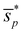Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unveiling the deformability of mussel plaque core: the role of pore distribution and hierarchical structure†
Yulan
Lyu
 ab,
Mengting
Tan
c,
Yong
Pang
b,
Wei
Sun
a,
Shuguang
Li
a and
Tao
Liu
ab,
Mengting
Tan
c,
Yong
Pang
b,
Wei
Sun
a,
Shuguang
Li
a and
Tao
Liu
 *b
*b
aFaculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
bSchool of Engineering and Materials Science, Queen Mary University of London, London E1 4NS, UK. E-mail: tao.liu@qmul.ac.uk
cSchool of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
First published on 27th August 2024
Abstract
The mussel thread-plaque system exhibits strong adhesion and high deformability, allowing it to adhere to various surfaces. While the microstructure of plaques has been thoroughly studied, the effect of their unique porous structure on the high deformability remains unclear. This study first investigated the porous structure of mussel plaque cores using scanning electron microscopy (SEM). Two-dimensional (2D) porous representative volume elements (RVEs) with scaled distribution parameters were generated, and the calibrated phase-field modelling method was applied to analyse the effect of the pore distribution and multi-scale porous structure on the failure mechanism of porous RVEs. The SEM analysis revealed that large-scale pores exhibited a lognormal size distribution and a uniform spatial distribution. Simulations showed that increasing the normalised mean radius value (ū) of the large-scale pore distribution can statistically lead to a decreasing trend in final failure strain, strength and strain energy density but cannot solely determine their values. The interaction between pores can lead to two different failure modes under the same pore distribution: progressive failure mode and sudden failure mode. Additionally, the hierarchical structure of multi-scale porous RVEs can further increase the final failure strain by 40–60% compared to single-scale porous RVEs by reducing stiffness, highlighting the hierarchical structure could be another key factor contributing to the high deformability. These findings deepen our understanding of how the pore distribution and multi-scale porous structure in mussel plaques contribute to their high deformability and affect other mechanical properties, providing valuable insights for the future design of highly deformable biomimetic materials.
1 Introduction
The mussel byssus system, consisting of protein threads and porous plaques (Fig. 1a and b), can anchor to almost any surface in harsh marine environments.1–4 This ‘anchoring’ system enables mussels to withstand a force equivalent to approximately 10 times their own weight (Fig. 1a).5 Meanwhile, the high deformability of mussel plaques allows them to undergo significant deformation without fracturing under the strong hydrodynamic forces exerted by the ocean.6 In nature, mussel plaques undergo directional tensions with pulling angles ranging from 0° to 90°. Our previous study developed a customized microscope system to apply quasi-static tension to mussel plaques and found that they can experience substantial deformation,6 exhibiting up to a 2.8-fold increase in volume when the pulling angle reaches or exceeds 45° (Fig. 1c). | ||
| Fig. 1 (a) Mussel byssus system attached on a rock, (b) schematic diagram of the mussel plaques microstructure,5 (c) large deformation of mussel plaque under tension, (d) the distribution of normalized x and y coordinates for large pore centres within the mussel plaque core, (e) the SEM photo showing the multi-scale porous structure of mussel plaque core and (f) the distribution of normalized radius for both large-scale (mirco) and small-scale (nano) pores within the mussel plaque core. | ||
However, despite thorough studies on the adhesive performance of mussel plaques,7–11 the cause of their high deformability remains unclear.
Mussel plaques consist of a porous core and a protective cuticle layer (Fig. 1b).12–15 The cuticle layer, approximately 4 μm thick, is covered by granules about 0.5 μm in size.5 The plaque features randomly distributed nano- (small-) and micro- (large-) scale pores, with diameters approximately ranging from 50–800 nm to 1–3 μm, respectively (Fig. 1d–f). The obtained pore size ranges are consistent with previous studies.13,16 The formation of porous structures is closely related to seawater temperature and pH levels.13,16 The plaque core and cuticle layer work together to enhance the deformability and establish a robust load-bearing capacity.5,7,17 The pore structure of significantly deformed plaques has been reported in previous work.15,18 However, the evolution of the pore deformation under external loads, leading to high deformability, remains unclear.
Previous research has suggested that the pore arrangement within the plaque cores might influence the stress heterogeneity and thus have a significant impact on their deformability.19 However, this study mainly applied ordered pores rather than the natural pore arrangement found in mussel plaques. It is, therefore, crucial to understand the role of the natural porous structure (Fig. 1e) on the mechanical behaviours of plaque cores.
This study is motivated by the need to investigate the impact of the plaque core's porous structure on its mechanical performance, with a focus on deformability. We investigated the effects of pore distribution (Fig. 1d and f) and multi-scale porous structure (Fig. 1e) on the mechanical properties of plaque cores. The actual pore distribution within plaque cores was determined using scanning electron microscope (SEM) analysis. Scaled distribution parameters were then applied to create two-dimensional (2D) porous representative volume elements (RVEs) for subsequent numerical and experimental investigations of the porous structures. The validated phase field method, incorporating the Neo-Hookean model, was used in the simulations to investigate the effect of pore distribution and multi-scale structure on the failure mechanism of porous RVEs. By fully understanding how the pore distribution and multi-scale porous structure influence the mechanical performance, this study provides valuable insights for designing highly deformable metamaterials inspired by mussel plaques.
2 SEM characterisation of mussel plaque core
2.1 SEM sample preparation
Blue mussels (Mytilus edulis) were collected from the intertidal zone off the coast of Hunstanton, UK. Subsequently, they were tied to small acrylic plates and kept in a water tank with cold (8–10 °C), oxygenated, and continuously circulated and filtered artificial seawater. Sea salt (Tropic Marin Pro-Reef Sea Salt, UK) was mixed with fresh water to replicate the salinity and pH levels seen in natural seawater (salinity = 33 ppt and pH = 8). The plaques were separated from the acrylic plates using a razor blade (Accu-Edge® Disposable Microtome Blades S35). To prevent damage when removing the plaques from hard acrylic plates, a thin layer of polydimethylsiloxane (PDMS) was coated on the acrylic plates. The PDMS substrates with mussel plaque deposits were precisely cut using surgical blades for fixation and cryo-sectioning. Cutting was carried out with a 5 mm margin from the target plaque to prevent any damage to the plaque/substrate interface and microstructures. The collected plaques were fixed in a solution containing 3.7% formaldehyde and 2.5% glutaraldehyde for approximately four hours.5,13 After that, plaque samples were placed in Milli-Q water at 4 °C for three days.The plaques were then sectioned into 20 μm thick slices at a temperature of −20 °C using a cryostat (Leica CM1850) and immediately immersed in Milli-Q water to remove the mounting medium.13 The plaque slices underwent dehydration through sequential concentrations of ethanol and were subjected to two drying cycles of hexamethyldisilane (HDMS).13 The dehydrated samples were sputter-coated with a 10 nm thick iridium layer for 120 seconds using a Quorum Q150V Plus and imaged using a JEOL 7100F FEG-SEM with an accelerating voltage set at 5 kV.
2.2 The pore distribution analysis for mussel plaque core
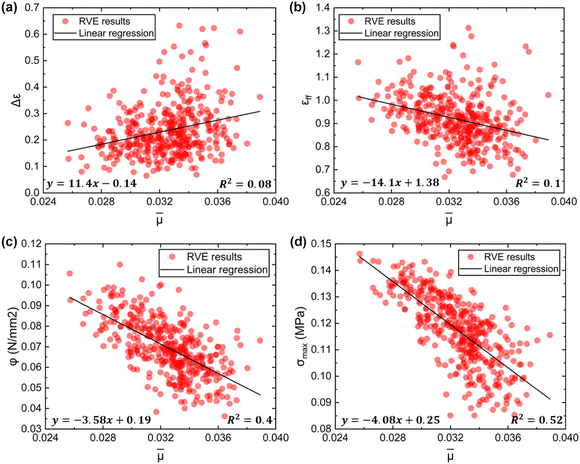
Two-dimensional (2D) SEM images have suggested that the pores within the plaque cores are of two different scales, ranging in diameter from 50–800 nm (small-scale pores) to 1–3 μm (large-scale pores) (Fig. 1e). The pore distribution of large-scale pores within those SEM photos was first examined. A total of nine SEM photographs from various plaques and different locations within the same plaque were analysed to minimize the impact of cut position on the large-scale pore distribution, ensuring that the SEM analysis results were representative (Fig. 1e, 2 and Fig. S1, S2 in the ESI†). The irregular large-scale pores were simplified into circular shapes, as shown by the pore outlines in Fig. 2. The simplification facilitates a more direct method for obtaining important distribution factors for large-scale pores such as porosity, pore radius, pore number and the coordinates of pore centres, which in turn ensures consistency of analysis. Despite the simplification to circular pores, the main geometric features of plaque cores were retained, thus ensuring that the pore distribution remained consistent with the original complex structure (Fig. S3 in the ESI†).Meanwhile, the radii of large-scale pores and the coordinates of the pore centres were normalised by dividing the length of the squared SEM image edges (ls) for the distribution analysis. The normalised mean value 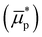 and normalised standard deviation value
and normalised standard deviation value  of the large-scale pores radius were calculated as:
of the large-scale pores radius were calculated as:
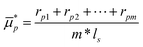 | (1) |
 | (2) |
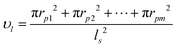 | (3) |
It can be observed that the large-scale pore radius consistently follows a lognormal distribution (Fig. 1e, 2 and Fig. S1, S2 in the ESI†). However, the distribution parameters and porosity may be affected by the position of the slices or plaques considered (see Table 1 and Tables S1, S2 in the ESI†). The range of 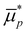 within the plaques is approximately 0.021–0.043, while the range of
within the plaques is approximately 0.021–0.043, while the range of  is approximately 0.005–0.014. The porosity of large-scale pores (υl) ranges from 23% to 33%. Additionally, the Q–Q plots (quantile–quantile plots) (Fig. S4 in the ESI†) comparing the x and y coordinates of large-scale pore centres in the nine SEM images (Fig. 1e, 2 and Fig. S1, S2 in the ESI†) show that both the x and y coordinates are consistent with a uniform distribution.
is approximately 0.005–0.014. The porosity of large-scale pores (υl) ranges from 23% to 33%. Additionally, the Q–Q plots (quantile–quantile plots) (Fig. S4 in the ESI†) comparing the x and y coordinates of large-scale pore centres in the nine SEM images (Fig. 1e, 2 and Fig. S1, S2 in the ESI†) show that both the x and y coordinates are consistent with a uniform distribution.
 and normalised standard deviation of radius
and normalised standard deviation of radius  of simplified large-scale pores within the SEM images for different plaques
of simplified large-scale pores within the SEM images for different plaques
Therefore, it can be concluded that the radius of large-scale pores is lognormally distributed, and the coordinates of the large-scale pore centres are uniformly distributed within the mussel plaque core. Because the distribution parameters and porosity vary for each SEM photo, the parameters of Fig. 1e were selected and scaled to generate the porous RVEs for further study: υl = 27%,  and
and  .
.  and
and  are the mean and standard deviation values of the lognormal distribution of the large-scale pores within Fig. 1e, respectively.
are the mean and standard deviation values of the lognormal distribution of the large-scale pores within Fig. 1e, respectively.
The pore radius distribution of the small-scale pores also follows a lognormal distribution with a mean value of 150 nm and a standard deviation value of 190 nm (Fig. 1f). The porosity of the small-scale pores υs in Fig. 1e was calculated using ImageJ as 5%. The analysis for the small-scale pore distribution ensured that our main focus remained on the comprehensive study of large-scale pore distributions while still gaining relevant insights into the characteristics of small-scale pores.
3 The generation of the porous RVEs
Two types of Two-dimensional (2D) porous RVEs were generated for the numerical study. The first RVE type investigates the effect of large-scale pores, while the second RVE type examines the impact of the multi-scale architecture of the mussel plaque core.3.1 Generation of single-scale porous RVEs and post-processing procedure
To overcome manufacturing limitations, the plaque pore sizes were scaled up by a factor of 1000, transitioning from microns to millimetres, to enable 3D printing of the test samples. Two-dimensional (2D) square-shaped porous RVEs were generated by using the scaled distribution parameters of the large-scale pores (vl = 27%, and
and  ). The dimensions of the RVEs are 30 × 30 mm, comprising solely large-scale pores with the remaining volume filled with solid material.
). The dimensions of the RVEs are 30 × 30 mm, comprising solely large-scale pores with the remaining volume filled with solid material.
The size effect of the RVEs was investigated by studying the responses of the RVEs with ordered pore arrangement and uniform pore size (details shown in the ESI†). The ordered porous RVEs featured porosity that was consistent with that of the large-scale pores obtained in the SEM image (vl = 27%). The pore size within these RVEs was consistent with the scaled mean value of the large-scale pores  , and the spacing between adjacent pores was the same (Fig. S5 in the ESI†). The results obtained from the simulations showed that the RVEs with the 30 × 30 mm dimension could reflect the macroscopic stress–strain relation of the porous structures (Fig. S6 in the ESI†). The macroscopic stress was determined by dividing the reaction force in the tensile direction by the cross-sectional area of the RVE, while the macroscopic strain was calculated by dividing the displacement in the tensile direction by the side length of the RVE.
, and the spacing between adjacent pores was the same (Fig. S5 in the ESI†). The results obtained from the simulations showed that the RVEs with the 30 × 30 mm dimension could reflect the macroscopic stress–strain relation of the porous structures (Fig. S6 in the ESI†). The macroscopic stress was determined by dividing the reaction force in the tensile direction by the cross-sectional area of the RVE, while the macroscopic strain was calculated by dividing the displacement in the tensile direction by the side length of the RVE.
The commercial FE package ABAQUS was employed to create the single-scale RVEs using Python scripts. Within the Python scripts, the function random.lognormvariate (μp, sp) was used to generate pores in the RVEs following a lognormal distribution, where μp is the scaled mean value of the normal distribution corresponding to the lognormal distribution within the SEM image:
 | (4) |
 | (5) |
The coordinates of pore centres follow a uniform distribution in accordance with the coordinate distribution observed in the SEM images (Fig. 1d, 2 and Fig. S1, S2 in the ESI†). The function random.uniform (low, high) was applied in the Python scripts to identify the locations of pores in the RVEs, where ‘low’ and ‘high’ are the min value and max value of pore centre coordinates, respectively.
Therefore, in order to ensure all the pores are contained within the RVE, each pores centre coordinates (xi, yi) must adhere to the following relation:
| (x, y) ∈ {(xi, yi)|ri ≤ xi ≤ w − ri, ri ≤ yi ≤ w − ri}, i ∈ n | (6) |
Moreover, the distance between the centres of any two pores θ in the RVE must be greater than the sum of their radii to avoid overlapping:
 | (7) |
Consequently, the RVEs created through the ABAQUS Python scripts were required to fulfil all the previously mentioned criteria before being subjected to the FE analysis in ABAQUS.
The generated single-scale RVEs were discretised using 2D triangular plane stress elements including temperature effects, i.e. CPS3T20 in ABAQUS notation and analysed using the phase field modelling method via analogy to a coupled heat transfer-displacement analysis.21 The phase field method is described in more detail in Section 4 below.
Following the completion of the ABAQUS calculation, a further Python script was developed with the objective of obtaining the following data from ABAQUS.odb files:
1. The coordinates (xi, yi) of all pore centres for each RVE (i = 1, 2, 3…, n).
2. The radii ri of all pores for each RVE.
3. The number of pores for each RVE.
4. The macroscopic stress–strain curves for each RVE.
Furthermore, a MATLAB algorithm was created to extract and calculate various parameters from the stress–strain data sets. These include the strain energy density (φ), strength (σmax), final failure strain (εff), and the strain difference (Δε) between the initial failure strain and the final failure strain for each RVE. In particular, the strain energy density (φ) was calculated as the area under the stress–strain curve. The initial failure strain was defined as the strain value corresponding to the peak strength, and the final failure strain (εff) was the strain value corresponding to the point that stress decreased to 0. Additionally, the normalised mean value (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and normalised standard deviation value (
) and normalised standard deviation value (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) of the pores radius within each single-scale RVE were calculated as:
) of the pores radius within each single-scale RVE were calculated as:
 | (8) |
 | (9) |
3.2 Generation of multi-scale porous RVEs and post-processing procedure
To further investigate the influence of multi-scale porous structures on mussel plaque behaviour, three different single-scale RVE FE models were selected. The multi-scale porous structures were 3D in nature, and the cell walls were 2D surfaces. As an approximation, a 2D idealisation was made for the 3D porous structures. The multi-scale porous structures were generated by removing 2D elements in the FE models and reconnecting the nodes using lines. In the simulation, the walls of the pores were represented by these lines. The approximation is a simple way as a first step into the study, and it should be capable of offering some qualitative assessment of the behaviour of such structures. As a result of such idealisation, 2D wall surfaces were subsequently simulated using 1D elements in the finite element (FE) models, connecting the nodes to form 2D porous structures (Fig. 3). Additionally, for cellular solids made of rubber-like materials, the type of unit cell primarily determines whether stretch- or bending-governed behaviours during the elastic deformation stage. However, rubber-like materials are highly stretchable, with a failure strain of approximately 1.2. Under large deformations, they ultimately exhibit stretch-governed behaviour regardless of the unit cell type.22,23 In this scenario, the walls of the small pores mainly experience axial tension, similar to the behaviour of truss elements in finite element (FE) simulations. Therefore, truss elements (T2D2T elements20) are a good approximation in FE simulations, as they effectively capture the stretch deformations of the walls. | ||
| Fig. 3 Schematic drawing of multi-scale porous RVE generation (The mesh element type switched from 2D triangular plane stress elements CPS3T to coupled temperature-displacement truss element T2D2T). | ||
The radius of the truss elements was determined to ensure that the newly generated RVEs reflected the same overall porosity (υ = υs + υl = 32%) with the SEM image (Fig. 1e). The approximate size of the small-scale pores within the multi-scale porous RVEs was set to 0.5 mm, which falls within the scaled range of small-scale pore sizes observed in mussel plaques (0.05–0.8 mm). A size effect study, detailed in the ESI,† confirmed that the size of the small-scale pores within the multi-scale porous RVEs has an insignificant impact on the macroscopic material behaviours (Fig. S7 in the ESI†). Notably, the structural configuration adopted in the multi-scale porous RVEs serves as an approximation for examining the multi-scale porous structure of the mussel plaque. This simplified model was utilised to explore characteristic behaviours of such structures rather than a precise duplication of the plaques hierarchical structures.
Building on the same material properties and periodic conditions24–26 used in the single-scale RVE FE models, the phase field method was applied to analyse the failure behaviour of the multi-scale porous RVEs (Section 4). The stress–strain curves of multi-scale porous RVEs were extracted from the ABAQUS.odb files, and fracture paths were analysed using the Abaqus/CAE graphical user interface.
4 ABAQUS implementation and experimental calibration of the phase field modelling method
4.1 Theory of phase field method for fracture modelling
The phase field method was applied to analyse the failure mechanism of test samples and RVEs. The parent material was assumed to be an incompressible Neo-Hookean material. Therefore, in this section, a phase-field method for the incompressible Neo-Hookean material is introduced.According to the theory of energy conservation, when a crack grows in an arbitrary body Ω, the energy per time unit Ė provided externally is equal to the rate of the strain energy ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) stored in the material and the rate of the energy Ḋdiss dissipated from the crack:
stored in the material and the rate of the energy Ḋdiss dissipated from the crack:
Ė = ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) + Ḋdiss + Ḋdiss | (10) |
Let c denote the phase field variable. The value of c is between 0 and 1, with c = 0 and c = 1 denoting undamaged materials and fully damaged materials, respectively. The quadratic degradation function g(c) is introduced to control the material stiffness, i.e.,
| g(c) = (1 − c)2 | (11) |
Therefore, the strain energy stored in the material can be written as the following:
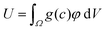 | (12) |
For incompressible 2D plane stress studies in this research, the strain energy density φ can be expressed as ref. 27:
| φ = φiso(F) | (13) |
Therefore, based on the vector calculus identity28 and divergence theorem,29 the rate of the stored strain energy is given by:
 | (14) |
![[u with combining dot above]](https://www.rsc.org/images/entities/b_char_0075_0307.gif) is the velocity field presenting the rate of change of the displacement field u with respect to time, ∂Ω is the surface of the volumetric body Ω and n is the outward normal to the surface ∂Ω. The derivation process for eqn (14) is shown in the ESI.†
is the velocity field presenting the rate of change of the displacement field u with respect to time, ∂Ω is the surface of the volumetric body Ω and n is the outward normal to the surface ∂Ω. The derivation process for eqn (14) is shown in the ESI.†
Meanwhile, the dissipated crack formation energy density τ was given by Miehe et al. (2010):30
 | (15) |
Therefore, the energy dissipated by the crack formation Df and the rate of the dissipated energy from crack formation Ḋf can be written as:
 | (16) |
 | (17) |
Again, based on the vector calculus identity28 and divergence theorem,29eqn (17) can be rewritten as:
 | (18) |
Moreover, a rate of dissipation energy for crack growth Ḋg was introduced by Pascal et al. (2019):27
 | (19) |
 | (20) |
Additionally, external energy can be broadly classified into work done by surface tractions (forces acting on the boundary of the body) and body forces (forces acting throughout the volume of the body). Hence, the rate of external energy Ė can be expressed as:
 | (21) |
Therefore, based on eqn (10), (14), (20) and (21), it can be obtained as follows:
 | (22) |
Given the macroforce and microforce balances, we can finally obtain the following equations:
 | (23) |
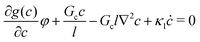 | (24) |
 | (25) |
4.2 Finite element (FE) analysis implementation
| φ = C1(I1 − 3) | (26) |
Combing eqn (11), (24) and (26),
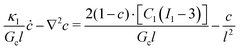 | (27) |
The time derivative term of phase field variable ċ can be expressed as:
 | (28) |
Because the focus of our research is the progressive and slow fracture of 2D porous structures, it was assumed vx ≈ vy ≈ vz ≈ 0. Therefore, eqn (28) can be simplified as:
 | (29) |
Furthermore, eqn (27) can be rewritten as:
 | (30) |
Meanwhile, the field equation of heat transfer given by the first law of thermodynamics reads as,
 | (31) |
 is the rate of the temperature field, k is the thermal conductivity, cp is the specific heat, ρ is the density, and q is the heat source.
is the rate of the temperature field, k is the thermal conductivity, cp is the specific heat, ρ is the density, and q is the heat source.
Given the similarity of eqn (30) and (31), the phase field model can be implemented via the heat transfer analogy by letting the temperature variable T represent the phase field variable c. Assuming k = 1, the equation for the heat source q can be expressed as:
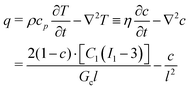 | (32) |
 .
.
 | (33) |
Meanwhile, the heat flux (q) and the changing rate of the heat flux (χ) were defined in the HETVAL subroutine as follows:
 | (34) |
 | (35) |
4.3 Material parameters acquisition and model calibration
Single-edge notched tension (SENT) tests34 with different notch lengths were carried out to obtain the material parameters of TangoBlack Plus FLX980, including the material constant C1, critical energy release rate Gc, and length scale l. Rectangular strips used in the SENT tests had a total length of 100 mm (clamp distance 80 mm), a width of 25 mm, a thickness of 1 mm, a notch width of 0.3 mm, and variable notch lengths (α) ranging from 0 mm to 4 mm (Fig. 4a).34,35 The sample size was designed based on the rubber fracture experiments conducted by Rivlin and Thomas (1953)35 and Roucou et al. (2019).34 Samples were 3D printed using TangoBlack Plus FLX980. SENT tests were displacement-controlled with a fixed strain rate of 100% strain per min using an INSTRON tensile machine. Since the primary focus of this study does not involve the parent material, the effect of the global strain rate on the parent material was not discussed. Instead, we ensured that the global strain rate was consistent for both SENT tests and following porous sample tensile tests to exclude the effects from the parent material. A Thorlabs DCC1545M CMOS camera, equipped with an imaging lens (focal length of 100 mm), was employed to monitor specimen deformation.36–38 The CMOS camera was configured at a frame rate of 10 fps and a special resolution of 9.6 pixels per mm.
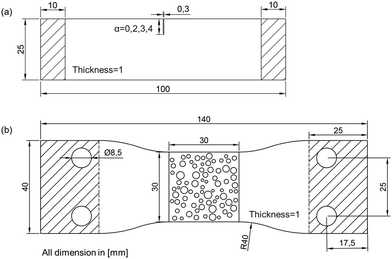 | ||
| Fig. 4 Schematic drawings of (a) the SENT test samples and (b) the porous samples for tensile testing. | ||
C
1 and Gc were determined by analysing the nominal stress–strain curves obtained from SENT tests. C1 was derived by fitting the tensile stress–strain curves prior to failure, and the critical strain energy release rate Gc was computed using the equation below:34,35
| G = 2αK(λ)W(λ) |
| Gc = G(λc) | (36) |
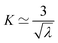 | (37) |
 | ||
| Fig. 5 The numerical and experimental stress–strain curves for samples with different notch lengths during SENT tests. | ||
In addition, three porous samples with the same scaled distribution parameters and porosity (Fig. 6) were 3D printed to validate the rate-dependent phase field model and to calibrate the fracture parameter η. The results showed that when η = 0.4, both the stress–strain curves and the failure paths of the simulated and experimental results were in good agreement for all three porous structures (Fig. 6). The material parameters for TangoBlack Plus FLX980 used in the phase field based numerical simulations are summarised in Table 2.
 | ||
| Fig. 6 Comparison between the (a)–(c) numerical and experimental stress–strain curves and (d)–(f) fracture paths for three porous samples in tension (elements with NT11 ≥ 1 were deleted). | ||
| Material parameters | Values |
|---|---|
| k | 1 |
| C 1 (MPa) | 0.09 |
| G c (N mm−1) | 0.27 |
| l (mm) | 1 |
| η | 0.4 |
5 The failure mechanism analysis of generated RVEs
5.1 The effect of large-scale pore distribution on mechanical behaviour
The normalised mean (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and standard deviation (
) and standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) of the pore radius reflect the statistic characteristic of the pore distribution within the single-scale porous RVEs, raising the question of whether these two parameters have a dominant effect on mechanical behaviour. To address this, Fig. 7 presents the simulation results for 400 generated RVEs based on Section 3, showing the difference between the initial and final failure strain (Δε), final failure strain (εff), strength (σmax), and strain energy density (φ) as functions of the normalised mean (
) of the pore radius reflect the statistic characteristic of the pore distribution within the single-scale porous RVEs, raising the question of whether these two parameters have a dominant effect on mechanical behaviour. To address this, Fig. 7 presents the simulation results for 400 generated RVEs based on Section 3, showing the difference between the initial and final failure strain (Δε), final failure strain (εff), strength (σmax), and strain energy density (φ) as functions of the normalised mean (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and standard deviation (
) and standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ). The range of
). The range of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) (0.025–0.038) and
(0.025–0.038) and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (0.007–0.015) of the RVE results shown in Fig. 7 closely mirrors the range of
(0.007–0.015) of the RVE results shown in Fig. 7 closely mirrors the range of  and
and  observed in the SEM images (Fig. 1e, 2 and Fig. S1, S2 in the ESI†), indicating that the RVE results could reflect the geometrical effect of the microstructures on the mussel plaques.
observed in the SEM images (Fig. 1e, 2 and Fig. S1, S2 in the ESI†), indicating that the RVE results could reflect the geometrical effect of the microstructures on the mussel plaques.
3D linear regression analysis was used as an estimation method to evaluate the trend of data as functions of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) and
and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (Fig. 7):39
(Fig. 7):39
ô = a0 + a1![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) + a2 + a2![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) | (38) |
The coefficient of determination R2 was calculated to measure how well the regression model predicts the real data points (Fig. 7):40
 | (39) |
R 2 ranges from 0 to 1, where 1 indicates perfect fit, and 0 indicates that the regression model cannot account for any of the variation in the response data around its mean.41 The nonlinear regression analysis was also conducted to fit the data. However, there was little improvement in the value of R2. For simplicity, only the results of the linear regression analysis are presented in Fig. 7.
The results of the linear regression, as shown in Fig. 7, demonstrate that the overall effects of the normalised standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) on Δε, εff, σmax, and φ were statistically insignificant for the 400 samples. Conversely, the regression analysis indicates that an increase in the normalised mean radius (
) on Δε, εff, σmax, and φ were statistically insignificant for the 400 samples. Conversely, the regression analysis indicates that an increase in the normalised mean radius (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) led to an overall decreasing trend in strength (σmax), strain energy density (φ), and final failure strain (εff), respectively (Fig. 8b–d). While a different overall trend was observed for Δε: as
) led to an overall decreasing trend in strength (σmax), strain energy density (φ), and final failure strain (εff), respectively (Fig. 8b–d). While a different overall trend was observed for Δε: as ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) increased, the value of Δε exhibited a slight increase (Fig. 8a).
increased, the value of Δε exhibited a slight increase (Fig. 8a).
It is important to note that linear regression analysis only illustrates the overall trend of the effect of the normalised mean (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and standard deviation (
) and standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) on macroscopic material properties and cannot capture the high dispersion of the results (Fig. 7 and 8). It can be seen from Fig. 8 that the same
) on macroscopic material properties and cannot capture the high dispersion of the results (Fig. 7 and 8). It can be seen from Fig. 8 that the same ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) can always return scattered Δε, εff, σmax, or φ values. This may suggest that while the normalised mean value (
can always return scattered Δε, εff, σmax, or φ values. This may suggest that while the normalised mean value (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) of the pore radius can influence the final failure strain or other macroscopic material properties of the single-scale RVE, it might not be the sole determining factor. Other factors, such as the interactions between pores or the multi-scale structure, could also play an important role.
) of the pore radius can influence the final failure strain or other macroscopic material properties of the single-scale RVE, it might not be the sole determining factor. Other factors, such as the interactions between pores or the multi-scale structure, could also play an important role.
5.2 Sudden and progressive failure modes within the single-scale porous RVEs
To better understand the failure mechanism of the single-scale porous RVEs, Fig. 9 shows the macroscopic stress–strain curve and crack propagation of Sample A, which had the highest values of Δε, εff, and φ among the 400 RVE results. For comparison, the stress–strain curves and crack propagation of two additional samples, B and C, are also presented in Fig. 9. It is noted that samples A, B and C have nearly identical normalised standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) and mean (
) and mean (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) values, with a difference of only ±0.001.
) values, with a difference of only ±0.001.
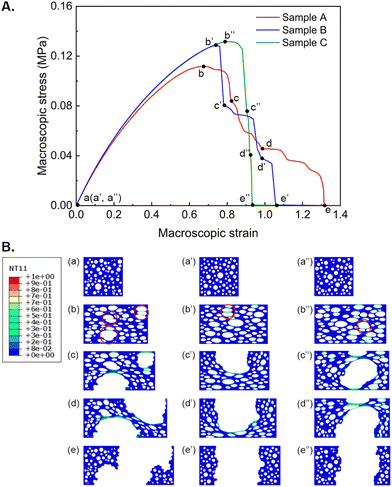 | ||
| Fig. 9 (A) The macroscopic stress–strain curves, and (B) crack paths of selected samples with different failure modes. | ||
Two different failure modes were identified from the stress–strain curves of the samples: progressive failure and sudden failure (Fig. 9A). For the progressive failure sample (Sample A), the Δε value was approximately 50% of the final failure strain. In contrast, the Δε value for the sudden failure sample (Sample C) was close to 0 (Fig. 9A). The final failure strain of the progressive failure sample (Sample A) was about 1.5 times that of the sudden failure sample (Sample C), but its strength was only approximately 85% of Sample Cs strength (Fig. 9A). Interestingly, the strength of these samples decreased with increasing Δε (Fig. 9A), indicating that the high deformability of the plaques may have been achieved by sacrificing strength.
The crack propagation of Samples A, B and C are presented in Fig. 9B to further investigate their failure mechanisms. It can be seen from Fig. 9B that although the normalised standard deviation (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) and mean (
) and mean (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) of Samples A, B and C are nearly identical, their underlying failure mechanisms are distinct. The damage observed in Sample A was initiated at three distinct locations: large pores or closely spaced pores aligned perpendicular to the tensile direction (Fig. 9B). The scattered locations of the initial damage caused a diffused crack pattern with an elongated fracture path, resulting in the progressive failure mode of Sample A. In Sample C, the initial damage occurred at closely clustered pores perpendicular to the tensile direction (Fig. 9B), rapidly forming a complete fracture path, i.e., a concentrated crack pattern. Although another damage was also observed during the failure process, it played a minor role as the initial damage was the primary cause of the failure (Fig. 9B).
) of Samples A, B and C are nearly identical, their underlying failure mechanisms are distinct. The damage observed in Sample A was initiated at three distinct locations: large pores or closely spaced pores aligned perpendicular to the tensile direction (Fig. 9B). The scattered locations of the initial damage caused a diffused crack pattern with an elongated fracture path, resulting in the progressive failure mode of Sample A. In Sample C, the initial damage occurred at closely clustered pores perpendicular to the tensile direction (Fig. 9B), rapidly forming a complete fracture path, i.e., a concentrated crack pattern. Although another damage was also observed during the failure process, it played a minor role as the initial damage was the primary cause of the failure (Fig. 9B).
Sample B exhibited a fracture path similar to Sample C (Fig. 9B). However, unlike the rapidly developing failure observed in Sample C, the failure in Sample B was more progressive (Fig. 9A). It might be because the blunted cracking observed in Sample B enabled the stress to be distributed and absorbed more energy. While the pore distribution in Sample C may cause blunted cracking to be insufficient to prevent rapid crack growth and stress concentration. In addition to the distribution of large-scale pores, the interactions among pores might also influence the failure mechanisms of the RVEs.
5.3 The effect of multi-scale porous structures on mechanical behaviour
The SEM images of the mussel plaque core revealed the presence of two different scales of pores (Fig. 1e). In addition to the large-scale pores that were analysed above, small-scale pores were found to fill the remaining areas of mussel plaques. New multi-scale porous RVEs based on the three samples selected in Section 5.2 were regenerated and analysed to understand the effect of the multi-scale porous structure on the failure mechanism (Fig. 10). | ||
| Fig. 10 (A) The macroscopic stress–strain curves of single and multi-scale porous samples, and (B) crack paths of multi-scale porous samples. | ||
A comparison of the fracture paths shown in Fig. 9B and 10B reveals that the failure modes were almost identical for all three samples, despite the structural change from the single-scale porous RVE to the multi-scale porous RVE. This suggests that the failure mechanism could be dominated by the large-scale pores.
The stress–strain curves for both multi-scale and single-scale porous RVEs are presented in Fig. 10A. The multi-scale porous RVEs with 32% porosity exhibited significantly lower stiffness compared to the single-scale porous RVEs with 27% porosity, despite having only a 5% difference in porosity (Fig. 10A). To understand this mechanism, numerical simulations of solid RVE and small-scale porous RVE with 5% porosity were conducted. These simulations demonstrate that even a small increase in porosity can lead to a substantial decrease in material stiffness due to microstructural changes (Fig. S8 in the ESI†). The reduction in stiffness, however, enhanced the final failure strain of the multi-scale porous RVEs (Fig. 10A). Specifically, the final failure strains of the three multi-scale porous samples increased by 40% (Sample A), 50% (Sample B), and 60% (Sample C), respectively, compared to the single-scale samples (Fig. 10A). Meanwhile, the strength of the three multi-scale porous samples decreased by 33% (Sample A′), 31% (Sample B′), and 32% (Sample C′), respectively, due to the reduction in stiffness. This may suggest that the multi-scale porous structure of mussel plaques might improve the deformability by reducing their stiffness, but this could also result in a reduction in strength.
6 Discussion
Researchers have consistently focused on understanding the structural and chemical compositions of mussel plaques and their impact on adhesion.7,8,13,42 Previous study has suggested that the pore arrangement within the plaque core might influence the adhesion ability.19 However, limited attention has been paid to understanding how pore arrangement affects the mechanical behaviours of the plaque core. Tensile testing of the thread-plaque system reveals that mussel plaques can withstand considerable deformation before detachment, underscoring their high deformability (Fig. 1c).5,17 This led us to hypothesise that the pore distribution and hierarchical structure of the plaque core might also contribute to its high deformability and potentially impact other tensile properties.Elbanna et al. (2015) conducted a semi-analytical approach to understand the effect of void arrangement on the adhesion of mussel plaques.19 They found that plates with larger voids near the attached interface display higher stress heterogeneities, which can trap cracks in regions with low stress, thereby slowing down the propagation of cracks and resulting in higher maximum forces, increased deformability, and enhanced energy dissipation. However, the ordered and graded pores were used in the study, which differs from the natural pore distribution found in the plaque core and may influence the mechanical behaviour.19
In this research, extensive SEM analysis was employed to obtain the pore distribution of the plaque core. Porous RVEs were generated using scaled distribution parameters to present the main geometric characteristics of the plaque core and conduct the qualitative analysis. Our results demonstrate that large-scale pore distribution significantly impacts the mechanical behaviour of single-scale porous RVEs, including final failure strain, strength, and strain energy density.
As mentioned above, Elbanna et al. (2015) reached the conclusion that larger voids near the attached interface can lead to higher strength, final failure strain, and strain energy density.19 Our RVE-based numerical studies have suggested that increasing the normalised mean value (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) of pore radius can statistically lead to a decreasing trend in these macroscopic material properties: final failure strain, strength, and strain energy density. While the normalised standard deviation value (
) of pore radius can statistically lead to a decreasing trend in these macroscopic material properties: final failure strain, strength, and strain energy density. While the normalised standard deviation value (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) of the pore radius had an insignificant effect on these properties. Additionally, it was found that the same normalised mean value (
) of the pore radius had an insignificant effect on these properties. Additionally, it was found that the same normalised mean value (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) or normalized standard deviation value (
) or normalized standard deviation value (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) can always return highly scattered macroscopic material property values. This indicates that the values of
) can always return highly scattered macroscopic material property values. This indicates that the values of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) and
and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) can not solely determine the mechanical behaviour of single-scale porous RVEs. Other factors, such as the interactions between pores and the hierarchical structure, could also play an important role.
can not solely determine the mechanical behaviour of single-scale porous RVEs. Other factors, such as the interactions between pores and the hierarchical structure, could also play an important role.
Regarding the interactions between pores, our FE simulation results suggest that two types of failure mechanisms might occur under the same pore distribution, i.e. diffused crack pattern and concentrated crack pattern. The diffuse crack pattern elongated the crack path, which in turn led to the progressive failure mode and an increase in the final failure strain of RVEs. While the concentrated crack pattern led to rapid crack propagation and resulted in a sudden failure mode. The observed findings highlight the crucial role played by pore interactions in influencing mechanical behaviours.
Another factor, i.e. the hierarchical structure, was also examined in this research. The results indicate that the failure modes of the porous RVEs are dominated by the large-scale pores, however, the hierarchical structure can further increase the final failure strain of porous RVEs by reducing stiffness, suggesting it is also a crucial factor in achieving the high deformability of mussel plaques.
This study advances the understanding of how pore distribution and hierarchical structure within the mussel plaque core contribute to its high deformability and other material properties. These insights are crucial for mimicking the unique microstructure in the design of advanced materials. For instance, Bosnjak and Silberstein (2021) presented two chemical pathways to develop highly deformable materials with high toughness. Our research shows that altering the pore distribution or introducing the hierarchical structure might be another potential pathway to design materials with combined strong properties.43
However, several limitations remain. For instance, the porous RVEs serve as an approximation rather than an exact replication of the porous structure of mussel plaques for the qualitative analysis in this research. In simplified SEM images of large-scale pores (Fig. 2), the exclusion of overlapping, damaged or incomplete pores at the boundaries may lead to discrepancies between measured and true porosity. Future studies could focus on analysing RVEs that accurately replicate the porous structure of the mussel plaque core for quantitative analysis.44,45 Extending the simplified two-dimensional structural analysis to a three-dimensional framework represents another significant future research direction.46 It should be noted that the sectioning, fixing, and dehydration processes could potentially alter pore size. The embedding medium used for frozen plaques may expand at low temperatures, enlarging the pore size. Sectioning can introduce mechanical loads that may close the pores in the loading direction. Additionally, dehydration can cause warping in plaque samples. Therefore, future studies are recommended to characterize the 3D microstructures in mussel plaques using non-destructive methods, such as Nano-CT and confocal laser scanning. Once the accurate 3D structure of mussel plaque is obtained, a comprehensive analysis comparing the mussel plaque pore distribution with other potential distributions could be conducted in the future. Additionally, understanding the scalability of the porous structure is also the focus of future research.
7 Conclusions
This study has systematically explored the influence of the pore distribution and hierarchical porous structures within the mussel plaque core on its tensile properties, with a specific emphasis on enhancing deformability. Our main conclusions are summarized as follows:1. The SEM analysis of the mussel plaque core shows there are two different scales of pores within the plaque core: small-scale pores with diameters ranging from 50 nm to 800 nm and large-scale pores with diameters ranging from 1 μm to 3 μm. The size of large-scale pores follows a lognormal distribution, while the location of them follows a uniform distribution.
2. The large-scale pore distribution can significantly influence the final failure strain, strength, and strain energy density of the porous RVEs. Statistically, increasing the normalised mean value (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) of the pore radius can lead to a decreasing trend in the value of the final failure strain, strength and strain energy density. However, the normalised standard deviation value (
) of the pore radius can lead to a decreasing trend in the value of the final failure strain, strength and strain energy density. However, the normalised standard deviation value (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) of the pore radius had an insignificant effect on these properties. Additionally, the same values of
) of the pore radius had an insignificant effect on these properties. Additionally, the same values of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) or
or ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) can always return scattered values of the final failure strain, strength and strain energy density, indicating that they cannot solely determine the macroscopic material properties.
can always return scattered values of the final failure strain, strength and strain energy density, indicating that they cannot solely determine the macroscopic material properties.
3. Two distinct failure modes (sudden and progressive) were identified under the same pore distribution. The interactions between pores led to two different crack patterns: diffused and concentrated. The diffused crack pattern extended the crack path and delayed the failure, which led to a progressive failure mode and higher final failure strain. While the concentrated crack pattern had rapid crack propagation, resulting in a sudden failure mode but with higher strength. This indicates that mussels may enhance the deformability of their plaques by sacrificing the plaques strength to form the porous plaque core.
4. The multi-scale porous RVEs exhibited identical failure modes to the single-scale porous RVEs, indicating that the failure mechanism of the mussel plaque could be dominated by the large-scale pores. Compared to the single-scale porous RVEs, the multi-scale porous RVEs had 40–60% higher final failure strain but lower stiffness and strength. This suggests that the hierarchical structure of mussel plaques might enhance their deformability by reducing the stiffness.
Author contributions
Y. L.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review and editing; M. T.: conceptualization, investigation, methodology, software, writing – review and editing; Y. P.: formal analysis, investigation, methodology, validation, writing – review and editing; W. S.: supervision, writing – review and editing; S. L: supervision, writing – review and editing; T. L.: conceptualization, data curation, funding acquisition, investigation, methodology, project administration, supervision, validation, writing – original draft, writing – review and editing.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the support provided by the Leverhulme Trust Research Grant Scheme (RPG-2020-235), the NanoCAT Research Grant of the University of Nottingham, and the Centre for Additive Manufacturing of the University of Nottingham. We acknowledge Professor Robert McMeeking from the University of California, Santa Barbara for early discussions to initiate this research.Notes and references
- C. V. Benedict and J. H. Waite, J. Morphol., 1986, 189, 261–270 CrossRef CAS PubMed.
- J. H. Waite and M. J. Harrington, Can. J. Chem., 2022, 100, 197–211 CrossRef CAS.
- N. Cohen, J. H. Waite, R. M. McMeeking and M. T. Valentine, Philos. Trans. R. Soc., B, 2019, 374, 20190202 CrossRef CAS PubMed.
- N. Aldred, L. Ista, M. Callow, J. Callow, G. Lopez and A. Clare, J. R. Soc., Interface, 2006, 3, 37–43 CrossRef CAS PubMed.
- Y. Pang, W. Sun and T. Liu, Proc. R. Soc. A, 2024, 480, 20230465 CrossRef.
- Y. Pang, J. Busfield and T. Liu, Proc. R. Soc. A, 2024 DOI:10.1098/rspa.2024.0257.
- K. W. Desmond, N. A. Zacchia, J. H. Waite and M. T. Valentine, Soft Matter, 2015, 11, 6832–6839 RSC.
- J. H. Waite, J. Exp. Biol., 2017, 220, 517–530 CrossRef PubMed.
- D. A. Qureshi, S. Goffredo, Y. Kim, Y. Han, M. Guo, S. Ryu and Z. Qin, Matter, 2022, 5, 710–724 CrossRef.
- N. Bandara, H. Zeng and J. Wu, J. Adhes. Sci. Technol., 2013, 27, 2139–2162 CrossRef CAS.
- H. G. Silverman and F. F. Roberto, Mar. Biotechnol., 2007, 9, 661–681 CrossRef CAS PubMed.
- A. Tamarin, P. Lewis and J. Askey, J. Morphol., 1976, 149, 199–221 CrossRef CAS PubMed.
- E. Filippidi, D. G. DeMartini, P. Malo de Molina, E. W. Danner, J. Kim, M. E. Helgeson, J. H. Waite and M. T. Valentine, J. R. Soc., Interface, 2015, 12, 20150827 CrossRef PubMed.
- N. R. Martinez Rodriguez, S. Das, Y. Kaufman, J. N. Israelachvili and J. H. Waite, Biofouling, 2015, 31, 221–227 CrossRef CAS PubMed.
- M. H. Wilhelm, E. Filippidi, J. H. Waite and M. T. Valentine, Soft Matter, 2017, 13, 7381–7388 RSC.
- J. H. Bernstein, E. Filippidi, J. H. Waite and M. T. Valentine, Soft Matter, 2020, 16, 9339–9346 RSC.
- Y. Lyu, Y. Pang, T. Liu and W. Sun, Soft Matter, 2024, 20, 2442–2454 RSC.
- Y. Kwon, J. H. Bernstein, N. Cohen and M. T. Valentine, ACS Biomater. Sci. Eng., 2021, 7, 5099–5106 CrossRef CAS PubMed.
- A. Ghareeb and A. Elbanna, J. Appl. Mech., 2018, 85, 121003 CrossRef.
- A. S. U. Manual, http://130.149, 2012, 89, v6.
- Y. Navidtehrani, C. Betegón and E. Martnez-Pañeda, Appl. Eng. Sci., 2021, 6, 100050 Search PubMed.
- Y. Zhang, K. Yu, K. H. Lee, K. Li, H. Du and Q. Wang, J. Mech. Phys. Solids, 2022, 159, 104782 CrossRef CAS.
- T. Li, Y. Jiang, K. Yu and Q. Wang, Soft Matter, 2017, 13, 7731–7739 RSC.
- A. S. Bhuwal, Y. Pang, I. Ashcroft, W. Sun and T. Liu, J. Mech. Phys. Solids, 2023, 175, 105294 CrossRef.
- A. S. Bhuwal, Y. Pang, I. Maskery, I. Ashcroft, W. Sun and T. Liu, Adv. Eng. Mater., 2023, 2300643 CrossRef.
- A. Bhuwal, Y. Pang, T. Liu, I. Ashcroft and W. Sun, Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems, CRC Press, 2022, pp. 333–338 Search PubMed.
- P. J. Loew, B. Peters and L. A. Beex, J. Mech. Phys. Solids, 2019, 127, 266–294 CrossRef.
- J. Bonet and R. D. Wood, Nonlinear continuum mechanics for finite element analysis, Cambridge University Press, 1997 Search PubMed.
- W. Pfeffer, Trans. Am. Math. Soc., 1986, 295, 665–685 CrossRef.
- C. Miehe, M. Hofacker and F. Welschinger, Comput. Methods Appl. Mech. Eng., 2010, 199, 2765–2778 CrossRef.
- L. R. G. Treloar, Trans. Faraday Soc., 1943, 39, 36–41 RSC.
- Y. Navidtehrani, C. Betegón and E. Martinez-Paneda, Materials, 2021, 14, 1913 CrossRef CAS PubMed.
- Stratasys Object260, Connex3 Objet260 3D Printer for Multi-color Multi-material Models, https://www.stratasys.com/3d-printers/objet260-connex3, [Online; accessed 26-July-2024].
- D. Roucou, J. Diani, M. Brieu and A. Mbiakop-Ngassa, Int. J. Fract., 2019, 216, 31–39 CrossRef.
- R. S. Rivlin and A. G. Thomas, J. Polym. Sci., 1953, 10, 291–318 CrossRef CAS.
- Y. Pang, S. Huang, H. Li, T. Liu and W. Sun, Theor. Appl. Fract. Mech., 2024, 104532 CrossRef.
- Y. Pang, B. K. Chen, S. F. Yu and S. N. Lingamanaik, Opt. Lett., 2020, 45, 2331–2334 CrossRef PubMed.
- Y. Pang, B. K. Chen, W. Liu, S. F. Yu and S. N. Lingamanaik, NDT & E Int., 2020, 111, 102219 CrossRef.
- D. A. Freedman, Statistical models: theory and practice, Cambridge University Press, 2009 Search PubMed.
- J. L. Devore, Probability and Statistics for Engineering and the Sciences, Brooks Cole Pub. Co., 8th edn, 2011 Search PubMed.
- N. J. Nagelkerke, et al. , Biometrika, 1991, 78, 691–692 CrossRef.
- J. R. Burkett, J. L. Wojtas, J. L. Cloud and J. J. Wilker, J. Adhes., 2009, 85, 601–615 CrossRef CAS.
- N. Bosnjak and M. N. Silberstein, Science, 2021, 374, 150–151 CrossRef CAS PubMed.
- A. Wongsto and S. Li, Composites, Part A, 2005, 36, 1246–1266 CrossRef.
- S. Li and E. Sitnikova, Representative volume elements and unit cells: concepts, theory, applications and implementation, Woodhead Publishing, 2019 Search PubMed.
- S. Li and A. Wongsto, Mech. Mater., 2004, 36, 543–572 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00832d |
| This journal is © The Royal Society of Chemistry 2024 |