Open Access Article
Open Access ArticleUnconstrained dynamic gel swelling generates transient surface deformations†
Alyssa
VanZanten
 a,
Shih-Yuan
Chen
a,
Shih-Yuan
Chen
 b,
Michelle M.
Driscoll
b,
Michelle M.
Driscoll
 b and
Caroline R.
Szczepanski
b and
Caroline R.
Szczepanski
 *a
*a
aDepartment of Chemical Engineering and Materials Science, Michigan State University, East Lansing, MI, USA. E-mail: szcz@msu.edu
bDepartment of Physics and Astronomy, Northwestern University, Evanston, IL, USA
First published on 5th August 2024
Abstract
Polymer gels are comprised of a three-dimensional, cross-linked network that can typically withstand the mechanical deformation associated with both swelling and de-swelling. Thus, gels can be designed with smart behaviors that require both stress generation and dissipation, making them well-suited to many applications including membrane technology, water capture devices, and drug delivery systems. In contrast to the fully swelled equilibrium state, limited research characterizes the unsteady-state swelling regime prior to equilibrium. It is in this regime where unique surface deformations can occur. Here we show how internal network constraints and external diffusive pressure can be leveraged to manipulate swelling kinetics and surface deformations in poly(ethylene glycol) gels during unconstrained, three-dimensional swelling. We find that increasing cross-linker molecular weight and swelling in ethanol, as opposed to water, are both effective routes to increase the time it takes to reach equilibrium but do so through different mechanisms. Networks with fewer internal constraints, manipulated via cross-linker chain-length, imbibe more solvent over a longer time. In contrast, swelling in ethanol reduces the amount of solvent imbibed by the network while increasing the time to reach equilibrium. Measurements of surface patterns during swelling establishes that an immediate, fast relaxation at the surface occurs during the first five minutes of swelling. However, the density and persistence of these features varies with solvent quality. These results establish a framework for how soft materials undergo dynamic deformation. Engineering transient surface properties while mitigating unwanted instabilities opens the door for emerging technologies such as smart anti-fouling and sensors.
1 Introduction
The development of smart soft materials in recent years has largely focused on utilizing stimuli-responsive polymers, because of the numerous synthetic pathways available to tailor their responsive behavior.1–4 For example, hydrogels, which are cross-linked, elastic polymer networks capable of absorbing large amounts of liquid, can be designed to swell and de-swell in response to external stimuli, like heat, solvent quality, and light.5,6 These qualities make hydrogels attractive for targeted drug delivery systems7,8 and tissue engineering.9,10 For instance, controlled release in delivery applications requires precise tailoring of transport kinetics11 and internal forces,12 such as the generation and dissipation of stresses during gel swelling. Interestingly, the significant internal stresses that arise during swelling are known to induce instabilities, such as bulk buckling and surface deformation.13–15 These instabilities are relevant and must be understood at a fundamental level, since changes at the surface of a material can dramatically impact its interactions with surrounding fluids. Thus, establishing how synthetic handles, such as cross-link density, impact surface deformation is critical when tailoring gels for specific application fields. This work utilizes hydrogel swelling as a platform to establish the fundamental stress generation and dissipation mechanics that lead to reversible surface deformation in soft materials.To understand swelling of a polymer network at a fundamental level, researchers often turn to Flory–Rehner polymer solution theory, which posits that gel swelling is driven by two opposing forces: (1) the force of mixing that results from the attraction between the polymer network and the solvent, and (2) the opposing elastic force that is due to the resistance of the elastic network to stretching during swelling.16–18 This theory successfully summarizes the complex interplay of forces that govern swelling, and therefore captures a broad range of gel swelling phenomena, such as the existence of continuous and discontinuous volume phase changes, and the effects of temperature, pH, and salt concentration on swelling.19 However, while Flory–Rehner describes the fully swelled, equilibrium state, there are systems to which this theory cannot be applied. For example, the use of macromeric (e.g., longer) cross-linkers, which are common in hydrogel development, deviates from the small-chain cross-links proposed by Flory–Rehner.20,21 Furthermore, the derivation of the Flory–Rehner theory assumes that a polymer network is in an equilibrium state where the chemical potential (μ) is equivalent inside and outside of the gel. When considering the unsteady-state swelling regime prior to equilibrium, this assumption no longer holds true. Some models combine kinetic behavior with Flory–Rehner fundamentals;22 however, assumptions of local equilibrium are still typically required. Thus, understanding transient swelling behavior prior to an equilibrium state remains a challenge. Bulk instabilities such as spontaneous fracture and dynamic surface deformation arise during non-equilibrium swelling, which highlights the need to understand this transient behavior.13,23 Understanding the origin of these instabilities will provide information on how localized stress gradients arise during swelling, as well as the mechanisms by which mismatched internal stresses are dissipated during transient swelling.
Despite the limited characterization of transient swelling, prior studies on equilibrium systems provide guidance as to what parameters can significantly impact gel swelling. For instance, we know that equilibrium swelling depends on cross-linking,24 polymer–solvent interaction,25 and environmental conditions.18,26 Additionally, studies that analyze the kinetics of swelling show that geometry,27 polymer–solvent interaction,17,28 and diffusion rate29 strongly impact swelling, but more work is needed to understand how these factors influence the dynamics of internal stress during the entire swelling process. Building upon this foundation, here we examine the changes in transient swelling and instability behaviors (e.g. surface deformations such as wrinkling, creasing, and folding) due to variations in both network constraints and solvent quality.
Many models of hydrogel swelling have been developed to capture these instability behaviors, which are driven both by solvent diffusion and non-linear, viscoelastic deformation of the polymer network.28,30–35 However, these models typically assume a two-dimensional material geometry either consisting of a thin ‘skin’ layer adhered to a softer foundation, or a bi-layer material consisting of two layers with finite thickness.36 With this geometry, the wavelength and amplitude of wrinkles on the surface are related to the compressive force in the skin layer.37 Furthermore, in many two-dimensional systems, surface deformations are engineered by imposing bulk strain, either manually through stretching38,39 or by constraining a gel to a substrate during swelling,12,15,38,40–44 as well as by creating a depth-wise cross-linking gradient.15,45–47 While these models and prior works characterize and describe behaviors such as wrinkling in coatings and thin films, assumptions that the elastic modulus and skin layer thickness are at steady-state do not apply to the system presented herein, which features free, unconstrained gel swelling, where material parameters are transient. While characterizing surface deformations in a transient, unconstrained system is challenging, it is crucial for engineering applications as these instabilities can be leveraged to impart anti-fouling or adhesive properties.37,48
To describe the network response during swelling, we can consider three aspects that evolve dynamically and are inter-related: (1) swelling kinetics, (2) stress dynamics, and (3) surface deformation mechanics. (1) Swelling kinetics defines the rate at which solvent is transported into and through a gel, and is dependent on many factors, such as cross-link density and polymer–solvent attraction.11,27,29,47,49 Swelling kinetics depend on how effectively polymer chains can move and stretch in response to swelling, as well as diffusion of solvent molecules. When swelling begins, the surface of a gel becomes saturated and stretches to accommodate diffusing solvent while being constrained by the inner portion of the material that is not yet expanding or responding to swelling, since the solvent molecules have not yet diffused to the interior. (2) These kinetics broadly influence stress dynamics, such as the stress that builds up due to mismatched swelling in the outer versus inner regions and the compressive stress experienced at the surface of the gel.7 The magnitude of stress experienced locally changes based on the speed at which the saturated outer region diffuses inwards toward the unsaturated center. As a result of internal stress changing and dissipating, surface deformation is observed to be transient as swelling progresses. (3) The solvent-saturated outer layer becomes softer than the bulk,17,44 and this mismatch between layers results in a buildup of compressive stress at the surface, thus leading to deformation (e.g., creasing).14,40,41,50 The evolution of surface instabilities is directly linked to swelling kinetics, stress dynamics, and therefore network relaxation. Measurements of how creasing patterns evolve during swelling can give us a window into the mechanics of dynamic deformation.
The work presented here utilizes a three-dimensional bulk swelling setup, where the samples are not constrained during swelling and therefore imbibe water on all faces. We present unique, transient creasing of poly(ethylene glycol)-based gels and characterize both the swelling kinetics and surface deformation evolution. In Section 3.1 we characterize the instability behaviors that occur during transient swelling, focusing on the three-stages of surface deformation. We highlight a grid-like surface pattern that emerges after 20 minutes of swelling, which has only been described in a limited context prior to this work.13 The impact of network constraints on swelling kinetics and capacity is investigated in Section 3.2 by manipulating cross-link fraction and molecular weight of the cross-linker employed. We also characterize how external diffusive pressure can be modulated via (co)solvent quality in Section 3.3. Specifically, swelling in ethanol as opposed to water is shown to decrease the rate of solvent imbibement, while the rate of swelling in water–ethanol (co)solvents changes non-monotonically with respect to ethanol content. Finally, crease evolution and kinetics are quantified through imaging measurements to infer stress dynamics in Section 3.4. This study will be used to understand the fundamental factors, both internal and external, that drive network relaxation during swelling.
2 Experimental
2.1 Materials
The base monomer employed in this study is poly(ethylene glycol) methyl ether acrylate (PEGMA) with a molecular weight of 400 g mol−1. To form a network structure (gel), a cross-linker was incorporated into the polymerization. Two different poly(ethylene glycol) diacrylate (PEGDA) cross-linkers were employed, one with an average molecular weight of 700, and the other 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1. In all formulations, the photoinitiater used was 2,2-dimethoxy-2-phenylacetophenone (DMPA). All materials were obtained from Sigma-Aldrich and were used as received. For swelling experiments, deionized (DI) water was obtained via an in-house DI water source and 200-proof ethanol was obtained from Koptec. (Co)solvent solutions were prepared by mixing DI water and 200-proof ethanol at the following volume ratios: 90
000 g mol−1. In all formulations, the photoinitiater used was 2,2-dimethoxy-2-phenylacetophenone (DMPA). All materials were obtained from Sigma-Aldrich and were used as received. For swelling experiments, deionized (DI) water was obtained via an in-house DI water source and 200-proof ethanol was obtained from Koptec. (Co)solvent solutions were prepared by mixing DI water and 200-proof ethanol at the following volume ratios: 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 75
10, 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, 50
25, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 25
50, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, and 10
75, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 (water
90 (water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol).
ethanol).
2.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), as shown in Table 1. Throughout the remainder of the manuscript, formulations will be referenced by their name, which follows the pattern PEGDA(mol%):PEGMA(mol%). If the formulation was made with PEGDA-10
000), as shown in Table 1. Throughout the remainder of the manuscript, formulations will be referenced by their name, which follows the pattern PEGDA(mol%):PEGMA(mol%). If the formulation was made with PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, it is noted by the use of “10k” at the beginning of the name. If this notation is absent, PEGDA-700 was used in the formulation.
000, it is noted by the use of “10k” at the beginning of the name. If this notation is absent, PEGDA-700 was used in the formulation.
The photoinitiator loading in all formulations was 0.5 wt%, meaning that the loadings listed for PEGMA and PEGDA in Table 1 constitute 99.5 wt% of the total mass. Resins made with the 700 g mol−1 PEGDA were prepared neat (i.e., without solvent). In brief, the appropriate mass of DMPA, PEGMA, and PEGDA-700 were incorporated into a glass vial and magnetically stirred until homogeneous (∼15 min). To achieve a homogeneous resin formulation when employing the high molecular weight cross-linker (PEGDA-10k), water was included in the resin. This was incorporated to homogenize all resin constituents during mixing. After achieving a homogeneous mixture, the resin was dried at 65 °C overnight, resulting in at least 95% of the water being removed as evidenced by the mass change after drying.
All polymerized samples were prepared in glass molds with approximate dimensions of 25 × 10 × 2 mm (l × w × t). Samples were photocured at an intensity of 0.1 W cm−2 in the UV-A region (λ ∼ 315 to 400 nm). UV irradiation intensity was verified with a UV radiometer (Power Puck II, Electronic Instrumentation and Technology, Inc.). Prior works suggest that this photoinitiator concentration and UV intensity results in relatively homogeneous depth-wise cross-link density at this thickness.51,52
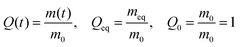 | (1) |
Swelling data was collected in triplicate for every formulation (Table 1) and solvent condition. The average and standard deviation of the swelling ratio at a each time point (t) were used to calculate  , the normalized swelling ratio (eqn (2)) and its associated error.
, the normalized swelling ratio (eqn (2)) and its associated error.
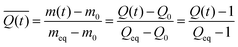 | (2) |
In this equation, the relative swelling ratio increase at time (t) is divided by the total relative swelling ratio increase at equilibrium. Therefore, the normalized swelling ratio  represents the fraction of the total swelling capacity that is reached at each time point.
represents the fraction of the total swelling capacity that is reached at each time point.
Lastly, initial swelling kinetics were characterized via the swelling rate (e.g., Q as a function of time) during the first 30 minutes of solvent exposure in order to describe the entire range of swelling during which surface deformation (i.e., creasing) is observed. To obtain this rate, a linear equation was fit to the Q data during the first 30 minutes of swelling. The y-intercept of the linear fit was fixed at 1 as Q0 = 1 (see, eqn (1)). These initial swelling rate calculations are shown in Fig. S1, ESI.†
 | (3) |
FTIR transmission spectra before and after photopolymerization for two gel formulations are also included in Fig. S6 (ESI†) to confirm that the vinyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) peak at 6165 cm−1 completely disappears after photopolymerization, even in the most densely cross-linked formulations.
C) peak at 6165 cm−1 completely disappears after photopolymerization, even in the most densely cross-linked formulations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99, PEGDA-700 samples were swelled while microscope images (with a field of view of 6656 μm × 6656 μm) were captured every 20 seconds during the first 31.6 minutes of swelling. To ensure that there was no contact with the surrounding vessel inhibiting diffusion, each hydrogel sample was suspended off the bottom of the dish during swelling. The plane of focus of the microscope was aligned with the bottom of the sample, meaning that creases on the bottom appeared as thin, dark lines, whereas the out-of-focus creases on the top surface show up as larger, dark splotches. See Fig. S3 and S4, ESI† for a clear depiction of the surface features we measured, in which the crease tracings in orange are overlaid on the microscope images.
99, PEGDA-700 samples were swelled while microscope images (with a field of view of 6656 μm × 6656 μm) were captured every 20 seconds during the first 31.6 minutes of swelling. To ensure that there was no contact with the surrounding vessel inhibiting diffusion, each hydrogel sample was suspended off the bottom of the dish during swelling. The plane of focus of the microscope was aligned with the bottom of the sample, meaning that creases on the bottom appeared as thin, dark lines, whereas the out-of-focus creases on the top surface show up as larger, dark splotches. See Fig. S3 and S4, ESI† for a clear depiction of the surface features we measured, in which the crease tracings in orange are overlaid on the microscope images.
To extract quantitative data from these microscope images, the crease lines were manually traced using MS Paint on a Microsoft Surface tablet. This process binarizes the images and provides accurate locations for the crease lines. Using a custom Python code, the geometric mean point of each line was identified from the images. Then, the closest neighboring point was identified, any duplicate reported distances were eliminated, and the average distance between neighboring creases was calculated. Once an ensemble of the distance between each crease line was established, the ensemble was averaged to obtain the characteristic “wavelength” or distance between observed crease patterns. Three samples were imaged for each solvent mixture. Given the complexity associated with the tracing process, seven equally spaced time points (20, 320, 640, 940, 1300, 1600, and 1900 seconds) were chosen for analysis to capture the range of instability behaviors.
3 Results and discussion
3.1 Instability behaviors during transient swelling
Qualitative observation of swelling behavior for each gel formulation (Table 1) reveals two types of instabilities during transient solvent diffusion; complex surface deformation (e.g., Fig. 1a–h) and catastrophic rupture (e.g., Fig. 1i and j). Surface deformations were observed for six formulations during swelling in water: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99, 5
99, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95, and all formulations employing the 10k cross-linker (pink entries, Table 1). The remaining formulations (10
95, and all formulations employing the 10k cross-linker (pink entries, Table 1). The remaining formulations (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90, 20
90, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, and 40
80, and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, gray entries, Table 1) did not typically exhibit macroscopic surface deformations during swelling in water, but often exhibited self-rupture. Catastrophic rupture of PEG-based gels during swelling has been reported to occur mainly due to the networks inability to utilize viscous stress dissipation coupled with large volume change during swelling.23 In rare cases, gels with 5–10 mol% PEGDA can exhibit surface deformation at early swelling times prior to self-rupture.
60, gray entries, Table 1) did not typically exhibit macroscopic surface deformations during swelling in water, but often exhibited self-rupture. Catastrophic rupture of PEG-based gels during swelling has been reported to occur mainly due to the networks inability to utilize viscous stress dissipation coupled with large volume change during swelling.23 In rare cases, gels with 5–10 mol% PEGDA can exhibit surface deformation at early swelling times prior to self-rupture.
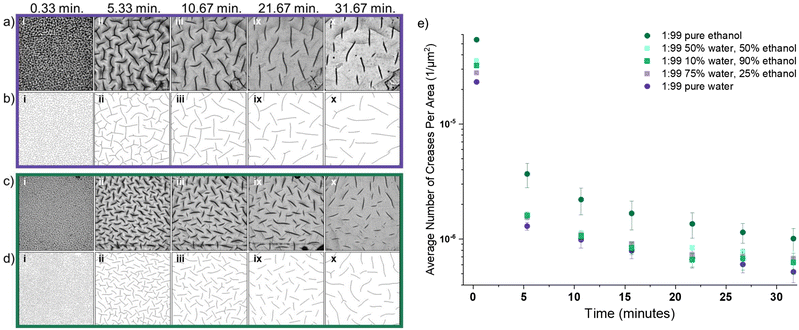
All samples that underwent surface deformation during transient swelling exhibited the same three-stage surface feature evolution: creasing, grid, and equilibrium. Immediately after being placed in an excess of solvent (e.g., on the order of seconds), small creases (detectable with the naked eye) appeared (see Fig. 1b). As swelling progressed (e.g., over many minutes), these surface features grew and coalesced, and additional self-contact occurred between “cells” as seen in Fig. 1c and d. As swelling continued, a long-range grid pattern emerged (see Fig. 1e–g). At later swelling stages (e.g. 70 minutes of swelling or longer), the grid was still visible, although it became less distinct. Finally, the surface of the gel became smooth again (Fig. 1h) once the gel reached its final, equilibrium state. Equilibrium swelling is verified by constant Q(t) values (e.g., plateauing to Qeq).
Prior experimental work describes related surface deformations, such as creasing in gels that are attached to a substrate15,40,42,43 or under constraint,53,54 as well as bulk buckling in gels with an engineered gradient in cross-link density45,47 or layered structure.50,55 However, to the best of our knowledge, the observed “grid” surface patterning during swelling has only been seen in one previous study, which found that this instability pattern was coupled to bulk buckling of hydrogel discs.13 The similar, anisotropic grid-like crease pattern in our system provides perspective on how other sources of anisotropic internal stresses can be engineered. Prior studies,56 as well as our ongoing work, indicates that crease patterns are dependent on the geometry of the sample. As one example, we observe that in thin samples (e.g. low thickness) surface instabilities during swelling are eliminated due to a lack of strain mismatch between inner and outer layers.
Self-rupture behavior is addressed in computational studies on constrained swelling leading to fracture,31 and in experimental studies where rupture occurred during free swelling,23 as well as pre-programmed rupture induced by non-uniform swelling.57 Theory has been developed to understand how stress due to swelling contributes to surface deformation in free-swelling spheres32 and in constrained gel blankets,44 and how in soft materials internal stresses are often dissipated through instabilities (e.g. creases, wrinkles, or buckling). Here, we explore how surface deformations are coupled to both material properties (network architecture) and swelling kinetics (solvent selection) in a free-swelling gel, where no mechanical constraints are applied during the swelling process. Understanding the coupling between these swelling control parameters in an unconstrained system is necessary to design and tailor structured and dynamic material interfaces.
3.2 Impact of internal network constraints
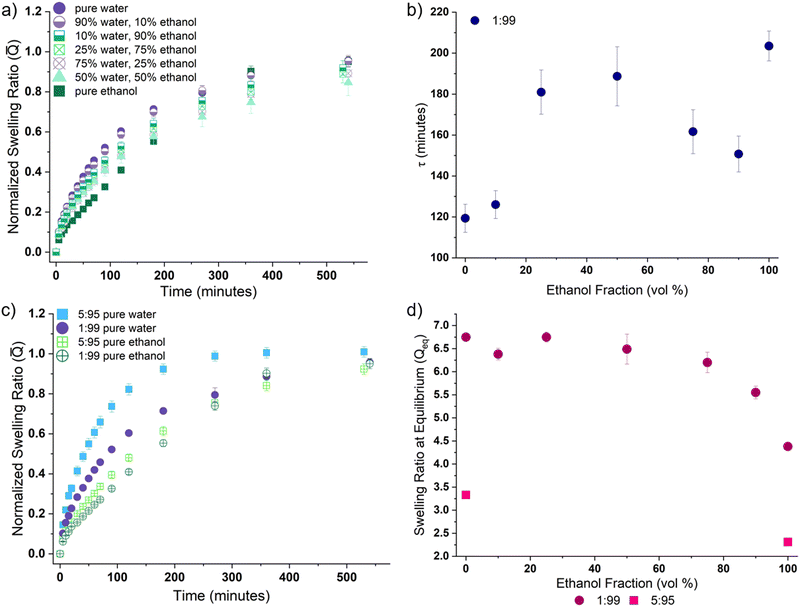
All samples containing the high MW cross-linker (PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, denoted by “10k” in our sample notation) exhibited surface creasing and deformation during swelling in water; no rupture events were observed regardless of cross-linker fraction (mol%). This is in contrast to formulations containing the lower molecular weight cross-linker (PEGDA-700), where high cross-linker content (10 mol% or greater) corresponds to a high likelihood of rupture and no observable surface creasing or deformation. This indicates that internal network constraints significantly impact swelling kinetics and solvent diffusion. To quantify this behavior, we measure the swelling ratio Q(t) (eqn (1) and Fig. S1, ESI†); we report swelling for all samples as the normalized swelling ratio
000, denoted by “10k” in our sample notation) exhibited surface creasing and deformation during swelling in water; no rupture events were observed regardless of cross-linker fraction (mol%). This is in contrast to formulations containing the lower molecular weight cross-linker (PEGDA-700), where high cross-linker content (10 mol% or greater) corresponds to a high likelihood of rupture and no observable surface creasing or deformation. This indicates that internal network constraints significantly impact swelling kinetics and solvent diffusion. To quantify this behavior, we measure the swelling ratio Q(t) (eqn (1) and Fig. S1, ESI†); we report swelling for all samples as the normalized swelling ratio ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) , which is 0 in a dry gel and 1 for a fully swollen (equilibrium) gel (Fig. 2a and b). At each time point,
, which is 0 in a dry gel and 1 for a fully swollen (equilibrium) gel (Fig. 2a and b). At each time point, ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) indicates the fraction of the total swelling capacity the gel has obtained. Higher
indicates the fraction of the total swelling capacity the gel has obtained. Higher ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) at earlier times indicate samples that quickly reach a high fraction of equilibrium swelling ratio (Qeq), which is often a result of the total swelling capacity being relatively small (e.g., Qeq for the 40
at earlier times indicate samples that quickly reach a high fraction of equilibrium swelling ratio (Qeq), which is often a result of the total swelling capacity being relatively small (e.g., Qeq for the 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 gels is 1.88, whereas for 1
60 gels is 1.88, whereas for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 gels this value is 6.75 – Fig. 2d). Thus only a small amount of water is imbibed to reach a high
99 gels this value is 6.75 – Fig. 2d). Thus only a small amount of water is imbibed to reach a high ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) .
.
 | ||
Fig. 2 Tuning internal network constraints leads to measurable differences in swelling behavior (i.e. normalized swelling ratio (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) ), time to equilibrium (τ), and equilibrium swelling ratio (Qeq)). (a) Normalized swelling ratio ( ), time to equilibrium (τ), and equilibrium swelling ratio (Qeq)). (a) Normalized swelling ratio (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) ) vs. time, which represents the fraction of the total swelling capacity for gel formulations containing the 700MW PEGDA cross-linker. (b) Normalized swelling ratio ( ) vs. time, which represents the fraction of the total swelling capacity for gel formulations containing the 700MW PEGDA cross-linker. (b) Normalized swelling ratio (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) ) vs. time for gel formulations utilizing the 10 ) vs. time for gel formulations utilizing the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000MW PEGDA cross-linker. Here the 1 000MW PEGDA cross-linker. Here the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation with the 700MW cross-linker is also plotted for reference. (c) τ, the characteristic time parameter for 99 formulation with the 700MW cross-linker is also plotted for reference. (c) τ, the characteristic time parameter for ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) (eqn (4)), is plotted versus the fraction of cross-linker (PEGDA) in all gel formulations. An example fitting to obtain τ is provided in Fig. S2 (ESI†). Generally, these data show that a decrease in cross-linker fraction corresponds to a decrease in (eqn (4)), is plotted versus the fraction of cross-linker (PEGDA) in all gel formulations. An example fitting to obtain τ is provided in Fig. S2 (ESI†). Generally, these data show that a decrease in cross-linker fraction corresponds to a decrease in ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) at early swelling times, as well as an increase in the total time required to reach equilibrium. (d) The equilibrium swelling ratio (Qeq) for all gel formulations are plotted as a function of cross-linker fraction. All data are for gels swelled in water. at early swelling times, as well as an increase in the total time required to reach equilibrium. (d) The equilibrium swelling ratio (Qeq) for all gel formulations are plotted as a function of cross-linker fraction. All data are for gels swelled in water. | ||
The influence of cross-linker MW can be understood by comparing the ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) data for PEGDA-700 formulations (Fig. 2a) with PEGDA-10
data for PEGDA-700 formulations (Fig. 2a) with PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 formulations (Fig. 2b). Overall, we find that
000 formulations (Fig. 2b). Overall, we find that ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) is higher at early times for the PEGDA-700 samples. While most formulations with the PEGDA-700 cross-linker reach equilibrium relatively quickly, the 1
is higher at early times for the PEGDA-700 samples. While most formulations with the PEGDA-700 cross-linker reach equilibrium relatively quickly, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation takes a much longer time. Similar behavior is observed if the cross-linker MW is increased (PEGDA-10
99 formulation takes a much longer time. Similar behavior is observed if the cross-linker MW is increased (PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 – Fig. 2b). Gels with 1 mol% of the higher MW cross-linker (10k 1
000 – Fig. 2b). Gels with 1 mol% of the higher MW cross-linker (10k 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99) are slower to achieve equilibrium, and increasing cross-linker fraction generally decreases the time to equilibrium.
99) are slower to achieve equilibrium, and increasing cross-linker fraction generally decreases the time to equilibrium.
To quantify the differences in time to equilibrium across various network architectures, each ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) dataset was fit with the following equation:
dataset was fit with the following equation:
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation experiences a much larger time to reach equilibrium (τ ≃ 120 minutes) than the formulations with higher PEGDA-700 content (all τ ≤ 61 minutes). Similarly, when PEGDA-10
99 formulation experiences a much larger time to reach equilibrium (τ ≃ 120 minutes) than the formulations with higher PEGDA-700 content (all τ ≤ 61 minutes). Similarly, when PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is used as the cross-linker, the 10k 1
000 is used as the cross-linker, the 10k 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation exhibits the highest τ value (τ ≃ 190 minutes), and increasing cross-linker fraction lowers τ. Overall, networks with lower cross-linker content imbibe a higher fraction of water (see Fig. 2d), and also take more time to reach equilibrium. In other words, when the constraints in the network are increased (via increased cross-linking), the total capacity to swell decreases and therefore less solvent is required to reach equilibrium.
99 formulation exhibits the highest τ value (τ ≃ 190 minutes), and increasing cross-linker fraction lowers τ. Overall, networks with lower cross-linker content imbibe a higher fraction of water (see Fig. 2d), and also take more time to reach equilibrium. In other words, when the constraints in the network are increased (via increased cross-linking), the total capacity to swell decreases and therefore less solvent is required to reach equilibrium.
At all cross-linker loadings, the formulations using the PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cross-linker have a larger τ, which demonstrates that increasing the length of the cross-linker (PEGDA) corresponds to an increase in the time to reach equilibrium. The increased flexibility afforded by a higher MW cross-linker (PEGDA-10
000 cross-linker have a larger τ, which demonstrates that increasing the length of the cross-linker (PEGDA) corresponds to an increase in the time to reach equilibrium. The increased flexibility afforded by a higher MW cross-linker (PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) means that the network has more freedom to accommodate solvent during swelling.
000) means that the network has more freedom to accommodate solvent during swelling.
3.3 Effect of external diffusive pressure on swelling
The![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) and τ behavior for swelling PEGDA-700 and PEGDA-10
and τ behavior for swelling PEGDA-700 and PEGDA-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 gels in water highlight how the rate of solvent imbibement during swelling is influenced by the internal constraints of the polymer network. This is consistent with the Flory–Rehner (FR) polymer solution thermodynamics model, which postulates that gel swelling is described by an overall osmotic pressure (Π), that is composed of two main terms: the pressure of mixing (Πmix) and the pressure of elasticity (Πel) (see eqn (5) and Table 2).18,19,63–66 The sum of the pressure of mixing (Πmix) and the pressure of elasticity (Πel) equals the overall osmotic pressure (Π) that the material experiences during swelling. Total osmotic pressure (Π) and mixing pressure (Πmix) are positive values that represent the forces that drive swelling, while (Πel) is always negative, representing the resistance to swelling that the elasticity of the polymer network asserts.
000 gels in water highlight how the rate of solvent imbibement during swelling is influenced by the internal constraints of the polymer network. This is consistent with the Flory–Rehner (FR) polymer solution thermodynamics model, which postulates that gel swelling is described by an overall osmotic pressure (Π), that is composed of two main terms: the pressure of mixing (Πmix) and the pressure of elasticity (Πel) (see eqn (5) and Table 2).18,19,63–66 The sum of the pressure of mixing (Πmix) and the pressure of elasticity (Πel) equals the overall osmotic pressure (Π) that the material experiences during swelling. Total osmotic pressure (Π) and mixing pressure (Πmix) are positive values that represent the forces that drive swelling, while (Πel) is always negative, representing the resistance to swelling that the elasticity of the polymer network asserts. | (5) |
| Π = Πmix + Πel |
| Term | Definition |
|---|---|
| k B | Boltzmann's constant |
| α | Effective solvent diameter |
| ϕ | Volume fraction of polymer |
| ϕ 0 | Initial volume fraction (equals 1 for neat polymer) |
| χ | Flory–Huggins interaction parameter |
| N c | Number of chains in the polymer network |
| V 0 | Initial volume |
Π mix represents the driving force for swelling that originates from the attraction between the polymer network and the solvent, which is often characterized by the Flory–Huggins interaction parameter χ. Πmix also accounts for how the size of a solvent molecule impacts physical mixing. Inspired by the equilibrium FR model, we believe that both the external diffusive pressure during swelling and the elastic network both can be leveraged, even in the transient state, to manipulate the rate of solvent imbibement.
The experiments presented up to this point explicitly manipulate the elastic contribution to swelling (i.e., network constraints). To systematically vary the external diffusive pressure and establish how that impacts instability behaviors, PEGDA-700 samples were swelled in varying (co)solvents comprised of water and ethanol. Initial swelling rates, which were estimated by performing a linear fit to the first 30 minutes of the swelling ratio Q(t), were calculated for all gel formulations with PEGDA-700 as the cross-linker, and are plotted in Fig. S1 (ESI†). Overall, swelling in ethanol, as opposed to water, resulted in a significant decrease in initial swelling rate at all PEGDA-700 fractions. Additionally, for swelling in both water and ethanol, the initial rate of swelling decreases as cross-linker fraction increases. This data demonstrates how the external diffusive pressure, which can be manipulated via solvent selection, is a means to further manipulate the timescale of swelling.
To better understand the impact of external diffusive pressure, particularly on transient surface instabilities, the PEGDA-700 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation was chosen for further analysis. Specifically,
99 formulation was chosen for further analysis. Specifically, ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) was characterized for the 1
was characterized for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation when swelling was conducted in pure water, pure ethanol, and 5 co-solvent mixtures (Fig. 3a). The solvent-driven changes in
99 formulation when swelling was conducted in pure water, pure ethanol, and 5 co-solvent mixtures (Fig. 3a). The solvent-driven changes in ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) are consistent with the initial swelling rate and are further reflected in the τ parameters (Fig. 3b); swelling in ethanol increases the time required to reach equilibrium. To explore the effect of changing network architecture, we measured swelling for two different cross-link densities; 1
are consistent with the initial swelling rate and are further reflected in the τ parameters (Fig. 3b); swelling in ethanol increases the time required to reach equilibrium. To explore the effect of changing network architecture, we measured swelling for two different cross-link densities; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 and 5
99 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95. As shown in Fig. 3c, increasing cross-link density leads to faster equilibration times. This may be attributed to the fact that the network imbibes less overall solvent (Qeq, Fig. 3d). Interestingly, swelling in pure ethanol also decreases Qeq, but leads to slower equilibration times. This contrasting relationship between Qeq and time to equilibrium indicates that swelling in ethanol, as opposed to water, fundamentally changes the diffusion kinetics.
95. As shown in Fig. 3c, increasing cross-link density leads to faster equilibration times. This may be attributed to the fact that the network imbibes less overall solvent (Qeq, Fig. 3d). Interestingly, swelling in pure ethanol also decreases Qeq, but leads to slower equilibration times. This contrasting relationship between Qeq and time to equilibrium indicates that swelling in ethanol, as opposed to water, fundamentally changes the diffusion kinetics.
Water is commonly used as a good solvent for PEG gels,11 and thus we expect that as the fraction of ethanol in the (co)solvent mixture increases, ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) will decrease and τ will increase. Surprisingly, we find instead that τ changes non-monotonically with ethanol vol% (Fig. 3b). This indicates that there are competing interactions between water and ethanol that interfere with diffusion into the polymer network during swelling in a mixed solvent.
will decrease and τ will increase. Surprisingly, we find instead that τ changes non-monotonically with ethanol vol% (Fig. 3b). This indicates that there are competing interactions between water and ethanol that interfere with diffusion into the polymer network during swelling in a mixed solvent.
To understand this non-monotonic relationship, we must quantify the attraction between the (co)solvent molecules and the polymer network. The standard method of quantifying interactions is the Flory–Huggins (FH) interaction parameter (χ). χ can be estimated between two species (α and β) using eqn (6):67
 | (6) |
| α ≡ A, B, β ≡ B, C ≠ α |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 g mol−1 are reported in Table 3.68 While these measurements are for linear PEG systems, and may not directly correspond to χ measured for a cross-linked PEG system, they can help us understand how our ternary mixture interacts.
600 g mol−1 are reported in Table 3.68 While these measurements are for linear PEG systems, and may not directly correspond to χ measured for a cross-linked PEG system, they can help us understand how our ternary mixture interacts.
| Flory–Huggins interaction parameter | PEG 8650 | PEG 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
|---|---|---|
| χ water–PEG | 1.0001 | 0.6318 |
| χ water–ethanol | −4.4412 | −4.2339 |
| χ PEG–ethanol | −0.6862 | −0.7451 |
Table 3 shows that mixing of water and PEG is slightly unfavorable, mixing PEG and ethanol is favorable, and mixing water and ethanol is significantly favorable (due to the large, negative (−) χwater–ethanol). This can explain the non-monotonic swelling behavior we observe in (co)solvent mixtures: water and ethanol are significantly attracted to one another, meaning the interaction between these solvent species likely competes with the driving force of swelling.67 The normalized swelling ratio (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) ) data for swelling in (co)solvent mixtures supports this finding (Fig. 3a). The
) data for swelling in (co)solvent mixtures supports this finding (Fig. 3a). The ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) behavior for 10/90 and 90/10 (vol/vol, water/ethanol) (co)solvents are very similar to pure water behavior (Fig. 3a), which is similar to findings from ternary mixtures with linear PEG polymers.67 More specifically, when (co)solvent species experience significant interaction with each other, the miscibility between the (co)solvent mixture and the polymer network is decreased, and immiscibility reaches its maximum when the volume ratio between the (co)solvent species is equal to one. Indeed, Fig. 3b shows that the 50/50 (vol/vol) (co)solvent mixture exhibits the highest τ value, indicating that the ternary mixture reaches its peak immiscibility when water and ethanol are mixed in equal parts. This is particularly interesting, as this behavior does not follow established co-non-solvency and co-solvency behaviors in gel swelling,69–71 as our two (co)solvents have differing interactions with the gel (e.g. positive (+) vs. negative (−) χ).
behavior for 10/90 and 90/10 (vol/vol, water/ethanol) (co)solvents are very similar to pure water behavior (Fig. 3a), which is similar to findings from ternary mixtures with linear PEG polymers.67 More specifically, when (co)solvent species experience significant interaction with each other, the miscibility between the (co)solvent mixture and the polymer network is decreased, and immiscibility reaches its maximum when the volume ratio between the (co)solvent species is equal to one. Indeed, Fig. 3b shows that the 50/50 (vol/vol) (co)solvent mixture exhibits the highest τ value, indicating that the ternary mixture reaches its peak immiscibility when water and ethanol are mixed in equal parts. This is particularly interesting, as this behavior does not follow established co-non-solvency and co-solvency behaviors in gel swelling,69–71 as our two (co)solvents have differing interactions with the gel (e.g. positive (+) vs. negative (−) χ).
While the χ values for water–PEG and PEG–ethanol indicate mixing should be favored when gels are swollen in ethanol, our data shows reduced Qeq and initial swelling rate in ethanol (Fig. 3d and Fig. S1, ESI,† respectively). This could be due to the solvent molecular size. Flory–Rehner theory (see eqn (5)) states that the pressure of mixing (Πmix) is inversely proportional to the solvent diameter cubed, meaning that increasing the size of the solvent molecule would decrease the pressure of mixing (i.e., the driving force for swelling). The effective diameter of a water molecule is 2.75 Å,72 and the diameter of an ethanol molecule is 4.5 Å.73 This means that swelling in ethanol is less entropically favorable than swelling in water, which is consistent with our experimental observation that the network swells considerably more in water. Although ethanol has a negative (−) χ for linear PEG chains, its larger size may hinder its ability to mix with the three-dimensional, cross-linked PEG network.
3.4 Examining surface creasing during swelling
Changing the solvent mixture changes the rate of solvent imbibement, and thus impacts transient material stress. To quantify these changes, we studied the evolution of surface instabilities during swelling in water, ethanol, and (co)solvent mixtures. We used light microscopy to image surface instabilities in situ and characterize pattern evolution. The surface deformation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99, PEGDA-700 formulation was characterized during swelling in ethanol, water, and (co)solvent mixtures (Fig. 4).
99, PEGDA-700 formulation was characterized during swelling in ethanol, water, and (co)solvent mixtures (Fig. 4).
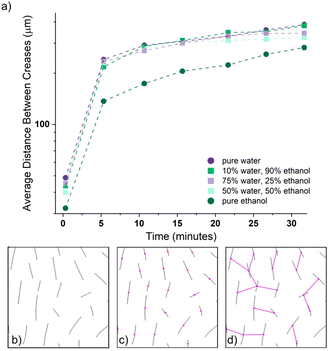
The observed crease evolution in water (Fig. 4a, corresponding binary tracings Fig. 4b) and in ethanol (Fig. 4c, corresponding binary tracings Fig. 4d), show that surface deformation began rapidly once the gel was placed in solvent. We note that the images show creasing on both the bottom (in-focus sharp lines) and top of the sample (larger, darker out-of-focus lines); analysis was done on the creases on the bottom of the sample as highlighted in Fig. S3 and S4, ESI.†Fig. 4 shows that swelling in ethanol leads to a higher number of creases when compared to swelling in water. This is quantified in Fig. 4e, which shows the mean density of creases as a function of swelling time in the various (co)solvent mixtures. The density of creases rapidly decreases in time. This large, relatively fast decrease is due to relaxation of the outermost layer of the gel as diffusion of the solvent continues deeper into the network. At all time points, swelling in pure ethanol results in significantly more creases than any other (co)solvent, and swelling in pure water shows the lowest number of creases. The three co-solvent mixtures explored fell between these extremes and are statistically similar.
As shown in Fig. S1, ESI,† swelling the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 formulation in water significantly increases the initial rate of swelling compared to ethanol. The slower imbibement of ethanol corresponds to a lower driving force for swelling and less mixing pressure (Πmix) forcing the network to relax and dissipate the compressive stress at the surface. Despite the fact that the network imbibes significantly less fluid during swelling in ethanol as compared to water, this results in twice the number of surface creases at 0.33 min (Fig. 4e). This suggests that (co)solvent selection and the associated diffusivity within a gel network is a significant parameter when tailoring the scale of instabilities that form.
99 formulation in water significantly increases the initial rate of swelling compared to ethanol. The slower imbibement of ethanol corresponds to a lower driving force for swelling and less mixing pressure (Πmix) forcing the network to relax and dissipate the compressive stress at the surface. Despite the fact that the network imbibes significantly less fluid during swelling in ethanol as compared to water, this results in twice the number of surface creases at 0.33 min (Fig. 4e). This suggests that (co)solvent selection and the associated diffusivity within a gel network is a significant parameter when tailoring the scale of instabilities that form.
Wrinkling of soft materials under compression is well-characterized, and theories have been developed to connect wrinkling wavelength directly with material properties.37 The features we observe in this gel system are creases (as opposed to wrinkles), as evidenced by their random orientation. This indicates the material has made self-contact, which presents a challenge for connecting these patterns to network material properties. However, the assumption from classical wrinkling relating wrinkle wavelength to material properties and compressive forces for a skin layer atop a foundation is similar and can be applied to this system during the initial states of swelling when only the thin, outermost layer of the gel has imbibed solvent. Wrinkling theory predicts that the compressive force at the surface is related to the skin thickness, the elastic modulus and Poisson's ratio of both the skin and the bulk;37 therefore, higher compressive forces generally lead to smaller wavelength of wrinkles. Thus, applying this theory to our gel system at early time points means that when we observe a lower number of features (Fig. 4e), and higher spacing (i.e., “wavelength”) when swelling in water, as opposed to ethanol, it likely represents lower compressive forces at the surface.
To further quantify crease spacing, we measure the mean inter-crease distance for each solvent condition (Fig. 5a). This analysis shows that the average crease spacing at all times is lowest for ethanol, which indicates higher compressive stress if classical wrinkling theory is applied to early time points of swelling. In other words, because ethanol has a lower driving force for swelling (Πmix) than water, the compressive stress generated during swelling persists longer due to the slow diffusion of ethanol through the gel. As time passes and swelling evolves, the crease distance rapidly increases, which correlates to a relaxation of the polymer network with time. Similar to the average number of creases, all solvent conditions show a dramatic increase in the distance between creases between 0.33 min and 5.33 min (i.e., between a 300% and a 400% increase). This increase in distance between creases (our analogue to wavelength) indicates an immediate, fast decrease in compressive stress at the surface due to the initial relaxation that occurs at the surface of the gel. This fast, initial relaxation followed by a slower, secondary relaxation that occurs after 5.33 min is consistent with the two modes of deformation proposed by Hong et al.22
Interestingly, at late times, the 50/50 water/ethanol (co)solvent plateaued and diverged slightly from the grouping of the pure water and other (co)solvent mixtures. A similar trend appeared in the number of creases (Fig. 4a). This result can be understood in the context of the (co)solvent theory that immiscibility is greatest when the ratio  is equal to 1. The interaction between water and ethanol that competes with swelling is greatest when the (co)solvent contains equal parts of water and ethanol. This significant interference leads to the (co)solvent mixture behaving as a worse solvent.
is equal to 1. The interaction between water and ethanol that competes with swelling is greatest when the (co)solvent contains equal parts of water and ethanol. This significant interference leads to the (co)solvent mixture behaving as a worse solvent.
4 Conclusions
We explore the impact of internal network constraints (cross-linking) and external diffusive pressure (solvent quality) on swelling kinetics and surface deformation dynamics in PEG-based gels. We find that networks with fewer internal constraints (which have a higher overall capacity for swelling, Qeq), experience much longer transient swelling. Increasing the molecular weight between cross-links decreases the elastic pressure, and thus increases the time it takes to reach equilibrium. We find that ethanol, despite having a large negative (−) χ, exhibits less imbibement into the network than water (which has a positive (+) χ). This demonstrates that while imbibement is a function of chemical affinity (χ), this competes with the effect of molecular size. Swelling experiments in water–ethanol (co)solvent mixtures reveal that the strong affinity between water and ethanol competes with the driving force of swelling.Measurements of surface instabilities show that immediately after being placed in a solvent, densely packed creases rapidly appear on the surface of the gel. The inter-crease spacing increases in time as diffusion progresses and the material begins to relax. Furthermore, we find that swelling in ethanol results in a higher crease density, which likely indicates that larger compressive stresses are present. Thus, swelling in ethanol not only slows down swelling kinetics, but it also alters the dynamics of surface deformations. This reveals that the driving force for mixing is lower for swelling in ethanol as compared to water, and therefore the hydrogel network experiences less pressure to relax and dissipate the stress that builds due to swelling and solvent diffusion. The physics involved in generating macroscopic surface deformations is complex, and thus it is challenging to use the geometry of these features to directly quantify material stresses. However, this work establishes a path towards understanding the complex dynamics at play during transient swelling and offers a new way to quantify material response.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
During this study, Alyssa VanZanten was supported by the NSF/DMR (Award 2311697) and Shih-Yuan Chen was partially supported by the NSF/DMR (Award 2311698). The authors would like to thank our labmates Sabrina Curley, Denghao Fu, and Samira Kahn, for their support and rigorous discussions.Notes and references
- B. Xin and J. Hao, Chem. Soc. Rev., 2010, 39, 769–782 RSC
.
- S. Zeng, R. Li, S. G. Freire, V. M. Garbellotto, E. Y. Huang, A. T. Smith, C. Hu, W. R. Tait, Z. Bian, G. Zheng, D. Zhang and L. Sun, Adv. Mater., 2017, 29, 1700828 CrossRef PubMed
.
- Y. Huang, B. B. Stogin, N. Sun, J. Wang, S. Yang and T. S. Wong, Adv. Mater., 2017, 29, 1604641 CrossRef PubMed
.
- T. Manouras and M. Vamvakaki, Polym. Chem., 2017, 8, 74–96 RSC
.
- Z. Jiang, M. L. Tan, M. Taheri, Q. Yan, T. Tsuzuki, M. G. Gardiner, B. Diggle and L. A. Connal, Angew. Chem., Int. Ed., 2020, 59, 7049–7056 CrossRef CAS PubMed
.
- X.-Q. Wang, S. Yang, C.-F. Wang, L. Chen and S. Chen, Macromol. Rapid Commun., 2016, 37, 759–768 CrossRef CAS PubMed
.
- C. S. Brazel and N. A. Peppas, Polymer, 1999, 40, 3383–3398 CrossRef CAS
.
- P. Colombo, R. Bettini, G. Massimo, P. L. Catellani, P. Santi and N. A. Peppas, J. Pharm. Sci., 1994, 84(8), 991–997 CrossRef PubMed
.
- R. Devolder and H. J. Kong, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2012, 4, 351–365 CAS
.
- A. Gargava, C. Arya and S. R. Raghavan, ACS Appl. Mater. Interfaces, 2016, 8, 18430–18438 CrossRef CAS PubMed
.
- M. Saidi, A. Dabbaghi and S. Rahmani, Polym. Bull., 2020, 77, 3989–4010 CrossRef CAS
.
- H. Tanaka, H. Tomita, A. Takasu, T. Hayashi and T. Nishi, Am. Phys. Soc., 1992, 68, 2794–2797 CAS
.
- R. Takahashi, Y. Ikura, D. R. King, T. Nonoyama, T. Nakajima, T. Kurokawa, H. Kuroda, Y. Tonegawa and J. P. Gong, Soft Matter, 2016, 12, 5081–5088 RSC
.
- F. Weiss, S. Cai, Y. Hu, M. K. Kang, R. Huang and Z. Suo, J. Appl. Phys., 2013, 114, 073507 CrossRef
.
- J. Kim, J. Appl. Polym. Sci., 2014, 131(13), 40482 CrossRef
.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 512–520 CrossRef CAS
.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 521–526 CrossRef CAS
.
- J.-F. Louf, N. B. Lu, M. G. O’connell, H. J. Cho and S. S. Datta, Sci. Adv., 2021, 7, 11 Search PubMed
.
- M. Quesada-Pérez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 10536–10547 RSC
.
- F. T. P. Borges, G. Papavasiliou and F. Teymour, Biomacromolecules, 2020, 21, 5104–5118 CrossRef CAS PubMed
.
- F. T. P. Borges, G. Papavasiliou and F. Teymour, Biomacromolecules, 2023, 24, 1585–1603 CrossRef CAS PubMed
.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS
.
- K.-A. Leslie, R. Doane-Solomon, S. Arora, S. J. Curley, C. Szczepanski and M. M. Driscoll, Soft Matter, 2021, 17, 1513–1520 RSC
.
- N. A. Peppas and E. W. Merrill, J. Appl. Polym. Sci., 1977, 21, 1763–1770 CrossRef CAS
.
- M. T. Punter, H. M. Wyss and B. M. Mulder, Phys. Rev. E, 2020, 102, 062607 CrossRef CAS PubMed
.
- M. J. Molina, M. R. Gómez-Antón and I. F. Piérola, J. Phys. Chem. B, 2007, 111, 12066–12074 CrossRef CAS PubMed
.
- Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365–1371 CrossRef CAS
.
- A. Drozdov, A. Papadimitriou, J. Liely and C.-G. Sanporean, Mech. Mater., 2016, 102, 61–73 CrossRef
.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS
.
- S. A. Chester, Soft Matter, 2012, 8, 8223–8233 RSC
.
- A. Plummer, C. Adkins, J.-F. Louf, A. Košmrlj and S. S. Datta, Soft Matter, 2024, 20(7), 1425–1437 RSC
.
- M. Curatolo, P. Nardinocchi, E. Puntel and L. Teresi, J. Appl. Phys., 2017, 122, 145109 CrossRef
.
- J. Guo, A. T. Zehnder, C. Creton and C. Y. Hui, Soft Matter, 2020, 16, 6163–6179 RSC
.
- M. R. Islam, S. Tanveer and C. C. Chen, Chem. Eng. Sci., 2021, 242, 116744 CrossRef CAS
.
- P. Yang, Y. Fang, Y. Yuan, S. Meng, Z. Nan, H. Xu, H. Imtiaz, B. Liu and H. Gao, J. Mech. Phys. Solids, 2021, 151, 104401 CrossRef
.
- Z. Y. Huang, W. Hong and Z. Suo, J. Mech. Phys. Solids, 2005, 53, 2101–2118 CrossRef CAS
.
- J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310–323 RSC
.
- S. Yang, K. Khare and P. C. Lin, Adv. Funct. Mater., 2010, 20, 2550–2564 CrossRef CAS
.
- E. Cerda and L. Mahadevan, Phys. Rev. Lett., 2003, 90, 4 CrossRef PubMed
.
- V. Trujillo, J. Kim and R. C. Hayward, Soft Matter, 2008, 4, 564–569 RSC
.
- J. Ju, K. Sekimoto, L. Cipelletti, C. Creton and T. Narita, Phys. Rev. E, 2022, 105, 034504 CrossRef CAS PubMed
.
- B. Xu and R. C. Hayward, Adv. Mater., 2013, 25, 5555–5559 CrossRef CAS PubMed
.
- S. J. Dupont, R. S. Cates, P. G. Stroot and R. Toomey, Soft Matter, 2010, 6, 3876–3882 RSC
.
- W. Toh, Z. Ding, T. Y. Ng and Z. Liu, J. Appl. Mech., 2015, 82, 061004 CrossRef
.
- M. Guvendiren, S. Yang and J. A. Burdick, Adv. Funct. Mater., 2009, 19, 3038–3045 CrossRef CAS
.
- J. Gu, X. Li, H. Ma, Y. Guan and Y. Zhang, Polymer, 2017, 110, 114–123 CrossRef CAS
.
- M. Guvendiren, J. A. Burdick and S. Yang, Soft Matter, 2010, 6, 2044–2049 RSC
.
- J. Rodríguez-Hernández, Prog. Polym. Sci., 2015, 42, 1–41 CrossRef
.
- H. Scholt, J. Pharm. Sci., 1992, 407, 467–470 Search PubMed
.
- A. Ilseng, V. Prot, B. H. Skallerud and B. T. Stokke, J. Mech. Phys. Solids, 2019, 128, 219–238 CrossRef CAS
.
- L. Lecamp, P. Lebaudy, B. Youssef and C. Bunel, Polymer, 2001, 42, 8541–8547 CrossRef CAS
.
- M. D. Goodner and C. N. Bowman, Chem. Eng. Sci., 2002, 57, 887–900 CrossRef CAS
.
- N. Zalachas, S. Cai, Z. Suo and Y. Lapusta, Int. J. Solids Struct., 2013, 50, 920–927 CrossRef CAS
.
- Y. Kashihara, T. A. Asoh and H. Uyama, Macromol. Rapid Commun., 2022, 43, 2100848 CrossRef CAS PubMed
.
- Z. L. Wu, M. Moshe, J. Greener, H. Therien-Aubin, Z. Nie, E. Sharon and E. Kumacheva, Nat. Commun., 2013, 4, 1586 CrossRef PubMed
.
- J. Kim, J. A. Hanna, R. C. Hayward and C. D. Santangelo, Soft Matter, 2012, 8, 2375–2381 RSC
.
- U. K. D. Silva and Y. Lapitsky, ACS Appl. Mater. Interfaces, 2016, 8, 29015–29024 CrossRef PubMed
.
- A. R. Berens and H. B. Hopfenberg, Diffusion and relaxation in glassy polymer powders: 2. Separation of diffusion and relaxation parameters, 1978.
- K. Zhang, W. Feng and C. Jin, MethodsX, 2020, 7, 100779 CrossRef CAS PubMed
.
- J. Sievers, K. Sperlich, T. Stahnke, C. Kreiner, T. Eickner, H. Martin, R. F. Guthoff, M. Schünemann, S. Bohn and O. Stachs, J. Appl. Polym. Sci., 2021, 138, 50326 CrossRef CAS
.
- F. Ganji, S. V. Farahani, E. Vasheghani-Farahani and S. Vasheghani-Farahani, Theoretical Description of Hydrogel Swelling: A Review, 2010, https://journal.ippi.ac.ir Search PubMed.
- D. M. Gruber, M. S. Ferris and G. Zabow, Polymer, 2023, 281, 126108 CrossRef CAS
.
-
P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed
.
-
T. Sakai, Physics of Polymer Gels, John Wiley and Sons Ltd, 2020 Search PubMed
.
- S. Hirotsu, Phase Transitions, 1994, 47, 183–240 CrossRef CAS
.
-
M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed
.
- J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 143, 131101 CrossRef PubMed
.
-
S. P. Luh, The Cloud Point Composition and Flory-Huggins Interaction Parameters of Polyethylene Glycol and Sodium Lignin Sulfonate in Water-Ethanol Mixtures, Master's thesis, Oregon State University, 1988 Search PubMed
.
- D. Mukherji, C. M. Marques and K. Kremer, J. Phys.: Condens. Matter, 2018, 30, 024002 CrossRef PubMed
.
- Y. Higaki, T. Masuda, M. Nakamura and M. Takahashi, Macromolecules, 2023, 56, 6208–6216 CrossRef CAS
.
- L. Steinbeck, H. J. M. Wolff, M. Middeldorf, J. Linkhorst and M. Wessling, Macromol. Rapid Commun., 2024, 45, 2300680 CrossRef CAS PubMed
.
- P. Schatzberg, J. Phys. Chem., 1967, 4569–4570 CrossRef CAS
.
- Z. Song, Y. Huang, W. L. Xu, L. Wang, Y. Bao, S. Li and M. Yu, Sci. Rep., 2015, 5, 13981 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00762j |
| This journal is © The Royal Society of Chemistry 2024 |