Open Access Article
Open Access ArticleFlow and clogging of capillary droplets
Yuxuan
Cheng
 *a,
Benjamin F.
Lonial
*a,
Benjamin F.
Lonial
 b,
Shivnag
Sista
a,
David J.
Meer
b,
Anisa
Hofert
b,
Eric R.
Weeks
b,
Shivnag
Sista
a,
David J.
Meer
b,
Anisa
Hofert
b,
Eric R.
Weeks
 b,
Mark D.
Shattuck
b,
Mark D.
Shattuck
 c and
Corey S.
O'Hern
c and
Corey S.
O'Hern
 adef
adef
aDepartment of Physics, Yale University, New Haven, Connecticut 06520, USA. E-mail: yuxuan.cheng@yale.edu
bDepartment of Physics, Emory University, Atlanta, GA 30322, USA
cBenjamin Levich Institute and Physics Department, The City College of New York, New York, New York 10031, USA
dDepartment of Mechanical Engineering and Materials Science, Yale University, New Haven, Connecticut 06520, USA
eProgram in Computational Biology and Bioinformatics, Yale University, New Haven, Connecticut 06520, USA
fDepartment of Applied Physics, Yale University, New Haven, Connecticut 06520, USA. E-mail: Corey.ohern@yale.edu
First published on 12th September 2024
Abstract
Capillary droplets form due to surface tension when two immiscible fluids are mixed. We describe the motion of gravity-driven capillary droplets flowing through narrow constrictions and obstacle arrays in both simulations and experiments. Our new capillary deformable particle model recapitulates the shape and velocity of single oil droplets in water as they pass through narrow constrictions in microfluidic chambers. Using this experimentally validated model, we simulate the flow and clogging of single capillary droplets in narrow channels and obstacle arrays and find several important results. First, the capillary droplet speed profile is nonmonotonic as the droplet exits the narrow orifice, and we can tune the droplet properties so that the speed overshoots the terminal speed far from the constriction. Second, in obstacle arrays, we find that extremely deformable droplets can wrap around obstacles, which leads to decreased average droplet speed in the continuous flow regime and increased probability for clogging in the regime where permanent clogs form. Third, the wrapping mechanism causes the clogging probability in obstacle arrays to become nonmonotonic with surface tension Γ. At large Γ, the droplets are nearly rigid and the clogging probability is large since the droplets can not squeeze through the gaps between obstacles. With decreasing Γ, the clogging probability decreases as the droplets become more deformable. However, in the small-Γ limit, the clogging probability increases since the droplets are extremely deformable and wrap around the obstacles. The results from these studies are important for developing a predictive understanding of capillary droplet flows through complex and confined geometries.
1 Introduction
Capillary droplets, which consist of immiscible liquid droplets dispersed in another continuous phase, are ubiquitous in food science,1,2 the pharmaceutical industry,3,4 petroleum products,5,6 and pollution remediation.7 Being able to control how capillary droplets flow and interact with their surroundings is crucial for enhancing food emulsion stability, optimizing drug production and delivery, and improving oil recovery rates, while minimizing environmental risks associated with oil exploration. For example, the flow rate of capillary droplets can be tuned by varying the channel width and by designing obstacle arrays in microfluidic chambers,8–13 cell sorting instruments,14–16 and cell encapsulation devices.17–19 However, we do not yet have a fundamental understanding of the dynamics of capillary droplets flowing through complex, confined geometries as a function of the droplet properties.Flows of hard, frictional grains through narrow constrictions, such as hoppers, silos, and obstacle arrays, display complex spatiotemporal dynamics.20–22 Over 50 years ago, Beverloo and co-workers23 carried out experimental studies of hopper flows for a wide range of dry granular materials and proposed an empirical form for the flow rate Q (in the continuous flow rate regime) versus the orifice width w: Q ∼ (w/σavg − k)β, where σavg is the mean grain size, the flow arrests for w/σavg ≲ k, k ≳ 1.5 for rigid grains, and β is the power-law scaling exponent that can be tuned by varying the ratio of the dissipation from particle–particle contacts and from the background fluid.24 In addition, researchers have found that placing an obstacle ∼3σavg above the orifice can reduce clogging in silo flows of hard, frictional grains.25–31 Experimental and computational studies have also shown that the permeability of an obstacle array to granular flow can be tuned by varying the density, shape, and size of the obstacles.32–35
In contrast, for deformable particles, it is possible to obtain Q > 0 with no clogging even for w/σavg < 1. Unlike hard grains, deformable particles can change their shapes to squeeze through narrow constrictions that are much smaller than their undeformed diameters. However, there have been few studies of flows of deformable particles through narrow constrictions. Many experimental studies have instead focused on hydrogel particle flows in hoppers and silos with w/σavg ∼ 2–3, which do not give rise to large particle deformation. For example, recent studies have found that hydrogel particles with smaller elastic moduli are less likely to clog36–38 and possess flow rates that are much faster than those for hard particles, such as glass beads.39 These prior results for hydrogel particles do not address how particle flow rates are affected by large particle deformation. Thus, an important open question is: does significant particle shape change (i.e. by more than 50%) still enhance flow through narrow constrictions and other confined geometries?
The interplay between particle deformability and the geometry of obstacle arrays can give rise to a new physical mechanism, particle wrapping, which can strongly influence the dynamics of capillary droplets as they flow through obstacle arrays. When colliding with an obstacle, the highly deformable droplet can wrap around the obstacle with both ends of the droplet elongating in the flow direction until the energy penalty from the droplet surface tension matches the work done by the fluid driving force. At this point, both ends of the droplet become stationary, and then one end of the droplet moves in the opposite direction of the driving force, causing the particle to unwrap. Particle wrapping can even lead to single-particle clogging in obstacle arrays. In this case, the droplet is in force balance after wrapping around an obstacle, where the fluid forces on the droplet are supported by contact forces on the droplet from neighboring obstacles. Thus, particle wrapping can lead to much longer transit times through obstacle arrays compared to those for hard particles with the same undeformed diameter. Despite its importance, the particle wrapping mechanism has not been studied in detail in droplet flows through obstacle arrays.
A key factor that contributes to the knowledge gap concerning flows of highly deformable particles in confined geometries is the lack of an accurate and efficient computational model for these flows. At submicron length scales, e.g. within microfluidic devices, inertial forces are typically much smaller than capillary forces generated by particle surface tension, which strongly influences the behavior of multi-phase fluid flows. Computational models for multi-phase fluid flows include grid-based Eulerian techniques, such as the volume-of-fluid40 and Lattice Boltzmann methods,41,42 and particle-based Lagrangian techniques, such as the smoothed particle hydrodynamics method.43–45 Grid-based methods determine the amount of fluid and gas in each cell and calculate the surface energy by reconstructing the fluid-gas interface. However, this method does not strictly conserve mass, and the surface energy can depend on the interface reconstruction algorithm.40 For particle-based methods, the multi-phase system is discretized into “particles” with each particle assigned as gas or liquid with a specified mass. Therefore, interface tracking is not needed, and the multi-phase fluid behavior is governed by particle–particle interactions. However, it is challenging to determine a priori the particle–particle interactions that yield the correct contact angles at the multi-phase interfaces.43,46 Particle-based methods are also computationally demanding since they simulate the droplet interiors in addition to the interfaces. As a result, most particle-based simulations of multi-phase fluids are limited to short time scales and small systems.
In this article, we describe combined experimental and computational studies that enable the development of new efficient computational methodologies and provide new insights for flows of deformable particles through narrow constrictions and obstacle arrays. In the experimental studies, we measure the speed and shape of capillary droplets as they flow through narrow openings as a function of the orifice width and gravitational driving force. For the computational studies, we develop a new deformable particle (DP) model47–49 with surface tension (in two dimensions, 2D) that can be implemented to efficiently model thousands of capillary droplets flowing through complex, confined geometries. Varying surface tension in the experiments by more than a factor of 2 is challenging, and thus we carry out simulations of extremely deformable particles with surface tensions that vary by more than a factor of 103, which accentuates the particle wrapping mechanism. We first validate the DP simulations by comparing the droplet shape dynamics in experiments and simulations for a single droplet flowing through narrow constrictions. We then investigate the important physical parameters that control the flow rate and clogging propensity of single deformable particles moving through obstacle arrays using the experimentally validated DP simulations. Through this article, we seek to encourage future experimental studies that will investigate droplet squeezing and wrapping behavior of capillary droplets flowing through obstacle arrays.
We find several important results. First, when a capillary droplet is pushed by gravity (or buoyancy) through a narrow constriction, its speed initially decreases as it enters the orifice and deforms. After it reaches a minimum speed, the droplet begins to speed up as it exits the orifice. However, as the speed increases, it can overshoot the droplet's terminal speed. We find that the amplitude of the overshoot decreases with increasing gravitational driving force (relative to the capillary forces). Second, we show that highly deformable droplets flow more slowly in obstacle arrays compared to droplets with larger surface tension, due to the wrapping mechanism. Thus, for capillary droplets flowing through obstacle arrays, the clogging probability, as characterized by the average distance λ traveled by a droplet before it clogs, is non-monotonic as a function of surface tension. For small values of surface tension, λ first increases with increasing surface tension, reaches a peak that depends on the obstacle spacing, and then decreases with continued increases in surface tension. In contrast, models of soft particles that do not model explicit changes in particle shape cannot capture particle wrapping,50,51 and thus cannot accurately model flows of capillary droplets moving through obstacle arrays in the low surface tension limit.
The remainder of the article is organized as follows. In Section 2, we describe the computational methods including descriptions of the deformable particle model47–49 for droplets and the soft (semi-rigid) particle model50,51 and the equations of motion and boundary conditions for discrete element method (DEM) simulations of droplet flows through narrow channels and obstacle arrays. In Section 3, we introduce the experimental setup and method to generate capillary droplets and flows. In Section 4, we describe the main results from the combined experimental and simulation studies. We first characterize the droplet speed and shape dynamics as a function of the distance h from the orifice for both oil-in-water experiments and DPM simulations of droplet flows through narrow channels. We calibrate the results for the droplet speed and shape from the DP simulations to those from the experiments. Using the experimentally validated DP simulations, we quantify the nonmonotonic behavior in the droplet speed profile and the clogging probability of single droplets flowing through obstacle arrays as a function of the droplet surface tension. In Section 5, we provide conclusions and propose future research directions, including studies of multi-droplet flows through obstacle arrays with droplet breakup and coalescence that can predict the steady-state droplet size distribution. We also include five Appendices to supplement the discussion in the main text. In Appendix A, we present experimental data for the near-wall droplet speed profile. In Appendix B, we investigate how the results of the DP simulations depend on the number of vertices Nv in each deformable particle and the perimeter elasticity Kl. In Appendix C, we provide additional details concerning the definition of a clogging event and the clogging probability for droplets flowing through obstacle arrays. In Appendix D, we identify the surface tension regime for which the simulations can achieve continuous flows in obstacle arrays. In Appendix E, we quantify the dependence of the steady-state speed of the droplets on the near-wall drag coefficient.
2 Simulation methods
In this section, we describe the methods for simulating 2D gravity-driven flows of a single droplet through narrow channels and obstacle arrays. We first illustrate the geometry of the narrow channels and obstacle arrays. We then introduce two models for describing the droplet shape and interactions with the walls: (1) the deformable particle (DP) model that treats each droplet as a polygon with Nv vertices, employs a shape-energy function to penalize changes in droplet area and changes in the separations between vertices, and enforces excluded volume interactions using pairwise purely repulsive forces between the droplet vertices and walls and (2) the soft particle (SP) model, which tracks the centers of mass of the droplets and enforces excluded volume interactions using pairwise purely repulsive forces that increase with the overlap between a droplet and the walls. For both models, we define the forces on the droplets that arise from the shape-energy function, droplet-wall interactions, and dissipative forces from the background fluid, and provide the equations of motion for the droplet trajectories. Finally, we describe the method for initializing the droplet positions and velocities in narrow channels and obstacle arrays.2.1 Geometry for flows through narrow channels and obstacle arrays
The narrow channels in the 2D simulations are constructed using two infinitely long wedges, one on the top and one on the bottom that form an orifice between them with width w < σ, where σ is the diameter of the undeformed droplet [see Fig. 1(a)]. The obstacle arrays are located within L × L simulation boxes with periodic boundary conditions and L = 500σ. The circular obstacles with diameter σob are placed inside the simulation box using a Poisson sampling procedure with separations w > wob [see Fig. 1(b)].2.2 Deformable particle model
When droplets squeeze through narrow constrictions, they can experience dramatic shape changes. To efficiently describe large changes in shape that occur during gravity-driven droplet flows, we employ the recently developed deformable particle (DP) model.47–49 In 2D, the droplets are modeled as deformable polygons with Nv vertices. The shape-energy function Us for each deformable particle includes three terms: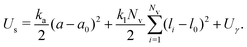 | (1) |
 , where
, where ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 1 for a circle. The third term gives the energy arising from line tension:
= 1 for a circle. The third term gives the energy arising from line tension:| Uγ = γsolso + γsw(L − lso) + γowlow, | (2) |
We assume that there are purely repulsive forces between the droplets and hopper walls or obstacles, which are modeled using the following pairwise interaction potential:
 | (3) |
The total potential energy U for the droplet is the sum of the shape-energy function Us, gravitational potential energy Ug, and particle-wall interactions Uw,
| U = Us + Ug + Uw, | (4) |
We also consider dissipative forces from the background fluid acting on each droplet vertex i:
 | (5) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i is the velocity of vertex i and ζi is the viscous drag coefficient:
i is the velocity of vertex i and ζi is the viscous drag coefficient: | (6) |
Thus, for the DP model, the equations of motion for the position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i of droplet vertex i is
i of droplet vertex i is
 | (7) |
From eqn (1)–(3), we introduce the dimensionless line tension Γ = γ/(gρσ2) and three additional dimensionless energy scales for the DP model in a gravitational field in 2D: the dimensionless area compressibility Ka = kaσ/(gρ), the dimensionless perimeter elasticity Kl = kl/(gρσ), and the dimensionless wall interaction energy Ew = εw/(gρσ3). In these studies, we vary Γ in the range 10−2 < Γ < 10. We set Ka > 104 so that the fluctuations in the droplet areas are small, Kl/Γ < 10−3 so that the line tension energy dominates the perimeter elasticity (see Appendix B), and Ew = 104 to minimize the vertex-wall (and vertex-obstacle) overlaps. The time t is measured in units of  and the equations of motion are integrated using a modified velocity-Verlet algorithm with time step Δt = 10−3t0.
and the equations of motion are integrated using a modified velocity-Verlet algorithm with time step Δt = 10−3t0.
2.3 Soft particle model
We will also describe gravity-driven single-droplet flows through obstacle arrays using the soft particle (SP) model, and compare the results from the SP model to those of the DP model to better understand the influence of droplet shape change on the flows. In general, there are three contributions to the total potential energy: (1) the shape-energy function Us, (2) the gravitational potential energy Ug, and (3) the droplet-obstacle interaction energy Uw. For the SP model, Us = 0 and excluded volume interactions between the droplet and obstacles are generated by allowing overlaps between them.36,37,50,51 The pairwise droplet-obstacle interaction energy is | (8) |
| U = Ug + Uw. | (9) |
For the SP model, we consider following form for the viscous drag forces on droplets moving in a background viscous fluid:
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ζ = −ζsp ζ = −ζsp![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) , , | (10) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) is the velocity of the SP droplet. We note that, unlike eqn (6) for the DP model, we set ζsp = b∞. In contrast to the DP model, the SP model considers droplet deformation by allowing overlaps between the droplets and obstacles, which makes it difficult to describe distance-dependent viscous drag. For the SP model, the equations of motion for the droplet position
is the velocity of the SP droplet. We note that, unlike eqn (6) for the DP model, we set ζsp = b∞. In contrast to the DP model, the SP model considers droplet deformation by allowing overlaps between the droplets and obstacles, which makes it difficult to describe distance-dependent viscous drag. For the SP model, the equations of motion for the droplet position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i are
i are | (11) |
2.4 Simulation initialization
For the DP model, we initialize the droplets in narrow channels and obstacle arrays in the shape of regular polygons with edge lengths equal to their equilibrium values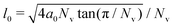 . For droplet flows in narrow channels, we initially place the droplet far from the orifice, typically at h = − 10σ, so that the droplet reaches terminal speed before touching the channel walls. For droplets in obstacle arrays, we initially place the droplet in the center of the simulation box. However, this placement typically causes overlaps between the droplet and nearby obstacles. Therefore, after the initial placement of the droplet, we carry out energy minimization (in the absence of gravity) to eliminate overlaps between the droplet and obstacles. We then integrate the equations of motion with gravity and the droplet begins to flow through the obstacle array until it reaches steady state or clogs (see Section 4.2).
. For droplet flows in narrow channels, we initially place the droplet far from the orifice, typically at h = − 10σ, so that the droplet reaches terminal speed before touching the channel walls. For droplets in obstacle arrays, we initially place the droplet in the center of the simulation box. However, this placement typically causes overlaps between the droplet and nearby obstacles. Therefore, after the initial placement of the droplet, we carry out energy minimization (in the absence of gravity) to eliminate overlaps between the droplet and obstacles. We then integrate the equations of motion with gravity and the droplet begins to flow through the obstacle array until it reaches steady state or clogs (see Section 4.2).
3 Experimental methods
Below, we will compare the SP and DP simulation results for gravity-driven droplet flows in narrow channels and obstacle arrays to experimental studies of quasi-2D gravity-driven flows of octane oil droplets in water. In this section, we describe the details of our experimental studies. Note that quantitative experimental studies were performed on flows of capillary droplets through narrow orifices. In contrast, only qualitative experimental studies of droplets flowing through obstacle arrays were performed to illustrate the droplet squeezing and wrapping mechanisms. The experimental studies of droplets in obstacle arrays were only featured in the images in Fig. 5(a) and (c).For the experiments studying droplet flows through narrow constrictions, we construct the sample chambers using laser-cut plastic film with thickness 400 μm, sandwiched between two glass microscope slides. The film is attached to the slides using Norland Optical Adhesive.24 The film is cut into two triangular shapes and placed such that they form a narrow orifice, as shown in Fig. 1(a). The slope of the walls coming into the orifice is 45°. The diameters of the droplets are tuned so that they are larger than the chamber thickness to ensure that each droplet is quasi-two-dimensional when confined by the microscope slides.
We also conduct qualitative experiments of droplets flowing through obstacle arrays to illustrate the physical mechanisms of droplet squeezing and wrapping. For these qualitative experiments, the obstacles are produced by placing small drops of UV adhesive between the slides, which then cure into solid cylinders spanning the sample chamber thickness. In addition, we do not observe any influence of gravity in how the obstacles cure. The chamber is sufficiently thin such that surface tension determines the obstacle shapes. The maximum diameter at the obstacle center is no more than 10% larger than the diameter at the glass walls.
Our experiments focus on individual oil droplets passing through the microfluidic chamber, and thus we do not need to produce a large number of droplets. We form single oil droplets by direct injection of the oil into the chamber via a hand-held syringe. The droplet diameter is subsequently measured in situ. Different experiments typically use different chambers with their own oil droplet, allowing us to vary the orifice width w and droplet diameter σ. We use octane with density ρo = 0.703 g mL−1 suspended in water with density ρw = 0.997 g mL−1. Despite the absence of other oil droplets, we find that it is still necessary to use a 0.5% Tween 20 nonionic detergent solution to prevent sticking of the oil droplets to the microscope slide surfaces.
We image the droplets using a 1.6 × lens (0.05 Numerical Aperture) attached to a Leica DM4500 B inverted microscope. Movies are acquired by attaching a 0.35 × C-mount to a ThorLabs DCC1545M camera, and recording at a frame rate commensurate with the droplet speed. The microscope is tilted slightly from the horizontal to cause gravitationally driven motion of the droplet. In particular, the tilt angle of the microscope is changed by placing a spacer underneath the front edge of the microscope, and the angle is measured relative to the ground via a Wixley digital angle gauge. As the droplet density is less than water, the droplets rise in the sample chamber due to the buoyant force. In all images presented in this article, the direction of droplet motion is in the direction of the arrow labeled by f.
The droplet motion is affected by viscous drag from the water phase (viscosity ηw ≈ 1 mPa s) and viscous drag between the oil and glass plates (ηo ≈ 100 mPa s). The droplets try to remain round due to surface tension (γow ≈ 10 mJ m−2, as measured by the “Dropometer” from Droplet Labs). However, under gravity, the droplets deform when pressed against the sample chamber walls. We do not observe droplet break-up in these experiments.
We incorporate quasi-2D effects in the simulations by defining an effective 2D surface tension based on the 3D surface tension γexp from the experiments. The droplet surface energy can be split into two parts, E = E′ + Eoop, where E′ = γexp(atop + abottom) is the surface energy of the top and bottom surfaces of the droplet, and Eoop = γexpaoop is the surface energy of the out-of-plane surface of the droplet with area aoop as shown in Fig. 1(d). In the quasi-2D limit, the droplet thickness satisfies H ≪ P, where P is the perimeter of the droplet from the top view and aoop ≈ PH. Note that atop + abottom is roughly constant due to fluid incompressibility. Thus, when the droplet deforms, the change in surface energy δE = δE′ + δEoop ≈ γexpδaoop ≈ γexpHδP, and the effective 2D surface tension is γ = γexpH. We nondimensionalize γ by the buoyancy force such that the dimensionless surface tension is defined as:
 | (12) |
4 Results
In this section, we describe the results from the numerical simulations of gravitationally-driven droplet flows through narrow channels and obstacle arrays. We first present a method to calibrate the DP simulations to experimental results for droplet flows through narrow channels. We then show results for the droplet speed in the direction of the driving νg as a function of distance from the orifice. We find that the droplet speed profile is nonmonotonic and can even possess an overshoot, such that the droplet speed exceeds the terminal speed νt as it exits the orifice. Using the DP and SP models, we also investigate gravity-driven droplet flows through obstacle arrays. For the DP simulations, we find non-monotonic behavior for the clogging probability as a function of the dimensionless line tension Γ. We show that droplets can clog at small Γ when they are highly deformable and can wrap around the obstacles. We emphasize that the SP model does not include the wrapping mechanism since wrapping requires significant changes in the droplet shape. As shown in many previous studies of flows of nearly hard particles in confined geometries, the droplets can also clog when they are nearly rigid at large Γ. At intermediate Γ, we find a regime of continuous droplet flows through the obstacle arrays. We observe qualitatively similar results over a wide range of obstacle densities.4.1 Calibration of DP model using experiments of a single droplet flowing through narrow channels
We first carried out both experiments and DP simulations of a single droplet flowing through narrow channels under the influence of gravity. To enable a comparison between the experimental and simulation results, we define the root-mean-square deviations in the droplet shape parameter Δ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and speed Δν:
and speed Δν: | (13) |
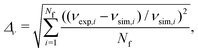 | (14) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) exp,i is the droplet shape parameter in the ith frame in the experimental video, and
exp,i is the droplet shape parameter in the ith frame in the experimental video, and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) sim,i is the droplet shape parameter in the DP simulations when the droplet center of mass is at the same location as it is in the experiments at frame i. Similarly, νexp,i and νsim,i are the droplet speed in the direction of gravity at the ith frame in the experiments and simulations. The summations in eqn (13) and (14) are over all Nf frames in the experimental videos. Despite using a small time step in the DP simulations, we might not find a frame in the simulations where the droplet has the same position as that in the experiments. In this case, we use linear interpolation between frames to generate
sim,i is the droplet shape parameter in the DP simulations when the droplet center of mass is at the same location as it is in the experiments at frame i. Similarly, νexp,i and νsim,i are the droplet speed in the direction of gravity at the ith frame in the experiments and simulations. The summations in eqn (13) and (14) are over all Nf frames in the experimental videos. Despite using a small time step in the DP simulations, we might not find a frame in the simulations where the droplet has the same position as that in the experiments. In this case, we use linear interpolation between frames to generate ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) sim,i and νsim,i.
sim,i and νsim,i.
We seek to minimize Δ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and Δν by tuning the dimensionless line tension Γ and near-wall drag coefficient b0/b∞ in the DP simulations. In practice, Δ
and Δν by tuning the dimensionless line tension Γ and near-wall drag coefficient b0/b∞ in the DP simulations. In practice, Δ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is more than an order of magnitude smaller than Δν, and thus we only minimize Δν over Γ and b0/b∞. b∞ is determined by matching the droplet's terminal speed far from wall in the DP simulations and experiments. In particular, we equate the dimensionless terminal speed,
is more than an order of magnitude smaller than Δν, and thus we only minimize Δν over Γ and b0/b∞. b∞ is determined by matching the droplet's terminal speed far from wall in the DP simulations and experiments. In particular, we equate the dimensionless terminal speed,
 | (15) |
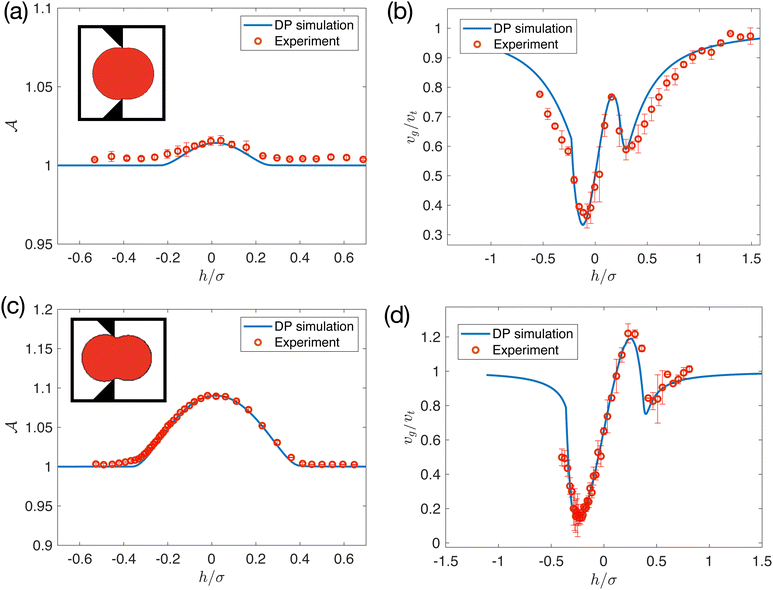
In Fig. 2(a) and (b), we show the droplet shapes as a function of distance h from the orifice (with width w = 0.4σ) from trajectories of gravity-driven droplet flows through narrow channels in experiments and DP simulations using the values Γ* = 0.16 ± 0.01 and b0*/b∞ = 0.064 ± 0.003 that minimize Δν. The error bars for Γ* and b0* are the standard deviations in Γ* and b0* from fitting the DP simulations to at least five independent experimental trials. For the experiments in Fig. 2(a), the terminal velocity νt ≈ 7 mm s−1 far from the wall, undeformed droplet diameter σ ≈ 3.5 mm, and tilt angle θ ≈ 28°. Thus, for the data in Fig. 2(a), we estimate the dimensionless surface tension for the droplets to be Γexp ≈ 0.57 and the dimensionless terminal velocity to be Vt ≈ 0.08. In Fig. 2(c) and (d), we plot ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and νg as a function of h/σ for both the calibrated DP simulations and experiments for the data presented in Fig. 2(a) and (b). We find that the droplet shapes and speed profiles for the DP simulations and experiments are similar over the full range of h, with Δ
and νg as a function of h/σ for both the calibrated DP simulations and experiments for the data presented in Fig. 2(a) and (b). We find that the droplet shapes and speed profiles for the DP simulations and experiments are similar over the full range of h, with Δ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≈ 0.01 and Δν ≈ 0.09. Note that despite the simplicity of the 2D DP simulations, Γ* is comparable to Γexp (with Γ*/Γexp ≈ 0.3), emphasizing the predictive power of 2D DP simulations. We also note that, in general the shape parameter is not symmetric about h = 0. For example, in Fig. 2(c) the shape parameter at h ≈ 0.5σ is
≈ 0.01 and Δν ≈ 0.09. Note that despite the simplicity of the 2D DP simulations, Γ* is comparable to Γexp (with Γ*/Γexp ≈ 0.3), emphasizing the predictive power of 2D DP simulations. We also note that, in general the shape parameter is not symmetric about h = 0. For example, in Fig. 2(c) the shape parameter at h ≈ 0.5σ is ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≈ 1.07, whereas at h ≈ − 0.5σ, it is
≈ 1.07, whereas at h ≈ − 0.5σ, it is ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≈ 1.00.
≈ 1.00.
In Fig. 3, we compare the results for the calibrated DP simulations and experiments of gravity-driven droplet flows in narrow channels for two additional experiments with different droplet sizes, orifice widths and tilt angles. In Fig. 3(a) and (b), we show ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and νgversus h/σ for w/σ = 0.90, θ ≈ 8.5°, σ ≈ 1.98 mm, νt ≈ 0.97 mm s−1, Vt ≈ 0.028, and Γexp ≈ 5.80. In Fig. 3(c) and (d), we show
and νgversus h/σ for w/σ = 0.90, θ ≈ 8.5°, σ ≈ 1.98 mm, νt ≈ 0.97 mm s−1, Vt ≈ 0.028, and Γexp ≈ 5.80. In Fig. 3(c) and (d), we show ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and νgversus h/σ for w/σ = 0.70, θ ≈ 5.0°, σ ≈ 3.30 mm, νt ≈ 1.1 mm s−1, Vt ≈ 0.032, and Γexp ≈ 3.47. In the DP simulations we can obtain the dimensionless line tension Γ** for droplets in the two additional experiments that minimizes Δν for the experimental data in Fig. 3 using Γ**/Γ* = (σ*)2sinθ*/((σ**)2sinθ**), where θ*, σ* and Γ* are the tilt angle, undeformed droplet diameter and fitted dimensionless line tension for the data in Fig. 2, and θ**, σ** are the tilt angle and undeformed droplet diameter for the two additional experiments in Fig. 3. We find Γ** = 1.7 ± 0.1 for θ** = 8.5° and σ** ≈ 1.98 mm (with Γexp ≈ 5.8) and Γ** = 1.08 ± 0.09 for θ** = 5.0° and σ** = 3.30 mm (with Γexp ≈ 3.47). For all tilt angles and droplet diameters studied, we find that the ratio of the dimensionless line tension that minimizes Δν to the dimensionless surface tension in experiments satisfies Γ**/Γexp ≈ 0.3, which likely stems from the fact that we compare values of the dimensionless line tension in 2D to values of the dimensionless surface tension in 3D. We find that the near-wall drag coefficients that minimize Δν do not depend strongly on droplet diameter and tilt angle, b0*/b∞ ≈ 0.06–0.2.
and νgversus h/σ for w/σ = 0.70, θ ≈ 5.0°, σ ≈ 3.30 mm, νt ≈ 1.1 mm s−1, Vt ≈ 0.032, and Γexp ≈ 3.47. In the DP simulations we can obtain the dimensionless line tension Γ** for droplets in the two additional experiments that minimizes Δν for the experimental data in Fig. 3 using Γ**/Γ* = (σ*)2sinθ*/((σ**)2sinθ**), where θ*, σ* and Γ* are the tilt angle, undeformed droplet diameter and fitted dimensionless line tension for the data in Fig. 2, and θ**, σ** are the tilt angle and undeformed droplet diameter for the two additional experiments in Fig. 3. We find Γ** = 1.7 ± 0.1 for θ** = 8.5° and σ** ≈ 1.98 mm (with Γexp ≈ 5.8) and Γ** = 1.08 ± 0.09 for θ** = 5.0° and σ** = 3.30 mm (with Γexp ≈ 3.47). For all tilt angles and droplet diameters studied, we find that the ratio of the dimensionless line tension that minimizes Δν to the dimensionless surface tension in experiments satisfies Γ**/Γexp ≈ 0.3, which likely stems from the fact that we compare values of the dimensionless line tension in 2D to values of the dimensionless surface tension in 3D. We find that the near-wall drag coefficients that minimize Δν do not depend strongly on droplet diameter and tilt angle, b0*/b∞ ≈ 0.06–0.2.
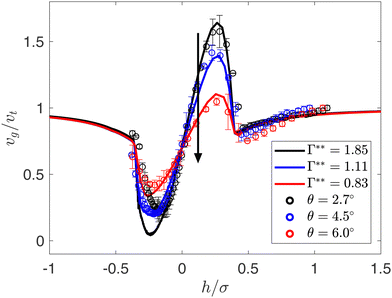
A key feature of the droplet speed profile νg is that it can possess nonmonotonic behavior and νg can even exceed the terminal speed νt as the droplet exits the orifice. For example, in Fig. 3(d), νg overshoots νt near h/σ ≈ 0.3. Similar phenomena have been observed in pressure-driven droplet flows in obstacle arrays, where the pressure drop across the orifice changes from positive to negative, which indicates that the droplet speed exceeds the background fluid velocity.42 To further investigate the effects of the gravitational driving on the nonmonotonic speed profile, we show νgversus h/σ for fixed w/σ = 0.7 for several values of the tilt angle: θ = 2.7°, 4.5°, and 6° in Fig. 4. The nonmonotonic droplet speed profile can be understood by analyzing energy transfer while the droplet moves through the narrow channel. The droplet first impacts the chamber wall at h/σ < 0 and deforms while squeezing through narrow orifice. During this process, the kinetic and gravitational energy of the droplet transfers into surface energy of the deformed droplet, which corresponds to the first speed minimum near h/σ ≈ −0.25. The large surface energy is transferred into kinetic energy as the droplet continues to move through the orifice, which can give rise to speeds that exceed the terminal velocity near h/σ ≈ 0.3. However, the excess kinetic energy is quickly dissipated by viscous drag, and νg decreases again, reaching a second local minimum near h/σ ≈ 0.5. Finally, the speed increases again, approaching νt as the droplet moves far from the orifice since the drag coefficient ζ decreases toward b∞ for h/σ ≫ 1 (see eqn (6)).
As shown in Fig. 4, the amplitude of the overshoot in the droplet speed increases with decreasing g and θ. The excess shape energy ΔUs gained during droplet deformation is largely determined by the width of the orifice, w/σ. In contrast, the droplet kinetic energy at the terminal speed Et decreases with increasing g. Thus, for h > 0, the excess surface energy ΔUs transferred into kinetic energy Ek ∼ ΔUs, generates enhanced droplet speed overshoots  as g or θ decreases. These results are consistent with the intuition that, the dimensionless surface tension Γexp in eqn (12) is inversely proportional to the gravitational acceleration g, which in turn is proportional to the tilt angle. Thus, Γexp is inversely proportional to the tilt angle. As a result, increasing the tilt angle, decreases Γexp, which in turn decreases the optimal fit Γ** and reduces the overshoot.
as g or θ decreases. These results are consistent with the intuition that, the dimensionless surface tension Γexp in eqn (12) is inversely proportional to the gravitational acceleration g, which in turn is proportional to the tilt angle. Thus, Γexp is inversely proportional to the tilt angle. As a result, increasing the tilt angle, decreases Γexp, which in turn decreases the optimal fit Γ** and reduces the overshoot.
4.2 Clogging of single droplets in obstacle arrays
Droplet shape dynamics plays an important role in determining the motion and clogging of droplets flowing through obstacle arrays. For example, in Fig. 5(a) and (c), we show that droplets can wrap around obstacles and squeeze through narrow constrictions formed by adjacent obstacles. These shape change mechanisms do not occur for nearly rigid particles and can be accurately modeled using the calibrated DP simulations with surface tension described in Section 4.1, as shown in Fig. 5(b) and (d).For minimum obstacle separation wob/σ ≫ 1, single droplets flow continuously through obstacle arrays without clogging. However, when wob/σ < 1, single droplets can become permanently clogged within the obstacle array. We assume that as the droplet moves through the obstacle array, it successively interacts with each obstacle, with each interaction contributing to the probability of clogging. This scenario suggests that particle clogging is a Poisson process, confirmed by numerous prior studies.52–54 This means that the droplet can move a distance r > 0 without clogging with cumulative probability distribution function,
| P(r) = e−r/λ, | (16) |
Several previous studies of clogging of soft particles in hoppers have shown that softer particles (i.e. with smaller elastic moduli) are less likely to form clogs,36–38 and thus would possess larger values of the clogging decay length λ. Does this result also hold for the highly deformable droplets considered in this study? To address this question, we carry out numerical simulations of single droplets (using the SP and DP models) moving through obstacle arrays in the clogging regime with wob/σ ≤ 0.5. We measure λ as a function of Γ (for the DP model), Kw (for the SP model), and the deformability δs/σ, given by the fraction of the droplet diameter that deforms under its own weight. We find that the wrapping mechanism plays an important role in determining the clogging statistics for single droplets moving through obstacle arrays. In particular, clogs can form when droplets wrap around an obstacle as shown in Fig. 6(a). The droplet is mainly supported by the obstacle around which the droplet has wrapped, with additional stabilizing forces from adjacent obstacles. For less deformable particles, clogs form when droplets cannot squeeze through narrow channels between adjacent obstacles as shown in Fig. 6(b).
In Fig. 6(c), we plot λ/σ as a function of the line tension Γ from DP model simulations of single droplets moving through obstacle arrays for σob/σ = 0.3 and wob/σ = 0.2, 0.3, 0.4, and 0.5. We find that λ/σ versus Γ is non-monotonic. At large Γ, where droplet shape deformation is small, decreasing Γ increases λ, which implies that softer particles are less likely to clog. However, at small Γ, where droplet shape deformation is large, we find the opposite behavior. In this regime, decreasing Γ decreases λ, which implies that softer particles are more likely to clog. The nonmonotonic behavior of λ(Γ) is caused by the two different mechanisms for clogging (wrapping versus squeezing) as shown in Fig. 6(a) and (b). At large Γ, droplets become clogged when squeezing between obstacles. It is easier for nearly rigid droplets to squeeze through the gaps between obstacles as Γ decreases, which gives rise to decreased clogging probability and increased λ. In contrast, at small Γ, highly deformable droplets can easily squeeze through narrow gaps between obstacles, but they can wrap around an obstacle and clog. Thus, increased deformability enhances the wrapping mechanism, increasing the clogging probability, and decreasing λ. In Fig. 6(c), we also show that λ increases with wob as expected, since wider gaps between obstacles reduce clogging. We also find that the transition from wrapping to squeezing behavior shifts to larger values of Γ as wob/σ increases. This shift occurs because wrapping is primarily a single-obstacle phenomenon. Larger separation between obstacles makes wrapping more prevalent, while narrower gaps between obstacles promotes squeezing behavior.
We also carry out SP simulations of single droplets moving through the same obstacle arrays in Fig. 6 to understand the effects of droplet stiffness versus deformability on clogging. In Fig. 7(a), we plot λ/σ versus the dimensionless stiffness Ew for the SP model; λ/σ decreases monotonically with increasing Ew over the full range of Ew, and as expected, λ/σ increases with wobs/σ. These results emphasize that the SP model can only generate clogs via the squeezing mechanism, not the wrapping mechanism.
To directly compare the results for single droplet motion through obstacle arrays using the SP and DP models, we consider the droplet deformation δs caused by its own weight36 (see Fig. 7(b)). To calculate δs, we initially turn off gravity and place an SP droplet or a DP droplet with diameter σ next to a wall. We then turn on gravity and measure the distance δs that the droplet sinks. In Fig. 7(c), we plot λ/σ versus δs/σ for both the SP and DP models of single droplet motion through obstacle arrays. λ/σ versus δs is similar for the SP and DP models for δs/σ < 0.25, but the results differ significantly for δs/σ > 0.25. At large δs/σ, overlaps between the obstacles and SP droplets are not strongly penalized, clogs are highly unlikely, and λ/σ → ∞. However, at large δs/σ, DP droplets are extremely deformable, can wrap around obstacles, and thus λ/σ → 0. Comparing the results for the SP and DP models allows us to assess the importance of shape deformability, particle softness, and volume conservation in determining the clogging probability.
4.3 Continuous single-droplet flows in obstacle arrays
We now investigate continuous flows of single droplets through obstacle arrays (using the SP and DP models). We calculate the average droplet speed 〈νg〉 (over each droplet trajectory and multiple random obstacle arrays, see Appendix D) as a function of the size and placement of the obstacles. For simplicity, we set Vt = 0.03 and b0 = 0, but the results also hold for non-zero b0. (See Appendix E.) Intuitively, one might expect that increasing the line tension Γ would lead to increased resistance to droplet shape changes, and thus decreases in 〈νg〉. However, in Fig. 8(a), we find that 〈νg〉 increases with Γ for wob/σ ≥ 1. The decrease in 〈νg〉 with decreasing Γ occurs because droplets with small surface tension can easily wrap around an obstacle. When droplets wrap around an obstacle, the two ends of the droplet extend in the flow direction until the droplet surface energy matches the work done by the driving force. After the ends of droplet stop moving in the flow direction, one end of the droplet moves in the opposite direction of the driving force, which allows the droplet to unwrap. This wrapping and unwrapping process significantly slows droplet movement and decreases 〈νg〉.Numerous studies have characterized droplet flows as a function of the capillary number Ca, which can be expressed in terms of the dimensionless line tension,
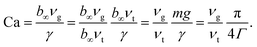 | (17) |
In Fig. 8(b), we quantify continuous flows after fixing wob/σ = 1.0 and varying σob/σ. We plot 〈νg〉/νtversus Γ for σob/σ = 0.3, 0.6, and 0.9. We find that increasing σob/σ increases 〈νg〉 at small Γ, indicating that it is more difficult for droplets to wrap around larger obstacles. In the large-Γ limit, the single-droplet flows for all σobs/σ approach the same wobs-dependent plateau value in 〈νg〉. Droplet wrapping does not occur in this regime since droplet deformation would require large surface energy.
In Fig. 9(a), we show 〈νg〉/νtversus the droplet-obstacle stiffness Ew using the same obstacle arrays in Fig. 8 for the SP model. In contrast to the DP simulations, we find that 〈νg〉/νt decreases with increasing Ew, which indicates that softer particles flow more rapidly for the SP model. This result stems from the fact that droplet softness in the SP model is represented by larger allowed overlaps between the droplet and obstacles. Therefore, in the Ew → 0 limit, droplets would flow through obstacles without slowing down, resulting in 〈νg〉/νt → 1. In contrast, in the Γ → 0 limit in DP simulations, the droplets wrap around each obstacle that they encounter. This difference in the flow behavior of single SP and DP droplets emphasizes the importance of modeling explicit deformability in droplet flows through obstacle arrays. In Fig. 9(b), we plot 〈νg〉/νtversus droplet deformation δs/σ at wob/σ = 1.1 for both the DP and SP models. We find that 〈νg〉/νt for the SP and DP models converge to same value in the rigid-droplet limit (δs/σ → 0), but they possess diverging behavior for large droplet deformation, δs/σ → 1.
5 Discussion and conclusions
In this article, we carried out coordinated experiments and numerical simulations of gravity-driven flows of single droplets in narrow channels and obstacle arrays. We first developed deformable particle (DP) simulations with line tension in 2D and calibrated them to the experiments. The DP simulations recapitulate the experimental results for the droplet shape and speed for flows within narrow channels with an error of less than 10%. Using the calibrated DP simulations, we find several important results concerning single-droplet flows in narrow channels and obstacle arrays. First, the droplet speed possesses nonmonotonic behavior as the droplet traverses the narrow channels. The droplet speed can even overshoot the terminal speed and the overshoot is enhanced as the gravitational driving is decreased. Second, we showed that the clogging probability is nonmonotonic with the line tension for droplets flowing through obstacle arrays. The nonmonotonic behavior is caused by two distinct clogging mechanisms (droplet wrapping and squeezing) in obstacle arrays. Stiffer droplets become trapped when they cannot squeeze in between obstacles, while highly deformable droplets clog when they wrap around obstacles, resulting in high clogging probabilities for droplets with both large and small deformabilities. We also compared the DP simulation results for flows in obstacle arrays to those for the frequently used soft particle (SP) model, which does not include explicit shape deformability. The DP and SP simulations of single-droplet flows in obstacle arrays are similar in the rigid-droplet limit, but diverge for deformable droplets since the SP model can only model clogging via the squeezing mechanism (and not the wrapping mechanism).These results suggest several promising future research directions. First, the current numerical simulations employ the DP model with line tension in 2D. When calibrating the 2D DP model to the experimental results, we obtain values for the dimensionless line tension Γ* that are a factor of ∼3 smaller than the dimensionless surface tension Γexp in experiments. Thus, in future work we will develop the 3D DP model49 with surface tension to describe quasi-2D flows of droplets in narrow channels and obstacle arrays. Second, In the current work, we do not quantitatively model the background fluid. However, the hydrodynamics of the background fluid can influence the droplet dynamics, such as causing the droplets to follow stream lines, which can prevent droplet-obstacle contact. Therefore, in the future, we can include the effects of Stokesian dynamics of the background fluid on the droplet motion.
Third, we observe in experiments that droplets undergoing sufficiently large deformations (larger than those considered in the Results section) break up into smaller droplets. However, our current numerical simulations do not account for this phenomenon. In future studies, we will develop a quantitative framework to predict the conditions under which droplet breakup occurs and use it to determine the size distribution of daughter droplets emerging from obstacle arrays. This improved understanding of droplet breakup will be valuable in microfluidic applications,55,56 where generating droplets of a specific size is required.57 We also plan to investigate multi-droplet flows through obstacle arrays. The efficiency of the DP model will enable us to simulate systems consisting of thousands of droplets, and explore under what conditions droplet interactions give rise to coalescence, where two droplets in contact merge to form a larger droplet.58 Droplet breakup and coalescence play competing roles in determining the equilibrium size distribution of droplets moving through obstacle arrays.59,60 In future studies, we will investigate their combined effects to quantitatively predict the droplet size distribution exiting from the obstacle arrays.
Fourth, we observe cases where both wrapping and squeezing mechanisms occur simultaneously during droplet flows. These hybrid cases occur at intermediate values of the line tension, i.e. where the wrapping and squeezing branches connect in Fig. 6(c). The occurrence of hybrid behavior also depends on the obstacle density. For example, at sufficiently high density, a droplet could unwrap around one obstacle and the side of the droplet that is unwrapping can become squeezed between two obstacles that are further downstream. In the future, we will investigate the conditions that cause these hybrid cases and their effects on the flow and clogging of capillary droplets.
Finally, the droplet squeezing and wrapping mechanisms can be exploited in deterministic-lateral-displacement (DLD) devices to separate droplets spatially and/or temporally based on their surface tension. Currently, DLD devices separate droplets based on their size and response to fluid streamlines. Our results pave the way for separating droplets or cells in DLD devices at fixed size but varying surface tension.
Data availability
Simulation code used in this article is available at GitHub repository DPM_OMP at https://github.com/YUXUANCHENG/DPM_OMP. Experimental images and data are stored in https://drive.google.com/drive/folders/18Mx9t6MyRM45tAprRDykjGwZpQPCdnZ8.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A
In this Appendix, we show experimental measurements of the power-law exponent α that appears in eqn (6) for the distance-dependent drag coefficient. In the low Reynolds number (overdamped) regime, eqn (6) can be rewritten as: | (18) |
After rearranging eqn (18), we find
 | (19) |
 | (20) |
Appendix B
In this Appendix, we investigate the effects of the number of vertices Nv and perimeter elasticity Kl on the results for droplet flows through narrow channels using the DP simulations. The DP model with Nv → ∞ and Kl → 0 is the most accurate for describing droplet flows. However, to limit computational time, we choose Nv such that it is sufficiently large that further increases do not significantly change the results. In Fig. 11, we show the droplet speed profile, νg/νtversus h/σ, for Nv = 32, 64, 128, 256, 512, and 1024. We find that for Nv ≤ 64, the velocity profile is quite noisy. For Nv ≥ 128, the velocity profile is smooth on a linear scale. For the DP simulations presented here, we use Nv = 256.For the DP simulations to accurately model line tension, it is important that Kl/Γ → 0. However, the perimeter elasticity in eqn (1) is important for ensuring the stability of the DP simulations. If the DP model only includes line tension without perimeter elasticity, the droplet vertices can aggregate in the direction of gravity, which gives rise to an uneven distribution of vertices around the droplet perimeter and can cause the droplet to overlap the side walls. Thus, we need to select a non-zero value of Kl to uniformly distribute vertices on the droplet surface, but small enough such that the results for the DP model are dominated by line tension and do not depend on Kl. In Fig. 12, we show the root-mean-square deviations in the droplet speed Δv between the DP simulations and experiments of flow in narrow channels plotted as a function of Kl/Γ. Δv ∼ 0.08 reaches a plateau for Kl/Γ ≲ 10−2. In the present work, we set Kl/Γ = 10−3.
Appendix C
In this Appendix, we include additional details concerning the definition of a permanent clog and the clogging decay length λ for droplets moving in obstacle arrays. In the simulations, a clog occurs when the droplet kinetic energy Ek (normalized by the kinetic energy at the terminal speed) decays below a threshold Ek/Et < 10−17. In Fig. 13(a), we show examples of Ek/Etversus time t/t0 for cases when the droplet clogs (wob/σ = 0.3) and does not clog (wob/σ = 1.1).To determine the clogging decay length λ, we first measure the cumulative probability P that the droplet does not clog as a function of the droplet displacement r in the obstacle array. We run Ns = 50 simulations for a total time T = 2 × 105t0 with different randomized initial droplet positions and randomized obstacle arrays. P(r) = 1 − Nclog(r)/Ns, where Nclog is the number of times that the droplet clogs before it moves a distance r. In Fig. 13(b), we plot P versus r/σ for DP simulations with Γ ≈ 1.09, σob/σ = 0.3, and wob/σ = 0.2. At the beginning of each simulation, r = 0 and P = 1. As each droplet traverses the obstacle array, the cumulative probability P of not clogging decreases exponentially with increasing r.
Appendix D
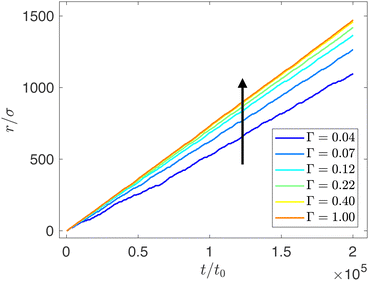
In this Appendix, we show that the DP simulations of single droplet flows in obstacle arrays can reach a continuous flow regime (with no permanent clogs) for minimum obstacle spacing wob/σ > 1. In Fig. 14, we plot the droplet displacement r versus time t for DP simulations with Γ = 0.04–1. We determine the steady state speed νg for a single-droplet trajectory in a given obstacle array by measuring the slope of r/σ versus t/t0. 〈νg〉 is averaged over 10 random obstacle arrays.Appendix E
In this Appendix, we show that the choice of the near-wall drag coefficient b0 does not qualitatively affect the results in Section 4.3. As discussed previously, the SP model does not include distance-dependent drag forces (eqn (6)). In Fig. 9(c) and Fig. 7(b), we set b0 = 0 in the DP simulations so that when we compare the DP and SP simulations, both have the same form for the drag force. In Fig. 15, we plot 〈νg〉/νtversus Γ for single droplets flowing through obstacle arrays with wob/σ = 1.0. All other parameters are the same as those in Fig. 8(a), except the near-wall drag coefficient varies: b0/b∞ = 0, 0.2, and 0.4. We find that increasing b0/b∞ decreases 〈νg〉/νt, but it monotonically increases with Γ for all b0/b∞.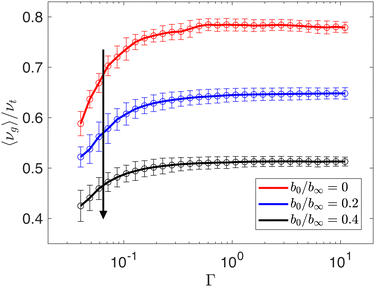 | ||
| Fig. 15 Average speed of the center mass of the droplet in the flow direction 〈νg〉 normalized by the terminal velocity νt plotted as a function of the dimensionless line tension Γ for obstacle arrays with wob/σ = 1.0. All other parameters are the same as those used in Fig. 8(a), except we vary the near-wall drag coefficient: b0/b∞ = 0 (red), 0.2 (blue), and 0.4 (black). The arrow indicates increasing b0/b∞. | ||
Acknowledgements
We acknowledge support from NSF Grants No. CBET-2002782 (Y. C., S.S., and C. S. O.), No. CBET-2002815 (B. L., P. H., and E. R. W.), No. CBET-2306371 (D. M.), and No. CBET-2002797 (M. D. S.). This work was also supported by the High Performance Computing facilities operated by Yales Center for Research Computing.References
- C. Chung and D. J. McClements, Food Struct., 2014, 1, 106–126 CrossRef.
- L. Bai, S. Huan, O. J. Rojas and D. J. McClements, J. Agric. Food Chem., 2021, 69, 8944–8963 CrossRef CAS PubMed.
- S. Freitas, G. Hielscher, H. P. Merkle and B. Gander, Ultrason. Sonochem., 2006, 13, 76–85 CrossRef CAS.
- C. Albert, M. Beladjine, N. Tsapis, E. Fattal, F. Agnely and N. Huang, J. Controlled Release, 2019, 309, 302–332 CrossRef CAS PubMed.
- M. A. Krawczyk, D. T. Wasan and C. Shetty, Ind. Eng. Chem. Res., 1991, 30, 367–375 CrossRef CAS.
- A. A. Umar, I. B. M. Saaid, A. A. Sulaimon and R. B. M. Pilus, J. Pet. Sci. Eng., 2018, 165, 673–690 CrossRef CAS.
- B. Cerff, D. Key and B. Bladergroen, Sustainability, 2021, 13, 12339 CrossRef CAS.
- A. D. Bick, J. W. Khor, Y. Gai and S. K. Y. Tang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2017822118 CrossRef CAS.
- S. Sohrabi, N. Kassir and M. Keshavarz Moraveji, RSC Adv., 2020, 10, 27560–27574 RSC.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- X. Casadevall, I. Solvas and A. deMello, Chem. Commun., 2011, 47, 1936–1942 RSC.
- Y. Ding, P. D. Howes and A. J. deMello, Anal. Chem., 2020, 92, 132–149 CrossRef CAS PubMed.
- T. Schneider, J. Kreutz and D. T. Chiu, Anal. Chem., 2013, 85, 3476–3482 CrossRef CAS.
- C. Xue, J. Wang, Y. Zhao, D. Chen, W. Yue and J. Chen, Micromachines, 2015, 6, 1794–1804 CrossRef.
- J.-C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak, L. Frenz, C. Rick, M. L. Samuels, J. B. Hutchison, J. J. Agresti, D. R. Link, D. A. Weitz and A. D. Griffiths, Lab Chip, 2009, 9, 1850–1858 RSC.
- W. Beattie, X. Qin, L. Wang and H. Ma, Lab Chip, 2014, 14, 2657–2665 RSC.
- H. N. Joensson and H. Andersson Svahn, Angew. Chem., Int. Ed., 2012, 51, 12176–12192 CrossRef CAS.
- T. S. Kaminski, O. Scheler and P. Garstecki, Lab Chip, 2016, 16, 2168–2187 RSC.
- K. Matuła, F. Rivello and W. T. S. Huck, Adv. Biosyst., 2020, 4, 1900188 CrossRef.
- C. C. Thomas and D. J. Durian, Phys. Rev. E, 2016, 94, 022901 CrossRef CAS PubMed.
- A. Pascot, N. Gaudel, S. Antonyuk, J. Bianchin and S. Kiesgen De Richter, Chem. Eng. Sci., 2020, 224, 115749 CrossRef CAS.
- J. Tang and R. P. Behringer, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2011, 21, 041107 Search PubMed.
- W. Beverloo, H. Leniger and J. van de Velde, Chem. Eng. Sci., 1961, 15, 260–269 CrossRef CAS.
- Y. Cheng, J. D. Treado, B. F. Lonial, P. Habdas, E. R. Weeks, M. D. Shattuck and C. S. O'Hern, Soft Matter, 2022, 18, 8071–8086 RSC.
- I. Zuriguel, A. Janda, A. Garcimartín, C. Lozano, R. Arévalo and D. Maza, Phys. Rev. Lett., 2011, 107, 278001 CrossRef PubMed.
- C. Lozano, A. Janda, A. Garcimartín, D. Maza and I. Zuriguel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031306 CrossRef PubMed.
- G.-J. J. Gao, F.-L. Yang, M. C. Holcomb and J. Blawzdziewicz, Phys. Rev. E, 2021, 103, 062904 CrossRef CAS.
- S. D. Alessio, Eur. J. Phys., 2021, 42, 065808 CrossRef.
- Y. Gai, A. Montessori, S. Succi and S. K. Y. Tang, Phys. Rev. Fluids, 2022, 7, 080501 CrossRef.
- G.-J. J. Gao, J. Blawzdziewicz, M. C. Holcomb and S. Ogata, Granular Matter, 2019, 21, 25 CrossRef.
- A. D. Bick, J. W. Khor, Y. Gai and S. K. Y. Tang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2017822118 CrossRef CAS.
- C. Reichhardt and C. J. O. Reichhardt, Phys. Rev. Lett., 2018, 121, 068001 CrossRef CAS.
- H. T. Nguyen, C. Reichhardt and C. J. O. Reichhardt, Phys. Rev. E, 2017, 95, 030902 CrossRef CAS PubMed.
- C. Reichhardt and C. J. O. Reichhardt, Soft Matter, 2021, 17, 1548–1557 RSC.
- H. Péter, A. Libál, C. Reichhardt and C. J. O. Reichhardt, Sci. Rep., 2018, 8, 10252 CrossRef PubMed.
- X. Hong, M. Kohne, M. Morrell, H. Wang and E. R. Weeks, Phys. Rev. E, 2017, 96, 062605 CrossRef.
- R. Tao, M. Wilson and E. R. Weeks, Phys. Rev. E, 2021, 104, 044909 CrossRef CAS.
- S. Alborzi, B. G. Clark and S. M. Hashmi, Soft Matter, 2022, 18, 4127–4135 RSC.
- J. Wang, B. Fan, T. Pongó, K. Harth, T. Trittel, R. Stannarius, M. Illig, T. Börzsönyi and R. Cruz Hidalgo, Soft Matter, 2021, 17, 4282–4295 RSC.
- C. Hirt and B. Nichols, J. Comput. Phys., 1981, 39, 201–225 CrossRef.
- D. P. F. Silva, R. C. V. Coelho, I. Pagonabarraga, S. Succi, M. M. Telo da Gama and N. A. M. Araújo, Soft Matter, 2024, 20, 2419–2441 RSC.
- R. C. V. Coelho, D. P. F. Silva, A. M. R. Maschio, M. M. Telo da Gama and N. A. M. Araújo, Phys. Fluids, 2023, 35, 013304 CrossRef CAS.
- T. Breinlinger, P. Polfer, A. Hashibon and T. Kraft, J. Comput. Phys., 2013, 243, 14–27 CrossRef CAS.
- R. A. Gingold and J. J. Monaghan, Mon. Not. R. Astron. Soc., 1977, 181, 375–389 CrossRef.
- J. J. Monaghan, Rep. Prog. Phys., 2005, 68, 1703–1759 CrossRef.
- J. P. Morris, Int. J. Numer. Methods Fluids, 2000, 33, 333–353 CrossRef.
- A. Boromand, A. Signoriello, F. Ye, C. S. O'Hern and M. D. Shattuck, Phys. Rev. Lett., 2018, 121, 248003 CrossRef.
- A. Boromand, A. Signoriello, J. Lowensohn, C. S. Orellana, E. R. Weeks, F. Ye, M. D. Shattuck and C. S. O'Hern, Soft Matter, 2019, 15, 5854–5865 RSC.
- D. Wang, J. D. Treado, A. Boromand, B. Norwick, M. P. Murrell, M. D. Shattuck and C. S. O'Hern, Soft Matter, 2021, 17, 9901–9915 RSC.
- D. J. Durian, Phys. Rev. Lett., 1995, 75, 4780–4783 CrossRef CAS PubMed.
- D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 1739–1751 CrossRef CAS.
- X. Hong, K. W. Desmond, D. Chen and E. R. Weeks, Phys. Rev. E, 2022, 105, 014603 CrossRef CAS.
- C. C. Thomas and D. J. Durian, Phys. Rev. Lett., 2015, 114, 178001 CrossRef CAS PubMed.
- A. Marin, H. Lhuissier, M. Rossi and C. J. Kähler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2018, 97, 021102 CrossRef CAS PubMed.
- D. R. Link, S. L. Anna, D. A. Weitz and H. A. Stone, Phys. Rev. Lett., 2004, 92, 054503 CrossRef CAS PubMed.
- C. Chung, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2009, 162, 38–44 CrossRef CAS.
- A. Tazikeh Lemeski, S. M. Seyyedi, M. Hashemi-Tilehnoee and A. S. Naeimi, Sci. Rep., 2024, 14, 13324 CrossRef CAS PubMed.
- P. V. Dolganov, A. S. Zverev, K. D. Baklanova and V. K. Dolganov, Phys. Rev. E, 2021, 104, 014702 CrossRef CAS PubMed.
- N. Barai and N. Mandal, Int. J. Multiphase Flow, 2019, 111, 1–15 CrossRef CAS.
- Z. Deng, S. Wu and Y. Chen, Int. J. Multiphase Flow, 2024, 104953 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |