Dynamics of poly(methyl acrylate)/poly(methyl methacrylate)-grafted-Fe₃O₄ nanocomposites

Abstract

We investigated the dynamics of nanocomposites prepared through mixing poly(methyl methacrylate) grafted Fe₃O₄ nanoparticles (PMMA-g-Fe₃O₄) with poly(methyl acrylate) (PMA). A key feature here different from previous dynamics measurements of polymer nanocomposites is the different chemistry between the matrix polymer and the polymer grafts, which introduces chemical heterogeneity. Transmission electron microscopy shows clear evidence of nanoparticle clustering due to the poor miscibility between the bulk PMA and the bulk PMMA. At the same time, broadband dielectric spectroscopy measurements detect two leading relaxations, i.e. the α and α* processes, where the α process is associated with the bulk PMA and the α* process from the PMA interacting with the grafted PMMA in the nanoparticle clustering region. Interestingly, the characteristic time of α*, τ_α*, is slightly slower than that of the α, τ_α, at high temperatures, and exhibits near Arrhenius temperature dependence at low temperatures. As a result, τ_α* and τ_α cross each other in the activation plot upon cooling and τ_α* ≪ τ_α is observed at temperatures approaching the glass transition temperature of PMA. These observations suggest the presence of component dynamics and the dynamics confinement effect between PMA and PMMA in the nanoparticle clustering region, highlighting an active interaction between PMA and PMMA at the interface despite their poor miscibility. These results thus suggest new routes to control interface dynamics through immiscible polymer pairs.

---

1. Introduction

Polymer nanocomposites (PNCs) are an important class of materials that can exhibit many functionalities and properties not accessible by the corresponding matrix polymers or nanoparticles.^1–7 Many of these advanced functionalities and macroscopic properties of PNCs are known to correlate strongly with particle dispersion and the interphase between nanoparticles and the matrix polymer.^8–12 Extensive work has been conducted to elucidate the structures and dynamics of polymers at the interphase. An interphase polymer layer with a thickness of ∼3–5 nm has been widely acknowledged and exhibits a distinct structure, dynamics, and properties from the bulk matrix polymer.^13–21 However, most existent efforts have focused on PNCs with chemically homogeneous interphases where the matrix polymer shares the same chemistry as the adsorbed or grafted polymers at the interphase, leaving PNCs with heterogeneous interphases consisting of grafted polymer chains chemically different from the matrix polymers largely unexplored.

Recent work showed that poly(methyl methacrylate) (PMMA)-adsorbed SiO₂ nanoparticles dispersed in poly(ethylene oxide) (PEO) exhibited mechanical stiffening when the temperature sweeps across the glass transition temperature, T_g, of PMMA.^22–24 Rheological measurements of poly(methyl acrylate) (PMA) composites containing nanoparticles with adsorbed PMMA chains exhibited both intermixing and dynamics interplay.^25–27 Studies on the interphase dynamics of immiscible polymer pairs also suggest long-range effects on the dynamics of chemically heterogeneous interphases, which is qualitatively different from that of the polymer/solid substrates.^28,29 Hence, it is important to understand the effect of chemical heterogeneity at the interphase of PNCs, where grafted canopy and matrix chains mix.

In this article, we characterize the dynamics of PNCs with chemically heterogeneous interphases by blending PMMA-grafted nanoparticles with PMA and compare them with the PMA/PMMA blends. For PMA/PMMA blends, differential scanning calorimetry (DSC) measurements give two distinct glass transition temperatures, T_g, suggesting the presence of macrophase separation. We would like to emphasize that for miscible polymer blends with a large T_g separation between two components, one sees two distinct, T₁₀₀, where the structural relaxation times of each component reach 100 s.^30–35 This is true for polymer mixtures with high and low molecular weights of the same polymer, such as polystyrene/oligostyrene.^36,37 However, these miscible polymer blends give one glass transition step in the DSC measurements. Therefore, one should not mix the two T₁₀₀ of miscible blends with the two DSC T_gs from polymer blends with macrophase separation. Furthermore, broadband dielectric spectroscopy (BDS) measurements of the PMA/PMMA blend demonstrate (i) similar segmental dynamics of the PMA phase with that of the neat PMA at all temperatures, (ii) a speeding up in β relaxation of the PMMA phase, and (iii) a smaller β relaxation activation energy of the PMMA phase, E^B_β,PMMA, than that of the neat PMMA.

On the other hand, transmission electron microscopy (TEM) measurements of PMA/PMMA-g-Fe₃O₄ nanocomposites demonstrate the clustering of PMMA-g-Fe₃O₄ nanoparticles in the PMA matrix. BDS measurements capture two primary relaxations of the PMA/PMMA-g-Fe₃O₄ nanocomposites, α and α*. We attribute α relaxation to the structural relaxation of the PMA matrix and α* the structural relaxation of PMA in the nanoparticle clustering region. Interestingly, the characteristic time of the α* process, τ_α*, exhibits a crossover from a super-Arrhenius temperature dependence to near-Arrhenius temperature dependence at temperatures close to T_g of bulk PMMA. As a result, τ_α* is larger than the characteristic time of the α process, τ_α, at high temperatures and can become much smaller than τ_α at temperatures close to T_g of the bulk PMA. These results suggest the presence of component dynamics of the PMA and PMMA in the nanoparticle clustering region and a strong dynamics confinement effect of the vitrified PMMA component imposed on the PMA component below the T_g of PMMA. Furthermore, temperature modulated DSC measurements of PMA/PMMA-g-Fe₃O₄ nanocomposites at different cooling rates only capture a single sharp glass transition, T_g, and no signs of T_g of the PMMA, implying a strong influence of the PMA on the T_g of the grafted PMMA. These results suggest an interesting interplay between the PMA and the grafted PMMA in the nanoparticle clustering region and highlight the qualitatively different dynamic features of the PNCs with chemically heterogeneous interphases.

2. Materials and methods

2.1 Materials

The synthesis of the PMMA-g-Fe₃O₄ nanoparticle and the preparation of their composites in PMA matrices were published in previous work.²⁶ Iron oxide (Fe₃O₄) nanoparticles (15 ± 3 nm in diameter) purchased from Rosecreek Technologies Inc. were modified with (3-aminopropyl)-triethoxysilane (APTES, 99%, Sigma-Aldrich). The average molecular weight (M̄_w) of grafted PMMA chains is 39 kg mol⁻¹ with a polydispersity index (PDI) of 1.48 and the grafting density is 0.045 chains per nm². Poly(methyl acrylate) (PMA) at 20, 80, and 160 kDa were synthesized by reversible addition–fragmentation chain transfer (RAFT) polymerization, and their molecular weights were estimated from rheology data since the dn/dc value is negative for PMA and we cannot determine the absolute molecular weight using the gel permeation chromatography (GPC) instrument.²⁶ In the following presentation, we use the abbreviation of the polymer and its molecular weights to represent this polymer. For instance, PMA40k represents neat PMA with a molecular weight of 40 kg mol⁻¹.

2.2 Preparation of PMA nanocomposites and particle dispersion

PMA/PMMA-g-Fe₃O₄ nanocomposites and PMA40k/Fe₃O₄ nanocomposites with bare Fe₃O₄ nanoparticles were solution cast to form their bulk films. The compositional specifications and T_g of polymer nanocomposites and polymer blends are presented in Table 1. We chose PMA as the matrix and PMMA as the grafted polymer as they have large disparities in their glass transition temperatures T_g,PMA ≈ 287 K and T_g,PMMA ≈ 385 K. We fixed the loading of Fe₃O₄ as 3 vol% (volume fraction), which corresponds to 90 vol% PMA and 10 vol% of PMMA in the polymer phase of the PMA/PMMA-g-Fe₃O₄ nanocomposites. In addition, we also prepared a polymer blend, PMA40k/PMMA53k with 90 vol% PMA and 10 vol% PMMA. The polymer blend was prepared through solution casting of PMA/PMMA in tetrahydrofuran (THF). The dispersion of nanoparticles in the PMA/PMMA-g-Fe₃O₄ nanocomposites was characterized through small-angle X-ray scattering (SAXS) measurements²⁶ and transmission electron microscopy (TEM) analysis. The SAXS measurements showed signs of aggregation of Fe₃O₄ in the nanocomposites. A power-law of the scattering intensity of I(Q) ∼ Q⁻⁴ has also been observed in the unified fitting to I(Q) where Q is the scattering wavevector, indicating the Fe₃O₄ nanoparticle form fractals with diffusive interphases.²⁶ We cryosectioned the composite using a diamond knife and imaged ∼100 nm thick sections in TEM (JEOL 2100 Plus S/TEM). Fig. 1 shows the aggregated state of grafted nanoparticles and this aggregation state is consistent with the aggregation seen in the adhesion force maps of the composites obtained in AFM in previous work.²⁶ Thus, the PMA/PMMA-g-Fe₃O₄ nanocomposites have a bulk PMA region and a PMMA-g-Fe₃O₄ nanoparticle clustering region. As discussed in the following sections, the microstructure can lead to an interesting influence on the dynamics of PMA/PMMA-g-Fe₃O₄ nanocomposites.

Table 1 Basic characterization of polymer nanocomposites and polymer blend

Samples	Polymer matrix or component A	φ P or φA	Nanoparticle or component B	φ NP or φB	T g (K) (DSC)	T g (K) (BDS)	E β,PMA (kJ mol^−1)	E β,PMMA (kJ mol^−1)
a For PMA40k/PMMA53k (9 : 1) blend, component A: PMA and component B: PMMA.
PMA40k	PMA40k	1	—	—	287	287	40	—
PMMA53k	PMMA53k	1	—	—	385	385	—	132
PMA20k/PMMA-g-Fe3O4	PMA20k	0.905	PMMA-g-Fe3O4	0.095	288	288	45	—
PMA40k/PMMA-g-Fe3O4	PMA40k	0.905	PMMA-g-Fe3O4	0.095	291	293	43	—
PMA80k/PMMA-g-Fe3O4	PMA80k	0.905	PMMA-g-Fe3O4	0.095	291	292	47	—
PMA160k/PMMA-g-Fe3O4	PMA160k	0.905	PMMA-g-Fe3O4	0.095	294	294	60	—
PMA40k/Fe3O4	PMA40k	0.97	Fe3O4	0.03	288	NA	—	—
PMA40k/PMMA53k (9 : 1)^a	PMA40k	0.9	PMMA53k	0.1	288 and 380	290 for PMA	—	83

---

Fig. 1 (a) TEM image of PMA80k/PMMA-g-Fe₃O₄. (b) An illustration of PMMA-grafted-Fe₃O₄ nanoparticle (NP) sub-micron aggregates in the PMA matrix with limited interphase mixing. Color mapping qualitatively indicates the distribution of PMMA graft chains and PMA matrix chains. NPs are represented by black spheres.

2.3 Differential scanning calorimetry (DSC)

The glass transition temperatures, T_g, of all samples were identified using a temperature-modulated differential scanning calorimeter (TMDSC) DSC250 (TA Instruments) from 453 K to 253 K at a cooling rate of 2 K min⁻¹ and a modulation amplitude of 1 K every 60 s. The T_g values were determined from the inflection point of the reversible specific heat capacity jump (C_p). The T_g values of all samples are summarized in Table 1.

2.4 Broadband dielectric spectroscopy (BDS)

BDS was employed to quantify the dynamics of the neat polymers, the polymer blend, and the polymer nanocomposites. Specifically, disk-like thin films with a thickness of 0.14 mm and a diameter of 16 mm were prepared using a Carver Press at 453 K and sandwiched between two gold electrodes with a diameter of 20 mm. A hollow Teflon spacer of the same thickness of 0.14 mm, an inner diameter of 16 mm, and an outer diameter of 24 mm was placed between the two gold electrodes to prevent shortage. The sandwiched samples were then loaded into the ZGS sample holder of the Novocontrol Concept-40 system with an Alpha-A impedance analyzer and a Quatro Cryosystem temperature controller that has a temperature accuracy of ±0.1 K. The frequency range of all the measurements was from 10⁷ Hz to 10⁻² Hz. The measurements were conducted from 453 K to 213 K with an interval of 5 K upon cooling and from 213 K to 453 K at an interval of 10 K upon heating. A thermal annealing of 20 min was applied before each measurement to assure thermal equilibrium. The dielectric spectra of PMA/PMMA-g-Fe₃O₄ at the same temperature upon heating and cooling overlap nicely with each other, confirming the negligible changes of the microstructure during the measurements. To further confirm the reproducibility of the measurements, we repeat the BDS measurements of PMA40k/PMMA-g-Fe₃O₄ with different sample sizes, where excellent agreement has been observed between different measurements (Fig. S1, ESI†). These results thus suggest the reproducibility of the results that do not depend on the specimen used.

The obtained complex dielectric permittivity, ε*(ω), were analyzed through a fit to a set of Havriliak–Negami (HN) functions:

where ε₀ and ε_∞ are the vacuum permittivity and the dielectric constant of the polymer at infinitely high frequency, ε′(ω) and ε′′(ω) are the dielectric storage permittivity and loss permittivity, ω is the angular frequency, Δε_k, τ_HN,k, β_k, and γ_k are the dielectric relaxation amplitude, the HN time, and the shape parameters of the k^th relaxation process, σ_dc is the dc-conductivity, and A and s are constants to describing the electrode polarization.³⁸ The characteristic relaxation time of the k^th relaxation process can then be obtained from the HN relaxation time:

In addition, Maxwell–Wagner–Sillar's (MWS) interfacial polarization is very common in multicomponent polymeric materials,^39,40 including both immiscible blends and polymer nanocomposites that were also analyzed using eqn (1) as a separate relaxation process.

3. Results and discussion

3.1 Glass transition of the polymer blends and polymer composites

Fig. 2 presents the specific heat capacity, C_p, of the PMA40k/PMMA-g-Fe₃O₄ nanocomposite and its comparison with neat PMA40k, the PMA40k/PMMA53k (9 : 1) blend, pure PMMA-g-Fe₃O₄ nanoparticles, and the PMA40k/Fe₃O₄ nanocomposite. PMMA53k has comparable T_g to PMMA-g-Fe₃O₄ nanoparticles (see Table 1). The PMA40k/PMMA53k blend shows clear signs of two T_g steps at 288 K and 380 K, consistent with previous literature on the phase diagram of PMA/PMMA blends.⁴¹ Interestingly, the T_g of the PMMA phase is significantly broadened in the blend and has a slightly lower T_g than the neat PMMA. On the other hand, only one T_g has been observed for PMA/PMMA-g-Fe₃O₄ nanocomposites as determined from the temperature derivative of the specific heat capacity, dC_p/dT (Fig. S2, ESI†). Similar results of one T_g of PMA/PMMA-g-Fe₃O₄ nanocomposites have been observed for TMDSC tests at different cooling rates (Fig. S3, ESI†). Interestingly, an ∼4 K increase in T_g (defined through the inflection point) has been observed in PMA40k/PMMA-g-Fe₃O₄ compared with the neat PMA40k (the inset of Fig. 2a). In contrast, there is less than 1 K increment in the T_g of the PMA40k/Fe₃O₄ nanocomposite with 3 vol% of bare Fe₃O₄ nanoparticles. The small changes in the T_g of PMA40k/Fe₃O₄ with bare Fe₃O₄ nanoparticles agree well with previous experiments on the influence of nanoparticles of similar sizes on the glass transition of the matrix polymer.^5,42 A single T_g has been observed in other PMA/PMMA-g-Fe₃O₄ nanocomposites with different molecular weights of PMA (Fig. 2b). Given the distinct regions of the bulk PMA and the PMMA-g-Fe₃O₄ nanoparticle aggregation (Fig. 1b) and the clear detection of macrophase separation in the PMA/PMMA blends from DSC (Fig. 2a), a single T_g of the PMA/PMMA-g-Fe₃O₄ indicates an intriguing influence of PMA on T_g of the grafted PMMA that makes DSC insensitive to detect it.

Fig. 2 (a) Shifted specific heat capacity, C_p, of neat PMA40k (blue squares), PMMA-g-Fe₃O₄ (olive diamonds), PMA40k/PMMA-g-Fe₃O₄ (red circles), PMA40k/PMMA53k (9 : 1) blend (pink pentagons), and PMA40k/Fe₃O₄ (purple triangles). The arrows point to the two T_gs of the PMA40k/PMMA53k blend. The inset provides a comparison of the T_g of the neat PMA40k and PMA40k/PMMA-g-Fe₃O₄. (b) Vertically shifted C_p of other PMA/PMMA-g-Fe₃O₄ nanocomposites, where only one T_g is observed.

3.2 Dynamics of the PMA/PMMA blend

To quantify the dynamics of the PMA40k/PMMA53k (9 : 1) blend, we turned to BDS. Fig. 3a provides the dielectric loss permittivity, ε′′(ω), of the PMA40k/PMMA53k (9 : 1) blend (the pink left triangles) at T = 313 K and the corresponding spectra of the neat PMA40k (the blue squares). The dielectric spectra of neat PMA at T = 213 K (blue circles) have also been presented to reveal the characteristics of β relaxation. Fig. 3b provides the dielectric loss permittivity, ε′′(ω), and derivative spectra, , of the PMA/PMMA (9 : 1) blend (the pink left triangles) and the neat PMMA53k (the olive diamonds) at T = 393 K. The dashed and the dashed-dotted lines of Fig. 3a are HN functions fit to the spectra that signify the α process of the PMA and the β process of the PMA, respectively. The solid black lines are the sum of relaxation processes through eqn (1). For Fig. 3b, the dashed lines represent the HN functions fit to the β relaxation of the PMMA of the blend and the neat PMMA. The dotted line represents the HN function fit to the MWS process of the blend, and the dash-dotted line represents the HN function fit to the α relaxation of the neat PMMA. The α relaxation of the PMMA phase is not visible in the PMA/PMMA blend due to the weak dielectric relaxation strength of the PMMA.⁴³ In addition, the characteristic time and shapes of the segmental relaxation of PMA in the blend do not seem to be affected by PMMA, consistent with the immiscibility between PMA and PMMA. On the other hand, the characteristic time of β relaxation of the PMA/PMMA (9 : 1) blend, τ^B_β,PMMA, is noticeably smaller than that of the neat PMMA, τ^N_β,PMMA, pointing to an interesting dynamics interplay between the PMA and PMMA in the blend.

Fig. 3 (a) Dielectric loss spectra, ε′′(ω), of PMA40k/PMMA53k (9 : 1) blend (pink left triangles) as well as their comparison with neat PMA40k at T = 313 K (blue squares) and T = 213 K (blue circles). The dashed lines signify the Havriliak–Negami (HN) function fit to the α process of PMA and the PMA/PMMA blend. The dashed-dotted line is the HN-function fit to the β process of the PMA. The solid black lines are the sum of the fit taking into account the conductivity and electrode polarization contributions. (b) Dielectric loss spectra (pink left triangles), ε′′(ω), and the derivative of dielectric storage spectra of the PMA40k/PMMA53k blend (pink circles) as well as their comparison with neat PMMA53k (olive diamonds) at 393 K. The pink dashed line is the HN-function fit to the β relaxation of the PMMA in the PMA/PMMA blend, the olive dashed line represents the HN-function fit to the β relaxation of the neat PMMA, the olive dash-dotted line gives the HN-function fit to the α relaxation of the neat PMMA, and the pink dotted line represents the MWS of the PMA/PMMA blend. The solid black lines are the sum of the fit taking into account the conductivity and electrode polarization contributions. (c) Temperature dependence of the τ^B_α,PMA (pink circles) and τ^B_β,PMMA (pink squares) of the blend, τ^N_α,PMMA (olive circles) and τ^N_β,PMMA (olive squares) of the neat PMMA53k, and τ^N_α,PMA (blue circles) and τ^N_β,PMA (blue triangles) of the neat PMA40k.

To be more quantitative, Fig. 3c summarizes the temperature dependence of τ^B_α,PMA and τ^B_β,PMMA of the blend as well as the α and β relaxation time of the neat PMA, τ^N_α,PMA and τ^N_β,PMA and the β relaxation time of the neat PMMA53k, τ^N_β,PMMA. For polymer blends with strong macrophase separation τ^B_α,PMA ≈ τ^N_α,PMA has been observed as expected⁴⁴ and they follow Vogel–Fulcher–Tammann (VFT) relation. τ^N_β,PMA, τ^B_β,PMMA, and τ^N_β,PMMA follow Arrhenius temperature dependence. The τ^B_β,PMMA is ∼10 times faster than τ^N_β,PMMA at high temperatures of ∼400 K which increases with cooling, highlighting their different activation energies. Applying the Arrhenius law, , the apparent activation energy of τ^B_β,PMMA is E^B_β,PMMA ≈ 83 kJ mol⁻¹ that is between that of τ^N_β,PMMA with E^N_β,PMMA ≈ 132 kJ mol⁻¹ and that of τ^N_β,PMA with E^N_β,PMA ≈ 40 kJ mol⁻¹. The activation energies of the β relaxation of neat PMA and neat PMMA agree well with previous literature.⁴⁵ Here, τ₀ is a prefactor constant, E_β is the apparent activation energy, and R is the gas constant. The changes in both τ_β and E_β indicate a modification of the chain packing of the PMMA phase in the blend. Since β relaxation is very sensitive to the local packing of polymers, the large influence of β relaxation of the PMMA phase in the blend may also indicate some miscibility between PMA and PMMA, despite the global macrophase separation between them.

3.3 Dynamics of PMA/PMMA-g-Fe₃O₄ nanocomposites

Fig. 4a and b present ε′′(ω) and of the PMA40k/PMMA-g-Fe₃O₄ at different temperatures from 293 K to 333 K. Two processes can be visualized from the low-frequency and the high-frequency side of the spectra. The low frequency one exhibits similar characteristics to the structural relaxation of the neat PMA and represents the α process of the matrix PMA. For the high-frequency process, we assign it an α* process, whose molecular origin will be discussed in detail in the following section. Fig. 4c and d give the representative ε′′(ω) and spectra of the PMA40k/PMMA-g-Fe₃O₄ (the red circles) at T = 313 K. The corresponding spectra of the neat PMA40k (the blue squares) are also given for comparison. Fig. 4e gives ε'_der(ω) of the PMA40k/PMMA-g-Fe₃O₄ at a representative high temperature T = 373 K, and ε'_der(ω) at other temperatures are presented in Fig. S4 (ESI†). The solid and the dashed red lines are the HN fit to the α and α* process of the nanocomposite and the solid blue lines are the HN fit to the α process of the neat PMA. The solid black lines are the sum of the HN function along with the contributions of the MWS process, the dc-conductivity, and the electrode polarization. The α relaxation time of the composite is slightly larger than that of the neat PMA. The small influence of nanoparticles on segmental dynamics of the matrix polymer away from the surface of nanoparticles in nanocomposites has been widely observed previously.^14,46–48 The broad dielectric dispersion of the α relaxation of polymer composites is also well-known, which reflects a large dynamics heterogeneity of composites.^{14–16,39,49–51} The α relaxation of the PMMA phase cannot be captured by dielectric measurements due to the low PMMA (∼10 vol%) in the nanocomposites and the weak dielectric relaxation amplitude.⁴³ To resolve the α relaxation of the PMMA of the nanocomposites, we have also performed rheological measurements on the linear viscoelastic spectra (Fig. S5, ESI†). However, the rheology cannot provide signatures of α relaxation of the PMMA probably due to the pronounced flow characteristic of the nanocomposites at temperatures close to the T_g of the PMMA. In addition, PMA40k/PMMA-g-Fe₃O₄ shows a clear α* shoulder peak at higher frequencies than its α relaxation at T = 313 K, implying the emergence of a faster relaxation process of the nanocomposites. At high temperatures, the α* process overlaps strongly with the α relaxation of the composite, which makes it challenging to characterize. To better resolve the α* process at high temperatures, we plot in the inset of Fig. 4e the normalized dielectric derivative spectra, , at T = 343 K, 353 K, and 373 K, where ω_p is the angular frequency at the peak position of . Compared with T = 343 K and T = 353 K, the spectra at the T = 373 K has a shoulder peak appearing at the low frequency side of the main α peak. Note that the α process is well-separated from the α* process at low temperatures (see Fig. 4a and b), such as at T = 343 K or T = 353 K. One thus can quantify the exact dielectric function of the α process (the dashed grey line in the inset of Fig. 4e) from these low temperature measurements. As a result, the dielectric function of the α* process can be obtained at temperatures where α and the α* process overlap strongly. In particular, the HN function shape parameters of the α* process obtained from this deconvolution agree well with those at low temperatures (Fig. S6, ESI†) where the α* process is well resolved (Fig. 4a). Comparing the results of Fig. 4a, b and e, one can find a very different temperature dependence of the α* from the α process. The observations of τ_α* > τ_α at high temperatures also rule out the α* process as a secondary relaxation of PMA. At the same time, one can clearly observe the β relaxation of PMA/PMMA-g-Fe₃O₄ at low temperaures, such as T = 233 K (see Fig. 4f). The β relaxation of neat PMA is also presented in Fig. 4f for comparison, which has a slightly smaller characteristic relaxation time than that of PMA40k/PMMA-g-Fe₃O₄. These observations further confirm that the α* process cannot be the β relaxation of PMA in the PMA40k/PMMA-g-Fe₃O₄ composite.

Fig. 4 (a) Dielectric loss spectra, ε′′(ω), (b) derivative of dielectric storage spectra of PMA40k/PMMA-g-Fe₃O₄ at 333 K (red circles), 323 K (blue squares), 313 K (olive diamonds), 303 K (pink triangles), and 293 K (wine left triangles). (c) Dielectric loss spectra, ε′′(ω), (d) derivative of dielectric storage spectra of PMA40k/PMMA-g-Fe₃O₄ (red circles) at 313 K as well as their comparison with neat PMA40k (blue squares). The dashed lines and dashed-dotted lines represent the Havriliak–Negami (HN) function fits to the α process of PMA and the α* process. (e) Derivative spectra of PMA40k/PMMA-g-Fe₃O₄ (blue squares) at 373 K. The dotted, dashed, and dashed-dotted lines signify the Havriliak–Negami (HN) function fits to the Maxwell–Wagner–Silliar's (MWS) process, the α process, and the α* process. The inset represents of PMA40k/PMMA-g-Fe₃O₄ (red circles) at three representative temperatures. (f) Dielectric loss spectra, ε′′(ω), of PMA40k/PMMA-g-Fe₃O₄ (red circles) as well as its comparison with neat PMA40k (blue squares) at T = 233 K. The dashed line represents the Havriliak–Negami (HN) function fits to their β process.

Fig. 5a summarizes the temperature dependence of τ^P_α,PMA, 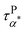, and τ^P_β,PMA of the PMA40k/PMMA-g-Fe₃O₄ nanocomposites. The α and β relaxation time of the neat PMA, τ^N_α,PMA and τ^N_β,PMA, and the α relaxation time of the neat PMMA-g-Fe₃O₄, τ^N_α,PMMA, are presented as references. The representative HN-function fit to these processes is given in Fig. 3a and b. Although there are six relaxation times presented in Fig. 5a, only three of them, τ^P_α,PMA, , and τ^P_β,PMA, are from the nanocomposites (see Fig. 4c–f for the representative fit). Both τ^P_α,PMA and τ^N_α,PMMA follow the Vogel–Fulcher–Tammann (VFT) relation, and (at least at low temperatures), τ^P_β,PMA, and τ^N_β,PMA follow nearly Arrhenius temperature dependence. The τ^P_α,PMA is slower than τ^N_α,PMA, which becomes significant at temperatures approaching T_g of the PMA of the PNC. This is consistent with the shift in T_g from TMDSC measurements. On the other hand, the τ^P_β,PMA is around three times slower than the τ^N_β,PMA, implying an influence of the grafted PMMA on the local dynamics of PMA. Interestingly, 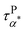is larger than τ^P_α,PMA at high temperatures and exhibit a cross with τ^P_α,PMA upon cooling. As a result, is much faster than τ^P_α,PMA at temperatures close to the T_g of the PMA. Furthermore, the apparent activation energies of 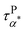(at low temperatures), τ^P_β,PMA, and τ^N_β,PMA, are , E^P_β,PMA ≈ 35 kJ mol⁻¹, and E^N_β,PMA ≈ 40 kJ mol⁻¹, respectively. The observed Arrhenius temperature dependence of the α* process and its crossing τ^P_α,PMA at intermediate temperatures are interesting. Another interesting observation is that the activation energy of the α* process is only slightly larger than the apparent activation energy of the β relaxation of PMA. All these observations point to the strong influence of the grafted PMMA on the dynamics of PMA in the nanoparticle clustering region.

Fig. 5 (a) Temperature dependence of the τ^P_α,PMA (red circles), (red diamonds), and τ^P_β,PMA (red left triangles) of the PMA40k/PMMA-g-Fe₃O₄ nanocomposite, τ^N_α,PMMA (olive squares) of the neat PMMA-g-Fe₃O₄, and τ^N_α,PMA (blue circles) and τ^N_β,PMA (blue triangles) of the neat PMA40k (b) temperature dependence of the dielectric relaxation amplitude of the α (red circles) and the α* process (red diamonds) of the PMA40k/PMMA-g-Fe₃O₄ nanocomposite, the α (blue circles) and β (blue trianlges) process of neat PMA, and the β process (olive diamonds) of neat PMMA.

In addition, we summarize in Fig. 5b the dielectric amplitudes of α (Δε^P_α,PMA) and the α* process of the PMA40k/PMMA-g-Fe₃O₄ nanocomposite, as well as the α process of the neat PMA (Δε^N_α,PMA). Δε^P_α,PMA and Δε^N_α,PMA have comparable dielectric amplitude and similar temperature dependence. They both increase with cooling. On the other hand, the dielectric relaxation amplitudes of the neat PMA, Δε^P_β,PMA, and neat PMMA, Δε^P_β,PMMA, decrease with cooling. All these are well-known features of dielectric properties of polymers.⁴⁰ Interestingly, increases with cooling, which does not favor secondary relaxation for the α* process. One can obtain a similar conclusion from the dielectric relaxation amplitudes: Δε^N_β,PMA ∼ 0.9–1.3 and Δε^N_β,PMMA ∼ 0.7–1.2. Since there is only 10% PMMA in the polymer matrix phase, if α* belongs to β relaxation of either the PMA or the PMMA one should not anticipate over the temperature range of the measurements. On the other hand, the values of 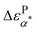are only a fraction of Δε^N_α,PMA and the temperature dependence of follows closely with that of the Δε^N_α,PMA. Based on these analyses, we conclude the α* process from the structural relaxation of the PMA in the PMA/grafted PMMA mixing region (i.e., the nanoparticle clustering region).

We have further noticed that a recent study⁵² on dielectric properties of thin films observed an Arrhenius process across the α relaxation of the film that has been attributed to the tightly adsorbed polymer layer at the polymer/substrate interface. Since the nanocomposites involve nanoparticles with a large surface curvature (i.e. radius R_NP ∼ 7.5 ± 1.5 nm) and grafted polymers of different chemistry from the matrix polymer, it is unlikely that a layer of tightly adsorbed matrix polymer would form on the surface of nanoparticles. In addition, there are only 3 vol% of nanoparticles in the nanocomposites. Even if there are tightly adsorbed polymer on the surface of the nanoparticles, it will be difficult for one to capture such a small amount of adsorbed polymers. In fact, the authors of the same article⁵² have demonstrated that the Arrhenius process from the tightly adsorbed polymers is too weak to be captured when the polymer film thickness increases to ∼110 nm. Therefore, we do not believe that the observed strong α* process has a similar origin as the Arrhenius process discussed in this thin film measurement.⁵²

Furthermore, we have varied the molecular weight of the PMA matrices. Fig. 6a and b present the dielectric loss permittivity, ε′′(ω), and derivative spectra, , of the PMA20k/PMMA-g-Fe₃O₄ (the magenta triangles), PMA80k/PMMA-g-Fe₃O₄ (the orange left triangles), and PMA160k/PMMA-g-Fe₃O₄ (the wine hexagons) at T = 313 K. The dashed and dashed-dotted lines are the fit to the spectra through Havriliak–Negami (HN) functions. The dielectric spectra have been shifted vertically for clarity. Varying the molecular weight of the PMA matrix from 20 kg mol⁻¹ to 160 kg mol⁻¹ leads to small variations in their τ^P_α,PMA as well as the α* process. Fig. 6c summarizes the temperature dependence of τ^P_α,PMA and , both of which show little influence of the PMA molecular weight. This observation is interesting since a higher tendency for phase separation is anticipated between a higher molecular weight PMA and the grafted PMMA.

Fig. 6 (a) Dielectric loss spectra, ε′′(ω), (b) derivative of dielectric storage spectra of PMA20k/PMMA-g-Fe₃O₄ (the magenta triangles), PMA80k/PMMA-g-Fe₃O₄ (the orange left triangles), and PMA160k/PMMA-g-Fe₃O₄ (the wine hexagons) at T = 313 K. The dashed and dashed-dotted lines give the Havriliak–Negami (HN) function fits to the α process of PMA and the α* process (c) temperature dependence of the τ^P_α,PMA of PMA20k/PMMA-g-Fe₃O₄ (pink circles), PMA80k/PMMA-g-Fe₃O₄ (orange circles), and PMA160k/PMMA-g-Fe₃O₄ (wine circles), and of PMA20k/PMMA-g-Fe₃O₄ (pink squares), PMA80k/PMMA-g-Fe₃O₄ (orange squares), and PMA160k/PMMA-g-Fe₃O₄ (wine squares). The τ^N_α,PMA of the neat PMA40k (blue circles) is also presented for comparison.

3.4 Molecular origin of the α* process in PMA/PMMA-g-Fe₃O₄

The above measurements and analyses point out the following characteristics of the structures and the dynamics of PMA/PMMA-g-Fe₃O₄: (i) TEM measurements provide evidence of NP clustering in the PMA/PMMA-g-Fe₃O₄ nanocomposites. (ii) DSC measurements detect a single T_g of the PMA/PMMA-g-Fe₃O₄ composites, regardless of the molecular weights of PMA. (iii) BDS measurements detect an α relaxation, an α* relaxation, and a β relaxation of the PMA. Below we discuss the understanding of these features, especially the molecular origin of the newly observed α* relaxation.

Firstly, one sees a single T_g of each nanocomposite from DSC measurements. At the same time, the TEM and BDS results revealed two different environments of PMA. The bulk PMA matrix should be a main contributor to the DSC signal due to its large population, as confirmed by the T_g values. The question here is why PMMA does not contribute to a second T_g step like the PMA/PMMA (9 : 1) blend. One possibility is the PMA in the NP clustering region strongly impacts the dynamics of PMMA, which gives an extremely broad T_g step of the PMMA phase, and the T_g step of the PMMA phase is not obvious in the conventional DSC measurements. This explanation agrees with the emergence of the α* process in the PMA/PMMA-g-Fe₃O₄ nanocomposites and the comparable values of τ^P_α,PMA and τ^N_α,PMA as well as τ^P_β,PMA and τ^N_β,PMA. The appearance of the α* process is also consistent with the strong clustering of the NPs in the TEM measurements.

More importantly, the large differences between τ^P_α,PMA and point to the strong dynamics interplay between the trapped PMA and the grafted PMMA in the NP clustering region. Despite the positive interaction parameter of χ ≈ 0.03 between PMA and PMMA (see Appendix A), one would anticipate some interpenetration at the interface between the PMA and the grafted PMMA.⁴¹ According to Helfand et al., immiscible blends can interpenetrate with each other at the interphase of depth, δ, due to an entropy-driven force.^53,54 In the large molecular weight limit,

where b is the average Kuhn length of the polymers and χ is the interaction parameter between the two polymers. For PMA and the grafted PMMA, b ≈ 1.5 nm and χ ≈ 0.03 (see Appendix A), which gives δ ≈ 7.1 nm that is slightly larger than the R_g,PMMA ≈ 5.0 nm of the grafted PMMA. Note that the interphase width can be even larger for the PMA/PMMA blend with finite molecular weights as , where N_PMA and N_PMMA are the degree of polymerization of PMA and PMMA.^55,56 For PMA with a molecular weight of 20 kg mol⁻¹ to 160 kg mol⁻¹, N_PMA ≈ 232–1860, and grafted PMMA with a molecular weight of 39 kg mol⁻¹, N_PMMA ≈ 390, this gives δ′ ≈ 7.6–8.2 nm > R_g,PMMA. Thus, one can anticipate some swelling of the grafted PMMA by the PMA chains in the nanoparticle clustering region, resembling a scenario of a “miscible” blend. The entropy-driven interpenetration between the grafted PMMA and the PMA explains the different time scales of the α* process from τ^P_α,PMA. Since the above argument is in the limit of infinitely high molecular weight, it also explains the little impact of the PMA molecular weight on the α* process.

Can the entropy-driven miscibility between the PMA and the grafted PMMA explain the Arrhenius temperature dependence of 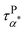at temperatures approaching the T_g of the neat PMA? In miscible blends, the effective structural relaxation (i.e. component dynamics) of the low-T_g component can switch from super-Arrhenius to Arrhenius when the testing temperature is lower than the effective glass transition temperature of the high-T_g component. Although the origin of this dynamics switch is not entirely clear, the crossover between super-Arrhenius to Arrhenius is quite common experimentally and has been observed in the polystyrene (PS)/poly(vinyl methyl ether) (PVME) blend,⁵⁷ poly(vinylidene fluoride) (PVDF)/poly(methyl methacrylate) (PMMA) blend,⁵⁸ PEO/PMMA blend,⁵⁹ poly(ethylene oxide) (PEO)/poly(vinyl acetate) (PVAc) blend,^60,61 and PS/oligostyrene.⁶² We anticipate a similar scenario here in the mixture of the PMA and grafted PMMA at the nanoparticle interface. Specifically, due to the influence of the high-T_g component (PMMA), the dynamics of the lower-T_g component (PMA) are slower than the neat PMA at temperatures higher than the T_g of the PMMA. Below the effective T_g of the high-T_g component, the dynamics of the low-T_g component follows Arrhenius temperature dependence, leading to a cross between the low-T_g component dynamics and the dynamics of neat low-T_g material. Our experiments agree well with all these features as demonstrated in the activation plots of the relaxation times (Fig. 5 and 6), where the onset of Arrhenius temperature dependence of the α* process starts at around T_g of the neat PMMA, which should serve as a good approximation of the T_g of the PMMA component in the nanocomposite. Thus, the entropy-driven miscibility at the interface between two immiscible blends can help explain the emergence of the α* process as well as its Arrhenius temperature dependence. Furthermore, the above analyses suggest the presence of component dynamics and the dynamics confinement in immiscible blends at the interpenetration interface, which has not been revealed before. At this moment, it is not clear whether the component dynamics and the dynamics confinement of the interface-mediated miscibility between immiscible blends follow the same characteristics as the miscible blends.^32,33,63 Our future studies will focus on this point. Nevertheless, these observations suggest the interface-mediated miscibility of immiscible blends, leading to interesting component dynamics and dynamic confinement effects.

If the entropy-driven interpenetration at the PMA–PMMA interface is the leading origin of the α* process, one should also anticipate an α* process in the PMA/PMMA blends. However, our dielectric measurements of PMA/PMMA blends do not find such a process. We believe this is due to the small volume fraction of the PMA–PMMA interfacial region in the PMA/PMMA blend with macrophase separation. Interestingly, recent quasi-elastic neutron scattering experiments⁶⁴ on the protonated PMA(hPMA)/deuterated PMMA (d-PMMA) blend have observed a slowing down in dynamics of hPMA compared with the neat hPMA at high temperatures, i.e. T = 403 K. In addition, the mean-squared displacement of the hydrogens in the blend is slightly larger than the neat PMA at low temperatures (temperature below 300 K), indicating a larger segmental jump distance of hPMA in the hPMA/dPMMA blend than the neat hPMA. These results are aligned with the observations of at high temperatures and at low temperatures (Fig. 5a and 6c) due to the interpenetration of the PMA/grafted PMMA in the nanoparticle clustering region, providing further support to our assignment on the molecular origin of the α* process.

4. Conclusion

In conclusion, we have studied the dynamics of a set of polymer/polymer-grafted nanoparticle nanocomposites, i.e. PMA/PMMA-g-Fe₃O₄ with different PMA molecular weights. The macrophase separation between the bulk PMA and the bulk PMMA is a key feature that leads to nanoparticle clustering and intriguing interface dynamics. TEM measurements showed clear evidence of nanoparticle clustering. DSC measurements, on the other hand, can only detect a single T_g step for all polymer nanocomposites associated with the PMA phase and no signs of T_g of PMMA, suggesting a strong influence of the PMA on the glass transition of the grafted PMMA. In addition to the primary and secondary relaxations of the PMA phase in the PMA/PMMA-g-Fe₃O₄ nanocomposites, BDS measurements reveal a new dielectric active process, α*, that is slower than τ^P_α,PMA at high temperatures and faster than τ^P_α,PMA at low temperatures. Moreover, τ_α* follows an intriguing Arrhenius temperature dependence at temperatures approaching the T_g of the bulk PMA. Further analyses showed that the characteristics of the α* process does not alter with the PMA molecular weights. We attribute the origin of the α* process to the structural relaxation of the PMA in the nanoparticle clustering region, which experiences component dynamics and dynamic confinement observed in the miscible blends. Although the component dynamics and dynamic confinement are commonly observed in miscible blends with large separations in T_g, we are not aware of any previous report of the similar features in immiscible blends. Our results thus reveal an interesting interface effect on the dynamics of immiscible polymers, providing new ways of tailoring the properties of polymers at the interfaces. At this moment, we do not know how the molecular weights of the grafted polymer or the thickness of the interphase could affect the α* process. We believe the local polymer concentration distribution at the polymer–polymer interface plays an important role. Future work is planned to clarify these questions.

Data availability

All the data reported in this article have been included in the figures and tables of the main context and the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Appendix A: estimation of the interaction parameter, χ, between PMA and PMMA

The phase behavior of polymer and copolymer blends can be described by an extension of the Flory expression for the free energy of mixing which is governed by the segmental interaction energy (B_ij).⁴¹ The interaction energy is estimated from the empirical equation obtained from the constants k, B₀ and B₁ from

B_ij = B₀ + B₁ϕ + k × B₁ϕ²

Segments		B0 (J cm^−3)	B1 (J cm^−3)	k
i	j
Methyl methacrylate	Methyl acrylate	1.47	−0.78	−0.1

where ϕ is the volume fraction of the matrix.

The solubility parameter (δ_ij) is defined as^41,65

B_ij = (δ_i − δ_j)².

The interaction parameter (χ) is thus

where M is the molecular weight of the matrix; ρ is the density of the matrix; R is the ideal gas constant. For our PMA/PMMA blend, PMA is the matrix with B_ij = 0.831 J cm⁻³. As a result,
which agrees with the previous literature results.²⁵

Acknowledgements

This work was supported by the National Science Foundation with Award Number NSF-DMR 2211573. C. M. is funded by the Stevens Provost Fellowship Program. P. A. acknowledges the NSF-CMMI 1825250 award for partially funding this work.

References

1. A. C. Balazs, T. Emrick and T. P. Russell, Nanoparticle Polymer Composites: Where Two Small Worlds Meet, Science, 2006, 314(5802), 1107–1110.
2. S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, 50th Anniversary Perspective: Are Polymer Nanocomposites Practical for Applications?, Macromolecules, 2017, 50(3), 714–731.
3. S. K. Kumar, V. Ganesan and R. A. Riggleman, Perspective: Outstanding theoretical questions in polymer-nanoparticle hybrids, J. Chem. Phys., 2017, 147, 020901.
4. R. Sun, M. Melton, N. Safaie, R. C. Ferrier, S. Cheng, Y. Liu, X. Zuo and Y. Wang, Molecular View on Mechanical Reinforcement in Polymer Nanocomposites, Phys. Rev. Lett., 2021, 126(11), 117801.
5. S. Cheng, S.-J. Xie, J.-M. Y. Carrillo, B. Carroll, H. Martin, P.-F. Cao, M. D. Dadmun, B. G. Sumpter, V. N. Novikov, K. S. Schweizer and A. P. Sokolov, Big Effect of Small Nanoparticles: A Shift in Paradigm for Polymer Nanocomposites, ACS Nano, 2017, 11(1), 752–759.
6. S. Cheng, V. Bocharova, A. Belianinov, S. Xiong, A. Kisliuk, S. Somnath, A. P. Holt, O. S. Ovchinnikova, S. Jesse, H. Martin, T. Etampawala, M. Dadmun and A. P. Sokolov, Unraveling the Mechanism of Nanoscale Mechanical Reinforcement in Glassy Polymer Nanocomposites, Nano Lett., 2016, 16(6), 3630–3637.
7. J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Current issues in research on structure–property relationships in polymer nanocomposites, Polymer, 2010, 51(15), 3321–3343.
8. S. Wang, Z. Luo, J. Liang, J. Hu, N. Jiang, J. He and Q. Li, Polymer Nanocomposite Dielectrics: Understanding the Matrix/Particle Interface, ACS Nano, 2022, 16(9), 13612–13656.
9. E. J. Bailey and K. I. Winey, Dynamics of polymer segments, polymer chains, and nanoparticles in polymer nanocomposite melts: A review, Prog. Polym. Sci., 2020, 105, 101242.
10. Q. Chen, S. Gong, J. Moll, D. Zhao, S. K. Kumar and R. H. Colby, Mechanical Reinforcement of Polymer Nanocomposites from Percolation of a Nanoparticle Network, ACS Macro Lett., 2015, 4(4), 398–402.
11. J. Yang, M. Melton, R. Sun, W. Yang and S. Cheng, Decoupling the Polymer Dynamics and the Nanoparticle Network Dynamics of Polymer Nanocomposites through Dielectric Spectroscopy and Rheology, Macromolecules, 2020, 53(1), 302–311.
12. L. Song, S. Patil, Y. Song, L. Chen, F. Tian, L. Chen, X. Li, L. Li and S. Cheng, Nanoparticle Clustering and Viscoelastic Properties of Polymer Nanocomposites with Non-Attractive Polymer–Nanoparticle Interactions, Macromolecules, 2022, 55(17), 7626–7636.
13. K. S. Schweizer and D. S. Simmons, Progress towards a phenomenological picture and theoretical understanding of glassy dynamics and vitrification near interfaces and under nanoconfinement, J. Chem. Phys., 2019, 151, 240901.
14. S. Cheng, B. Carroll, V. Bocharova, J.-M. Carrillo, B. G. Sumpter and A. P. Sokolov, Focus: Structure and dynamics of the interfacial layer in polymer nanocomposites with attractive interactions, J. Chem. Phys., 2017, 146, 203201.
15. S. Cheng, A. P. Holt, H. Wang, F. Fan, V. Bocharova, H. Martin, T. Etampawala, B. T. White, T. Saito, N.-G. Kang, M. D. Dadmun, J. W. Mays and A. P. Sokolov, Unexpected Molecular Weight Effect in Polymer Nanocomposites, Phys. Rev. Lett., 2016, 116(3), 038302.
16. B. Carroll, S. Cheng and A. P. Sokolov, Analyzing the Interfacial Layer Properties in Polymer Nanocomposites by Broadband Dielectric Spectroscopy, Macromolecules, 2017, 50(16), 6149–6163.
17. S. Cheng and A. P. Sokolov, Correlation between the temperature evolution of the interfacial region and the growing dynamic cooperativity length scale, J. Chem. Phys., 2020, 152, 094904.
18. S. Gong, Q. Chen, J. F. Moll, S. K. Kumar and R. H. Colby, Segmental Dynamics of Polymer Melts with Spherical Nanoparticles, ACS Macro Lett., 2014, 3(8), 773–777.
19. A. Papon, H. Montes, F. Lequeux, J. Oberdisse, K. Saalwächter and L. Guy, Solid particles in an elastomer matrix: impact of colloid dispersion and polymer mobility modification on the mechanical properties, Soft Matter, 2012, 8(15), 4090–4096.
20. M. Krutyeva, A. Wischnewski, M. Monkenbusch, L. Willner, J. Maiz, C. Mijangos, A. Arbe, J. Colmenero, A. Radulescu, O. Holderer, M. Ohl and D. Richter, Effect of Nanoconfinement on Polymer Dynamics: Surface Layers and Interphases, Phys. Rev. Lett., 2013, 110(10), 108303.
21. S. Cheng, D. Kogut, J. Zheng, S. Patil, F. Yang and W. Lu, Dynamics of polylactic acid under ultrafine nanoconfinement: The collective interface effect and the spatial gradient, J. Chem. Phys., 2024, 160, 114904.
22. E. Senses, A. Faraone and P. Akcora, Microscopic Chain Motion in Polymer Nanocomposites with Dynamically Asymmetric Interphases, Sci. Rep., 2016, 6(1), 29326.
23. E. Senses, A. Isherwood and P. Akcora, Reversible Thermal Stiffening in Polymer Nanocomposites, ACS Appl. Mater. Interfaces, 2015, 7(27), 14682–14689.
24. S. Yang, S. Liu, S. Narayanan, C. Zhang and P. Akcora, Chemical heterogeneity in interfacial layers of polymer nanocomposites, Soft Matter, 2018, 14(23), 4784–4791.
25. D. Wu, Y. Feng, R. Li, R. Ozisik and P. Akcora, Entanglement density and particle dynamics in rigid interfacial layers of polymer nanocomposites, J. Appl. Phys., 2021, 130, 064701.
26. D. Wu, Y. Ge, R. Li, Y. Feng and P. Akcora, Thermally Activated Shear Stiffening in Polymer-Grafted Nanoparticle Composites for High-Temperature Adhesives, ACS Appl. Polym. Mater., 2022, 4(4), 2819–2827.
27. D. Wu, D. G. Weiblen, R. Ozisik and P. Akcora, Local Viscosity of Interfacial Layers in Polymer Nanocomposites Measured by Magnetic Heating, ACS Appl. Polym. Mater., 2020, 2(12), 5542–5549.
28. Y. J. Gagnon, J. C. Burton and C. B. Roth, Development of broad modulus profile upon polymer–polymer interface formation between immiscible glassy–rubbery domains, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(1), e2312533120.
29. C. B. Roth, Polymers under nanoconfinement: where are we now in understanding local property changes?, Chem. Soc. Rev., 2021, 50(14), 8050–8066.
30. G. C. Chung, J. A. Kornfield and S. D. Smith, Compositional Dependence of Segmental Dynamics in a Miscible Polymer Blend, Macromolecules, 1994, 27(20), 5729–5741.
31. G. C. Chung, J. A. Kornfield and S. D. Smith, Component Dynamics Miscible Polymer Blends: A Two-Dimensional Deuteron NMR Investigation, Macromolecules, 1994, 27(4), 964–973.
32. T. P. Lodge and T. C. B. McLeish, Self-Concentrations and Effective Glass Transition Temperatures in Polymer Blends, Macromolecules, 2000, 33(14), 5278–5284.
33. S. Shenogin, R. Kant, R. Colby and S. Kumar, Dynamics of Miscible Polymer Blends: Predicting the Dielectric Response, Macromolecules, 2007, 40(16), 5759–5766.
34. A. Zetsche and E. W. Fischer, Dielectric studies of the α-relaxation in miscible polymer blends and its relation to concentration fluctuations, Acta Polym., 1994, 45(3), 168–175.
35. G. Katana, E. W. Fischer, T. Hack, V. Abetz and F. Kremer, Influence of Concentration Fluctuations on the Dielectric.alpha.-Relaxation in Homogeneous Polymer Mixtures, Macromolecules, 1995, 28(8), 2714–2722.
36. Y. Wang, S. Patil, S. Cheng and C. Do, The influence of elongation-induced concentration fluctuations on segmental friction in polymer blends, Soft Matter, 2024, 20(21), 4257–4269.
37. L. A. Wall, Roestamsjah and M. H. Aldridge, The Glass Transition Temperature of Monodispersed Polystyrenes and Their Binary Mixtures, J. Res. Natl. Bur. Stand., Sect. A, 1974, 78a(4), 447–451.
38. I. I. Popov, R. R. Nigmatullin, E. Y. Koroleva and A. A. Nabereznov, The generalized Jonscher's relationship for conductivity and its confirmation for porous structures, J. Non-Cryst. Solids, 2012, 358(1), 1–7.
39. S. Cheng, Broadband Dielectric Spectroscopy of Polymer Nanocomposites, Broadband Dielectric Spectroscopy: A Modern Analytical Technique, American Chemical Society, 2021, vol. 1375, pp. 157–183.
40. I. Popov, S. Cheng and A. P. Sokolov, Broadband Dielectric Spectroscopy and Its Application in Polymeric Materials, Macromolecular Engineering, 2022, pp. 1–39.
41. J. M. G. Cowie, R. Ferguson, M. D. Fernandez, M. J. Fernandez and I. J. McEwen, Miscibility of some methacrylate and acrylate homopolymer blends, Macromolecules, 1992, 25(12), 3170–3173.
42. H. Emamy, S. K. Kumar and F. W. Starr, Diminishing Interfacial Effects with Decreasing Nanoparticle Size in Polymer-Nanoparticle Composites, Phys. Rev. Lett., 2018, 121(20), 207801.
43. R. Bergman, F. Alvarez, A. Alegría and J. Colmenero, The merging of the dielectric α- and β-relaxations in poly-(methyl methacrylate), J. Chem. Phys., 1998, 109(17), 7546–7555.
44. H. Yin and A. Schönhals, Broadband Dielectric Spectroscopy on Polymer Blends, in Polymer Blends Handbook, ed. L. A. Utracki and C. A. Wilkie, Springer, Netherlands, Dordrecht, 2014, pp. 1299–1356.
45. L. Monnerie, F. Lauprêtre and J. L. Halary, Investigation of Solid-State Transitions in Linear and Crosslinked Amorphous Polymers, in Intrinsic Molecular Mobility and Toughness of Polymers I, ed. H.-H. Kausch, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 35–213.
46. M. Füllbrandt, P. J. Purohit and A. Schönhals, Combined FTIR and Dielectric Investigation of Poly(vinyl acetate) Adsorbed on Silica Particles, Macromolecules, 2013, 46(11), 4626–4632.
47. A. P. Holt, J. R. Sangoro, Y. Wang, A. L. Agapov and A. P. Sokolov, Chain and Segmental Dynamics of Poly(2-vinylpyridine) Nanocomposites, Macromolecules, 2013, 46(10), 4168–4173.
48. S. Cheng, B. Carroll, W. Lu, F. Fan, J.-M. Carrillo, H. Martin, A. Holt, N.-G. Kang, V. Bocharova, J. Mays, B. Sumpter, M. Dadmun and A. Sokolov, Interfacial Properties of Polymer Nanocomposites: Role of Chain Rigidity and Dynamic Heterogeneity Length Scale, Macromolecules, 2017, 50(6), 2397–2406.
49. S. Cheng, S. Mirigian, J.-M. Y. Carrillo, V. Bocharova, B. G. Sumpter, K. S. Schweizer and A. P. Sokolov, Revealing spatially heterogeneous relaxation in a model nanocomposite, J. Chem. Phys., 2015, 143, 194704.
50. I. Popov, B. Carroll, V. Bocharova, A.-C. Genix, S. Cheng, A. Khamzin, A. Kisliuk and A. P. Sokolov, Strong Reduction in Amplitude of the Interfacial Segmental Dynamics in Polymer Nanocomposites, Macromolecules, 2020, 53(10), 4126–4135.
51. E. U. Mapesa, D. P. Street, M. F. Heres, S. M. Kilbey II and J. Sangoro, Wetting and Chain Packing across Interfacial Zones Affect Distribution of Relaxations in Polymer and Polymer-Grafted Nanocomposites, Macromolecules, 2020, 53(13), 5315–5325.
52. S. Madkour, P. Szymoniak, M. Heidari, R. von Klitzing and A. Schönhals, Unveiling the Dynamics of Self-Assembled Layers of Thin Films of Poly(vinyl methyl ether) (PVME) by Nanosized Relaxation Spectroscopy, ACS Appl. Mater. Interfaces, 2017, 9(8), 7535–7546.
53. E. Helfand and Y. Tagami, Theory of the Interface between Immiscible Polymers. II, J. Chem. Phys., 2003, 56(7), 3592–3601.
54. E. Helfand and Y. Tagami, Theory of the interface between immiscible polymers, J. Polym. Sci., Part B: Polym. Lett., 1971, 9(10), 741–746.
55. D. Broseta, G. H. Fredrickson, E. Helfand and L. Leibler, Molecular weight and polydispersity effects at polymer–polymer interfaces, Macromolecules, 1990, 23(1), 132–139.
56. I. Alig, G. Floudas, A. Avgeropoulos and N. Hadjichristidis, Junction Point Fluctuations in Microphase Separated Polystyrene−Polyisoprene−Polystyrene Triblock Copolymer Melts. A Dielectric and Rheological Investigation, Macromolecules, 1997, 30(17), 5004–5011.
57. I. Cendoya, A. Alegría, J. M. Alberdi, J. Colmenero, H. Grimm, D. Richter and B. Frick, Effect of Blending on the PVME Dynamics. A Dielectric, NMR, and QENS Investigation, Macromolecules, 1999, 32(12), 4065–4078.
58. J. W. Sy and J. Mijovic, Reorientational Dynamics of Poly(vinylidene fluoride)/Poly(methyl methacrylate) Blends by Broad-Band Dielectric Relaxation Spectroscopy, Macromolecules, 2000, 33(3), 933–946.
59. A. C. Genix, A. Arbe, F. Alvarez, J. Colmenero, L. Willner and D. Richter, Dynamics of poly(ethylene oxide) in a blend with poly(methyl methacrylate): A quasielastic neutron scattering and molecular dynamics simulations study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(3), 031808.
60. M. Tyagi, A. Arbe, J. Colmenero, B. Frick and J. R. Stewart, Dynamic Confinement Effects in Polymer Blends. A Quasielastic Neutron Scattering Study of the Dynamics of Poly(ethylene oxide) in a Blend with Poly(vinyl acetate), Macromolecules, 2006, 39(8), 3007–3018.
61. M. Tyagi, A. Arbe, A. Alegría, J. Colmenero and B. Frick, Dynamic Confinement Effects in Polymer Blends. A Quasielastic Neutron Scattering Study of the Slow Component in the Blend Poly(vinyl acetate)/Poly(ethylene oxide), Macromolecules, 2007, 40(13), 4568–4577.
62. V. A. Harmandaris, K. Kremer and G. Floudas, Dynamic Heterogeneity in Fully Miscible Blends of Polystyrene with Oligostyrene, Phys. Rev. Lett., 2013, 110(16), 165701.
63. S. K. Kumar, S. Shenogin and R. H. Colby, Dynamics of Miscible Polymer Blends:  Role of Concentration Fluctuations on Characteristic Segmental Relaxation Times, Macromolecules, 2007, 40(16), 5759–5766.
64. C. Mbonu, N. C. Osti, D. Wu and P. Akcora, Quasi-elastic neutron scattering study on dynamically asymmetric polymer blends, J. Polym. Sci., 2024, 62(18), 4177.
65. D. R. Paul and J. W. Barlow, A binary interaction model for miscibility of copolymers in blends, Polymer, 1984, 25(4), 487–494.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00731j

---