Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanical characterization of freestanding lipid bilayers with temperature-controlled phase†
Arash
Yahyazadeh Shourabi
a,
Roland
Kieffer
a,
Djanick
de Jong
a,
Daniel
Tam
 *b and
Marie-Eve
Aubin-Tam
*b and
Marie-Eve
Aubin-Tam
 *a
*a
aDepartment of Bionanoscience, Kavli institute of Nanoscience, Delft University of Technology, Van der Maasweg 9, 2629 HZ, Delft, The Netherlands. E-mail: m.e.aubin-tam@tudelft.nl
bLaboratory for Aero and Hydrodynamics, Faculty of Mechanical Engineering, Delft University of Technology, 2628 CD, Delft, The Netherlands. E-mail: d.s.w.tam@tudelft.nl
First published on 17th October 2024
Abstract
Coexistence of lipid domains in cell membranes is associated with vital biological processes. Here, we investigate two such membranes: a multi-component membrane composed of DOPC and DPPC lipids with gel and fluid separated domains, and a single component membrane composed of PMPC lipids forming ripples. We characterize their mechanical properties below their melting point, where ordered and disordered regions coexist, and above their melting point, where they are in fluid phase. To conduct these inquiries, we create lipid bilayers in a microfluidic chip interfaced with a heating system and optical tweezers. The chip features a bubble trap and enables high-throughput formation of planar bilayers. Optical tweezers experiments reveal interfacial hydrodynamics (fluid-slip) and elastic properties (membrane tension and bending rigidity) at various temperatures. For PMPC bilayers, we demonstrate a higher fluid slip at the interface in the fluid-phase compared to the ripple phase, while for the DOPC:DPPC mixture, similar fluid slip is measured below and above the transition point. Membrane tension for both compositions increases after thermal fluidization. Bending rigidity is also measured using the forces required to extend a lipid nanotube pushed out of the freestanding membranes. This novel temperature-controlled microfluidic platform opens numerous possibilities for thermomechanical studies on freestanding planar membranes.
1. Introduction
In both eukaryotic and prokaryotic plasma membranes, coexistence of ordered and disordered regions within the lipid bilayer impacts the membranes’ properties and plays a role in several biological processes, such as protein transport, signal transduction, and the fusion of viruses into cells.1–3 Coexistence of lipid regions in the membrane depends on lipid composition and it can appear in the form of gel domains emergence in lipid mixtures, or ripple-state conformation in single component membranes4,5 In particular, binary lipid mixtures containing 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) promote phase separation resulting in the presence of in-plane gel phase and fluid phase domains. Coexistence of gel and fluid regions presents as patches enriched in highly-ordered saturated lipids, e.g. DPPC, which exist alongside fluid-phase lipid domains, e.g. DOPC.4 Such DOPC:DPPC containing mixtures are often models for biological cell membranes.6,7The ripple phase is another manifestation of ordered–disordered coexisting lipid regions,5,8 more recently described as the coexistence of an ordered phase and a complex mixed phase.9 The ripple phase can occur in single lipid composition bilayers just below the melting temperature (Tm), i.e. in between a pre-transition temperature (Tpre) and Tm, and has been reported for both supported8 and un-supported lipid bilayers.10,11 Unlike the gel-fluid separation in a DOPC–DPPC binary mixture, the ripple-state membrane presents a structure with corrugations with a periodicity of ∼10–30 nm,5,12 and long-range orientation correlation of its hexagonal lattice packed domains.13 For instance, palmitoyl-myristoyl-PC (PMPC, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0–14
0–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC, Tm = 27 °C, Tpre = 17 °C) is a mixed-chain (sn-1 and sn-2 acyl chains of different lengths14) lipid that forms a ripple structure below its Tm.15 Although PMPC is abundant in the mammalian pulmonary system and is involved in COVID-19 infection prevention,16 it is scarcely characterized mechanically especially below the Tm.
0 PC, Tm = 27 °C, Tpre = 17 °C) is a mixed-chain (sn-1 and sn-2 acyl chains of different lengths14) lipid that forms a ripple structure below its Tm.15 Although PMPC is abundant in the mammalian pulmonary system and is involved in COVID-19 infection prevention,16 it is scarcely characterized mechanically especially below the Tm.
It has been shown that membranes with coexisting ordered–disordered regions exhibit complex thermomechanical properties different from what is observed in single-phase ones.17 Yet, the overall literature on the contribution of such lipid sub-domains to the bilayers’ mechanical properties is still limited.18–21 Such studies are thus needed because many biological functions depend on the mechanical properties of the membrane22–24 determined by the spatial phase heterogeneity of bilayers.21,25 The hydrodynamics at the interface (interfacial fluid slip) and elastic properties (membrane tension and bending rigidity) are two subgroups of such mechanical properties, which influence numerous biological processes.26,27 Interfacial fluid slip is an indicator of the bilayer response to the surrounding flow.28In vivo, this response is dependent on bilayer composition/physical properties27 and influences a broad range of biological processes such as ion channel gating, signaling, molecular transport, protein activation, and cell–drug interaction.29–33 On the other hand, membrane tension influences cell polarity,34,35 membrane fusion,36 and trafficking,37 while bending rigidity influences cell growth rate and division instabilities.38 Membrane tension and bending rigidity together also define geometrical and physical properties of lipid nanotubes (LNTs), which are structures also present in cells for molecular transport and intercellular communication.39
Measuring the mechanical characteristics of a membrane in vitro, while altering the phase of the bilayer represents a technical challenge. Two conventional in vitro settings for the study of membrane properties are vesicles and supported bilayers. These systems present limitations for measurements of mechanical and phase-related properties.40,41 In vesicles, controlling membrane curvature can be challenging and usually requires specific custom technology.42,43 Membrane curvature is known to impact lipid ordering and to interfere with phase separation, and more specifically may shift the pre-transition temperature at which the ripple structure occurs.10,44 In supported bilayers, the contact between one leaflet and the solid substrate exerts influences on their phase behavior;45 this results in a strong dependency of the bilayer phase and the related mechanical properties on the substrate topography.46 For example, substrate contact was reported to affect ripple phase formation in supported bilayers.47
The use of planar freestanding membranes formed in microchannels represents a reliable alternative for phase-related studies, as they have minimal curvature and do not contact a surface. This configuration has been used for measurements of room-temperature mechanical properties of single-phase bilayers,28,48,49 but phase-associated mechanical studies using this approach have not been reported. To enable this, an improved microfluidic system is required, to provide precise and controlled heating, while preventing thermal-related instabilities leading to the loss of the membrane, including: membrane instability below the melting point,50 and the management of air bubbles in microchannels for thermal experiments.51 Additionally, the design should robustly handle the often low success rate of membrane formation in microchannels with non-fluid lipid compositions,50,52 aiming for high-throughput and comprehensive characterization in each experiment. It should be noted that in all these artificial systems (freestanding bilayers, vesicles, supported bilayers), the membrane is at equilibrium, as opposed to cell membranes in vivo.53
Here, we study the thermomechanical properties of lipid membranes in a freestanding, planar configuration. We present a microfluidic chip (integrated with a bubble trap and a temperature sensor) compatible with optical tweezers, as a high-throughput tool for the on-chip formation of long-term stable non-fluid bilayers and phase-related investigations. The lipid bilayers are formed by the contact of two lipid monolayers at organic-aqueous interfaces inside a microchannel. This results in artificial lipid membranes perpendicular with respect to the imaging plane enabling physical manipulation with optical tweezers, accessibility to either leaflet independently, and straightforward imaging of the membrane deformations. Two distinct lipid bilayer compositions are used in this study: the gel-fluid domain-forming DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (
DPPC (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3:
3:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) lipid mixture, and the ripple phase-forming PMPC lipid. For both compositions, phase change takes place approximately at the same temperature (Tm ≈ 27 °C54). The chip is mounted on an optical tweezer setup with a coiled objective to heat it, inducing temperature-driven phase changes in the membranes. We study the temperature-related elastic properties (membrane tension and bending rigidity) and interfacial hydrodynamics (fluid slip) for temperatures below and above their melting points (i.e. between 21 °C and 32 °C). We first perform a study on how the fluid-slip at the interface depends on the temperature of the bilayer by shearing the membranes with the optically trapped bead. Then, beads are pushed against these bilayers bidirectionally to extract biologically relevant mechanical properties namely surface tension, membrane-to-tube and tube-to-membrane transition force-barriers, and bending rigidity at the aforementioned temperatures.
2 molar ratio) lipid mixture, and the ripple phase-forming PMPC lipid. For both compositions, phase change takes place approximately at the same temperature (Tm ≈ 27 °C54). The chip is mounted on an optical tweezer setup with a coiled objective to heat it, inducing temperature-driven phase changes in the membranes. We study the temperature-related elastic properties (membrane tension and bending rigidity) and interfacial hydrodynamics (fluid slip) for temperatures below and above their melting points (i.e. between 21 °C and 32 °C). We first perform a study on how the fluid-slip at the interface depends on the temperature of the bilayer by shearing the membranes with the optically trapped bead. Then, beads are pushed against these bilayers bidirectionally to extract biologically relevant mechanical properties namely surface tension, membrane-to-tube and tube-to-membrane transition force-barriers, and bending rigidity at the aforementioned temperatures.
Other well-established techniques, such as cDICE55,56 and eDICE,57 also rely on the contact of two monolayers at an organic–aqueous interface for membrane formation. These techniques are increasingly used to synthesize GUVs that model minimal cells.57,58 For mechanical characterization of membranes formed by monolayers zipping at an organic–aqueous interface, the planar freestanding configuration of the present study offers enhanced opportunities.
2. Results and discussion
2.1. High-throughput formation of freestanding planar membranes
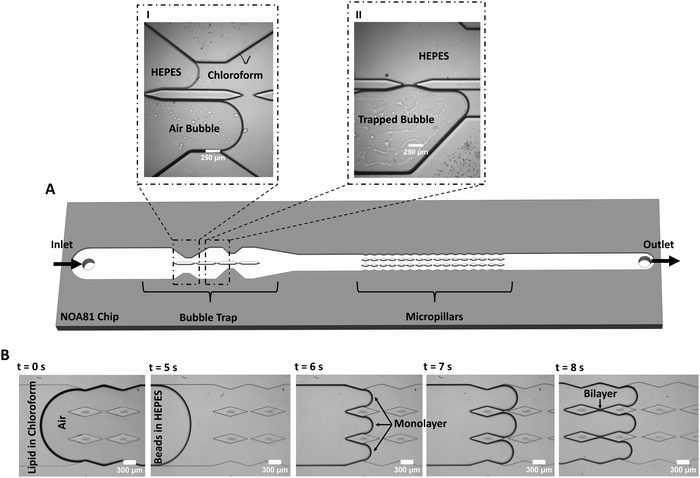
The freestanding lipid bilayers are formed in a microfluidic device by the contact of two lipid monolayers based on a reported method28,49 that is here modified for increased lipid membrane formation and stability (Fig. 1). The core of the improvement revolves around tackling three primary challenges that existed in previous systems.The first challenge is to deal with unwanted bubbles in the channels often formed at the interface between the aqueous and organic phases, disrupting the contact process between monolayers. Air bubbles are a common hurdle in microfluidics,59 in particular for experiments conducted at varying temperatures.51 The bubbles have several possible origins: air trapping due to the geometry and various components of the system (tubing, connection, inlet, microchannels), wettability properties of the chip material, temperature variations, and injecting both an organic and an inorganic solution into the chip.60 To capture and/or remove air bubbles from microfluidic systems, bubble traps are often used. They are categorized as passive or active traps with regards to their function,59 and as in-plane or out-of-plane with regards to their configuration.29,51 Here, a novel passive bubble trap with an in-plane configuration is designed with an asymmetric architecture (discussed more in details later on).
The second challenge is the frequent low success rate of membrane formation in microchips, specifically with cholesterol-free non-fluid lipid compositions or non-conical lipids.50,52 To tackle this issue, a chamber filled with several pillars was designed downstream of the bubble trap. This results in a high-throughput membrane formation, with several stable membranes forming per microchannel at a time. Using multiple membranes on a single chip allows various experiments on different membranes without the time-consuming process of forming new membranes for each new experiment.28,49 Having several membranes on the chip is a key point here, since designs with a single membrane per microchannel have reproducibility and throughput issues making them unsuitable for mechanical characterization when a large number of experiments with different lipid compositions are usually required. However, we should mention that single-membrane designs are still usually necessary for electrical measurements,61,62 for asymmetric membrane formation,52 and for membrane protein channels studies.63
Finally, the third challenge is to ensure that the pressure and the flow velocity on each side of the bilayer are comparable, during and after membrane formation. This is a requirement for smooth leaflets zipping, and it ensures the flatness and improves the membrane long-term stability under ongoing flow. To do so, we designed the pillar chamber with an architecture that follows the fluid-flow pattern (contracting – expanding width of walls in the chamber, see Fig. 1B) making the flow at the gaps fully symmetric (i.e. balanced fluidic pressure at the gap), thus ideal for membrane formation.
To form membranes, a solution of lipids dissolved in chloroform is flown into the chip followed by the aqueous buffer HEPES. During this process, air bubbles are often observed at the organic/aqueous interface or in the chloroform. If air bubbles are not captured and reach the pillars, they affect the flow and prevent membrane formation. The bubble trap is divided into two channels of unequal widths, enabling the trapping of air bubbles in the upstream section of the chip (Fig. 1). Due to the strong wettability of NOA81 for chloroform, the chloroform solution flows into both channels almost simultaneously (Fig. 1A, panel I). Subsequently, we observe that any air bubble present in the system will enter one of the channels, preferably the wider one (Fig. 1A, panel I). Bubbles are trapped and slowed down at the constricted sections of the channel (Fig. 1A, panel II), enabling the aqueous phase to freely flow in the other channel and resulting in a continuous bubble-free buffer-chloroform interface in the pillars section (Fig. 1B). Lipid bilayers can then be formed by the junction of two monolayer leaflets that ‘zip’ together after each pillar (Fig. 1B).
To demonstrate the added value of using the bubble trap, we compare DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) lipid bilayers formed either with the bubble trap or without (by infusing from the outlet). With the use of the bubble trap, a continuous leaflet-leaflet zipping allows the formation of several stable, flat membranes on the chip (Video S1, ESI†). Without the bubble trap, due to the highly asymmetric flow at the gap and the fluidic disturbances generated by the bubbles, the membranes are either not forming, are very short lived (Video S2, ESI†), or are highly curved. The bubble trap design substantially enhances the formation of stable flat membranes even at flowrates as high as 5 μL min−1 (at the inlet). In general, we find that membranes composed of phosphatidylcholines (PC) lipid compositions that are in liquid phase at room temperature (e.g., 16
2) lipid bilayers formed either with the bubble trap or without (by infusing from the outlet). With the use of the bubble trap, a continuous leaflet-leaflet zipping allows the formation of several stable, flat membranes on the chip (Video S1, ESI†). Without the bubble trap, due to the highly asymmetric flow at the gap and the fluidic disturbances generated by the bubbles, the membranes are either not forming, are very short lived (Video S2, ESI†), or are highly curved. The bubble trap design substantially enhances the formation of stable flat membranes even at flowrates as high as 5 μL min−1 (at the inlet). In general, we find that membranes composed of phosphatidylcholines (PC) lipid compositions that are in liquid phase at room temperature (e.g., 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 18
0 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC, 18
0 PC, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 18
1 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PC, 18
1 PC, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 18
0 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PC, and 16
1 PC, and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 18
0 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 PC) remain stable for weeks in our chip if all ports are sealed with silicon grease.
2 PC) remain stable for weeks in our chip if all ports are sealed with silicon grease.
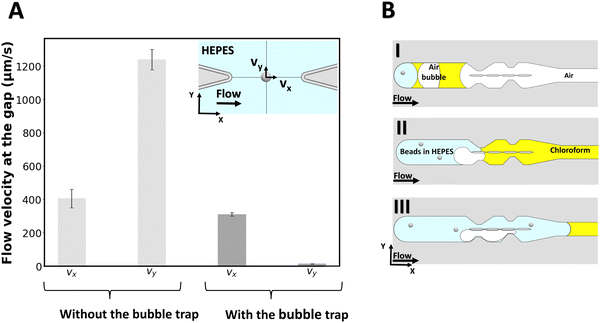
To measure the local flow velocities in the gap, a polystyrene bead of 2 μm diameter is optically trapped at the center of the gap's midline as indicated in the inset of Fig. 2A, while liquid is flown through the chip from the outlet (for the case with no bubble trap) and from the inlet (for the case with the bubble trap). For this purpose, a similar procedure as for lipid bilayer formation is followed, except that no lipid is added to the organic solvent. Then, while a flow of 2 μL min−1 is applied with the syringe pump, the displacement of the beads from the center of the optical trap is measured for a 6-second period and converted to flow velocity for both cases (N = 3 experiments for each case). Fig. 2 reports the velocity components of the flow at the gap for both cases. Without the bubble trap, the velocity along the y-axis (vy) reaches 1216 ± 153 μm s−1, which indicates that fluid flows across the gap because of a pressure imbalance between the two channels caused by the presence of bubbles in the system. With the bubble trap however, bubbles are trapped upstream in the system (Fig. 2B) and no bubble can reach the pillars section to disturb the flow pattern. We find a significantly lower vy of 16 ± 9 μm s−1 in the case of using a bubble trap, which demonstrates that the pressure in both channels is almost equal. This pressure balance shows the benefits of using the bubble trap for membrane formation.
We can directly estimate the pressure difference in the two channels from a hydraulic circuit analysis. From the geometry of our channel, we find a value for the hydraulic resistance of each channel section on the order of Rh ≈ 1.6 × 1010 kg m−4 s−1. We can estimate the volumetric flow rate from the velocity measurement, which yields an estimate for the pressure difference between the channels of ΔP ≈ 10−3 Pa for vy = 16 μm s−1 (with bubble trap) and on the order of ΔP ≈ 10−1 Pa for vy = 1216 μm s−1 (without bubble trap).
These estimates of the pressure difference in the channels can be directly related to the curvature of the membrane that will form in the gap. Given the membrane tensions previously measured in similar freestanding membranes (ranging between σ = 3–6 × 10−6 N m−1),49 we can estimate the radius of curvature of a membrane formed in the device with bubble trap to be on the order of ∼1 mm, which can be approximated as a flat membrane given the size of the gap. For the device without bubble trap, the radius of curvature of the membrane formed would be ∼10 μm, which is smaller than the gap size and we therefore do not expect a membrane to form.
2.2. Hydrodynamics at the interface of membranes
We start characterizing our lipid membranes by investigating the hydrodynamics at their interface (fluid slip). We have previously shown that the fluid slip at the interface of freestanding planar membranes depends on lipid composition and lies in between a full-slip (equivalent to no wall) and a no-slip (solid wall) boundary condition.28 Here, we compare the flow behavior at the interface of gel-fluid and ripple membranes at 21 °C and show how fluidizing them by increasing the temperature to 32 °C affects fluid slip.For this purpose, we use PMPC and DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) bilayers, which were both reported to experience a phase transition at 27 °C.66,67 It should be noted that Tm may deviate slightly depending on the solvent used, the membrane configuration, and the interactions between the membranes and the platform on which they are formed. For instance, freestanding planar DOPC
2) bilayers, which were both reported to experience a phase transition at 27 °C.66,67 It should be noted that Tm may deviate slightly depending on the solvent used, the membrane configuration, and the interactions between the membranes and the platform on which they are formed. For instance, freestanding planar DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) membranes formed in microchannels by contacting monolayers followed by subsequent drainage of the solvent, showed a Tm that deviates ∼0.4 °C on average from the Tm observed on giant unilamellar vesicles (GUVs).54 We therefore do not rule out the possibility that our method of membrane formation and the presence of residual solvent may influence phase separation or shift slightly the transition point. For this reason, we probed a range of several degrees around 27 °C, i.e. from 21 °C to 32 °C. Also, one indication that we likely cross Tm is that when heating from 21 °C to 32 °C, membrane buds were occasionally observed (Fig. S3, ESI†), as reported for lipid vesicles when going through phase transition.68 Note that our mechanical testing was not performed in the vicinity of such buds, but only on flat membranes.
2) membranes formed in microchannels by contacting monolayers followed by subsequent drainage of the solvent, showed a Tm that deviates ∼0.4 °C on average from the Tm observed on giant unilamellar vesicles (GUVs).54 We therefore do not rule out the possibility that our method of membrane formation and the presence of residual solvent may influence phase separation or shift slightly the transition point. For this reason, we probed a range of several degrees around 27 °C, i.e. from 21 °C to 32 °C. Also, one indication that we likely cross Tm is that when heating from 21 °C to 32 °C, membrane buds were occasionally observed (Fig. S3, ESI†), as reported for lipid vesicles when going through phase transition.68 Note that our mechanical testing was not performed in the vicinity of such buds, but only on flat membranes.
We optically trap a polystyrene bead of diameter 2a = 2 μm at a specific distance d between the center of the bead and the freestanding lipid bilayer. The membrane is then moved parallel to its plane with the use of a piezostage (inset of Fig. 3A and Video S3, ESI†). The drag force experienced by the bead (D) is measured with the optical trap and is normalized with Stokes’ drag (FD = 6πμUa, where μ is the dynamic viscosity, U is bead's relative velocity). We call this force ratio Cδ and use it to describe the fluid slip at the interface of the aqueous medium with the membrane as previously described.28Cδ can be described as follows:
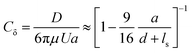 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) membranes with a high-speed camera while a 2 μm optically trapped bead was translated at velocities U between 5–100 μm s−1 in the plane of the membrane. This experiment was repeated with a distance d varying from 1.1 μm to 11.1 μm between the bead's center and the bilayer. Video analysis showed that no significant membrane deformation was obtained at any value of U or d tested (Fig. S4, ESI†).
2) membranes with a high-speed camera while a 2 μm optically trapped bead was translated at velocities U between 5–100 μm s−1 in the plane of the membrane. This experiment was repeated with a distance d varying from 1.1 μm to 11.1 μm between the bead's center and the bilayer. Video analysis showed that no significant membrane deformation was obtained at any value of U or d tested (Fig. S4, ESI†).
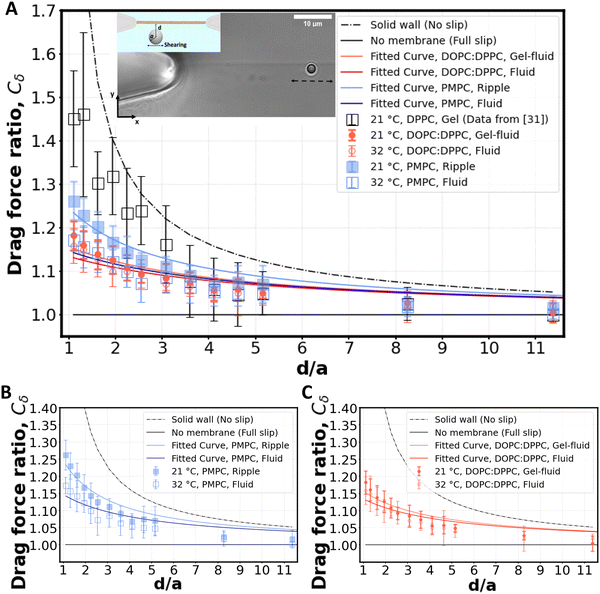 | ||
Fig. 3 Shearing experiment. (A) An optically trapped bead of radius a is used to shear the membrane at various distances d (as shown in inset). The graph shows the ratio of the experimentally measured drag force on a bead of diameter 2a = 2 μm to the Stokes’ force at different bead-membrane distances d. Fitted curve of eqn (1) is also plotted on the experimental data. R2 values are 0.84, 0.80, 0.91, 0.78 for gel-fluid DOPC:DPPC, fluid DOPC:DPPC, ripple PMPC, and fluid PMPC respectively. The dashed line represents the no-slip condition (ls = 0) that happens at the boundary of a solid wall based on Faxén's law.69 The solid line represents what we would expect for a free gap (no membrane), where a full slip (ls = ∞) happens. For the lipid membranes tested, the behaviour lies between a solid wall and a free gap (no membrane) condition depending on composition and temperature as indicated with red and blue data points. (B and C) Drag ratio of PMPC and DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (same data as (A), plotted independently for better visualization). DPPC (same data as (A), plotted independently for better visualization). | ||
For our membranes, Cδ was deduced from our experimental measurements at varying distances d/a from the bilayer (Fig. 3). For the rippled-phase PMPC membrane at 21 °C, we measure Cδ = 1.26 ± 0.05 at a distance d = 1.1 μm between the bead's center and the bilayer, resulting in a fitted slip length ls = 1.9a, higher than the previously reported value for DPPC (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC) bilayers (Cδ = 1.46 ± 0.15 at d = 1.1 μm, and ls = 0.83a)28 at 21 °C. Therefore, we find that the mixed-chain PMPC (16
0 PC) bilayers (Cδ = 1.46 ± 0.15 at d = 1.1 μm, and ls = 0.83a)28 at 21 °C. Therefore, we find that the mixed-chain PMPC (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 14
0 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC) lipid allows for higher fluid slippage compared to its symmetric-chain counterpart, i.e. DPPC (16
0 PC) lipid allows for higher fluid slippage compared to its symmetric-chain counterpart, i.e. DPPC (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC). When increasing the temperature to 32 °C, PMPC bilayers transition to the fluid phase and we find a significant reduction in the drag ratio at 32 °C (Cδ = 1.18 ± 0.03 at d = 1.1 μm, ls = 3.4a). Our observation of a decrease in the drag force experienced by the bead at the interface upon heating is consistent with previous reports on the decrease of drag force experienced by a bead attached to a DMPC giant vesicle transitioning from the ripple to the liquid-disordered phase.71 We performed the same experiment with DOPC
0 PC). When increasing the temperature to 32 °C, PMPC bilayers transition to the fluid phase and we find a significant reduction in the drag ratio at 32 °C (Cδ = 1.18 ± 0.03 at d = 1.1 μm, ls = 3.4a). Our observation of a decrease in the drag force experienced by the bead at the interface upon heating is consistent with previous reports on the decrease of drag force experienced by a bead attached to a DMPC giant vesicle transitioning from the ripple to the liquid-disordered phase.71 We performed the same experiment with DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) membranes. Unlike PMPC, we find drag ratios that are not significantly different below and above Tm, i.e. Cδ = 1.18 ± 0.03 (ls = 3.2a) at 21 °C and Cδ = 1.16 ± 0.04 (ls = 3.8a) at 32 °C.
2) membranes. Unlike PMPC, we find drag ratios that are not significantly different below and above Tm, i.e. Cδ = 1.18 ± 0.03 (ls = 3.2a) at 21 °C and Cδ = 1.16 ± 0.04 (ls = 3.8a) at 32 °C.
The values measured for Cδ at intermediate temperatures between 21 °C and 32 °C are also provided in Fig. S6A (ESI†) for both lipid compositions. We observe a continuous decrease of Cδ with temperature for PMPC. For DOPC:DPPC, the drag ratio remains almost constant at all the temperatures. Similarly, FRAP experiments on DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (1
DPPC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) lipid bilayers showed no correlation of lipid diffusion coefficient with temperature when the temperature was increased from 22 °C to 38 °C.72
1) lipid bilayers showed no correlation of lipid diffusion coefficient with temperature when the temperature was increased from 22 °C to 38 °C.72
When comparing PMPC and DOPC:DPPC bilayers, we find that both bilayers exhibit a behavior at the water interface which is far from a solid boundary (no-slip), with ripple-phase PMPC showing a lower slip-length at the interface in comparison to the two-phase DOPC:DPPC membrane. We attribute this lower drag ratio obtained for the two-phase DOPC:DPPC membranes to the presence of kinks in the unsaturated lipid DOPC.
The interfacial drag ratios enable us to estimate membrane viscosity (ηb in Pa s m) and its variation with temperature. For this purpose, we assume an intermonolayer friction coefficient b in the range of 0.3 × 103 ≤ b ≤ 1.7 × 103 Pa s m−1 (ref. 28) (which was reported experimentally for DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (2
DPPC (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) bilayers using a similar microfluidic setup). With the methodology provided by Amador et al.28 we estimate a membrane viscosity of 3.4 × 10−9 Pa s m ≤ ηb ≤ 9.8 × 10−9 Pa s m for PMPC at 21 °C, 1.3 × 10−9 Pa s m ≤ ηb ≤ 5.5 × 10−9 Pa s m for PMPC at 32 °C, 1.0 × 10−9 Pa s m ≤ ηb ≤ 5.6 × 10−9 Pa s m for DOPC:DPPC at 21 °C, and 0.46 × 10−9 Pa s m ≤ ηb ≤ 5.1 × 10−9 Pa s m for DOPC:DPPC at 32 °C. For comparison, a membrane viscosity of 3 nPa s m was reported for SOPC (18
1) bilayers using a similar microfluidic setup). With the methodology provided by Amador et al.28 we estimate a membrane viscosity of 3.4 × 10−9 Pa s m ≤ ηb ≤ 9.8 × 10−9 Pa s m for PMPC at 21 °C, 1.3 × 10−9 Pa s m ≤ ηb ≤ 5.5 × 10−9 Pa s m for PMPC at 32 °C, 1.0 × 10−9 Pa s m ≤ ηb ≤ 5.6 × 10−9 Pa s m for DOPC:DPPC at 21 °C, and 0.46 × 10−9 Pa s m ≤ ηb ≤ 5.1 × 10−9 Pa s m for DOPC:DPPC at 32 °C. For comparison, a membrane viscosity of 3 nPa s m was reported for SOPC (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 18
0 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PC) GUVs measured using falling ball viscometry,73 13 nPa s m for SOPC GUVs measured using probe diffusion method,74 and 0.15 nPa s m for DOPC LUVs measured via Fluorescence lifetime of dye.75
1 PC) GUVs measured using falling ball viscometry,73 13 nPa s m for SOPC GUVs measured using probe diffusion method,74 and 0.15 nPa s m for DOPC LUVs measured via Fluorescence lifetime of dye.75
2.3. Surface tension and bending rigidity of membranes
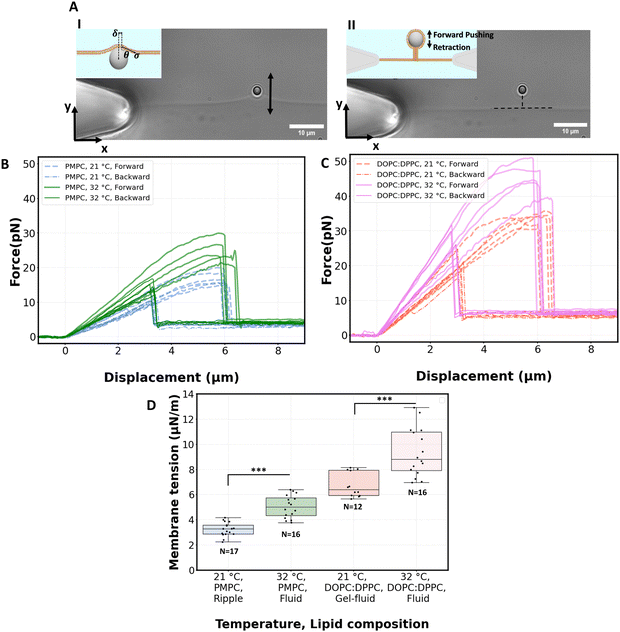
We proceed by performing measurements of membrane tension (σ) and bending rigidity (k) on bilayers at temperatures between and including 21 °C and 32 °C. For measuring membrane tension and rigidity, we used the optical trap to push a 2 μm bead against a planar, freestanding bilayer. The force-displacement curve of the trapped bead provides a direct measurement of the surface tension and the subsequent calculation of the tube radius and bending rigidity.49 First, the bead is pushed ‘forward’ and enters in contact with the membrane, the force increases as the membrane deforms and gradually wraps around the bead (panel I of Fig. 4A corresponding to the linear region of solid lines in Fig. 4B). After reaching a maximum force, the force drops abruptly, corresponding to the complete wrapping of the membrane around the bead and the formation of a lipid nanotube (Fig. 4A, panel II). The lipid nanotube can then be extended at constant force while the bead is moved further away from the freestanding bilayer (Video S4, ESI†). After being displaced to a distance of 9 μm from the lipid bilayer, the direction of motion of the optical trap relative to the bilayer is reversed and the bead moves ‘backward’ towards the lipid bilayer (the dashed lines in Fig. 4B). The lipid tube first retracts, and eventually disappears (Video S5, ESI†), resulting in an abrupt increase of the measured force. At this stage, the bilayer is partially wrapped around the bead. As the bead continues to move backward, the force decreases linearly with the same slope as for the forward motion (Fig. 4B and C) until the force goes back to zero when the bead is fully released from the membrane.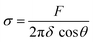 | (2) |
For PMPC, we find membrane tensions of 3.3 ± 0.6 μN m−1 and 5.04 ± 0.9 μN m−1, at 21 °C and 32 °C respectively. For the binary DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC (3
DPPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) mixture, we find the tensions to be 6.75 ± 1 μN m−1 and 9.35 ± 1.9 μN m−1, at 21 °C and 32 °C respectively. The membrane tensions at temperatures in between 21 °C and 32 °C are presented in Fig. S6 (ESI†). For both lipid compositions the significant increase in tension takes place when heating membranes over 27 °C.
2) mixture, we find the tensions to be 6.75 ± 1 μN m−1 and 9.35 ± 1.9 μN m−1, at 21 °C and 32 °C respectively. The membrane tensions at temperatures in between 21 °C and 32 °C are presented in Fig. S6 (ESI†). For both lipid compositions the significant increase in tension takes place when heating membranes over 27 °C.
The values of tension that we obtained are similar to tensions measured via laser-induced surface deformation for other planar, freestanding membranes composed of PC/PE lipid mixtures (i.e. 1.3 to 68.1 μN m−1 for bilayers with cholesterol molar fractions varying from 0 to 33%).76
As a control, we did the same experiment on 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 18
0 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PC (POPC, Tm = −2 °C) bilayers. The measured membrane tensions (5.93 ± 2.07 μN m−1 at 21 °C) show good temperature stability in the range from 21 °C to 32 °C, where POPC is expected to remain in the fluid phase (Fig. S7A, ESI†). When comparing PMPC, DOPC:DPPC, and POPC, the measured surface tension is the lowest for the mixed-chain lipid PMPC.
1 PC (POPC, Tm = −2 °C) bilayers. The measured membrane tensions (5.93 ± 2.07 μN m−1 at 21 °C) show good temperature stability in the range from 21 °C to 32 °C, where POPC is expected to remain in the fluid phase (Fig. S7A, ESI†). When comparing PMPC, DOPC:DPPC, and POPC, the measured surface tension is the lowest for the mixed-chain lipid PMPC.
It should be noted that the tension depends on several factors including the experimental platform, the lipid composition, the interactions of the lipid monolayers/bilayers with the surface of the chip, and the diffusion of lipids from the annulus into the membrane to compensate for the increase in surface area caused by pushing the membrane. Although tension is not an intrinsic property of a membrane, calculating it remains important for two key reasons. First, there is a current interest in obtaining membrane tension values in freestanding planar bilayers,77 in particular for protein-embedded membrane experiments.78 Second, it serves as an essential intermediate step in determining the bending rigidity when using the lipid tube (or tether) pulling approach.
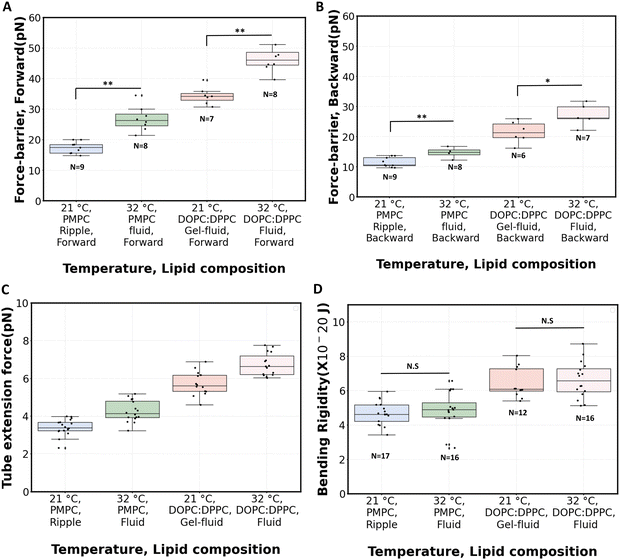
Fig. 5C shows the measured tube extension forces (Ft). For PMPC, the average tube extension force (forward and backward) increased by about 25% when going from ripple phase to the fluid phase. For the binary mixture, this increase is about 18% after fluidization. The magnitude of tube extension forces that we obtained is similar to the values reported when pushing optically trapped beads on planar DOPC:DPPC membranes (3.8 pN)49 or on DOPC:DOPG vesicles (5.7 pN).81
The radius of the lipid nanotubes (Rt) pushed out of membranes at both temperatures can be deduced from the measured membrane tension and tube extension force via the formula 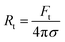 .82 Tube radii were previously reported to be in the range of 10–100 nm when tubes were pulled from DOPC or DOPC:DPPC bilayers with either optical tweezers,49,80 an atomic force microscope83 or by the action of actomyosin filaments.84 For PMPC membranes, the formed nanotube was calculated to have the radius of 84 ± 9 nm in ripple phase and decreased to 70 ± 12 nm in the fluid phase. For the binary mixture, we calculated the radius to be 71 ± 4 nm in its two-phase state and 60 ± 8 nm in the single fluid phase. In summary, for both membrane compositions, we measured a decrease in the LNT average radius in the fluid phase compared to their phase below melting point.
.82 Tube radii were previously reported to be in the range of 10–100 nm when tubes were pulled from DOPC or DOPC:DPPC bilayers with either optical tweezers,49,80 an atomic force microscope83 or by the action of actomyosin filaments.84 For PMPC membranes, the formed nanotube was calculated to have the radius of 84 ± 9 nm in ripple phase and decreased to 70 ± 12 nm in the fluid phase. For the binary mixture, we calculated the radius to be 71 ± 4 nm in its two-phase state and 60 ± 8 nm in the single fluid phase. In summary, for both membrane compositions, we measured a decrease in the LNT average radius in the fluid phase compared to their phase below melting point.
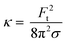 | (4) |
The bending rigidity for both lipid compositions at both temperatures are reported in Fig. 5D. Our value of κ measured from DOPC:DPPC bilayer (6.4 ± 0.9 × 10−20 J) is similar to that measured on oriented stacks of DOPC bilayers with X-ray scattering method, i.e. 7.3 × 10−20 J.85 For PMPC, we find a κ value of 4.7 ± 0.7 × 10−20 J, which is in the range previously reported for DPPC and DMPC when measured experimentally utilizing flicker noise spectroscopy.86
Interestingly, the measured values of bending rigidities remain constant in the range between 21 °C to 32 °C (Fig. S6 and S7, ESI†). Previous work has reported a lowering of κ when lipid bilayers transition from gel to liquid phase.71,87,88 In our experiments with PMPC, we probe the transition from ripple to fluid phase (as opposed to gel to fluid), which possibly explain our temperature-stable values of κ, also consistent with a previous observation that the decrease in κ appears to be sharper around Tpre than Tm.87 Also, PMPC is a saturated mixed-chain lipid, and molecular dynamics simulations have shown less variation of κ around Tm for a mixed-chain lipid compared to its symmetric-chain counterpart.89 Interestingly, a sizeable fraction of PC lipids constituting biological membranes are saturated mixed-chain lipids,90,91 just like PMPC; and they are shown to provide temperature stability to membranes.92,93
In addition to the tether pulling approach,94 several other methods have been used to measure bending stiffness (e.g. fluctuation spectroscopy, optical dynamometry) using different assumptions and leading to different values for the measured κ. An inherent limitation of the tether pulling approach is that the phase and composition of the lipid bilayer is uncertain at the junction between the flat membrane and the newly formed tube. In PMPC bilayers, ripples possibly do not form in the vicinity of the tube. As for the phase-separated DOPC:DPPC mixture (below Tm), the area where the tube is being pulled from the freestanding membrane is possibly always in a specific phase due to lipid sorting,95,96 and therefore the bending rigidity value calculated below Tm could represent only one specific phase within the phase-separated DOPC:DPPC bilayer.
3. Conclusion
We used optical tweezers to investigate the mechanical properties of two types of vertical freestanding membranes with coexisting ordered–disordered lipid regions: (i) domain-forming DOPC:DPPC and (ii) ripple PMPC. For this purpose, we developed a thermally controlled microchip that enables robust and highly reproducible bilayer formation in a high-throughput manner due to its integration with a bubble trapping system and its fluidic design.Utilizing optical tweezers on the chip, we characterized how the fluid slip at the interface of ripple PMPC lipid bilayers increases after they undergo a fluid transition. Additionally, we showed that the mixed-chain counterpart of DPPC, i.e. PMPC, possesses a higher degree of fluid slip. We also studied the force barrier for membrane-to-nanotube and nanotube-to-membrane transition in freestanding planar bilayers. We showed in both compositions, that the membrane-to-tube force barrier is higher in the fluid phase compared to the phase below the melting point. Further, we demonstrate that for both lipid compositions, the membrane tension increases upon heating.
PMPC membranes show a temperature stable rigidity, while being mechanically more flexible (lower tension and bending rigidity) and also less susceptible to oxidations due their saturated structure,97 making them good candidates for various drug-carrier applications.97–99
The novel tools developed here are well suited for the systematic mechanical characterization of diverse lipid compositions during phase transition, which could elucidate other uncharted aspects of cell membrane biophysics.
4. Methods and experimental
4.1. Microfabrication
We fabricated NOA81 microfluidic chips integrated with thermocouples for our experiments. The fabrication of the NOA81 chip requires the preparation of a master and a minor mold which are described in this section. This is because casting NOA81 directly on the conventional SU-8 master molds would not allow for easy demolding due to the high stiffness of both the silicon wafer and the NOA81 cured polymer. We therefore used an intermediate minor mold made of PDMS.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio were well mixed, degassed in vacuum, and then casted on the master mold and degassed again. Afterwards it was cured in an oven at 85 °C during 8 hours. Finally we diced out the PDMS from the master mold and performed surface silanization (tri-chloro (1H,1H,2H,2H-perfluorooctyl)silane (PFOTS, Sigma-Aldrich)) in a desiccator under vacuum. For the silanization, we connected 50 μL of the silane in a glass tube to the vacuumed chamber with a well-sealed connector for at least 2 hours such that the silane is vaporized and treats the surface of the mold.
1 ratio were well mixed, degassed in vacuum, and then casted on the master mold and degassed again. Afterwards it was cured in an oven at 85 °C during 8 hours. Finally we diced out the PDMS from the master mold and performed surface silanization (tri-chloro (1H,1H,2H,2H-perfluorooctyl)silane (PFOTS, Sigma-Aldrich)) in a desiccator under vacuum. For the silanization, we connected 50 μL of the silane in a glass tube to the vacuumed chamber with a well-sealed connector for at least 2 hours such that the silane is vaporized and treats the surface of the mold.
4.2. Heating and temperature control
To precisely control the temperature of the chip, a proportional integral derivative (PID) heating system was installed on the objective. Two k-type thermocouple were used to monitor the temperature inside the chip at the edge of the objective. During the experiment, the top layer of the chip was in contact with the condenser. The room temperature was maintained at 21 °C. The chip was mounted on the optical tweezers setup. Then, the objective wrapped in wire elements was heated by applying voltage (Fig. S1, ESI†). For thermal stabilization, the chip was kept at each temperature for 120 minutes and then the optical tweezers experiments were started. We set the heat flux at 0.3 °C min−1 when assigning any specific temperatures to the membrane.4.3. Lipids and membrane formation
1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), and palmitoyl-myristoyl-PC (PMPC) in chloroform (10 mg mL−1) and 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) in chloroform (25 mg mL−1) were all purchased from Avanti (Sigma-Aldrich), stored at −20 °C, and used directly without further purification. For the mixture, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of DOPC
2 molar ratio of DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPPC was prepared at 10 mg mL−1. To prepare the aqueous phase, a 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonicacid (HEPES) solution was adjusted to pH 7.4 with concentrated KOH, and KCl (150 mM) and bovine serum albumin (BSA, 0.5 mg mL−1) were added, and the aqueous buffer was filtered with a 0.2 μm sterile filter. Afterwards, 2 μm beads (real diameter = 1.93 μm, Polysciences Inc.) were diluted 25
DPPC was prepared at 10 mg mL−1. To prepare the aqueous phase, a 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonicacid (HEPES) solution was adjusted to pH 7.4 with concentrated KOH, and KCl (150 mM) and bovine serum albumin (BSA, 0.5 mg mL−1) were added, and the aqueous buffer was filtered with a 0.2 μm sterile filter. Afterwards, 2 μm beads (real diameter = 1.93 μm, Polysciences Inc.) were diluted 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times in the aqueous buffer. A ProSense NE-30 syringe pump was used to infuse the flow into the chip. To do so, a syringe connected to tubing is filled with the buffer and mounted on the syringe pump. Using another syringe, lipid containing chloroform is injected at the tip of the tube, which is later connected to the chip inlet. Immediately after the membrane formation, the interface appeared optically as a thick dark-bright film. In the first few minutes, the solvent was absorbed rapidly until only a thin, nearly invisible interface remains. While membranes were formed, the pump was running at high-flow rates (5 μL min−1) until all the chloroform has been pushed out of the chip. During this time, the membranes were vibrating slightly due to the instabilities caused by the pulsatile nature of the syringe pump's flow. After the chloroform has been pushed out completely, the pump was stopped. Experiments were conducted on membranes between 2 to 8 hours old.
000 times in the aqueous buffer. A ProSense NE-30 syringe pump was used to infuse the flow into the chip. To do so, a syringe connected to tubing is filled with the buffer and mounted on the syringe pump. Using another syringe, lipid containing chloroform is injected at the tip of the tube, which is later connected to the chip inlet. Immediately after the membrane formation, the interface appeared optically as a thick dark-bright film. In the first few minutes, the solvent was absorbed rapidly until only a thin, nearly invisible interface remains. While membranes were formed, the pump was running at high-flow rates (5 μL min−1) until all the chloroform has been pushed out of the chip. During this time, the membranes were vibrating slightly due to the instabilities caused by the pulsatile nature of the syringe pump's flow. After the chloroform has been pushed out completely, the pump was stopped. Experiments were conducted on membranes between 2 to 8 hours old.
4.4. Optical tweezers experiments
The optical tweezers (OT) methods for both the shearing and pushing experiments are described previously.28,49 All experiments were performed at 30 μm above the surface of the flow cell. For the shearing experiment, the traveling distance was 25 μm with a rate of 100 μm s−1. A 1.2 NA water immersion objective (FI Plan Apo VC 60×, Nikon) was used to optically trap a bead inside microchannels mounted on a piezostage (NANO-LPS100, Mad City Labs) with a 1064 nm trapping laser (YLR-10-LP-Y12, IPG Laser) and a 830 nm detection laser (LDT830-30GC, TOPAG). Anti-aliasing filtering and pre-amplification (10 dB) was performed with a KROHN-HITE 3364 on the voltage signals from a position sensitive detector (PSD, DL100-7-PCBA3, First Sensor). In the pushing experiment, fine positioning of the bead relative to the membrane was controlled with the piezo stage. The stage was moved sequentially in steps from 0.03 μm to 0.08 μm, and at each position, the data collection was done in a quasi-static manner by recording the PSD signal during 0.5 second, at a sampling rate of 1 kHz with a cut-off frequency of 500 Hz. For setup calibration, trap stiffness calculation, bubble trap quantification (flow measurement through the gap), and shearing experiments, signals were sampled at 50 kHz with a cut-off frequency of 24.5 kHz. All the signals from the PSD were processed and converted to nm and pN with a custom-made python code.For the flow measurements to quantify the effect of the bubble trap, a similar process to the membrane formation procedure was followed. This time, chloroform, free of lipids, was injected into the channels followed by HEPES containing 2 μm beads. After stabilization, the inlet port remained connected to the pumping line and the outlet was not sealed. A 2 μm bead was trapped at the centre of a gap while the pump was pushing at 2 μL min−1 and the signal was measured during 6 seconds.
4.5. Image processing for surface tension measurements
To track the membrane and the bead, a CMOS camera (DCC1545M, Thorlabs GmbH) with 11.5 px μm−1 resolution was used to record videos of pushing experiments at 14 fps. Videos are converted to tiff format, cropped, and filtered with a FFT band pass filter for contrast enhancement in ImageJ. Modified tiff files were then analysed with a custom Matlab script to obtain the deformation angle (Fig. S5 and Video S6, ESI†). To track membrane deformation while being sheared, a high-speed sCMOS camera (LaVision PCO.edge, 75 fps) was used. AVI videos were recorded and analysed directly in ImageJ.4.6. COMSOL simulation
COMSOL Multiphysics 6.2 simulation was conducted using a 3D stationary heat transfer in solid model. The objective, microfluidic chip and condenser were reproduced using built-in thermal properties of the COMSOL library: aluminium for the objective and condenser core (density: 2700 kg m−3, thermal conductivity: 238 W m−1 k−1, heat capacity: 900 J kg−1 k−1), silica glass for the lenses and the chip (density: 2203 kg m−3, thermal conductivity: 1.38 W m−1 k−1, heat capacity: 703 J kg−1 k−1). The thermal properties of NOA81 were approximated to be the same as those of acrylic plastic (density: 1190 kg m−3, thermal conductivity: 0.18 W m−1 k−1, heat capacity: 1470 J kg−1 k−1) and condenser oil as vegetable oil (temperature-dependant physical properties were directly used from the COMSOL library). All surfaces not assigned with fixed temperatures as boundaries were assigned as surface-to-ambient radiation boundary conditions.4.7. Statistical
Results shown on Fig. 2 were obtained from experiments repeated 3 times for each condition. Results shown on Fig. 3–5 were obtained from experiments repeated on at least 4 membranes from at least 3 different chips. For each experiment, a new bead was trapped. A Kruskal–Wallis one-way statistical analysis was executed, utilizing a significance criterion of p = 0.05 to ascertain significance. Calculated p-values for data presented in Fig. 3, 4B, 4C, 5A and B are tabulated in the ESI† (Tables S1 and S2). P-Values on the graphs are represented via * for p < 0.05, ** for p < 0.01 and *** for p < 0.001. Error bars in all figures represent the standard deviation of the data. In the box plots in all figures, the box shows the quartiles, the horizontal line is the median, and the whiskers are extending to the most extreme data points.Data availability
The data that supports the findings of this study are available from the corresponding authors upon reasonable request.Conflicts of interest
Two patents have been filed in relation with the present study.Acknowledgements
The authors want to thank Sarah L. Keller and Guillermo J. Amador for useful discussion.References
- M. Gohrbandt, A. Lipski, J. W. Grimshaw, J. A. Buttress, Z. Baig and B. Herkenhoff, et al., Low membrane fluidity triggers lipid phase separation and protein segregation in living bacteria, EMBO J., 2022, 41(5), e109800 CrossRef CAS.
- S. Yang, V. Kiessling and L. Tamm, Line tension at lipid phase boundaries as driving force for HIV fusion peptide-mediated fusion, Nat. Commun., 2016, 7, 11401 CrossRef CAS.
- M. B. Stone, S. A. Shelby, M. F. Núñez, K. Wisser and S. L. Veatch, Protein sorting by lipid phase-like domains supports emergent signaling function in B lymphocyte plasma membranes, eLife, 2017, 6, e19891 CrossRef.
- S. L. Veatch and S. L. Keller, Seeing spots: complex phase behavior in simple membranes, Biochim. Biophys. Acta, Mol. Cell Res., 2005, 1746(3), 172–185 CrossRef CAS.
- K. Akabori and J. F. Nagle, Structure of the DMPC lipid bilayer ripple phase, Soft Matter, 2015, 11(5), 918–926 RSC.
- C. Peetla, A. Stine and V. Labhasetwar, Biophysical interactions with model lipid membranes: applications in drug discovery and drug delivery, Mol. Pharmaceutics, 2009, 6(5), 1264–1276 CrossRef CAS.
- L. Scheidegger, L. Stricker, P. J. Beltramo and J. Vermant, Domain size regulation in phospholipid model membranes using oil molecules and hybrid lipids, J. Phys. Chem. B, 2022, 126(31), 5842–5854 CrossRef CAS.
- T. Kaasgaard, C. Leidy, J. H. Crowe, O. G. Mouritsen and K. Jørgensen, Temperature-controlled structure and kinetics of ripple phases in one-and two-component supported lipid bilayers, Biophys. J., 2003, 85(1), 350–360 CrossRef CAS.
- M. Davies, A. Reyes-Figueroa, A. A. Gurtovenko, D. Frankel and M. Karttunen, Elucidating lipid conformations in the ripple phase: Machine learning reveals four lipid populations, Biophys. J., 2023, 122(2), 442–450 CrossRef CAS.
- T. Heimburg, Mechanical aspects of membrane thermodynamics. Estimation of the mechanical properties of lipid membranes close to the chain melting transition from calorimetry, Biochim. Biophys. Acta, Biomembr., 1998, 1415(1), 147–162 CrossRef CAS.
- D. Chen and M. M. Santore, Large effect of membrane tension on the fluid–solid phase transitions of two-component phosphatidylcholine vesicles, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(1), 179–184 CrossRef CAS.
- U. Bernchou, H. Midtiby, J. H. Ipsen and A. C. Simonsen, Correlation between the ripple phase and stripe domains in membranes, Biochim. Biophys. Acta, Biomembr., 2011, 1808(12), 2849–2858 CrossRef CAS.
- J. Zasadzinski and M. Schneider, Ripple wavelength, amplitude, and configuration in lyotropic liquid crystals as a function of effective headgroup size, J. Phys., 1987, 48(11), 2001–2011 CrossRef CAS.
- K. Tada, E. Miyazaki, M. Goto, N. Tamai, H. Matsuki and S. Kaneshina, Barotropic and thermotropic bilayer phase behavior of positional isomers of unsaturated mixed-chain phosphatidylcholines, Biochim. Biophys. Acta, Biomembr., 2009, 1788(5), 1056–1063 CrossRef CAS.
- E. Serrallach, G. De Haas and G. Shipley, Structure and thermotropic properties of mixed-chain phosphatidylcholine bilayer membranes, Biochem, 1984, 23(4), 713–720 CrossRef CAS.
- K. Du, L. Sun, Z. Luo, Y. Cao, Q. Sun, K. Zhang, A. Faizy, D. Piomelli, X. Lu, J. Shan and Q. Yang, Reduced DMPC and PMPC in lung surfactant promote SARS-CoV-2 infection in obesity, Metabolism, 2022, 131, 155181 CrossRef CAS.
- J. D. Nickels, M. D. Smith, R. J. Alsop, S. Himbert, A. Yahya, D. Cordner, P. Zolnierczuk, C. B. Stanley, J. Katsaras, X. Cheng and M. C. Rheinstadter, Lipid rafts: buffers of cell membrane physical properties, J. Phys. Chem. B, 2019, 123(9), 2050–2056 CrossRef CAS.
- V. Betaneli, R. Worch and P. Schwille, Effect of temperature on the formation of liquid phase-separating giant unilamellar vesicles (GUV), Chem. Phys. Lipids, 2012, 165(6), 630–637 CrossRef CAS.
- Y. Z. Yoon, J. P. Hale, P. G. Petrov and P. Cicuta, Mechanical properties of ternary lipid membranes near a liquid–liquid phase separation boundary, J. Phys.: Condens. Matter., 2010, 22(6), 062101 CrossRef.
- N. Shimokawa, M. Nagata and M. Takagi, Physical properties of the hybrid lipid POPC on micrometer-sized domains in mixed lipid membranes, Phys. Chem. Chem. Phys., 2015, 17(32), 20882–20888 RSC.
- D. Chen and M. M. Santore, Hybrid copolymer–phospholipid vesicles: phase separation resembling mixed phospholipid lamellae, but with mechanical stability and control, Soft Matter, 2015, 11(13), 2617–2626 RSC.
- P. Bassereau, R. Jin, T. Baumgart, M. Deserno, R. Dimova and V. A. Frolov, et al., The 2018 biomembrane curvature and remodeling roadmap, J. Phys. D: Appl. Phys., 2018, 51(34), 343001 CrossRef.
- J. J. Thottacherry, A. J. Kosmalska, A. Kumar, A. S. Vishen, A. Elosegui-Artola and S. Pradhan, et al., Mechanochemical feedback control of dynamin independent endocytosis modulates membrane tension in adherent cells, Nat. Commun., 2018, 9(1), 4217 CrossRef.
- C. Dinet, A. Torres-Sánchez, R. Lanfranco, L. Di Michele, M. Arroyo and M. Staykova, Patterning and dynamics of membrane adhesion under hydraulic stress, Nat. Commun., 2023, 14(1), 7445 CrossRef.
- E. J. Miller, A. M. Ratajczak, A. A. Anthony, M. Mottau, X. I. R. Gonzalez and A. R. Honerkamp-Smith, Divide and conquer: How phase separation contributes to lateral transport and organization of membrane proteins and lipids, Chem. Phys. Lipids, 2020, 233, 104985 CrossRef CAS.
- C. Roffay, G. Molinard, K. Kim, M. Urbanska, V. Andrade and V. Barbarasa, et al., Passive coupling of membrane tension and cell volume during active response of cells to osmosis, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(47), e2103228118 CrossRef CAS.
- K. Yamamoto and J. Ando, Endothelial cell and model membranes respond to shear stress by rapidly decreasing the order of their lipid phases, J. Cell Sci., 2013, 126(5), 1227–1234 CrossRef CAS.
- G. J. Amador, D. van Dijk, R. Kieffer, M. E. Aubin-Tam and D. Tam, Hydrodynamic shear dissipation and transmission in lipid bilayers, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 21 CrossRef.
- A. Y. Shourabi, N. Kashaninejad and M. S. Saidi, An integrated microfluidic concentration gradient generator for mechanical stimulation and drug delivery, J. Sci.: Adv. Mater. Devices, 2021, 6(2), 280–290 Search PubMed.
- A. V. Nguyen, A. Y. Shourabi, M. Yaghoobi, S. Zhang, K. W. Simpson and A. Abbaspourrad, A high-throughput integrated biofilm-on-a-chip platform for the investigation of combinatory physicochemical responses to chemical and fluid shear stress, PLoS One, 2022, 17(8), e0272294 CrossRef CAS.
- H. E. Boycott, C. S. Barbier, C. A. Eichel, K. D. Costa, R. P. Martins and F. Louault, et al., Shear stress triggers insertion of voltage-gated potassium channels from intracellular compartments in atrial myocytes, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(41), E3955–E3964 CrossRef CAS.
- B. Cross, A. Steinberger, C. Cottin-Bizonne, J.-P. Rieu and E. Charlaix, Boundary flow of water on supported phospholipid films, Europhys. Lett., 2006, 73(3), 390 CrossRef CAS.
- C. R. White and J. A. Frangos, The shear stress of it all: the cell membrane and mechanochemical transduction, Philos. Trans. R. Soc. London, Ser. B, 2007, 362(1484), 1459–1467 CrossRef CAS.
- W.-J. Rappel and L. Edelstein-Keshet, Mechanisms of cell polarization, Curr. Opin. Syst. Biol., 2017, 3, 43–53 CrossRef.
- A. R. Houk, A. Jilkine, C. O. Mejean, R. Boltyanskiy, E. R. Dufresne and S. B. Angenent, et al., Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration, Cell, 2012, 148(1), 175–188 CrossRef CAS.
- T. A. Masters, B. Pontes, V. Viasnoff, Y. Li and N. C. Gauthier, Plasma membrane tension orchestrates membrane trafficking, cytoskeletal remodeling, and biochemical signaling during phagocytosis, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(29), 11875–11880 CrossRef CAS.
- P. Shendrik, G. Golani, R. Dharan, U. S. Schwarz and R. Sorkin, Membrane Tension Inhibits Lipid Mixing by Increasing the Hemifusion Stalk Energy, ACS Nano, 2023, 17(19), 18942–18951 CrossRef CAS.
- S. Salinas-Almaguer, M. Mell, V. G. Almendro-Vedia, M. Calero, K. C. M. Robledo-Sánchez and C. Ruiz-Suarez, et al., Membrane rigidity regulates E. coli proliferation rates, Sci. Rep., 2022, 12(1), 933 CrossRef CAS.
- C. Zurzolo, Tunneling nanotubes: Reshaping connectivity, Curr. Opin. Cell Biol., 2021, 71, 139–147 CrossRef CAS.
- J. F. Nagle, M. S. Jablin, S. Tristram-Nagle and K. Akabori, What are the true values of the bending modulus of simple lipid bilayers?, Chem. Phys. Lipids, 2015, 185, 3–10 CrossRef CAS.
- R. Dimova, Recent developments in the field of bending rigidity measurements on membranes, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS.
- N. Yandrapalli, J. Petit, O. Bäumchen and T. Robinson, Surfactant-free production of biomimetic giant unilamellar vesicles using PDMS-based microfluidics, Commun. Chem., 2021, 4(1), 100 CrossRef CAS.
- S. Deshpande, Y. Caspi, A. E. Meijering and C. Dekker, Octanol-assisted liposome assembly on chip, Nat. Commun., 2016, 7(1), 10447 CrossRef CAS.
- R. Parthasarathy, C.-H. Yu and J. T. Groves, Curvature-modulated phase separation in lipid bilayer membranes, Langmuir, 2006, 22(11), 5095–5099 CrossRef CAS.
- A. Mangiarotti and N. Wilke, Energetics of the phase transition in free-standing versus supported lipid membranes, J. Phys. Chem. B, 2015, 119(28), 8718–8724 CrossRef CAS.
- M. O. Ogunyankin, A. Torres, F. Yaghmaie and M. L. Longo, Lipid domain pixelation patterns imposed by e-beam fabricated substrates, Langmuir, 2012, 28(18), 7107–7113 CrossRef CAS.
- S. D. Connell and D. A. Smith, The atomic force microscope as a tool for studying phase separation in lipid membranes, Mol. Membr. Biol., 2006, 23(1), 17–28 CrossRef CAS.
- N. Khangholi, R. Seemann and J.-B. Fleury, Simultaneous measurement of surface and bilayer tension in a microfluidic chip, Biomicrofluidics, 2020, 14(2), 024117 CrossRef CAS.
- A. Dols-Perez, V. Marin, G. J. Amador, R. Kieffer, D. Tam and M.-E. Aubin-Tam, Artificial cell membranes interfaced with optical tweezers: A versatile microfluidics platform for nanomanipulation and mechanical characterization, ACS Appl. Mater. Interfaces, 2019, 11(37), 33620–33627 CrossRef CAS.
- A. Blicher, K. Wodzinska, M. Fidorra, M. Winterhalter and T. Heimburg, The temperature dependence of lipid membrane permeability, its quantized nature, and the influence of anesthetics, Biophys. J., 2009, 96(11), 4581–4591 CrossRef CAS.
- C. Lochovsky, S. Yasotharan and A. Günther, Bubbles no more: in-plane trapping and removal of bubbles in microfluidic devices, Lab Chip, 2012, 12(3), 595–601 RSC.
- P. Heo, S. Ramakrishnan, J. Coleman, J. E. Rothman, J. B. Fleury and F. Pincet, Highly reproducible physiological asymmetric membrane with freely diffusing embedded proteins in a 3D-printed microfluidic setup, Small, 2019, 15(21), 1900725 CrossRef.
- H. Noguchi, Nonequilibrium membrane dynamics induced by active protein interactions and chemical reactions: A review, ChemSystemsChem, 2024, e202400042 CrossRef.
- P. J. Beltramo, R. Van Hooghten and J. Vermant, Millimeter-area, free standing, phospholipid bilayers, Soft Matter, 2016, 12(19), 4324–4331 RSC.
- M. C. Blosser, B. G. Horst and S. L. Keller, cDICE method produces giant lipid vesicles under physiological conditions of charged lipids and ionic solutions, Soft Matter, 2016, 12(35), 7364–7371 RSC.
- L. Van de Cauter, Y. K. Jawale, D. Tam, L. Baldauf, L. van Buren, G. H. Koenderink, M. Dogterom and K. A. Ganzinger, High-speed imaging of giant unilamellar vesicle formation in cDICE, ACS Omega, 2024, 9(41), 42278–42288 CrossRef CAS.
- L. Baldauf, F. Frey, M. A. Perez, T. Idema and G. H. Koenderink, Branched actin cortices reconstituted in vesicles sense membrane curvature, Biophys. J., 2023, 122(11), 2311–2324 CrossRef CAS.
- Z. Yu, A. V. Baptist, S. C. Reinhardt, E. Bertosin, C. Dekker and R. Jungmann, et al., Compliant DNA origami nanoactuators as size-selective nanopores, Adv. Mater., 2024, 2405104 CrossRef CAS.
- M. Yang, N. Sun, Y. Luo, X. Lai, P. Li and Z. Zhang, Emergence of debubblers in microfluidics: A critical review, Biomicrofluidics, 2022, 16(3), 031503 CrossRef CAS.
- Y. Wang, D. Lee, L. Zhang, H. Jeon, J. E. Mendoza-Elias and T. A. Harvat, et al., Systematic prevention of bubble formation and accumulation for long-term culture of pancreatic islet cells in microfluidic device, Biomed. Microdevices., 2012, 14, 419–426 CrossRef.
- V. Marin, R. Kieffer, R. Padmos and M.-E. Aubin-Tam, Stable free-standing lipid bilayer membranes in Norland optical adhesive 81 microchannels, Anal. Chem., 2016, 88(15), 7466–7470 CrossRef CAS.
- N. Khangholi, M. Finkler, R. Seemann, A. Ott and J.-B. Fleury, Photoactivation of cell-free expressed archaerhodopsin-3 in a model cell membrane, Int. J. Mol. Sci., 2021, 22(21), 11981 CrossRef CAS.
- K. Ogishi, T. Osaki, Y. Morimoto and S. Takeuchi, 3D printed microfluidic devices for lipid bilayer recordings, Lab Chip, 2022, 22(5), 890–898 RSC.
- S. Silvestrini, D. Ferraro, T. Tóth, M. Pierno, T. Carofiglio and G. Mistura, et al., Tailoring the wetting properties of thiolene microfluidic materials, Lab Chip, 2012, 12(20), 4041–4043 RSC.
- P. Wägli, A. Homsy and N. F. de Rooij, Norland optical adhesive (NOA81) microchannels with adjustable surface properties and high chemical resistance against IR-transparent organic solvents, Procedia Eng., 2010, 5, 460–463 CrossRef.
- K. Keough and P. Davis, Gel to liquid-crystalline phase transitions in water dispersions of saturated mixed-acid phosphatidylcholines, Biochem, 1979, 18(8), 1453–1459 CrossRef CAS.
- D. Chen and M. M. Santore, Three dimensional (temperature–tension–composition) phase map of mixed DOPC–DPPC vesicles: Two solid phases and a fluid phase coexist on three intersecting planes, Biochim. Biophys. Acta, Biomembr., 2014, 1838(11), 2788–2797 CrossRef CAS.
- C. Leirer, B. Wunderlich, V. Myles and M. F. Schneider, Phase transition induced fission in lipid vesicles, Biophys. Chem., 2009, 143(1–2), 106–109 CrossRef CAS.
- H. Faxén, Der Widerstand gegen die Bewegung einer starren Kugel in einer zähen Flüssigkeit, die zwischen zwei parallelen ebenen Wänden eingeschlossen ist, Ann. Phys., 1922, 373(10), 89–119 CrossRef.
- B. Rallabandi, N. Oppenheimer, M. Y. Ben Zion and H. A. Stone, Membrane-induced hydroelastic migration of a particle surfing its own wave, Nat. Phys., 2018, 14(12), 1211–1215 Search PubMed.
- R. Dimova, B. Pouligny and C. Dietrich, Pretransitional effects in dimyristoylphosphatidylcholine vesicle membranes: optical dynamometry study, Biophys. J., 2000, 79(1), 340–356 CrossRef CAS.
- J. L. Kure, C. B. Andersen, T. E. Rasmussen, B. C. Lagerholm and E. C. Arnspang, Defining the diffusion in model membranes using line fluorescence recovery after photobleaching, Membranes, 2020, 10(12), 434 CrossRef CAS.
- R. Dimova, C. Dietrich, A. Hadjiisky, K. Danov and B. Pouligny, Falling ball viscosimetry of giant vesicle membranes: finite-size effects, Eur. Phys. J. B, 1999, 12, 589–598 CrossRef CAS.
- Y. Gambin, R. Lopez-Esparza, M. Reffay, E. Sierecki, N. Gov and M. Genest, et al., Lateral mobility of proteins in liquid membranes revisited, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(7), 2098–2102 CrossRef CAS.
- G. Chwastek, E. P. Petrov and J. P. Sáenz, A method for high-throughput measurements of viscosity in sub-micrometer-sized membrane systems, ChemBioChem, 2020, 21(6), 836–844 CrossRef CAS.
- T. Takei, T. Yaguchi, T. Fujii, T. Nomoto, T. Toyota and M. Fujinami, Measurement of membrane tension of free standing lipid bilayers via laser-induced surface deformation spectroscopy, Soft Matter, 2015, 11(44), 8641–8647 RSC.
- A. Griffo, C. Sparn, F. Lolicato, F. Nolle, N. Khangholi and R. Seemann, et al., Mechanics of biomimetic free-standing lipid membranes: insights into the elasticity of complex lipid compositions, RSC Adv., 2024, 14(19), 13044–13052 RSC.
- A. Anishkin, S. H. Loukin, J. Teng and C. Kung, Feeling the hidden mechanical forces in lipid bilayer is an original sense, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(22), 7898–7905 CrossRef CAS.
- G. Koster, M. VanDuijn, B. Hofs and M. Dogterom, Membrane tube formation from giant vesicles by dynamic association of motor proteins, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(26), 15583–15588 CrossRef CAS.
- G. Koster, A. Cacciuto, I. Derényi, D. Frenkel and M. Dogterom, Force barriers for membrane tube formation, Phys. Rev. Lett., 2005, 94(6), 068101 CrossRef.
- Y. Shitamichi, M. Ichikawa and Y. Kimura, Mechanical properties of a giant liposome studied using optical tweezers, Chem. Phys. Lett., 2009, 479(4–6), 274–278 CrossRef CAS.
- I. Derényi, F. Jülicher and J. Prost, Formation and interaction of membrane tubes, Phys. Rev. Lett., 2002, 88(23), 238101 CrossRef.
- J. W. Armond, J. V. Macpherson and M. S. Turner, Pulling nanotubes from supported bilayers, Langmuir, 2011, 27(13), 8269–8274 CrossRef CAS.
- K. Jahnke, S. J. Maurer, C. Weber, J. E. H. Bücher, A. Schoenit and E. D’Este, et al., Actomyosin-assisted pulling of lipid nanotubes from lipid vesicles and cells, Nano Lett., 2022, 22(3), 1145–1150 CrossRef CAS.
- Y. Lyatskaya, Y. Liu, S. Tristram-Nagle, J. Katsaras and J. F. Nagle, Method for obtaining structure and interactions from oriented lipid bilayers, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63(1), 011907 CrossRef.
- D. Drabik, G. Chodaczek, S. Kraszewski and M. Langner, Mechanical properties determination of DMPC, DPPC, DSPC, and HSPC solid-ordered bilayers, Langmuir, 2020, 36(14), 3826–3835 CrossRef CAS.
- J. Daillant, E. Bellet-Amalric, A. Braslau, T. Charitat, G. Fragneto and F. Graner, et al., Structure and fluctuations of a single floating lipid bilayer, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(33), 11639–11644 CrossRef CAS.
- C.-H. Lee, W.-C. Lin and J. Wang, All-optical measurements of the bending rigidity of lipid-vesicle membranes across structural phase transitions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64(2), 020901 CrossRef CAS.
- H.-L. Wu, H.-K. Tsao and Y.-J. Sheng, Dynamic and mechanical properties of supported lipid bilayers, J. Chem. Phys., 2016, 144(15), 154904 CrossRef.
- C. Huang, Mixed-chain phospholipids and interdigitated bilayer systems, Klin. Wochenschr., 1990, 68, 149–165 CrossRef CAS.
- J. Reinhard, C. Mattes, K. Väth, T. Radanović, M. A. Surma and C. Klose, et al., A quantitative analysis of cellular lipid compositions during acute proteotoxic ER stress reveals specificity in the production of asymmetric lipids, Front. Cell Dev. Biol., 2020, 8, 756 CrossRef.
- S. Hui, J. Mason and C. Huang, Acyl chain interdigitation in saturated mixed-chain phosphatidylcholine bilayer dispersions, Biochem, 1984, 23(23), 5570–5577 CrossRef CAS.
- S. Ali, J. M. Smaby, M. M. Momsen, H. L. Brockman and R. E. Brown, Acyl chain-length asymmetry alters the interfacial elastic interactions of phosphatidylcholines, Biophys. J., 1998, 74(1), 338–348 CrossRef CAS.
- E. Evans and D. Needham, Physical properties of surfactant bilayer membranes: thermal transitions, elasticity, rigidity, cohesion and colloidal interactions, J. Phys. Chem., 1987, 91(16), 4219–4228 CrossRef CAS.
- M. Heinrich, A. Tian, C. Esposito and T. Baumgart, Dynamic sorting of lipids and proteins in membrane tubes with a moving phase boundary, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(16), 7208–7213 CrossRef CAS.
- H. Jiang and T. R. Powers, Curvature-driven lipid sorting in a membrane tubule, Phys. Rev. Lett., 2008, 101(1), 018103 CrossRef.
- P. Smith, D. M. Owen, C. D. Lorenz and M. Makarova, Asymmetric glycerophospholipids impart distinctive biophysical properties to lipid bilayers, Biophys. J., 2021, 120(9), 1746–1754 CrossRef CAS.
- V. K. Sharma, K. K. Sarwa and B. Mazumder, Fluidity enhancement: a critical factor for performance of liposomal transdermal drug delivery system, J. Liposome Res., 2014, 24(2), 83–89 CrossRef CAS.
- A. M. Bodratti and P. Alexandridis, Amphiphilic block copolymers in drug delivery: Advances in formulation structure and performance, Expert Opin. Drug Delivery, 2018, 15(11), 1085–1104 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00706a |
| This journal is © The Royal Society of Chemistry 2024 |