Shear thickening in suspensions of particles with dynamic brush layers

Abstract

Control of frictional interactions among liquid-suspended particles has led to tunable, strikingly non-Newtonian rheology via the formation of strong flow constraints as particles come into close proximity under shear. Typically, these frictional interactions have been in the form of physical contact, controllable via particle shape and surface roughness. We investigate a different route, where molecular bridging between nearby particle surfaces generates a controllable constraint to relative particle movement. This is achieved with surface-functionalized colloidal particles capable of forming dynamic covalent bonds with telechelic polymers that comprise the suspending fluid. At low shear stress this results in particles coated with a uniform polymer brush layer. Beyond an onset stress σ* the telechelic polymers become capable of bridging and generate shear thickening. Over the size range investigated, we find that the dynamic brush layer leads to dependence of σ* on particle diameter that closely follows a power law with exponent −1.76. In the shear thickening regime, we observe an enhanced dilation in measurements of the first normal stress difference N₁ and reduction in the extrapolated volume fraction required for jamming, both consistent with an effective particle friction that increases with decreasing particle diameter. These results are discussed in light of predictions for suspensions of hard spheres and of polymer-grafted particles.

---

1 Introduction

Shear thickening fluids are materials with a viscosity that rises with increasing shear stress or shear rate.¹ Dense suspensions of solid particles suspended in a Newtonian liquid have emerged as the prototypical fluid exhibiting strong shear thickening and have been studied extensively over the last two decades. Understanding the flow of suspensions is critically important in both industrial applications and natural processes. Frictional interaction between particles has been implicated as the dominant contribution to dramatic increases in viscosity during shear thickening, whereby applied stress leads to a growing population of particles interacting frictionally and resisting the applied shear.^2–5

Advances in the understanding of shear thickening in dense suspensions have been facilitated primarily by studying spherical particles as a model system. This is the most straightforward for theoretical calculations and computational modeling as well as being relatively simple to synthesize and measure experimentally. Spherical particle suspensions also have the virtue of making it relatively easy to isolate how changes to particle level characteristics such as particle roughness, particle size, and particle surface chemistry impact shear thickening. For example, by tuning particle roughness,^6–9 varying contact friction,¹⁰ or incorporating enhanced lubrication hydrodynamics in simulations^11,12 it has been shown how the shear thickening response can be controlled. Another way to alter the shear thickening response is to tune the particle size, which controls the stress σ* required to make frictional contact and thus to induce shear thickening. For hard sphere suspensions this stress is found to scale as , where the effective applied force σ*d² has to exceed the effective stabilizing force F₀ at contact.^13,14 Whenever local frictional contacts exist between contacting particles, i.e., whenever σ > σ*, relative movement is hindered and this acts as a stress-activated constraint for the associated degree of freedom.^13,15

Typically, such stress-induced constraints have their origin in physical contact friction. However, friction can also be created by chemical bridging between suitably functionalized surfaces.¹⁶ For example, hydrogen bonding between the particles can enhance the effective friction to the point of inducing shear jamming.¹⁷ However, hydrogen bonds are weak and have a very short lifetime. Comparatively new and less studied are suspensions in which the chemistry of particles and suspending polymeric liquid has been designed to enable bridging via dynamic covalent bonds that can be significantly stronger and have longer lifetimes than non-covalent interactions. These polymers have groups at both ends that bond to the particle surfaces.^18,19 The effective friction induced by such dynamic covalent bridging has been termed “chemical friction” because the constraint is generated by solvent molecules that chemically attach to contacting particle surfaces in a reversible manner. The shear-induced bridging bond results in constraints resistant to relative particle motions. Such a chemical bond can then be viewed as friction (i.e., as an effective, chemical friction), similar to the physical friction of hard spheres. These dynamic bonds establish quickly and release more slowly, resulting in a longer lifetime. In addition to strong shear thickening such suspensions also can exhibit anti-thixotopic responses owing to the slow release.^18,19 The focus of the present work is, however, only on the suspension behavior with increasing applied stress and investigates how dynamic bridging affects the onset of shear thickening, enables a cross-over from lubrication- to friction-dominated rheological behavior, and changes the propensity for jamming. Our experiments show how bridging interactions provide a means of systematically tuning the effective friction in sheared suspensions and, in particular, make it possible to change this effective friction simply by changing particle size.

2 Experiments

2.1 Materials preparation

Five sets of silica spheres with hydroxyl surface groups were purchased from fiber optic center (New Bedford, MA) with diameters in the range 300 nm < d < 2000 nm. These particles were surface-functionalized with thiol groups as reported previously (see ESI†).¹⁸ The size of thiol-functionalized particles was measured as d = 340 ± 4 (SP3), 620 ± 10 (SP6), 870 ± 10 (SP9), 1210 ± 40 (SP12), and 1930 ± 90 nm (SP19) using dynamic light scattering.

The suspending medium for these spheres was a telechelic polymeric liquid comprised of p-nitrobenzalcyanoacetamide (N-BCAm)-endcapped poly(propylene glycol) (number-averaged molecular weight, M_n ≈ 5300 g mol⁻¹).¹⁸ A dynamic brush layer is formed on the surface of the particles via the catalyst free, room temperature dynamic thia-Michael reaction between the thiol and the BCAm group. In contrast to a covalently attached brush layer, the dynamic brush continually forms and releases due to the kinetics of the thia-Michael bond at room temperature (Fig. 1a). The equilibrium constant K_eq of this thia-Michael reaction was measured as K_eq ≈ 8000 M⁻¹.¹⁸ From a thermodynamic perspective, we note that, for all suspensions reported here, the stoichiometric amount of the BCAm Michael-acceptor group is at least 5-fold larger than the surface thiol (1–2 thiol-per-nm², see the nuclear magnetic resonance spectroscopy study in the ESI†). In this concentration limit and K_eq, the telechelic polymers form dynamic bonds with the surface thiol, resulting in the brush layer.

Fig. 1 (a) Schematic of silica particles (grey) whose surfaces are functionalized with thiol groups (red triangles) suspended in p-nitrobenzalcyanoacetamide (N-BCAm)-endcapped poly(propylene glycol) (blue polygons). The polymers form dynamic brushes at the particle surface through the dynamic thia-Michael reaction, which convert to bridging bonds when sheared. (b)–(d) Viscosity η as a function of applied shear stress σ for thiol-functionalized silica particles suspended in N-BCAm-endcapped poly(propylene glycol) for different particle volume fraction ϕ. Particle diameter d is 620 nm (SP6, (b)), 1210 nm (SP12, (c)), and 1930 nm (SP19, (d)). Vertical red dashed lines refer to the average onset stress for shear thickening. Shaded area in left-top corner indicates inaccessible range due to the rheometer minimum rate limit [small gamma, Greek, dot above] < 0.001 s⁻¹.

2.2 Rheology measurement

Suspensions with different volume fractions ϕ were prepared by measuring masses of particles and solvents and converting to volumes using their densities. The rheology over all accessible shear stresses, typically σ = 10⁻¹ Pa to σ = 10³ Pa, was measured using a rheometer (Anton Paar, MCR 302 or MCR 702) in cone and plate geometry (25 mm diameter, 2° angle). Owing to the high yield stress, the measurements were performed in rate-controlled mode at low stress prior to the shear thickening regime and otherwise using stress control. For suspensions with the smallest particles, d = 340 nm, the rheology was measured in rate-controlled mode throughout, given the particularly high yield stress. The onset stress for shear thickening was determined from the minimum viscosity.

3 Results

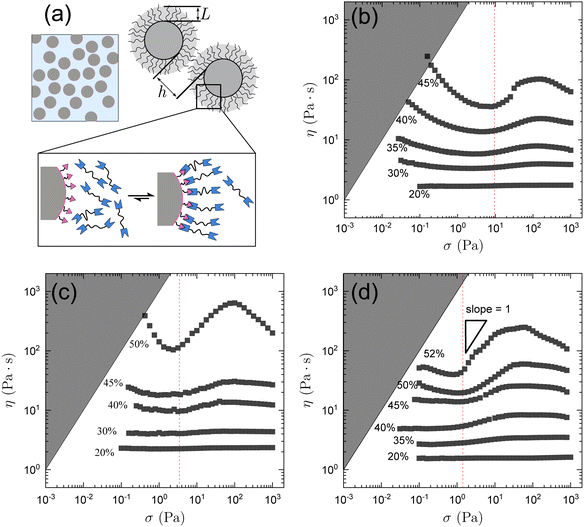
Fig. 1b shows the rheology of SP6 at different volume fractions ϕ defined here using the volume of the thiol-functionalized particles without the attached brush layer of telechelic solvent molecules. For ϕ = 0.30, the suspension exhibits a mild thinning and thickens slightly at larger stresses. The magnitude of shear thickening increases with ϕ, as seen in the slope d log η/d log σ. At ϕ = 0.45 the slope reaches 1, which corresponds to discontinuous shear thickening when viscosity is plotted as a function of shear rate. For all ϕ, the suspension starts to shear thicken at σ* ≈ 10 Pa (red dashed line). Also observed is an increase in the yield stress with increasing ϕ. This is in line with the increased ability to form inter-particle bonds already at rest as the packing fraction becomes high.

A second shear-thinning regime appears at high stress. While similar behavior has been found in suspensions of anisotropic,²⁰ irregular,²¹ or soft²² particles, this second thinning in the dynamic suspensions studied here is most likely attributable to the breaking of the bridging interactions at high shear stress. Probing larger particles, SP12 (Fig. 1c) and SP19 (Fig. 1d), analogous behavior is observed. However, the shear thickening behavior for given ϕ becomes weaker with increasing d. Similarly, the low stress yielding behavior is weaker for larger d, even at larger ϕ.

Physically, the onset stress σ* signals the stress level at which the particles have been sheared into sufficiently close distance, h*, to start forming frictional contact. In Fig. 2 we plot the onset stress for shear thickening, σ*, as a function of particle diameter d. Over the size range measured, for our particles (blue symbols) this onset closely follows a power law σ* ∝ d^α with best fit exponent α = −1.76. Also shown in that figure are results from prior work^{13,14,23–28} with particles where the brush layer was attached with permanent covalent bonds (black symbols), and for which a best fit exponent α ≈ −1.9 has been reported.¹³ We believe that one of the reasons for our data to exhibit very little scatter is that the dynamic brush layers is formed by the exact same N-BCAm-endcapped polymers for all particle sizes.

Fig. 2 Onset stress for shear thickening σ* in suspensions with dynamic covalent bonds (blue diamonds). Also shown are data from prior studies^{13,14,23–28} using suspension with particles having permanently attached covalent brush layers (black symbols). Solid lines are least-squares fits.

As σ increases, particles are necessarily pushed closer together, thus promoting bridging by the telechelic macromonomers via dynamic bonds at σ > σ*. This generates constraints to relative particle movement, similar to the constraints arising from a network of frictional contacts. In the following, we further explore the dynamic-bond-induced shear thickening state through the first normal stress difference N₁ ≡ σ_xx − σ_zz. Here σ_xx and σ_zz refer to the stress tensor components in the shear flow direction (x) and its gradient direction (z). Prior work has suggested that the sign of N₁ distinguishes states where particles interact via lubrication (N₁ < 0) or form system-spanning networks of frictional contacts that lead to dilation of the overall sample volume (N₁ > 0).^3,29,30 In Fig. 3a, we plot N₁ − N_1,0 for the largest particles, 1930 nm, at different volume fractions 0.3 ≤ ϕ ≤ 0.52, where the initial value N_1,0 at the lowest applied shear stress has been subtracted. For ϕ ≤ 0.5, we find N₁ < 0 even beyond the stress σ* ≈ 1.3 Pa that indicates the onset of shear thickening. We interpret this as indicating that system-spanning networks of frictional contacts can only form for σ > σ*. This changes once ϕ ≥ 0.52 where now the sign of N₁ reverses from negative to positive as σ ≥ σ*.

Fig. 3 (a) First normal stress difference N₁ as a function of shear stress σ for suspensions of 1930 nm particles (SP19) with volume fractions ϕ = 0.3 to 0.52. The value measured at the lowest applied shear stress, N_1,0, has been subtracted. (b) N₁ − N_1,0 is plotted for suspensions of particles with diameter d = 620 nm (SP6), 1210 nm (SP12), and 1930 nm (SP19) at fixed ϕ = 0.45.

The effect on N₁ of changing particle size is shown in Fig. 3b for fixed ϕ = 0.45. Strikingly, the sign of N₁ in the shear thickening regime reverses from negative to positive for particles with d < 1210 nm (see ESI† for other particle packing fractions).

The size-dependent magnitude of the effective friction seen in the behavior of N₁ is also observed in the approach to jamming as the particle volume fraction ϕ is increased. This can be seen in plots of the high-stress viscosity η_t, measured at the upper end of the shear thickened state (i.e., the maximum viscosity in the shear thickening regime), as a function of particle volume fraction ϕ, which diverges at a friction-dependent jamming volume fraction ϕ^μ_J.³¹ The ϕ^μ_J divergence shifts to a lower value with increased interparticle friction and can therefore be taken as another indicator of the effect of dynamic-bond-induced constraints. In Fig. 4 we plot data for the three particle systems measured and fit them to a power-law relation, η = A(1 − ϕ/ϕ_J)⁻ⁿ (ref. 31–33) to extract ϕ^μ_J. The fits, with n = 1.7–1.8 (see ESI†), give ϕ^μ_J = 0.54, 0.51, and 0.48 for SP19, SP12 and SP6, respectively.

Fig. 4 Viscosity η_t at the thickened state versus volume fraction ϕ for SP6 (black), SP12 (blue), and SP19 (red). Lines are least-squares fits to η = A(1 − ϕ/ϕ_J)⁻ⁿ. The jamming volume fraction ϕ_J are ϕ_J,SP6 = 0.48, ϕ_J,SP12 = 0.51, and ϕ_J,SP19 = 0.54.

4 Discussion

For particles coated with a polymer brush layer we can expect that shearing them into contact produces a balance between the applied stress and the counteracting stress from the stiffness of the brush. Balancing the force σ*d² with the restoring force derived from gradient of the interparticle potential for brush-layer stabilized particles¹⁴ gives

Different interparticle potentials will produce different scalings σ* ∝ d^α of the onset stress as a function of particle diameter d. For example, stabilization by steric interactions with distance-independent forces leads to σ* ∝ d⁻². The data shown Fig. 2 by the black symbols therefore has been interpreted as the result of behavior close to the hard sphere limit. Another much-studied limit is that for compressed semidilute polymer brush layers^14,34 with polymer brush thickness L and surface-to-surface distance h (see Fig. 1a). In this case the stabilizing potential gradient between polymer brush layers was found consistent with . This gradient gives a scaling σ* ∝ d^−1.75.¹⁴ Intriguingly, this closely matches our data for dynamic brushes. Notably, however, the power law exponent −0.25 in this scaling argument requires semidilute, good solvent conditions for the brush, which are difficult to justify in our system, where we have a very different situation: the particles are dispersed in a melt of N-BCAm endcapped polymers and these polymers also form the dynamic brush layer. In addition, we see that the shear thickening in these suspensions is stress-dependent. The rates of bond association/dissociation do not impact the onset of shear thickening, particularly at this high K_eq where the majority of dynamic bonds is in the bonded state, as shown in a previous study¹⁹ with a library of benzalcyanoacetamide Michael-acceptors with different K_eq.

The size dependence of the sign reversal in N₁ (Fig. 3b) suggests that the strength of the effective friction produced by the bridging linkers increases with decreasing d. To rationalize this, we consider how particle–particle interactions due to polymer linkages depend on the total energy density associated with bridging. This energy density (ρ_B) depends on the energy per bridging bond ε_B, the interparticle contact area A ∼ Ld for d ≫ L, and the number of particles per unit volume, which is proportional to d⁻³, and it scales as ρ_B ∼ ε_BLd/d³ = ε_BLd⁻². As a result, although telechelic polymers on larger particles with less curved surfaces have a stronger attractive pair potential, particularly in the regime of d ≫ R_g,³⁵ the overall bridging energy density scales inversely with particle size, ρ_B ∼ d⁻². Hence, per unit volume smaller particles are more strongly interacting by bridging and behave more frictional, i.e., they experience stronger constraints to relative motion under shear. This then decreases the volume fraction required for the formation of system-spanning frictional networks and thus for the observation of behavior with N₁ > 0. Conversely, at fixed ϕ, suspensions of larger particles behave less frictional, thus exhibit less pronounced shear thickening and may not show a transition to positive N₁. We also see from Fig. 3 that in suspensions where N₁ < 0 initially, there can be a sign reversal at larger shear stresses. We take this as an indication that telechelic linkers make it possible to establish extended network structures even under large applied shear. However, the decrease in viscosity seen in Fig. 1 at these large stress levels suggests that such networks structures deform more easily under shear than hard spheres would.

The fits to the data in Fig. 4 make it possible to estimate the associated effective friction coefficient μ, using the simulation data by Singh et al.³⁶ Taking ϕ^∞_J ≈ 0.47 as obtained for infinite sliding friction μ_s = ∞ at fixed rolling friction μ_r = 0.3,¹⁵ the resulting values are μ = 3.5, 0.9, and 0.5 for SP6, SP12, and SP19, respectively. The finding that the extracted effective friction coefficient can be larger than unity again highlights that we are dealing with friction due to chemical bridging, as opposed to physical contact friction for which μ ≤ 1 can typically be expected. We note that it is possible to attribute some of the decrease in ϕ^μ_J with particle diameter d also to the brush layer effectively increasing the volume fraction of particles in the suspension. Accounting for the brush layer would then shift ϕ to ϕ_eff = ϕ(1 + 2L/d)³. However, this shift is too small to fully explain the observed particle size dependence in ϕ^μ_J (see ESI†).

5 Summary and conclusions

We investigated shear thickening for a class of dense suspensions with particles designed to interact through chemical bridging interactions. In these systems silica particles are surface-functionalized with thiol groups and suspended in a N-BCAm-endcapped poly(propylene glycol). This combination of particle surface and solvent chemistry allows for a dynamic brush layer to be established at the particle surface. At low shear this brush layer stabilizes the particles. As larger stress is applied to the suspension, particles come into sufficiently close proximity that dynamic bridging interactions are formed. These bridges introduce an effective interparticle friction and promote shear thickening. We find that the onset stress of shear thickening for suspensions with dynamic brush layers scales with particle size as d^−1.76. It is intriguing that this lines up closely with the theoretical model for covalently-attached brush stabilized particles, which predicts d^−1.75 but applies to a rather different regime. The degree to which this model can be generalized is currently unknown. Our results show that bridging interactions can give rise to dilatancy and form system-spanning networks, just as in shear thickening suspensions where the particles interact sterically through direct contact friction. However, owing to the increase in the overall area of contact for fixed brush thickness, and in contrast to steric interactions, the effective bridging-induced friction increases as particle size decreases. Consequently, also the onset of jamming is shifted to smaller ϕ^μ_J for smaller particles.

Our findings demonstrate that dynamic bridging interactions provide a direct, highly tunable means for controlling the effective particle friction. For fixed particle and solvent chemistry, this friction can be changed straightforwardly by changing the particle size and it can become as large as or even exceed physical friction produced by particle surface roughness. While we reported on one specific dynamic covalent chemistry, the results introduce a versatile way to design the non-Newtonian rheology of shear thickening fluids, and we expect that this approach can be extended further by tuning the molecular structure of the suspending polymer medium, including the molecular weight (length scale of bridging interaction), persistence length (rolling friction), and thermodynamic reaction equilibrium (effective friction lifetime). Furthermore, the shear-induced bridging discussed here can be seen as a form of adhesive interaction as it shows a long relaxation timescale to break once formed under shear. The distinct stress- and time-dependent conformations of dynamic bonds therefore open a new window to explore particle–polymer composites with adhesive interactions that are dynamic.

Author contributions

HK, SJR, and HMJ conceived the research project; HK and FAB performed the experiments; HK, MvdN, TAW, SJR, and HMJ analyzed the data; all authors participated in the discussion and writing the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Norman Wagner for fruitful discussion. This work was primarily supported by the University of Chicago Materials Research Science and Engineering Center, which is funded by National Science Foundation under award number DMR-2011854. This work was partially supported by National Science Foundation under award DMR-2104694. Parts of this work were carried out at the Soft Matter Characterization Facility and at the MRSEC Characterization Facility at the University of Chicago (award number DMR-2011854).

Notes and references

1. J. Mewis and N. J. Wagner, Colloidal suspension rheology, Cambridge University Press, 2012.
2. R. Seto, R. Mari, J. F. Morris and M. M. Denn, Phys. Rev. Lett., 2013, 111, 218301.
3. J. R. Royer, D. L. Blair and S. D. Hudson, Phys. Rev. Lett., 2016, 116, 188301.
4. N. Y. Lin, B. M. Guy, M. Hermes, C. Ness, J. Sun, W. C. Poon and I. Cohen, Phys. Rev. Lett., 2015, 115, 228304.
5. C.-P. Hsu, J. Mandal, S. N. Ramakrishna, N. D. Spencer and L. Isa, Nat. Commun., 2021, 12, 1477.
6. D. Lootens, H. Van Damme, Y. Hémar and P. Hébraud, Phys. Rev. Lett., 2005, 95, 268302.
7. L. C. Hsiao, S. Jamali, E. Glynos, P. F. Green, R. G. Larson and M. J. Solomon, Phys. Rev. Lett., 2017, 119, 158001.
8. P. Bourrianne, V. Niggel, G. Polly, T. Divoux and G. H. McKinley, Phys. Rev. Res., 2022, 4, 033062.
9. C.-P. Hsu, S. N. Ramakrishna, M. Zanini, N. D. Spencer and L. Isa, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5117–5122.
10. Y.-F. Lee, Y. Luo, T. Bai, C. Velez, S. C. Brown and N. J. Wagner, Phys. Fluids, 2021, 33, 033316.
11. S. Jamali and J. F. Brady, Phys. Rev. Lett., 2019, 123, 138002.
12. M. Wang, S. Jamali and J. F. Brady, J. Rheol., 2020, 64, 379–394.
13. B. M. Guy, M. Hermes and W. C. Poon, Phys. Rev. Lett., 2015, 115, 088304.
14. L.-N. Krishnamurthy, N. J. Wagner and J. Mewis, J. Rheol., 2005, 49, 1347–1360.
15. A. Singh, G. L. Jackson, M. van der Naald, J. J. de Pablo and H. M. Jaeger, Phys. Rev. Fluids, 2022, 7, 054302.
16. U. Raviv, R. Tadmor and J. Klein, J. Phys. Chem. B, 2001, 105, 8125–8134.
17. N. M. James, E. Han, R. A. L. de la Cruz, J. Jureller and H. M. Jaeger, Nat. Mater., 2018, 17, 965–970.
18. G. L. Jackson, J. M. Dennis, N. D. Dolinski, M. van der Naald, H. Kim, C. Eom, S. J. Rowan and H. M. Jaeger, Macromolecules, 2022, 55, 6453–6461.
19. H. Kim, M. van der Naald, N. D. Dolinski, S. J. Rowan and H. M. Jaeger, Soft Matter, 2023, 19, 6797–6804.
20. E. Brown, N. A. Forman, C. S. Orellana, H. Zhang, B. W. Maynor, D. E. Betts, J. M. DeSimone and H. M. Jaeger, Nat. Mater., 2010, 9, 220–224.
21. S. R. Raghavan and S. A. Khan, J. Colloid Interface Sci., 1997, 185, 57–67.
22. S. Jamali, A. Boromand, N. Wagner and J. Maia, J. Rheol., 2015, 59, 1377–1395.
23. J. Mewis and J. Vermant, Prog. Org. Coat., 2000, 40, 111–117.
24. W. J. Frith, P. Haene, R. Buscall and J. Mewis, J. Rheol., 1996, 40, 531–548.
25. T. Strivens, J. Colloid Interface Sci., 1976, 57, 476–487.
26. M. Smith, R. Besseling, M. Cates and V. Bertola, Nat. Commun., 2010, 1, 114.
27. L. Isa, PhD thesis, University of Edinburgh, 2008.
28. P. d'Haene, J. Mewis and G. Fuller, J. Colloid Interface Sci., 1993, 156, 350–358.
29. D. R. Foss and J. F. Brady, J. Fluid Mech., 2000, 407, 167–200.
30. N. Park, V. Rathee, D. L. Blair and J. C. Conrad, Phys. Rev. Lett., 2019, 122, 228003.
31. R. Mari, R. Seto, J. F. Morris and M. M. Denn, J. Rheol., 2014, 58, 1693–1724.
32. B. Andreotti, J.-L. Barrat and C. Heussinger, Phys. Rev. Lett., 2012, 109, 105901.
33. E. Lerner, G. Düring and M. Wyart, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4798–4803.
34. G. H. Fredrickson and P. Pincus, Langmuir, 1991, 7, 786–795.
35. X.-X. Meng and W. B. Russel, J. Rheol., 2006, 50, 169–187.
36. A. Singh, R. Mari, M. M. Denn and J. F. Morris, J. Rheol., 2018, 62, 457–468.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00624k

---