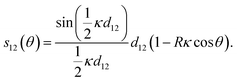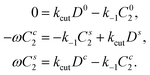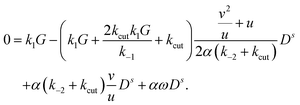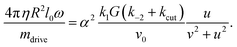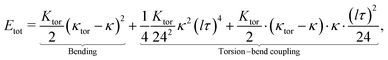Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reshaping and enzymatic activity may allow viruses to move through the mucus
Falko
Ziebert
 ab,
Kenan G.
Dokonon
c and
Igor M.
Kulić
ab,
Kenan G.
Dokonon
c and
Igor M.
Kulić
 de
de
aInstitute for Theoretical Physics, Heidelberg University, Philosophenweg 19, 69120 Heidelberg, Germany. E-mail: f.ziebert@thphys.uni-heidelberg.de
bBioQuant, Heidelberg University, Im Neuenheimer Feld 267, 69120 Heidelberg, Germany
cDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Cambridge CB3 0AS, UK
dInstitut Charles Sadron UPR22-CNRS, 67034 Strasbourg, France
eInstitute Theory of Polymers, Leibniz-Institute of Polymer Research, D-01069 Dresden, Germany. E-mail: kulic@unistra.fr
First published on 23rd August 2024
Abstract
Filamentous viruses like influenza and torovirus often display systematic bends and arcs of mysterious physical origin. We propose that such viruses undergo an instability from a cylindrically symmetric to a toroidally curved state. This “toro-elastic” state emerges via spontaneous symmetry breaking under prestress due to short range spike protein interactions magnified by surface topography. Once surface stresses are sufficiently large, the filament buckles and the curved state constitutes a soft mode that can potentially propagate through the filament's material frame around a Mexican-hat-type potential. In the mucus of our airways, which constitutes a soft, porous 3D network, glycan chains are omnipresent and influenza's spike proteins are known to efficiently bind and cut them. We next show that such a non-equilibrium enzymatic reaction can induce spontaneous rotation of the curved state, leading to a whole body reshaping propulsion similar to – but different from – eukaryotic flagella and spirochetes.
1. Introduction
Thin fibers are common structural elements in biology, from biofilaments to body shapes of viruses and bacteria. Notably, biological filaments like the bacterial flagellar hook,1–3 microtubules,4,5 and intermediate filaments6 exhibit an unusual, common motif: their straight ground state can become unstable, reshaping them into polymorphic toroids and superhelices. Not less surprisingly, when driven out of equilibrium, stimuli-responsive but otherwise straight fibers can acquire a dissipative toroidal steady state of spontaneous rotation.7,8 Visually inspecting the shapes of filamentous viruses like influenza C (IV-C)9,10 or Torovirus,11 see Fig. 1a and c, the natural question arises if viral envelopes posses a similar symmetry-broken, toroidal ground state. And as viruses like influenza A (IV-A) and C,12–14 as well as paramyxovirus15 have been shown to be able to roll on surfaces due to their spike proteins' catalytic activity, can their toroidal state be driven catalytically and used for virus propulsion? | ||
| Fig. 1 Emergent toroidal shapes of various biofilaments (a)–(c), a filamentous influenza virus in its natural environment – the mucus (d), and geometry of the virus and the toroidal mode (e) and (f). (a) Torovirus.16 (b) The bacterial flagellar hook.2 (c) Influenza C: long filamentous viruses display both straight and oscillatory shapes10; the inset shows a shorter, curved influenza C that is actively rolling on a glycan-coated surface.13 (d) The mucus environment that the influenza virus has to bypass forms a loose protein fiber network decorated with sticky glycan chains. (e) In the considered filamentous virus, spike proteins are arranged on a typically staggered column lattice with spacing l0 and effective radius R (including the spikes). (f) Curving the lattice by a curvature κ allows some spikes to interact at the inside of the bend (left). Which particular spikes can interact depends on their orientation angle θ (right) with respect to the angle ϕ of the curvature vector κ. | ||
In the following we consider a plausible model for the emergence of curved states, that arise via a spontaneous symmetry breaking, represent a soft mode around the virus axis and which we call the “toro-elastic” state of the viral envelope. It relies on surface switchability via spike protein contacts and a mismatch-stress with layers further inside the virus. Notably, recently resolved surface structures of influenza C17 have shown extensive spike–spike contacts, establishing a hexagonal lattice on the envelope. The switch corresponds to the making-and-breaking of any reversible physical bond – including hydrogen bonds, screened-electrostatic, van der Waals bonds – as well as protein-tail-mediated interactions. After demonstrating the mechanism giving rise to the toro-elastic state, we explain how its continuous ground state can act as a “wheel within the material”,7 mirroring the “universal joint” model of the bacterial flagellar hook.1–3
Finally, we consider such a filamentous virus with a toroidal mode embedded into a loose 3D mucus network, cf. (Fig. 1d). In this environment, polymeric ligands that can be bound to and cut by the enzymatic spikes on the viral envelope can induce dynamic force imbalances. This situation reflects what influenza is confronted within the mucus of our airways, a highly viscous environment containing polymers with sugary ends (glycans) the virus spikes interact with. We show that the cutting of glycans by enzymatic spikes can force the toroidally curved state to spontaneously rotate, once enzymatic activity surpasses a certain threshold. This dynamic shape rotation should allow the virus to move at small but noticeable speeds, and could explain why catalytic activity increases mucus penetration so strongly for influenza.18,19
2. Toro-elastic state
We focus here on influenza C, whose spike protein is called Hemagglutinin-esterase-fusion protein (HEF), for which spike–spike interactions have been experimentally evidenced.17 We consider a virus whose surface is covered with radial spikes with initial axial spacing l0 (see Fig. 1e). If the virus curves, variations of strains ε and thus distances along the axis between spikes are amplified proportional to the effective radius of the cylindrical virus, R, and the centerline curvature κ like l(κ) ≈ εl0 = κRl0. In addition, there is a geometric “shortcut factor” for finite deformations: For spiky surface elements that interact along the shortest spatial distance, this distance is given by the secant line, see Appendix A for details.Introducing the vectorial curvature perpendicular to the axis κ = (κx, κy) = κ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, sin
ϕ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) with orientation angle ϕ and magnitude κ, and parameterizing the material-fixed spike positions with angle θ (with θ = ϕ corresponding to the orientation of the curvature vector, i.e. towards the bend), the spacing between surface contacts along the axis is given by, see Fig. 1f and Appendix A,
ϕ) with orientation angle ϕ and magnitude κ, and parameterizing the material-fixed spike positions with angle θ (with θ = ϕ corresponding to the orientation of the curvature vector, i.e. towards the bend), the spacing between surface contacts along the axis is given by, see Fig. 1f and Appendix A,
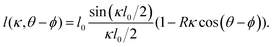 | (1) |
The spikes are assumed to be uniformly distributed over the surface, cf.Fig. 1f on the right, and every spike can interact with its axial neighbors that are within range, letting them gain a binding energy (per unit length), v(l). On the flip side, binding along its long axis implies a curving of the cylindrical virus, which costs elastic bending energy. Modeling the latter contribution as a harmonic term with bending stiffness B, the total energy per cross section is hence given by
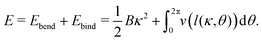 | (2) |
 | (3) |
Inserting eqn (1) and (3) into eqn (2), the energy can be calculated analytically.† Importantly, for suitable parameters its shape is of Mexican-hat-type, see the inset showing the energy shape in the light green region of Fig. 2b. This is what we call the “toro-elastic” state: a finite curvature is preferred, whose direction (i.e., angle ϕ) is arbitrary and hence corresponds to a soft mode. Fig. 2b shows the different energy landscapes/shapes when varying the depth, v0, and the minimum position, σ, of the potential for fixed spike distance l0 and virus stiffness B. This phase diagram displays: (i) an elastic state (dark green) where κ = 0 is the energy minimum, corresponding to a straight virus; (ii) the toro-elastic region (light green), where the minimum is a circle with |κ| = κtor and arbitrary angle ϕ; and (iii) a coexistence region (yellow), where both previous states are local minima, with a barrier in between. Fig. 2c shows a similar phase diagram in the plane spike distance l0vs. minimum position of the potential σ, now for fixed potential depth v0.
To understand when the straight state becomes unstable, we expand the energy up to second order in curvature, yielding 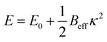 with
with 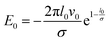 and an effective bending stiffness Beff = B + Bbind with
and an effective bending stiffness Beff = B + Bbind with  . This binding-induced part of the effective stiffness can become negative. In fact, this can be always satisfied for l0 ≳ 2σ if in addition the interaction is sufficiently large, v0 ≫ el0/σB/l02: then Bbind overrules B and the filament curves, with higher order terms stabilizing a finite toroidal curvature κtor.
. This binding-induced part of the effective stiffness can become negative. In fact, this can be always satisfied for l0 ≳ 2σ if in addition the interaction is sufficiently large, v0 ≫ el0/σB/l02: then Bbind overrules B and the filament curves, with higher order terms stabilizing a finite toroidal curvature κtor.
This toro-elastic state generically appears for short ranged potentials; a general condition can be determined by expanding an arbitrary potential v(l) around its straight state l0, see Appendix B. Then for  , Beff = B + πv′′(l0)l02R2, implying that the curvature v′′(l0) of the potential must be sufficiently negative,
, Beff = B + πv′′(l0)l02R2, implying that the curvature v′′(l0) of the potential must be sufficiently negative,
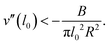 | (4) |
The virus curvature in the toro-elastic state adjusts such that a significant portion of the cross-section (typically half of it), benefits from the surface interactions. For that, the elements of the surface need to shift from their unperturbed distance l0 to σ, i.e. by an amount l0 − σ ∼ κtorRl0, which yields an estimate for the curvature of the toro-elastic state
| κtor ∼ R−1(1 − σ/l0). | (5) |
 , and the binding energy by δE ≈ |E0|. Equating
, and the binding energy by δE ≈ |E0|. Equating  then yields
then yields | (6) |
Considering numbers, typical scales are l0 = 25 nm, σ = 10 nm and R = 50 nm; potential strength around v0 = 1kBT nm−1. The bending rigidity of a virus is hard to measure,20 but considering the virus as a membrane tube we estimate B = 2πR × 10kBT ≃ 3kBT μm. Using these values, one finds Bbind ≃ −5.7kBT μm, hence indeed Beff < 0 is at reach. Further we estimate from eqn (5) and (6) that κtor ≃ (100 nm)−1 and the toro-elastic stiffness Ktor ≃ 100kBT μm, which is much larger than the usual bending rigidity.
3. Toroelastic state driven by ligand dynamics
Having seen how the toro-elastic, curved state arises, we now show how the orientation angle of the curved state – representing a soft mode due to the Mexican-hat-type potential – can be driven to rotate in an out-of-equilibrium situation. For this we assume that the virus is embedded in a solvent that contains a substantial concentration of glycan-coated polymers which the virus spikes’ can attach to and enzymatically cut. This reflects the situation in the mucus, which is a gel/network of long and heavily (up to 80%) glycosilated mucins,21 having a pore size of 100–500 nm,22 hence larger than the virus diameter. For simplicity, we model this situation via di-glycan “dumbbells” floating in solution, representing attachment to glycans from the same mucin backbone. We would like to stress that we consider the virus to be embedded in a 3D environment, cf. (Fig. 1d). This should be contrasted to the catalytic spike-induced motion of viruses on surfaces.12,13,23 In the latter case, strategies like the burnt-bridge mechanism, employing the trail of cut glycans behind to rectify the motion, or rolling14,24 can be used. In contrast, in the absence of surfaces both mechanisms are not possible or not effective (with the trail in 3D having a mathematical measure close to zero).The argument for rotation involves two steps: first, when glycan dumbbells attach to two axially neighboring spikes, they introduce longitudinal tensions on top of the toro-elastic state, creating a torque. Second, the cutting of the glycan dumbbells leads to a release of tension with a certain dead time for new binding, since cut glycans have yet to detach. Like that, torque is maintained by breaking of detailed balance and the dead time gives the system a “directional memory”, once a direction of rotation is picked.‡
To calculate the torque due to dumbbell attachment, we assume the di-glycans to be harmonic polymer springs with spring constant S and vanishing preferred length. They can be unbound (state B0), bound to one spike (state B1) or to two neighboring spikes – along the backbone – defining the double bound state D, see the upper part of the reaction scheme in Fig. 3b. In the double bound state, glycans stretch out to a non-zero length given by eqn (1), with ϕ the orientation of the curvature κ and θ the angular position of the spike it attaches to in the considered cross-section.
Note that, for simplicity, we consider here only relevant spike-glycan interactions, which are the ones along the virus axis, or having, when projected, a component along the axis. Couplings along the azimuthal direction are neglected, since they do not contribute to axial bending. Note that this simplification introduces effective, phenomenological binding rates.
As the spikes are assumed to be uniformly distributed over the surface, all states have to be described by a function of the azimuthal angle θ. In general, a cross-section will have an azimuthal imbalance of the (double-)bound density D(θ). The total glycan stretching energy per cross-section of thickness l0 then reads  . Assuming small curvatures κR, κl0 ≪ 1 and applying a mode ansatz D(θ) = D0 + Ds
. Assuming small curvatures κR, κl0 ≪ 1 and applying a mode ansatz D(θ) = D0 + Ds![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Dc
θ + Dc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, to linear order
θ, to linear order  . The corresponding torque (per l0 section) is given by
. The corresponding torque (per l0 section) is given by  and in the frame co-moving with the toro-elastic curvature evaluates to
and in the frame co-moving with the toro-elastic curvature evaluates to
 | (7) |
This is the driving torque from the inhomogeneously distributed double bound glycans, with mdr the characteristic torque scale. Assuming a Kuhn length of a glycan chain of b ∼ 0.5 nm25 and a number of bonds of N ∼ 40 or larger one expects typical spring constants  . Together with the above parameters and κ = κtor, we estimate mdr ≃ 2–20kBT, which is much larger than the hydrodynamic resistance of such a small cross-section.§ In view of this, we will first study the case, where resistance can be completely neglected, implying that the total torque is zero. It should be however noted that the attachment–detachment dynamics to the sticky mucin network elements of the mucus can contribute an additional friction term due to dragging a portion of the mucins along with the virus. Therefore, in a next step, we will add the (rotational) resistance perturbatively.
. Together with the above parameters and κ = κtor, we estimate mdr ≃ 2–20kBT, which is much larger than the hydrodynamic resistance of such a small cross-section.§ In view of this, we will first study the case, where resistance can be completely neglected, implying that the total torque is zero. It should be however noted that the attachment–detachment dynamics to the sticky mucin network elements of the mucus can contribute an additional friction term due to dragging a portion of the mucins along with the virus. Therefore, in a next step, we will add the (rotational) resistance perturbatively.
To describe the possible steady-state torque generation, we now consider the enzymatic glycan cutting activity of the HEF spike. The reaction scheme just discussed has to be extended by two more states associated to the cutting reaction, as sketched in the lower part of Fig. 3(b): First, a double bound glycan can be cut into two, to a state C2 that still blocks both spikes for further attachments. If one of these cut parts detaches, or if a single bound glycan is cut, this yields state C1. Importantly, only if all cut parts have left, one recovers state B0 and the spike can be “reused” for attachment.
 | ||
| Fig. 3 (a) Interaction of tension-inducing polymeric ligand springs (glycan dumbbells) with the virus spikes. (b) The reaction kinetics of equilibrium binding and catalytic cutting. | ||
The full reaction scheme of Fig. 3b translates into
 | (8) |
We now consider the steady-state, where the virus curvature κ is rotating with constant angular frequency ω – that has to be determined, and could of course be zero – implying ϕ(t) = ωt, and where κ = const. as suggested by the high stiffness of the toroidal state estimated above. We hence transform eqn (8) into the co-moving frame, ϕ = 0, where steady states become time independent and the total time derivative transforms into an advective derivative 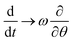 .
.
The double binding rate, k2(θ) in the co-moving frame, can be specified as follows: we expect a relation
k2(θ) = k02(1 + α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), θ), | (9) |
 . Matching this result with eqn (9),
. Matching this result with eqn (9),  , yields the estimate
, yields the estimate | (10) |
The equations for the steady state dynamics in the co-moving coordinate system can be solved by applying a mode ansatz, similar as above for the driving torque. Now all chemical species are expressed as X = X0 + Xc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Xs
θ + Xs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ for X = B1, D, C1, C2. In the case of negligible fluid friction, and fast binding of the second bond of the dumbbell, k02 ≫ kothers, the solution can be given analytically, see appendix C. One finds that ω = 0 – i.e. no rotation – is always a solution. However, solutions with finite angular velocity, given by
θ for X = B1, D, C1, C2. In the case of negligible fluid friction, and fast binding of the second bond of the dumbbell, k02 ≫ kothers, the solution can be given analytically, see appendix C. One finds that ω = 0 – i.e. no rotation – is always a solution. However, solutions with finite angular velocity, given by
 | (11) |
 | (12) |
Rephrasing eqn (12) as  , the first ratio demands a sufficiently large effective attachment rate (k1G) to supply for new D (for large k2, B1 converts to D fast) and the second a sufficiently large cutting rate to maintain non-equilibrium. Due to the product, faster attachment can compensate for slower cutting and vice versa. Notably, the rotating state also requires a sufficiently long “dead time” interval tdt = 1/k−1, i.e. a sufficiently small off-rate k−1 compared to kcut. This is intuitively understandable, as large dead times allow for the maintenance of the angular direction (clockwise/anticlockwise rotation), while too short dead times would effectively erase the directional memory of the main force-generating “power-stroke” sequence B0 → D → Ci → B0 and the time-ordering of the force-generating state D(θ, t) in the azimuthal direction necessary for persistent rotation.
, the first ratio demands a sufficiently large effective attachment rate (k1G) to supply for new D (for large k2, B1 converts to D fast) and the second a sufficiently large cutting rate to maintain non-equilibrium. Due to the product, faster attachment can compensate for slower cutting and vice versa. Notably, the rotating state also requires a sufficiently long “dead time” interval tdt = 1/k−1, i.e. a sufficiently small off-rate k−1 compared to kcut. This is intuitively understandable, as large dead times allow for the maintenance of the angular direction (clockwise/anticlockwise rotation), while too short dead times would effectively erase the directional memory of the main force-generating “power-stroke” sequence B0 → D → Ci → B0 and the time-ordering of the force-generating state D(θ, t) in the azimuthal direction necessary for persistent rotation.
It is also possible to solve the problem in the presence of the small, hydrodynamic rotational resistance. Assuming a hydrodynamic (Stokes) rotational friction torque Mh = ξhω = 4πηR2l0ω and equating it with the driving torque, eqn (7), one gets kccut = kc,0cut + kc,1cut(η). The correction is to leading order linear in fluid viscosity η, proportional to  and in addition depends on the chemical rates. See Appendix C for the result, eqn (46), and how it is obtained.
and in addition depends on the chemical rates. See Appendix C for the result, eqn (46), and how it is obtained.
Fig. 4a shows the angular velocity ω as a function of the cutting rate kcut: the red curve shows (the positive branch of) eqn (11) and the black curve are numerical results including the frictional torque. Since the kinetic parameters of IV-C have not been characterized, we had to resort to estimates for IV-A here: G = 3 mM; k1 = 0.1 mM−1 s−1, k−1 = 0.1 s−1;26,27k02 = 1 mM−1 s−1, k−2 = 0.1 s−1. Note that cutting rates are estimated conservatively, IV-A's neuraminidase reaches rates of up to kcut = 15 s−1.28
 | ||
| Fig. 4 (a) The toroidal mode's angular frequency as a function of the cutting rate kcut (both in units s−1). Red curve: analytical result, eqn (11), obtained without friction. Black curve: numerical result with realistic frictional torque coefficient ξh/mdr = 0.01. Parameters as described in the main text. Inset: The angular dependence of the steady-state populations. Right hand side: Scaled and shifted populations for visual comparison. Note their typical phase lag. (b) The polar plot of the double-bound and cut state populations, D(θ,t) and C2(θ,t) respectively, shows their characteristic phase-shift determining the direction of toroidal rotation. Polar plots are schematic and not to scale. (c) The latter kinetics induces a uniform, shape-invariant rotation of a short toroidal virus or an elongated helical virus with frequency ω. When embedded in a viscous fluid the rotation leads to a swimming kinematics similar to fluid vortex lines.29,30 | ||
We have shown that dynamic force imbalances, caused by interactions of the virus spikes with glycans from the 3D environment, can lead to a rotation of the toroidal state. We note that in Section 2, we considered the toroidal state to be caused by spike–spike interactions. Hence the creation of the toroidal state, and its rotation outside of equilibrium, have different causes: spike–spike vs. spike–glycan interactions. While the former needs localized, anharmonic interactions, for the additional imbalance caused by the latter linear spings are sufficient. Experimental evidence shows strong spike–spike interactions, at least for IV-C.17 Nevertheless, one could also imagine the toroidal state to be caused (or modulated) by spike-glycan interactions as well. In that case, the rotation is probably less stable: when the virus moves, its rear will be exposed to fewer uncut glycans, and the helix at the rear may unfold. Such effects, as well as considering a varying density of the enzymatic spikes along the virus backbone – or a phase-separated one, as in IV-A23 – would be interesting to investigate in the future.
4. Helix formation
Let us now come back to the helical shapes of IV-C as shown in Fig. 1c, noting that also filamentous IV-A sometimes displays curvature.31 So far, we considered a single cross-section, hence the natural question arises how different cross-section are coupled. As sketched in Fig. 1e as pairs 1–2 and 3–4, in general viruses have staggered spike sub-lattices.Assuming for simplicity two sub-lattices, I and II, these experience the mean effective curvature induced by the other sub-lattice over their length scale (l) as 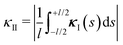 and analogously for κI, implying a smearing-out of sectional curvature over the two lattices. For a curvature vector of constant amplitude slowly winding with a torsion rate τ ≪ l−1 like κ(s) = κ(cos(τs)ex + sin(τs)ey), the total energy of the two sub-lattices can be calculated to be, see Appendix D, as
and analogously for κI, implying a smearing-out of sectional curvature over the two lattices. For a curvature vector of constant amplitude slowly winding with a torsion rate τ ≪ l−1 like κ(s) = κ(cos(τs)ex + sin(τs)ey), the total energy of the two sub-lattices can be calculated to be, see Appendix D, as
 | (13) |
This energy is positive definite. Its ground state is curved and untwisted, κ = κtor and τ = 0. The first term is similar to classical bending energy, followed by a torsion–bend coupling that is quartic for κ = κtor. Notably, for curvatures larger than optimal, κ > κtor, the torsion becomes bistable with two new preferred states 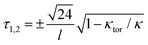 . Hence external bending torques – like those due to the above-discussed glycan binding – will turn the toroidal ground state into a bistable helix. The symmetry between the two helical states is likely broken by a geometrical chirality of the natural spike lattice – an effect neglected here for simplicity.
. Hence external bending torques – like those due to the above-discussed glycan binding – will turn the toroidal ground state into a bistable helix. The symmetry between the two helical states is likely broken by a geometrical chirality of the natural spike lattice – an effect neglected here for simplicity.
5. Discussion and conclusions
There is an old question from biology asking “why nature does not have wheel and axles”. In the light of what we know about the emergence of toroidal zero-energy modes in the bacterial flagellar hook2,3 (and possibly microtubules4,5), the question can be tentatively answered by: Nature has something better – the “wheel within (the filament)”. In fact, to implement and maintain bi-component wheel-axle system is hard to achieve biologically, but a very practical replacement exists: any elastic object equipped with a circularly symmetric zero-energy mode. Such structures have the great advantage of being single piece continuous structures that are containing both an axle (the material frame of the structure), and the wheel – the deformation propagating (rotating) with respect to the material frame at virtually no elastic energy cost. The simplest of such ZEEMs7 (zero elastic energy modes) seems to be the toro-elastic mode we revisited here for filamentous viruses.We have shown that such a mode can generically appear for any rough surface spiked cylinder – like a filamentous influenza virus – for sufficiently strong and short ranged spike interactions, competing with elastic restoring forces of the elastic core of the cylinder. Once this toro-elastic ZEEM emerges and equilibrium detailed balance is somehow broken – as by the spike-catalysed glycan-cutting investigated here – it becomes possible for this “wheel-like” mode to actively rotate in a particular direction, randomly picked by a non-equilibrium bifurcation as investigated here. The resulting spatial motion, that could be seen as a shape invariant, constant angular velocity “re-bending” dynamics of the filament perpendicular to its axis is similar to the anholonomic body reshaping of a falling cat32,33 and has been described in various terms and contexts in the literature. Other examples include the “eversion/inversion” for self-rolling polymer fibers,8,34 “wobbling motion” in clamped, superhelical microtubules4 and the “ideal joint” rotation for the bacterial flagellar hook driven by the flagellar motor.3 A related active re-bending/eversion motion in the soft, body reshaping bacterium spiroplasma has been also recently described.35
Furthermore we have shown that the toro-elastic mode in a long filament equipped with a sticky surface lattice can induce helix formation in addition to toroids. The spontaneous emergence of multi-stable and rearranging helices is very common in biological filaments and their origins have been studied in various systems including bacterial flagella,36–39 microtubules,4,5 intermediate filaments6 and spiroplasma.35 Looking at the wealth of examples, one is tempted to suspect that the cylindrically symmetric filament shape could be structurally unstable against perturbations and that the superhelical filament is the rule rather than the exception in Nature. The common theme behind the emergent helicity in these filaments seems to be some form of core–shell stress mismatch combined with various forms of elastic anharmonicity, that originates from mechanical, geometric or molecular nonlinearities. In contrast to these previous examples, in the proposed virus model, the helical states are still subcritical or “evanescent”, that is, only upon (arbitrary small) additional stresses, the straight state spontaneously breaks the symmetry and picks one of two handed helices. However, it appears possible or even likely that specific spike-lattice arrangement and chiral spike–spike interactions would give rise to more specific, additional effects, so far neglected here. This would lead to definite handedness helices in the ground state of the virus and be described by similar physics as in the other helical systems.36,37,39,40
Finally, if – via the enzymatic drive described above – the toroidal or helical virus uniformly rotates its body keeping its shape invariant, see (Fig. 4c), we expect it to self-propel and swim. Whether the motion corresponds to a toroidal or a helical rotation depends on the presence (or absence) of angular shift between the directions of curving of two subsequent cross-sections. In the case that all curvature directions are found in a single (osculating) plane, an ideal toroidal rotation occurs, see (Fig. 4c) on the left. If the plane of curvature is changing along the contour, the rotation is helical, see (Fig. 4b) on the right. The swimming kinematics will be that of a helically shaped spinning cable. Mathematically this is a vortex line of fixed vorticity ∝ ω, self-advecting through the fluid.29 In leading order the self-propulsion is independent of the (small) helical torsion and occurs at typical velocities of spinning tori v ∼ ωκR2.30,41 Note that the predicted shape invariant swimming contrasts body-reshaping swimmers (like spirochetes) using propagating bending waves, where the velocity depends on undulation amplitude and wavelength but not on radius.42
The described motility mechanism should be directly applicable to IV-C. It could also be relevant for influenza A, where, however, the two dynamic properties of the spike – the binding to/unbinding from glycan and the cutting of glycan residues – are not co-localized in a single HEF spike. In IV-A, these tasks are performed by two different spike proteins, hemaglutinin (HA) for the binding/unbinding and neuraminidase (NA) for the cutting. This makes the surface structure of IV-A more complex, and in fact, HA and NA are often phase-separated on the virus surface,23 implying that the theory developed here has to be generalized to inhomogeneous spike distributions. Our theory is also relevant for the design of synthetic self-propelled objects, where the adhesion–cutting mechanism has been already implemented, e.g., via DNA–RNA hybridization (binding/unbinding) and catalytic action of RNase H (selectively cutting duplexes), to induce surface-based motion.43–46 The here-described 3D toroidal motion should be at reach for DNA nano-tubes floating in a solution of RNA, able to bind to two DNAs along the backbone, and RNase H. One could also think of synthetically motorizing the flagellar hook.2,3
Coming back to viruses, while IV-C has rarely been studied, many studies on IV-A suggest that the enzymatic activity (of NA in case of IV-A) is important for mucus penetration, both on the macroscopic level,18,19 as well as by observing filamentous viruses directly.23 For purely spherical viruses, however, it seems that NA is less relevant and it is rather the mesh size of the mucus that determines the diffusion, as reported in ref. 47. This finding is in accordance with our model and the one by Vahey and Fletcher,23 where only filamentous viruses can profit from enzymatic mechanisms. We note that the mechanism described in ref. 23 is ratchet-based, hence the longer the filament, the slower the motion – since then the virus engages many links, causing increasing friction, proportional to virus length. In contrast, the mechanism proposed here would be effective independent of virus length.
In future studies, the nature of the mucus as a natural habitat environment for filamentous influenza viruses needs some deeper considerations. Regardless of the detailed motility mechanism, the mucus poses a significant barrier to viral motion. Depending on its mesoscale morphological features, like its pore size47 or glycan density and type,21 it will impose different constraints to the viral filament in various shapes and modes of motion. Large scale motion through such an environment would not be easily possible for a virus that is straight or a piece of a torus, while a helical filament could easily “follow its own footprint” and reptate its way through the mucus pores.
In conclusion, filamentous viruses like influenza C, possessing the toro-elastic state due to axial interactions can develop helical shapes and can attain a spontaneous rotation upon binding and cutting interactions with the glycans floating in the mucus. The predicted angular velocities are comparable to the rolling angular velocities of surface attached viruses (fractions of s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,14). The expected swimming velocity of tens of nm/s is rather modest compared to swimming speeds of microorganisms, yet still of the order of one virus size per second and hence preferable to staying immobilized in the extremely viscous, sticky environment faced in the mucus. The proposed mechanism adds another possible motility mode – effective in 3D surroundings such as loose mucus networks – to the existing repertoire of the influenza family and torovirus, beyond ratchet-like motion23 and rolling,12,13 which both employ glycan-coated surfaces.
13,14). The expected swimming velocity of tens of nm/s is rather modest compared to swimming speeds of microorganisms, yet still of the order of one virus size per second and hence preferable to staying immobilized in the extremely viscous, sticky environment faced in the mucus. The proposed mechanism adds another possible motility mode – effective in 3D surroundings such as loose mucus networks – to the existing repertoire of the influenza family and torovirus, beyond ratchet-like motion23 and rolling,12,13 which both employ glycan-coated surfaces.
Author contributions
F. Z. and I. M. K. developed the model. F. Z., K. G. D. and I. M. K. performed the calculations. All authors wrote the paper.Data availability
The data supporting this article have been included as part of the Appendices at the end of the article.Conflicts of interest
There are no conflicts to declare.Appendix
A. Derivation of the “shortcut factor”: surface–surface contact spacing
To derive the formula for the spacing between surface contacts from the main text, eqn (1), we assume that deformations are linear, keeping the “neutral line” arc-length contour distances unchanged, i.e. d12 = const., independent of κ. After uniformly bending the virus with a center line curvature κ, cf.Fig. 5, the surface elements on the outside of the bend (found at a radial spacing R from the neutral line) change their distances along the circular contour proportional to the curvature κ | ||
| Fig. 5 Sketch of the geometry of a strongly bent cylinder (the virus capsid/envelope) and the emergence of the short-cut factor. | ||
For spiky surface elements that interact along the shortest spatial distance, the relevant spatial distance s12 between two spikes is shorter than the surface arc-length  : it is given by the length of the secant line corresponding to an opening angle
: it is given by the length of the secant line corresponding to an opening angle 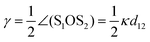 with length
with length
The spatial distance can be simply generalized to any azimuthal orientation θ of the bent cylinder (where θ = 0 points to the “inside” of the bend) such that
With d12 = l0 and giving the curvature direction another angle, ϕ, this is eqn (1) from the main text.
B. Influence of the potential shape on the emergence of the toro-elastic state
Gaussian potential
We investigated a more general potential of Gaussian form,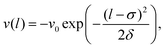 | (14) |
Unfortunately, the energy cannot be calculated analytically anymore. Fig. 6 shows results for the “phase” diagrams obtained by numerical minimization. The color code is the same as in Fig. 2. The left figure shows the plane l0vs. variance δ for fixed σ = 10 nm. One can see a certain symmetry with respect to l0 = 10 nm: now, the spikes can also induce the toro-elastic state by stretching out towards the minimum of the potential. The toro-elastic state is easiest to attain for a short ranged (variance) δ of the potential, but on the other hand its existence region shrinks for small δ and the region of coexistence increases. The right figure shows the plane l0vs. σ for fixed δ = 10 nm2. One can see interesting series of transitions. For instance, choosing σ = 15 nm, upon increasing l0 from a small value one finds first the elastic state, then coexistence, then the toro-elastic state, again an elastic region and a toro-elastic region (and again coexistence for larger l0, beyond the region visible in the figure).
 | ||
| Fig. 6 (a) l0 in nm and δ in nm2 for σ = 10 nm. (b) l0 and σ in nm for δ = 10 nm2. Color-code is according to the energy minima, as in Fig. 2b and c. Dark green: elastic state, straight state is stable; light green: toro-elastic state, with an energy minimum at finite κ; yellow: coexistence region. Parameters: virus radius R = 50 nm; virus bending rigidity B = 3kBT μm; contact potential strength v0 = 1kBT nm−1. | ||
The additional study of the Gaussian potential shows that the shape of the potential of course matters, but that the three states described in the main text – elastic, toro-elastic and coexistence – are again found.
Harmonic potential
To shed some light on which properties the binding potential has to fulfill in order for the toro-elastic instability to occur, let us study the simplest case of a harmonic binding potential. Note that a harmonic v(l) is not physically realistic, as every realistic binding potential will have a finite range. Using v(l) = a(l − b)2 with some spring stiffness 2a and preferred length b, the binding energy reads (note that l = l(κ,θ))The two integrals can be evaluated
 | (15) |
with u = κl0/2. Expanding for small u shows that in the relevant limit R > l0 and for any positive preferred length b of the harmonic spring, the quadratic term is always positive.
But in principle, a negative quartic term could still induce an instability. To investigate this, adding the bending stiffness term  yields the total energy
yields the total energy
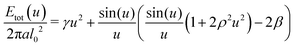 | (16) |
where ρ > 1, typically even ρ ≫ 1.
Taylor expanding for small u yields, neglecting a constant,
When the (negative) quartic and the (positive) quadratic term become comparable, we expect a barrier u ≈ ubar to occur which for the special case of β = 0 can be given as
In summary, we have just shown that for a harmonic potential, the straight state increases in stability and cannot show an instability.
Criterion for toro-elasticity for a general potential
Let us now assume a general potential v(l) and investigate, when the straight state can become unstable. For that we expand v(l) around its straight state l = l0, | (17) |
The binding energy can again be evaluated, expanding the functions L1, L2 defined in eqn (15) in powers of κ. Again dropping constant energy contributions, we get
 | (18) |
Interestingly, going on in the expansion of eqn (17), the contribution from v′′′(l0) cancels in O(κ2). Furtheron, it is easy to check that, using eqn (18) for the linear-exponential potential, eqn (3), exactly recovers the criterion discussed in the main text. This both corroborates that the contributions from v′(l0) and v′′(l0) are the most relevant contributions.
For the toro-elastic state to emerge, the prefactor of the term ∝κ2 in eqn (18) has to be negative. In general, the second term is the dominant one, due to its large geometric prefactor  . As a generic neccessary condition for the toro-elastic instability – in the relevant parameter range for a thin virus – one can hence state that v′′(l0) < 0 should hold. A harmonic potential is strictly convex and v′′(l0) > 0 forbids the instability, as shown before. But v′′(l0) < 0 is of course possible for a short ranged potential in its concave region. In fact, all short ranged potentials have a concave region, namely when crossing over from the minimum to the zero-level plateau at large distances.
. As a generic neccessary condition for the toro-elastic instability – in the relevant parameter range for a thin virus – one can hence state that v′′(l0) < 0 should hold. A harmonic potential is strictly convex and v′′(l0) > 0 forbids the instability, as shown before. But v′′(l0) < 0 is of course possible for a short ranged potential in its concave region. In fact, all short ranged potentials have a concave region, namely when crossing over from the minimum to the zero-level plateau at large distances.
Including the bending rigidity, the total potential reads
 is dominated by the first two terms. The toroelastic state then emerges for
is dominated by the first two terms. The toroelastic state then emerges for | (19) |
C. Perturbation theory for the rotating state
We now consider the case where the toro-elastic curvature κ may rotate in the lab frame with angular velocity ω, due to the chemical reactions (attachment and cutting of glycan dumbbells). We place ourselves in the co-moving coordinate system where κ is stationary and can rewrite the dynamics by replacing the time derivative in terms of the advective derivative . As we are only interested in the steady state, the partial time derivative drops out and we are left with the replacement rule
. As we are only interested in the steady state, the partial time derivative drops out and we are left with the replacement rulefor the chemical reactions in the main manuscript. Eliminating B0 by using B0 = 1 − B1 − C1 − C2 − D, eqn (8) in the stationary, co-moving frame now read
 | (20) |
Now we make the simple mode ansatz already mentioned in the main part: all chemical species X = B1, D, C1, C2 can have a constant, a cos- and a sin-mode,
X = X0 + Xc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Xs θ + Xs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ. | (21) |
The amplitudes X0, Xc, Xs need to be determined, except for the Ds – mode – existing in the presence of external torques – which is fixed by the torque balance: in the general case, where an external torque is present, we have (in the co-moving frame)
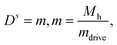 | (22) |
We exemplify the method for the equation for C2. One inserts the mode ansatz into  , to obtain
, to obtain
Now we project on the modes by performing integrations like 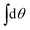 ,
,  and
and  . This yields three conditions – for the constant, sin- and cos-mode, respectively:
. This yields three conditions – for the constant, sin- and cos-mode, respectively:
Note that terms ∝ Ds are only present in the case of an external torque. The equations can be solved and simplified.
Proceeding the same way for all equations, one gets expressions for B1, C1, C2 as functions of D0, Dc, Ds
 | (23) |
 | (24) |
 | (25) |
 | (26) |
| −ωBc1 = −k1GCs1 − k1GCs2 − (k1G + k−1 + k02 + kcut)Bs1 + (k−2 − k1G)Ds, | (27) |
| ωBs1 = −k1GCc1 −k1GCc2 + (k−2 − k1G)Dc − (k1G + k−1 + k02 + kcut)Bc1 + k02αB01, | (28) |
Approximation of fast binding rate k2
To be able to proceed, we now assume that the binding of the second “leg” of a glycan dumbbell that is already attached to the virus, k2, is faster than all other processes. More specifically, we assume k02 ≫ kothers, ω while kothersB1 → 0, ωB1 → 0 and only B1k02 ∼ O(1) stays finite.The effect is that we can drop all terms with kothersB1, express everything in terms of D0, Dc, Ds and get  and
and
 | (29) |
 | (30) |
| 0 = −k1G(Cs1 + Cs2) − k02Bs1 + (k−2 − k1G)Ds, | (31) |
| 0 = −k1G(Cc1 + Cc2) + (k−2−k1G)Dc − k02Bc1 + k02αB01. | (32) |
From eqn (29), we can now extract
and inserting all known fields into eqn (30)–(32) results in three closed equations for D0, Dc and ω for given Ds:
 | (33) |
 | (34) |
 | (35) |
Case of negligible external torque/friction
The simplest result can be obtained, if one assumes that the external torque – which is due to hydrodynamic friction, and for such a small object as a 100 nm thin virus should be very small – is negligible. m = 0 then immediately implies Ds = 0, cf.eqn (22).In this case, from eqn (34), we immediately get the following instructive result:
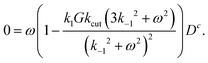 | (36) |
First of all, ω = 0 – i.e. no rotation at all – is always a solution, as it should. The term in brackets could yield non-trivial solutions, but only in case that Dc ≠ 0. This also makes sense, since otherwise D would be constant and no torque is created. In fact, for α ≠ 0 one has Dc ≠ 0 – which can be seen from eqn (33) and (35). There is one more condition: k−1 > 0 has also to be finite. Otherwise one can show that D(ω) = 0, which reflects a “blocking effect”: all initially existing double bound states were cut and the cut glycans never can detach.
In total, this yields (in case α, k−1 ≠ 0) three possible solutions for the angular velocity ω:
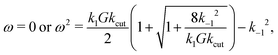 | (37) |
 | (38) |
This is the pitchfork bifurcation explained in the main manuscript: for sufficiently large cutting rate kcut, namely if
 | (39) |
General case and obtaining the motor relation
To treat the general case, we consider the limit of small α, i.e. small variations of k2(θ) with θ. We expand eqn (33)–(35) to linear order in α, and notice that a certain symmetry emerges: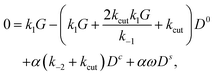 | (40) |
| 0 = u(ω)Dc − v(ω)Ds, | (41) |
| 0 = −v(ω)Dc − u(ω)Ds + 2α(k−2 + kcut)D0, | (42) |
 | (43) |
From (41) we immediately get 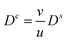 , inserting into (42) yields
, inserting into (42) yields
Dropping orders O(α2) we solve for
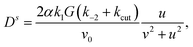 | (44) |
 | (45) |
It relates any external torque (here the hydrodynamic frictional torque Mh) to the kinetics of the rotation.
Dynamics under Stokes friction
Assuming the external torque is Stokes friction in a fluid of viscosity η, yields the explicit expression| Mh = 4πηR2l0ω |
Considering that for small torques, u is small as well – note that u(ω) = 0 was the relation determining ω in the case of no frictional torque, cf.eqn (36) – we drop the u2 – term in the denominator and expand the r.h.s. for ω2 small (close to the onset of motion). The leading order constant term O(ω0) cancels on both sides for the motion to occur
 ):
): | (46) |
D. Details on helix formation
In general a virus surface displays multiple interdigitated and mutually staggered sub-lattices of switchable spike-pairs, as sketched in (Fig. 1e) (pairs 1–2 and 3–4). We assume here for simplicity just two sub-lattices, I and II.In the following we make the intuitive assumption that the curvature vector is a smooth function along the contour s, regardless of how it is measured, over sub-lattice I or II. This in particular implies that one sub-lattice will experience the mean effective curvature of the other sub-lattice (averaged over the smallest characteristic length scale ∼l). Due to the smoothness, the curvature vector felt by sub-lattice II at some position s can be formally expressed by the mean of curvature vector over the sub-lattice I in its close vicinity, i.e. as
 | (47) |
For a constant modulus κI, and a slowly rotating curvature vector on the sub-lattice I,
| κI(s) = κI(cos(τs)ex + sin(τs)ey) |
 | (48) |
That is, the curvature felt by lattice II from the one at lattice I becomes effectively reduced by an amount 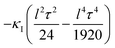 .
.
The overall energy penalty per length l can then be written as the average over the two sub-lattices, with Ktor given by eqn (6), and evaluates to
Dropping the index I and rearranging,
 | (49) |
The torsion–bend coupling suggests an unusual mechanics: (i) for optimal curvature κ = κtor the torsional term has a weak quartic stiffness O(τ4) indicating some flexibility in this degree of freedom. (ii) For curvature larger than optimal, i.e. for κtor − κ < 0, a torsion (of any sign) is favorable, given by
 | (50) |
 in leading order, forcing it strongly towards the τ = 0 state.
in leading order, forcing it strongly towards the τ = 0 state.
Overall this indicates some highly unusual spatial dynamics of the toro-elastic state, very much different from usual semiflexible filaments. Note that case (ii), i.e. larger curvature than κtor, is the one that should be relevant for a virus in a mucus environment, where glycan ligands cause additional tensile stresses, leading to increased curvatures.
Acknowledgements
I. M. K. thanks Jens-Uwe Sommer for continuous discussion and support.References
- H. C. Berg and R. Anderson, Nature, 1973, 245, 380–382 CrossRef CAS PubMed.
- S. Shibata, H. Matsunami, S.-I. Aizawa and M. Wolf, Nat. Struct. Mol. Biol., 2019, 26, 941 CrossRef CAS PubMed.
- T. Kato, F. Makino, M. Tomoko, P. Horvath and K. Namba, Nat. Commun., 2019, 10, 5295 CrossRef PubMed.
- H. Mohrbach, A. Johner and I. Kulić, Phys. Rev. Lett., 2010, 105, 268102 CrossRef PubMed.
- F. Ziebert, H. Mohrbach and I. Kulić, Phys. Rev. Lett., 2015, 114, 147101 CrossRef PubMed.
- L. Bouzar, M. M. Müller, R. Messina, B. Nöding, S. Köster, H. Mohrbach and I. M. Kulić, Phys. Rev. Lett., 2019, 122, 098101 CrossRef CAS PubMed.
- A. Baumann, A. Sánchez-Ferrer, L. Jacomine, P. Martinoty, V. Le Houerou, F. Ziebert and I. M. Kulić, Nat. Mater., 2018, 17, 523 CrossRef CAS PubMed.
- A. Bazir, A. Baumann, F. Ziebert and I. M. Kulić, Soft Matter, 2020, 16, 5210 RSC.
- M. D. Badham and J. S. Rossman, Curr. Clin. Microbiol. Rep., 2016, 3, 155 CrossRef PubMed.
- M. L. Martin, E. L. Palmer and A. P. Kendal, J. Clin. Microbiol., 1977, 6, 84 CrossRef CAS PubMed.
- A. E. Hoet and M. C. Horzinek, Torovirus, in Encyclopedia of Virology, 3rd edn, 2008, p. 151 Search PubMed.
- T. Sakai, S. I. Nishimura, T. Naito and M. Saito, Sci. Rep., 2017, 7, 45043 CrossRef CAS PubMed.
- T. Sakai, H. Takagi, Y. Muraki and M. Saito, J. Virol., 2018, 92, e01522–17 CrossRef PubMed.
- F. Ziebert and I. M. Kulić, Phys. Rev. Lett., 2021, 126, 218101 CrossRef CAS PubMed.
- X. Wu, M. Goebbels, L. Chao, T. Wennekes, F. J. M. van Kuppeveld, E. de Vries and C. A. M. de Haan, PLoS Pathog., 2023, 19, e1011273 CrossRef CAS PubMed.
- D. Rodriguez Aguirre, Virus Taxonomy - Classification and Nomenclature of Viruses. Online-Edition. Chp. “Coronaviridae”, in ICTV Reports. International Committee on Taxonomy of Viruses, 2011, adapted from: https://en.wikipedia.org/wiki/Torovirus Search PubMed.
- S. Halldorsson, K. Sader, J. Turner, L. J. Calder and P. B. Rosenthal, Nat. Commun., 2021, 12, 1694 CrossRef CAS PubMed.
- M. Cohen, X.-Q. Zhang, H. P. Senaati, H.-W. Chen, N. M. Varki, R. T. Schooley and P. Gagneux, Virol. J., 2013, 10, 321 CrossRef PubMed.
- X. Yang, L. Steukers, K. Forier, R. Xiong, K. Braeckmans, K. Van Reeth and H. Nauwynck, PLoS One, 2014, 9, e110026 CrossRef PubMed.
- I. A. T. Schaap, F. Eghiaian, A. des Georges and C. Veigel, J. Biol. Chem., 2012, 287, 41078 CrossRef CAS PubMed.
- R. Bansil and B. S. Turner, Adv. Drug Delivery Rev., 2018, 124, 3–15 CrossRef CAS PubMed.
- W. M. Saltzman, M. L. Radomsky, K. J. Whaley and R. A. Cone, Biophys. J., 1994, 66, 508 CrossRef CAS PubMed.
- M. D. Vahey and D. A. Fletcher, eLife, 2019, 8, e43764 CrossRef PubMed.
- P. A. Soria Ruiz, F. Ziebert and I. M. Kulić, Phys. Rev. E, 2022, 105, 054411 CrossRef PubMed.
- H. Li, M. Rief, F. Oesterhelt, H. E. Gaub, X. Zhang and J. Shen, Chem. Phys. Lett., 1999, 305, 197 CrossRef CAS.
- N. K. Sauter, M. D. Bednarski, B. A. Wurzburg, J. E. Hanson, G. M. Whitesides, J. J. Skehel and D. C. Wiley, Biochemistry, 1989, 28, 8388 CrossRef CAS PubMed.
- N. K. Sautera, J. E. Hanson, G. D. Glick, J. H. Brown, R. L. Crowther, S. J. Park, J. J. Skehel and D. C. Wiley, Biochemistry, 1992, 31, 9609 CrossRef PubMed.
- S. E. Adams, N. Lee, V. Y. Lugovtsev, A. Kan, R. P. Donnelly and N. A. Ilyushina, Antiviral Res., 2019, 169, 104539 CrossRef CAS PubMed.
- C. Pozrikidis, Fluid Dynamics: Theory, Computation and Numerical Simulation, Springer, 2nd edn, 2009 Search PubMed.
- R. Thaokar, H. Schiessel and I. Kulić, Eur. Phys. J. B, 2007, 60, 325 CrossRef CAS.
- L. V. Kordyukova, R. R. Mintaev, A. A. Rtishchev, M. S. Kunda, N. N. Ryzhova, S. S. Abramchuk, M. V. Serebryakova, V. V. Khrustalev, T. A. Khrustaleva, V. V. Poboinev, S. G. Markushin and O. L. Voronina, Microsc. Microanal., 2020, 26, 297 CrossRef CAS PubMed.
- E. J. Marey, La Nature, 1894, 119, 714 Search PubMed.
- T. R. Kane and M. P. Scher, Int. J. Solids Struct., 1969, 5, 663 CrossRef.
- K. Li, Z. Chen, Z. Wang and S. Cai, Phys. Rev. E, 2021, 103, 033004 CrossRef CAS PubMed.
- P. M. Ryan, J. W. Shaevitz and C. W. Wolgemuth, Phys. Rev. Lett., 2023, 131, 178401 CrossRef CAS PubMed.
- C. Calladine, J. Theoret. Biol., 1976, 57, 469–489 CrossRef CAS PubMed.
- S. V. Srigiriraju and T. R. Powers, Phys. Rev. E, 2006, 73, 011902 CrossRef PubMed.
- H. Wada and R. R. Netz, Europhys. Lett., 2008, 82, 28001 CrossRef.
- C. Speier, R. Vogel and H. Stark, Phys. Biol., 2011, 8, 046009 CrossRef CAS PubMed.
- B. Friedrich, J. Math. Biol., 2006, 53, 162 CrossRef PubMed.
- A. Chwang and W. Hwang, Phys. Fluids, 1990, 8, 1309 CrossRef.
- D. K. Vig and C. W. Wolgemuth, Phys. Rev. Lett., 2012, 109, 218104 CrossRef PubMed.
- K. Yehl, A. Mugler, S. Vivek, Y. Liu, Y. Zhang, M. Fan, E. R. Weeks and K. Salaita, Nat. Nanotechnol., 2016, 11, 184 CrossRef CAS PubMed.
- A. Bazrafshan, T. A. Meyer, H. Su, J. M. Brockman, A. T. Blanchard, S. Piranej, Y. Duan, Y. Ke and K. Salaita, Angew. Chem., 2020, 132, 9601 CrossRef.
- P. Zhan, K. Jahnke, N. Liu and K. Göpfrich, Nat. Chem., 2022, 14, 958 CrossRef CAS PubMed.
- C. S. Korosec, I. N. Unksov, P. Surendiran, R. Lyttleton, P. M. G. Curmi, C. N. Angstmann, R. Eichhorn, H. Linke and N. R. Forde, Nat. Commun., 2024, 15, 1511 CrossRef CAS PubMed.
- L. Kaler, E. Iverson, S. Bader, D. Song, M. A. Scull and G. A. Duncan, Commun. Biol., 2022, 5, 249 CrossRef CAS PubMed.
Footnotes |
† The result is  where where  and I0, I1 are the modified Bessel functions of the first kind. and I0, I1 are the modified Bessel functions of the first kind. |
| ‡ Jumping bit ahead, as we will see later in this section, the direction of rotation is set by the phase-shift of certain ligand-binding populations introduced in Fig. 3 and plotted in Fig. 4. |
| § Note that this value is large, considering that it acts on a short section of size l0. As a reference, the rotational friction at an angular frequency ω = 2πs−1 in a rather viscous medium of η = 0.1 Pa s (100 times of water) for R = 50 nm is approximately M ≈ 0.05kBT, i.e. largely subdominant compared to the linker-induced torque Mdr for not too low Ds. |
| This journal is © The Royal Society of Chemistry 2024 |