Spreading of volatile droplets in a humidity-controlled environment

Abstract

When a pure ethanol droplet is deposited on a dry, wettable and conductive substrate, it is expected to spread into a thin, uniform film. Here, we demonstrate that this uniform spreading behaviour can be altered significantly by controlling the ambient relative humidity. We show that higher relative humidity not only promotes faster spreading of the droplet, it also destabilizes the moving contact line, resulting in a fingering instability. We observe that these effects primarily emerge due to the hygroscopic nature of the pure droplet, which eventually leads to solutal-Marangoni effects. Additionally, heat transfer between the evaporating droplet and the underlying substrate also plays a crucial role in the overall dynamics. Thus, the overall spreading of a pure hygroscopic droplet is determined by a delicate interplay between solutal and thermal Marangoni effects.

---

1 Introduction

Evaporating droplets on solid surfaces hold a central role in a diverse range of applications spanning various technological domains. From inkjet printing^1–3 to pharmaceuticals,⁴ from microfluidic devices⁵ to advanced coatings,^6,7 the behaviour of evaporating droplets on solid surfaces emerges as a pivotal determinant of product quality and overall performance. Consequently, this seemingly simple problem has witnessed a noteworthy surge in interest, with a particular emphasis on achieving a quantitative understanding of the complex interplay between heat and mass transfer during the phase change.^8–11 It is worth noting that the current understanding of this phenomenon hinges not only on the inherent properties of the fluid^12–17 but also on the characteristics of the substrate^18–20 and the surrounding environment. While the influence of substrate properties on droplet evaporation has been intensively studied, the influence of ambient conditions such as humidity on droplet spreading and evaporation has received limited attention. Moreover, previous investigations^21–24 have been focused on more complex scenarios, involving droplets of binary mixtures or colloidal droplets in humid conditions, or micro-droplets of pure liquids. In contrast, our investigation examines the evaporation of larger, millimetric-sized droplets of a pure liquid, offering a broader understanding of this fundamental interaction between the surrounding environment and an evaporating droplet.

In this letter, we focus on the role of ambient humidity and show that by tuning it the overall spreading behaviour of a pure, volatile droplet deposited on a solid substrate can be significantly altered. We find that elevating ambient humidity not only accelerates the spreading rate but also induces a tendency for initially uniform spreading droplets to manifest fingering instabilities. We attribute these fundamental changes in the spreading behaviour of pure, volatile droplets to interfacial activity driven primarily by solutal-Marangoni effects. For a pure droplet, these solutal effects emerge from a combination of non-uniform evaporation of the droplet along its interface and absorption of water into the droplet at high relative humidity (hygroscopicity). Additionally, we find that thermal-Marangoni effects arising from heat transfer between droplet and substrate also influence the spreading behaviour of volatile droplets.

2 Experimental method

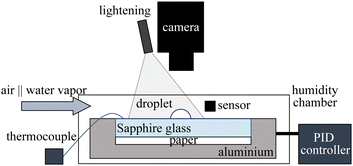
The experiments reported here involve the deposition of a 5 μl drop of pure ethanol (100% analytical grade) on various substrates, with different thermal properties. During an experiment, the substrate is placed inside a closed, transparent chamber to achieve precise control over ambient relative humidity (RH) as shown in Fig. 1. Experiments are performed for RH ranging from 10% to 60% and at different substrate temperatures. Two humidity sensors are placed inside the chamber: one near the droplet and the other near the chamber wall. Based on the difference between the desired RH and the sensor readings, air or DI water vapour is introduced. To ensure a stable environment with no strong background flow, the pump is turned off once the target RH is achieved. The droplet is then deposited after the sensors confirm a stable RH value. The substrate temperature T_s is controlled using a PID controller and is measured during the experiments via thermocouples attached to the top and the bottom of the substrate. The spreading and evaporation of the droplet are recorded from above (top-view) via a high-speed camera (Photron Mini). From recorded images, we then measure the equivalent diameter d of the spreading droplet, defined as the diameter of a circle with the same aggregate area. Experiments are performed on sapphire and acrylic substrates to elucidate the effect of the substrate properties on the spreading and evaporation of deposited droplets. Since the evaporation rate of the droplet is strongly influenced by the thickness of the substrate,²⁰ substrates of the same thickness of 3 mm are used in the experiments. Observing the very thin droplet height, we estimate it to be much less than the capillary length of ethanol (l_c = (σ/ρg)^1/2 ∼ 1.7 mm), where σ is the liquid surface tension, ρ is the liquid density, and g is the gravitational acceleration. This indicates a negligible influence of gravity.

Fig. 1 Schematic of the experimental setup.

3 Results and discussion

A comparison of sequences of experimental snapshots shown in Fig. 2(a)–(c) reveals the variability in the spreading behaviour of an ethanol droplet on a sapphire substrate under different ambient relative humidity (RH) conditions. At a low RH of 10% (Fig. 2(a)), after deposition, the droplet initially spreads into an axisymmetric thin film. Subsequently, as it reaches its maximum footprint area, the droplet undergoes a retraction phase, resulting in the formation of a distinctive doughnut-shaped ring by the end of its lifespan, suggesting the evaporation occurs via a constant contact angle mode.^12,25 Remarkably, an elevation in ambient RH brings about a substantial modification in the overall spreading behaviour. At RH = 40% (Fig. 2(b)), the deposited droplet spreads into a thin film with a larger footprint area, indicating unexpected modification in the wettability of the substrate. Moreover, the absence of the distinct retraction phase observed at lower RH also indicates a change in evaporation mode to constant contact radius mode.²⁶ Continuing in a similar fashion, a further increase in ambient humidity to RH = 60% causes the droplet to spread over an even larger area; however, in this case, the moving contact line loses its stability (Fig. 2(c)). We find that soon after deposition the wetted area no longer remains axisymmetric as shallow azimuthal undulations of small wavelength (λ ∼ 100 μm) appear at the moving contact line. These corrugations at the periphery gradually evolve into finger-like protrusions as the droplet continues to spread. Moreover, at high RH, as the deposited ethanol evaporates it leaves behind a myriad of small residual droplets distributed across its footprint area. Remarkably, these small droplets persist for a very long time, much greater than the expected time it takes to evaporate the deposited ethanol.

Fig. 2 Time sequence images of evaporating ethanol droplets on sapphire at a substrate temperature of T_s = 25 °C and different ambient relative humidities: (a) RH = 10%, (b) 40%, and (c) 70%.

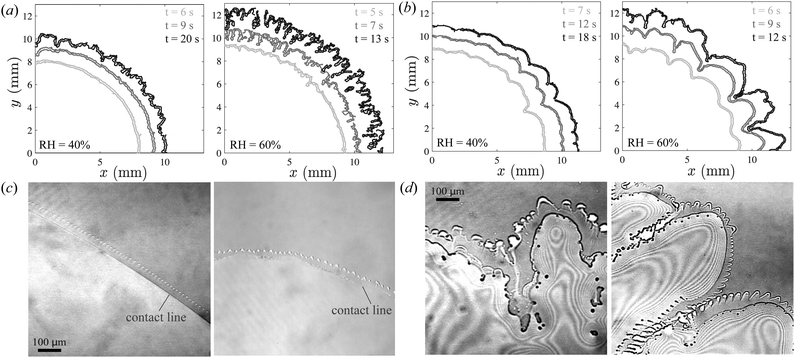
Importantly, our experiments uncover that the fingering instability of pure ethanol droplets transpires irrespective of the thermal properties of the underlying substrate which were unchanged in Fig. 2. These observations are in stark contrast to the findings of Gotkis et al.,¹⁸ who found that substrates with higher heat conductivity in fact suppress the instability of pure volatile droplets and to which our experiments add a new dimension. In Fig. 3(a) and (b), we show the temporal evolution of azimuthal undulations along the contact line as ethanol droplets spread on sapphire and acrylic substrates under varying ambient conditions. The data shown in Fig. 3(a) and (b) clearly demonstrate that initial perturbations along the contact line lead to the formation of thick fingers on the acrylic substrate, while fine structures emerge on the sapphire substrate. This indicates that, while the material properties of the underlying substrate do not determine the onset of the fingering instability of the spreading droplet, they certainly influence the ensuing dynamics. We must also point out that similar fingering instability of pure, iso-propanol alcohol (IPA) micro-droplets on the glass surface was also reported recently by Yang et al.²⁴ They concluded that the instability observed in their experiments arises because of the formation of a liquid rim at the edge of the droplet, which is destabilized by a mechanism similar to that of classical Rayleigh–Plateau instability. However, it is difficult to conclude if the instability is driven by a similar mechanism in our experiments. Our experiments indicate that at the inception of azimuthal perturbation at the contact line, a thick rim-like feature indeed persists at the droplet edge for a brief time, however, it vanishes soon after, as the fingers continue to split and merge.

Fig. 3 Temporal evolution of the moving contact line of ethanol droplets evaporating on (a) sapphire and (b) acrylic substrate of equal temperature T_s = 27 °C. The zoomed-in image in (c) and (d) illustrate the presence of a pre-cursor film while an ethanol droplet spreads on a sapphire substrate at different experimental conditions (c) T_s = 25 °C, RH = 10% and (d) T_s = 25 °C, RH = 60%.

To investigate events occurring near the contact line in detail, we record the spreading of ethanol droplets via a confocal microscope. Through this imaging method, we reveal that the contact line of a spreading ethanol droplet is consistently preceded by a thin precursor film irrespective of ambient humidity level. Interestingly, despite the apparent uniformity of droplet spreading at low RH, confocal imaging reveals unstable features within the precursor film, manifesting as finger-like perturbations (Fig. 3(c)). Moreover, we note that the precursor film becomes more prominent and exhibits increased instability at elevated levels of relative humidity (Fig. 3(d)). Notably, these precursor films are more conspicuous when droplets spread on the high-thermal conductivity sapphire substrates compared to acrylic substrates, where their presence is less apparent. For droplets spreading on acrylic substrates, we observe tiny islands of fluid masses distributed alongside the contact line instead of a continuous precursor film, see ESI.†

Measuring the temporal evolution of the equivalent diameter d of spreading ethanol droplets at different RH reveals another intriguing characteristic of our system. Typically, the spreading of a (non-volatile) droplet on a solid substrate is anticipated to be governed by a balance between viscous dissipation and capillary action, resulting in a power-law, R ∼ t^1/10, also referred to as Tanner's law.^27,28 Ideally, such behaviour is also expected for an ethanol droplet spreading on a sapphire substrate, at least on time scales where the evaporative mass flux can be considered small. However, we measure a significantly different power law, see Fig. 4(a) and (b). Interestingly, at elevated RH levels, ethanol droplets spread at a faster rate than predicted by Tanner's law. Fitting the experimental data results in a power-law R ∼ t^α with an exponent α varying in the range of [0.3–0.4]. Note that this observed behaviour is found to be consistent for different substrates—sapphire and acrylic—possessing vastly different thermal properties. The only exception is formed by the spreading at the lowest humidity on an acrylic substrate, where for a brief period of time, the measured exponent is consistent with α = 1/10 predicted by Tanner's law. Furthermore, data reported by Yang et al.²⁴ suggests the power-law exponent could be as high as 0.5 in the case of micro-droplets.

Fig. 4 Accelerated spreading: temporal evolution of the equivalent diameter d(t) measured in experiments for ethanol droplets spreading and evaporating under different ambient relative humidity conditions on (a) sapphire and (b) acrylic substrate at two different substrate temperatures (T_s = 25 °C and T_s = 40 °C). In these plots, time is normalized by the droplet lifetime t_f. Each time series represents the averaged data over five experimental runs.

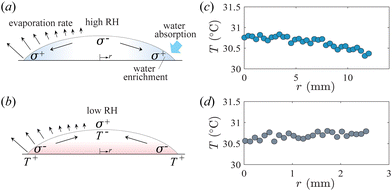
The key physical interactions controlling the enhanced spreading and contact line instability of pure volatile droplets, as described above, are shown schematically in Fig. 5(a). We hypothesize that the instability of pure, evaporating droplets, as discussed in this context, is influenced by an interplay between solutal-Marangoni and thermal-Marangoni flows. The solutal-Marangoni effects emerge due to the hygroscopic nature of ethanol, which leads to the absorption of water from the ambient environment into the droplet.^23,24 This, coupled with the non-uniform evaporation along the droplet interface, which is well-known to be particularly intensified near the contact line,^8,9 results in a higher water concentration near the contact line region. Consequently, a spatial gradient in composition induces a surface tension gradient along the droplet interface. This localized increase in surface tension near the droplet edge instigates outward Marangoni stresses, facilitating the transport of the liquid from the centre to the periphery, thereby enhancing the droplet spreading dynamics. Note that, through systematic experiments, Mouat et al.²⁹ showed that fingering instability can also occur for a volatile droplet with a small amount of solute. In such cases, the solutal-Marangoni effect drives the instability. Correspondingly, in our experiments, the water absorbed into the ethanol from the surroundings acts as a solute, eventually leading to contact line instability through solutal-Marangoni effects.

Fig. 5 Schematic diagram highlighting different physical interactions governing the spreading behaviour of an ethanol droplet on a high-thermal-conductivity substrate. (a) The hygroscopicity of an ethanol droplet allows the absorption of water from its surroundings. Combined with non-uniform evaporation along the interface, the enrichment of water near the contact line induces solutal Marangoni flow. (b) The high thermal conductivity of the substrate results in higher temperatures near the contact line, leading to thermal Marangoni contraction. To quantify the above effects, temperature distribution measurements were obtained using an infrared camera at the interface of droplets deposited on sapphire glass, covering the range from the droplet's centre r = 0 to its edge for (c) Marangoni spreading (T_s = 30 °C, RH = 30% at t = 15 s) and (d) Marangoni contracting (T_s = 30 °C, RH = 10% at t = 70 s).

Another crucial aspect for a droplet deposited on a thermally conductive substrate, such as sapphire, is that the temperature near the contact line is expected to be higher than in the central part of the droplet, which is due to the fact that the high thermal conductivity of the substrate allows heat to be transferred rapidly to the edge to compensate for evaporative heat loss.¹⁹ As illustrated in Fig. 5(b), this temperature difference between the droplet edge and its centre induces a surface tension gradient and consequent directional flow of the liquid from the edge of the droplet to the centre. Noticeably, this thermally induced Marangoni contraction is in the opposite direction to the solutal Marangoni spreading. Therefore, it is expected that in cases when thermal-Marangoni effects are dominant, we will observe no contact line instability. In our experiments, to identify conditions when thermal Marangoni effects are dominant we use infrared imaging to quantitatively measure the thermal map of the droplet interface. Note that for solutal-Marangoni, the droplet is cooled near the contact line (Fig. 5(c)), whereas the temperature near the edge is slightly higher than in the centre when the thermal Marangoni contraction plays a role (Fig. 5(d)).

The phase diagram shown in Fig. 6 summarizes the different spreading behaviours observed for an ethanol droplet when it is deposited on a sapphire plate at different ambient relative humidity and substrate temperatures. Through this phase map, we can distinguish the conditions under which, dominated by solutal-Marangoni effects, the deposited droplet spreads at an accelerated rate from those where thermal-Marangoni effects drive the contraction of the droplet. It is easily seen that at lower substrate temperatures T_s = 25–27 °C when thermal-Marangoni effects are absent, a deposited droplet spreads uniformly at an accelerated rate. It is only at sufficiently high RH > 40%, that finger-like structures appear at the contact line. We see the threshold RH at which fingering occurs critically depends on the substrate temperature. We find that with an increase in substrate temperature, the critical RH at which fingering occurs also increases. Also, it is important to note that the phenomenon where a myriad of droplets are left on the substrate after the deposition of the primary droplet occurs at very high relative humidity and lower substrate temperatures. At higher substrate temperatures, we did not observe the residual droplets after the evaporation of the primary ethanol droplet. This stands to reason as presumably, these droplets have water as their main constituent, the volatility of which rapidly increases with (substrate) temperature. On the acrylic surface, droplets exhibit significantly less fingering instability compared to those on sapphire surfaces under the same conditions (see ESI†).

Fig. 6 Regime maps in a space spanned by the surface temperature T_s across the relative humidity RH for sapphire glass surface. The different symbol shapes indicate the different behaviour of the evaporating droplets.

4 Conclusions

In conclusion, our study sheds light on the intricate interplay between ambient humidity and the spreading behaviour of pure, volatile droplets on solid substrates. By systematically varying the relative humidity, we have demonstrated significant alterations in the spreading dynamics, including both acceleration and destabilization of the moving contact line leading to fingering instabilities. These findings underscore the importance of considering environmental factors such as humidity alongside inherent fluid and substrate properties in understanding droplet behaviour during evaporation. Our results illustrate the dependence of fingering instability on solutal-Marangoni effects driven by the hygroscopic nature of pure droplets, as well as the thermal-Marangoni effects arising due to heat transfer between the droplet and substrate. Moving forward, a deeper understanding of these complex phenomena will not only enrich our fundamental understanding of droplet dynamics but also inform the design and optimization of various technological applications reliant on controlled droplet behaviour. Moreover, our findings emphasize the need for further exploration into the effects of ambient conditions on droplet spreading, opening avenues for future research aimed at elucidating the broader environmental factors influencing this ubiquitous phenomenon.

Data availability

The datasets used in this study are available at the Open Science Framework repository (DOI: https://doi.org/10.17605/OSF.IO/3CSAK).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dennis van Gils for providing the humidity chamber, and Gert-Wim Bruggert and Thomas Zijlstra for their technical assistance. We also acknowledge Pim Dekker for his support with confocal microscopy. This publication is part of the Vici project IMBOL (Project No. 17070) which is partly financed by the Dutch Research Council (NWO).

References

1. D. Lohse, Annu. Rev. Fluid Mech., 2022, 54, 349–382.
2. M. Singh, H. M. Haverinen, P. Dhagat and G. E. Jabbour, Adv. Mater., 2010, 22, 673–685.
3. H. Wijshoff, Curr. Opin. Colloid Interface Sci., 2018, 36, 20–27.
4. D. Bolleddula, A. Berchielli and A. Aliseda, Adv. Colloid Interface Sci., 2010, 159, 144–159.
5. A. Karbalaei, R. Kumar and H. J. Cho, Micromachines, 2016, 7, 13.
6. H. Kim, F. Boulogne, E. Um, I. Jacobi, E. Button and H. A. Stone, Phys. Rev. Lett., 2016, 116, 124501.
7. E. Y. Gatapova, A. M. Shonina, A. I. Safonov, V. S. Sulyaeva and O. A. Kabov, Soft Matter, 2018, 14, 1811–1821.
8. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829.
9. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E, 2000, 62, 756.
10. Y. O. Popov, Phys. Rev. E, 2005, 71, 036313.
11. A.-M. Cazabat and G. Guena, Soft Matter, 2010, 6, 2591–2612.
12. G. Guéna, C. Poulard and A.-M. Cazabat, Colloids Surf., A, 2007, 298, 2–11.
13. A. Williams, G. Karapetsas, D. Mamalis, K. Sefiane, O. Matar and P. Valluri, J. Fluid Mech., 2021, 907, A22.
14. A. A. Pahlavan, L. Yang, C. D. Bain and H. A. Stone, Phys. Rev. Lett., 2021, 127, 024501.
15. J. Shi, L. Yang and C. D. Bain, Langmuir, 2021, 37, 4091–4101.
16. D. A. Baumgartner, S. Shiri, S. Sinha, S. Karpitschka and N. J. Cira, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2120432119.
17. F. Wang and Q. Yuan, J. Colloid Interface Sci., 2023, 637, 522–532.
18. Y. Gotkis, I. Ivanov, N. Murisic and L. Kondic, Phys. Rev. Lett., 2006, 97, 186101.
19. W. Ristenpart, P. Kim, C. Domingues, J. Wan and H. A. Stone, Phys. Rev. Lett., 2007, 99, 234502.
20. S. Shiri, S. Sinha, D. A. Baumgartner and N. J. Cira, Phys. Rev. Lett., 2021, 127, 024502.
21. S. Karpitschka, F. Liebig and H. Riegler, Langmuir, 2017, 33, 4682–4687.
22. V. H. Chhasatia, A. S. Joshi and Y. Sun, Appl. Phys. Lett., 2010, 97, 231909.
23. S. K. Parimalanathan, S. Dehaeck, A. Rednikov and P. Colinet, J. Colloid Interface Sci., 2021, 592, 319–328.
24. L. Yang, A. A. Pahlavan, H. A. Stone and C. D. Bain, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302653120.
25. C. Liu, E. Bonaccurso and H.-J. Butt, Phys. Chem. Chem. Phys., 2008, 10, 7150–7157.
26. R. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350.
27. L. Tanner, J. Phys. D: Appl. Phys., 1979, 12, 1473.
28. D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739.
29. A. P. Mouat, C. E. Wood, J. E. Pye and J. C. Burton, Phys. Rev. Lett., 2020, 124, 064502.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00583j

---