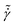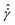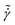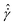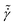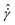Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics description of startup flow of soft particles glasses†
Nazanin
Sadeghi
 a,
Hrishikesh
Pable
a,
Hrishikesh
Pable
 a and
Fardin
Khabaz
a and
Fardin
Khabaz
 *ab
*ab
aSchool of Polymer Science and Polymer Engineering, The University of Akron, The United States, OH 44235, USA. E-mail: fkhabaz@uakron.edu; Tel: +1 330 972-5410
bDepartment of Chemical, Biomolecular, and Corrosion Engineering, The University of Akron, The United States, OH 44235, USA
First published on 3rd September 2024
Abstract
Particle dynamics simulations are used to study the startup flow of jammed soft particle suspensions in shear flow from a thermodynamic perspective. This thermodynamic framework is established using the concept of the two-body excess entropy extracted from the transient pair distribution function and elastic energy of the suspension as a function of strain at different shear rates and suspension volume fractions. Although the evolution of the elastic energy in these soft particle glasses closely mimics the stress–strain behavior at different shear rates and volume fractions, there are several differences corresponding to their overshoots in terms of the broadness and location of the peaks. The transient excess entropy shows an anisotropic behavior due to the anisotropic distribution of contacts at high shear rates. The excess entropy at high shear rates increases as a function of the strain and attains a steady state. On the other hand, it is nearly constant and isotropic in the quasi-static regime, where the stress response is close to the dynamic yield stress. Using the transient elastic energy and excess entropy, a transient temperature is defined to establish a relationship between thermodynamics and the static yield stress data. This transient temperature increases with the strain and then diverges at strains close to the static yield point at high shear rates.
1 Introduction
Yield stress fluids, such as slurries, pastes, and certain food products (like ketchup and mayonnaise), and geological materials, such as lava flows, are a class of non-Newtonian fluids that exhibit solid-like response at rest and flow when the applied stress or force, exceeds a critical value known as dynamic yield stress σy.1–5 A particular type of these fluids categorized as soft particle glasses (SPGs) are suspensions composed of soft particles suspended in Newtonian fluids and are jammed in disorder phase at volume fractions above the random close packing ϕrcp = 0.64 of equivalent hard spheres.3,6–8 These soft particles can be in the form of swollen microgels suspended in water, emulsions, star polymers with many arms, and block copolymers, and can maintain disordered microstructure above volume fraction of ϕrcp.1,9 In this regime, each particle is surrounded by a strong cage formed by neighboring particles at contact; the strength of the cage scales with the contact modulus of the particles and is much stronger than thermal energy.3 Thus, these suspensions are athermal and show weak elastic solid behavior at rest and low stresses. At stresses larger than the dynamic yield threshold, σy, they flow according to the Herschel–Bulkley (HB) equation σ = σy + k![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n, where
n, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, k is the consistency index, and n is the HB exponent which is close to 0.5.3,10–12
is the shear rate, k is the consistency index, and n is the HB exponent which is close to 0.5.3,10–12
Prior studies in this area have shown that interparticle contact and lubrication forces govern the shear rheology of SPGs.3,7,13–19 The viscoelastic properties of SPGs are controlled by particle properties such as softness, their volume fractions, and macroscopic parameters such as deformation rate, and these macroscopic rheological properties are correlated with the microdynamics of individual soft particles in flow.7 The shear-induced dynamics of suspensions in these systems show two distinct flow regimes:7,20 (1) the dynamics are dictated by the transport of mobility between domains formed by the mobile and immobile particles, or avalanches, which have also been reported in shear simulations of two-dimensional jammed suspensions21,22 and granular materials.23,24 The stress response is nearly constant in this quasi-static regime, which covers several orders of magnitude in shear rate, and corresponds to the dynamic yield stress, σy, which is the minimum stress required to keep SPGs flowing. (2) Particles show very localized dynamics at high shear rates, which gives rise to the appearance of a power-law regime in the flow curve. The key observation is that a unique dimensionless number ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ηs/G0, where ηs is the viscosity of solvent and G0 is the low-frequency modulus of SPGs, separates these two regimes of flow.
ηs/G0, where ηs is the viscosity of solvent and G0 is the low-frequency modulus of SPGs, separates these two regimes of flow.
Apart from the steady state flow behavior of soft glasses, understanding the static yield behavior, which corresponds to the stress required to flow the suspensions from rest and is highlighted with an overshoot in shear stress at a given rate, is crucial since controlling the startup flow response can avoid pressure overshoot and subsequent damage to the processing tools in manufacturing these materials.19,25 In addition, the transient response of soft glasses reveals key physical mechanisms of their complex rheology. Statistical physics links the yield behavior of thermally annealed amorphous materials to phase transitions.26 Depending on the annealing degree of structure at rest, brittle or ductile yielding can be observed. In this regard, the fluidity model associates stress overshoots with shear band formation near moving walls due to nonlocal effects.27 Stress overshoots follow power laws with different exponents at low and high shear rates. Theoretical approaches like shear-transformation-zone theory,28 mode coupling theory,29 elastically collective nonlinear Langevin equation theory,30 molecular dynamics simulations,31,32 and micromechanical models18,33 emphasize nonaffine deformations in amorphous materials during startup flow. The microstructure of SPGs continuously changes until shear stress reaches a steady state in the startup flow.18 During this period, shear stress exhibits an overshoot, which corresponds to static yield at intermediate and high shear rates,18,19 while at low shear rates, the overshoot is not detected. At the overshoot point, the anisotropy of the pair distribution function is maximum. Furthermore, the magnitude of the stress overshoot and corresponding strain is a function of the mechanical history of the SPGs, and the magnitude of the stress overshoot decreases with the internal stress stored in the material at the onset of the shear flow.18 Furthermore, the direction of the preshear flow also plays an important role in the overshoot magnitude.19
The onset of the shear flow rearranges the microstructure of SPGs by redistributing the contacts between the particles and inducing anisotropy.18 The latter is correlated with the macroscopic stress response of the SPGs in shear flow.3 On the other hand, microstructural signatures can be utilized to extract thermodynamic properties, such as excess entropy, to provide a thermodynamic description for the measured macroscopic property, i.e., an equation of state (EOS). Simulation studies have shown that the concept of the excess entropy, SE, proposed by Rosenfeld34,35 is applicable to correlate the dynamics properties with the entropy in several complex fluids, such as hard-spheres,36 star-like polymers,37 metallic glasses,38 Gaussian core fluids,39 supercooled liquids,40 soft spheres,41,42 and this method can be reliably used for SPGs in shear flow. In SPGs at steady-state,17 this framework provides an EOS which relates the excess entropy to the shear stress at steady-state according to −SE = −SEy − B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(σ/σy), where B is a constant close to 1.35. Thus, the excess entropy can be used in these suspensions to provide a thermodynamic framework to determine the shear stress flow curve. The remarkable achievement of the scaling law determined by correlating excess entropy to rheological properties of SPGs is that these suspensions are athermal, and the generality of the thermodynamic framework is extended in a shear-flow case which is a nonequilibrium state. This success of the correlation with excess entropy becomes more important when one considers the properties at the dynamic yield point, or the quasi-static regime, since the shear viscosity and normal stress functions diverge, and the diffusivity vanishes at a critical excess entropy, corresponding to the yield stress of the suspension. An effective temperature is defined based on the derivative of the elastic energy (U) with respect to the excess entropy, i.e.,
ln(σ/σy), where B is a constant close to 1.35. Thus, the excess entropy can be used in these suspensions to provide a thermodynamic framework to determine the shear stress flow curve. The remarkable achievement of the scaling law determined by correlating excess entropy to rheological properties of SPGs is that these suspensions are athermal, and the generality of the thermodynamic framework is extended in a shear-flow case which is a nonequilibrium state. This success of the correlation with excess entropy becomes more important when one considers the properties at the dynamic yield point, or the quasi-static regime, since the shear viscosity and normal stress functions diverge, and the diffusivity vanishes at a critical excess entropy, corresponding to the yield stress of the suspension. An effective temperature is defined based on the derivative of the elastic energy (U) with respect to the excess entropy, i.e., 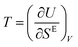 , which is found to vary linearly with the shear stress and the elastic energy of the sheared SPGs. Furthermore, it was shown that a universal behavior based on Dzogootov's theory43 for particle diffusivity versus excess entropy unifies observations for systems at equilibrium and nonequilibrium.
, which is found to vary linearly with the shear stress and the elastic energy of the sheared SPGs. Furthermore, it was shown that a universal behavior based on Dzogootov's theory43 for particle diffusivity versus excess entropy unifies observations for systems at equilibrium and nonequilibrium.
Similarly, Khabaz and Bonnecaze44 used this framework and described the shear-induced phase transition of SPGs with a low degree of polydispersity in particle size distribution. These jammed SPGs transform into a layered phase in strong shear flow.45,46 After sufficient exposure to shear flow, the shear stress decreases and reaches a steady state in a layered phase. The latter creates a discontinuity in the flow curves. Using the two-body excess entropy formulation, a clear discontinuity in the excess entropy is observed at this phase transition. The entropy of the system decreases significantly upon layering, that is an indicator of the formation of an ordered microstructure. At the transition, the effective temperature at steady-state, T, shows a discontinuity as a function of the shear rate. This discontinuity in the T–![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) curves is similar to the discontinuity observed in the flow curve. At a fixed temperature, where there is a transition from glassy to layered phase, the Helmholtz free energy is equal in two phases, which reveals that this transformation is a first-order thermodynamic phase transition. Furthermore, the elastic energy, shear stress, and Helmholtz free energy correlate with the temperature in stable/metastable glassy and layered phases. The latter emphasizes the importance of this thermodynamic framework not only in building useful relationships between rheological properties of disordered systems but also in capturing flow-induced transitions and structures with short-range ordering.
curves is similar to the discontinuity observed in the flow curve. At a fixed temperature, where there is a transition from glassy to layered phase, the Helmholtz free energy is equal in two phases, which reveals that this transformation is a first-order thermodynamic phase transition. Furthermore, the elastic energy, shear stress, and Helmholtz free energy correlate with the temperature in stable/metastable glassy and layered phases. The latter emphasizes the importance of this thermodynamic framework not only in building useful relationships between rheological properties of disordered systems but also in capturing flow-induced transitions and structures with short-range ordering.
Inspired by prior works,17–19,44 here we study the transient response of the excess entropy and elastic energy during the startup flow at different shear rates and five different volume fractions above the random close-packing fraction. The anisotropy of the microstructure in strong shear flow is fully captured in the excess entropy, and the results highlight the distinction between the thermodynamic response at high shear rates and the quasi-static regime. We establish a thermodynamic description of the static yield point appearance at different flow regimes for SPGs. Our results suggest that a transient temperature can be constructed by the concept of transient excess entropy.
2 Simulations methods
The model system comprises N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polydisperse soft particles with a contact modulus of E* and an average radius of R suspended in a Newtonian fluid with a viscosity of ηs (Fig. 1). The polydispersity in the particle size distribution is 20% of the average radius to avoid the formation of ordered structures.45,46 Five different volume fractions in the range of ϕ ∈ [0.70–0.90] are selected. Particles in contact interact via generalized elastic Hertz force, FE, and elastohydrodynamic force, FEHD, which depends on the magnitude of the relative velocities of two particles in contact and overlap distance.3
000 polydisperse soft particles with a contact modulus of E* and an average radius of R suspended in a Newtonian fluid with a viscosity of ηs (Fig. 1). The polydispersity in the particle size distribution is 20% of the average radius to avoid the formation of ordered structures.45,46 Five different volume fractions in the range of ϕ ∈ [0.70–0.90] are selected. Particles in contact interact via generalized elastic Hertz force, FE, and elastohydrodynamic force, FEHD, which depends on the magnitude of the relative velocities of two particles in contact and overlap distance.3
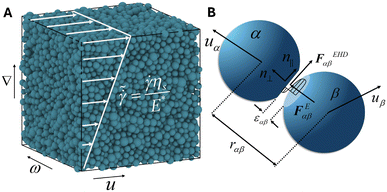 | ||
Fig. 1 (A) Configuration of suspensions with volume fraction of ϕ = 0.80 in a cubic simulation box that is in the shear flow with an applied shear rate of 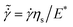 , where E* is the particle contact modulus and ηs is the suspending fluid viscosity. The flow (u), gradient (∇), and vorticity (ω = ∇ × u) directions are shown. (B) Two particles form flat facet at a contact and interact via generalized Hertzian contact and elastohydrodynamic lubrication forces.3 , where E* is the particle contact modulus and ηs is the suspending fluid viscosity. The flow (u), gradient (∇), and vorticity (ω = ∇ × u) directions are shown. (B) Two particles form flat facet at a contact and interact via generalized Hertzian contact and elastohydrodynamic lubrication forces.3 | ||
Following our previous works on this topic,3,45,46 we utilize the methodology for simulating SPGs in shear flow governed by the generalized Hertzian elastic contact according to:47
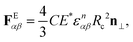 | (1) |
| FEHDαβ = −(ηsuαβ‖E*Rc3)(2n+1)/4ε(2n+1)/4αβn‖, | (2) |
Considering these two forces, and the far-field shear flow 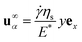 , where ex is the basis vector in the flow direction equation. Using the scales of the particle size R, time ηs/E*, the dimensionless equation of motion for particles becomes:
, where ex is the basis vector in the flow direction equation. Using the scales of the particle size R, time ηs/E*, the dimensionless equation of motion for particles becomes:
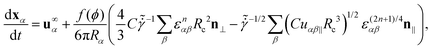 | (3) |
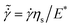 emerges from these equations of motion and is used to impose the shear rate on the suspensions by applying the Lees–Edwards boundary conditions.48 The stress tensor is computed as a function time using the Kirkwood formula,49i.e.,
emerges from these equations of motion and is used to impose the shear rate on the suspensions by applying the Lees–Edwards boundary conditions.48 The stress tensor is computed as a function time using the Kirkwood formula,49i.e., 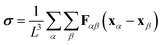 , where L is the length of the cubic box and Fαβ = FEHDαβ + FEαβ is the total force acting on particle α from β. The maximum shear strain of two is set as the final time in all simulations. A wide range of shear rate
, where L is the length of the cubic box and Fαβ = FEHDαβ + FEαβ is the total force acting on particle α from β. The maximum shear strain of two is set as the final time in all simulations. A wide range of shear rate 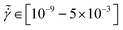 , which translates to
, which translates to 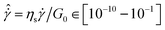 when the low-frequency modulus of SPGs, G0(ϕ),20 is used for collapsing the data obtained at different volume fractions. The time step of simulations is chosen to produce 107 steps per strain at each shear rate. The initial configuration of the particles is in a minimized elastic energy at the beginning of the shear flow to avoid the effect of mechanical aging on the startup flow.3 The stress tensor and trajectories of the particles are monitored at regular strain interval of Δγ = 0.001. All results are averaged over five independent replicas.
when the low-frequency modulus of SPGs, G0(ϕ),20 is used for collapsing the data obtained at different volume fractions. The time step of simulations is chosen to produce 107 steps per strain at each shear rate. The initial configuration of the particles is in a minimized elastic energy at the beginning of the shear flow to avoid the effect of mechanical aging on the startup flow.3 The stress tensor and trajectories of the particles are monitored at regular strain interval of Δγ = 0.001. All results are averaged over five independent replicas.
3 Results and discussion
3.1 Transient shear stress and elastic energy in startup flow
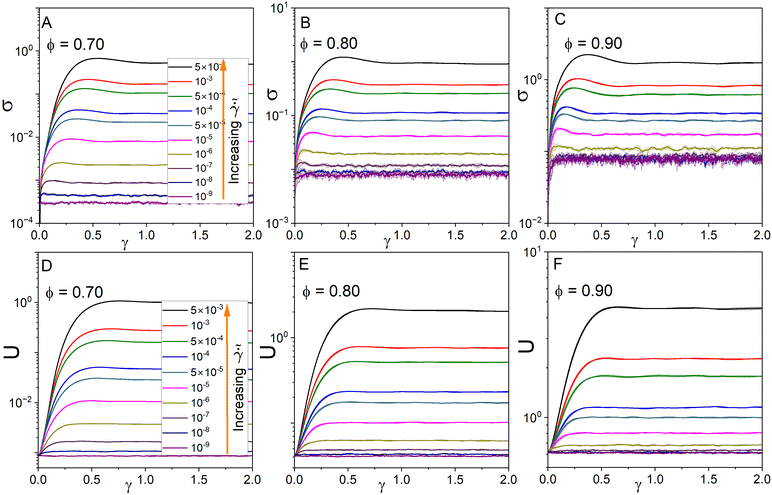
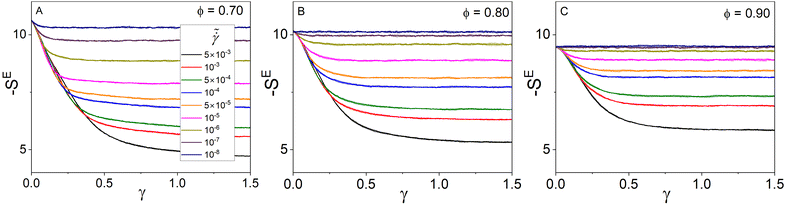
The shear stress, σ, as a function of the strain, γ, is plotted in Fig. 2A–C for suspensions with volume fractions of ϕ = 0.70–0.9 (σ–γ data for ϕ = 0.75 and 0.85 are not shown here). The general trend in σ–γ curves is that shear stress increases in the linear regime and then shows an overshoot, which is marked by σp, at a strain of γσp, and then decreases to the steady-state value. This stress overshoot highlights the energy barrier required to initiate the plastic flow of SPGs in shear. Similarly, the elastic energy, U, is determined from the contacts between the particles as a function of the shear strain as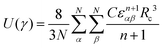 , and it is scaled by E*R3. At γ = 0 (Fig. 2D–F), the elastic energy value is U0, which increases with the volume fraction of suspensions and shows a linear relationship with G0. The transient elastic energy follows a very similar trend as the shear stress, except that overshoots are slightly milder and broader than those in σ–γ curves since the number of the contacts per particle shows a minimum, while the overlap distance between the particles shows a mild maximum at the overshoot point (see Fig. S1 in ESI† for the plots on the linear scales).18 Furthermore, the evolution of the first and second normal stresses, i.e., N1(γ) and −N2(γ) as well as the osmotic pressure, Π(γ), are shown in Fig. S2 in ESI.†
, and it is scaled by E*R3. At γ = 0 (Fig. 2D–F), the elastic energy value is U0, which increases with the volume fraction of suspensions and shows a linear relationship with G0. The transient elastic energy follows a very similar trend as the shear stress, except that overshoots are slightly milder and broader than those in σ–γ curves since the number of the contacts per particle shows a minimum, while the overlap distance between the particles shows a mild maximum at the overshoot point (see Fig. S1 in ESI† for the plots on the linear scales).18 Furthermore, the evolution of the first and second normal stresses, i.e., N1(γ) and −N2(γ) as well as the osmotic pressure, Π(γ), are shown in Fig. S2 in ESI.†
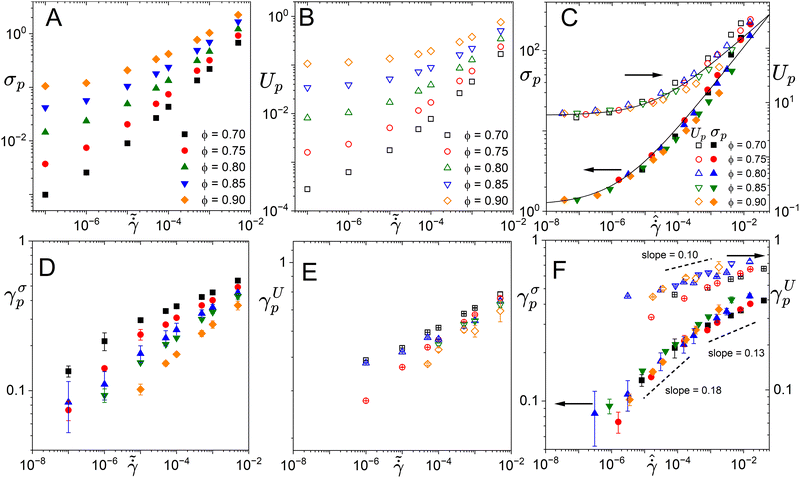
As seen in Fig. 3A and B, the stress and elastic energy overshoots at different volume fractions show limiting values and power-law behaviors at low and high shear rates, respectively. Using the corresponding values in the quasi-static regime and steady-state (i.e., σy and Uy), and utilizing the rescaled shear rate, 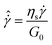 , all data collapsed onto master curves in Fig. 3C. These behaviors are described by HB relationships, i.e.,
, all data collapsed onto master curves in Fig. 3C. These behaviors are described by HB relationships, i.e., 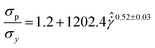 and
and 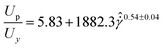 . These HB exponents are similar to those reported in simulations and experiments for SPGs (see Fig. S3 in ESI† for the master curve of the steady-state flow curve).7,18,19 The strains corresponding to these overshoots in transient stress, γσp, and elastic energy, γUp, also increase with the shear rate (Fig. 3D and E) and decrease with the volume fraction at a given shear rate. We also note that at lower shear rates, detecting these overshoots becomes challenging, especially for the elastic energy (it does not show overshoot at the low shear rates), and uncertainty in the data increases. Albeit the latter point, the data show reasonable collapse at high shear rates, and dispersion increases at low rates (Fig. 3F). At high shear rates, both peak strains show power-law relationships with the rescaled shear rate:
. These HB exponents are similar to those reported in simulations and experiments for SPGs (see Fig. S3 in ESI† for the master curve of the steady-state flow curve).7,18,19 The strains corresponding to these overshoots in transient stress, γσp, and elastic energy, γUp, also increase with the shear rate (Fig. 3D and E) and decrease with the volume fraction at a given shear rate. We also note that at lower shear rates, detecting these overshoots becomes challenging, especially for the elastic energy (it does not show overshoot at the low shear rates), and uncertainty in the data increases. Albeit the latter point, the data show reasonable collapse at high shear rates, and dispersion increases at low rates (Fig. 3F). At high shear rates, both peak strains show power-law relationships with the rescaled shear rate: 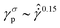 and
and 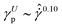 . At low and intermediate shear rates, the exponent for the γσp slightly increases to 0.20. The values of γUp are almost twice γσp. Note that the scaling exponents are weakly dependent on the mechanical history of the pastes, as discussed by Di Dio et al.19
. At low and intermediate shear rates, the exponent for the γσp slightly increases to 0.20. The values of γUp are almost twice γσp. Note that the scaling exponents are weakly dependent on the mechanical history of the pastes, as discussed by Di Dio et al.19
3.2 Thermodynamics in startup flow behavior
Since shear flow induces anisotropy of the configuration of the particles in contact, the pair distribution function is determined in the flow-gradient plane, i.e., g(x,y), at low and high shear rates over the startup flow period for suspensions with a volume fraction of ϕ = 0.80 (Fig. 4). At a low shear rate of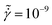 (Fig. 4A–C) particles show symmetric distribution at rest, and increasing the strain does not make major rearrangement in the contacts. On the other hand, at a high shear rate of
(Fig. 4A–C) particles show symmetric distribution at rest, and increasing the strain does not make major rearrangement in the contacts. On the other hand, at a high shear rate of 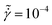 (Fig. 4D–F), the distribution of the contacts for a reference particle becomes anisotropic as soon as shear stress increases. In strong shear flow, neighboring particles tend to accumulate in the upstream compressive quadrant,
(Fig. 4D–F), the distribution of the contacts for a reference particle becomes anisotropic as soon as shear stress increases. In strong shear flow, neighboring particles tend to accumulate in the upstream compressive quadrant, 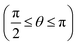 , where they are more compressed, and deplete along the extension axis,
, where they are more compressed, and deplete along the extension axis, 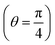 , where they are less distorted. The particles are also more compressed by increasing the strain up to the γσp. This anisotropy is maximum at γσp and then slightly decreases and reaches steady-state (see Fig. S4 in ESI† for the polar plots of g(r,θ)). Alternatively, this anisotropy of the pair distribution function between the compression and extension axes can be captured by the g2,−2(r) coefficient of the spherical harmonics expansion of g(r), as shown in Fig. S6 and S7 in ESI† and prior works.3,18 This behavior is consistently observed when the suspensions undergo strong shear deformation, which corresponds to the power-law flow regime at all volume fractions.18
, where they are less distorted. The particles are also more compressed by increasing the strain up to the γσp. This anisotropy is maximum at γσp and then slightly decreases and reaches steady-state (see Fig. S4 in ESI† for the polar plots of g(r,θ)). Alternatively, this anisotropy of the pair distribution function between the compression and extension axes can be captured by the g2,−2(r) coefficient of the spherical harmonics expansion of g(r), as shown in Fig. S6 and S7 in ESI† and prior works.3,18 This behavior is consistently observed when the suspensions undergo strong shear deformation, which corresponds to the power-law flow regime at all volume fractions.18
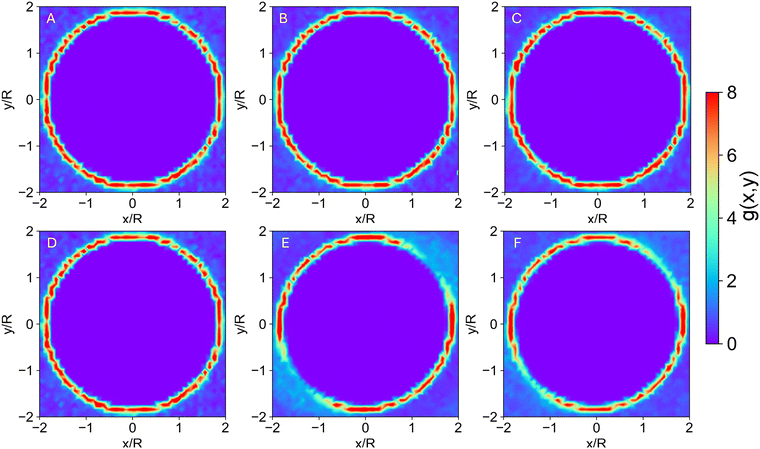 | ||
Fig. 4 Two dimensional pair distribution function, g(x,y), at shear rate of (A)–(C) 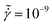 and (D)–(F) and (D)–(F) 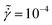 for ϕ = 0.80 at different strains: (A) and (D) γ = 0, (B) and (E) γ = γσp, and (C) and (F) γ = γst. for ϕ = 0.80 at different strains: (A) and (D) γ = 0, (B) and (E) γ = γσp, and (C) and (F) γ = γst. | ||
The dimensionless excess entropy is calculated using the two-body approximation as 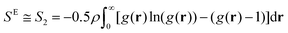 ,34,35,42 where ρ is the number density of the suspensions. The excess entropy is non-dimensionalized by the Boltzmann factor kB. Since the shear flow induces anisotropy in the flow-gradient plane, we consider g(r) = g(r,θ), where θ is defined with respect to the flow direction and capture the anisotropy in the flow-gradient plane.50 Considering the latter, the dependence of the excess entropy on θ is given by:
,34,35,42 where ρ is the number density of the suspensions. The excess entropy is non-dimensionalized by the Boltzmann factor kB. Since the shear flow induces anisotropy in the flow-gradient plane, we consider g(r) = g(r,θ), where θ is defined with respect to the flow direction and capture the anisotropy in the flow-gradient plane.50 Considering the latter, the dependence of the excess entropy on θ is given by:
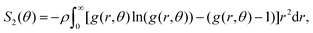 | (4) |
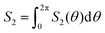 . In the above equation the g(r,θ) is calculated using:
. In the above equation the g(r,θ) is calculated using: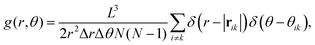 | (5) |
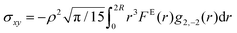 .3
.3
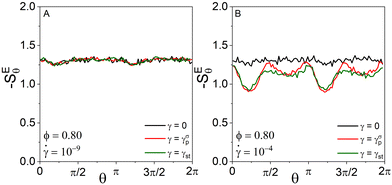 | ||
Fig. 5 Excess entropy, −SE, as a function of θ, at (A) 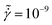 and (B) and (B) 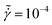 for suspensions with volume fraction of ϕ = 0.80. for suspensions with volume fraction of ϕ = 0.80. | ||
By integrating the S2(θ) over θ, the total excess entropy is determined as a function of strain (Fig. 6) at different shear rates and volume fractions. At low shear rates, the excess entropy reaches a steady state quickly since the microstructure shows minor adjustment in this regime of the shear flow. On the other hand, SE initially increases with the strain and then attains a steady state at higher shear rates (note that −SE decreases as a function of the strain). Although the pair distribution function shows an anisotropic distribution and S2(θ) clearly shows a θ-dependence at high shear rates, the total excess entropy as a function of strain does not show a measurable overshoot, due to the compensation of the contribution from extension and compression axes at large strains and shear rates. In addition, the SE(γ) increases with an increase in the volume fraction at a given shear rate and strain.
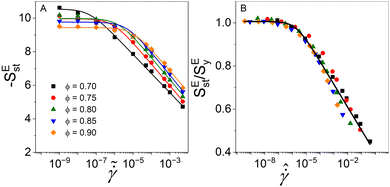
Now, we turn our attention to the scaling behavior of the steady state value of excess entropy, SEst, and correlate that with the shear rate, 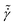 . At low shear rates, data suggest that there is a limiting value for SEst, and then it shows a logarithmic increase as a function of
. At low shear rates, data suggest that there is a limiting value for SEst, and then it shows a logarithmic increase as a function of 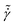 at all volume fractions (Fig. 7A). The dependence of the SEst on
at all volume fractions (Fig. 7A). The dependence of the SEst on 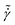 is expressed by a logarithmic function in the form of
is expressed by a logarithmic function in the form of 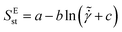 , where a, b, and c are fitting parameters and are presented in the ESI.† By scaling the excess entropy at steady-state with the value obtained in a quasi-static regime, SEy, as a function of the rescaled shear rate,
, where a, b, and c are fitting parameters and are presented in the ESI.† By scaling the excess entropy at steady-state with the value obtained in a quasi-static regime, SEy, as a function of the rescaled shear rate, 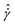 , a universal behavior for different volume fractions is obtained (Fig. 7B). This relationship is well-described by a logarithmic function in the form of
, a universal behavior for different volume fractions is obtained (Fig. 7B). This relationship is well-described by a logarithmic function in the form of 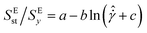 , where a = 0.396 ± 0.013, b = 0.046 ± 0.001, and c = 1.84 × 10−6 ± 6.09 × 10−7.
, where a = 0.396 ± 0.013, b = 0.046 ± 0.001, and c = 1.84 × 10−6 ± 6.09 × 10−7.
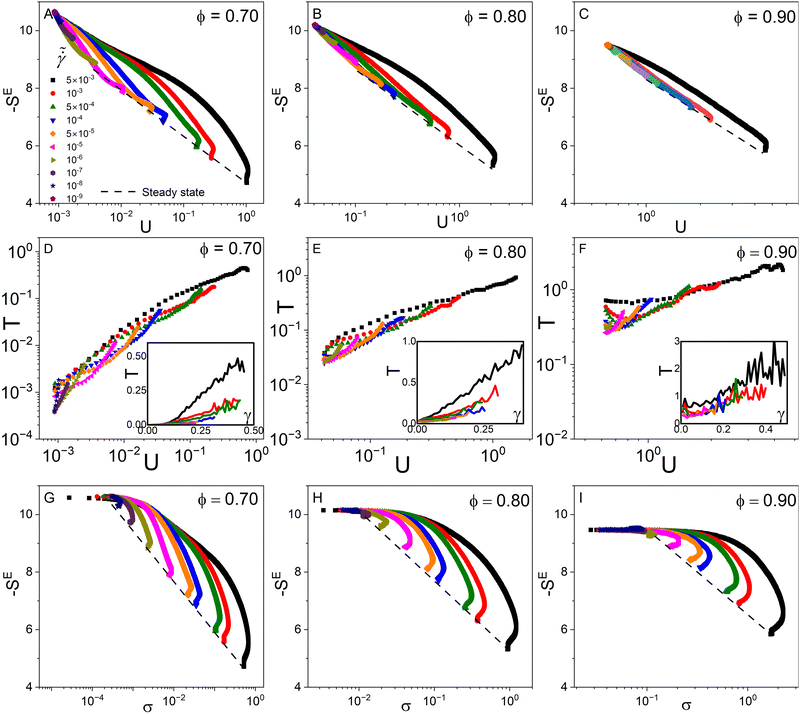
As shown in Fig. 8, the excess entropy increases with the elastic energy in the startup flow. Since there is a weak overshoot in U and SE smoothly increases and reaches steady behavior as a function of strain, the SE–U curves show a hook-like shape near and after the overshoot points, especially at the lowest volume fraction, ϕ = 0.70 (Fig. 8A). The steady-state condenses to a single point on the SE–U plot. This trend occurs at all shear rates and volume fractions. Interestingly, the initial part of the transient SE = SE(U) data obtained at different shear rates that approximately correspond to elastic deformation follows a universal behavior. Thus the departure from this trend can be considered as an indication of plastic flow.
Next, we utilize the thermodynamic definition of temperature, i.e., 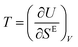 , with a goal to define a transient temperature during the startup flow as a function of the strain. Considering the scales for the SE and U, this transient temperature is normalized with E*R3/kB. Note that these calculations have been performed over the period that shear stress and elastic energy show a transient behavior, i.e., 0 ≤ γ ≤ 1.0; thus, we call this parameter transient temperature to distinguish this definition from the prior definition obtained based on the steady-state properties.17,44 At volume fraction of ϕ = 0.70 and high shear rates, T monotonically increases as a function of the elastic energy, until it reaches the point which corresponds to the steady-state of the steady state point of SE–U diagram. This behavior consistently occurs at shear rates which a clear overshoot in the stress–strain data is observed. Furthermore, the transient temperatures at different rates show overlap in the T–U plot in the linear part of the stress–strain data. At higher volume fractions (ϕ = 0.80 and 0.90), the transient temperature generally increases with elastic energy. At low rates, where the shear stress reaches steady-state behavior rather over smaller strains, T shows a minor increase-note that the range of U or SE is significantly limited when determining the temperature. The latter is more severe for data obtained at higher volume fractions. In other words, the data on the SE–U diagram is limited to one thermodynamical state point. Thus, the transient temperature does not exist. At a high shear rate, the T–U diagram is more extended to higher temperatures at high elastic energy values. One should note that these calculations are performed up to strain values that elastic energy and excess entropy show steady-state since T can diverge when SE becomes steady or it can fluctuate about zero when U shows an overshoot. This behavior can be explained by considering the chain rule of differentiation applied to the transient temperature as
, with a goal to define a transient temperature during the startup flow as a function of the strain. Considering the scales for the SE and U, this transient temperature is normalized with E*R3/kB. Note that these calculations have been performed over the period that shear stress and elastic energy show a transient behavior, i.e., 0 ≤ γ ≤ 1.0; thus, we call this parameter transient temperature to distinguish this definition from the prior definition obtained based on the steady-state properties.17,44 At volume fraction of ϕ = 0.70 and high shear rates, T monotonically increases as a function of the elastic energy, until it reaches the point which corresponds to the steady-state of the steady state point of SE–U diagram. This behavior consistently occurs at shear rates which a clear overshoot in the stress–strain data is observed. Furthermore, the transient temperatures at different rates show overlap in the T–U plot in the linear part of the stress–strain data. At higher volume fractions (ϕ = 0.80 and 0.90), the transient temperature generally increases with elastic energy. At low rates, where the shear stress reaches steady-state behavior rather over smaller strains, T shows a minor increase-note that the range of U or SE is significantly limited when determining the temperature. The latter is more severe for data obtained at higher volume fractions. In other words, the data on the SE–U diagram is limited to one thermodynamical state point. Thus, the transient temperature does not exist. At a high shear rate, the T–U diagram is more extended to higher temperatures at high elastic energy values. One should note that these calculations are performed up to strain values that elastic energy and excess entropy show steady-state since T can diverge when SE becomes steady or it can fluctuate about zero when U shows an overshoot. This behavior can be explained by considering the chain rule of differentiation applied to the transient temperature as 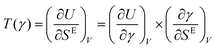 (see the insets of Fig. 8D–F for T = T(γ)). Thus, T(γ) → ∞ when
(see the insets of Fig. 8D–F for T = T(γ)). Thus, T(γ) → ∞ when 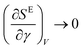 . Generally, at shear rates lower than
. Generally, at shear rates lower than 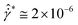 , this transition temperature shows a value fluctuating about zero since no significant adjustment in the microstructure occurs.
, this transition temperature shows a value fluctuating about zero since no significant adjustment in the microstructure occurs.
We also observe that the rate of the excess entropy change, 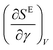 , at high shear rates shows at least one maximum before descending to zero, i.e., steady-state behavior in SE, while at low shear rates, this parameter decays to zero (Fig. S8 in ESI†). This result is important since it shows this measurement can separate two flow regimes: (1) at
, at high shear rates shows at least one maximum before descending to zero, i.e., steady-state behavior in SE, while at low shear rates, this parameter decays to zero (Fig. S8 in ESI†). This result is important since it shows this measurement can separate two flow regimes: (1) at 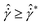 at high and intermediate shear rates where shear stress shows an overshoot and nonaffine dynamics of particles are localized and (2) at
at high and intermediate shear rates where shear stress shows an overshoot and nonaffine dynamics of particles are localized and (2) at 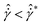 where flow is driven by the avalanches in dynamics of the particles at low stresses close to the dynamic yield limit and stress overshoot is suppressed.7,20
where flow is driven by the avalanches in dynamics of the particles at low stresses close to the dynamic yield limit and stress overshoot is suppressed.7,20
Finally, the transient shear stress and excess entropy of SPGs with different shear rates and volume fractions are correlated in Fig. 8G–I. Similar to the SE–U data, the SE–σ diagrams at different shear rates show a hook-like shape in the plastic flow regime and approximately collapse in the elastic part of the deformation. Other transient rheological properties, such as first normal stress, N1, second normal stress, N2, and osmotic pressure, Π, can also be correlated with the SE as shown in Fig. S9 (ESI†). Furthermore, the steady-state points at different rates can be explained by a logarithmic relationship in the form of SEy − SEst = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(σ/σy). Notably, the thermodynamic path to reach a steady state at a given volume fraction becomes longer on SE–σ by increasing the shear rate and decreasing the volume fraction. This path essentially reaches a single thermodynamic state point close to the dynamic yield stress value in the quasi-static regime.
ln(σ/σy). Notably, the thermodynamic path to reach a steady state at a given volume fraction becomes longer on SE–σ by increasing the shear rate and decreasing the volume fraction. This path essentially reaches a single thermodynamic state point close to the dynamic yield stress value in the quasi-static regime.
4 Summary and concluding remarks
Our study explores the thermodynamics of startup shear flow in jammed suspensions comprising soft particles using particle dynamics simulations. Results reveal that the excess entropy proposed by Rosenfeld34,35 not only explains the steady-state rheology behavior as reported by Bonnecaze et al.17 but also effectively captures the stress–strain behaviors in transient flow regimes at different shear rates and volume fractions. The transient excess entropy, SE(γ), derived from the pair distribution function, exhibits an overshoot whose magnitude generally increases with the shear rate. Notably, the magnitudes of these overshoots in stress, elastic energy, and excess entropy collapse onto master curves when the shear rate is scaled by the parameter G0/ηs, reflecting the ratio of elastic to viscous forces in the paste. In these master curves, either determined from transient rheology or thermodynamics, two behaviors reflecting the dominant flow mechanisms at the quasi-static regime and high shear rates are observed. These two regimes are separated at a critical shear rate of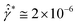 .
.
From a thermodynamic perspective, our analysis reveals the variation of the excess entropy as a function of the elastic energy, i.e., SE–U data, follows a universal behavior when data from different shear rates are limited to small deformations. Any departure from this generic behavior can be considered a thermodynamic indication of nonlinear flow and the onset of plastic deformation in these materials. Furthermore, a transient temperature can be defined using the thermodynamic definition of temperature from SE–U data. This transient temperature, T, is not defined at steady-state. In the transient flow regime, it increases with an increase in the elastic energy (equivalently increasing strain or stress), while at low rates corresponding to the quasi-static regime, it shows fluctuating behavior about zero.
The scaling relationships and thermodynamic framework established in this work provide valuable insights into the transient flow behavior of athermal, flow-driven systems across various conditions. Our findings suggest a promising route for exploring the applicability of this framework to thermally activated and flow-driven systems for future research. Given the similarities between SPGs and other flow-driven systems, such as granular materials,24 where particle dynamics are driven by avalanches in a jammed state, it would be constructive to apply this method to correlate the transient macroscopic rheology with the microstructure. We also note that the definition of the granular temperature, which is related to the kinetic energy of the particles, cannot reproduce the trend seen here since the average nonaffine velocity of the particles does not change as a function of the strain at a given rate. These suspensions also share similarities with hard spheres when under shear, exhibiting anisotropy of microstructural and arrested state in the shear flow. While this similarity exists, there are specific differences in the transient stress response when the volume fraction of hard spheres approach the random close-packing; the stress overshoot magnitude decreases with the increasing the ϕ, while as we have shown, the overshoot is monotonically increased with volume fraction. The latter is due to the difference in the origin of the stress, which arises from the purely entropic origin in hard spheres, while in SPGs, particles can deform at contact and accumulate elastic energy. Nevertheless, this framework can be tested for these hard-sphere suspensions, in which particles experience the caging behavior in the flowing state,51–55 and show shear-driven microstructural changes in form of structuring into layers. This phenomenon also occurs in SPGs when the distribution of the particle size is narrow, and they show a similar trend in terms of the existence of an induction period, where stress gradually decreases before attaining a steady state in the layered phase.45,46,56 We also note that hard-sphere colloidal gels57,58 and glass forming systems59 that show caging behavior can be used to establish these correlations between the transient thermodynamics and macroscopic rheology.
Author contributions
Nazanin Sadeghi: writing – review, formal analysis, visualization. Hrishikesh Pable: formal analysis and visualization. Fardin Khabaz: conceptualization, methodology, visualization, writing – review & editing, formal analysis, funding acquisition, investigation, project administration.Data availability
Data are available upon reasonable request from the authors.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
The authors thank Roger T. Bonnecaze and Michel Cloitre for discussing the static yield and excess entropy of SPGs. We also thank the National Science Foundation (grant numbers: CBET-2240760 and NRT-2152210) for providing financial support for this research. The authors also acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing computational resources that contributed to the research results reported in this paper.Notes and references
- D. Vlassopoulos and M. Cloitre, Theory and Applications of Colloidal Suspension Rheology, Cambridge University Press, Cambridge, 2021, ch. 6, pp. 227–290 Search PubMed.
- R. T. Bonnecaze and M. Cloitre, High Solid Dispersions, Springer, Berlin, Heidelberg, 2010, ch. 3, pp. 117–161 Search PubMed.
- J. R. Seth, L. Mohan, C. Locatelli-Champagne, M. Cloitre and R. T. Bonnecaze, Nat. Mater., 2011, 10, 838–843 CrossRef CAS PubMed.
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631 CrossRef CAS PubMed.
- D. Bonn and M. M. Denn, Science, 2009, 324, 1401–1402 CrossRef CAS PubMed.
- M. Cloitre, R. Borrega, F. Monti and L. Leibler, Phys. Rev. Lett., 2003, 90, 068303 CrossRef PubMed.
- F. Khabaz, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2020, 64, 459–468 CrossRef CAS.
- J. G. Berryman, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 1053 CrossRef CAS.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- M. Cloitre and R. T. Bonnecaze, Rheol. Acta, 2017, 56, 283–305 CrossRef CAS.
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed.
- N. J. Balmforth, I. A. Frigaard and G. Ovarlez, Annu. Rev. Fluid Mech., 2014, 46, 121–146 CrossRef.
- L. Mohan, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2014, 58, 1465–1482 CrossRef CAS.
- L. Mohan, R. T. Bonnecaze and M. Cloitre, Phys. Rev. Lett., 2013, 111, 268301 CrossRef PubMed.
- L. Mohan, C. Pellet, M. Cloitre and R. Bonnecaze, J. Rheol., 2013, 57, 1023–1046 CrossRef CAS.
- T. Liu, F. Khabaz, R. T. Bonnecaze and M. Cloitre, Soft Matter, 2018, 14, 7064–7074 RSC.
- R. T. Bonnecaze, F. Khabaz, L. Mohan and M. Cloitre, J. Rheol., 2020, 64, 423–431 CrossRef CAS.
- F. Khabaz, B. F. Di Dio, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2021, 65, 241–255 CrossRef CAS.
- B. F. Di Dio, F. Khabaz, R. T. Bonnecaze and M. Cloitre, J. Rheol., 2022, 66, 717–730 CrossRef CAS.
- H. Pable, N. Sadeghi, M. Cloitre and F. Khabaz, Under review, 2024 Search PubMed.
- A. Lematre and C. Caroli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 036104 CrossRef PubMed.
- A. Lematre and C. Caroli, Phys. Rev. Lett., 2009, 103, 065501 CrossRef PubMed.
- P. Coussot, Q. D. Nguyen, H. Huynh and D. Bonn, Phys. Rev. Lett., 2002, 88, 175501 CrossRef PubMed.
- O. Dauchot, G. Marty and G. Biroli, Phys. Rev. Lett., 2005, 95, 265701 CrossRef CAS PubMed.
- A. Kurokawa, M. Ichihara and K. Kurita, J. Non-Newtonian Fluid Mech., 2015, 217, 14–22 CrossRef CAS.
- M. Ozawa, L. Berthier, G. Biroli, A. Rosso and G. Tarjus, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6656–6661 CrossRef CAS PubMed.
- R. Benzi, T. Divoux, C. Barentin, S. Manneville, M. Sbragaglia and F. Toschi, Phys. Rev. Lett., 2021, 127, 148003 CrossRef CAS PubMed.
- M. Jiang, G. Wilde and L. Dai, Mech. Mater., 2015, 81, 72–83 CrossRef.
- C. P. Amann, M. Siebenbürger, M. Krüger, F. Weysser, M. Ballauff and M. Fuchs, J. Rheol., 2013, 57, 149–175 CrossRef CAS.
- A. Ghosh and K. S. Schweizer, J. Rheol., 2023, 67, 559–578 CrossRef CAS.
- N. Koumakis, M. Laurati, S. Egelhaaf, J. Brady and G. Petekidis, Phys. Rev. Lett., 2012, 108, 098303 CrossRef CAS PubMed.
- N. Koumakis, M. Laurati, A. R. Jacob, K. J. Mutch, A. Abdellali, A. Schofield, S. U. Egelhaaf, J. F. Brady and G. Petekidis, J. Rheol., 2016, 60, 603–623 CrossRef CAS.
- A. Zaccone, P. Schall and E. Terentjev, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 140203 CrossRef.
- Y. Rosenfeld, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 2545 CrossRef.
- Y. Rosenfeld, J. Phys.: Condens. Matter, 1999, 11, 5415 CrossRef CAS.
- R. V. Vaz, A. L. Magalhães, D. L. Fernandes and C. M. Silva, Chem. Eng. Sci., 2012, 79, 153–162 CrossRef CAS.
- G. Foffi, F. Sciortino, P. Tartaglia, E. Zaccarelli, F. L. Verso, L. Reatto, K. Dawson and C. Likos, Phys. Rev. Lett., 2003, 90, 238301 CrossRef CAS PubMed.
- J. Hoyt, M. Asta and B. Sadigh, Phys. Rev. Lett., 2000, 85, 594 CrossRef CAS PubMed.
- W. P. Krekelberg, T. Kumar, J. Mittal, J. R. Errington and T. M. Truskett, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031203 CrossRef PubMed.
- I. R. Graham, P. E. Arratia and R. A. Riggleman, J. Chem. Phys., 2023, 158(20), 204504 CrossRef CAS PubMed.
- L. Berthier, A. J. Moreno and G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 060501 CrossRef PubMed.
- W. P. Krekelberg, M. J. Pond, G. Goel, V. K. Shen, J. R. Errington and T. M. Truskett, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061205 CrossRef PubMed.
- M. Dzugutov, Nature, 2001, 411, 720 CrossRef CAS.
- F. Khabaz and R. T. Bonnecaze, Phys. Fluids, 2021, 33(1), 013315 CrossRef CAS.
- F. Khabaz, T. Liu, M. Cloitre and R. T. Bonnecaze, Phys. Rev. Fluids, 2017, 2, 093301 CrossRef.
- F. Khabaz, M. Cloitre and R. T. Bonnecaze, Phys. Rev. Fluids, 2018, 3, 033301 CrossRef.
- K. Liu, D. Williams and B. Briscoe, J. Phys. D: Appl. Phys., 1998, 31, 294 CrossRef CAS.
- A. Lees and S. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef.
- R. Larson, The Structure and Rheology of Complex Fluids, OUP, USA, 1999 Search PubMed.
- T. S. Ingebrigtsen and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 87–92 CrossRef CAS PubMed.
- B. Ackerson, J. Phys.: Condens. Matter, 1990, 2, SA389 CrossRef.
- B. J. Ackerson, J. Rheol., 1990, 34, 553–590 CrossRef.
- S. D. Kulkarni and J. F. Morris, J. Rheol., 2009, 53, 417–439 CrossRef CAS.
- S. Marenne, J. F. Morris, D. R. Foss and J. F. Brady, J. Rheol., 2017, 61, 477–501 CrossRef CAS.
- A. Sierou and J. F. Brady, J. Rheol., 2002, 46, 1031–1056 CrossRef CAS.
- R. Alrashdan, H. K. Yankah, M. Clotre and F. Khabaz, Phys. Fluids, 2024, 36(7), 073333 CrossRef CAS.
- L. C. Johnson, B. J. Landrum and R. N. Zia, Soft Matter, 2018, 14, 5048–5068 RSC.
- R. N. Zia, B. J. Landrum and W. B. Russel, J. Rheol., 2014, 58, 1121–1157 CrossRef CAS.
- J. Zausch, J. Horbach, M. Laurati, S. U. Egelhaaf, J. M. Brader, T. Voigtmann and M. Fuchs, J. Phys.: Condens. Matter, 2008, 20, 404210 CrossRef.
Footnote |
† Electronic supplementary information (ESI) available: Elastic energy as a function of strain on linear scales, strain dependence of first and second normal stresses and osmotic pressure, fit parameters for SE–![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) curves, flow curve, two-dimensional pair distribution function, expansion of pair distribution function based on spherical harmonics at high and low shear rates, derivative of excess entropy as a function of strain, correlation of excess entropy with first and second normal stresses as well as osmotic pressure, linear scale of elastic energy as a function of strain. See DOI: https://doi.org/10.1039/d4sm00514g curves, flow curve, two-dimensional pair distribution function, expansion of pair distribution function based on spherical harmonics at high and low shear rates, derivative of excess entropy as a function of strain, correlation of excess entropy with first and second normal stresses as well as osmotic pressure, linear scale of elastic energy as a function of strain. See DOI: https://doi.org/10.1039/d4sm00514g |
| This journal is © The Royal Society of Chemistry 2024 |