Open Access Article
Open Access ArticleAutonomous engulfment of active colloids by giant lipid vesicles†
Florent
Fessler
 *a,
Martin
Wittmann
b,
Juliane
Simmchen
c and
Antonio
Stocco
*a,
Martin
Wittmann
b,
Juliane
Simmchen
c and
Antonio
Stocco
 *d
*d
aInstitut Charles Sadron, CNRS UPR-22, 23 rue du Loess, Strasbourg, France. E-mail: florent.fessler@ics-cnrs.unistra.fr
bPhysical Chemistry, TU Dresden, Zellescher Weg 19, 01069 Dresden, Germany
cPure and Applied Chemistry, University of Strathclyde, Cathedral Street, Glasgow, UK
dInstitut Charles Sadron, CNRS UPR-22, 23 rue du Loess, Strasbourg, France. E-mail: stocco@unistra.fr
First published on 19th June 2024
Abstract
Our ability to design artificial micro/nanomachines able to perform sophisticated tasks crucially depends on our understanding of their interaction with biosystems and their compatibility with the biological environment. Here, we design Janus colloids fuelled only by glucose and light, which can autonomously interact with cell-like compartments and trigger endocytosis. We evidence the crucial role played by the far-field hydrodynamic interaction arising from the puller/pusher swimming mode and adhesion. We show that a large contact time between the active particle and the lipid membrane is required to observe the engulfment of a particle inside a floppy giant lipid vesicle. Active Janus colloids showing relatively small velocities and a puller type swimming mode are able to target giant vesicles, deform their membranes and subsequently get stably engulfed. An instability arising from the unbound membrane segment is responsible for the transition between partial and complete stable engulfment. These experiments shed light on the physical criteria required for autonomous active particle engulfment in giant vesicles, which can serve as general principles in disciplines ranging from drug delivery and microbial infection to nanomedicine.
1. Introduction
Catalytic microswimmers are micron-sized objects, that can self-propel and perform a variety of tasks on the micro-scale including drug delivery and environmental remediation. They achieve self-propulsion through chemical reactions that create concentration gradients that induce fluid flows in the surrounding solution. Efficient propulsion of the microswimmer requires a high reaction rate, which is usually achieved by the addition of highly reactive compounds such as hydrogen peroxide (H2O2)1 or hydrazine (N2H4),2 which are decomposed by the microswimmer. However, these toxic compounds limit potential applications e.g. in biological systems. Therefore, several works have focused on extending the range of propulsion reactions for catalytic microswimmers, including galvanic exchange reactions,3 photodeposition,4 the degradation of organic pollutants5,6 or the oxidation of amines to imines.7One very promising approach for powering of catalytic microswimmers in biological media is the use of a fuel that is also used by nature – glucose. Wang et al.8 have shown, that Cu2O microspheres can move in aqueous solutions of glucose under irradiation with visible light. The motion was explained with a photocatalytic oxidation of glucose to formic acid and the corresponding shorter monosaccharides arabinose, erythrose and glyceraldehyde. In their work, Wang et al. used symmetrical spherical particles, and the symmetry breaking necessary for propulsion was introduced by shining light on one side of the particle. Due to self-shadowing effects, asymmetric reaction rates would indeed result in a directed motion away from the light source. Here, we introduce Cu@SiO2 Janus particles that can move in an aqueous glucose solution under visible light irradiation. The Cu is converted to photocatalytic copper oxides when the particles are dispersed in water. Due to their asymmetric Janus structure, they have an intrinsic ability to move in any direction independent of the light source, allowing us to observe more complex biologically relevant interactions with the surroundings. In particular, interactions with fluid interfaces such as phospholipid membranes of cells represent a situation of confinement encountered in many processes. It was found that Janus swimmers are able to deform giant lipid vesicles when enclosed inside them,9 a response that has also been confirmed for biological active matter10 and by theoretical considerations.11,12 Freely swimming Janus particles however, showed interactions that resemble the generic interactions of active matter with obstacles.13–15 For pusher type swimmers, persistent orbital motion of Janus swimmers around giant vesicles was reported,16 and active transportation of the vesicles by a single particle could be achieved after applying strong forces.17 To the best of our knowledge, no other behavior was reported upon interaction of freely swimming active Janus particles with cell-like compartments. While in previous experiments the Janus particles were usually made from Pt@SiO2, which swim away from the metal cap and generally are considered to be pushers,18 we use a new combination of Cu@SiO2 particles with glucose fuel. Similar to differently fuelled Cu Janus particles,19–21 these swimmers move towards the catalyst cap. This different swimming mode enables different types of interactions with vesicles, and allows to observe endocytic-like behaviors.
2. Results and discussion
2.1. Glucose fuelled Cu@SiO2 Janus colloid self-propulsion
Cu@SiO2 Janus particles were fabricated by thermal deposition of a 30 nm metallic Cu layer on a monolayer of commercial SiO2 particles of radius RP ≈ 1.5 μm, covering one hemisphere. These particles can self-propel catalytically when immersed in H2O2 and swim towards the metal cap,20 which can be interpreted as behaviour as puller type swimmers because we assume the strongest slip is on the lead face.22 Here, we observe self-propelled motion in a different fuel. When immersed in a glucose aqueous solution at physiological concentration (25–100 mM), under homogeneous light irradiation provided by standard microscope illumination conditions, these particles show active propulsion as shown in Fig. 1A. The sedimented particles navigate in a two dimensional plane close to the glass substrate, which allows to image them with bright field microscopy and track their center of mass with image treatment techniques (ESI†). During some segments of the trajectory, the plane defined by the Janus boundary is orthogonal to the imaging plane. The hemisphere of the particle coated with the Cu layer appears darker than the bare hemisphere and allows to track the in-plane orientation of the particle (ESI†). The strong correlation between the particle orientation and its direction of motion, after filtering out the Brownian diffusion, confirms the existence of a directional active propulsion (ESI†). The out-of-equilibrium nature of Cu@SiO2 dynamics in glucose can be assessed, and their projected active velocity quantified, by plotting the center of mass mean squared displacement (MSD = 〈(xt+Δt − xt)2〉 + 〈(yt+Δt − yt)2〉) for single particles. For an active Brownian particle and for times shorter than the rotational diffusion time (τro = 1/Dro = 8πηRP3/kBT = 21 s) reads:1| MSD(Δt) = 4DtrΔt + V2Δt2, | (1) |
 | ||
| Fig. 1 (A) Bright field microscopy snapshot and trajectory (green) of a Cu@SiO2 Janus swimmer in a 100 mM glucose solution. Inset sketches the active motion mechanism. The scale bar is 5 μm in length. (B) Mean squared displacement as a function of lag time in log–log scale for three representative trajectories of particles immersed in 100 mM glucose with only white light (grey circles), white light and 0.46 mW blue light radiation (light blue up-pointing triangles) and white light and 1.96 mW blue light radiation (dark blue down-pointing triangles). Inset shows a linear scale representation with fits (white plain lines) allowing to extract projected velocity using eqn (1). For these three cases, fit yields V = 0.48 μm s−1, V = 1.23 μm s−1 and V = 2.33 μm s−1 (bottom to top). (C) Projected active velocity V extracted from MSD fits for particles immersed in glucose solutions of increasing concentration in normal illumination conditions. Black squares stand for averages on 10 trajectories. (D) Projected active velocity measured for particles immersed in a 100 mM glucose solution under different blue light illumination powers. | ||
2.2. Particle-vesicle encounter and engulfment phenomenon
In this section, we illustrate the phenomenon observed when an active Cu@SiO2 particle in a glucose solution spontaneously interacts with a giant unilamellar vesicle (GUV). This phenomenon can be described as composed of two steps: (i) the hydrodynamic capture, and (ii) the particle being wrapped by the vesicle membrane. Note that the particle activity depends on exposure to visible light and physiological glucose concentrations. Hence, we got rid of the limitations of using H2O2 as a fuel, which is not biocompatible and generally harmful for cells.24,25 In all experiments, we used GUVs made of phospholipids in the low-tension membrane regime (σ ∼ 10−8 N m−1, ESI†), which are pertinent systems to study endocytic-like phenomena26,27 in the absence of receptor-mediated interaction or large external forces.28–30Fig. 2A illustrates a typical result obtained few minutes after the spontaneous interaction between active particles and GUVs. Some active particles are already engulfed by GUVs and for one isolated particle we could track its active trajectory before and after encountering a GUV. The impact of the activity on the encounter rate is evident as it allows the particles to explore larger areas in a given time with respect to passive Brownian particles. The impact of far-field hydrodynamic interactions on the encounter rate is hard to evidence, because directional changes can be due either to hydrodynamic interaction or Brownian rotational diffusion. Still, even in diluted situations this kind of event happens at a high rate and after few minutes, most of the active particles in the sample are engulfed by GUVs (Fig. 2). In the first step of the interaction, the particle moves in the wedge defined by the bottom wall and the GUV membrane, which is slightly deformed by the particle, as sketched in Fig. 2B. The first two snapshots at times t1 and t2 in Fig. 2C correspond to bright field microscopy images of the capture. After the hydrodynamic capture, which can last several tens of seconds, a transition occurs and a sudden radial displacement of the particle towards the projected GUV center of mass is observed at the time t3 in Fig. 2C (showing snapshots of the Movie S1, ESI†). At time t4, the particle appears completely dark, evidencing a change of orientation and the trajectory shows a more confined diffusion than previously. Using confocal microscopy, we can show that at this final stage, the particle is inside the GUV volume while being fully wrapped by the lipid membrane (Fig. 2D), and remains in this stable state indefinitely. Movie S2 (ESI†) shows the whole wrapping process in fluorescence microscopy, together with a particle that was already engulfed. Note that in our experimental conditions, the wrapped particle is connected to the mother vesicle with a small neck or tube.30 Particle engulfment occurs only for floppy GUVs showing low tensions (σ < 10−7 N m−1) and as shown in Fig. 2, it occurs at the GUV periphery in the wedge defined by the bottom wall and the lipid membrane. In the next sections, we will describe quantitatively the two different steps of the phenomenon introduced here.2.3. Active particle hydrodynamic docking at the vesicle periphery
In order to elucidate on the mechanism responsible for capture of the particle at the GUV periphery, we quantify here the particle motion focusing our attention on the rotational dynamics. During the capture phase, the Cu cap of the particle is indeed systematically facing the GUV membrane. A top view of the situation is sketched in Fig. 3A, together with the definition of the particle orientation angle φ in the observation plane. The azimuthal angle of the particle radial position β and the distance between the particle and GUV projected centers L are also defined. An additional particle angle θ for the out-of-plane orientation can be defined as sketched in the inset of Fig. 3A (θ = 0 when the Janus boundary is parallel to the observation plane and the Cu hemisphere points towards the substrate). A component of the active propulsion force is oriented towards the lipid membrane and promotes the deformation of the latter. This orientation can be observed in bright field microscopy as in Fig. 2C and deformation of the vesicle can be confirmed using fluorescence microscopy as shown in Fig. 3B.The time evolution of the angular difference φ − β, plotted in Fig. 3C, shows a zero mean value 〈φ − β〉 ≈ 0, and a clear orientational confinement of the particle with the Cu cap facing towards the GUV projected center. The confinement effect is apparent when comparing φ − β to the time evolution of the orientation φ − φ0 (where φ0 = φ(t = 0) is a reference angle) of an active particle far from the GUV, also shown in Fig. 3C. Here, the in-plane particle orientation during capture 〈φ − β〉 ≈ 0 is very different from the one observed for pusher type swimmers, which align as 〈φ − β〉 ≈ π/2 performing orbital motion around GUVs (ESI†) or solid spherical obstacles.14,16,31,32 These results point to a self-propulsion mechanism of Cu@SiO2 colloids in glucose generating puller-type swimmer flow-fields, as it is in H2O2 with the Cu cap forward. Far-field hydrodynamics models indeed predict that puller type swimmers encountering a spherical obstacle should be trapped by the interface and remain motionless even for reasonably low dipole strengths and small obstacles.33 Hence, the capture observed in our experiments can be attributed to the far-field hydrodynamic attraction expected for puller active particles close to obstacles. The additional complexity arising from the softness and fluidity of the GUV membrane does not seem to modify the attractive nature of those interactions.
The particle orientation is however not frozen and φ − β show significant fluctuations, which indicates rotational diffusion at short times while experiencing an effective restoring torque at long times. Hence, we calculated the mean squared angular displacement (MSAD) of φ − β. At short times, the slope of the MSAD allows to extract the in-plane rotational friction ζφ experienced by the particle during the capture phase. The fit yields ζφ = 7.3 × 10−20 N s m (ESI†) which is close to the theoretical value expected for the rotational friction experienced by a spherical RP = 1.5 μm particle in the bulk ζro,b = 8πηRP3 = 8.5 × 10−20 N s m. Hence, no additional dissipations due to the GUV membrane are experienced by the particle during the capture, that points to a large water gap (>100 nm) between the membrane and the particle surface,34 which does not permit adhesive surface interactions to play a role and agrees with a far-field hydrodynamic interaction.
The magnitude of the MSAD(φ − β) plateau at long times provides an angular range  , which describes the competition between the Brownian diffusion that tends to randomize the particle orientation and an effective restoring torque tending to align the particle towards φ − β = 0. As described before, the origin of this restoring torque can be purely hydrodynamic. In this first stage of the interaction between the active colloid and the GUV characterized by far-field hydrodynamic effects, the adhesion energies between the two particle faces (Cu and SiO2) and the GUV membrane, quantified by an adhesive energy per unit area w, are not expected to play a significant role for the particle orientational confinement.
, which describes the competition between the Brownian diffusion that tends to randomize the particle orientation and an effective restoring torque tending to align the particle towards φ − β = 0. As described before, the origin of this restoring torque can be purely hydrodynamic. In this first stage of the interaction between the active colloid and the GUV characterized by far-field hydrodynamic effects, the adhesion energies between the two particle faces (Cu and SiO2) and the GUV membrane, quantified by an adhesive energy per unit area w, are not expected to play a significant role for the particle orientational confinement.
Note that our ability to unequivocally determine the in-plane orientation φ during capture relies on the out-of-plane orientation θ ≈ π/2 (see inset in Fig. 3A), which makes the Janus boundary visible under the microscope in bright field. While θ ≈ π/2 is a signature of an hydrodynamic interaction with the lipid vesicle membrane, the bright field acquisitions do not allow to univocally determine if the Cu hemisphere is pointing upwards or downwards. In bright-field microscopy, particles show the same aspect for θ − Δθ and θ + Δθ. Hence, we cannot determine whether the particle is slightly oriented towards the lipid membrane as shown in Fig. 2B, or towards the glass substrate. Still, in our experiments 〈φ − β〉 ≈ 0 shows that the interaction with the lipid membrane dictates the engulfment behavior of the active particle by the GUV.
The transition to full wrapping is evidenced by an abrupt variation of the distance L in Fig. 3D at the end of the capture phase. The approaching of the particle is however not always a direct effect of the transition to full wrapping. It happens that the particle first moves towards the GUV projected center of mass and remains confined between the GUV and the substrate before undergoing the full wrapping transition. It can also be seen in Fig. 3C that after the transition (represented by the vertical dashed line), the in-plane orientation φ can not be precisely measured and show large variations as a result of the out-of-plane reorientation of the particle, which does not allow to image the Janus boundaries, see Fig. 2C. During the capture step, there is a dynamics associated with the drainage of the water film such that the particle–membrane distance is not the equilibrium one. Indeed, the particle–membrane surface interaction potential, in the case of non-specific adhesion, is minimal at separation distances in the range 20–100 nm35,36 while the basin of attraction associated to the hydrodynamic capture is of the order of the swimmer body size (few micrometers here).33 The characteristic time τd associated to the drainage of the water film can be estimated from Reynolds law37 and yields τd ≈ 101 s with the active propulsion as driving force. To investigate the dynamics towards the wrapping transition, measurements on the membrane profile upon wrapping and the driving forces of the process will be discussed in the following section.
2.4. Wrapping transition dynamics
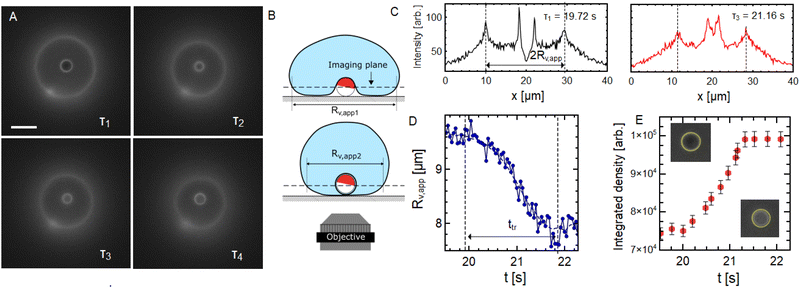
The dynamics of the GUV wrapping the active particle can be followed using fluorescence microscopy. In most cases, the transition to full wrapping takes place at the periphery of the vesicle, as it can clearly be seen in the Movie S2 (ESI†) and in Fig. 2D. In some rare cases for GUVs of small sizes (7–10 μm radii), the particle can slowly crawl underneath the vesicle and reach the GUV projected center, as depicted in Fig. 4A and B. In this case, one can take advantage of the geometry to monitor the evolution of the projected GUV area and particle fluorescence during the wrapping dynamics. In Fig. 4A, one can see fluorescence microscopy snapshots of an active particle that came in contact with a relatively small GUV, and during the capture phase reaches the center of the circular projected GUV area. At time τ1 = 19.72 s after the start of the acquisition, the particle is not wrapped yet and the situation corresponds to the one depicted on the top panel of Fig. 4B. At time τ4 = 22.08 s, the particle is fully wrapped and the situation corresponds to the situation of the lower panel in Fig. 4B, while intermediate times correspond to the dynamics of full wrapping transition (τ2 = 21.12 s and τ3 = 21.16 s). In Fig. 4C, we show representative intensity profiles passing through the projected GUV center of fluorescence microscopy images from Fig. 4A. The two external peaks correspond to the bright circle coming from the GUV projection in the imaging plane. Such profiles allow to follow the evolution of an apparent projected radius Rv,app(t) during the full wrapping transition from the distance between these two peaks.Plotting the evolution of Rv,app during the transition (from τ1 to τ4) in Fig. 4D shows a decrease of more than a micron, which is a signature of the full wrapping transition. Indeed, fully enveloping the particle with membrane requires pulling more membrane surface area to the wrapping site resulting in a decrease of the apparent vesicle projected radius (as depicted in Fig. 4B) as the GUV sphericity increases. Conversely, the fluorescence signal emitted from the region corresponding to the particle projected area (quantified by the so-called pixel integrated density in Fig. 4E) increases following the same dynamics, confirming the full wrapping of the particle. During this transition, the contact line advances from the equator of particle (the Janus boundary) to its pole. We show here that this transition occurs in a time tin ≈ 2 s, resulting in a contact line velocity vc = πRP/2tin = 1.17 μm s−1. This is comparable to contact line velocities measured in the system of Spanke et al.,38 where wrapping was triggered by depletion attraction with adhesion energy densities w of the order of 10−6 N m−1 for similar particle size (RP = 1 μm).
In order to evaluate the adhesion energy densities in our system, we performed adhesion experiments of GUVs on planar SiO2 and Cu surfaces.37,39,40 We are able to thermally deposit a nanometric Cu layer on glass slides over several cm2 surface area using the same technique employed to deposit the cap on the SiO2 particles. Fig. 5A shows the analogy between our situation and the experiment we performed to determine w illustrated in Fig. 5B, where we also define the quantity Rco which will be of interest here. Using a confocal microscope, we can extract the full 3-dimensional shape of the adhesive vesicles. If we compare typical side view profiles (x–z plane) acquired with confocal microscopy of an initially floppy vesicle on Cu (Fig. 5C) or on SiO2 glass (Fig. 5D), it is clear that the interaction with the bottom substrate is very different leading to different vesicle shapes. The shape of the unbound part of the membrane is very close to a spherical cap (expected in the limit of high adhesion37) in the case of Cu substrate, while the shape is more elongated and the membrane appears more fluctuating for SiO2. Indeed, the bending energy that tends to maximize the membrane curvature radius over the whole surface area is in competition with the adhesion energy that tends to maximize the membrane area in contact with the surface. The curvature radius at contact therefore reads:39
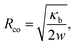 | (2) |
Hence, the associated adhesion energy density wCu is several orders of magnitude larger than wSiO2 in this geometry. This attractive interaction potential between a POPC lipid bilayer and a Cu surface results from many contributions including electrostatic double-layer, van der Waals, hydration, hydrophobic and steric repulsion.42 Electrostatic attraction alone between the slightly positively charged Cu (zeta potential ζCu ≈ +14 mV20,21) and the zwitterionic POPC (reported to show slightly negative zeta potential ζPOPC ≈ −7 mV43) could hardly explain the measured adhesion. Other short range chemical interactions could play a role. For example, it was shown that Cu2+ ions can bind to PC and PE lipid headgroups44,45 and induce structural changes on the membrane. It is not obvious however how to quantify these effects in terms of an effective adhesion.
2.5. Theoretical modelling of the wrapping energy landscape
In the previous sections, we showed that active Cu@SiO2 Janus particles are able to deform GUV membranes until reaching a stable complete engulfment. We also measured the adhesion energy densities and the characteristic capture time. By using these experimental values, in this section, we model the driving energies and costs associated to the particle engulfment, in order to understand its stability. Our model will also allow to address questions regarding the dynamics of the phenomenon, in particular the duration of the capture time tc before the wrapping transition.The system considered in our model is composed of a particle and a fluid membrane with bending rigidity κb, tension σ and particle–membrane adhesive energy per unit area w. If one assumes a flat membrane and negligible volume conservation constraints, the free energy of the system can be described with the following Helfrich–Canham Hamiltonian:46
 | (3) |
Let us first consider that the adhesion, bending and tension contributions of the membrane segment bound to the particle dictate the wrapping angle α defined in the inset of Fig. 6A. Thus, we ignore at the moment the contribution of the free segment (the vesicle area that is not bound to the particle). This simplification is expected to apply to infinite planar membranes with vanishing tension and spontaneous curvature,47,48 and has been used to explain the experimental wrapping phase diagram of isotropic particles adhering to floppy vesicles with small spontaneous curvature |m| ≤ 4 × 104 m−1.29 In the case of a spherical particle with radius RP, the energies associated with tension and bending for the bound membrane area Ab = 2πRP2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) are: Eσ = πσRP2(1 − cos
α) are: Eσ = πσRP2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)2 and Eb = 4πκb(1 + mRP)(1 − cos
α)2 and Eb = 4πκb(1 + mRP)(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) respectively, where m is a membrane spontaneous curvature. These two contributions can be calculated in our system using a standard value of the bending rigidity κb = 27.3 ± 5.1kBT ≈ 10−19 J for POPC vesicles in glucose/sucrose solutions49 and a tension σ = 10−8 N m−1 as a representative value accounting for the tension distribution from previous force measurements on floppy vesicles prepared with the same protocol30 and confirmed by analyzing the thermal undulations of the vesicle membrane (ESI†). The two negative (energetically favorable) contributions to the free energy of the system can also be estimated. The work done by the propulsion force f can be expressed as a function of α as Ef = −fRP(1 − cos
α) respectively, where m is a membrane spontaneous curvature. These two contributions can be calculated in our system using a standard value of the bending rigidity κb = 27.3 ± 5.1kBT ≈ 10−19 J for POPC vesicles in glucose/sucrose solutions49 and a tension σ = 10−8 N m−1 as a representative value accounting for the tension distribution from previous force measurements on floppy vesicles prepared with the same protocol30 and confirmed by analyzing the thermal undulations of the vesicle membrane (ESI†). The two negative (energetically favorable) contributions to the free energy of the system can also be estimated. The work done by the propulsion force f can be expressed as a function of α as Ef = −fRP(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α). Here, an upper bound of the active force f in our system can be calculated by taking it to be equal to the translational friction force when the particle is far from a GUV at the highest measured projected velocity V. We then have f = ζtr,bV = 6πηRPV ≈ 0.1 pN. Considering the Janus geometry of the particle, the adhesion energy density w is not constant throughout the wrapping process (as shown previously). Indeed, the adhesion energy density of Cu wCu and SiO2wSiO2 with the membrane are very different, as shown in the previous section. The adhesion energy then reads:
α). Here, an upper bound of the active force f in our system can be calculated by taking it to be equal to the translational friction force when the particle is far from a GUV at the highest measured projected velocity V. We then have f = ζtr,bV = 6πηRPV ≈ 0.1 pN. Considering the Janus geometry of the particle, the adhesion energy density w is not constant throughout the wrapping process (as shown previously). Indeed, the adhesion energy density of Cu wCu and SiO2wSiO2 with the membrane are very different, as shown in the previous section. The adhesion energy then reads:
 | (4) |
 | ||
| Fig. 6 (A) Energy associated to the membrane segment bound to the particle Ebo as a function of wrapping angle. Plain line stands for spontaneous curvature m = 0 and dashed one to m = −105 m−1. Insets show the adhesion energy between the membrane and the particle as a function of wrapping angle considering the particle is wrapped with the Cu facing towards the membrane. (B) Illustration of the shape of the total energy (Ebo + Efree) and definition of the energy barrier Eb between the partial and full wrapping states. (C) Temporal evolution of L/L0 (where L0 = L(t = 0)) for three wrapping experiments with t0 taken as the moment the particle undergoes the full wrapping transition. (D) Height of the energy barrier Eb as a function of the inverse hopping rate 1/Γ = thop using the Kramers theory50,51 of escape over an energy barrier using stiffness and diffusivity extracted from curves in (C). Vertical dashed line stands for average tc from (C). | ||
Taking wCu = 0.2 μN m−1 the lower bound inferred from confocal microscopy acquisitions and wSiO2 = 0.88 nN m−1 allows to have a full description of the wrapping energy landscape for the bound membrane segment. In Fig. 6A we plot the sum of the contributions for the bound membrane segment together with the active force and adhesion contributions Ebo = Eb + Eσ + Ef + Ead as a function of wrapping angle α defined in the sketch. Inset shows the evolution of Ead alone when taking into account the Janus geometry (eqn (4)). It appears clearly that using values of wCu inferred from experiments, the adhesion is what drives the wrapping and not the active force as it is much weaker, |Ead| > |Ef|. However, due to the Janus geometry and the difference in the Cu and SiO2 affinities with the membrane, the only minimum is predicted at α = π/2 as shown by the Ebovs. α curves in Fig. 6A. Note that the evolution of Ebo(α) is qualitatively the same in the presence of a negative spontaneous curvature m = −105 m−1 expected in our system due to the inner sucrose/outer glucose solution asymmetry across the membrane.30,52 In other terms, when considering only the bound membrane segment, a stable partial wrapping up to the equator is predicted due to the anisotropy in particle adhesive properties (wCu ≫ wSiO2), and the full wrapping state α = π appears highly unstable and energetically costly. This is not consistent with our observations at long times, showing that particles can undergo a transition to full wrapping (α = π, see Fig. 3C, D and 4). The minimum at α = π/2 may however describe the transitory state observed experimentally in Fig. 3B. Hence, the assumption that the energy associated to the shape of the free membrane segment Efree is negligible does not hold for our system.
In Fig. 6B, we sketch the shape of the total energy profile for a Janus particle Etot(α) = Ebo(α) + Efree(α) which would be consistent with our experimental observations, with a global minimum at α = π. The shapes adopted by the unbound (free) membrane segment for 0 < α < π might be costly in regards to both tension and bending in the presence of a spontaneous curvature.47 However, when α = π (full wrapping), a narrow neck is formed behind the particle and the rest of the vesicle adopts a shape with M ≈ 1/Rv. Narrow necks are highly curved shapes, but the principal curvatures being of opposite signs lead to vanishing mean curvatures and in turn low bending energies, which explains the lower energetic cost of the α = π configuration from the unbound membrane segment standpoint.47,53 This gives rise to an energy barrier Eb that separates the metastable partial wrapping state and the stable full wrapping state. Theoretical and numerical works considering isotropic adhesive particles and the full vesicle shape already reported the existence of bistable regimes, where an energy barrier separates the free/partially engulfed and the completely engulfed states which are therefore (meta)stable.54–56 Taking into account the presence of a negative spontaneous curvature, the calculations performed in ref. 54 indeed predict a bistable regime in our range of particle and vesicle sizes, and considering the particle to be isotropic with w = wCu ∼ 10−7 N m−1. Even if these models consider vesicle shapes simpler than the ones observed in our systems and do not account for the Janus particle geometry, they allow to explain the stability of the fully wrapped state.
While calculation of the full energy associated to both the particle–membrane interaction and the full membrane shape is impossible with our experimental data (the full membrane shape can not be determined), we could estimate the energy barrier Eb separating the partial wrapping state and the full wrapping state. Indeed, for cases when the capture time is large compared to the fast local relaxation processes in the potential well (∼1 s) around α = π/2 (such as for the cases in Fig. 6C), we can use the Kramers theory of escape over an energy barrier. The latter links a hopping rate Γ, i.e. the inverse average time spent by the particle in the metastable state before hopping 〈thop〉, to Eb such as:50,51
 | (5) |
 | (6) |
| ΔL = −RPΔα | (7) |
Hence, we can plot the distribution of α inferred from L and translate it in an effective potential ΔU(α), which we can fit assuming it is quadratic around α = π/2 to extract the stiffness k. The average stiffness of the quadratic trapping potential using our data is k = 38 ± 4kBT (ESI†). Diffusivity Dα can be inferred from a linear fit at short times of the mean squared angular displacement curves of α as a function of lag time. The mean diffusivity Dα measured here is Dα = 0.021 ± 0.002 rad2 s−1 (ESI†). We can plot Eb as a function of thop (Fig. 6D) by reversing eqn (5) and by plugging in the calculated k and Dα. This allows to visualize the expected magnitude of Eb for hopping times few tens of seconds long which is what we observe in experiments as a lower bound. Note that tc can be larger than thop as it might take some time for the water gap between the particle and the membrane to drain and the adhesion measured in equilibrium to be effective. Still, tc provides an upper bound for thop and this reasoning allows to estimate that the full energy profile considering the full (bound and free) membrane shape leads to an energy barrier Eb ≈ 2kBT, see Fig. 6D.
3. Conclusion
To conclude, we designed a system that autonomously reproduces endocytosis and the wrapping of artificial active swimmers by giant vesicles, only by providing visible light and physiological glucose concentrations. We showed that the velocity of the active particle is not the quantity to maximize in order to observe engulfment by cell-like compartments. In fact, our results evidence the key role of long contact times between the swimmer and the wrapping host. Long contact times during which an active propulsion force component of the particle is directed towards the membrane indeed allow the liquid film between the two objects to drain and physicochemical interactions to be triggered leading to adhesion between the two surfaces. Additionally, time is needed for the system to overcome energy barriers separating two wrapping states. It is therefore crucial that far-field interactions, such as the long-range hydrodynamic attraction between the puller swimmer and the soft obstacle here, prevent the particle to swim away from the vesicle membrane. To generalize, for future investigations we can predict that bigger particles sizes would facilitate the hydrodynamic docking of the particle at the vesicle periphery, due to reduced magnitude of the orientational and translational Brownian noise. However, the associated increase in tension cost will lead to a higher energy barrier57 and therefore increase the average hopping time over the barrier. This leads to a more effective but slower overall process. For tenser membranes, this energy barrier could be lowered by increasing the adhesion of the particle via designing Janus colloids with both faces showing w ≥ σ. Increasing the membrane negative spontaneous curvature m could also facilitate the full wrapping transition. However, one must bare in mind that spontaneous curvature gives rise to a spontaneous tension![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 2κbm2, which might be significant for large values of m. For smaller particle sizes, the decrease of the tension energetic cost is followed by an increase of the bending energy cost, leading to a similar barrier height. The enhanced translational and rotational diffusion would however prevent the slow processes to occur as the particle is more likely to diffuse away or reorient before adhesion is triggered. Note that from Reynold's law of drainage, we expect the duration of the film drainage step to be larger for larger spherical particles. However, non-spherical particle shapes could minimize the drainage time to trigger adhesion faster.
= 2κbm2, which might be significant for large values of m. For smaller particle sizes, the decrease of the tension energetic cost is followed by an increase of the bending energy cost, leading to a similar barrier height. The enhanced translational and rotational diffusion would however prevent the slow processes to occur as the particle is more likely to diffuse away or reorient before adhesion is triggered. Note that from Reynold's law of drainage, we expect the duration of the film drainage step to be larger for larger spherical particles. However, non-spherical particle shapes could minimize the drainage time to trigger adhesion faster.
Overall, this research provides insights on the physical criteria required to trigger autonomous full and stable wrapping of active particles, when their direction of motion is not prescribed by an external field. Such findings are of particular interest for interactions of swimmers in general with biological units to perform tasks at the cellular level in contexts such as drug delivery and nanomedicine, or in the case of microbial infections. In the scope of micromotors design for wastewater treatments, being able to get all particles stably wrapped by fluid membranes once they performed a given task could constitute an efficient way to remove them from any environment, by removing the membrane enclosing them as a whole instead of individually removing particles.
4. Materials and methods
4.1. Janus particles
Janus colloids were fabricated by drop casting a diluted solution of SiO2 microspheres of radius RP = 1.5 μm (Sigma Aldrich) on a plasma clean glass slide. After evaporation of the solvent, a nanometric (30 nm) Cu layer was subsequently thermally deposited on the microspheres monolayer. The half Cu-coated microspheres were released in MilliQ water thanks to ultrasonic pulses and stored at 4 °C until use.4.2. Giant unilamellar vesicles assembly
The giant unilamellar vesicles were prepared using a PVA (Polyvinyl alcohol) gel-assisted formation method.58 The PVA gel is prepared by dissolving PVA in pure water (MilliQ water) at 5% w/v concentration. The prepared PVA gel is spread uniformly in PTFE (polytetrafluoroethylene) troughs and dried for 45 minutes at 80 °C in an oven. In the case of POPC/POPC-NBD vesicles, 5 μL of a 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (molar) mixture of POPC (1-palmitoyl-2-oleoylphosphatidylcholine) and POPC-NBD (POPC fluorescently labelled with nitrobenzoxadiazole) lipids in chloroform (1 g L−1) are spread on the PVA gel and vacuum dried in a desiccator for 15 minutes. At this stage, the lipids under solvent evaporation spontaneously form stacks of lipid layers supported by the dried PVA gel film. This lipid system obtained is then hydrated with 200 μL of sucrose (50–150 mM) and allowed to grow for 2 hours while remaining sealed to avoid water evaporation that would lead to sucrose solution concentration increase. The vesicle suspension is then collected and sedimented in 1 mL of glucose solution with matching concentration to have isotonic conditions. They are stored in isotonic conditions for optimal stability and osmotically deflated when preparing the sample (see below). The slight density mismatch between the sucrose solution inside the vesicle and the sucrose/glucose solution in the outer aqueous medium allows the vesicles to sediment at the bottom of the observation cell without strongly deforming them.
1 (molar) mixture of POPC (1-palmitoyl-2-oleoylphosphatidylcholine) and POPC-NBD (POPC fluorescently labelled with nitrobenzoxadiazole) lipids in chloroform (1 g L−1) are spread on the PVA gel and vacuum dried in a desiccator for 15 minutes. At this stage, the lipids under solvent evaporation spontaneously form stacks of lipid layers supported by the dried PVA gel film. This lipid system obtained is then hydrated with 200 μL of sucrose (50–150 mM) and allowed to grow for 2 hours while remaining sealed to avoid water evaporation that would lead to sucrose solution concentration increase. The vesicle suspension is then collected and sedimented in 1 mL of glucose solution with matching concentration to have isotonic conditions. They are stored in isotonic conditions for optimal stability and osmotically deflated when preparing the sample (see below). The slight density mismatch between the sucrose solution inside the vesicle and the sucrose/glucose solution in the outer aqueous medium allows the vesicles to sediment at the bottom of the observation cell without strongly deforming them.
4.3. Sample cell preparation
The sample cell consists in a thin glass coverslip (0.17 mm thickness, Menzel-Gläser) on top of which a self-adhesive silicon imaging chamber (CoreWell Imaging Chamber) of 0.9 cm diameter and 1.6 mm thickness is placed. The whole forms a sealed through which can then be filled with 150 μL of a glucose solution with concentration matching the vesicle outer solution concentration. 1–5 μL of concentrated GUVs solution can then be added as well as 2 μL of particles solution. The whole is then left open for an hour to allow evaporation of the water in the glucose phase and induce the deflation of the GUVs.4.4. Optical setup
The microscope used here is a Nikon Eclipse TE2000 confocal microscope which was used both as a standard inverted microscope for bright field and epifluorescence visualization of the sample and as a confocal microscope. Objectives used are Nikon ×40 air objective, ×60 water objective and ×100 oil objective. Bright field illumination light source was a LHS-H100P-1 12V100W halogen lamp. The fluorescence excitation light source is the Nikon C-HGFI Intensilight, combined with the appropriate set of filters (Semrock optical filters as exciter, emitter and dichroic) to shine blue light on the sample. Bright field as well as epifluorescence acquisitions were done using a Hamamatsu C13440 Orca-Flash 4.0 digital camera.4.5. Acquisition and tracking
Videos were acquired at frequencies ranging from 25 to 100 frames per second (fps). Tracking of the Janus Cu@SiO2 particles center of mass required an appropriate thresholding of the microscope acquisitions for the tracking algorithm not to be influenced by the particle orientation changes. Fitting the raw images indeed led to additional unphysical motion of the center of mass due to the orientation variations correlated with a change in aspect of the particle. To get rid of this effect, microscopy acquisitions were thresholded using ImageJ so that the particle would appear as a plain circular dark spot and the tracking was insensitive to orientation changes. The center of mass tracking of these dark spots was then achieved using the open source software Blender v 3.0.0 (Blender, Inc.). Orientation tracking was performed using a homemade ImageJ routine (ESI†) consisting in inverting the image and subsequently threshold appropriately in order to track the orientation of the Cu coated hemisphere whose 2D projection is close to an ellipsoid.Author contributions
Florent Fessler: conceptualization, data curation, formal analysis, investigation, methodology, writing – original draft, writing – review & editing. Martin Wittman: conceptualization, data curation, investigation, methodology, writing – review & editing. Juliane Simmchen: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing – review & editing. Antonio Stocco: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We wish to acknowledge funding from the Ecole Doctorale Physique Chimie-Physique of Strasbourg, Agence Nationale de la Recherche EDEM (Grant No. ANR-21-CE06-0042-01) and ITI HiFunMat (Université de Strasbourg).References
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- W. Gao, A. Pei, R. Dong and J. Wang, J. Am. Chem. Soc., 2014, 136, 2276–2279 CrossRef CAS PubMed.
- L. Feuerstein, C. G. Biermann, Z. Xiao, C. Holm and J. Simmchen, J. Am. Chem. Soc., 2021, 143, 17015–17022 CrossRef CAS PubMed.
- M. Wittmann, M. Voigtmann and J. Simmchen, Small, 2023, 19, 2206885 CrossRef CAS.
- Y. Wu, R. Dong, Q. Zhang and B. Ren, Nano-Micro Lett., 2017, 9, 30 CrossRef.
- Q. Zhang, R. Dong, Y. Wu, W. Gao, Z. He and B. Ren, ACS Appl. Mater. Interfaces, 2017, 9, 4674–4683 CrossRef CAS PubMed.
- M. Wittmann, S. Heckel, F. Wurl, Z. Xiao, T. Gemming, T. Strassner and J. Simmchen, Chem. Commun., 2022, 58, 4052–4055 RSC.
- Q. Wang, R. Dong, C. Wang, S. Xu, D. Chen, Y. Liang, B. Ren, W. Gao and Y. Cai, ACS Appl. Mater. Interfaces, 2019, 11, 6201–6207 CrossRef CAS PubMed.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS PubMed.
- L. Le Nagard, A. T. Brown, A. Dawson, V. A. Martinez, W. C. Poon and M. Staykova, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2206096119 CrossRef CAS PubMed.
- S. Y. Lee, P. W. Schönhöfer and S. C. Glotzer, Sci. Rep., 2023, 13, 22773 CrossRef CAS.
- P. Iyer, G. Gompper and D. A. Fedosov, Soft Matter, 2022, 18, 6868–6881 RSC.
- S. Makarchuk, V. C. Braz, N. A. Araújo, L. Ciric and G. Volpe, Nat. Commun., 2019, 10, 4110 CrossRef PubMed.
- J. Simmchen, J. Katuri, W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Sánchez, Nat. Commun., 2016, 7, 10598 CrossRef CAS PubMed.
- C. van Baalen, W. E. Uspal, M. N. Popescu and L. Isa, Soft Matter, 2023, 19, 8790–8801 RSC.
- V. Sharma, E. Azar, A. P. Schroder, C. M. Marques and A. Stocco, Soft Matter, 2021, 17, 4275–4281 RSC.
- V. Sharma, C. M. Marques and A. Stocco, Nanomaterials, 2022, 12, 1434 CrossRef CAS PubMed.
- A. I. Campbell, S. J. Ebbens, P. Illien and R. Golestanian, Nat. Commun., 2019, 10, 3952 CrossRef PubMed.
- K. Xiao, R. Ma and C.-X. Wu, Phys. Rev. E, 2022, 106, 044411 CrossRef CAS PubMed.
- P. Sharan, Z. Xiao, V. Mancuso, W. E. Uspal and J. Simmchen, ACS Nano, 2022, 16, 4599–4608 CrossRef CAS PubMed.
- P. Sharan, A. Daddi-Moussa-Ider, J. Agudo-Canalejo, R. Golestanian and J. Simmchen, Small, 2023, 19, 2300817 CrossRef CAS PubMed.
- E. Lauga, The Fluid Dynamics of Cell Motility, Cambridge University Press, 2020 Search PubMed.
- S. Ketzetzi, J. D. Graaf and D. J. Kraft, Phys. Rev. Lett., 2020, 125, 238001 CrossRef CAS PubMed.
- E. R. Block, J. Cell. Physiol., 1991, 146, 362–369 CrossRef CAS PubMed.
- G. Valen, A. Sondén, J. Vaage, E. Malm and B. Kjellström, Free Radicals Biol. Med., 1999, 26, 1480–1488 CrossRef CAS PubMed.
- J. Dai, H. P. Ting-Beall and M. P. Sheetz, J. Gen. Physiol., 1997, 110, 1–10 CrossRef CAS PubMed.
- B. Pontes, P. Monzo and N. C. Gauthier, Semin. Cell Dev. Biol., 2017, 71, 30–41 CrossRef CAS.
- A. Meinel, B. Tränkle, W. Römer and A. Rohrbach, Soft Matter, 2014, 10, 3667–3678 RSC.
- H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 198102 CrossRef CAS PubMed.
- F. Fessler, V. Sharma, P. Muller and A. Stocco, Phys. Rev. E, 2023, 107, L052601 CrossRef CAS PubMed.
- S. Das, A. Garg, A. I. Campbell, J. Howse, A. Sen, D. Velegol, R. Golestanian and S. J. Ebbens, Nat. Commun., 2015, 6, 8999 CrossRef CAS PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411 RSC.
- V. Sharma, F. Fessler, F. Thalmann, C. M. Marques and A. Stocco, J. Colloid Interface Sci., 2023, 652, 2159–2166 CrossRef CAS PubMed.
- J. O. Rädler, T. J. Feder, H. H. Strey and E. Sackmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4526–4536 CrossRef PubMed.
- I. Cantat, K. Kassner and C. Misbah, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 10, 175–189 CrossRef CAS PubMed.
- A. L. Bernard, M. A. Guedeau-Boudeville, L. Jullien and J. M. D. Meglio, Langmuir, 2000, 16, 6809–6820 CrossRef CAS.
- H. T. Spanke, J. Agudo-Canalejo, D. Tran, R. W. Style and E. R. Dufresne, Phys. Rev. Res., 2022, 4, 023080 CrossRef CAS.
- R. Lipowsky and U. Seifertt, Langmuir, 1991, 7, 1867–1873 CrossRef CAS.
- T. Gruhn, T. Franke, R. Dimova and R. Lipowsky, Langmuir, 2007, 23, 5423–5429 CrossRef CAS PubMed.
- J. Steinkühler, J. Agudo-Canalejo, R. Lipowsky and R. Dimova, Biophys. J., 2016, 111, 1454–1464 CrossRef PubMed.
- T. H. Anderson, Y. Min, K. L. Weirich, H. Zeng, D. Fygenson and J. N. Israelachvili, Langmuir, 2009, 25, 6997–7005 CrossRef CAS PubMed.
- B. Klasczyk, V. Knecht, R. Lipowsky and R. Dimova, Langmuir, 2010, 26, 18951–18958 CrossRef CAS PubMed.
- X. Jiang, J. Zhang, B. Zhou, P. Li, X. Hu, Z. Zhu, Y. Tan, C. Chang, J. Lü and B. Song, Sci. Rep., 2018, 8, 14093 CrossRef PubMed.
- M. F. Poyton, A. M. Sendecki, X. Cong and P. S. Cremer, J. Am. Chem. Soc., 2016, 138, 1584–1590 CrossRef CAS PubMed.
- K. Xiao, R. Ma and C.-X. Wu, Phys. Rev. E, 2022, 106, 044411 CrossRef CAS PubMed.
- M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef PubMed.
- A. H. Bahrami, M. Raatz, J. Agudo-Canalejo, R. Michel, E. M. Curtis, C. K. Hall, M. Gradzielski, R. Lipowsky and T. R. Weikl, Adv. Colloid Interface Sci., 2014, 208, 214–224 CrossRef CAS PubMed.
- H. A. Faizi, A. Tsui, R. Dimova and P. M. Vlahovska, Langmuir, 2022, 38, 10548–10557 CrossRef CAS PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- A. T. Brown, I. D. Vladescu, A. Dawson, T. Vissers, J. Schwarz-Linek, J. S. Lintuvuori and W. C. K. Poon, Soft Matter, 2016, 12, 131 RSC.
- H. G. Döbereiner, O. Selchow and R. Lipowsky, Eur. Biophys. J., 1999, 28, 174–178 CrossRef.
- M. Deserno and T. Bickel, Europhys. Lett., 2003, 62, 767 CrossRef CAS.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS PubMed.
- Q. Yu, S. Othman, S. Dasgupta, T. Auth and G. Gompper, Nanoscale, 2018, 10, 6445–6458 RSC.
- J. Agudo-Canalejo, Soft Matter, 2021, 17, 298–307 RSC.
- Q. Yu, S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2020, 20, 1662–1668 CrossRef CAS PubMed.
- A. Weinberger, F. C. Tsai, G. H. Koenderink, T. F. Schmidt, R. Itri, W. Meier, T. Schmatko, A. Schröder and C. Marques, Biophys. J., 2013, 105, 154–164 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00337c |
| This journal is © The Royal Society of Chemistry 2024 |