Open Access Article
Open Access ArticleFoam coarsening in a yield stress fluid†
Alice
Requier
 *a,
Chiara
Guidolin‡
*a,
Chiara
Guidolin‡
 a,
Emmanuelle
Rio
a,
Emmanuelle
Rio
 a,
Nicolò
Galvani
a,
Nicolò
Galvani
 bc,
Sylvie
Cohen-Addad
bc,
Sylvie
Cohen-Addad
 bd,
Olivier
Pitois
bd,
Olivier
Pitois
 c and
Anniina
Salonen
c and
Anniina
Salonen
 *a
*a
aUniversité Paris-Saclay, CNRS, Laboratoire de Physique des Solides, 91405 Orsay, France. E-mail: anniina.salonen@universite-paris-saclay.fr
bSorbonne Université, CNRS-UMR 7588, Institut des NanoSciences de Paris, 4 Place Jussieu, 75005 Paris, France
cUniversité Gustave Eiffel, ENPC, CNRS, Laboratoire Navier, 5 Bd Descartes, Champs-sur-Marne, F-77454 Marne-la-Vallée Cedex 2, France
dUniversité Gustave Eiffel, 5 Bd Descartes, Champs-sur-Marne, F-77454 Marne-la-Vallée Cedex 2, France
First published on 13th July 2024
Abstract
Foams coarsen because of pressure differences between bubbles of different sizes. We study the coarsening of quasi-2D foams made from model yield stress fluids: concentrated oil-in-water emulsions. We show that increasing the yield stress of the foamed emulsion continuous phase leads to both slower coarsening and irreversible structural change. The impact of the continuous phase rheology is stronger when the foamed emulsion is wetter or more confined. The bubble growth and organisation both become highly heterogeneous with an excess of small bubbles. We present a model that rationalises the impact of these three parameters by taking into account a resisting pressure required to displace the yield stress fluid around the bubbles.
1 Introduction
Liquid foams are dense dispersions of gas bubbles within a continuous liquid phase. Their structure and stability mainly depend on bubble size and liquid volume fraction ε = Vliq/Vfoam (with Vliq the volume of liquid contained in a foam volume Vfoam). Depending on the foam liquid fraction, bubbles can either be spherical, moving freely in the liquid medium, or polyhedral and in contact. In the latter configuration, bubbles are compressed together and separated by thin liquid films, connected three by three through liquid channels called Plateau borders. Surfactants, which adsorb at the gas–liquid interfaces, are required to produce a stable foam. Yet liquid foams are still fragile materials that irreversibly evolve in time. Three possibly entangled mechanisms alter their structure and eventually lead to foam destabilisation: gravitational liquid drainage, bubble coalescence and foam coarsening.1 Pioneering foam ageing experiments performed with dry horizontal quasi-2D foams (single monolayers of confined bubbles) showed that this configuration allows neglecting gravitational drainage during the foam evolution.2 Moreover, the rupture of the liquid films between bubbles, causing bubble coalescence, can be minimised using a surfactant that generates stable films.1 This means that working in the quasi-2D geometry allows to specifically study foam coarsening.Foam coarsening is a process driven by Laplace pressure differences between bubbles of different sizes, that cause gas transfer from smaller to larger bubbles. This mechanism leads to a decrease in the number of bubbles with time along with growth of the average bubble size. Coarsening bubble dispersions eventually reach a scaling state where the bubble growth becomes statistically self-similar. All dimensionless geometrical and topological distributions become time invariant, and the average bubble size 〈R〉 grows in time as a power law 〈R〉 ∼ tα, where α depends on the mechanism of gas transfer between bubbles. For dry foams, i.e., with small liquid fraction, gas diffusion through liquid films dominates and theory predicts that the mean bubble size evolves with time as 〈R〉 ∼ t1/2.3–5 This prediction is experimentally verified for the limiting case of a very dry foam ε ∼ 1%.6,7 This coarsening law is also derived in a 2D configuration8 and measured in quasi-2D foams.9,10
Liquid foams exhibit unusual mechanical properties based on their typical cellular structure and the rearrangement dynamics of the bubbles.11–15 Combined with their lightness and high interfacial area, this makes them interesting for many personal and industrial applications, including cosmetics, oil recovery, pharmaceutics and food industry. In many of these applications, the foam continuous phase is a complex fluid with non-Newtonian rheology.16 These materials may exhibit a threshold in applied stress, called the yield stress, below which they behave like solids, and above which they flow. Foaming such fluids can be beneficial as they can improve foam stability and change their rheology.17,18 A yield stress fluid can prevent entrapped bubbles from rising,19,20 or stop coarsening.21 Moreover, most solid foams are made from fluid precursors, which are subsequently solidified, hence the continuous phase passes through a variety of stages of rheological behaviour. Bubbles in materials result in lighter foams and better insulating properties,22 but their presence can also be detrimental, as trapped bubbles may negatively affect material physical properties.23
Emulsions are good candidates of non-Newtonian fluids to foam. Different types of foamed emulsions exist, depending on the continuous phase surrounding the bubbles: the latter can be either a water-in-oil emulsion, an oil-in-water emulsion or even a bi-continuous oil and water phase.24 Dispersions of bubbles in mixtures of oil and water, stabilised by particles rather than surfactants, are also widely studied.25,26 In particular, highly concentrated oil-in-water emulsions are a good example of yield stress fluids. Previous studies have shown that swapping a foam aqueous phase for an emulsion dramatically changes its behaviour and properties,27,28 and in particular the emulsion yield stress can be high enough to stop foam gravitational drainage, making very stable foams.29 The coarsening of single bubbles is also expected to slow down or stop in complex fluids.30,31 The study of bubbles suspensions in silicone oil-in-water emulsions also showed that their rheological behaviour depends on the stress applied to the sample: the coupling between bubble deformation and bulk rheology is different whether the emulsion yields or not.32 All this work suggests that the ageing undergone by the trapped bubbles may be impacted by the rheology of the foam continuous phase.
In this paper, we study coarsening of quasi-2D foamed emulsions. The continuous phase is a concentrated oil-in-water emulsion, which is a model yield stress fluid. We have recently shown that foams made from emulsions with high oil volume fractions ϕ coarsen more slowly and evolve into highly heterogeneous structures.28 In this work we explore the effect of varying the foamed emulsion liquid fraction ε and the confining gap d on its ageing and we rationalise the impact of ϕ, ε and d on the foamed emulsion structure and evolution. To do so, we follow the evolution of the average bubble radius and the bubble size distributions with time.
2 Materials and methods
2.1 Emulsion generation
Concentrated oil-in-water emulsions with varying oil volume fractions are prepared by mixing the freshly-made aqueous phase, composed of sodium dodecyl sulfate (SDS, Sigma Aldrich) at 30 g L−1, and deionised water (Purelab, resistivity 18.2 MΩ cm), with oil (rapeseed oil from Brassica Rapa or sunflower oil from Helianthus Annuus, Sigma Aldrich) with the double-syringe method.33 Syringes in polypropylen with a 60 mL volume (Codan, VWR) are connected with a double Luer Lock junction (VWR) and the emulsion is generated by pushing the aqueous and the oil phase back and forth through the connector thirty times at constant velocity. The oil fraction ϕ = Voil/Vcp (with Voil the volume of oil dispersed in the emulsion volume Vcp) ranges between 70% and 85%.2.2 Emulsion characterisation
The size and polydispersity of the emulsion drops are measured using laser diffraction granulometry with a Mastersizer 3000E (Malvern Panalytical) equipped with a Hydro SM wet dispersion unit. The surface-weighted mean drop diameter decreases slightly from 5 to 2 μm with increasing ϕ up to 85%.The rheological properties of the emulsions are measured with a rheometer (MCR 302, Anton Paar) using a cylindrical Couette geometry (CC27, Anton Paar). The surface of the measuring tool has been sand-blasted to ensure a no-slip condition for the measurement. Oscillatory strain sweep tests are performed increasing the strain amplitude from 10−3% to 102% at a constant frequency of 1 Hz. The gap width is equal to 1.1 mm and the temperature is set to (20.5 ± 0.5) °C. The storage and loss moduli, G′ and G′′ are determined in the limit of small strain amplitude. The stress versus strain amplitude curves also give access to the emulsion yield stress τy by determining the cross-over between the linear regime at low strain and the non-linear regime at high strain. The emulsion storage modulus varies from 114 to 506 Pa and the yield stress from 1 to 23 Pa as ϕ increases from 70% to 85%. We note that the average droplet size also varies as ϕ changes. The ϕ-dependence of G′, G′′, and τy is shown in Fig. 1. The storage modulus and yield stress follow the classical scalings  34 and
34 and  ,35 which are shown in Fig. S1 in ESI.†Fig. 1 (circles) show that the rheological parameters of emulsions made with sunflower oil are similar to the ones of emulsions made with rapeseed oil (squares).
,35 which are shown in Fig. S1 in ESI.†Fig. 1 (circles) show that the rheological parameters of emulsions made with sunflower oil are similar to the ones of emulsions made with rapeseed oil (squares).
2.3 Foam generation
The emulsion is foamed using a planetary kitchen mixer (Kenwood KMIX750AW, 1000 W). The double rotation of the whisk slowly entraps air pockets in the continuous phase.36 The final liquid (emulsion) fraction ε can be controlled by adjusting the mixing protocol: gradually increasing the mixing speed up to the maximum level along with a long mixing time (around 35 minutes) leads to foams at ε ≃ 9%, whereas mixing for less time at low speed leads to wetter ones. The liquid fraction is measured by weight immediately after foam generation and ranges between 9% and 25%. The different samples studied are listed in Table 1. Experiments where we vary the liquid fraction are made with sunflower oil. The oil drop size distribution is measured after foaming and after the end of the coarsening experiments.28 It is unchanged from the original distribution, therefore the emulsion is stable throughout the foam generation and ageing process.| ϕ [%] | ε [%] | d [mm] | t 0 [h] | 〈R0〉 [mm] | μ R 3,0 × 10−2 |
|---|---|---|---|---|---|
| 0 | 10 | 1 | 2.3 | 0.89 | 4.8 |
| 70 | 10 | 1 | 3.0 | 0.89 | 2.6 |
| 75 | 10 | 1 | 3.2 | 0.88 | 3.2 |
| 80 | 10 | 1 | 3.6 | 0.98 | 3.2 |
| 85 | 10 | 1 | 5.1 | 0.82 | 3.1 |
| 70 | 9 | 1 | 2.6 | 0.89 | 7.8 |
| 70 | 13 | 1 | 3.8 | 0.84 | 3.6 |
| 70 | 20 | 1 | 5.3 | 0.85 | 2.4 |
| 70 | 25 | 1 | 6.9 | 0.85 | 3.9 |
| 75 | 25 | 1 | 7.6 | 0.87 | 0.5 |
| 80 | 25 | 1 | 7.7 | 0.91 | 0.9 |
| 80 | 10 | 1 | 3.2 | 1.07 | 5.7 |
| 80 | 10 | 2 | 8.0 | 1.52 | 2.9 |
| 80 | 10 | 3 | 15.8 | 2.20 | 2.4 |
2.4 Foam coarsening experiments
Once the foamed emulsion is prepared, it is squeezed between two transparent horizontal glass plates. The plates are square with 24 cm sides, and they are separated by a rubber seal of thickness d. We measure the resulting gap between the plates, and find that it corresponds to d within 10% uncertainty. Most of the experiments are done with d = 1 mm, however the impact of d has been tested using d = 2 or 3 mm. The plates are fixed between two duralumin frames. The cell is illuminated from above by a square of LED lights and placed under a high-resolution camera (Basler acA3800 – 14 um, 3840 × 2748 pixels) equipped with a lens (Fujinon 16 mm f/1.4).We let the foam coarsen and we follow its evolution over time by recording a photograph every 3 or 5 minutes at the early stages and every 30 minutes or one hour at later stages. At very early times, the foam exhibits a 3D structure and multi-layers of small bubbles can be observed in the cell. After a certain time, that we call t0, as the foam coarsens most of the bubbles in the foam become larger than the gap d and we have a monolayer of bubbles. The average bubble radii 〈R0〉 = 〈R(t = t0)〉 and times t0 are summarised in Table 1 for the different samples. We can note that 〈R0〉 are slightly smaller than the gap size, indicating that the bubble diameters are almost twice the gap width. This ensures that in the polydisperse bubble size distribution most of the bubbles are indeed quasi-2D. All of the presented results refer to the regime t ≥ t0.
In addition, to test whether the mechanical boundary condition has an effect on the coarsening dynamics in our confined geometry, we carried out an experiment where the glass plates have been previously roughened with glass beads, leading to a roughness depth around 30 μm. For this test, we use a foamed emulsion with ϕ = 70% and ε = 13%, confined within a gap d = 1 mm.
2.5 Image analysis
Custom Matlab scripts are used to analyse the photographs. A first pre-treatment, in which the raw pictures are cropped and contrast-adjusted, is necessary to get a proper image segmentation. The foam skeleton is then obtained from the segmented pictures through a watershed algorithm. The latter is detected to be in the middle of the foam Plateau borders, no matter their thickness. The area A of each polygonal bubble is then retrieved using the built-in function regionprops. The bubble equivalent radius is then calculated as .
.
3 Results and discussion
We have studied the effects of changing the emulsion oil fraction ϕ, the foam liquid fraction ε and the gap between the glass plates d on the different features of the foam.3.1 Foam evolution during coarsening
Photographs of an aqueous foam and three foamed emulsions, together with the corresponding bubble size distributions, are shown in Fig. 2 for different foam ages. The times chosen are t0, the time at which the foam structure becomes 2D, t0 + 72 h and tf, the time of the last recorded photograph. We chose t0 + 72 h as the foams have evolved, but this instant does not coincide with the end of the measurement for any of the foams. | ||
| Fig. 2 Photographs of foams at three different times and the corresponding bubble size distributions for an aqueous foam (a)–(d) and foamed emulsions (e)–(p). Top line (a)–(c) shows photographs of a dry SDS foam with ε = 10% liquid. Second line (e)–(g) corresponds to a dry foamed emulsion: ε = 10% and ϕ = 70%. Third line (i)–(k) is a dry foamed emulsion (ε = 10%) with a more viscoelastic continuous phase (ϕ = 80%). Bottom row (m)–(o) corresponds to a wet foamed emulsion with ε = 20% and ϕ = 70%. For each foam, time increases in the photographs from left to right: t0 the time at which the foam structure becomes quasi-2D, three days later and tf the time of the last recorded photograph. The values of t0 are given in Table 1. The instants tf are shown on photographs (c), (g), (k) and (o). Edge of the photographs is 70 mm. The last column on the right shows the bubble size distributions, represented as a function of the normalised radius R/〈R〉, corresponding to each sample: the pale grey is at t0, dark grey at t0 + 72 h and black at tf. | ||
The top row (a–c) shows the temporal evolution of a dry aqueous foam made from an SDS solution and with a liquid fraction of ε = 10%. We see that in time, the bubble size increases and the number of bubbles decreases. We observe the typical cellular structure of a 2D dry aqueous foam. This means polygonal bubbles packed together with a characteristic local equilibrium structure. The bubble size distributions, represented as a function of the normalised radius R/〈R〉, are shown in Fig. 2d. They are invariant in time, as it has been observed in quasi-2D foams with similar liquid fractions.37
The second row (e–g) shows the structural evolution of a dry foamed emulsion (ε = 10% and ϕ = 70%). As for the aqueous foam, the bubble size increases with time while the number of bubbles decreases. If we compare the foamed emulsion structure to the one of the aqueous foam, the photographs look alike. However, a closer look reveals some tiny bubbles and a hint of heterogeneity in the Plateau border thicknesses in the foamed emulsion (g) that we do not see in the aqueous foam (c). The bubble size distribution (h) at tf is also a bit different, as it has become slightly triangular with a peak that has shifted towards the left compared to the initial distribution.
Photographs of the third row (i–k) show the evolution of a dry foamed emulsion (ε = 10%) with a higher oil fraction in the continuous phase (ϕ = 80%) and thus with a higher yield stress and elastic modulus (cf.Fig. 1). This time the foamed emulsion structure at t0 (i) looks different compared to the one at ϕ = 70% (e), even though the bubble size distributions (pale grey, h and l) are similar. We start to see hints of the impact of the oil with the apparition of peculiar features, such as elongated bubble shapes. The effect of high ϕ is clearly visible when it comes to t = t0 + 72 h (photograph j). Not only are the bubbles smaller than in the other foams but the bubble organisation is also very different between f and j. Indeed for ϕ = 80% a structural heterogeneity becomes visible with two populations of bubbles: big ones, separated by very thin Plateau borders, and localised areas of very small bubbles surrounded by much more liquid. This suggests that the liquid is not distributed within the foam during coarsening. Finally, the photograph at tf (k) shows a foamed emulsion that is very similar to photograph (j) even though separated in time by a hundred hours. The coarsening process is significantly slowed down, and specifically the small bubbles seem to linger. This excess of small bubbles within the foam becomes visible in the bubble size distributions in (l). The distributions become increasingly asymmetric and the peak shifts left with time, meaning it is shifted towards smaller bubbles.
Finally, the bottom row shows the impact of increasing liquid fraction on the evolution of a foam with ϕ = 70% (m–o). A higher liquid fraction (ε = 20%) results in slower coarsening, and the bubbles are much smaller at t0 + 72 h (n) when compared to the sample at ϕ = 70% and ε = 10% (f). Although tf is much larger at 1548 h in (o) versus 385 h in (g), the final bubble sizes are much smaller. In this last sample we can also notice the accumulation of small bubbles which is confirmed by the shape of the bubble size distributions at long times in (p).
We observe the slowing down of coarsening, and changes in the foam structure with increased oil volume fraction. A higher foam liquid fraction amplifies the impact of the emulsion.
3.2 Temporal evolution of bubble size and skewness
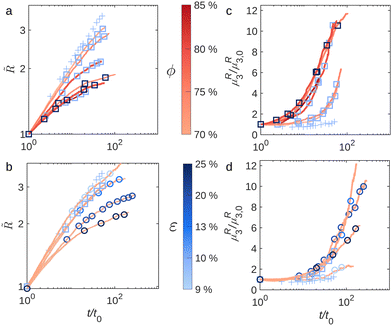
In order to quantify the temporal evolution of the foams, we measure the average bubble size 〈R〉. Fig. 3a and b show the evolution of the normalised average bubble radius![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = 〈R〉/〈R0〉, where 〈R0〉 = 〈R(t0)〉, as a function of normalised time t/t0. Fig. 3a shows the effect of varying the oil fraction ϕ at constant liquid fraction (ε = 10%). The pale blue crosses represent the evolution of
= 〈R〉/〈R0〉, where 〈R0〉 = 〈R(t0)〉, as a function of normalised time t/t0. Fig. 3a shows the effect of varying the oil fraction ϕ at constant liquid fraction (ε = 10%). The pale blue crosses represent the evolution of ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) with the normalised time for an aqueous SDS foam with ε = 10%. The average radius of the aqueous foam evolves with something resembling a power law, with an exponent close to 1/3, which starts to flatten out at longer times. This is in contrast to dry aqueous foams in 2D or 3D, which should evolve as
with the normalised time for an aqueous SDS foam with ε = 10%. The average radius of the aqueous foam evolves with something resembling a power law, with an exponent close to 1/3, which starts to flatten out at longer times. This is in contrast to dry aqueous foams in 2D or 3D, which should evolve as ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ∼ t1/2.7,38 Indeed we do not expect a power-law coarsening due to the quasi-2D geometry of the foam. As the bubble size increases, the Plateau borders thicken.39 The increase in the Plateau borders radius rPB results in a decrease of the height of the contact film between bubbles h = d − 2rPB (d being the gap between the plates). The induced reduction in thin film area leads to a border-blocking effect which slows down gas transfer, thus resulting in a lower coarsening rate.37 Therefore, the growth of an even moderately wet quasi-2D aqueous foam does not follow the 1/2 power law.40,41
∼ t1/2.7,38 Indeed we do not expect a power-law coarsening due to the quasi-2D geometry of the foam. As the bubble size increases, the Plateau borders thicken.39 The increase in the Plateau borders radius rPB results in a decrease of the height of the contact film between bubbles h = d − 2rPB (d being the gap between the plates). The induced reduction in thin film area leads to a border-blocking effect which slows down gas transfer, thus resulting in a lower coarsening rate.37 Therefore, the growth of an even moderately wet quasi-2D aqueous foam does not follow the 1/2 power law.40,41
We now have a look at the bubble size evolution in foamed emulsions with increasing oil volume fraction ϕ, shown in Fig. 3a. We can see the effect of varying the elastic modulus G′ and the yield stress τy of the continuous phase since both are increasing functions of ϕ (cf.Fig. 1). We notice that as ϕ increases the bubble growth becomes weaker and the growth rate at early times decreases. The higher ϕ, the earlier ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) starts to flatten. This suggests that the presence of emulsion strongly affects the bubble growth and significantly slows down the coarsening process.
starts to flatten. This suggests that the presence of emulsion strongly affects the bubble growth and significantly slows down the coarsening process.
For its part, Fig. 3b shows the effect of varying the foam liquid fraction ε keeping the oil fraction constant (at ϕ = 70%). The pale blue crosses still represent ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) (t/t0) for the aqueous SDS foam with ε = 10%. We saw that the presence of oil in the foam continuous phase contributes to slow down the coarsening process and Fig. 3b shows that increasing ε amplifies this effect. This is confirmed by the decrease of the growth rate and the flattening of
(t/t0) for the aqueous SDS foam with ε = 10%. We saw that the presence of oil in the foam continuous phase contributes to slow down the coarsening process and Fig. 3b shows that increasing ε amplifies this effect. This is confirmed by the decrease of the growth rate and the flattening of ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) at an earlier time with increasing ε: a wetter foamed emulsion coarsens significantly more slowly, consistent with what is shown in the photographs in Fig. 2f and n.
at an earlier time with increasing ε: a wetter foamed emulsion coarsens significantly more slowly, consistent with what is shown in the photographs in Fig. 2f and n.
We saw in Fig. 2(d), (h), (l) and (p) that in contrast to aqueous foams, the normalised bubble size distributions for the foamed emulsions vary in time. They become highly asymmetrical and develop a peak at small R/〈R〉, reflecting an excess of small bubbles within the foam. A recent study of 3D aqueous foam coarsening revealed an excess of small bubbles roaming in the interstices between bigger jammed bubbles within the foam in the scaling state.42 However here the observed excess of small bubbles has a different origin since it results from their shrinkage slowdown due to a thick layer of emulsion surrounding them. There are different ways to quantify the change in the distributions shape along the coarsening. A first method based on the shift of the distribution peak is described in ESI.† Here, we quantify this change using the bubble size distribution third moment  , which is sensitive to its asymmetry. For an aqueous foam in the scaling state, μR3 is constant in time and its value depends on the liquid fraction of the foam.43 By contrast, in the foamed emulsions μR3 starts off constant, but deviates at a certain time, as seen in Fig. 3c and d, where the normalised third moment μR3/μR3,0 (with μR3,0 = μR3(t0)) is shown as a function of t/t0. The two methods give comparable results as seen in Fig. S2 and S5 of ESI† and we choose to continue with μR3(t).
, which is sensitive to its asymmetry. For an aqueous foam in the scaling state, μR3 is constant in time and its value depends on the liquid fraction of the foam.43 By contrast, in the foamed emulsions μR3 starts off constant, but deviates at a certain time, as seen in Fig. 3c and d, where the normalised third moment μR3/μR3,0 (with μR3,0 = μR3(t0)) is shown as a function of t/t0. The two methods give comparable results as seen in Fig. S2 and S5 of ESI† and we choose to continue with μR3(t).
We plot the normalised third moment μR3/μR3,0 as a function of t/t0 for samples with varying oil fraction at ε = 10% and ε = 25% (Fig. 3c) and for samples with a fixed oil fraction ϕ = 70% and varying liquid fraction (Fig. 3d). The pale blue crosses in both graphs still represent the evolution of normalised μR3 with normalised time for an aqueous SDS foam with ε = 10%. Values of μR3,0 for the different experiments are given in Table 1. We observe that the third moment of foamed emulsion systematically departs from its initial plateau after a certain time, which depends on the sample. The steep increase of μR3 is evidence that these foamed emulsions are not evolving towards a self-similar regime. The shift of the bubble size distribution peak due to the accumulation of the small bubbles, observed for these samples in Fig. 2(h), (l) and (p) is responsible for the significant rise of the third moment μR3.
3.3 Evolution of μR3(R)
We saw that in all the foamed emulsions μR3 departed from its constant value during the coarsening process. The average bubble size sets the average Laplace pressure difference between the bubbles, and hence the coarsening rate. For this reason, we plot now the evolution of μR3, not as a function of t, but as a function of 〈R〉.By plotting the normalised μR3/μR3,0 as a function of the average bubble radius 〈R〉 (cf.Fig. 4), we can also observe its departure from an initial plateau for all foamed emulsions. The higher ϕ and the higher ε, the smaller the average bubble size at which the skew deviates. For example, for a foamed emulsion with ϕ = 70% and ε = 10%, μR3/μR3,0 deviates at a radius around 2 mm. If the foamed emulsion is wetter (ϕ = 70% and ε = 20%), it deviates at around 1.4 mm. Finally, for a continuous phase with a higher yield stress and elastic modulus (ϕ = 80% and ε = 10%), the radius at which we observe the deviation of μR3/μR3,0 is close to 1 mm. We define an experimental critical radius as the average radius at which μR3/μR3,0 has increased by 50% from its plateau (corresponding to μR3/μR3,0 = 1) and call it Rsk. Therefore, Rsk is, by construction, a relative parameter which enables us to identify the characteristic average radius at which the foamed emulsion behaviour has deviated from the one of aqueous foam.
 | ||
| Fig. 4 Normalised third moment of the bubble radius distributions μR3/μR3,0 (μR3,0 = μR3(t0)) plotted as a function of the average bubble size 〈R〉. The evolution is shown for all the samples in Fig. 3 with the same symbols. The solid grey line shows the initial average plateau at early times. The dashed grey line indicates 150% of this value; Rsk is found by the intersection between the curves and the dashed line. | ||
The values of Rsk for all samples studied are plotted in Fig. 5. Fig. 5a shows the evolution of Rsk as a function of the emulsion oil fraction ϕ and Fig. 5b represents Rskvs. the foam liquid fraction ε. Note that an uncertainty is given for each value of Rsk, coming from Fig. 4 taking 120% and 180% of the initial plateau instead of 150%. It is worth noticing that a difference of about 15% can be found in the value of Rsk for the same experiment repeated twice. We find that Rsk systematically decreases with increasing ϕ (and so with increasing G′ and τy, see Fig. 1a and b) and ε. This means that the accumulation of small bubbles within the sample, as well as the foam structure change, happen at smaller average radii as the yield stress of the emulsion gets higher (increasing ϕ) or the amount of the yield stress fluid in the foam increases (increasing ε). The impact of foam confinement on the evolution of μR3/μR3,0 with 〈R〉 is also studied using d = 2 and d = 3 mm. Increasing the gap between the plates results in an increase of Rsk: the larger the confining gap, the larger the average radius at which small bubbles accumulate. Results are shown in Fig. S3 and S5 of ESI.†
3.4 Impact of emulsion on local foam structure
We can summarise the impact of the continuous fluid on the evolution of the foamed emulsions as follows: (1) the growth of the average bubble radius slows down compared to aqueous foams, (2) the shrinkage of smaller bubbles slows down, making them accumulate, and leading to a visible impact on the bubble size distribution once 〈R〉 ∼ Rsk and (3) the foamed emulsion structure exhibits unusual bubble patterns at high ϕ.Let us have a closer look to what happens to the foamed emulsion at early times and describe qualitatively how it evolves. The foam is very polydisperse as we make it, so smaller and larger bubbles coexist (see left column in Fig. 2). As part of the coarsening process smaller bubbles transfer their gas to larger ones, shrink and eventually disappear. Fig. 6 shows photographs of an aqueous foam (ε = 10%, top row) and a foamed emulsion (ϕ = 80%, ε = 10%, bottom row) during the coarsening process. We observe in photographs c–f a global increase of the bubble size with time and the disappearance of smaller bubbles. However, we want to concentrate on the local organisation of the bubbles during the coarsening. In the aqueous foam, when a bubble disappears the liquid is redistributed and the bubbles rearrange to return to the equilibrium foam structure (see Fig. 6c and e, white dashed circle).1 By contrast, in the foamed emulsion when small bubbles disappear they leave behind the emulsion that surrounded them and the bubbles do not reorganise (see Fig. 6d and f, white dashed circle, where bubbles are replaced by white patches of emulsion). Thus, as the small bubbles disappear, a progressive thickening of the emulsion layers is observed in localised areas of the foamed emulsion. Bubbles that have not already disappeared are then surrounded by more emulsion, and at a certain point the foam structure becomes highly heterogeneous. This structural heterogeneity is visible in Fig. 6f, where two populations of bubbles coexist: big ones, separated by very thin Plateau borders (Fig. 6f yellow arrow 1), and localised areas of very small bubbles surrounded by more liquid (Fig. 6f yellow arrow 2). This is in contrast to the aqueous foam, in which the Plateau borders have very similar thicknesses (Fig. 6e). This heterogeneity in the foam structure is associated with heterogeneous foam growth. Indeed, the shrinkage of smaller bubbles is significantly slowed down by the stiffness of the thick zones of emulsion they are embedded in, while the bigger bubbles keep coarsening. Fig. 6d and f (white solid circle) show an example of two bubbles slowly shrinking for about a hundred hours. The coarsening process is hindered by the rheology of the emulsion that is not redistributed. In the following part, we build a model to formalise these experimental observations.
 | ||
| Fig. 6 Photographs of an aqueous foam (top row) (ε = 10%) and foamed emulsion (bottom row) (ϕ = 80%, ε = 10%) during the coarsening process. Left column (a) and (b) shows pictures taken at t = t0 + 72 h, with t0 the time at which the foam structure becomes 2D (see Table 1). Edge is 70 mm. Middle column (c) and (d) shows zoomed photographs of (a) and (b). Zoomed photographs taken at the final time of the experiment tf are shown in right column (e) and (f). Edge of zoomed photographs is 29 mm. White dashed circles in (c)–(f) point out bubbles disappearing during the coarsening in an aqueous foam (c) and (e) and in a foamed emulsion (d) and (f). White solid circles in (d) and (f) show bubbles shrinking extremely slowly. Finally yellow arrows in photograph (f) show the heterogeneity in the Plateau border thickness in a foamed emulsion: 1 points out a very thin Plateau border separating two big bubbles and 2 a cluster of tiny bubbles surrounded by much more liquid. | ||
3.5 Model for hindered foam coarsening
We propose a simplified model for foamed emulsion coarsening to extract a critical radius at which the emulsion rheology hinders the foam coarsening process, and compare it with the experimental one Rsk.First, to describe why the small bubbles dissolve so slowly into the larger bubbles, we consider the Laplace pressure difference between small bubbles and big ones, that is the driving force of the gas transfer:44
 | (1) |
We model the regions of foam with high liquid fraction as consisting of bubbles surrounded by an elastic shell composed of emulsion with yield stress τy. We consider that an extra pressure ΔPy is then required for a bubble to change size (grow or shrink) and to make the shell made of emulsion flow. We assume that the shell is a ring with width ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) that has uniform mechanical properties. To induce the flow of the shell between the two plates, the stress at the plate (where it reaches its maximum value in the gap) must be larger than the yield stress. Thus the extra pressure can be obtained from the force balance (at yield) by assuming no-slip condition at walls:
that has uniform mechanical properties. To induce the flow of the shell between the two plates, the stress at the plate (where it reaches its maximum value in the gap) must be larger than the yield stress. Thus the extra pressure can be obtained from the force balance (at yield) by assuming no-slip condition at walls:
2πRdΔPy ≈ 2 × (2πR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )τy, )τy, | (2) |
 | (3) |
With such an excess stress, the pressure difference for gas transfer from smaller to larger bubble becomes:
| ΔP = ΔPL − ΔPy. | (4) |
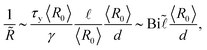 | (5) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = 〈R〉/〈R0〉,
= 〈R〉/〈R0〉, 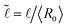 and Bi = τy〈R0〉/γ is the Bingham capillary number.
and Bi = τy〈R0〉/γ is the Bingham capillary number.
We expect the width ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to increase with the number of bubbles that have disappeared around the bubble. Let us consider now how
to increase with the number of bubbles that have disappeared around the bubble. Let us consider now how  varies with
varies with ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) : at time t0 the average bubble radius is 〈R0〉 and the total number of bubbles in the sample is n0. At time t > t0, 〈R〉 > 〈R0〉 and the total number of bubbles in the foam is n. As the gas volume fraction is constant, and neglecting structural changes to the foam, the surface area covered by those bubbles is constant, so we get:
: at time t0 the average bubble radius is 〈R0〉 and the total number of bubbles in the sample is n0. At time t > t0, 〈R〉 > 〈R0〉 and the total number of bubbles in the foam is n. As the gas volume fraction is constant, and neglecting structural changes to the foam, the surface area covered by those bubbles is constant, so we get:
 | (6) |
 | (7) |
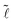 :
: | (8) |
 in eqn (5) gives:
in eqn (5) gives: | (9) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ys = Rys/〈R0〉 at which coarsening is stopped by emulsion rheology:
ys = Rys/〈R0〉 at which coarsening is stopped by emulsion rheology: | (10) |
So we have a scaling for the average radius at which the coarsening process should be stopped by the yield-stress fluid composing the foam continuous phase. We now compare this predicted critical radius to the experimental ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) sk = Rsk/〈R0〉 obtained in Section 3.3, at which coarsening has not stopped but is certainly influenced by the yield stress fluid. Therefore, we expect the predicted radius Rys to be larger than Rsk.
sk = Rsk/〈R0〉 obtained in Section 3.3, at which coarsening has not stopped but is certainly influenced by the yield stress fluid. Therefore, we expect the predicted radius Rys to be larger than Rsk.
The comparison between ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) sk and
sk and ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ys is shown in Fig. 7. We observe a linear relation between the two radii, meaning that our model captures the impact of continuous phase rheology, liquid fraction and confinement (cf. Fig. S5 in ESI†). We note that the scaling overestimates the datapoints with ϕ = 70% and underestimates the ones for ϕ > 70%. We expect this to be the signature of the incomplete description of the foam structure. The prefactor is around 5, which again confirms the validity of the scaling law. We stress that we expect
ys is shown in Fig. 7. We observe a linear relation between the two radii, meaning that our model captures the impact of continuous phase rheology, liquid fraction and confinement (cf. Fig. S5 in ESI†). We note that the scaling overestimates the datapoints with ϕ = 70% and underestimates the ones for ϕ > 70%. We expect this to be the signature of the incomplete description of the foam structure. The prefactor is around 5, which again confirms the validity of the scaling law. We stress that we expect ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ys to be larger than
ys to be larger than ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) sk as they do not characterise the same moment in the foamed emulsion ageing. It should finally be mentioned that we would experimentally observe this predicted stop in the coarsening only if the foamed emulsion kept an average structure as considered for the model. Yet in our experiments the structure gradually deviates and becomes highly heterogeneous; therefore we observe the foamed emulsion coarsening significantly slowing down but never really stopping.
sk as they do not characterise the same moment in the foamed emulsion ageing. It should finally be mentioned that we would experimentally observe this predicted stop in the coarsening only if the foamed emulsion kept an average structure as considered for the model. Yet in our experiments the structure gradually deviates and becomes highly heterogeneous; therefore we observe the foamed emulsion coarsening significantly slowing down but never really stopping.
 | ||
Fig. 7 Normalised theoretical critical radius ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ys = Rys/〈R0〉 plotted as a function of the normalised experimental critical radius ys = Rys/〈R0〉 plotted as a function of the normalised experimental critical radius ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) sk = Rsk/〈R0〉. Here, the slope of the dashed line is 5.5. sk = Rsk/〈R0〉. Here, the slope of the dashed line is 5.5. | ||
4 Conclusion
We studied the coarsening of a quasi-2D foam made from a model yield stress fluid, a concentrated oil-in-water emulsion. We explored the impact of the emulsion oil fraction ϕ, the foam liquid fraction ε and the confining gap d on the foamed emulsion coarsening process. Our experiments show that increasing the yield stress τy of the interstitial emulsion leads to slower foam coarsening. This slowing down happens together with an accumulation of small bubbles that induces an increasingly asymmetric bubble size distribution. A high oil fraction ϕ also leads to a significant heterogeneity in the foamed emulsion structure: we find large bubbles separated by very thin Plateau borders and accumulated small bubbles clustered and surrounded by much more liquid. While bigger bubbles keep coarsening, the shrinking rate of smaller bubbles is significantly slowed down by the emulsion stiffness. The impact of the continuous phase rheology is stronger as we increase the amount of yield stress fluid in the foam by making the foam wetter.We extract a critical radius Rsk, which characterises the onset of the structural change in the foamed emulsion. The experiments show that Rsk decreases with increasing ϕ, increasing ε, but increases with increasing gap size. To rationalise the variation of Rsk with these parameters we consider that an extra pressure is required to displace the yield stress fluid that had accumulated around the bubbles. This can be used to predict a critical radius for the arrest of coarsening, which we find scales linearly with Rsk. This suggests that the resistance of the yield stress fluid is the dominant mechanism through which coarsening is impacted.
The experiments carried out and presented in this paper show highly heterogeneous materials that do not follow Plateau's laws. Understanding how these complex foams coarsen is of great interest for all the applications requiring the solidification of a liquid foam, as the latter will age before solidifying. Moreover the unrelaxed internal structures that result from complex foam ageing will be transferred to the foams once solidified, impacting the mechanical properties of the final material.45,46 Controlling the structural evolution is then crucial to tune the features of the final foamy material.
Data availability
The videos of the coarsening foams used in this study can be found in the Zenodo database using the following links https://zenodo.org/records/12680668 (variation of liquid fraction) and https://doi.org/10.5281/zenodo.7535841 (variation of oil volume fraction).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Space Agency (ESA) through project Soft Matter Dynamics. The French space agency CNES is acknowledged for the PhD grant of N. Galvani and its support in the frame of the GDR “Micropesanteur Fondamentale et Appliqué” with the project “Hydrodynamics of wet foams”.Notes and references
- I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Foams: structure and dynamics, Oxford University Press, Oxford, 2013 Search PubMed.
- J. Stavans, Rep. Prog. Phys., 1993, 56, 733 CrossRef CAS.
- J. Von Neumann, Metal interfaces, American Society for Metals, Cleveland, 1952, vol. 108, pp. 108–110 Search PubMed.
- C. Wagner, Z. Elektrochem., 1961, 65, 581–591 CrossRef CAS.
- W. Mullins, J. Appl. Phys., 1986, 59, 1341–1349 CrossRef CAS.
- D. J. Durian, D. Weitz and D. Pine, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, R7902 CrossRef CAS.
- J. Lambert, R. Mokso, I. Cantat, P. Cloetens, J. A. Glazier, F. Graner and R. Delannay, Phys. Rev. Lett., 2010, 104, 248304 CrossRef CAS PubMed.
- W. W. Mullins, J. Appl. Phys., 1956, 27, 900–904 CrossRef.
- J. A. Glazier, S. P. Gross and J. Stavans, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 306–312 CrossRef.
- J. Stavans, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 5049–5051 CrossRef PubMed.
- R. Prud'homme and S. Khan, Foams: Theory, Measurements, and Applications, Marcel Dekker Inc., New York, 1996, vol. 57 Search PubMed.
- D. Weaire and S. Hutzler, The Physics of Foams, Oxford University Press, Oxford, 1999 Search PubMed.
- A. Saint-Jalmes, D. Durian and D. Weitz, Kirk-Othmer Encyclopedia of Chemical Technology, Wiley, 2005 Search PubMed.
- S. Cohen-Addad, R. Höhler and Y. Khidas, Phys. Rev. Lett., 2004, 93, 028302 CrossRef PubMed.
- M. Le Merrer, S. Cohen-Addad and R. Höhler, Phys. Rev. Lett., 2012, 108, 188301 CrossRef PubMed.
- S. Cohen-Addad, R. Höhler and O. Pitois, Annu. Rev. Fluid Mech., 2013, 45, 241–267 CrossRef.
- F. Gorlier, Y. Khidas and O. Pitois, J. Rheol., 2017, 61, 919–930 CrossRef CAS.
- H. Bey, F. Wintzenrieth, O. Ronsin, R. Hohler and S. Cohen-Addad, Soft Matter, 2017, 13, 6816–6830 RSC.
- N. Dubash and I. Frigaard, J. Non-Newtonian Fluid Mech., 2007, 142, 123–134 CrossRef CAS.
- D. Sikorski, H. Tabuteau and J. Bruyn, J. Non-Newtonian Fluid Mech., 2009, 159, 10–16 CrossRef CAS.
- I. Lesov, S. Tcholakova and N. Denkov, J. Colloid Interface Sci., 2014, 426, 9–21 CrossRef CAS.
- G. Samson, A. Phelipot-Mardelé and C. Lanos, Mag. Concr. Res., 2017, 69, 201–216 CrossRef.
- C. Arriagada, I. Navarrete and M. Lopez, Constr. Build. Mater., 2019, 228, 116746 CrossRef.
- A. Salonen, Curr. Opin. Colloid Interface Sci., 2020, 50, 101381 CrossRef CAS.
- O. Okesanjo, G. Aubry, S. Behrens, H. Lu and J. C. Meredith, Lab Chip, 2023, 23, 4434–4444 RSC.
- Y. Si, J. R. Royer, T. Li and P. S. Clegg, J. Colloid Interface Sci., 2023, 646, 671–678 CrossRef CAS PubMed.
- A. Salonen, R. Lhermerout, E. Rio, D. Langevin and A. Saint-Jalmes, Soft Matter, 2012, 8, 699–706 RSC.
- C. Guidolin, J. Mac Intyre, E. Rio, A. Puisto and A. Salonen, Nat. Commun., 2023, 14, 1125 CrossRef CAS PubMed.
- J. Goyon, F. Bertrand, O. Pitois and G. Ovarlez, Phys. Rev. Lett., 2010, 104, 128301 CrossRef CAS.
- W. Kloek, T. van Vliet and M. Meinders, J. Colloid Interface Sci., 2001, 237, 158–166 CrossRef CAS PubMed.
- D. C. Venerus, J. Non-Newtonian Fluid Mech., 2015, 215, 53–59 CrossRef CAS.
- L. Ducloué, O. Pitois, J. Goyon, X. Chateau and G. Ovarlez, J. Non-Newtonian Fluid Mech., 2015, 215, 31–39 CrossRef.
- T. Gaillard, M. Roché, C. Honorez, M. Jumeau, A. Balan, C. Jedrzejczyk and W. Drenckhan, Int. J. Multiphase Flow, 2017, 96, 173–187 CrossRef CAS.
- H. M. Princen and A. Kiss, J. Colloid Interface Sci., 1986, 112, 427–437 CrossRef CAS.
- T. Mason, J. Bibette and D. Weitz, J. Colloid Interface Sci., 1996, 179, 439–448 CrossRef CAS.
- N. Politova, S. Tcholakova, Z. Valkova, K. Golemanov and N. D. Denkov, Colloids Surf., A, 2018, 539, 18–28 CrossRef CAS.
- A. E. Roth, C. D. Jones and D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042304 CrossRef CAS PubMed.
- N. Isert, G. Maret and C. M. Aegerter, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 116 CrossRef CAS.
- J. A. Glazier and J. Stavans, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 7398–7401 CrossRef CAS PubMed.
- C. D. Schimming and D. J. Durian, Phys. Rev. E, 2017, 96, 032805 CrossRef CAS.
- C. Gay, P. Rognon, D. Reinelt and F. Molino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1–11 CrossRef PubMed.
- N. Galvani, M. Pasquet, A. Mukherjee, A. Requier, S. Cohen-Addad, O. Pitois, R. Höhler, E. Rio, A. Salonen, D. J. Durian and D. Langevin, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2306551120 CrossRef CAS.
- C. Guidolin, PhD thesis, Université Paris-Saclay, 2022.
- A. J. Webster and M. E. Cates, Langmuir, 2001, 17, 595–608 CrossRef CAS.
- S. Heitkam, W. Drenckhan, T. Titscher, D. Weaire, D. C. Kreuter, D. Hajnal, F. Piechon and J. Fröhlich, Eur. J. Mech. A Solids, 2016, 59, 252–264 CrossRef.
- M. Jouanlanne, A. Egelé, D. Favier, W. Drenckhan, J. Farago and A. Hourlier-Fargette, Soft Matter, 2022, 18, 2325–2331 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00296b |
| ‡ Present address: Department of Medical Biotechnology and Translational Medicine, University of Milan, Segrate, Italy. |
| This journal is © The Royal Society of Chemistry 2024 |