Dynamic duos: the building blocks of dimensional mechanics

Abstract

Mechanics studies the relationships between space, time, and matter. These relationships can be expressed in terms of the dimensions of length 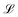, time 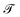, and mass 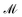. Each dimension broadens the scope of mechanics. Historically, mechanics emerged from geometry, which considers quantities like lengths or areas, with dimensions of the form 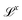. With the Renaissance, quantities combining space and time were considered, like speed, acceleration and later diffusivity, all of the form 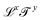. Eventually, mechanics reached its full potential by including “mass-carrying” quantities such as mass, force, momentum, energy, action, power, viscosity, etc. These standard mechanical quantities have dimensions of the form 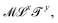where x and y are integers. In this contribution, we show that, thanks to this dimensional structure, these mass-carrying quantities can be readily arranged into a table such that x and y increase along the row and column, respectively. Ratios of quantities in the same rows provide characteristic lengths, while those in the same columns yield characteristic times, encompassing a great variety of physical phenomena from atomic to astronomical scales. Most generally, we show that selecting duos of mechanical quantities that are neither on the same row nor column of the table yields dynamics, where one mechanical quantity is understood as impelling motion, while the other impedes it. The force and the mass are the prototypes of impelling and impeding factors, but many other duos are possible. We present examples from the physical and biological realms, including planetary motion, sedimentation, explosions, fluid flows, turbulence, diffusion, cell mechanics, capillary and gravity waves, and spreading, pinching, and coalescence of drops and bubbles. This review provides a novel synthesis revealing the power of scaling or dimensional analysis, to understand processes governed by the interplay of two mechanical quantities. This elementary decomposition of space, time and motion into pairs of mechanical factors is the foundation of “dimensional mechanics”, a method that this review wishes to promote and advance. Pairs are the fundamental building blocks, but they are only a starting point. Beyond this simple world of mechanical duos, we envision a richer universe that beckons with an interplay of three, four, or more quantities, yielding multiple characteristic lengths, times, and kinematics. This review is complemented by online video lectures, which initiate a discussion on the elaborate interplay of two or more mechanical quantities.

---

1 Introduction

Mechanics is the bedrock of physics and exerts influence across all sciences. Mechanics has had such a far reaching impact on our understanding of the natural world that it is hard to contain it under a single definition. In the 19th century, an effort to bring new disciplines like thermodynamics and electromagnetism into its fold prompted Fourier,¹ Gauss and Weber,² Maxwell and Kelvin,^3,4 and their contemporaries to formulate one of the most commonly accepted definitions of mechanics.^3,5 Mechanics deals with the relationships between space, time and matter, usually quantified by the dimensions of length , time , and mass .

Mechanics in a general sense includes geometric quantities, with dimensions of the form (lengths, areas, etc.). More broadly, mechanics also includes kinematic quantities, with dimensions (speed, acceleration, diffusivity, etc.). These kinematic quantities describe motion, but without any reference to the “causes” of these motions. The quest for these causes led to the definition of mass, and all its derivatives: force, density, momentum, energy, action, power, stiffness, pressure, viscosity, etc. The bestiary of mechanics includes many creatures, all cast from the same mold. All these mechanical quantities have dimensions of the form ; they are “mass-carrying quantities”. As we will see in this review, this shared structure allows a representation of the mechanical quantities in a plane with coordinates x and y, representing the exponents of the space and time dimensions. Moreover, since x and y are usually integers, the standard mechanical quantities can be arranged into a table, which can act as a great guide for researchers and teachers, and a perfect cheat sheet for students. We have spent the last three years toying with this enigmatic map of mechanical quantities. We constructed this table in order to provide a Rosetta stone to help translate knowledge across the boundaries of the diverse sub-fields of science. We invite readers to contribute to this table, and to suggest additions or modifications.

Our investigations led us to reformulate the dimensional approach to mechanics, which we are sharing through a series of lectures on a https://www.youtube.com/@naturesnumbers channel that we created for this purpose (https://www.youtube.com/@naturesnumbers). These lectures explain in detail how to use this table to identify the “causes” of a wide range of motions, enabling the transformation of a kinematic description into a dynamical understanding. These videos serve as a supplementary material to this review, which focuses on the decomposition of geometric or kinematic quantities into ratios of mechanical quantities. From a dimensional perspective, this kind of decomposition is elementary, but it has far reaching consequences on the understanding of the relationship between mechanics and motion, and it provides a systematic way to approach the “causes” of motion.

The basis for this dimensional approach to mechanics dates back to Archimedes. To measure volume Ω, Archimedes proposed expressing it as a ratio, Ω = m/ρ, where m is the mass of the object and ρ is its density. This old formula seems so elementary today that we do not realize the great leap that it encompasses: a geometric quantity (the volume) is derived from a ratio of two mechanical quantities (the mass and the density). Dimensionally, the logic is flawless: where the brackets return the dimensions of their content. The extra dimension of mass is a sort of “dummy” dimension, disappearing from the final result, a very useful intermediary in the computation.

Almost two thousand years after Archimedes, Newton extended this logic even further. What Newton sought to compute was not a geometric quantity, but a kinematic one, acceleration a; however, he used the same principle. He expressed acceleration as the ratio between two mechanical quantities: a = F/m. Again, the dimensions match: . The example is so classical that it may not seem too impressive today.

Fast forward almost three centuries to the 1940s and consider this other example, often found in textbooks on dimensional analysis.⁶ The Second World War is raging and the British physicist G. I. Taylor is trying to compute the dynamics of an explosion blast. Experiments suggest that the radius of explosion follows a ‘power law’ of time, d(t) ≃ Kt^α. To understand the value of the kinematic prefactor K, Taylor uses the old trick again. In this context, Taylor identifies the energy E of the bomb and the density ρ of the ambient air as the relevant mechanical parameters. Then, the dimensions of the mechanical ratio provide an answer: . Taylor concludes that , that is .^7,8 Not so trivial anymore!

From Archimedes to Newton and Taylor, the procedure remains the same. A geometric or more broadly kinematic quantity (without any mass dimension) can always be expressed as a ratio of mechanical quantities. The only thing that varies from one example to another is the pair of mechanical quantities that are involved in the decomposition. In any case, the dimension of mass comes to the rescue, providing a means to understand sizes, durations and motions of all sorts, from a ratio, or “balance”, or “struggle”, between “competing” mechanical factors.

Even if we restrict ourselves to the standard mechanical quantities in Table 1, there are hundreds of possible pairs, and quite a few with a rich history. The purpose of this review is to discuss a few of these pairs. Each pair tells a unique story, synthesizing different “physics”, and retracing the steps of those who sought to explore this mechanical landscape.

Table 1 Table of standard mechanical quantities, with dimensions . Values of the exponents x and y refer to the columns and rows. A given quantity associated with a choice of couple (x, y) usually has several names. The symbol and the name in bold are the one we chose when generically referring to that quantity in this review. The dimensions of a mechanical quantity dictate its symbol. We systematically use the same symbols for all the mechanical quantities that share the same dimensions. For instance, we do not use “P” for pressure, “G” for elastic modulus and “σ” for shear stress, we just use Σ for all quantities with dimensions . We have found useful to define the levity and strength, which are respectively discussed in Sections 4.4.2 and 3.1.7. Please feel free to complete this table in any way you see fit

---

Pairs of mechanical quantities are the building blocks of the relationship between mechanics and kinematics, but they are only a starting point. If motion can be understood from the interplay of mechanical quantities, what can we expect from the interaction of three, four or even more quantities? We asked ourselves these very questions three years ago and we have been working on answering them ever since; our https://www.youtube.com/@naturesnumbers documents this journey. In this review, we solely focus on the interplay of pairs of mechanical quantities, but we will return later with more on the impact of additional players.

To illustrate the scope of a dimensional analysis of mechanics we will use examples from a wide spectrum of fields. This diversity constrains us to limit our citations to a few papers, which can be used as gates toward larger bodies of literature. Our background in fluid dynamics, soft matter, and biophysics, has biased us toward references from these fields. For instance, we are indebted to several reviews and textbooks on spreading, pinching and coalescence, including works by Dussan,⁹ de Gennes,¹⁰ Leger and Joanny,¹¹ Middleman,¹² Oron et al.,¹³ McKinley,¹⁴ Starov et al.,¹⁵ Kalliadasis and Thiele,¹⁶ Craster and Matar,¹⁷ Bonn et al.,¹⁸ Popescu et al.,¹⁹ de Gennes et al.,²⁰ Snoeijer and Andreotti,²¹ Lu et al.,²² Bico et al.,²³ Andreotti and Snoeijer,²⁴ Lohse et al.,²⁵ and Lohse and Zhang.²⁶ However, we have tried as much as possible to diversify our references to include a literature more familiar to biologists and engineers. In particular, for explosions we relied on works by Bethe et al.,²⁷ Glasstone et al.,²⁸ Sedov,²⁹ Krehl,³⁰ Westine et al.,³¹ Kinney and Graham³² and Sachdev.³³ For biological systems, we relied on works by Thompson,³⁴ Mitchison and Cramer,³⁵ Alt,³⁶ Sheetz,³⁷ Roberts et al.,³⁸ Lecuit and Lenne,³⁹ Le Clainche and Carlier,⁴⁰ Pollard and Cooper,⁴¹ Phillips et al.,⁴² Marchetti et al.⁴³ and Schwarz and Safran.⁴⁴ We have also benefited from seminal texts on dimensional analysis, including those by Fourier,¹ Maxwell,³ Buckingham,⁴⁵ Rayleigh,⁴⁶ Bridgman,⁴⁷ Barenblatt,^6,48 and Santiago.⁴⁹

In this review, terms first appearing between ‘single quotes’ are technical terms from the literature. A search for this term on the Web will generally yield its definition. Terms appearing in italics are those we first define here, or which substantially deviate from traditional usage. Terms appearing between “double quotes” are actual quotes, or colloquialisms. The sign ‘≡’ symbolizes a definition, where the left-hand side is a shorthand notation for the right-hand side. The sign ‘≃’ means that the two sides of the equation are expected to be of the same ‘order of magnitude’ (other authors may use ∝ or ∼). The sign ‘∼’ will be used to state an incomplete scaling relation, as in d ∼ t^α, where “incomplete” means that the left and right-hand sides do not have the same dimensions. The sign ‘=’ refers to a standard equality, which is presumably exact.

Links to the https://www.youtube.com/@naturesnumbers are given at the beginning of each associated section.

2 The mechanical quantities

https://youtu.be/XDQ21ngtpkI?si=a1PeLW6ICFV8bP5i

Mechanics includes geometry, kinematics and everything beyond, if it can be expressed with the inclusion of the dimension of mass. So the most generous definition of the term “mechanical quantity” could encompass any quantity with dimensions of the form , where x, y and z could a priori be real numbers. However, this is not how we will use this term in this review. We will refer to quantities with dimensions of the form as mechanical quantities. We will use the term kinematic quantities to describe quantities with dimensions of the form , with x ≠ 0 and y ≠ 0. And we will use the adjectives geometric/spatial and chronometric/temporal to describe and (x ≠ 0 and y ≠ 0), respectively. What about quantities like (z ≠ 0, z ≠ 1)? We will disregard them due to the fact that they can be reduced to mechanical quantities by factorization: .

Examples of geometric quantities include not only the well-known length area and volume but also more technical quantities like the ‘wavenumber’ . Chronometric quantities include the duration or period or the frequency . The three most well-known examples of kinematic quantities are speed or velocity acceleration and diffusivity . Progressive time derivatives of the position beyond acceleration lead to the so-called ‘jerk’, ‘snap’, ‘crackle’ and ‘pop’, but these colorful terms are seldom used. More broadly, as we will see later, there are many more possible kinematic quantities, although they are less known and rarely have names.

Now, what about mechanical quantities ? In a colloquial sense, mechanical quantities are the “forces” that in turn push or pull, drive or resist, impel or impair, all the processes at play behind space, time and their combination: motion. We have seen a few examples of these mechanical quantities in the introduction: mass (x = 0, y = 0), density (x = −3, y = 0), force (x = 1, y = −2), and energy (x = 2, y = −2). Each quantity is specified by its coordinates (x, y), so mechanical quantities can be represented as points on a plane. As we said, a priori, the coordinates x and y could take any value, but the small integers are of notable importance. Indeed the well-known geometric, kinematic and mechanical quantities have integer exponents. Investigating the reasons for this preference for integers is a fascinating task, but it goes beyond the scope of this review. In this review, we will only take note of this fact, and we will use it to our advantage. Because if the coordinates are small integers, we can represent the standard mechanical quantities they correspond to in a table. Thus, standard mechanical quantities refer to mechanical quantities where the exponents x and y are small integers, but since these are the only mechanical quantities we will be dealing with here, we will drop the adjective “standard”.

In Table 1, we have tabulated the mechanical quantities we could find in the literature, highlighting the fact that they may bear different names depending on the context. Surprisingly, such a table does not seem to have been drawn before, although, as we will see, it provides a great way to understand the mechanical underpinning of space-time. The table is organized around mass (x = y = 0), with columns determined by the exponent x, and rows by the exponent y. You can think of each mechanical quantity as being located in the dimensional space with two coordinates (x, y). We will use the symbol Q(x,y) to designate the mechanical quantity with dimensions , and the symbol K(x, y) to designate the kinematic quantity with dimensions or simply Q and K when the exponents are implicit.

Table 1 is a map of the explorations of mechanics in the past centuries, but this mechanical universe is still mostly uncharted territory. The quantities on this table were discovered step by step. Just a few centuries ago, the table would have been mostly empty. Beyond mass, density, force and momentum, contemporaries of Newton had very little to work with. Newton himself formalized the concept of ‘viscosity’, while his rival Hooke was quantifying the concept of ‘stiffness’. It is the painstaking recording of natural phenomena that progressively enlarged the mechanical cartography. And this exploration is still ongoing. There are blank spots to fill. We took the liberty of naming two quantities we felt deserved their place, but for which we could not find names in the literature: levity and strength. A famous example of levity is the inverse of the gravitational constant G. Almost equally famous examples of strength are ℏc, and k_ce², where ℏ, k_c, c and e are respectively the Planck and Coulomb constants, the speed of light, and the elementary charge. These two expressions respectively represent the “strength” of the nuclear and electromagnetic interactions. We will return to these important examples later in the review.

Each mechanical quantity can a priori be independent from the others. However, as we shall see, mechanical quantities are revealed through their interactions with one another. The most elementary form of such interaction is between pairs of mechanical quantities. Ratios of different mechanical quantities can produce space, time and motion.

Ratios of quantities in the same row produce purely spatial results:

We will discuss examples of such lengths in Section 3.1. The symbol [small script l] will generally be used to refer to any kind of length, size or distance, when this length is constant. We will rather use the symbol d when referring to a variable length. When multiple lengths are present, we may occasionally use alternate symbols for lengths, like h for height, or r for radius.

Ratios of quantities in the same column produce purely temporal results:

We will discuss examples of such times in Section 3.2. The symbol τ is used to refer to any kind of constant time, duration or period. We will rather use t to refer to a variable time.

Ratios of quantities on a diagonal of slope −1 produce speeds:

We will discuss examples of such speeds in Section 4.2. We will use the symbol u to designate any constant speed, and v to refer to a variable speed.

Ratios of quantities on a diagonal of slope −2 produce acceleration:

We will discuss examples of such acceleration in Section 4.3. We will use the symbol g to designate constant acceleration, and a for variable acceleration.

These ratios giving rise to length, time, speed, and acceleration are the most well-known, but we shall see that others are of interest. Note also that the relationship between two mechanical quantities is sometimes encoded in the very names of these quantities. In particular, the quantity Q(x − 2, y − 1) can be thought of as the flux of Q(x, y). For instance, stress can be thought of as a flux of momentum. The quantity Q(x − 3, y) can be thought of as the density of the quantity Q(x, y). For instance, stress can be thought of as a density of energy. However, except in a few instances where traditions obliged us (as with the mass flux, or the force–density), we tried to use names that did not explicitly refer to a parent quantity. All quantities on the table are related to another, but every quantity exists in its own right.

As illustrated by the different names of the mechanical quantities shown in Table 1, the overall spatial dimension of a particular context can lead to confusing usage of the same words. For instance, in a 2D setting, one may call the stiffness Q(0, −2) an elasticity (this is very common in the study of cells and tissues^43,44). Our choice here will be to use the 3D naming conventions written in bold in Table 1. Note that the existence of many names for a quantity with the same dimensions is correlated to the existence of many units as well. For instance, Table 1 will make it quite obvious that stiffness is sometimes expressed in N m⁻¹, where a Newton is a unit of force, or in J m⁻², where a Joule is a unit of energy. Although less conventional, it could very well be given in poise m s⁻¹, where a poise is a unit of viscosity. We have found that the table of mechanical quantities can make it easier to juggle with all these overlapping names and units.

3 The mechanics of space or time

Before addressing the relationship between mechanics and kinematics that is between mass-carrying quantities and motion, we should first discuss how space or time can be separately understood mechanically. Any constant length or duration can be decomposed into a pair of mechanical factors. At the very least, these factors are interpreted as providing a way to compute the values of lengths or durations, but they can also be regarded as the “origin”, or “reason”, or “cause” behind these lengths or durations.

3.1 Simple lengths

https://youtu.be/QiZ--8tkMdo?si=2IERNoMuT8Jq1A6w

As mentioned in the introduction, Archimedes showed us the way when it comes to relating geometry and mechanics, when he expressed volume as the ratio of mass and density Ω = m/ρ. The story has been told a thousand times; it is the original “Eureka!” moment. https://math.nyu.edu/~crorres/Archimedes/Crown/bilancetta.html shows the importance it had on the mechanical Renaissance.⁵⁰

If the mass and density of an object are known, then its volume is known. For a simple volume, like that of a cube, we can simply compute the volume from the knowledge of the length of the side [small script l], as Ω = [small script l]³. Conversely, for a given volume, we can always compute the length of the side of a cube with the same volume, as , which represents a sort of “average size” of the object. Using the notations introduced in the previous section (eqn (1)), we can write:

We will use the symbol [small script l] to denote any length, when no confusion is possible. Once we shall start dealing with multiple such lengths simultaneously, we will introduce more specific notations. In particular, the length built from the quantities Q₁ and Q₂ shall be called [small script l]_Q1Q2. So in the example from Archimedes, the average size is [small script l]_mρ, and the volume is [small script l]_mρ³. Note that the order of the indices does not matter, so [small script l]_mρ = [small script l]_ρm. We will come back to this important point in Section 4.4.

Objects can have all sorts of shapes, with different heights, widths and lengths. When a measurement of the “size” of this object is performed, this measure may not exactly coincide with the size . For instance, if the object is spherical, its volume will be Ω = (4π/3)r³, where r is the radius, so . If we call radius r the “size”, then this size is only approximately given by the ratio of mass and density, . Because tracking the fine effects of shape is often challenging, and because we do not seek precision but generality, we will often rely on this approximate equality sign ‘≃’.

In all generality, lengths can be built by combining an arbitrary number of quantities (geometric, kinematic, mechanical and even beyond) such that the overall dimension is a length. However, in this review, we will focus on cases where the decomposition only involves two mechanical quantities. We will refer to these lengths as simple lengths, and as we will see they have been useful in a very wide range of situations. Even if we restrict ourselves to the standard mechanical quantities tabulated in Table 1, there are over sixty pairs that can produce lengths. We will only discuss a few, enough to illustrate the generality of this mechanical approach to space:

Each of these characteristic lengths have several famous examples, and some are presented in detail below. We invite the reader to add to this list.

3.1.1 Energy and stress: explosions and ideal gases. The length [small script l]_EΣ applies particularly in the context of explosions. In the introduction, we mentioned the scaling derived by Taylor for the dynamics of the radius of an explosion, . We will return to this scaling later in the review; it concerns a type of motion connected to a ratio of energy and density. Evidently, this motion cannot continue indefinitely and eventually a ‘final blast radius’ is reached.^{28,31,32,51–54} This radius gives the extent of the zone where most damages occur. For the nuclear test studied by Taylor (Trinity), the energy is that of the bomb, around E ≃ 10¹⁴ J, and the stress is the bulk modulus of the air, which is not far from the atmospheric pressure Σ ≃ 10⁵ Pa. Overall, this gives: . As a comparison, bombs of 1 Mt, 10 Mt and 100 Mt of TNT (where 1 ton of TNT is equal to 4.184 gigajoules) correspond to blasts radii of 3 km, 8 km, and 16 km, respectively.²⁸ The length [small script l]_EΣ also applies to blast cavities of underground explosions, where Σ is the elastic modulus of the ground materials.⁵⁵

As illustrated in Fig. 1a, the same formula can be applied all the way up to supernovae explosions,^56,57 which release energies on the order of 10⁴⁴ J, and can extend their blast to a distance of at least 10¹⁹ m (i.e., over 300 parsecs). This gives a pressure of the interstellar medium of E/[small script l]³ ≃ 10⁴⁴/10^19×3 ≃ 10⁻¹³ Pa, which is the right order of magnitude.⁵⁷ In regions of interstellar space with even smaller pressures, the supernova remnants can extend even further.

Fig. 1 Examples of simple lengths. (a) The Crab nebula, a supernova remnant, which will grow for millennia up to a size (here [small script l] ≃ 10¹⁷ m). Image credit: NASA (public domain). (b) Earth, Titan and the Moon, three astronomical bodies with sizes of the form [small script l] ≃ Σ/Ψ (here [small script l] ≃ 6371, 2575, 1737 km). Image credit: NASA (public domain). (c) Manilius crater on the Moon, an example of length given by (here [small script l] ≃ 19 km). Image credit: NASA (public domain). (d) Illustration of the capillary length on a pendant drop before its fall (public domain), with size (here [small script l] ≃ 3 mm). (e) An elastic substrate is deformed by capillarity at the contact line, over a distance [small script l] ≃Γ/Σ (here [small script l] ≃ 10 μm).²³ (f) A thin film of oil on water produces an interference pattern testifying of its small thickness expressed as (public domain). (g) Beyond the optical resolution, the diffraction pattern of an atomic crystal obtained by electron crystallography reveals the typical size of the atoms (public domain). This size if of the form [small script l] ≃ S/E or [small script l] ≃ H/p (here [small script l] ≃ 0.1 nm).

The length [small script l]_EΣ can also be used in situations far from explosions. For instance, in microscopic physics influenced by thermal effects, E can be the thermal energy E = k_BΘ, where k_B is the Boltzmann constant and Θ is the temperature. This Boltzmann constant conveniently enables the translation of a temperature into an energy, incorporating thermodynamics into the realm of mechanics. In this context, the equation is better known as Σ[small script l]³ ≃ k_BΘ, which is called the ‘ideal gas law’, and is usually written as ‘PV = nk_BT’, where V/n ≃ [small script l]³ is the average volume associated with each microscopic constituent, n is the number of these constituents, and P, V and T are the symbols usually used for pressure, volume and temperature, respectively (note that we shall not use these notations in this review). This denomination is a bit misleading since this formula is not restricted to ideal gases but can be useful for connecting (thermal) energy, pressure, and microscales, for a wide variety of materials. For instance, in 1905, Einstein's theory of Brownian motion was developed with the postulate that the osmotic pressure due to a dilute suspension of particles was analogous to that of molecular solutes.^58a In some cases, the stress Σ can then be interpreted as an elastic modulus. For instance, in polymer physics, [small script l]_EΣ gives the typical ‘blob size’. Assuming room temperature (E ≃ 4 × 10⁻²¹ J) and a modulus around Σ ≃ 100 Pa, which is typical for soft gels, then a scale characteristic of the biological frontier of physics.⁵⁹ Clearly, the same formula can underpin very different interpretations. Similar formulas have also been used to explain the size of cells, where the thermal energy is multiplied with the effective number of proteins in the cell.^60–62

3.1.2 Energy and force–density: craters and Brownian particles. The length given in this equation describes a situation where energy is balanced by force–density. The force–density is usually the weight per unit volume, that is Ψ = ρg₀, where g₀ is the standard acceleration due to gravity. This length scale is, for instance, relevant to the size of the crater of an explosion,^63,64 if the density ρ is taken at the value of the ground materials. Indeed, this type of simple length is used to study all sorts of craters from explosions or impacts, including those of asteroids on the moon, as illustrated in Fig. 1c.⁶⁵ Studies of cratering in granular media also found the same length scale, when the impactors have moderate speeds.^66,67 The same scaling can also be applied to the size of the cavity created by explosions at the surface of liquids.⁶⁸

The length [small script l]_EΨ can also be used to describe the average ‘height of a Brownian particle’ in sedimentation or centrifugation. There, E is the thermal energy and the force–density is Ψ ≃ ρg, with g = g₀ for sedimentation and g = rω² for centrifugation (where r is the distance from the axis of rotation at rate ω).⁶⁹ For instance, at room temperature E ≃ 4 × 10⁻²¹ J, and if ρ ≃ 10³ kg m⁻³, then . Particles below this size are ‘Brownian’, and they remain suspended or dispersed, with a number distribution at any height set by the sedimentation–diffusion equilibrium.⁷⁰

Note that for objects embedded in a fluid, the force–density will generally be built from ‘buoyancy’, i.e., from the difference in density with the surrounding medium Ψ ≃ |ρ_f − ρ|g. In particular, in the case of Brownian particles, the density difference between dispersed particles and the outside medium determines the length scale that can be identified as the upper limit to the size of Brownian particles. The argument explains why metal nanoparticles are Brownian only below 100 nm, whereas polymer microbeads can be over a micron. Centrifugation can provide a much larger value of effective g, and therefore leads to sedimentation and separation.⁶⁹

An example of a characteristic size of the form [small script l]_EΨ for which the force–density is not the weight density occurs for drop impact. When the viscosity of the drop is negligible compared to its inertia and surface-tension, some studies have found that the maximum drop radius after impact is given by where E ≃ ρr³u² is the kinetic energy of the impacting drop of radius r, speed u and density ρ. The force–density Ψ ≃ Γ/r² originates from capillarity.⁷¹ We will see in Section 3.1.6 that other studies suggest a different scaling.

3.1.3 Stress and force–density: the hydrostatic equilibrium. In this length, the force–density is here again often the weight per unit volume, giving [small script l] ≃ Σ/ρg₀. The simplest examples consider that the stress is the isotropic pressure. Such a formula is particularly useful in the context of the formation of astronomical objects like planets or stars.⁷² In these cases, the size of a ball of matter is understood as a compromise between the compression by gravity and the resistance of an internal pressure. The size is then that of the planet or star. In this context, eqn (8) is sometimes referred to as ‘the hydrostatic equilibrium’ and written as Σ ≃ [small script l]Ψ, where the internal pressure equilibrates the weight per unit volume,⁷³ as in the context of barometers where pressure was first defined.⁷⁴ As an example, in the case of Earth, ρg₀ ≃ 5 × 10⁴ N m⁻³, and [small script l] ≃ 6 × 10⁶ m, giving Σ ≃ 10¹¹ Pa. Such pressure typically corresponds to the elastic modulus of metallic or amorphous solids constituting the Earth (≃100 GPa). Through this scaling, the various sizes of astronomical objects shown in Fig. 1b are directly related to their densities and elastic moduli.⁷² For more information, we refer the reader to a pedagogical presentation on scaling approaches to the size of stars and planets, which some of us have recently published.⁷⁵

3.1.4 Stiffness and force–density: the capillary length. Usually Ψ ≃ ρg₀ and the stiffness Γ is typically understood as a surface energy, also called ‘surface tension’. In the context of the wetting of fluids, such length is called the ‘capillary length’.²⁰ This capillary length sets the scale where surface energy and gravity exert comparable influence. For instance, at the water–air interface, the typical surface-tension is Γ ≃ 7 × 10⁻² N m⁻¹, the density is ρ ≃ 10³ kg m⁻³, and g₀ ≃ 9.8 m s⁻², such that the capillary length is around 3 mm. On the moon, where g ≃ 1.6 m s⁻², the capillary length of water is more than twice bigger.

When a drop hangs from a leaf as shown in Fig. 1d, it may grow in size only up to the capillary length, after which it will fall. Generally, gravitation flattens drops of size larger than [small script l]_ΓΨ, forming puddles, while capillarity keeps smaller drops spherical. The capillary length also influences the shape of a meniscus near an immersed or floating object.²⁰ Understanding the interplay between gravity and capillarity can actually be used to determine surface tension, using pendant drop analysis or using capillary rise.²⁰

3.1.5 Stiffness and stress: the elasto-capillary and elasto-adhesive lengths. This length provides a balance between stiffness (i.e., surface energy) and stress (i.e., volume energy). The relevant surface energy can be dominated by the contact with a solid substrate (in which case it is sometimes called ‘adhesion energy’), or with a fluid medium (in which case it is usually referred to as ‘surface tension’). Since Γ is in the numerator, it is the “driving” term. Larger values of Γ lead to larger lengths. One particular instance of this kind of length scale is when the stiffness is understood as an adhesion energy, and when the stress is elastic. The elasticity generates a recoil that is balanced by adhesion. In this context, [small script l]_ΓΣ may be called the ‘elasto-adhesive’ length.⁷⁶

When Γ comes from surface-tension, the length [small script l]_ΓΣ is often called the ‘elasto-capillary length’.²³ This length is relevant for the spreading of drops on soft substrates, associating surface energy and elasticity.²⁴ The elasticity can be that of the spreading object or of its environment. For instance, as illustrated in Fig. 1e, [small script l]_ΓΣ applies to the height of the wetting ridge near the solid–liquid–air triple line,⁷⁷ where the surface tension Γ acts perpendicularly to a substrate of elastic modulus Σ. Experimentally, a drop of glycerol (Γ ≃ 63 mN m⁻¹) on a soft silicone gel (Σ ≃ 2.4 kPa) produces a ridge of about 12 μm.⁷⁸ Other orders of magnitude can be obtained, for instance, a length of 30 nm was found for tricresyl phosphate (Γ ≃ 28.5 mN m⁻¹) on a silicone elastomer (Σ ≃ 0.6 MPa).⁷⁹

3.1.6 Energy and stiffness: Scheludko–Vrij length. This length is particularly relevant for thin films, where it can be called the ‘Scheludko–Vrij length’.^80,81 One example involves the energy E arising from van der Waals interactions and is called the ‘Hamaker constant’.^20,82 For typical fluids, this length is around a few angstroms. In this context, one usually defines a ‘disjoining pressure’ Σ ≃ E/[small script l]³, where [small script l] is the film thickness. Disjoining pressure and the Hamaker constant play an important role in the climbing and spreading of thin films,^11,19,83 and in setting the nano-topography of foam films.⁸⁴

Note that the linear stability analysis of both freestanding and supported ultra-thin films results in a prediction of a spinodal-like instability into thick-thin regions, with a typical size [small script l]_ΓΨ given in eqn (9), where the force–density is defined as the gradient of disjoining pressure, i.e. Ψ ≃ E/[small script l]_EΓ⁴. This length scale has been observed experimentally in spinodal dewetting and spinodal stratification.^16,85

As mentioned in Section 3.1.2, in the context of drop impact, when the viscosity of the drop is negligible, some studies have found that the maximum drop radius after impact is a simple length of the form [small script l]_EΨ, where E is the kinetic energy of the drop. In contrast, other studies suggest that the maximum radius may be of the form given by [small script l]_EΓ.^86–88

3.1.7 Strength and energy: Bohr radius and Bjerrum length. This length has profound origins since it can be used to express the size of the atom. This length also gives us the opportunity to say a few words about the mechanical quantity S = Q(3, −2). To the best of our knowledge, this quantity does not have a standard name in the literature. In the context of the deformations of elastic beams, it is sometimes called the ‘flexural rigidity’.⁸⁹ We call S the strength because it is often used to compare the relative strength of fundamental forces.⁹⁰ Newton's force of gravity between two masses m₁ and m₂ separated by a distance r can be expressed as Gm₁m₂/r², whereas Coulomb's force between two charges q₁ and q₂ can be expressed as k_Cq₁q₂/r², where G and k_C = 1/4πε₀ are respectively the gravitational and Coulomb constants (with ε₀ being the vacuum permittivity). Both Gm₁m₂ and k_Cq₁q₂ have the dimensions of strength. Most notably, if the charges q₁ and q₂ are elementary, then S₀ = k_Cq₁q₂ = k_Ce² ≃ 2 × 10⁻²⁸ kg m³ s⁻². In the microscopic realm one says that electromagnetism has a greater strength than gravity because S₀ ≫ Gm², where m is, for instance, the mass of a proton.

The length [small script l]_SE can then be used to express the size of an atom, using S₀ and the Hartree energy E = m_eu², where m_e is the mass of the electron and where u = α₀c is the semi-classical speed of the electron (α₀ ≃ 1/137 is the ‘fine structure constant’ we shall discuss later, c is the speed of light). Under these assumptions eqn (12) gives [small script l] = e²/(4πε₀m_eu²), which is the first historical expression of the ‘Bohr radius’⁹¹ (an alternate way of writing this radius will be given in the next sub-section).

In plasma and electrolytes, the strength S₀ also appears in the definition of the Bjerrum and Debye lengths.⁸² The ‘Bjerrum length’ follows eqn (12) with S = S₀/ε_r, which takes into account the dimensionless relative dielectric constant ε_r, and E = k_BΘ. This length provides the scale at which the electrostatic and thermal effects exert comparable influence. It arises in the context of electrolytes and colloidal dispersions.^82,92 For water at room temperature, ε_r ≃ 80 and the Bjerrum length is around 0.7 nm. The different assumptions leading from S/E to the Bohr or Bjerrum lengths are summarized here:

In the context of plasmas and electrolytes, the ‘Debye length’ also involves a strength S₀. The Debye length characterizes the screening of electrostatic interactions between two charges in the presence of other charges. In colloidal dispersions, the Debye length depends on ion concentration, making it a property of the solution, unlike the Bjerrum length which depends on the solvent and its dielectric constant.⁹² In this context one can define an effective stiffness as a density of strength, Γ = S₀/r³, which is then combined with the thermal energy using eqn (11). Here, the distance r is the mean distance between electrons and 1/r³ is the electron number density, so Γ can be understood as a charge density expressed in units of mass, length and time. The Debye length can vary widely, from the atomic scale in the solar core to thousands of kilometers in the intergalactic medium. In electrolyte media, encountered in soft matter and within cells, the strength is built from the number density of ions, whereas in semiconductors, the number density of dopants makes the relevant contribution.^93,94

3.1.8 Action and momentum: Bohr radius and de Broglie wavelength. We have seen in the preceding sub-section that the size of the atom can be expressed as a ratio of two mechanical quantities. More precisely, the Bohr radius can be expressed as a ratio between the electromagnetic strength and the kinetic energy of the electron, [small script l] ≃ S₀/E. The kinetic energy can be written in terms of the mass m_e of the electron and its speed u = α₀c, so [small script l] ≃ S₀/(m_euα₀c) ≃ S₀/(pα₀c), where p = m_eu is the momentum of the electron. Historically, the dimensionless ‘fine structure constant’ α₀ was understood precisely in this fashion, as the ratio between the speed of the electron and the speed of light.⁹⁵ However, α₀ quickly showed up in other situations, particularly in the comparison between the electromagnetic strength S₀ and the nuclear strength ℏc, since α₀ = S₀/ℏc. Using this formula we can rewrite the Bohr radius as [small script l] ≃ ℏ/p. Expressed in this way the Bohr radius is understood as the ‘de Broglie wavelength of the electron’. Generally, when H is the quantum of action ℏ, eqn (14) encompasses one of the central concept of quantum mechanics, the relationship between waves and particles.⁹⁶

We have seen that the Bohr radius can be expressed by two different pairs of mechanical quantities, S and E or H and p. The existence of multiple mechanical decompositions is not at all unique to this case. Any length can always be decomposed into a ratio of two mechanical quantities, but this decomposition is not unique, and this plurality encourages a diversity of mechanical models. The pair chosen in a particular situation depends on the broader context in which the length is found, and on historical circumstances. A more complete investigation of this “plurality” would require more than two mechanical quantities and is therefore out of the scope of this review. We will say a few more words about this in the conclusion.

3.1.9 Action and viscosity: viscosity as a density of action. As we said in Section 2, a mechanical quantity of the form Q(x − 3, y) can always be thought as a 3D density of the quantity Q(x, y). This is famously true for density itself, which is a mass-density and the template for all the others. This is also true for stress, which can be understood as a density of energy, as we saw with eqn (6). It is also true in less traditional cases, as with viscosity η ≡ Q(2 − 3, −1), which can be thought of as a density of action H ≡ Q(2, −1). Take water as an example. Water has a viscosity of around η ≃ 10⁻³ Pa s (where 1 Pa s ≡ 1 kg m⁻¹ s⁻¹). A water molecule has a radius of around [small script l] ≃ 1 Å. So if we multiply the viscosity with the typical volume of a water molecule we get an action: H ≃ η[small script l]³ ≃ 10⁻³³ J s. This value is not far from the quantum of action, ℏ ≃ 10⁻³⁴ J s, so the viscosity of water almost corresponds to one quantum of action per molecule. Although this link between viscosity and action is here only sketched by rough orders of magnitude, it can be formalized more rigorously, as exemplified in a recent paper by Trachenko and Brazhkin.⁹⁷

3.1.10 Old lengths under new light. These last examples provide ratios that are well known but often represented differently.

In eqn (16), Γ can be interpreted as the stiffness of a material behaving as a spring, then eqn (16) is just Hooke's law, F = Γ[small script l]_FΓ, where F and [small script l]_FΓ are usually understood as variables. In the context of spreading drops or cells, this ratio can represent a balance between a driving force F and surface tension or stiffness Γ. For cell spreading, the length [small script l]_FΓ can be used to characterize the portion of the cell behind the edge, which is rich in a very dynamic polymer called ‘actin’.^35,38,41 The polymerization of actin can be associated with a ‘protrusion force’ F, which is balanced by a surface energy Γ, with contributions form the plasma membrane, the cell stiffness, and the adhesion with the substrate.^98,99

In eqn (17), the length is [small script l]_ζη ≡ ζ/η, which is a ratio between ‘friction’ or ‘mobility’ and viscosity. This equation is more often seen in the form ζ = η[small script l]_ζη, in the context of Stokes drag,^100,101 where it gives the effective friction ζ on an object of size [small script l]_ζη moving slowly in a fluid of viscosity η. Indeed, at high viscosity and low speed, the frictional force is proportional to speed u, and given by F ≃ ζu ≃ η[small script l]_ζηu. This connection is the basis for Brownian motion in the Stokes Einstein relation,¹⁰¹ and thus lies at the heart of colloidal physics and chemistry.¹⁰²

In eqn (18), length is defined as the ratio between a force and a stress. This formula is more often seen as Σ ≃ F/[small script l]², which defines stress from the force F over the area [small script l]². From this perspective, the stress is typically understood as intensive, whereas the force is extensive but normalized by the area. When F and Σ are independent constants, [small script l]_FΣ is a simple length in its own right. This is, for instance, the case in the physics of nematic and polar materials, which includes a large class of living systems.^43,44 In this context, [small script l]_FΣ is sometimes called the ‘nematic length’, where F is understood as the ‘Frank constant’, which represents 1D elasticity associated with differences in alignment, and where Σ represents the energy per unit volume associated with the alignment of the nematic components.¹⁰³ This length scale determines the typical extent of orientational boundary layers.⁴³ Another important simple length in the study of active matter is the crossover from ‘wet’ to ‘dry’ active particles, which can be written as [small script l]_ηχ, where η is the viscosity of the embedding fluid, and χ is understood as a so-called ‘frictional drag’.⁴³

3.2 Simple times

https://youtu.be/KNeNx9mi2ao?si=CSSXh1kCe7_DcNKv

We have seen that ratios of mechanical quantities can produce length scales that show up in a wide variety of situations. In these examples, a length emerges from a sort of “balance” between conflicting “forces”, where the term “force” is used quite generously to encompass any mechanical quantity . Similarly, pairs of mechanical quantities can be used to understand time, durations and periods, leading to what we can call simple times. We will use the symbol τ when no ambiguity is possible, and τ_Q1Q2 when specificity is required. Over thirty such simple times can be derived from the standard quantities of Table 1. We list here the ones we shall discuss in this section:

3.2.1 Mass and stiffness: Hooke–Rayleigh time. This time is the archetypal example of a simple time. When Γ is interpreted as the stiffness of a spring to which a mass m is attached, eqn (19) represents the familiar expression of the period of oscillation. The standard formula found in textbooks usually uses the symbol ‘k’ instead of Γ, and includes a prefactor of 2π, so τ_mΓ is more precisely the inverse of ‘angular frequency’.

In the context of the dynamics of droplets, the mass is usually given by m ≃ ρr³, where ρ is the density of the fluid and r is the radius of the droplet. In this context one speaks of the ‘Rayleigh time’,¹⁰⁴ which applies to the oscillation frequency of drops, as well as to the contact time of rebounding drops.¹⁰⁵ Despite very different rebound profiles depending on the impact speed, the contact time remains the same and is set by τ_mΓ. The timescale also appears in capillarity-driven flows of ‘inviscid fluids’ (i.e., negligible viscosity).^{12,14,104,106,107}

3.2.2 Energy and power: energy consumption and Ritter–Kelvin–Helmholtz time. The power relates to a transfer or conversion of energy over time, and so the dimension of E/P is naturally . Common units of energy, like kilowatt-hour, reflect this proximity, with 1 kW h = 3.6 × 10⁶ J s⁻¹ s, so simply 3.6 × 10⁶ J. For a given energy E, the time scale in eqn (20) gives the expected time range when the energy consumption rate is the power P. This time scale can be used for a wide variety of purposes, to estimate how long you can drive on a full tank, as well as the life expectancy of the Sun.

A typical small car will have something like 70 horsepower, so P ≃ 53 × 10³ W. The energy comes from the fuel. Assuming a gas tank of 35 liters of standard fuel, with 8.9 kW h liter⁻¹, yields E ≃ 10⁹ J per gas tank. Then, τ_EP ≃ 5 hours. This is roughly how long this car can drive without refueling.

The principle behind the formula in eqn (20) remains the same for all kinds of fuel and all kinds of systems consuming this fuel. In particular, this formula can also be used to obtain an estimate of the lifetime of a star like the Sun. In this case, the power is well estimated by the solar luminosity, and P ≃ 3.8 × 10²⁶ W.⁷³ If the fuel of the Sun were standard gasoline as in the car, then the lifetime of the Sun would only be around 3000 years, according to eqn (20). This is obviously not the case.

So what is the fuel of the Sun? The quest to answer this question spanned from the mid 19th to the mid 20th century and involved some of the greatest minds of that time. The story has been told beautifully in a paper by Shaviv.¹⁰⁸ An important step in the quest was to consider the energy to be due to the self-gravitation of the Sun, so E ≃ Gm²/[small script l], where m and [small script l] are respectively the mass and size of the Sun. In this scenario, the power of the Sun, that is its luminosity is due to the gravitational potential energy. This time scale is sometimes called the ‘thermal timescale’, or the ‘Kelvin–Helmholtz timescale’, to honor Kelvin and Helmholtz contributions to this field of research. However, as noted by Shaviv,¹⁰⁸ August Ritter was the first to derive this formula. This timescale plays an important role in astronomy, in particular to set the timescale of the collapse of protostars; however, it fails to estimate the age of the Sun and similar stars. Indeed, using [small script l] ≃ 7 × 10⁸ m and m ≃ 2 × 10³⁰ kg, we get τ_EP ≃ 30 million years. The inadequacy of this figure with the geological records led to intense debate, and the controversy was only resolved at the beginning of the 20th century, when it was realized that the fuel of the Sun is nuclear.¹⁰⁸ By considering the conversion of hydrogen into helium, it was estimated that the energy of the Sun is around E ≃ 6 × 10⁻⁴mc², giving τ_EP ≃ 10 billion years, which is the currently accepted order of magnitude, and is sometimes called the ‘nuclear time scale’.⁷³

3.2.3 Action and energy: Planck relation. Staying on the same column of Table 1 as in the previous example, we have the pair combining action and energy. The part of physics where a constant action is most dramatically felt is quantum mechanics, where the action is the Planck constant ℏ. Using this value, we can rearrange eqn (21) to express the energy from the Planck constant and the inverse of time, which is usually written as frequency, E = hω. This equation started the whole quantum revolution; it is the Planck relation, which gives the energy of a photon of frequency ω, or the frequency from the energy. This is the formula behind Einstein's Nobel prize-winning work on the photoelectric effect.^58b With this relationship, Einstein calculated the frequency of a photon required to eject an electron from a metallic target. For instance, if the target is made of zinc, the binding energy of an electron is around E ≃ 9 electronvolts, so E ≃ 10⁻¹⁸ J. Thus, according to eqn (21) the frequency of light above which electrons can be extracted is around 10¹⁶ Hz, corresponding to ultraviolet light.

In the special case where the energy is the thermal energy (E = k_BΘ), the time τ = ℏ/k_BΘ is called the ‘Debye time’.¹⁰⁹ The inverse of this time scale provides an important thermal cut-off in the propagation of waves in crystal lattices. At room temperature, the Debye time is around twenty femtoseconds. Note that the term ‘Debye time’ can also be used in a slightly different way, as the time for charge relaxation, for diffusion across the Debye length.¹¹⁰ The two formulas could be reconciled by using the relationship between viscosity and action, as given in eqn (15).

3.2.4 Viscosity and stress: rheological time. This ratio most notoriously applies to Newton's relation, where [small gamma, Greek, dot above] is the deformation rate. The time scale is then [small gamma, Greek, dot above]⁻¹. In general, the deformation rate is not a constant. However, in complex fluids there are often remarkable values of [small gamma, Greek, dot above]. For instance, many materials display rather elastic properties on short time scales, and are viscous on longer time scales.¹¹¹ These materials are usually called ‘visco-elastic’, and the threshold between short and long time scales is the ‘relaxation time’ τ. In ‘Maxwell's model’, which is the simplest model of visco-elastic fluid, the elasticity of the material Σ, the viscosity, and the relaxation time are connected by the equation τ ≃ η/Σ.^111,112 The greater the viscosity, the longer the time, and the greater the elasticity, the shorter the time. The relaxation time scale of visco-elastic fluids can range from milliseconds to decades.^111,112 At any rate, in simple visco-elastic fluids the time τ is a constant of the material and it can be used to understand the transition between different flow regimes.^14,111,113

In more complex visco-elastic fluids beyond Maxwell's model, there can be more than one relaxation time.^111,114 Polymer solutions typically exhibit a spectrum of relaxation times. In addition, some materials may behave as Maxwell fluids under small deformations, but display flow-induced changes in their structure at higher deformations. For instance, worm-like micelle¹¹¹ solutions have a viscosity η₁ at low deformation rates, and above a threshold [small gamma, Greek, dot above]₁ a different flow-induced “phase” of viscosity η₂ is generated and coexists at constant stress Σ_p with the original one until a second threshold [small gamma, Greek, dot above]₂. Above this threshold the whole material has viscosity η₂. This phenomenon is usually called ‘shear-banding’.¹¹⁵ Both [small gamma, Greek, dot above]₁⁻¹ ≃ η₁/Σ_p and [small gamma, Greek, dot above]₂⁻¹ ≃ η₂/Σ_p are time scales of the form η/Σ. More broadly, remarkable values of viscosity or stress can occur in a large class of ‘complex’ or ‘non-Newtonian’ fluids, including shear-thinning, shear-thickening and yield-stress fluids. In turn, these quantities provide multiple ways to construct time scales of the form given in eqn (22).¹¹¹

3.2.5 Viscosity and normal stresses: Weissenberg time. In addition to the visco-elastic time scales they are often associated with, non-Newtonian materials can also display quite remarkable ‘normal stress effects’.^111,112 In ‘Newtonian fluids’, shear stresses are of the form Σ_s ≃ η[small gamma, Greek, dot above], where [small gamma, Greek, dot above] ≃ u/[small script l] is a velocity gradient over the distance [small script l]. In contrast, normal stresses arise from inertia and are usually of the form Σ_n ≃ ρu² ≃ ρ[small script l]²[small gamma, Greek, dot above]². This stress is sometimes called the ‘dynamic pressure’, or the ‘Ram pressure’ in astrophysics.¹¹⁶ For Newtonian or non-Newtonian fluids, normal stresses can be expressed as Σ_n ≃ Φ[small gamma, Greek, dot above]², such that , the same dimensions as a 1D mass-density. In the Newtonian case, Φ ≃ ρ[small script l]², but in non-Newtonian fluids, including magnetic fluids relevant to astrophysics, the normal stress coefficient Φ can be completely independent of ρ and inertia in general.¹¹⁷ Whereas the positive value of Φ for Newtonian fluids tend to generate centrifugal forces pushing a rotating fluid outward, for non-Newtonian fluids, Φ can be negative and push the material inward in the so-called ‘rod-climbing’ or ‘Weissenberg effect’.^111,112 This is but one among many examples of non-Newtonian normal stress effects.

For non-Newtonian fluids, the normal stress coefficient Φ is a material property as important as viscosity, and disconnected from the density. It is an independent mechanical quantity, from which a time scale τ_Φη can be constructed, as in eqn (23). In simple visco-elastic models like Maxwell's model, this time scale is identical to the relaxation time τ_ηΣ. Indeed, in Maxwell's model, one has Φ ≃ ητ_ηΣ.¹¹¹ This identity is not true in general. Currently, the differences between the two non-Newtonian time scales are most often investigated in the context of flows with an extensional component, where the dual effects of normal stresses and relaxation time are factored into the differences between shear and extensional rheology.^14,118

3.2.6 Friction and stiffness: damping time. One way to understand this time scale is as the 2D equivalent of τ_ηΣ. For fluid films, the details of the dynamics of the height can usually be neglected when the horizontal extent is much larger than the thickness. Under the ‘lubrication approximation’,^13,119,120τ_ζΓ can be understood as the characteristic time separating the short time dynamics driven by the stiffness, and the long time scales dominated by friction. In the most elementary expression of this time scale, Γ is the stiffness of a spring, and ζ is the damping coefficient. If the spring is initially compressed, it first snaps back fast until a cross-over time ζ/Γ, after which it relaxes more slowly. A time scale of this nature is, for instance, observed for the dewetting time of islands of cells on unwelcoming substrates.¹²¹ In this situation, a monolayer of cells progressively retracts into a 3D aggregate. In this context, the friction is ζ ≃ ηh, where h is the cell height, and the stiffness is the ‘tension’ over the portion of the monolayer close to the edge, Γ ≃ Σ[small script l], where Σ is the ‘traction stress’ exerted by the cells on the substrate, and the width [small script l] near the edge is given by the nematic length discussed with eqn (18).

3.2.7 Density and its variation: proliferation time. Because the standard name we have chosen for the mechanical quantity χ ≡ Q(−3, −1) is density change, the fact that this ratio is a time scale seems trivial. It is the time scale over which the density changes. This time scale is particularly useful in dynamics due to the proliferation of objects with a characteristic mass m and a ‘number density’ n (dimension or in 2D). If the mass is constant, then τ_ρχ ≡ ρ/χ ≃ n/ṅ, where ṅ ≃ ∂n/∂t. Thus, the time scale reflects the rate of change of the number of objects. For instance, in tissues of cells the time scale τ_ρχ is associated with the characteristic time separating two cell divisions. This time scale is relevant for the spreading of tissues,¹²² as well as for some organisms like ants.¹²³

4 The mechanics of motion

In the previous section, we investigated the mechanics of space or time, taken separately. Here, we will see how mechanical quantities can be used to rationalize motion, so we will address the connection between mechanics and kinematics, that is between mass-carrying quantities and space-time.

We will present a few instructive examples of dynamic scalings from the literature, in particular those illustrated in Fig. 2.

Fig. 2 Examples of dynamics associated with scalings of the form d ∼ t^α, from the pinching of viscous liquid threads, to atomic explosions and the motions of living cells. (a) Side view of the pinching dynamics of a viscous glycerol filament,¹²⁴ governed by d ≃ (Γ/η)t (eqn (31)), where the time t is the duration before pinch-off, so in this example the “actual time” runs from right to left. The length d is the radius of the filament, and Γ and η are the surface tension and viscosity of the fluid, respectively. (b) Side view of the first atomic explosion (Trinity test, 1945), discussed in the introduction.⁷ The dynamics of the blast radius d follow where E is the yield of the explosion and ρ is the density of the surrounding air. (c) Top view of the spreading of a silicon oil droplet that is being spin coated.¹²⁵ The dynamics of the contact radius d follows (eqn (38)), where E is the centrifugal energy and φ ≃ η/[small script l] is an interfacial friction derived from the viscosity and size of the drop. (d) Top view of the spreading of a cell onto a rigid substrate covered with an extracellular matrix.⁹⁹ The dynamics of the contact radius d follows (eqn (51)), where F is the ‘protrusion force’ and η is the viscosity of the cell. (e) Top view of the spreading of an aggregate of cells onto a rigid substrate covered by extracellular matrix.¹²⁶ The dynamics of the contact radius d follows (eqn (39)), where E ≃ Γ[small script l]² is the adhesion energy, and η is the viscosity of the aggregate.

4.1 General formula

In the previous section we only considered pairs of mechanical quantities on the same lines or on the same columns of Table 1. Pairs on the same line yield simple lengths, and pairs on the same column yield simple times. We now consider any arbitrary pair of mechanical quantities, Q₁(x₁, y₁) and Q₂(x₂, y₂). In this general case, the dimensions of the mechanical ratio combine space and time, and the dimension of mass naturally disappears:This general formula includes simple lengths in the case where y₁ = y₂ (same line), and simple times when x₁ = x₂ (same column). Also included are all sorts of fully kinematic results, where x₁ ≠ x₂ and y₁ ≠ y₂. As we will see now, these kinematic cases provide a deep connection between mechanical quantities and motion.

4.2 Simple speeds

https://youtu.be/VvMKwZSNEX4?si=l6aLuzYAhzjqjxfv

Similarly, just as pairs of mechanical quantities can combine to give simple lengths or times, they can also produce speeds. Indeed, for pairs of mechanical quantities satisfying x₁ − x₂ = y₂ − y₁, eqn (26) implies

Graphically, the constraint on the exponents, x₁ − x₂ = y₂ − y₁, means that the two quantities Q₁ and Q₂ reside on the same diagonal of slope −1 in Table 1. So in this case, the ratio of such a pair of mechanical quantities results in a speed or powers of a speed. Taking the appropriate root we can systematically express the result as a simple speed, since:We shall discuss five important examples:
These speeds give us a preview of the relationship between mechanics and motion, in the special case where this motion is ‘uniform’, i.e., at constant speed.

4.2.1 Energy and mass: kinetic energy and projectiles. The combination of energy and mass results in a speed, which underlies the concept of kinetic energy, and which can be used to derive the speed of projectiles of known mass and energy. The standard unit of energy is Joule, which is defined as 1 kg m² s⁻². This definition connects the energy to the mass, [E] = [m][u]², where u represents some speed. The most famous example of this formula is the most famous formula: E = mc², the mass–energy equivalence. Another more ancient example of this connection between energy, mass, and speed is the kinetic energy, . In this context, the speed u is much smaller than the speed of light. Usually, this formula is used to compute the energy from a known mass m and speed u. However, the formula can be rearranged to express the speed from the mass and energy, as in eqn (29). The mass can be that of a projectile, like a canon ball, or a bullet, and the energy is that delivered by the gun.

The speed u_Em can be used to rationalize the speed of all sorts of projectiles, including bullets racing in a straight line, as well as debris flying in all directions, as in the case of explosions–small, large, or even astronomical. This kind of speed can, for instance, be used to describe the early stage of supernova explosions. For some types of supernovae (type Ia), both the mass and energy are known with some confidence. The mass of the ‘progenitor’, i.e., the exploding star, is around the same as that of our Sun, so m ≃ 2 × 10³⁰ kg, and the energy is around E ≃ 2 × 10⁴⁴ J. In this context, the early speed of the leading edge of the supernova remnant can be estimated from eqn (29), reaching a daunting 10 000 km per second!

4.2.2 Stress and density: sound speed. This is probably one of the most well-known example. The speed u_Σρ is the ‘sound speed’, taken in its most general sense. The sound waves can be associated with either compression or shear, depending on whether the stress Σ is considered to be a shear stress or a pressure. Some materials, typically gaseous can only sustain compression waves. For air, with ρ ≃ 1.2 kg m⁻³, and Σ ≃ 1.4 × 10⁵ Pa, the sound speed u_Σρ would be about 340 m s⁻¹ (the stress Σ is the bulk modulus of the air, which is given by the product between the atmospheric pressure and the ‘adiabatic index’ around 1.4). The order of magnitude of the sound speed in various materials can be computed from values of densities and elasticity/pressure/shear modulus, etc. In general, there can be different elastic moduli depending on the directions of deformation. Nevertheless, for isotropic and homogeneous materials, only two moduli are enough to characterize the material.⁸⁹ Many pairs are possible. For instance, inside the Earth, the sound waves are ‘seismic waves’, called ‘P-waves’ (compression) and ‘S-waves’ (shear), with speeds obtained using the formula in eqn (30), by choosing Σ to be respectively the P-wave modulus and shear modulus. For granite, the P-wave speed is typically around 5000 m s⁻¹, whereas the S-wave speed is 3000 m s⁻¹. In contrast, for medical ultrasounds, the relevant stress is the shear modulus of tissues, around Σ ≃ 10⁴ Pa, with density ρ ≃ 10³ kg m⁻³, giving a sound speed of around 3 m s⁻¹.

The sound speed u_Σρ can also appear in other fields, for instance, in astrophysics, and magnetohydrodynamics, where it is sometimes called the ‘Alfvén speed’, when the stress is built from a magnetic field strength B as Σ = B²/μ₀, where μ₀ is the permeability of the vacuum.¹²⁷ Note that just like the Boltzmann constant was used to translate a temperature into an energy ([k_B] = [E]/[Θ]), and the permittivity ε₀ was used to translate charges into a strength ([ε₀] = [e]²/[S]), here the permeability is used to translate a magnetic field into a stress ([μ₀] = [B]²/[Σ]). These translation constants allow one to remain within the system.

4.2.3 Stiffness and viscosity: visco-capillary speed. This speed plays a crucial role in the dynamics of capillary driven flows. In this context the stiffness is interpreted as surface tension, and the speed may be called the ‘visco-capillary speed’.^12,14,20 At the interface between pure water and air, the surface tension is typically Γ ≃ 7 × 10⁻² N m⁻¹, and the viscosity of water is η ≃ 10⁻³ Pa s, such that the capillary speed is Γ/η ≃ 10² m s⁻¹. In contrast, the sound speed in water would be around 1400 m s⁻¹, and the molecular speed would be 600 m s⁻¹. Note that such molecular speed would be expressed as u_Em (eqn (29)), using the thermal energy and the mass of the molecules as factors. For glycerol, since the surface tension is similar and the viscosity is a thousand times greater, the visco-capillary speed would be around 10 cm s⁻¹. When there is no other significant mechanical quantity beyond Γ and η, the visco-capillary speed is the natural speed scale. For instance, u_Γη is the speed at which viscous filaments gets thinner,^106,124,128 as depicted in Fig. 2a. This speed also manifests itself during the dynamics of spreading and coalescing droplets.¹⁰⁷ Note that in the context of dilute surfactant solutions, a difference in surface tension is used and the speed can be called the Marangoni speed.^10,129–131

4.2.4 Force and friction: terminal or active speed. This pair is more often found in the form F ≃ ζu, where u is the drift speed or terminal speed. Usually, ζ is understood as a constant, whereas F and u are variables. This viewpoint corresponds well with passive fluids, where the force is usually applied by the experimenter or set by gravity.^100,120 One famous example of this speed is in the context of an object falling inside a viscous fluid, like a steel ball in corn syrup. In this context, F = mg₀, where m is the mass of the ball. The friction or drag coefficient ζ can be estimated if we know the weight and the speed. For instance, for a ball of steel with a diameter of 1 cm, the weight is around F ≃ 0.04 N and the speed in syrup around u ≃ 2.6 cm s⁻¹, so ζ ≃ F/u ≃ 1.5 kg s⁻¹. Note that when the density of the falling object is comparable to that of the fluid, the driving force F must also account for buoyancy.

In eqn (32), the force F needs not be the weight. For instance, the standard acceleration of gravity can be superseded by a centrifugal acceleration, g ≃ rω², which can be orders of magnitude larger than the standard g₀. Then eqn (32) can be written as u ≃ mrω²/ζ, a formula very useful in biology, chemistry, and physics, to separate objects based on their different sedimentation speeds. The equation can be rearranged as u/g ≃ m/ζ. On the left, the sedimentation speed is divided by the effective acceleration, and is sometimes called the sedimentation coefficient, measured in Svedberg, after Theodor Svedberg, the Swedish chemist who got a Nobel prize for his study of colloids and proteins and the development of the ultracentrifuge.^69,132,133 By definition, one Svedberg is equal to 10⁻¹³ s, and indeed speed divided by acceleration yields time. The right hand side of the equation reveals that this kinematic ratio of speed and acceleration can also be understood mechanically as a ratio of mass and friction. So the sedimentation coefficient is a simple time, τ_ζm, built from the mass and friction, both belonging to a pair on the same column of Table 1, which we can add to the list of simple times we started in the previous section.

Note that the most general formulation of this simple speed does not require the force to be connected to any mass. For sedimentation and centrifugation the force is known, but in recent years, this simple formula has also been used the other way around, to estimate the magnitude of an unknown driving force F from a known friction, as in the case of motile cells or organisms. For instance, consider a swimming bacterium; between turning points, the bacterium moves at an approximately constant speed, u ≃ 30 μm s⁻¹. From eqn (32), we can obtain an estimate of the driving force F from the speed u, if we also know friction ζ. In viscous fluids, as we saw in eqn (17), the friction can be related to the size [small script l] of the moving object and to the viscosity of the fluid, as ζ ≃ [small script l]η. The driving force can then be expressed as F ≃ η[small script l]u. For a swimming E. coli with u ≃ 30 μm s⁻¹ and [small script l] ≃ 2 μm, the surrounding medium is around 10 times more viscous than water, so η ≃ 10⁻² Pa s. Overall, F ≃ 10⁻¹² N, i.e., one piconewton, which is indeed the correct order of magnitude, although the numerical prefactors we ignored can increase this force to a few tens of piconewtons.^43,44

4.2.5 Strength and action: the speed of light. This last example yields a simple speed as a ratio between a strength and an action. We have already seen an example of such speed with the semi-classical speed of the electron, u = α₀c, with α₀ being the fine structure constant, which can be expressed as α₀ = S₀/ℏc, where we recall that S₀ = k_Ce² is the electromagnetic strength between two elementary charges. Thus the electron speed is u = S₀/ℏ, an important example of simple speed derived from strength and action.

Note that the speed of light itself can be expressed using eqn (33). Since c = S₀/ℏα₀, we can define an action H = hα₀, or a strength S = S₀/α₀, which would provide slightly different ways to think about the speed of light.

4.3 Non-uniform motion

https://youtu.be/jv6IKH7aO5s?si=55dEy2nCWsS_51GT

From Antiquity to the Middle Ages, motion was practically synonymous with uniform motion, where distances grow linearly with time, as d = ut. The great leap made by Galileo, Kepler and Newton was in no small part driven by their departure from this narrow focus on motion at constant speed. Generations of thinkers had been fascinated by speed, with dimensions but the Renaissance shifted the attention toward acceleration, in particular with the study of free-fall, where the fallen distance grows quadratically, as . Unfortunately, this revolutionary takeover turned into a new dogma, and for centuries acceleration became the imposed kinematic metric of motion. It was only toward the end of the 19th century that the existence of other types of motion resurfaced with the study of diffusion.¹³⁴ For diffusive processes, distances grow proportionally to the square root of time, , which is usually written as , introducing the ‘diffusivity’ or ‘diffusion coefficient’ , with .^69,70,135 For reasons beyond our scope, kinematic quantities just like standard mechanical quantities are usually defined in such a way as to have integer exponents.

Motions characterized by constant speed, constant acceleration, or “diffusive behavior” are the three most historically significant examples of motion, but they are in no way more fundamental than other types of motions discovered subsequently. For instance, following Taylor,^7,8 we have seen that the blast of an explosion may advance according to a ‘power law’ . In this case, the kinematic parameter K is neither a speed, nor acceleration, nor given by a diffusivity. The kinematic quantity (or if we prefer integer exponents) is a more unusual combination of time and space. Like most kinematic quantities, K⁵ does not have a standard name, but it deserves a specific designation. In our https://www.youtube.com/playlist?list=PLbMiQs7eX-bbNTc-7HwdWzohUs8yPw300, we took the liberty of calling it explosivity. An explosion as the one studied by Taylor corresponds to a motion at constant explosivity. Just like speed, acceleration, or diffusivity, explosivity can be understood as a ratio of a pair of mechanical quantities. In Taylor's analysis, K⁵ ≃ E/ρ, where E is the energy of the bomb and ρ the density of the ambient medium. This relationship is a direct consequence of eqn (26). Indeed, since energy and density are five columns and two lines apart in Table 1, we have:

We can understand Taylor's relation, , as being the natural expression of the ratio E/ρ when time is measured by t and space by d. We shall use these two symbols, t and d, instead of τ and [small script l], in order to underline the fact that the length and time are variable here.

This way of representing kinematics as an evolution law for a size d(t) is pretty visual, so we will adopt it in this entire subsection, but as we shall see in Section 5 it is by no means the only perspective on kinematics. From this length versus time perspective the general formula in eqn (26) can be expressed as a ‘scaling law’ or regime:

Q₁/Q₂ ≃ d^x₁−x₂t^y₁−y₂ (35)

This formula includes simple lengths, simple times and simple speeds as special cases, and it also includes all sorts of non-uniform motions. Any choice of two mechanical quantities immediately yields a regime. The mechanical quantity in the numerator drives motion, while the quantity in the denominator slows things down. We will say that the numerator is the impelling factor, while the denominator is the impeding factor, and we shall return to the subtleties of this duality in Section 4.4.

Note the use of the approximate equality ‘≃’ in eqn (36), which underlines the fact that this relationship may not be exact, depending on the precise definitions of the mechanical parameters (Q₁ and Q₂) and kinematic variables (d and t). For now, we will consider that the mechanical quantities Q₁ and Q₂ provide a satisfying model of the dynamics if the two sides of eqn (36) only differ by numerical factors ‘of order 1’. We will return to this point in Section 6.3.2.

Note also that eqn (36) includes growing regimes, where (y₂ − y₁)/(x₁ − x₂) > 0, and shrinking regimes, where (y₂ − y₁)/(x₁ − x₂) < 0. In these shrinking regimes, the length d diverges at initial time, and it only converges to zero for t → ∞. In this review, we will focus on growing regimes. We differ a discussion of shrinking regimes to a future publication.

In Table 1, we have defined 25 widely used mechanical quantities. Considering all pairs, would generate more than 300 regimes. If we remove the simple lengths, times, and speeds, and if we only focus on dynamics where the size grows over time (d ∼ t^α with α > 0), there are still more than 100 possible regimes. This large number reflects the great diversity of “physics” that can be at play in different situations. In the following sub-sections, we will evidently not discuss all possibilities, but we will show that regimes of all sorts have already been used to describe dynamics across scales and disciplines.

4.3.1 Dynamics impelled by energy. Let us first present a few regimes impelled by energy. If we put aside the simple lengths and times, we have seen two cases so far: the uniform regime given by energy and mass, i.e., and Taylor's regime of explosions, . Taylor's regime is depicted in Fig. 2b, and the scaling is plotted in Fig. 3a.

Fig. 3 Growth of a length d over time t for regimes observed in dynamics from atomic explosions to living cells. The lengths and times are respectively measured by the vertical and horizontal axes, in meters and seconds for all plots. All plots show power laws of the form d = Kt^α. On each plot the value of α is represented by a triangle giving the slope of the line. The pair of mechanical quantities invoked to rationalize the slopes are given at the bottom-right corner. Note that in some cases the data have been truncated to isolate the range of validity of the regime in focus, undisturbed by the effect of additional mechanical quantities (see the conclusion of the review for a discussion of this point). (a) Blast radius of the Trinity explosion.⁸ (b) Initial spreading of a spherical aggregate of cells under ‘partial wetting’ conditions.¹²⁶ (c) Grain size growth for the ‘Ostwald ripening’ regime of ‘sintering’.¹³⁶ (d) Spreading of the ‘precursor film’ of motile cells for the ‘complete wetting’ of a spherical aggregate of cells.¹²⁶ (e) Inertio-capillary pinching of a bridge of liquid mercury.¹³⁷ In this case, the time t is the duration before pinch-off, so the “actual time” runs from right to left. (f) Spreading of a water droplet.¹³⁸ (g) Spreading of a single cell.⁹⁸ (h) Distance traveled by a debris flow down an incline.¹³⁹ (i) Radius of the neck for the coalescence of two air bubbles in silicone oil.¹⁴⁰

If we seek additional regimes impelled by energy, quantities on the same line or column as E cannot be included since they yield simple lengths and times. Quantities represented on the line with an index y = −3 cannot be included because they result in shrinking behavior (d ∼ t^α, with α < 0) rather than growth (α > 0). Of the quantities that are left, we have chosen to highlight the 2D density Λ ≡ Q(−2, 0), the mass flux φ ≡ Q(−2, −1) (understood as an interfacial friction Q(−2, −1) = Q(0 − 2, −1)), and the viscosity η ≡ Q(−1, −1):

The first regime in eqn (37) can be understood as the equivalent of Taylor's regime in cylindrical geometry.²⁹ In the case of explosions confined inside a cylinder of radius [small script l], one can define a 2D density as Λ ≃ ρ[small script l], leading to a regime with . This regime can be used to describe exploding-bridgewire detonators.¹⁴¹

The second example can be used to describe the dynamics of the radius of contact of ‘spin-coated’ drops, as illustrated in Fig. 2c.¹²⁵ In this case, the spinning is associated with a centrifugal energy E = ρ[small script l]⁵ω², where [small script l]³ is the volume of a drop and ω is the rotational frequency. One can then define a form of ‘interfacial friction’ from the fluid viscosity as φ = η/[small script l]. With these definitions, the spreading of the spun drop follows eqn (38). Note that quantities with the same dimensions have been used to study the “friction” of fluids, polymers and elastomers on solid boundaries.^142,143 In this context, one can also define the so-called Navier slip length, [small script l] ≃ η/φ, a form of simple length measured by extrapolating the velocity profile beyond the boundary.¹⁴⁴ We will see another use of this kind of ‘interfacial friction’ φ in eqn (47).

The third example in eqn (39) describes a regime where viscosity prevents the spreading of a source of energy. This regime could be relevant for point-like inputs of energy in very viscous fluids. This input could, for instance, come from explosions, lasers,¹⁴⁵ or ultrasounds.^146,147 Interestingly, this regime has also been applied to contexts far from explosions, to describe the spreading of aggregates of cells, as illustrated in Fig. 2e.¹²⁶ In this context, a ball of cells comes in contact with a substrate, on which it starts spreading through cell migration. The cell–substrate adhesion Γ and the size [small script l] of the ball can be used to define an adhesion energy E ≃ Γ[small script l]², such that the spreading abides eqn (39), where η is the aggregate viscosity. A comparison between this mechanical model and the data is shown in Fig. 3b.

4.3.2 Dynamics impelled by power. We now turn our attention to dynamics driven by constant power rather than constant energy. Many choices for resisting quantities could be useful. We here choose to highlight four possibilities:Eqn (40) can be found in a slightly different form in the context of turbulent mixing. In the design of stirrers for mixing liquids inside vessels, it has been found that the mechanical input power P required for mixing is given by P ≃ ρd⁵t⁻³, where d is the agitator diameter, t its period of rotation and ρ is the density of the fluid.¹⁴⁸ Note that in this case the scaling does not relate a variable length and time, unlike the approach adopted in the examples discussed so far. We will see in Section 5 that any pair of mechanical quantities can be expressed from multiple perspectives. The mixing scaling, P ≃ ρd⁵t⁻³, serves as a first example of what we will generically call a “mechanical perspective” in Section 5.2.

Eqn (41) gives another example of a regime based on power. This equation defines the simple speed so we could have put it in Section 4.2. This speed is relevant to dynamics characterized by a constant friction ζ. In many situations, the friction ζ is not constant and depends on speed. In general one can define ζ from the friction force F as ζ = F/u, where u is the speed. In the ‘inertial regime’, the friction force is proportional to the square of the speed, such that ζ ≃ ρud². Using u ≃ d/t this definition of the friction would lead back to eqn (40). In contrast, in the ‘viscous regime’, the friction force is proportional to speed and given by ζ ≃ ηd.¹⁰⁰ If d is the variable distance, this leads to the regime given in eqn (42). However, in some cases d is a constant length, for instance, connected to the size of a vehicle. The quantity ζ would then be a constant parameter and eqn (41) may apply.

Eqn (43) gives yet another example of a regime driven by power, where the impeding quantity is stress. This equation may be applicable to ‘sintering’.¹³⁶ In this process, the typical size of grains grows as where in the so-called ‘Ostwald ripening’ regime, the grain growth rate can be written as . The parameter R is the ideal gas constant, and Ω is the molar volume, such that Σ ≡ RT/Ω is a characteristic thermal stress. The constant C is a dimensionless solubility, Γ is the solid–liquid surface energy and is the solid diffusivity in the liquid. Thus, one can define the power associated with an increase in the size of the grains as such that the sintering equation becomes an example of eqn (43). An example of this regime is given in Fig. 3c.¹³⁶

4.3.3 Dynamics impelled by force–density.

d ≃ (Ψ/ρ)t² (44)

Because of its position in the table of mechanical quantities, force–density only allows a few regimes where it acts as the motor. In eqn (44), force–density is balanced by density. Since force–density is often taken to be Ψ = ρg, the equation just states d ≃ gt², which is the ‘free-fall’ equation. This regime applies to the early dynamics of materials driven by gravity before dissipation can set in. It applies, for instance, to the early dam-break flow,¹⁴⁹ and to the debris flow down an incline,¹³⁹ as depicted in Fig. 3h. In the first case, one of the walls of a reservoir of fluid is removed and one records the dynamics of the surge on a horizontal plane. In the second case, a mixture of fragmented rock and muddy water is similarly released, but down a steep incline plane.

Note that eqn (44) may also describe rises rather than falls, in the context of buoyancy. In this case, the force–density takes into account a difference in density between two materials Ψ ≃ |ρ_f − ρ|g. This version of eqn (44) would, for instance, be useful for understanding the initial rise of a mushroom cloud after a nuclear explosion such as Trinity.⁸ Indeed, the blast generates a zone of very low density, which acts as a bubble inside the comparatively denser air.

4.3.4 Dynamics impelled by stress. Of the possible regimes driven by stress, we have already seen the uniform regime associated with the sound speed, . Let us also mention the following ‘diffusive’ regime:Like the regime at a constant sound speed, this additional regime is most commonly found in aerodynamics.¹⁰¹Eqn (45) is appropriate in situations where the density of the medium uniformly changes at a rate χ (either compressing if χ > 0 or expanding if χ < 0). This situation is particularly relevant to some scenarios of star formation.¹⁵⁰

4.3.5 Dynamics impelled by stiffness. In the dynamics of drops and bubbles, surface tension is often understood as a “driving force”. We here highlight three possible regimes impelled by surface tension/stiffness:

d ≃ (Γ/Φ)t² (48)

The first equation has been studied in great detail in the context of spreading, pinching and coalescence of simple liquids like water.^{11,18,21,106,107,151–154} We have seen with eqn (31) that combining surface tension and viscosity yields a simple speed, which underlines what is sometimes called the ‘visco-capillary’ regime, where viscosity is the principal impeding force. In contrast, eqn (46) describes the ‘inertio-capillary’ regime. In the context of the spreading, pinching and coalescence of drops, eqn (46) dictates the dynamics unencumbered by viscosity, where the main impeding factor is ‘inertia’, represented by density ρ. This regime is, for instance, observed in the pinching of liquids with low viscosity,¹⁵⁵ like water, or mercury as shown in the example in Fig. 3e.¹³⁷ This regime has also been observed for spreading^156,157 and coalescence of low viscosity fluids.¹⁵⁸ Note that although the neck of a pinching drop decreases over time, its dynamics can be represented by a growing regime, d ∼ t^α, with α > 0, when the variable time t is understood as the duration before pinch-off.¹⁰⁷

The regime given in eqn (47) describes dynamics driven by a surface energy Γ, but impaired by a mass flux or momentum density φ. An example of this regime is shown in Fig. 3d.¹²⁶ In this example, the dynamics describe the spreading of the ‘precursor film’ composed of motile cells moving away in 2D after the contact of a spherical aggregate. In this context, the surface energy arises from the adhesion of cells with the substrate, and the parameter φ is understood as a form of “friction”.¹²⁶

In eqn (48) the term ‘1D density’ Φ can be interpreted as a ‘normal stress coefficient’, as mentioned in Section 3.2. The ratio Γ/Φ yields acceleration, which has some relevance to the free-surface flows of visco-elastic liquids. In particular, eqn (48) has been discussed in the context of the pinching of the so-called ‘second order fluids’.¹⁴

4.3.6 Dynamics impelled by force. Of the possible regimes driven by force, we choose to highlight three cases:

d ≃ (F/m)t² (49)

In eqn (49), Newton's second law is barely disguised. Like eqn (44), this spreading law just describes dynamics at constant acceleration a = F/m. We recall that under the assumption that d ∼ t^α, F = ma just translates to F ≃ md/t². As mentioned in the introduction, this pair is of great historical significance, since it records the first time a kinematic—and not just geometric—quantity was understood mechanically. The force is the prototype for all impelling factors, and mass is the prototype for all impeding factors.

In eqn (50), the force is balanced by density rather than mass. This regime applies to spreading, coalescence and pinching of drops when the whole size of the drop has a substantial impact.^{18,106,107,151–153} In this context, the force can be expressed as F ≃ Γ[small script l], where Γ is the surface-tension and [small script l] is the size of the drop. An example of this regime is given in Fig. 3f for the spreading of a water drop.¹³⁸

In eqn (51), the force is balanced by viscosity. This regime has been observed in a few different contexts. For instance, this regime describes the coalescence of drops in a viscous outer fluid, where η is the viscosity of the outer fluid, as shown in Fig. 3i.¹⁴⁰ A similar regime can be used to describe the spreading of thin films, where F/η is understood as an effective diffusivity, with F ≃ E/[small script l], where E is the Hamaker constant and [small script l] the film thickness.^19,159 Since the Hamaker constant is usually on the order of the thermal energy, the effective diffusivity matches with Stokes diffusivity. The same equation was also used to describe the early spreading of single cells, as illustrated in Fig. 2d.⁹⁹ In this case, the viscosity corresponds to that of the cell and the force can be attributed either to the stiffness of the cytoskeleton, or to a ‘protrusion force’ originating from the polymerization of ‘actin’.^98,99 An example of such scaling in the early spreading of cells is given in Fig. 3g.⁹⁸

4.4 Impelling and impeding

https://youtu.be/J5tm6IXt_fU?si=bPbBS5hD6SkaO3wm

If two mechanical quantities are given, there is a unique regime associated with them. For this reason, we may use the notation {Q₁, Q₂} to denote the regime associated with the pair of mechanical quantities Q₁ and Q₂. For instance, Taylor's regime is {E, ρ}, or {ρ, E}. The order of the quantities between brackets does not matter. In the pair {E, ρ}, the energy will always be the motor, or impelling factor, in accordance with eqn (36). Let us recall this equation here so there is no need to turn the pages:

In this equation, the mechanical quantity Q₁ is really in the numerator if x₁ − x₂ > 0, that is, if x₁ > x₂. Graphically, this means that the impelling factor of a pair is always the quantity located at the rightmost part of Table 1. For instance, if the pair is {E, ρ}, since E is on the right of ρ, then energy will be the impelling factor.

Although in a pair, one quantity is always driving; what is driving in one situation can be resisting in another and vice versa. This fact was clearly not understood when the first few mechanical quantities were defined, and to this day it remains the source of a lot of confusion. We only need to look at the historical names of the quantities in Table 1 to see that some of them are quite heavily connoted. On the right of the table, where these quantities are more likely to be impelling motion, the names are markedly positive, like ‘action’, ‘energy’, ‘force’, or ‘power’. All these “macho” terms in the English language are here to remind us that these quantities were thought as movers. For a lot of early scientists they were nothing short of the hand of God in the physical world. In contrast, terms like ‘friction’, ‘mass’, or ‘viscosity’, were initially thought of as sticky, gooey, resisting or at most inert rather than active. In fact, these quantities can be active; they can be impelling motion rather than impeding it, under the right circumstances. We shall illustrate this versatility on two historically significant examples.

4.4.1 Boundary layers. We have seen a few examples of dynamical regimes where viscosity was involved: {Γ, η}, {E, η}, and {F, η}. In all these cases, viscosity appeared as an impeding factor, living up to its name (“viscous” comes from Latin “viscosus”, meaning “sticky”). However, in some situations the viscosity can actually drive motion; it can be the impelling factor. We just have to pair viscosity with a mechanical quantity on its left in Table 1. One such pairing with great historical significance is as follows:Here, viscosity is paired with density, and the resulting regime is central to the understanding of ‘boundary layers’.¹⁰¹ In this context, the viscosity and density are that of a fluid and eqn (53) describes the thickness of the sheared layer of that fluid near a boundary. For instance, if a plate starts moving at t = 0 in a quiescent fluid, the fluid in the immediate vicinity of the plate will start moving too (in the absence of slip), but the fluid far away will remain immobile. As time goes by, the size of the moving layer of fluid near the boundary will grow, according to eqn (53). Since the power law has an exponent of this motion can be said to be ‘diffusive’, and the mechanical ratio ν ≡ η/ρ can be interpreted as (‘momentum’) diffusivity. It is also called ‘kinematic viscosity’. The greater the viscosity the greater the diffusivity, so indeed, viscosity is here impelling motion! It is surprising that eqn (53) does not involve the speed of the moving boundary. The dynamics of the boundary layer are actually independent of this speed only up to a point, where the flow becomes turbulent. So eqn (53) only refers to ‘laminar boundary layers’.¹⁰¹

4.4.2 Kepler's law and levity. The mass was originally understood as ‘inertial’, a word from the beginning of the 18th century based on the adjective “inert”, in-art, without art, without skill, from Latin “inertem”, meaning “unskilled, incompetent, inactive, helpless, weak, sluggish, worthless”, a long list of pretty negative attributes given by the etymological dictionary. This was how mass was initially perceived: as the paradigm of the impeding factor, the exemplar of what is resisting motion. This view on mass changed during the Renaissance, as it was realized that mass could also be the source of motion, in the context of gravity.

At the end of the 16th century, building on the observations of his master Tycho Brahe, Kepler had established his now famous ‘third law of planetary motion’: t² ∼ d³. The square of a planet's orbital period, t, is proportional to the cube of the length of the semi-major axis of its orbit, d.¹⁶⁰ If we want we can of course express this law in the following fashion: , where the unknown kinematic prefactor K must have dimensions , so a rather odd kinematic quantity that is nowadays called the ‘gravitational parameter’. In the case of the solar system the data available to Kepler established that K³ ≃ 3 × 10¹⁸ m³ s⁻². The mechanical interpretation of this kinematic quantity had to wait for one more generation, with the work of Newton.

Fig. 4a demonstrates the validity of Kepler's law for the orbits of the planets of the solar system. Also included are the characteristics (periods and semi-major axes) of the orbits of the satellites of the various planets of the solar system. Concomitantly with Kepler's investigations, Galileo had discovered the four largest moons of Jupiter,¹⁶¹ now called the ‘Galilean moons’. As evident in Fig. 4a, the Galilean moons, as well as the moons of other planets also follow power laws of the form but the value of the kinematic prefactor K changes from one system to another.

Fig. 4 (a) Kepler's law , i.e., the square of the orbital period, t, is proportional to the cube of the length of the semi-major axis of its orbit, d. The law is verified for the ‘solar system’, where the represented orbiting bodies are the planets and the dwarf planets (small grey disks). The law is also verified for the orbits of the satellites of the planets, represented by stars of a color corresponding to the associated planet. These satellites include the Galilean moons of Jupiter (orange). The values of the prefactor K differ depending on the orbital system. (b) The values of K³ for the solar system and for the satellite systems are plotted against the mass m of the central object, which is the planet for its satellites, and the Sun for the orbiting planets. One finds that K³ ∼ m. For instance, the data point for Jupiter corresponds to the value of the prefactor K of the power law for the Galilean moons in (a) (small orange squares).

It was Newton who first realized that the prefactor K is not a “universal” constant, but that it depends on the “world” under study.¹⁶² Newton then set out to find a decomposition of the kinematic quantity K into mechanical quantities. Using the notation introduced in this review, we could say that Newton sought a pair of mechanical quantities Q₁(x₁, y₁) and Q₂(x₂, y₂) such that . As shown in Fig. 4b, Newton realized that K³ ∼ m, with the impelling mechanical quantity being the central mass of the orbit, Q₁ = m, where m is for instance the mass of the Sun for the solar system.¹⁶²

Since and Newton's second mechanical quantity had to have the following dimensions: . Thus, Q₂ = Q(−3, 2). Looking back at Table 1, we see that this mechanical quantity occupies an odd position in comparison to all the others, which probably explains its peculiar fate. A quantity Q(−3, 2) is what we refer to as levity, denoted by the symbol . Since this mysterious quantity is on the left of the mass (in the table), it is impeding motion, whereas mass is impelling it:

Kepler's law is here understood as a regime based on pairing mass and levity. Using a notation introduced at the end of the 19th century and still in use today,¹⁶³ we can identify the levity with the inverse of the so-called ‘universal constant of gravity’ G. More precisely, (assuming the central mass is much more massive than the orbiting objects).

The purpose of defining such “levity” is to stress that Kepler's law—like any other regime—can be expressed from a pair of standard mechanical quantities with dimensions of the form . In contrast, the universal constant of gravity has dimensions . Other mechanical quantities with similar negative power of the mass have been occasionally used, like the ‘fluidity’ with dimensions .¹⁶⁴ These quantities are absolutely valid, but they are unnecessary, since they can be reduced to standard quantities through inversion. We do believe that the “levity” deserves its place in Table 1 and should be free to interact with all the other quantities. As we saw, pairing levity and mass leads to Kepler's law for orbital motion, but we invite the reader to try different pairings. For instance, gives rise to a simple time , which is called the ‘free-fall time’, with important applications in astrophysics.⁷³

5 Perspectives on motion

https://youtu.be/lVLjflQI41w?si=m3h0d3Kvm6hI_2e6

Since eqn (36), we have presented mechanics from a particular kinematic perspective. The assumption was that we observed some kind of motion, like an explosion, or the pinching of a water droplet, or the fall of an object, or the orbit of a planet. With these examples, we represented motion by plotting length d versus time t, as in Fig. 3. That length could be a size or a distance, and the time could be an indefinite duration, or a recurring period. We have seen that the interplay of a pair of mechanical quantities Q₁ and Q₂ produces a single kinematic power law, d = Kt^α, where the kinematic prefactor K and the dimensionless exponent α are obtained from the underlying mechanical quantities. As soon as we know the relative dimensions of the two mechanical quantities Q₁ and Q₂, we know the scaling connecting kinematics and mechanics.

Describing motion as the time series of a distance d(t) is quite visual; however, not all dynamics can easily be understood in this fashion, and it is sometimes much more practical to use different pairs of kinematic variables. Each pair of kinematic variables corresponds to a different perspective on the dynamics. In some situations, it may even be useful to manipulate mechanical rather than kinematic variables. These different kinematic and mechanical perspectives provide complementary approaches on the same physics. The “physics” is set by the quantities Q₁ and Q₂, and the perspectives are set by the choice of variables. The exact forms of the scaling differ from one perspective to another, but they are always the direct consequence of dimensional analysis.

5.1 Kinematic perspectives

For a given pair of mechanical quantities, we know since eqn (26) that the dimensions of their ratio can be expressed as a combination of space and time: . So far, we have considered cases where the spatial dimension could be associated with a variable size d, and the time dimension could be associated with a variable time t. However, in some situations the more obvious variables are different kinematic combinations.

5.1.1 Velocity profiles. Let us first come back to the example of an explosion studied by Taylor. When the explosion is initially supersonic, Taylor showed that the radius of the blast will extend for some time according to . This perspective on the dynamics is convenient, because the validity of this regime can simply be checked by measuring the radius of the blast on pictures captured at different instants,^8,165 as those reproduced in Fig. 2b. However, one may rather choose to record this explosion by measuring the speed of the blast, v, as it passes by detectors placed at different distances d from ground zero. What should we expect for v(d)? If v is defined as the instantaneous speed of the front, then v ≡ ∂d/∂t = 2d/5t, which can be expressed solely from the variable length d, as (where numerical factors are absorbed by the approximate equality). This equation still displays the same physics combining energy and density, but it is expressed from the perspective of speed versus distance, rather than distance versus time. We may write this shift in perspective by adding indices to the pair of mechanical quantities underlining this type of motion:In the second equation, one of the variables is speed, and the other is distance. One important application of this perspective is in hydrodynamics, where one is interested in representing the so-called ‘velocity profiles’.^101,112 The scaling {E,ρ}_vd provides an example of such an approach, although it is rather exotic. Let us now consider two more famous cases.

We have seen in eqn (22) that combining a viscosity and a stress yields a simple time . In the case of a Newtonian fluid like water under normal conditions, this simple time can be understood as the inverse of the deformation rate on a fluid with viscosity η, upon applying a shear stress Σ at the boundary. The deformation rate can in turn be interpreted as a ‘velocity gradient’, since . So the interplay between viscosity and stress can also be written as v/d ≃ Σ/η, or as:

In other words if a flow is determined by the interplay between a viscosity and a stress, the ‘velocity profile’ in this flow is linear. This scaling goes back all the way to Newton's definition of viscosity, but when this combination of stress and viscosity is expressed as a speed over distance, one speaks of the ‘Couette profile’ or ‘Couette flow’.¹⁰¹ This simple shear-flow naturally emerges from the interplay of stress and viscosity. Speed varies linearly with distance.

Another very useful flow is the pipe flow. Here, the profile is not linear but parabolic. Why? In this situation, the viscosity of the fluid is still relevant, but the flow is not driven by a stress at the boundary, but by a difference in pressure along the conduit. The impelling factor behind these dynamics is the gradient of pressure, which is also a force–density Ψ, since . Then, indeed, the combination of a force–density and a viscosity leads to a parabolic profile:

When the interplay of viscosity and force–density is represented from this perspective, it is referred to as the ‘Hagen–Poiseuille flow’.¹⁰¹ Note that in this equation, the distance d is defined from the center of the pipe, and v is the speed in the co-moving frame, that is, the maximum speed at the center minus the speed in the lab frame.

The scalings {Ψ,η}_vd, {Σ,η}_vd and {E,ρ}_vd give three examples of velocity profiles, illustrating a general principle that can be applied to any pair of mechanical quantities.

5.1.2 Dispersion relations. Another important kinematic perspective is that of ‘dispersion relations’.²⁰ This viewpoint on kinematics is rooted in the study of waves, where one is interested in relating the frequency of waves and their wavenumber, that is the inverse of their wavelength. We will use the symbol ω for the frequency and k for the wavenumber. So this perspective connects the inverse of time to the inverse of length . We will give two famous examples related to the waves on the surface of liquids like water.

For small waves, also called ‘ripples’,¹⁶⁶ the relevant mechanical quantities are surface tension Γ, and density ρ. We have seen this pair already, in eqn (46), in the context of pinching, coalescence and spreading of low viscosity fluids. In these cases, we saw that the interplay of the pair of mechanical quantities could be expressed as a power law of the form , where the length d was the radius of the neck for pinching and coalescence, or the radius of contact for spreading. The time t was either the time elapsed since contact for spreading and coalescence, or the time remaining before pinch-off. For ripples, the size d ≃ k⁻¹ and the time t ≃ ω⁻¹ are understood as the wavelength and period of the waves, so the perspective we started with, {Γ, ρ}_dt, can be translated to a dispersion relation {Γ,ρ}_ωk:

The regime {Γ, ρ}_ωk was first studied theoretically by Lord Kelvin,¹⁶⁷ but it is Rayleigh who first tested this regime experimentally.¹⁶⁶ An example of modern measurements of such scaling is given in Fig. 5.¹⁶⁸ The dynamics of these small ripples have exactly the same underlying physics as the dynamics of droplets, they are all due to the interplay of surface-tension and density, but this mechanical struggle is seen from different angles.

Fig. 5 Examples of dispersion relations of ‘capillary ripples’¹⁶⁸ and ‘gravity waves’¹⁶⁹ on the surface of water. The capillary ripples correspond to the pair . The gravity waves correspond to .

For Newtonian liquids like water, the dynamics of waves change when their wavelength becomes substantially larger than the capillary length which we introduced in eqn (9). In this regime, the dominant impelling factor becomes the weight density Ψ ≃ ρg, while the impeding factor remains the ‘inertia’ of the fluid encapsulated in its density ρ. Thus, the struggle is between Ψ and ρ, and we have seen this balance before in eqn (44). Just as we did for ripples, we can compare the initial scaling with how the dynamics look when given as a dispersion relation:

The waves described by this regime are famously observed not only on the surface of oceans, seas, lakes and other bodies of water, but also in the sky.²⁰ We could not find a clear reference for the first use of this regime, but it was already used as a matter of fact by Kelvin at the end of the 19th century. Fig. 5 gives an example of this scaling in the case of oceanic surface waves.¹⁶⁹

The cases discussed here provide two historically important examples of dispersion relations. Nevertheless, here again the procedure is general, and any regime can be expressed from such perspective if need be. We invite the reader to select any pair from Table 1, to derive the associated dispersion relation and to investigate if such a relation has been observed.

5.1.3 Power spectra. In the case of velocity profiles or dispersion relations, the variables used (v(d) or ω(k)) are not too distant from the initial variables (d(t)), so it is not too difficult to identify the kinship between the resulting regimes. However, for practical or historical reasons, some perspectives may use comparatively complicated kinematic variables. This is for instance the case when considering the so-called “energy” or “power” spectra, which are very useful in turbulence studies.¹⁷⁰

In the context of turbulence, one often measures what is routinely called an ‘energy spectrum’ . The first variable, k, is a wavenumber, as in the case of dispersion relations, so with . The misleadingly called “energy” is actually a kinematic quantity, with ,¹⁷⁰ so it could be thought of as a specific strength (strength over mass). Fig. 6a gives a famous example of such an energy spectrum measured in the case of turbulence in a tidal channel.¹⁷¹ These measurements were among the first to validate a prediction from Kolmogorov,¹⁷⁰ about the spectrum to be expected in the case where the turbulence is impelled by a power per unit volume Π and impaired by the density of the fluid ρ:

Note that one usually uses a so called ‘dissipation rate’ or ‘transfer rate’ ε ≡ Π/ρ, which is a ‘specific power’, i.e., power per unit mass, such that .¹⁷⁰ This kinematic notation unfortunately obscures the underlying mechanical quantities, so we shall not adopt it. As we will see now, the spectrum given in eqn (63) provides a great exercise in translation between different perspectives.

Fig. 6 (a) Kolmogorov's spectrum of ‘inertial turbulence’ {Π, ρ}_{[scr E, script letter E]k} (eqn (63)), observed in a tidal channel by Grant et al.¹⁷¹ (b) Translation of the spectrum into the evolution law for the size of strained “blobs” {Π, ρ}_dt, using d ≡ k⁻¹ and . Note that since the translation formulas neglect numerical factors, the resulting plot is only qualitative. In both (a) and (b) the grey data points deviate from Kolmogorov's scaling due to the effect of a third mechanical quantity: the viscosity of the fluid. We refer the reader to the https://youtu.be/1WP7k1VUf3Q?si=Muusfb3EDpNHB2I2 of our Mechanics series for a discussion on this crossover. It is beyond the scope of this review.

The variable is called “energy” because its integral over all wavenumbers is defined by the variance of the flow speed, also understood as ‘specific energy’: . If we maintain our neglect for numerical factors, all the subtleties of this integration should not concern us, and we can simply write . The variable is connected to the magnitude v of velocity fluctuations for each wavenumber k. Larger wavenumbers are in turn related to smaller distances, with k ≃ 1/d. Thus, we can use Kolmogorov's spectrum given in eqn (63), and to express the interplay of power-density and mass-density from a relationship between the amplitude of velocity fluctuations and the size of these fluctuations:

Velocity fluctuations over longer distances have larger amplitude. This equation encompasses the same physics as the initial Kolmogorov spectrum but it provides a slightly different perspective on the pair {Π, ρ}. From this alternate vantage point, we can more easily translate the dynamics to the perspective of a length versus a time, which we adopted for most of this review. Let us do this with an intermediate step in between:These two perspectives are quite useful for the study of so-called ‘coherent structures’, like the vortices, whirls, or eddies, which populate turbulent flows.¹⁷² These structures have attracted a lot of attention in the last 30 years, and they provide an alternative way to think about turbulence, complementary to the statistical style of spectral perspectives.¹⁷³ These coherent structures are the face of velocity fluctuations in turbulent flows. The vortices can rotate at different rates ω, which is called ‘vorticity’, with ω ≃ v/d, so .¹⁰¹ This variable ω is also connected to the zones between vortices. Here, ω is the extension rate, when the vortices rotate in different directions, or the shear rate where locally the vortices rotate in the same direction. Through shear, extension, or rotation, ω is connected to the strain rate. So eqn (65) can be interpreted as relating the strain rate to the characteristic size of the strained region, whether it is a ‘vortex filament’, or a ‘shear layer’, or some more complicated structure.^172–174

To conclude, we can mention the perspective given in eqn (66), size d versus time t, which is the initial approach of this review. In Table 1 the mass–density ρ and power–density Π are two columns apart and three lines apart so we get a size growing like time with a power . We know that one way to think about the variable d is as the size of a strained region. We know that we can think of t as the period of velocity fluctuations at this length scale, but also as the inverse of the strain rate ω on a fluid region of size d. Yet another way to think about it is following the evolution of a strained “blob” of varying size d. We do not know a priori if the blobs are getting bigger or smaller, pinching like droplets. Some blobs might grow while other deflate, but in any case dimensional analysis gives us the power law relating size and time. Although tracking this process for a single blob entangled in a sea of countless others may be challenging, we can actually estimate what we would get by translating the measured energy spectrum, as shown in Fig. 6. For each measured values of [scr E, script letter E] and k, we can compute the associated values of d ≃ k⁻¹ and . Of course, since these translation formulas neglect all numerical factors, the resulting plot in Fig. 6b can only be regarded as qualitative, but the scaling is ensured.

The four perspectives on turbulence given in eqn (63)–(66) – and any others we may like to adopt – are formally equivalent, but they collectively contribute to a richer and finer appreciation of the interplay between power–density and mass–density, the mechanical pair behind ‘inertial turbulence’. What we see is influenced by the perspective we have taken, and greater insight is reached by comparing what is perceived from different perspectives. We have seen this in some detail for the case of ‘inertial turbulence’ but the lesson is again general. In particular, we invite the reader to investigate the scalings associated with the growing number of ‘non-inertial’ types of turbulence, from visco-elastic fluids¹⁷⁵ to active matter.¹⁷⁶ Although these more exotic turbulent flows might be represented as energy spectra, [scr E, script letter E] ∼ k^α, in these cases one finds that , because mechanical pairs beyond {Π, ρ} are involved—finding which pair is the subject of current research.

5.2 Mechanical perspectives

We have seen in the previous sub-section that the effects of any one pair of mechanical quantities can be expressed from different perspectives. So far, all the perspectives we considered were kinematic, which is to say that the pair of chosen variables always had dimensions of the form (allowing x or y to be zero). For instance, we saw that Taylor's regime of explosions, could also be expressed as a velocity profile, . In the first perspective the variables are d and t, and in the second, v and d. In both cases they are kinematic quantities in a broad sense (i.e. including geometric and chronometric quantities). In some circumstances one may rather prefer to focus on mechanical variables.

A proper discussion of mechanical perspectives would lead us astray from our purpose, but let us say a few words about it here, keeping explosions as our example. To illustrate our purpose, we shall consider the following equations, all equivalent formulations of Taylor's regime:

E ≃ (ρd³)(d/t)² (67)

E/d ≃ (ρd³)(d/t²) (68)

E/d³ ≃ ρ(d/t)² (69)

E/t ≃ (ρd³)(d/t²)(d/t) (70)

The terms of a regime can be reshuffled and grouped in countless ways. Some outcomes from this reshuffling can be interpreted in terms of mechanical variables, like the four cases above.

Let us first consider eqn (67). There, the dynamics of the explosion are presented as an energy balance. On the left-hand side is the constant input of energy E coming from the bomb. On the right-hand side, the variables are grouped in such a way as to compensate each other and yield a constant result. The combination can be understood as a mechanical variable, representing the variable mass m̃ of ambient air swept-away by the blast (we use tildes for mechanical variables to differentiate them from the constant mechanical parameters of the regimes).¹⁷⁷ The entirety of the right-hand side can then be understood as the kinetic energy of the swept-up air, Ẽ ≃ m̃v², and Taylor's regime as E ≃ Ẽ, which can be interpreted as saying that the energy of the bomb is converted into the kinetic energy of the blast front.

If we now consider eqn (68), we can recover the Newtonian perspective on mechanics, a viewpoint cherished in so many textbooks. The terms of this equation are now forces, since [E/d] = [F]. We can introduce the variable “explosion force” F̃ ≃ E/d. The term ρd³ ≃ m̃ is still the variable swept-up mass, and d/t² ≃ a is the acceleration of the explosion front. Overall eqn (68) can be written as a force balance, similar to Newton's second law: F̃ ≃ m̃a.

In eqn (69), the dynamics are now described as a balance of pressures. The left-hand side, is the energy density of the explosion. The right-hand side, is the dynamic pressure emerging from the speed of the front, v ≃ d/t. Taylor's regime corresponds to a front moving in such a way that the varying energy density equals the dynamic pressure.

In eqn (70), the dynamics are described as a balance of power. The power of the explosion P̃ ≃ E/t is countered by m̃av.

In these four examples we illustrated how a given regime can be interpreted in terms of mechanical variables. Here these mechanical variables are just built from algebraic manipulations, but in some cases they can be measured using instruments designed for this purpose. For instance, in the context of explosions one may perform pressure measurements at various distances from ground zero. Many such measurements were, for instance, performed for the Trinity test, enough to confirm the validity of eqn (69) from this perspective (cf. Barschall (1945) LA-352, Graves (1945) LA-354, Manley (1945) LA-360, Bright (1945) LA-366, Marley (1945) LA-431; all these reports are available in the Los Alamos National Laboratory https://sgp.fas.org/othergov/doe/lanl/).

For more information on this topic, we invite the reader to watch our lecture series on explosions, and more particularly the episode dedicated to kinematic and mechanical perspectives (https://youtu.be/bvVCvdB5Uzk?si=7BpPAD6HsvfYjpUe).

6 Simple dimensionless numbers

https://youtu.be/aun0CHanq94?si=w6CXSKyvzqmlqrqk

We have seen in the previous section that different perspectives provide complementary approaches on the same “physics”. In the framework of this review, these “physics” are conveniently expressed by a pair of mechanical quantities {Q₁, Q₂}, taken from Table 1, and these mechanical parameters manifest themselves as regimes. The exact forms of the regimes or ‘scalings’ differ from one perspective to another, but they are always the direct consequence of dimensional analysis. They can be re-derived with a few lines of algebra. When we briefly considered mechanical variables, we observed that the kinematic components of a scaling could be combined in such a particular way as to yield a constant outcome. For instance, in the case of Taylor's regime, we saw that E ≃ (ρd³)(d/t)², and since the energy E and density ρ were constant, this meant that d³(d/t)² was also constant, despite being constructed from variables, d and t. Even if we restrict ourselves to kinematic variables, for any pair of mechanical parameters {Q₁, Q₂}, there is always a perspective that can be built to exploit this property. Kinematic variables and mechanical parameters can combine to form mechanical variables, but they can also combine in such a way as to provide a so-called ‘dimensionless number’, which provides a useful angle on the dynamics.

6.1 Constant variables

Let us consider the free fall as an example. In this context an object—like an apple—falls down to the ground. Galileo had discovered that before any significant friction can set in, the trajectory is characterized by a constant acceleration. Because this fact is now taught in pretty much all schools throughout the world, it is easy to overlook that a “constant acceleration” would have sounded like a complete oxymoron back then. Indeed “acceleration” is derived from the Latin word “accelerare”, meaning “to hasten, quicken”, whereas “constant” comes from “constantem”, meaning “standing firm”. What did Galileo mean? The distance traveled since the object was dropped increases as the square of the elapsed time, d = Kt². If instead of following the distance over time we track the speed over time, we would find that it increases linearly, v ≃ d/t ≃ Kt. Now, if we track acceleration over time, we find that it is indeed independent of time, since a ≃ v/t ≃ K. All these considerations may sound trivial if we solely consider this one example of the free fall. However, the remarks made in this particular case can be generalized to any sort of regime.

We just saw the famous example of constant acceleration, but there are “constant variables” of all kinds. If we agree to say “constant acceleration”, we should welcome this apparent contradiction as well. For any pair of mechanical quantities, for any regime, there is always a way to combine the initial variables to define a new variable, which will remain constant in the range of validity of the regime. The recipe to build such combination is simple. If we have two mechanical quantities Q₁(x₁, y₁) and Q₂(x₂, y₂), then assuming that the kinematics can be described by a variable length d and time t, we know from eqn (35) that Q₁/Q₂ ≃ d^x₁−x₂t^y₁−y₂. Since both Q₁ and Q₂ are constant parameters, the combination of variables κ ≡ d^x₁−x₂t^y₁−y₂ is also constant. The new kinematic variable κ is the constant variable of this regime.

In the case of Taylor's regime, the constant variable is thus κ ≡ d⁵t⁻², which we called “explosivity”. As shown in Fig. 7, if we plot the values of this variable for the Trinity test, we find that it remains roughly constant over time. In fact, this “constant variable” is not only constant over time, but also for all sizes d, all speeds v ≃ d/t, etc. In Fig. 7, changing the horizontal axis does not change the shape of the plot. For the x-axis, we could actually choose any kinematic quantity as long as it is not a power of explosivity, which would just replicate the y-axis. The horizontal axis is largely arbitrary. The dimensions of the selected variable are inconsequential, as are its units. In contrast, for the vertical axis, the mechanics underlying this motion suggest a particular unit for explosivity: κ₀ ≡ E/ρ, with [κ₀] = [κ], the ratio of energy and density is an explosivity. So we can use the ratio of energy and density as our “natural” or “objective” unit of explosivity (a term we shall specify in Section 6.3). Another way to say this is that N_Eρ ≡ κ/κ₀ ≡ ρd⁵/Et² provides a ‘dimensionless number’ for the pair {E, ρ}. Indeed, which is to say that the quantity N_Eρ has no dimensions. As we will see now these numbers are quite useful.

Fig. 7 The “constant variable” of the Trinity explosion, i.e., “explosivity” κ ≡ d⁵t⁻² plotted against the time since detonation t, the blast size d, the average front speed d/t, or the average front acceleration d/t². Note that the axes for speed and acceleration run from right to left, since the speed and acceleration are initially greater. The horizontal red line is the “unit of explosivity” κ₀ ≡ E/ρ. The data correspond to the set used by Taylor,⁸ and are shown as d(t) in Fig. 3a.

6.2 Dimensionless numbers

In their simplest expression, dimensionless numbers provide a privileged perspective on each particular regime. Nevertheless, the term “dimensionless number” is also used to describe more complex combinations of kinematic and mechanical quantities, with no overall dimensions of space, time or mass. In this review, we will focus on simple dimensionless numbers. For any pair of mechanical quantities {Q₁, Q₂}, we assume an initial perspective with two variables, d and t, and we define the simple dimensionless number from eqn (35) as follows:By construction we have N_Q1Q2 ≃ 1 in the range of validity of the regime.

6.2.1 The Reynolds number. To illustrate the concept of simple dimensionless numbers, let us come back to the boundary layer regime, .¹⁰¹ The dimensionless number associated with this regime is the ‘Reynolds number’ Re, which is probably one of the most famous of its kind.¹⁷⁸

According to eqn (71) the dimensionless number associated with the pair {η, ρ} is:

The dynamics of a laminar boundary layer are such that N_ηρ ≃ 1. Here, the dimensionless number is initially expressed in terms of the size d of the boundary layer, and the time t since deformation started. However, as we saw in Section 5.1.1, in hydrodynamics the scalings are more often expressed from ‘velocity profiles’, using speed v ≃ d/t and distance d. With these alternative variables N_ηρ ≃ ρdv/η, which is the better known formula for the Reynolds number. The reader is invited to check that the following expressions are also satisfying formulations of the Reynolds number: , etc. The form used depend on the choice of kinematic variables, and so on the context.

All too often, the Reynolds number is narrowly defined from one particular perspective. For instance, Wikipedia states that “The Reynolds number is the ratio of inertial forces to viscous forces”. In fact, because dimensionless numbers are dimensionless, they can be understood as ratios of any pair of quantities with the same dimensions. So the Reynolds number can indeed be defined as a ratio of (variable) forces, but it can also as a ratio of a number of other quantities. Here are some of the different ways to interpret the Reynolds number:

You can check that all these quantities have correct dimensions by using Table 1. Each particular formulation of the Reynolds number underscores a different way to think about the interplay of viscosity and density.

Among the various ways of interpreting the Reynolds number, one has a stronger standing than the others. As we saw in Section 4.4.1, the ratio of viscosity and density gives rise to ‘diffusivity’ (ν ≡ η/ρ, with ). The most natural way to express the Reynolds number is as a ratio of diffusivities:

The diffusivity ν_k is traditionally called ‘advection’ or ‘convection’ and is written as ν_k ≡ dv, or with alternate variables as ν_k ≡ d²/t or v²t, depending on context. This combination of variables provides the “constant variable” of the pair {η, ρ}, and ν ≡ η/ρ is its “objective unit” (a term we shall specify in Section 6.3).

6.2.2 The Taylor–Sedov number. The procedure we followed to construct the Reynolds number can be carried out for any regime. As we will see in the next sub-section some of the ensuing dimensionless numbers also have their own name, but most do not. Surprisingly, to the best of our knowledge the dimensionless number associated with Taylor's regime of explosions does not have a name. Since the ‘Taylor number’ refers to something else already,¹¹³ let us call it the Taylor–Sedov number, named after a Soviet physicist whom also contributed substantially to the understanding of explosion blasts.^29,179

According to eqn (71), the dimensionless number associated with the pair {E, ρ} is:

The right-most expression gives the Taylor–Sedov number from the traditional “hydrodynamic perspective”, with speed and length as variables. Dynamics following Taylor's regime correspond to a constant Taylor–Sedov number, N_Eρ ≃ 1. Contrary to the Reynolds number, this dimensionless number is not naturally expressed as a ratio of diffusivities, but as a ratio of explosivities.

6.2.3 Multitudes of dimensionless numbers. To each pair of mechanical quantities corresponds a simple dimensionless number. Even if we restrict ourselves to the standard quantities in Table 1 we can build over three hundred different dimensionless numbers. Some of the most well-known are represented in Table 2, with some listed here with a comparison between the traditional hydrodynamic formulations and the standard definitions following eqn (71):The first two examples correspond to simple lengths (Bo and Ec). The third example corresponds to a simple time (Wi). The forth and fifth examples correspond to simple speeds (Ma and Ca). The sixth example corresponds to a regime at constant acceleration (Fr). The last example corresponds to a more “exotic” regime, where the associated constant variable is a quantity with no standard name, and dimensions .

Table 2 Simple dimensionless numbers as relations between pairs of mechanical quantities. Some representative dimensionless numbers are shown to connect the mechanical quantities of Table 1: Bo = Ψd²/Γ (Bond number), Ec = Γ/(Σd) (elasto-capillary number), (Froude number), (Mach number), Wi = ηv/(Σd) (Weissenberg number), Ca = ηv/Γ (Capillary number), Re = ρdv/η (Reynolds number), We = ρv²d/Γ (Weber number), Ne = P/(ρv³d²) (Newton or Power number), Se = ρd³v²/E (Taylor–Sedov), C₁ = F/(ρv²d²) (inertial drag coefficient), C₂ = F/(ηvd) (viscous drag coefficient). All numbers shown are standard, except for the Taylor–Sedov, which we defined in this review. The notation ‘Se’ is here to imitate the traditional style, but as mentioned in the text we recommend the standard notation introduced in eqn (71). The structure constant α₀ = S/Hv is usually defined in the special case where H = ℏ, v = c and S = S₀ = k_Ce², and in this case it is called the ‘fine structure constant.’

---

As we first observed with the Reynolds number, Re, dimensionless numbers are often referred to using the first two letters of the person most often associated with that number. This is true for the Bond, Mach, Froude or Weber numbers. This is almost true for the Weissenberg number, which uses Wi, instead of We, to avoid confusion with the Weber number. Some numbers, like elasto-capillary or capillary numbers imitate the style of one capitalized letter followed by a lower case letter, although no surnames are attached to it. This odd nomenclature can become quite unpractical when dealing with an increasing number of regimes, and can be the source of bitter priority disputes. It is one of the reasons why we advocate the more neutral and less reverent notation N_Q1Q2, as defined in eqn (71). Note also that in some cases the name used for a particular dimensionless number depends on the choice of kinematic variables. For instance, one usually refers to the ‘Weissenberg number’ to describe Wi ≡ ηv/Σd, but to the ‘Deborah number’ for De ≡ η/Σt.^180,181

As is apparent, for a given pair {Q₁,Q₂}, the traditional dimensionless numbers usually coincide with the definitions of N_Q1Q2. However, in certain cases they differ by some power, which is a vestige of historical circumstances. Indeed, dimensionless numbers are defined modulo an overall power, meaning that if a combination of kinematic variables and mechanical parameters is dimensionless, then any power of that combination is also necessarily dimensionless. So for a dimensionless number N, N^α will also be dimensionless for all values of α. Underneath this trivial fact, if κ is a constant variable for a regime, the κ^α will also be constant.

The general definition provided in eqn (71) ensures that all dimensionless numbers constructed in that way are linear in the underlying mechanical quantities, unlike Ma or Fr. In addition, since both N and N⁻¹ can be equally valid definitions, eqn (71) ensures that the impelling and impeding factors always occupy the same place from one number to another. For instance, historically, the ‘elasto-capillary number’ Ec = Γ/(Σd)¹⁴ has been defined in contrast to the Bond number, such that Ec < 1 means that d > [small script l]_ΓΣ, whereas Bo < 1 means that d < [small script l]_ΓΨ. When we use traditional definitions, all these little discrepancies pile up and end up seriously obstructing the use of these dimensionless quantities. This is another reason to prefer the notation introduced in eqn (71).

6.3 Numbers and units

We have seen that given a pair of mechanical quantities we can derive its kinematic outcome and express it from a number of perspectives. One of these perspectives combines all variables and parameters into a dimensionless number. How is this last viewpoint special? How to use dimensionless numbers to further our understanding of the relationship between mechanics and kinematics?

6.3.1 Rescaling. So far we have illustrated regimes associated with pairs of mechanical quantities, {Q₁, Q₂}, by giving single examples where the mechanical parameters took set values. For instance, when we discussed Taylor's regime {E, ρ}, we focused—like him—on the Trinity explosion, where E ≃ 10¹⁴ J and ρ ≃ 1 kg m⁻³.⁸ To gain greater insight into the use of dimensionless numbers, we need to consider a collection of dynamics governed by the same mechanical pair, but with different values for the impelling and impeding factors. We will review the case of explosions in detail in an upcoming article, so let us here consider the ‘visco-capillary’ regime as an example, i.e., the regime combining surface tension and viscosity, {Γ,η}, which we mentioned in Section 4.2 on simple speeds.

As shown in Fig. 8a, the visco-capillary regime has been observed in a number of situations where viscous fluids are driven by surface tension.¹⁰⁷ As mentioned in Section 4.2, this regime is, for instance, observed for the pinching of viscous liquid bridges.¹²⁴ In that case, t is the duration before pinch-off, and so the “actual time” runs from right to left. This pinching configuration is just one out of many possible set-ups exhibiting the regime {Γ, η}. Similar visco-capillary dynamics can also occur with rising bubbles pinching-off.^182,183 In that case, the viscosity corresponds to that of the outer fluid. This regime has also been found in a number of slightly different configurations of droplet coalescence.^184–188 For these examples, the neck between the drop grows, indicating the passage of time from left to right. As we will see shortly, the differences in setups actually have a marginal impact. The visco-capillary regime is observed during pinching, coalescence, and spreading of drops onto substrates.¹⁵⁷ For spreading the size d is the radius of contact.

Fig. 8 Illustration of “rescaling” on a set of data exhibiting the visco-capillary regime {Γ, η}. The data include various configurations of pinching,^124,182,183 coalescence^184–188 and spreading.¹⁵⁷ The data sets are available in the supplementary files of our recent review of this subject.¹⁰⁷ (a) The visco-capillary regime seen from the “canonical perspective” of a length versus a time, {Γ, η}_dt. The length d is the radius of the neck or contact area. The time t is the duration since contact for spreading and coalescence, and the duration before pinch-off for pinching. (b) The speed of the neck or of the edge of the contact area is plotted against time, {Γ, η}_vt. Since the speed is the “constant variable” of this regime, the data sets fall on plateaus. (c) Upon using the mechanical ratio Γ/η as an “objective unit” of speed, the data sets are all found to be close to 1, ηv/Γ ≃ 1. The vertical axis can also be interpreted as giving the value of the simple dimensionless number of the regime, N_Γη = Ca. The actual ordinates of each plateau give the value of the scaling constant δ_Γη in each experiment. (d) When the scaling constant is included in the definition of the dimensionless number , all data sets naturally collapse on a single plateau given by . Note that in (c) and (d), the size d is used as the horizontal axis, but any variable other than the speed v or powers of it could have been used (cf.Fig. 7).

All lines in Fig. 8a have the same slope but the intercepts are different, because the values of viscosity and surface tension are different in each case, giving rise to visco-capillary speeds ranging from over 10 m s⁻¹ for water with a bit of glycerol, in dark green,¹⁸⁷ to slightly over 1 μm s⁻¹ for colloid–polymer mixtures, in faint green.¹⁸⁶ What we observe in Fig. 8a is how all these experiments look like from the perspective of length versus time, the “canonical perspective” of this review. But we are free to adopt a different perspective, particularly a perspective where one of the axis is the “constant variable”, which in this case is the speed v ≃ d/t. In Fig. 8b we have kept the time t as the other variable, but we could have chosen the size d, or anything we want other than speed (or powers of the speed). As we have observed already in Fig. 7 the second variable is largely irrelevant. The data sets would have still looked the same: horizontal lines. Since {Γ, η} → v ≃ Γ/η, in Fig. 8b, the different ordinates of the horizontal lines associated with each experiment reflect the different values of Γ/η. Experiments found higher on the plot correspond to higher values of surface-tension or lower values of viscosity.

In Fig. 8b, regardless of the fluid and set-up, the speeds are measured in meters per second. Of course, we could have used any arbitrary unit we want like cm/min or feet/hour. The choice of unit is completely subjective. We can—if we want—measure the speed of these pinching, coalescing and spreading droplets in relation to the length of our feet (ft), and to a fraction of the rotation period of our planet (hour). We are allowed to do this, but we should recognize how presumptuous we are to expect that the dynamics of droplets would be best described by such provincial choices. When, for instance, we say that the pinching of glycerol happens at a speed around 54 feet per hour, the number we get, 54, is due to two different things. First, and hopefully, it is related to an actual natural phenomenon, which was recorded sometime around the turn of the millennium.¹²⁴ Second, the number 54 is connected to the choice of unit. If we choose different units, we get a different number, like 27.6 cm min⁻¹. So these two concepts of units and numbers are obviously related. That is not really contentious. Whether it is 54 or 27.6, these numbers are a bit random, much like our choice of units.

Can we instead find a way to define more “objective” or “natural” units, less bound to our preferences? Units that would be set by the mechanics at play? Yes we can, this unit of speed is given by the ratio of surface tension and viscosity, v₀ ≡ Γ/η. For each experiment we know the surface tension, and viscosity, so we can compute their ratio and use it directly as our unit. This unit is more objective than any of our choices because it is directly determined by the mechanical quantities dictating the dynamics.

In contrast to subjective units like meters per second, the value of the objective unit changes from one experiment to another. Once we have our objective units we can then plot all curves together, as shown in Fig. 8c. The curves now start to overlap, revealing their inherent similarity. With these objective units, all speeds are reasonably “close to 1”. Also note that plotting the speed v “in units of Γ/η” is the same as plotting the dimensionless number of the regime, which in this case is the capillary number Ca = N_Γη. In Fig. 8c, it is often said that the dynamics from Fig. 8a or b have been ‘rescaled’.

Nevertheless, the overlap between the different curves in Fig. 8c is not perfect. For all curves we may say that N_Γη ≃ 1, but not that N_Γη = 1. Now that we are reaching the end of our exploration of scalings based on pairs of mechanical quantities, it is time to come back to the difference between the approximate equality, ‘≃’, which we have been relying on, and a stricter kind of equality, ‘=’.

6.3.2 Scaling constants. Throughout this review, except on rare occasions, we have used approximate equalities, ‘≃’, which connect left and right-hand sides with the same ‘order of magnitude’. This sign has helped us absorb a number of numerical factors ‘of order 1’, which tend to cloud the expressions of regimes. For instance, in a formula such as Ω = (4π/3)r³, giving the volume of a sphere of radius r, the symbols within the brackets should not be given the same status as the term r³. When focusing on scaling, we would just write Ω ≃ r³, neglecting the numerical factors. However, as we have just seen with Fig. 8, in the end if we want to neatly overlap all dynamics pertaining to the same underlying mechanics we need to pay more attention to these factors.

A dimensional equation like [E/ρ] = [d]⁵[t]⁻² is unimpeachable and exact regardless of the values of energy, density, size and time. This is why we use the sign ‘=’. When the brackets are dropped, E/ρ ≃ d⁵t⁻², the approximate equality ‘≃’ is not so much an expression of imprecision as it is a requirement for adequacy between the chosen kinematic variables d and t, and the values of the mechanical quantities E and ρ. One may say that if the dynamics of an explosion blast are due to the interplay of energy and density, then E/ρ and d⁵t⁻² must indeed have the same order of magnitude. More generally, assuming for simplicity that we have identified a variable length d and a variable time t to describe the kinematics, if we have Q₁/Q₂ ≃ d^x₁−x₂t^y₁−y₂, we can safely assume that the dynamics are impelled by Q₁ and impeded by Q₂. However, the agreement between the two sides may not be exact. We can write this from the “canonical perspective” of length versus time:

This equation is identical to eqn (36), but we have introduced a (dimensionless) numerical correction δ_Q1Q2, in order to be able to use a strict equality. This kind of prefactor has been called by different names, like the ‘similarity constant’, or the ‘scaling constant’, or even the “fudge factor” by more facetious commentators. In contrast to the rest of the equation, this constant cannot be derived from dimensional analysis; however, dimensional analysis imposes that its value remains ‘of order 1’, roughly between 0.1 and 10. Unfortunately, making this constraint more precise would go beyond the scope of this review since it requires considering more than two mechanical quantities. Nevertheless, we can already clarify a few things about this scaling constant.

The scaling constant δ_Q1Q2 of a regime is a black box, containing all sorts of influences beyond that of the mechanical pair underlying the dynamics. For instance, consider Archimedes’ simple length . Suppose we are dealing with a sphere of diameter d, so its volume is Ω = (π/6)d³, and its mass is m = ρΩ, and so with . In this case, the scaling constant δ includes shape effects. Its value would be different if we were dealing with a cube or a pyramid, or some more complicated figure. The description of shapes may require more than a single length (height, width, etc.) and would then involve more than a pair of mechanical quantities.

When we discussed the Hooke–Rayleigh time τ_mΓ, we observed a similar effect in the time rather than the space dimension. The period of oscillation of a spring and mass system is , with δ = 2π ≃ 6.3. Such correction can very well be absorbed by redefining the variables. For instance here, we can use the angular frequency ω ≡ 2π/τ to reach where there is no more correction factor.

In some cases, as in previous two examples, the scaling constant can be disposed off by an appropriate redefinition of the variables. In other cases, a redefinition of the mechanical quantities may also be helpful. For instance, if the standard way for measuring the energy (or ‘yield’) of an explosion involved fitting the dynamics of the blast by a power law and then to set E ≡ ρK⁵, then obviously we would have with δ = 1, as long as our measurement of the air density ρ is correct. Whenever we encounter a regime with a scaling constant that conveniently reduces to one, it is probably because the mechanical quantities of this regime are actually defined in that context. However, this is rarely the case, since mechanical quantities are free to interact with so many partners, like all those given in Table 1. The difficulties in understanding the value of the scaling constant δ then lie in the fact that δ usually connects a given regime to other manifestations of its mechanical factors, beyond the range of validity of the regime. For instance, for explosions, the energy may be defined from measurements of the final blast radius [small script l], as , where Σ is the bulk modulus of the air (according to eqn (6)), or from the initial speed u, as where m is the ejected mass (according to eqn (29)). The numerical factors used in these definitions (, or ) get carried over from one equation to another and end up pilling up in the scaling constant δ.

In the case of the pinching, coalescing and spreading fluids in Fig. 8c, the ordinates of the plateaus in each data set give an average value of the scaling constant δ_Γη for each experiment. We refer the reader to our recent meta-analysis of this subject, where values of the constant are listed for all experiments shown in Fig. 8c.¹⁰⁷ The constants are all reasonably “close to 1”, but they are influenced by the geometric details of each set-up. For instance, in the case of the pinching of a liquid thread between two plates, theoretical analyses proposed slightly different values of δ_Γη depending on subtle differences: δ_Γη = 0.1666,¹²⁴δ_Γη = 0.0709,¹²⁸δ_Γη = 0.0304,^189,190 and δ_Γη = 0.0108.¹⁹⁰ The experiment on the pinching of glycerol reproduced in Fig. 8 (▲) seemed to favor Papageorgiou's value.¹²⁴

Ultimately, one may decide to include the scaling constants into the definition of the objective unit or constant variable, that is, into the definition of the simple dimensionless number, in order to achieve a more satisfying overlap of the data, as shown in Fig. 8d for the visco-capillary regime. If the scaling constant is defined from the canonical perspective in eqn (89), then amending eqn (71) we may write:

Then all data sets naturally collapse on a single plateau given by . Systematic deviations from this plateau may indicate the growing effect of mechanical quantities beyond the initial pair, for instance, the effect of the density of the fluid ρ, or the ‘Laplace force’ F ≃ Γ[small script l], when approaching the size [small script l] of the whole drop.¹⁰⁷ Since no regime extends forever, such deviations are bound to happen; however, this topic is beyond the scope of this review.

7 Conclusion

With Archimedes, Newton, Taylor, and all those who sought to explore the mechanical underpinning of space and time, this review has demonstrated the parsimonious efficiency of dimensional analysis. Whether we want to explain the magnitude of a particular volume, acceleration, or the more exotic motion of an explosion blast, the mechanical philosophy suggests a bold idea: to invoke an extra dimension, the dimension of mass [scr M, script letter M], beyond the visible dimensions of space, and time, . The scope of this simple idea is immense.

What we see as motion, size, or duration is understood as a form of shadow, cast on a plane by a much broader play. The players are the mechanical quantities, inferred by generations of researchers from their effects. The table of mechanical quantities that we built for this review provides an initial map, drawn from centuries of exploration of this mechanical pantheon. We hope that this table will incite historians of science to trace back the steps of past thinkers from one spot on the map to another, to define pressure, energy, power, action, etc. Why did so many great minds sailed these waters? How does this mechanical chart relate to the world we live in? We wish to do our part in answering these questions, and this review is a first step. In this review, we have shown what emerges from the interplay of pairs of mechanical quantities. This type of pair interaction is the elementary building block of a dimensional analysis of mechanics, to which we can refer to more succinctly as dimensional mechanics.

As we observed, numerous experiments have shown that a range of complex motions can be cast as single lines on a logarithmic scale. These straight regimes are drawn on a plane of space and time, yet we find that they can be more deeply understood as a “reflection”, or “projection”, or “shadow” of phenomena occurring at a higher dimension. What is going on is a “struggle”, or “balance”, between “competing” mechanical factors. Dimensional mechanics help us in formalizing all these colloquialisms and help us find the “causes” behind these scalings. These causes are embodied by the mechanical quantities. Any pair of mechanical quantities is associated with a regime, represented as a line in the kinematic plane. The slope of this line is given by the dimensions of the mechanical ratio. Because the standard mechanical quantities all share a dimension of mass [scr M, script letter M], such mass disappears from their ratio:

Hence kinematics emerge from a confrontation of mechanical terms. Motion, change, arises from ratios of constant mechanical parameters. Mathematical division formalizes the age-old intuition that motion results from a “tug of war” between “forces” and “masses”, between what we more generally called impelling and impeding factors.

The type of scaling observed in a particular context depends on the dimensions of the underlying mechanical parameters. Some experiments may evidence characteristic lengths, or times, or speeds, but others may record more intricate relationships between space and time. For instance, from the “canonical perspective” of a variable length measured relative to a variable time one may see scalings of the form d ∼ t^α, with or or or or etc. These exponents are not fundamentally stranger than the more traditional α = 1 of uniform motion, or α = 2 of uniformly accelerated motions. We just had less time to get used to them. In this review, we have tried to find a diverse array of examples from different fields, but the lists of scalings that we compiled represent only a fraction of what could be gathered from a more thorough investigation. We invite readers to participate in this encyclopedic enterprise, and we will welcome any correspondence to that end.

Throughout this review, we have assumed that the “relevant” mechanical quantities were known in each particular context, and so from these parameters the regimes could be derived through dimensional analysis. We understood the “play” so that we could make sense of its “shadow”, as observed from different perspectives. For instance, in the case of the Trinity explosion, knowing the energy E of the bomb and the density ρ of the air to be the relevant parameters, Taylor could derive that or . We have shown how a knowledge of mechanics implies the kinematics. But how is such knowledge gained in the first place? Mechanics implies kinematics, but the reverse is not so simple. Assuming a “canonical perspective”, we can symbolize this as follows:

Mechanical Kinematic {Q₁, Q₂} d ≃ Kt^α (92)

For a given pair of mechanical quantities {Q₁, Q₂}, there is a single associated kinematic regime. However, a single regime can be associated with a multitude of possible mechanical models (what we symbolized with the squiggly arrow). We encountered this concept in passing with the Bohr radius, which could be expressed from the electromagnetic strength and the kinetic energy of the electron, {S, E} (eqn (12)), or from the Planck constant and the momentum of the electron, {H, p} (eqn (14)). Both models gave the same result. This “redundancy” is not at all unique to the Bohr radius, it is fundamentally entrenched in the asymmetric relationship between mechanics and kinematic.

Kinematics have a lower dimension than mechanics. What we perceive as motion is only a projection of what goes on, and information is lost in this shadow play. We might see a dog or a duck on the screen, but it may actually be the hand of the puppeteer. For a given pair of mechanical quantities, Q₁(x₁, y₁) and Q₂(x₂, y₂), the resulting regime is d ≃ Kt^α, with α = (y₂ − y₁)/(x₁ − x₂). Only the relative dimensions of the mechanical quantities matter, i.e., the differences y₂ − y₁ and x₁ − x₂. Thus, a given exponent α may actually stem from an array of mechanical pairs. For instance, we saw diffusive regimes due to {E, Λ}, {Σ, χ}, {Γ, φ}, {F, ρ}, {F, η}, or {η, ρ}. Reviewing the table of mechanical quantities will confirm that these pairs have the same relative placement. So, if we do observe how can we know which mechanical pair is behind this motion? We cannot, that is, if we only observe a single regime…

On paper, power laws such as d ≃ Kt^α are ‘self-similar’;⁶ they seemingly extend to arbitrarily small or large scales. In practice, no single regime extends indefinitely. For instance, Taylor showed that the Trinity explosion of July 1945 in New Mexico followed . As shown in Fig. 3a, the data do support this model, but only for the selected time range, from a fraction of a millisecond to a fraction of a second after detonation. Taylor knew very well that this regime was only transient.^7,8 If extended indefinitely in the future, the blast would have reached New York by now! And if extended to the instant of detonation, this regime would predict a diverging front speed, since . Evidently, the balance between energy and density cannot account for the whole dynamics of the explosion. We actually know what we should expect. At small time scales, the mass of the bomb will have an effect and we would get a constant initial speed from {E, m}, according to eqn (29). At a large scale, we would reach the final blast radius set by the ambient pressure, {E, Σ}, according to eqn (6). Dynamics are never truly ‘self-similar’, because the complete play always involves more than two players.

We have learned much by focusing on pairs of mechanical quantities, and we would be right to expect that a deeper understanding of dimensional mechanics may emerge by progressively enlarging our set of mechanical parameters. We have already started exploring the effects of trios and quartets, and they greatly extend the reach of dimensional mechanics. Our https://www.youtube.com/playlist?list=PLbMiQs7eX-bbNTc-7HwdWzohUs8yPw300 on explosions documents this progression for this particular example, and starting with https://youtu.be/1WP7k1VUf3Q?si=Muusfb3EDpNHB2I2, the series on mechanics generalizes our findings. We are planning to summarize these investigations in upcoming publications, but we can already mention a few salient points, which may resonate with some of the questions that this review might have raised.

When considering three mechanical quantities, two cases should be distinguished: whether the three quantities are aligned or not. When the quantities are aligned they lead to three parallel regimes. For instance, in the special case where the quantities align on the same line in Table 1, this configuration can be used to rationalize shapes with distinct dimensions along different directions, and more generally to explore the mechanical basis of geometry. Readers wishing to delve deeper may investigate situations characterized by trios such as {E, Σ, Ψ}, which may be useful for cratering,⁶⁴ or {E, Γ, Ψ}, which may be useful for drop impact.⁸⁸ When considering trios of mechanical quantities that are not aligned, the three regimes associated with the three pairs of the trio intersect at a single point, a special event where dynamics take a turn, and which can serve as the locus of fully objective units. For instance, looking back at the dispersion relation in Fig. 5, we can easily envision that the regimes of waves {Ψ, ρ} and ripples {Γ, ρ} will intersect at a wavenumber given by the inverse of the capillary length implied by the pair {Γ, ρ}. The coordinates of the point of intersection are fully characterized by the trio {Ψ, Γ, ρ}. Another example involves considering the trio {Γ, ρ, η}, to capture the combined effects of inertia and viscosity on capillary flows. We discussed this case in a recent publication.¹⁰⁷

The key insight brought by considering a fourth quantity is even more intriguing. Quartets of mechanical quantities include four connected trios associated with intersections. The six associated regimes connect these turning points to one another, enabling, for instance, the tracking of the sequence of events in an explosion from the initial dynamics driven by the energy of the bomb E and impaired by the ejected mass m, to the gradual transformation of the blast into a simple sound wave, depending solely on the density ρ and pressure Σ of the ambient air. As shown in our https://www.youtube.com/playlist?list=PLbMiQs7eX-bbNTc-7HwdWzohUs8yPw300, a quartet such as {E, m, ρ, Σ} also provides a new kind of dimensionless number, depending solely on the constant mechanical parameters. In this particular instance, this number would be (modulo an overall power). Such dimensionless numbers enable the distinction between two broad classes of dynamics: detonations and deflagrations . More profoundly, such dimensionless numbers provides an “objective number base”, to use instead of 10 in logarithmic representations. Base 10 is an international convention for numbers, just like kilograms, meters, and seconds are international conventions for mass, length and time. If dimensional analysis is practiced beyond the mechanical duos we have been focusing on here, these four conventions are replaced with standards set by the physics of the situation under consideration.

Although the role of the mass dimension and the associated mechanical quantities is initially to “explain” the kinematics, what dimensional analysis reveals is that the “physics” of a situation also dictate the appropriate ways to represent what is observed. The kind of rescaling displayed in Fig. 8 can be brought to a whole new level by enlarging the experimental range, including the effects of more than two mechanical quantities.

Dimensional analysis is so much more than a trick to circumvent the more “rigorous” use of differential equations. Dimensions provide the fundamental structure of physics, and the dimensions of mechanics are its most robust backbone.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

VS thanks UIC and UChicago students who enrolled in his many courses and provided student perspectives in discussions on dimensions and dimensional analysis, as well as feedback on the supplementary videos. VS also wishes to thank his Soft Matter ODES-lab students. VS acknowledges Matt Tirrell, Juan de Pablo, Paul Nealey, and the Pritzker School of Molecular Engineering at UChicago for financial support during his sabbatical. MH thanks DGAPA-UNAM for funding his sabbatical, which initiated this review. VS, MH and MAF acknowledge the joyful atmosphere of the Ladoux-Mège lab, the stimulating haven that made this project possible. We owe a great debt to our predecessors and mentors, and many in the fluid mechanics, soft matter, and biophysics communities for inspiration and exemplary applications of dimensional analysis.

Notes and references

1. J. B. J. Fourier, Théorie de la chaleur, 1822.
2. A. K. T. Assis, K. Reich and K. H. Wiederkehr, 21st Century, 2002, 15, 40–48.
3. J. C. Maxwell, A treatise on electricity and magnetism, Clarendon Press, 1873, vol. 1.
4. D. J. Mitchell, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 2017, 58, 63–79.
5. E. O. Macagno, J. Franklin Institute, 1971, 292, 391–402.
6. G. I. Barenblatt, Scaling, Cambridge University Press, 2003, vol. 34.
7. G. I. Taylor, Proc. R. Soc. London, Ser. A, 1950, 201, 175–186.
8. G. I. Taylor, Proc. R. Soc. London, Ser. A, 1950, 201, 175–186.
9. E. Dussan, Annu. Rev. Fluid Mech., 1979, 11, 371–400.
10. P.-G. de Gennes, Rev. Mod. Phys., 1985, 57, 827.
11. L. Leger and J. Joanny, Rep. Prog. Phys., 1992, 55, 431.
12. S. Middleman, Modeling axisymmetric flows: dynamics of films, jets, and drops, Academic Press, 1995.
13. A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931.
14. G. H. McKinley, Rheol. Rev., 2005, 1, 1–48.
15. V. Starov, M. Velarde and C. Radke, Wetting and Spreading Dynamics, CRC Press, 2007.
16. S. Kalliadasis and U. Thiele, Thin films of soft matter, Springer, 2007, vol. 1.
17. R. V. Craster and O. K. Matar, Rev. Mod. Phys., 2009, 81, 1131.
18. D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739.
19. M. N. Popescu, G. Oshanin, S. Dietrich and A. Cazabat, J. Phys.: Condens. Matter, 2012, 24, 243102.
20. P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer Science & Business Media, 2013.
21. J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292.
22. G. Lu, X.-D. Wang and Y.-Y. Duan, Adv. Colloid Interface Sci., 2016, 236, 43–62.
23. J. Bico, É. Reyssat and B. Roman, Annu. Rev. Fluid Mech., 2018, 50, 629–659.
24. B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308.
25. D. Lohse and X. Zhang, et al. , Rev. Mod. Phys., 2015, 87, 981.
26. D. Lohse and X. Zhang, Nat. Rev. Phys., 2020, 2, 426–443.
27. H. A. Bethe, K. Fuchs, J. O. Hirschfelder, J. L. Magee and R. V. Neumann, Blast wave, Los alamos national lab nm technical report, 1958.
28. S. Glasstone, P. J. Dolan, et al., The effects of nuclear weapons, US Department of Defense, 1977, vol. 50.
29. L. I. Sedov, Similarity and dimensional methods in mechanics, CRC Press, 1993.
30. P. O. Krehl, History of shock waves, explosions and impact: a chronological and biographical reference, Springer Science & Business Media, 2008.
31. P. S. Westine, F. Dodge and W. Baker, Similarity methods in engineering dynamics: theory and practice of scale modeling, Elsevier, 2012.
32. G. F. Kinney and K. J. Graham, Explosive shocks in air, Springer Science & Business Media, 2013.
33. P. Sachdev, Shock waves & explosions, Chapman and Hall/CRC, 2016.
34. D. Thompson, On Growth and Form, Namaskar Books, 1917.
35. T. Mitchison and L. Cramer, Cell, 1996, 84, 371–379.
36. W. Alt, Dynamics of cell and tissue motion, Springer Science & Business Media, 1997.
37. M. P. Sheetz, Nat. Rev. Mol. Cell Biol., 2001, 2, 392–396.
38. K. Roberts, B. Alberts, A. Johnson, P. Walter and T. Hunt, Molecular biology of the cell, Garland Science, New York, 2002.
39. T. Lecuit and P.-F. Lenne, Nat. Rev. Mol. Cell Biol., 2007, 8, 633–644.
40. C. Le Clainche and M.-F. Carlier, Physiol. Rev., 2008, 88, 489–513.
41. T. D. Pollard and J. A. Cooper, Science, 2009, 326, 1208–1212.
42. R. Phillips, J. Kondev, J. Theriot and H. Garcia, Physical biology of the cell, Garland Science, 2012.
43. M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143.
44. U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327.
45. E. Buckingham, Phys. Rev., 1914, 4, 345.
46. L. Rayleigh, Nature, 1915, 95, 202–203.
47. P. W. Bridgman, Dimensional analysis, Yale University Press, 1922.
48. G. I. Barenblatt, Scaling, self-similarity, and intermediate asymptotics: dimensional analysis and intermediate asymptotics, Cambridge University Press, 1996.
49. J. G. Santiago, A First Course in Dimensional Analysis: Simplifying Complex Phenomena Using Physical Insight, Mit Press, 2019.
50. A. Mottana, Philosophia Scientiæ. Travaux d'histoire et de philosophie des sciences, 2017, 165–179.
51. B. Hopkinson, The National Archives, Kew, UK, 1915, 11.
52. C. Cranz, Lehrbuch der Ballistik, II Band, 1926.
53. R. G. Sachs, The dependence of blast on ambient pressure and temperature, Army ballistic research lab aberdeen technical report, 1944.
54. T. Wei and M. J. Hargather, Shock Waves, 2021, 31, 231–238.
55. V. Fokin, Atomic Energy, 2000, 89, 924–927.
56. S. P. Reynolds, Annu. Rev. Astron. Astrophys., 2008, 46, 89–126.
57. A. I. Asvarov, Astron. Astrophys., 2014, 561, A70.
58. (a) A. Einstein, Ann. Phys., 1905, 17, 549; (b) A. Einstein, Ann. Phys., 1905, 17, 132.
59. R. Phillips and S. R. Quake, Phys. Today, 2006, 59, 38–43.
60. M. Guo, A. F. Pegoraro, A. Mao, E. H. Zhou, P. R. Arany, Y. Han, D. T. Burnette, M. H. Jensen, K. E. Kasza and J. R. Moore, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8618–E8627.
61. K. Xie, Y. Yang and H. Jiang, Biophys. J., 2018, 114, 675–687.
62. R. M. Adar and S. A. Safran, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5604–5609.
63. K. Housen, R. Schmidt and K. Holsapple, J. Geophys. Res.: Solid Earth, 1983, 88, 2485–2499.
64. K. A. Holsapple, Annu. Rev. Earth Planet. Sci., 1993, 21, 333–373.
65. H. Katsuragi, et al., Physics of soft impact and cratering, Springer, 2016.
66. J. Uehara, M. Ambroso, R. Ojha and D. J. Durian, Phys. Rev. Lett., 2003, 90, 194301.
67. H. Takita and I. Sumita, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022203.
68. A. Benusiglio, D. Quéré and C. Clanet, J. Fluid Mech., 2014, 752, 123–139.
69. V. Sharma, K. Park and M. Srinivasarao, Mater. Sci. Eng., R, 2009, 65, 1–38.
70. J. B. Perrin, Nobel Lectures, 1926, 1, 2.
71. C. Clanet, C. Béguin, D. Richard and D. Quéré, J. Fluid Mech., 2004, 517, 199–208.
72. A. R. Choudhuri, Astrophysics for physicists, Cambridge University Press, 2010.
73. R. Kippenhahn, A. Weigert and A. Weiss, Stellar structure and evolution, Springer, 1990, vol. 192.
74. C. Frontali, Phys. Educ., 2013, 48, 484.
75. M.-A. Fardin and M. Hautefeuille, Am. J. Phys., 2022, 90, 914–920.
76. C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601.
77. E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 186103.
78. M. Coux and J. M. Kolinski, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 32285–32292.
79. A. Carré, J.-C. Gastel and M. E. Shanahan, Nature, 1996, 379, 432–434.
80. A. Sheludko, Adv. Colloid Interface Sci., 1967, 1, 391–464.
81. A. Nikolov and D. Wasan, Adv. Colloid Interface Sci., 2014, 206, 207–221.
82. J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2015.
83. V. M. Starov and M. G. Velarde, Wetting and spreading dynamics, CRC Press, 2019.
84. Y. Zhang and V. Sharma, Langmuir, 2018, 34, 1208–1217.
85. S. Yilixiati, E. Wojcik, Y. Zhang and V. Sharma, Mol. Syst. Des. Eng., 2019, 4, 626–638.
86. T. Bennett and D. Poulikakos, J. Mater. Sci., 1993, 28, 963–970.
87. J. Eggers, M. A. Fontelos, C. Josserand and S. Zaleski, Phys. Fluids, 2010, 22, 062101.
88. N. Laan, K. G. de Bruin, D. Bartolo, C. Josserand and D. Bonn, Phys. Rev. Appl., 2014, 2, 044018.
89. L. D. Landau, E. M. Lifshitz, et al., Theory of elasticity, Pergamon Press, Oxford New York, 1986, vol. 7.
90. P. A. Dirac, Nature, 1937, 139, 323.
91. D. J. Griffiths and D. F. Schroeter, Introduction to quantum mechanics, Cambridge University Press, 2018.
92. M. Muthukumar, Physics of Charged Macromolecules, Cambridge University Press, 2023.
93. R. Robinson and R. Stokes, Electrolyte Solutions, Dover Publications, Incorporated, 2nd edn, 2012.
94. P. C. Clemmow, Electrodynamics of particles and plasmas, CRC Press, 2018.
95. H. Kragh, Archive History Exact Sci., 2003, 57, 395–431.
96. L. de Broglie, Ann. Phys., 1925, 22–128.
97. K. Trachenko and V. Brazhkin, Sci. Adv., 2020, 6, eaba3747.
98. D. Cuvelier, M. Théry, Y.-S. Chu, S. Dufour, J.-P. Thiéry, M. Bornens, P. Nassoy and L. Mahadevan, Curr. Biol., 2007, 17, 694–699.
99. M. Fardin, O. Rossier, P. Rangamani, P. Avigan, N. Gauthier, W. Vonnegut, A. Mathur, J. Hone, R. Iyengar and M. Sheetz, Soft Matter, 2010, 6, 4788–4799.
100. G. Stokes, Trans. Camb. Philos. Soc., 1850, 9, 106.
101. L. Landau and E. Lifshitz, Fluid Mechanics, Pergamon, 1959, vol. 61.
102. W. B. Russel, W. Russel, D. A. Saville and W. R. Schowalter, Colloidal dispersions, Cambridge University Press, 1991.
103. P.-G. de Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993.
104. L. Rayleigh, et al. , Proc. R. Soc. London, 1879, 29, 71–97.
105. D. Richard, C. Clanet and D. Quéré, Nature, 2002, 417, 811.
106. J. Eggers, Rev. Mod. Phys., 1997, 69, 865.
107. M. A. Fardin, M. Hautefeuille and V. Sharma, Soft Matter, 2022, 18, 3291–3303.
108. G. Shaviv, New Astron. Rev., 2008, 51, 803–813.
109. C. Kittel, Introduction to solid state physics, John Wiley & Sons, Inc, 2005.
110. M. Z. Bazant, K. Thornton and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 021506.
111. R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999, vol. 150.
112. R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids, Fluid mechanics, John Wiley and Sons Inc., New York, NY, 1987, vol. 1.
113. M. Fardin, C. Perge and N. Taberlet, Soft Matter, 2014, 10, 3523–3535.
114. M. Doi, S. F. Edwards and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988, vol. 73.
115. T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103.
116. C. Clarke and B. Carswell, Principles of astrophysical fluid dynamics, Cambridge University Press, 2007.
117. G. I. Ogilvie and M. R. Proctor, J. Fluid Mech., 2003, 476, 389–409.
118. J. Dinic and V. Sharma, Macromolecules, 2020, 53, 4821–4835.
119. B. J. Hamrock, B. J. Schmid and B. O. Jacobson, Fundamentals of fluid film lubrication, CRC Press, 2004, vol. 169.
120. L. G. Leal, Advanced transport phenomena: fluid mechanics and convective transport processes, Cambridge University Press, 2007, vol. 7.
121. C. Pérez-González, R. Alert, C. Blanch-Mercader, M. Gómez-González, T. Kolodziej, E. Bazellieres, J. Casademunt and X. Trepat, Nat. Phys., 2019, 15, 79–88.
122. A. Puliafito, L. Hufnagel, P. Neveu, S. Streichan, A. Sigal, D. K. Fygenson and B. I. Shraiman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 739–744.
123. N. J. Mlot, C. A. Tovey and D. L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7669–7673.
124. G. H. McKinley and A. Tripathi, J. Rheol., 2000, 44, 653–670.
125. F. Melo, J. Joanny and S. Fauve, Phys. Rev. Lett., 1989, 63, 1958.
126. S. Douezan, K. Guevorkian, R. Naouar, S. Dufour, D. Cuvelier and F. Brochard-Wyart, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7315–7320.
127. S. Chandrasekhar, Hydrodynamic and hydromagnetic stability, Courier Corporation, 2013.
128. D. T. Papageorgiou, J. Fluid Mech., 1995, 301, 109–132.
129. D. A. Edwards, H. Brenner and D. T. Wasan, Interfacial transport processes and rheology, Butterworth-Heinemann, 1991.
130. H. Manikantan and T. M. Squires, J. Fluid Mech., 2020, 892, P1.
131. A. D. Nikolov, D. T. Wasan and P. Wu, Curr. Opin. Colloid Interface Sci., 2021, 51, 101387.
132. T. Svedberg, Nobel Lectures, 1966.
133. S. Claesson and K. O. Pedersen, Biogr. Mem. Fellows R. Soc., 1972, 18, 594–627.
134. R. Bird, W. Stewart and E. Lightfoot, Transport Phenomena, Wiley, 2006.
135. A. Einstein, Ann. Phys., 1905, 17, 549.
136. R. M. German, P. Suri and S. J. Park, J. Mater. Sci., 2009, 44, 1–39.
137. J. Burton, J. Rutledge and P. Taborek, Phys. Rev. Lett., 2004, 92, 244505.
138. A.-L. Biance, C. Clanet and D. Quéré, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 016301.
139. R. M. Iverson, M. E. Reid, M. Logan, R. G. LaHusen, J. W. Godt and J. P. Griswold, Nat. Geosci., 2011, 4, 116–121.
140. J. D. Paulsen, R. Carmigniani, A. Kannan, J. C. Burton and S. R. Nagel, Nat. Commun., 2014, 5, 1–7.
141. M. J. Murphy and R. J. Adrian, Exp. Fluids, 2010, 49, 193–202.
142. L. Bocquet and J.-L. Barrat, Soft Matter, 2007, 3, 685–693.
143. M. Hénot, E. Drockenmuller, L. Léger and F. Restagno, ACS Macro Lett., 2018, 7, 112–115.
144. C.-L. Navier, Mem. Acad. Sci. Inst. Fr., 1823, 6, 389–416.
145. B. Campanella, S. Legnaioli, S. Pagnotta, F. Poggialini and V. Palleschi, Atoms, 2019, 7, 57.
146. W. Lauterborn and C.-D. Ohl, Ultrason. Sonochem., 1997, 4, 65–75.
147. T. Gibaud, N. Dagès, P. Lidon, G. Jung, L. C. Ahouré, M. Sztucki, A. Poulesquen, N. Hengl, F. Pignon and S. Manneville, Phys. Rev. X, 2020, 10, 011028.
148. J. Seinfeld, J. Wei, J. Anderson and K. Bischoff, Advances in Chemical Engineering, Elsevier Science, 1992.
149. I. M. Jánosi, D. Jan, K. G. Szabó and T. Tél, Exp. Fluids, 2004, 37, 219–229.
150. M.-M. Mac Low and R. S. Klessen, Rev. Mod. Phys., 2004, 76, 125.
151. O. A. Basaran, AIChE J., 2002, 48, 1842.
152. E. Villermaux, Annu. Rev. Fluid Mech., 2007, 39, 419–446.
153. J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601.
154. H. P. Kavehpour, Annu. Rev. Fluid Mech., 2015, 47, 245–268.
155. J. B. Keller and M. J. Miksis, SIAM J. Appl. Math., 1983, 43, 268–277.
156. L. Courbin, J. C. Bird, M. Reyssat and H. Stone, J. Phys.: Condens. Matter, 2009, 21, 464127.
157. A. Eddi, K. G. Winkels and J. H. Snoeijer, Phys. Fluids, 2013, 25, 013102.
158. A. Eddi, K. Winkels and J. Snoeijer, Phys. Rev. Lett., 2013, 111, 144502.
159. F. Feslot, A. Cazabat and N. Fraysse, J. Phys.: Condens. Matter, 1989, 1, 5793.
160. J. Kepler, Astronomia nova, American Philosophical Society, 1609, vol. 209.
161. G. Galilei, Dialogue concerning the two chief world systems, Univ. of California Press, 1632.
162. I. Newton, The Principia: mathematical principles of natural philosophy, Univ. of California Press, 1687.
163. C. V. Boys, Nature, 1894, 50, 571.
164. L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001.
165. J. E. Mack, Semi-popular motion-picture record of the Trinity explosion, Technical Information Division, Oak Ridge Directed Operations, 1946, vol. 221.
166. L. Rayleigh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1890, 30, 386–400.
167. W. Thomson, London, Edinburgh Dublin Philos. Mag. J. Sci., 1871, 42, 362–377.
168. D. Nikolić and L. Nešić, Eur. J. Phys., 2012, 33, 1677.
169. D. W. Wang and P. A. Hwang, J. At. Oceanic Technol., 2004, 21, 1936–1945.
170. U. Frisch, Turbulence: the legacy of AN Kolmogorov, Cambridge University Press, 1995.
171. H. Grant, R. Stewart and A. Moilliet, J. Fluid Mech., 1962, 12, 241–268.
172. O. Métais and M. Lesieur, Turbulence and coherent structures, Springer Science & Business Media, 2013, vol. 2.
173. P. A. Davidson, Y. Kaneda, K. Moffatt and K. R. Sreenivasan, A voyage through turbulence, Cambridge University Press, 2011.
174. B. Dubrulle, J. Fluid Mech., 2019, 867, P1.
175. V. Steinberg, Annu. Rev. Fluid Mech., 2021, 53, 27–58.
176. R. Alert, J. Casademunt and J.-F. Joanny, Ann. Rev. Condens. Matter Phys., 2022, 13, 143–170.
177. H. A. Bethe, K. Fuchs, J. O. Hirschfelder, J. L. Magee, R. Peieris and J. von Neumann, Blast wave, Los Alamos National lab. (lanl), Los Alamos, NM (United States) technical report, 1947.
178. N. Rott, Annu. Rev. Fluid Mech., 1990, 22, 1–12.
179. M. A. Deakin, Int. J. Math. Educ. Sci. Technol., 2011, 42, 1069–1079.
180. J. M. Dealy, Rheol. Bull., 2010, 79, 14–18.
181. R. Poole, Rheol. Bull., 2012, 53, 32–39.
182. J. Burton, R. Waldrep and P. Taborek, Phys. Rev. Lett., 2005, 94, 184502.
183. R. Bolanos-Jiménez, A. Sevilla, C. Martnez-Bazán, D. Van Der Meer and J. Gordillo, Phys. Fluids, 2009, 21, 072103.
184. W. Yao, H. Maris, P. Pennington and G. Seidel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 016309.
185. D. G. Aarts, H. N. Lekkerkerker, H. Guo, G. H. Wegdam and D. Bonn, Phys. Rev. Lett., 2005, 95, 164503.
186. D. G. Aarts and H. N. Lekkerkerker, J. Fluid Mech., 2008, 606, 275–294.
187. J. D. Paulsen, J. C. Burton and S. R. Nagel, Phys. Rev. Lett., 2011, 106, 114501.
188. M. M. Rahman, W. Lee, A. Iyer and S. J. Williams, Phys. Fluids, 2019, 31, 012104.
189. J. Eggers, Phys. Rev. Lett., 1993, 71, 3458.
190. M. P. Brenner, J. R. Lister and H. A. Stone, Phys. Fluids, 1996, 8, 2827–2836.

---