Open Access Article
Open Access ArticleInelastic effects in bulge formation of inflated polymer tubes†
Fatemeh
Rouhani‡
a,
Jack Wurster
Pazin‡
a,
Brian A.
Young
c,
Qihan
Liu
 a and
Sachin S.
Velankar
a and
Sachin S.
Velankar
 *ab
*ab
aDepartment of Mechanical Engineering and Material Science, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: velankar@pitt.edu
bDepartment of Chemical Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA
cPlastics Engineering and Technology Department, Penn State University Behrend, Erie, PA 16563, USA
First published on 6th May 2024
Abstract
When a soft tube is inflated, it may sometimes show a bulge instability wherein a portion of the tube inflates much more than the rest. The bulge instability is well-understood for hyperelastic materials. We examine inflation of polyurethane tubes whose material behavior is not strictly hyperelastic. Upon inflating at constant rate, the tubes deform into a variety of shapes including irregular axisymmetric shapes with multiple localized bulges, a single axially-propagating bulge, or homogeneous cylindrical shapes. In all cases regardless of the inflation mode, the pressure first rises to a maximum, and then gradually reduces towards a plateau. We document numerous differences as compared to hyperelastic tubes. Most notably a pressure maximum can appear even without bulging, whereas for hyperelastic tubes, a pressure maximum is necessarily accompanied by bulging. Further, the decrease in pressure beyond the maximum occurs gradually over timescales as long as an hour, whereas bulging of hyperelastic tubes induces an instantaneous drop in pressure. We also observe permanent deformation upon deflation, a decrease in the pressure maximum during a subsequent second inflation, and more severe bulge localization at low inflation rates. Existing theory of hyperelastic tube inflation cannot capture the observed behaviors, even qualitatively. Finite element simulations suggest that many of the observations can be explained by viscoelasticity, specifically that a slow material response allows the pressure to remain high for long durations, which in turn allows growth of multiple bulges.
1. Introduction
When a long elastomeric tube such as a rubber hose is inflated without constraining its length, it can exhibit two limiting behaviors: homogeneous expansion maintaining a cylindrical shape (not shown), or coexistence between two cylindrical regions one of which is much more inflated than the other (Fig. 1(a)). The latter behavior is often called a propagating instability because as the tube is inflated, the more-inflated region propagates axially with no change in pressure or diameter of either region.1–11 A third behavior – a localized bulge that expands to bursting7,12 – may be regarded as a special case of Fig. 1(a) where the more-inflated region of the tube ruptures before coexistence between the two states is achieved. These behaviors can be captured by hyperelastic models of material behavior where the degree of strain hardening and the tube geometry (i.e. ratio of inner to outer diameter) determine which of these behaviors appear. If the ends of the tube are constrained, e.g. by providing a fixed axial stretch, the tubes may also buckle upon inflation.13–16 Previous articles by Fu and coauthors have provided a succinct summary of the sequence of research starting from the 1960s regarding bulging of elastic tubes.10,17 | ||
| Fig. 1 (a) Bulge propagation in a natural rubber tube in which a more-bulged region coexists with a less-inflated region. As fluid is pumped in, the bulged region propagates axially with no change in diameter. The pressure–volume curve for this inflation is shown in Fig. 8(a). (b)–(d) Irregular expansion of three polyurethane tubes inflated under the same conditions. All three were cut from the same spool of tubing and had similar initial length. Both tubes had uninflated diameter of 0.25′′ = 6.35 mm. The dark splotches on each tube are ink marks to help visualize the local area changes. | ||
However, these limiting cases are overly-simplistic and more complex behavior may appear, as illustrated in Fig. 1(b)–(d). Even though all three specimens were cut from the same spool of polyurethane tubing and inflated identically, they show distinct inflations. These behaviors do not cleanly resemble either homogeneous inflation or the bulge propagation instability of Fig. 1(a); instead, the tubes inflated in an irregular fashion, sometimes with multiple bulges separated by less-inflated regions. More strikingly than the irregular inflation, the bulges in the polyurethane tubes grow over timescales of minutes to hours, whereas in hyperelastic tubes, bulge growth is almost instantaneous. These tubes also show rate dependent inflation behavior, permanent deformation upon unloading, and loading-reloading hysteresis, all of which will be discussed below. None of these complexities can be captured by existing theories based on hyperelastic material models because hyperelastic models necessarily require the mechanical behavior to be captured by the instantaneous strain state with no dependence on deformation rate or deformation history.
This paper is an experimental study of tube inflation that includes mechanical behaviors beyond hyperelasticity. We examine the role of inelastic deformation, viscoelasticity, and strain-induced damage (i.e. permanent changes in properties upon first inflation) on the inflation behavior of polyurethane elastomer tubes. These non-elastic behaviors induce numerous differences as compared to hyperelastic tubes. Yet, the bulges are axisymmetric, which remains qualitatively similar to hyperelastic tubes. In later research to be published separately but available in a thesis,18 we will also examine large deformation inflation of polyethylene “plastic” tubes which inflate in a non-axisymmetric manner which differ from hyperelastic tubes even qualitatively.19,20
Incidentally we note that even ordinary rubber balloons – which are often cited in the literature on inflation instabilities of hyperelastic tubes – can sometimes show some of these complexities. For example, inflating a rubber balloon into the bulge propagation regime such as Fig. 1(a) and then deflating it induces a permanent increase in diameter. A second inflation can then yield three coexisting diameters, the smallest of which corresponds to the portion of the balloon that has never experienced large inflation (Fig. S1, ESI†). Such complexities are rarely discussed in the literature. Indeed, experimental papers on inflation instabilities sometimes mention that they “preconditioned” their samples by stretching them repeatedly prior to inflation,6,21–25 and it is only this preconditioning that allows them to be modeled as hyperelastic.
2. Experimental details
2.1. Tensile testing
Polyurethane tubes, with an outer diameter of 1/4 inch (6.35 mm) and an inner diameter of 5/32 inch (3.97 mm) with the product number of 5648K25, were purchased from McMaster-Carr Supply Co. The polyurethane has a durometer rating of 95A. The vendor states that the tubing was manufactured by Freelin Wade, and is a polyether-based polyurethane. The tubes were available in the form of rolled spools and hence have an intrinsic radius of curvature of 120–130 mm in their stress-free configuration. This intrinsic curvature had no noticeable effect on the inflation behavior. The rubber tube of Fig. 1(a) (outer diameter 1/4 inch, inner diameter 1/8 inch, product number 5546K42) was also purchased from the same vendor.Uniaxial tests were conducted using an Instron model 34TM-30 tensile testing machine equipped with a 30 kN load cell. The clamp-to-clamp length of the samples was 50 mm, and they were stretched at 25 mm min−1 (i.e. a nominal rate of 50% per minute) to various strains. The corresponding tensile data (Fig. 2(a)) give a tensile modulus of 56 MPa. As with many polymeric materials, the material is strongly strain hardening at strains exceeding 200%.
As mentioned in the Introduction, the tubes had readily-visible permanent deformation upon deflation. To test for inelastic behavior, the same specimens were also unloaded at the same speed. Pronounced loading–unloading hysteresis was noted, Fig. 2(a). A signature of inelastic deformation is that the force during unloading reduces to zero when the nominal strain is still non-zero. By this criterion, significant inelastic behavior (e.g. permanent strain exceeding 10%) appeared when the true strain exceeded about 50%.
The effect of elongation rate, ranging from nominal rate of 10% min−1 to 250% min−1 is shown in ESI,† Fig. S2. The tensile behavior remains qualitatively similar to that in Fig. 2, with a modest decrease in stress at lower rate.
2.2. Inflation testing
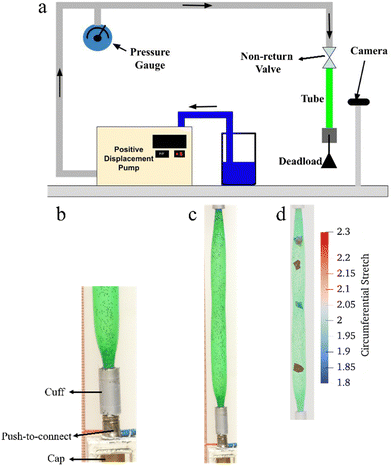
The experimental setup is shown in Fig. 3(a). Tubes were inflated using a constant-flow rate piston pump (Isco Reaxys LS). A pressure gauge (Ralston LC10-GR2M) was used to continuously monitor pressure at 1 Hz frequency. The entire inflation process was imaged, either using a video camcorder (Panasonic HC-V180 operating at 60 frames per s) or a camera (Panasonic DC-FZ80 operating with a 1–10 s duration between successive photos).All tubes were cut to a length of 200 mm, and the water was supplied from the top of the tube, whereas the bottom was capped. The fittings on both ends were of the push-to-connect type. To reduce the chance of leakage at the connections, the end section immediately adjacent to the connectors was restrained by snugly fitting aluminum “cuffs” (Fig. 3(b)). The section within the cuffs could only inflate axially, not radially. Thus, accounting for the cuff lengths and the length at each end that is inserted into the push-to-connect fittings, the section of the undeformed tube that could inflate freely was 115 mm long, corresponding to an undeformed aspect ratio L/R of 52.7, and an initial internal volume of 1.42 mL. Inflation rates ranged from 0.1 to 20 mL min−1, with a majority of the experiments being conducted at 2 mL min−1. Incidentally, if the tubes expanded circumferentially only the rate of 2 mL s−1 corresponds to an initial expansion rate of 70% per minute on the inner surface of the tube, which is comparable to the tensile testing rate in Fig. 2.
All experiments were conducted with a load of 2.44 N suspended from the bottom of the tube, which served to keep the tube approximately taut even before inflation was started. While previous experiments and theory show that inflation behavior can change with axial load,3,5,6,15,26 in fact the axial load used here is negligible. This may be judged by two criteria. First, the stress corresponding to this load is 0.13 MPa, which is too small to induce significant axial strain as judged from the uniaxial tensile data (Fig. 2(a)). Second, typical pressures during inflation are on the order of 3 MPa, which (even using the cross-sectional area of the uninflated tube diameter) corresponds to an “internal” axial force of 37.7 N, which far exceeds the 2.44 N weight suspended from the ends. Incidentally we note that past literature has considered inflation with fixed axial load as well as fixed axial stretch.14,15,23,27 We only consider the former situation in this paper. In fact, we will show that the tubes undergo significant elongation during inflation, and therefore are expected to buckle if length was fixed. The axial stretch needed to avoid such inflation-induced buckling would be sufficiently large to induce inelastic effects even without inflation.
Prior to conducting the test, the tube was sprayed with droplets of paint, or with flakes of black “glitter” to serve as markers for motion-tracking. Subsequently, the displacement of these markers was monitored using digital correlation software (Blender). The radial and axial stretch of selected regions could then be calculated from these displacement fields as shown in Fig. 3(d).
As a measure of sample-to-sample variability, we note that at an inflation rate of 2 mL min−1 (which was used for most of the experiments in this paper), a total of 24 experiments were conducted. These showed a peak pressure of 2.93 MPa with a standard deviation of 0.16 MPa, which corresponds to a 5% variation in peak pressure. Tests conducted in succession, i.e. from adjacent sections of tubing, tended to show closer agreement suggesting that at least a part of the variation may be due to small variations or imperfections in the geometry or in the mechanical properties of the tube over long lengths.
3. Results
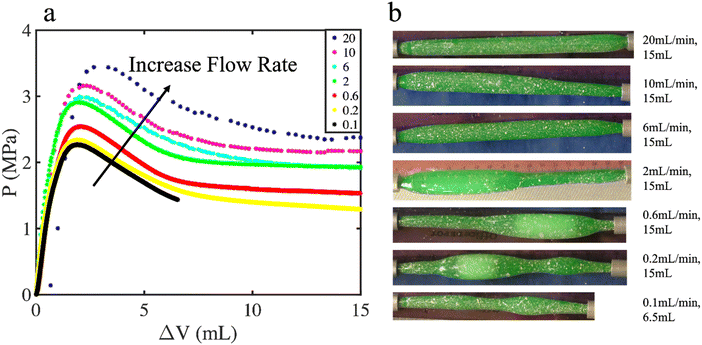
Fig. 4(a) illustrates an exemplary inflation of a polyurethane tube at a rate of 2 mL min−1, with ΔV denoting the increase in volume of the tube. Fig. 4(b) shows a rise in pressure at low inflation volumes, followed by a peak at a volume of roughly ΔV = 3 mL and a pressure of roughly 2.8 MPa. Subsequently, the pressure decreases gradually towards a plateau value of about 1.8 MPa. This decrease in pressure is denoted pressure-unloading in the rest of this paper. During this inflation, the macroscopic length of the tube increased monotonically. At the final volume of ΔV = 40 mL, the increase in length corresponds to an average axial strain of roughly 80% based on the length of the uncuffed tube at the beginning of the experiment.The evolution of pressure and tube length during inflation is qualitatively similar to that of hyperelastic tubes undergoing stable propagation of an inflated region, and similar to hyperelastic tubes, the tube develops a distinct bulge after the pressure maximum. Yet, there are some key differences. First, the pressure-unloading is gradual, occurring over several mL of volume inflation, i.e. a period of 3–5 minutes. This is in sharp contrast to the behavior of rubber tubes where the pressure-unloading is nearly instantaneous6,22,23 (also Fig. 8(a) discussed later). The second is that the inflation is irregular as was already mentioned in the Introduction. In the case of Fig. 4(a), the mid-section of the tube inflated less than the ends, and this was seen most frequently. In some cases, the inflation approximately resembled a bulge propagation instability where a more-bulged region coexists with a less-inflated region (two examples shown in Fig. 5). Furthermore, although repeated trials on identical specimens had significant variations in shape, they all had very similar pressure evolutions suggesting that the pressure is primarily related to material behavior rather than the geometric details of bulging.
To quantify the irregular deformation, Fig. 4(c) and (d) shows the circumferential and the axial stretches at four distinct locations along the tube. Up to ΔV of roughly 5 mL, all marker positions show similar deformation, indicating uniform expansion. Beyond ΔV of 5 mL, deformations at the various locations steeply deviate from each other. Later during the inflation, the least-deformed region does “catch up” with the more deformed regions, but at the final volume, there is still a difference of almost 0.8 units in the circumferential stretch of the most vs. least inflated region.
Next we examine the role of inflation rate. Tube specimens were inflated at rates ranging from 0.1 to 20 mL min−1. Fig. 5(a) shows that the peak pressure and the plateau pressure both increase modestly with increasing flow rate. At the lowest rates examined, the pressure does not show a true plateau, but instead continues to reduce gradually with continued inflation. The inflation rate strongly affects the tube shapes, with low rates promoting a greater degree of localized bulging, and high rates appearing relatively more homogeneous. It is noteworthy that the volume required for pressure-unloading remains roughly 5 mL regardless of rate, and by implication, the time required for pressure-unloading increases sharply as the flow rate reduces. For the lowest flow rate examined, the duration from the pressure peak to the end of the experiment (when the pressure had still not plateaued) exceeded 1 hour. This long timescale for unloading can be seen clearly in ESI,† Fig. S4a in which the same data are shown with time on the x-axis. A remarkable observation from Fig. 5 is that despite the diverse inflation behaviors, all cases share similar pressure–volume curves. Even the cases of 6 mL min−1 and 20 mL min−1, which happen to show nearly homogeneous inflation, still show a clear maximum in the PV curve followed by pressure-unloading. In contrast, homogeneous inflation of hyperelastic tubes gives monotonically increasing PV data. This will be discussed further in Section 4.
We also examined the extent to which inflation induces irreversible softening (henceforth called strain-induced damage) of the material such that a second inflation is different from the first. Loading–unloading–reloading experiments were conducted where tubes were inflated by various volumes ΔV1 (ranging from 1.5 mL to 15 mL), then deflated to atmospheric pressure, and then reinflated. Fig. 6(a) shows the images of the samples at three stages: at the volume ΔV1 during the first inflation, at zero pressure after deflation, and at volume ΔV1 during the second inflation. Fig. 6(b) shows the pressures during the second inflation. Increasing ΔV1 first reduces, and then eliminates, the pressure peak during inflation.
Turning to the tube shapes, at first glance, the first and the second inflation appear similar, i.e. images in the third row of Fig. 6(a) are almost identical to those in the first row. However closer examination reveals that for volumes exceeding 6 mL, the regions that were more (or less) inflated after the first inflation become even more inflated (or even less inflated) during the second. This is quantified Fig. 6(c) which shows the difference in the profile between the first and second inflation for the 6 mL case.
This issue of loading–unloading–reloading behavior was tested more thoroughly elsewhere.18 Briefly, tubes were repeatedly cycled between two states: inflation by ΔV = 6 mL, and zero pressure. Over 10 cycles, the bulge grew steadily suggesting a slow but incremental damage that caused an increasing degree of bulge localization.
Finally, we also observed that tubes deflated from a large volume did not return back to their original diameter, but were distinctly distorted. Accordingly, we examined (see ESI,† Fig. S3) inelastic deformation in more detail. Briefly, ΔV values exceeding 10 mL induced significant permanent deformation. Notably, a ΔV of 6 mL that completely eliminated the pressure peak (Fig. 6(b)) did not induce significant permanent deformation, i.e. strain-induced damage precedes inelastic deformation.
4. Discussion
4.1. Interpretation based on theory of hyperelastic tubes
Fig. 4–6, and Fig. S3 (ESI†) show that the inflation behavior of these polyurethane tubes have several features that deviate from those of hyperelastic tubes. However, before discussing these deviations, it is useful to consider whether some of the observations can be predicted by existing theory of hyperelastic tubes. Accordingly, this section proceeds on the assumption that the tubes are hyperelastic, with properties corresponding to the loading curve measured experimentally (Fig. 2). The corresponding predictions for the pressure and for the deformation can then be compared against experimental measurements.We adopt the incompressible Ogden model28 for the constitutive behavior,
 | (1) |
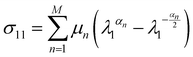 | (2) |
The parameters μn and αn can now be obtained by fitting experimental data. Fig. 7(a) shows the same data as the loading portion of the tensile data in Fig. 2, but converted to true stress by multiplying the engineering stress by the stretch (1 + ε). As a first attempt, we fitted these data to eqn (2) with no constraints on μn and αn. Adequate fits were obtained with M = 3 (dashed black line in Fig. 7(a)), and the second column of Table 1 lists the corresponding fitting parameters. These parameters, and the corresponding predictions, are referred to as unconstrained.
 | ||
| Fig. 7 (a) Fits of the loading portion of the tensile testing data to the Ogden model. All four datasets corresponding to Fig. 2(a) are shown in light colors, whereas the two fitted models are shown as the dashed black and solid purple lines. (b)–(d) Comparison of experimental data and theoretical predictions. In c and d, the green data are the average of the four markers in Fig. 4(c) and (d), wheres the green shaded region encompasses the range spanned by the markers. The inset in b shows the same pressure–volume graph, but up to higher volumes to show the dashed line Maxwell construction. | ||
The thin-wall approximation model developed by Kyriakides and Chang6 (see ESI,† Section S2 for a derivation) was then applied wherein the pressure–volume behavior of homogenous inflation regime is obtained from three equations
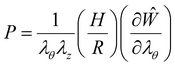 | (3) |
 | (4) |
 | (5) |
The prediction for pressure and λz can be compared against experiments such as Fig. 4 directly. The predictions for the circumferential deformation cannot be compared against experiments directly because experiments measure the stretch on the outer surface, whereas λθ in the model corresponds to the mean radial location Rm. (Note that λz is independent of radius, and hence there is no need to distinguish between the axial stretch at the outer vs. the mean radial position.) The circumferential stretch on the outer surface is related to the stretch at the mean radius by
 | (6) |
 | (7) |
Fig. 7(b)–(d) now compare the predictions for pressure and the two stretches against experiments. The model significantly overpredicts the initial rise in pressure. Beyond this quantitative error however, a more significant qualitative discrepancy is that the predicted PV curve has a very weak maximum, indeed the curve becomes almost flat before rising again, whereas the measured pressure shows a clear maximum followed by pressure-unloading. The predictions for λθo are also much higher than experiments. Perhaps the greatest discrepancy is that the model predicts λz < 1, whereas experimentally the tube lengthens upon inflation.
We therefore sought to fit the tensile data with a different set of μn, αn parameters that guarantee that the tube lengthens at the beginning of the inflation. The ESI,† Section S3 shows that the requirement that the initial inflation be accompanied by tube lengthening (not shortening) leads to the inequality
 | (8) |
Applying this inequality constraint when fitting the tensile data gives the parameters listed in the third column of Table 1, and the corresponding fit is shown as the solid purple curve in Fig. 7. This model is referred to as constrained. It is noteworthy that the fit to the constrained model cannot capture the small-strain behavior of the uniaxial tensile tests accurately, i.e. no combination of μn, αn that satisfies eqn (8) can reproduce the initial curvature of the stress–strain data. Further, a careful inspection of Fig. 7(a) shows that the purple curve overpredicts the stress between a stretch of 2 and 2.5. The corresponding prediction for pressure is shown as the solid purple curve in Fig. 7(b). While there is still a discrepancy at the earliest stages of inflation, the value of the maximum pressure is in reasonable agreement with experiments. Fig. 7(c) shows a better prediction of the experimental λθo, although the predicted λz in Fig. 7(d) still remains lower than experimental values. It must be emphasized that strictly, comparisons of the model are only reasonable up to the pressure maximum. Beyond that, the model predicts non-homogeneous inflation and should not be compared against experiments.
The purple PV curve in Fig. 7(b) is shown only to small values of volume. The inset to Fig. 7(b) shows that at larger volumes, the pressure predicted by the constrained model rises to values above the peak pressure indicating that the bulge that initiates at the pressure maximum is limited by strain hardening. Thus, the model predicts that eventually the tube must show coexistence between a bulged and an unbulged state. The coexistence pressure calculated using the Maxwell construction (inset to Fig. 7(b)) was found to be 1.76 MPa. This latter value is in remarkably good agreement with the plateau value of the pressure, even though the experiments do not actually show coexistence between a bulged and unbulged state! The corresponding stretches are found to be λθ = 3.45 (corresponding to λθo = 2.8 and λz = 1.97), values that are larger than the stretches in Fig. 4(c) and (d). Thus, as per this interpretation, the stretches in Fig. 4 have not yet reached the limiting values needed for stable coexistence and bulge propagation. Yet the qualitative behavior of Fig. 4 does not suggest stable bulge propagation will be approached at all; instead the tube already approaches homogeneity by the end of the inflation.
To summarize, the existing theory of thin-walled hyperelastic tubes, simply using the tensile loading curve to inform the constitutive behavior, is in qualitative and quantitative disagreement with experiments. If an additional constraint that the tubes must lengthen upon inflation is imposed, the small-strain tensile data are not well-captured by the constitutive equation. Yet, this ill-fitting model gives reasonable predictions for the value of the maximum pressure and the stable coexistence pressure.
Finally, note that the above judgements about the accuracy of the hyperelastic model depend on the tube radius R selected for the analysis. Eqn (3)–(5) show that for F = 0, the λθ − λz relationship is independent of the geometry, the magnitude of the predicted pressure scales with H/R, whereas the volume V0 used for normalizing the experimental data scales with R2. Our calculations all used the value of the mean radius Rm. If on the other hand the value of Ri was used for the calculations, the predicted pressure curve would increase by a factor of Rm/Ri = 1.3 whereas the value of V0 would reduce by a factor of (Ri/Rm)2 = 0.59. Accordingly, the constrained model (purple curves) would overestimate the peak pressure, but give good predictions for the value of the ΔV/V0 at the pressure maximum.
4.2. Inelastic effects and one further experiment
We now turn to the two noteworthy aspects of the inflation behavior that strongly differ from past experiments on rubber tubes.3,6,22,23 The first is that multiple specimens cut from the same spool of tubing show distinct behaviors even under identical inflation conditions. For the inflation rate of 2 mL min−1, in more than 40 experiments, we have observed several examples of tubes with irregular shapes such as in Fig. 1, several examples that approximately resemble bulge propagation, and occasional examples of nearly-homogeneous inflation. Even tubes that resemble bulge propagation show up to 20% variation in the diameter of the more-bulged and less-inflated regions. In contrast, hyperelastic tubes can only show coexistence of two well-defined strain states. Despite this variability in deformation however, all these specimens show very similar pressure–volume curves. Especially remarkable are two cases in Fig. 5 where the inflation proceeds almost homogeneously even though the PV curve shows a prominent maximum. In contrast, for hyperelastic tubes, a pressure–volume curve with a negative slope is necessarily unstable and incompatible with homogeneous inflation. This suggests that pressure-unloading is attributable not just to bulging, but also to material behavior. This notion, that material behavior is a strong contributor to pressure-unloading is also supported by the observation (Fig. 5) that despite a wide difference in the degree of bulging and a 100-fold difference in experimental timescales, the pressure-unloading remains similar, and always requires roughly 5 mL of inflation volume.A second noteworthy aspect is the simultaneous inflation of two or more bulges along a single tube. Intuition suggests that once a bulge starts growing, three factors encourage further localization. First, a bulge has a larger diameter and a thinner wall, both of which increase the local wall stress as per Laplace equation. This effect is present even in hyperelastic tubes. Second, if the material has a yield point (or undergoes strain-induced damage), the bulged region becomes more compliant. Third, as a consequence of the prior two factors, the pressure within the tube reduces, thus making it impossible to initiate new bulges. Accordingly, we expect that when a single bulge starts growing, the formation or growth of other bulges must be suppressed. Despite this however, we have noted numerous examples where more than one bulge grows simultaneously (although one always grows more than the others).
We propose that both these unusual aspects, sample-to-sample variability in bulging behavior and multiple bulges, are related to the remarkably slow pressure-unloading behavior of these tubes as compared to hyperelastic tubes. To illustrate this, Fig. 8(a) compares the pressure–volume response of the polyurethane tubing with natural rubber tubing of similar diameter and wall thickness. The natural rubber tubing (same sample as shown in Fig. 1(a)) was found to bulge “instantaneously”, i.e. the pressure reduces more steeply than can be resolved by the 1 Hz data acquisition rate. Such rapid bulging was also reported in previous studies6,22,23 and also appears in our own rubber balloon experiments from ESI,† Fig. S1. In contrast, the decrease in pressure of the polyurethane tubing occurs over several tens of seconds in Fig. 8(a), but might take over an hour at low flow rates.
 | ||
| Fig. 8 Delayed strain response of polyurethane tubes. (a) Comparison of pressure–volume curves of polyurethane tubes vs. natural rubber tubes. Note that the right and left y-axes have different scales because the natural rubber tube is much softer. The axes were scaled to approximately superpose the data at small inflation. The green data for the polyurethane tube in a is identical to Fig. 4(b). The rubber tube experiment corresponds to Fig. 1(a). (b) The axial strain measured when a tube is subjected to a rapid increase in axial load from 40 N to 140 N. | ||
Such slow unloading likely results from an intrinsically slow strain response of the polyurethane material to applied stress. To quantify this, we conducted an experiment where a polyurethane tube was first loaded with a weight of 40 N for several minutes, and then abruptly (within less than 2 s) the weight was raised to 140 N. This is conceptually similar to a creep experiment except that the force (rather than stress) is held constant. The strain evolution was obtained from quantitative analysis of images of ink marks on the tube taken during the experiment. Fig. 8(b) shows that strain increases gradually over tens of minutes before approaching a stable value.
The consequence of the slow response to load is that in the inflation experiment, the strain in the tube wall lags behind the instantaneous pressure. Once the pressure reaches the maximum value expected from homogeneous expansion, the entire tube becomes susceptible to bulging, and at some location (presumably a small defect), a bulge initiates. However, the crucial point is that because this bulge grows slowly, the tube stays at high pressure for a long duration. Thus, locations sufficiently remote from the first bulge can also initiate bulging independently. Only when one or more bulges grows sufficiently does the pressure reduce gradually, and new bulges are no longer viable; beyond this point a single bulge grows more than the others. Nevertheless, some of the other bulges can still continue growing gradually. We hypothesize that this is because strain-induced damage has already rendered these regions softer, and local creep allows a steady increase in strain with time.
4.3. Simulations of viscoelastic tubes
To flesh out the physical picture from the previous paragraph, finite element simulations were conducted. The goal was not to reproduce all the physical phenomena quantitatively, but to test whether viscoelasticity can reproduce the qualitative differences between the inflation of the polyurethane tubes vs. the theoretical expectations of hyperelastic tubes. Accordingly, we adopted the two simplest constitutive models that can highlight viscoelastic effects without confounding effects. In the first, denoted “hyperelastic”, the material was taken to be neo-Hookean with a small-strain modulus of μ∞. The second model, denoted “viscoelastic”, used the same strain-dependence as the neo-Hookean model, but the shear modulus was now taken to be time-dependent: | (9) |
 | ||
| Fig. 9 (a) Spring dashpot model corresponding to the viscoelastic constitutive behavior of eqn (9). (b) Geometry of the tube used for simulations. (c) Pressure evolution during inflation of tubes at the Wi values increasing from bottom to top as per the legend on the right of the graph. The lowest curve corresponds to the hyperelastic model. (d) Configurations of each tube at a volume ΔV/V0 of 3.9 with Wi values increasing from bottom to top. | ||
The tube was represented by a shell of radius R with hemispherical ends (Fig. 9(b)). The straight section (i.e. excluding the hemispherical ends) had length L ≫ R. The inner volume of the tube was increased at a fixed rate dV/dt. This inflation rate can be represented in non-dimensional terms as follows. Ignoring the hemispherical ends, the volume of the uninflated tube is V0 = πR2L. If the tube expands homogeneously, V = λθ2λzV0. Since the initial expansion is expected to occur without axial stretching, at the early stages of expansion, λz remains 1, and hence
 | (10) |
 | (11) |
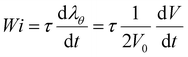 | (12) |
Having defined the constitutive models, we can now pin down the parameters that affect inflation behavior. Assuming material incompressibility, and L ≫ R, dimensional analysis requires that for the hyperelastic tube, the non-dimensional pressure P/μ∞ must depend only on ΔV/V0 with no further parameters. In contrast, for viscoelastic tubes, P/μ∞ must depend on ΔV/V0, g, and Wi. Thus the specific choice of μ∞, τ, L and R are not expected to affect the results when represented in non-dimensional terms.
Simulations were conducted using the Abaqus software with a 3D model of the geometry of Fig. 9(b), using 4-node shell elements. The geometric parameters were set to R = 2.58 mm (same as the mean value Rm for the experimental tube) and L = 150 mm. μ∞ was set to be 18 MPa for both the hyperelastic and the viscoelastic model; this value is close to the measured modulus of the experimental tube. τ was set to 1 s. However, we reiterate that, as per the previous paragraph, these parameter values are not expected to affect the non-dimensional pressure P/μ∞ presented below. The Poisson's ratio was set to 0.5 to approximate incompressible behavior. The material parameter g was set to 0.9, and more comments on this are made below. Volume-controlled inflation was simulated by thermal expansion of a virtual fluid cavity inside the closed-end tube. The virtual fluid was assigned a thermal expansion coefficient, and a temperature rise was prescribed with a constant ramp rate. Accordingly, the cavity volume increased linearly with time, and the resulting pressure within the tube was reported.
Fig. 9(c) and (d) show the evolution of the non-dimensional pressure P/μ∞ and the tube configurations during inflation for the hyperelastic (i.e. neo-Hookean) model, and for the viscoelastic model at various Wi values. As expected, the neo-Hookean tube inflates homogeneously up to a non-dimensional volume of ΔV/V0 of 1.8, upon which a bulged stage appears abruptly, i.e. the pressure–volume curve unloads almost discontinuously. The viscoelastic model shows bulge formation only at low Wi, but the bulge initiates at a larger volume than the hyperelastic tube, and the bulge grows gradually (rather than abruptly) as reflected in the gradual decrease in pressure with increasing volume. Increasing Wi raises the pressure early during inflation, and also raises the volume at which the bulge grows; this was also observed in experiments and simulations of spherical membranes.29,30 These changes are qualitatively consistent with Fig. 5. Most notably, since the bulge initiates at larger volume with higher Wi, at any selected volume, the tube inflation appears to become more homogeneous as rate increases, in agreement with experiments. Finally, at higher Wi values, a pressure maximum appears without bulge initiation, i.e. purely due to constitutive behavior of the material. This is in agreement with previous research on inflation of shells or tubes which also confirm that viscoelastic effects can give a pressure maximum even while the inflation remains homogeneous.29,30
The previous section hypothesized that multiple bulges appear because the pressure remains high for long periods, and hence can initiate other bulges. To test this hypothesis, separate simulations were conducted where the tube was endowed with two axisymmetric defects lengths of 0.46Rm and 0.39Rm separated by a tube length of 24.4Rm (Fig. 10(a)). Both defects had a local modulus that was 5.5% smaller than μ∞ and hence can serve as bulge initiation sites. In the hyperelastic case, the longer of the two defects initiated a bulge at a ΔV/V0 value of 1.7, which is close to that of the defect-free tube in Fig. 9. This single bulge abruptly reduced the pressure (Fig. 10(b)), thus suppressing growth of a second bulge, and only one bulge grew (Fig. 10(c), lowest frame). The simulation was repeated with the viscoelastic model, inflated at a Wi value of 0.006. In this case, the pressure remained high for an extended period after bulge initiation and – even though the longer defect initiated a larger bulge – both bulges started growing. Only later during the inflation did the larger bulge grow faster, causing the smaller bulge to disappear (Fig. 10(c), second frame from bottom). Raising the Wi value caused the second bulge to grow less and disappear sooner, until at Wi = 0.06, the tube expanded almost homogeneously, ignoring the defects altogether disappear (Fig. 10(c), topmost frame). A video comparing all three simulations is available as ESI.† In summary, simulations support the physical picture that multiple bulges can grow because viscoelasticity causes the pressure to remain high for relatively long durations.
 | ||
| Fig. 10 (a) Tube showing defects (in red) where local modulus is lower than the rest of the tube. Overall tube dimensions are identical to that in Fig. 9. (b) Pressure evolution during inflation of tubes with defects. (c) Configurations of each tube at selected volumes indicated by the filled points in b. | ||
Limited simulations with shorter tubes show that, consistent with previous research,7 the pressure unloading becomes more gradual as the tube length reduces, but qualitatively, the effects of increasing Wi remain the same. Simulations were also conducted with the same tube geometry at three other g values: 0.75, 0.8 and 0.95. As g approaches 1, the initial modulus increased as μ∞/(1 − g) and hence at any given Wi value, the pressure rose to a larger extent during the early, homogeneous phase of the expansion. The bulging behavior (ESI,† Fig. S5) remained qualitatively similar, except that when compared at fixed Wi, low g values caused the bulge to appear at a lower ΔV/V0 value.
Although viscoelastic simulations are in qualitative agreement with the results, viscoelasticity alone cannot fully describe the experiments. In the simulations, the bulge develops over the same timescale independent of the inflation rate. This is seen more clearly when the data of Fig. 9(c) are plotted in the form of pressure vs. time (ESI,† Fig. S4b). As a consequence, when plotted as a pressure–volume curve, the pressure-unloading appears increasingly sharp as rates reduces, e.g. compare the Wi values of 0.0006 and 0.0015 in Fig. 9(c). In stark contrast, Fig. 5 shows that the pressure unloading occurs over a similar range of volumes, which corresponds to timescales as short as few ten seconds and as long as tens of minutes (ESI,† Fig. S4a). A possible reason for the discrepancy may be that strain-induced damage plays a significant role so that significant pressure unloading happens only once the material has reached a certain minimum strain, an effect that is not captured by the linear viscoelastic model. Finally we note that inelastic deformation is not incorporated into the model, and hence the permanent diameter change noted experimentally (Fig. S3, ESI†) is not captured.
5. Summary and conclusions
To summarize, this paper explores the inflation behavior of tubes whose material behavior deviates from strict hyperelasticity. Hyperelastic tubes inflated under volume-controlled conditions are known to inflate along three possible pathways: tubes that are sufficiently strain-hardening inflate uniformly, maintaining their cylindrical shape. Tubes that have insufficient strain-hardening develop a bulge, which may either inflate to failure with a monotonic decrease in pressure, or propagate axially at constant pressure. This paper explores how the inflation behavior changes when the material comprising the tube wall has inelastic behaviors such as rate-dependent mechanical properties, strain-induced damage, and plastic deformation.Experiments with polyurethane elastomer tubes inflated at fixed flow rate show that the pressure within the tubes first rises to a maximum, and then reduces towards a plateau. While this behavior is qualitatively similar to that of hyperelastic tubes undergoing axial bulge propagation, in fact there are major differences. First, the decrease in pressure from its peak value towards a plateau value can take from tens of seconds to tens of minutes, depending on the inflation rate. In contrast, rubber tubes inflate almost instantaneously they bulge. Second, the polyurethane tubes deform into a variety of shapes: uniform inflation maintaining cylindrical shape, irregular axisymmetric shapes with multiple bulges, or axial propagation of a bulge. In all these cases – even when tubes inflate uniformly – the pressure shows a maximum value followed by unloading. In contrast, for hyperelastic tubes at fixed axial force, a peak in pressure is a necessary and sufficient condition for bulge formation. Third, if tubes are reinflated a second time, the pressure–volume curve does not show a maximum, indicating that the first inflation induced damage, i.e. a permanent change in mechanical properties due to strain. Finally, after sufficient inflation, tubes are left permanently deformed indicating plastic deformation. One observation that underpins some of these behaviors is that the polyurethane material responds to an applied load relatively slowly, on the order of many minutes. We propose that it is this slow response that causes the pressure to remain high for a long duration during inflation, and hence allow multiple bulges to grow. In contrast, since a single bulge instantaneously reduces the pressure in hyperelastic tubes, growth of multiple bulges is suppressed. This physical picture is supported by finite element simulations using a linearly viscoelastic constitutive model with a single-relaxation time.
We also tested the extent to which existing theory of hyperelastic models of tube inflation can predict the first-inflation behavior of the tubes. The first-loading uniaxial tensile testing data were fitted to the Ogden model, and the corresponding predictions were tested against the observed behavior. The theory was found to underpredict the pressure and the deformations. More significant than the quantitative discrepancy, the theory does not predict a maximum in pressure, and predicts that the tubes shorten when inflated, contrary to experiments. We show that the Ogden model can make more reasonable predictions, but only at the cost of poorly-fitting the initial portion of the uniaxial tensile testing data.
Broadly, we conclude that the tube-inflation characteristics noted in this paper appear from a complex coupling of all four phenomena: bulge formation, strain hardening, time-dependent relaxation of the material, and strain-induced damage. The first of these is a purely geometric effect, whereas the other three are material behaviors. The latter two phenomena are (by definition) absent in hyperelastic models. An especially interesting qualitative result from this paper is that a pressure peak followed by a pressure plateau – a signature of bulge initiation and propagation in hyperelastic tubes – may appear without bulge formation, and due to mechanical properties alone. While this article is fundamental in nature, it may guide the design of actuators, e.g. used in soft robotics. In those applications, consistently-repeatable actuation requires fully-reversible inflation behavior, whereas any inelastic effects may build up over time to reduce reproducibility. In addition, a large deformation even for a brief period (e.g. exposure to high pressure, local kinking) may permanently change their behavior.
The polyurethane tubes studied here showed relatively modest deviations from hyperelastic behavior. They retained one key feature of hyperelastic tube inflation, viz. the inflated tubes remain axisymmetric. In contrast, if the tubes have a relatively large yield stress, non-axisymmetric deformations appear. These will be explored in a separate publication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by NSF-DMR-2036164. We are grateful to Prof. Andrew Bunger, University of Pittsburgh, for the use of his positive displacement pump during the early portion of this research and to Mr Charles Hager, University of Pittsburgh for assistance with some of the mechanical testing. We are grateful to Dr Nhung Nguyen, University of Chicago, for her suggestion to use thermal expansion of a cavity to simulate volume-controlled inflation of the tube, and also for suggestions on an early draft.References
- A. D. Kydoniefs, Q. J. Mech. Appl. Math., 1968, 22, 319–331 CrossRef
.
- A. D. Kydoniefs and A. J. M. Spencer, Q. J. Mech. Appl. Math., 1969, 22, 87–95 CrossRef
.
- H. Alexander, Int. J. Mech. Sci., 1970, 13, 87–95 CrossRef
.
- W. L. Yin, J. Elastoplast., 1977, 7, 265–282 CrossRef
.
- D. M. Haughton and R. W. Ogden, J. Mech. Phys. Solids, 1979, 27, 179–212 CrossRef
.
- S. Kyriakides and Y.-C. Chang, Int. J. Solids Struct., 1990, 26, 975–991 CrossRef
.
- S. Kyriakides and Y.-C. Chang, Int. J. Solids Struct., 1991, 27, 1085–1111 CrossRef
.
- F. Schmidt, A. Rodriguez-Villa, F. Agassant and M. Bellet, Eur. J. Mech., 2000, 19, 89–104 CrossRef
.
- Y. B. Fu, S. P. Pearce and K. K. Liu, Int. J. Non-Linear Mech., 2008, 43, 697–706 CrossRef
.
- Y. Ye, Y. Liu and Y. Fu, J. Mech. Phys. Solids, 2020, 135, 103804 CrossRef
.
- A. H. Corneliussen and R. T. Shield, Arch. Ration. Mech. Anal., 1961, 7, 273–304 CrossRef
.
- A. A. Alhayani, J. Rodríguez and J. Merodio, Int. J. Eng. Sci., 2014, 85, 74–89 CrossRef
.
- H. Dehghani, D. Desena-Galarza, N. K. Jha, J. Reinoso and J. Merodio, Finite Elem. Anal. Des., 2019, 161, 51–60 CrossRef
.
- A. Font, N. K. Jha, H. Dehghani, J. Reinoso and J. Merodio, Mech. Res. Commun., 2021, 111, 103643 CrossRef
.
- M. Hejazi, Y. Hsiang and A. Srikantha Phani, Proc. R. Soc. A, 2021, 477, 20200837 CrossRef
.
- Y. Seddighi and H. C. Han, Front. Physiol., 2021, 12, 712636 CrossRef PubMed
.
- Y. B. Fu, J. L. Liu and G. S. Francisco, J. Mech. Phys. Solids, 2016, 90, 45–60 CrossRef
.
-
J. W. Pazin, Master thesis “An Experimental Study on the Inflation of Non-Elastic Tubes”, University of Pittsburgh, 2024
.
- M. Takla, Int. J. Pressure Vessels Piping, 2018, 159, 73–83 CrossRef
.
- B. Lindgreen, V. Tvergaard and A. Needleman, Modell. Simul. Mater. Sci. Eng., 2008, 16, 085003 CrossRef
.
- L. Horný and M. Netušil, Int. J. Mech. Sci., 2016, 106, 95–106 CrossRef
.
- Z. Guo, J. Gattas, S. Wang, L. Li and F. Albermani, Int. J. Mech. Sci., 2016, 115–116, 665–675 CrossRef
.
- S. Wang, Z. Guo, L. Zhou, L. Li and Y. Fu, J. Mech. Phys. Solids, 2019, 124, 536–554 CrossRef
.
- T. Voňavková and L. Horný, Comput. Methods Biomech. Biomed. Engin., 2020, 23, 81–91 CrossRef PubMed
.
- Z. Petřivý and L. Horný, Eur. J. Mech., 2022, 96, 104763 CrossRef
.
- D. M. Haughton and R. W. Ogden, J. Mech. Phys. Solids, 1979, 27, 489–512 CrossRef
.
- H. Demirkoparan and J. Merodio, Math. Mech. Solids, 2017, 22, 666–682 CrossRef
.
- R. W. Ogden, Proc. R. Soc. A, 1972, 326, 565–584 CAS
.
- E. Benet, H. Zhu and F. J. Vernerey, Phys. Rev. E, 2019, 99, 042502 CrossRef PubMed
.
- R. De Pascalis, W. J. Parnell, I. David Abrahams, T. Shearer, D. M. Daly and D. Grundy, Proc. R. Soc. A, 2018, 474, 20180102 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00241e |
| ‡ These authors contributed equally to the research. |
| This journal is © The Royal Society of Chemistry 2024 |