Open Access Article
Open Access ArticleThe influence of elongation-induced concentration fluctuations on segmental friction in polymer blends
Yangyang
Wang
 *a,
Shalin
Patil
b,
Shiwang
Cheng
*a,
Shalin
Patil
b,
Shiwang
Cheng
 *b and
Changwoo
Do
*b and
Changwoo
Do
 c
c
aCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA. E-mail: wangy@ornl.gov
bDepartment of Chemical Engineering and Materials Science, Michigan State University, East Lansing, MI 48824, USA. E-mail: chengsh9@msu.edu
cNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
First published on 7th May 2024
Abstract
Recent experimental studies have revealed a lack of universality in the extensional behavior of linear polymers, which is not envisioned by classical molecular theories. These surprising findings, particularly the sharp contrast between polymer melts and solutions, have catalyzed the development of new theoretical ideas, including the concept of friction reduction in highly stretched polymer melts. By presenting evidence from rheology and small-angle neutron scattering, this work shows that deformation-induced demixing, which is due to the viscoelastic asymmetry in binary mixtures, contributes to the observed nonuniversality. In the case of polystyrene/oligostyrene blends, demixing increases the effective glass transition temperature of the long chain, leading to an apparent friction enhancement. On the other hand, the opposite case is found for the polystyrene/poly(α-methylstyrene) blend. These results highlight the important influence of deformation-induced concentration fluctuations on polymer segmental friction.
1 Introduction
The dynamic properties of polymeric liquids exhibit remarkable universalities and can often be understood using coarse-grained models.1–11 In particular, universality has been found in both linear and nonlinear shear rheology of polymer melts and solutions.2,4,10–20 It is against this backdrop that the observations of lack of universality in the extensional rheology of polymers,20–33 especially entangled polymers, come as a surprise. Several theoretical ideas, notably interchain pressure34 and friction reduction,31,35–41 have been proposed to reconcile these experimental results, but a clear understanding has not been achieved.The goal of this work is to investigate the potential role of deformation-induced demixing in the apparent lack of universality in extensional rheology of polymers. Although deformation-induced demixing and concentration fluctuations are ubiquitous and well-known phenomena,42–73 their impact on the rheological behavior of polymers has not been seriously contemplated. As we shall demonstrate below, deformation-induced demixing can not only be present in extensional flow of polymer solutions, but can also affect the rheological response. To illustrate the first point, we have carried out small-angle neutron scattering measurements of entangled polystyrene solutions during continuous uniaxial extension as well as step-strain relaxation. It is found that the viscoelastic asymmetry between the long and short chains drives the deformation-induced demixing, which occurs on time scales longer than the Rouse relaxation time of the short-chain, oligomeric styrene. Most importantly, demixing leads to a change in the effective glass transition temperature of the long chain. A qualitative theoretical picture is offered to rationalize the anomalous rheological behavior, which exhibits apparent dependence on sample composition (chemistry) and violates the principle of time–temperature equivalence. These results point to the crucial influence of deformation-induced concentration fluctuations on polymer segmental friction.
This paper is organized as follows. The Materials and methods section gives an account of the sample preparation procedures, characterization methods, and equilibrium properties of the polymer solutions. The results of the small-angle neutron scattering experiments are presented and discussed in the first part of the Results and discussion section, and the underlying physics of the deformation-induced demixing is explained. Next, the rheological consequences of demixing are discussed. The change of local glass transition temperature due to the deformation-induced concentration fluctuations turns out to be a key for understanding many aspects of the apparent lack of universality in extensional rheology of polymers, including the molecular weight and temperature effects. Lastly, to put the current investigation into a proper context, we reexamine the literature data in light of the demixing phenomenon. It is shown that these existing experimental studies indeed should involve deformation-induced demixing, whose influence on the segmental friction should be of vital importance.
2 Materials and methods
2.1 Materials
Hydrogenous (h) and deuterated (d) polystyrenes (PS) with narrow molecular weight distributions were purchased from Polymer Source, Inc. and Scientific Polymer Products Inc., along with a hydrogenous, low molecular weight poly(α-methylstyrene) (PαMS). The molecular characteristics of these samples, including the number average molecular weight (Mn), weight average molecular weight (Mw), and glass transition temperature (Tg), are provided in Table 1. Four binary polymer blends, each consisting of long and short chains, were prepared by dissolving the two components in toluene and subsequently precipitating the polymers in methanol. Due to the lack of a complete set of melt density data for all the samples, the following glassy state densities (ρ0) were used in the sample preparation and the other calculations: 1.05 g cm−3 for h-PS,74 1.065 g cm−3 for h-PαMS,74 and 1.12 g cm−3 for d-PS.75 The precipitated polymer blends were dried in a heated vacuum oven above the glass transition temperatures for at least 24 hours to remove any residual solvents. The compositions of these polymer blends are described in Table 2, where Z is the number of entanglements per chain, and ϕL and ϕS are the volume fractions of the long and short chains, respectively. The PS790K/PS4K, PS790K/PS23K, and PS130K/PS12K blends were used in the small-angle neutron scattering (SANS) experiments, whereas the melt uniaxial extension behavior of PS790K/PS4K, PS790K/PS23K, and PS790K/PαMS11K blends was examined with an SER3 fixture (Xpansion Instruments).76| Sample name | M n (kg mol−1) | M w (kg mol−1) | M w/Mn | T g [°C] |
|---|---|---|---|---|
| h-PS790K | 790 | 853 | 1.08 | 104.0 ± 0.9 |
| d-PS23K | 23.0 | 24.4 | 1.06 | 100.3 ± 1.4 |
| d-PS4K | 4.00 | 4.30 | 1.07 | 80.0 ± 0.8 |
| d-PS130K | 125 | 133 | 1.06 | 101.8 ± 1.4 |
| h-PS12K | 12.0 | 12.1 | 1.01 | 89.4 ± 0.4 |
| h-PαMS11K | 10.6 | 11.8 | 1.11 | 156.1 ± 1.2 |
| Blend name | Long chain | Short chain | ϕ L | ϕ S | Z |
|---|---|---|---|---|---|
| PS790K/PS4K | h-PS790K | d-PS4K | 0.56 | 0.44 | 21 |
| PS790K/PS23K | h-PS790K | d-PS23K | 0.56 | 0.44 | 24 |
| PS130K/PS12K | d-PS130K | h-PS12K | 0.50 | 0.50 | 2.7 |
| PS790K/PαMS11K | h-PS790K | h-PαMS11K | 0.56 | 0.44 | 26 |
The samples for the SANS experiments were molded into rectangular strips in a Carver hydraulic press at 180 °C. The prepared specimens were uniaxially stretched on a RSA-G2 solid analyzer (TA Instruments) equipped with an environmental test chamber, following well-established procedures.77–80 In each extension experiment, the polymer sample was stretched with a constant crosshead velocity to a stretching ratio of λ = 1.8 in the melt state, allowed to relax for a certain amount of time trelax, and then immediately quenched into the glassy state by pumping cold gas into the test chamber. For “continuous” extension experiments, the waiting time (i.e., stress relaxation time) trelax = 0. The initial strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0 is given by the crosshead velocity v0 and initial length of the sample l0 as
0 is given by the crosshead velocity v0 and initial length of the sample l0 as ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0 = v0/l0. Additionally, the quenching time was always significantly shorter than the waiting time as well as the Rouse relaxation time of the sample. This kind of stretch–quench method thus effectively preserved the “instantaneous” polymer structures for the ex situ SANS characterization.
0 = v0/l0. Additionally, the quenching time was always significantly shorter than the waiting time as well as the Rouse relaxation time of the sample. This kind of stretch–quench method thus effectively preserved the “instantaneous” polymer structures for the ex situ SANS characterization.
Because of the constraint of test chamber size, the stretching experiments on RSA-G2 were limited to moderate strains. Therefore, a more complete set of melt extension data was collected with a SER3 fixture fitted on an MCR302 rheometer (Anton Paar). The temperature control was achieved using a CTD600 environmental chamber, with an accuracy of ±0.1 °C. The samples were prepared in the form of filaments (1 mm in diameter) by melt extrusion with a Monsanto capillary rheometer at T = 160 °C.81 Continuous uniaxial extension experiments were carried out under constant Hencky strain rates ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) with nitrogen as the gas source.
with nitrogen as the gas source.
2.2 Differential scanning calorimetry
Differential scanning calorimetry (DSC) measurements of the neat polymers as well as the polymer blends were carried out on a DSC Q2000 from TA Instruments with aluminum hermetic pans. The glass transition temperature (Tg) was determined from the heat flow during the heating scan using the “half extrapolated tangents” method. For each sample, three heating scans were performed with rates 10 °C min−1, 5 °C min−1, and 2 °C min−1, respectively, and the glass transition temperatures reported in Table 1 are based on linear extrapolations to zero heating rate. To further illustrate the influence of molecular weight on the glass transition temperature, the data of all the polystyrene samples are also plotted in the inset of Fig. 1. | ||
| Fig. 1 (a) Linear viscoelastic spectra of the PS790K/PS4K and PS790K/PS23K blends at T = 200 °C. The inset shows that the dynamic moduli of the two samples can be overlapped with appropriate horizontal shifts. (b) SANS spectra of the polymer blends in the isotropic, undeformed state. Symbols: experimental data. Lines: Fittings with the RPA equation. The inset presents the glass transition temperature Tgs of PS4K (square), PS12K (down triangle), PS23K (circle), PS130K (up triangle), and PS790K (diamond). The black hollow circles are the Tg data from the literature.82,83 | ||
The low-molecular-weight PS4K has the lowest Tg among all the samples, around 80 °C. On the other hand, the Tg of PS23K is only slightly lower than that of PS790K. In these polystyrene–polystyrene (oligostyrene) blends, the Tg of the short chain (solvent) is always lower than that of the long chain. In contrast, in the PS790K/PαMS11K blend, the short PαMS11K has higher Tg (156.1 ± 1.2 °C) than the long chain (Tg = 104.0 ± 0.9 °C). As we shall see later, this kind of “reversed” blend provides important insight into the influence of deformation-induced demixing on rheology.
2.3 Rheology
Small-amplitude oscillatory shear measurements were carried out on an HR2 (TA Instruments) rheometer with parallel plates to evaluate the linear viscoelastic properties of the polystyrene samples. The time–temperature superposition (TTS) principle4 is used to construct master curves of the measured dynamic moduli (G* = G′ + iG′′). The linear viscoelastic spectra of PS790K/PS4K and PS790K/23K blends are shown in Fig. 1. These two samples have similar entanglement plateau moduli and widths, and their linear viscoelastic spectra can be overlapped with appropriate shifts in angular frequency [inset of Fig. 1(a)]. Additional results for the PS790K/PS4K, PS790K/PS23K, PS130K/PS12K, and PS790K/PαMS11K blends, as well as those for the neat PS4K, PS23K, PS12K, and PαMS11K melts, are included in Appendix A. The rubbery plateau modulus GN is determined from the storage modulus G′(ω) at the frequency where tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′/G′ exhibits a minimum. The average number of entanglements per chain Z = Mw/Me is estimated from the weight-average molecular weight Mw and entanglement molecular weight Me, with Me = ρ0ϕLRT/GN.4 Here, ρ0 and ϕL are respectively the density and volume fraction of the long chain, R is the gas constant, and T is the absolute temperature.
δ = G′′/G′ exhibits a minimum. The average number of entanglements per chain Z = Mw/Me is estimated from the weight-average molecular weight Mw and entanglement molecular weight Me, with Me = ρ0ϕLRT/GN.4 Here, ρ0 and ϕL are respectively the density and volume fraction of the long chain, R is the gas constant, and T is the absolute temperature.
For the entangled polymer blends, the terminal relaxation time τ of the long chain is determined from the low-frequency crossover of the storage and loss moduli as τ = ωc−1, where ωc is the crossover angular frequency. For the neat, unentangled polymers (PS4K, PS12K, PS23K, and PαMS11K), the terminal relaxation time is calculated from the steady-state creep compliance J0e and zero-shear viscosity η0 as: τ = J0eη0.4 The J0e and η0 are obtained by fitting the low-frequency dynamic mechanical spectrum:4
 | (1) |
2.4 Small-angle neutron scattering
Small-angle neutron scattering experiments were performed on the EQ-SANS beamline of the Oak Ridge National Laboratory's Spallation Neutron Source.86,87 For the PS790K/PS4K and PS790K/PS23K blends, two configurations were used to cover a scattering wavenumber (Q) range of 0.006–0.4 Å−1. The sample to detector distance was fixed at 4 m and two wavelength bands defined by the minimum wavelength of 10 Å and 2.5 Å were used. For the PS130K/PS12K blend, three configurations were used with a Q coverage of 0.003–0.5 Å−1. Here, the sample to detector distance was varied to 2.5 m, 4 m, and 9 m with wavelength bands defined by minimum wavelengths of 2.5 Å, 10 Å, and 15 Å, respectively. The obtained scattering intensities were normalized by the sample thickness, corrected by the detector sensitivity and background contributions, and placed on an absolute scale using measurements of a standard sample.88,89The results of SANS measurements of the isotropic, undeformed polymer blends PS790K/PS4K and PS790K/PS23K are shown in Fig. 1(b). These SANS spectra can be fitted with the widely used random-phase-approximation (RPA) formula:90,91
 | (2) |
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) α(Q) are respectively the volume fraction, degree of polymerization, and single-chain structure factor of component α (α = a, b). In the current context, component a is the long chain (L), and b is the short chain (S). With the Gaussian-chain assumption, the single-chain structure factor
α(Q) are respectively the volume fraction, degree of polymerization, and single-chain structure factor of component α (α = a, b). In the current context, component a is the long chain (L), and b is the short chain (S). With the Gaussian-chain assumption, the single-chain structure factor ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) α(Q) takes the form of a Debye function:
α(Q) takes the form of a Debye function: | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rg0,α = 0.4175 + 0.5076 × log10
Rg0,α = 0.4175 + 0.5076 × log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nα, which is obtained by a linear fit of the literature data.77–79,92 The resulting fitting curves from eqn (2) are presented in Fig. 1(b). The corresponding fitting parameters are: Iiso(0) = 9.23
Nα, which is obtained by a linear fit of the literature data.77–79,92 The resulting fitting curves from eqn (2) are presented in Fig. 1(b). The corresponding fitting parameters are: Iiso(0) = 9.23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, Iinc = 0.34
cm−1, Iinc = 0.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, and χ = 5.6 × 10−3 for the 790K/4K blend; Iiso(0) = 44.30
cm−1, and χ = 5.6 × 10−3 for the 790K/4K blend; Iiso(0) = 44.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, Iinc = 0.32
cm−1, Iinc = 0.32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, and χ = 5.4 × 10−4 for the 790K/23K blend. The SANS spectrum of the isotropic, undeformed PS130K/PS12K blend (not shown here) is fitted by the same procedure, and the result is: Iiso(0) = 23.19
cm−1, and χ = 5.4 × 10−4 for the 790K/23K blend. The SANS spectrum of the isotropic, undeformed PS130K/PS12K blend (not shown here) is fitted by the same procedure, and the result is: Iiso(0) = 23.19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, Iinc = 0.26
cm−1, Iinc = 0.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1, and χ ≈ 0. The success of the RPA formula and the relatively low values of χ indicate that the short and long chains are well mixed in the equilibrium, undeformed state. Although we do not have SANS data for the PS790K/PαMS11K blend, our DSC measurement and the previous studies in the literature93–96 suggest that this particular pair of PS and PαMS should be miscible at ϕL = 0.56.
cm−1, and χ ≈ 0. The success of the RPA formula and the relatively low values of χ indicate that the short and long chains are well mixed in the equilibrium, undeformed state. Although we do not have SANS data for the PS790K/PαMS11K blend, our DSC measurement and the previous studies in the literature93–96 suggest that this particular pair of PS and PαMS should be miscible at ϕL = 0.56.
3 Results and discussion
3.1 Evidence of demixing during continuous extension
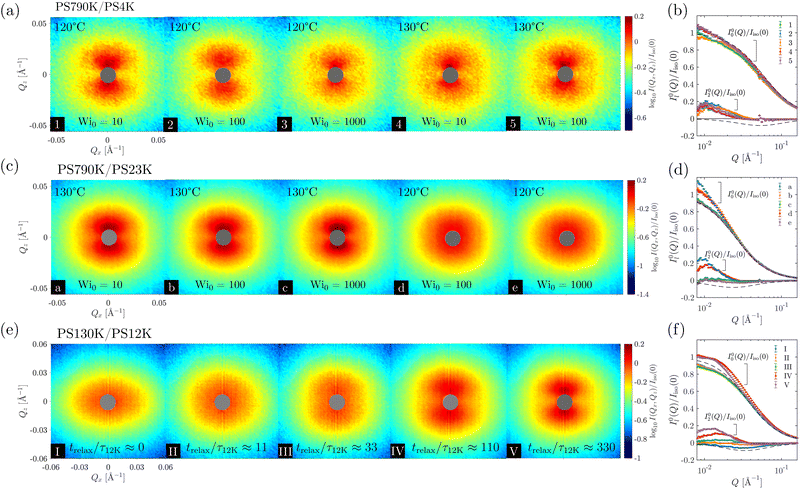
The results of SANS measurements of the PS blends during continuous uniaxial extension at various initial Weissenberg numbers (Wi0 ≡![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0τ, defined with respect to the long chain here) are shown in Fig. 2(a) and (b). As noted in the experimental section, all the spectra were taken at a stretching ratio of 1.8. With the exception of the PS790K/PS23K blend at 120 °C and Wi0 = 100 and Wi0 = 1000, butterfly patterns can be observed in all cases. Additionally, the time–temperature superposition principle does not hold in the nonlinear viscoelastic regime, as the scattering pattern is dependent on not only the effective strain rate Wi0, but also the temperature.
0τ, defined with respect to the long chain here) are shown in Fig. 2(a) and (b). As noted in the experimental section, all the spectra were taken at a stretching ratio of 1.8. With the exception of the PS790K/PS23K blend at 120 °C and Wi0 = 100 and Wi0 = 1000, butterfly patterns can be observed in all cases. Additionally, the time–temperature superposition principle does not hold in the nonlinear viscoelastic regime, as the scattering pattern is dependent on not only the effective strain rate Wi0, but also the temperature.
To quantify the structural changes under uniaxial extension and better illustrate the failure of TTS, the measured 2D SANS spectra are analyzed with the spherical harmonic expansion technique.72,77,79,97 Specifically, the scattering intensity I(Q) is expanded as  where θ is the polar angle, ϕ is the azimuthal angle, Y0l(θ,ϕ) is the spherical harmonic function of degree l and order zero, and I0l(Q) is the corresponding coefficient. The definitions of the spherical harmonic functions follow the ones used in our previous work,77 where the normalization condition is
where θ is the polar angle, ϕ is the azimuthal angle, Y0l(θ,ϕ) is the spherical harmonic function of degree l and order zero, and I0l(Q) is the corresponding coefficient. The definitions of the spherical harmonic functions follow the ones used in our previous work,77 where the normalization condition is 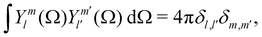 with δl,l′ and δm,m′ being the Kronecker δ-functions. In the case of uniaxial extension, the spherical coordinates are placed in such a way that the z axis is along the stretching direction, and the xz plane is perpendicular to the incident beam and parallel to the sample.77 The expansion coefficient I0l(Q) is related to the experimentally measured scattering intensity from the xz plane Ixz(Q,θ) as:
with δl,l′ and δm,m′ being the Kronecker δ-functions. In the case of uniaxial extension, the spherical coordinates are placed in such a way that the z axis is along the stretching direction, and the xz plane is perpendicular to the incident beam and parallel to the sample.77 The expansion coefficient I0l(Q) is related to the experimentally measured scattering intensity from the xz plane Ixz(Q,θ) as:
 | (4) |
To further enhance insight, we compute the spherical harmonic expansion coefficients of the blends using the random-phase approximation, where the mixing state is assumed to be unaffected by the deformation. The normalized anisotropic scattering intensity I(Q)/Iiso(0) is given by
 | (5) |
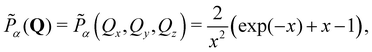 | (6) |
| x = Rg0,α2(λα−1Qx2 + λα−1Qy2 + λα2Qz2). | (7) |
 | (8) |
Several observations from the spherical harmonic expansion analysis are worth noting. First, our previous study demonstrated that positive I02(Q) is associated with butterfly scattering patterns whereas negative I02(Q) produces ellipsoidal patterns.72 The current results in Fig. 2 are consistent with this prior finding: the anisotropic expansion coefficients I02(Q) are positive within the experimental Q range for the butterfly patterns (spectra 1–5, a, b, and c); the I02(Q) is close to zero for the SANS spectrum of the PS790K/PS23K blend at Wi0 = 100 and 120 °C (spectrum d); and the I02(Q) is slightly negative for the ellipsoidal spectrum of PS790K/PS23K at Wi0 = 1000 and 120 °C (spectrum e). Second, the failure of TTS becomes quite evident, when the 2D SANS spectra are quantified by the spherical harmonic expansion technique. The expansion coefficients I00(Q) and I02(Q) are not identical for the same sample stretched under the same Wi0. Third, the short-chain molecular weight clearly plays a role in the structural evolution during extension, even when Wi0 and temperature are kept the same (e.g., spectra 3 and e). This behavior is consistent with the previous reports of a lack of universality in the uniaxial extension of entangled polymers,26,33 where the solvent molecular weight effect was observed. Lastly, a comparison with the RPA reference curves (dashed lines) suggests that some degree of deformation-induced demixing is still present in the samples that do not exhibit butterfly patterns [spectra (d) and (e)], as their anisotropic coefficients I02(Q) are substantially smaller than the RPA predictions (in magnitude). This is due to the cancellation effect from intramolecular and intermolecular correlations.72
The emergence of butterfly patterns is a direct result of deformation-induced demixing,72 which has been attributed to the asymmetric stress division in polymer blends that drives diffusion of short chains in the direction perpendicular to stretching.98–102 Our previous investigation72 indicates that Wi0 ≪ 1 for the short chain is a necessary condition for generating butterfly patterns, i.e., deformation-induced demixing in polymer blends. Using the Lodge–McLeish model, the short-chain relaxation time in the blend can be estimated (see Appendix B for details). Combined with the long-chain relaxation time directly measured by small-amplitude oscillatory shear, we find that the ratio of long chain and short chain terminal relaxation times is approximately 3.3 × 105 for the PS790K/PS4K at the experimental temperatures, and 1.0 × 104 for the PS790K/PS23K. The condition of Wi0 ≪ 1 is thus satisfied for both PS4K and PS23K in these blends. Nevertheless, the difference in the glass transition temperature and relaxation time of the short chains should play an important role in the lack of universality in the extensional rheology of these polymer blends. The full consequence of deformation-induced demixing on the rheological behavior will be discussed in detail in Section 3.3. It is worth noting that the deformation-induced demixing is directly connected to the diffusive kinetics of the short chains and the enhanced concentration fluctuations at lower Wi0 [Fig. 2(a)–(d)] are a result of the prolonged time for molecular diffusion.72
3.2 Evidence of demixing during stress relaxation
To illustrate the ubiquity of the deformation-induced demixing in polymer blends, we now turn our attention to stress relaxation. In this case, the PS130K/PS12K blend was uniaxially stretched to an extension ratio of λ = 1.8 at 110 °C with an effective initial Weissenberg number Wi0 = 1.9 × 102 for the long chain (Wi0 ≪ 1 for the short chain), allowed to relax for trelax = 0, 100, 300, 1000, and 3000 s, and subsequently quenched into the glassy state for ex situ SANS measurements. The terminal relaxation times τ of the long and short chains are about 1.9 × 104 and 9 s respectively at the experimental temperature of 110 °C. Therefore, even at the longest time of trelax = 3000 s, the long chains still retain a substantial amount of stress whereas the short chains have sufficient time to relax and diffuse over a large distance. The results of the SANS experiments are shown in Fig. 2(e) and (f), and the corresponding stress data are presented in Fig. 3.Immediately after the step deformation (trelax ≈ 0), the SANS spectrum displays an ellipsoidal pattern, suggesting that the coherent scattering is dominated by the intramolecular correlations of the stretched chain [spectrum I of Fig. 2(e)]. Nevertheless, a weak degree of demixing may have occurred during the step extension, as the duration of the deformation is longer than the relaxation time of the short chain. Quantitative analysis with the spherical harmonic expansion technique seems to confirm this conclusion [Fig. 2(f)], as the experimental structural anisotropy I02(Q) is still smaller than the RPA prediction. With the progression of stress relaxation, the short chains continue to migrate in the direction perpendicular to stretching, due to the viscoelastic asymmetry between long and short chains. Consequently, butterfly patterns start to develop. This process is clearly captured by the spherical harmonic expansion analysis—demixing leads to a change of sign in I02(Q) and an enhancement of the isotropic, zero-angle scattering intensity.72
The stress relaxation experiment is a powerful demonstration of the nature of deformation-induced demixing—it is not caused by convection itself, but the viscoelastic asymmetry of the two components, i.e., the coexistence of fast- and slow-relaxing chains.98–101 Since the underlying physics here is entirely general, deformation-induced demixing should be present in many polymer blends and solutions—a fact that is often underappreciated in rheological measurements at large deformations. In the next section, we will explore the consequence of deformation-induced demixing and explain its important role in the loss of universality in extensional rheology of entangled polymers.
In passing, we note that a previous SANS investigation of PS blends during stress relaxation did not reveal any butterfly patterns.103 A closer look at their experimental conditions indicates, however, that the SANS spectra were taken up to only two times of the relaxation time of the short chain, which would be insufficient for full development of deformation-induced demixing. In other words, there is no contradiction between the current and previous reports.
3.3 Consequence of demixing: change of local friction
Now we ask the most important question: what is the consequence of deformation-induced demixing and how is it related to the lack of universality in extensional rheology of polymers? We observe that in many polymer blends and solutions, the short chains or solvent molecules have a much lower glass transition temperature than the long chains. As the long chain and solvent demix under deformation, the effective glass transition temperature of the long chain, which controls the rheological response, should start to increase. In other words, deformation-induced demixing leads to an increase of the local friction of the long chain in such blends or solutions. This picture offers an important clue for understanding the sharp contrast between polymer melts and solutions in steady extensional flow, where melts display thinning behavior and solutions exhibit hardening behavior.24 Since the “standard” tube model predicts a hardening behavior of steady-state extensional viscosity of entangled polymers when the Rouse Weissenberg number is greater than unity,34 which is in apparent, qualitative agreement with the experimental data on polymer solutions but at odds with the data on polymer melts, recent research attention has been focused on searching for a friction reduction mechanism in polymer melts to explain its extensional thinning behavior. We argue that the effect of deformation-induced demixing is also of great importance in understanding the differences in the rheological behaviors among polymer blends, solutions, and melts, where the presence of viscoelastic asymmetry is almost ubiquitous in the former two.69,104,105To further test the proposed picture, we now take a closer look at the rheological behavior of deformed polymer blends. In the present analysis, we will highlight two noteworthy consequences of deformation-induced demixing. One concerns the effect of short-chain molecular weight on the rheological behavior of polymer blends, and the other relates to the failure of time–temperature superposition (TTS) in the large-deformation limit. Both of them derive from the change in local friction associated with demixing.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kg mol−1, the lower molecular weight solvent should produce a larger increase of the effective Tg for the long chain upon demixing. At the same Weissenberg/Rouse Weissenberg number as determined from the equilibrium state, the effective rate would be much higher for the solution with short chains of lower molecular weight.
kg mol−1, the lower molecular weight solvent should produce a larger increase of the effective Tg for the long chain upon demixing. At the same Weissenberg/Rouse Weissenberg number as determined from the equilibrium state, the effective rate would be much higher for the solution with short chains of lower molecular weight.
The above explanation is not only consistent with the steady-state data in the literature26 but is also supported by the transient stress–strain data from the current investigation. Fig. 4(a) compares the stress–strain behavior of PS790K/PS4K and PS790K/PS23K at Weissenberg numbers (Wi ≡ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) τ) of 63 and 1000 at 140 °C. Here, the Weissenberg number is computed using the terminal relaxation time of the long chain (blend) in the equilibrium, mixed state. The DSC measurements (Table 1) indicate that the d-PS4K has a glass transition temperature around 80 °C, whereas the d-PS23K has a Tg around 100 °C, which is fairly close to that of the h-PS790K (104 °C). Therefore, deformation-induced demixing should have a much larger impact on the effective Tg of PS790K in PS790K/PS4K than in PS790K/PS23K. In accordance with our expectation, the PS790K/PS4K exhibits higher stress than the PS790K/PS23K at large strains. Therefore, a proper understanding of such phenomena should require consideration of the change in local effective glass transition temperature due to demixing, besides the potential influence of nematic interactions.26,106–109
τ) of 63 and 1000 at 140 °C. Here, the Weissenberg number is computed using the terminal relaxation time of the long chain (blend) in the equilibrium, mixed state. The DSC measurements (Table 1) indicate that the d-PS4K has a glass transition temperature around 80 °C, whereas the d-PS23K has a Tg around 100 °C, which is fairly close to that of the h-PS790K (104 °C). Therefore, deformation-induced demixing should have a much larger impact on the effective Tg of PS790K in PS790K/PS4K than in PS790K/PS23K. In accordance with our expectation, the PS790K/PS4K exhibits higher stress than the PS790K/PS23K at large strains. Therefore, a proper understanding of such phenomena should require consideration of the change in local effective glass transition temperature due to demixing, besides the potential influence of nematic interactions.26,106–109
An example of such a breakdown is illustrated in Fig. 4(b). As described in the Materials and methods section, constant Hencky-strain-rate extension experiments were carried out on the PS790K/PS4K blend up to a stretching ratio of at least λ = 20. Fig. 4(b) compares the stress–strain curves produced with the same Weissenberg number Wi = 31 at 120 °C, 130 °C, 140 °C, and 150 °C. The linear and quasi-linear responses at relatively small strains are essentially identical at different temperatures, which is in agreement with the time–temperature superposition principle. However, clear differences are observed at large strains, as the stress level increases with the decrease of temperature—this is an apparent violation of the TTS principle. Similar trends have been found for both PS790K/PS4K and PS790K/PS23K at other Weissenberg numbers.
This seemingly perplexing phenomenon can be qualitatively understood in terms of the demixing-induced change of local friction. In the current case of mixtures of high-Tg long chains and low-Tg short chains, the stress response is dominated by the long chains, which acquire a higher effective glass transition temperature ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) effg,L upon deformation-induced demixing. Here, the hat symbol denotes properties associated with the demixed states. Fig. 5 schematically illustrates the temperature dependence of the local friction of the long chain in both the equilibrium (ζL(T), solid line) and demixed states (
effg,L upon deformation-induced demixing. Here, the hat symbol denotes properties associated with the demixed states. Fig. 5 schematically illustrates the temperature dependence of the local friction of the long chain in both the equilibrium (ζL(T), solid line) and demixed states (![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) L(T), dashed line). It is easy to see that for two temperatures T1 and T2 (T1 < T2), the following relationship should be true for the local frictions in the equilibrium and nonequilibrium states:
L(T), dashed line). It is easy to see that for two temperatures T1 and T2 (T1 < T2), the following relationship should be true for the local frictions in the equilibrium and nonequilibrium states:
 | (9) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T1) = ζL(T2)
(T1) = ζL(T2)![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T2). Therefore, following the inequality in eqn (9), the effective rate in the demixed state at the low temperature T1 must be higher than that at the high temperature T2:
(T2). Therefore, following the inequality in eqn (9), the effective rate in the demixed state at the low temperature T1 must be higher than that at the high temperature T2: ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) L(T1)
L(T1)![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T1) >
(T1) > ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) L(T2)
L(T2)![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T2). This partially explains the observed failure of TTS—it breaks down as a result of a change in local friction associated with deformation-induced demixing.
(T2). This partially explains the observed failure of TTS—it breaks down as a result of a change in local friction associated with deformation-induced demixing.
To provide further support to the preceding argument, we turn to the PS790K/PαMS11K blend. In this system, the short PαMS11K chain has a higher Tg than the long PS790K chain, while the terminal relaxation times of the short and long chains remain widely separated in the blend (Fig. 6 and 7). Therefore, the viscoelastic asymmetry should still drive demixing under deformation, but the long chain should experience a decrease in effective Tg and thus a reduction of local friction in the nonequilibrium state—exactly the opposite case of the PS/PS blend. For extension experiments at the same Weissenberg number at T1 and T2 (T1 < T2), the effective rate should now be lower at the low temperature T1: ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) L(T1)
L(T1)![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T1) <
(T1) < ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) L(T2)
L(T2)![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (T2) (Fig. 5). This prediction is indeed verified experimentally in the PS790K/PαMS11K blend, as shown in Fig. 4(c).
(T2) (Fig. 5). This prediction is indeed verified experimentally in the PS790K/PαMS11K blend, as shown in Fig. 4(c).
We note that our argument about the dependence of the temperature sensitivity of ζL on Tg [e.g.eqn (9)] can be placed on a firm mathematical basis with the aid of the Williams–Landel–Ferry (WLF) equation,4 by assuming that the change of local composition alters the reference temperature but not the coefficients C1 and C2. This is in fact a common assumption in the context of the concentration fluctuation effect on segmental dynamics in miscible polymer blends.85,113
3.4 Ubiquity of demixing: a literature survey
Lastly, it is important to recognize that deformation-induced demixing is present in many polymer blends and solutions of practical interest. For example, the recent discussions of nonuniversal extensional rheology of polymers polystyrene/oligostyrene blends,26,27,29,30 poly(methyl methacrylate)/oligo(methyl methacrylate) blends,32,114 and polymer solutions with marginal solvent quality, including PS/diethyl phthalate (DEP),21,22,28 PS/dibutyl phthalate (DBP),21,22,27 PS/dioctyl phthalate (DOP),21 PS/tricresyl phosphate (TCP),23 and polyisoprene/squalene.28 The majority of these systems have been shown to go through demixing (concentration fluctuations) under either extensional60,65,72 or shear deformation.55,56,59,61,62,115,116 In particular, light-scattering experiments have revealed deformation-induced demixing of the PS/DOP solutions in both shear and extensional flows.60,115 Additionally, what the polystyrene/oligostyrene blends and the aforementioned polymer solutions have in common is that the solvent has a lower glass transition temperature than the long-chain solute. Deformation-induced demixing is thus expected to elevate the Tg of the long chain, giving rise to enhanced local friction. Conceptually, the coupling between stress and diffusion69,100,117 exists, regardless of the mode of deformation.69,99,101,102,118 As a result, deformation-induced demixing should be prevalent in multicomponent polymeric systems, including polymer blends and solutions.4 Summary
In summary, small-angle neutron scattering experiments demonstrate that deformation-induced demixing occurs in polystyrene–oligostyrene blends both during continuous stretching and after a step extension. This process is driven by the coupling between stress and diffusion, and takes place on time scales longer than the characteristic relaxation time of the short chain. Demixing changes the effective glass transition temperature and thereby the local friction of the long chain. Two consequences associated with the friction change are discussed, namely, the molecular weight effect and temperature effect. A survey of the literature further suggests that deformation-induced demixing should be present in the majority of the polymer blends and solutions recently investigated by extensional rheology. These findings call attention to the influence of deformation-induced demixing on polymer segmental friction, and offer important clues for understanding the nonuniversal behavior of polymers in extensional flow. It is worth noting that the present study by no means suggests that deformation-induced demixing is the only mechanism for changing segmental friction. Indeed, an apparent reduction in segmental friction has been observed by Matsumiya et al. in unentangled polymer melts,31 where demixing is evidently absent. More studies are clearly desired to fully resolve the variation of local friction of polymers in the nonlinear rheological regime.The presence of deformation-induced demixing poses significant theoretical challenges for the rheology of polymeric mixtures. For example, the spatial distribution of local friction and entanglement density in systems undergoing demixing is still an open question. The existing hydrodynamic theories98–102 are formulated on the continuum level, and do not have any “feedback” mechanism to incorporate the effect of concentration fluctuations on segmental friction or entanglement density. Moreover, when clear phase boundaries are formed, the influence of surface tension119,120 on the rheological response may also be considered.
Finally, we point out that the influence of concentration fluctuations on the segmental dynamics of miscible polymer blends in the equilibrium state has been well recognized and widely discussed in the literature.113,121–124 In this context, the present work can be regarded as a conceptual extension of this effect to the nonequilibrium state, where the coupling between stress and diffusion drives large concentration fluctuations (demixing) in polymer blends and solutions with viscoelastic asymmetry. The large deformation-induced concentration fluctuations have profound influences on the polymer segmental friction, and pose a tremendous challenge to the theoretical modeling of multicomponent polymeric materials.
Author contributions
Y. Wang: conceptualization (lead); data curation (equal); investigation (equal); methodology (equal); formal analysis (equal); writing – original draft (lead); writing – review & editing (equal). S. Patil: data curation (equal); investigation (equal); methodology (equal); formal analysis (equal). C. Do: data curation (equal); writing – review & editing (equal). S. Cheng: data curation (equal); investigation (equal); methodology (equal); formal analysis (equal); writing – review & editing (equal).Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: Linear viscoelasticity
This section provides additional information about the linear viscoelastic properties of the polymer blends as well as the neat short-chain “solvents”. As stated in the main text, small-amplitude oscillatory shear measurements were employed to evaluate the dynamic mechanical spectra of these samples, and the resulting master curves are shown in Fig. 6. In all cases, including the PS790K/PαMS11K blend, the time–temperature superposition principle works reasonably well, which is consistent with the miscible nature of these blends. It is also apparent from the linear viscoelastic spectra that in the PS/PS blends the short chains have lower glass transition temperatures than the blends, whereas the opposite scenario is encountered in the PS790K/PαMS11K blend.Appendix B: Component dynamics in equilibrium
Analysis of the nonlinear rheological behavior of binary polymer blends requires an estimation of the characteristic relaxation times of both components in equilibrium. The terminal relaxation time of the long chain in the blends can be conveniently calculated from the low-frequency crossover (ωc) of the storage and loss moduli in the linear viscoelastic spectra as τ = 1/ωc. However, the determination of the short-chain relaxation time is often not straightforward, due to the lack of clear viscoelastic signatures of short chain motions. To gain insights into the component dynamics of the polymer blends, the Lodge–McLeish model84 is employed.The key concept in this model is the self-concentration ϕself, which describes the deviation of the local environment of a segment in a miscible polymer blend as a result of chain connectivity. The self-concentration can be estimated as84
 | (B.1) |
For a miscible polymer blend consisting of two components A and B, the effective, “local” volume fraction of a segment is given by
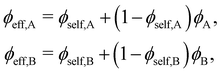 | (B.2) |
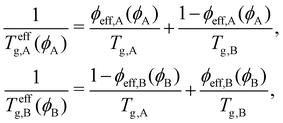
Using the Fox equation,84,126,127 the effective glass transition temperature Teffg for each component can be calculated as
 | (B.3) |
To estimate the terminal relaxation time of the short, unentangled chain in the blend, we follow the approach of Pathak et al.,85 and make the assumption that the terminal relaxation time τ is determined by the effective glass transition temperature Teffg and can be described by the Williams–Landel–Ferry (WLF) equation:4
 | (B.4) |
Acknowledgements
Y. W. is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Early Career Research Program Award KC0402010, under Contract DE-AC05-00OR22725. S. C. acknowledges the support by the National Science Foundation with the Award Number NSF-DMR 2211573. Part of the polymer characterization work was performed at Oak Ridge National Laboratory's Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. This research also used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-publicaccess-plan).Notes and references
- G. C. Berry and T. G. Fox, Adv. Polym. Sci., 1968, 5, 261–357 CrossRef.
- W. W. Graessley, Adv. Polym. Sci., 1974, 16, 1–179 CrossRef.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1979 Search PubMed.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley & Sons, New York, 1980 Search PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986 Search PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids. Fluid Mechanics, John Wiley & Sons, New York, 2nd edn, 1987, vol. 1 Search PubMed.
- R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Kinetic Theory, John Wiley & Sons, New York, 2nd edn, 1987, vol. 2 Search PubMed.
- R. G. Larson, Constitutive Equations for Polymer Melts and Solutions, Butterworths Publishers, Stoneham, 1988 Search PubMed.
- H. Watanabe, Prog. Polym. Sci., 1999, 24, 1253–1403 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- W. W. Graessley, Polymeric Liquids and Networks: Dynamics and Rheology, Garland Science, New York, 2008 Search PubMed.
- M. Takahashi, T. Masuda, N. Bessho and K. Osaki, J. Rheol., 1980, 24, 517–520 CrossRef.
- W. W. Graessley, Adv. Polym. Sci., 1982, 47, 67–117 CrossRef CAS.
- E. Menezes and W. Graessley, J. Polym. Sci., Part B: Polym. Phys., 1982, 20, 1817–1833 CAS.
- K. Osaki, Rheol. Acta, 1993, 32, 429–437 CrossRef CAS.
- K. Osaki, T. Inoue and T. Isomura, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 1917–1925 CrossRef CAS.
- S. Ravindranath and S.-Q. Wang, J. Rheol., 2008, 52, 681–695 CrossRef CAS.
- D. Auhl, J. Ramirez, A. E. Likhtman, P. Chambon and C. Fernyhough, J. Rheol., 2008, 52, 801–835 CrossRef CAS.
- P. E. Boukany, S.-Q. Wang and X. Wang, J. Rheol., 2009, 53, 617–629 CrossRef CAS.
- S. Costanzo, Q. Huang, G. Ianniruberto, G. Marrucci, O. Hassager and D. Vlassopoulos, Macromolecules, 2016, 49, 3925–3935 CrossRef CAS.
- P. Bhattacharjee, J. Oberhauser, G. H. McKinley, L. Leal and T. Sridhar, Macromolecules, 2002, 35, 10131–10148 CrossRef CAS.
- P. Bhattacharjee, D. A. Nguyen, G. H. McKinley and T. Sridhar, J. Rheol., 2003, 47, 269–290 CrossRef CAS.
- X. Ye, R. G. Larson, C. Pattamaprom and T. Sridhar, J. Rheol., 2003, 47, 443–468 CrossRef CAS.
- A. Bach, K. Almdal, H. K. Rasmussen and O. Hassager, Macromolecules, 2003, 36, 5174–5179 CrossRef CAS.
- J. K. Nielsen, H. K. Rasmussen, O. Hassager and G. H. McKinley, J. Rheol., 2006, 50, 453–476 CrossRef CAS.
- Q. Huang, N. J. Alvarez, Y. Matsumiya, H. K. Rasmussen, H. Watanabe and O. Hassager, ACS Macro Lett., 2013, 2, 741–744 CrossRef CAS PubMed.
- Q. Huang, O. Mednova, H. K. Rasmussen, N. J. Alvarez, A. L. Skov, K. Almdal and O. Hassager, Macromolecules, 2013, 46, 5026–5035 CrossRef CAS.
- T. Sridhar, M. Acharya, D. A. Nguyen and P. K. Bhattacharjee, Macromolecules, 2014, 47, 379–386 CrossRef CAS.
- Q. Huang, L. Hengeller, N. J. Alvarez and O. Hassager, Macromolecules, 2015, 48, 4158–4163 CrossRef CAS.
- Q. Huang and H. K. Rasmussen, J. Rheol., 2016, 60, 465–471 CrossRef CAS.
- Y. Matsumiya, H. Watanabe, Y. Masubuchi, Q. Huang and O. Hassager, Macromolecules, 2018, 51, 9710–9729 CrossRef CAS.
- H. K. Rasmussen, S. L. Wingstrand and O. Hassager, Rheol. Acta, 2019, 58, 333–340 CrossRef CAS.
- R. Yuan, J. Liu, Y. Wang and S.-Q. Wang, Soft Matter, 2020, 16, 3705–3716 RSC.
- G. Marrucci and G. Ianniruberto, Macromolecules, 2004, 37, 3934–3942 CrossRef CAS.
- G. Ianniruberto, A. Brasiello and G. Marrucci, et al., Proc. 7th Annu. Eur. Rheol. Conf, 2011, p. 61 Search PubMed.
- G. Ianniruberto, A. Brasiello and G. Marrucci, Macromolecules, 2012, 45, 8058–8066 CrossRef CAS.
- G. Ianniruberto, Macromolecules, 2015, 48, 6306–6312 CrossRef CAS.
- G. W. Park and G. Ianniruberto, Macromolecules, 2017, 50, 4787–4796 CrossRef CAS.
- T. Yaoita, T. Isaki, Y. Masubuchi, H. Watanabe, G. Ianniruberto and G. Marrucci, Macromolecules, 2012, 45, 2773–2782 CrossRef CAS.
- Y. Masubuchi, Y. Matsumiya and H. Watanabe, Macromolecules, 2014, 47, 6768–6775 CrossRef CAS.
- G. Ianniruberto, A. Brasiello and G. Marrucci, Macromolecules, 2019, 52, 4610–4616 CrossRef CAS.
- A. Silberberg and W. Kuhn, Nature, 1952, 170, 450–451 CrossRef CAS.
- J. Eliassaf, A. Silberberg and A. Katchalsky, Nature, 1955, 176, 1119 CrossRef CAS.
- A. Lodge, Polymer, 1961, 2, 195–201 CrossRef CAS.
- A. Peterlin and D. Turner, J. Polym. Sci., Part B: Polym. Lett., 1965, 3, 517–520 CrossRef CAS.
- I. Steg and D. Katz, J. Appl. Polym. Sci., 1965, 9, 3177–3193 CrossRef CAS.
- Y. Go, S. Matsuzawa, Y. Kondo and K. Nakamura, Kobunshi Kagaku, 1967, 24, 577 CrossRef CAS.
- F. Frank, A. Keller and M. Mackley, Polymer, 1971, 12, 467–473 CrossRef CAS.
- C. Rangel-Nafaile, A. Metzner and K. Wissbrun, Macromolecules, 1984, 17, 1187–1195 CrossRef CAS.
- J. D. Katsaros, M. F. Malone and H. H. Winter, Polym. Bull., 1986, 16, 83–88 CrossRef CAS.
- M. Tirrell, Fluid Phase Equilib., 1986, 30, 367–380 CrossRef CAS.
- M. G. Brereton, T. A. Vilgis and F. Boué, Macromolecules, 1989, 22, 4051–4053 CrossRef CAS.
- J. Bastide, L. Leibler and J. Prost, Macromolecules, 1990, 23, 1821–1825 CrossRef CAS.
- F. Boué, J. Bastide, M. Buzier, A. Lapp, J. Herz and T. Vilgis, Colloid Polym. Sci., 1991, 269, 195–216 CrossRef.
- X.-L. Wu, D. Pine and P. Dixon, Phys. Rev. Lett., 1991, 66, 2408 CrossRef CAS PubMed.
- T. Hashimoto and T. Kume, J. Phys. Soc. Jpn., 1992, 61, 1839–1843 CrossRef CAS.
- I. Hindawi, J. Higgins and R. Weiss, Polymer, 1992, 33, 2522–2529 CrossRef CAS.
- R. Larson, Rheol. Acta, 1992, 31, 497–520 CrossRef CAS.
- J. J. Magda, C. S. Lee, S. J. Muller and R. G. Larson, Macromolecules, 1993, 26, 1696–1706 CrossRef CAS.
- J. W. van Egmond and G. G. Fuller, Macromolecules, 1993, 26, 7182–7188 CrossRef CAS.
- F. Boué and P. Lindner, Europhys. Lett., 1994, 25, 421 CrossRef.
- E. Moses, T. Kume and T. Hashimoto, Phys. Rev. Lett., 1994, 72, 2037–2040 CrossRef CAS PubMed.
- D. Wirtz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 50, R1755 CrossRef CAS PubMed.
- A. Ramzi, F. Zielinski, J. Bastide and F. Boué, Macromolecules, 1995, 28, 3570–3587 CrossRef CAS.
- C. Hayes, L. Bokobza, F. Boué, E. Mendes and L. Monnerie, Macromolecules, 1996, 29, 5036–5041 CrossRef CAS.
- E. Mendes, R. Oeser, C. Hayes, F. Boué and J. Bastide, Macromolecules, 1996, 29, 5574–5584 CrossRef CAS.
- K. Migler, C.-H. Liu and D. Pine, Macromolecules, 1996, 29, 1422–1432 CrossRef CAS.
- H. Murase, T. Kume, T. Hashimoto, Y. Ohta and T. Mizukami, Macromol. Symp., 1996, 159–182 CrossRef CAS.
- A. Onuki, J. Phys.: Condens. Matter, 1997, 9, 6119 CrossRef CAS.
- I. Morfin, P. Lindner and F. Boué, Macromolecules, 1999, 32, 7208–7223 CrossRef CAS.
- N. Jouault, F. Dalmas, S. Said, E. Di Cola, R. Schweins, J. Jestin and F. Boué, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031801 CrossRef PubMed.
- Y. Wang, W. Wang, K. Hong and Y. Liu, Macromolecules, 2021, 54, 3531–3542 CrossRef CAS.
- S. Liu, L. Peng, S. Xiang, H. Chen, Y. Huang, X. Huang and Q. Huang, ACS Macro Lett., 2024, 13, 138–143 CrossRef CAS PubMed.
- D. W. Van Krevelen and K. Te Nijenhuis, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier, Amsterdam, 4th edn, 2009 Search PubMed.
- W. Wallace, N. Beck Tan, W. Wu and S. Satija, J. Chem. Phys., 1998, 108, 3798–3804 CrossRef CAS.
- M. L. Sentmanat, Rheol. Acta, 2004, 43, 657–669 CrossRef CAS.
- Z. Wang, C. N. Lam, W.-R. Chen, W. Wang, J. Liu, Y. Liu, L. Porcar, C. B. Stanley, Z. Zhao, K. Hong and Y. Wang, Phys. Rev. X, 2017, 7, 031003 Search PubMed.
- C. N. Lam, W.-S. Xu, W.-R. Chen, Z. Wang, C. B. Stanley, J.-M. Y. Carrillo, D. Uhrig, W. Wang, K. Hong, Y. Liu, L. Porcar, C. Do, G. S. Smith, B. G. Sumpter and Y. Wang, Phys. Rev. Lett., 2018, 121, 117801 CrossRef PubMed.
- Y. Wang, W. Wang, K. Hong, C. Do and W.-R. Chen, Polymer, 2020, 204, 122698 CrossRef CAS.
- R. Sun, M. Melton, N. Safaie, R. C. Ferrier Jr, S. Cheng, Y. Liu, X. Zuo and Y. Wang, Phys. Rev. Lett., 2021, 126, 117801 CrossRef CAS PubMed.
- Y. Wang, P. Boukany, S.-Q. Wang and X. Wang, Phys. Rev. Lett., 2007, 99, 237801 CrossRef PubMed.
- P. Santangelo and C. Roland, Macromolecules, 1998, 31, 4581–4585 CrossRef CAS.
- Y. Ding, A. Kisliuk and A. Sokolov, Macromolecules, 2004, 37, 161–166 CrossRef CAS.
- T. P. Lodge and T. C. McLeish, Macromolecules, 2000, 33, 5278–5284 CrossRef CAS.
- J. A. Pathak, S. K. Kumar and R. H. Colby, Macromolecules, 2004, 37, 6994–7000 CrossRef CAS.
- J. K. Zhao, C. Y. Gao and D. Liu, J. Appl. Cryst., 2010, 43, 1068–1077 CrossRef CAS.
- W. T. Heller, M. Cuneo, L. Debeer-Schmitt, C. Do, L. He, L. Heroux, K. Littrell, S. V. Pingali, S. Qian, C. Stanley, V. S. Urban, B. Wu, W. Bras and IUCr, J. Appl. Crystallogr., 2018, 51, 242–248 CrossRef CAS.
- O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- W. T. Heller, J. Hetrick, J. Bilheux, J. M. B. Calvo, W.-R. Chen, L. DeBeer-Schmitt, C. Do, M. Doucet, M. R. Fitzsimmons, W. F. Godoy, G. E. Granroth, S. Hahn, L. He, F. Islam, J. Lin, K. C. Littrell, M. McDonnell, J. McGaha, P. F. Peterson, S. V. Pingali, S. Qian, A. T. Savici, Y. Shang, C. B. Stanley, V. S. Urban, R. E. Whitfield, C. Zhang, W. Zhou, J. J. Billings, M. J. Cuneo, R. M. F. Leal, T. Wang and B. Wu, SoftwareX, 2022, 19, 101101 CrossRef.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1979 Search PubMed.
- J. S. Higgins and H. Benoît, Polymers and Neutron Scattering, Clarendon Press, Oxford, 1994 Search PubMed.
- J. Cotton, D. Decker, H. Benoit, B. Farnoux, J. Higgins, G. Jannink, R. Ober, C. D. Picot and J. Des Cloizeaux, Macromolecules, 1974, 7, 863–872 CrossRef.
- S. Saeki, J. Cowie and I. McEwen, Polymer, 1983, 24, 60–64 CrossRef CAS.
- J.-M. Widmaier and G. Mignard, Eur. Polym. J., 1987, 23, 989–992 CrossRef CAS.
- L. Lanzavecchia and E. Pedemonte, Thermochim. Acta, 1988, 137, 123–128 CrossRef CAS.
- A. Rameau, Y. Gallot, P. Marie and B. Farnoux, Polymer, 1989, 30, 386–392 CrossRef CAS.
- C. N. Lam, L. He, C. Do, W.-R. Chen, W. Wang, K. Hong and Y. Wang, J. Appl. Crystallogr., 2023, 56, 1168–1179 CrossRef CAS.
- A. Onuki, Phys. Rev. Lett., 1989, 62, 2472 CrossRef CAS PubMed.
- E. Helfand and G. H. Fredrickson, Phys. Rev. Lett., 1989, 62, 2468 CrossRef CAS PubMed.
- S. T. Milner, Phys. Rev. Lett., 1991, 66, 1477 CrossRef CAS PubMed.
- H. Ji and E. Helfand, Macromolecules, 1995, 28, 3869–3880 CrossRef CAS.
- M. Cromer, M. C. Villet, G. H. Fredrickson, L. G. Leal, R. Stepanyan and M. J. H. Bulters, J. Rheol., 2013, 57, 1211–1235 CrossRef CAS.
- J. J. Kirkensgaard, L. Hengeller, A. Dorokhin, Q. Huang, C. J. Garvey, K. Almdal, O. Hassager and K. Mortensen, Phys. Rev. E, 2016, 94, 020502 CrossRef PubMed.
- H. Tanaka, T. Araki, T. Koyama and Y. Nishikawa, J. Phys.: Condens. Matter, 2005, 17, S3195 CrossRef CAS.
- H. Tanaka and T. Araki, Chem. Eng. Sci., 2006, 61, 2108–2141 CrossRef CAS.
- J. A. Kornfield, G. G. Fuller and D. S. Pearson, Macromolecules, 1989, 22, 1334–1345 CrossRef CAS.
- M. Doi, D. Pearson, J. Kornfield and G. Fuller, Macromolecules, 1989, 22, 1488–1490 CrossRef CAS.
- M. Doi and H. Watanabe, Macromolecules, 1991, 24, 740–744 CrossRef CAS.
- J. Cao and A. E. Likhtman, Phys. Rev. Lett., 2010, 104, 207801 CrossRef PubMed.
- R. H. Colby, Polymer, 1989, 30, 1275–1278 CrossRef CAS.
- X. Yang, S.-Q. Wang and H. Ishida, Macromolecules, 1999, 32, 2638–2645 CrossRef CAS.
- X. Yang, A. Halasa, W.-L. Hsu and S.-Q. Wang, Macromolecules, 2001, 34, 8532–8540 CrossRef CAS.
- S. K. Kumar, R. H. Colby, S. H. Anastasiadis and G. Fytas, J. Chem. Phys., 1996, 105, 3777–3788 CrossRef CAS.
- S. L. Wingstrand, N. J. Alvarez, Q. Huang and O. Hassager, Phys. Rev. Lett., 2015, 115, 078302 CrossRef PubMed.
- J. W. van Egmond, D. E. Werner and G. G. Fuller, J. Chem. Phys., 1992, 96, 7742–7757 CrossRef CAS.
- A. Nakatani, J. Douglas, Y.-B. Ban and C. Han, J. Chem. Phys., 1994, 100, 3224–3232 CrossRef CAS.
- M. Doi and A. Onuki, J. Phys. II, 1992, 2, 1631–1656 CrossRef CAS.
- M. Cromer, G. H. Fredrickson and L. Gary Leal, J. Rheol., 2017, 61, 711–730 CrossRef CAS.
- D. Graebling, R. Muller and J. Palierne, Macromolecules, 1993, 26, 320–329 CrossRef CAS.
- W. Yu, W. Zhou and C. Zhou, Polymer, 2010, 51, 2091–2098 CrossRef CAS.
- S. Kamath, R. H. Colby, S. K. Kumar, K. Karatasos, G. Floudas, G. Fytas and J. E. Roovers, J. Chem. Phys., 1999, 111, 6121–6128 CrossRef CAS.
- S. Salaniwal, R. Kant, R. H. Colby and S. K. Kumar, Macromolecules, 2002, 35, 9211–9218 CrossRef CAS.
- R. Kant, S. K. Kumar and R. H. Colby, Macromolecules, 2003, 36, 10087–10094 CrossRef CAS.
- S. K. Kumar, S. Shenogin and R. H. Colby, Macromolecules, 2007, 40, 5759–5766 CrossRef CAS.
- M. Kurata and Y. Tsunashima, in Viscosit-ymolecular weight relationships and unperturbed dimensions of linear chain molecules, ed. J. Brandrup, E. H. Immergut, E. A. Grulke, A. Abe and D. R. Bloch, John Wiley & Sons, New York, 1999 Search PubMed.
- G. Fox, Bull. Am. Phys. Soc., 1956, 1, 123 Search PubMed.
- H. A. Schneider and E. A. Di Marzio, Polymer, 1992, 33, 3453–3461 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |