DOI:
10.1039/D4SM00213J
(Paper)
Soft Matter, 2024,
20, 3161-3174
Steering droplets on substrates with plane-wave wettability patterns and deformations†
Received
15th February 2024
, Accepted 15th March 2024
First published on 15th March 2024
Abstract
Motivated by strategies for targeted microfluidic transport of droplets, we investigate how sessile droplets can be steered toward a preferred direction using travelling waves in substrate wettability or deformations of the substrate. To perform our numerical study, we implement the boundary-element method to solve the governing Stokes equations for the fluid flow field inside the moving droplet. In both cases we find two distinct modes of droplet motion. For small wave speed the droplet surfs with a constant velocity on the wave, while beyond a critical wave speed a periodic wobbling motion occurs, the period of which diverges at the transition. These observation can be rationalized by the nonuniform oscillator model and the transition described by a SNIPER bifurcation. For the travelling waves in wettability the mean droplet velocity in the wobbling state decays with the inverse wave speed. In contrast, for travelling-wave deformations of the substrate it is proportional to the wave speed at large speed values since the droplet always has to move up and down. To rationalize this behavior, the nonuniform oscillator model has to be extended. Since the critical wave speed of the bifurcation depends on the droplet radius, this dependence can be used to sort droplets by size.
1 Introduction
Liquid droplets on a solid substrate occur naturally during, e.g., rain and condensation1,2 or artificially in printing of ink3 or medical testing.4 Depending on their interaction with the substrate and gas phase, they either sit on a substrate, spread, contract, or even move laterally along the substrate.5 Lateral motion can be induced by a variety of mechanisms; through nonuniform electric fields (electrowetting),6 gravity,7 Marangoni advection,8,9 gradients in wettability,4,10,11 or deformations of the substrate itself.12,13 Here, we focus on the latter two mechanisms.
In our previous work, we used the gradient in a wettability step to move a droplet forward using a feedback loop, which synchronizes step and droplet motion.14 However, due to surface imperfections at which droplets get pinned, such a motion can be difficult to realize in an experiment.5 Yet, pinning can be avoided by a large wettability gradient,15e.g., induced by structural changes of the substrate,16 or by using homogeneously clean and flat surfaces.17
Deformations of the substrate itself also move a droplet.18 In ref. 19 it has been demonstrated that capillary forces attract droplets towards regions with large inward curvature. An example of this are pipettes. It is possible to externally control such substrate deformations, e.g., using gels that reversibly swell and unswell in response to light with specific wavelengths.13,20,21 Already more than three decades ago wetting of curved rigid substrates was investigated.22 In more recent work, elastic substrates were studied that deform in contact with a liquid droplet.23–25 Internal tension builds up as a substrate deforms, which changes its surface tension what is known as Shuttleworth effect.26,27 Here, we just consider curved rigid substrates, where this effect does not occur.
In this article we compare two mechanisms for inducing droplet motion by imposing the spatio-temporal pattern of a travelling wave onto the substrate; first in wettability and thereafter in the height profile of the substrate. This enables to steer the droplet into a prescribed direction; a typical task in lab-on-a-chip applications.28 For possible experimental realizations of travelling waves in wettability and deformations, we refer the reader to Sections 4 and 5, respectively. Because the travelling wave is spatially periodic, the droplet is continuously driven out of equilibrium and cannot settle into a sessile state. Instead, the droplet can be considered as a driven nonuniform oscillator,29 as we show, the driving force of which depends on its position relative to the travelling wave. In Fig. 1 we display two series of snapshots that illustrate the two possible modes of motion, which we term wobbling (left in Fig. 1) and surfing (right in Fig. 1), respectively. In ref. 14 and 30 we applied the boundary element method (BEM)31 to a wetting droplet on a plane substrate with a spatio-temporal wettability pattern. To describe deformation waves of the substrate, we needed to extend our approach to substrates with a spatio-temporal curvature pattern. However, we also needed to completely reformulate our formalism in order to guarantee conservation of the droplet volume.
 |
| | Fig. 1 Time series (top to bottom) of snapshots for wettability waves travelling at different speeds: (left) wobbling motion at large speeds and (right) surfing motion of the droplet at small speeds. The greyscale shading indicates wettability and the red lines indicate the contact line of the droplet. The same two states are also observed for a travelling deformation wave. | |
First, in Section 2 we describe the theory of dynamic wetting for small droplets and our numerical approach based on the BEM. Next, in Section 3 we introduce the so-called nonuniform oscillator, which we use as an analytic model to interpret the observed droplet dynamics. We present and analyze the effect of travelling waves in wettability in Section 4 and travelling-wave deformations in Section 5. Finally, we comment on implications of our findings for the sorting of droplets by size in Section 6 and conclude with Section 7.
2 Boundary element method for dynamic wetting
We consider the motion of viscous droplets at small scales in the creeping flow regime, where viscous forces dominate, while inertia is negligible. Accordingly, fluid flow within droplets are described by the Stokes equations and the incompressibility condition,| | | η∇2v = ∇p and ∇·v = 0. | (1) |
Here, we use fluid velocity field v, pressure p, and shear viscosity η. In addition, appropriate boundary conditions have to be chosen, most importantly, describing forces acting at the fluid boundary. Notably, the flow fields determined by the Stokes equations adapt instantaneously to the boundary conditions because the equations do not contain any time derivatives.
In ref. 14 we formulated the boundary-element method for dynamic wetting. When extending this approach to droplets on deforming substrates, we encountered difficulties with the conservation of the droplet volume. This forced us to reformulate the boundary-element method in a more formalized way. As a result, for any point on the droplet surface we can write a force balance
| |  | (2) |
where the friction force
is linear in the surface velocity field
Ṙ and
G is a linear operator that does not depend on
v, since the Stokes equations are linear in the fluid velocity field
v.
32,33 The force

derives from the droplet free energy, as we explain in Section 2.2, and provides the Laplace pressure, Young's force at the contact line, and constraint forces. Finally,
F governs the dynamics induced by deforming substrates.
After discretizing the droplet surface by a mesh, K,  and F become vectors and G a friction matrix. In the following we systematically determine all these quantities, which will give us a systematic approach for calculating the motion of the droplet. We start with the mesh discretization in Section 2.1, then continue with the droplet free energy in Section 2.2 and discuss the relevant Lagrange parameters for the volume and rigidity constraint of droplet and deforming substrate, respectively, in Section 2.3. In Section 2.4 we analyze the boundary conditions at the droplet surface, which confirms the force balance of eqn (2), and we formulate the vectors K and F. In Section 2.5 we calculate the complete friction matrix by considering shear friction in the fluid using the boundary integral equation for the Stokes equation, as well as liquid–substrate and contact-line friction. In Section 2.6 we present the final dynamic equations, which we use in our simulations, and in Section 2.7 we collect the parameters used.
and F become vectors and G a friction matrix. In the following we systematically determine all these quantities, which will give us a systematic approach for calculating the motion of the droplet. We start with the mesh discretization in Section 2.1, then continue with the droplet free energy in Section 2.2 and discuss the relevant Lagrange parameters for the volume and rigidity constraint of droplet and deforming substrate, respectively, in Section 2.3. In Section 2.4 we analyze the boundary conditions at the droplet surface, which confirms the force balance of eqn (2), and we formulate the vectors K and F. In Section 2.5 we calculate the complete friction matrix by considering shear friction in the fluid using the boundary integral equation for the Stokes equation, as well as liquid–substrate and contact-line friction. In Section 2.6 we present the final dynamic equations, which we use in our simulations, and in Section 2.7 we collect the parameters used.
Before we proceed we add two comments. In our previous implementation of volume conservation we directly constrained the velocities of the droplet's mesh vertices following ref. 34. However, when the substrate deforms, this ad hoc constraint introduces spurious flows on the droplet's surface. Our current approach resolves this issue by properly introducing the volume constraint with the pressure as a Lagrange parameter in the droplet free energy as explained in Section 2.3. It constrains the restoring forces acting on the droplet's mesh vertices. This approach also allows us to directly incorporate an additional constraint that links the droplet to the height profile of the substrate. Thus, our reformulation of the boundary-element method puts an increased focus on forces rather than solely on velocities.
In parallel, we needed to modify our approach to contact-line friction. Whereas in ref. 14 we simply prescribed the velocity of the contact line using the Cox–Voinov law, now we first calculate the Young force acting on the contact line and then calculate its velocity with a Cox–Voinov type friction law (see Section 2.5.3).
2.1 Mesh discretization
As noted above, our aim is to reduce the droplet motion to the dynamics of its boundary consisting of the liquid–substrate and liquid–gas interfaces as well as the three-phase contact line, which requires special consideration. To treat the droplet dynamics numerically, we describe the entire droplet surface by a triangular mesh. Each triangle consists of three vertices and three edges, which it shares with its direct neighbour triangles. As long as the triangular mesh stays intact, the shape of the droplet is completely specified by the positions of the vertices ri, which define the configuration vector R = (r1, r2, r3, …).
In general, the part of the surface force field acting on the droplet at the liquid–solid and liquid–gas interactions derives from the functional derivative of a surface energy w.r.t. the configuration field R. However, since the droplet surface is discretized, the functional derivative becomes gradients w.r.t. the vertex positions. To continue, we construct an expression for the surface energy using surface integrals and discretize the integrals for our mesh in the following part.
2.2 Droplet free energy and discretization
The free energy of an incompressible liquid droplet at constant temperature can be written as| |  | (4) |
where γ is the surface tension and the area A encompasses all the surfaces of the droplet. The bulk free energy is kept constant here. The surface integral can be split up into two parts: the liquid–gas (lg) interface and the solid–liquid interface (sl) with the respective surface tensions γlg and γsl. The solid–gas interface of the substrate not in contact with the droplet contributes to the free energy with surface tension γsg. Whenever part of this interface is covered by the droplet, the surface energy changes by γsl − γsg. Thus we obtain| | 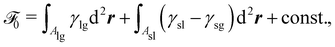 | (5) |
where Alg and Alg are the areas of the respective interfaces. Young's law for the equilibrium contact angle θeq is a force balance in the substrate plane that states that γsl − γsg = −γlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq.‡ Using it together with γlg = const., we obtain
θeq.‡ Using it together with γlg = const., we obtain| |  | (6) |
where θeq is determined by the local value of γsg − γsl. Because we want to study movable droplets on substrates with nonuniform wettability, the remaining integral cannot be further simplified here.
We now turn our attention toward the constraints on the shape of the droplet. They are two-fold: first, the volume of the droplet is conserved and, second, the normal forces on the liquid–solid interface sum up to zero since any fluid forces are compensated by the forces exerted by the rigid substrate that resists any elastic deformation. Using the method of Langrangian multipliers, each constraint gives rise to an additional term in the energy functional:
| |  | (7) |
Here, the second term on the right-hand side constrains the droplet volume to the value
V0 and the pressure
p0 serves as the Langrange multiplier. The third term firmly connects the vertical position
z of the liquid–solid interface to the height variations
h(
x) of the substrate written in Monge representation with
x = (
x,
y). In the case of a flat substrate,
h = 0, this term reduces to
| |  | (8) |
which guarantees that the solid–liquid interface
Asl is defined by
z = 0. Finally, note that the volume of the droplet can be expressed by the surface integral
| |  | (9) |
as one verifies immediately with Gauss's theorem.
Now, the functional derivative of  is one part of the force balance of eqn (3). In our simulations we always calculate it numerically as detailed below. However, to illustrate its content, we perform the derivative and explicitely write it as
is one part of the force balance of eqn (3). In our simulations we always calculate it numerically as detailed below. However, to illustrate its content, we perform the derivative and explicitely write it as
| |  | (10) |
The last term on the right-hand side results from the rigidity constraint, which only affects the solid–liquid interface, and
G(
x) is the Jacobian determinant of the height profile
h(
x) of the curved substrate. The three contributions in
eqn (10) are illustrated in
Fig. 2, where the derivative of

gives the acting forces due to surface tension and the Young force (see below). Their normal components acting on the substrate compensate the rigidity-constraint force and, as we demonstrate in Appendix D, the remaining terms of the functional derivative can be written as
| |  | (11) |
In thermal equilibrium it is zero, while in non-equilibrium it drives the dynamics of the droplet. The first term contains the balance at the liquid–gas interface between static pressure
p0, which we introduced with the volume constraint, and the force due to surface tension. Here,
κ is the local mean curvature of the liquid–gas interface, which is negative for the unit normal
n pointing out of the droplet. The second term on the right-hand side of
eqn (11) is the Young force acting locally on the contact line. It points in direction of unit vector
t, which is perpendicular to the contact line and tangential to the substrate. In equilibrium the Young force vanishes (cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq
θeq = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ) and
p0 becomes the Laplace pressure
pL = −2
κγlg =
p0.
 |
| | Fig. 2 Schematic illustrating the three force contributions to  in eqn (10) acting on the different interfaces of the droplet (black outline): static pressure p0 (red), surface tension and Young force in eqn (10) acting on the different interfaces of the droplet (black outline): static pressure p0 (red), surface tension and Young force  (blue), and rigidity-constraint force λGn at the solid–liquid interface (green). The rigid substrate is shaded in gray. (blue), and rigidity-constraint force λGn at the solid–liquid interface (green). The rigid substrate is shaded in gray. | |
To discretize all the surface integrals of the free energy  we use the triangular mesh of the droplet surface and sum up the contributions from each triangle so that
we use the triangular mesh of the droplet surface and sum up the contributions from each triangle so that
| | 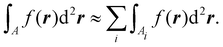 | (12) |
Here, we have to distinguish between functions
f, the values of which are known for any position
r and those functions, the values of which are only known at the vertices. In the first case, an example is cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq
θeq, we use Gaussian quadrature with 4 sample values of the prescribed profile to calculate the integral on each triangle. The sample values are taken at positions (1/3, 1/3, 1/3), (3/5, 1/5, 1/5), (1/5, 3/5, 1/5), and (1/5, 1/5, 3/5) in barycentric coordinates of the triangle and weighted by −27/48, 25/48, 25/48, and 25/48, respectively.
35 In the second case, an example is the calculation of the volume
V, we linearly interpolate between the values at the vertices. If
f has a constant value
fi on the area of the triangle, for example, in the case of
γlg, we simply use
Aifi.
Note, after discretizing the free energy  in terms of all positions of the vertices R, the functional derivative of
in terms of all positions of the vertices R, the functional derivative of  becomes
becomes  .
.
2.3 Method of lagrange multipliers
After having discretized all contributions to 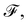 we obtain terms as a function of the configuration vector R, including all the constraint terms, which we write as λjgj(R) = 0. For convenience, we label λ0 = p0 and assign the remaining multipliers to the rigidity constraint. Thus, eqn (7) becomes
we obtain terms as a function of the configuration vector R, including all the constraint terms, which we write as λjgj(R) = 0. For convenience, we label λ0 = p0 and assign the remaining multipliers to the rigidity constraint. Thus, eqn (7) becomes| |  | (13) |
We discretize the surface integral of the rigidity constraint in eqn (7),
| |  | (14) |
where we subsume the area
Ai surrounding each vertex into the
λi, respectively, and we sum over all
N vertices on the solid–liquid interface. The force due to this constraint is guaranteed to be normal to the substrate, since ∇
igi =
ni, as shown in Appendix B, and therefore equivalent to the desired rigidity constraint.
§ This construction greatly simplifies the procedure below because ∇
Rgi is easily accessible.
The purpose of the Lagrange multipliers λi is to constrain the force  such that it does not have a component perpendicular to the manifold defined by the constraints gi(R) = 0, otherwise the constraints would be violated.¶ Therefore, the condition
such that it does not have a component perpendicular to the manifold defined by the constraints gi(R) = 0, otherwise the constraints would be violated.¶ Therefore, the condition
| |  | (15) |
must hold. Using
eqn (13) for

in this condition with
| |  | (16) |
we obtain a set of linear equations for the Lagrange multipliers
λi (including
λ0),
| |  | (17) |
which we solve numerically. With this,

is known up to a constant.
||
2.4 Boundary condition and dynamic equation
So far we looked at the forces, which derive from the droplet free energy. They are part of the boundary condition of the Stokes equations, eqn (1), which balances all the forces acting at each point on the different interfaces of the droplet. There are three contributions to this force balance. First, we have the traction of the liquid on the interface, σn, where σij = −pδij + η(∂ivj + ∂jvi) is the stress tensor, n the unit normal vector, and δij is the Kronecker symbol. For the following argumentation, we split the stress tensor into a part −p0n, where p0 is the spatially uniform static pressure due to the volume constraint already introduced in Section 2.2, and a spatially varying part ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n = σn + p0n. Second, there is the traction of the substrate at the substrate–liquid interface. It consists of the constraint force frigid = λGn|sl, already introduced in Section 2.2, with which the substrate resists deformations induced by the droplet, and fdeform, which acts on the liquid when the substrate deforms in time according to the prescribed height profile h. Finally and third, there is the traction due to the surface tension of both interfaces, which includes the Young force acting on the contact line and which we denoted
n = σn + p0n. Second, there is the traction of the substrate at the substrate–liquid interface. It consists of the constraint force frigid = λGn|sl, already introduced in Section 2.2, with which the substrate resists deformations induced by the droplet, and fdeform, which acts on the liquid when the substrate deforms in time according to the prescribed height profile h. Finally and third, there is the traction due to the surface tension of both interfaces, which includes the Young force acting on the contact line and which we denoted 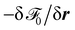 in Section 2.2. Note that we neglect the vapour pressure of the gas phase surrounding the droplet, here and in the following.
in Section 2.2. Note that we neglect the vapour pressure of the gas phase surrounding the droplet, here and in the following.
In total, we have the force balance at each point of the droplet surface,
| |  | (18) |
where
frigid +
fdeform is zero at the gas–liquid interface. Note that
fdeform is due to the boundary conditions at the liquid–substrate interface, which include continuity of the normal velocity component and a slip boundary condition of the tangential component, as we will specify in Section 2.5.2. At the liquid–gas interface
eqn (18) gives zero tangential stresses or traction forces, while the normal forces obey the usual Neumann boundary condition,
n·
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n
n −
p0 = 2
κγlg, where we have used
eqn (11). Finally, using
eqn (10) the first two terms on the r.h.s. of
eqn (18) together with
p0n can be rewritten as
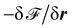
and we obtain
| | 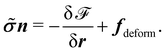 | (19) |
The equilibrium case with zero dynamic stresses,
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n
n = 0, and
fdeform = 0 gives

and was already discussed in Section 2.2.
We now rephrase boundary condition (19) for the discretized droplet surface. At each vertex i the traction ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) ini from the fluid is multiplied by area Ai and collected in the friction vector
ini from the fluid is multiplied by area Ai and collected in the friction vector
| | K = (−![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n1A1, − n1A1, −![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n2A2, − n2A2, −![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n3A3, …), n3A3, …), | (20) |
Similarly, we collect the substrate traction
fdeform in a force vector
| | | F = (f(1)deformA1, f(2)deformA2, f(3)deformA3, …). | (21) |
Our method to calculate
F is described in detail in Section 2.5. As usual, the gradient of

describes a force

which takes the place of the functional derivative

. Thus, condition
(19) is rewritten as

which proves the force balance of
eqn (2), with which we started. In the next section we will show that
K = −
GṘ and thereby calculate the friction matrix. This completes the reformulation of our boundary element approach.
2.5 Friction matrix
Now, we specify the friction matrix G such that all sources of friction related to the droplet are accounted for. Three types of friction are relevant in our setup. First, there is shear friction or viscous shear stresses in the droplet fluid, when neighboring fluid layers move relative to each other. Second, there is slip friction between the substrate and the directly adjacent fluid layer. And finally, there is friction of the moving contact line. The latter should naturally arise from the first and second mechanisms. However, so far this has proved difficult to show analytically5 and also to implement numerically due to the flow singularity that arises at the contact line.36 Therefore, we use a hydrodynamically motivated friction law for the contact line. It is closely related to the Cox–Voinov law,37 which has successfully been matched to experiments, e.g., in ref. 38.
2.5.1 Shear friction.
We start with shear friction in the droplet fluid. The solution of the Stokes equations within a given domain is equivalent to a boundary-integral equation that relates flow velocity v(r) to surface forces σ(r)n and force/source dipoles at the domain surface,31| | 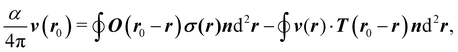 | (22) |
where α is the inward solid angle, O the Oseen tensor, and T the associated stress tensor. For the surface velocities relevant here, α = 2π at the fluid interface and α = 2θ at the contact line, while inside the droplet α = 4π. We note that σn in eqn (22) can be replaced by ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n since a constant pressure does not contribute to the integral as shown in Appendix A. To discretize the boundary-integral equation, we proceed as in our previous work.14 We assign to each surface vertex parts of the surrounding triangles such that the resulting polygonal cells with area Aj do not overlap and cover the whole region of integration. The result is a set of linear equations for the vertex velocities vj,
n since a constant pressure does not contribute to the integral as shown in Appendix A. To discretize the boundary-integral equation, we proceed as in our previous work.14 We assign to each surface vertex parts of the surrounding triangles such that the resulting polygonal cells with area Aj do not overlap and cover the whole region of integration. The result is a set of linear equations for the vertex velocities vj,| | 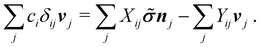 | (23) |
Recalling the definition of K in eqn (20) and introducing block matrices, which we specify in Appendix C,| |  | (24) |
| |  | (25) |
we are able to rewrite eqn (23) asor aswhere X−1(C + Y) is the shear contribution to the friction matrix.
2.5.2 Liquid–substrate friction.
We now turn to friction between liquid and substrate due to a non-zero slip velocity. The conventional slip boundary condition, also called Navier condition, is lsPtσn = ηPtv, where ls is the slip length and Pt = 1 − n⊗n the projection operator on the tangential plane. Note that the surface normal n points out of the fluid according to ref. 39 and that Ptσn = Pt![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n. However, since we are interested in moving substrates, the fluid motion relative to the local substrate velocity vsubs and the deforming traction fdeform become relevant and we have lsPt(
n. However, since we are interested in moving substrates, the fluid motion relative to the local substrate velocity vsubs and the deforming traction fdeform become relevant and we have lsPt(![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n − fdeform) = ηPt(v − vsubs). On the discretized solid/fluid interface of the substrate using eqn (20) and (21), the boundary condition becomes
n − fdeform) = ηPt(v − vsubs). On the discretized solid/fluid interface of the substrate using eqn (20) and (21), the boundary condition becomes| | | P‖(Kls + F) = −QP‖(Ṙ − Vsubs). | (28) |
Here,  is the projection operator from all the n droplet vertices onto the tangential space of the substrate with m vertices. For consistency, we defined Vsubs = (v(1)subs, v(2)subs,…) as the vector of the substrate velocities at the vertices, which also includes the vertices on the liquid–gas interface with v(i)subs = 0. Finally,
is the projection operator from all the n droplet vertices onto the tangential space of the substrate with m vertices. For consistency, we defined Vsubs = (v(1)subs, v(2)subs,…) as the vector of the substrate velocities at the vertices, which also includes the vertices on the liquid–gas interface with v(i)subs = 0. Finally,| |  | (29) |
is the slip contribution to the friction matrix, where δij is the Kronecker symbol and i, j refer to vertices on the substrate. Here we consider that, according to eqn (3), K must vanish if Ṙ = 0, and similarly, the parallel components of vector F in eqn (2) must vanish if there is no substrate deformation, i.e., if Vsubs = 0. We therefore conclude that P‖F = QP‖Vsubs which satisfies both conditions.
So far, we have not addressed the continuity condition for the normal velocity component, v·n = vsubs·n, at the liquid–substrate interface, which we already mentioned in Section 2.4. Similar to P‖, it is convenient to introduce the projection operator onto the normal space of the substrate vertices  . The boundary condition can then be restated for our discretized mesh as P⊥Ṙ = P⊥Vsubs. It directly determines the normal components of the vertex velocities at the substrate, which are contained in Ṙ. However, the condition also means that the substrate pushes or pulls on the liquid as it deforms its height profile h and the liquid resists with friction. We have already introduced the traction forces due to the substrate deformations. Their normal components are contained in the vector F⊥ = PT⊥P⊥F, which has to be calculated numerically at the same time as those components of Ṙ which are still unknown.
. The boundary condition can then be restated for our discretized mesh as P⊥Ṙ = P⊥Vsubs. It directly determines the normal components of the vertex velocities at the substrate, which are contained in Ṙ. However, the condition also means that the substrate pushes or pulls on the liquid as it deforms its height profile h and the liquid resists with friction. We have already introduced the traction forces due to the substrate deformations. Their normal components are contained in the vector F⊥ = PT⊥P⊥F, which has to be calculated numerically at the same time as those components of Ṙ which are still unknown.
For completeness we give the normal velocity component of the substrate velocity for a deforming substrate with height profile z = h(x, t). It amounts to vsubs(x)·n = ∂th(x,t)ez·n.
2.5.3 Contact-line friction.
Finally, we address the friction of the contact line. In 1964 Moffatt solved the Stokes flow at the contact line of a moving wedge filled with a viscous liquid and found an analytic expression for the traction σn along the liquid–gas interface,40| |  | (30) |
Here, H is the distance of the interface from the substrate, θ the contact angle, and vcl the tip velocity of the wedge along the substrate. Voinov relied on eqn (30) to derive the well-known Cov–Voinov law,37 which we have previously used to prescribe contact line velocity in ref. 14. However, since in our reformulated approach the Young forces appear explicitely through the droplet free energy, we derive a direct relationship between Young forces and contact line velocity based on eqn (30). As in the Cox–Voinov law we do not take into acount contact angle hysteresis and pinning, which are not our focus here.
Again, if the substrate moves, we have vcl = v − vsubs and its deforming traction fdeform, which modify eqn (30). The velocity lies in the tangential plane of the substrate and is normal to the contact line. To proceed, we integrate the traction over height H along the liquid/gas interface from a microscopic length ls, i.e., the slip length, up to a mesoscopic length ζ
| |  | (31) |
In the discretized representation of the droplet surface, we choose for the integral the surface force
σini assigned to the vertex
i on the contact line, which is contained in the friction vector
K,
i.e.,
| |  | (32) |
For the contact line, we therefore have the additional contribution
| | | Pcl(Kcl + F) = −MPcl(Ṙ − Vsubs), | (33) |
where

is the projection operator on the direction normal to the contact line and tangential to the substrate, where
k is the number of vertices on the contact line. Obviously, these vertices contribute with
| |  | (34) |
to the friction matrix. Here we use the Kronecker symbol
δij, which means that
M is diagonal. As in Section 2.5.2, we identify
PclF =
MPclVsubs as contribution to
F in
eqn (2). Note that the instantaneous local contact angle
θi is determined by the shape of the droplet mesh,
i.e., the value of
R and so
Mij is not a function of the contact line velocity
vcl. However,
θi also appears in the driving Young force [see second line of
eqn (11)] and thereby determines
vcl.
We summarize here our result for the substrate traction force F. While the components tangential to the substrate are determined by the tangential velocity of the substrate, the normal component needs to be determined. Thus we have
| | | F = (PT‖QP‖ + PTclMPcl)Vsubs + F⊥ | (35) |
where
T indicates matrix transposition.
2.6 Final dynamic equations
Finally, we are able to formulate the full set of dynamic equations. Collecting all the contributions to the friction force K linear in Ṙ from eqn (27), (28) and (33), the total friction matrix G becomes| | | G = X−1(C + Y) +PT‖QP‖ + PTclMPcl. | (36) |
Thus the force balance of eqn (2) is completely determined and reads| |  | (37) |
where he have used the specific expression for F from eqn (35). To solve this equation for the velocities Ṙ for a static substrate (Vsubs = 0 and F = 0), one just needs to invert the friction matrix G. To test our reformulated implementation of the boundary-element method, in Appendix E we simulated the relaxation of a droplet towards its equilibrium shape. The relaxation of the dynamic contact angle is in very good agreement with experimental measurements.
For substrates deforming in time, the right-hand side of eqn (37) contains the unknown non-zero components of F⊥, while on the left-hand side in Ṙ the normal velocity components at the solid–liquid interface are given by the normal substrate velocity components, i.e., P⊥Ṙ = P⊥Vsubs. By introducing the projector  that projects Ṙ onto the subspace of its unknown entries, we can reorder eqn (37) so that on the right-hand side only known quantities appear
that projects Ṙ onto the subspace of its unknown entries, we can reorder eqn (37) so that on the right-hand side only known quantities appear
| |  | (38) |
where we used
P⊥Ṙ =
P⊥Vsubs as well as
PuVsubs =
PuF⊥ = 0.
Eqn (36) further simplifies the right-hand side so that
| |  | (39) |
Now, one first solves for
PuṘ by inverting −
PuGPTu and then uses
PuṘ in the first row to determine
P⊥F⊥ if needed. This is a procedure, which we implemented in our computer code.
2.7 Nondimensionalization and parameters
We choose characteristic units, which derive from the motion of the droplet surfaces. First, as a unit of length l, we choose the initial radius R0 of the liquid–solid interface of the droplet. The dominant time scale for the deformation of the droplet is determined by the motion of the contact line. A good estimate for the speed of the contact line was derived by Voinov in ref. 37 using eqn (30) and (18). He ultimately arrives the Cox–Voinov law| | 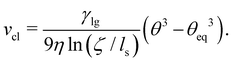 | (40) |
From the prefactor of the Cox–Voinov law and R0, we obtain an inherent time scale| | τ = 9γlg−1ηR0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ζ/ls). ln(ζ/ls). | (41) |
for the motion of the contact line. Furthermore, a characteristic force follows from combining the liquid–gas surface tension γlg and R0 as fc = γlgR0. Now, writing eqn (1) in nondimensional form using these characteristic units, gives rise to a dimensionless viscosity ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = [9
= [9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ζ/ls)]−1. Thus, our results become independent from specific values of γlg and R0. They only depend on the ratios
ln(ζ/ls)]−1. Thus, our results become independent from specific values of γlg and R0. They only depend on the ratios ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) , ζ/R0 and ls/R0, for which we choose appropriate values.
, ζ/R0 and ls/R0, for which we choose appropriate values.
As in ref. 14 the parameters of our system are matched to droplets from a 90%-glycerol/10%-water mixture for which de Ruijter et al.38 measured in experiments ln(ζ/ls) = 44, η = 209 mPa s, ls = 1 nm, γlg = 65.3 mN m−1, and mass density ρ = 1.24 g ml−1. To determine a value for ζ needed in the friction matrix of eqn (34), we fitted the experimental data for the droplet relaxation in ref. 38 in our simulations and obtained ζ = 0.17R0. All simulations are performed using a surface mesh of 1199 vertices which, in their initial configuration, have an average distance of 0.094R0 from the nearest neighbor. In the following, we use R0 = 100 μm.
From the characteristic parameters, we determine the Reynolds number as
| |  | (42) |
which matches the assumption of negligible inertia inherent in
eqn (1).
3 Driven droplets as nonuniform oscillators
Our droplets are driven by travelling waves either in wettability or in deformations of the substrate. For small wave speeds they are strongly connected to and surf on the wave, while for large speeds they can no longer follow and perform a wobbling motion. Before we describe the phenomenology of both substrate types, we introduce and study a simplified model for the motion of a droplet under a spatially periodic external stimulus. Neglecting inertia, we start with a simplified force balance for the center of mass y of the droplet, −Γẏ + F(y, t) = 0, where Γ is a friction constant and F is the effective force exerted by the substrate, on which the droplet is moving. The travelling wave pattern is modeled by the effective force| |  | (43) |
with wavelength λ and wave speed vwave. It models that there are specific positions in the travelling wave, y − vwavet = nπ with n = 0, 1, …, where no force is excerted on the droplet. For our specific wave patterns, these are the minima and maxima. In the co-moving reference frame of the substrate pattern, ycom = y − vwavet, the droplet's velocity ẏcom = ẏ − vwave generally oscillates around −vwave, i.e.,| |  | (44) |
with amplitude vc = F0/Γ. Depending on its position on the pattern, the droplet's speed is increased or reduced. In particular, for ycom = nλ/2 the force on the droplet is zero, which means ẏ = 0 or ẏcom = −vwave. Although ẏcom oscillates around −vwave, that is not its time average. Instead −vwave is the spatial average of ẏcom.
We can map eqn (44) onto the so-called ideal nonuniform oscillator29 for phase variable φ with constants a and c by identifying
| |  | (45) |
This results into the expression
also called the Adler equation.
41 Unlike the uniform (harmonic) oscillator, the phase of which has a constant rate of change,
φ determines its own rate of change. In particular, the oscillation stops for |
c| ≥ |
a| when the two terms on the r.h.s. balance each other.
42
Strogatz derives the period T of the nonuniform oscillator in ref. 29 and following his derivation we find with our parameters
| |  | (47) |
To predict the long-time behavior of the droplet, for example, its position, the time averaged droplet speed
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
is useful, which we derive now. Generally, in steady state the droplet position oscillates relative to the substrate pattern with a period
| |  | (48) |
where the difference between
vwave and
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
gives the droplet's speed relative to the substrate pattern with wavelength
λ. Differently speaking,
T is the period of the forcing experienced by the droplet through the travelling wave. Setting
eqn (47) equal to
eqn (48), we obtain
| |  | (49) |
which relates
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
to
vwave with only a single free parameter,
vc. Consequently, in this model
vc contains all material properties of the driving mechanism and droplet-substrate interaction. The limiting case for large
vwave is
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
≈
vc2/(2
vwave) and therefore
| |  | (50) |
which is useful to find
vc in the simulations but also in experiments.
However, vc is not just a fitting parameter because it also marks a change in the dynamics of the droplet. For vwave ≤ vc the oscillation stops, as predicted by the non-uniform oscillator, which means ẏcom = 0 or, equivalently, ẏ = vwave = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) . In our following analysis, we will refer to this stationary dynamics as ‘surfing’ and to the oscillatory dynamics as ‘wobbling’.
. In our following analysis, we will refer to this stationary dynamics as ‘surfing’ and to the oscillatory dynamics as ‘wobbling’.
The main limitation of the nonuniform oscillator model is that the constant vc is a priori unknown and has to be determined, e.g., from experimental or (in our case) simulation data. From its definition vc = F0/Γ we see that it is specific for the periodic forcing, eqn (43), which is applied to the droplet. Consider the case of deforming substrates with a travelling-wave height profile. On a deforming substrate, the amplitude of the driving force F0 comes from the substrate curvature. However, the curvature is determined by the amplitude of the travelling wave and its wavelength λ. Therefore, vc is not a independently tunable parameter but also a function of λ. Similarly, in the case of travelling waves in wettability, λ determines the local gradient in wettability and thereby F0. Because vc generally depends on λ this means that the relations expressed in eqn (47), (49) and (50) are only useful for predictions as long as λ (and therefore vc) is kept constant.
4 Travelling waves in wettability
We first study how travelling waves in wettability can move droplets on a completely flat substrate, similar to our earlier study of moving steps in wettability in ref. 14. However, there are clear differences, which we explain in the following.
4.1 Substrate dynamic
Here, we impose a travelling wave in wettability on a flat substrate such that the prescribed equilibrium contact angle varies according to| |  | (51) |
with wavelength λ = 2R0, vwave the speed of the wave in y-direction, the Heaviside or Θ-function, the amplitude Δθ = 30°, and θ0 = 90°.**
In experiment such a travelling wave can be generated, for example, by first exposing an azobenzene-coated substrate (cmp. ref. 11) to structured blue light with a plane-wave intensity profile, then UV light of uniform intensity, then again structured blue light with a slightly shifted intensity profile, and so on. By alternating between these UV and blue light patterns, one produces a wettability profile which slowly changes in time.
The droplet moves toward regions of high wettability, which means the valleys of the travelling wave in θeq. Because these valleys are steadily moving forward in y-direction, the droplet is biased to also move in that direction. However, as noted in Section 3, the droplet can perform different kinds of motion under the influence of this driving mechanism, namely surfing and wobbling motion (see Fig. 1), which we will analyse in detail now.
4.2 Surfing and wobbling
We first review the basic phenomenology. A surfing droplet moves at the same speed as the travelling wave. Consequently, its shape remains constant and a stationary flow field exists inside the droplet (see Movie M1 in the ESI†). This stationary state is identical to the surfing dynamics we observed in ref. 14.
A wobbling droplet moves at a slower speed than the travelling wave pattern. It oscillates in speed and shape as it repeatedly passes over the peaks and valleys of the wave (see Movie M2 in the ESI†). The wobbling dynamics was not present in our previous study of moving steps in wettability14 because it requires a periodic wettability pattern.
According to the nonuniform oscillator model, we outlined in Section 3, wobbling occurs above a critical speed of the travelling wave pattern. As the speed of the travelling wave pattern decreases, the period at which the droplet shape oscillates grows and it diverges exactly at the transition. So, the resulting surfing state can be considered as a wobbling which is frozen in time. This bifurcation is analyzed in detail in Section 4.4.
4.3 Quantitative analysis
One characteristic quantity of the surfing and wobbling dynamics is the droplet speed and we ask how it relates to the speed of the wave pattern. The droplet speed needs to be defined carefully, especially for wobbling, because it varies periodically over time. It is appropriate to average the droplet speed over one period of oscillation T. The period of oscillation refers to the shortest duration between two identical shapes of the droplet, albeit not identical positions in the lab reference frame. The average droplet speed is then formally given by| |  | (52) |
where the starting time t is set after the decay of any transients and the number of periods n is chosen according to the available simulation data. Note that, for the case of a surfing droplet, we have y(t) = vwavet + y0 with position y0 at t = 0. Here, the time interval T is arbitrary and the definition above reduces to ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = vwave.
= vwave.
In Fig. 3(a) we plot the speed ratio ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwaveversus vwave as determined from our BEM simulations. The speed ratio is 1 in the surfing state and it decays as vwave−2 in the wobbling state (dashed line), as predicted from the nonuniform oscillator model and eqn (49) in the limit vwave ≫ vc. This means
/vwaveversus vwave as determined from our BEM simulations. The speed ratio is 1 in the surfing state and it decays as vwave−2 in the wobbling state (dashed line), as predicted from the nonuniform oscillator model and eqn (49) in the limit vwave ≫ vc. This means ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is inversely proportional to vwave for wobbling and equal to vwave for surfing. The time-averaged speed of the droplet decays to zero which also matches our observation from an earlier article that droplets are less susceptible to rapid changes in wettability.30 For a full quantitative comparison with our model, we need to determine the velocity vc. Following eqn (50), we plot
is inversely proportional to vwave for wobbling and equal to vwave for surfing. The time-averaged speed of the droplet decays to zero which also matches our observation from an earlier article that droplets are less susceptible to rapid changes in wettability.30 For a full quantitative comparison with our model, we need to determine the velocity vc. Following eqn (50), we plot  versus vwave in Fig. 3(b) and read off vc = 2.65R0τ−1 at large wave speeds (dash-dotted red line). The dashed line in Fig. 3(a) is the prediction from eqn (49) using the determined value for vc.
versus vwave in Fig. 3(b) and read off vc = 2.65R0τ−1 at large wave speeds (dash-dotted red line). The dashed line in Fig. 3(a) is the prediction from eqn (49) using the determined value for vc.
 |
| | Fig. 3 Diagrams of (a) the mean droplet speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , (b) the helper quantity , (b) the helper quantity  and (c) the wobbling oscillation period T plotted versus vwave for a travelling wave in wettability with wavelength λ = 2R0. Blue dots indicate our results from BEM simulation, the dashed black lines indicate predictions from the nonuniform oscillator model and the dash-dotted red line indicates the critical wave speed vc, which is the sole fitting parameter of the model. and (c) the wobbling oscillation period T plotted versus vwave for a travelling wave in wettability with wavelength λ = 2R0. Blue dots indicate our results from BEM simulation, the dashed black lines indicate predictions from the nonuniform oscillator model and the dash-dotted red line indicates the critical wave speed vc, which is the sole fitting parameter of the model. | |
The transition from surfing to wobbling appears continuous, meaning there is no jump in droplet speed, as predicted by the nonuniform oscillator model. However, the transient dynamics decays slowly close to the transition so that we lack data close to vwave = vc. If the transition is indeed continuous, the droplet moves fastest exactly at the critical wave speed vc. The period T of wobbling oscillations, displayed in Fig. 3(c), grows inversely proportional to vwave − vc as vwave approaches vc from above. These observations for the wobbling state again quantitatively match the prediction of the nonuniform oscillator model.
4.4 Comparison with travelling steps in wettability
In ref. 14 we observed a droplet surfing along a substrate on a wettability step that moves with velocity vstep and a sigmoidal profile σ(y). Similar to eqn (44) we can describe the droplet velocity in the co-moving frame of the step with| | 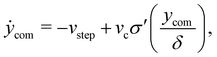 | (53) |
where for the sigmoidal function we chose σ(y) = (1 + e−y)−1, and δ is the step width. Most importantly, for vstep < vc two surfing states exist. They sit outside the center of the step and are stable and unstable fixed points, which eventually meet in a saddle-node bifurcation at vstep = vc. Furthermore, there is a sessile steady state where the droplet sits outside of the step. It occurs for any value of vstep in the limit |ycom/δ| ≫ 0 so that the contribution from σ′ vanishes. The saddle node bifurcation with the stable and unstable fixed points as well as the stable fixed point of the sessile droplet are schematically illustrated in Fig. 4(a) using an appropriate shape variable.
 |
| | Fig. 4 Schematic bifurcation diagrams for an appropriate droplet-shape variable plotted versus pattern velocity. (a) The droplet dynamics in the step wettability pattern (cf. ref. 14) corresponds to a saddle-node bifurcation at the critical velocity vc. (b) The travelling wave pattern generates an additional limit cycle that collides with the saddle and node, giving rise to a saddle-node-infinite-period (SNIPER) bifurcation. | |
Comparing the moving wettability step treated in ref. 14 to the travelling wettability wave considered here and modeled by eqn (44), we note that a sessile state is impossible due to the periodicity of the wave pattern. Instead, the wobbling dynamic takes the place of the sessile state for vwave > vc. In Fig. 4(b) the resulting bifurcation diagram is sketched. The saddle-node bifurcation of the moving wettability step is still present but for travelling waves it collides with the limit cycle associated with wobbling. This collision comprises a global bifurcation which is called Saddle-Node-Infinite-PERiod (SNIPER) bifurcation.29
A SNIPER bifurcation was previously observed for droplets exposed to an oscillating external force on a static heterogeneous substrate41 and for a droplet subject to a constant external force on a rotating cylinder43,44 with the force acting perpendicular to the cylinder's axis of rotation. In both cases, the bifurcation marks the transition from a pinned to a sliding droplet.
5 Travelling-wave deformations
We now turn to the second driving mechanism introduced in Section 2. The substrate deforms such that its height profile follows a travelling wave. The wettability is kept uniform and we solely rely on the travelling height profile to move the droplet. In experiment such a travelling wave can be generated, for example, by light-responsive liquid-crystal elastomers exposed to structured light patterns.20 The influence of gravity in such a deformation wave is negligible because the capillary length  is much larger than the droplet radius. This raises the question of the driving mechanism that moves the droplet forward.
is much larger than the droplet radius. This raises the question of the driving mechanism that moves the droplet forward.
For an equilibrium contact angle of θeq = 90°, which according to Young's law occurs at surface tensions γsl = γsg, only the liquid–gas interface is relevant and the droplet deforms to minimize the area of this interface. Hence, on a curved surface the droplet moves away from peaks and toward valleys because there the liquid–gas interface occupies less area compared to a droplet with the same volume sitting on a flat part or a peak of the substrate. For θeq < 90° the droplet is even more attracted to valleys in the substrate, as it is energetically advantageous to cover more of the solid with liquid, while for θeq > 90° the situation is less clear. In ref. 19 Lv et al. demonstrate how a droplet moves on the inside and outside of a conical substrate without any additional external stimulus. On the outside of the cone the liquid–substrate curvature is negative and on the inside of the cone it is positive. Notably, for all cases studied with θeq ranging from 30° to 120°, the droplets move in the direction of increasing curvature. The same behavior was recently confirmed for droplets on cylinders of varying size.45 Indeed, when we place a droplet onto a substrate peak with θeq = 120° in our BEM simulations and then perturb the droplet, the position is unstable. Lv et al. term this mechanism curvi-propulsion and in this section we investigate if it generates the same wobbling and surfing dynamics we found for the wettability waves in Section 4 and if there are any differences between the two cases.
5.1 Surfing and wobbling
Instead of a wettability profile, we now impose a travelling height profile of the substrate with amplitude h0,| | 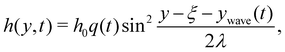 | (54) |
where ξ determines the initial phase shift or position of the wave relative to the droplet at y = 0. Especially, in the surfing dynamic we use a value of ξ = 0.3R0 to place the droplet close to its surfing position on the wave profile, while ξ is irrelevant for the wobbling dynamics. We introduce the factor| |  | (55) |
and| |  | (56) |
The purpose of the factor q(t) is to allow a continuous evolution of the surface deformation from a flat to the sinusoidal shape to which the droplet can adjust gradually starting at a specific position relative to the wave. Then, the deformation wave starts to travel at t = t0, where we choose t0 in the interval 0.1τ ≤ t0 ≤ 0.2τ. To be specific, we set λ = 4R0 for the wavelength, h0 = 0.1R0 for the amplitude, and an equilibrium contact angle of θeq = 90°.†† In Section 6, we will explore travelling deformation waves for a range of wavelengths.
With time the droplet again settles into either surfing or wobbling motion depending on the wave speed vwave. Because it is attracted to the valleys in the substrate, it tries to follow them as the travelling deformation wave progresses. If the travelling wave moves sufficiently slowly, the droplet can surf on a position behind the valley (see Movie M3 in the ESI†). If the travelling wave moves faster than a critical speed, the droplet is always overtaken by the peak behind it, relaxes into the closest valley, and falls back again giving rise to the wobbling motion (see Movie M4 in the ESI†).
5.2 Quantitative analysis
In analogy to the travelling wettability pattern, we analyze the time-averaged speed of the droplet as defined in eqn (52). In Fig. 5(a) we again plot ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwaveversus vwave. In contrast to the wettability wave, the speed of the wobbling droplet now grows linearly with vwave at large vwave. Due to this clear difference, we realize that our model needs to be adjusted.
/vwaveversus vwave. In contrast to the wettability wave, the speed of the wobbling droplet now grows linearly with vwave at large vwave. Due to this clear difference, we realize that our model needs to be adjusted.
 |
| | Fig. 5 Diagrams of (a) the mean droplet speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , (b) the helper quantity v*, and (c) the wobbling oscillation period T as functions of vwave for a travelling deformation wave with wavelength λ = 4R0. Blue dots indicate our results from BEM simulation, the dashed black line indicates the revised nonuniform oscillator model, eqn (59), the dash-dotted red line indicates the critical wave speed vc, and the dotted red line indicates the parameter ε. The latter two are the fitting parameters of the model. , (b) the helper quantity v*, and (c) the wobbling oscillation period T as functions of vwave for a travelling deformation wave with wavelength λ = 4R0. Blue dots indicate our results from BEM simulation, the dashed black line indicates the revised nonuniform oscillator model, eqn (59), the dash-dotted red line indicates the critical wave speed vc, and the dotted red line indicates the parameter ε. The latter two are the fitting parameters of the model. | |
To start, we re-examine the nonuniform oscillator model of eqn (44), where a spatially periodic force drives the droplet with a constant amplitude vc. For the deforming substrate we introduced a traction force F⊥ in eqn (37), which imposes the deformation of the substrate onto the droplet shape. However, this force depends on vwave: it is zero for vwave ≤ vc, where the droplet's shape is constant and beyond vc it grows with vwave as the droplet is deformed more rapidly. As before, the force is also spatially periodic since it originates from the wave pattern of the substrate's height profile. Therefore, to include the dependence of the amplitude of the driving force on vwave, we extend eqn (44) and write
| |  | (57) |
The dimensionless coefficient
ε ≪ 1 quantifies the relative strength of the wave-speed depending part of the amplitude. In analogy to
eqn (47), we find for the time period,
| |  | (58) |
which together with
eqn (48) gives the mean droplet speed,
| |  | (59) |
Here, we have used

in
eqn (58). The small parameter
ε means that
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
increases proportional to
vwave for large
vwave. Note that
ε does not affect the scaling of the wobbling period
T with the inverse wave speed well above
vc.
Now, our procedure to determine ε and vc, the central parameters of the model, is as follows. First, from eqn (59) we determine the limiting value of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwave = ε for large vwave, which we can directly read off from Fig. 5(a) as ε = 3.565 × 10−3. Then, we subtract εvwave from both sides of eqn (59),
/vwave = ε for large vwave, which we can directly read off from Fig. 5(a) as ε = 3.565 × 10−3. Then, we subtract εvwave from both sides of eqn (59),
| |  | (60) |
and expand the r.h.s. for large
vwave to obtain
| | 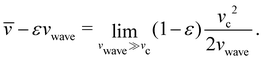 | (61) |
Solving for
vc yields
| | 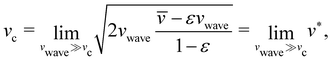 | (62) |
which for
ε = 0 indeed simplifies to
eqn (50). Accordingly, in
Fig. 5(b) we plot
v* as defined in
eqn (62). Because
ε appears as coefficient of
vwave2,
v* is sensitive to small errors in
ε at large
vwave. However, around
vwave/
R0τ−1 = 2 it takes on a constant value, from which we determine
vc = 0.185
R0τ−1. The dashed black line labelled model in
Fig. 5(a) shows that with these parameters our revised model quantitatively matches the BEM data (blue dots). Similarly, it also reproduces the wobbling period displayed in
Fig. 5(c). Because around
vwave =
vc, the original and the revised model behave the same, the latter also predicts a SNIPER bifurcation at
vwave =
vc for droplets driven by travelling substrate deformations.
Our revised model fits the BEM data well and thus provides an interpretation of the asymptotic behavior of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for large vwave. To capture the asymptote, we introduced an amplitude of the driving force, which depends on vwave. It accounts for the fact that a travelling substrate deformation always needs to displace the droplet, which requires a larger driving force with increasing vwave. This is the clear difference to travelling wettability patterns treated in Section 4, where the pattern can just pass beneath the droplet without the need to lift it up.
for large vwave. To capture the asymptote, we introduced an amplitude of the driving force, which depends on vwave. It accounts for the fact that a travelling substrate deformation always needs to displace the droplet, which requires a larger driving force with increasing vwave. This is the clear difference to travelling wettability patterns treated in Section 4, where the pattern can just pass beneath the droplet without the need to lift it up.
6 A note on particle sorting
In Sections 4 and 5 we described that droplets move in response to spatial gradients in wettability or curvature of the substrate, respectively. Both, gradient and curvature, change in magnitude when we adjust the wavelength λ of the travelling wave pattern. Therefore, we can expect that the speed of the droplet ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) also depends on λ. However, in the surfing state the droplet speed is identical to the wave speed vwave, regardless of λ. Therefore, we only need to consider a wobbling droplet.
also depends on λ. However, in the surfing state the droplet speed is identical to the wave speed vwave, regardless of λ. Therefore, we only need to consider a wobbling droplet.
In Fig. 6 we display for both driving mechanisms the mean droplet velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) as a function of R0/λ for vwave = 50R0τ−1, which places the droplet far into the regime of wobbling dynamics. For travelling deformation waves (green crosses in Fig. 6) no clear trend is discernible because mean droplet speed
as a function of R0/λ for vwave = 50R0τ−1, which places the droplet far into the regime of wobbling dynamics. For travelling deformation waves (green crosses in Fig. 6) no clear trend is discernible because mean droplet speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) has a minimum near R0 = 0.17λ. In contrast, for travelling waves in wettability (blue dots in Fig. 6) we observe that
has a minimum near R0 = 0.17λ. In contrast, for travelling waves in wettability (blue dots in Fig. 6) we observe that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) grows like (R0/λ)2. Further decreasing λ, one would expect
grows like (R0/λ)2. Further decreasing λ, one would expect ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) to decrease again. However, for larger ratios R0/λ the creeping flow approximation does not hold anymore for deforming substrates and one enters the regime of unsteady Stokes flow due to the increased oscillation frequency of the height profile.
to decrease again. However, for larger ratios R0/λ the creeping flow approximation does not hold anymore for deforming substrates and one enters the regime of unsteady Stokes flow due to the increased oscillation frequency of the height profile.
 |
| | Fig. 6 Diagram of mean droplet speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) as a function of R0/λ, i.e., the ratio between droplet radius and wavelength, for travelling waves with speed vwave = 50R0τ−1. Blue dots indicate results from BEM simulation with waves in wettability (right axis), and green crosses indicate results from BEM simulation with deformation waves (left axis) with h0 = 0.1R0. Connecting dotted and dashed lines are added to guide the eye. The solid black line indicates a quadratic scaling. as a function of R0/λ, i.e., the ratio between droplet radius and wavelength, for travelling waves with speed vwave = 50R0τ−1. Blue dots indicate results from BEM simulation with waves in wettability (right axis), and green crosses indicate results from BEM simulation with deformation waves (left axis) with h0 = 0.1R0. Connecting dotted and dashed lines are added to guide the eye. The solid black line indicates a quadratic scaling. | |
Now consider a poly-disperse collection of droplets with R0 in the range of 0.1λ to 0.5λ on a single substrate with a travelling wave in wettability with fixed λ. According to Fig. 6 there is a unique value of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for each droplet size. This means, after we let the droplets run for some time (and with sufficient distance between them to prevent mergers), the droplets will separate according to their size. Because small droplets lag behind larger droplets, this naturally leads to a sorting mechanism for such a poly-disperse collection of droplets.
for each droplet size. This means, after we let the droplets run for some time (and with sufficient distance between them to prevent mergers), the droplets will separate according to their size. Because small droplets lag behind larger droplets, this naturally leads to a sorting mechanism for such a poly-disperse collection of droplets.
7 Conclusions
We have studied liquid-droplet motion on substrates using two different mechanisms: travelling waves in wettability and travelling-wave deformations of the substrate. To that end, we first implemented the boundary element method (BEM) for the fluid velocity field inside the droplet starting from the free energy of the droplet, the balance of forces at the droplet interface, and the relevant friction contributions.
To interpret our numerical findings from applying the BEM, we first introduced an analytic model for a particle driven by a travelling-wave force, which maps onto the so-called nonuniform oscillator. For increasing wave velocity, the analytic model exhibits a bifurcation between two states, which we call surfing and wobbling and which directly connect to the phenomenology observed in our BEM simulations.
For travelling waves in wettability the results from BEM simulations for wobbling period and mean droplet speed are consistent with the analytic model and indeed confirm the bifurcation in the full dynamical system. This further implies that the motion of the droplet's center of mass can be characterized solely by the critical wave speed for the bifurcation, which is determined by the material properties of the droplet and substrate. For a specific set of parameters we determined the critical wave speed by varying the wave speed in the BEM simulations.
We also investigated travelling-wave deformations of the substrate, which give rise to what is called curvi-propulsion in ref. 19. Again, we could identify a transition from surfing to wobbling with increasing wave speed but, interestingly, the simulation results reveal that the droplet speed does not approach zero for large wave speeds. By including a speed-dependent amplitude of the driving force, the modified analytic model could account for this new behavior, as we demonstrated for a specific set of parameters in the BEM simulations.
Finally, we also performed simulations where we varied the wavelength λ of the travelling wave for both driving mechanisms in the wobbling regime. For waves in wettability the droplet speed decays as λ−2, which implies that the critical wave speed is proportional to droplet radius over wavelength. This suggests a potential sorting mechanism for a collection of droplets by droplet size. For travelling-wave deformations of the substrate, we could not observe a clear trend in droplet speed w.r.t. wavelength.
Our findings compare and contrast two different mechanisms for steering droplets toward a preferred direction, one based on switchable wettability and one based on externally-induced deformations of the substrate. They demonstrate that the relevant quantities such as droplet speed and wobbling period can be reproduced and interpreted with an analytic model using only one or two fitting parameters, respectively. Moving droplets is relevant for lab-on-a-chip applications. Our work suggest two methods for realizing this. Another attractive possibility to explore are substrates with switchable softness46 and the occurence of durotaxis since our reformulated approach is already well-adapted to deforming substrates. In particular, the elasticity of a soft substrate can be represented by an additional contribution to the free energy.
Conflicts of interest
There are no conflicts to declare.
Appendices
A Invariance of the boundary-integral equation
In eqn (22) one can replace σn by ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n = σn + p0n, where the constant pressure p0 does not contribute to the surface integral. To show this, we write for an arbitrary force vector f0,
n = σn + p0n, where the constant pressure p0 does not contribute to the surface integral. To show this, we write for an arbitrary force vector f0,| |  | (63) |
The closed surface integral of the Stokeslet flow field, uStokeslet(r) = O(r − r0)f0, vanishes, since uStokeslet(r) is incompressible by construction and after applying Gauss's theorem.
B Normal vector in Monge representation
We parameterize the substrate according to Monge representation by ![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) = (x,y,h(x,y)). The normal n then points perpendicular to both tangential vectors of the surface which are given by the derivatives of
= (x,y,h(x,y)). The normal n then points perpendicular to both tangential vectors of the surface which are given by the derivatives of ![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) w.r.t. x and y, respectively, so that
w.r.t. x and y, respectively, so that| |  | (64) |
Note that n, as written here, is generally not of unit length. However, as noted in Section 2.3, the normalization constant is subsumed into the Lagrange multiplier λ.
C Block matrices
The matrices in eqn (23) are defined as| | 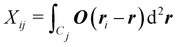 | (65) |
and| |  | (66) |
where the surface integral is performed over the polygonal cell Cj around vertex j and ri is the position of vertex i. Furthermore, in eqn (23), if vertex i is on the contact line, ci = θi/2π with contact angle θi and otherwise ci = 1/2.
D Functional derivative and rigidity constraint
The functional derivative of 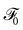 w.r.t. shape deformation is
w.r.t. shape deformation is| | 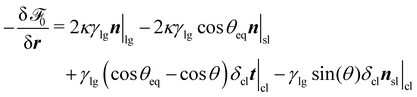 | (67) |
which contributes to the r.h.s. of eqn (10). The first and second terms are due to surface tension within the liquid–gas and liquid–solid interfaces of the droplet, respectively, and κ is the local curvature of the respective interface.47 The third and fourth terms on the right-hand side of eqn (67) comprise the Young force acting locally on the contact line, where δcl is the Dirac δ-function centered at the location of the contact line. The Young force has two components: one along unit vector t tangential to the plane of the substrate and one along unit vector nsl normal to the substrate.
In eqn (10) the last term is a rigidity force with which the substrate acts to keep its shape against the interior pressure p0, against the curvature force at the solid–liquid interface in the second term on the r.h.s. of eqn (67), and the normal component of the Young force in the fourth term. Because the rigidity constraint with the Lagrange multiplier λ needs to balance these forces, the rigidity-constraint force frigid = G(x)λ(x)n|sl introduced in Section 2.4 reads
| | frigid = (2κγlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq + γlg θeq + γlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)δcl|cl − p0)n|sl. sin(θ)δcl|cl − p0)n|sl. | (68) |
Together with
eqn (10) and (67) it results in
eqn (11).
E Validation
To test our method we compare its result to an experiment reported in ref. 38 and to a fit with our previous simulation approach in ref. 14. In the experiment, a glycerol droplet (with the material properties written in Section 2.7) is placed on a substrate with equilibrium contact angle 64.3° starting from a contact angle above this value. During the relaxation of the droplet, its dynamic contact angle is recorded over time. To transfer the parameters of the experiment to BEM, we simulate a droplet which is initially in equilibrium with a contact angle close to the first recorded angle in the experiment on a substrate with equilibrium contact angle 64.3°. As in the experiment, we measure the dynamic contact angle θ in our simulation by fitting a spherical cap shape to the discretized liquid–gas interface at each time step and then calculate θ from the cap's tangent at the contact line.
To compare our simulation to the experiment, we need to convert our timesteps to SI units by explicitely calculating the value of τ for the experimental data as specified in eqn (41). In the experiment, the volume of the droplet is reported to be at least V = 5 mm3 from which we calculate  . With this value for R0 and the material properties written in Section 2.7, we calculate τ = 1.7 s. We display both the experimental data and the result of our simulation in Fig. 7 where we can see good agreement, especially in the initial relaxation. The long-time relaxation of the experimental data appears to be a bit slower than our simulation data which may be due to defects on the substrate which we do not consider in our method. The test demonstrates that our method is able to reproduce the relaxation of a real droplet as it is observed in experiment. Notably, because we have carefully nondimensionalized our method, we do not need to alter any simulation parameters to simulate smaller or larger droplets; any change in droplet volume merely affects the conversion of our timescale from τ to seconds.
. With this value for R0 and the material properties written in Section 2.7, we calculate τ = 1.7 s. We display both the experimental data and the result of our simulation in Fig. 7 where we can see good agreement, especially in the initial relaxation. The long-time relaxation of the experimental data appears to be a bit slower than our simulation data which may be due to defects on the substrate which we do not consider in our method. The test demonstrates that our method is able to reproduce the relaxation of a real droplet as it is observed in experiment. Notably, because we have carefully nondimensionalized our method, we do not need to alter any simulation parameters to simulate smaller or larger droplets; any change in droplet volume merely affects the conversion of our timescale from τ to seconds.
 |
| | Fig. 7 Diagram of the dynamic contact angle θ over time t. Red dots indicate the experimental data visually extracted from Fig. 2(a) in ref. 38 and the solid blue line shows our simulation data which has been converted to ESI,† units with τ = 1.7 s, the time scale implied by the parameters of the experiment. The dash-dotted green line shows data from our previous simulation approach in ref. 14 and the dashed black line indicates the equilibrium contact angle θeq = 64.3°. | |
Acknowledgements
We thank Uwe Thiele and Akash Choudhary for fruitful discussions and acknowledge financial support from German Research Foundation (DFG) as part of priority program 2171 (project number 505839720).
Notes and references
- M. Alwazzan, K. Egab, B. Peng, J. Khan and C. Li, Int. J. Heat Mass Transf., 2017, 112, 991 CrossRef CAS.
- M. Edalatpour, L. Liu, A. Jacobi, K. Eid and A. Sommers, Appl. Energy, 2018, 222, 967 CrossRef.
- S. N. Varanakkottu, M. Anyfantakis, M. Morel, S. Rudiuk and D. Baigl, Nano Lett., 2016, 16, 644 CrossRef CAS PubMed.
- L. Qi, Y. Niu, C. Ruck and Y. Zhao, Lab Chip, 2019, 19, 223–232 RSC.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS.
- P. Teng, D. Tian, H. Fu and S. Wang, Mater. Chem. Front., 2020, 4, 140–154 RSC.
- U. Thiele, K. Neuffer, M. Bestehorn, Y. Pomeau and M. G. Velarde, Colloids Surf., A, 2002, 206, 87 CrossRef CAS.
- D. Baigl, Lab Chip, 2012, 12, 3637 RSC.
- A. Venancio-Marques and D. Baigl, Langmuir, 2014, 30, 4207–4212 CrossRef CAS PubMed.
- M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539 CrossRef CAS PubMed.
- K. Ichimura, S. Oh and M. Nakagawa, Science, 2000, 288, 1624 CrossRef CAS PubMed.
- J. Vialetto, M. Hayakawa, N. Kavokine, M. Takinoue, S. N. Varanakkottu, S. Rudiuk, M. Anyfantakis, M. Morel and D. Baigl, Angew. Chem., Int. Ed., 2017, 56, 16565–16570 CrossRef CAS PubMed.
- J. ter Schiphorst, J. Saez, D. Diamond, F. Benito-Lopez and A. P. H. J. Schenning, Lab Chip, 2018, 18, 699–709 RSC.
- J. Grawitter and H. Stark, Soft Matter, 2021, 17, 2454 RSC.
- H. B. Eral, D. J. C. M. t Mannetje and J. M. Oh, Colloid Polym. Sci., 2013, 291, 247 CrossRef CAS.
- H. S. Lim, J. T. Han, D. Kwak, M. Jin and K. Cho, J. Am. Chem. Soc., 2006, 128, 14458 CrossRef CAS PubMed.
- H.-J. Butt, J. Liu, K. Koynov, B. Straub, C. Hinduja, I. Roismann, R. Berger, X. Li, D. Vollmer, W. Steffen and M. Kappl, Curr. Opin. Colloid Interface Sci., 2022, 59, 101574 CrossRef CAS.
- S. Karpitschka, A. Pandey, L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7403–7407 CrossRef CAS PubMed.
- C. Lv, C. Chen, Y.-C. Chuang, F.-G. Tseng, Y. Yin, F. Grey and Q. Zheng, Phys. Rev. Lett., 2014, 113, 026101 CrossRef PubMed.
- S. Palagi, A. G. Mark, S. Y. Reigh, K. Melde, T. Qiu, H. Zeng, C. Parmeggiani, D. Martella, A. Sanchez-Castillo, N. Kapernaum, F. Giesselmann, D. S. Wiersma, E. Lauga and P. Fischer, Nat. Mater., 2016, 15, 647–653 CrossRef CAS PubMed.
- I. Rehor, C. Maslen, P. G. Moerman, B. G. van Ravensteijn, R. van Alst, J. Groenewold, H. B. Eral and W. K. Kegel, Soft Robot., 2021, 8, 10–18 CrossRef PubMed.
- M. P. Gelfand and R. Lipowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 8725–8735 CrossRef PubMed.
-
C. Duprat and H. A. Stone, Fluid-Structure Interactions in Low-Reynolds-Number Flows, The Royal Society of Chemistry, 2016, pp. 193–246 Search PubMed.
- J. Bico, É. Reyssat and B. Roman, Annu. Rev. Fluid Mech., 2018, 50, 629–659 CrossRef.
- S. Aland and D. Mokbel, Int. J. Numer. Methods Eng., 2021, 122, 903–918 CrossRef.
- R. Shuttleworth, Proc. Phys. Soc. Sect. A, 1950, 63, 444–457 CrossRef.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977 CrossRef CAS.
-
S. Strogatz, Nonlinear dynamics and Chaos, Westview Press, 1994 Search PubMed.
- J. Grawitter and H. Stark, Soft Matter, 2021, 17, 9469 RSC.
-
C. Pozrikidis, Boundary integral and singularity methods for linearized viscous flow, Cambridge University Press, 1992 Search PubMed.
- M. Doi, J. Phys.: Condens. Matter, 2011, 23, 284118 CrossRef PubMed.
- A. Zafferi, D. Peschka and M. Thomas, Z. Angew. Math. Mech., 2023, 103, e202100254 CrossRef.
- E. Alinovi and A. Bottaro, J. Comput. Phys., 2018, 356, 261–281 CrossRef CAS.
- in The Boundary Element Method for Engineers and Scientists, ed. J. T. Katsikadelis, Academic Press, Oxford, 2nd edn, 2016, pp. 403–421 Search PubMed.
- C. Huh and L. E. Scriven, J. Colloid Interface Sci., 1971, 35, 85 CrossRef CAS.
- O. V. Voinov, Fluid Dyn., 1976, 11, 714 CrossRef.
- M. J. de Ruijter, J. De Coninck, T. D. Blake, A. Clarke and A. Rankin, Langmuir, 1997, 13, 7293 CrossRef CAS.
- S. J. Bolaños and B. Vernescu, Phys. Fluids, 2017, 29, 057103 CrossRef.
- H. K. Moffatt, J. Fluid Mech., 1964, 18, 1–18 CrossRef.
- U. Thiele and E. Knobloch, Phys. Rev. Lett., 2006, 97, 204501 CrossRef PubMed.
- R. Adler, Proc. IRE, 1946, 34, 351 Search PubMed.
- U. Thiele, J. Fluid Mech., 2011, 671, 121 CrossRef.
- T.-S. Lin, S. Rogers, D. Tseluiko and U. Thiele, Phys. Fluids, 2016, 28, 082102 CrossRef.
- J. Liu, Z. Feng, W. Ouyang, L. Shui and Z. Liu, ACS Omega, 2022, 7, 20975–20982 CrossRef CAS PubMed.
- N. Nekoonam, G. Vera, A. Goralczyk, F. Mayoussi, P. Zhu, D. Böcherer, A. Shakeel and D. Helmer, ACS Appl. Mater. Interfaces, 2023, 15, 27234–27242 CrossRef CAS PubMed.
- K. Deckelnick, G. Dziuk and C. M. Elliott, Acta Numerica, 2005, 14, 139–232 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Consists of four animations, M1–M4, corresponding to specific BEM simuluations: M1 and M2 correspond to simulations with vwave = 1R0τ−1 (surfing) and vwave = 10R0τ−1 (wobbling) in Fig. 3, respectively. M3 corresponds to a simulation as described in Section 5 with ξ = 1R0, t0 = 0.2τ and vwave = 0.18R0τ−1 (surfing). M4 corresponds to the simulation with vwave = 70R0τ−1 (wobbling) in Fig. 5. See DOI: https://doi.org/10.1039/d4sm00213j |
‡ In fact, Young's law follows from minimizing  under a volume constraint. under a volume constraint. |
| § In the case of a flat substrate placed at a height h = 0, we have ni = ez and so the constraint reduces to λigi = λizi, which is aquivalent to eqn (8). |
| ¶ This is commonly referred to as the principle of virtual work. |
|| Note that we can reuse the gradients ∇Rgi from above in calculating  in eqn (16). Note also that in our previous study ref. 14 when we studied a droplet on a rigid flat substrate there was no need to calculate the constraint forces due to the rigid substrate because in that case we calculated the force on each vertex individually and imposed the volume constraint only on the resulting velocity field. That approach proved inapplicable for our current study. in eqn (16). Note also that in our previous study ref. 14 when we studied a droplet on a rigid flat substrate there was no need to calculate the constraint forces due to the rigid substrate because in that case we calculated the force on each vertex individually and imposed the volume constraint only on the resulting velocity field. That approach proved inapplicable for our current study. |
| ** Note that in ref. 14 we studied a moving wettability step and explored the influence of different contact angles θ0 and step widths Δθ on the surfing speed of a droplet. One important finding was that θ0 = 90° does not result in a qualitatively different result than other values of θ0. |
| †† Note that θeq = 90° is not a special case here because curvi-propulsion acts in the same direction regardless of wettability, i.e., regardless whether a substrate is hydrophobic or hydrophilic.19 |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Holger
Stark
* and
Holger
Stark


 derives from the droplet free energy, as we explain in Section 2.2, and provides the Laplace pressure, Young's force at the contact line, and constraint forces. Finally, F governs the dynamics induced by deforming substrates.
derives from the droplet free energy, as we explain in Section 2.2, and provides the Laplace pressure, Young's force at the contact line, and constraint forces. Finally, F governs the dynamics induced by deforming substrates.
 and F become vectors and G a friction matrix. In the following we systematically determine all these quantities, which will give us a systematic approach for calculating the motion of the droplet. We start with the mesh discretization in Section 2.1, then continue with the droplet free energy in Section 2.2 and discuss the relevant Lagrange parameters for the volume and rigidity constraint of droplet and deforming substrate, respectively, in Section 2.3. In Section 2.4 we analyze the boundary conditions at the droplet surface, which confirms the force balance of eqn (2), and we formulate the vectors K and F. In Section 2.5 we calculate the complete friction matrix by considering shear friction in the fluid using the boundary integral equation for the Stokes equation, as well as liquid–substrate and contact-line friction. In Section 2.6 we present the final dynamic equations, which we use in our simulations, and in Section 2.7 we collect the parameters used.
and F become vectors and G a friction matrix. In the following we systematically determine all these quantities, which will give us a systematic approach for calculating the motion of the droplet. We start with the mesh discretization in Section 2.1, then continue with the droplet free energy in Section 2.2 and discuss the relevant Lagrange parameters for the volume and rigidity constraint of droplet and deforming substrate, respectively, in Section 2.3. In Section 2.4 we analyze the boundary conditions at the droplet surface, which confirms the force balance of eqn (2), and we formulate the vectors K and F. In Section 2.5 we calculate the complete friction matrix by considering shear friction in the fluid using the boundary integral equation for the Stokes equation, as well as liquid–substrate and contact-line friction. In Section 2.6 we present the final dynamic equations, which we use in our simulations, and in Section 2.7 we collect the parameters used.
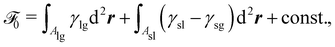
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq.‡ Using it together with γlg = const., we obtain
θeq.‡ Using it together with γlg = const., we obtain



 is one part of the force balance of eqn (3). In our simulations we always calculate it numerically as detailed below. However, to illustrate its content, we perform the derivative and explicitely write it as
is one part of the force balance of eqn (3). In our simulations we always calculate it numerically as detailed below. However, to illustrate its content, we perform the derivative and explicitely write it as
 gives the acting forces due to surface tension and the Young force (see below). Their normal components acting on the substrate compensate the rigidity-constraint force and, as we demonstrate in Appendix D, the remaining terms of the functional derivative can be written as
gives the acting forces due to surface tension and the Young force (see below). Their normal components acting on the substrate compensate the rigidity-constraint force and, as we demonstrate in Appendix D, the remaining terms of the functional derivative can be written as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq = cos
θeq = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and p0 becomes the Laplace pressure pL = −2κγlg = p0.
θ) and p0 becomes the Laplace pressure pL = −2κγlg = p0.

 in eqn (10) acting on the different interfaces of the droplet (black outline): static pressure p0 (red), surface tension and Young force
in eqn (10) acting on the different interfaces of the droplet (black outline): static pressure p0 (red), surface tension and Young force  (blue), and rigidity-constraint force λGn at the solid–liquid interface (green). The rigid substrate is shaded in gray.
(blue), and rigidity-constraint force λGn at the solid–liquid interface (green). The rigid substrate is shaded in gray. we use the triangular mesh of the droplet surface and sum up the contributions from each triangle so that
we use the triangular mesh of the droplet surface and sum up the contributions from each triangle so that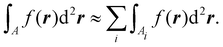
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq, we use Gaussian quadrature with 4 sample values of the prescribed profile to calculate the integral on each triangle. The sample values are taken at positions (1/3, 1/3, 1/3), (3/5, 1/5, 1/5), (1/5, 3/5, 1/5), and (1/5, 1/5, 3/5) in barycentric coordinates of the triangle and weighted by −27/48, 25/48, 25/48, and 25/48, respectively.35 In the second case, an example is the calculation of the volume V, we linearly interpolate between the values at the vertices. If f has a constant value fi on the area of the triangle, for example, in the case of γlg, we simply use Aifi.
θeq, we use Gaussian quadrature with 4 sample values of the prescribed profile to calculate the integral on each triangle. The sample values are taken at positions (1/3, 1/3, 1/3), (3/5, 1/5, 1/5), (1/5, 3/5, 1/5), and (1/5, 1/5, 3/5) in barycentric coordinates of the triangle and weighted by −27/48, 25/48, 25/48, and 25/48, respectively.35 In the second case, an example is the calculation of the volume V, we linearly interpolate between the values at the vertices. If f has a constant value fi on the area of the triangle, for example, in the case of γlg, we simply use Aifi.
 in terms of all positions of the vertices R, the functional derivative of
in terms of all positions of the vertices R, the functional derivative of 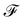 becomes
becomes 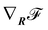 .
.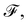 we obtain terms as a function of the configuration vector R, including all the constraint terms, which we write as λjgj(R) = 0. For convenience, we label λ0 = p0 and assign the remaining multipliers to the rigidity constraint. Thus, eqn (7) becomes
we obtain terms as a function of the configuration vector R, including all the constraint terms, which we write as λjgj(R) = 0. For convenience, we label λ0 = p0 and assign the remaining multipliers to the rigidity constraint. Thus, eqn (7) becomes

 such that it does not have a component perpendicular to the manifold defined by the constraints gi(R) = 0, otherwise the constraints would be violated.¶ Therefore, the condition
such that it does not have a component perpendicular to the manifold defined by the constraints gi(R) = 0, otherwise the constraints would be violated.¶ Therefore, the condition
 in this condition with
in this condition with

 is known up to a constant.||
is known up to a constant.||
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n = σn + p0n. Second, there is the traction of the substrate at the substrate–liquid interface. It consists of the constraint force frigid = λGn|sl, already introduced in Section 2.2, with which the substrate resists deformations induced by the droplet, and fdeform, which acts on the liquid when the substrate deforms in time according to the prescribed height profile h. Finally and third, there is the traction due to the surface tension of both interfaces, which includes the Young force acting on the contact line and which we denoted
n = σn + p0n. Second, there is the traction of the substrate at the substrate–liquid interface. It consists of the constraint force frigid = λGn|sl, already introduced in Section 2.2, with which the substrate resists deformations induced by the droplet, and fdeform, which acts on the liquid when the substrate deforms in time according to the prescribed height profile h. Finally and third, there is the traction due to the surface tension of both interfaces, which includes the Young force acting on the contact line and which we denoted 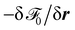 in Section 2.2. Note that we neglect the vapour pressure of the gas phase surrounding the droplet, here and in the following.
in Section 2.2. Note that we neglect the vapour pressure of the gas phase surrounding the droplet, here and in the following.

![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n − p0 = 2κγlg, where we have used eqn (11). Finally, using eqn (10) the first two terms on the r.h.s. of eqn (18) together with p0n can be rewritten as
n − p0 = 2κγlg, where we have used eqn (11). Finally, using eqn (10) the first two terms on the r.h.s. of eqn (18) together with p0n can be rewritten as 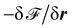 and we obtain
and we obtain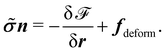
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n = 0, and fdeform = 0 gives
n = 0, and fdeform = 0 gives  and was already discussed in Section 2.2.
and was already discussed in Section 2.2.
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) ini from the fluid is multiplied by area Ai and collected in the friction vector
ini from the fluid is multiplied by area Ai and collected in the friction vector![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n1A1, −
n1A1, −![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n2A2, −
n2A2, −![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n3A3, …),
n3A3, …), describes a force
describes a force  which takes the place of the functional derivative
which takes the place of the functional derivative  . Thus, condition (19) is rewritten as
. Thus, condition (19) is rewritten as  which proves the force balance of eqn (2), with which we started. In the next section we will show that K = −GṘ and thereby calculate the friction matrix. This completes the reformulation of our boundary element approach.
which proves the force balance of eqn (2), with which we started. In the next section we will show that K = −GṘ and thereby calculate the friction matrix. This completes the reformulation of our boundary element approach.
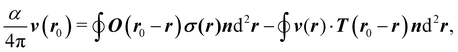
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n since a constant pressure does not contribute to the integral as shown in Appendix A. To discretize the boundary-integral equation, we proceed as in our previous work.14 We assign to each surface vertex parts of the surrounding triangles such that the resulting polygonal cells with area Aj do not overlap and cover the whole region of integration. The result is a set of linear equations for the vertex velocities vj,
n since a constant pressure does not contribute to the integral as shown in Appendix A. To discretize the boundary-integral equation, we proceed as in our previous work.14 We assign to each surface vertex parts of the surrounding triangles such that the resulting polygonal cells with area Aj do not overlap and cover the whole region of integration. The result is a set of linear equations for the vertex velocities vj,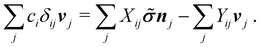


![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n. However, since we are interested in moving substrates, the fluid motion relative to the local substrate velocity vsubs and the deforming traction fdeform become relevant and we have lsPt(
n. However, since we are interested in moving substrates, the fluid motion relative to the local substrate velocity vsubs and the deforming traction fdeform become relevant and we have lsPt(![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n − fdeform) = ηPt(v − vsubs). On the discretized solid/fluid interface of the substrate using eqn (20) and (21), the boundary condition becomes
n − fdeform) = ηPt(v − vsubs). On the discretized solid/fluid interface of the substrate using eqn (20) and (21), the boundary condition becomes is the projection operator from all the n droplet vertices onto the tangential space of the substrate with m vertices. For consistency, we defined Vsubs = (v(1)subs, v(2)subs,…) as the vector of the substrate velocities at the vertices, which also includes the vertices on the liquid–gas interface with v(i)subs = 0. Finally,
is the projection operator from all the n droplet vertices onto the tangential space of the substrate with m vertices. For consistency, we defined Vsubs = (v(1)subs, v(2)subs,…) as the vector of the substrate velocities at the vertices, which also includes the vertices on the liquid–gas interface with v(i)subs = 0. Finally,
 . The boundary condition can then be restated for our discretized mesh as P⊥Ṙ = P⊥Vsubs. It directly determines the normal components of the vertex velocities at the substrate, which are contained in Ṙ. However, the condition also means that the substrate pushes or pulls on the liquid as it deforms its height profile h and the liquid resists with friction. We have already introduced the traction forces due to the substrate deformations. Their normal components are contained in the vector F⊥ = PT⊥P⊥F, which has to be calculated numerically at the same time as those components of Ṙ which are still unknown.
. The boundary condition can then be restated for our discretized mesh as P⊥Ṙ = P⊥Vsubs. It directly determines the normal components of the vertex velocities at the substrate, which are contained in Ṙ. However, the condition also means that the substrate pushes or pulls on the liquid as it deforms its height profile h and the liquid resists with friction. We have already introduced the traction forces due to the substrate deformations. Their normal components are contained in the vector F⊥ = PT⊥P⊥F, which has to be calculated numerically at the same time as those components of Ṙ which are still unknown.


 is the projection operator on the direction normal to the contact line and tangential to the substrate, where k is the number of vertices on the contact line. Obviously, these vertices contribute with
is the projection operator on the direction normal to the contact line and tangential to the substrate, where k is the number of vertices on the contact line. Obviously, these vertices contribute with

 that projects Ṙ onto the subspace of its unknown entries, we can reorder eqn (37) so that on the right-hand side only known quantities appear
that projects Ṙ onto the subspace of its unknown entries, we can reorder eqn (37) so that on the right-hand side only known quantities appear

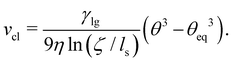
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ζ/ls).
ln(ζ/ls).![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = [9
= [9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ζ/ls)]−1. Thus, our results become independent from specific values of γlg and R0. They only depend on the ratios
ln(ζ/ls)]−1. Thus, our results become independent from specific values of γlg and R0. They only depend on the ratios ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) , ζ/R0 and ls/R0, for which we choose appropriate values.
, ζ/R0 and ls/R0, for which we choose appropriate values.




![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) = a − c
= a − c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is useful, which we derive now. Generally, in steady state the droplet position oscillates relative to the substrate pattern with a period
is useful, which we derive now. Generally, in steady state the droplet position oscillates relative to the substrate pattern with a period
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gives the droplet's speed relative to the substrate pattern with wavelength λ. Differently speaking, T is the period of the forcing experienced by the droplet through the travelling wave. Setting eqn (47) equal to eqn (48), we obtain
gives the droplet's speed relative to the substrate pattern with wavelength λ. Differently speaking, T is the period of the forcing experienced by the droplet through the travelling wave. Setting eqn (47) equal to eqn (48), we obtain
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) to vwave with only a single free parameter, vc. Consequently, in this model vc contains all material properties of the driving mechanism and droplet-substrate interaction. The limiting case for large vwave is
to vwave with only a single free parameter, vc. Consequently, in this model vc contains all material properties of the driving mechanism and droplet-substrate interaction. The limiting case for large vwave is ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ≈ vc2/(2vwave) and therefore
≈ vc2/(2vwave) and therefore
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) . In our following analysis, we will refer to this stationary dynamics as ‘surfing’ and to the oscillatory dynamics as ‘wobbling’.
. In our following analysis, we will refer to this stationary dynamics as ‘surfing’ and to the oscillatory dynamics as ‘wobbling’.

![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = vwave.
= vwave.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwaveversus vwave as determined from our BEM simulations. The speed ratio is 1 in the surfing state and it decays as vwave−2 in the wobbling state (dashed line), as predicted from the nonuniform oscillator model and eqn (49) in the limit vwave ≫ vc. This means
/vwaveversus vwave as determined from our BEM simulations. The speed ratio is 1 in the surfing state and it decays as vwave−2 in the wobbling state (dashed line), as predicted from the nonuniform oscillator model and eqn (49) in the limit vwave ≫ vc. This means ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is inversely proportional to vwave for wobbling and equal to vwave for surfing. The time-averaged speed of the droplet decays to zero which also matches our observation from an earlier article that droplets are less susceptible to rapid changes in wettability.30 For a full quantitative comparison with our model, we need to determine the velocity vc. Following eqn (50), we plot
is inversely proportional to vwave for wobbling and equal to vwave for surfing. The time-averaged speed of the droplet decays to zero which also matches our observation from an earlier article that droplets are less susceptible to rapid changes in wettability.30 For a full quantitative comparison with our model, we need to determine the velocity vc. Following eqn (50), we plot  versus vwave in Fig. 3(b) and read off vc = 2.65R0τ−1 at large wave speeds (dash-dotted red line). The dashed line in Fig. 3(a) is the prediction from eqn (49) using the determined value for vc.
versus vwave in Fig. 3(b) and read off vc = 2.65R0τ−1 at large wave speeds (dash-dotted red line). The dashed line in Fig. 3(a) is the prediction from eqn (49) using the determined value for vc.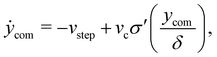

 is much larger than the droplet radius. This raises the question of the driving mechanism that moves the droplet forward.
is much larger than the droplet radius. This raises the question of the driving mechanism that moves the droplet forward.
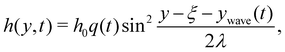


![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwaveversus vwave. In contrast to the wettability wave, the speed of the wobbling droplet now grows linearly with vwave at large vwave. Due to this clear difference, we realize that our model needs to be adjusted.
/vwaveversus vwave. In contrast to the wettability wave, the speed of the wobbling droplet now grows linearly with vwave at large vwave. Due to this clear difference, we realize that our model needs to be adjusted.

![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , (b) the helper quantity v*, and (c) the wobbling oscillation period T as functions of vwave for a travelling deformation wave with wavelength λ = 4R0. Blue dots indicate our results from BEM simulation, the dashed black line indicates the revised nonuniform oscillator model, eqn (59), the dash-dotted red line indicates the critical wave speed vc, and the dotted red line indicates the parameter ε. The latter two are the fitting parameters of the model.
, (b) the helper quantity v*, and (c) the wobbling oscillation period T as functions of vwave for a travelling deformation wave with wavelength λ = 4R0. Blue dots indicate our results from BEM simulation, the dashed black line indicates the revised nonuniform oscillator model, eqn (59), the dash-dotted red line indicates the critical wave speed vc, and the dotted red line indicates the parameter ε. The latter two are the fitting parameters of the model.


 in eqn (58). The small parameter ε means that
in eqn (58). The small parameter ε means that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) increases proportional to vwave for large vwave. Note that ε does not affect the scaling of the wobbling period T with the inverse wave speed well above vc.
increases proportional to vwave for large vwave. Note that ε does not affect the scaling of the wobbling period T with the inverse wave speed well above vc.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /vwave = ε for large vwave, which we can directly read off from Fig. 5(a) as ε = 3.565 × 10−3. Then, we subtract εvwave from both sides of eqn (59),
/vwave = ε for large vwave, which we can directly read off from Fig. 5(a) as ε = 3.565 × 10−3. Then, we subtract εvwave from both sides of eqn (59),
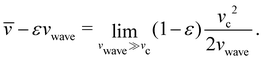
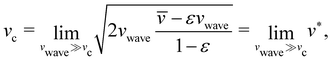
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for large vwave. To capture the asymptote, we introduced an amplitude of the driving force, which depends on vwave. It accounts for the fact that a travelling substrate deformation always needs to displace the droplet, which requires a larger driving force with increasing vwave. This is the clear difference to travelling wettability patterns treated in Section 4, where the pattern can just pass beneath the droplet without the need to lift it up.
for large vwave. To capture the asymptote, we introduced an amplitude of the driving force, which depends on vwave. It accounts for the fact that a travelling substrate deformation always needs to displace the droplet, which requires a larger driving force with increasing vwave. This is the clear difference to travelling wettability patterns treated in Section 4, where the pattern can just pass beneath the droplet without the need to lift it up.![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) also depends on λ. However, in the surfing state the droplet speed is identical to the wave speed vwave, regardless of λ. Therefore, we only need to consider a wobbling droplet.
also depends on λ. However, in the surfing state the droplet speed is identical to the wave speed vwave, regardless of λ. Therefore, we only need to consider a wobbling droplet.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) as a function of R0/λ for vwave = 50R0τ−1, which places the droplet far into the regime of wobbling dynamics. For travelling deformation waves (green crosses in Fig. 6) no clear trend is discernible because mean droplet speed
as a function of R0/λ for vwave = 50R0τ−1, which places the droplet far into the regime of wobbling dynamics. For travelling deformation waves (green crosses in Fig. 6) no clear trend is discernible because mean droplet speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) has a minimum near R0 = 0.17λ. In contrast, for travelling waves in wettability (blue dots in Fig. 6) we observe that
has a minimum near R0 = 0.17λ. In contrast, for travelling waves in wettability (blue dots in Fig. 6) we observe that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) grows like (R0/λ)2. Further decreasing λ, one would expect
grows like (R0/λ)2. Further decreasing λ, one would expect ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) to decrease again. However, for larger ratios R0/λ the creeping flow approximation does not hold anymore for deforming substrates and one enters the regime of unsteady Stokes flow due to the increased oscillation frequency of the height profile.
to decrease again. However, for larger ratios R0/λ the creeping flow approximation does not hold anymore for deforming substrates and one enters the regime of unsteady Stokes flow due to the increased oscillation frequency of the height profile.![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for each droplet size. This means, after we let the droplets run for some time (and with sufficient distance between them to prevent mergers), the droplets will separate according to their size. Because small droplets lag behind larger droplets, this naturally leads to a sorting mechanism for such a poly-disperse collection of droplets.
for each droplet size. This means, after we let the droplets run for some time (and with sufficient distance between them to prevent mergers), the droplets will separate according to their size. Because small droplets lag behind larger droplets, this naturally leads to a sorting mechanism for such a poly-disperse collection of droplets.![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) n = σn + p0n, where the constant pressure p0 does not contribute to the surface integral. To show this, we write for an arbitrary force vector f0,
n = σn + p0n, where the constant pressure p0 does not contribute to the surface integral. To show this, we write for an arbitrary force vector f0,
![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) = (x,y,h(x,y)). The normal n then points perpendicular to both tangential vectors of the surface which are given by the derivatives of
= (x,y,h(x,y)). The normal n then points perpendicular to both tangential vectors of the surface which are given by the derivatives of ![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) w.r.t. x and y, respectively, so that
w.r.t. x and y, respectively, so that
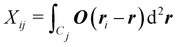

 w.r.t. shape deformation is
w.r.t. shape deformation is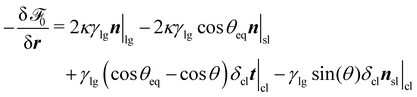
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeq + γlg
θeq + γlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)δcl|cl − p0)n|sl.
sin(θ)δcl|cl − p0)n|sl. . With this value for R0 and the material properties written in Section 2.7, we calculate τ = 1.7 s. We display both the experimental data and the result of our simulation in Fig. 7 where we can see good agreement, especially in the initial relaxation. The long-time relaxation of the experimental data appears to be a bit slower than our simulation data which may be due to defects on the substrate which we do not consider in our method. The test demonstrates that our method is able to reproduce the relaxation of a real droplet as it is observed in experiment. Notably, because we have carefully nondimensionalized our method, we do not need to alter any simulation parameters to simulate smaller or larger droplets; any change in droplet volume merely affects the conversion of our timescale from τ to seconds.
. With this value for R0 and the material properties written in Section 2.7, we calculate τ = 1.7 s. We display both the experimental data and the result of our simulation in Fig. 7 where we can see good agreement, especially in the initial relaxation. The long-time relaxation of the experimental data appears to be a bit slower than our simulation data which may be due to defects on the substrate which we do not consider in our method. The test demonstrates that our method is able to reproduce the relaxation of a real droplet as it is observed in experiment. Notably, because we have carefully nondimensionalized our method, we do not need to alter any simulation parameters to simulate smaller or larger droplets; any change in droplet volume merely affects the conversion of our timescale from τ to seconds.
 under a volume constraint.
under a volume constraint. in eqn (16). Note also that in our previous study ref. 14 when we studied a droplet on a rigid flat substrate there was no need to calculate the constraint forces due to the rigid substrate because in that case we calculated the force on each vertex individually and imposed the volume constraint only on the resulting velocity field. That approach proved inapplicable for our current study.
in eqn (16). Note also that in our previous study ref. 14 when we studied a droplet on a rigid flat substrate there was no need to calculate the constraint forces due to the rigid substrate because in that case we calculated the force on each vertex individually and imposed the volume constraint only on the resulting velocity field. That approach proved inapplicable for our current study.



