Open Access Article
Open Access ArticleDeformation-dependent gel surface topography due to the elastocapillary and osmocapillary effects†
Luochang
Wang
 and
Qihan
Liu
and
Qihan
Liu
 *
*
Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA 15213, USA. E-mail: qihan.liu@pitt.edu
First published on 11th April 2024
Abstract
Actively tuning surface topography is crucial for the design of smart surfaces with stimuli-responsive friction, wetting, and adhesion properties. This paper studies how elastocapillary deformation and osmocapillary phase separation can lead to rich deformation-dependent surface topography in polymeric gels. In a purely elastic material, stretching always flattens the surface due to the Poisson effect. We show that stretching can roughen the surface due to the elastocapillary and osmocapillary effects. The roughening can be tuned by the gel stiffness, the gel osmotic pressure, the deformation mode, and the initial amplitude of surface roughness. The rich deformation-dependent behavior of gel surface topography points to a new direction in designing smart surfaces.
1. Introduction
Surface topography governs many surface behaviors such as friction, wetting, adhesion, and transparency.1–7 Smart surfaces that actively control surface behavior through surface topography have been extensively studied. For example, swelling a polymeric gel expands surface features,8–12 and stretching a soft material deforms the surface topography with the bulk.13–17 Although deforming a piece of material is simple, predicting the deformation-dependent surface topography is not.12,14,18 By elastic deformation alone, stretching the material flattens surface topography due to the Poisson effect. However, if the material is sufficiently soft, surface tension can deform the surface topography, causing elastocapillary deformation.14,17–22 If the material is sufficiently swollen with a solvent, surface tension can pull the solvent out from the material bulk, leading to osmocapillary phase separation.12,23–25 While the elastocapillary and osmocapillary effects on a static surface are relatively well studied, how they affect surface topography during deformation remains unclear. Understanding the deformation-dependent elastocapillary and osmocapillary effects is crucial to predicting the deformation-dependent surface topography and designing novel smart surfaces.In general, a deformation can be decomposed into a volumetric and an incompressible part. This paper focuses on the surface topography change under incompressible deformation. The change under volumetric deformation have been recently reported.12 We perform novel finite element simulation that incorporates coupled elastocapillary and osmocapillary effects. We use a sinusoidal profile to reveal the length dependence of the elastocapillary and osmocapillary effects. The simulation shows that the elastocapillary and osmocapillary effects can lead to non-monotonic surface roughening and flattening with deformation. Here roughening or flattening means an increase or decrease in the amplitude of surface undulation. The findings point to new possibilities to program complex surface responses. Our findings also echo a recent experimental study that found PDMS gels can either roughen or flatten under stretch depending on the elastic moduli.14 The paper attributed the observation to strain-dependent surface tension and elastocapillary deformation alone. Our study shows that similar phenomena could happen under constant surface tension when both the elastocapillary and osmocapillary effects are considered.
2. Governing mechanisms for the deformation-dependent gel surface topography
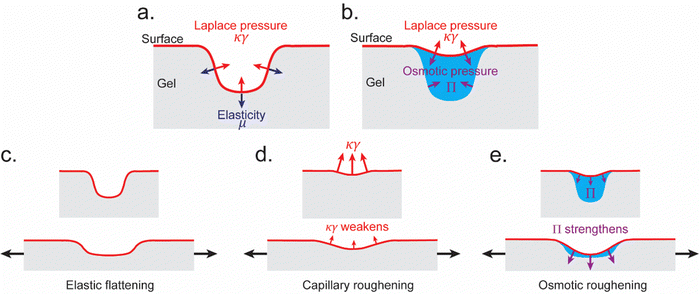
A polymeric gel consists of a polymer network infiltrated with a solvent. The polymer network leads to a solid-like elastic behavior;26 the solvent leads to a liquid-like capillary behavior, which dominates the gel surface at high solvent content;27 and the absorption of the solvent by the polymer network leads to an osmotic behavior.28 In the absence of external load, the gel surface topography is governed by the competition between elasticity, capillarity, and osmosis. Elasticity resists any deformation thus maintaining the stress-free surface topography. Capillarity tends to minimize the surface area by flattening the surface topography. The competition between elasticity and capillarity to deform the polymer network is known as elastocapillary deformation (Fig. 1a).20 Here capillarity is governed by the Laplace pressure γκ, where γ is surface energy and κ is the sum of the two principal curvatures of the surface. Elasticity is governed by the shear modulus μ of the gel. The elastocapillary effect is governed by the dimensionless number γκ/μ, where γκ ≫ μ leads to significant elastocapillary deformation. On the other hand, osmosis absorbs the solvent that covers surface asperities thus roughening the surface topography. The competition between osmosis and capillarity to move the surface solvent is known as osmocapillary phase separation (Fig. 1b).23 Here osmosis is governed by the osmotic pressure Π. The osmocapillary effect is governed by the dimensionless number γκ/Π, where γκ ≫ Π leads to significant osmocapillary phase separation. Due to the elastocapillary and osmocapillary effects, the equilibrium surface topography generally deviates from the stress-free surface topography.When the gel is externally loaded, elasticity, osmosis, and capillarity respond to the deformation differently. Consider a uniform stretch (Fig. 1c). Elasticity elongates the surface topography with the gel bulk and the Poisson effect flattens the surface. The elongation of the surface topography decreases the surface curvature κ. Consequently, the Laplace pressure γκ that flattens the surface is reduced, and the surface roughens (Fig. 1d). On the other hand, the tensile stress during stretch increases the osmotic pressure Π that resists phase separation.29 Consequently, the volume of solvent between asperity reduces, which also roughens the surface (Fig. 1e). The competition between elasticity, capillarity, and osmosis evolves with deformation, which can lead to complex deformation-dependent surface topography.
3. Finite element simulation of coupled elastocapillary and osmocapillary effects
This paper uses finite element simulation to study the coupled elastocapillary and osmocapillary effects in deformation-dependent surface topography. The elastocapillary and osmocapillary effects are characterized by elastocapillary length γ/μ and osmocapillary length γ/Π.20,23 To cleanly study the length dependence of the elastocapillary and osmocapillary effects, we study a sinusoidal surface profile, which only involves two length scales, the wavelength L0 and the peak-to-peak amplitude h0 in the stress-free state (Fig. 2a). Then the equilibrium surface amplitude h without external load is completely determined by three dimensionless numbers: | (1) |
 | (2) |
We perform finite element simulation to investigate the effects of each of the four dimensionless numbers in eqn (2).
A commercial finite element package, ABAQUS, is used for the simulation. We perform all simulations in the plane strain condition (λ3 = 1), then transform the results to generalized plane strain conditions with different λ3.30,31 Due to the symmetry and periodicity of a sinusoid, we only model half a period (Fig. 2b). We consider the common case that the surface amplitude is much smaller than the sample thickness and set the gel thickness is to be larger than 50h0. Then the bottom boundary negligibly affects the simulation. The gel bulk is modeled with neo-Hookean elasticity. 2D quadratic hybrid plane-strain element, CPE8H, is used to discretize the simulation domain. We only study the equilibrium state after the complete poroelastic relaxation. Consequently, there is no solvent flux, and the osmotic pressure is uniform everywhere. On the other hand, since the gel modulus depends on the solvent content,32 the near-surface solvent migration can lead to spatial variation in the gel modulus. For common low-roughness surfaces, the deformation and solvent migration to flatten the asperities are small. Consequently, we neglect the deformation-dependent gel modulus in the current study.
The gel surface is modeled with a layer of quadratic beam elements, B22. We ensure the beam behaves like the surface tension through three features:31 (1) a uniform prestress is applied so that the tension in the beam matches the surface tension γ, (2) the tensile stiffness of the beam is so low that the deformation in the simulation negligibly affects the prestress and the cross-section Poisson's ratio is set to 0 so that deformation does not change the cross-section area. Then surface tension γ is independent of deformation. (3) The bending stiffness of the beam is so low that the beam layer negligibly affects the deformation of the gel. For simplicity, we assume the surface tension of the gel is identical to that of the solvent, which is valid for gels of high solvent content.12,27 In gels of low solvent content, the gel surface stress can be different from the solvent surface tension and can be strain-dependent.14,33,34
To simulate coupled elastocapillary deformation and osmocapillary phase separation, the beam and the gel are pulled towards each other by a uniform pressure that matches the magnitude of the osmotic pressure Π (Fig. 2c). The “hard contact” interaction in ABAQUS is used to prevent the beam from penetrating the gel. We model the deformation-dependent osmotic pressure Π using the incompressible neo-Hookean model:29
| σ2 = μ(λ22 − 1) − Π0 + Π. | (3) |
 | (4) |
4. The elastocapillary effect: γ/μL0
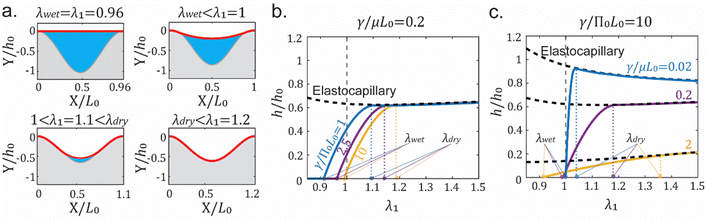
When osmotic pressure Π is sufficiently large (γ/Π0L0 ≪ 1), the solvent will be completely absorbed into the gel bulk. Then there is no osmocapillary phase separation. Elastocapillary deformation alone determines the deformation-dependent surface topography. Consider a fixed h0/L0 = 0.2 under plane strain deformation, eqn (2) simplified to h/h0 = G(λ1;γ/μL0), which can be easily studied by simulating a group of h(λ1)/h0 curves with various γ/μL0. Our simulations show that when the capillary effect is weak (γ/μL0 < 1, Fig. 3a), the surface is little deformed before stretching (left half of the subfigure with h/h0 = 0.88) and stretching the surface leads to flattening. This is expected from the Poisson effect. When the capillary effect is strong (γ/μL0 > 1, Fig. 3a), the surface is significantly flattened before stretching (left half of the subfigure with h/h0 = 0.06), and stretching the surface roughens the surface. This is because the capillary flattening is weakened.To quantitatively illustrate the deformation-dependent surface flattening in Fig. 3a, we plot h/h0 = G(λ1;γ/μL0) in Fig. 3b. It shows that a larger γ/μL0 results in more significant surface flattening (smaller h/h0) at all stretch levels. When the capillary effect is weak (γ/μL0 = 0.02), the surface monotonically flattens with stretch (decreasing h/h0) similar to an elastically deformed surface. However, when the capillary effect is strong (γ/μL0 = 0.2 or 2), the surface roughens with stretch for small deformation (increasing h/h0 for λ1 near 1), then flattens with stretch for large deformation (λ1 far from 1, either tensile or compressive). The range of roughening behavior broadens as γ/μL0 increases. We do not simulate λ1 < 0.85 because a crease forms at the bottom of the trough. Crease-induced surface topography change is a different topic that we will not investigate. Readers may refer to existing ref. 30, 31 and 35.
The non-monotonic behavior can be interpreted as the competition between the elastic flattening and capillary roughening. To separate the elastic and capillary contributions on the surface deformation, we divide the total change in surface profile amplitude, h − h0, into two parts: the capillary part h − he and the elastic part he − h0. Here he is the stretch-dependent surface profile amplitude without capillary effect (i.e., γ/μL0 = 0). Then he − h0 represents the contribution due to elastic deformation, and h − he represents the additional deformation induced by capillarity. Fig. 3c shows that elastic flattening due to the Poisson effect strengthens monotonically with stretch in both tensile (he − h0 < 0) and compressive (he − h0 > 0) directions. In contrast, the capillary flattening weakens monotonically with stretch in the tensile direction (approaches 0) because stretching reduces the local curvature. For small γ/μL0, the elastic part dominates over the capillary part at any stretch λ1 (the absolute value of the red curve dominates over the blue curves), leading to monotonically flattening with stretch. For larger γ/μL0, the capillary part dominates over the elastic part for small deformation (λ1 near 1), leading to stretch-dependent roughening. However, the elastic part still dominates over the capillary part for large deformation (λ1 far from 1), leading to stretch-dependent flattening.
5. Osmocapillary effect: γ/Π0L0
When osmotic pressure is sufficiently small, the solvent can be pulled out from the gel bulk by capillarity, leading to osmocapillary phase separation.23 Deforming the gel bulk impacts osmocapillary phase separation in two ways: (1) stretching the surface reduces the local curvature thus weakening the capillary effect, and (2) tensile stress increases the osmotic pressure thus strengthening the osmotic effect. Since both the weakening of the capillary effect and the strengthening of the osmotic effect roughen the surface, stretching always roughens the surface in the presence of osmocapillary phase separation (Fig. 4a). Since both effects reduce the amount of osmocapillary phase separation, there exists a critical λdry where osmocapillary phase separation disappears for λ1 > λdry. Then the surface deformation is purely elastocapillary, which has been discussed in Section 4. Based on the same argument, compression increases the amount of osmocapillary phase separation. There exists a critical λwet where Π = 0 and the solvent is squeezed out of the surface. When the solvent completely covers the surface, the liquid surface is completely flattened by capillarity.The deformation-dependent osmocapillary phase separation in Fig. 4a is governed by two dimensionless numbers, the same elastocapillary number γ/μL0, and the osmocapillary number γ/Π0L0. We first plot h(λ1)/h0 with the fixed γ/μL0 = 0.2 and varying γ/Π0L0 (Fig. 4b). It shows that a larger γ/Π0L0 corresponds to a larger amount of initial osmocapillary phase separation at λ1 = 1 and shifts both λdry and λwet to larger stretches (Fig. S2a, ESI†). The surface roughness is independent of γ/Π0L0 once phase separation disappears (λ1 > λdry) or inundates the surface (λ1 < λwet). Next, we plot h(λ1)/h0 with fixed γ/Π0L0 = 10 and varying γ/μL0 (Fig. 4c). It shows two trends: (1) a larger γ implies stronger elastocapillary flattening, thus lowering h/h0 when the surface is stretched (λ1 > 1). (2) According to eqn (4), a smaller μ results in a weaker stretch dependence of Π, thus a larger gap between λdry and λwet (Fig. S2b, ESI†).
6. The effect of Poisson's ratio
The two above sections illustrate the competition between the stretch-induced flattening caused by the Poisson effect and the stretch-induced roughening caused by elastocapillary and osmocapillary effects. So far, we have assumed the polymer network to be incompressible with a Poisson's ratio ν = 0.5. In general, the Poisson's ratio of a gel depends on the swelling ratio, as can be illustrated by the Flory–Rehner model (Section S3, ESI†). According to the Flory–Rehner model, polymer networks are nearly incompressible, i.e. shear is much easier than volumetric deformation, in most conditions even if free solvent exchange is allowed (Fig. S3, ESI†). This contradicts with much lower Poisson's ratios measured through some indentation tests.36–39 Such contradictions are expected because the Flory–Rehner model has been shown to severely underestimate the volumetric elasticity of the polymer network.40 In the lack of an accurate compressible constitutive model for polymer networks, here we use the classical compressible neo-Hookean model to qualitatively illustrate the effect of network compressibility.41 We tune the Poisson's ratio between ν = 0 to 0.5 and repeat the simulations for the elastocapillary and osmocapillary cases. Since the Poisson effect is responsible for the stretch-induced flattening and the capillary effect is responsible for the stretch-induced roughening, lowering the Poisson ratio will reduce the flattening effect. In the limit of ν = 0, the surface will monotonically roughen with stretch (Fig. 5a). On the other hand, a lower Poisson's ratio makes the gel more deformable under surface tension, thus rendering the surface flatter before stretching. The flatter surface makes osmocapillary phase separation easier to absorb, thus lowering λdry (Fig. 5b).7. The effect of out-of-plane deformation: λ3
So far, we have been concerned with the plane strain deformation where λ3 = 1. The results of plane strain deformation can be transformed into any generalized plane strain deformation with a uniform λ3 ≠ 1.30,31 We derive the transformation for osmocapillary phase separation as follows (Fig. 6). We take the reference state as the stress-free state with no surface energy, thus no elastocapillary deformation or osmocapillary phase separation. After applying a macroscopic plane strain stretch and relaxing the surface under surface tension γ and osmotic pressure Π, the bulk material will have an inhomogeneous field of F(PE) and there will be some osmocapillary phase separation. Consider a unit thickness of material in the reference state, the free energy after deformation is: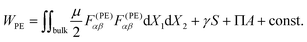 | (5) |
 | ||
| Fig. 6 A generalized plane strain deformation (GPE) can be decomposed into a uniaxial deformation (UA) followed by a plane strain deformation (PE). | ||
Consider the same piece of material undergoes a generalized plane strain deformation. The total deformation of the gel can be decomposed into a uniaxial deformation F(UA) followed by a plane strain deformation F(PE), F(GPE) = F(PE)F(UA). We assume the uniaxial deformation is uniform with no capillary effect. Then the following plane strain deformation relative to the intermediate state is governed by the same physics as the plane strain deformation relative to the reference state discussed above. The only difference is that after F(UA), the unit thickness in the reference state elongates to λ3 in the intermediate state and any in-plane dimension in the intermediate state is shrunk by compared to the reference state. Then eqn (5) should be modified as:
 | (6) |
 | (7) |
 directly follows from F(GPE) = F(PE)F(UA).
directly follows from F(GPE) = F(PE)F(UA).
The transformation eqn (7) allows us to study various loading conditions with arbitrary λ3. Most common loading conditions can be represented by the relation λ3 = 1/λα1. For example, α = 0 corresponds to the plane strain deformation (λ3 = 0) and α = −1 corresponds to equibiaxial deformation (λ3 = λ1). Fig. 7a lists a few common deformation modes and their corresponding α. In these cases, eqn (4) becomes:
 | (8) |
8. The effect of stress-free amplitude: h0/L0
Under the assumption of shallow amplitude h0/L0 ≪ 1, the elastocapillary effect is linear and h(λ1)/h0 is independent of h0/L0.14 However, the osmocapillary effect is intrinsically nonlinear due to the moving boundaries of phase separation.25 Consequently, h(λ1)/h0 is expected to show a strong dependence on h0/L0 for any amplitude in the presence osmocapillary phase separation. To illustrate this, we vary h0/L0 and simulate the evolution of h/h0 for a purely elastocapillary case (γ/μL0 = 0.2, γ/Π0L0 ≪ 1) and an osmocapillary case (γ/μL0 = 0.2, γ/Π0L0 = 10) under the plane strain condition and assume incompressible network. In the elastocapillary case (Fig. 8a), h(λ1)/h0 shows weak dependence on the amplitude h0/L0 when h0/L0 < 1. Yet, a large amplitude of h0/L0 > 1 is significantly harder to flatten. In the osmocapillary case (Fig. 8b), increasing h0/L0 significantly enhances the initial flattening (lower h/h0 at λ1 = 1) and delays the disappearance of osmocapillary phase separation at λdry. λwet is determined by setting Π = 0 in eqn (4), thus independent of amplitude h0/L0. The change in the initial flattening and λdry is significant even between the cases that have nearly identical elastocapillary behaviors (h0/L0 = 0.02 and 0.2). The strong amplitude dependence of osmocapillary phase separation is easy to understand (Fig. 8c): the competition between the osmotic and capillary effects dictates the surface radius of curvature to be the osmocapillary length γ/Π,23 thus the larger the h0/L0, the larger the amount of osmocapillary phase separation, and thus the more difficult it is to dry the surface.9. Conclusion
In this paper, we have performed systematic finite element analyses of how a sinusoidal surface deforms with stretch in the presence of the coupled elastocapillary and osmocapillary effects. When both the elastocapillary and osmocapillary effects are weak (γ/μL0 ≪ 1, γ/Π0L0 ≪ 1), the surface flattens with stretch due to the Poisson effect. Elastocapillary deformation alone can lead to surface roughening with stretching (γ/μL0 ∼ 0.1 or higher, γ/Π0L0 ≪ 1). However, such roughening is limited to relatively small deformation. For large tension and compression, the Poisson effect dominates over the capillary effect thus resuming the flattening. Osmocapillary phase separation also leads to surface roughening with stretching (γ/Π0L0 ∼ 1 or higher with any γ/μL0). The osmocapillary roughening happens over a limited stretch range bounded by λdry and λwet. Outside this range, the surface is either dry, thus purely elastocapillary, or inundated under exuded solvent, thus completely flat. The range between λdry and λwet is strongly affected by the out-of-plane constraint (λ3) and the surface amplitude (h0/L0). In common loading conditions such as uniaxial and equibiaxial deformations, osmocapillary phase separation leads to much stronger stretching-dependent roughening than elastocapillary deformation. The richness of deformation-dependent gel surface topography can be used to design novel stimuli-responsive surfaces with tunable surface topography.Conflicts of interest
There are no conflicts to declare.References
- B. N. Persson, Theory of rubber friction and contact mechanics, J. Chem. Phys., 2001, 115(8), 3840–3861 CrossRef CAS.
- D. E. Packham, Surface energy, surface topography and adhesion, Int. J. Adhes. Adhes., 2003, 23(6), 437–448 CrossRef CAS.
- K. Fuller and D. Tabor, The effect of surface roughness on the adhesion of elastic solids, Proc. R. Soc. London, Ser. A, 1975, 345(1642), 327–342 Search PubMed.
- M. Ramiasa, et al., The influence of topography on dynamic wetting, Adv. Colloid Interface Sci., 2014, 206, 275–293 CrossRef CAS PubMed.
- S. M. Lößlein, F. Mücklich and P. G. Grützmacher, Topography versus chemistry–How can we control surface wetting?, J. Colloid Interface Sci., 2022, 609, 645–656 CrossRef PubMed.
- X. Yao, et al., Adaptive fluid-infused porous films with tunable transparency and wettability, Nat. Mater., 2013, 12(6), 529–534 CrossRef CAS PubMed.
- Y. Lin, et al., Surface roughness and light transmission of biaxially oriented polypropylene films, Polym. Eng. Sci., 2007, 47(10), 1658–1665 CrossRef CAS.
- L. Chen, et al., Thermal-responsive hydrogel surface: tunable wettability and adhesion to oil at the water/solid interface, Soft Matter, 2010, 6(12), 2708–2712 RSC.
- D. Liu, et al., (Photo-) thermally induced formation of dynamic surface topographies in polymer hydrogel networks, Langmuir, 2013, 29(18), 5622–5629 CrossRef CAS PubMed.
- J. Comelles, et al., Microfabrication of poly (acrylamide) hydrogels with independently controlled topography and stiffness, Biofabrication, 2020, 12(2), 025023 CrossRef CAS PubMed.
- Y. Hu, J.-O. You and J. Aizenberg, Micropatterned hydrogel surface with high-aspect-ratio features for cell guidance and tissue growth, ACS Appl. Mater. Interfaces, 2016, 8(34), 21939–21945 CrossRef CAS PubMed.
- J. Zhu, C. Yang and Q. Liu, Experimental characterization of elastocapillary and osmocapillary effects on multi-scale gel surface topography, Soft Matter, 2023, 19(45), 8698–8705 RSC.
- S. Zhao, et al., Mechanical stretch for tunable wetting from topological PDMS film, Soft Matter, 2013, 9(16), 4236–4240 RSC.
- N. Bain, et al., Surface tension and the strain-dependent topography of soft solids, Phys. Rev. Lett., 2021, 127(20), 208001 CrossRef CAS PubMed.
- S. C. Truxal, Y.-C. Tung and K. Kurabayashi, High-speed deformation of soft lithographic nanograting patterns for ultrasensitive optical spectroscopy, Appl. Phys. Lett., 2008, 92(5), 051116 CrossRef.
- P. Goel, et al., Mechanical strain induced wetting transitions between anisotropic and isotropic on polydimethylsiloxane (PDMS) films patterned by optical discs, Appl. Surf. Sci., 2015, 356, 102–109 CrossRef CAS.
- N. Lapinski, et al., A surface with stress, extensional elasticity, and bending stiffness, Soft Matter, 2019, 15(18), 3817–3827 RSC.
- C.-Y. Hui, et al., How surface stress transforms surface profiles and adhesion of rough elastic bodies, Proc. R. Soc. A, 2020, 476(2243), 20200477 CrossRef PubMed.
- B. Andreotti, et al., Solid capillarity: when and how does surface tension deform soft solids?, Soft Matter, 2016, 12(12), 2993–2996 RSC.
- R. W. Style, et al., Elastocapillarity: Surface tension and the mechanics of soft solids, Annu. Rev. Condens. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- D. Paretkar, et al., Flattening of a patterned compliant solid by surface stress, Soft Matter, 2014, 10(23), 4084–4090 RSC.
- A. Jagota, D. Paretkar and A. Ghatak, Surface-tension-induced flattening of a nearly plane elastic solid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(5), 051602 CrossRef PubMed.
- Q. Liu and Z. Suo, Osmocapillary phase separation, Extreme Mech. Lett., 2016, 7, 27–33 CrossRef.
- R. W. Style, et al., The contact mechanics challenge: Tribology meets soft matter, Soft Matter, 2018, 14(28), 5706–5709 RSC.
- J. Zhu and Q. Liu, The osmocapillary effect on a rough gel surface, J. Mech. Phys. Solids, 2023, 170, 105124 CrossRef.
- M. Rubinstein and S. Panyukov, Elasticity of polymer networks, Macromolecules, 2002, 35(17), 6670–6686 CrossRef CAS.
- A. Chakrabarti and M. K. Chaudhury, Direct measurement of the surface tension of a soft elastic hydrogel: exploration of elastocapillary instability in adhesion, Langmuir, 2013, 29(23), 6926–6935 CrossRef CAS PubMed.
- M. Quesada-Pérez, et al., Gel swelling theories: the classical formalism and recent approaches, Soft Matter, 2011, 7(22), 10536–10547 RSC.
- W. Hong, et al., A theory of coupled diffusion and large deformation in polymeric gels, J. Mech. Phys. Solids, 2008, 56(5), 1779–1793 CrossRef CAS.
- W. Hong, X. Zhao and Z. Suo, Formation of creases on the surfaces of elastomers and gels, Appl. Phys. Lett., 2009, 95(11), 111901 CrossRef.
- Q. Liu, et al., Elastocapillary crease, Phys. Rev. Lett., 2019, 122(9), 098003 CrossRef CAS PubMed.
- J. Li, et al., Experimental determination of equations of state for ideal elastomeric gels, Soft Matter, 2012, 8(31), 8121–8128 RSC.
- Q. Xu, et al., Direct measurement of strain-dependent solid surface stress, Nat. Commun., 2017, 8(1), 555 CrossRef PubMed.
- Q. Xu, R. W. Style and E. R. Dufresne, Surface elastic constants of a soft solid, Soft Matter, 2018, 14(6), 916–920 RSC.
- X. Guan, et al., Rate-dependent creasing of a viscoelastic liquid, Extreme Mech. Lett., 2022, 55, 101784 CrossRef.
- Y. Hu, et al., Using indentation to characterize the poroelasticity of gels, Appl. Phys. Lett., 2010, 96(12), 121904 CrossRef.
- Y. Hu, et al., Indentation of polydimethylsiloxane submerged in organic solvents, J. Mater. Res., 2011, 26(6), 785–795 CrossRef CAS.
- S. Cai, et al., Poroelasticity of a covalently crosslinked alginate hydrogel under compression, J. Appl. Phys., 2010, 108(11), 113514 CrossRef.
- Y. Hu, et al., Poroelastic relaxation indentation of thin layers of gels, J. Appl. Phys., 2011, 110(8), 086103 CrossRef.
- Z. Shao and Q. Lin, Independent characterization of the elastic and the mixing parts of hydrogel osmotic pressure, Extreme Mech. Lett., 2023, 64, 102085 CrossRef.
- A. N. Gent, Engineering with rubber: how to design rubber components, Carl Hanser Verlag GmbH Co KG, 2012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00139g |
| This journal is © The Royal Society of Chemistry 2024 |