Dilute gel networks vs. clumpy gels in colloidal systems with a competition between repulsive and attractive interactions

Abstract

Using Brownian dynamics simulations we study gel-forming colloidal systems. The focus of this article lies on the differences of dense and dilute gel networks in terms of structure formation both on a local and a global level. We apply reduction algorithms and observe that dilute networks and dense gels differ in the way structural properties like the thickness of strands emerge. We also analyze the percolation behavior and find that two different regimes of percolation exist which might be responsible for structural differences. In dilute networks we confirm that solidity is mainly a consequence of pentagonal bipyramids forming in the network. In dense gels, tetrahedral structures also influence solidity.

---

1 Introduction

Gelation is an intensively studied phenomenon. It also has relevant applications in experimental and theoretical frameworks, for example in the study of the formation of non-equilibrium structures and their influence on ageing or rheology.¹ In a theoretical framework, a simple system to explore gelation is a colloid–polymer mixture, where there is a phase separation of a dilute and a dense phase. Gelation is observed – not necessarily exclusively – in the coexistence phase. Therefore, in this work we focus on the coexistence region while not studying dense systems where a slowdown of dynamics can also occur.^2,3 Gelation can for example occur in short-ranged purely attractive systems and is then governed by a non-equilibrium percolation process.^4,5 The depletion attractions between the colloids, that are mediated by the polymers, are usually modelled by AO-interactions^6–8 along with short-ranged repulsions and as in this article sometimes longer-ranged screened Coulomb repulsions^9,10 leading to the formation of numerous complex, partially or completely ordered structures and to a drastic slowdown of the dynamics in the system.^2,11–16

To be specific, the competition of the attraction and the short-ranged repulsion causes the phase separated regime and the additional longer-ranged repulsions lead to the formation of even more complex heterogeneous structures in this part of the phase diagram.^14,17 In experiments the competition of the different interactions can be controlled, e.g., by varying the polymer size and concentration to change the attractive forces or by increasing the salt concentration in the system such that the repulsive Coulomb force is decreased due to additional screening.¹⁶

In the rich phase behavior the following structures are observed: homogeneous fluids for attractions that are weaker than at the phase separating binodal line and a large zoo of heterogeneous structures for stronger attractions. Close to the binodal line or in case of purely attractive interactions cluster fluids are found,¹⁸ which consist of connected particle clusters surrounded by single, non-connected colloidal particles. For systems deep inside the phase separated region, gel networks that consist of thin, long strands of particles are found.^17,19–22 Depending on the attractive strength, these can be either weakly or strongly connected as shown in our recent article.²³ Due to the arrested dynamics deep inside the phase separated region, these structures are non-equilibrium structures undergoing slow evolution. Only close to the binodal line, the structures are expected to converge within a reasonable time towards the structures expected in an equilibrium phase diagram for a potential with short ranged attraction and long ranged repulsion.²⁴

Our main interest in this article is the structural differences between dilute gel networks at low densities and clumpy gels that occur at larger packing fractions.

In dilute systems, except for very high interparticle attraction strengths, particles can almost move freely during most of the equilibration process, i.e., there are no stresses due to percolating strands. Percolation might only set in at later times of the evolution. In contrast, the particles in dense systems percolate nearly instantaneously. Percolation constraints then lead to mechanical forces that modify the structural formation.^17,25 It was also observed that directed percolation slows down the relaxation dramatically¹⁶ for a system deep in the phase separated regime²⁶ and that it changes the behavior of the gel if subjected to shear.²⁷ Here, we investigate how percolation constraints influence the global as well as the local structure formation. In recent research on local structure formation in dilute gel networks, it was found that the hierarchical formation of local structures is responsible for macroscopic properties of gels.²⁸ In addition to our study of the differences between dilute and dense gel structures, we use our computer simulations to extend the recent experimental findings on the hierarchical structure formation²⁸ to dense gels with both weakly and strongly bound particles.

Our article is structured as follows. In Section 2, we introduce the investigated model system, the simulation procedure, and the methods used to calculate gel network skeletons and distribution functions. In Section 3, we show our results on structural differences for dilute and dense networks. First, we concentrate on skeletonized networks and present results on global properties like the thickness of strings, tortuosity and percolation behavior. We find that dilute and dense networks differ in their global properties and that there may be a smooth transition in the state diagram at around φ ≈ 0.10–0.15. The second part of the results section is dedicated to local structure formation extending the research of Tanaka et al.²⁸ to higher packing fractions and different interaction strengths. Here, we also show that packing fraction and interaction strength have an impact on the structure formation process. Before we conclude in Section 4, we investigate the impact of packing fraction and attraction strength on the onset of solidity by comparing local structures and the average coordination number of the system.

2 Methods and simulation procedure

2.1 Colloid–polymer mixture

We study a gel forming model system that is similar to the system considered in ref. 29 and that we have previously used in ref. 23. A colloid–polymer mixture is simulated with Brownian dynamics simulations. The colloids possess a polydispersity of 5% and the effective colloid–colloid interactions are modeled by summing a short-ranged square-well-potential U_SW(r) and a longer ranged repulsive Yukawa tail U_YK(r), such that U_tot(r) = U_SW(r) + U_YK(r), where

A sketch of the potential is shown in Fig. 1(b). Here, σ_ij = r_i + r_j, where r_i is the radius of particle i. The strength of the attraction is modeled by the parameter ε, which is the depth of the square well-potential. The range of attractive interaction is given by the width of the square well, i.e., δ_ij = 0.03σ. To avoid infinite forces, we smoothen the square-well potential by the additional parameter . In experimental setups, the screening length κ⁻¹ can be tuned by modifying salt concentration.¹⁶ In our theoretical setup, it is responsible for the strength and range of the repulsive force. For κ = ∞, the Yukawa-tail vanishes, and therefore, this represents the case of a purely attractive potential. The parameter C is chosen as 200k_BT. For our simulations, we choose a cut-off distance at as in ref. 29. In summary, the whole system can be characterized by choosing a triplet of parameters (ε,κ,φ), where is the packing fraction of the system with the box size L. Note that in the following ε is used in units of k_BT and κ in units of σ⁻¹. In contrast to the more complicated, but maybe more realistic AO-potential,⁶ we choose this combined potential as it has fewer parameters and the influence of each single parameter is more directly visible. The phase behavior can be mapped to that of the AO-potential.^26,29,30

Fig. 1 (a) State diagram of our gel forming model system. The insets show examples of gel networks at the marked parameter values far above the binodal line for ε = 15 after simulation time 2000τ_B. The opaque particles represent the complete network, while the non-opaque particles form the reduced network obtained by our backbone method.²³ Note that as gels are non-equilibrium structures, the structures shown here could still evolve, but due to dynamic arrest, they are quite stable and persist over large time scales. They are meant as a guide of which structures could be expected at which parameter values. The grey dotted arrows indicate lines along which we have simulated systems for analysis in this article. The blue and black lines show binodal lines for different screening lengths κ = ∞ and κ = 15. In the article, we always refer to the case κ = 15 (black). (b) shows the interaction potential for ε = 3 and different values of κ. (c)–(e) show the percolation time for systems simulated along the grey opaque arrows in (a) for a next neighbor distance of 1.1σ (c) ε = 15, (d) ε = 10, and (e) ε = 6. The red dotted line corresponds to the directed percolation threshold, while the blue dotted line represents the continuous percolation threshold. For all values of ε, the slope in the double logarithmic plots changes somewhere between φ = 0.1 and φ = 0.15. Systems for percolation analysis were simulated for at most 500τ_B and the smallest at least once percolating density was taken as the percolation threshold. The estimates for percolation transition lines are drawn as dashed lines in the state diagram and depend on the chosen next neighbor distance.

2.2 Brownian dynamics simulations

In our simulations, the motion of colloidal particles is determined by the overdamped Langevin equation for particle jwhich is numerically integrated. γ is the friction constant and F⃑_int models the effective force between colloidal particles as given by the pair interaction potential introduced in the previous subsection. Thermal fluctuations induce random motion of particles which have to obey two conditions, such that the correct diffusion behavior is reproduced. These random forces are denoted by F⃑_th and fulfill 〈F⃑_th〉 = 0⃑ and 〈F_th,i(t)F_th,j(t′)〉 = 2γk_BT[small delta, Greek, tilde]_ijδ(t − t′). Here [small delta, Greek, tilde]_ij is the Kronecker-δ and the tilde is used to distinguish it from δ_ij used in the model description above. Forces are calculated using a parallelized version of a combination of the Verlet-list algorithm and the linked-cell algorithm to minimize computation time.³¹ The time constant in our simulations is given by the Brownian time and we use a time resolution of Δt = 10⁻⁵τ_B, simulations are run for 2000τ_B. We use periodic boundary conditions and boxes of size 30σ × 30σ × 30σ, where σ is the mean particle diameter, for all considered packing fractions. The boxes are then randomly filled with particles until the considered packing fraction is reached. Due to the polydispersity of the system, the number of particles for a given packing fraction may vary slightly. The number of particles N as a function of packing fraction φ may be calculated using . For example in our simulations for φ = 0.05, we use N = 2567 particles, while for φ = 0.10, we use N = 5162 particles, and for φ = 0.20, the number of particles is N = 10 385.

2.3 Continuous and directed percolation

Fig. 1(a) shows the state diagram of the investigated system. The binodal lines (for κ = 15 (black) and κ = ∞ (blue)) in the state diagram were obtained by extracting coexistence densities from several simulations.²⁹ The additional dotted lines in blue and red show the percolation behavior of the system. The determination of the percolation behavior was done using a next neighbor distance of 1.036σ, 1.1σ and 1.2σ and depends on the choice of this distance. From the form of the interaction potential including a modified square-well potential, 1.036σ is the natural, physical choice which defines if two particles are bonded or not. We have chosen the bigger distances to account for the random, thermal motion of the particles which can lead to random splitting and reconnection of particle bonds within only a few timesteps. If the bonding threshold is chosen larger, this effect occurs less frequently and we can more certainly say if two particles are really unbonded or if this is just due to random effects and the distinct chosen timestep of the analysis. This choice has only a small effect on the percolation lines but gets more important later during the analysis of local order to smoothen the computation results. We distinguish continuous and directed percolation. In both cases, system spanning paths exist, but in the case of continuous percolation, steps in all directions – including backward steps – are allowed, while in directed percolation, only steps in a previously chosen arbitrary direction are considered, and backward steps are forbidden.¹⁶ The percolation time is defined as the time until the first continuous or directed percolating path in the network is found. This time is plotted for different attraction strengths as a function of packing fraction in Fig. 1(c)–(e). The dotted lines in these plots show an estimation for the percolation threshold at the given attraction strength. Simulations were carried out for at most 500τ_B. The simulation time also influences the exact position of the percolation lines in the state diagram. As a compromise between computational effort and equilibration of the system, we have chosen 500τ_B as the maximum simulation time. The different results for the different choices of neighbor distances are represented by the different lines in the state diagram in Fig. 1 and show that the exact position of the percolation threshold depends on these choices although the differences are small. Also, as gels are non-equilibrium systems, they still undergo slow dynamical changes and as a consequence, the exact value of the percolation threshold might depend on the simulation time. As the relaxation dynamics slow down at the directed percolation line,¹⁶ the waiting time dependence of this transition is most pronounced, especially in simulations of dilute systems and at low values of ε, as here strands of particles can split up and connect easily. As for the value of the percolation time, we have taken the first time step at which we could find percolation irrespective of how stable or unstable the percolating strands are. Note that continuously percolating strands often seem to be significantly more stable than strands with directed percolation. That means that at least for dilute networks at lower attraction strengths, the directed percolation connections were destroyed often in less than 1τ_B and eventually reformed again. Thus, constraints due to percolation are most important deep inside the phase separated region but not close to the binodal line (or even for attractions smaller than at the binodal line).

2.4 Methods and skeletonization process

In our global structural analysis of gel networks, we use two different skeletonization methods. The first method is on a particle level and was described in detail in our last article.²³ It is based on the idea of preserving only crucial connections in the network. Therefore, we delete colloids as long as the connectivity of the whole network is not destroyed. Like this, we get a backbone of the original network on a particle level. Examples of our algorithm for different packing fractions are shown in the insets in the state diagram in Fig. 1(a). The computation of reduced networks in this way is computationally expensive; therefore, we also use ArGSLab to calculate skeleton structures of gel networks.³² ArGSLab is a software designed for the quantitative comparison of experimental and computational data of particle networks and the determination of reduced structures. It is based on binarization of the original input and a thinning algorithm, which is explained in more detail in the original publication.³² The advantage is that it performs much faster than our reduction algorithm, its disadvantage is that it is pixel based and not particle based. Furthermore, it is mainly designed for experimental data and therefore does not take the periodic boundary conditions into account that we use in our simulations. Results obtained with the two methods are shown in Fig. 2. One of our goals is to show how these two inherently different methods can profit from each other and can be used together to get insight into different structural properties of complex network structures. The suitable type of skeletonization algorithm depends on the task which is of interest.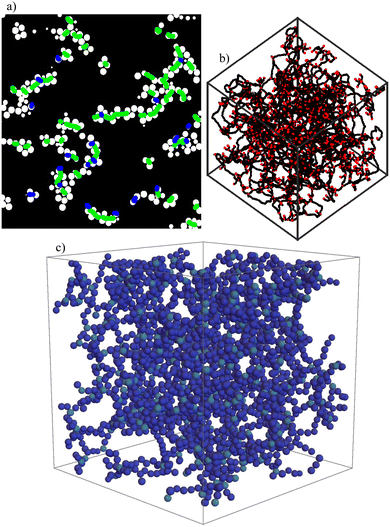

Fig. 2 Reduced networks obtained for a gel structure with packing fraction φ = 0.18 at time 2000τ_B obtained (a), (b) with ArGSLab³² and (c) with our backbone method introduced in ref. 23. While ArGSLab leads to a skeleton network of nodes and links (in the slice shown in (a) nodes are shown in blue and the links in green), our backbone method leads to a network of colloids that is obtained if all particles not needed for the essential connections are left away. Both methods are used in this article depending on the property that we want to determine.

The skeletons obtained from our analytical particle based method are used to calculate different distribution functions that we introduce in the following. In the following, we call two particles i and j neighbors, if their distance r_ij ≤ 1.036σ, i.e., if it is smaller than the width of the attractive step in the interaction potential.

For the loop size and the link length distribution, we interpret the particle network as a graph structure by identifying particles with nodes and connecting two nodes by an edge if the corresponding particle distance is smaller than the next neighbor distance. For loop size distribution, we then determine the minimal cycle basis of the graph structure, the weights on the edges are given by the particle distances. The minimal cycle basis is a set of loops with minimal weight, from which all loops in the network can be reconstructed. For link length distributions, we first determine all crossing points or terminal points in the network. These are found by neglecting all particles with next neighbor count two, because these have to be particles in the middle of strings. Then, the length of the shortest path from each crossing or terminal point to the next neighboring crossing or terminal point is calculated and interpreted as the link length.

The pore size distribution is obtained by choosing random points in the system and calculating the minimal distance from that point to any other point in the particle network. This is the size of the biggest sphere centered at the chosen point, not overlapping any particle in the system.^33–37

The last property we consider in this context is the link thickness. This is of course extracted not from skeletonized networks, but from the entire network structure by generalizing a 2-dimensional approach from ref. 38 to 3-dimensional systems. We insert random planes in the system and calculate which particles intersect the plane. From the intersecting particles, we determine connected components using the graph structure and interpret the size of the connected components as the string thickness. When interpreting the results from this calculation, one has to consider that the planes do not have to be perpendicular to the strings in the network; therefore, the tail of the distribution does also show an estimate for the longest straight connection.

3 Results

The phase behavior of the system has been discussed previously in ref. 23. The state diagram is shown in Fig. 1(a). The computation of binodal lines for different values of κ is done using the slab geometry method.²⁹ After equilibrating the slab geometry until the density profile is stable, the coexistence densities in the high density and low density regime for each ε are obtained by fitting the density profile. To improve the accuracy of the method, we averaged 4 independent simulations. For further details, we refer to ref. 29. As stated in the introduction, a rich phase behavior can be observed. The crossover between the dilute gel network and the clumpy gel case is not sharp but rather continuous and smooth and will be further analyzed in this article.

3.1 Analysis of reduced networks

State diagram and percolation times. We first evaluated the percolation time of the networks as a function of packing fraction in Fig. 1(c)–(e). As one would expect, the percolation time decreases with increasing packing fraction. For high densities, the network percolates almost immediately. The divergence of the percolation time for systems with ε = 6 at φ ≈ 0.1 is not surprising, as at this point, the line ε = 6 crosses the binodal in the state diagram and systems with φ < 0.1 are located below the phase separating line. Interestingly in the double-logarithmic plots, we see two different regimes and a crossover at a packing fraction between φ ≈ 0.1 and φ ≈ 0.15, depending slightly on the value of ε. Decreasing the value of ε leads to an increase in the crossover packing fraction φ. In both the low and the high density regime the percolation time decreases with increasing packing fraction. The different slopes in the two regimes may be a hint at the different mechanisms behind gelation. However, directly at the binodal line ε = 6, we do not see different regimes concerning the percolation behavior. As for larger attractions, the percolation behavior changes, we also want to find out which structural properties might change. To investigate this, we use ArGSLab and our backbone approach to analyze the gel structures.

Nodes and links in the reduced network. The dynamical evolution of the backbone structure is analyzed using ArGSLab. At first, we compare the number of nodes and links which remain in the network after applying the skeletonization algorithm. As expected, the number of remaining links and nodes decreases as a function of time for all considered packing fractions as the structure of the gel coarsens and therefore more links and particles get neglectable (see Fig. 3(a) and (b)). Therefore, during the dynamical evolution of the gel, particles form bigger clusters for all considered packing fractions. Interestingly if we plot the ratio of links and nodes (see Fig. 3(c)), we see a difference between dilute networks and dense networks. While in dilute networks (φ ∈ {0.05,0.08,0.10,0.12}), a constant ratio is approached from below, in dense gels (φ ∈ {0.15,0.18,0.20,0.25}), a constant value is approached from above. Therefore, evolution in dilute gel networks seems to occur by thinning out the network even further and especially getting rid of links. In contrast, evolution in clumpy gels is related to growing clusters such that the number of nodes is reduced faster than the number of links. The value for the node-to-link ratio that is approached depends on the packing fraction. Interestingly the differences between dilute networks and clumpy gels are much larger at small times but decrease during evolution. The remaining differences between dilute and dense systems seem to be stable over a long time. However, we cannot rule out the possibility that the node-to-link ratio might not be constant for very long times but that there may be a further approach due to evolution on much longer timescales. The change of the dynamics occurs around φ = 0.12–0.15. This value coincides with the dynamical percolation crossover point mentioned earlier and can be seen as the result of different dynamical pathways in gelation. We only show results for t ≥ 1τ_B as we focus on the long time behavior of the arrested gel networks and not the short-term limit, which may nevertheless also be interesting.

Fig. 3 (a) and (b) Evolution of node and link density calculated as the number of nodes and links after the skeletonization divided by the volume of the simulation box. (c) Ratio of nodes and links in the skeletons. In dense gels, a constant value is approached from above, while in dilute networks, the approach is from below. The data is taken from skeletons obtained with ArGSLab.

Thickness and tortuosity of strands. Using our analytic backbone construction method, we are able to get skeletons on a particle base. This can be used to get insight into the structure of the single connection strings in the network. To analyze how the thickness of these strings in the network changes as a function of packing fraction, we calculate the quantitywhere t(φ) stands for the thickness of the strings as a function of the packing fraction and is calculated by dividing the total number of particles in the non-skeletonized network N_tot(φ) by the total length of the skeletonized network L_skel(φ). The length of the skeletonized network can be calculated by summing up the diameters of all particles in the backbone structure. This gives an estimate of how many particles are on average found per particle diameter in the non-skeletonized network and can be seen as an approximation to the thickness of the strings. We find that the thickness decreases with increasing packing fraction. This shows that in dilute networks particles tend to cluster more easily, while in dense networks, the small number of particles and their pairwise interaction forces them to form thinner strings. Another observation we show in Fig. 4(b) is that in dilute networks, the strings get thinner with time, while in dense networks, they tend to get thicker. The evolution towards thicker strings in dense networks is nevertheless quite slow. Again the crossover point seems to be at approximately φ = 0.1–0.12. This may again be an indicator of different dynamical pathways in gelation. Dilute gel systems contain random clusters at the beginning of the evolution. Then, strands are formed that initially are loose and might be clumpy. As additional particles may move quite freely and strands can easily reorganize, the evolution leads to thinner and less bent strands in the network. In contrast in dense gels, there are more conditions concerning the movement of particles and therefore the confined movement leads to the early formation of strings. In other words, the initial random clumps are not compact clusters, but networks consisting of thin strands. The process to become more compact is very slow.

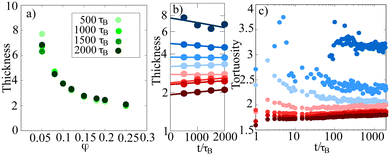Fig. 4 (a) Thickness of strings in the network as a function of the packing fraction at different simulation times. In general, strings tend to get thinner with increasing packing fraction. (b) Thickness of strings as a function of time. Fitted linear functions are shown to illustrate the general trend. As a function of time, the thickness decreases for dilute networks but increases slightly for dense gels. (c) Tortuosity of gel networks. Dense networks tend to form rather straight connections, while dilute networks are more erratic. The colors in (b) and (c) are the same as in Fig. 3(c).

We also show the tortuosity of the gel structures in Fig. 4(c), which is a measure of the erraticity of percolating strands between particles. For two particles A and B, it is calculated by dividing the distance along the backbone λ(A,B) by their euclidean distance λ_Euc(A,B), which would represent the distance along a straight line:³²

The average is taken over all such percolating paths in a given direction. Tortuosity can be interpreted as a measure of erraticity of percolating strands, and how much they deviate from straight connections. We see that dilute networks are in general more erratic than dense networks and that the tortuosity of dilute networks changes much more drastically during gelation, especially in the initial 10–20τ_B. According to the analysis with ArGSLab, the network at φ = 0.08 starts to percolate after approximately 100τ_B. Therefore, prior to that time, no data points can be calculated. Note that the tortuosity for very dilute packings like φ = 0.05 cannot be calculated using ArGSLab, as the analyzed network never percolates (except if periodic boundary conditions were taken into account, which ArGSLab does not do). The tortuosity of dense gels changes very little over time. It is even slightly increasing during temporal evolution, while the tortuosity of dilute networks decreases until it reaches a constant value. A general trend is visible in all data sets: the higher the packing fraction, the lower the tortuosity.

Structural distribution functions. After looking at the temporal evolution of the strings themselves, we focus on the global structure of the whole system. Therefore, we look at loop size, link length, pore size³³ and string thickness distributions. These are calculated as described in the methods part in Section 2. In Fig. 5, loop size and link length are shown as cumulated distributions, while pore size and link thickness are shown as a non-cumulative distribution. We observe the general trend that an increase in the density leads to a decrease in loop size, link length, pore size, and also link thickness which means that the network itself gets more compact and the void spaces in between get smaller. In particular, the decrease in loop size is very pronounced. The biggest loop for a network at φ = 0.05 is nearly twice as big as the biggest loop for the network with φ = 0.08 even if the difference in packing fraction is quite small. The distribution of the link thickness in Fig. 5(d) reveals two interesting properties. The first one can be seen from the behavior at small particle numbers – here the dilute systems show bigger values than the dense systems. This can be taken as a measure of the link thickness and agrees with our result from Fig. 4(a). The second interesting property is taken from the tail of the distribution. As the planes, which are used to calculate the distribution functions are chosen arbitrarily, it can happen that they do not intersect a string perpendicularly, but are rather parallel to the string direction. Therefore, the tail of the distribution can be seen as an approximation to the longest straight strings in the system. The result that dense networks have longer, straight links is in accordance with our result from the tortuosity calculation in Fig. 4(b) where we find smaller tortuosity values for dense systems.

Fig. 5 (a) Cumulative distribution of link length in reduced networks of packing fraction φ = 0.05–0.25. (b) Cumulative distribution of loop sizes in reduced networks of packing fraction φ = 0.05–0.25. (c) Distribution of pore sizes in reduced networks of packing fraction φ = 0.05–0.25. (d) Distribution of string thickness in non-reduced networks. The general trend can be seen in all of the distributions: the higher the density of the system, the shorter the links between nodes and the smaller the loops and pores in the network. The analysis of the string thickness confirms the result that individual strings in dilute networks are thicker than in dense networks, but dense networks show longer straight strings. All figures show distributions obtained from simulations after 2000τ_B and the colors are the same as in Fig. 3(c).

Concerning the number of branches which are connected to a single node in the graph, we use ArGSLab to calculate distributions for different packing fractions. In Fig. 6, the relative appearance of nodes with the given number of branches is shown. Nodes with one branch are therefore terminal nodes of strings and have no crossing points. Nodes with two branches are strongly suppressed and in a further idealized network should be exactly zero as these nodes correspond to particles inside a link, i.e., the outgoing links could be replaced by one link and the node could be neglected. But depending on the used cleaning routines in the algorithm, small branches can still contribute and non-zero values can arise.

Fig. 6 Relative number of branches connected to each node in the reduced network as calculated using ArGSLab. Different colors indicate different timesteps.

For nodes with more than two branches, we see that the relative appearance decreases exponentially as a function of branch number. But if the temporal evolution is considered we can again see a difference between dilute and dense systems. For dilute systems, the relative appearance of nodes with more branches increases with time, while for dense systems, it decreases slightly or stays constant. This is possible as the fraction of terminal nodes decreases for dilute systems and increases for dense systems with time. Therefore, while free ends and loose strands are reduced in dilute networks, in dense gels, the surface of growing clusters increases and thus the number of terminal nodes.

3.2 Occurrence of local ordering

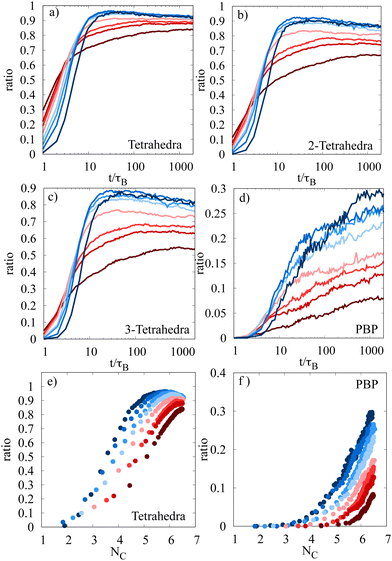
Local ordering plays a key role in understanding the way towards gelation and dynamical arrest. Recently, it was reported that experiments of dilute, stress-free gel networks show that local ordering happens in a hierarchical manner and that the different stages of the ordering process are responsible for distinct properties of gels.²⁸ Stress-free gel network means that the packing fraction is lower than φ = 0.1 where percolation only occurs after the gelation. Using our simulation results, we want to check the results obtained for dilute gel networks and in addition extend the range of studied packing fractions to denser networks. In this article, we extend the range of studied packing fractions up to φ = 0.25 and also look at differences between weakly or strongly bound particle networks.

As the most important local ordering structures which occur we consider tetrahedra, 2-tetrahedra, 3-tetrahedra and pentagonal bipyramids (PBP). These structures and especially the fractions of particles which are part of these structures are detected using the same analysis methods as in ref. 28. It is important to note that a particle can be part of several local orderings at the same time; therefore, the distribution curves do not add up to 1. During the analysis, two particles i and j are seen as neighbors if their distance r_ij < 1.1σ. This is in contrast to our previous definition of the neighborhood from the first part of the article where we choose r_ij ≤ 1.036σ. This difference is made to account for random, thermal motion which can lead to splitting and reconnection of particle bonds within a few time steps. Taking larger bonding thresholds reduces the influence of this effect as random splitting is unlikely and therefore ensures more stability in the calculations.

The hierarchical formation of local ordering mentioned in ref. 28 for dilute gel networks is reproduced not only for dilute networks, but also for dense gels. Initially, particles form tetrahedral clusters, which merge to 2-tetrahedral clusters, 3-tetrahedral clusters and finally pentagonal bipyramidal clusters. Fig. 7(a)–(d) shows that for dilute gel networks the fraction of particles inside local structures is higher than for dense networks, indicating a higher local order in dilute networks. In particular for the pentagonal bipyramids, the fraction of particles for the system with φ = 0.25 is only 10% after 2000τ_B, while for the dilute network with φ = 0.05, it is nearly 30%. A difference which can be seen between dilute and dense networks is that for all dilute networks (φ ≤ 0.12), the ratio of particles in local structures is approximately the same, while for dense networks, the final ratio depends on the packing fraction. Concerning the dynamics of local structure formation we see that for dense systems, the initial formation is fast, but later slows down, and is finally overtaken by the dilute systems. This may indicate differences in the evolution mechanism. Dense systems percolate quickly as already stated in Section 2. Therefore, mechanical stress due to percolation influences the evolution of the system and makes it more difficult to form new local structures (or to form local structures at all). This explains both the slower dynamics after rapid initial evolution and the lower fraction of particles in later stages of the hierarchical structure formation chain. Interestingly the fraction of particles in all of the tetrahedral states reaches a maximum and decreases afterwards, which means that tetrahedral order constitutes an intermediate stage during gelation and may slowly vanish during the further evolution of the system. In ref. 28, it is also stated that the formation of pentagonal bipyramids is connected to the onset of solidity, as the fraction of particles in PBP-clusters is directly proportional to the mean coordination number at the isostatic point 〈N_c〉 = 6. This behavior is reproduced for low packing fractions and also observed for higher packing fractions (see Fig. 7(f)). In contrast, in dense gels, also the fraction of particles in tetrahedral clusters is directly proportional to the mean coordination number at 〈N_c〉 = 6 (see Fig. 7(e)). This means that for dense gels, the formation of tetrahedral clusters may also play a role for the onset of solidity. Interestingly, for lower packing fractions the tetrahedral curves show a maximum at values 〈N_c〉 < 6, which means that for higher coordination numbers, the fraction of tetrahedral clusters decreases. For larger packing fractions, this maximum shifts to larger values of 〈N_c〉 and disappears for the largest considered packing fractions.

Fig. 7 (a)–(d) Fraction of particles inside distinct local structures. The hierarchical formation of local structures becomes apparent for all kinds of local structures analyzed. The packing fraction influences the fraction of particles in certain local structures and also the speed of local structure formation. (e) Particles in tetrahedral clusters as a function of coordination number N_c. The point of the maximum shifts with increasing packing fraction to higher values of 〈N_c〉. For dilute networks, the maximum is reached before 〈N_c〉 = 6. (f) The fraction of particles in PBP-clusters is directly proportional to 〈N_c〉, but the onset of the formation of PBP-structures shifts to higher values of 〈N_c〉 for increasing packing fractions.

Finally, we study how the formation of local structures depends on the interaction between the particles by changing the strength of the attractive forces. This means that we analyze how homogeneous fluids, cluster fluids and dilute gel networks differ structurally with identical packing fractions. Therefore, a system at φ = 0.05 is studied at different values of ε for 2000τ_B. As expected for homogeneous fluids, for a system simulated below the binodal and spinodal line at ε = 4.5, no structure formation at all is seen. As the phase separated regime of the state diagram is entered, we see structure formation both in cluster fluids (small values of ε) and in dilute gel networks (higher values of ε). We see a similar trend for all of the tetrahedral structures: the higher the attraction between the particles, the faster these local structures are formed and the higher the fraction of particles in these structures are. For the PBP structure, the trend seems to be different. Fig. 8(d) shows that for all the network states (ε > 7), the fraction of particles in PBP structures approaches the same value of about 0.25–0.3 in approximately the same time. In contrast, the cluster fluid states (ε = 6.5 and ε = 7) show a lower fraction of particles in the PBP structure. This means that the gelation and chain formation seem to be a consequence of the PBP-structure formation. The less clumpy a system is, the higher the fraction of pentagonal bipyramids. We again analyze the dependence of structural ordering on the mean coordination number of the system in Fig. 8(e) and (f). For the system with ε = 6.5, the solidity threshold 〈N_c〉 = 6 is never reached. We notice that for cluster fluids, the pentagonal ordering is already present at very small coordination numbers and increases linearly, while for the network states the pentagonal ordering becomes important at higher coordination numbers. This behavior seems to be more or less independent of the attractive strength, depending only on the regime (cluster fluid or network state) in the state diagram which is studied, similar to the results for the PBP-fraction in Fig. 8(d).

Fig. 8 (a)–(d) Fraction of particles inside distinct local structures for φ = 0.05 as a function of attraction strength ε. For the tetrahedral structures in (a)–(c), the fraction of particles inside the structure decreases with decreasing attraction ε. For the PBP structures, the particle fraction is similar for all network states (ε > 7) while it is lower for the cluster states (ε ≤ 7). (e) and (f) Fraction of particles in tetrahedral structures and in PBP-structures as a function of the mean coordination number. For PBP structures, all cluster fluids show similar behavior and all dilute gel networks show similar behavior, irrespective of the chosen attraction strength. So, this behavior seems to be a general feature of the studied structural regime not depending on the exact attractive strength ε.

4 Conclusions

Our simulations and analysis of gel networks at different packing fractions and intraparticle attractions reveal different pathways in gelation influencing dynamical properties on the one hand and structural properties of the emerging networks on the other hand.

Using two different skeletonization algorithms, we find that on a global scale at a packing fraction of approximately φ ≈ 0.12 the gelation dynamics changes. This is related to early percolation dynamics in the system. In Fig. 1(c)–(e), we show the percolation time of the system as a function of the packing fraction. Between φ ≈ 0.1 and φ ≈ 0.15 (depending on the chosen attractivity ε), the slope of the double logarithmic plot changes. This is an indicator for different dynamical regimes. For dense systems, the percolation time is very small (≤1τ_B) leading to relaxation which is restricted by mechanical stress. In contrast, for dilute networks, the system can first form disconnected clusters which can evolve freely and start to percolate later.

This has consequences for different properties of the gel. We find that the thickness of the strings decreases with increasing packing fraction. For dilute gel networks, the string thickness decreases with time, while for dense gels it increases. The crossover packing fraction is again around φ ≈ 0.12. Note that the overall structure of the gel networks gets more compact with increasing packing fraction, in the sense that loop size, link length, pore size and string thickness all decrease with increasing packing fraction.

Regarding the influence of the packing fraction on the local structure formation, we have analyzed the fraction of particles which are located inside different types of tetrahedral or pentagonal substructures. We find that for dilute gel networks φ < 0.15, the final fraction of particles in tetrahedral subclusters is more or less independent of the packing fraction, all of our systems approach similar values. Concerning the dynamics of structure formation in dilute gel networks, one notices that the more dilute the network is, the slower the initial structure formation, but once initial structures have formed, the curves are more or less parallel to each other. For dense systems, we see a different behavior. Here, we notice that the final fraction of particles in all of the mentioned local structures decreases with increasing packing fraction, which leads us to the assumption that dense networks show a weaker local order.

Turning away from the effect of packing fraction, we have also investigated the effect of attraction strength. Here we notice, as might be expected, that higher attraction strength leads to faster structure formation.

Dilute gel networks and clumpy gels probably have very different properties concerning their rheological and mechanical properties. Similarly, percolation and the evolution dynamics are known to have an impact on such properties.^16,27 However, more systematic studies are required in future to obtain a better insight into the mechanical properties of the different types of gel structures.

In this study, we have shown how the tuning of basic parameters can influence the structural and dynamical behavior of gel networks. We strengthen the assumption that distinct pathways in gelation, governed by the packing fraction of the network, have a major influence on the structural formation both on global and on local levels. As we have extended the experimental work by Tanaka et al.²⁸ with our computer simulations, it would be insightful to see how our results compare to further experiments. In addition, the influence of the observed phenomena on mechanical or rheological properties of the gel network might be interesting. Finally, gels usually are evolving very slowly and their formation differs from the behavior observed in other slowly relaxing systems like colloidal glasses thus they represent a separate class of non-equilibrium soft-matter systems.^28,39 Therefore, connecting our findings on the different types of structural and dynamical behavior to different characterizations of the non-equilibrium will be an important task for future research.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

Matthias Gimperlein: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, visualization. Jasper N. Immink: conceptualization, methodology, writing – review & editing. Michael Schmiedeberg: conceptualization, methodology, writing – review & editing, supervision, project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Stefan Egelhaaf for important discussions contributing to this article.

Notes and references

1. R. B. Jadrich, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2023, 159, 090401.
2. P. Lu, E. Zaccarelli, F. Ciulla, A. Schofield, F. Sciortino and D. Weitz, Nature, 2008, 453, 499.
3. G. Foffi, G. D. McCullagh, A. Lawlor, E. Zaccarelli, K. A. Dawson, F. Sciortino, P. Tartaglia, D. Pini and G. Stell, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 65, 031407.
4. J. Rouwhorst, C. Ness, S. Stoyanov, A. Zaccone and P. Schall, Nat. Commun., 2020, 11, 3558.
5. J. Rouwhorst, P. Schall, C. Ness, T. Blijdenstein and A. Zaccone, Phys. Rev. E, 2020, 102, 022602.
6. S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255.
7. A. Vrij, Pure Appl. Chem., 1976, 48, 471.
8. K. Binder, P. Virnau and A. Statt, J. Chem. Phys., 2014, 141, 140901.
9. B. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633.
10. E. Verwey and J. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, 1948.
11. N. Verhaegh, D. Asnaghi, H. Lekkerkerker, M. Giglio and L. Cipelletti, Physica A, 1997, 242, 104.
12. D. Richard, J. Hallett, T. Speck and C. Royall, Soft Matter, 2018, 14, 5554.
13. N. A. Verhaegh, J. S. van Duijneveldt, J. K. Dhont and H. N. Lekkerkerker, Physica A, 1996, 230, 409–436.
14. H. Tanaka, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6842–6852.
15. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
16. M. Kohl, R. Capellmann, M. Laurati, S. Egelhaaf and M. Schmiedeberg, Nat. Commun., 2016, 7, 11817.
17. M. E. Helgeson, et al. , Soft Matter, 2014, 10, 3122–3133.
18. P. J. Lu, J. C. Conrad, H. M. Wyss, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 028306.
19. A. Archer and N. Wilding, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 76, 031501.
20. J. F. Toledano, F. Sciortino and E. Zaccarelli, Soft Matter, 2009, 5, 2390.
21. I. Zhang, C. P. Royall, M. Faers and P. Bartlett, Soft Matter, 2013, 9, 2076.
22. E. Mani, W. Lechner, W. K. Kegel and P. G. Bolhuis, Soft Matter, 2014, 10, 4479–4486.
23. M. Gimperlein and M. Schmiedeberg, J. Chem. Phys., 2021, 154, 244903.
24. P. D. Godfrin, N. E. Valadez-Pérez, R. Castañeda-Priego, N. J. Wagner and Y. Liu, Soft Matter, 2014, 10, 5061–5071.
25. H. Tsurusawa, S. Arai and H. Tanaka, Sci. Adv., 2020, 6(41), eabb8107.
26. M. Schmiedeberg, J. Chem. Phys., 2022, 157, 027101.
27. M. Kohl and M. Schmiedeberg, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 71.
28. H. Tsurusawa and H. Tanaka, Nat. Phys., 2023, 19, 1171–1177.
29. D. Richard, C. Royall and T. Speck, J. Chem. Phys., 2018, 148, 241101.
30. N. Valadez-Pérez, A. Benavides, E. Schöll-Paschinger and R. Castaneda-Priego, J. Chem. Phys., 2012, 137, 084905.
31. M. P. Allen and D. J. Tildesley, Computer simulations of liquids, Oxford University Press, New York, 1990.
32. J. N. Immink, J. J. E. Maris, R. F. Capellmann, S. U. Egelhaaf, P. Schurtenberger and J. Stenhammar, Soft Matter, 2021, 17, 8354–8362.
33. V. Sorichetti, V. Hugouvieux and W. Kob, Macromolecules, 2020, 53, 2568–2581.
34. S. Torquato, B. Lu and J. Rubinstein, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2059.
35. S. Torquato and M. Avellaneda, J. Chem. Phys., 1991, 95, 6477–6489.
36. S. Torquato, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 3170.
37. S. Torquato, Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Springer Science & Business Media, 2013.
38. M. Wei, M. Y. B. Zion and O. Dauchot, Phys. Rev. Lett., 2023, 131, 018301.
39. M. Schmiedeberg, Nat. Phys., 2023, 19, 1078–1079.

---