Open Access Article
Open Access ArticleDynamics of self-propelled particles in vibrated dense granular media†
Kyungmin
Son
 a,
Yunsik
Choe
a,
Yunsik
Choe
 b,
Euijoon
Kwon
b,
Leonardo Garibaldi
Rigon
b,
Yongjoo
Baek
*b and
Ho-Young
Kim
b,
Euijoon
Kwon
b,
Leonardo Garibaldi
Rigon
b,
Yongjoo
Baek
*b and
Ho-Young
Kim
 *ac
*ac
aDepartment of Mechanical Engineering, Seoul National University, Seoul 08826, Korea. E-mail: hyk@snu.ac.kr
bDepartment of Physics and Astronomy & Center for Theoretical Physics, Seoul National University, Seoul 08826, Korea. E-mail: y.baek@snu.ac.kr
cInstitute of Advanced Machines and Design, Seoul National University, Seoul 08826, Korea
First published on 29th February 2024
Abstract
We study a system consisting of a few self-propelled particles (SPPs) placed among a crowd of densely packed granular particles that are vertically vibrated in a two-dimensional circular confinement. Our experiments reveal two important findings. First, an SPP exhibits a fractal renewal process within the dense granular medium, which induces a superdiffusive behavior whose diffusion exponent increases with its aspect ratio. Second, the SPPs eventually reach the boundary and form a moving cluster, which transitions from the moving state to the static state as the number of SPPs is increased. These results suggest a simple and effective method of modulating the fluidity and directionality of granular systems via controlling the shape and the number of SPPs.
I. Introduction
Various systems in nature exhibit self-organization, where complex structures emerge from simple interactions among individual elements without any centralized control.1 This has inspired the development of “swarm robotics”, which aims to design artificial systems whose milli-scale or larger components self-organize into a predetermined target structured through reprogrammable interactions.2–8 However, these approaches are based on components that only engage in weak mutual interactions, prioritizing a flexible structure at the cost of making it robust against external stress. Interestingly, many naturally occurring self-organized structures manage to maintain their overall shape, even as they remain flexible enough to carry out diverse functions. This is exemplified by various proteins that sit almost exactly at the rigidity transition in their native state.9,10 In this regard, the issue of reprogrammable self-organization still faces a core challenge: one must find a balance between structural stability, which demands solid-like rigidity, and structural flexibility, which requires the components to rearrange themselves in a fluid-like manner.Active granular media, comprised of polar particles that effectively self-propel on a vibrated surface, present a promising approach to this challenge. Neither fully solid-like nor liquid-like, granular materials generally exhibit a variety of mechanical properties depending on the physical situation.11–14 In particular, a two-dimensional (2D) layer of vibrated granular medium can be made to form both solid and liquid-like phases by tuning the vibration amplitude.15 Moreover, when such medium consists of self-propelled particles (SPPs), it exhibits a rich range of collective phenomena including flocking,16–18 clogging,19–21 crystallization,22 and phase separation.23,24 It should be noted that even a small fraction of SPPs mixed with the ordinary granular particles can dramatically alter the properties of the system, as exemplified by the promotion of crystallization,25,26 the acceleration of domain coarsening,27 and the generation of global nonequilibrium flux via positive feedback between the flocking of SPPs and the rectified currents of granular particles.28,29 Those motivate us to look into the physics of a granular medium with a small number of SPPs, which can be regarded as “active dopants” whose geometric and mechanical features can be adjusted to change the structure and function of the whole system.
In this study, as a minimal empirical representation of the granular media with active dopants, we study the dynamics of SPPs placed among a dense crowd of vibrated granular particles in a 2D circular confinement. Previous research has touched upon such systems in light of global ordering28,29 and microscopic fluctuations.30 However, the motion of an individual SPP within the granular medium, the emergent order when there are only a handful of SPPs within the system, and the effects of the shape of each SPP on these phenomena remain underexplored.
Our investigation reveals two distinct phenomena: first, the traversal of an SPP to the confinement boundary through a “fractal renewal process”,31 characterized by a power-law waiting time distribution influenced by the shape of the SPP. Second, when the number of SPPs is small enough, a single motile cluster forms at the boundary, exhibiting persistent unidirectional movement due to a positive feedback loop between the cluster's asymmetry and its motion. The underlying mechanism is reminiscent of the spontaneous symmetry-breaking motility involving active fluids.32–39 The phenomenon occurs even when the confinement boundary is simply circular, a setup that has been avoided in the previous research16–18,28,29 that employed a petal-shaped confinement instead to inhibit the boundary aggregation of SPPs.40 These results open up new avenues for controlling the fluidity and directionality of granular systems using a limited number of SPPs.
II. Experimental setup
A. Particle fabrication
As shown in Fig. 1a and b, each particle consists of two elliptic cylinders, the cap (height 5 mm) and the body (height 6 mm), joined on the same axis. For a circular particle, the diameters of the cap and the body are 20 mm and 12 mm, respectively, while the cap and the body of an elliptic particle have the same area, height, and mass as the corresponding parts of the circular particle. Eleven legs (length 8 mm, diameter 1 mm) are attached to the cap, which are tilted from the vertical direction by the identical angle less than 10°. All particles are manufactured by stereolithography 3D printing (Formlabs Form 3) using acrylate-based clear photopolymer. The geometric accuracy of the 3D printer employed in this work is approximately ±0.1 mm. For robust tracking of the position and the orientation of particles of interest, we mark them with one or two red squares at the top. Then the TrackMate plug-in for ImageJ41 is used to trace and analyze the trajectories. | ||
| Fig. 1 Dynamics of a single SPP placed in the center of densely packed isotropic particles. (a) Top and side views of a circular isotropic particle. (b) Top and side views of an elliptic SPP. Thicknesses of the disks and leg length are the same as the isotropic particle. (c) Trajectories of a single SPP as the leg tilt angle θL and the aspect ratio (AR) are varied (Movie S1, ESI†). (d) Time to reach the boundary, T, as θL and AR are varied. Error bars indicate standard deviation. (e) Time-averaged mean squared displacement of the SPP. (inset) Time-averaged mean squared angular displacement of the same SPP. (f) Interevent time probability P(τ) ∼ τ−α characterizing the axial motion of the SPP at θL = 10°. (inset) Example of the time evolution of the axial displacement for AR = 1.0. (g) Power spectrum S(f) ∼ f−β of the axial velocity of the SPP. (inset) Power-law exponents α and β are consistent with the relation α + β = 3 up to error bars. | ||
B. Vibrating table
The SPPs and the circular particles are excited by vertical vibration of the circular acrylic baseplate (diameter 350 mm, height 30 mm) attached to an electromagnetic shaker (Tira TV 5220). The plate is kept horizontal with an accuracy of 0.1°. Particle motion is restricted by an enclosing ring (diameter 300 mm). The shaker is attached to heavy concrete blocks to suppress resonances. Experiments are performed with vibrations at frequency f = 80 Hz and amplitude A = 70 μm, which guarantees stable excitation of particles.III. Motion of a single self-propelled particle
A. Experimental observations
We first observe how a single SPP moves amidst a crowd of vibrating granular particles. For this purpose, we placed a 2D circular confinement horizontally upon a vertically vibrating plate, with legged particles filling 75% of its area (170 particles in total). All but one of the particles (Fig. 1a) have a circular top and vertical legs, which move around randomly in an unbiased manner on the vibrating plate. In addition to these isotropic particles, there is a single particle whose legs are tilted from the vertical direction along the major axis of its elliptic top (Fig. 1b). Collisions of these tilted legs with the vibrating plate result in a fluctuating horizontal force that propels the particle in the direction indicated in Fig. 1b. Thus, this particle becomes an SPP exhibiting directed motion. The physical properties of the SPP can be controlled by varying the leg title angle θL and the aspect ratio (AR) of the elliptic top while maintaining its total area equal to that of an isotropic particle. In the absence of other particles, the axial velocity of the SPP increases with θL but does not vary significantly with the AR (see Fig. 5).The SPP is initially put at the center of the circular confinement. When the vibration is turned on, the SPP exhibits stochastic motion among the isotropic particles, always reaching the boundary of the confinement (Fig. 1c and Movie S1, ESI†). We note that, in contrast, an isotropic particle under the same conditions hardly moves from its initial position (see Fig. 6a). The virtual lack of diffusion indicates that the isotropic particles are in solid-like state via jamming, i.e., they barely exchange positions among themselves. The jammed state, however, is disrupted by the SPP, which penetrates through the granular medium of isotropic particles. The trajectories of the SPP clearly indicate the significance of θL and the AR: the higher θL or AR tends to produce straighter trajectories, while the lower θL or AR creates more wiggly trajectories. Their quantitative effects are more evident in the time T for the SPP to reach the boundary, which decreases rapidly as θL or AR of the SPP is increased (Fig. 1d); an increase in θL or AR shortens the distance traveled to reach the boundary and increases the time-averaged velocity (see Fig. 7). These results are at odds with what one would naively expect from the velocity of an isolated SPP, which increases by at most 20% as θL is increased from 4° to 10° and barely changes with the AR (see Fig. 5). In other words, using the granular medium in the jammed state, the motion of the SPP becomes far more sensitive to its controllable physical attributes.
B. Superdiffusion of the self-propelled particle
To characterize the motion of the single SPP in more detail, we measured its time-averaged mean squared displacement (MSD), which is defined as | (1) |
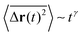 with 1 < γ < 2 for a time interval up to the order of seconds, which eventually crosses over to the normal diffusion with γ = 1 as time goes on. The diffusion exponent γ increases as the AR is increased, which is consistent with the visual observation shown in Fig. 1c that the SPP with a larger AR tends to exhibit a straighter trajectory. Such superdiffusion indicates the presence of nontrivial long-range temporal correlations in the motion of the SPP. To gain more information, we also separately examined the time-averaged mean squared angular displacement
with 1 < γ < 2 for a time interval up to the order of seconds, which eventually crosses over to the normal diffusion with γ = 1 as time goes on. The diffusion exponent γ increases as the AR is increased, which is consistent with the visual observation shown in Fig. 1c that the SPP with a larger AR tends to exhibit a straighter trajectory. Such superdiffusion indicates the presence of nontrivial long-range temporal correlations in the motion of the SPP. To gain more information, we also separately examined the time-averaged mean squared angular displacement | (2) |
 in a dense granular media. As shown in the inset of Fig. 1e, Dr of an SPP with AR = 2 is about 100.6 ≈ 25% of that of a circular SPP. One possible factor contributing to this decrease is the oscillation amplitude, which becomes slightly smaller when the AR is increased (see Fig. 8). However, for the case θL = 10° shown in Fig. 1e, the AR hardly affects Dr in the absence of the granular particles. Thus, the lower Dr for the higher AR in the granular medium is due to the angular motion of the elongated SPP being more strongly suppressed by the torque applied by the surrounding isotropic particles. Thanks to this effect, the SPP with a higher AR keeps its initial orientation for a longer time, traveling through a straighter route as shown in Fig. 1c.
in a dense granular media. As shown in the inset of Fig. 1e, Dr of an SPP with AR = 2 is about 100.6 ≈ 25% of that of a circular SPP. One possible factor contributing to this decrease is the oscillation amplitude, which becomes slightly smaller when the AR is increased (see Fig. 8). However, for the case θL = 10° shown in Fig. 1e, the AR hardly affects Dr in the absence of the granular particles. Thus, the lower Dr for the higher AR in the granular medium is due to the angular motion of the elongated SPP being more strongly suppressed by the torque applied by the surrounding isotropic particles. Thanks to this effect, the SPP with a higher AR keeps its initial orientation for a longer time, traveling through a straighter route as shown in Fig. 1c.
Now we move on to the axial motion of the SPP. For this purpose, we examine the properties of the axial velocity and the axial displacement of the SPP, which are respectively defined as
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) denotes the orientation of the self-propulsion force. By this definition, l‖ increases (decreases) if the SPP travels in the direction of (against) its self-propulsion. As exemplified for AR = 1.0 by the inset of Fig. 1f, l‖ rarely decreases in time but tends to increase via a series of steps alternating with plateaus of various lengths between adjacent pairs of steps. This indicates that the SPP is usually trapped by a cage composed of the surrounding particles but occasionally moves forward by cracking it.
θ) denotes the orientation of the self-propulsion force. By this definition, l‖ increases (decreases) if the SPP travels in the direction of (against) its self-propulsion. As exemplified for AR = 1.0 by the inset of Fig. 1f, l‖ rarely decreases in time but tends to increase via a series of steps alternating with plateaus of various lengths between adjacent pairs of steps. This indicates that the SPP is usually trapped by a cage composed of the surrounding particles but occasionally moves forward by cracking it.
To characterize such intermittent translation quantitatively, we measured the trapping time τ, here defined as the time it takes for l‖ to increase by a step of 20 mm (the diameter of each isotropic particle). See the inset of Fig. 1f for an illustration, where the spacing between every adjacent pair of vertical blue lines corresponds to an instance of τ. Its distribution, as shown in the main figure, exhibits a broad power-law tail P(τ) ∼ τ−α with 2 < α < 3. Moreover, we also examined the power spectrum S(f) = |![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) ‖(f)|2 obtained from the Fourier transform of the axial velocity:
‖(f)|2 obtained from the Fourier transform of the axial velocity:
 | (4) |
C. Effects of the particle shape on the cracking force
We see from the above analysis that α increases (β decreases) with the AR, which implies that a sharper SPP finds it easier to crack the cage. A step-by-step view of such cracking motion is shown in Fig. 2a, where the SPP (marked by a red tape) finds and widens a gap between a pair of neighboring isotropic particles highlighted in yellow dashed lines. To understand how a larger AR enhances the cracking motion, in the following we calculate the cracking force applied by the SPP that widens the gap between the two isotropic particles in front.For simplicity, we assume that the system is at static mechanical equilibrium. Although this assumption is not strictly true in the actual experiment, the results obtained from this assumption still give us a useful picture of how the AR of the SPP affects the cracking dynamics. As shown in Fig. 2b, we consider the situation where an elliptic SPP of AR = a propels itself to the right by self-propulsion force F and pushes the neighboring isotropic particles of radius R by cracking force P. Here, ϕ is the angle between the x-axis and a line passing through the center of the adjacent circle and the point of contact (X,Y), and (u,0) is the intersection between the line and the x-axis. We first use the properties of ellipses to represent the horizontal and vertical distances l and b in terms of just a and X. Using the coordinate system employed in Fig. 2b, the elliptic perimeter of the horizontal SPP centered at the origin is expressed by
 | (5) |
 , which implies
, which implies | (6) |
 . Combining this relation with eqn (5) and (6) and choosing the suitable root of the quadratic equation, we obtain
. Combining this relation with eqn (5) and (6) and choosing the suitable root of the quadratic equation, we obtain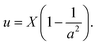 | (7) |
We then consider the angle ϕ. From the two points, (X,Y) and (u,0), sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and cos
ϕ and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ can be represented by Y/[(X − u)2 + Y2] and (X − u)/[(X − u)2 + Y2], respectively. Using eqn (5) and (7), we can relate the trigonometric functions to X and a by
ϕ can be represented by Y/[(X − u)2 + Y2] and (X − u)/[(X − u)2 + Y2], respectively. Using eqn (5) and (7), we can relate the trigonometric functions to X and a by
 | (8) |
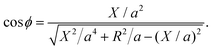 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and b = 2(Y + R
ϕ and b = 2(Y + R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ − R), the two distances l and b are represented as a function of a and X.
ϕ − R), the two distances l and b are represented as a function of a and X.
Now we express the cracking force P in terms of a and X. By the assumption of static mechanical equilibrium, the principle of virtual work42 states that the cracking force P and the self-propulsion force F must satisfy the relation
| Fδl + 2P(δb/2) = 0, | (10) |
 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and b = 2(Y + R
ϕ and b = 2(Y + R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ − R) along with eqn (8) and (9) in eqn (11), we finally obtain the curves shown in Fig. 2c.
ϕ − R) along with eqn (8) and (9) in eqn (11), we finally obtain the curves shown in Fig. 2c.
The behavior of P as a function of the AR and the gap b is shown in Fig. 2c. It shows that P monotonically increases with the AR; at b = 0, the magnitude of P applied by an SPP with AR = 2.5 is about twice as large as that exerted by the circular SPP. This ratio increases even more as b increases. We also note that P is smaller for a narrower gap (smaller b), which indicates that cracking becomes harder in more crowded environments. These results confirm our observation that the shape of the SPP greatly affects its mobility within a dense granular medium via the rotational and cracking characteristics.
D. Boundary motion of the self-propelled particle
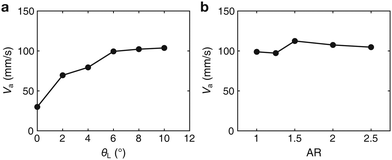
Finally, we briefly discuss how the SPP moves after reaching the confinement boundary. Using our setting, if there is no SPP, an isotropic particle initially located at the boundary stays there while exhibiting some diffusion only in the tangential direction (see Fig. 6b). This again confirms that the granular system satisfies the jamming condition, i.e., the relative positions of the particles do not change, although the entire cluster may exhibit rotational diffusion. In contrast, as shown in Fig. 3a, the SPP reaching the boundary exhibits a high mobility through the granular medium. The SPP tends to stay close to the boundary, as expected for a particle whose direction of motion exhibits a degree of persistence.43 But how close to the boundary the SPP stays depends on the AR and θL. Since the cracking ability and the orientational persistence of the SPP both increase with the AR, the SPP with a higher AR tends to stay closer to the boundary (Fig. 3a, b, Movie S2, ESI†) with a higher velocity Va tangential to the boundary (Fig. 3c). In addition, since the self-propulsion force monotonically increases with θL below 10°, the SPP tends to move faster along the boundary as θL is increased. We also note that the SPP deviates farther away from the boundary at higher AR, albeit at a reduced frequency (see Fig. 3b). This behavior is also attributable to the enhanced cracking ability and the orientational persistence of the SPP with a higher AR. | ||
| Fig. 3 Dynamics of a single SPP after reaching the boundary. (a) The SPP trajectories for 3 min after reaching the boundary as the leg tilt angle θL and the AR are varied (Movie S2, ESI†). (b) The time evolution of the radial position Pr of the SPP at θL = 8°. (c) The time-averaged velocity Va of the SPP moving along the boundary. The quantity is calculated only for particles moving on the boundary for 30 s without stopping or leaving the boundary. | ||
IV. Motion of multiple self-propelled particles at the boundary
A. Formation of the boundary cluster
As previously mentioned, when the AR is high enough, an individual SPP in the vibrated granular medium moves to the boundary and travels along it in a unidirectional manner. With this in mind, now we examine the collective behavior of multiple SPPs in a granular medium confined by a circular boundary. We place multiple SPPs with AR = 2.5 and θL = 10° in the bulk of the previously described experimental system, with each SPP replacing a single isotropic particle so that the packing fraction stays at 75% as in the single-SPP experiments. When the vibration is turned on, as shown in Fig. 4a (for t < 40 s), all the SPPs move from the bulk to the boundary, and then they collide with each other at the boundary. When they collide while moving in the opposite directions along the boundary, either they simply pass by, or one of them leaves the boundary and returns to the bulk (see Fig. 9a and b). On the other hand, if they collide while moving in the same direction along the boundary, they tend to stay close to each other and keep their original traveling direction even after the collision (see Fig. 9c). These imply that only a cluster of SPPs that used to travel in the same direction can form a stable structure, acting as the attractor of the collective dynamics of the SPPs. Indeed, our experiments show that the SPPs gradually merge into one large cluster (Fig. 4a, 40 s < t < 80 s) and travel together along the boundary (Fig. 4a, t > 80 s). | ||
| Fig. 4 Collective motion of multiple SPPs. (a) Five SPPs, initially located in the bulk, reach the boundary and form a cluster that persistently maintains its asymmetric structure and mobility in a single direction (Movie S3, ESI†). (b) A moving cluster of eight SPPs gets stuck after the leading SPP switches its direction and restores the symmetry. (c) The time-averaged velocity Va of the SPP cluster as the number N of the SPPs varies (Movie S4, ESI†). The velocity is calculated from the SPP cluster moving persistently in one direction for more than 2 min. Meanwhile, the red points indicate that the SPP clusters with N > 7 mostly stay stuck at the boundary after 5 min of observation time. Error bars indicate standard deviation. All SPPs in (a)–(c) have AR = 2.5 and θL = 10°. (d) An illustration of our simplified model of the SPP cluster dynamics. The effective outward force applied by the bulk granular particles is indicated by g. (e) An illustration of the effective process by which the moving SPP cluster gets stuck. (f) and (g) The magnitude of Va (f) and the mean lifetime τcl (g) of the moving SPP cluster as N and g vary. | ||
B. Motility of the boundary cluster
It is worthwhile to examine in more detail how a cluster of SPPs can persistently travel in a single direction along the boundary. In Fig. 4a, for t > 80 s, we observe that all the SPPs forming a cluster are tilted from the radial direction in an asymmetric manner. For example, the rearmost SPP, indicated by a yellow arrow, exhibits a significant tilt that makes it almost completely lean against the confinement boundary. In contrast, the frontmost SPP tends to tilt only slightly, usually leaning against an isotropic particle in front. Thus, whereas the rearmost SPP strongly pushes the cluster forward, the frontmost SPP provides only a weak resistance to the cluster motion. The cluster moves forward as a result of this force imbalance, which makes the isotropic particle in front of the cluster to stick more strongly to the frontmost SPP. Thus, despite the microscopic noise, the frontmost SPP maintains a limited tilt, keeping the asymmetric arrangement of the SPPs in the cluster. In short, there is a positive feedback between the structural asymmetry and the motility of the SPP cluster, which allows it to maintain a persistent motion via spontaneous symmetry breaking. This state of motion may be called the moving phase.However, the above mechanism fails to maintain the motion of the SPP cluster when the number N of SPPs is too large. The case of N = 8 is illustrated in Fig. 4b. For 0 < t < 3 s, the cluster maintains its motion according to the positive feedback mechanism described above. However, at approximately t = 3 s, the isotropic particle in front of the cluster happens to move sufficiently far away from the frontmost SPP. This allows the frontmost SPP to lean completely against the boundary, leading to both the rearmost and the frontmost SPPs exerting about the same magnitude of force on the SPP cluster in opposite directions. Thus the SPP cluster assumes a symmetric structure and loses its persistent mobility. This state of motion may be called the static phase.
How does N affect the phase of the SPP cluster, and what is the nature of the transition between the moving phase and the static phase? As shown in Fig. 4c, the time-averaged velocity Va of the SPP cluster tends to decrease as N is increased (with a notable exception created by a maximum Va attained at N = 3, which will be discussed later), with multiple metastable values observed for N > 7. To put it more precisely, for N > 7, the SPP cluster may exhibit a prolonged period of persistent motion, which eventually comes to a halt as the frontmost particle flips over to restore the cluster symmetry according to the mechanism described above. After that, the cluster is stuck, never resuming motion within the observation time. These results, especially the coexistence of multiple metastable states of motion for a range of N, indicate that the transition between the moving and the static phases is discontinuous. This is also corroborated by the results shown in Fig. 10, where the moving phase and the static phase seem to coexist for N ≥ 7, with the static phase becoming more likely than the moving phase as N increases from 7 to 8.
C. Simple model of cluster motility
Due to difficulties in increasing the number of samples and the observation time, we could not reliably estimate the stability of the moving SPP cluster as the number of SPPs, N, was increased, which is crucial for understanding the nature of the phases and the transition between them. To circumvent the difficulty, we consider a simplified model of the SPP cluster as shown in Fig. 4d. The model assumes that a one-dimensional ring is filled with a total of Ntot particles, where a series of Niso ≡ Ntot − N isotropic particles (grey disks) are followed by a series of N SPPs (red-blue rigid dimers) that propel themselves along the axial directions (green arrows). To represent the boundary accumulation of the particles, we assume that all grey and red disks stay in contact with the boundary, while the blue disks are allowed to move in two dimensions to model the flipping behavior of the SPPs. Noting that the outward pressure resulting from the random short-range movement of bulk granular matter tends to make the SPPs lean against the boundary, the effect is implemented by introducing an effective gravity g into the dynamics. Every pair of particles interacts via the Weeks–Chandler–Andersen (WCA) potential (orange arrows), and the microscopic noise originating from the plate vibration is modeled by the Gaussian white noise. See the Methods for more detailed description of the model. As Fig. 4d schematically shows, this model also exhibits persistent motion of the SPP cluster maintained by a symmetry-breaking mechanism very similar to the one observed in the experiment. Moreover, as illustrated in Fig. 4e, the cluster mobility is eventually lost when the isotropic particle (grey disk) in front of the traveling cluster (red elliptic disks) moves sufficiently far away from the frontmost SPP, allowing it to lean against the boundary.We first observe how the time-averaged velocity Va of the cluster changes depending on the number N of SPPs for different magnitudes of the gravity g. As shown in Fig. 4f, the model reproduces the existence of an optimal number of SPPs that maximizes the cluster velocity. This effect seems to be caused by the geometric shape of the SPPs. When N is small, each additional SPP means one more pusher and one less isotropic particle in front to be pushed, so Va increases with N. But when N is increased further, the elliptic shape of each SPP (narrower at the tip, fatter in the center) means that the SPPs farther away from the rear tends to tilt more and more against the motion of the cluster. When this happens, an additional SPP means an active obstacle pushing against the moving cluster in place of a passive obstacle simply staying in front. Thus, Va would eventually start to decrease when N goes above a certain threshold, which may be regarded as the “optimal” N. If the boundary shown in Fig. 4d bends upward (due to a finite radius of curvature), the optimal N would become smaller. This explains why the optimal N in the experiment (found to be 3 in Fig. 4c) is smaller than that found in our simplified model (found to be 5 in Fig. 4f). We also see that the increase in g, which tilts the SPPs more toward the boundary, makes the cluster move faster along the boundary.
Next, we turn to the question of how a large SPP cluster switches from a moving state to a static state. As schematically illustrated in Fig. 4e, for a moving cluster to be stuck, the Niso = Ntot − N isotropic disks in front should move sufficiently far away from the frontmost SPP of the cluster by the length l of the SPP, so that the SPP can fully lean against the boundary. This is like overcoming an effective potential barrier
| ΔE ∼ (Ntot − N)lVa/μm | (12) |
| τcl ∼ exp[ΔE/Teff] ∼ exp[−N × constant]. | (13) |
Although not implemented in our simplified model, a static, symmetric cluster of SPPs can be turned into a mobile, asymmetric cluster when the leftmost/rightmost SPP is kicked up via collision with the adjacent granular particle, inducing the cluster asymmetry. The time scale of this happening will not depend appreciably upon the number N of SPPs since it only concerns the two SPPs at both ends of the cluster. Thus, while the rate of a static cluster becoming mobile changes insignificantly with N, the rate of a moving cluster becoming static increases exponentially with N. For this reason, when N crosses a certain threshold, the relative stability of the moving phase and the static phase will change dramatically, leading to a phase coexistence behavior indicating a discontinuous transition.
V. Conclusions
We have presented experimental and numerical results that show how the easily tunable attributes of the SPPs, such as their AR and number, significantly change their individual and collective dynamics in a vibrated dense granular medium. Here follow comparisons between our findings and the notable results reported in the literature.In the absence of the granular medium, the motion of the single SPP on the vibrating plate can be faithfully described as the active Brownian motion with largely constant axial velocity and weak rotational diffusion, as already reported in previous studies.16,17 The velocity and the rotational diffusion coefficient of the SPP do not exhibit a strong dependence on its AR, especially when the self-propulsion is sufficiently strong (θL = 10°) (see Fig. 5 and 8). But, when surrounded by a dense granular medium of isotropic particles, we observed that the AR strongly affects both axial and rotational components of the SPP motion via cage formation and cracking. For this reason, the easily tunable microscopic attributes of the SPPs have far greater impact on the self-organization process in the presence of the dense granular medium than in its absence.
Previous studies also reported that a large number of SPPs, via direct mechanical interactions16,17 or indirect interactions mediated by the granular medium,28 develop a long-range orientational order. This phenomenon, called flocking, requires that the confining boundary of the system be designed so that the SPPs sticking to the boundary are constantly guided back into the bulk.16,17,28 Without such boundary, the SPPs eventually form a static cluster that sticks to the boundary and hardly move as a whole, preventing the formation of a flock. This precisely corresponds to the static boundary cluster for large N discussed in Section IV. Since these studies focused only on a system consisting of a macroscopically large number of SPPs, they missed the possibility of a small number of SPPs forming a motile cluster whose polarity and cohesion are maintained by the surrounding dense granular medium.
Our findings pave the way for a variety of interesting future investigations. First, the precise relation between the self-organized structure of the SPPs and the physical properties of the surrounding granular medium is yet to be clarified. While the enhanced effects of the SPP's shape on its dynamics and the formation of the traveling cluster at the boundary do seem to require the presence of caging, we still need to examine how these phenomena change depending on various characteristic time and length scales of the granular medium as its packing fraction and vibration protocols are varied. A related issue is how the presence of granular materials affects the boundary accumulation of the SPPs, which still occurs even without the granular materials.44,45 It would be interesting to check if local variations in the vibration protocols can allow us to control the form of the self-organized structure in a manner similar to the light-induced patterns formed by swimming bacteria.46 Second, we may explore the self-organization behaviors of the system for a flexible confinement boundary. We expect such systems to exhibit a rich range of collective dynamics via feedback between SPP ordering and membrane deformation. Their behaviors may also give us some clues as to the dynamical properties of cells and vesicles, which are by themselves crowded systems consisting of SPPs enclosed by flexible membranes. Finally, we also need to investigate whether our findings generalize to the case where the particles are even softer and thus highly deformable. This may give us a physical picture of how highly motile and invasive cells spread amidst a confluent tissue of epithelial cells, with ramifications for the mechanisms of morphogenesis and cancer metastasis.47
Author contributions
K. S., Y. B. and H.-Y. K. designed research and wrote the paper. K. S. performed experiments and analyzed experimental data. K. S. Y. C., E. K., L. G. R., and Y. B. performed theoretical analysis.Conflicts of interest
Authors declare no competing interest.Appendices
Appendix A: simulation details for the simple model of the SPP cluster
We consider a 2D system consisting of Ntot = 25 particles in total. N of them are rigid dimers (SPPs) that propel themselves along their axes, while the rest are isotropic particles without any self-propulsion (Fig. 4d). Each isotropic particle is a (grey) disk of radius a1 = 6. Each dimer consists of a smaller (red) disk of radius a2 = 4 and a larger (blue) disk of radius a3 = 4.6 separated by a fixed distance l = 4, so that the overall envelope of the dimer imitates the elliptic particle used in our experiments. The smaller (larger) particle corresponds to the front (rear) of the SPP, and the self-propulsion force F = 100 (green arrow) always acts from the center of the larger particle towards that of the smaller particle. Assuming that each SPP always stays in contact with the boundary, we constrain all isotropic (gray) particles and the smaller (red) particles of the dimers to move along the 1D periodic line, which is a zero-curvature simplification of the circular confinement boundary used in our experiments. The length of the periodic line is set to be| L = 2a1(Ntot − N) + 2a2(N − 1) + (a2 + a3 + l), | (A1) |
Now we describe three types of forces (other than the self-propulsion F) acting on each of the particles. First, given the distance rij between particles i and j, their short-range repulsion is given by the gradient of the Weeks–Chandler–Andersen (WCA) potential
 | (A2) |
Implementing all the above elements, and assuming every particle to be overdamped with a mobility coefficient μm = 4, their dynamics are numerically integrated using the Euler method.
Appendix B: supplemental figures
When the mass of the particle is fixed, the SPP's leg tilt angle θL and AR are main factors that affect its behavior. Fig. 5 shows the change in average velocity of a single SPP as a result of increasing θL and the AR when its movement is unimpeded by its surroundings. The axial velocity of the SPP increases with θL but converges as it approaches 10° (Fig. 5a), while it does not vary significantly with the AR (Fig. 5b). This indicates that the SPP's self-propulsion is only affected by θL, and the influence decreases as θL increases.Fig. 6 shows how particle move when only isotropic particles without SPP densely fill the circular arena. An isotropic particle located at the center can hardly exchange its position with other particles except by slight oscillation (Fig. 6a). For a particle situated at the boundary, it remains stationary, undergoing diffusion exclusively in the tangential direction (Fig. 6b). This affirms that isotropic particles are in a jammed state, even though the entire cluster may display rotational diffusion.
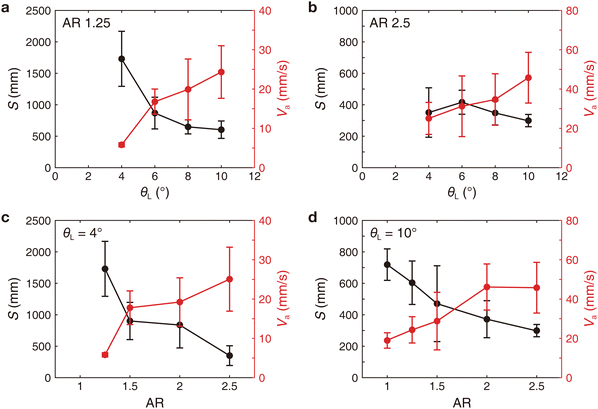
Fig. 7 shows the effect of θL and AR on the time-averaged speed Va and distance S traveled by a single SPP from the center of a dense environment to the boundary. At low AR, a rise in θL leads to both an increase in Va and a decrease in S (Fig. 7a). However, at high AR, x causes a significant change in Va only (Fig. 7b). On the other hand, an increase in AR significantly increases Va and decreases S for both low and high θL (Fig. 7c and d). This indicates that the SPP's AR has a considerable impact on both its ability to penetrate and redirect in a dense environment.
The θL and AR of the particle also affect its rotational properties. Fig. 8a shows that increasing both variables generally suppresses the rotational movement of the SPP. The cause of this effect can be found in Fig. 8b–d, which show that an increase in the two variables inhibits the particle's vertical movement generated by the vibrating plate. Increasing θL diminishes the vertical deformation of the particle legs, while elongating particles enhances the likelihood of certain legs adhering to the bottom plate. This impedes the rotation of the particle, a phenomenon primarily observed when the particle falls off the floor.
Fig. 9a and b shows how two SPPs moving in opposite directions at a boundary behave after a collision. Typically, they either traverse along the boundary without significant changes or, alternatively, one of them exits the boundary. The particle that returns to the bulk will eventually encounter the boundary again, and this process continues until they move in the same direction along the boundary. Unless the two particles are moving at precisely the same speed, they will eventually meet at a certain point. Subsequently, they will coalesce into a cluster and continue their motion in the original direction (Fig. 9c).
Fig. 10 depicts a time-dependent histogram of SPP cluster velocities along the boundary for each cluster size, initially exhibiting motion in a single direction. When N is 3 or less, all clusters maintain their initial direction, but as SPP is added, several clusters appear to switch their orientation. In particular, from N ≥ 8, many clusters switch from moving phase to static phase, and when N = 9, almost all clusters get stuck to the wall over time. The rise in the quantity of stationary clusters over time implies that once a large cluster transitions into a static phase, it faces difficulties returning to a moving phase.
Acknowledgements
This work was supported by the National Research Foundation of Korea (Grant no. 2018-052541, 2021-017476) via SNU SOFT Foundry Institute. We acknowledge an administrative support from SNU Institute of Engineering Research.References
- S. Camazine, J.-L. Deneubourg, N. R. Franks, J. Sneyd, G. Theraula and E. Bonabeau, Self-Organization in Biological Systems, Princeton University Press, 2003 Search PubMed.
- M. Brambilla, E. Ferrante, M. Birattari and M. Dorigo, Swarm Intell., 2013, 7, 1–41 CrossRef.
- M. Rubenstein, A. Cornejo and R. Nagpal, Science, 2014, 345, 795–799 CrossRef CAS PubMed.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2014, 14, 2–9 CrossRef PubMed.
- X. Tang, B. Rupp, Y. Yang, T. D. Edwards, M. A. Grover and M. A. Bevan, ACS Nano, 2016, 10, 6791–6798 CrossRef CAS PubMed.
- W. Wang, J. Giltinan, S. Zakharchenko and M. Sitti, Sci. Adv., 2017, 3, e1602522 CrossRef PubMed.
- I. Slavkov, D. Carrillo-Zapata, N. Carranza, X. Diego, F. Jansson, J. Kaandorp, S. Hauert and J. Sharpe, Sci. Rob., 2018, 3, eaau9178 CrossRef PubMed.
- U. Culha, Z. S. Davidson, M. Mastrangeli and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11306–11313 CrossRef CAS PubMed.
- A. J. Rader, B. M. Hespenheide, L. A. Kuhn and M. F. Thorpe, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 3540–3545 CrossRef CAS PubMed.
- M. V. Chubynsky, M.-A. Briére and N. Mousseau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 016116 CrossRef CAS PubMed.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259–1273 CrossRef.
- A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21–22 CrossRef CAS.
- I. S. Aranson and L. S. Tsimring, Rev. Mod. Phys., 2006, 78, 641–692 CrossRef CAS.
- B. Andreotti, Y. Forterre and O. Pouliquen, Granular Media: Between Fluid and Solid, Cambridge University Press, 2013 Search PubMed.
- P. Melby, F. V. Reyes, A. Prevost, R. Robertson, P. Kumar, D. A. Egolf and J. S. Urbach, J. Phys.: Condens. Matter, 2005, 17, S2689 CrossRef CAS.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef PubMed.
- J. Deseigne, S. Leonard, O. Dauchot and H. Chaté, Soft Matter, 2012, 8, 5629–5639 RSC.
- C. A. Weber, T. Hanke, J. Deseigne, S. Léonard, O. Dauchot, E. Frey and H. Chaté, Phys. Rev. Lett., 2013, 110, 208001 CrossRef CAS PubMed.
- G. A. Patterson, P. I. Fierens, F. S. Jimka, P. G. König, A. Garcimartín, I. Zuriguel, L. A. Pugnaloni and D. R. Parisi, Phys. Rev. Lett., 2017, 119, 248301 CrossRef CAS PubMed.
- L. Caprini, F. Cecconi, C. Maggi and U. M. B. Marconi, Phys. Rev. Res., 2020, 2, 043359 CrossRef CAS.
- C. Reichhardt and C. J. O. Reichhardt, Phys. Rev. E, 2021, 103, 062603 CrossRef CAS PubMed.
- G. Briand, M. Schindler and O. Dauchot, Phys. Rev. Lett., 2018, 120, 208001 CrossRef CAS PubMed.
- C. Scholz, M. Engel and T. Pöschel, Nat. Commun., 2018, 9, 931 CrossRef PubMed.
- C. Scholz, A. Ldov, T. Pöschel, M. Engel and H. Löwen, Sci. Adv., 2021, 7, eabf8998 CrossRef PubMed.
- R. Ni, M. A. Cohen Stuart and M. Dijkstra, Nat. Commun., 2013, 4, 2704 CrossRef PubMed.
- R. Ni, M. A. Cohen Stuart, M. Dijkstra and P. G. Bolhuis, Soft Matter, 2014, 10, 6609–6613 RSC.
- B. Van Der Meer, L. Filion and M. Dijkstra, Soft Matter, 2016, 12, 3406–3411 RSC.
- N. Kumar, H. Soni, S. Ramaswamy and A. K. Sood, Nat. Commun., 2014, 5, 4688 CrossRef CAS PubMed.
- H. Soni, N. Kumar, J. Nambisan, R. K. Gupta, A. K. Sood and S. Ramaswamy, Soft Matter, 2020, 16, 7210–7221 RSC.
- N. Kumar, H. Soni, S. Ramaswamy and A. K. Sood, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 030102 CrossRef PubMed.
- S. B. Lowen and M. C. Teich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 992 CrossRef PubMed.
- E. Tjhung, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12381–12386 CrossRef CAS PubMed.
- G. De Magistris, A. Tiribocchi, C. A. Whitfield, R. J. Hawkins, M. E. Cates and D. Marenduzzo, Soft Matter, 2014, 10, 7826–7837 RSC.
- N. Nikola, A. P. Solon, Y. Kafri, M. Kardar, J. Tailleur and R. Voituriez, Phys. Rev. Lett., 2016, 117, 098001 CrossRef PubMed.
- M. Shafiei Aporvari, M. Utkur, E. U. Saritas, G. Volpe and J. Stenhammar, Soft Matter, 2020, 16, 5609–5614 RSC.
- J. Howard, Annu. Rev. Biophys., 2009, 38, 217–234 CrossRef CAS PubMed.
- G. Foffano, J. S. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2012, 109, 028103 CrossRef CAS PubMed.
- O. Granek, Y. Kafri and J. Tailleur, Phys. Rev. Lett., 2022, 129, 038001 CrossRef CAS PubMed.
- K.-W. Kim, Y. Choe and Y. Baek, Phys. Rev. E, 2024, 109, 014614 CrossRef CAS PubMed.
- A. Kudrolli, G. Lumay, D. Volfson and L. S. Tsimring, Phys. Rev. Lett., 2008, 100, 058001 CrossRef PubMed.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
- C. Lanczos, The Variational Principles of Mechanics, Dover, Toronto, 4th edn, 1986 Search PubMed.
- G. Li and J. X. Tang, Phys. Rev. Lett., 2009, 103, 078101 CrossRef PubMed.
- L. Caprini and U. M. B. Marconi, Soft Matter, 2018, 14, 9044–9054 RSC.
- M. Leoni, M. Paoluzzi, S. Eldeen, A. Estrada, L. Nguyen, M. Alexandrescu, K. Sherb and W. W. Ahmed, Phys. Rev. Res., 2020, 2, 043299 CrossRef CAS.
- G. Frangipane, D. Dell’Arciprete, S. Petracchini, C. Maggi, F. Saglimbeni, S. Bianchi, G. Vizsnyiczai, M. L. Bernardini and R. Di Leonardo, eLife, 2018, 7, e36608 CrossRef PubMed.
- S. Grosser, J. Lippoldt, L. Oswald, M. Merkel, D. M. Sussman, F. Renner, P. Gottheil, E. W. Morawetz, T. Fuhs, X. Xie, S. Pawlizak, A. W. Fritsch, B. Wolf, L.-C. Horn, S. Briest, B. Aktas, M. L. Manning and J. A. Käs, Phys. Rev. X, 2021, 11, 011033 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01596c |
| This journal is © The Royal Society of Chemistry 2024 |