Dynamics of drying colloidal suspensions, measured by optical coherence tomography

Abstract

Colloidal suspensions are the basis of a wide variety of coatings, prepared as liquids and then dried into solid films. The processes at play during film formation, however, are difficult to observe directly. Here, we demonstrate that optical coherence tomography (OCT) can provide fast, non-contact, precise profiling of the dynamics within a drying suspension. Using a scanning Michelson interferometer with a broadband laser source, OCT creates cross-sectional images of the optical stratigraphy of a sample. With this method, we observed the drying of colloidal silica in Hele–Shaw cells with 10 μm transverse and 1.8 μm depth resolution, over a 1 cm scan line and a 15 s sampling period. The resulting images were calibrated to show how the concentration of colloidal particles varied with position and drying time. This gives access to important transport properties, for example, of how collective diffusion depends on particle concentration. Looking at early-time behaviours, we also show how a drying front initially develops, and how the induction time before the appearance of a solid film depends on the balance of diffusion and evaporation-driven motion. Pairing these results with optical microscopy and particle tracking techniques, we find that film formation can be significantly delayed by any density-driven circulation occurring near the drying front.

---

1 Introduction

The formation of a solid film from a liquid precursor is an indispensable industrial process, which can add a wide variety of functionality to products. Evaporation of the solvent from a colloidal suspension is one of the easiest ways to make a thin film with specific properties, including photonic materials, stratified films, textured surfaces, as well as more traditional paints and coatings.^1–4 In contrast to the versatility of this process, however, fundamental understanding of film formation is still lacking in many ways. Complicating matters, drying films dramatically change their appearance and structure as they evolve from a liquid to a solid, and the way in which they pass through intermediate states like gels or glasses can affect the final film properties.^5–8

An important challenge to understanding film formation is the difficulty of monitoring the structure of a colloidal suspension during drying. For example, two basic problems are understanding how particles pack near the liquid–solid transition^9–12 and how cracks develop in a solidified but still-wet film.^13–16 In both cases, changes in the concentration of particles in a drying film are of fundamental interest. Small-angle X-ray scattering (SAXS), in which an intense X-ray beam is scattered as it passes through a sample, has been a particularly successful means of measuring such changes.^6,17–20 The scattering spectrum provides information about the particle concentration¹⁷ and orientation,⁶ as well as the microstructure^19,20 of a colloidal film, and these properties can be mapped out by scanning the beam.^18,19 However, these measurements require the use of centralised synchrotron facilities. As alternatives, several means for observing particle concentrations have been proposed, including spectroscopic methods,^21,22 Mach-Zehnder interferometry,⁷ laser speckle imaging,²³ and imaging of the evolution of optical transmission²⁴ or structural colour.⁵

Here we show that Optical Coherence Tomography (OCT) can rapidly map the optical properties of a drying colloidal film, providing high-resolution, high-accuracy information of the drying process, including of the particle concentration field.

Optical coherence tomography was first developed for medical applications²⁵ but has been emerging as a powerful imaging method for applications in soft matter physics^26–31 and the heritage sciences.^32–36 Using OCT, dynamic measurements of surfaces or interfaces can be made, for example to monitor the roughness of a drying varnish layer,³³ or to measure the evaporation rates of droplets,³⁰ the spreading rates of extruded fluids,³¹ and the formation and decay of wrinkles during dielectrophoresis.²⁹ Internal features like shear bands can also be visualised.²⁸ Alternatively, it can be used to track reflective tracer particles, to measure fluid flows in liquids.^26,27

OCT is a non-invasive, non-contact technique employing a Michelson interferometer, as shown in Fig. 1(a). Light from the source is split into one beam directed towards a sample and another towards a reference mirror. The light reflected from various depths inside the sample interferes with that reflected from the mirror. Fourier-domain OCT uses a broadband laser source, which makes simultaneous measurement of the interference patterns over a range of wavelengths.^35,36 A suitable transformation of this signal then allows for the measurement of the optical distance between interfaces in the sample.

Fig. 1 Experimental and imaging methods. Schematic illustration of (a) the Fourier-domain optical coherence tomography (OCT) system and (b) a drying cell. (c) A cross-sectional OCT image is shown, of a drying KE-W10 suspension (d = 110 nm) inside a cell of height H = 300 μm. The initial volume fraction of the suspension is φ₀ = 0.18 and the image was captured after 40 minutes of drying. The optical thickness of the suspension is the distance between the bright reflections arising from the interfaces between the suspension and the glass plates. This distance increases towards the close-packed film region, as the volume fraction φ increases.

The optical distance experienced by a beam of light moving within a material is the product of that material's group refractive index, n, and the real distance travelled. As such, OCT can detect changes in the refractive index of a drying droplet of a polymer solution,²⁶ for example, as well as characterising dynamic wrinkling on the surface of liquid films.²⁹ Within a colloidal suspension any optical distance will depend on the concentration of colloidal particles, φ, and on the difference between the refractive indices of the particles and their solvent. With proper calibration, we will show that OCT can thus provide a means of dynamically measuring properties of suspensions, like particle concentrations.

A unidirectional drying cell, or Hele–Shaw cell, is often used to observe the film formation process of drying suspensions.^{6,18,19,37–44} As used here, and shown in Fig. 1(b), this is a thin rectangular channel into which a liquid suspension can be added. Evaporation occurs at one end of the cell (right side in figure), and the geometry simplifies film formation into a largely one-dimension problem. Particles flow with the solvent towards the drying surface, where a densely packed, solid film develops, and Brownian motion or diffusion smears out the sharp jump in particle concentration that would otherwise develop at the packing front. Additionally, even for gap thicknesses as small as H ∼ 100 μm, buoyancy effects along particle concentration gradients can lead to circulating flows within the cell.^7,21,44–46 Near the packing front, these flows involve particle-rich fluid settling and moving away from the front in the lower part of the cell, balanced by an enhanced flow towards the front in the upper part of the cell. In concentrated suspensions, this circulation is limited by higher viscosities.⁷

In this work we demonstrate that OCT can measure and map out how particle concentrations vary in drying suspensions. Using this method, we collect cross-sectional images of drying colloidal suspensions in Hele–Shaw cells, as in Fig. 1(c). Denser suspensions have higher particle concentrations, implying a higher refractive index and a larger optical thickness of the drying cell, and we show how to convert OCT data into measurements of particle concentration. We then study the particle concentration dynamics of drying films using different initial concentrations, cell thicknesses and particle sizes. The results are used to evaluate particle diffusivity. Finally, we use OCT to document the early stages of drying, including the development of the particle packing front, and demonstrate that buoyancy-driven circulation can significantly delay film formation.

2 Experimental

2.1 Colloidal suspensions

Two aqueous colloidal silica suspensions (KE-W10, Nippon Shokubai; Ludox SM-30, Sigma Aldrich) were used. Their average particle diameter and pH are d = 110 ± 56 nm, pH = 7 (KE-W10) and d = 10 ± 4 nm, pH = 10 (SM-30), as measured by dynamic light scattering (Zetasizer Nano-ZS, Malvern; range gives standard deviation of d). The full particle size distributions are shown in Fig. S1 of the ESI.† The volume fraction of particles, φ, was controlled by either adding solvent to or dialysing each suspension. In dialysis, suspension enclosed in a semi-permeable bag (Spectra/Por 4 dialysis membrane) was immersed in an aqueous solution of poly(ethylene glycol) with molecular mass of 35 000 u (PEG35000, Sigma Aldrich) and with pH = 10 controlled by addition of NaOH.⁴⁷ This gave an effective monovalent ionic strength of 0.1 mM to the dialysis solution. Estimations of the effective Debye length and compressibility factor of the resulting suspensions are shown in the ESI,† Fig. S2, as calculated using the non-linear Poisson–Boltzmann cell method.^18,48,49 We calculated the particle concentration of suspensions from the weight difference before and after drying samples in an oven at 80 °C overnight, assuming a mass density of 2.2 g cm⁻³ for the silica particles.⁴⁸ Concentration measurements were found to be repeatable to within 0.6%. At these low ionic strengths, samples with particle concentrations of φ > 0.43 (KE-W10) and φ > 0.26 (SM-30) were gel-like, and too viscous to manipulate easily.

2.2 Optical coherence tomography (OCT)

We used an ultra-high-resolution OCT system that is described in detail elsewhere,³⁶ and which was developed for applications in art conservation and archaeology. As sketched in Fig. 1(a), this is a Fourier-domain instrument, incorporating a fixed reference mirror and a broadband supercontinuum laser source with a centre wavelength of 810 nm and a FWHM bandwidth of 200 nm. The recombined light is dispersed through a grating onto a detector covering the wavelength range of 600–1000 nm; interference patterns are collected spectrally, and a Fourier transform is used to convert these patterns into details of the stratigraphy along the optical axis. A scanning mirror then enables fast optical cross-sectional imaging by moving the laser beam horizontally across the sample.^26,36

This instrument provides axial (i.e. along the optical axis, or depth) information with a resolution of 1.8 μm in air (1.35 μm in water). The axial resolution derives from the spectrum of the laser source.³⁶ The virtual cross-section images presented here have a 0.4 μm pixel size over a 1.5 mm depth of field. Depth profiles (A-scans) were captured with an integration time of 8 μs. Two-dimensional cross-section images (B-scans) were constructed at 10 μm per pixel in the transverse direction. This is larger than the instrument's optical transverse resolution of 4.4 μm. Field curvature due to the objective lens is corrected during post-processing.⁵⁰ For each image a time-average of 100 consecutive B-scans, taken over about 15 s, was used to reduce noise levels.

2.3 Calibration

The refractive indices of suspensions of known volume fractions φ were measured in rectangular glass capillaries (Vitrotubes, VitroCom Inc.). These capillaries had widths of 2–3 mm, gap thicknesses of H = 100–300 μm and wall thicknesses of 100–210 μm. For each test an empty capillary was stuck to a glass substrate and a cross-sectional OCT image was captured. Suspension was then injected into the capillary and another OCT image was taken at the same position. The refractive index of the suspension was calculated as the ratio of the optical thickness of the gap in the filled and empty conditions of the capillary. We used a MATLAB code to identify the glass-suspension and glass–air interfaces in the OCT images and measure these lengths (see Fig. S3 in the ESI† for more detail). For any depth profile (A-scan) the highest-intensity peaks, corresponding to the interfaces, were fit by a Gaussian function with a five-point window, to find their positions with sub-pixel accuracy.³³ The distance between the reflections from the top and bottom of the capillary gave the optical thickness across the cell, at a horizontal location. The accuracy achieved in optical thickness measurement was 2 nm for an empty cell and 10 nm for a filled cell. These procedures were repeated at different points along the B-scan, to map out the optical thickness along the scan line. For the calibrations, we averaged results across a 1 mm long cross-section, about 100 pixels, to give representative optical thicknesses Z_f and Z_e of each capillary when filled and empty, respectively. The group refractive index of the suspension was then calculated as n = Z_f/Z_e.

All measurements were repeated five times for each φ, with average values and standard deviations shown in Fig. 2. An upper limit on φ was set by the viscosity of the suspensions, and the ability to effectively fill a capillary cell. Linear least-squares fits of these data give the calibrations used to convert n into φ for the experiments involving drying suspensions. As shown in Section 3.1, this calibration is consistent with a linear superposition of two phases, corresponding to pure water and Stöber-manufactured silica, respectively.

Fig. 2 Calibration of the group refractive index, n, with the particle volume fraction, φ, for suspensions of (a) KE-W10 and (b) SM-30. Error bars indicate the standard deviation of n over five measurements. Linear least-squares fits to the data are shown as dashed lines. These correspond to calibrations of the form n = n_sφ + n_w(1 − φ), with effective indices of refraction n_s and n_w for the silica particles and water, respectively.

2.4 OCT measurements of drying suspensions

We used OCT to make time-lapse observations of suspensions drying in Hele–Shaw cells, using the setup sketched in Fig. 1(b). For each cell, two spacers (silicone rubber sheet, Kenis Ltd) were cut out and placed parallel to each other on a glass plate (S1127, Matsunami Glass Ind. Ltd) separated by a distance W ≈ 5 mm. The thicknesses of the spacers used, either 100 or 200 μm, determined the height of the cell, H. Cells with H = 300 μm were made by layering pairs of spacers. A thinner glass plate (Haemocytometer coverslip, Marienfeld) was placed above the spacers to make a narrow, covered channel. The layers were then fixed together by an adhesive (NOA61, Norland) to prevent any motion when suspension was injected into the cell.

For each experiment a drying cell was placed under the OCT instrument and a 10 mm long optical cross-section of the empty cell was recorded, perpendicular to its open, exposed end. Suspension was then added into the cell and a series of OCT images were taken at the same position as the first scan, as in Fig. 1(b). These were captured immediately after injection, 1, 2, 3, 5, 7 and 10 minutes later, then from 5–20 minute intervals until 80–300 minutes after injection; each image, like that in Fig. 1(c), represents a 15 s average of 100 consecutive B-scans. Evaporation from the open end of the channel concentrated the particles there, leading to the appearance of a solid, packed particle film that grew slowly into the drying cell. Optical thickness measurements of the empty and filled drying channels were made, as in Section 2.3, and their ratios were used to calculate the evolution of the refractive index of the suspension at every pixel along the horizontal scan line. The calibrations from Fig. 2 were used to convert these results into measurements of the particle concentration, φ, along the channel. We performed experiments using suspensions with two different diameters d (KE-W10, 110 nm and SM-30, 10 nm), each with three different initial particle concentrations φ₀ between 0.02–0.19, and for drying cells with three different heights, H (100, 200 and 300 μm).

In a few cases we detected signs of bending of the glass plates, due to the capillary pressure that developed within the drying suspension.⁴² These effects were typically confined to the smaller SM-30 particles, which could cause up to a few micrometres inward deformation of the cell, especially between the first appearance of a solid film and its delamination from the glass. Bending of the top glass plate was easily detectable with OCT, so we excluded any data where bending was observed.

2.5 Optical microscopy of drying suspensions

Complementary observations of the drying of SM-30 suspensions in H = 300 μm thick cells were made using an optical microscope (AZ-100, Nikon). In these experiments, the Hele–Shaw cell was placed on a thermally stabilised glass plate, kept at 20 °C by water circulating from a temperature-controlled bath (RE104, Lauda). A stream of dry air was continuously supplied across the top of the cell. Images of the drying suspension were recorded every 2 minutes with a digital camera (D5600, Nikon) equipped with the microscope. The areas covered by the liquid suspension and the solid film were found in each image using ImageJ.⁵¹ Dividing these areas by the width of the cell gave measures of the size of the liquid and solid film regions, x_l and x_f.

Particle tracking experiments in H = 100 μm thick cells used fluorescent tracer particles (sicastar-GreenF, micromod Partikeltechnologie GmbH, d = 500 nm) added to a SM-30 suspension at a 1 : 2500 volume ratio. We observed the flow of the tracer particles with fluorescence microscopy (Eclipse Ti2-E, Nikon), using 510–560 nm light for excitation and monitoring emission at wavelengths >580 nm.

3 Results

3.1 OCT images and calibrated concentration distributions

A typical cross-sectional OCT image of a drying experiment is given in Fig. 1(c). Here, a KE-W10 suspension had been drying for 40 minutes in a 300 μm thick cell. The bright lines represent reflections from the interfaces between the colloidal suspension and the glass cell, while the fainter lines are autocorrelation artefacts resulting from the mutual interference of light reflected from the drying cell interfaces. The optical thickness of the suspension – the distance between the two bright lines – increases from left to right, as the suspension becomes more concentrated and changes from a liquid to a solid. The most noticeable changes are over a region about one millimetre wide, between the relatively uniform suspension to the left, and a solid deposit that is developing near the drying interface at x = 0.

Calibrations of the particle concentrations φ with refractive index n show a simple linear relationship, for both KE-W10 and SM-30. Fig. 2 gives these data, with best-fit slopes of dn/dφ = 0.114 ± 0.002 for KE-W10 and 0.123 ± 0.003 for SM-30. The smaller value for KE-W10 likely reflects its fabrication by the Stöber process, which leads to a more nano-porous structure as compared to Ludox;^48,52 the inferred index of 1.458 ± 0.002 for the KE-W10 particles (i.e. extrapolating to φ = 1) is consistent with measured values of n_s = 1.45–1.46 for Stöber-fabricated colloidal silica.^52,53 The φ = 0 intercepts of the calibration fits are 1.3439 ± 0.0005 for KE-W10 and 1.3432 ± 0.0007 for SM-30. These values are consistent with the group refractive index of pure water, which spans n_w = 1.341 to 1.352 for wavelengths of light between 587–1014 nm at 20 °C, as calculated^50,54 from tabulated measurements of water's phase refractive index.⁵⁵

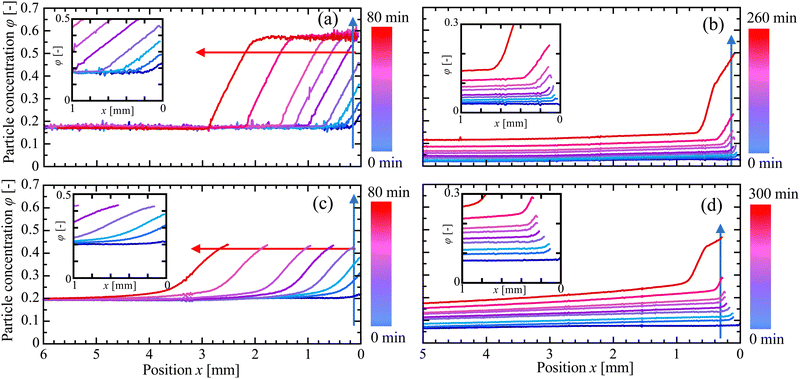
The results of several typical drying experiments are shown in Fig. 3. Each panel shows how the particle concentration, φ, of a particular experiment varied with the distance x from the drying edge and time t since drying began. In all cases φ increased rapidly near the air–liquid interface, developing into a steep drying front that gradually shifted into the cell as drying proceeded. When the initial concentration φ₀ was sufficiently large, as in Fig. 3(a) and (c), the concentration of the suspension far from the drying front remained constant. As shown in Fig. 3(b) and (d), however, in experiments with φ₀ less than 0.14, the concentration of suspension everywhere slowly increased with time, suggestive of convective mixing.^21,44 This bulk increase in the particle concentration was observed in several cases at sufficiently low φ₀. In these cases, density-driven motion was confirmed by particle tracking experiments, as detailed in Section 3.3. Finally, we note that cracks, or the delamination of the suspension from the top or bottom of the drying cell, complicated the OCT measurements by introducing additional interfaces (see Fig. S4 in the ESI†). As such, we limited our quantitative observations to the crack-free areas of the films, to avoid potential higher uncertainties in the derived refractive indices. This was important for the suspension with the smaller particles (SM-30), where we limited measurements to values of φ ≲ 0.42, to avoid such effects.

Fig. 3 Dynamical variation of the particle concentration, φ(x,t), in drying suspensions of (a), (b) KE-W10 and (c), (d) SM-30. Evaporation occurs at the drying interface, x = 0, and all cells are of height H = 300 μm. The initial volume fraction φ₀ is (a) 0.17, (b) 0.02, (c) 0.19 and (d) 0.06, respectively. The insets highlight the early development of the drying fronts, over the first millimetre of each drying cell. The red arrows show the values of φ used to track the advance of the drying front into the cell. The blue arrows show the position used to track the growth of φ near the drying interface.

In experiments without convection, the drying front developed into a dynamical steady-state, with a relatively fixed concentration distribution that slowly advanced into the drying cell. This is demonstrated in Fig. 4, where the data from Fig. 3(a) and (c) are superimposed, after shifting them to coincide at φ = 0.50 for KE-W10 and φ = 0.42 for SM-30. These values are indicated by red arrows in Fig. 3. For KE-W10 there is a point where the concentration steeply changes near x′ = 28 mm and all the data collapse onto a single curve, as in Fig. 4(a). For the SM-30, however, the concentration is more smooth and the drying fronts shown in Fig. 4(b) become slightly shallower with time. This is consistent with a gradual slowing-down of the growth of the packing layer, and the drying rate. We checked this interpretation by tracking the motion of the drying fronts over time. For this, Fig. 5 indicates how the position at which φ = 0.50 and φ = 0.42 advances with time for the KE-W10 and SM-30 suspensions, respectively. For the larger particles the packing front grew linearly with time, as in Fig. 5(a), but the film formation of the smaller particles, shown in Fig. 5(b), slowed somewhat as drying proceeded.

Fig. 4 Superimposed particle concentration distributions from (a) Fig. 3(a) and (b) Fig. 3(c). The data are taken well after the onset of film growth (20–80 min, colour scheme as in Fig. 3) and are shifted horizontally so that they overlap at (a) the first position where φ = 0.50 and (b) such that all plots start from φ = 0.42 at x′ = 0.

Fig. 5 Growth of the packed film region over time, as represented by the position x where (a) φ = 0.50 in Fig. 3(a) (KE-W10) and (b) 0.42 in Fig. 3(c) (SM-30). The corresponding particle concentrations are shown by red arrows in Fig. 3. For panel (a), the data are well-fit by a linear growth rate, with a slope of 0.0325 ± 0.0002 mm min⁻¹. The data in panel (b) show film growth that slows down over time, decreasing from an initial rate of 0.0412 ± 0.0008 mm min⁻¹ (solid line) to 0.0346 ± 0.0002 mm min⁻¹ (dashed line) later.

3.2 Characterising the collective diffusion coefficient

Concentrated suspensions of colloidal particles typically show a faster diffusion of particles across concentration gradients, as compared to more isolated particles.^18,21 The particle mobility is related to the strength of inter-particle interactions, and the concentration or collective diffusion coefficient is characteristic of the colloidal equation of state.^18,56–60 As an example application of OCT techniques, we used measurements of concentration gradients during drying, such as those shown in Fig. 3, to evaluate how the collective diffusion coefficient D varies with particle concentration φ, for our suspensions.

Assuming a one-dimensional flow with an average velocity v in the horizontal direction x, the mass and force balances of a colloidal suspension can be summarised as an advection-diffusion problem:

For drying in a Hele–Shaw cell, if the particle packing front is growing at a fixed velocity w into the cell, then the steady-state solution to eqn (1), in the frame of reference moving with the packing front, provides an estimate of the collective diffusion coefficient:¹⁸ This approximation will hold as long as any changes happen slowly, compared to the rate at which the particle packing front relaxes. Volume conservation implies that the relative speed of the evaporative flow is given here by (w − v) = (φ_f/φ₀)w, where φ_f is the final particle concentration, as measured in the fully-packed film. For this calculation, w was found by tracking the position of the packing front in time, as in Fig. 5, and the final concentration of SM-30 was estimated to be φ_f = 0.6, based on results from similar experiments.¹⁸ As evidenced in Fig. 4, we estimate any temporal dynamics in the late stages of drying to be happening at rate of ∂φ/∂t ≤ 10⁻⁵ s⁻¹, while the magnitude of the advective term in eqn (1) is of order 10⁻⁴ s⁻¹, so the quasi-steady state approximation given by eqn (2) is valid.

Measurements of D(φ), made using eqn (2), are shown in Fig. 6. Here, ∂φ/∂x was calculated as the numerical derivative of φ(x), using only results that had settled into a steady state, including the late-time data shown in Fig. 3(a) and (c); experiments where φ continued to increase everywhere were excluded, such as the cases in Fig. 3(b) and (d). We also excluded the flatter regions of the concentration distributions, where the numerical derivative used to evaluate eqn (2) becomes noisy. Finally, D was normalised by the Stokes–Einstein diffusion coefficient, D₀ = k_BT/(3πμ₀d), where k_B is Boltzmann's constant, T = 293 K is the temperature, μ₀ = 10⁻³ Pa s is the viscosity of the solvent, and d is the particle diameter. To check the consistency of the results, experiments were repeated for cell thicknesses of H = 100, 200 and 300 μm, which affected the evaporation rates and front velocities,⁴³ allowing w to vary from 1.1 μm s⁻¹ to 0.54 μm s⁻¹. For both suspensions, the results were consistent to within the experimental scatter.

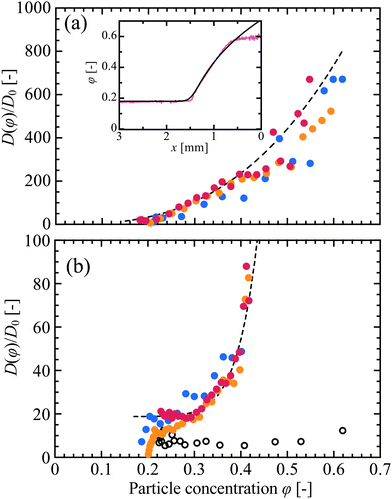Fig. 6 The collective diffusion coefficient, D(φ), normalised by the Stokes–Einstein diffusivity D₀, is shown for (a) KE-W10 and (b) SM-30. D is estimated from eqn (2) using late-time data for φ, such as is shown in Fig. 3, and using drying cells of heights H = 100 μm (blue), 200 μm (orange) and 300 μm (red). In (b) corresponding data acquired by SAXS¹⁸ are shown as open circles. Dashed lines show fits to the H = 300 μm data, of (a) D(φ)/D₀= 3070φ^2.80 and (b) D(φ)/D₀ = 18.8 + 269000φ^9.75. (inset) Based on this fitting, the particle concentration distribution of a drying front can be estimated (black line) by integrating eqn (2). This compares well to data from the corresponding experiment (magenta line, t = 40 min), from Fig. 3(a).

3.3 Film dynamics observed by optical microscopy

To complement the OCT results, we collected time-lapse sequences of similarly prepared experiments using optical microscopy. The drying of SM-30 suspensions in H = 300 μm thick cells are shown in Fig. 7, with corresponding Movies S1 and S2 in the ESI.† For suspensions with lower initial particle concentrations a solid film only appeared at the drying surface after a significant delay, or induction period. For example, Fig. 7(a) shows an experiment with φ₀ = 0.06, where the induction period was 78 minutes. At higher initial concentrations this delay was dramatically shorter, as in Fig. 7(b). Here, for the same conditions, but with φ₀ = 0.19, the induction period was only 10 minutes.

Fig. 7 Sequences of images of drying SM-30 suspension in a cell of height H = 300 μm, for initial concentrations of (a) φ₀ = 0.06, and (b) φ₀ = 0.19. Scale bars are 2 mm.

From the microscope images we extracted the areas covered by the solid and liquid regions (see Section 2.5) to give the effective locations of the air–liquid (x_l) and liquid–solid (x_f) interfaces within the drying cells. The motions of these interfaces, for the two experiments just described, are given in Fig. 8. In both cases the suspension evaporated at similar rates, as demonstrated by the rate of change of x_l. However, the general behaviour of the particle packing front changed with φ₀. For the case of φ₀ = 0.06, even after the lengthy induction period, the growth of the packed region started slowly and only gradually accelerated to a steady value. For the experiment with φ₀ = 0.19, in contrast, the packed region grew most rapidly to start with, and slowed slightly as it became more established. These trends in film growth kinetics were also observed in the drying of KE-W10 suspensions.

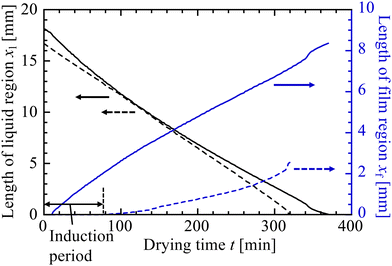Fig. 8 Time variation of the size of the liquid region, x_l (black lines), and solid film, x_f (blue lines), in the drying experiments shown in Fig. 7, for initial particle concentrations of φ₀ = 0.06 (dashed lines) and φ₀ = 0.19 (solid lines). At the lower φ₀ a long induction period of 78 min is observed, before any solid packed film appears, even though the evaporation rate (given by dx_l/dt) is similar in both cases.

The fluid flows within these experiments were further investigated with fluorescent tracer particles, as in Movies S3 and S4 in the ESI.† For SM-30 and φ₀ = 0.06, a circulating flow was seen around the packing front (Movie S3, ESI†), appearing as a steady stream of some particles moving opposite to the main advective flow. This situation resembles the buoyancy-driven flows reported elsewhere,^21,44 under similar conditions. However, such a circulating flow was not observed for larger particle concentrations, for example φ₀ = 0.19 (Movie S4, ESI†). These results are consistent with Section 3.1, where it was shown that a well-developed advection-diffusion front only developed at high enough φ₀.

4 Discussion

4.1 OCT and film drying

Optical coherence tomography has recently been showing its potential for the study of soft materials.^{26–32,34–36} While most applications, to date, have involved tracking particle motion or the shapes of surfaces or interfaces, we have shown that OCT can be a sensitive probe of the evolving composition of soft materials. Here, we compare our results with those obtained by other methods, chiefly SAXS (see introduction for a list of other methods recently applied to drying films), in order to demonstrate the strengths and limitations of OCT methods for the study of drying films and coatings.

As the main alternative, SAXS has been particularly successful in probing the dynamics and structure of colloidal films.^6,17–20,61 For example, a SAXS experiment at ESRF (ID02) mapped out the drying fronts of colloids in Hele–Shaw cells.¹⁸ Data from this experiment is reproduced alongside OCT data in the ESI,† Fig. S5. Despite differences in material preparation, and drying conditions, the shapes of the drying fronts are qualitatively similar, and the high resolution and low noise levels of the OCT are evident. By moving drying cells across the path of a fixed X-ray beam, the SAXS measurements had 50–200 μm spatial resolution, sampling one data point every 3 s, including the time to move the sample between imaging positions. Under these conditions, data along a 10 mm long scan took several minutes to acquire. A micro-focus beamline and high-speed stage can offer improved capacities¹⁹ but the challenges of a fixed beam remain, as do the constraints of using a synchrotron facility. The OCT tools demonstrated here measured the same type of concentration distribution with 10 μm resolution in ∼15 s, using a table-top system^33,36 and without moving the sample. Depending on the noise tolerance of an experiment, the sampling rate and spatial resolution of the imaging could be improved, in this case up to the instrumental limits of a 4 μm transverse resolution of A-scans acquired at ∼ 10 μs intervals.³⁶ Furthermore, although SAXS does offer exceptional access to structural information, such as particle orientation or crystal texture,^6,18–20 polarising OCT techniques could provide for some applications in this area as well.

For the larger KE-W10 particles we made measurements of particle concentration well into the solid, packed film. In these experiments we found a final packing of φ_f = 0.59 ± 0.01, by averaging particle concentration values over the first few millimetres of the solid film, for times above 30 minutes. This value is close to that of random close packing, φ = 0.64, and is consistent with final packing densities of between φ_f = 0.55 and 0.63 reported for similarly prepared films of KE-W10 and KE-W30, as estimated through mass conservation principles.^43,62 This agreement gives an independent validation of the accuracy of the OCT-based measurements of particle concentration.

4.2 Collective diffusivity

The collective diffusion coefficient of a colloidal suspension is a practical summary of its transport properties, and is linked to its thermodynamic equation of state. Specifically, D(φ)/D₀ = f(φ)∂(φZ(φ))/∂φ, where f(φ) is the hindered settling coefficient, which describes hydrodynamical interactions between nearby particles, and Z(φ) is a compressibility factor related to the osmotic pressure of the suspension, Π = nk_BTZ, for a particle number density n.^18,56–60 As such, the collective diffusivity D(φ) is a key point of contact between models of colloidal behaviour, and experimental measurements. Here, we discuss our observations of D(φ) for colloidal silica, in this context.

For SM-30, we can compare our results to the collective diffusion of the same type of particles, as measured from concentration gradients obtained using SAXS.¹⁸ As shown in Fig. 6(b), these data are in the range of D = (5–12)D₀, while our results lie between (10–80)D₀. Variations in preparation are likely the source of this difference: our suspensions were dialysed against deionised water (with 0.1 mM NaOH to control pH), while the SAXS particles were dialysed against solutions of 5 mM NaCl.¹⁸ Silica particles acquire a strong negative charge in water,^53,63 but any dissolved counter-ions will readily accumulate around the particles, screening their effective surface charge and reducing the Debye length of their electrostatic interaction. These effects weaken the osmotic pressure acting between particles, lowering D in the presence of additional salt.^18,60,64 The different results are within the range of values that can be reasonably expected, taking into account the differences in salt concentration.

In line with theoretical models⁶⁴ and other SAXS observations,¹⁸ the diffusivity of the larger (KE-W10, d = 110 nm) particles is strongly enhanced compared to the smaller ones (SM-30, d = 10 nm), for similarly prepared suspensions. We found here that the diffusivity of the KE-W10 particles, shown in Fig. 6(a), can reach up to several hundred times D₀, at intermediate volume fractions. Such high values of the collective diffusivity have not been reported before, but are comparable to the values of up to D/D₀ ≃ 500 predicted, for example, for 100 nm charged silica particles under very low salt conditions.⁶⁴ To further explore this observation, we modelled the osmotic compressibility, Z(φ), for colloidal silica with a bare surface charge density of 0.5 e⁻ nm⁻², in Donnan equilibrium with a 0.1 mM salt solution, using the non-linear Poisson–Boltzmann cell method.^18,48,49 As shown in Fig. S2(b) of the ESI,† the expected values of Z for the KE-W10 are between 10 and 20 times higher than for SM-30, and in line with the order-of-magnitude higher collective diffusivities seen in the KE-W10. These differences in compressibility can be attributed to the higher total surface charge, per particle, of the larger KE-W10 particles, moderated by some screening due to charge condensation.⁴⁹

For both sizes of particle studied here, D(φ)/D₀ increases monotonically with particle concentration and rises sharply as the particles become well-packed, as predicted.⁵⁸ To examine these results further we made empirical fits to the data from the H = 300 μm experiments; these trials had the lowest noise, as the optical thickness was larger, and as the effective evaporation was slower. The KE-W10 data was well fit by a simple power law, see Fig. 6(a), while the SM-30 was better fit by a power law with a constant offset at low φ, as in Fig. 6(b). Given a functional fit for D(φ), eqn (2) can be inverted to solve the time-independent advection-diffusion equation, corresponding to the case of a well-developed drying front advancing at a steady speed (see ESI† for derivation). As shown in the inset to Fig. 6(a), this result agrees well with the measured concentration gradients for KE-W10, at least until the film solidifies. The corresponding result for SM-30 also agrees well, see Fig. S6 in the ESI.† In Section 4.3, we show how similar calculations can accurately capture the first few minutes of drying, before the formation of a packed film. We only estimated D(φ)/D₀ for samples with high enough φ₀, due to the convective flows seen when φ₀ < 0.14, as in Movie S3 of the ESI.† These flows are induced by density gradients of the suspensions near the packing front,^21,44 and are not considered in the simple 1D advection-diffusion model of eqn (1) and (2). However, they were suppressed at higher particle concentrations, as in Movie S4 (ESI†), due to the smaller density difference and increased viscosity of these conditions (see also Section 4.3). The speed of these flows should scale²¹ with H³, and so by repeating observations in cells ranging in height from H = 100–300 μm, we confirmed the negligible effect of convection on the measurements of D(φ) reported in Fig. 6.

To summarise, OCT techniques enabled us to estimate the collective diffusion coefficient of silica suspensions, with results ranging from 10–600 times larger than the Stokes–Einstein coefficient. The effect of the collective diffusion of particles on the film formation process of a drying suspension is particularly important in the higher concentration range, where it acts to broaden out the particle compaction front.

4.3 Film formation and early-time behaviour

Once a drying experiment had been set up, a packed layer of particles took from several minutes to a few hours to appear. To highlight the initial dynamics of film formation we tracked how the particle concentration evolved near the drying interface, x = 0, as shown in Fig. 9. This initially increased at a roughly steady rate, in all experiments. For more concentrated suspensions φ continued to increase smoothly until reaching close packing, at which point a solid film began to form. The dilute suspensions, in contrast, showed two distinct steps in the rate at which φ developed, and had a much longer induction time before film formation. The differences between the two cases can be seen more clearly in the insets to Fig. 9, where we show how the near-surface particle concentration depends on the total volume of particles transported to the drying interface, per unit cross-sectional area.

Fig. 9 Evolution of the particle concentration φ near the drying interface, x = 0, in (a) KE-W10 and (b) SM-30 suspensions for higher (solid circles) and lower φ₀ (open circles). The original data are shown in Fig. 3 and taken from the positions indicated by the blue arrows in that figure. In the samples of lower φ₀ of both suspensions, φ increases gradually with time in the initial stage of drying (dashed lines give linear fits) but transitions to a sharper increase when φ reaches ∼ 0.20. Insets show the same data, rescaled to show how the results depend on the total volume of particles transported to the drying interface, per unit cross-sectional area.

With measurements of the collective diffusion coefficient, it is possible to predict how the particle packing front should develop, under the assumption of a simple advection-diffusion transport model. The time evolution of eqn (1) was simulated for a uniform initial condition of φ = φ₀, a no-flux boundary condition for the particles at x = 0 and a far-field boundary condition of φ → φ₀ at large x, using forward Euler time stepping and a second-order centred finite difference approximation of the spatial derivatives. The numerical methods were first validated by comparison to analytic solutions⁶⁵ for the special case of D = D₀. For comparison with experiments, we then assumed D(φ) as fit in Section 4.2 and Fig. 6.

For a constant flow towards the drying surface, at speed |v|, the total volume of particles near that surface should increase at a rate of |vφ₀|. We used this to estimate v, by integrating φ over x = 0 to 3 mm and fitting a slope to how the value of this integral changed over the first seven minutes of drying. The evaporation rates measured in this way, before any solid deposit formed, were |v| = (0.9 ± 0.1) μm s⁻¹ for KE-W10 and (0.7 ± 0.1) μm s⁻¹ for SM-30. These values are of similar magnitude to, but slightly lower than, the rates inferred for the late-time behaviours in Fig. 5, of (1.2 ± 0.01) μm s⁻¹ for KE-W10 and (1.5 ± 0.03) μm s⁻¹ for SM-30.

By numerically integrating the advection-diffusion system in time, we predicted the evolution of φ(x,t), up to the point where a packed film developed, under conditions corresponding to the experiments with the denser initial conditions of φ₀ ≈ 0.2. For KE-W10, the advection-diffusion model accurately predicts the shape of the concentration distribution, as shown in Fig. 10(a), and gives a reasonable estimate for the characteristic timescale over which it develops, as in Fig. 10(b). The SM-30 has a similar level of agreement, see Fig. 10(c) and (d), demonstrating the internal consistency of the data. As a further check on the self-consistency of D, we found that artificially increasing or decreasing the interpolated values of the collective diffusivity by a third, which is about the level of uncertainty permitted by the scatter of the measured data, gave noticeably poorer predictions for the drying front shape at these early times.

Fig. 10 Simulation of the initial growth in φ for (a), (b) KE-W10 and (c), (d) SM-30 suspensions with high φ₀, in the absence of circulation. Concentration distributions (dashed lines) are shown near the drying interface at (a) t = 10 min for KE-W10 and at (c) t = 7 min for SM-30, and compared with experimental data taken at the same times (solid lines, colours as in Fig. 3). Predictions (dashed lines) of how φ evolves at the drying interface (x = 0) are shown for the early period of drying of (b) KE-W10 (d) SM-30. The corresponding experimental data, from Fig. 9, are shown as black circles.

For the experiments at lower φ₀, we attribute the slower development of the particle packing layer, and the longer induction time, to the presence of circulating flows. This is consistent with the film growth observed by optical microscopy, as in Fig. 7 and 8. As drying proceeds, particles are concentrated near the drying interface and this gradient in the density of the suspension induces a flow. Recently, Salmon and Doumenc⁶⁶ have shown how this problem is analogous to Taylor dispersion, with an effective particle dispersion that is enhanced by a factor of

Here, α = 362 880 is a parameter accounting for the problem geometry, g = 9.8 m s⁻² is the gravitational acceleration, ν is the kinematic viscosity of the suspension, and for silica in water β = 1.2 gives the relative density difference between the particles and solvent.⁶⁶ As representative values, consider a cell height of H = 300 μm, and concentration gradients of ∂φ/∂x = 100 m⁻¹, of the same order as those in Fig. 10. Under these conditions, assuming a constant value of ν = 10⁻⁶ m² s⁻¹, for pure water, and if D = D₀, then for SM-30 eqn (3) predicts that the convective contributions to transport will be about 10⁵ times larger than the effects of particle diffusion. This is clearly an overestimate, however, as both ν and D are enhanced in dense suspensions. For example, if D = 20D₀, typical of the data in Fig. 6(b), then once the suspension viscosity is ∼ 20 times that of water, convection and diffusion are comparable in magnitude; convection will then become negligible as both ν and D increase any further. The argument for KE-W10 gives a similar result. Rheological measurements⁸ on SM-30 (as supplied, undialysed) shows that ν depends strongly on φ, and that this suspension would be viscous enough to effectively shut off the convective contributions to transport by particle concentrations of φ = 0.23.

When circulation is active, particles will accumulate near the drying interface, but also flow back into the cell, and so the rate of increase in particle concentration remains small. As evaporation proceeds, however, the particle concentration near the drying interface will still steadily increase. This leads to a higher viscosity, and faster diffusion of any gradients across the thickness of the cell. These effects, in turn, will slowly weaken the circulation flow, until it becomes ineffectual, after which time the rate of particle accumulation will speed up. In our present work, φ ∼ 0.20 is a threshold to shift to this more rapid increase, as shown in Fig. 9, although this threshold will vary depending on particle properties and drying conditions. The OCT measurements clearly demonstrate the two regimes, and how the different particle concentrations are related to the induction time before the first appearance of the solid film.

4.4 Late-stage drying

At later times, drying is controlled by the growth of a solid packed particle film, as shown in Fig. 5. While the solid film grew at a constant rate for KE-W10 (Fig. 5(a)), film growth slowed with time for SM-30 (Fig. 5(b) and 8). This retardation can be explained by a transition in the rate-limiting step of the film formation process. In the early stage of drying, the diffusion of water molecules in the air wholly determines the drying rate, but as the particles accumulate, the permeation of water through the packed film can also affect this rate. Dufresne et al. have demonstrated that the permeability depends strongly on particle sizes.³⁸ Recently, however, two additional causes have been proposed for the slowdown; the decrease in the water vapour pressure by Kelvin effect, or the recession of the evaporation interface into the porous layer of packed particles.^41,67

Regardless of the cause, the effects of variations in film growth rate can also be seen in Fig. 4. The particle concentration distributions of the KE-W10 suspension overlapped, once shifted into the co-moving reference frame, while those of the SM-30 became more gradual with time. Changes in the film propagation would affect the time that the particles take to cross the packing front. If the propagation speed is slower, more particles would be able to diffuse into the bulk suspension instead of packing, as the advection-diffusion length scale characterising the front width in eqn (1) scales as D/(w − v). Thus, the concentration gradients are correspondingly shallower as drying proceeds, as in Fig. 4(b).

One interesting feature in drying of KE-W10 suspension is that the concentration increases rather suddenly at x′ = 2.8 mm in Fig. 4(a). The corresponding drying front of the SM-30 is smoother, as are literature reports¹⁸ for Ludox with particle radii a of 5 to 14 nm. This is suggestive of some potentially interesting particle size effects. However, the origin of the discontinuity is unclear at present. It occurs at too low a particle concentration to attribute to a gelling transition, or the onset of e.g. shear resistance.^5,18 Similarly, it is difficult to attribute to convective mixing, as the feature is robust to changes in cell thickness that should cause a 27-fold variation in the strength of convection.^21,44,66

Finally, one aspect of the late-time concentration distributions that remains puzzling is the gradual increase in bulk concentration as drying proceeds, for experiments with a low initial volume fraction. Here we consider the bulk as the suspension at least 2–3 mm away from the packing front. In this region, φ remained constant in the samples of larger φ₀, while it steadily increased in the dilute samples, where convective mixing was also important. Using tracer particles, we have also confirmed that the circulation flow continued even 6–7 mm away from the drying interface, in these experiments. Theoretical models without circulation^18,64 do not predict this effect, at least not without assuming an unreasonably high value for the collective diffusivity. However, models that account for buoyancy-driven circulation still do not predict changes to the bulk particle concentrations, well ahead of the packing front.^21,45,66 A possible resolution is that these models use an asymptotic boundary condition in which the particles far away from the drying interface approach a constant φ₀. This boundary condition is not wholly appropriate for our experiments, where the volume of suspension was limited, and shrinking with time, as shown in Fig. 7. Alternatively, relaxing assumptions, for example by considering a concentration-dependent viscosity, may help explain this unusual observation of particles mixing readily into the bulk of the drying suspension.

5 Conclusions

The transparency of colloidal materials, especially when particle sizes are significantly smaller than the wavelength of visible light, means that the dynamics of colloidal film formation have consistently proven difficult to measure. We have shown here that optical coherence tomography, OCT, can make non-contact, rapid and dynamic measurements of the particle concentration field of drying colloids, with high precision. The particle concentrations are accessible by calibration against the group refractive index of the suspension. Given the small size of the particles used here, this refractive index is well-approximated as a linear sum of the refractive indices of the particles and the solvent. With OCT, we measured the time evolution of the concentration gradients of colloidal suspensions drying in fixed Hele–Shaw cells, and showed how this method can help address open issues in film formation, such as the particle diffusion during packing, and density-driven circulation. Possible related applications of these methods could include mapping out the particle compaction around cracks and shear bands, tracking the deformation caused by the high pressures generated in drying suspensions, exploring further the nature of collective diffusivity, or observation of the relaxation and reversibility of an arrested drying front.

From the shape of the particle concentration distributions under a steady state, we measured the collective diffusion coefficient of two silica suspensions. The diffusivity measured for the 10 nm SM-30 suspension compares favourably to similar observations made by SAXS methods.¹⁸ In line with recent predictions,⁶⁴ we found that diffusion in the 110 nm KE-W10 suspension is remarkably strong, reaching hundreds of times higher than the Stokes–Einstein diffusion constant that is typical for isolated Brownian particles. This demonstrates how OCT can provide a new way to characterise properties of drying suspensions, more easily than conventional SAXS methods.

The dynamics of the particle concentration distributions depended strongly on the initial particle concentration of the suspensions used. For the larger φ₀, a packed film began to grow after only a few minutes, without any increase in the bulk concentration of the suspension. In contrast, experiments with lower initial particle concentrations showed a significantly delayed film growth. Combined with observations by optical microscopy, these differences in the film growth kinetics were attributed to circulating flows near the drying interface. This shows the potential of OCT as a valuable complementary technique to traditional methods, providing quantitative insight into the dynamics of the film formation process.

Author contributions

Kohei Abe: methodology, investigation, formal analysis, funding acquisition, visualization, writing – original draft, writing – review and editing. Patrick Atkinson: methodology, software, writing – review and editing. Chi Shing Cheung: methodology, software, resources. Haida Liang: conceptualization, supervision, funding acquisition, writing – review and editing. Lucas Goehring: conceptualization, formal analysis, supervision, writing – original draft, writing – review and editing. Susumu Inasawa: conceptualization, funding acquisition, supervision, writing – original draft, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. A. thanks the Japan Society for the Promotion of Science (JSPS) Overseas Challenge Program for Young Researchers for the support to conduct research activities in the UK. This work is financially supported by JSPS KAKENHI grant no. JP21J10968, JP21K18843, JP23KJ2128 and JP23H01742. The development of the ultra-high-resolution OCT was funded by the AHRC/EPSRC cross-council funding (AH/H032665/1) and the subsequent upgrade was supported by AHRC (AH/V012460/1). We thank Carole C. Perry for access to dynamic light scattering, Megha Emerse and Fouzia F. Ouali for experimental consumables and Yu Yamamoto and Masahiko Tanaka for assistance with the international logistics of the project.

Notes and references

1. A. F. Routh, Rep. Prog. Phys., 2013, 76, 046603.
2. P. Bacchin, D. Brutin, A. Davaille, E. D. Giuseppe, X. D. Chen, I. Gergianakis, F. Giorgiutti-Dauphiné, L. Goehring, Y. Hallez, R. Heyd, R. Jeantet, C. L. Floch-Fouéré, M. Meireles, E. Mittelstaedt, C. Nicloux, L. Pauchard and M.-L. Saboungi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 94.
3. M. Schulz and J. L. Keddie, Soft Matter, 2018, 14, 6181–6197.
4. R. G. Larson, AIChE J., 2014, 60, 1538–1571.
5. L. Goehring, W. J. Clegg and A. F. Routh, Langmuir, 2010, 26, 9269–9275.
6. F. Boulogne, L. Pauchard, F. Giorgiutti-Dauphiné, R. Botet, R. Schweins, M. Sztucki, J. Li, B. Cabane and L. Goehring, Europhys. Lett., 2014, 105, 38005.
7. B. Sobac, S. Dehaeck, A. Bouchaudy and J.-B. Salmon, Soft Matter, 2020, 16, 8213.
8. E. D. Giuseppe, A. Davaille, E. Mittelstaedt and M. François, Rheol. Acta, 2012, 52, 451–465.
9. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829.
10. T. P. Bigioni, X.-M. Lin, T. T. Nguyen, E. I. Corwin, T. A. Witten and H. M. Jaeger, Nat. Mater., 2006, 5, 265–270.
11. P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Nature, 2011, 476, 308–311.
12. W. Liu, J. Midya, M. Kappl, H.-J. Butt and A. Nikoubashman, ACS Nano, 2019, 13, 4972–4979.
13. W. P. Lee and A. F. Routh, Ind. Eng. Chem. Res., 2006, 45, 6996–7001.
14. L. Goehring, W. J. Clegg and A. F. Routh, Soft Matter, 2011, 7, 7984–7987.
15. F. Giorgiutti-Dauphiné and L. Pauchard, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 39.
16. P. Bourrianne, P. Lilin, G. Sintès, T. Nîrca, G. H. McKinley and I. Bischofberger, Soft Matter, 2021, 17, 8832–8837.
17. J. Li, B. Cabane, M. Sztucki, J. Gummel and L. Goehring, Langmuir, 2012, 28, 200–208.
18. L. Goehring, J. Li and P.-C. Kiatkirakajorn, Philos. Trans. R. Soc., A, 2017, 375, 20160161.
19. B. Yang, N. D. Smith, A. Johannes, M. Burghammer and M. I. Smith, Sci. Rep., 2018, 8, 12979.
20. A. J. Carr, W. Liu, K. G. Yager, A. F. Routh and S. R. Bhatia, ACS Appl. Nano Mater., 2018, 1, 4211–4217.
21. C. Loussert, A. Bouchaudy and J.-B. Salmon, Phys. Rev. Fluids, 2016, 1, 19.
22. M. Lehtihet, E. Abisset, S. Chevalierb, A. Sommierb, C. Pradereb and J. Leng, Chem. Eng. J., 2021, 403, 126167.
23. H. M. van der Kooij, R. Fokkink, J. van der Gucht and J. Sprakel, Sci. Rep., 2016, 6, 34383.
24. K. Hatakeyama, K. Tanaka, T. Takahashi, S. Wakaki and A. F. Routh, Colloids Surf., A, 2022, 648, 129263.
25. D. Huang, E. A. Swanson, C. P. Lin, J. S. Schuman, W. G. Stinson, W. Chang, M. R. Hee, T. Flotte, K. Gregory, C. A. Puliafito and J. G. Fujimoto, Science, 1991, 254, 1178–1181.
26. S. Manukyan, H. M. Sauer, I. V. Roisman, K. A. Baldwin, D. J. Fairhurst, H. Liang, J. Venzmer and C. Tropea, J. Colloid Interface Sci., 2013, 395, 287–293.
27. A. M. J. Edwards, P. S. Atkinson, C. S. Cheung, H. Liang, D. J. Fairhurst and F. F. Ouali, Phys. Rev. Lett., 2018, 121, 184501.
28. H. Huang, Y. Huang, W. Lau, H. D. Ou-Yang, C. Zhou and M. S. El-Aasser, Sci. Rep., 2018, 8, 12962.
29. A. Saxena, C. Tsakonas, D. Chappell, C. S. Cheung, A. M. J. Edwards, H. Liang, I. C. Sage and C. V. Brown, Micromachines, 2021, 12, 1583.
30. E. J. Sewalt, J. Kalkman, J. van Ommen, G. M. Meesters and V. van Steijn, Food Res. Int., 2022, 157, 111049.
31. J. van der Kolk, D. Tieman and M. Jalaal, J. Fluid Mech., 2023, 958, A34.
32. H. Liang, M. G. Cid, R. G. Cucu, G. M. Dobre, A. G. Podoleanu, J. Pedro and D. Saunders, Opt. Express, 2005, 13, 6133–6144.
33. S. Lawman and H. Liang, Appl. Opt., 2011, 50, 6039–6048.
34. H. Liang, M. Sax, D. Saunders and M. Tite, J. Archaeol. Sci., 2012, 39, 3683–3690.
35. P. Targowski and M. Iwanicka, Appl. Phys. A: Mater. Sci. Process., 2012, 106, 265–277.
36. C. S. Cheung, M. Spring and H. Liang, Opt. Express, 2015, 23, 10145–10157.
37. C. Allain and L. Limat, Phys. Rev. Lett., 1995, 74, 2981–2984.
38. E. R. Dufresne, E. I. Corwin, N. A. Greenblatt, J. Ashmore, D. Y. Wang, A. D. Dinsmore, J. X. Cheng, X. S. Xie, J. W. Hutchinson and D. A. Weitz, Phys. Rev. Lett., 2003, 91, 224501.
39. E. R. Dufresne, D. J. Stark, N. A. Greenblatt, J. X. Cheng, J. W. Hutchinson, L. Mahadevan and D. A. Weitz, Langmuir, 2006, 22, 7144–7147.
40. P.-C. Kiatkirakajorn and L. Goehring, Phys. Rev. Lett., 2015, 115, 088302.
41. P. Lidon and J.-B. Salmon, Soft Matter, 2014, 10, 4151–4161.
42. S. Inasawa and Y. Yamaguchi, Soft Matter, 2012, 8, 2416–2422.
43. K. Abe and S. Inasawa, Phys. Chem. Chem. Phys., 2018, 20, 8935–8942.
44. K. Inoue and S. Inasawa, RSC Adv., 2020, 10, 15763–15768.
45. B. Selva, L. Daubersies and J.-B. Salmon, Phys. Rev. Lett., 2012, 108, 198303.
46. A. Bouchaudy and J.-B. Salmon, Soft Matter, 2019, 15, 2768–2781.
47. J. Li, M. Turesson, C. A. Haglund, B. Cabane and M. Skepö, Polymer, 2015, 80, 205–213.
48. B. Cabane, J. Li, F. Artzner, R. Botet, C. Labbez, G. Bareigts, M. Sztucki and L. Goehring, Phys. Rev. Lett., 2016, 116, 208001.
49. E. Trizac, L. Bocquet, M. Aubouy and H. H. von Grünberg, Langmuir, 2003, 19, 4027–4033.
50. M. K. Faluweki, C. S. Cheung and H. Liang, Eur. Phys. J. Plus, 2023, 138, 825.
51. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Meth., 2012, 9, 671–675.
52. A. van Blaaderen and A. Vrij, J. Colloid Interface Sci., 1993, 156, 1–18.
53. The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica, ed. R. K. Iler, Wiley, New York, 1979, p.896.
54. S. J. Lawman, Optical and material properties of varnishes for paintings, PhD thesis, Nottingham Trent University, 2011.
55. M. Daimon and A. Masumura, Appl. Opt., 2007, 46, 3811–3820.
56. G. K. Batchelor, J. Fluid Mech., 1976, 74, 1–29.
57. W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal dispersions, Cambridge University Press, Cambridge, 1989, p.525.
58. S. S. L. Peppin, J. A. W. Elliott and M. G. Worster, J. Fluid Mech., 2006, 554, 147–166.
59. R. Style and S. Peppin, Proc. R. Soc. London, Ser. A, 2011, 467, 174–193.
60. C. Keita, Y. Hallez and J.-B. Salmon, Phys. Rev. E, 2021, 104, L062601.
61. J. D. Forster, H. Noh, S. F. Liew, V. Saranathan, C. F. Schreck, L. Yang, J.-G. Park, R. O. Prum, S. G. J. Mochrie, C. S. OHern, H. Cao and E. R. Dufresne, Adv. Mater., 2010, 22, 2939–2944.
62. S. Inasawa, Y. Oshimi and H. Kamiya, Soft Matter, 2016, 12, 6851–6857.
63. G. H. Bolt, J. Phys. Chem., 1957, 61, 1166–1169.
64. J. Sui, Phys. Rev. E, 2019, 99, 062606.
65. R. A. Wooding, S. W. Tyler, I. White and P. A. Anderson, Water Resour. Res., 1997, 33, 1199–1217.
66. J.-B. Salmon and F. Doumenc, Phys. Rev. Fluids, 2020, 5, 024201.
67. H. Pingulkar and J.-B. Salmon, Soft Matter, 2023, 19, 2176–2185.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01560b

---