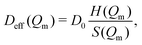DOI:
10.1039/D3SM01510F
(Paper)
Soft Matter, 2024,
20, 1309-1319
Structure and short-time diffusion of concentrated suspensions consisting of silicone-stabilised PMMA particles: a quantitative analysis taking polydispersity effects into account
Received
8th November 2023
, Accepted 13th January 2024
First published on 19th January 2024
Abstract
We characterise structure and dynamics of concentrated suspensions of silicone-stabilised PMMA particles immersed in index-matching decalin–tetralin mixtures by means of static and quasielastic light scattering experiments. These particles can reproducibly be prepared via a comparatively easy route and are thus promising model systems with hard-sphere interaction. We demonstrate the hard-sphere behaviour of dense suspensions of these systems rigorously taking polydispersity effects into account. Structure factors S(Q) can in the entire range of volume fractions with liquid-like structure quantitatively be modelled using a multi-component Percus–Yevick ansatz regarding the particle size distribution and the form factor assuming a core–shell model with a scattering length density gradient in the PMMA core. Herewith, hydrodynamic functions H(Q) are in the whole accessible Q-range beyond the second maximum of H(Q) quantitatively modelled using a rescaled δγ-approach for all investigated volume fractions. With these data, previously provided characterisation of dilute systems is extended: the excellent agreement of structural and dynamic properties with theoretical predictions for hard spheres demonstrates the suitability of these particles as a model system for hard spheres.
1 Introduction
Colloidal suspensions have attracted wide interest as highly defined and tunable model systems for the investigation of condensed matter. The hard-sphere model is of special interest, as it describes, despite its simplicity, the most fundamental properties of dense, simple liquids with a dominating repulsive interaction potential.1,2 Initiated by the pioneering work of Pusey and van Megen,3,4 suspensions of sterically stabilised poly(methyl methacrylate) (PMMA) particles in non-polar solvents are the most commonly used colloidal model systems for experimental studies of hard spheres, which encompass investigations of the bulk phase behaviour,3,5 the fluid structure, both in reciprocal space via scattering experiments6,7 and in real space via microscopy,8–10 structure-dynamics relations,11–14 crystalline15,16 and glass-like17–22 structures as well as the study of non-equilibrium phenomena such as sedimentation under gravity23 or rheological properties.24,25
Synthesis via dispersion polymerisation26 yields particles which are composed of a solid PMMA core, surrounded by a shell of stabiliser molecules, whose steric hindrance prevents the aggregation of particles upon close contact, leading to steep repulsive forces. The most commonly employed stabiliser is a poly(12-hydroxystearic acid) (PHSA) comb polymer whose synthesis is well studied27 but nevertheless considered difficult and a major obstacle for a reproducible particle synthesis with the detailed complications being described in depth elsewhere.28,29
In the pursuit of alternatives, a class of poly(dimethylsiloxane) (PDMS)-based stabilisers recently gained attention. Unlike their PHSA counterpart, these PDMS-stabilisers are commercially available and can directly be copolymerised with MMA due to their reactive end-group functionalisation which considerably simplifies the preparation of suspensions. The synthesis of these PMMA–PDMS particles and the influence of varying reaction conditions on the particle size and polydispersity is well documented.30,31 In a recent small-angle neutron scattering (SANS)-study,29 the particles were confirmed to exhibit a core–shell structure analogue to the well known PMMA–PHSA colloids. Furthermore, the study revealed several characteristics of the novel dispersions: The size distribution of submicron-sized particles suitable for scattering experiments is generally slightly broader and the stabiliser shell is slightly thicker than for PMMA–PHSA particles of comparable size. On the other hand, there is an enhanced difference of the scattering contrast between the core and the shell, which generally enables a clearer determination of the scattering form factor. It is worth mentioning that the shell thickness and thus the core-to-shell ratio of these particles can to a certain degree be tuned by employing PDMS-stabilisers with different molecular weight. Particles of this type are already adopted in multiple studies concerning the gelation of colloid-polymer mixtures,32–36 the formation of crystalline structures37 or the particle transport in microfluidic channels.38
In comparison to the established, thoroughly characterised PMMA–PHSA colloids, studies of PDMS-stabilised particles' topology and dynamics are rather limited. In this work, we investigate structure-dynamics relations of these particles in dense, fluid-like suspensions via static and dynamic light scattering. By studying concentrated systems, not only information on the particle morphology, but also on their local ordering is attainable from the scattered intensity. Thus, by comparing experimentally obtained static structure factors with theoretical predictions, the suitability of PDMS-stabilised PMMA particles as a hard-sphere model system can be tested. Dynamic scattering experiments give access to the wavevector-dependent diffusion of the particles which is influenced both by potential and solvent-mediated, hydrodynamic interactions. By investigating the relation between structural and hydrodynamic features, it can be assessed if the hard-sphere character of these particles also manifests itself in the hydrodynamics of the system.
2 Theoretical background
2.1 Scattering of polydisperse particles
Consider a multicomponent system consisting of n distinct species of isotropically interacting, spherical particles, where the composition is specified by the number fraction xα = Nα/N, which is the ratio of the number of particles Nα of species α to the total number of particles N. For such a system, the wavevector-dependent mean intensity,| |  | (1) |
probed in a static scattering experiment, is proportional to the weighted sum of the scattering amplitudes bα(Q), describing the scattering function of a single particle of species α, and the partial structure factors Sαβ(Q), representing interparticle correlations.39 The scattering amplitude| | 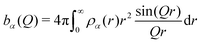 | (2) |
is given by the Fourier–Bessel transform of the scattering contrast ρα(r), which for light scattering is proportional to the difference between the refractive index of the particle and the refractive index of the surrounding medium. The partial structure factors can in principle be retrieved from computer simulations or by employing integral equation schemes. For hard spheres, an analytical solution for Sαβ(Q) for an arbitrary number of components can be obtained by solving the multicomponent Ornstein–Zernike equation employing the Percus–Yevick closure.40–43
In the absence of particle interactions, with Sαβ(Q) = δαβ, where δαβ denotes the Kronecker symbol, eqn (1) reduces to
| |  | (3) |
the squared scattering amplitude averaged over the size distribution. Similar to a monodisperse system, formally, the factorisation
I(
Q) ∝
P(
Q)
SM(
Q) into the normalised average form factor
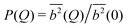
and the measurable structure factor,
| |  | (4) |
can be employed for polydisperse suspensions. This structure factor is experimentally accessible by dividing the scattered intensity of a concentrated suspension by the intensity of a diluted system, weighted by the concentration ratio of the two samples. Within this procedure, special care has to be taken that the particle morphology in the concentrated sample is the same as in the diluted state.
SM(
Q) is influenced not only by the interparticle correlations but also by the scattering properties on a single particle level, which also means that samples with the same particle interactions but different form factors yield disparate measurable structure factors. A measure for the overall local ordering of the suspension, irrespective of the individual particle sizes and shapes, is the total structure factor,
| |  | (5) |
which is independent of the scattering amplitudes.
For the particle size distribution, a reasonable choice for polymeric colloids is given by the Schulz–Flory distribution, originally derived to describe the molecular weight distribution of polymers,44,45
| | 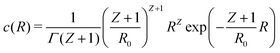 | (6) |
as the probability density function (pdf) of the total particle radius
R, where
Γ(
x) denotes the Gamma function.
R0 = 〈
R〉 is the mean radius and the parameter
Z is related to the polydispersity
p of the suspension as
p2 = (〈
R2〉 − 〈
R〉
2)/〈
R〉
2 = 1/(
Z + 1). We discretise the pdf to a more tractable
n-component mixture, where the radii and number fractions for the resulting histogram are chosen such that the first 2
n − 1 moments of the discrete and the continuous distribution match. This is essentially the application of an
n-point Gaussian quadrature rule to integrate over the size distribution. For the Schulz–Flory distribution in particular, the roots of the generalised Laguerre polynomials can be employed.
46,47 Because of the rather small wavevector range accessible in static light scattering experiments, only a small number of nodes is necessary for convergence.
2.2 Short-time dynamics and hydrodynamic function
Photon correlation spectroscopy probes dynamical properties by analysing the time-dependent fluctuations of the scattered intensity I(Q,t). The normalised measurable intermediate scattering function (ISF) ΦM(Q,t) = SM(Q,t)/SM(Q,0) is accessible from the intensity correlation function g2(Q,t) accessed in a homodyne dynamic scattering experiment. For ergodic systems, g2(Q,t) is connected to ΦM(Q,t) by the Siegert relation,48| | 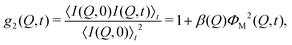 | (7) |
where the factor β(Q) depends on the coherence properties of the radiation and the detector's aperture. The angular brackets 〈…〉t denote a time average. Similar to eqn (4), SM(Q,t) is related to the scattering amplitudes bα(Q) and the partial ISFs Sαβ(Q,t):| |  | (8) |
In the short-time regime, for correlation times larger than the momentum relaxation time but smaller than the structural relaxation time, the particles exhibit simple translational Brownian motion and the normalised ISF is characterised by the exponential form| | | ΦM(Q,t) = exp[−Deff(Q)Q2t], | (9) |
with an effective, collective diffusion coefficient Deff(Q), which for polydisperse samples can be written as| |  | (10) |
and is also called extended de Gennes relation.39,49 Here,  denotes the mean Stokes–Einstein diffusion coefficient, which can be expressed as a weighted average of the diffusion coefficients of the single species,
denotes the mean Stokes–Einstein diffusion coefficient, which can be expressed as a weighted average of the diffusion coefficients of the single species,| | 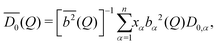 | (11) |
with| | 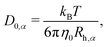 | (12) |
where kB indicates Boltzmann's constant, T the temperature, η0 the viscosity of the surrounding medium and Rh,α the hydrodynamic radius of the particles of species α. The measurable hydrodynamic function| |  | (13) |
is experimentally accessible if Deff(Q), 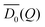 and SM(Q) are known from static and dynamic scattering experiments. HM(Q) is related to the partial hydrodynamic functions Hαβ(Q) whose calculation however, remains a computationally challenging task. For monodisperse systems, the hydrodynamic function H(Q) can be calculated with the semi-analytical δγ-scheme proposed by Beenakker and Mazur,50,51 which gives a satisfactory approximation for the wavevector-dependent short-time diffusion of hard spheres, but can in principle be employed for any interaction potential, as the scheme only depends on the structure factor of the system as an external input.52H(Q) can be decomposed into the sum of a wavevector-independent self part and a wavevector-dependent distinct part according to
and SM(Q) are known from static and dynamic scattering experiments. HM(Q) is related to the partial hydrodynamic functions Hαβ(Q) whose calculation however, remains a computationally challenging task. For monodisperse systems, the hydrodynamic function H(Q) can be calculated with the semi-analytical δγ-scheme proposed by Beenakker and Mazur,50,51 which gives a satisfactory approximation for the wavevector-dependent short-time diffusion of hard spheres, but can in principle be employed for any interaction potential, as the scheme only depends on the structure factor of the system as an external input.52H(Q) can be decomposed into the sum of a wavevector-independent self part and a wavevector-dependent distinct part according to| |  | (14) |
where the self part contains the short-time self diffusion coefficient Ds. Within the δγ-scheme, the distinct part of the hydrodynamic function can be calculated from the static structure factor S(Q) with the relation| |  | (15) |
where φ is the volume fraction, x = 2QR is a reduced wavevector with the particle radius R and μ = ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ·
·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ′ is the cosine of the angle enclosed by the unit vectors
′ is the cosine of the angle enclosed by the unit vectors ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and
and ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ′. The calculation of the function Sγ0(x) is described ref. 52. Although the self part of H(Q) can in principle also be calculated employing the δγ-scheme, the method can be significantly improved if instead more accurate, semi-empirical expressions for Ds are used or if Ds is directly fitted to experimental data or simulation results.53,54 It has been shown that the combination of the δγ-approach with a more elaborate description of Ds produces hydrodynamic functions in satisfactory agreement with computer simulations.55
′. The calculation of the function Sγ0(x) is described ref. 52. Although the self part of H(Q) can in principle also be calculated employing the δγ-scheme, the method can be significantly improved if instead more accurate, semi-empirical expressions for Ds are used or if Ds is directly fitted to experimental data or simulation results.53,54 It has been shown that the combination of the δγ-approach with a more elaborate description of Ds produces hydrodynamic functions in satisfactory agreement with computer simulations.55
3 Experimental section
3.1 Materials
Dodecane, methyl methacrylate (MMA), 2,2′-azobis(2-methylpropionitrile) (AIBN), 1-octanethiol and 1,2,3,4-tetrahydronaphthalene (tetralin) were purchased from Sigma-Aldrich, monomethacryloxypropyl-terminated poly(dimethylsiloxane) (PDMS-MA) (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) from ABCR and decahydronaphthalene (decalin, cis/trans-mixture) from Carl Roth. Tetralin and decalin were thoroughly filtered through 0.2 μm syringe filters to remove dust particles, other than that, all chemicals were used as received.
000 g mol−1) from ABCR and decahydronaphthalene (decalin, cis/trans-mixture) from Carl Roth. Tetralin and decalin were thoroughly filtered through 0.2 μm syringe filters to remove dust particles, other than that, all chemicals were used as received.
3.2 Dispersion polymerisation
The particles are synthesised by radical dispersion polymerisation following previously reported procedures.29–31
In a round bottom flask, 140 ml dodecane and 3.0 ml PDMS-MA were degassed with nitrogen for 30 min and afterwards heated to 80 °C under magnetic stirring. Simultaneously, a mixture of 15.0 ml MMA, 145 mg AIBN and 175 μl 1-octanethiol was prepared in a round bottom flask and also degassed with nitrogen for 30 min at room temperature. To start the reaction, the monomer solution was added to the stabiliser solution with a syringe. After 5 min, the initially transparent solution turned opaque, indicating the start of the polymerisation. The reaction was maintained in a nitrogen atmosphere at 80 °C for 4 h. After cooling down, the dispersion was purified by 4 cycles of centrifugation and redispersion in fresh decalin.
3.3 Sample preparation
A stock suspension of the particles was refractive-index matched in a mixture of decalin (n20D = 1.474) and tetralin (n20D = 1.541). This solvent mixture is known to cause a slight swelling of the particles, induced by the partial diffusion of the solvent molecules into the particle core.5,56 The final refractive index of the suspension was adjusted to n20D = 1.496 after a swelling period of one week after which the optical transparency persisted for several months even at high particle concentrations with no indication of polymer degradation due to the solvent. From the index-matched stock dispersion, samples of different particle concentrations in the fluid range were prepared either by concentration via centrifugation or by dilution with the index-matching solvent directly inside cylindrical quartz cuvettes. We additionally prepared from the same batch one highly concentrated suspension as a metastable colloidal glass. The fluid-like samples were gently mixed employing a vortex mixer to ensure sample homogeneity before the light scattering measurements. The mass density of the solvent mixture is slightly lower than that of the particles, however, no significant sedimentation effects and additionally no signs of crystallisation could be detected over a span of 48 h for the submicron sized colloids.
3.4 Light scattering
Light scattering experiments were performed with a CGS-3 goniometer supplied by ALV GmbH, Langen (Germany), employing an ALV/LSE-5004 multiple tau digital correlator, an avalanche photodiode single-photon detector with an optical fibre based detection unit and a frequency doubled Nd:YAG-Laser (wavelength 532 nm) as a light source. The cuvettes were placed in a temperated index matching vat filled with filtered toluene. All measurements were conducted at 20 °C, where the temperature was monitored with a Pt-100 sensor. The temperature stability of the setup is better than ±0.1 K.
For static light scattering experiments, the scattered intensity was recorded at 90 distinct scattering angles for 30 s each, in a range between 30° and 150° such that the resulting scattering vectors Q = (4πn/λ)sin(θ/2) are equidistantly spaced. The sample cuvettes were continuously rotated during the measurement to achieve ensemble averaging through the illumination of many independent scattering volumes. The recorded mean intensity was corrected for the intensity of the incident beam, the size of the illuminated sample volume and for background contributions of the cuvette and the pure solvent. In dynamic light scattering experiments, the intensity autocorrelation function g2(Q,t) was measured under the same conditions at the same scattering angles for 20 min each, however, without rotation of the sample cell.
4 Results and discussion
To model the scattering function of the particles, we employ an extended core–shell model, which also takes into account a possibly inhomogeneous core contrast caused by permeation of the decalin–tetralin mixture. For simplicity, it is assumed that this refractive-index gradient can be described by a linear decay inside the core, while the refractive index of the shell is assumed to be constant. This coarse-grained description of the particle is appropriate for the restricted wavevector-range accessible with static light scattering, where, in particular, detailed features of the surface morphology of the grafted stabiliser shell cannot be resolved. With these assumptions, the scattering contrast ρ(r) in dependence on the distance r from the particle center is represented by| |  | (16) |
where Rc is the core radius, Δ is the shell thickness and ρ0, ρR and ρΔ denote the contrast at the center of the core, at the boundary between core and shell and inside the shell, respectively. A Schulz–Flory function [eqn (6)] is used to model the size distribution of the particle cores while the stabiliser shell thickness is assumed to be identical for all particles. The partial structure factors Sαβ(Q) are obtained from the analytical solution of the Percus–Yevick equation for an n-component mixture of hard spheres in combination with a multicomponent version of the Verlet–Weis correction.57,58 A model for the scattering cross section, given by eqn (1) as a product of form factor and measurable structure factor, can then directly be fitted to experimentally obtained intensities, as demonstrated in Fig. 1. The model shows excellent agreement with the experimental data and because of the unique combination of the features from both structure factor and form factor, the particle size distribution and the effective hard-sphere volume fraction can for each sample be accurately determined from the light scattering experiments, even with the restricted wavevector range compared to small-angle scattering, employing neutrons or X-rays as a probe.
 |
| | Fig. 1 Mean intensity I(Q) of the investigated PMMA–PDMS particles, obtained by static light scattering, for effective hard-sphere volume fractions in a range from 0.24 < φeff < 0.59, as indicated in the legend. The solid lines are the result of a least squares fit of the combined hard-sphere/core–shell model described in the text. For clarity of presentation, the curves are scaled by an arbitrary factor. | |
Fig. 2 provides a more detailed depiction of the core–shell morphology of the particles. The radius of the PMMA core is independent of the effective volume fraction φeff and takes a mean value of (248 ± 3) nm for this particular sample. From the model fit, the polydispersity of the cores is determined to be approximately 7%. Unlike the particle cores, the thickness of the monodisperse shell is surprisingly observed to be affected by the particle concentration. At lower concentrations, the thickness has a limiting plateau value of (37 ± 5) nm, which is nearly independent of the volume fraction up to a critical value of φeff ≈ 0.5, after which the shell begins to shrink. In a highly concentrated glass-like suspension at φeff = 0.59, the thickness is reduced to only (25 ± 2) nm. It is possible that the crowded environment in such dense particle suspensions favours a more coiled conformation of the PDMS polymer chains. For a more detailed understanding of this behaviour, further investigations are required. As can be seen from the visual representation of the particle contrast at the top of Fig. 2, the effect is rather small when comparing the change in the shell thickness to the change of the total radius of the particles. In terms of the mean volume of a single particle, however, this still implies a decrease to about 88% of its initial volume, so the relationship between the particle number density and the volume fraction is noticeably nonlinear. For particles with even smaller cores in comparison to the shell, this effect is likely to be more prominent, especially when studying highly concentrated suspensions.
 |
| | Fig. 2 Top: A false-color representation of the scattering contrast of the investigated particles to get an idea of the core-to-shell ratio in a dilute (left) and a concentrated sample (right). The dashed line indicates the contour of the particle in the dilute state. Bottom: The mean radius of the particle cores Rcore and the thickness of the shell Δshell in dependence of the effective volume fraction φeff. The solid lines are a guide to the eye. | |
An upper bound for the shell thickness can be estimated from the fully elongated contour length of the PDMS-stabiliser.29 If the functionalised stabiliser is approximated by a simple PDMS chain, where each repetition unit has a projected length of approximately 0.32 nm (taken from hexamethyldisiloxane in the gas phase59) and a molar mass of 74 g mol−1, the total molecular weight of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 corresponds to a maximum possible length of 46 nm. The shell thickness estimated from the model fits is therefore realistic.
000 g mol−1 corresponds to a maximum possible length of 46 nm. The shell thickness estimated from the model fits is therefore realistic.
The extracted form factor P(Q) of a dilute sample is depicted in Fig. 3, together with the corresponding radial profile of the scattering contrast. The form factor displays a somewhat uncommonly encountered shape, where the peak of the first local maximum exceeds the zero-wavevector limit. This is a result of the contrast matching procedure, where the refractive index of the decalin–tetralin solvent mixture is chosen to minimise the overall scattering of the suspension. This leads for the core–shell particles to a refractive index of the surrounding medium which lies between the index of the PDMS shell and the PMMA core, with a greatly reduced forward scattering contribution. The additional swelling causes a gradient of the refractive index inside the core, but does not qualitatively change the scattering pattern of the form factor. The relation between the different contrast contributions is better visualised in the contrast profile at the bottom of Fig. 3. It shows that the contrast of the shell to the suspending medium is similar in magnitude to the contrast between the core center and suspending medium, however, with opposite sign. Further, it reveals the extent of solvent permeation inside the PMMA core, where the contrast at the boundary between core and shell is almost halfway between the contrast of the core center and of the pure suspending medium.
 |
| | Fig. 3 Top: Extracted form factor P(Q) of a dilute suspension of the investigated particles. The solid line is the form factor contribution of the employed model function which was fitted to the intensities in Fig. 1. From the extended wavevector-range, the characteristic scattering pattern of an index-matched core–shell particle is clearly visible. Bottom: Radial profile of the scattering contrast ρ(r) in dependence on the distance r from the particle center, normalised to ρ(0). The dotted line is a guide to the eye for the location of the solvent background ρsolv.(r) = 0. | |
Fig. 4 exemplarily displays the measurable structure factor SM(Q) of a concentrated suspension. SM(Q) is for polydisperse systems influenced by both the partial structure factors and the scattering amplitudes of all present species. A visualisation of SM(Q) is therefore mainly useful for the assessment of the fit quality when comparing the experimental data and the theoretical prediction. A good agreement between the experimental data and the employed model is obvious and as such, the liquid-like suspension can be well described by an effective, polydisperse hard-sphere model within the Percus–Yevick theory. For comparison, the polydispersity-averaged total structure factor Stot(Q) and the structure factor of a corresponding monodisperse suspension with the same volume fraction are also shown. In the region around the main peak, SM(Q) and Stot(Q) behave very similarly, so for this particular model particle, the measurable structure factor provides a decent estimate of the ordering on length scales corresponding to the particle contact distance. The monodisperse structure factor overestimates the ordering as it neglects any polydispersity effects which generally diminish the peak height. Beyond the first maximum, Stot(Q) shows considerably stronger oscillations than SM(Q). The pronounced dampening of the oscillations in SM(Q) results mostly from the influence of the core–shell scattering amplitudes, the dampening resulting from the polydispersity on the other hand is much weaker, as is evident when comparing Stot(Q) to its monodisperse equivalent.
 |
| | Fig. 4 Measurable structure factor SM(Q), exemplarily for a sample with an effective volume fraction of φeff = 0.50 and a mean radius of R = 282 nm. The solid line is the SM(Q) corresponding to the model fit to the intensities in Fig. 1, the dashed line represents the total structure factor Stot(Q) with the same partial structure factors and the dash-dotted line describes a monodisperse structure factor with the same radius and volume fraction. | |
Dynamic light scattering experiments give access to the diffusional properties of the system. To analyse the short-time diffusion of the particles, the effective short-time diffusion coefficient Deff(Q) is obtained from the measurable intermediate scattering function SM(Q,t) using the cumulant method. In Fig. 5, Deff(Q), normalised to the apparent Stokes–Einstein diffusion coefficient  , is displayed together with the experimental structure factor from Fig. 4. In accordance to the de Gennes relation [eqn (10)], Deff(Q) and SM(Q) show an alternating progression: The collective diffusion is decelerated on length scales with stable configurations, precisely where the local maxima of the structure factor occur.
, is displayed together with the experimental structure factor from Fig. 4. In accordance to the de Gennes relation [eqn (10)], Deff(Q) and SM(Q) show an alternating progression: The collective diffusion is decelerated on length scales with stable configurations, precisely where the local maxima of the structure factor occur.
 |
| | Fig. 5 Comparison between the normalised effective diffusion coefficient  and the measurable structure factor SM(Q), for a suspension with effective volume fraction φeff = 0.50. The shaded area indicates the uncertainty of the experimental data. The dashed horizontal line is a guide to the eye for both SM(Q → ∞) = 1 and the location of the reduced self-diffusion coefficient and the measurable structure factor SM(Q), for a suspension with effective volume fraction φeff = 0.50. The shaded area indicates the uncertainty of the experimental data. The dashed horizontal line is a guide to the eye for both SM(Q → ∞) = 1 and the location of the reduced self-diffusion coefficient  . . | |
The inverse relation, however, is not exact for this particular system, as the diffusion of the particles is not only influenced by their local interaction potential but also by indirect, hydrodynamic interactions mediated by diffusion-induced flow patterns in the suspending medium. With both Deff(Q) and SM(Q) known from independent experiments, the measurable hydrodynamic function HM(Q) is accessible. An exemplary visualisation of the resulting hydrodynamic function of a concentrated suspension is displayed in Fig. 6. It is possible to fully resolve the oscillating HM(Q) up to the second maximum and as expected for a hard-sphere system, the hydrodynamic interactions slow down the dynamics on all investigated length scales. The theoretical description of hydrodynamics in strongly interacting colloidal suspensions is still a very challenging task. We avoid a real multicomponent treatment of the hydrodynamic interactions and prefer an effective one-component approach, which involves the δγ-scheme proposed by Beenakker and Mazur.50,51 We choose the size-averaged total structure factor Stot(Q) to serve as the structure factor of a hypothetical monodisperse system in hope that most of the polydispersity effects can be accounted for by the pre-averaging of this S(Q). This input is then used to calculate the distinct part of the hydrodynamic function Hd(Q) according to eqn (15). The self part Ds/D0 is determined by a least-squares fit to the experimental data. The resulting prediction for HM(Q) is displayed in Fig. 6 as the dotted line and already shows a remarkably good agreement with the experiment. The general shape and especially the location of the main peak Qm is reflected accurately, however, its amplitude is overestimated for this sample with φeff = 0.50 and, although much more subtly, there is a slight phase mismatch of the oscillation beyond the second maximum, which is more noticeable at lower effective volume fractions. As a further improvement, we decided to employ an empirical rescaling of the original δγ-H(Q). Similar rescaling procedures have previously been employed in conjunction with δγ-theory, for example for studying solvent-permeable particles like microgels.60,61 The rescaled hydrodynamic function in our approach reads as
| |  | (17) |
with
Q* =
α(
Q −
Qm) +
Qm. Besides the reduced self-diffusion coefficient
Ds/
D0 as an adjustable parameter, two additional parameters are introduced: The factor
A adjusts the height of the distinct part
Hd(
Q) and the factor
α scales the spatial frequency about
Qm so that the location of the principal peak remains constant. These two parameters are also determined with a least-squares fit to the experimental
HM(
Q), so in total, three adjustable parameters are fitted simultaneously in our approach. The resulting curve is displayed in
Fig. 6 as the solid line. The agreement of this rescaled δγ-approach with the experimental data is excellent up until the second maximum. For larger
Q, the deviation between experiment and theory is difficult to assess because of the high experimental uncertainty.
 |
| | Fig. 6 Measurable hydrodynamic function HM(Q) of a suspension with an effective hard-sphere volume fraction of φeff = 0.50. The shaded area indicates the uncertainty of the experimental data. The dashed line is the theoretical prediction according to the original δγ-theory while the solid line is the rescaled modification [eqn (17)]. | |
The volume-fraction dependence of the scaling parameters A and α of the rescaled δγ-approach is displayed in Fig. 7. Both scaling factors can be parameterised, within experimental uncertainty, as a linear function. The two factors show opposing trends: α, which scales H(Q) along the Q-axis, increases with higher volume fraction, whereas A, which scales the amplitude of H(Q), decreases with rising φeff, with a much steeper slope. There exists a crossover region around φeff ≈ 0.45 where both scaling factors are very similar and incidentally also close to unity. Thus, in this regime, the original δγ-theory in conjunction with a fitted self-diffusion coefficient is already accurate without any rescaling. For volume fractions smaller than that, the height of the principal peak is underestimated by the original theory, while for larger φeff the peak height is overestimated instead. This is in accordance to results of a comparison between δγ-theory and accelerated Stokesian dynamics simulations,54 where the same trends are observed.
 |
| | Fig. 7 The scaling parameters A and α from the rescaled δγ-scheme introduced in the text in dependence on the effective volume fraction φeff. The dashed lines are linear least-squares fits, their fit parameters are indicated in the legend. | |
Fig. 8 exemplarily shows selected extracted hydrodynamic functions together with the theoretical prediction from the introduced rescaled δγ-scheme. The theory describes the experimental data well for all investigated volume fractions within experimental accuracy, which supports the success of the employed rescaling approach. In the glassy state at φeff = 0.59, practically no Q-dependence of the hydrodynamic function except a small maximum coinciding with the maximum of S(Q) is observed. An estimate for the self part of H(Q) is indicated by a dashed line.
 |
| | Fig. 8 Selected measurable hydrodynamic functions HM(Q) for effective hard-sphere volume fractions in a range from 0.24 < φeff < 0.59, as indicated in the legend. The solid lines are results from the rescaled δγ-theory described in the text. The shaded areas indicate the uncertainty of the experimental data. The horizontal dashed line is an estimate for the self part of H(Q) for the glassy sample. | |
From the experimental structure factors and hydrodynamic functions, the principal peak values S(Qm), H(Qm) and Deff(Qm) can be extracted as characteristic properties, which, together with the reduced self-diffusion coefficient Ds/D0, can be readily compared to semi-empirical expressions from the literature:54,62
| |  | (18a) |
| | 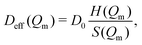 | (18c) |
| |  | (18d) |
The expressions are accurate at least up to the freezing transition of monodisperse hard spheres at
φ = 0.494. The comparison between these theoretical predictions and experimental values [
Fig. 9] therefore provides valuable insight into the influence of the particle polydispersity on these properties. As presumed,
S(
Qm) is overestimated by the expression for monodisperse spheres. It can instead be well described by the predictions of the multicomponent Percus–Yevick theory for hard spheres, as established previously. Altogether, all investigated properties follow closely the expected hard-sphere behavior. As a surprising observation, both
H(
Qm) and
Ds/
D0 are well described by the predictions for monodisperse systems over the whole volume fraction range. The hydrodynamic interactions in this investigated system are therefore practically undisturbed by the moderate polydispersity. The effective diffusion coefficient
Deff(
Qm) results from the combination of potential and hydrodynamic interactions. Looking at the two possible theoretical descriptions, depending on whether the monodisperse or the multicomponent expression for
S(
Qm) is used for the structural part, it is evident that the polydispersity only causes minimal deviations in the volume-fraction dependence of the diffusion coefficient. Variations in
H(
Qm) on the other hand would have a much more pronounced effect.
 |
| | Fig. 9 Experimentally obtained characteristic properties in dependence on the effective hard-sphere volume fraction φeff with theoretical predictions from eqn (18). Top left: Principle peak height of the structure factor S(Qm), together with the theoretical predictions for monodisperse (dashed lines) and polydisperse (dashed-dotted lines) hard spheres. Bottom left: Hydrodynamic function H(Qm) at the structure factor main peak, together with the monodisperse prediction (dashed lines). Top right: Reduced effective diffusion coefficient Deff(Qm)/D0, together with the monodisperse (dashed lines) and polydisperse (dashed-dotted lines) predictions, which are a combination of the theoretical curves from S(Qm) and H(Qm). Bottom right: Reduced self diffusion coefficient Ds/D0, together with the monodisperse prediction (dashed lines). | |
5 Conclusions
Colloidal PMMA particles grafted with PDMS-stabilisers are a promising alternative for established PMMA–PHSA particles. With the combination of MMA as monomer and PDMS which is commercially available with defined molecular weight and thus chain length, in a dispersion polymerisation reaction, particles with tunable size of PMMA-core and PDMS-shell are accessible in a reproducible way with acceptable polydispersity.
Self-organisation of these PMMA–PDMS particles leads to liquid-like ordered colloidal suspensions whose structural and dynamic properties are investigated employing static and dynamic light scattering. Start values for the topological parameters of the particles are determined via static light scattering experiments with highly-diluted suspensions with neglectable particle interactions and thus uncorrelated particles. The scattering function of single particles or form factor can be described employing a core–shell model with a gradient of scattering length density in the PMMA-core induced by swelling in the index-matched suspending medium. With the form factor, regarding the size-distribution of the ensemble, the scattered intensity resulting from liquid-like ordered systems can quantitatively be described in the whole range of volume fractions up to the glass transition employing a Percus–Yevick ansatz for polydisperse hard spheres. Hence, the structure of self-organised systems can quantitatively be described employing hard-sphere interactions.
Since dynamic properties are even more sensitive to particle interactions, we investigated collective diffusion by means of dynamic light scattering experiments. Hydrodynamic functions are determined from the intermediate scattering functions, structure factors and polydispersity-weighted Einstein diffusion coefficients. The determined hydrodynamic functions can in the whole range of volume fractions investigated accurately be modeled using a rescaled δγ-scheme based on hard-sphere interactions. Using a polydisperse Percus–Yevick ansatz, not only the principal peak of the hydrodynamic function, but also beyond its second maximum can for the first time quantitatively be described within experimental uncertainties. Also the amplitudes S(Qm) and H(Qm) of structure factor and hydrodynamic function as well as the reduced short-time self diffusion coefficient Ds/D0 are in excellent agreement to predictions for hard-sphere systems. Hence, in addition to the structure, also the dynamic properties can quantitatively be described using a hard-sphere model. In conclusion, the PMMA–PDMS system is not only a comparatively easy accessible, but also a highly suitable hard-sphere model system.
Small-angle X-ray and neutron scattering experiments with practically no limitation with respect to Qmax are promising experiments giving access to the shell structure with enlarged spatial resolution. Since optical index matching is not mandatory for these techniques, apolar suspending media leading to higher contrast can facilitate such experiments. Herewith, additional insights to the mechanism of sterical stabilisation and shrinking of the shell thickness at high volume fractions can be expected. Static and dynamic X-ray scattering experiments such as X-ray photon correlation spectroscopy (XPCS) would also enable the investigation of systems with comparable size of core diameter and shell thickness, where the validity of a simple hard-sphere description is still an open question.
Further investigations on dynamics of glassy systems and rheological properties of liquid-like structured and glassy systems are promising remaining tasks. A certain degree of polydispersity is needed to stabilise metastable glassy systems in order to prevent crystallisation. Since for these systems with still acceptable polydispersity, structural and dynamic properties can quantitatively be modeled by theoretical approaches regarding their size distribution, they are promising, comparatively easy accessible systems to systematically investigate structure-dynamics relations in colloidal glasses combining theory such as the mode coupling scheme and experiment. The availability of accurate experimental data can stimulate the development of theoretic approaches for glass dynamics and hydrodynamics rigorously taking polydispersity at high volume fractions into account which would also improve the prediction of macroscopic, rheological properties.
Author contributions
J. Diaz Maier: conceptualisation, data curation, formal analysis, investigation, methodology, software, validation, visualisation, writing – original draft. J. Wagner: conceptualisation, methodology, project administration, resources, supervision, validation, writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Notes and references
- J. G. Kirkwood and E. M. Boggs, J. Chem. Phys., 1942, 10, 394–402 CrossRef CAS.
- B. Widom, Science, 1967, 157, 375–382 CrossRef CAS PubMed.
- P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- P. N. Pusey and W. van Megen, Phys. Rev. Lett., 1987, 59, 2083–2086 CrossRef CAS PubMed.
- S.-E. Phan, W. B. Russel, Z. Cheng, J. Zhu, P. M. Chaikin, J. H. Dunsmuir and R. H. Ottewill, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6633–6645 CrossRef CAS PubMed.
- D. J. Cebula, J. W. Goodwin, R. H. Ottewill, G. Jenkin and J. Tabony, Colloid Polym. Sci., 1983, 261, 555–564 CrossRef CAS.
- A. Moussaïd and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5670–5676 CrossRef PubMed.
- A. van Blaaderen and P. Wiltzius, Science, 1995, 270, 1177–1179 CrossRef CAS.
- C. P. Royall, A. A. Louis and H. Tanaka, J. Chem. Phys., 2007, 127, 044507 CrossRef PubMed.
- S. Kale, A. Lederer, M. Oettel and H. J. Schöpe, Soft Matter, 2023, 19, 2146–2157 RSC.
- W. van Megen, S. M. Underwood, R. H. Ottewill, N. S. J. Williams and P. N. Pusey, Faraday Discuss. Chem. Soc., 1987, 83, 47–57 RSC.
- R. H. Ottewill and N. S. J. Williams, Nature, 1987, 325, 232–234 CrossRef CAS.
- X. Qiu, X. L. Wu, J. Z. Xue, D. J. Pine, D. A. Weitz and P. M. Chaikin, Phys. Rev. Lett., 1990, 65, 516–519 CrossRef CAS PubMed.
- P. N. Segrè, O. P. Behrend and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 5070–5083 CrossRef PubMed.
- Z. Cheng, P. M. Chaikin, J. Zhu, W. B. Russel and W. V. Meyer, Phys. Rev. Lett., 2001, 88, 015501 CrossRef PubMed.
- S.-E. Phan, W. B. Russel, J. Zhu and P. M. Chaikin, J. Chem. Phys., 1998, 108, 9789–9795 CrossRef CAS.
- W. van Megen and S. M. Underwood, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 248–261 CrossRef CAS PubMed.
- W. van Megen and S. M. Underwood, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 4206–4220 CrossRef CAS PubMed.
- W. van Megen, T. C. Mortensen, S. R. Williams and J. Müller, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6073–6085 CrossRef CAS.
- M. Leocmach and H. Tanaka, Nat. Commun., 2012, 3, 974 CrossRef PubMed.
- J. E. Hallett, F. Turci and C. P. Royall, Nat. Commun., 2018, 9, 3272 CrossRef PubMed.
- F. Lehmkühler, B. Hankiewicz, M. A. Schroer, L. Müller, B. Ruta, D. Sheyfer, M. Sprung, K. Tono, T. Katayama, M. Yabashi, T. Ishikawa, C. Gutt and G. Grübel, Sci. Adv., 2020, 6, eabc5916 CrossRef PubMed.
- C. P. Royall, J. Dzubiella, M. Schmidt and A. van Blaaderen, Phys. Rev. Lett., 2007, 98, 188304 CrossRef PubMed.
- P. Ballesta, R. Besseling, L. Isa, G. Petekidis and W. C. K. Poon, Phys. Rev. Lett., 2008, 101, 258301 CrossRef CAS PubMed.
- E. Di Cola, A. Moussaïd, M. Sztucki, T. Narayanan and E. Zaccarelli, J. Chem. Phys., 2009, 131, 144903 CrossRef CAS PubMed.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78 CrossRef CAS.
- M. T. Elsesser and A. D. Hollingsworth, Langmuir, 2010, 26, 17989–17996 CrossRef CAS PubMed.
- L. Palangetic, K. Feldman, R. Schaller, R. Kalt, W. R. Caseri and J. Vermant, Faraday Discuss., 2016, 191, 325–349 RSC.
- J. E. Hallett, I. Grillo and G. N. Smith, Langmuir, 2020, 36, 2071–2081 CrossRef CAS PubMed.
- S. M. Klein, V. N. Manoharan, D. J. Pine and F. F. Lange, Colloid Polym. Sci., 2003, 282, 7–13 CrossRef CAS.
- A. P. Richez, L. Farrand, M. Goulding, J. H. Wilson, S. Lawson, S. Biggs and O. J. Cayre, Langmuir, 2014, 30, 1220–1228 CrossRef CAS PubMed.
- H. Tsurusawa, J. Russo, M. Leocmach and H. Tanaka, Nat. Mater., 2017, 16, 1022–1028 CrossRef CAS PubMed.
- H. Tsurusawa, M. Leocmach, J. Russo and H. Tanaka, Sci. Adv., 2019, 5, eaav6090 CrossRef PubMed.
- H. Tsurusawa, S. Arai and H. Tanaka, Sci. Adv., 2020, 6, eabb8107 CrossRef CAS PubMed.
- M. Tateno, T. Yanagishima and H. Tanaka, J. Chem. Phys., 2022, 156, 084904 CrossRef CAS PubMed.
- H. Tsurusawa and H. Tanaka, Nat. Phys., 2023, 19, 1171–1177 Search PubMed.
- N. H. P. Orr, T. Yanagishima, E. Maire and R. P. A. Dullens, Phys. Rev. Mater., 2021, 5, 123605 Search PubMed.
- T. Lin, T. E. Kodger and D. A. Weitz, Soft Matter, 2013, 9, 5173–5177 RSC.
-
P. N. Pusey, in Liquids, Freezing and Glass Transition, ed. J. Z.-J. J. P. Hansen and D. Levesque, North-Holland, Amsterdam, 1991, pp. 765–942 Search PubMed.
- A. Vrij, J. Chem. Phys., 1978, 69, 1742–1747 CrossRef CAS.
- A. Vrij, J. Chem. Phys., 1979, 71, 3267–3270 CrossRef CAS.
- L. Blum and G. Stell, J. Chem. Phys., 1979, 71, 42–46 CrossRef CAS.
- L. Blum and G. Stell, J. Chem. Phys., 1980, 72, 2212 CrossRef.
- G. Schulz, Z. Phys. Chem., 1949, 46, 155–193 Search PubMed.
- J. Wagner, J. Appl. Crystallogr., 2012, 45, 513–516 CrossRef CAS.
- B. D'Aguanno and R. Klein, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 7652–7656 CrossRef PubMed.
- B. D'Aguanno, Phys. Scr., 1993, 1993, 84 CrossRef.
-
B. J. Berne and R. Pecora, Dynamic light scattering: with applications to chemistry, biology and physics, Dover Publications, 1976 Search PubMed.
-
J.-P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic Press, 2013 Search PubMed.
- C. W. J. Beenakker and P. Mazur, Phys. A, 1983, 120, 388–410 CrossRef.
- C. W. J. Beenakker and P. Mazur, Phys. A, 1984, 126, 349–370 CrossRef.
- U. Genz and R. Klein, Phys. A, 1991, 171, 26–42 CrossRef.
- J. Gapinski, A. Wilk, A. Patkowski, W. Häußler, A. J. Banchio, R. Pecora and G. Nägele, J. Chem. Phys., 2005, 123, 054708 CrossRef CAS PubMed.
- A. J. Banchio and G. Nägele, J. Chem. Phys., 2008, 128, 104903 CrossRef PubMed.
- M. Heinen, P. Holmqvist, A. J. Banchio and G. Nägele, J. Appl. Crystallogr., 2010, 43, 970–980 CrossRef CAS.
- W. B. Russel, P. M. Chaikin, J. Zhu, W. V. Meyer and R. Rogers, Langmuir, 1997, 13, 3871–3881 CrossRef CAS.
- L. Verlet and J.-J. Weis, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 939–952 CrossRef.
- E. W. Grundke and D. Henderson, Mol. Phys., 1972, 24, 269–281 CrossRef.
- K. B. Borisenko, B. Rozsondai and I. Hargittai, J. Mol. Struct., 1997, 406, 137–144 CrossRef CAS.
- G. C. Abade, B. Cichocki, M. L. Ekiel-Jeżewska, G. Nägele and E. Wajnryb, J. Chem. Phys., 2010, 132, 014503 CrossRef PubMed.
- J. Riest, T. Eckert, W. Richtering and G. Nägele, Soft Matter, 2015, 11, 2821–2843 RSC.
- M. Heinen, A. J. Banchio and G. Nägele, J. Chem. Phys., 2011, 135, 154504 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Joachim
Wagner
and
Joachim
Wagner
 *
*

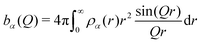

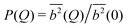 and the measurable structure factor,
and the measurable structure factor,

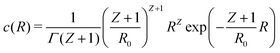
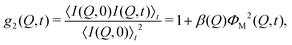


 denotes the mean Stokes–Einstein diffusion coefficient, which can be expressed as a weighted average of the diffusion coefficients of the single species,
denotes the mean Stokes–Einstein diffusion coefficient, which can be expressed as a weighted average of the diffusion coefficients of the single species,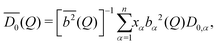
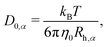

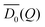 and SM(Q) are known from static and dynamic scattering experiments. HM(Q) is related to the partial hydrodynamic functions Hαβ(Q) whose calculation however, remains a computationally challenging task. For monodisperse systems, the hydrodynamic function H(Q) can be calculated with the semi-analytical δγ-scheme proposed by Beenakker and Mazur,50,51 which gives a satisfactory approximation for the wavevector-dependent short-time diffusion of hard spheres, but can in principle be employed for any interaction potential, as the scheme only depends on the structure factor of the system as an external input.52H(Q) can be decomposed into the sum of a wavevector-independent self part and a wavevector-dependent distinct part according to
and SM(Q) are known from static and dynamic scattering experiments. HM(Q) is related to the partial hydrodynamic functions Hαβ(Q) whose calculation however, remains a computationally challenging task. For monodisperse systems, the hydrodynamic function H(Q) can be calculated with the semi-analytical δγ-scheme proposed by Beenakker and Mazur,50,51 which gives a satisfactory approximation for the wavevector-dependent short-time diffusion of hard spheres, but can in principle be employed for any interaction potential, as the scheme only depends on the structure factor of the system as an external input.52H(Q) can be decomposed into the sum of a wavevector-independent self part and a wavevector-dependent distinct part according to

![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ·
·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ′ is the cosine of the angle enclosed by the unit vectors
′ is the cosine of the angle enclosed by the unit vectors ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and
and ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ′. The calculation of the function Sγ0(x) is described ref. 52. Although the self part of H(Q) can in principle also be calculated employing the δγ-scheme, the method can be significantly improved if instead more accurate, semi-empirical expressions for Ds are used or if Ds is directly fitted to experimental data or simulation results.53,54 It has been shown that the combination of the δγ-approach with a more elaborate description of Ds produces hydrodynamic functions in satisfactory agreement with computer simulations.55
′. The calculation of the function Sγ0(x) is described ref. 52. Although the self part of H(Q) can in principle also be calculated employing the δγ-scheme, the method can be significantly improved if instead more accurate, semi-empirical expressions for Ds are used or if Ds is directly fitted to experimental data or simulation results.53,54 It has been shown that the combination of the δγ-approach with a more elaborate description of Ds produces hydrodynamic functions in satisfactory agreement with computer simulations.55
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) from ABCR and decahydronaphthalene (decalin, cis/trans-mixture) from Carl Roth. Tetralin and decalin were thoroughly filtered through 0.2 μm syringe filters to remove dust particles, other than that, all chemicals were used as received.
000 g mol−1) from ABCR and decahydronaphthalene (decalin, cis/trans-mixture) from Carl Roth. Tetralin and decalin were thoroughly filtered through 0.2 μm syringe filters to remove dust particles, other than that, all chemicals were used as received.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 corresponds to a maximum possible length of 46 nm. The shell thickness estimated from the model fits is therefore realistic.
000 g mol−1 corresponds to a maximum possible length of 46 nm. The shell thickness estimated from the model fits is therefore realistic.

 , is displayed together with the experimental structure factor from Fig. 4. In accordance to the de Gennes relation [eqn (10)], Deff(Q) and SM(Q) show an alternating progression: The collective diffusion is decelerated on length scales with stable configurations, precisely where the local maxima of the structure factor occur.
, is displayed together with the experimental structure factor from Fig. 4. In accordance to the de Gennes relation [eqn (10)], Deff(Q) and SM(Q) show an alternating progression: The collective diffusion is decelerated on length scales with stable configurations, precisely where the local maxima of the structure factor occur.