Modulating photothermocapillary interactions for logic operations at the air–water interface

Abstract

We demonstrate a system for performing logical operations (OR, AND, and NOT gates) at the air–water interface based on Marangoni optical trapping and repulsion between photothermal particles. We identify a critical separation distance at which the trapped particle assemblies become unstable, providing insight into the potential for scaling to larger arrays of logic elements.

---

A powerful mechanism for manipulating microscale objects at the interface between two media is provided by the Marangoni effect – i.e., convective flows arising from gradients in surface tension.^1–7 Mechanisms of generating surface tension gradients generally involve either the inhomogeneous distribution of surface-active species or the localized generation of heat. The former method has been employed to realize active droplets^8,9 and Marangoni boats^10,11 that release oil or solvent molecules to generate a local surface tension gradient and solutocapillary flow, thereby driving autonomous motion. The latter mechanism is especially promising because photothermal effects can be used to transform light into heat, thereby providing opportunities for high resolution spatiotemporal control over Marangoni forces. Light-driven thermocapillary actuation has been used to demonstrate high-speed colloidal surfers,^4,12,13 self-assembled robots,² and cell manipulators.¹⁴ Interaction and cooperation between multiple swimmers at the interface have also been examined to realize collective motion and synchronization.^15–23 Despite the promise of this area, efforts to exploit thermocapillary actuation of multiple microscale objects to conduct desired tasks remain in their early stages.

A rising area of interest in soft matter systems is the design of unconventional mechanisms for performing logical computations that can be directly embedded in material systems, thereby eliminating the need for connected electrical control systems. Basic logic gates have been engineered using a variety of systems including micro-mechanical elements,^24–26 metamaterials,^27–29 origami designs,³⁰ molecules,^31,32 DNA,^33,34 enzymes,³⁵ thermal elements,^36,37 topological defects in liquid crystals,^38,39 and microfluidic devices.^40–42 Despite these advances, progress toward systems capable of performing more complex computations remains limited, and hence the development of new modalities for computation is of interest. Although the ability to rapidly and simultaneously address many strongly-interacting objects via thermocapillary forces presents an intriguing platform for realizing complex logic operations in a material, to our knowledge this direction has been largely unexplored.

In this communication, we demonstrate that thermocapillary forces can be harnessed to design interactions between collections of particles in Marangoni optical traps and thereby realize basic logic elements. The spatiotemporal control of light intensity allows us to engineer Marangoni forces on photothermal particles via two modes: particle trapping and interparticle repulsion. Particle trapping is achieved by generating a dark pattern surrounded by an illuminated region, providing a greater surface tension in the cooler unilluminated regions. Interparticle repulsion is generated due to the temperature gradient around each particle, and the corresponding surface tension gradient across a neighbouring particle. We design a bistable trap defined by a dark pattern and place an output particle in the trap. Then we use the repulsive force from an input particle that determines the position of the output particle in the bistable trap. By tuning the geometry of the trap and the position of the input particle, we demonstrate basic logic elements – AND, OR, and NOT gates. We also investigate the possibility of scaling such a system to larger 2D arrays of trapped particles. Because of the long-ranged nature of the Marangoni repulsion between particles, we find that the repulsive ‘potential’ per particle increases with the system size in a 2D arrangement of trapped particles. We identify a critical neighbouring distance at which a particle assembly becomes unstable causing the particles to escape their traps.

The microparticles used in our experiment are photo-responsive hydrogel nanocomposite disks (HNDs) that generate thermocapillary flows at the air–water interface under visible light irradiation. The HNDs are fabricated using two-step photolithographic patterning of a polymer film - poly(diethylacrylamide-co-N-(4-benzoylphenyl)acrylamide-co-acrylic acid) containing gold (Au) salt precursors. First, the polymer film (thickness ≈ 6 μm) is crosslinked and then the gold salt is photochemically reduced to form gold nanoparticles (Au NP) inside the crosslinked film.^16,43 After development and release, the fabricated microscale HNDs (diameter d = 2a = 375 μm) are placed at a planar air–water interface (see Section S1 and S2 of the ESI† for detailed experiment methods and ref. 43 for nanoparticle-polymer characterization data). When irradiated with a white light source, the HNDs generate heat due to the surface plasmon resonance of the gold nanoparticles, introducing a gradient in temperature, and therefore surface tension, around them. If a small dark region is placed within an illuminated region, the dark region acts as Marangoni optical trap because a portion of the HND in the dark will experience higher surface tension, therefore tending to hold it in the trap. The mechanism of this Marangoni optical trap and its influence on a particle is shown in Fig. 1a, and demonstration of trapping a particle is presented in Fig. 1b, and Movie S1 (ESI†). The Marangoni force that operates to restore an off-centre particle can be expressed as F_trap ≈ γ_TaΔT, where a is the disk radius, γ_T is the variation in surface tension with temperature (0.14 mN m⁻¹ K⁻¹ for an air/water interface near room temperature), and ΔT is the temperature difference between the leading and the trailing edge of the disk.^44,45 We design the trap size to be close to the particle diameter (w = 0.6d − d) and keep the light intensity in the range of 0.6–1.3 W cm⁻². In prior work we have studied how smaller traps (w < 0.5d) and higher light intensities (>2.0 W cm⁻²) lead to oscillation of particles within the trap;¹⁶ while here we seek to hold the particles static.

Fig. 1 (a) Schematic illustration of a trap showing that a disk-shaped particle (dark red color) experiences an attractive force towards the dark (gray color) circular region due to the Marangoni force. The orange/yellow colored region around the particle illustrates the temperature increase around it. (b) Experiment showing an HND remains trapped inside the illuminated region when the stage moves to the right (shown by the displacement of the tracer particle at the top in the dark region of the screen). A small circular dark region with a width of w = 0.7d located concentrically inside the illuminated region performs the function of the trap. (c) Schematic illustration of the repulsive interaction between two HNDs. (d) Experiment result showing two particles moving away in opposite directions as the repulsive interaction is turned on with light irradiation.

When two HNDs are placed in proximity in an illuminated region, the surface tension gradient around each particle gives rise to a repulsive force on the neighbouring particle (Fig. S2 and S3, ESI†). Assuming purely diffusive heat transfer, the temperature profile around each particle at the interface can be expressed as , where Q is the total heat generation by the particle (Q ∝ I, I: light intensity), k is the thermal conductivity of water (0.6 W m⁻¹ K⁻¹), and r is the distance from the particle centre.^12,45,46 From the expression of Marangoni force F ≈ γ_TaΔT, we can estimate the repulsive Marangoni force on a particle exerted by its neighbour: , where we have neglected a geometric prefactor of order 1. Fig. 1c schematically depicts the mechanism of this repulsive interaction between two HNDs in a fully illuminated region. Demonstration of the repulsive interaction is presented in Fig. 1d and Movie S2 (ESI†), where two closely located particles move away from each other upon light illumination. We find that even particles initially separated by a distance of 3d show a measurable repulsion upon illumination (Fig. S4, ESI†), consistent with the long-ranged nature of the interaction. We modelled particle displacement over time using the abovementioned expression of Marangoni repulsive force and found good agreement with experimental observations over relevant separation distances (Fig. S5, ESI†). Using a far-field approximation (r ≫ a), we can express this interaction in terms of a pseudo-potential energy . In making this estimate of U(r), we ignored capillary attraction because the displacements of two adjacent particles in the absence of light illumination have found to be negligible at experimentally relevant timescales (1–2 s).

The motion of the HNDs can be programmed if the Marangoni trapping and repulsive interactions are combined together. The Marangoni trap is designed with an “H” shape using patterned illumination to ensure stable trapping conditions at either of the vertically-oriented sides. Because the height h of these sides is larger than the height of the rectangle that connects them (h ≥ 117 μm, as shown in Fig. 2b), the area of the dark region as well as the trapping potential energy must be lower at the sides. This design allows for the trap to function as a bistable element (Fig. 2a). If a neighbouring particle is moved close enough to a particle placed on one side of the bistable trap, the additional energy due to thermocapillary repulsion will cause the particle to become unstable in the original position and switch its position to the other side of the bistable trap.

Fig. 2 (a) Schematic illustration showing that the output particle moves its position from one trap to the other due to repulsion from the input particle. (b) The geometry of an “H”-shaped bistable trap. (c) For h = 184 μm, the output particle moves from “0” to “1”, as the input particle A moves from “0” to “1”. (d) For h = 250 μm, the output particle stays at “0”, as the input particle A moves from “0” to “1”. (e) Operation of gates with six different trap heights is demonstrated by the output particle displacement over time during approach of one input. All scale bars are 300 μm.

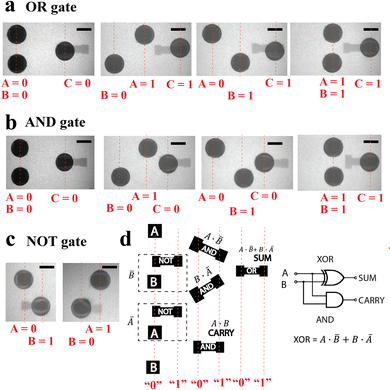
To design basic logic gates such as OR and AND, we need to understand the interplay between trapping and repulsive potential that a trapped ‘output’ particle experiences as a function of the bistable trap geometry and the location of two ‘input’ particles. If the approach of only one input particle is sufficient to shift the position of the output particle, then the bistable will serve as an OR gate. If the particle requires two neighbouring particles for the repulsive potential to exceed the trapping potential, the bistable trap will function as an AND gate. To establish suitable designs, we first set initial conditions where two input particles (‘A’ and ‘B’) are placed at positions ‘0’ in separate Marangoni traps, and one output particle (output ‘C’) is placed at the left side (position ‘0’) of the “H”-shaped trap at time t = 0 s (Fig. 2c and d). One of the input particles (input ‘A’) is then guided toward the output particle ‘C’ at ‘0’ by shifting the trap position at a speed of 160 μm s⁻¹, which is sufficiently slow for the input particle to follow the trap location (Movie S3 and S4, ESI†). As shown in Fig. 2e, the value of h determines whether the gate functions as an OR gate or not. For all values of h ≤ 184 μm, setting particle A to 1 causes particle C to shift from 0 to 1, while for all values of h ≥ 209 μm, C remains at 0. The total time required to move the input particle and have the output particle reach its final state is approximately 1 s.

Based on the design parameters established in Fig. 2, we next use bistable traps to demonstrate operation of three fundamental logic gates: AND, OR, and NOT. We first choose h = 184 μm, which based on the above is expected to serve as an OR gate. Indeed, as shown in Fig. 3a, when either or both input particles are set to 1, the output particle successfully reached 1. Notably, the additional repulsive force from the second particle is not sufficient to destabilize the particle in the second trap state (Movie S3, ESI†). To design an AND gate, we choose a larger trap height of h = 250 μm. Again, as expect from Fig. 2, when only one of the input particles is set to 1, the output remains at 0. Now, however, when both particles are set to 1, the output particle is forced to 1 (Fig. 3b and Movie S4, ESI†). We find successful signal operation up to h = 300 μm for the input (1,1). However, if both h and the width of the trap (previously fixed at 117 μm) are increased, a (1,1) input is no longer sufficient to push the output particle to 1 (Fig. S6, ESI†), causing the AND gate to fail. Finally, we designed a NOT gate using a value of h = 130 μm, however, we placed the gate directly above the input signal such that the distance between the input and output particles is longer when one of the particles is at 1 and the other is at 0 compared to the case when the particles are both at 0, or both at 1 (Fig. 3c and Movie S5, ESI†). This arrangement of a NOT gate still allows for the cascading of multiple different gates in a logic architecture, as shown by the proposed design of a half adder circuit in Fig. 3d. A half-adder circuit can add two input bits and produces two outputs– a sum and a carry. In contrast to the prior demonstrations of half-adder circuits based on molecular systems,^47–49 our proposed half-adder circuit will require ten particles in total – six of them must be placed at logic gates (two NOT, three AND, and one OR gate) and four of them must be used as inputs, since we do not currently have a route to split one input into multiple signals. In any case, engineering complex logic architecture in this manner will require scaling up the number of particles positioned in a given region of the interface.

Fig. 3 (a) For an OR gate, the output particle C reaches 1 when either or both of the input particles, A and B are 1. (b) For an AND gate, the output particle C reaches 1 only when both of the input particles, A and B are 1. (c) For a NOT gate, the output particle B reaches 1 when the input A is 0 and B remains at 0 when A is 1. (d) Design of a half-adder circuit that adds inputs A and B to produce two outputs—sum of A and B (A XOR B) and carry (A AND B). The XOR gate can be designed as a combinatino of AND, OR, and NOT gates. All scale bars are 300 μm.

To better understand the possibilities for extending to more complex logic operations, we must consider the stability of large two-dimensional arrays of trapped particles. In particular, due to the long-ranged repulsive interactions which scale the same way as the Coulomb potential between two charges, the repulsive energy of the system scales superextensively, i.e., the energy per particle increases with the system size. For a fixed trapping energy, the increase in repulsive energy will cause the particles to escape from their traps at a critical density.

To demonstrate this fundamental limitation, we place N particles (N = 2, 3, 4, 5, or 6) at the equidistant points of a ring with radius R, and then gradually reduce R by projecting different light patterns in a sequential manner (Movie S6, ESI†). This experiment allows the particles to approach each other while keeping all interparticle separation distances uniform. We find that for each N, there exists a critical separation (centre-to-centre distance between traps) between nearest neighbours D_c, at which at least one particle becomes unstable and escapes its trap, as shown in Fig. 4a and b. We also find that D_c increases with the system size N, indicating that the additional repulsive energy from the neighbouring particles combining with the long-range nature of the repulsive potential can cause the trap arrangement to become unstable even at longer interparticle separation distances (D_c ≅ 400 μm for N = 6). The particle trap diameter in this experiment was chosen to be w = 0.68d and the light intensity was 0.72 W cm⁻².

Fig. 4 Stability of 2D particle arrangement in Marangoni optical traps. (a) N = 3 particle arrangement becomes unstable when interparticle separation distance becomes smaller than D_c. (b) N = 6 particle arrangement becomes unstable when interparticle separation distance becomes smaller than D_c. D_c for N = 6 is longer than D_c for N = 3. (c) Repulsive potential energy of a particle in the ring arrangement for N = 2,3,4,5,6 for different interparticle separation distances. (d) Experiment results and model show that the critical separation distance increases with N. All scale bars are 300 μm.

To provide a deeper understanding of the superextensive energy increase with the system size, we estimate the repulsive potential energy per particle for the ring arrangement as , where r_i is the distance between the particle of interest and the ith particle on the ring. From the numerically calculated repulsive potential plotted as a function of the distance between the nearest neighbours D, in Fig. 4c, we see that the potential energy per particle grows with increasing N at a constant nearest neighbour distance D. We next posit that when this energy equals the (constant) value of the pseudo-potential energy holding each particle in its trap, U_trap, at least one particle will escape, i.e., corresponding to the experimental measurement of D_c. Thus, using U_trap as a fitting parameter in our model, we compare measured and predicted values of D_c as a function of N in Fig. 4d, and find good agreement between the two. The best-fit value of U_trap = 1.8 × 10⁻¹² J is represented by a dashed horizontal line in Fig. 4c, while the measured values of D_c for each N are represented as circles along this line. The fact that each point lies very close to the corresponding solid curve of inter-particle repulsive potential provides another way of visualizing the good agreement between the measurements and this simple model.

In summary, we have exploited thermocapillary actuation to program precise motion of interfacially-adsorbed particles via spatiotemporal control of light intensity. Dark regions inside an illuminated area near a particle serve as Marangoni optical traps, while the bright regions lead to interparticle repulsive interaction. The interplay between trapping and repulsion allowed us to demonstrate AND, OR, and NOT logic gates at the air–water interface for the first time. Additionally, we found a critical stability condition that indicates that the nearest-neighbour distance between the traps must be kept longer than a critical value that increases with system size. This has important implications for designing complex logic architectures that require many particles, as well as other devices based on thermocapillary interactions. The effect of long-ranged repulsive interactions can be likely be at least partially mitigated in future work if the devices are arranged in geometries that are extended in one dimension and compact in the other to weaken the superextensive energy growth, or if mechanisms are exploited to screen the long-range interparticle interactions while preserving short-range repulsion. Future experiments on scaling up the number of logic gates will also require careful consideration of relevant experimental parameters, i.e., trap dimensions, light intensity, and particle size. This platform of thermocapillary logic gates may find intriguing applications in providing computation capabilities to the transport of drugs, cells, and other biomaterials.

This work was supported by the Army Research Office through grants W911NF-21-1-0068 and W911NF-19-1-0348. K. K. was supported by the Interdisciplinary Quantitative Biology (IQ Biology) PhD program at the BioFrontiers Institute, University of Colorado Boulder, and the National Science Foundation NRT Integrated Data Science Fellowship (award 2022138). The authors thank Hyunki Kim, Christian Santangelo and Ji-Hwan Kang for helpful discussions.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. L. E. Scriven and C. V. Sternling, Nature, 1960, 187, 186.
2. F. N. Piñan Basualdo, A. Bolopion, M. Gauthier and P. Lambert, Sci. Robot., 2021, 6, eabd3557.
3. L. Zhang, Y. Yuan, X. Qiu, T. Zhang, Q. Chen and X. Huang, Langmuir, 2017, 33, 12609.
4. K. Dietrich, N. Jaensson, I. Buttinoni, G. Volpe and L. Isa, Phys. Rev. Lett., 2020, 125, 098001.
5. Y. Choi, C. Park, A. C. Lee, J. Bae, H. Kim, H. Choi, S. W. Song, Y. Jeong, J. Choi, H. Lee, S. Kwon and W. Park, Nat. Commun., 2021, 12, 4724.
6. R. T. Mallea, A. Bolopion, J.-C. Beugnot, P. Lambert and M. Gauthier, IEEE/ASME Trans. Mechatron., 2018, 23, 1543.
7. A. S. Basu and Y. B. Gianchandani, J. Microelectromech. Syst., 2009, 18, 1163.
8. C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171.
9. B. V. Hokmabad, R. Dey, M. Jalaal, D. Mohanty, M. Almukambetova, K. A. Baldwin, D. Lohse and C. C. Maass, Phys. Rev. X, 2021, 11, 011043.
10. H. Ender, A.-K. Froin, H. Rehage and J. Kierfeld, Eur. Phys. J. E, 2021, 44, 21.
11. D. Boniface, C. Cottin-Bizonne, R. Kervil, C. Ybert and F. Detcheverry, Phys. Rev. E, 2019, 99, 062605.
12. A. Girot, N. Danné, A. Würger, T. Bickel, F. Ren, J. C. Loudet and B. Pouligny, Langmuir, 2016, 32, 2687.
13. G. Koleski, A. Vilquin, J.-C. Loudet, T. Bickel and B. Pouligny, Phys. Fluids, 2020, 32, 092108.
14. W. Hu, Q. Fan and A. T. Ohta, Lab Chip, 2013, 13, 2285.
15. M. A. Rahman, J. Cheng, Z. Wang and A. T. Ohta, Sci. Rep., 2017, 7, 3278.
16. H. Kim, S. Sundaram, J.-H. Kang, N. Tanjeem, T. Emrick and R. C. Hayward, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024581118.
17. K. Lippera, M. Benzaquen and S. Michelin, Phys. Rev. Fluids, 2020, 5, 032201.
18. M. Bourgoin, R. Kervil, C. Cottin-Bizonne, F. Raynal, R. Volk and C. Ybert, Phys. Rev. X, 2020, 10, 021065.
19. Y. Hirose, Y. Yasugahira, M. Okamoto, Y. Koyano, H. Kitahata, M. Nagayama and Y. Sumino, J. Phys. Soc. Jpn., 2020, 89, 074004.
20. K. Lippera, M. Morozov, M. Benzaquen and S. Michelin, J. Fluid Mech., 2020, 886,  DOI:10.1017/jfm.2019.1055.
21. C. H. Meredith, P. G. Moerman, J. Groenewold, Y.-J. Chiu, W. K. Kegel, A. van Blaaderen and L. D. Zarzar, Nat. Chem., 2020, 12, 1136.
22. C. M. Wentworth, A. C. Castonguay, P. G. Moerman, C. H. Meredith, R. V. Balaj, S. I. Cheon and L. D. Zarzar, Angew. Chem., Int. Ed., 2022, 61, e202204510.
23. S. Soh, K. J. M. Bishop and B. A. Grzybowski, J. Phys. Chem. B, 2008, 112, 10848.
24. Y. Song, R. M. Panas, S. Chizari, L. A. Shaw, J. A. Jackson, J. B. Hopkins and A. J. Pascall, Nat. Commun., 2019, 10, 882.
25. Y. Jiang, L. M. Korpas and J. R. Raney, Nat. Commun., 2019, 10, 128.
26. J. R. Raney, N. Nadkarni, C. Daraio, D. M. Kochmann, J. A. Lewis and K. Bertoldi, PNAS, 2016, 113, 9722.
27. U. Waheed, C. W. Myant and S. N. Dobson, Extreme Mech. Lett., 2020, 40, 100865.
28. T. Mei, Z. Meng, K. Zhao and C. Q. Chen, Nat. Commun., 2021, 12, 7234.
29. C. El Helou, P. R. Buskohl, C. E. Tabor and R. L. Harne, Nat. Commun., 2021, 12, 1633.
30. B. Treml, A. Gillman, P. Buskohl and R. Vaia, PNAS, 2018, 115, 6916.
31. A. P. de Silva and S. Uchiyama, Nat. Nanotechnol., 2007, 2, 399.
32. C.-Y. Yao, H.-Y. Lin, H. S. N. Crory and A. P. de Silva, Mol. Syst. Des. Eng., 2020, 5, 1325.
33. A. Okamoto, K. Tanaka and I. Saito, J. Am. Chem. Soc., 2004, 126, 9458.
34. J. Chen, S. Fu, C. Zhang, H. Liu and X. Su, Small, 2022, 18, 2108008.
35. E. Katz, Chem. Phys. Chem., 2017, 18, 1688.
36. A. Hamed and S. Ndao, Sci. Rep., 2020, 10, 2437.
37. C. Kathmann, M. Reina, R. Messina, P. Ben-Abdallah and S.-A. Biehs, Sci. Rep., 2020, 10, 3596.
38. Ž. Kos and J. Dunkel, Sci. Adv., 2022, 8, eabp8371.
39. R. Zhang, A. Mozaffari and J. J. de Pablo, Sci. Adv., 2022, 8, eabg9060.
40. E. Asghari, A. Moosavi and S. K. Hannani, Sci. Rep., 2020, 10, 9293.
41. N. El-Atab, J. C. Canas and M. M. Hussain, Adv. Sci., 2020, 7, 1903027.
42. G. Katsikis, J. S. Cybulski and M. Prakash, Nat. Phys., 2015, 11, 588.
43. H. Kim, J.-H. Kang, Y. Zhou, A. S. Kuenstler, Y. Kim, C. Chen, T. Emrick and R. C. Hayward, Adv. Mater., 2019, 31, 1900932.
44. A. W. Hauser, S. Sundaram and R. C. Hayward, Phys. Rev. Lett., 2018, 121, 158001.
45. A. Würger, J. Fluid Mech., 2014, 752, 589.
46. G. Baffou, R. Quidant and C. Girard, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165424.
47. A. Prasanna de Silva and N. D. McClenaghan, J. Am. Chem. Soc., 2000, 122, 3965.
48. D. Margulies, G. Melman and A. Shanzer, J. Am. Chem. Soc., 2006, 128, 4865.
49. D. C. Magri and A. A. Camilleri, Chem. Commun., 2023, 59, 4459.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01487h

---