 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synergistic effects between a non-ionic and an anionic surfactant on the micellization process and the adsorption at liquid/air surfaces†
Kristo
Kotsi
 a,
Teng
Dong
a,
Takeshi
Kobayashi
a,
Teng
Dong
a,
Takeshi
Kobayashi
 b,
Ian
Mc Robbie
c,
Alberto
Striolo
b,
Ian
Mc Robbie
c,
Alberto
Striolo
 bd and
Panagiota
Angeli
bd and
Panagiota
Angeli
 *a
*a
aThAMeS Multiphase, Department of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK. E-mail: p.angeli@ucl.ac.uk
bDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK
cInnospec Ltd, Oil Sites Road, Ellesmere Port, Cheshire, CH65 4EY, UK
dSchool of Sustainable Chemical, Biological and Materials Engineering, Sarkeys Energy Center, The University of Oklahoma, Norman, OK 73019, USA
First published on 20th December 2023
Abstract
Predicting the behaviour of solutions with surfactants of significantly different critical micelle concentration (CMC) values remains a challenge. The study of the molecular interactions within micelles and interfaces in surfactant combinations used in everyday products is essential to understand these complex systems. In this work, the equilibrium and dynamic surface tension in the presence of mixed non-ionic (tristyrylphenol ethoxylates) and anionic (sodium benzene sulfonate with alkyl chain lengths of C10–C13) surfactants, commonly encountered as delivery systems in agrochemicals, were studied and their CMC values were determined. For the surfactant mixtures, four molar ratios were examined: nEOT/nNaDDBS = 0.01, 0.1, 1, 4 and two different cases were analysed, the premixed and the add one by one surfactant. The surface tension for single surfactants stabilised quickly, while the mixtures needed a long time to reach equilibrium; up to 15 h for the premixed mixtures and 40 min when surfactants were added one by one. The CMC values for the nEOT/nNaDDBS = 0.01, 0.1 premixed surfactant mixtures were found to be in between the CMC values of the single surfactants, but those for the nEOT/nNaDDBS = 1 and 4 mixtures were lower than the CMCs of both single surfactants. Calculations based on the regular solution theory suggested that there are attractive forces in the mixed micelles and at the interface layers, while the supramolecular assemblies in the bulk (i.e., micelles) and at interfaces (surfactant films) are preferentially enriched in EOT.
Introduction
Surfactants are widely used in products such as detergents, paints, agrochemicals, cosmetics, personal care, pharmaceuticals, and in processes including enhanced oil recovery,1–3 flocculation, controlled drug delivery, corrosion inhibition, emulsification, and nanolithography. Very often, surfactant mixtures are preferred to single surfactants4,5 because of their synergistic properties.3,6–8 Cost is also a major factor in designing surfactant mixtures. The synergism, at mixed monolayers or in mixed micelles, which arises from interactions between differently charged surfactant headgroups (non-ionic/ionic or cationic/anionic), affects adsorbance to interfaces, surface tension, as well as the formation of micelles in the bulk.9–11Ideally mixed micelles, where the free energy of mixing results only from the entropy change during the mixing of the surfactants,12 are expected to form in solutions of surfactants of homologous series, i.e., surfactant molecules with similar chemical properties, or surfactants with similar headgroups.12,13 However, non-ionic/ionic,14 anionic/cationic,15 and zwitterionic/ionic16 surfactant mixtures, form mixed micelles that deviate from ideality because of the attractive/repulsive forces among the dissimilar surfactant headgroups.17
In mixed systems, the composition of the solution affects the micellization process,18 the counter-ion binding in micelles,19 and likely other properties as well. When non-ionic surfactant molecules are added to ionic micellar systems, they enter the pure micelles of the ionic surfactants, where the non-ionic hydrophilic headgroups separate the charged ionic hydrophilic ones (also known as the charge separation effect).20 This reduces the electrical repulsions among the ions in the Stern layer, next to the micellar interface. This decrease in charge density facilitates the formation of mixed micelles, as less work is needed for ionic monomers to enter into them than in pure ionic micelles.17
The critical micelle concentration (CMC) of surfactant mixtures depends on the CMC of each of the single surfactants,21 as well as on the interactions among the surfactants. For surfactants with similar CMC values and no interactions among the surfactant molecules, the CMC of their mixtures is the same for all surfactant concentration ratios. When the CMC values of the individual surfactants differ, the CMC of the mixture may fall between them. In this case, the mixture CMC is affected by the CMC of the most surface-active substance,13 which is also preferably adsorbed at the water/air interface and reduces surface tension at low bulk concentrations.22
Kesarwani et al.,23 carried out experiments involving a non-ionic and an anionic surfactant with CMC values differing by two orders of magnitude. They determined the CMC of binary surfactant mixtures by adding certain amounts of the non-ionic surfactant to the prepared anionic surfactant solutions. They concluded that the CMC of the mixtures fell in-between those of the single surfactants. Moreover, Mahajan & Nandni24 investigated the micellization process of a binary system of different non-ionic and anionic surfactants with comparable CMCs by measuring the surface tension of surfactant mixtures with different mole ratios and used regular solution theory (RST) to explain the data. They reported that the addition of a non-ionic surfactant in anionic micellar solutions led to the formation of mixed micelles by reducing the electrostatic interactions among the charged anionic headgroups. They also found that the micellar shape was affected by the ratio of the non-ionic/anionic surfactants in the system. Other studies focused on non-ionic/cationic surfactant mixtures and calculated the surface parameters derived from RST in the premicellar region,25 or optimised the anionic/cationic mole ratios to achieve low surface tension values while avoiding precipitation.1
All the above studies on surfactant mixtures only focus on the equilibrium surface tension values and not on the dynamic ones, which can be of great importance for industrial processes,26 and can help us better understand the interactions between surfactant molecules. In this work, we study both the equilibrium and dynamic surface tension of binary ionic/non-ionic surfactant mixtures. The surfactants used are relevant to the agrochemical sector. Their CMC values differ by two orders of magnitude, meaning that the surfactant with lower CMC is preferentially adsorbed at the interface. This makes the prediction of the CMC values of their mixtures difficult and affects the time needed for the surface tension to reach equilibrium when mixed surfactant systems are present in solution. To elucidate dynamic phenomena, the dynamic surface tension is studied here implementing two complementary approaches, one in which the surfactants are premixed and then added to the system to be investigated, and the other in which one surfactant is added first, and then the other is, sequentially. The regular solution theory is implemented to explain the experimental results for the premixed surfactants case, as in the add one by one process long-lived metastable states might prevent reaching equilibrated systems. The results are used to explore how mixing surfactants can affect the dynamic surface tension, the equilibrium surface tension, as well the CMCs of the newly formed surfactant systems.
Experimental section
Materials
Tristyrylphenol ethoxylates (EOT) (Innospec UK, MW = 1122 g mol−1) and sodium benzene sulfonate with alkyl chain lengths between C10–C13 (NaDDBS), (Innospec UK, MW = 348 g mol−1) were used as non-ionic and anionic surfactants, respectively. The non-ionic surfactant product is composed of 98% wt/wt tristyrylphenol ethoxylates, with their molecules mostly incorporating sixteen ethoxylate groups. The anionic surfactant product consists of 25% wt/wt sodium benzene sulfonates with C10–C13 alkyl derivatives. In the majority, these derivatives have twelve carbon atoms in their alkyl chains. Water comprises the remaining components. The reported molecular weight for each surfactant product corresponds to the weight of the most abundant molecule in the sample. In Fig. S1 and S2, in the ESI,† representative structures of these molecules are shown. The surfactants are received as concentrated aqueous solutions and diluted in deionised water (of conductivity: κ = 0.055 μS cm−1) before use. No additional purification steps were attempted. Surfactant aqueous solutions were prepared on the same day of the measurements to avoid any changes,27 such as surfactants aging.28Experimental setup
A Force Balance K100C tensiometer (Krüss Scientific, Germany), equipped with a plate made of roughened platinum, was used for the surface tension measurements. Surface tension σ is extracted from the experimental data by the relationship: | (1) |
For the measurements, a volume of 20 ml of the surfactant laden solutions was placed in a sample vessel. Since surface tension measurements are very sensitive to impurities, both the plate and the vessel were first rinsed with deionised water, then with methanol (≥99%), and finally exposed to a flame. To ensure accurate measurements and confirm the cleanliness of the sample vessel, the surface tension of deionised water was measured at room temperature before and at the end of each set of experiments. The results are consistent with literature values.
All surface tension measurements were carried out at room temperature (∼21 °C) and ambient pressure. The densities of the single surfactant stock solutions and of the surfactant mixtures stock solutions were very close to the density of deionised water (ρ = 998 kg m−3).
Surface tension measurements
Measurement of surface tension for premixed surfactant mixtures. In this case, the anionic and the non-ionic surfactants at the required concentrations were added into 1000 ml deionised water and mixed. Before the experimental measurements, the stock solution was diluted to the desired final concentrations. For each set of experiments, the following mole ratios of the non-ionic over the anionic surfactant were used: 0.01, 0.1, 1 and 4. In contrast to the surface tension measurements of the single surfactants, which reached equilibrium in seconds, it took hours for the surface tension of the premixed surfactant mixtures to equilibrate, so a cover plate was used to reduce changes in the surfactant concentration due to water evaporation.
Measurement of surface tension for add one by one surfactant mixtures. Two different stock solutions were prepared, one for the non-ionic (c1 = 9.71 × 10−6 mol m−3) and one for the anionic (c2 = 1.28 × 10−5 mol m−3) surfactant, by adding a certain amount of each surfactant to 100 ml deionised water. Two procedures were followed. In Case 1, the non-ionic surfactant solution was added to the anionic one, while in Case 2 the order was reversed. The experimental procedure was as follows. 20 ml of deionised water was initially added to the measuring vessel and almost 5 min later a droplet of the stock solution of one of the surfactants, formed with a 0.1–2.5 μl, 0.5–10 μl or a 20–200 μl pipette (Eppendorf Research® plus, Germany), was released on the water surface. When the surface tension equilibrated, a droplet of the stock solution containing the other surfactant was released on the aqueous system surface. The measurement finished when the surface tension of the mixture reached a plateau. For these experiments a cover plate could not be used to eliminate deionised water evaporation. The surfactant mole fractions were chosen based on the mole fractions studied in the premixed surfactant mixtures case.
Results and discussion
Surface tension measurements for single surfactants
The surface tension values for the single surfactants are shown in Fig. 1. From the surface tension measurements, we extract the CMC for the individual surfactants in deionised water. The CMC is estimated from the interception of the regression line of the pre-micellar region and the line passing through the plateau of the post-micellar region, as shown in Fig. 1. The CMC of the non-ionic surfactant (EOT) is 3.68 × 10−2 mol m−3 whereas that of the anionic surfactant (NaDDBS) is 1.28 mol m−3. Differences in the CMC between non-ionic and anionic surfactants seem to be consistent with literature expectations, as described later. The data show that the non-ionic surfactant is able to decrease the surface tension at lower bulk surfactant concentrations, although NaDDBS achieves lower surface tensions than EOT at concentrations above the CMC. The surface tension reduction in the pre-micellar region, at concentrations lower than the CMC, indicates that the surfactants adsorbance at the water/air interface precedes the micellar formation in the bulk, as reported by Scamehorn,17 especially for EOT, for which the surface tension decreases more gradually in the semi-log plot compared to the results for NaDDBS.The equilibrium data shown in Fig. 1 can be used to extract, indirectly, the amount of surfactant adsorbed as a function of the bulk surfactant concentration and as a function of the measured surface tension. The first step requires fitting the data in Fig. 1 to the Langmuir–Szyskowski equation:27,29,30
σ(c) = σ0 − nΓmaxRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KLc + 1) ln(KLc + 1) | (2) |
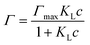 | (3) |
| EOT – non-ionic | NaDDBS – anionic | ||
|---|---|---|---|
| a Surface tension values for the single surfactants at their CMCs. | |||
| K L (m3 mol−1) | 2028.5 ± 376.5 | K L (m3 mol−1) | 1.20 ± 0.29 |
| Γ max (mol m−2) | 3.77 × 10−6 ± 2.63 × 10−7 | Γ max (mol m−2) | 8.65 × 10−6 ± 1.59 × 10−6 |
| R 2 | 0.994 | R 2 | 0.992 |
| σ non-nionic (N m−1) | 0.042 | σ anionic (N m−1) | 0.037 |
The equilibrium surface tension at the CMC for the non-ionic surfactant is σnon-nionic ≅ 0.042 N m−1, whereas for the anionic one it is σanionic ≅ 0.037 N m−1. The value for the non-ionic surfactant is larger than that obtained for the anionic one, because as can be seen in Table 1, the surface excess of the non-ionic surfactant at the deionised water/air interface is lower than that of the anionic surfactant. For the anionic surfactant, Γmax is larger at CMC because, as mentioned by Zhu et al.,33 the hydrophilic surfactant headgroups are compressed due to ion-condensation effects within the surrounding electrical double layer.
As also shown in Table 1, the KL value of the non-ionic surfactant is three orders of magnitude higher than that of the anionic surfactant, suggesting that the non-ionic surfactant is preferably adsorbed at the deionised water/air interface compared to the ionic one. This can explain the lower CMC value of EOT compared to the CMC value of NaDDBS. Kronberg et al.13 mentioned that the CMC of non-ionic surfactants is expected to be lower than the CMC of anionic ones (roughly two orders of magnitude is the initial reference point), which agrees with our findings. Another reason for the higher CMC value of the anionic surfactants lies in the fact that for anionic micelles to form, the hydrocarbon tail interactions (e.g., attractive van der Waals forces) inside the micelles should be stronger than the headgroup electrostatic repulsions on the micelles interface. In contrast, for non-ionic micelles, Scamehorn et al.,20 suggest that hydrophobic repulsions must overcome problems related only to space requirements of the hydrophilic headgroups.
Surface tension measurements for premixed surfactant mixtures
In the premixed surfactant mixtures case, as shown in Fig. 3, the surface tension decreases as the total molar concentration of the surfactants increases. A similar trend is reported by Jia et al.1 who studied mixed surfactant systems consisting of a cationic surfactant (N-dodecyl-N-methylpyrrolidinium bromide, L12) and an anionic one (sodium dodecyl sulfate, SDS). At low total surfactant concentrations (up to ctotal = 3.70 × 10−2 mol m−3), the reduction of surface tension is more noticeable in the case of surfactant mixtures than in the case of the single anionic surfactant. According to Kesarwani et al.23 and Mahajan & Nandni24 the addition of a non-ionic surfactant reduces the repulsive forces among the negatively charged headgroups of the anionic surfactant molecules, causing a more compact arrangement of the molecules at the surface. Thus, surface tension decreases more effectively as surfactant molecules are efficiently packed at the water/air interface among the deionised water molecules. | ||
| Fig. 3 Equilibrium surface tension vs. total molar surfactant concentration for the system EOT/NaDDBS at various mole ratios for solutions in which the surfactants were premixed. | ||
Similar behaviour was observed by Aaraadhya et al.34 for solutions containing 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of cationic (hexadecyltrimethylammonium chloride, CTAC) and non-ionic (pentaethyleneglycol monododecyl ether, C12E5) surfactants, where the CMC values of the surfactant mixtures decrease as the molar fraction of the non-ionic surfactant in the mixtures increases.
1 mixtures of cationic (hexadecyltrimethylammonium chloride, CTAC) and non-ionic (pentaethyleneglycol monododecyl ether, C12E5) surfactants, where the CMC values of the surfactant mixtures decrease as the molar fraction of the non-ionic surfactant in the mixtures increases.
As shown in Fig. 3, for nEOT/nNaDDBS = 0.01, 0.1 and 1 the equilibrium surface tension values fall in between those of the individual single surfactants. From Table 2, the mixture CMC values for nEOT/nNaDDBS = 0.01 and 0.1 are between the CMC values of the single surfactants, but for nEOT/nNaDDBS = 1 they are slightly lower than the CMC of the non-ionic surfactant. For nEOT/nNaDDBS = 4 the equilibrium surface tension values are below those of the single surfactants at the same total surfactant concentration. For this composition ratio, the CMC value is much lower than the CMC values of the single surfactants.
| Single surfactant/surfactant mixture | CMC (mol m−3) |
|---|---|
| EOT | 3.68 × 10−2 |
| NaDDBS | 1.28 |
| n EOT/nNaDDBS = 0.01 | 1.06 |
| n EOT/nNaDDBS = 0.1 | 3.92 × 10−2 |
| n EOT/nNaDDBS = 1 | 1.72 × 10−2 |
| n EOT/nNaDDBS = 4 | 9.10 × 10−4 |
The regular solution theory can interpret the experimentally determined CMC values of the surfactant mixtures, by calculating the interaction parameter βM (see eqn (S3)35 in Appendix A, ESI†) within the mixed micelles, which is an indication of the interactions between different surfactant molecules relative to the self-interactions of the individual surfactants under the same conditions.36 As shown in Table 3, for nEOT/nNaDDBS = 0.01, 0.1, and 1, when the mole fraction aEOT of the non-ionic surfactant EOT in the solution increases, its micellar mole fraction XMEOT (see eqn (S4)36 in Appendix A, ESI†) increases. At the same time, the interaction parameter βM decreases, indicating that the forces between the different surfactant molecules in the mixed micelles become more attractive20,37 than the self-interactions between the individual surfactants before mixing.36
For systems with nEOT = 0.01nNaDDBS, the mole fraction of the anionic surfactant in the micelles is XMNaDDBS = 0.801, suggesting that the anionic surfactant molecules occupy most of the mixed micelles for this system. The interaction parameter, βM, is slightly positive (βM = +0.58), meaning that the forces among the surfactant molecules in the mixed micelles are slightly more repulsive than those among the molecules of the single surfactants. Because of this, the CMC value of the mixture (CMCexp = 1.06 mol m−3) is close to the CMC value (CMCexp = 1.28 mol m−3) of the single anionic surfactant, albeit a bit lower.
For the system in which nEOT = 0.1nNaDDBS, the interaction parameter becomes negative (βM = −8.7), suggesting that the attractive forces among the anionic and non-ionic surfactant molecules are stronger relative to those among the molecules of the individual surfactants. Correspondingly, the CMC value for this surfactant mixture decreases by two orders of magnitude (CMCexp = 3.92 × 10−2 mol m−3). For nEOT = nNaDDBS, the interaction parameter remains negative (βM = −9.0), indicating again strong attractive forces between the molecules of the different surfactants in the mixed micelles compared to the individual ones while the CMC value of the mixture is further reduced (CMCexp = 1.72 × 10−2 mol m−3). When nEOT = 4nNaDDBS the interaction parameter is still negative with the largest absolute value among all three cases (βM = −21.8) while the CMCexp = 9.10 × 10−4 mol m−3 value of the surfactant mixture is by two orders of magnitude lower than the CMC of the non-ionic surfactant (CMCexp = 3.68 × 10−2 mol m−3). Finally, for nEOT/nNaDDBS = 0.1, 1 and 4 the mole fraction of the non-ionic (EOT) surfactant in the micelles was estimated to be higher than the mole fraction of the anionic (NaDDBS) surfactant (Table 3), based on the regular solution theory results. These observations suggest that the CMCs for the mixed surfactant systems depend on the relative interactions between different surfactant molecules within the micelles. Interestingly, these interactions depend on system composition and seem to be more pronounced when the CMCs of the single surfactants differ significantly, as is the case for the system chosen for the present work.
In general, our results are consistent with literature observations. For example, Azum et al.,38 reported that negative values of the interaction parameter suggest that mixed micelles are thermodynamically more stable than micelles formed from single surfactants. Zhou and Rosen36 concluded that negative values of the β parameter are observed in systems of non-ionic and anionic surfactants after mixing, because the non-ionic compounds screen the repulsions among the like-charged anionic headgroups. Furthermore, Kronberg et al.13 proposed that when the CMC values of surfactants are comparable, the CMC values of their mixtures should fall in between those of the single surfactants, and the interaction parameter values will be close to βM = −2. However, when the CMCs of the surfactants differ a lot, as happens in this study, it has been reported by Azum et al.38 that the interaction parameter βM acquires large negative values. The latter group38 studied anionic/non-ionic, cationic/non-ionic and anionic/cationic surfactant mixtures, with the CMC value of the anionic surfactant higher by two and one orders of magnitude than those of the non-ionic and the cationic surfactants, respectively. Vanjara & Dixit39 also obtained negative βM values between βM = −9.6 and βM = −13.8 in mixtures of p-dodecyl benzene sulfonate (anionic) and Brij 58, 78 and 99 (non-ionic) surfactants. On the other hand, Zheng et al.,40 reported highly negative values between βM = −5 and βM = −11 but for systems of zwitterionic gemini and anionic (SDS) or non-ionic (diglycolamide laurate, CDA) surfactants, while Sachin et al.,41 studied mixed SDS and DTAB (dodecyltrimethylammonium bromide) micelles and showed that the composition of the solution affects βM; the DTAB-rich systems exhibited slightly positive values, while negative βM values were calculated for the SDS-rich systems.
Rosen & Zhu9 discussed that when βM is negative and  , attractive forces are exerted between surfactants, and, as a result, the surface tension is efficiently reduced, i.e., a target surface tension value can be achieved at lower total bulk surfactant concentrations. Accordingly, as shown in Table 3, for nEOT/nNaDDBS = 0.1, 1, and 4, the absolute βM values are greater than
, attractive forces are exerted between surfactants, and, as a result, the surface tension is efficiently reduced, i.e., a target surface tension value can be achieved at lower total bulk surfactant concentrations. Accordingly, as shown in Table 3, for nEOT/nNaDDBS = 0.1, 1, and 4, the absolute βM values are greater than  . In detail, for nEOT/nNaDDBS = 4,
. In detail, for nEOT/nNaDDBS = 4,  , while for nEOT/nNaDDBS = 0.1 and 1,
, while for nEOT/nNaDDBS = 0.1 and 1,  , which indicate a better synergism when the mole ratio of the two surfactants is equal to four.
, which indicate a better synergism when the mole ratio of the two surfactants is equal to four.
Lastly, another way to interpret negative or positive deviation from ideality for surfactant mixtures is by invoking Clint's model (see the ESI,† Appendix A, eqn (S2)42). If the experimental CMC value (CMCexp) for the mixture is lower than the CMC value calculated from Clint's model (CMCideal), synergistic effects are expected among surfactants,38 while the opposite denotes antagonistic effects in the mixed micelles.17 For the mixtures studied here, when nEOT = 0.01nNaDDBS the CMCexp is higher than CMCideal, suggesting repulsive interactions among the molecules. In contrast, for nEOT/nNaDDBS = 0.1, 1, and 4, CMCexp is lower than CMCideal, suggesting synergisms between the surfactant molecules.
According to Rosen and Hua,14 the regular solution theory can also be applied to interpret the interactions between the surfactant molecules at the mixed layers on the water/air interface, by calculating the interaction parameter (βS) and the mole fraction of the non-ionic surfactant (XSEOT) (see eqn (S5)14 and (S6)14 in Appendix A, ESI†). The calculations were performed for four surface tension values in the premicellar region of the single surfactants and surfactant mixtures, where the slopes of the curves are constant and are given in Table 4.
| n EOT/nNaDDBS | σ (N m−1) | β S | X SEOT | X SNaDDBS |
|---|---|---|---|---|
| 0.01 | 0.060 | −9.4 | 0.535 | 0.465 |
| 0.055 | −8.6 | 0.520 | 0.480 | |
| 0.050 | −6.5 | 0.503 | 0.497 | |
| 0.045 | −4.5 | 0.462 | 0.538 | |
| 0.1 | 0.060 | −10.0 | 0.633 | 0.367 |
| 0.055 | −9.2 | 0.625 | 0.375 | |
| 0.050 | −7.9 | 0.623 | 0.377 | |
| 0.045 | −7.8 | 0.596 | 0.404 | |
| 1 | 0.060 | −6.6 | 0.801 | 0.199 |
| 0.055 | −5.3 | 0.826 | 0.174 | |
| 0.050 | −5.1 | 0.812 | 0.188 | |
| 0.045 | −4.9 | 0.785 | 0.215 | |
| 4 | 0.060 | −16.3 | 0.685 | 0.315 |
| 0.055 | −16.6 | 0.672 | 0.328 | |
| 0.050 | −17.1 | 0.675 | 0.343 | |
| 0.045 | −18.1 | 0.635 | 0.365 |
Based on our calculations (Table 4), for all the surfactant mixtures studied, the interaction parameter βS is negative, indicating that the attractive interactions between the surfactant molecules are stronger than the electrostatic or steric self-interactions of the molecules of the individual surfactants before mixing.36 Upon mixing, due to the dilution effect, repulsive forces are weakened and attractive ones between the hydrophobic tails,25 but also between headgroups,36 become more pronounced. According to Rosen and Hua14 negative values of βS can be attributed to the protonation of oxygen atoms in the ether groups of the polyoxyethylene chain of EOT, which causes the non-ionic surfactant to act as a cationic one.
According to Zhou and Rosen36 different negative values of βM and βS can be attributed to surfactants packing in the mixed micelles and at the mixed layers. A bulky hydrophobic group can more easily adapt to the water/air surface, whereas a bulky hydrophilic group can better adjust on the micellar surface. Branched hydrophobic tails are more difficult to pack within mixed micelles. In this study, EOT has a bulky hydrophilic ethoxylated group and a bulky hydrophobic tristyrylphenol group, whereas NaDDBS surfactant consists of a branched hydrophobic hydrocarbon tail and a hydrophilic benzene sulfonate head. The regular solution theory indicates that when nEOT/nNaDDBS = 0.01 and 0.1, surfactant molecules can be better accommodated at the mixed water/air interface, as βS is more negative than βM, while when nEOT/nNaDDBS = 1 and 4 βM is more negative than βS, so surfactants pack more easily in the mixed micelles,36 since the fraction of NaDDBS decreases.
From Table 4, it can also be seen that the mole fraction of EOT at the water/air interface is higher than that of NaDDBS, for all the surfactant mixtures studied. Even when nEOT = 0.01nNaDDBS, the mole fractions of the non-ionic surfactant at the water surface are almost equal to the fractions of the anionic surfactant, suggesting that the non-ionic surfactant molecules preferably adsorb at the water/air interface in the system considered here.
Dynamics surface tension measurements
A similar trend can also be observed for the nEOT = 0.1nNaDDBS and nEOT = nNaDDBS premixed surfactant mixtures cases, shown in the ESI,† Appendix B (Fig. S3), where up to 15 h are needed for equilibration at some total surfactant concentrations, e.g., when nEOT = 0.1nNaDDBS and ctotal = 1.31 × 10−3 mol m−3.
For nEOT = 4nNaDDBS, as illustrated in Fig. 4b, for the lowest total concentration ctotal = 7.57 × 10−5 mol m−3 studied, the surface tension reaches a constant value of around σ = 0.071 N m−1 very quickly. However, for higher total surfactant concentrations, i.e., for ctotal = 3.03 × 10−4 mol m−3 and ctotal = 6.06 × 10−4 mol m−3, it takes more time for the surface tension to reach a steady state. Finally, the time needed is reduced for concentrations above the CMC of the mixture, e.g., ctotal = 3.03 × 10−1 mol m−3.
Scamehorn17 described in detail the formation of surfactant monolayers at interfaces for surfactant mixtures and suggested that the mechanism (orientation of hydrophilic headgroups and hydrophobic tails) for the formation of mixed monolayers is similar to that responsible for the formation of mixed micelles. During the formation of a mixed monolayer at low surfactant bulk concentrations (≪CMC), surfactant molecules individually adsorb at the interface and do not interact significantly with each other. Thus, for concentrations much lower than the CMC of the mixtures, e.g., for ctotal = 1.28 × 10−3 mol m−3 in Fig. 4a, and for ctotal = 7.57 × 10−5 mol m−3 in Fig. 4b, the surface tension slightly decreases and equilibrates in several seconds, hence no change with time is observed within the time scale accessible to our instrumentation.
On the other hand, when the total concentration in the bulk increases, but it remains below the mixture CMC, it takes longer for the surface tension to equilibrate. According to Zhou and Rosen36 the long timescales observed for these concentrations can be correlated to surfactant interactions. Ion-dipole interactions between the anionic and non-ionic surfactant molecules, electrostatic interactions between the ionic hydrophilic headgroups, steric interactions between the hydrophilic headgroups or hydrophobic tails, van der Waals interactions between the hydrophobic groups and hydrogen bonding in the surfactant molecules, are all intermolecular interactions present in surfactant solutions. These interactions, especially at high total concentrations, can affect the adsorption of surfactants from the bulk to the water/air interface, i.e., (a) the diffusion from the bulk to the subsurface43 (a layer with a thickness of a few molecular diameters, below the surface44), (b) the adsorption from the subsurface to the water/air interface26 and (c) the reorientation of the molecules at the water surface.45 In addition, a wrong orientation of the molecules and steric effects of the non-ionic (EOT) and anionic (NaDDBS) surfactants, because of the size or the length of their alkyl chains, may cause molecules to diffuse back to the bulk instead of adsorbing at the water/air interface and thus increase the time needed for the surface tension of the mixture to stabilise. For instance, if the alkyl chain of a molecule is entangled within itself, the molecule could diffuse back to the bulk, rearrange itself and then once an adsorbed state is reached, diffuse back to the surface.26
Furthermore, limited availability of ‘vacant sites’ on the surface can also affect the time needed for the surface tension to equilibrate.26 At low total concentrations, based on Ward and Tordai,44 molecules from the subsurface can easily adsorb at empty sites at the water surface. As the bulk concentration increases, the number of vacancies at the water/air interface decreases, so molecules arrive at already occupied sites, interact with the molecules at the interface and may diffuse back in the bulk; thus, the timescale for the surface tension decay can further increase. Moreover, when the total concentration in the bulk increases, the surface excess of the non-ionic (EOT) and anionic (NaDDBS) monomers increases, and the molecules pack tightly at the water/air interface. This causes surface pressure to increase, and the formation of an energy barrier at the surface. Therefore, monomers coming from the subsurface need to overcome this energy barrier to adsorb,26,46,47 increasing the surface tension equilibration time.
The presence of impurities in the surfactants also needs to be considered, as impurities may disrupt intermolecular interactions that can affect surfactants surface activity. They might compete with surfactant molecules at the water/air interface leading to the creation of heterogeneous surface layers; thus, further modifying solution stability. Impurities can also impact adsorption kinetics and influence the whole performance of the surfactant mixtures (e.g., the time needed for them to reach a certain surface tension value).
Above the mixture CMC, e.g., for ctotal = 1.51 mol m−3 for Fig. 4a or ctotal = 3.03 × 10−1 mol m−3 for Fig. 4b, surface tension equilibrates in less than t = 1 h. In these cases, the molar concentration difference between the bulk and the interface increases, so surfactant diffusion is enhanced, and the equilibrium state is reached quickly. The rate of exchange of surfactants between the bulk and the surface can be further enhanced when micelles have a certain lifetime for break-up.48 However, when stable micelles are formed, and their lifetime is longer than the time needed for the dynamic surface tension to stabilise, then surfactant molecules in the micelles will not be able to adsorb to the surface, increasing the time needed to reach equilibrium.49 Consequently, the formation of stable mixed micelles (see βM value in Table 3), of non-ionic (EOT) and anionic (NaDDBS) surfactants, can increase the time needed for the surface tension of the mixtures to equilibrate, as noticed in Fig. 4b.
The changes in surface tension with time are shown in Fig. 5a and 6a for the case of the non-ionic surfactant added to the ionic one and in Fig. 5b and 6b for the case of the anionic surfactant added to the non-ionic one for two molar ratios (nEOT = 0.01nNaDDBS and nEOT = 4nNaDDBS). As shown in both Fig. 5 and 6, in all the add one by one surfactant mixtures cases there is initially a steep decrease in surface tension, once the surfactant laden droplet is deposited on the water/air interface. This decrease is attributed to the mass transfer of the surfactant molecules on the surface because of Marangoni forces caused by surface tension gradients. To exclude any effects on the measurements from the deposition of the droplet, the surface tension of deionised water was measured during the deposition of a pure water droplet on it. It was found that the surface tension is not affected by the drop deposition and remains constant at σ = 0.072 N m−1.
As shown in Fig. 5a, when the NaDDBS laden droplet is deposited on the water/air interface, at around t = 5 min, a sudden decrease in surface tension is observed. It is believed that spreading of the surfactant molecules on the surface precedes their desorption to the bulk and thus, once the anionic surfactant laden droplet is deposited the surface tension decreases. The higher the concentration of the anionic surfactant in the droplet, the more abrupt the decrease in surface tension, because of the increase in the number of surfactant molecules distributed on the surface. After this initial decrease, the surface tension increases slowly to its equilibrium value. During this time, NaDDBS molecules adsorb at and desorb from the surface; KL = 1.20 m3 mol−1 (Table 1) is slightly higher than 1, thus the adsorption rate is similar to the desorption rate. The final equilibrium surface tension value is equal to the one obtained when the same concentration of the anionic surfactant is diluted in deionised water and the surface tension of the solution is measured. For example, when ctotal = 1.54 × 10−2 mol m−3, the concentration of NaDDBS in the solution is cNaDDBS = 1.52 × 10−2 mol m−3 and the surface tension is equal to the equilibrium value σ = 0.071 N m−1 for this concentration of NaDDBS (see Fig. 1).
When a droplet that contains EOT is deposited, a second rapid decrease of the surface tension is seen in Fig. 5a, due to the Marangoni forces and the consequent spreading of the EOT molecules on the surface. However, after this reduction, surface tension remains almost constant for all the total concentrations studied, probably because mixed layers are formed on the water/air interface, where the non-ionic surfactant molecules are dispersed among the charged anionic surfactant headgroups and stabilise them.
When the non-ionic EOT surfactant is added first at around t = 5 min, the surface tension equilibrates quickly (Fig. 5b), as the non-ionic surfactant molecules spread and preferably adsorb at the water/air interface because of their high KL = 2028.5 m3 mol−1 value (Table 1). Once NaDDBS is added, then for the lower concentrations ctotal = 1.28 × 10−3 mol m−3 and ctotal = 3.21 × 10−3 mol m−3, there is no observable change in surface tension. These trends are similar for molar ratios nEOT = 0.1nNaDDBS and nEOT = nNaDDBS as well, which are shown in the ESI,† Appendix B and in Fig. S4 and S5. However, at the higher two concentrations ctotal = 8.97 × 10−3 mol m−3 and ctotal = 1.54 × 10−2 mol m−3, there is a small increase in surface tension after the addition of NaDDBS before the solutions acquire their final equilibrium surface tension values (Fig. 5b).
For concentrations nEOT = 4nNaDDBS in the add one by one surfactant mixtures (Fig. 6a), when NaDDBS is added first at around t = 5 min, the surface tension of the newly formed solution is not affected but remains almost constant at σ = 0.072 N m−1. Once the non-ionic surfactant is added at approximately t = 15 min, surface tension suddenly decreases but then remains constant at σ = 0.042 N m−1 for both concentrations studied. After their spreading on the water surface, the non-ionic surfactant molecules adsorb at the interface and stabilise it, because KL = 2028.5 m3 mol−1 and their adsorption rate is higher than the desorption one (Table 1). Therefore, the repulsive forces between the anionic surfactant headgroups are reduced. When the non-ionic EOT surfactant is added first at around t = 5 min (Fig. 6b), the surface tension decreases from the initial value of σ = 0.072 N m−1 to σ = 0.042 N m−1. Finally, the addition of NaDDBS at approximately t = 13 min, does not affect the surface tension.
The results suggest that the surface tension of the mixtures, in both cases of adding surfactants one by one, is determined for the most part by EOT, as the equilibrium value σ = 0.042 N m−1 is the same to the surface tension of aqueous solutions containing only EOT at concentrations equal to and above its CMC = 3.68 × 10−2 mol m−3 (see Fig. 1). Once the non-ionic surfactant is added, molecules are adsorbed at the interface because of their amphiphilic structure. The hydrocarbon chain interactions and electrostatic interactions among the non-ionic and anionic surfactants, promote the stability of the surface and reduce the surface tension of the final mixture to σ = 0.041–0.043 N m−1, for all the systems analysed.
For all the add one by one surfactant mixtures cases analysed, it can be concluded that when the anionic surfactant is added first followed by the non-ionic surfactant, it takes more time for the surface tension of the final mixture to reach equilibrium (20–40 min), compared to the reverse order of addition, where the required time in most cases is around 15–20 min. An exception is seen for nEOT = 0.01nNaDDBS, and concentrations ctotal = 8.97 × 10−3 mol m−3 or ctotal = 1.54 × 10−2 mol m−3 (Fig. 5b), where EOT is added first, and 40 min are needed to reach equilibrium; this is attributed to the high concentration of NaDDBS which possibly delays the time needed to reach equilibrium.
As shown in Table 5, when surfactants are added one by one, the final equilibrium surface tension (σeq) values are lower than those of the premixed mixtures, for the same total surfactant concentrations. As mentioned above, this can be attributed to metastable phenomena due to the stabilisation of the layers on the water/air interface once the non-ionic surfactant is added.
| n EOT/nNaDDBS | c total (mol m−3) | Case | ||
|---|---|---|---|---|
| Premixed | Add one by one | |||
| (1) NaDDBS–(2) EOT | (1) EOT–(2) NaDDBS | |||
| σ eq (N m−1) | σ eq (N m−1) | σ eq (N m−1) | ||
| 0.01 | 1.28 × 10−3 | 0.071 | 0.041 | 0.042 |
| 3.21 × 10−3 | 0.066 | 0.042 | 0.042 | |
| 8.97 × 10−3 | 0.061 | 0.043 | 0.043 | |
| 1.54 × 10−2 | 0.057 | 0.043 | 0.043 | |
| 0.1 | 1.31 × 10−3 | 0.064 | 0.042 | 0.041 |
| 3.92 × 10−3 | 0.056 | 0.042 | 0.043 | |
| 1.20 × 10−2 | 0.047 | 0.042 | 0.042 | |
| 1 | 1.43 × 10−3 | 0.062 | 0.038 | 0.041 |
| 4.30 × 10−3 | 0.054 | 0.040 | 0.041 | |
| 1.29 × 10−2 | 0.045 | 0.039 | 0.041 | |
| 1.72 × 10−2 | 0.044 | 0.040 | 0.041 | |
| 4 | 3.03 × 10−4 | 0.057 | 0.042 | 0.042 |
| 6.04 × 10−4 | 0.052 | 0.042 | 0.042 | |
Conclusions
Predicting the behaviour of solutions containing surfactant combinations with significantly different CMC values remains a challenge. Therefore, a comprehensive examination of how molecular interactions influence the phenomena taking place in the bulk but also at the air/water interfaces of such mixtures is essential towards understanding these complex systems.In this study, the equilibrium and dynamic surface tension of a non-ionic (EOT) and an anionic (NaDDBS) emulsifier, commonly employed in the delivery systems of agrochemical products, and of their mixtures were examined at different mole ratios, i.e., nEOT/nNaDDBS = 0.01; 0.1; 1; 4. For each molar ratio two different cases were analysed: namely premixed surfactant mixtures and add one by one surfactant mixtures. In the first case, surfactants were mixed before each measurement while in the latter, the surfactants were added in deionised water, one by one during the measurements.
It was found that the CMC of the non-ionic surfactant EOT was two orders of magnitude lower than that of NaDDBS, which suggests that EOT preferably adsorbs at the deionised water/air interface. The surface tension of the single surfactants was found to equilibrate quickly, while the surfactant mixtures needed a long time (usually hours) to reach equilibrium.
The experimental data were interpreted using the regular solution theory. Analysis showed that for the mixed micelles and the mixed layers, and for most of the mole ratios studied, negative βM and βS values were obtained, suggesting more attractive interactions between the surfactants after mixing, than the self-interactions of the two single surfactants before mixing. Furthermore, for most of the mole ratios studied, the mole fraction of the non-ionic (EOT) surfactant was found to be greater than that of the anionic (NaDDBS) surfactant, both in the mixed micelles and at the mixed layers.
The data obtained from the add one by one surfactant mixtures case suggested that EOT was preferably adsorbed at the interface and showed that the necessary time for the surface tension of these mixtures to equilibrate was less compared to the time needed in the premixed surfactant mixtures case. By adding surfactants one by one a lower surface tension value at equilibrium was obtained, for all the cases studied. Overall, this approach highlights how adding surfactants one by one can greatly impact molecular interactions in the solutions and affect the performance of the final mixtures. Surfactant mixtures are common in the production of many everyday products, and the interactions between their molecules can affect key properties such as surface or interfacial tension, wetting, spreading, foaming, stability, emulsification, and solubilisation.
This study explores the impact of mixing surfactants with significantly different CMC values on the final solutions. It reveals that when surfactants are premixed, their interactions can be unpredictable. Adding the surfactants one by one can help to better understand their interactions and could enable the creation of customised formulations with desired properties, such as specific surface tension values that enhance stability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the UKRI agency for supporting the research via the Sustainable Formulation of Agri-Chemicals via Dynamic Molecular Interfaces, SusAgriChem grant (EPSRC, EP/V032909/1) and Innospec for providing the surfactant products. K. Kotsi also acknowledges UCL for his studentship. This research was supported, in part, by the Asahi Glass Chair in Chemical Engineering at the University of Oklahoma, awarded to AS.References
- H. Jia, X. Leng, M. Hu, Y. Song, H. Wu, P. Lian, Y. Liang, Y. Zhu, J. Liu and H. Zhou, Colloids Surf., A, 2017, 529, 621–627 CrossRef CAS.
- M. Mulqueen and D. Blankschtein, Langmuir, 2002, 18, 365–376 CrossRef CAS.
- Z. Ye, F. Zhang, L. Han, P. Luo, J. Yang and H. Chen, Colloids Surf., A, 2008, 322, 138–141 CrossRef CAS.
- D. López-Díaz, I. García-Mateos and M. M. Velázquez, Colloids Surf., A, 2005, 270–271, 153–162 CrossRef.
- S. R. Patil, N. Buchavzov, E. Carey and C. Stubenrauch, Soft Matter, 2008, 4, 840–848 RSC.
- P. C. Griffiths, M. L. Whatton, R. J. Abbott, W. Kwan, A. R. Pitt, A. M. Howe, S. M. King and R. K. Heenan, J. Colloid Interface Sci., 1999, 215, 114–123 CrossRef CAS PubMed.
- P. D. T. Huibers and D. O. Shah, Langmuir, 1997, 13, 5762–5765 CrossRef CAS.
- Y. J. Nikas, S. Puvvada and D. Blankschtein, Langmuir, 1992, 8, 2680–2689 CrossRef CAS.
- M. J. Rosen and Z. H. Zhu, J. Colloid Interface Sci., 1989, 133, 473–478 CrossRef CAS.
- A. Khan and E. F. Marques, Curr. Opin. Colloid Interface Sci., 1999, 4, 402–410 CrossRef CAS.
- B. Jańczuk, A. Zdziennicka and W. Wójcik, Colloids Surf., A, 2003, 220, 61–68 CrossRef.
- K. L. Mital, Solution Chemistry of Surfactants, 1979 Search PubMed.
- B. Kronberg, K. Holmberg and B. Lindman, Surface Chemistry of Surfactants and Polymers, 2014 Search PubMed.
- M. J. Rosen and X. Y. Hua, J. Colloid Interface Sci., 1982, 86, 164–172 CrossRef CAS.
- G. Kume, M. Gallotti and G. Nunes, J. Surfactants Deterg., 2008, 11, 1–11 CrossRef CAS.
- A. M. Misselyn-Bauduin, A. Thibaut, J. Grandjean, G. Broze and R. Jerome, Langmuir, 2000, 16, 4430–4435 CrossRef CAS.
- J. F. Scamehorn, An Overview of Phenomena Involving Surfactant Mixtures, 1986 Search PubMed.
- J. Ferreira, A. Mikhailovskaya, A. Chenneviere, F. Restagno, F. Cousin, F. Muller, J. Degrouard, A. Salonen and E. F. Marques, Soft Matter, 2017, 13, 7197–7206 RSC.
- G. Basu Ray, I. Chakraborty, S. Ghosh and S. P. Moulik, Colloid Polym. Sci., 2007, 285, 457–469 CrossRef CAS.
- J. F. Scamehorn, R. S. Schechter and W. H. Wade, J. Dispersion Sci. Technol., 1982, 3, 261–278 CrossRef CAS.
- M. Bergström, Langmuir, 2001, 17, 993–998 CrossRef.
- J. K. Ferri and K. J. Stebe, Adv. Colloid Interface Sci., 2000, 85, 61–97 CrossRef CAS PubMed.
- H. Kesarwani, A. Saxena, A. Mandal and S. Sharma, Energy Fuels, 2021, 35, 3065–3078 CrossRef CAS.
- R. K. Mahajan and D. Nandni, Ind. Eng. Chem. Res., 2012, 51, 3338–3349 CrossRef CAS.
- A. Bagheri and P. Khalili, RSC Adv., 2017, 7, 18151–18161 RSC.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef CAS PubMed.
- M. Kalli, L. Chagot and P. Angeli, J. Colloid Interface Sci., 2022, 605, 204–213 CrossRef CAS PubMed.
- L. Dong, Z. Xu, W. Qiao, Z. Li and L. Cheng, Energy Sources, Part A, 2007, 29, 1407–1413 CrossRef CAS.
- T. Dong, W. H. Weheliye and P. Angeli, Phys. Fluids, 2019, 31, 012106 CrossRef.
- K. Giribabu and P. Ghosh, Chem. Eng. Sci., 2007, 62, 3057–3067 CrossRef CAS.
- M. A. Muherei and R. Junin, Mod. Appl. Sci., 2009, 3, 158–167 CAS.
- H. Jin, W. Wang, F. Liu, Z. Yu, H. Chang, K. Li and J. Gong, Int. J. Multiphase Flow, 2017, 94, 44–52 CrossRef CAS.
- Y. P. Zhu, M. J. Rosen, S. W. Morrall and J. Tolls, J. Surfactants Deterg., 1998, 1, 187–193 CrossRef CAS.
- D. Arabadzhieva, P. Tchoukov and E. Mileva, Colloids Interfaces, 2020, 4, 53 CrossRef CAS.
- A. Thibaut, A. Misselyn-Bauduin, J. Grandjean, G. Broze and R. Jérôme, Langmuir, 2000, 16, 9192–9198 CrossRef CAS.
- Q. Zhou and M. J. Rosen, Langmuir, 2003, 19, 4555–4562 CrossRef CAS.
- M. Bergström and J. C. Eriksson, Langmuir, 2000, 16, 7173–7181 CrossRef.
- N. Azum, M. A. Rub and A. M. Asiri, J. Mol. Liq., 2016, 216, 94–98 CrossRef CAS.
- A. K. Vanjara and S. G. Dixit, Adsorpt. Sci. Technol., 1996, 13, 377–395 CrossRef CAS.
- Y. Zheng, X. Lu, L. Lai, L. Yu, H. Zheng and C. Dai, J. Mol. Liq., 2020, 299, 112108 CrossRef CAS.
- K. M. Sachin, S. A. Karpe, M. Singh and A. Bhattarai, R. Soc. Open Sci., 2019, 6, 181979 CrossRef CAS PubMed.
- J. H. Clint, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 1327–1334 RSC.
- C. H. Chang and E. I. Franses, Colloids Surf., A, 1995, 100, 1–45 CrossRef CAS.
- A. F. H. Ward and L. Tordai, J. Chem. Phys., 1946, 14, 453–461 CrossRef CAS.
- S. N. Moorkanikkara and D. Blankschtein, J. Colloid Interface Sci., 2006, 302, 1–19 CrossRef CAS PubMed.
- J. Eastoe, J. S. Dalton and R. K. Heenan, Langmuir, 1998, 14, 5719–5724 CrossRef CAS.
- S. Y. Lin, T. L. Lu and W. B. Hwang, Langmuir, 1995, 11, 555–562 CrossRef CAS.
- K. D. Danov, P. M. Vlahovska, T. Horozov, C. D. Dushkin, P. A. Kralchevsky, A. Mehreteab and G. Broze, J. Colloid Interface Sci., 1996, 183, 223–235 CrossRef CAS.
- V. B. Fainerman, Colloids Surf., 1992, 62, 333–347 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01454a |
| This journal is © The Royal Society of Chemistry 2024 |





