Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase transitions of fluorotelomer alcohols at the water|alkane interface studied via molecular dynamics simulation†
Stephen A.
Burrows
 ,
Jang Won
Shon
,
Jang Won
Shon
 ,
Boyan
Peychev
,
Boyan
Peychev
 ,
Radomir I.
Slavchov
,
Radomir I.
Slavchov
 * and
Stoyan K.
Smoukov
* and
Stoyan K.
Smoukov
 *
*
Centre for Sustainable Engineering, School of Engineering and Materials Science, Queen Mary University of London, Mile End Road, London, E1 4NS, UK. E-mail: r.slavchov@qmul.ac.uk; s.smoukov@qmul.ac.uk
First published on 6th February 2024
Abstract
Fluorosurfactants are long-lasting environmental pollutants that accumulate at interfaces ranging from aerosol droplet surfaces to cell membranes. Modeling of adsorption-based removal technologies for fluorosurfactants requires accurate simulation methods which can predict their adsorption isotherm and monolayer structure. Fluorotelomer alcohols with one or two methylene groups adjacent to the alcohol (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH and 6
1 FTOH and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, respectively) are investigated using the OPLS-AA force field at the water|hexane interface, varying the interfacial area per surfactant. The acquired interfacial pressure isotherms and monolayer phase behavior are compared with previous experimental results. The results are consistent with the experimental data inasmuch as, at realistic adsorption densities, only 7
2 FTOH, respectively) are investigated using the OPLS-AA force field at the water|hexane interface, varying the interfacial area per surfactant. The acquired interfacial pressure isotherms and monolayer phase behavior are compared with previous experimental results. The results are consistent with the experimental data inasmuch as, at realistic adsorption densities, only 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH shows a phase transition between liquid-expanded (LE) and 2D crystalline phases. Structures of the LE and crystalline phases are in good agreement with the sticky disc and Langmuir defective crystal models, respectively, used previously to interpret experimental data. Interfacial pressure of the LE phase agrees well with experiment, and sticky disc interaction parameters indicate no 2D LE–gas transition is present for either molecule. Conformation analysis reveals 7
1 FTOH shows a phase transition between liquid-expanded (LE) and 2D crystalline phases. Structures of the LE and crystalline phases are in good agreement with the sticky disc and Langmuir defective crystal models, respectively, used previously to interpret experimental data. Interfacial pressure of the LE phase agrees well with experiment, and sticky disc interaction parameters indicate no 2D LE–gas transition is present for either molecule. Conformation analysis reveals 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH favors conformers where the OH dipole is perpendicular to the molecular backbone, such that the crystalline phase is stabilized when these dipoles align.
1 FTOH favors conformers where the OH dipole is perpendicular to the molecular backbone, such that the crystalline phase is stabilized when these dipoles align.
1 Introduction
Since the discovery of polytetrafluoroethylene (PTFE) in 1938, fluorinated organic molecules have increasingly become key ingredients of many everyday products. Per- and polyfluoroalkyl substances (PFAS) are a diverse range of fluorinated compounds commonly used in industry, many of which are amphiphilic and have a high potential for bioaccumulation.1,2 PFAS have been injected as part of fracking operations3,4 and detected far away from original sources of pollution, leading to concerns about contamination of the environment and water supply.5 Recent studies have demonstrated multiple mechanisms of toxicity including suppression of the immune system and increased incidence of certain cancers.6,7 Therefore, there is an increasing need to overcome the challenges associated with the prevention and remediation of PFAS pollution.Fluorosurfactants are characterized by a tail of a partially or fully fluorinated alkyl chain attached to a hydrophilic head group such as a carboxylic acid or alcohol, giving them amphiphilic properties. The larger van der Waals radius for the fluorine atom compared to hydrogen (ca. 1.47 Å vs. 1.20 Å, respectively) gives fluorocarbon chains a higher molar volume compared to hydrocarbon chains (248 ml mol−1 for perfluorooctane vs. 163 ml mol−1 for octane). Fluorine's additional size also alters the conformation, with fluorocarbon chains typically found in a slightly twisted/helical conformer, similar to the straight all-trans conformation but with C–C–C–C dihedral angles deviating 10–15° from trans.8 This relieves some steric energy, but the helical conformation remains highly rigid due to the high energy barrier to forming gauche C–C bonds. A very strong C–F bond gives fluorocarbon chains high chemical and thermal resistance, allowing them to be used in various industries where alkyl-tail surfactants would be unstable.9 The unique properties of fluorinated groups, such as simultaneous hydrophobicity and oleophobicity, make them difficult to replace with alternative chemistries and have allowed their application in non-stick cookware, waterproof textile coatings and greaseproof food packagings.10,11
This work is concerned with the behavior of fluorotelomer alcohols (FTOH), a specific class of PFAS surfactant. These may be referred to as ‘diblock’ surfactants as the tail can be divided into two segments—the fluorinated part terminating in a CF3 group, and the chain of CH2 groups connecting the fluorinated tail to the alcohol hydroxyl. Therefore, the tail can be characterized by two numbers: m denoting the number of fluorinated carbons and n the number of CH2 carbons. Hence, they are abbreviated as m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n FTOH,1,12 having the chemical structure CF3(CF2)m−1(CH2)nOH. The junction between the CHx and CFx groups creates a strong ‘FC-HC’ dipole which affects the ordering and wettability of the partially fluorinated tails in adsorbate films.13 FTOHs can originate from the breakage of FTOH-based polymers during biodegradation processes in wastewater treatment facilities or landfills.14,15 FTOHs are probable precursor compounds that readily biodegrade to produce toxic and bio-accumulative unsaturated fluorotelomer acids and perfluoroalkyl carboxylic acids (PFCAs). Therefore, the fate of FTOHs as a raw material in the environment must be understood to determine the potential harms from it.14–16 The replacement of CH2 with CF2 groups (with extremely strong C–F bonds) alters the reactivity and stability of neighboring functional groups which can have a significant effect on the potential for metabolic transformations, leading to non-biodegradability.17 There is also considerable interest in establishing the source of FTOHs in the atmosphere and understanding their transport and behavior.16 Savvaides et al. have recently shown that PFAS exposure occurs via airborne particulates originating from building materials and stain-repellent coatings on furniture, raising concerns about the high exposure levels and impact on health.10
n FTOH,1,12 having the chemical structure CF3(CF2)m−1(CH2)nOH. The junction between the CHx and CFx groups creates a strong ‘FC-HC’ dipole which affects the ordering and wettability of the partially fluorinated tails in adsorbate films.13 FTOHs can originate from the breakage of FTOH-based polymers during biodegradation processes in wastewater treatment facilities or landfills.14,15 FTOHs are probable precursor compounds that readily biodegrade to produce toxic and bio-accumulative unsaturated fluorotelomer acids and perfluoroalkyl carboxylic acids (PFCAs). Therefore, the fate of FTOHs as a raw material in the environment must be understood to determine the potential harms from it.14–16 The replacement of CH2 with CF2 groups (with extremely strong C–F bonds) alters the reactivity and stability of neighboring functional groups which can have a significant effect on the potential for metabolic transformations, leading to non-biodegradability.17 There is also considerable interest in establishing the source of FTOHs in the atmosphere and understanding their transport and behavior.16 Savvaides et al. have recently shown that PFAS exposure occurs via airborne particulates originating from building materials and stain-repellent coatings on furniture, raising concerns about the high exposure levels and impact on health.10
The exposure to long-chain PFAS (LC-PFAS) and its persistence in human tissues leading to immunotoxicity, carcinogenicity and developmental toxicity has attracted regulatory attention regarding uses of LC-PFAS.18–20 Many studies have shown the association of FTOH exposure with hepatotoxicity,21,22 increased breast cancer proliferation23,24 and estrogenic activity.24,25 Toxicity and exposure concerns led many industries to voluntarily replace LC-PFAS with short-chain PFAS (SC-PFAS) in 2011, followed by the 2016 FDA regulation restricting uses of LC-PFAS and substances based on them.7 The SC-PFAS whose chains contain 6 carbons or less are thought to have similar oleophobic and hydrophobic properties as the LC-PFAS based compounds with reduced toxicity and carcinogenicity. However, recent studies have shown some SC-PFAS are more persistent and mobile than long-chain analogues.26 Furthermore, there are still controversies about the toxicity of SC-PFAS in the body27 and the lack of knowledge of these compounds suggests that adverse effects may continue to be discovered.28
Considering the potential for toxicity and bioaccumulation, there is an urgent need to deploy remediation strategies to remove PFAS from drinking water and other sources of human exposure. Many remediation methods make use of PFAS's amphiphilic properties to adsorb them at interfaces, such as in porous solids or foams. Examples of existing PFAS removal technologies include activated carbon (AC) and ozofractionation.29 AC is an effective adsorbent for LC-PFAS but may be less effective for SC-PFAS.30
The 2D phase behavior of fluorinated surfactants and their alkyl counterparts differs dramatically. Amphiphiles with hydrocarbon hydrophobic tails exhibit pronouncedly non-cohesive behavior,31–33i.e., the lateral interactions in their monolayers are dominated by the steric repulsion as the van der Waals interaction between hydrocarbon entities through a hydrocarbon medium is small. A non-cohesive monolayer behaves as a two-dimensional fluid of hard discs, normally with neither gas–liquid nor liquid–solid phase transition taking place upon compression (supercritical monolayer32). Only at temperatures close to the freezing point of the bulk alkane phase will a liquid–solid phase transition be observed (e.g., in droplet shape transformations34,35), which involves not only the surfactant but also the alkane phase. In contrast, two fluorinated chains will be attracted to each other through an alkane phase; therefore, FTOH monolayers behave as a 2D layer of cohesive particles, demonstrating a distinctive complex phase behavior which is very rare for monolayers at the water|oil interface. The cohesive behavior of FTOH monolayers differs not only from noncohesive alkanols at water|oil, but also from cohesive alkanol monolayers at water|air.36 Cohesive monolayers of normal alcohols at water|air, for example, show a liquid–gas and solid–liquid phase transitions when the hydrocarbon tail is of length >12–14 carbons (depending on temperature).37,38 Fluorosurfactant monolayers appear to show a much more stable 2D solid phase while never exhibiting a gas–liquid phase transition,36 probably a result of the more rigid nature of the fluorinated chain—unlike alkyl tail surfactants, there is no conformational change during phase transition.
Takiue et al.39 demonstrated these surprising surface phase transitions of FTOH at the water|oil interface. Moreover, they showed contrasting phase behavior in the films of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH. They determined phase transition points by looking for discontinuities in the gradient of the interfacial tension vs. surfactant concentration, then used these gradients to determine the change in surface density at the transition points. They concluded that 7
2 FTOH. They determined phase transition points by looking for discontinuities in the gradient of the interfacial tension vs. surfactant concentration, then used these gradients to determine the change in surface density at the transition points. They concluded that 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH undergoes two phase transitions, the first presumably a 2D gas to liquid-expanded (LE) transition, and the second being LE to crystalline (C). However, the gas–LE transition has been questioned;36 at least in some cases, the respective kink in the surface tension isotherm was connected to bulk association of FTOH in the oil. Unlike 6
1 FTOH undergoes two phase transitions, the first presumably a 2D gas to liquid-expanded (LE) transition, and the second being LE to crystalline (C). However, the gas–LE transition has been questioned;36 at least in some cases, the respective kink in the surface tension isotherm was connected to bulk association of FTOH in the oil. Unlike 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, LE–C transitions in monolayers of 8
2 FTOH, LE–C transitions in monolayers of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 10
2 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH which have longer fluorinated tails were confirmed by independent experiments: brewster angle microscopy confirmed the existence of two monolayer phases at the water|oil interface,40 and X-ray reflectivity confirmed that one of these is condensed and solid—confirming the presence of a LE–C transition.41 Pingali et al.42 studied the competitive adsorption and phase behavior of the long chain alcohol C20OH and the fluorotelomer alcohol 8
2 FTOH which have longer fluorinated tails were confirmed by independent experiments: brewster angle microscopy confirmed the existence of two monolayer phases at the water|oil interface,40 and X-ray reflectivity confirmed that one of these is condensed and solid—confirming the presence of a LE–C transition.41 Pingali et al.42 studied the competitive adsorption and phase behavior of the long chain alcohol C20OH and the fluorotelomer alcohol 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH at the water–hexane interface. They found the low-temperature (<24 °C) behavior to be highly sensitive to the molar ratio of the two surfactants in the hexane solution, with each capable of fully displacing the other at the interface. At the water|air interface, long chain FTOH have been shown to aggregate into condensed ordered domains even at very low surface density and it was suggested that the rigidity of the perfluorinated tail facilitates this ordering.43
2 FTOH at the water–hexane interface. They found the low-temperature (<24 °C) behavior to be highly sensitive to the molar ratio of the two surfactants in the hexane solution, with each capable of fully displacing the other at the interface. At the water|air interface, long chain FTOH have been shown to aggregate into condensed ordered domains even at very low surface density and it was suggested that the rigidity of the perfluorinated tail facilitates this ordering.43
Molecular dynamics (MD) force fields are readily available for simple perfluoroalkanes and PTFE, including the widely used OPLS all-atom force field of Watkins and Jorgensen.44 Alternative force fields include COMPASS,45 which uses a 9-6 Lennard-Jones (LJ) potential for intermolecular interactions, in contrast to the 12-6 LJ potential of OPLS. Borodin et al. developed a force field for perfluoroalkanes and PTFE, reporting more accurate conformational energetics than OPLS.46 Computationally efficient coarse-grained force fields for diblock fluorocarbons have been developed to simulate self-assembly of large molecular aggregates (such as micelles) over microsecond time scales.47 In comparison, force fields validated for PFAS simulation are less widely available because perfluoroalkane/PTFE force fields may not have suitable parameters for the surfactant head group. The COMPASS force field has been used to model adsorption of perfluorinated sulfonic acids on water|oxide interfaces.48 For FTOH specifically, Zygmunt and Potoff49 computed densities, heats of vaporization (ΔHv) and free energies of hydration using MD, comparing the performance of the united-atom TraPPE and all-atom OPLS force fields. They found both models generally reproduced the density and ΔHv of most FTOH well, but strangely overestimated ΔHv by nearly a factor of two for FTOHs with two non-fluorinated groups, i.e., the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 6
2, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 8
2, and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH. Optimizations to FTOH/PFAS force fields have been proposed to account for deviations in ideal mixture behavior arising from the mutual phobicity of the alkyl and fluoroalkyl groups.50 To be reliable models for simulating adsorption-based PFAS remediation methods, force fields must be able to reproduce the phase behavior of FTOH at interfaces, where amphiphiles naturally concentrate.
2 FTOH. Optimizations to FTOH/PFAS force fields have been proposed to account for deviations in ideal mixture behavior arising from the mutual phobicity of the alkyl and fluoroalkyl groups.50 To be reliable models for simulating adsorption-based PFAS remediation methods, force fields must be able to reproduce the phase behavior of FTOH at interfaces, where amphiphiles naturally concentrate.
In this paper, we aim to compare the behavior of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH and 6
1 FTOH and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, studying specifically the phase transitions in their monolayers at the water|hexane interface. We perform all-atom MD simulations and compute interfacial pressure isotherms, radial distribution functions and orientational order parameters, comparing MD predictions to previous experimental and theoretical results. Visualizing the trajectories also allows us to investigate the coexistence region of condensed 2D crystalline and 2D fluid phases (LE–C coexistence), giving the first MD evidence for this phase transition at the water|oil interface. Visualization and quantification of these domains also permits the analysis and explanation of non-monotonic surface pressure isotherms which deviate from ideal equilibrium behavior due to line tension present at the domain boundaries.51 We also apply our previous theoretical thermodynamic approach36 to make sense of the MD data, and demonstrate the contrasting behavior for 7
2 FTOH, studying specifically the phase transitions in their monolayers at the water|hexane interface. We perform all-atom MD simulations and compute interfacial pressure isotherms, radial distribution functions and orientational order parameters, comparing MD predictions to previous experimental and theoretical results. Visualizing the trajectories also allows us to investigate the coexistence region of condensed 2D crystalline and 2D fluid phases (LE–C coexistence), giving the first MD evidence for this phase transition at the water|oil interface. Visualization and quantification of these domains also permits the analysis and explanation of non-monotonic surface pressure isotherms which deviate from ideal equilibrium behavior due to line tension present at the domain boundaries.51 We also apply our previous theoretical thermodynamic approach36 to make sense of the MD data, and demonstrate the contrasting behavior for 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH and 6
1 FTOH and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH.
2 FTOH.
2 Methods
2.1 Molecular dynamics
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 115 water molecules.
115 water molecules.
Simulations of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH were performed at 293, 303 and 313 K. An equivalent batch of 6
1 FTOH were performed at 293, 303 and 313 K. An equivalent batch of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH simulations were performed at 293 K to compare with 7
2 FTOH simulations were performed at 293 K to compare with 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH at the same temperature. Initial areas per molecule from 28 to 60 Å2 were used, spaced by 1 Å2 from 28 to 40 Å2, then in steps of 2 when >40 Å2. These areas were corrected to account for any displacement of FTOH into the oil phase, although this was generally a small effect (<0.5 Å2). The diffusion coefficient, D, was found to be a suitable way to do this, with D being 1–10 × 10−9 m2 s−1 for FTOH in the bulk hexane and 0.01–1 × 10−9 m2 s−1 at the interface, depending on the surface density. Therefore, FTOH molecules with D above a chosen cut-off are assumed to be in the hexane. Cut-offs of 1.0, 1.4, and 1.8 × 10−9 m2 s−1 at temperatures of 293 K, 303 K, and 313 K, respectively, were found to be consistent with visual inspection in identifying the number of FTOH in the hexane.
1 FTOH at the same temperature. Initial areas per molecule from 28 to 60 Å2 were used, spaced by 1 Å2 from 28 to 40 Å2, then in steps of 2 when >40 Å2. These areas were corrected to account for any displacement of FTOH into the oil phase, although this was generally a small effect (<0.5 Å2). The diffusion coefficient, D, was found to be a suitable way to do this, with D being 1–10 × 10−9 m2 s−1 for FTOH in the bulk hexane and 0.01–1 × 10−9 m2 s−1 at the interface, depending on the surface density. Therefore, FTOH molecules with D above a chosen cut-off are assumed to be in the hexane. Cut-offs of 1.0, 1.4, and 1.8 × 10−9 m2 s−1 at temperatures of 293 K, 303 K, and 313 K, respectively, were found to be consistent with visual inspection in identifying the number of FTOH in the hexane.
Each simulation begins with a 10 ns equilibration period using the Berendsen barostat59 with a time constant of 1 ps. Then a 20 ns simulation was performed for data collection, using the Parrinello–Rahman barostat60 with a time constant of 4 ps. The Bussi–Donadio–Parrinello thermostat,61 denoted v-rescale in GROMACS, was used to control the temperature using a time constant of 0.1 ps. An integration time step of 2 fs was used, matching the L-OPLS publication.53 The LJ interaction is truncated at 1.3 nm using the force-switch option to smoothly reduce the force to zero from 1.1 to 1.3 nm.
Initial observations demonstrated a significant run-to-run variance in the computed interfacial tension, especially at low areas per molecule (<35 Å2) where 2D crystalline order appears. Longer production simulations of 40 ns (vs. 20 ns) were tested to try and reduce this variance, finding that the result from the extended simulations was highly correlated with the shorter ones they continued from. At low area per molecule the correlation was especially strong, as shown in Fig. S6 (ESI†). In other words, not much new information was gained by extending the length of the simulations. Here we discuss the origin and mitigation of this run-to-run variance.
In general, the unit cell of the crystalline C phase will not be able to tile the xy-plane exactly, as the simulation box vectors are not linear combinations of the C phase unit cell vectors. Therefore, if the C phase fully spans the simulation box in the x and/or y dimension, it has to deform slightly to achieve consistency with the periodic simulation cell. The resulting elastic stress in the crystal affects the average pressure tensor and therefore the interfacial tension. We tested several strategies to diminish this variance. The magnitude of the elastic stress is dependent on the orientation of the C phase with respect to the simulation box which varies from run to run. Therefore it was decided to repeat each simulation 10 times, rerunning the Packmol script each time with a different random seed in order to randomize the starting positions. The initial velocities are also randomized using the ‘gen-vel’ option in GROMACS. Reported interfacial tensions are therefore an average of 10 runs (200 ns in total). More importantly, for the densely packed monolayers with area per molecule 28–35 Å, two different methods were used to generate the starting configuration. The first is the random packing of surfactants generated by Packmol, with the condition that all atoms must be at least 2 Å apart from each other. The second involves creating a hexagonal lattice of surfactants using the lattice parameter obtained from the first peak of the C phase surfactant radial distribution function (RDF), as illustrated in Fig. 2. In that case, the x and y dimensions of the box are defined so that the 2D unit cell tiles the xy-plane exactly (but are still approximately 80 Å). For area per molecule >35 Å2, the C phase was not observed to fully span the simulation box and therefore there was no significant difference between the two starting configurations; however, at <35 Å2, the effect is significant, as discussed in the isotherm results section.
2.2 Simulation analysis
 | (1) |
Computed values of σ0 for water|hexane were found to be 54.9 ± 0.3, 54.4 ± 0.3, and 54.3 ± 0.2 mN m−1 at 293, 303, and 313 K, respectively. Experimental data from Takiue et al.39 shows σ0 = 50.8 mN m−1 at 293 K, consistent with data from Zeppieri et al.63 which also finds σ0 = 50.8 mN m−1 at 293 K. This suggests the MD force field overestimates the water|hexane interfacial tension by ≈8%. The interfacial entropy,
 | (2) |
The treatment of the long-range LJ interactions can have a significant effect on the measured surface tension in simulations of liquid|vapor systems where there is a large density difference between the two phases. This is because the standard LJ tail correction assumes a homogenous mean-field beyond the cutoff distance.65 In our case, we have two condensed phases (water and hexane, both in liquid state), so the homogeneous approach is a better approximation. Still, we investigated the effect of the LJ cutoff by varying it from the standard 1.3 nm up to 2.1 nm (in 0.2 nm steps) and measuring the water|hexane interfacial tension for each value. The results are given in Table S3 (ESI†). We find no significant dependence of σ on the cutoff distance, with all values being within the computed error bars (of size ≈0.3 mN m−1) of the value obtained using the standard 1.3 nm cutoff.
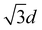 and 2d where d is the nearest-neighbor spacing. For each surfactant molecule, the centroid of the backbone chain (the C and O atoms) is used to define the position of that molecule. The separations, r, of every unique pair of molecules are binned into a histogram with a bin size dr of 0.01 nm. The RDF is obtained by normalization of this histogram with respect to the average number density of surfactants (for the entire volume), ρn, multiplied by the volume of a spherical shell between radii r and r + dr. The RDF, g(r), is therefore given by
and 2d where d is the nearest-neighbor spacing. For each surfactant molecule, the centroid of the backbone chain (the C and O atoms) is used to define the position of that molecule. The separations, r, of every unique pair of molecules are binned into a histogram with a bin size dr of 0.01 nm. The RDF is obtained by normalization of this histogram with respect to the average number density of surfactants (for the entire volume), ρn, multiplied by the volume of a spherical shell between radii r and r + dr. The RDF, g(r), is therefore given by | (3) |
 | (4) |
2.3 Conformer analysis
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH differ considerably in their phase behavior, yet the only chemical difference is the fluorination of a single carbon atom.36,39 To help understand why these differences arise, the conformations of the surfactant heads are measured and compared between the two molecules. Firstly, we measure the distribution of gauche and trans bonds along the entire backbone of the molecules. The method used to define and compute the dihedral angle ϕ is explained in the ESI† (Section S1). Then we pay special attention to the conformation of the surfactant head, as measured by the final two dihedrals, C–C–C–O and C–C–O–H. Each of these dihedrals can be assigned gauche+ (G+), trans (T), or gauche− (G−) which correspond to ϕ being within the intervals 0–120°, 120°–240°, and 240°–360°, respectively. Using this measure, dihedrals in the ‘helical’ conformation will be categorized as trans because their dihedral angle differs only slightly from 180°. As we are mainly concerned with significant changes in surfactant geometry due to gauche bonds near the head group, this approximation should not affect the conclusions. The pair of conformations for these two dihedrals (C–C–C–O and C–C–O–H) is denoted by two letters, such as TG+ for trans-gauche+. Conformations which are equivalent due to mirror symmetry, such as TG+ and TG−, are grouped together and denoted TG. The fractional population of the five possible conformers, TT, TG, GG, G+G− and GT, was computed for 7
2 FTOH differ considerably in their phase behavior, yet the only chemical difference is the fluorination of a single carbon atom.36,39 To help understand why these differences arise, the conformations of the surfactant heads are measured and compared between the two molecules. Firstly, we measure the distribution of gauche and trans bonds along the entire backbone of the molecules. The method used to define and compute the dihedral angle ϕ is explained in the ESI† (Section S1). Then we pay special attention to the conformation of the surfactant head, as measured by the final two dihedrals, C–C–C–O and C–C–O–H. Each of these dihedrals can be assigned gauche+ (G+), trans (T), or gauche− (G−) which correspond to ϕ being within the intervals 0–120°, 120°–240°, and 240°–360°, respectively. Using this measure, dihedrals in the ‘helical’ conformation will be categorized as trans because their dihedral angle differs only slightly from 180°. As we are mainly concerned with significant changes in surfactant geometry due to gauche bonds near the head group, this approximation should not affect the conclusions. The pair of conformations for these two dihedrals (C–C–C–O and C–C–O–H) is denoted by two letters, such as TG+ for trans-gauche+. Conformations which are equivalent due to mirror symmetry, such as TG+ and TG−, are grouped together and denoted TG. The fractional population of the five possible conformers, TT, TG, GG, G+G− and GT, was computed for 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH at 34 Å2 per molecule.
2 FTOH at 34 Å2 per molecule.
2.4 Equation of state
We have previously shown that the intra-layer lateral interactions for 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH on the water|oil interface are too weak to cause a first order gas-to-liquid (gas–LE) phase transition,32i.e. the liquid monolayer is a 2D-supercritical fluid. Such fluid can be described well with the sticky disc (SD) model of Gurkov and Ivanov.68 The SD equation of state (EoS), relating the interfacial pressure ΠSD to the state parameters adsorption Γ and temperature T, reads
2 FTOH on the water|oil interface are too weak to cause a first order gas-to-liquid (gas–LE) phase transition,32i.e. the liquid monolayer is a 2D-supercritical fluid. Such fluid can be described well with the sticky disc (SD) model of Gurkov and Ivanov.68 The SD equation of state (EoS), relating the interfacial pressure ΠSD to the state parameters adsorption Γ and temperature T, reads | (5) |
At high monolayer densities, the behaviors of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH are different: only 7
2 FTOH are different: only 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH has been reported to exhibit a liquid-to-crystalline (LE–C) phase transition. In our previous work we showed that the crystalline 7
1 FTOH has been reported to exhibit a liquid-to-crystalline (LE–C) phase transition. In our previous work we showed that the crystalline 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH monolayer behaves as a 2D van der Waals crystal.36 The free energy Fpc of a perfect (defect-free) 2D van der Waals crystal of N molecules is
1 FTOH monolayer behaves as a 2D van der Waals crystal.36 The free energy Fpc of a perfect (defect-free) 2D van der Waals crystal of N molecules is
 | (6) |
 is the lattice energy. For this system, the interaction potential uint is dominated by van der Waals interactions between neighboring F-blocks.36 For a hexagonal lattice, it can be assumed equal to six times the pair interaction between immediate neighbors. Ivanov's model for the London pair potential between two parallel –(CF2)– chains standing normal to the surface36,69 predicts that:
is the lattice energy. For this system, the interaction potential uint is dominated by van der Waals interactions between neighboring F-blocks.36 For a hexagonal lattice, it can be assumed equal to six times the pair interaction between immediate neighbors. Ivanov's model for the London pair potential between two parallel –(CF2)– chains standing normal to the surface36,69 predicts that: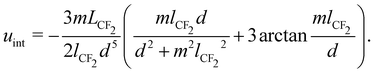 | (7) |
 | (8) |
3 Results and discussion
3.1 2D visualization of surfactant distribution and phase behavior
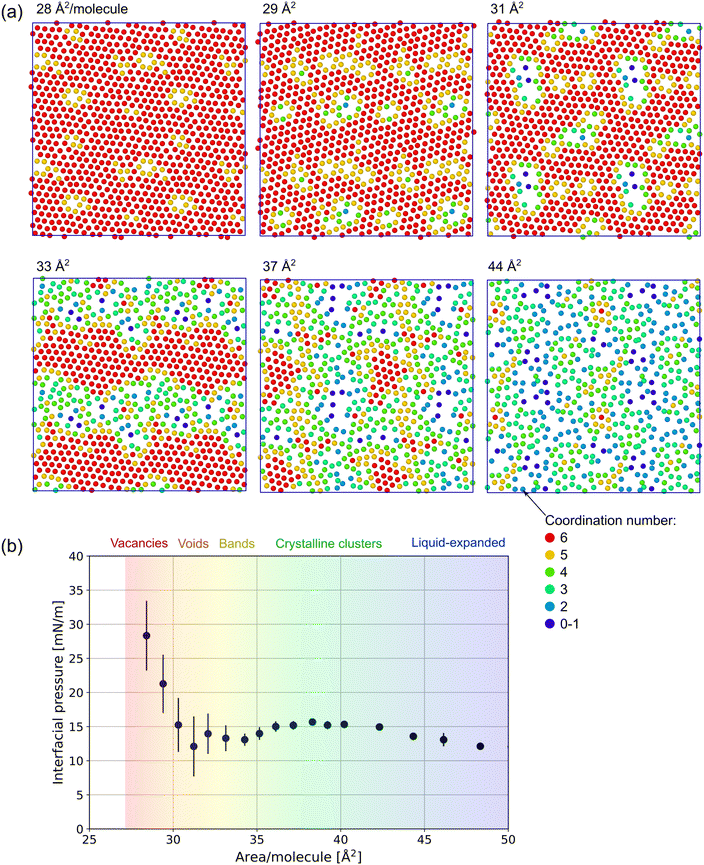
In Fig. 3, the distribution of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH surfactant at 293 K is visualized in the xy-plane. The molecules are represented by a single dot and colored according to their coordination number nc using a cutoff of 7 Å to help highlight regions of hexagonal crystalline phase in which nc = 6. The distance between the molecules is computed in the xy-plane only (ignoring the z coordinate), so this cutoff is slightly smaller than is later used in analyzing the first peak of the full 3D RDF.
1 FTOH surfactant at 293 K is visualized in the xy-plane. The molecules are represented by a single dot and colored according to their coordination number nc using a cutoff of 7 Å to help highlight regions of hexagonal crystalline phase in which nc = 6. The distance between the molecules is computed in the xy-plane only (ignoring the z coordinate), so this cutoff is slightly smaller than is later used in analyzing the first peak of the full 3D RDF.
In the range 28–30 Å2 per molecule, the surfactants appear to be entirely in the crystalline C phase and the change in density is achieved by a change in the number of vacancies. Above 30 Å2, where the interfacial pressure's steep decrease stops, the vacancies evolve into larger 2D domains of LE phase embedded within the C phase. LE is characterized by the lower density, lack of hexagonal crystalline order and coordination nc < 6. At ≈33 Å2, equal amounts of each phase appear to be present, typically forming bands which span the system in only one dimension. 37–38 Å2 is a local maximum in the simulated interfacial pressure (at 293 K), and visual inspection shows globular crystalline clusters surrounded by the LE phase. Beyond ≈40 Å2, the interfacial pressure is a monotonically decreasing function of the area per molecule and no crystalline clusters are seen beyond ≈50 Å2.
Fig. S7 (ESI†) shows the structure of the interface using the density profile, ρ(z), of each component. At 30 Å2 per 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH molecule, where the FTOH is in the crystalline phase, the density profile of the hexane at the FTOH|hexane boundary shows a pronounced peak (at z = 55 Å) characteristic of a sharp interface. At 60 Å2 per FTOH (LE phase), the interface is less sharp and the monolayer contains a mixture of hexane and FTOH. Within the monolayer (corresponding to z ≈ 40–55 Å), the amount of hexane decreases monotonically and approximately linearly when approaching the water interface.
1 FTOH molecule, where the FTOH is in the crystalline phase, the density profile of the hexane at the FTOH|hexane boundary shows a pronounced peak (at z = 55 Å) characteristic of a sharp interface. At 60 Å2 per FTOH (LE phase), the interface is less sharp and the monolayer contains a mixture of hexane and FTOH. Within the monolayer (corresponding to z ≈ 40–55 Å), the amount of hexane decreases monotonically and approximately linearly when approaching the water interface.
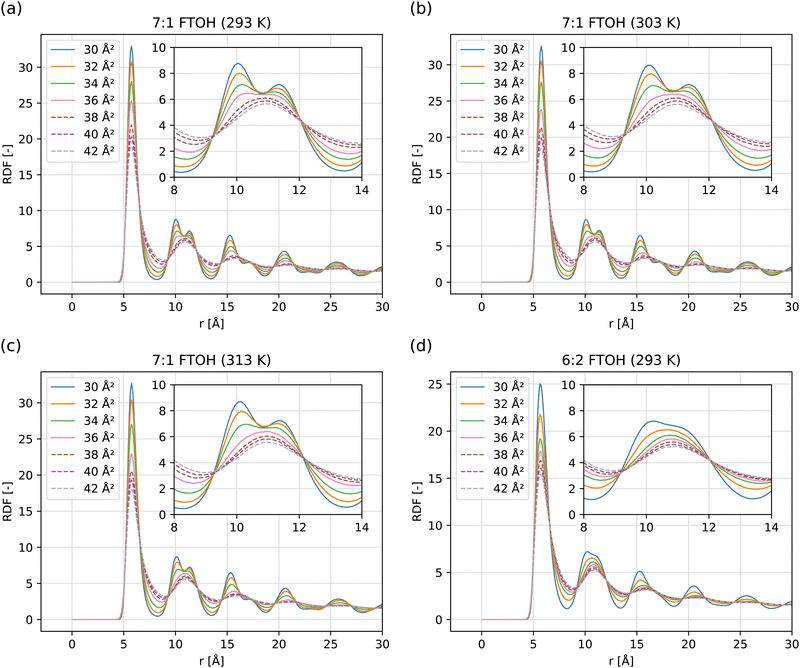
3.2 Interfacial pressure isotherms
In Fig. 4, the interfacial pressure isotherm as a function of area per molecule is given for the four systems studied in this work. In the homogeneous crystalline (area/molecule <30 Å2) and LE (area/molecule >45 Å2) phase regions, the interfacial pressure decreases monotonically with the increase in area per molecule. In the two-phase region between ≈30–45 Å2 (see Fig. 3), a complex behavior with two extrema is observed. This feature is typical for 2D dispersions and can be explained with a 2D Kelvin pressure effect (similar to the one in heterogeneous gas–liquid monolayers analyzed by Pethica70). In three dimensions, the pressure inside a small drop is increased by the capillary pressure 2σ/R. In two dimensions, the interfacial pressure in a 2D droplet is similarly increased by interfacial capillary pressure of τ/R due to the line tension τ of the boundary between the two phases. This pressure produces a simultaneous increase in the chemical potential of both phases, see the ESI† (Section S2). If this capillary pressure were negligible, the first-order phase transition would appear as a horizontal line defined by the equilibrium (binodal) value Π = Πpt. When present, it results in the observed shape with two extrema, as demonstrated in Fig. S4 (ESI†). | ||
| Fig. 4 Interfacial pressure isotherms with theoretical model of Peychev and Slavchov36 fit to both simulation (this work) and experimental data (Takiue et al.39). Red curves (open hexagon markers) include the simulations initialized using a crystalline monolayer in the 28–35 Å2 range (see Fig. 2b). Error bars correspond to two standard deviations. | ||
This shape of isotherm can also be found in existing MD studies of phospholipid surface pressure vs. area isotherms at the water|air interface. For example, the dipalmitoylphosphatidylcholine (DPPC) isotherm computed by Baoukina et al.71 showed a LE–C phase coexistence region in which the gradient of surface pressure vs. area per lipid was positive—this is again a result of the heterogeneity of the simulated monolayer. Similar surface pressure curves were obtained earlier by da Silva et al. during the expansion of diblock polymer monolayers at the water|air interface.72 In that case, the hysteresis was explained by entanglement of chains during expansion and differing conformation of the polymer chain during expansion vs. contraction of the monolayer.
The effect of simulation box size (x, y dimensions from 40 to 120 Å) on the interfacial pressure at 36 Å2 per molecule and 303, 313 K is shown in Table S4 and Fig. S8 (ESI†). These conditions were chosen as they approximately correspond to the local maxima in the interfacial pressure where deviations from Πpt are larger, especially at higher temperature. At this area per molecule, the system generally contains a crystalline cluster surrounded by LE phase. The results show that the interfacial pressure decreases with increasing system size, approaching the equilibrium value Πpt more closely. The radius of the crystalline cluster also increases with system size, so the effect of line tension (which is inversely proportional to the radius) becomes less significant. Therefore, the line tension can be considered a finite-size effect which explains the system size dependence.
The simulation of the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH monolayers predicts a LE–C phase transition in qualitative agreement with the one that follows from the σ vs. concentration data of Takiue et al.;39 however, the simulated crystalline phase is clearly more cohesive, resulting in lower interfacial pressure in the C region and lower phase equilibrium interfacial pressure Πpt (when above 293 K) compared to the ones derived from the experiment. The simulations where the initial surfactant state was crystalline (with vacancies) rather than a random packing (see Fig. 2) produce interfacial tension that better agrees with the experiment, suggesting that the discrepancy is due to slow equilibration of the 2D crystal structure and the associated elastic stresses which remain. Direct tests with longer 50 ns simulations showed that the discrepancy between the two types of starting configuration remained—further indicating that equilibration is limited by the possible mismatch between lattice constant and simulation box size; therefore, this must be accepted as a general limitation of MD when applied to crystalline monolayers at constant area per molecule.
1 FTOH monolayers predicts a LE–C phase transition in qualitative agreement with the one that follows from the σ vs. concentration data of Takiue et al.;39 however, the simulated crystalline phase is clearly more cohesive, resulting in lower interfacial pressure in the C region and lower phase equilibrium interfacial pressure Πpt (when above 293 K) compared to the ones derived from the experiment. The simulations where the initial surfactant state was crystalline (with vacancies) rather than a random packing (see Fig. 2) produce interfacial tension that better agrees with the experiment, suggesting that the discrepancy is due to slow equilibration of the 2D crystal structure and the associated elastic stresses which remain. Direct tests with longer 50 ns simulations showed that the discrepancy between the two types of starting configuration remained—further indicating that equilibration is limited by the possible mismatch between lattice constant and simulation box size; therefore, this must be accepted as a general limitation of MD when applied to crystalline monolayers at constant area per molecule.
Another visible difference is that the simulated Πpt has much less pronounced temperature dependence than the experimental one. In 2D, the Clausius–Clapeyron relation is
 | (9) |
In Table 1, eqn (5) and (8) are used to fit the simulated data in order to extract the model parameters and compare them with those calculated from the experimental data. Overall, there is quantitative agreement between the experiment and simulation in the LE phase and qualitative agreement in the C phase. Whatever the initial state, the condensed phase appears to be more cohesive than the experimental data suggests (Πexpcoh < Πsimcoh). However, the agreement is significantly improved when using the crystalline initial conditions. As Πcoh depends on the gradient of the C phase section of the isotherm, the obtained value of Πcoh will be influenced by the excessively low interfacial pressure at 30–33 Å2, an effect which may be amplified by line tension at the LE–C boundary (see Fig. S4, ESI†).
| T [K] | α [Å2] | β [−] | Π coh [mN m−1] | Π pt [mN m−1] | A C [Å2] | A LE [Å2] | ||
|---|---|---|---|---|---|---|---|---|
| a Random init. and crystal init. refer to the initial surfactant packing methods in Fig. 2(a) and (b), respectively. | ||||||||
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH 1 FTOH |
293 | Experiment | 24.5 | 5.20 | 6.8 | 12.91 | 36.9 | 46.9 |
| Simulation (crystal init.) | 23.27 | 3.92 | 10.13 | 14.46 | 32.4 | 45.4 | ||
| Simulation (random init.) | 24.66 | 4.63 | 17.74 | 14.28 | 30.7 | 46.0 | ||
| 303 | Experiment | 24.5 | 4.39 | 6.8 | 19.57 | 33.0 | 41.5 | |
| Simulation (crystal init.) | 24.36 | 4.72 | 11.02 | 16.18 | 32.5 | 43.9 | ||
| Simulation (random init.) | 25.24 | 4.93 | 22.07 | 15.33 | 30.3 | 45.5 | ||
| 313 | Experiment | 24.5 | 3.6 | 6.8 | 26.67 | 30.8 | 39.0 | |
| Simulation (crystal init.) | 24.80 | 4.68 | 10.26 | 17.83 | 32.9 | 43.4 | ||
| Simulation (random init.) | 25.44 | 4.79 | 23.18 | 16.74 | 30.3 | 45.0 | ||
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
293 | Experiment | 24.5 | 3.80 | — | — | — | — |
| Simulation (random init.) | 23.51 | 4.06 | 4.54 | 24.51 | 30.6 | 37.5 | ||
As it can be seen, the hard disc area α, which accounts for the close-range repulsion, is very well reproduced by the simulation. Within the simulation, the attraction parameter β appears to increase with temperature, opposite to what should be expected: the simulated monolayers show β = 3.9–4.6 at 293 K to 4.7–4.8 at 313 K, compared to the experimental decrease from 5.2 to 3.6. The obtained value of β is influenced by α, which was assumed constant in the experimental fits (α = 24.5 Å2), but treated as an adjustable parameter for the simulation fits. α was found to increase with temperature, but if α is fixed to 24.5 Å2, all simulation fits result in 4.5 < β < 5.0.
Since the LE phase is in quantitative agreement with the experiment, we could assume that the interaction potential uint is reasonably well reproduced by the simulation. Therefore, we posit that the difference in Πcoh is also due to the inability of the simulated condensed monolayer to heal itself. Within the simulation the surfactant molecules are less able to tilt and compensate for vacancies, and instead we observe interdigitation of hexane into the monolayer. The penalty per vacancy is higher and, therefore, the monolayer is more resistant to expansion (cohesive). On the other hand, the higher energy per vacancy means that when the simulated LE monolayer freezes there is less heat released compared to the experiment (ΔHexp > ΔHsim).
The simulated results for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH also show a possible phase transition with the LE–C line spanning 30–37 Å2. This cannot be compared to the available experimental data, as the highest monolayer density available is ca. 37 Å2, most likely close to the solubility limit of the surfactant. It is possible that the simulated cases of high surfactant density represent a metastable state that should relax to a state of lower surface density given sufficient time, with the excess surfactant being released into the oil as solute or as 3D crystals. Neither surfactant shows a 2D gas–LE phase transition at high molecular areas, but this hypothetical transition occurs at areas above the range used in our simulation. In the experimental interfacial pressure vs. total concentration isotherms, there is a characteristic kink at low concentration and interfacial pressures that has been ascribed to such a transition.39 Previously, we argued that the kink is due to an onset of bulk association and the expanded monolayers are actually supercritical.36
2 FTOH also show a possible phase transition with the LE–C line spanning 30–37 Å2. This cannot be compared to the available experimental data, as the highest monolayer density available is ca. 37 Å2, most likely close to the solubility limit of the surfactant. It is possible that the simulated cases of high surfactant density represent a metastable state that should relax to a state of lower surface density given sufficient time, with the excess surfactant being released into the oil as solute or as 3D crystals. Neither surfactant shows a 2D gas–LE phase transition at high molecular areas, but this hypothetical transition occurs at areas above the range used in our simulation. In the experimental interfacial pressure vs. total concentration isotherms, there is a characteristic kink at low concentration and interfacial pressures that has been ascribed to such a transition.39 Previously, we argued that the kink is due to an onset of bulk association and the expanded monolayers are actually supercritical.36
3.3 Radial distribution functions
In Fig. 5, RDFs are computed using the surfactant centroid separation distance. Particular attention is given to the range of distances from 9–12 Å, where the contrasting behavior between the crystal and LE phases is most clear. At high density (low area/molecule), 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH shows an RDF characteristic of a 2D hexagonal lattice similar to graphene,73 just with a different lattice parameter. The location of the first peak maxima is at r = 5.72 ± 0.05 Å. Therefore, an ideal hexagonal phase will demonstrate a second peak at
1 FTOH shows an RDF characteristic of a 2D hexagonal lattice similar to graphene,73 just with a different lattice parameter. The location of the first peak maxima is at r = 5.72 ± 0.05 Å. Therefore, an ideal hexagonal phase will demonstrate a second peak at  and third peak at 2r = 11.44 Å, which agrees with the second and third peaks in the Fig. 5 inlay.
and third peak at 2r = 11.44 Å, which agrees with the second and third peaks in the Fig. 5 inlay.
As the area per molecule is increased, the sharpness of the second and third peaks is seen to reduce until they eventually merge into a single peak at a separation of ≈11 Å, characteristic of a 2D liquid rather than a hexagonal crystalline phase. By contrast, the RDF for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH does not demonstrate two well-separated peaks in the 9–12 Å range, even at 30 Å2 per molecule, showing that the separation of adjacent molecules is more variable. This may be because the 6
2 FTOH does not demonstrate two well-separated peaks in the 9–12 Å range, even at 30 Å2 per molecule, showing that the separation of adjacent molecules is more variable. This may be because the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH molecules are more anisotropic in shape (less cylindrical or rod-like) due to their conformation. As discussed later, the lack of fluorine atoms on the beta carbon reduces steric hindrance and allows more gauche dihedrals to form about the final C–C bonds. This may also indicate the solid phase formed by 6
2 FTOH molecules are more anisotropic in shape (less cylindrical or rod-like) due to their conformation. As discussed later, the lack of fluorine atoms on the beta carbon reduces steric hindrance and allows more gauche dihedrals to form about the final C–C bonds. This may also indicate the solid phase formed by 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH is more defectuous, as molecules partially moving or tilting into vacant sites will contribute to variance of the nearest-neighbor spacing.
2 FTOH is more defectuous, as molecules partially moving or tilting into vacant sites will contribute to variance of the nearest-neighbor spacing.
We compare these results to the van der Waals crystal model, as follows. By combining eqn (6) and (7), one can calculate the free energy of a perfect m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n FTOH 2D van der Waals crystal at different lattice constants. The assumptions made are that only the F-blocks of the tails attract each other, the defects are ignored and the free area is calculated for fixed position of the nearest neighbours. Fig. S9 (ESI†) shows the free energy vs. lattice constant for several lengths of the perfluorinated segment using the effective London interaction constant calculated from the fits of the experimental results (10.5 × 10−78 J m6).36 For 7
n FTOH 2D van der Waals crystal at different lattice constants. The assumptions made are that only the F-blocks of the tails attract each other, the defects are ignored and the free area is calculated for fixed position of the nearest neighbours. Fig. S9 (ESI†) shows the free energy vs. lattice constant for several lengths of the perfluorinated segment using the effective London interaction constant calculated from the fits of the experimental results (10.5 × 10−78 J m6).36 For 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH (m = 7), the location of the minimum in the free energy is slightly higher than predicted by the first peak in the RDF, i.e. 6.16 Å versus 5.72 Å. For 6
1 FTOH (m = 7), the location of the minimum in the free energy is slightly higher than predicted by the first peak in the RDF, i.e. 6.16 Å versus 5.72 Å. For 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, m = 6, there is no minimum of the free energy vs. lattice constant profile, so the hypothetical perfect 2D van der Waals crystal is not stable. However, the curve is clearly close to inflection and even slightly higher lateral attraction should lead to a shallow minimum and a stable crystalline phase of 6
2 FTOH, m = 6, there is no minimum of the free energy vs. lattice constant profile, so the hypothetical perfect 2D van der Waals crystal is not stable. However, the curve is clearly close to inflection and even slightly higher lateral attraction should lead to a shallow minimum and a stable crystalline phase of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH.
2 FTOH.
3.4 Orientational order parameter
The orientational order parameter is plotted as a function of area per molecule in Fig. 6a. Firstly we observe the effect of temperature on the order of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH, then we compare 7
1 FTOH, then we compare 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH and 6
1 FTOH and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH at the same temperature (293 K).
2 FTOH at the same temperature (293 K).
For the crystalline phase of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH (28–30 Å2 per molecule), the order parameter is ≈ 0.9 and does not vary much between 293 K and 313 K. This may be due to the molecules being mostly constrained in a close-packed monolayer with little freedom to tilt as the temperature is increased. At intermediate areas per molecule (≈33–50 Å2), the effect of temperature is more pronounced with higher temperature seen to reduce the order parameter. This is the multiphase region and, therefore, the higher temperature will reduce the amount of crystalline phase present, i.e. at a given area per molecule the system is closer to the liquid phase region along the binodal line when the temperature is higher. At high area per molecule, where 7
1 FTOH (28–30 Å2 per molecule), the order parameter is ≈ 0.9 and does not vary much between 293 K and 313 K. This may be due to the molecules being mostly constrained in a close-packed monolayer with little freedom to tilt as the temperature is increased. At intermediate areas per molecule (≈33–50 Å2), the effect of temperature is more pronounced with higher temperature seen to reduce the order parameter. This is the multiphase region and, therefore, the higher temperature will reduce the amount of crystalline phase present, i.e. at a given area per molecule the system is closer to the liquid phase region along the binodal line when the temperature is higher. At high area per molecule, where 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH is entirely in the LE phase, the dependence on temperature is fairly weak.
1 FTOH is entirely in the LE phase, the dependence on temperature is fairly weak.
At all monolayer densities, the order parameter is significantly lower for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH compared to 7
2 FTOH compared to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH, and this reduction is much greater than is seen by increasing the temperature from 293 K to 313 K for 7
1 FTOH, and this reduction is much greater than is seen by increasing the temperature from 293 K to 313 K for 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH. In Fig. 6b, the tilting of FTOH molecules is visualized at 34 Å2 per molecule. This area per molecule was chosen as it shows the contrast between the two surfactants, with the 7
1 FTOH. In Fig. 6b, the tilting of FTOH molecules is visualized at 34 Å2 per molecule. This area per molecule was chosen as it shows the contrast between the two surfactants, with the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH monolayer being phase-separated between the crystal and LE phases whereas the 6
1 FTOH monolayer being phase-separated between the crystal and LE phases whereas the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH monolayer appears to be entirely in the LE phase and therefore more orientationally disordered.
2 FTOH monolayer appears to be entirely in the LE phase and therefore more orientationally disordered.
In the LE phase, the orientational order parameter is still >0 and as high as ≈0.5 when close to the LE–C transition. This level of orientational order is similar to a 3D nematic phase, but with the positional order resembling a 2D liquid as the molecules are confined to a monolayer. Supplementary calculations are provided which also compute the 2D nematic order parameter74 by considering the projection of the orientation vectors in the xy-plane (Section S3 and Fig. S5, ESI†). We find the 2D nematic order parameter is close to zero (≈0.05) for a range of areas spanning the full LE–C transition. Therefore, while the surfactants do have orientational order in 3D, there is no such order when considering only the projection in the xy-plane. The orientational order of the surfactants in the z direction is due to the order enforced by the interface (orienting the hydrophillic OH towards the water).
3.5 Conformer analysis
Fig. 7a shows the distribution of gauche and trans dihedrals along the surfactant backbone. Compared to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH, 6
1 FTOH, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH contains more gauche dihedrals for the C–C bonds closest to the alcohol OH (bonds 2 and 3), which can be attributed to the removal of one fluorinated group, reducing the steric energy of gauche bonds. In Fig. 7b, energy-minimized geometries of 7
2 FTOH contains more gauche dihedrals for the C–C bonds closest to the alcohol OH (bonds 2 and 3), which can be attributed to the removal of one fluorinated group, reducing the steric energy of gauche bonds. In Fig. 7b, energy-minimized geometries of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH are shown in each of the five conformers alongside the computed conformer populations. A significant difference is seen in the conformer populations of 7
1 FTOH are shown in each of the five conformers alongside the computed conformer populations. A significant difference is seen in the conformer populations of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, with 7
2 FTOH, with 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH having approximately 85% of the molecules in the two conformers TG and GG, whereas they are more evenly distributed for 6
1 FTOH having approximately 85% of the molecules in the two conformers TG and GG, whereas they are more evenly distributed for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH. The TG and GG conformers minimize the distance between the positive OH hydrogen and the nearby fluorine atoms bonded to the second carbon. This is expected considering the negative charge of −0.12|e| applied to F atoms in this model. For 6
2 FTOH. The TG and GG conformers minimize the distance between the positive OH hydrogen and the nearby fluorine atoms bonded to the second carbon. This is expected considering the negative charge of −0.12|e| applied to F atoms in this model. For 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, these two atoms are hydrogens instead of fluorine, with a slight positive charge of 0.06|e|, so the effect is reversed.
2 FTOH, these two atoms are hydrogens instead of fluorine, with a slight positive charge of 0.06|e|, so the effect is reversed.
It can be seen that the hydroxyl group dipole is oriented perpendicular to the backbone of the surfactant for the TG and GG conformers; therefore, the simulation predicts that the vast majority of the molecules have the OH dipole located in the interfacial plane for the crystalline phase of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH. This orientation minimizes the normal dipole moment of the monolayer which produces electrostatic repulsion75 (while tangential orientation corresponds to an overall attraction). However, it is difficult to isolate the effect of these surfactant–surfactant OH dipole interactions from the interactions of the surfactant OH with the water phase.
1 FTOH. This orientation minimizes the normal dipole moment of the monolayer which produces electrostatic repulsion75 (while tangential orientation corresponds to an overall attraction). However, it is difficult to isolate the effect of these surfactant–surfactant OH dipole interactions from the interactions of the surfactant OH with the water phase.
4 Conclusions
All-atom molecular dynamics using the OPLS-AA force field can reproduce the LE–C phase transition of FTOH surfactants at the water|hexane interface. Visualization of molecular positions, each colored according to their coordination number, showed clear evidence of two phases—one crystalline with the molecules packed in a hexagonal lattice and another with the behavior of a supercritical 2D fluid. Analysis of the RDF showed a clear change from 2D crystalline to liquid order as the area per molecule was increased from 30 to 42 Å2.The interfacial pressure isotherm was also characteristic of a system with a first order phase transition, showing a region in which the interfacial pressure was non-monotonic, with an inflection point and two extrema. This region coincided with the range of areas per molecule in which two phases were observed. The majority of previous MD studies reporting surfactant pressure-area isotherms are for monolayers of phospholipids71,76–78 or lipid mixtures such as pulmonary surfactant79–81 at the water|air interface. Of those showing phase transitions, some show a similar characteristic to the isotherm reported in this work,71,78 with the gradient of surface pressure vs. area per lipid becoming positive in the coexistence region. Here, this complex behavior of the interfacial pressure during coexistence was explained qualitatively by the effect of line tension and the resulting 2D Kelvin (capillary) pressure at the LE-C boundary.
The LE section of the isotherm was in good agreement with the experiment and, therefore, with the sticky disc model parameters determined previously.36 The sticky disc attraction parameter β ≈ 5 is well below the critical value for a 2D gas–LE phase transition to be present (β > 38.1 to be subcritical with respect to the gas–LE transition.32) Therefore, we maintain that the kink in the experimental isotherm at low concentration (high area per molecule) reported in ref. 39 may correspond to the onset of FTOH association in the hexane phase rather than a gas–LE transition at the interface.
On the other hand, the crystalline part of the isotherm was in qualitative but not quantitative agreement with the experiment. Visualization showed a defectuous hexagonal lattice, with expansion of the monolayer accomplished by an increase in the number of vacancies rather than an increase in lattice parameter, which is consistent with the Langmuir defective crystal model.36 The cohesiveness of the monolayer as quantified by Πcoh was larger than experiment, with the discrepancy being reduced when using a crystalline initial packing of surfactants. As attractive forces between FTOH molecules appeared to be modeled well in the LE phase, we hypothesize this deficiency was specifically due to the energy penalty of lattice vacancy formation.
To better understand the effect of fluorination of the beta carbon on the behavior of the monolayers, the surfactant head conformations were analyzed. 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH (fluorinated beta carbon) was found to have a higher population of TG and GG conformers compared to 6
1 FTOH (fluorinated beta carbon) was found to have a higher population of TG and GG conformers compared to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH, which are the conformers where the OH dipole is perpendicular to the molecular backbone. This means that in the crystalline phase of 7
2 FTOH, which are the conformers where the OH dipole is perpendicular to the molecular backbone. This means that in the crystalline phase of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH, where the molecules lie normal to the interface, the OH dipoles of the TG and GG conformers lie in the interfacial plane and are able to align. The higher number of TG and GG conformers for 7
1 FTOH, where the molecules lie normal to the interface, the OH dipoles of the TG and GG conformers lie in the interfacial plane and are able to align. The higher number of TG and GG conformers for 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 over 6
1 over 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH may be due to intramolecular coulomb interactions between the negatively charged fluorines and the OH hydrogen, since the closer proximity of the fluorines to the OH group in the beta-fluorinated 7
2 FTOH may be due to intramolecular coulomb interactions between the negatively charged fluorines and the OH hydrogen, since the closer proximity of the fluorines to the OH group in the beta-fluorinated 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH would result in a stronger interaction.
1 FTOH would result in a stronger interaction.
4.1 Future work
The main factor determining if a LE–C transition is present is the length of the fluorinated segment, with m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n FTOH where m ≥7 expected to have the transition.36 Here it is also proposed that the length of the short alkyl segment (1 vs. 2 CH2 groups) is a factor due to differences in the surfactant head conformations. To test this hypothesis further, simulations of 6
n FTOH where m ≥7 expected to have the transition.36 Here it is also proposed that the length of the short alkyl segment (1 vs. 2 CH2 groups) is a factor due to differences in the surfactant head conformations. To test this hypothesis further, simulations of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 FTOH would allow a comparison to 6
1 FTOH would allow a comparison to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH in which the length of the alkyl segment is the only variable.
2 FTOH in which the length of the alkyl segment is the only variable.
These results indicate that the OPLS-AA force field is an encouraging model for further study of fluorosurfactant monolayer phase behavior, but also identified areas in which quantitative agreement with experimental data can be improved. The dependence of Πpt on temperature was underestimated, meaning the heat of the LE–C transition was too low compared to experiment (see eqn (9)). An analogous issue was seen in the case of the surfactant-free water|hexane interface as well: the (negative) gradient of σ with temperature was underestimated, i.e., surface entropy was underestimated (see eqn (2)). The TIP4P/2005 water model used here has been shown to reproduce the surface entropy of water well (to within 6%82), which raises the question of why this is not true for the water|hexane interface. Hu et al. showed that low or even negative entropy water surfaces can be induced by surfactants which cause the water dipole to orient parallel (or anti-parallel) to the interface normal.83 Although interactions between alkane and water are much weaker, it should be investigated if there is a connection between the increased charge of alkyl hydrogens used by L-OPLS53 and an increased ordering of water molecules at the water|alkane interface. It would then be useful to determine which parameters of the FTOH force field influence ΔH for the LE–C transition most strongly. For example, Fontaine et al.84 proposed a more negative charge on the fluorine atoms (−0.15 compared to −0.12|e|) in order to simulate phase equilibria of long perfluorinated fatty acids on the water surface.
Finally, as was shown in the ESI,† it is possible to relate the LE–C boundary line tension to interfacial pressure in the case where a single approximately circular domain of one phase is embedded in another. Further work could therefore involve quantitative calculation of the line tension of the LE–C boundary85 and the resulting effect on the interfacial pressure isotherm. More generally, methods for computing line tension would enable comparison to experimental measurements such as those by Sriram and Schwartz,86 as well as investigation of the molecular mechanism behind line tension reducing compounds (linactants).87
Author contributions
Stephen A. Burrows: conceptualization, investigation, software, visualization, writing – original draft, review & editing; Jang Won Shon: investigation, visualization, writing – original draft; Boyan Peychev: conceptualization, methodology, writing – original draft, review & editing; Radomir I. Slavchov: conceptualization, methodology, writing – review & editing; Stoyan K. Smoukov: conceptualization, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the EPSRC Fellowship No. EP/R028915/1 and the ESA MAP project WHISKIES.Notes and references
- R. C. Buck, J. Franklin, U. Berger, J. M. Conder, I. T. Cousins, P. D. Voogt, A. A. Jensen, K. Kannan, S. A. Mabury and S. P. van Leeuwen, Integr. Environ. Assess. Manage., 2011, 7, 513–541 CrossRef CAS PubMed.
- J. C. Costa, M. Fulem, B. Schröder, J. A. Coutinho, M. J. Monte and L. M. Santos, J. Chem. Thermodyn., 2012, 54, 171–178 CrossRef CAS.
- C. Hogue, C&EN Global Enterprise, 2021, 99, 17 Search PubMed.
- J. Glüge, M. Scheringer, I. T. Cousins, J. C. DeWitt, G. Goldenman, D. Herzke, R. Lohmann, C. A. Ng, X. Trier and Z. Wang, Environ. Sci.: Processes Impacts, 2020, 22, 2345–2373 RSC.
- Y. Xu, K. Jakobsson, F. Harari, E. M. Andersson and Y. Li, Environ. Res., 2023, 115525 CrossRef CAS PubMed.
- S. E. Fenton, A. Ducatman, A. Boobis, J. C. DeWitt, C. Lau, C. Ng, J. S. Smith and S. M. Roberts, Environ. Toxicol. Chem., 2021, 40, 606–630 CrossRef CAS PubMed.
- P. A. Rice, J. Aungst, J. Cooper, O. Bandele and S. V. Kabadi, Food Chem. Toxicol., 2020, 138, 111210 CrossRef CAS PubMed.
- U. Röthlisberger, K. Laasonen, M. L. Klein and M. Sprik, J. Chem. Phys., 1996, 104, 3692–3700 CrossRef.
- N. Kovalchuk, A. Trybala, V. Starov, O. Matar and N. Ivanova, Adv. Colloid Interface Sci., 2014, 210, 65–71 CrossRef CAS PubMed.
- T. Savvaides, J. P. Koelmel, Y. Zhou, E. Z. Lin, P. Stelben, J. J. Aristizabal-Henao, J. A. Bowden and K. J. Godri Pollitt, Curr. Environ. Health Rep., 2022, 1–13 Search PubMed.
- P. de Voogt and M. Sáez, TrAC, Trends Anal. Chem., 2006, 25, 326–342 CrossRef CAS.
- N. Wang, B. Szostek, R. C. Buck, P. W. Folsom, L. M. Sulecki, V. Capka, W. R. Berti and J. T. Gannon, Environ. Sci. Technol., 2005, 39, 7516–7528 CrossRef CAS PubMed.
- O. Zenasni, M. D. Marquez, A. C. Jamison, H. J. Lee, A. Czader and T. R. Lee, Chem. Mater., 2015, 27, 7433–7446 CrossRef CAS.
- M. J. A. Dinglasan, Y. Ye, E. A. Edwards and S. A. Mabury, Environ. Sci. Technol., 2004, 38, 2857–2864 CrossRef CAS PubMed.
- N. Wang, B. Szostek, R. C. Buck, P. W. Folsom, L. M. Sulecki, V. Capka, W. R. Berti and J. T. Gannon, Environ. Sci. Technol., 2005, 39, 7516–7528 CrossRef CAS PubMed.
- Y. D. Lei, F. Wania, D. Mathers and S. A. Mabury, J. Chem. Eng. Data, 2004, 49, 1013–1022 CrossRef CAS.
- S. Dimitrov, V. Kamenska, J. Walker, W. Windle, R. Purdy, M. Lewis and O. Mekenyan, SAR QSAR Environ. Res., 2004, 15, 69–82 CrossRef CAS PubMed.
- G. Yuan, H. Peng, C. Huang and J. Hu, Environ. Sci. Technol., 2016, 50, 942–950 CrossRef CAS PubMed.
- United States Environmental Protection Agency, National Service Center for Environmental Publications, 2014, pp. 1–10.
- K. M. Annunziato, C. E. Jantzen, M. C. Gronske and K. R. Cooper, Aquat. Toxicol., 2019, 208, 126–137 CrossRef CAS PubMed.
- G. S. Ladics, J. C. Stadler, G. T. Makovec, N. E. Everds and R. C. Buck, Drug Chem. Toxicol., 2005, 28, 135–158 CrossRef CAS PubMed.
- W. J. Fasano, S. C. Carpenter, S. A. Gannon, T. A. Snow, J. C. Stadler, G. L. Kennedy, R. C. Buck, S. H. Korzeniowski, P. M. Hinderliter and R. A. Kemper, Toxicol. Sci., 2006, 91, 341–355 CrossRef CAS PubMed.
- C. Vanparys, M. Maras, M. Lenjou, J. Robbens, D. Van Bockstaele, R. Blust and W. De Coen, Toxicol. In Vitro, 2006, 20, 1238–1248 CrossRef CAS PubMed.
- M. Maras, C. Vanparys, F. Muylle, J. Robbens, U. Berger, J. L. Barber, R. Blust and W. De Coen, Environ. Health Perspect., 2006, 114, 100–105 CrossRef CAS PubMed.
- A. K. Rosenmai, C. Taxvig, T. Svingen, X. Trier, B. M. A. van Vugt-Lussenburg, M. Pedersen, L. Lesné, B. Jégou and A. Vinggaard, Andrology, 2016, 4, 662–672 CrossRef CAS PubMed.
- M. Nian, K. Luo, F. Luo, R. Aimuzi, X. Huo, Q. Chen, Y. Tian and J. Zhang, Environ. Sci. Technol., 2020, 54, 8291–8299 CrossRef CAS PubMed.
- S. Liu, R. Yang, N. Yin and F. Faiola, J. Environ. Sci., 2020, 88, 187–199 CrossRef CAS PubMed.
- M. Ateia, A. Maroli, N. Tharayil and T. Karanfil, Chemosphere, 2019, 220, 866–882 CrossRef CAS PubMed.
- I. Ross, J. McDonough, J. Miles, P. Storch, P. Thelakkat Kochunarayanan, E. Kalve, J. Hurst, S. S. Dasgupta and J. Burdick, Remediation J., 2018, 28, 101–126 CrossRef.
- D. M. Wanninayake, J. Environ. Manage., 2021, 283, 111977 CrossRef CAS PubMed.
- R. I. Slavchov, S. I. Karakashev and I. B. Ivanov, Surfactant science and technology: Retrospects and prospects, Taylor & Francis Group, New York, 2014, pp. 53–117 Search PubMed.
- R. I. Slavchov and I. B. Ivanov, Soft Matter, 2017, 13, 8829–8848 RSC.
- V. Pradines, V. B. Fainerman, E. V. Aksenenko, J. Krägel, N. Mucic and R. Miller, Colloids Surf., A, 2010, 371, 22–28 CrossRef CAS.
- N. Denkov, S. Tcholakova, I. Lesov, D. Cholakova and S. K. Smoukov, Nature, 2015, 528, 392–395 CrossRef CAS PubMed.
- D. Cholakova, D. Glushkova, Z. Valkova, S. Tsibranska-Gyoreva, K. Tsvetkova, S. Tcholakova and N. Denkov, J. Colloid Interface Sci., 2021, 604, 260–271 CrossRef CAS PubMed.
- B. Peychev and R. I. Slavchov, J. Colloid Interface Sci., 2021, 594, 372–388 CrossRef CAS PubMed.
- I. L. Minkov, D. Arabadzhieva, I. E. Salama, E. Mileva and R. I. Slavchov, Soft Matter, 2019, 15, 1730–1746 RSC.
- R. I. Slavchov and I. B. Ivanov, J. Colloid Interface Sci., 2018, 532, 746–757 CrossRef CAS PubMed.
- T. Takiue, K. Sugino, T. Higashi, T. Toyomasu, Y. Hayami, N. Ikeda and M. Aratono, Langmuir, 2001, 17, 8098–8103 CrossRef CAS.
- S. Uredat and G. H. Findenegg, Langmuir, 1999, 15, 1108–1114 CrossRef CAS.
- S. Venkatesh Pingali, T. Takiue, G. Luo, A. M. Tikhonov, N. Ikeda, M. Aratono and M. L. Schlossman, J. Dispersion Sci. Technol., 2006, 27, 715–722 CrossRef.
- S. V. Pingali, T. Takiue, G. Luo, A. M. Tikhonov, N. Ikeda, M. Aratono and M. L. Schlossman, J. Phys. Chem. B, 2005, 109, 1210–1225 CrossRef CAS PubMed.
- P. Silva, D. Nova, M. Teixeira, V. Cardoso, P. Morgado, B. Nunes, R. Colaço, M.-C. Fauré, P. Fontaine and M. Goldmann, et al. , Nanomaterials, 2020, 10, 2257 CrossRef CAS PubMed.
- E. K. Watkins and W. L. Jorgensen, J. Phys. Chem. A, 2001, 105, 4118–4125 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- O. Borodin, G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2002, 106, 9912–9922 CrossRef CAS.
- H. O. Yadav, S. Harada, A.-T. Kuo, S. Urata and W. Shinoda, Mol. Phys., 2021, 119, e1910355 CrossRef.
- H. Feng, Y. Lin, Y. Sun, H. Cao, J. Fu, K. Gao and A. Zhang, Water Res., 2017, 114, 144–150 CrossRef CAS PubMed.
- W. Zygmunt and J. J. Potoff, Fluid Phase Equilib., 2016, 407, 314–321 CrossRef CAS.
- P. Morgado, A. R. Garcia, L. M. Ilharco, J. Marcos, M. Anastácio, L. F. G. Martins and E. J. M. Filipe, J. Phys. Chem. B, 2016, 120, 10091–10105 CrossRef CAS PubMed.
- D. J. Benvegnu and H. M. McConnell, J. Phys. Chem., 1992, 96, 6820–6824 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- S. W. Siu, K. Pluhackova and R. A. Böckmann, J. Chem. Theory Comput., 2012, 8, 1459–1470 CrossRef CAS PubMed.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- J. Alejandre and G. A. Chapela, J. Chem. Phys., 2010, 132, 014701 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- T. King, S. Butcher and L. Zalewski, Apocrita – High Performance Computing Cluster for Queen Mary University of London, 2017 Search PubMed.
- L. Martnez, R. Andrade, E. G. Birgin and J. M. Martnez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- H. J. Berendsen, J. V. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. Bekker, E. Dijkstra, M. Renardus and H. Berendsen, Mol. Simul., 1995, 14, 137–151 CrossRef CAS.
- S. Zeppieri, J. Rodrguez and A. López de Ramos, J. Chem. Eng. Data, 2001, 46, 1086–1088 CrossRef CAS.
- R. Aveyard and D. Haydon, Trans. Faraday Soc., 1965, 61, 2255–2261 RSC.
- E. A. Muller, Å. Ervik and A. Meja, Living J. Comput. Mol. Sci., 2020, 2, 21385 Search PubMed.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303–1334 CrossRef CAS.
- S. A. Burrows, I. Korotkin, S. K. Smoukov, E. Boek and S. Karabasov, J. Phys. Chem. B, 2021, 125, 5145–5159 CrossRef CAS PubMed.
- T. Gurkov and I. Ivanov, Proceedings of the 4th World Congress on Emulsions, Lyon, France, 2006, p. 509 Search PubMed.
- I. B. Ivanov, K. D. Danov, D. Dimitrova, M. Boyanov, K. P. Ananthapadmanabhan and A. Lips, Colloids Surf., A, 2010, 354, 118–133 CrossRef CAS.
- B. Pethica, Colloids Surf., A, 1994, 88, 147–155 CrossRef CAS.
- S. Baoukina, L. Monticelli, S. J. Marrink and D. P. Tieleman, Langmuir, 2007, 23, 12617–12623 CrossRef CAS PubMed.
- A. Gonçalves da Silva, E. Filipe, J. d'Oliveira and J. Martinho, Langmuir, 1996, 12, 6547–6553 CrossRef.
- Z. Luo, S. A. Burrows, X. Fan, S. K. Smoukov and E. S. Boek, Carbon, 2021, 183, 438–448 CrossRef CAS.
- D. Frenkel and R. Eppenga, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1776 CrossRef CAS PubMed.
- R. I. Slavchov, I. M. Dimitrova and T. Ivanov, J. Chem. Phys., 2015, 143, 154707 CrossRef PubMed.
- D. Mohammad-Aghaie, E. Mace, C. A. Sennoga, J. M. Seddon and F. Bresme, J. Phys. Chem. B, 2010, 114, 1325–1335 CrossRef CAS PubMed.
- A. Olżyńska, M. Zubek, M. Roeselova, J. Korchowiec and L. Cwiklik, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 3120–3130 CrossRef PubMed.
- M. Javanainen, A. Lamberg, L. Cwiklik, I. Vattulainen and O. S. Ollila, Langmuir, 2018, 34, 2565–2572 CrossRef CAS PubMed.
- A. Stachowicz-Kuśnierz, S. Trojan, L. Cwiklik, B. Korchowiec and J. Korchowiec, Chem. – Eur. J., 2017, 23, 5307–5316 CrossRef PubMed.
- J. Hu, H. Liu, P. Xu, Y. Shang and H. Liu, Langmuir, 2019, 35, 13452–13460 CrossRef CAS PubMed.
- A. Stachowicz-Kuśnierz, B. Korchowiec, E. Rogalska and J. Korchowiec, Adv. Colloid Interface Sci., 2022, 102659 CrossRef PubMed.
- T. A. Pascal and W. A. Goddard III, J. Phys. Chem. B, 2014, 118, 5943–5956 CrossRef CAS PubMed.
- D. Hu, A. Mafi and K. C. Chou, J. Phys. Chem. B, 2016, 120, 2257–2261 CrossRef CAS PubMed.
- P. Fontaine, E. J. Filipe, M.-C. Fauré, T. Rego, S. Taßler, A. C. Alves, G. M. Silva, P. Morgado and M. Goldmann, Molecules, 2019, 24, 3590 CrossRef CAS PubMed.
- C. M. Rosetti, G. G. Montich and C. Pastorino, J. Phys. Chem. B, 2017, 121, 1587–1600 CrossRef CAS PubMed.
- I. Sriram and D. K. Schwartz, Surf. Sci. Rep., 2012, 67, 143–159 CrossRef CAS.
- S. Trabelsi, S. Zhang, T. R. Lee and D. K. Schwartz, Phys. Rev. Lett., 2008, 100, 037802 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01444d |
| This journal is © The Royal Society of Chemistry 2024 |