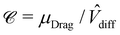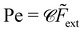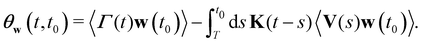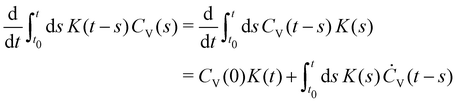Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Force renormalization for probes immersed in an active bath
Jeanine
Shea
 *a,
Gerhard
Jung
*a,
Gerhard
Jung
 b and
Friederike
Schmid
b and
Friederike
Schmid
 *c
*c
aInstitut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: j.shea@tu-berlin.de
bLaboratoire Charles Coulomb (L2C), Université de Montpellier, CNRS, 34095 Montpellier, France
cInstitut für Physik, Johannes Gutenberg-Universität Mainz, 55099 Mainz, Germany. E-mail: friederike.schmid@uni-mainz.de
First published on 2nd February 2024
Abstract
Langevin equations or generalized Langevin equations (GLEs) are popular models for describing the motion of a particle in a fluid medium in an effective manner. Here we examine particles immersed in an inherently nonequilibrium fluid, i.e., an active bath, which are subject to an external force. Specifically, we consider two types of forces that are highly relevant for microrheological studies: A harmonic, trapping force and a constant, “drag” force. We study such systems by molecular simulations and use the simulation data to extract an effective GLE description. We find that within this description, in an active bath, the external force in the GLE is not equal to the physical external force, but rather a renormalized external force, which can be significantly smaller. The effect cannot be attributed to the mere temperature renormalization, which is also observed.
1 Introduction
Microrheology focuses on linking the microscopic dynamics of a system to its macroscopic response. The goal of microrheological studies is then to investigate the behavior of an immersed and experimentally detectable probe particle to gain knowledge about the surrounding medium which is made up of smaller particles.1–3 Microrheological techniques have been used to study a variety of different mediums ranging from complex fluids4–7 to granular matter.8–12In general, microrheological studies can be classified in two categories: passive and active.13,14 Passive microrheology monitors the diffusive motion of an immersed probe to extract information about fluctuations and transport properties of the medium. Active microrheology relies on subjecting a probe to an external force to determine the properties of the immersive medium. This is true for both experimental and computational microrheological studies. The external forces often take the form of either constant, drag forces15–17 or harmonic, trapping forces.18 Microrheological studies employing these forms of external forces have also recently been applied to probe the properties of active systems.19–24
Since microrheology focusses on investigating a small number of immersed probes, usually described by their positions and velocities, the extracted information will correspond to a strongly coarse-grained description, in which the surrounding medium is replaced by effective friction coefficients and fluctuations. In previous studies, for example, the system of a passive probe immersed in an active bath and subject to a harmonic potential has been mapped onto an overdamped Langevin equation.25–27 However, in other studies, it has been shown that, under certain conditions, the dynamics of a probe immersed in an active bath cannot be assumed to be Markovian.28,29 In this case, the Langevin equation is no longer sufficient and, instead, a generalized Langevin equation (GLE) is required to capture the system dynamics in a coarse-grained model.30,31
A simple and popular Ansatz for such a GLE is to assume the form17,31–36
 | (1) |
In this work we will take a complementary approach and use the GLE (1) as a starting point to extract effective equations of motion for the coarse-grained variables from microscopic simulations. Thus, our goal is not to derive a GLE model (1) from a microscopic Hamiltonian (which may not be rigorously possible), but to map an ensemble of microscopic trajectories onto the model (1) such that important static properties, such as the distribution of particle positions, and important dynamic properties, such as the average drift and velocity correlation functions, are reproduced by the dynamical system defined by the GLE. All averages, 〈…〉, will therefore refer to the average over this, possibly non-equilibrium, ensemble. One should note that one has some freedom as to how to distribute the total force between f, K and Γ.17,30,49 At equilibrium, a popular Ansatz33,48,50,51 is to assume that f subsumes all reversible interactions (which also include medium-mediated interactions) and therefore correspond to the force emerging from static coarse-graining. The other two terms then characterize the thermal coupling with the medium; i.e., they can be seen as a thermostat52 with colored noise.
What happens in active systems far from equilibrium? This question has been intensely discussed in the literature,19,22,23,47,49,53–57 often focusing on the question of whether the 2FDT is still fulfilled. However, as mentioned above, one has some freedom as to how to distribute the net bath forces between the different terms of the GLE. In the absence of drift forces, it has been shown17,58 that many memory reconstruction methods18,58–62 will yield GLEs that automatically satisfy a generalized 2FDT,
| 〈Γ(t0)Γ(t)〉 = MK(t − t0)〈VV〉 | (2) |
In the present paper, we then address the following question: How does the active bath affect the drift force f on the probe in the presence of external drag forces? As prototype test systems, we consider a passive probe in a homogeneous bath of active Langevin particles63–65 subject to two typical types of external forces Fext: a constant drag force and a harmonic trap force.
Our main result can be summarized as follows: we can obtain a consistent GLE mapping of this system, but only if we renormalize the force: the drift force differs from the applied force by a factor α which is much smaller than one. The factor does not depend on whether the potential is linear or harmonic. Physically, this means that the active bath particles help the probe particle to access high potential regions not only by increasing its kinetic energy (i.e., effectively increasing its temperature), but also by actively pushing it into these regions.
By a mathematical analysis, we identify a generalized equipartition theorem which characterizes the relation between the renormalized force and the kinetic energy of the particle. The analysis also shows that the generalized 2FDT in our model may acquire an extra term in non-equilibrium systems, consistent with ref. 36, 54 and 55, which however vanishes within the error in the systems considered here.
Our results are of high importance for the interpretation of active microrheology in active systems, as they show how to extract information about an active bath by observing transport of immersed tracer particles. Our results are particularly pertinent to systems in which the constituents are of non-negligible mass, i.e. where the constituents are meso- or macroscopic. Examples of such systems include synthetic active robots66–68 and granular active matter.69–72 Whereas there exist previous studies on the microrheological properties of active granular matter,8–12 synthetic active robots is an emerging field and we are not aware of any studies of microrheological studies of such systems.
2 Model and simulation details
We consider a three dimensional system of a passive probe immersed in a bath of active Langevin particles (ALPs) of mass m and radius R, which propel themselves with a constant force F0 subject to rotational diffusion with a diffusion constant DR.63–65,73–78 An analogous model in the overdamped limit (a probe immersed in a bath of active Brownian particles with mass m → 0) has often been focused on in previous studies.25,79–84 These ABP fluids have a number of similar properties to ALP fluids, including the quadratic scaling of the effective temperature (or effective diffusion constant in the case of an ABP) with the bath activity and the velocity correlations.65The ALPs are coupled to a thermal bath with temperature kBT via a Markovian, Langevin thermostat, and they interact with each other and with the immersed probe by repulsive hard core interactions of the Weeks–Chandler–Anderson (WCA) type.85 Specifically, we follow ref. 63–65 and set the rotational inertia of ALPs to zero for simplicity. The equations of motion for an ALP, n, in the bath, are thus given by
 | (3) |
 | (4) |
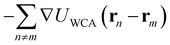 in eqn (3) describe the WCA interactions with the probe and with all other ALPs, respectively.
in eqn (3) describe the WCA interactions with the probe and with all other ALPs, respectively.
The time evolution of the orientation of the ALP, e(t), is governed by rotational diffusion,
| ė(t) = N(t) × e(t), | (5) |
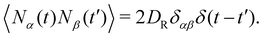 | (6) |
All simulations are performed using LAMMPS.86 The length, energy, and mass scales in the simulation system are defined by the Lennard-Jones (LJ) diameter σ, energy ε, and ALP mass m, respectively, which defines the LJ time scale 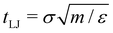 . We use truncated and shifted LJ potentials with the energy scale ε which are cut off at
. We use truncated and shifted LJ potentials with the energy scale ε which are cut off at 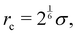 resulting in purely repulsive WCA interactions as described above. The cubic simulation box has periodic boundary conditions in all three dimensions and a side length based on the desired density of the bath. The probe has a mass of M = 100m and is defined as a rigid body with a radius Rp = 3σ. The body of the probe is constructed so that its surface is smooth, resulting in full slip boundary conditions for the LJ fluid. The active bath consists of ALPs with a mass of mALP = 1m and a radius of R = 0.5σ. The number of ALPs in the bath is determined by the desired density of the bath. The parameters of the thermal bath are chosen such that kBT = 1
resulting in purely repulsive WCA interactions as described above. The cubic simulation box has periodic boundary conditions in all three dimensions and a side length based on the desired density of the bath. The probe has a mass of M = 100m and is defined as a rigid body with a radius Rp = 3σ. The body of the probe is constructed so that its surface is smooth, resulting in full slip boundary conditions for the LJ fluid. The active bath consists of ALPs with a mass of mALP = 1m and a radius of R = 0.5σ. The number of ALPs in the bath is determined by the desired density of the bath. The parameters of the thermal bath are chosen such that kBT = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε and η = 1m/(σtLJ), resulting in γ = 3πm/tLJ, DT = (3π)−1σ2/tLJ, and DR = π−1/tLJ. For the active bath, we choose an active force of F0 = 50mσ2/tlJ because ref. 65 showed that this force is sufficiently large to induce non-equilibrium probe dynamics, but not large enough to cause motility induced phase separation in the active bath.
ε and η = 1m/(σtLJ), resulting in γ = 3πm/tLJ, DT = (3π)−1σ2/tLJ, and DR = π−1/tLJ. For the active bath, we choose an active force of F0 = 50mσ2/tlJ because ref. 65 showed that this force is sufficiently large to induce non-equilibrium probe dynamics, but not large enough to cause motility induced phase separation in the active bath.
In the following, for consistency with previous work,65 we will often also use dimensionless quantities ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = tγ/m,
= tγ/m, 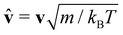 ,
, 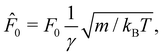 and
and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) R = Dm/γ. Dimensionless quantities will be denoted with a hat. Density values and the spring constant of the harmonic potential, and all distances are given in LJ units. In these cases, the LJ units are explicitly written with the value.
R = Dm/γ. Dimensionless quantities will be denoted with a hat. Density values and the spring constant of the harmonic potential, and all distances are given in LJ units. In these cases, the LJ units are explicitly written with the value.
3 Results
The behavior of free particles in the ALP bath has been reported in previous work65 for different bath densities and active forces F0. One important result of this study was that the bath transmits a kinetic temperature to the probe (kBTeff = M〈V2〉/3 in 3D), which, somewhat unexpectedly, can be significantly higher than the effective kinetic temperature of the ALP bath particles. In the present article, we will analyze the probe dynamics in the presence of external forces as described below.3.1 Harmonic potential
We trap the immersed probe in a harmonic potential such that its equation of motion is: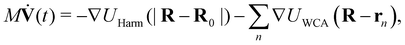 | (7) |
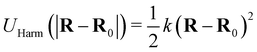 is the harmonic, trapping potential with trapping constant k and trap center R0. We test three different values of k: k = 1, 5, and 10 in LJ units of εσ−2.
is the harmonic, trapping potential with trapping constant k and trap center R0. We test three different values of k: k = 1, 5, and 10 in LJ units of εσ−2.
We map our system dynamics onto the GLE:18,31
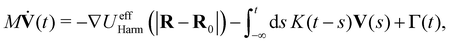 | (8) |
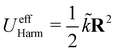 may differ from UHarm, as is known also for non-linear systems.30,87 Here and throughout, we will use the stationary GLE,58i.e., the initial time T in eqn (1) is taken to be in the infinite past. Following a strategy outlined in ref. 58 (see also Appendix C), we use eqn (8) to construct a Volterra equation of the second kind,
may differ from UHarm, as is known also for non-linear systems.30,87 Here and throughout, we will use the stationary GLE,58i.e., the initial time T in eqn (1) is taken to be in the infinite past. Following a strategy outlined in ref. 58 (see also Appendix C), we use eqn (8) to construct a Volterra equation of the second kind,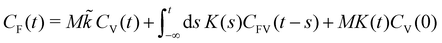 | (9) |
![[V with combining dot above]](https://www.rsc.org/images/entities/b_char_0056_0307.gif) ), the velocity autocorrelation function (VACF) CV(t) = 〈V(t)·V(0)〉, and the cross correlation CFV(t) = 〈F(t)·V(0)〉. Eqn (9) can then be used to determine K(t) following a modification of an algorithm presented in ref. 58. Details are shown in Appendix A.
), the velocity autocorrelation function (VACF) CV(t) = 〈V(t)·V(0)〉, and the cross correlation CFV(t) = 〈F(t)·V(0)〉. Eqn (9) can then be used to determine K(t) following a modification of an algorithm presented in ref. 58. Details are shown in Appendix A.
The corresponding 2FDT for GLE (8) in the presence of a harmonic potential is derived in Appendix A:
〈Γ(0)Γ(t)〉 = MK(t)〈VV〉 + ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) I(t)〈VR〉 I(t)〈VR〉 | (10) |
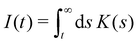 . It differs from eqn (2) by an additional term which is proportional to the instantaneous correlations between the position and the velocity. This term is zero at equilibrium due to time reversal symmetry, but could, in principle, be relevant in stationary active systems. In the systems considered in the present work, however, 〈VR〉 was always found to be zero within the statistical error (data not shown). We infer that the additional term can be neglected and the coarse-grained GLE for our systems satisfies the usual generalized 2FDT, eqn (2).
. It differs from eqn (2) by an additional term which is proportional to the instantaneous correlations between the position and the velocity. This term is zero at equilibrium due to time reversal symmetry, but could, in principle, be relevant in stationary active systems. In the systems considered in the present work, however, 〈VR〉 was always found to be zero within the statistical error (data not shown). We infer that the additional term can be neglected and the coarse-grained GLE for our systems satisfies the usual generalized 2FDT, eqn (2).
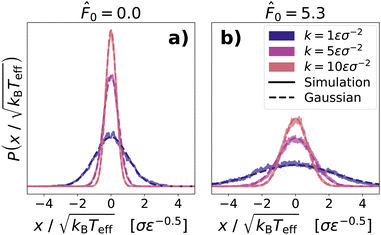
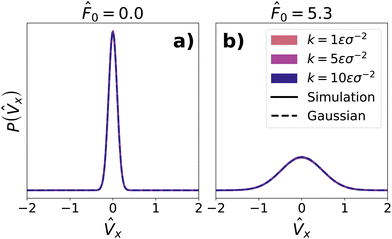
We see in (Fig. 1b), that the position distribution of the probe remains Gaussian and centered around the trap center even in an active bath, as in equilibrium. However, the variance of the probe position distribution is higher than that of a probe immersed in a passive bath. These results are consistent with previous studies of a harmonically confined probe immersed in an active bath.88–90 We note that, for higher values of k when the range of confinement is comparable to the persistence length of the active particles, the distribution has been shown to become non-Gaussian.90 However, all our values of k remain within this limit.
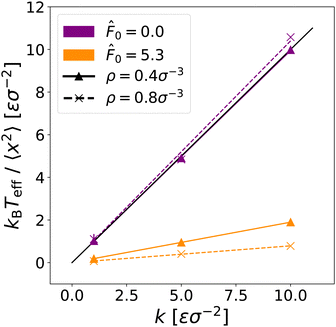
These previous studies have attributed the enhanced variance of the position distribution to an enhanced temperature. However, when we use the definition of the enhanced kinetic temperature as quoted earlier from ref. 65, we find that kBTeff/〈x2〉 ≠ k, as can be seen in Fig. 2 where we plot kBTeff/〈x2〉 as a function of k. Furthermore, we see in Fig. 2 that the value of kBTeff/〈x2〉 for a given constraint k is not density independent in the active case, as we would expect in equilibrium.
Nevertheless, it does appear that kBTeff/〈x2〉 ∝ k. We therefore posit that, due to the activity of the bath particles, the external force on the probe needs to be renormalized in our coarse-grained GLE model. Then, kBTeff/〈x2〉 = ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) for the active bath, where
for the active bath, where ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = αk is the renormalized spring constant of the harmonic potential with renormalization factor α.
= αk is the renormalized spring constant of the harmonic potential with renormalization factor α.
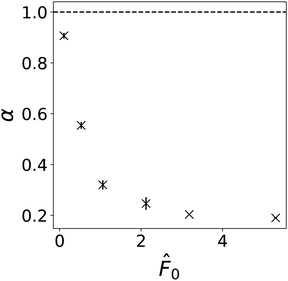
To determine the renormalization factor α, we fit our data in Fig. 2 to a line with zero offset. As expected, in the passive case, α ≈ 1 for both bath densities, i.e., the external force does not need to be renormalized and is density independent. In the active case, we find that for a bath with density ρ = 0.4σ−3, α0.4 = 0.190 ± 0.001 and for a bath with density ρ = 0.8σ−3, α0.8 = 0.079 ± 0.002. In both cases, α < 1, meaning that the activity of the bath effectively decreases the spring constant of the harmonic potential and, thereby, decreases the trapping force exerted on the probe. In Appendix B, we show how α varies as a function of ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0. We find that α decreases from the equilibrium value α = 1 as a function of
0. We find that α decreases from the equilibrium value α = 1 as a function of ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0. Furthermore, we find that a renormalization factor is necessary even for very small bath activities (
0. Furthermore, we find that a renormalization factor is necessary even for very small bath activities (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 1).
0 = 1).
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) obtained from Section 3.1.1. Interestingly, we find that the reconstructed memory kernel fails to go to zero in the long time limit if we insert the bare spring constant or omit the spring potential altogether. In Appendix A, we analyze this problem more generally. We show that, for any confining renormalized external potential Ueff, inverting the Volterra equation to extract the corresponding memory kernel is bound to fail unless the following (tensorial) condition is fulfilled:
obtained from Section 3.1.1. Interestingly, we find that the reconstructed memory kernel fails to go to zero in the long time limit if we insert the bare spring constant or omit the spring potential altogether. In Appendix A, we analyze this problem more generally. We show that, for any confining renormalized external potential Ueff, inverting the Volterra equation to extract the corresponding memory kernel is bound to fail unless the following (tensorial) condition is fulfilled:| 〈R∇Ueff〉 = M〈VV〉. | (11) |
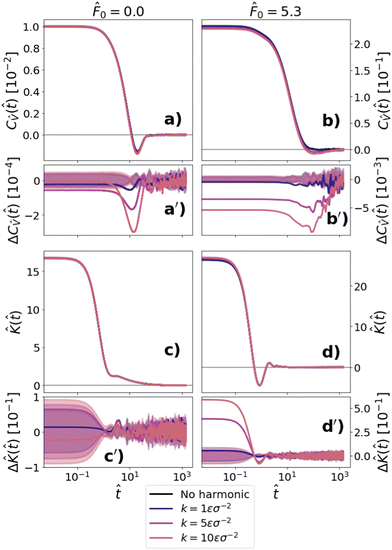
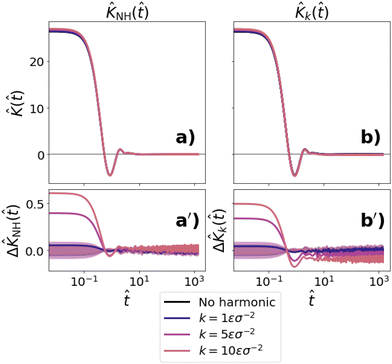
From Fig. 3(a) and (c), we see that, when immersed in a passive bath, the VACF/memory kernel of a harmonically constrained probe only differs slightly from that of an unconstrained probe. Namely, the oscillation of the VACF for a harmonically constrained probe is slightly deeper than that for an unconstrained probe. The increased depth of this oscillation relates to the restoring force on the probe; therefore, we expect that its depth would increase with an increased value of k, which agrees with what we see in (Fig. 3a). The memory kernel of a free vs. trapped probe in a passive bath exhibits even fewer differences. In fact, the differences between the memory kernel of a free vs. trapped particle all fall within our error bounds.
When immersed in an active bath, the VACF of the harmonically constrained probe depends more significantly on the confinement strength than in the passive case. In the inlay of (Fig. 3b), it can be observed that the trapped probe has a decreased local kinetic temperature, CV(0), in comparison with that of a free probe. Furthermore, the local kinetic temperature decreases as the trapping strength k increases. Within the range of k values we studied, however, this effect is relatively small (two orders of magnitude smaller than that of the kinetic temperature) and cannot be readily seen in the probe velocity distributions (see Appendix D). Therefore, this change in the kinetic temperature cannot account for the necessary rescaling of k. The memory also slightly depends on k at small times, but the differences are again smaller than the error at times ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) > 0.1.
> 0.1.
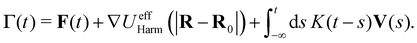 | (12) |
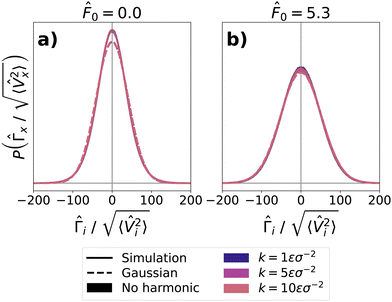
In Fig. 4, we see that in both the case of a passive and an active bath, the stochastic force distribution calculated from simulation data (solid lines) approximately matches a zero-centered Gaussian with the same standard deviation (dashed lines). The only deviations from the zero-centered Gaussian are an enhanced peak at the center of the distribution, which we infer results from the low density of the bath and which was also seen for an unconstrained probe in ref. 65.
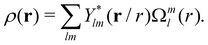 | (13) |
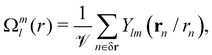 | (14) |
 runs over all bath particles in a spherical shell δr around the particle (i.e., their distance from the probe center lies within the interval [r − δr/2
runs over all bath particles in a spherical shell δr around the particle (i.e., their distance from the probe center lies within the interval [r − δr/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r + δr/2]), and
r + δr/2]), and 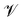 is the volume of the shell,
is the volume of the shell, 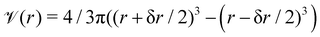 . Specifically, the radial average of ρ(r) can be obtained from
. Specifically, the radial average of ρ(r) can be obtained from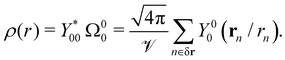 | (15) |
We first characterize the bath in the case that the probe is free. In comparing the radially averaged density curves for a passive and an active bath surrounding a free probe in (Fig. 5a), we see that the first peak of the density curve is higher in an active bath. Hence adding activity to the bath leads to a higher density of bath particles in the vicinity of the probe. We also see that the first shell of active particles is shifted slightly closer to the probe center in comparison with that of the passive bath. Furthermore, the spacing between the first and second shells of the active bath particles are closer together. This – in combination with the forward shifted first shell – leads to the coincidence of a peak in the density profile of the active bath with a trough in the density profile of the active bath at r ≈ 4.9σ. These closer shells indicate that ALPs are able to move closer to the probe, and each other, than passive bath particles. We infer that this ability stems from the higher kinetic energy of ALPs due to their active force, which allows them to overcome more of the repulsive potential from WCA interactions with the probe.
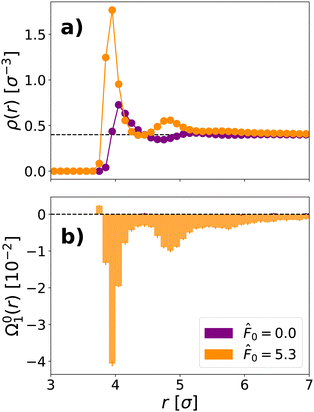 | ||
Fig. 5 (a) Radially averaged density (ρ(r), see eqn (15)) and (b) dipole moment (Ω01(r), see eqn (14)), surrounding a free probe immersed in a bath with activities ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 0.0 (indigo) and 0 = 0.0 (indigo) and ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3 (orange). The probe has a radius Rp = 3.0σ and is immersed in a bath with global density ρ = 0.4σ−3. The black dashed lines mark the global density in (a) and the zero baseline in (b). 0 = 5.3 (orange). The probe has a radius Rp = 3.0σ and is immersed in a bath with global density ρ = 0.4σ−3. The black dashed lines mark the global density in (a) and the zero baseline in (b). | ||
In a passive bath, all higher order moments of the bath are zero. However, in an active bath, the active fluid acquires a negative dipole moment surrounding the probe, which is sustained to large values of r, as can be seen in (Fig. 5b). This negative dipole moment indicates that ALPs collect behind the probe relative to its instantaneous velocity, even at large distances from the probe. The phenomenon of active particles gathering behind an immersed passive probe has previously been seen for a probe dragged through an ABP bath in ref. 20, where it is framed as a difference between the forces behind and in front of the probe. We find no significant structure in higher order spherical harmonics for either the active or passive bath.
Returning to the system of a probe immersed in an active bath and subject to a harmonic constraint, we find that in spite of the additional harmonic force on the probe, the density profile of the ALP bath (as calculated from eqn (15)) remains identical for a trapped and a free probe (see Fig. 6(b)). Additionally, its dipole moment remains the same whether the probe is trapped or free (see Fig. 6(b)). This is most likely due to the fact that the forces exerted by the harmonic trap are relatively small, i.e., within the linear regime. We will see in Section 3.2 that the situation changes if we subject the probe to very large forces.
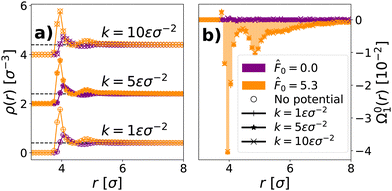 | ||
Fig. 6 (a) Radially averaged density (eqn (15)) and (b) dipole moment (Ω01(r)), see (eqn (14)), surrounding a harmonically confined probe immersed in a bath with global density ρ = 0.4σ−3 and activity level ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 0.0 (indigo) and 0 = 0.0 (indigo) and ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3 (orange). The probe has a radius Rp = 3.0σ. Different symbols show different harmonic trapping strengths k = 1εσ−3 (plus symbol), k = 5εσ−3 (star symbol), k = 10εσ−3 (x symbol). The results for a free probe are shown in (a) by open circles and in (b) by bars. For ease of visualization, in (a) we add different vertical shifts to the density profiles for different trapping strengths and mark the global density with black dashed lines. 0 = 5.3 (orange). The probe has a radius Rp = 3.0σ. Different symbols show different harmonic trapping strengths k = 1εσ−3 (plus symbol), k = 5εσ−3 (star symbol), k = 10εσ−3 (x symbol). The results for a free probe are shown in (a) by open circles and in (b) by bars. For ease of visualization, in (a) we add different vertical shifts to the density profiles for different trapping strengths and mark the global density with black dashed lines. | ||
3.2 Constant drag force
Next we consider a passive probe which is pulled through a bath of interacting ALPs with a constant ‘drag’ force along the x-axis: F = Fextex (see Fig. 7). Thus, the equation of motion for the probe is: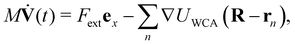 | (16) |
![[V with combining macron]](https://www.rsc.org/images/entities/b_char_0056_0304.gif) .
.
 | ||
| Fig. 7 Cartoon of a passive probe dragged by a constant, external force through a bath of active Langevin particles. | ||
In our coarse-graining approach we map this system onto a stationary GLE of the form
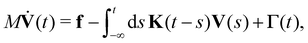 | (17) |
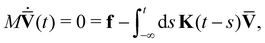 | (18) |
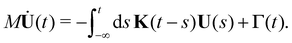 | (19) |
![[V with combining macron]](https://www.rsc.org/images/entities/b_char_0056_0304.gif) such that
such that ![[V with combining macron]](https://www.rsc.org/images/entities/b_char_0056_0304.gif) is the drift velocity of the probe. Eqn (19) has exactly the same form as the GLE for an unconstrained probe. The only difference is that the velocity U(t) is now the velocity of the probe in a co-moving frame with velocity
is the drift velocity of the probe. Eqn (19) has exactly the same form as the GLE for an unconstrained probe. The only difference is that the velocity U(t) is now the velocity of the probe in a co-moving frame with velocity ![[V with combining macron]](https://www.rsc.org/images/entities/b_char_0056_0304.gif) . Since the equations are of the same form, eqn (19) can also be transformed into a Volterra equation, which can then be inverted to find the memory kernel of the probe. The generalized 2FDT is fulfilled by construction.17 Using such a mapping, the effective drift force on the probe can then be calculated from eqn (18), as
. Since the equations are of the same form, eqn (19) can also be transformed into a Volterra equation, which can then be inverted to find the memory kernel of the probe. The generalized 2FDT is fulfilled by construction.17 Using such a mapping, the effective drift force on the probe can then be calculated from eqn (18), as 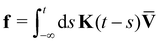 .
.
At equilibrium, the behavior of the probe at small drag velocities can be described by linear response theory. One purpose of the present study is to examine whether a similar behavior can be found in an active bath, if we renormalize the force according to the prescription found in the previous Section 3.1. In linear response theory, the drift velocity of the probe in response to a constant drag force Fext is given by the linear relation 〈V〉 = μeqFext with the mobility 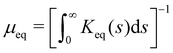 . Here Keq is the equilibrium memory kernel evaluated at Fext = 0.
. Here Keq is the equilibrium memory kernel evaluated at Fext = 0.
The analogous behavior in an active bath would be 〈V〉 = μ0Feffext, where μ0 is determined from the integrated memory kernel of the free probe and Feffext = αFext is renormalized according to Section 3.1. We should note that that linear response theory is not generally valid in our system.65 Our goal here is to probe the existence of a linear regime where 〈V〉 ∝ Fext, and test the relation 〈V〉/Fext = αμ0 in that regime.
In ref. 20, a probe dragged through a 2D bath of ALPs has been studied for drag forces well beyond the linear regime. Here, we focus on small to intermediate forces and possible transitions between linear and nonlinear regimes.
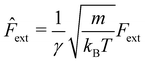 and
and 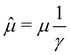 . Furthermore, to unify the notation for active and passive bath particles, we define a dimensionless renormalized force
. Furthermore, to unify the notation for active and passive bath particles, we define a dimensionless renormalized force ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext, which is given by
ext, which is given by ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext =
ext = ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext in a passive bath and
ext in a passive bath and ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext = α
ext = α![[F with combining circumflex]](https://www.rsc.org/images/entities/char_0046_0302.gif) ext in an active bath. We will consider three values of the mobility (in dimensionless form): (i) the drag mobility
ext in an active bath. We will consider three values of the mobility (in dimensionless form): (i) the drag mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag defined by
Drag defined by〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉 = x〉 = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag Drag![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext, ext, | (20) |
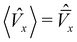 is the dimensionless average velocity along the x-axis;
is the dimensionless average velocity along the x-axis;
(ii) the linear GLE mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 0 defined by
0 defined by
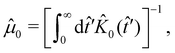 | (21) |
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) 0 is the (isotropic) dimensionless memory kernel of a free probe (at
0 is the (isotropic) dimensionless memory kernel of a free probe (at ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext = 0); and (iii) the tensorial GLE mobility
ext = 0); and (iii) the tensorial GLE mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) K defined by
K defined by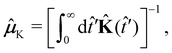 | (22) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉/
x〉/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff, where the diffusion velocity scale
diff, where the diffusion velocity scale ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff is given by
diff is given by 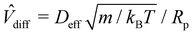 and depends on the probe radius Rp = 3.0σ and the effective diffusion coefficient of an isolated ALP, DALPeff = kBTALPeff/γ with kBTALPeff = kBT[1 +
and depends on the probe radius Rp = 3.0σ and the effective diffusion coefficient of an isolated ALP, DALPeff = kBTALPeff/γ with kBTALPeff = kBT[1 + ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 02/(3 + 6
02/(3 + 6![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) R)] as calculated in ref. 65. In terms of
R)] as calculated in ref. 65. In terms of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext, the Peclet number is given by Pe =
ext, the Peclet number is given by Pe = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag
Drag![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext/
ext/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff (see Appendix E).
diff (see Appendix E).
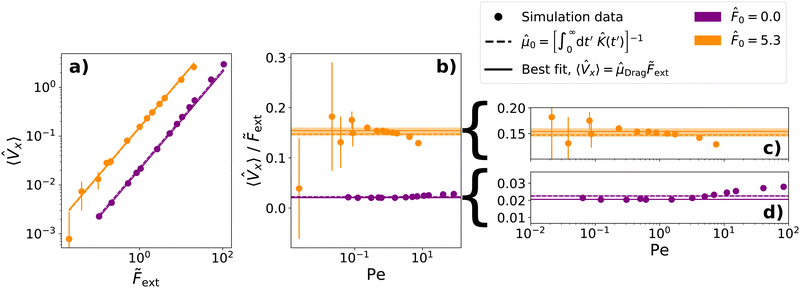
In (Fig. 8a), we graph 〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉 as a function of
x〉 as a function of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext to determine the drag mobility
ext to determine the drag mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag within the linear regime using eqn (20). We note that, for low values of Fext in an active bath, the stochastic motion of the active bath particles dominates the applied external force. Hence, the deviation of 〈
Drag within the linear regime using eqn (20). We note that, for low values of Fext in an active bath, the stochastic motion of the active bath particles dominates the applied external force. Hence, the deviation of 〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉 is significantly larger for low values of Fext, resulting in larger errors in our data.
x〉 is significantly larger for low values of Fext, resulting in larger errors in our data.
We extract a mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag = 0.02057 ± 0.00006 for a probe immersed in a passive bath (
Drag = 0.02057 ± 0.00006 for a probe immersed in a passive bath (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 0.0) with a density ρ = 0.4σ−3. For a probe in an active bath (
0 = 0.0) with a density ρ = 0.4σ−3. For a probe in an active bath (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3) of density ρ = 0.4σ−3, we extract a mobility of
0 = 5.3) of density ρ = 0.4σ−3, we extract a mobility of ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag = 0.154 ± 0.006. Comparing these values, we see that increasing the activity of the bath also increases the mobility of the probe particle.
Drag = 0.154 ± 0.006. Comparing these values, we see that increasing the activity of the bath also increases the mobility of the probe particle.
On the other hand, using the memory kernels of a free probe and eqn (21), we obtain the linear GLE mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 0 = 0.0226 ± 0.0003 for a probe in a passive bath of density ρ = 0.4σ−3 and
0 = 0.0226 ± 0.0003 for a probe in a passive bath of density ρ = 0.4σ−3 and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 0 = 0.147 ± 0.002 for a probe in an active bath of density ρ = 0.4σ−3 with
0 = 0.147 ± 0.002 for a probe in an active bath of density ρ = 0.4σ−3 with ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3. These values for the mobility agree well with those calculated from eqn (20). The slight discrepancy between values is most likely due to the reconstruction of the memory, which becomes less accurate at longer times. We emphasize that renormalizing the drift force in eqn (20) is essential for reaching this agreement.
0 = 5.3. These values for the mobility agree well with those calculated from eqn (20). The slight discrepancy between values is most likely due to the reconstruction of the memory, which becomes less accurate at longer times. We emphasize that renormalizing the drift force in eqn (20) is essential for reaching this agreement.
For high forces, the drag mobility is no longer a fixed value. In (Fig. 8b), we show the force dependent drag mobility (![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag(
Drag(![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext) = 〈
ext) = 〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉/
x〉/![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext) as a function of the Peclet number. We expect
ext) as a function of the Peclet number. We expect ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag(
Drag(![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext) to be constant within the linear response regime for a probe immersed in a passive bath. The figure shows that this is indeed the case for Peclet number up to Pe ∼ 1. For probes immersed in an active bath, we observe a very similar behavior, i.e., a crossover from roughly constant drag mobility to force dependent drag mobility around Pe ∼ 1. Identifying this crossover is more difficult in this case because the measured values for
ext) to be constant within the linear response regime for a probe immersed in a passive bath. The figure shows that this is indeed the case for Peclet number up to Pe ∼ 1. For probes immersed in an active bath, we observe a very similar behavior, i.e., a crossover from roughly constant drag mobility to force dependent drag mobility around Pe ∼ 1. Identifying this crossover is more difficult in this case because the measured values for ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag fluctuate strongly for low values of Pe. These fluctuations reflect the fact that the activity of the bath induces larger variations in the probe velocity.
Drag fluctuate strongly for low values of Pe. These fluctuations reflect the fact that the activity of the bath induces larger variations in the probe velocity.
We should note that, due to the enhanced diffusion of the active bath particles in comparison to the passive bath particles, equivalent Peclet numbers for a probe in an active and a passive bath correspond to different external drag forces (see also Appendix E). Much larger drag forces are required to achieve the same Peclet number for an active bath in comparison with a passive bath.
Fig. 8(c) and (d) show that the behavior beyond the linear response regime is qualitatively different for a probe immersed in an active vs. a passive bath. A probe dragged through a passive bath exhibits thinning behavior (increased mobility), whereas a probe dragged through a bath of ALPs exhibits thickening behavior (reduced mobility). Due to these opposite behaviors, the values of ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag(
Drag(![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext) for a passive and an active bath at the same Peclet number approach each other beyond the linear regime. We will discuss and analyze this further at the end of Section 3.2.5.
ext) for a passive and an active bath at the same Peclet number approach each other beyond the linear regime. We will discuss and analyze this further at the end of Section 3.2.5.
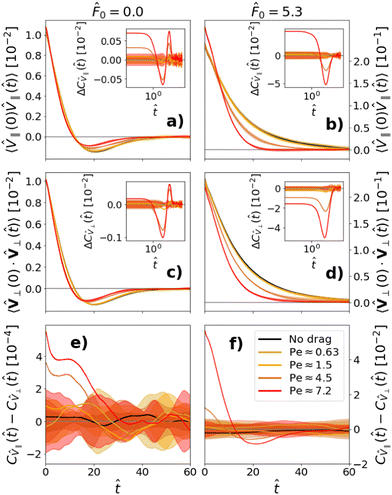
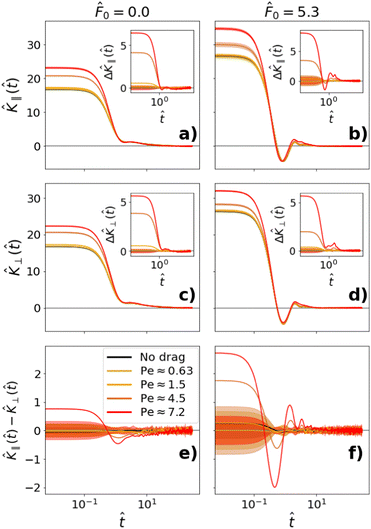
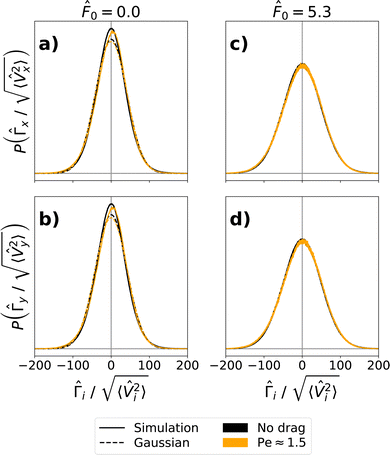
As we would expect, within the linear regime (Pe < 1), the VACF and memory kernel are isotropic and independent of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext for a probe dragged through a passive bath. We note that, in Fig. 10(a) and (b), the memory kernel for a probe dragged with Pe ≈ 1.5 through a passive bath already deviates slightly from the memory kernel of the undragged probe. This suggests that the transition from the linear to the nonlinear regime in a passive bath is a relatively sharp transition at Pe = 1. Because these deviations are primarily visible in the memory kernel as opposed to the VACF, this suggests that the transition to the nonlinear regime is primarily due to the stochastic force distribution. In fact, for a probe dragged through a passive bath at Pe ≈ 1.5, we can already see a slight asymmetry in the probe's stochastic force distribution (see Appendix F). This asymmetry is a signature of the nonlinear regime, as will be discussed in the next Section 11.
ext for a probe dragged through a passive bath. We note that, in Fig. 10(a) and (b), the memory kernel for a probe dragged with Pe ≈ 1.5 through a passive bath already deviates slightly from the memory kernel of the undragged probe. This suggests that the transition from the linear to the nonlinear regime in a passive bath is a relatively sharp transition at Pe = 1. Because these deviations are primarily visible in the memory kernel as opposed to the VACF, this suggests that the transition to the nonlinear regime is primarily due to the stochastic force distribution. In fact, for a probe dragged through a passive bath at Pe ≈ 1.5, we can already see a slight asymmetry in the probe's stochastic force distribution (see Appendix F). This asymmetry is a signature of the nonlinear regime, as will be discussed in the next Section 11.
For the active bath, we also see that the VACF and memory kernel are isotropic and independent of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext within the linear regime. Furthermore, in this case, the linear regime appears to hold for Peclet numbers of up to at least Pe ≈ 1.5 (Fig. 9 and 10), suggesting that the transition from the linear to nonlinear regime is less sharp in an active bath.
ext within the linear regime. Furthermore, in this case, the linear regime appears to hold for Peclet numbers of up to at least Pe ≈ 1.5 (Fig. 9 and 10), suggesting that the transition from the linear to nonlinear regime is less sharp in an active bath.
Beyond the linear regime, however, the VACF and memory kernel are neither isotropic (see Fig. 9(e), (f) and 10(e), (f)) nor independent of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext for both passive and active systems. In both cases, a large drag force causes the VACF to decay more rapidly in both its parallel and perpendicular components. The memory kernel is primarily affected at short times, where it is greater than the memory kernel of a free probe. This is, again, true for both a probe dragged through a passive and an active bath. However, the other aspects of the VACF/memory kernel form differ for passive and active baths. In a passive bath, we see that the dragged probe acquires an increased local kinetic temperature in both its parallel and perpendicular components. In an active bath, on the other hand, the dragged probe only acquires an increased local kinetic temperature in its parallel component. In its perpendicular component, the probe dragged through an active bath actually experiences a decrease in local kinetic temperature.
ext for both passive and active systems. In both cases, a large drag force causes the VACF to decay more rapidly in both its parallel and perpendicular components. The memory kernel is primarily affected at short times, where it is greater than the memory kernel of a free probe. This is, again, true for both a probe dragged through a passive and an active bath. However, the other aspects of the VACF/memory kernel form differ for passive and active baths. In a passive bath, we see that the dragged probe acquires an increased local kinetic temperature in both its parallel and perpendicular components. In an active bath, on the other hand, the dragged probe only acquires an increased local kinetic temperature in its parallel component. In its perpendicular component, the probe dragged through an active bath actually experiences a decrease in local kinetic temperature.
As a consequence of the changes in the memory kernel, the GLE mobility becomes anisotropic at high Peclet numbers, and both its parallel and perpendicular components increase (data not shown). In the linear regime, however, the tensorial and linear GLE mobility are identical: ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) K = 1
K = 1![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 0 for Pe < 1, where 1 is the unit tensor.
0 for Pe < 1, where 1 is the unit tensor.
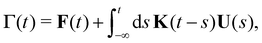 | (23) |
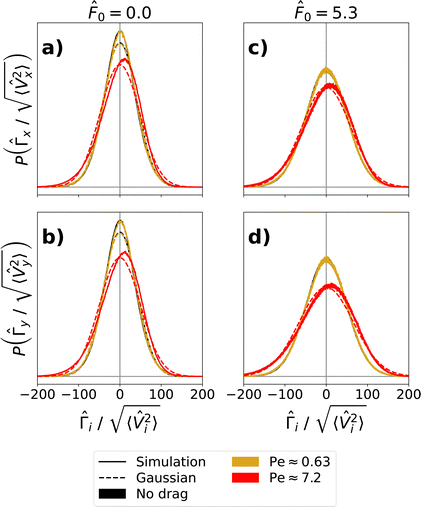
However, at higher drag forces, the distribution calculated from simulation data develops an asymmetry in both components parallel and perpendicular to the drag force. This asymmetry has already been seen for a passive bath in ref. 17. Our results here show that it also occurs for an active bath, although the magnitude of the asymmetry appears to be lower in the active case. We infer that the lower asymmetry in the active case stems from the already enhanced fluctuations due to the bath activity.
The asymmetry takes the form of a long tail in the negative forces of the distribution. This long tail occurs because, outside of the linear regime, bath particles in the vicinity of the probe do not necessarily travel at the same relative velocity as the probe.91 This leads some bath particles to ‘crash,’ with relatively high forces, into the probe, promoting the long tail. Because the average of the stochastic force distribution remains zero, the distribution also exhibits a slightly enhanced probability for positive forces. The distribution outside the linear regime can be described by a split normal Gaussian.17
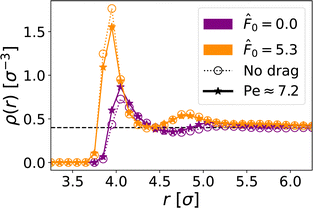 | ||
Fig. 12 Radially averaged density, see (eqn (15)) of the immersed probe in baths with activities ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 0.0 (indigo) and 0 = 0.0 (indigo) and ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3 (orange). Open circles with dotted lines show ρ(r) for a probe which is not dragged, whereas solid lines with stars show ρ(r) for a probe dragged with Pe ≈ 7.2. The probe has a radius Rp = 3.0σ. The black dashed line marks the global density, ρ = 0.4σ−3. 0 = 5.3 (orange). Open circles with dotted lines show ρ(r) for a probe which is not dragged, whereas solid lines with stars show ρ(r) for a probe dragged with Pe ≈ 7.2. The probe has a radius Rp = 3.0σ. The black dashed line marks the global density, ρ = 0.4σ−3. | ||
It has previously been shown that a probe dragged with sufficient force through a passive bath experiences an increased density of particles in front of it.17,92 By examining the dipole moment in the vicinity of the probe (see Fig. 13, calculated from eqn (14)), we verify this buildup of particles in front of a probe dragged through a passive bath with Pe > 1. A similar frontal buildup is exhibited by a probe dragged through an active bath with Pe ≈ 7.2. However, for lower Peclet numbers (Pe ≈ 1.5 and Pe ≈ 4.5), it is no longer observed. In spite of the drag force, we still see an accumulation of ALPs behind the probe for Pe ≲ 1.5.
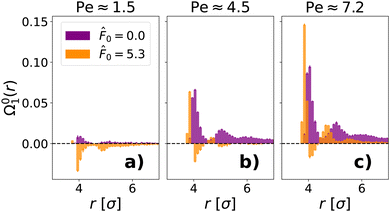 | ||
Fig. 13 Dipole moment (Ω01(r), see eqn (14)) of the bath as a function of distance from the center of the immersed probe (r) for a probe dragged with a Peclet number (a) Pe ≈ 1.5, (b) Pe ≈ 4.5, and (c) Pe ≈ 7.2 for both a passive (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 0.0, indigo) and an active ( 0 = 0.0, indigo) and an active (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3, orange) bath. Each bath has average density ρ = 0.4σ−3 and the probe has a radius Rp = 3.0σ. The black dashed line marks the zero baseline. 0 = 5.3, orange) bath. Each bath has average density ρ = 0.4σ−3 and the probe has a radius Rp = 3.0σ. The black dashed line marks the zero baseline. | ||
We reason this qualitative difference in the bath behavior at the probe interface following the arguments of ref. 20. For small Peclet numbers, the speed of the ALPs is greater than that of the dragged probe. Thus, the ALPs are able to accumulate behind the probe and push, as was the case for a probe without an external drag force. Consequently, we still see a negative dipole moment in the active bath for Pe ≈ 1.5 in (Fig. 13a). For intermediate Peclet numbers, the dragged probe and the ALPs move at similar speeds. Therefore, the dipole moment of the active bath approaches zero, which we see happening for Pe ≈ 4.5 in (Fig. 13b). Although for this value of Pe the dipole moment is not entirely zero, we can see that its magnitude and range are smaller. For large Peclet numbers, ALPs can no longer catch up to the probe and, consequently, the active bath acquires a positive dipole moment in the vicinity of the probe, as seen for Pe ≈ 7.2 in (Fig. 13c).
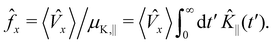 | (24) |
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) ‖(t) is the parallel component of the dragged probe's memory kernel shown in Fig. 10(a) and (b) and we have exploited the fact that
‖(t) is the parallel component of the dragged probe's memory kernel shown in Fig. 10(a) and (b) and we have exploited the fact that ![[K with combining circumflex]](https://www.rsc.org/images/entities/b_char_004b_0302.gif) and hence
and hence ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) are diagonal. In the linear regime, we have already established
are diagonal. In the linear regime, we have already established ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag =
Drag = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) K,‖ =
K,‖ = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 0 in Sections 3.2.1 and 3.2.2, hence
0 in Sections 3.2.1 and 3.2.2, hence ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x =
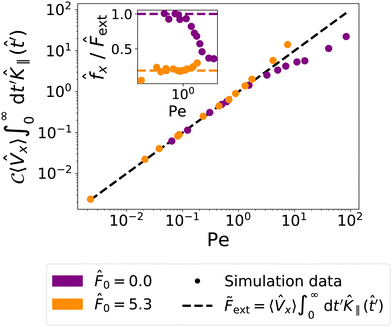
x = ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext. Our goal in this section is to test this relation in the nonlinear regime. To this end, we plot
ext. Our goal in this section is to test this relation in the nonlinear regime. To this end, we plot 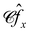 versus
versus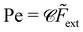 in Fig. 14. Here we rescale by
in Fig. 14. Here we rescale by 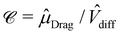 (see Appendix E) in order to be able to compare the nonlinear effects in the passive and active bath case.
(see Appendix E) in order to be able to compare the nonlinear effects in the passive and active bath case.
The figure shows that the relation ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x =
x = ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext holds in the linear regime as expected, but breaks down at high Peclet numbers. In the case of the a passive bath,
ext holds in the linear regime as expected, but breaks down at high Peclet numbers. In the case of the a passive bath, ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x is smaller than
x is smaller than ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext =
ext = ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext at large drag forces. In the case of an active bath,
ext at large drag forces. In the case of an active bath, ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x is larger than
x is larger than ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext = α
ext = α![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext. As a result, the values of
ext. As a result, the values of ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x in the active and passive bath at given physical drag force
x in the active and passive bath at given physical drag force ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext approach each other. This is shown in the inset of Fig. 14, where the ratio
ext approach each other. This is shown in the inset of Fig. 14, where the ratio ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x/
x/![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext is plotted as a function of the high Peclet number.
ext is plotted as a function of the high Peclet number.
We conclude that the change of the drag mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Drag = 〈
Drag = 〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉/Fext in the nonlinear regime, which has been reported in Fig. 8, can be decomposed into two factors: first the GLE mobility
x〉/Fext in the nonlinear regime, which has been reported in Fig. 8, can be decomposed into two factors: first the GLE mobility ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) K decreases with increasing Peclet number, both in a passive and in an active bath (cf.Fig. 10). Second, the force renormalization factor
K decreases with increasing Peclet number, both in a passive and in an active bath (cf.Fig. 10). Second, the force renormalization factor ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x/
x/![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext increases in an active bath, and decreases in a passive bath. In the nonlinear regime, Fext thus must be renormalized even in the passive system. In a passive bath, both factors result in thinning behavior. In an active bath, they compete with each other, but the force renormalization effect dominates; hence one effectively observes thickening. The latter can be associated with the redistribution of bath particles around the probe, from back end to front end, shown in Fig. 13.
ext increases in an active bath, and decreases in a passive bath. In the nonlinear regime, Fext thus must be renormalized even in the passive system. In a passive bath, both factors result in thinning behavior. In an active bath, they compete with each other, but the force renormalization effect dominates; hence one effectively observes thickening. The latter can be associated with the redistribution of bath particles around the probe, from back end to front end, shown in Fig. 13.
In the literature, both ‘thinning’ (increased mobility)20,24,27,92–96 and ‘thickening’ (decreased mobility)17,92,95,97,98 behavior have been observed for different systems beyond the linear regime. In general, systems which are not dominated by hydrodynamics exhibit thinning behavior.95 This aligns with our finding that a probe dragged through a passive bath exhibits thinning behavior. However, in spite of the fact that our system neglects hydrodynamics, we find that a probe dragged through a bath of ALPs exhibits thickening behavior. This thickening behavior is in contrast to what has been previously observed in an ABP bath, where particle inertia is also neglected.20,24,27 Thickening has, however, been observed in microrheological studies of granular active systems, where inertia plays an important role.12,98
4 Discussion and outlook
In sum, we have analyzed the dynamics of a probe particle immersed in a bath of active Langevin particles in the presence of external forces by molecular dynamics simulations. We found that it is possible to map this system onto a GLE that satisfies a 2FDT. However, in order to achieve full consistency, we must(i) Rescale the temperature such that kBTeff = M〈V2〉/d, with d being the dimensionality of the system. More generally, we must replace the equilibrium 2FDT by a generalized 2FDT, eqn (2).
(ii) Renormalize the external force, Feffext = αFext. It must be chosen such that the distribution of probe positions in a confining renormalized potential Ueff(R) satisfies a generalized equipartition theorem, eqn (11). We have identified a linear regime of small to moderate forces where the renormalization factor α does not depend on the amplitude of the force.
If these two conditions are fulfilled, the positions of the probe in a confining potential are Boltzmann distributed according to a Boltzmann-like distribution, P(R) ∝ exp(−Ueff/kBTeff), the mobility of the particle can be determined consistently as semi-infinite integral over the memory kernel, and the 2FDT ensures that the mobility μ and long-time diffusion constant D of a free particle are connected by a generalized Einstein relation, D = μkBTeff (see eqn (34) in the appendix).
The ability to map this non-equilibrium system onto a GLE that satisfies the generalized 2FDT enables the use of many recently developed coarse-grained methods which rely on its fulfillment.61,99,100
We emphasize that both temperature and force renormalization are necessary to achieve full consistency. This is because the effective temperature and the force renormalization depend on each other via the generalized equipartition theorem. On less formal grounds, we can also argue as follows: if we only rescale the temperature, as is commonly done, the probe particle will have the correct velocity distribution in the GLE model, but the position distribution will deviate from the true distribution. If we only renormalize the potential, the probe will not have the correct velocity distribution.
It is instructive to discuss our findings in relation to another popular type of coarse-grained model for particles immersed in an active fluid, i.e., the overdamped Markovian Langevin equation (OLE).27 An OLE for such a system should reproduce three target quantities: (i) the diffusion constant of a free probe, (ii) the drift velocity in the presence of a slowly varying drag force, (iii) the position distribution in the presence of a confining potential. Since the OLE can be derived from a GLE in certain limits, we can use our results to propose a suitable OLE:
Ṙ = μKαFext + Ξ(t) =: ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Fext + Ξ(t). Fext + Ξ(t). | (25) |
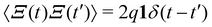 with q = kBTeffμK = kB
with q = kBTeffμK = kB![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif)
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) and we have defined the OLE mobility
and we have defined the OLE mobility ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) = μKα and the OLE temperature kB
= μKα and the OLE temperature kB![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = kBTeff/α. This analysis shows that, in the overdamped limit, it is not possible to distinguish between a renormalization of the mobility and a renormalization of the force, as long as the renormalized temperature is adjusted accordingly. Physically, this means that the separate effect of force renormalization – as opposed to just temperature renormalization101 – only becomes relevant if inertial effects are important. As such, our results are most experimentally relevant for systems in which the constituents are of the meso- or macroscopic scale, such as active granular matter systems8–12,69–72 or systems of synthetic active robots.66–68 However, in principle force renormalization can be distinguished from temperature renormalization for any system in which you can independently measure the kinetic temperature.
= kBTeff/α. This analysis shows that, in the overdamped limit, it is not possible to distinguish between a renormalization of the mobility and a renormalization of the force, as long as the renormalized temperature is adjusted accordingly. Physically, this means that the separate effect of force renormalization – as opposed to just temperature renormalization101 – only becomes relevant if inertial effects are important. As such, our results are most experimentally relevant for systems in which the constituents are of the meso- or macroscopic scale, such as active granular matter systems8–12,69–72 or systems of synthetic active robots.66–68 However, in principle force renormalization can be distinguished from temperature renormalization for any system in which you can independently measure the kinetic temperature.
The coarse-grained GLE for a single probe particle in a renormalized potential is equivalent to a GLE for an equilibrium system, therefore we cannot expect to find interesting nonequilibrium effects in such a model. However, the renormalization of temperature and forces has interesting consequences for systems of several interacting particles. We found that the kinetic temperature of the probe particle not only depends on the parameters of the bath such as density and activity level, but also on the properties of the probe, such as the size.102 A similar behavior can also be expected for the force renormalization factor α. If probes of different size interact with each other, we therefore expect the forces to be rescaled differently, implying that the effective forces are non-reciprocal. This is a common signature of nonequilibrium103–109 whose consequences for our particular type of system yet remain to be explored.
Furthermore, we have seen that the GLE mapping with constant renormalization parameter α breaks down for very large external forces. If α depends on the force, the renormalization may turn a conservative force into a non-conservative drift force, i.e., it may no longer be possible to rewrite the renormalized force as a gradient of a renormalized potential. Developing coarse-grained methods for external forces beyond the linear response regime will be an important area for future research. Moreover, theoretical arguments (Appendix A) suggest that it might sometimes be necessary to modify the 2FDT by adding another force-dependent term, e.g., as in eqn (10). In the case studies considered in the present work, the additional term was found to vanish; in general, it might be nonzero and generate true nonequilibrium signatures even in a single-particle model.
It has been shown that a harmonically confined active particle exhibits different behavior from a harmonically confined passive particle.110–112 Namely, the radial probability distribution of the active particle exhibits two ‘phases’ which depend on the particle activity and the trap strength: a ‘passive’ phase described by a Boltzmann-like distribution around the trap center, and an ‘active’ phase described by a non-Boltzmann distribution which is peaked away from the trap center.112 Given the shared behaviors of a probe immersed in an active bath with an active particle itself,82,113,114 it would be interesting to determine whether there exists an ‘active’ phase probability distribution for a probe immersed in an active bath for other values of activity and spring potentials, and whether this can be described by a a GLE with a modified 2FDT and/or a force-dependent α-parameter.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: generalized equipartition theorem and modified 2FDT
We consider an ensemble of trajectories of particles subject to an external, possibly position dependent force Fext. The underlying fine-grained system is taken to be in (possibly nonequilibrium) steady state (NESS). Our goal is to map this trajectory ensemble onto a GLE that reproduces certain ensemble averages (denoted by 〈…〉) of interest. Specifically, our target coarse-grained model is a stationary GLE58 of the form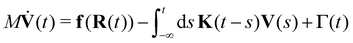 | (26) |
| Ṙ(t) = V(t). | (27) |
(I) We define tensorial correlation functions
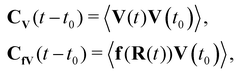 | (28) |
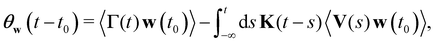 | (29) |
By multiplying the GLE, (26), with V(t0) and taking the trajectory ensemble average, we obtain the equation
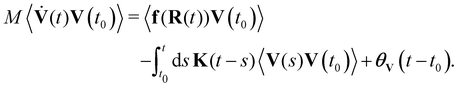 | (30) |
In order to define the memory kernel unambiguously, we impose the Volterra equation,
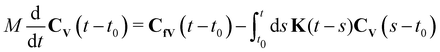 | (31) |
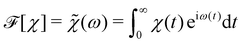 | (32) |
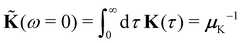 is the inverse tensorial GLE mobility as defined in eqn (21). We consider the GLE mapping to be successful if μK−1 exists and does not diverge. Additionally, for a successful mapping, the limit
is the inverse tensorial GLE mobility as defined in eqn (21). We consider the GLE mapping to be successful if μK−1 exists and does not diverge. Additionally, for a successful mapping, the limit 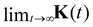 must exist, which implies
must exist, which implies 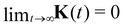 . We also note that
. We also note that 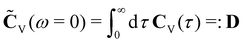 is the diffusion tensor for diffusing particles.
is the diffusion tensor for diffusing particles.
Applying the Fourier transform to the Volterra equation, we obtain
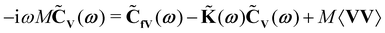 | (33) |
(II) We first discuss the case of a free particle with Ueff ≡ 0. In that case, the Volterra equation in the limit ω → 0 reads M〈VV〉 = ![[K with combining tilde]](https://www.rsc.org/images/entities/b_char_004b_0303.gif) (ω = 0)
(ω = 0)![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) V(ω = 0) and hence we obtain a generalized Einstein relation between the mobility and diffusion tensors,
V(ω = 0) and hence we obtain a generalized Einstein relation between the mobility and diffusion tensors,
| D = μKM〈VV〉 | (34) |
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) (0) is not bounded if
(0) is not bounded if ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) V(0) = 0. In this case, both the diffusion constant and the mobility are zero.
V(0) = 0. In this case, both the diffusion constant and the mobility are zero.
(III) Next we consider a confined particle subject to a confining potential U(R), such that 〈R2〉 < ∞, e.g., a particle in an external potential with infinite barrier height. It does not diffuse, hence ![[C with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0043_0303.gif) V(ω = 0) = 0. Since
V(ω = 0) = 0. Since ![[K with combining circumflex]](https://www.rsc.org/images/entities/b_char_004b_0302.gif) (ω = 0) is finite (one of our basic assumptions) and
(ω = 0) is finite (one of our basic assumptions) and ![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) V(ω = 0) = 0, the memory term in eqn (33) vanishes, and so does the term −iωM
V(ω = 0) = 0, the memory term in eqn (33) vanishes, and so does the term −iωM![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) V on the left hand side of the equation. Thus the Volterra equation only has a solution if
V on the left hand side of the equation. Thus the Volterra equation only has a solution if 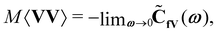 which implies
which implies
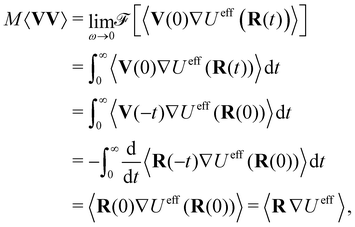 | (35) |
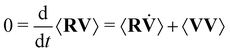 .
.
Applying the general result (11) to the harmonic oscillator potential, 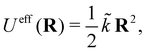 we find that the effective spring constant must fulfill
we find that the effective spring constant must fulfill ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = M〈V2〉/〈R2〉 = kBTeff/〈x2〉, which corresponds to the renormalization of the spring constant in the main text.
= M〈V2〉/〈R2〉 = kBTeff/〈x2〉, which corresponds to the renormalization of the spring constant in the main text.
(IV) Finally, we analyze the implications of (31) for the fluctuations of the stochastic noise Γ(t). We have analyzed the force free case in ref. 17 and shown that the Volterra equation then enforces a generalized 2FDT
| 〈Γ(t)Γ(t0)〉 = MK(t − t0)CV(0), | (36) |
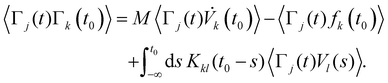 | (37) |
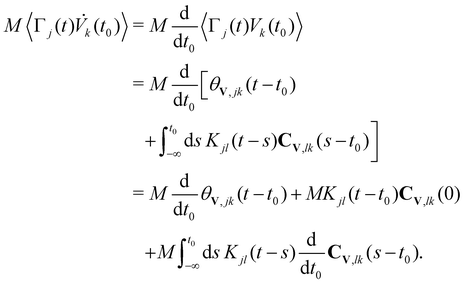 | (38) |
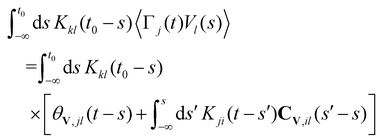 | (39) |
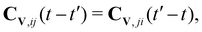 we rewrite the second term on the r.h.s. of (39) as
we rewrite the second term on the r.h.s. of (39) as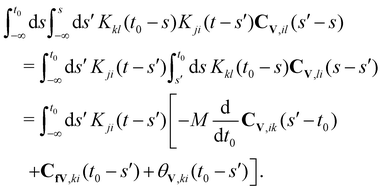 | (40) |
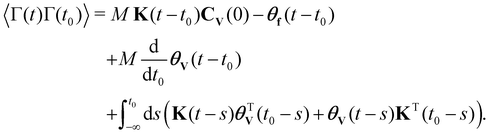 | (41) |
| 〈Γ(t)Γ(t0)〉 = MK(t − t0)CV(0) − θf(t − t0). | (42) |
We now specifically consider the case of the (possibly renormalized) harmonic potential, where the drift force can be expressed as f = −![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) R. Then we have θf(t − t0)harm. = −
R. Then we have θf(t − t0)harm. = −![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) θR(t − t0). θR(t − t0) can be calculated explicitly as follows: We first take the derivative of θR(t − t0) with respect to t0, and obtain
θR(t − t0). θR(t − t0) can be calculated explicitly as follows: We first take the derivative of θR(t − t0) with respect to t0, and obtain
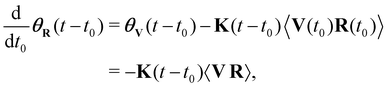 | (43) |
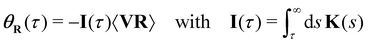 | (44) |
Inserting this result into eqn (42), we finally obtain the following expression for the modified 2FDT in the presence of a harmonic potential:
〈Γ(t)Γ(t0)〉 = MK(t − t0) 〈VV〉 + ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) I(t − t0)〈VR〉 I(t − t0)〈VR〉 | (45) |
At equilibrium, we have 〈VR〉 = 0 due to time reversal symmetry. Therefore, the last term vanishes and one recovers the force-free generalized 2FDT, eqn (2) in the main text. In active systems, this is not necessarily the case. For example, active particles have a tendency to accumulate at boundaries in a state where the active velocity points towards the boundary, which creates a clear correlation between position and velocity. If such a correlation were present for a harmonically trapped particle, omitting the last term in eqn (45) in the corresponding coarse-grained GLE would effectively map the system onto an equilibrium system, where 〈VR〉 = 0 by construction. In such cases, we can only recover 〈VR〉 ≠ 0 by using the full modified 2FDT. We note that it may be possible to define projection operators which formally lead to other definitions of the memory kernel and thus other FDTs in which the 〈VR〉 term may or may not be present. Here, however, we do not apply projection operator techniques, but rather analyze the GLE under the sole assumption that the memory is given by the Volterra equation. In this case, provided that the system is not at equilibrium, the 〈VR〉 term cannot generally be eliminated.
Numerically, however, we found the additional term in the 2FDT to be negligible in the systems considered in the present work. The value of 〈VR〉 was always zero within the error. We note that, due to eqn (44), this also implies θR(t − t0) ≡ 0 (noise orthogonality with respect to the position). On the other hand, the force renormalization in an active bath was substantial, as reported in the main paper, and moreover, the correct implementation of the force renormalization was crucial for the memory reconstruction, see Appendix C.
Appendix B: renormalization constant as a function of ![[F with combining circumflex]](https://www.rsc.org/images/entities/h3_i_char_0046_0302.gif) 0
0
In the main part of this manuscript, we focus on the system of a probe either immersed in a passive bath or immersed in an active bath with activity ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0 = 5.3. This same type of analysis can be performed for baths of different activities, i.e. with different activities
0 = 5.3. This same type of analysis can be performed for baths of different activities, i.e. with different activities ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0. In particular, the necessity of force renormalization is also applicable to baths with different activities. To illustrate this point, we calculated the value the renormalization constant α for baths with different activities
0. In particular, the necessity of force renormalization is also applicable to baths with different activities. To illustrate this point, we calculated the value the renormalization constant α for baths with different activities ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0. We calculated α using eqn (24) and the fact that, effectively, α =
0. We calculated α using eqn (24) and the fact that, effectively, α = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) x/
x/![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) ext. For each value of
ext. For each value of ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 0, we calculated α using two values of Fext where 0.1 < Pe < 0.5. The results are shown in Fig. 15. From Fig. 15, we can see that, even for low activity baths, a renormalized force is necessary.
0, we calculated α using two values of Fext where 0.1 < Pe < 0.5. The results are shown in Fig. 15. From Fig. 15, we can see that, even for low activity baths, a renormalized force is necessary.
Appendix C: numerical reconstruction of the memory kernel of a harmonically trapped particle
Our starting point is a scalar and steady-state version of the Volterra equation, (31):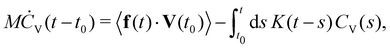 | (46) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) R, take the derivative with respect to t, and use M
R, take the derivative with respect to t, and use M![[V with combining dot above]](https://www.rsc.org/images/entities/b_char_0056_0307.gif) = F. Furthermore, we exploit the relations
= F. Furthermore, we exploit the relationsfor W = F and W = R and the relation
Setting t0 = 0, this gives the Volterra equation of the second kind quoted in the main text,
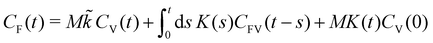 | (47) |
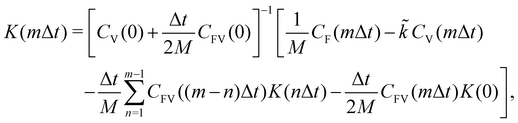 | (48) |
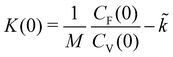 .
.
In Section 3.1.2, we used the the renormalized harmonic constraint ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in eqn (48) to solve for the probe memory kernel based on our findings in Section 3.1.1. Additionally, we tried solving the memory kernel without a harmonic constraint (
in eqn (48) to solve for the probe memory kernel based on our findings in Section 3.1.1. Additionally, we tried solving the memory kernel without a harmonic constraint (![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) NH(
NH(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )) as well as with the imposed harmonic constraint k (
)) as well as with the imposed harmonic constraint k (![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) k(
k(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )). The results are shown in Fig. 16(a) and (b) respectively. Although Fig. 16(a) and (b) both look qualitatively the same as Fig. 3(d), comparing the Fig. 16(a′) and (b′) with Fig. 3(d′) reveals that they are not the same. In Fig. 3(d′), where we define
)). The results are shown in Fig. 16(a) and (b) respectively. Although Fig. 16(a) and (b) both look qualitatively the same as Fig. 3(d), comparing the Fig. 16(a′) and (b′) with Fig. 3(d′) reveals that they are not the same. In Fig. 3(d′), where we define ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) with
) with ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , the difference between the memory kernel of the constrained probe and that of a free probe goes to zero. However, this difference converges to a finite value at late times in the case that we either neglect the harmonic constraint (Fig. 16(a′)) or we define
, the difference between the memory kernel of the constrained probe and that of a free probe goes to zero. However, this difference converges to a finite value at late times in the case that we either neglect the harmonic constraint (Fig. 16(a′)) or we define ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) with k (Fig. 16(b′)). This finding is similar to the renormalization/linearization within the Mori–Zwanzig formalism in the presence of non-linear external potentials.30,87 We know that the memory kernel of the free probe goes to zero in the long time limit.65 Therefore, the fact that
) with k (Fig. 16(b′)). This finding is similar to the renormalization/linearization within the Mori–Zwanzig formalism in the presence of non-linear external potentials.30,87 We know that the memory kernel of the free probe goes to zero in the long time limit.65 Therefore, the fact that ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) NH(
NH(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) and Δ
) and Δ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) k(
k(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) go to finite values, indicates that they do not approach zero in the long time limit as they should. Comparing Fig. 16(a′) to that of Fig. 16(b′), we see that
) go to finite values, indicates that they do not approach zero in the long time limit as they should. Comparing Fig. 16(a′) to that of Fig. 16(b′), we see that ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) NH(
NH(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) approaches a smaller (in terms of magnitude) finite value than Δ
) approaches a smaller (in terms of magnitude) finite value than Δ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) k(
k(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ). This can be understood given that, in our case, the value of
). This can be understood given that, in our case, the value of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) is closer to zero than to k. We conclude that consistent force renormalization is essential for the successful reconstruction of a memory kernel via the Volterra equation formalism, i.e., the successful derivation of a GLE that satisfies the 2FDT.
is closer to zero than to k. We conclude that consistent force renormalization is essential for the successful reconstruction of a memory kernel via the Volterra equation formalism, i.e., the successful derivation of a GLE that satisfies the 2FDT.
Appendix D: velocity distribution of the harmonically trapped probe
We saw in Fig. 3(b) that the kinetic temperature of the probe is dependent on the strength of the harmonic potential, k. However, within our range of k values this effect is marginal. In fact, as can be see in Fig. 17, the velocity distributions of the probe do not show any apparent deviations across the different values of k tested. Although there is a slight quantitative difference in the mean squared velocity (as seen from the different initial values of the VACF in Fig. 3(b)), this difference is too small to be qualitatively noticeable.Appendix E: peclet number as a function of drag force
In Section 3.2.1, we define the Peclet number Pe = 〈![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) x〉/
x〉/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff for the dragged probe, with
diff for the dragged probe, with  . Given that the average force exerted on the probe can be related to its average velocity through eqn (20), we can rewrite the Peclet number in terms of
. Given that the average force exerted on the probe can be related to its average velocity through eqn (20), we can rewrite the Peclet number in terms of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext as Pe = μDrag
ext as Pe = μDrag![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext/
ext/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff. We found in Section 3.2.1 that, for both a probe immersed in an passive and an active bath, μDrag is a constant within the linear response regime. Therefore, we expect that Pe is proportional to
diff. We found in Section 3.2.1 that, for both a probe immersed in an passive and an active bath, μDrag is a constant within the linear response regime. Therefore, we expect that Pe is proportional to ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext with proportionality constant μDrag/
ext with proportionality constant μDrag/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff within the linear response regime. This is indeed what we see in Fig. 18.
diff within the linear response regime. This is indeed what we see in Fig. 18.
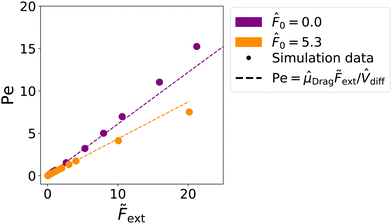 | ||
Fig. 18 Peclet number (Pe) as a function of the renormalized external drag force (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext). The dotted lines show Pe = μDrag ext). The dotted lines show Pe = μDrag![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ext/ ext/![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) diff in the linear response regime, where μDrag is constant. diff in the linear response regime, where μDrag is constant. | ||
Appendix F: stochastic force distribution at Pe ≈ 1.5
In Fig. 10(a) and (b), we see that the memory kernel of a probe dragged through a passive bath with Pe ≈ 1.5 already shows slight deviations from that of an undragged probe. Given that these deviations are not as visible in the VACF of the probe in comparison with the memory kernel, we infer that the deviations in the memory kernel were primarily due to the stochastic force distribution on the probe. Indeed, we see in Fig. 19 that the stochastic force distribution at Pe ≈ 1.5 in a passive bath already shows a slight asymmetry, a signature of the nonlinear regime, whereas that in an active bath does not. This indicates that the transition to the nonlinear regime in a passive bath occurs more sharply at Pe = 1 in comparison with an active bath.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG) via Grant 233630050, TRR 146, Project A3. Computations were carried out on the Mogon Computing Cluster at ZDV Mainz. We thank Martin Hanke, Niklas Bockius, and Thomas Speck for useful discussions.Notes and references
- F. MacKintosh and C. Schmidt, Curr. Opin. Colloid Interface Sci., 1999, 4, 300–307 CrossRef CAS.
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685 CrossRef.
- P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449–1455 RSC.
- C. Gutsche, F. Kremer, M. Krüger, M. Rauscher, R. Weeber and J. Harting, J. Chem. Phys., 2008, 129, 084902 CrossRef PubMed.
- A. S. Khair and T. M. Squires, Phys. Rev. Lett., 2010, 105, 156001 CrossRef PubMed.
- J. S. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2010, 105, 178302 CrossRef CAS PubMed.
- J. P. Rich, J. Lammerding, G. H. McKinley and P. S. Doyle, Soft Matter, 2011, 7, 9933–9943 RSC.
- O. Zik, J. Stavans and Y. Rabin, Europhys. Lett., 1992, 17, 315 CrossRef.
- R. Candelier and O. Dauchot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011304 CrossRef PubMed.
- R. Candelier and O. Dauchot, Phys. Rev. Lett., 2009, 103, 128001 CrossRef CAS PubMed.
- A. Seguin, Y. Bertho, P. Gondret and J. Crassous, Phys. Rev. Lett., 2011, 107, 048001 CrossRef CAS PubMed.
- A. Fiege, M. Grob and A. Zippelius, Granular Matter, 2012, 14, 247–252 CrossRef CAS.
- L. G. Wilson and W. C. K. Poon, Phys. Chem. Chem. Phys., 2011, 13, 10617–10630 RSC.
- R. N. Zia, Annu. Rev. Fluid Mech., 2018, 50, 371–405 CrossRef.
- U. Seifert and T. Speck, Europhys. Lett., 2010, 89, 10007 CrossRef.
- A. Córdoba, T. Indei and J. D. Schieber, J. Rheol., 2012, 56, 185–212 CrossRef.
- G. Jung and F. Schmid, Soft Matter, 2021, 17, 6413–6425 RSC.
- J. O. Daldrop, B. G. Kowalik and R. R. Netz, Phys. Rev. X, 2017, 7, 041065 Search PubMed.
- D. T. N. Chen, A. W. C. Lau, L. A. Hough, M. F. Islam, M. Goulian, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2007, 99, 148302 CrossRef CAS PubMed.
- M. Knežević, L. Podgurski and H. Stark, Sci. Rep., 2021, 11, 22706 CrossRef PubMed.
- Z. Peng and J. F. Brady, J. Chem. Phys., 2022, 157, 104119 CrossRef CAS PubMed.
- H. Seyforth, M. Gomez, W. B. Rogers, J. L. Ross and W. W. Ahmed, Phys. Rev. Res., 2022, 4, 023043 CrossRef CAS.
- E. Burkholder and J. Brady, J. Chem. Phys., 2019, 150, 184901 CrossRef PubMed.
- E. W. Burkholder and J. F. Brady, Soft Matter, 2020, 16, 1034–1046 RSC.
- S. Ye, P. Liu, F. Ye, K. Chen and M. Yang, Soft Matter, 2020, 16, 4655–4660 RSC.
- C. Maggi, M. Paoluzzi, N. Pellicciotta, A. Lepore, L. Angelani and R. Di Leonardo, Phys. Rev. Lett., 2014, 113, 238303 CrossRef CAS PubMed.
- A. Jayaram and T. Speck, Europhys. Lett., 2023, 143, 17005 CrossRef.
- J. Reichert and T. Voigtmann, Soft Matter, 2021, 17, 10492–10504 RSC.
- A. Abbasi, R. R. Netz and A. Naji, Phys. Rev. Lett., 2023, 131, 228202 CrossRef CAS PubMed.
- R. Zwanzig, Nonequilibrium Statistical Physics, Oxford University Press, 2001 Search PubMed.
- V. Klippenstein, M. Tripathy, G. Jung, F. Schmid and N. van der Vegt, J. Phys. Chem. B, 2021, 125, 4931 CrossRef CAS PubMed.
- S. Izvekov, J. Chem. Phys., 2013, 138, 134106 CrossRef PubMed.
- T. Kinjo and S.-a Hyodo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051109 CrossRef PubMed.
- S. Izvekov, Phys. Rev. E, 2021, 104, 024121 CrossRef CAS PubMed.
- H. Vroylandt, Europhys. Lett., 2022, 140, 62003 CrossRef.
- R. R. Netz, Derivation of the non-equilibrium generalized Langevin equation from a generic time-dependent Hamiltonian, arXiv, 2023, preprint, arXiv:2310.00748, DOI:10.48550/arXiv.2310.00748.
- H. Vroylandt and P. Monmarché, J. Chem. Phys., 2022, 156, 244105 CrossRef CAS PubMed.
- H. Mori, Progress Theor. Phys., 1965, 33, 423–455 CrossRef.
- S. Kim and I. Oppenheim, Physica, 1972, 57, 469–482 CrossRef CAS.
- P. Español, J. Chem. Phys., 2023, 159, 024111 CrossRef PubMed.
- F. Koch, J. Erle and T. Schilling, The non-equilibrium solvent response force: What happens if you push a Brownian particle, arXiv, 2023, preprint, arXiv:2309.14873, DOI:10.48550/arXiv.2309.14873.
- H. Meyer, T. Voigtmann and T. Schilling, J. Chem. Phys., 2017, 147, 214110 CrossRef PubMed.
- T. Schilling, Phys. Rep., 2022, 972, 1–45 CrossRef.
- Y. Zhu and H. Lei, Discrete. Contin. Dyn. Syst. – S, 2022, 15, 959–982 CrossRef.
- Y. Zhu, H. Lei and C. Kim, Phys. Scr., 2023, 98, 115402 CrossRef.
- F. Glatzel and T. Schilling, Europhys. Lett., 2022, 136, 36001 CrossRef.
- G. Jung, J. Phys.: Condens. Matter, 2022, 34, 204004 CrossRef CAS PubMed.
- V. Klippenstein and N. F. A. van der Vegt, J. Chem. Phys., 2021, 154, 191102 CrossRef CAS PubMed.
- B. G. Mitterwallner, C. Schreiber, J. O. Daldrop, J. O. Rädler and R. R. Netz, Phys. Rev. E, 2020, 101, 032408 CrossRef CAS PubMed.
- V. Klippenstein and N. F. A. van der Vegt, J. Chem. Theory Comput., 2023, 19, 1099–1110 CrossRef CAS PubMed.
- M. Tripathy, V. Klippenstein and N. F. A. van der Vegt, J. Chem. Phys., 2023, 159, 094904 CrossRef CAS PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, J. Chem. Theory Comput., 2010, 6, 1170–1180 CrossRef CAS.
- C. Maggi, M. Paoluzzi, L. Angelani and R. Leonardo, Sci. Rep., 2017, 7, 17588 CrossRef PubMed.
- C. Maes and S. Steffenoni, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022128 CrossRef PubMed.
- S. Steffenoni, K. Kroy and G. Falasco, Phys. Rev. E, 2016, 94, 062139 CrossRef PubMed.
- T. J. Doerries, S. A. M. Loos and S. H. L. Klapp, J. Stat. Mech.: Theory Exp., 2021, 2021, 033202 CrossRef.
- M. Baldovin, L. Caprini, A. Puglisi, A. Sarracino and A. Vulpiani, Nonequilibrium Thermodynamics and Fluctuation Kinetics: Modern Trends and Open Questions, Springer, 2022, pp. 29–57 Search PubMed.
- H. K. Shin, C. Kim, P. Talkner and E. K. Lee, Chem. Phys., 2010, 375, 316–326 CrossRef CAS.
- A. Carof, R. Vuilleumier and B. Rotenberg, J. Chem. Phys., 2014, 140, 124103 CrossRef PubMed.
- G. Jung, M. Hanke and F. Schmid, J. Chem. Theory Comput., 2017, 13, 2481–2488 CrossRef CAS PubMed.
- G. Jung, M. Hanke and F. Schmid, Soft Matter, 2018, 14, 9368–9382 RSC.
- N. Bockius, J. Shea, G. Jung, F. Schmid and M. Hanke, J. Phys.: Condens. Matter, 2021, 33, 214003 CrossRef CAS PubMed.
- S. C. Takatori and J. F. Brady, Phys. Rev. Fluids, 2017, 2, 094305 CrossRef.
- S. Shankar and M. C. Marchetti, Phys. Rev. E, 2018, 98, 020604(R) CrossRef PubMed.
- J. Shea, G. Jung and F. Schmid, Soft Matter, 2022, 18, 6965–6973 RSC.
- C. Scholz, S. Jahanshahi, A. Ldov and H. Löwen, Nat. Commun., 2018, 9, 5156 CrossRef PubMed.
- M. Leoni, M. Paoluzzi, S. Eldeen, A. Estrada, L. Nguyen, M. Alexandrescu, K. Sherb and W. W. Ahmed, Phys. Rev. Res., 2020, 2, 043299 CrossRef CAS.
- C. Tapia-Ignacio, L. L. Gutierrez-Martinez and M. Sandoval, J. Stat. Mech.: Theory Exp., 2021, 2021, 053404 CrossRef.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef PubMed.
- C. A. Weber, T. Hanke, J. Deseigne, S. Léonard, O. Dauchot, E. Frey and H. Chaté, Phys. Rev. Lett., 2013, 110, 208001 CrossRef CAS PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- A. Kudrolli, G. Lumay, D. Volfson and L. S. Tsimring, Phys. Rev. Lett., 2008, 100, 058001 CrossRef PubMed.
- H. Löwen, J. Chem. Phys., 2020, 152, 040901 CrossRef PubMed.
- C. Scholz, S. Jahanshahi, A. Ldov and H. Löwen, Nat. Commun., 2018, 9, 5156 CrossRef PubMed.
- A. Baskaran and M. C. Marchetti, Phys. Rev. Lett., 2008, 101, 268101 CrossRef PubMed.
- S. Mandal, B. Liebchen and H. Löwen, Phys. Rev. Lett., 2019, 123, 228001 CrossRef CAS PubMed.
- S. Das, G. Gompper and R. Winkler, Sci. Rep., 2019, 9, 6608 CrossRef PubMed.
- A. R. Sprenger, S. Jahanshahi, A. V. Ivlev and H. Löwen, Phys. Rev. E, 2021, 103, 042601 CrossRef CAS PubMed.
- T. Speck and A. Jayaram, Phys. Rev. Lett., 2021, 126, 138002 CrossRef CAS PubMed.
- W. Yan and J. F. Brady, Soft Matter, 2018, 14, 279–290 RSC.
- W. Yan and J. F. Brady, The force on a body in active matter, 2015 Search PubMed.
- S. Steffenoni, K. Kroy and G. Falasco, Phys. Rev. E, 2016, 94, 062139 CrossRef PubMed.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Phys. Chem., 1971, 54, 5237–5247 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, 1995, https://lammps.sandia.gov Search PubMed.
- B. Jung and G. Jung, J. Chem. Phys., 2023, 159, 084110 CrossRef CAS PubMed.
- C. Maggi, M. Paoluzzi, N. Pellicciotta, A. Lepore, L. Angelani and R. Di Leonardo, Phys. Rev. Lett., 2014, 113, 238303 CrossRef CAS PubMed.
- S. Paul, A. Jayaram, N. Narinder, T. Speck and C. Bechinger, Phys. Rev. Lett., 2022, 129, 058001 CrossRef CAS PubMed.
- A. Argun, A.-R. Moradi, E. M. C. C. V. Pinçe, G. B. Bagci, A. Imparato and G. Volpe, Phys. Rev. E, 2016, 94, 062150 CrossRef PubMed.
- T. Squires and J. Brady, Phys. Fluids, 2005, 17, 073101 CrossRef.
- T. Wang and M. Sperl, Phys. Rev. E, 2016, 93, 022606 CrossRef PubMed.
- I. Carpen and J. Brady, J. Rheol., 2005, 49, 1483–1502 CrossRef CAS.
- D. Winter, J. Horbach, P. Virnau and K. Binder, Phys. Rev. Lett., 2012, 108, 028303 CrossRef CAS PubMed.
- A. M. Puertas and T. Voigtmann, J. Phys.: Condens. Matter, 2014, 26, 243101 CrossRef CAS PubMed.
- C. J. Harrer, D. Winter, J. Horbach, M. Fuchs and T. Voigtmann, J. Phys.: Condens. Matter, 2012, 24, 464105 CrossRef PubMed.
- V. Buchholtz and T. Pöschel, Granular Matter, 1997, 1, 33–41 CrossRef.
- T. Wang, M. Grob, A. Zippelius and M. Sperl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 042209 CrossRef PubMed.
- Z. Li, X. Bian, X. Li and G. Karniadakis, J. Chem. Phys., 2015, 143, 243128 CrossRef PubMed.
- S. Wang, Z. Ma and W. Pan, Soft Matter, 2021, 17, 6404–6412 RSC.
- A. Shakerpoor, E. Flenner and G. Szamel, J. Chem. Phys., 2021, 154, 184901 CrossRef CAS PubMed.
- J. Shea, PhD thesis, Johannes Gutenberg University of Mainz, 2023.
- S. A. M. Loos and S. H. L. Klapp, New J. Phys., 2020, 22, 123051 CrossRef.
- Z. Zhang and R. Garcia-Millan, Phys. Rev. Res., 2023, 5, L022033 CrossRef CAS.
- C. Godrèche and J.-M. Luck, J. Phys. A: Math. Theor., 2018, 52, 035002 CrossRef.
- T. Kano, K. Osuka, T. Kawakatsu and A. Ishiguro, J. Phys. Soc. Jpn., 2017, 86, 124004 CrossRef.
- A. Dinelli, J. O'Byrne, A. Curatolo, Y. Zhao, P. Sollich and J. Tailleur, Non-reciprocity across scales in active mixtures, 2022 Search PubMed.
- R. K. Gupta, R. Kant, H. Soni, A. K. Sood and S. Ramaswamy, Phys. Rev. E, 2022, 105, 064602 CrossRef CAS PubMed.
- S. Saha, J. Agudo-Canalejo and R. Golestanian, Phys. Rev. X, 2020, 10, 041009 CAS.
- S. Takatori, R. De Dier, J. Vermant and J. Brady, Nat. Commun., 2016, 7, 10694 CrossRef CAS PubMed.
- M. Caraglio and T. Franosch, Phys. Rev. Lett., 2022, 129, 158001 CrossRef CAS PubMed.
- K. Malakar, A. Das, A. Kundu, K. V. Kumar and A. Dhar, Phys. Rev. E, 2020, 101, 022610 CrossRef CAS PubMed.
- A. Callegari and G. Volpe, in Numerical Simulations of Active Brownian Particles, ed. F. Toschi and M. Sega, Springer International Publishing, Cham, 2019, pp. 211–238 Search PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |