Open Access Article
Open Access ArticleUnderstanding the application of covalent adaptable networks in self-repair materials based on molecular simulation†
Xiang
Cui‡
,
Lu
Zhang‡
,
Yuliang
Yang
and
Ping
Tang
 *
*
State Key Laboratory of Molecular Engineering of Polymers, Department of Macromolecular Science, Fudan University, Shanghai 200433, China. E-mail: pingtang@fudan.edu.cn
First published on 12th January 2024
Abstract
Covalent adaptable networks (CANs) are widely used in the field of self-repair materials. They are a group of covalently cross-linked associative polymers that undergo reversible chemical reactions, and can be further divided into dissociative CANs (Diss-CANs) and associative CANs (Asso-CANs). Self-repair refers to the ability of a material to repair itself without external intervention, and can be classified into self-adhesion and self-healing according to the utilization of open stickers. Unlike conventional materials, the viscoelastic properties of CANs are influenced by both the molecular structure and reaction kinetics, ultimately affecting their repair performance. To gain deeper insight into the repair mechanism of CANs, we conducted simulations by using the hybrid MC/MD algorithm, as previously proposed in our research. Interestingly, we observed a significant correlation between reaction kinetics and repair behavior. Asso-CANs exhibited strong mechanical strength and high creep resistance, rendering them suitable as self-adhesion materials. On the other hand, Diss-CANs formed open stickers that facilitated local relaxation, aligning perfectly with self-healing processes. Moreover, the introduction of crosslinkers in the form of small molecules enhanced the repair efficiency. Theoretically, it was found that the repair timescale of Asso-CANs is slower than that of Diss-CANs with identical molecular structures. Our study not only clarifies the similarities and differences between Diss-CANs and Asso-CANs in terms of their self-repairing capabilities, but more importantly, it provides valuable insights guiding the effective utilization of CANs in the development of self-repair materials.
1. Introduction
Self-repair refers to the capability of a material to autonomously repair its own damage or defects. This process is commonly observed in biological systems, such as the natural healing of human skin injuries, the regeneration of damaged organs in animals, and the grafting process in plants. Inspired by nature, self-repair materials exhibit great prospects in fields like biomedical treatment,1–3 materials engineering,4–6 and environmental protection.7–9 The self-repairing process can be achieved either by intrinsic structural changes within the material itself, which mostly rely on inner reversible chemical reactions,10–14 or by the use of external stimuli or triggers, such as healing agents.15–17 However, the development of self-repair materials faces challenges in complex chemical synthesis and the design of well-defined self-repairing processes. The key to achieving ideal self-repair materials lies in the meticulous design of suitable, controllable reversible chemical reactions within the self-repair system. One of the main challenges is the trade-off between mechanical strength and self-repairing capability, as materials typically possess one or the other. Therefore, achieving ideal self-repair materials requires careful design of suitable and controllable reversible chemical reactions within the self-repair system.Covalent adaptable networks (CANs) are special kinds of associative polymers (APs), which present unique rheological behavior due to the incorporation of dynamic covalent bonds.18–22 In contrast to traditional polymers, CANs demonstrate outstanding solvent resistance, mechanical properties, and reprocessability. These materials find wide applications in areas such as stimuli responsiveness,23–25 shape memory,26–28 molecular transport,29–31etc. According to the reaction mechanism, CANs can be further classified into dissociative CANs (Diss-CANs) and associative CANs (Asso-CANs, also known as vitrimers). Diss-CANs undergo reversible sticker dissociation and association, thus leading to the formation of open stickers and the loss of network integrity. In contrast, Asso-CANs only involve bond swap processes, and as a result, the network integrity will be constant. Interestingly, the macroscopic rheology of Asso-CANs shows Arrhenius-type dependence, which is rarely seen in polymers. Owing to the mechanical strength brought by covalent bonding and the controllable inner reversible chemical reactions, CANs are increasingly applied in self-repair materials.32–36
On the one hand, these materials exhibit rapid recovery of injured sites while maintaining mechanical strength through rearrangement of polymeric networks. For example, Guo et al.32 proposed a supramolecular elastomer composed of a polydimethylsiloxane (PDMS) polymer backbone embedded with multiple dynamic bonds, including disulfide metathesis, strong crosslinking H-bonds, and weak crosslinking H-bonds. This synergistic interaction enables the material to achieve rapid self-repair while maintaining its mechanical strength. It is shown that the synergistic effects of dynamic bonds endow the elastomer with high stretchability (∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000%) as well as fast autonomous self-healing ability under universal conditions, including at room temperature (10 min for healing), ultralow temperature (−40 °C), underwater (93% healing efficiency), supercooled high-concentrated saltwater (30% NaCl solution at −10 °C, 89% efficiency), and a strong acid/alkali environment (pH = 0 or 14, 88% or 84% efficiency).
000%) as well as fast autonomous self-healing ability under universal conditions, including at room temperature (10 min for healing), ultralow temperature (−40 °C), underwater (93% healing efficiency), supercooled high-concentrated saltwater (30% NaCl solution at −10 °C, 89% efficiency), and a strong acid/alkali environment (pH = 0 or 14, 88% or 84% efficiency).
On the other hand, reversible chemical reactions can be triggered by the temperature, which endows CANs with mechanical strength at room temperature and simultaneously adjustable self-repairing ability when heating.37 For instance, Leibler et al.33 made a quantitative comparison between permanently cross-linked epoxidized natural rubbers (ENR) and dicarboxylic acids cross-linked ENR (DA (diamine)-cured ENR). They demonstrated that, by introducing transesterification, the ENR cured with DA showed large stress relaxation at high temperatures, while the use of the zinc acetate catalyst promoted the relaxation dynamics. These rubber materials exhibit excellent mechanical properties without undesired creeping at room and moderate temperatures. However, at high temperatures, they also show adhesion and potential healability. Furthermore, the architecture of topological structures of these materials can also provide particular self-repairing capability. Ciarella and Ellenbroek34 designed star-like vitrimers applied in self-repair coating and found that a single bond swap process was sufficient to build a bridge and stick the damaged surface, while multiple swaps were required to relax the whole network. Apparently, the CANs exhibit excellent mechanical properties under moderate conditions, whereas they also show superior adhesion or healing abilities when subjected to external stimuli, such as heat, pressure, light, etc. or in the presence of catalysts. This indicates the controllable repairing ability of CAN materials.
Improving our understanding of the self-repairing process at the molecular level is crucial for designing self-repair materials with tailored functions. However, at present, the interpretation of the chemical and/or physical mechanisms involved in CANs applied in self-healing materials is still insufficient. Rubinstein et al.38 developed scaling theories for self-repair based on hybrid reversible/permanent networks in associative polymers. They emphasize the significance of the match between the waiting time and relaxation time. Hinton et al.39 extended Rubinstein's model to entangled systems by using a modified filament stretching rheometer. According to these studies, self-adhesion and self-healing are both possible in typical associative polymers. The major difference lies in the presence of open stickers upon damage. When bonded stickers are forced to dissociate, they form a large number of open stickers at the interface. These open stickers are highly active and tend to reassociate with each other, resulting in significant healing effects. Over time, the open stickers become deactivated, transitioning the healing process into adhesion. However, in the case of CANs, the distinction between Diss-CANs and Asso-CANs leads to different adhesion and healing behaviors compared to typical associative polymers. On the basis of the sticky Rouse model,40–43 the network relaxation of CANs results from the superposition of strand motion and chemical reaction.
We believe that there is always a contradiction between the bulk relaxation of the entire network and the local relaxation on the damaged surface, as they both involve the same chemical reaction. As a result, the structure and kinetics can play a crucial role in determining the repair ability of these materials, which, unfortunately, is challenging to characterize in experiments and is often less emphasized by researchers. Here, to precisely simulate chemical reactions and molecular dynamics simultaneously, we deeply analyze the self-repair behavior of Diss-CANs and Asso-CANs by using the hybrid MC/MD algorithm.22,38,44–46 By examining the distinct kinetics of these molecular architectures, we present a systematic description of CANs when used for self-repairing. The results of our study demonstrate that the repair ability of CANs is strongly influenced by their structures and kinetics. Our work not only highlights the similarities and differences between Diss-CANs and Asso-CANs in self-repairing applications, but also more importantly, offers valuable insights for guiding the application of CANs in self-repair materials.
The rest of the manuscript is organized as follows. In Section 2, we present detailed hybrid MC/MD algorithms simulating the Diss-CANs and Asso-CANs, and the simulation of their repair process. In Section 3, we analyze the repair process of Diss-CANs and Asso-CANs, evaluating the repair effect by using the triaxial extension. We further discuss the influence of chemical reactions on the repairing kinetics, where the impacts of activation energy and temperature are emphasized. Finally, the conclusions are summarized in Section 4.
2. Simulation model and method
We adopt the coarse-grained Kremer–Grest (KG) bead-spring model for presenting polymer networks.47 A total of 2000 chains with a length of N = 5 and 300 chains with a length of N = 50, which is at or below the best estimates of the entanglement length 50 ≤ Ne ≤ 85,44,48 are constructed separately in two cubic periodic box with period Li > 2 〈Ree〉 to ensure that the topological structure of the chain is not affected by the box size. Here 〈Ree〉 is the mean end-to-end distance. The choice of box size is to ensure that further increasing the box size will not influence the final calculation results. The interaction energy between each unbonded monomer employs the Lennard-Jones (LJ) potential energy ULJ: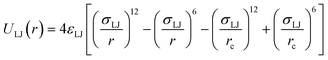 | (1) |
 . The covalent bonding between neighbor beads is modeled with the finitely extensible nonlinear elastic (FENE) potential as follows:
. The covalent bonding between neighbor beads is modeled with the finitely extensible nonlinear elastic (FENE) potential as follows: | (2) |
To highlight the repair effect of CANs, telechelic short chains with 5-mer and crosslinkers such as with four functional groups are firstly constructed, as shown in Fig. 1. Stickers are distributed at the end of each chain and crosslinker, and can only additionally heteroassociate with one other sticker (namely one-to-one) to avoid phase separation. The premixed chains and crosslinkers are cross-linked for 108 steps to ensure forming a fully cross-linked network. This is the prepared initial network for both Asso-CANs and Diss-CAN.
The hybrid MC/MD algorithm is employed to simulate the reversible network in both Asso-CANs and Diss-CANs. To model Asso-CANs, similar to Perego et al.45,46 and our previous work,22 we consider that the rearrangement of the network is accomplished via bond exchange reactions, ensuring the integrity of the network. When modeling Diss-CANs, we adopt the same approach as Hoy and Fredrickson.44 In Diss-CANs, the rearrangement of the network depends on the dissociation and association of stickers, which is simulated through the breaking and creation of sticky bonds. Both methods involve the movement of beads governed by MD equations, while chemical reactions take place in an MC step where the reaction probability is calculated independently.
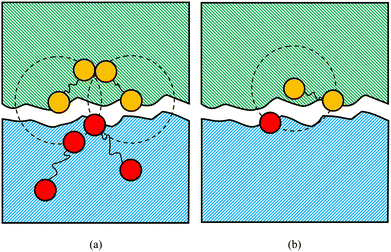
For the simulation of the repair process, we conducted equilibrium molecular dynamics (EMD) simulations with a timestep of δt = 0.01τLJ. Initially, at t = 0, two identical simulation boxes are stacked in the z-direction with fixed boundary conditions to simulate the damaged interface. Subsequently, at t = t1, the fixed boundary conditions are converted into periodic boundary conditions to initiate the chemical reaction. The repair process continued until t = t2, when the chemical reaction is terminated. The snapshots before and after the repair process are shown in Fig. 2(a) and (b), respectively.
 | ||
| Fig. 2 Snapshots of the simulation box (a) before and (b) after the self-repairing process. The two identical simulation boxes are stacked in the z-direction with fixed boundary conditions to simulate the damaged interface. The types of beads are the same as Fig. 1. The blue beads represent the regular beads in the box below. | ||
Triaxial stretching along the z-axis is often used to characterize the repair effect under non-equilibrium molecular dynamics (NEMD) simulation,51–53 where the tensile stress is expressed by Pzz. Because bond breakage is not allowed in FENE potential, the quartic potential is adopted to obtain the stress–strain curves:
| UQ(r) = K(r − Rc)2(r − Rc)(r − Rc − B) + U0 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.01τLJ−1.
= 0.01τLJ−1.
3. Results and discussion
As mentioned above, the self-repairing process involves a competition between the recovery of damaged sites and the overall relaxation of the network. To create a superior self-repair material, it is essential to have both rapid repair ability as well as robust mechanical properties, characterized by fast local site relaxation and slow overall network relaxation. However, conventional CANs face a contradiction in achieving these two kinds of relaxations, as they mainly depend on the same reversible chemical reaction. Indeed, diverse molecular structures and chemical mechanisms are better suited for different types of self-repair behavior based on specific applications and materials. The existence of open stickers further highlights the distinction between self-adhesion and self-healing, making the application of CANs in self-repair materials particularly intriguing.3.1. Asso-CAN system suitable for self-adhesion
To achieve self-adhesion such as in coatings, it is desirable to have arbitrary bonding positions and universal bonding conditions. Homogenous CANs without orientation can easily meet the requirement for sticky positions since chemical reactions can occur everywhere within the network. However, to meet the universal conditions for self-adhesion, the adhesion behavior should be triggered under specific conditions that are relatively easy to achieve and maintain stable behavior under working conditions. To draw an analogy, when using glue, people are willing to wait longer for the glue to cure as long as it provides a strong bond. This means that for self-adhesion, the slower relaxation of the entire network is more important compared to the local relaxation, which is suitable for Asso-CANs because of their conservative crosslinking density.We firstly investigate the influence of bond exchange reaction kinetics on self-adhesion. Fig. 3(a) displays snapshots at various healing times. When t = 0τLJ, there is a clear boundary (representing the interface to be bonded) between the two simulation boxes. As adhesion starts, the interface gradually merges and becomes indistinguishable within t = 1000τLJ. The number of bridge chains that connect the two surfaces, Nbridge, and the depth of sticker diffusion, dbridge, are shown in Fig. 3(b). It is found that Nbridge increases logarithmically with time initially, reaching a maximum at t = 500τLJ, before approaching saturation. Note that the adhesion of Asso-CANs does not need long-distance diffusion, as evidenced by the fact that dbridge is only 2% at t = 500τLJ.
The snapshots of the triaxial extension process are shown in Fig. 4(a). When the sample is pulled apart, voids will form in the middle and at the ends of the box. Crack propagation can be clearly observed during triaxial extension. For unstuck samples i.e., with adhesion time t = 0τLJ, the two simulation boxes can be easily separated by an external force. At short times (t = 50 or 100τLJ), bridge chains start forming, but the number of these bridges (Nbridge) is too small to effectively hold the two parts together. As the adhesion time increases, the separation between the boxes becomes more difficult. The stress–strain curves in Fig. 4(b) show that the maximum stress for samples with adhesion time t ≥ 500τLJ is almost identical to that of the undamaged sample, indicating an excellent adhesion effect.
According to Arrhenius equation:
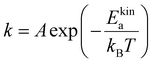 | (4) |
The impact of external stimulus on the self-repairing process can be theoretically observed through the changes in both activation energy and temperature. Therefore, we further explored the adhesion kinetics under various activation energies and temperatures. Fig. 5(a) and (b) show the effect of activation energies on the adhesion processes. With an increase in the adhesion time (t), Nbridge also increases. However, as the activation energies increase, both Nbridge and dbridge experience a significant decrease. This decrease indicates a reduction in the number of bridge chains and the extent of sticker diffusion due to the higher reaction barrier. Consequently, it becomes more difficult for exchange reactions to occur.
The temperature-dependence of the adhesion processes is analyzed in Fig. 5(c) and (d). As the temperature rises, Nbridge and dbridge increase, indicating the acceleration of the exchange reactions. Eqn (4) reveals that the exchange reaction is accelerated at low kinetic activation energies and high temperatures, resulting in an increase in Nbridge and dbridge, which enhance adhesion. When the temperature exceeds a certain threshold (T ≥ 1.0εLJ/kB), the effect of heating on the reactions becomes insignificant. Since crosslinking density remains constant in Asso-CANs, there is a characteristic transition temperature known as the topology freezing temperature (Tv), which is above Tg for commonly used Asso-CANs. Tv determines whether the bond exchange reaction can proceed. In our simulation, we calculated Tv = 0.88εLJ/kB for Asso-CANs, as shown in Fig. S1 (ESI†). Once Tv is reached, the impact of temperature on the system diminishes. It is noticed that this characteristic actually gives vitrimers an advantage in self-repair applications. As long as the temperature is above Tv, the self-repairing process can be triggered.
The triaxial extension is also simulated under different kinetics, and the snapshots at t = 500τLJ are depicted in Fig. 6(a) and (b). When T > 1.0εLJ/kB, as time progresses, the two simulation boxes exhibit minimal separation and the stress–strain curves shown in Fig. 6(c) agree with the snapshots. It should be noted that because of the periodic boundary conditions, the repairing behavior in the middle of the box and the boundaries is the same, and as a result, the overall repairing effect should be the synergistic repairing effect of both the parts. For T = 1.0εLJ/kB in Fig. 6(a), although the bridge chains in the middle of the box seems as many as T > 1.0εLJ/kB, it showed a worse repairing effect since the bridge chains on boundaries are much fewer than under other conditions. In terms of activation energy, Asso-CANs can be classified into different levels of association strength. According to the snapshots in Fig. 6(b) and the corresponding Nbridge in Fig. 5(a), at t = 500τLJ, strong association (Ekina = 8 and 10) results in almost no adhesion, while medium association (Ekina = 4 and 6) leads to a few bridge chains and poor adhesion performance. However, weak association (Ekina = 2) shows a vague interface between the two simulation boxes, and the maximum stress shown in Fig. 6(d) is almost the same as that of the undamaged sample. These results demonstrate that this low activation energy requirement for Asso-CANs is crucial for self-adhesion.
As has been emphasized above, the network relaxation of CANs is due to the superposition of strand motion and chemical reaction. This implies that the calculation of the activation energy for viscous flow, obtained from the terminal relaxation time, involves both the activation energy for strand motion and that for the chemical reaction.22 It should be noted that the activation energy for viscous flow can be considered as the combined effect of strand motion and chemical reaction based on the mean-field theory. However, when a polymer chain is dynamically crosslinked along the backbone, the mean-field theory becomes inapplicable. Consequently, the viscous activation energy may not be simply considered as the sum of strand motion and reaction in this scenario. Nevertheless, it is obvious that the strand motion is closely related to the molecular structure. To further reduce the activation energy for strand motion and enhance the diffusivity, small crosslinkers in the form of stickers are introduced into the bond exchange reaction. In order to compare the adhesion ability, two sets of unentangled pendant crosslinked long linear chains (N = 50) are designed, one with crosslinkers and the other without, but with the same crosslinking density. This comparison is shown in Fig. 7(a) and (b), respectively.
The snapshots shown in Fig. 8(a) and (b) reveal that much longer bridge chains can enhance the toughness through conformational transformation when extended. However, the adhesion performance of the sample without crosslinkers deteriorates, requiring almost t = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τLJ to achieve the same strength as the undamaged sample, as shown in Fig. 8(c). Despite having the same sticker content, the motion is restrained for longer chains, leading to higher activation energy for strand motion and hindering the adhesion behavior. In contrast, the addition of crosslinkers dramatically shortens the adhesion time to t = 1000τLJ, which is nearly 50 times quicker than the long-chain sample and only one time slower than the short-chain sample. This is evident that involvement of small molecules in chemical reactions accelerates the kinetics and shortens the relaxation time by bypassing the activation energy of strand motion. Note that the yield strain is γy ≈ 3.5, representing a two-fold improvement compared to short-chain samples. However, the maximum stress is reduced to σmax ≈ 1.0.
000τLJ to achieve the same strength as the undamaged sample, as shown in Fig. 8(c). Despite having the same sticker content, the motion is restrained for longer chains, leading to higher activation energy for strand motion and hindering the adhesion behavior. In contrast, the addition of crosslinkers dramatically shortens the adhesion time to t = 1000τLJ, which is nearly 50 times quicker than the long-chain sample and only one time slower than the short-chain sample. This is evident that involvement of small molecules in chemical reactions accelerates the kinetics and shortens the relaxation time by bypassing the activation energy of strand motion. Note that the yield strain is γy ≈ 3.5, representing a two-fold improvement compared to short-chain samples. However, the maximum stress is reduced to σmax ≈ 1.0.
 | ||
| Fig. 8 Extension process snapshots and stress–strain curves with long-chains without (a) and (c) and with crosslinkers (b) and (d). The types of beads are the same as in Fig. 7 and the blue beads represent the regular beads in the box below. | ||
3.2. Diss-CANs for self-healing
Unlike self-adhesion, self-healing emphasizes the spontaneous healing behavior of the wound surface without any external intervention, but it requires even more universal conditions. An example from organisms is the healing of the skin. When the skin is damaged, it starts to heal as quickly as possible to stop bleeding. However, the newly healed skin usually has lower strength. In this case, fast local relaxation hence becomes crucial, and it is significantly different from self-adhesion.The conservative crosslinking density of Asso-CANs provides enhanced creep resistance, while, reduction of crosslinks can actually prompt the healing performance. When subjected to external forces and deformation, Diss-CANs tend to dissociate into open stickers even before the strain rate reaches the inverse pre-factor of the terminal relaxation time.22 These open stickers have a strong tendency to react with one another, facilitating easier healing even under challenging conditions like low temperatures. Local relaxation can be greatly accelerated through this mechanism.
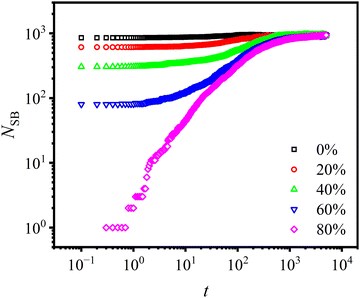
The influence of the concentration of open stickers, Copen, on the bonding rate is investigated, as shown in Fig. 9. In the simulation, sticky bonds near the interface are removed partially or completely resulting in the presence of open stickers. It is found that under strong association energy (Ekina = 10εLJ) more than 90% of open stickers are bonded after t = 104τLJ. This indicates that the presence of open stickers promotes bond formation, and the bonding rate increases with their content. As a result, the bonding rate at the interface is much faster than that in the bulk region due to the large number of exposed bonding sites at the interface, as illustrated in Fig. S3 (ESI†). These findings support our claim that Diss-CANs are suitable for self-healing materials.
In our previous study, we found a strong correlation between the concentration of open stickers and the association energy.22 In a weak-associated system, the interaction between stickers is not sufficiently strong to maintain them together, resulting in a significant presence of open stickers and hence poor healing behavior. To address this issue, it is crucial to establish a state of strong association that can promote effective self-healing. In Fig. 10, the equilibrium concentration of open stickers is plotted under various temperatures and activation energies. As the temperature decreases and the activation energy increases, the concentration of open stickers decreases accordingly. Here, to quantify the level of strong association, we define it as a state where the concentration of open stickers is below 10%.
The healing dynamics are investigated by comparing the changes in the concentration of open stickers at the interface with the corresponding mean-squared distance (MSD) under conditions of strong and weak association, as shown in Fig. 11. In the case of strong association, the concentration of open stickers decreases dramatically after some healing time, while for weak associations, it remains almost unchanged. Interestingly, the timescale at which the concentration of open stickers changes rapidly is similar to the timescale at which MSD reaches a plateau, indicating that the scale of the motion unit is predominantly strands. For Diss-CANs, this suggests that direct bonding between open stickers is the fastest mode of association. In contrast, no plateau is found for weak association, showing unhindered diffusion. This is actually why both Nbridge and dbridge are used to quantify adhesion or the healing effect, as the depth of diffusion is insignificant for weak association. Evidently, stronger associations are necessary for the self-healing of Diss-CANs, which is opposed to the self-adhesion of Asso-CANs.
 | ||
| Fig. 11 Open sticker concentration as a function of time (t) and its corresponding MSD for strong and weak associations. | ||
The stress–strain curves are plotted to examine the influence of various open sticker concentrations on the healing behavior of self-healing polymers at shorter healing time t = 100τLJ, as shown in Fig. 12(a). It is observed that the level of open stickers has a great impact on the healing effect. For samples without open stickers that rely solely on dissociation and reassociation, the healing process did not commence within this time scale. Conversely, the samples with 80% open stickers exhibit almost half the strength compared to the undamaged sample, indicated by the maximum stress σmax ≈ 0.7. Moreover, Fig. 12(b) shows the relationship between the concentration of open stickers and Nbridge, demonstrating a nearly proportional relationship.
 | ||
| Fig. 12 (a) Stress–strain curves under various concentrations of open stickers. (b) Nbridge as a function of concentration of open stickers (Copen). | ||
Note that self-healing behavior is not limited to Diss-CANs. Asso-CANs also have open stickers on the damaged surface. However, it is generally believed that Diss-CANs exhibit superior healing performance to Asso-CANs. This is due to two key factors. Firstly, as discussed above, Diss-CANs tend to form more open stickers when damaged. Secondly, the bond exchange rate in Asso-CANs is not significantly affected by the presence of open stickers, whereas in Diss-CANs, open stickers can easily bond together due to strong association energy. Wu et al.60 conducted a study indicating that the influence of sticker concentration on healing performance is not as significant as temperature or activation energy. Additionally, in some cases, Asso-CANs may have separate crosslinking and bond exchange reactions. In other words, it is uncertain whether the crosslinking reaction can occur during the bond exchange reaction, resulting in the formation of open stickers that may not be able to participate in the rearrangement of the network.61
In addition, the healing efficiency can be influenced by the molecular structure. It is important to note that the dissociated small molecules remain unaffected by strand motion, resulting in a faster reaction rate. However, it is crucial to emphasize that the primary factor for self-healing is the kinetics of the chemical reaction. Therefore, we have provided less discussion on the molecular structure, focusing instead on the significance of reaction rates in the self-healing process.
3.3. Repair timescale of self-adhesion and self-healing processes
After conducting independent simulations, we have compared the timescale of self-adhesion for Asso-CANs and the self-healing for Diss-CANs theoretically. In the case of Asso-CANs, the repair (self-adhesion) timescale is solely determined by the bond exchange kinetics: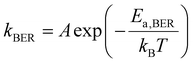 | (5) |
 | (6) |
For the self-healing of Diss-CANs, as shown in Fig. 13(b), bond breakage becomes unnecessary, and we only need to consider the kinetics of bond creation. In this scenario, the repair timescale is solely dependent on the association between stickers. The reaction rate and corresponding relaxation time are as follows:
 | (7) |
 | (8) |
Therefore, considering both the activation energy and pre-factor in Arrhenius equation, it can be concluded that the repair timescale of Asso-CANs is generally slower than that of Diss-CANs when the molecular structure remains the same. However, this conclusion relies on the assumption that both damage and healing occur simultaneously at the interface of Diss-CANs. If the open stickers on one side of the interface cannot access the open stickers on the other side, they can deactivate by bonding to each other instead. Once the majority of the open stickers have transformed into bonded stickers after a characteristic time τs,create, the self-healing behavior becomes indistinguishable from self-adhesion.
Polymer melt welding, similar to self-adhesion, involves the joining of entangled polymers. However, it requires higher temperatures and depends on long-distance diffusion for the welding effect to occur. Consequently, the timescale for welding is generally closer to the terminal relaxation time of entangled polymers, which is typically slower than the repair timescale of CANs.
4. Conclusion
Building upon our previous work,22 we utilize the linear and nonlinear viscoelastic properties of CANs to simulate the self-repair behavior by using a hybrid MC/MD algorithm. CANs exhibit diverse repair mechanisms, namely self-adhesion and self-healing, both of which are closely related to the kinetics of chemical reactions.For self-adhesion, the emphasis is on bonding strength, as it determines the mechanical strength and creep resistance of Asso-CANs below Tv, making them suitable for self-adhesion materials. The kinetics play a crucial role in adhesion efficiency. Above Tv, the decrease of activation energy leads to an improved adhesion performance. By introducing small molecules, the adhesion time can be significantly reduced, as their diffusion is not affected by strand motion. At this point, the activation energy for viscous flow is almost equal to the activation energy for kinetics.
In self-healing materials, the local healing efficiency becomes the top priority. Dissociation is permitted, and the presence of open stickers on the damaged surface is inevitable, making Diss-CANs a suitable choice for self-healing materials perfectly. The healing process is primarily driven by the encounter of open stickers through walking diffusion across the surface. As a result, the healing efficiency is significantly influenced by the concentration of open stickers and the strength of association energy between them. Interestingly, in contrast to the self-adhesion behavior observed in Asso-CANs, an increase in the association energy actually improves the healing effect. Additionally, our work demonstrates that Diss-CANs exhibit a shorter self-healing timescale compared to the self-adhesion timescale observed in Asso-CANs. These findings have significant implications for the development of self-repair materials, as they can serve as a valuable guide for understanding the molecular design of CANs to enhance their self-repairing capabilities.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from the National Natural Science Foundation of China (grant no. 21973017 and 22373023).References
- C. Jiang, L. Zhang, Q. Yang, S. Huang, H. Shi, Q. Long, B. Qian, Z. Liu, Q. Guan, M. Liu, R. Yang, Q. Zhao, Z. You and X. Ye, Nat. Commun., 2021, 12, 4395 CrossRef CAS PubMed.
- N. Tang, R. Zhang, Y. Zheng, J. Wang, M. Khatib, X. Jiang, C. Zhou, R. Omar, W. Saliba, W. Wu, M. Yuan, D. Cui and H. Haick, Adv. Mater., 2022, 34, 2106842 CrossRef CAS PubMed.
- Y. Liang, H. Xu, Z. Li, A. Zhangji and B. Guo, Nanomicro Lett., 2022, 14, 185 CAS.
- H. Chen, Z. Z. Wu, Z. Su, S. Chen, C. Yan, M. Al-Mamun, Y. B. Tang and S. Q. Zhang, Nano Energy, 2021, 81, 105654 CrossRef CAS.
- J. Xu, X. Wang, X. Zhang, Y. Zhang, Z. Yang, S. Li, L. Tao, Q. Wang and T. Wang, Chem. Eng. J., 2023, 451, 138673 CrossRef CAS.
- R. Guo, Q. Zhang, Y. Wu, H. Chen, Y. Liu, J. Wang, X. Duan, Q. Chen, Z. Ge and Y. Zhang, Adv. Mater., 2023, 35, 2212130 CrossRef CAS PubMed.
- W. J. Ma, Y. C. Ding, Y. S. Li, S. T. Gao, Z. C. Jiang, J. X. Cui, C. B. Huang and G. D. Fu, J. Membr. Sci., 2021, 634, 119402 CrossRef CAS.
- L. W. Ma, J. K. Wang, D. W. Zhang, Y. Huang, L. Y. Huang, P. J. Wang, H. C. Qian, X. G. Li, H. A. Terryn and J. M. C. Mol, Chem. Eng. J., 2021, 404, 127118 CrossRef CAS.
- B. Li, S. Xue, P. Mu and J. Li, ACS Appl. Mater. Interfaces, 2022, 14, 30192–30204 CrossRef CAS PubMed.
- P. Reutenauer, E. Buhler, P. J. Boul, S. J. Candau and J. M. Lehn, Chemistry, 2009, 15, 1893–1900 CrossRef CAS PubMed.
- G. Du, A. Mao, J. Yu, J. Hou, N. Zhao, J. Han, Q. Zhao, W. Gao, T. Xie and H. Bai, Nat. Commun., 2019, 10, 800 CrossRef PubMed.
- R. Xue, H. Zhao, Z. W. An, W. Wu, Y. Jiang, P. Li, C. X. Huang, D. Shi, R. K. Y. Li, G. H. Hu and S. F. Wang, ACS Nano, 2023, 17, 5653–5662 CrossRef CAS PubMed.
- X. Y. Ding, G. Li, P. Zhang, E. Jin, C. S. Xiao and X. S. Chen, Adv. Funct. Mater., 2021, 31, 2011230 CrossRef CAS.
- X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698–1702 CrossRef CAS PubMed.
- C. Dry, Compos. Struct., 1996, 35, 263–269 CrossRef.
- S. R. White, N. R. Sottos, P. H. Geubelle, J. S. Moore, M. R. Kessler, S. R. Sriram, E. N. Brown and S. Viswanathan, Nature, 2002, 415, 817 CrossRef CAS.
- K. S. Toohey, N. R. Sottos, J. A. Lewis, J. S. Moore and S. R. White, Nat. Mater., 2007, 6, 581–585 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- A. Jourdain, R. Asbai, A. Omaima, M. M. Chehimi, E. Drockenmuller and D. Montarnal, Macromolecules, 2020, 53, 1884–1900 CrossRef CAS.
- L. E. Porath and C. M. Evans, Macromolecules, 2021, 54, 4782–4791 CrossRef CAS.
- A. Rao, J. Ramirez and B. D. Olsen, Macromolecules, 2021, 54, 11212–11227 CrossRef CAS.
- X. Cui, N. F. Jiang, J. Y. Shao, H. D. Zhang, Y. L. Yang and P. Tang, Macromolecules, 2023, 56, 772–784 CrossRef CAS.
- M. Podgorski, B. D. Fairbanks, B. E. Kirkpatrick, M. McBride, A. Martinez, A. Dobson, N. J. Bongiardina and C. N. Bowman, Adv. Mater., 2020, 32, 1906876 CrossRef CAS PubMed.
- Y. H. Wu, S. Zhang, Y. Yang, Z. Li, Y. Wei and Y. Ji, Sci. Adv., 2022, 8, eabo6021 CrossRef CAS PubMed.
- S. S. Chen, M. Y. Zhang, Q. Y. Li, J. C. Li, S. P. Wu, J. Zhou, G. Q. Jin, Z. B. Zhang, X. Q. Pan and J. Zhu, Macromolecules, 2023, 56, 5765–5773 CrossRef CAS.
- R. Dolog and R. A. Weiss, Macromolecules, 2013, 46, 7845–7852 CrossRef CAS.
- W. Alabiso, T. M. Hron, D. Reisinger, D. Bautista-Anguis and S. Schlogl, Polym. Chem., 2021, 12, 5704–5714 RSC.
- Y. C. Mao, Y. Kubota, R. Q. Feng, J. Gong, A. Ishigami, Y. Kobayashi, T. Watabe, D. Aoki, H. Otsuka and H. Ito, Macromolecules, 2022, 55, 3948–3957 CrossRef CAS.
- J. R. Huang, N. Ramlawi, G. S. Sheridan, C. Chen, R. H. Ewoldt, P. V. Braun and C. M. Evans, Macromolecules, 2023, 56, 1253–1262 CrossRef CAS.
- Y. J. Lin, Y. L. Chen, Z. A. Yu, Z. J. Huang, J. C. Lai, J. B. H. Tok, Y. Cui and Z. N. Bao, Chem. Mater., 2022, 34, 2393–2399 CrossRef CAS.
- H. L. Wang, Z. Shi, K. R. Guo, J. R. Wang, C. L. Gong, X. L. Xie and Z. G. Xue, Macromolecules, 2023, 56, 2494–2504 CrossRef CAS.
- H. Guo, Y. Han, W. Zhao, J. Yang and L. Zhang, Nat. Commun., 2020, 11, 2037 CrossRef CAS PubMed.
- L. Imbernon, S. Norvez and L. Leibler, Macromolecules, 2016, 49, 2172–2178 CrossRef CAS.
- S. Ciarella and W. G. Ellenbroek, Coatings, 2019, 9, 114 CrossRef.
- M. K. McBride, B. T. Worrell, T. Brown, L. M. Cox, N. Sowan, C. Wang, M. Podgorski, A. M. Martinez and C. N. Bowman, Annu. Rev. Chem. Biomol., 2019, 10, 175–198 CrossRef CAS PubMed.
- Y. Yang, H. M. Wang, S. Zhang, Y. Wei, X. M. He, J. L. Wang, Y. Y. Zhang and Y. Ji, Matter, 2021, 4, 3354–3365 CrossRef CAS.
- N. Roy, B. Bruchmann and J. M. Lehn, Chem. Soc. Rev., 2015, 44, 3786–3807 RSC.
- E. B. Stukalin, L. H. Cai, N. A. Kumar, L. Leibler and M. Rubinstein, Macromolecules, 2013, 46, 7525–7541 CrossRef CAS PubMed.
- Z. R. Hinton, A. Shabbir and N. J. Alvarez, Macromolecules, 2019, 52, 2231–2242 CrossRef CAS.
- Q. Chen, G. J. Tudryn and R. H. Colby, J. Rheology, 2013, 57, 1441–1462 CrossRef CAS.
- N. F. Jiang, H. D. Zhang, P. Tang and Y. L. Yang, Macromolecules, 2020, 53, 3438–3451 CrossRef CAS.
- N. F. Jiang, H. D. Zhang, Y. L. Yang and P. Tang, J. Rheology, 2021, 65, 527–547 CrossRef CAS.
- J. Y. Shao, N. F. Jiang, H. D. Zhang, Y. L. Yang and P. Tang, Macromolecules, 2022, 55, 535–549 CrossRef CAS.
- R. S. Hoy and G. H. Fredrickson, J. Chem. Phys., 2009, 131, 224902 CrossRef PubMed.
- A. Perego and F. Khabaz, Macromolecules, 2020, 53, 8406–8416 CrossRef CAS.
- A. Perego, D. Lazarenko, M. Cloitre and F. Khabaz, Macromolecules, 2022, 55, 7605–7613 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823–826 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. I. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271 Search PubMed.
- LAMMPS Home Page, (accessed 2023-08-02).
- Z. Y. Zhang, J. Liu, S. Li, K. Gao, V. Ganesan and L. Q. Zhang, Macromolecules, 2019, 52, 4154–4168 CrossRef CAS.
- Y. Fang, T. K. Yue, S. Li, Z. Y. Zhang, J. Liu and L. Q. Zhang, Macromolecules, 2021, 54, 1095–1105 CrossRef CAS.
- J. He, Q. Chen, J. Qu, S. Li, Z. Fu, Y. Wei, S. Hu, A. Feng, L. Zhang and J. Liu, ACS Appl. Poly. Mater., 2023, 5, 3161–3172 CrossRef CAS.
- S. W. Sides, G. S. Grest and M. J. Stevens, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 050802 CrossRef CAS PubMed.
- M. J. Stevens, Macromolecules, 2001, 34, 2710–2718 CrossRef CAS.
- M. J. Stevens, Macromolecules, 2001, 34, 1411–1415 CrossRef CAS.
- J. Rottler, S. Barsky and M. O. Robbins, Phys. Rev. Lett., 2002, 89, 148304 CrossRef PubMed.
- C. Creton, E. J. Kramer, C. Y. Hui and H. R. Brown, Macromolecules, 1992, 25, 3075–3088 CrossRef CAS.
- T. Yan, K. Schröter, F. Herbst, W. H. Binder and T. Thurn-Albrecht, Macromolecules, 2017, 50, 2973–2985 CrossRef CAS.
- J. B. Wu, S. J. Li, H. Liu, H. J. Qian and Z. Y. Lu, Phys. Chem. Chem. Phys., 2019, 21, 13258–13267 RSC.
- M. Rottger, T. Domenech, R. van der Weegen, A. Breuillac, R. Nicolay and L. Leibler, Science, 2017, 356, 62–65 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01364b |
| ‡ X. Cui and L. Zhang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |