 Open Access Article
Open Access ArticleModeling photo-generated charge extraction in bulk heterojunction nanoparticles
Nigel
Clarke
 a and
Gavin A.
Buxton
b
a and
Gavin A.
Buxton
b
aDepartment of Physics and Astronomy, University of Sheffield, S3 7RH, Sheffield, UK. E-mail: n.clarke@sheffield.ac.uk
bScience Department, Robert Morris University, Moon Township, PA 15108, USA
First published on 22nd December 2023
Abstract
We present a drift-diffusion model for predicting currents generated through the absorption of solar energy inside bulk heterojunction organic nanoparticles, which are, for example, promising nanomaterials for photo-catalytic water splitting. By coupling a model of the internal microstructure of the nanoparticle with the electronic properties, we show how different characteristics of the microstructure influence the efficiency of the conversion of solar energy into electrical energy. Our model provides a foundation for using computational modeling to optimize the design of photocatalytic nanoparticles.
1 Introduction
The transition towards renewable, but intermittent, energy sources is motivating efforts to improve energy storage technologies. Pioneering research by Fujishima and Honda1 exemplified how solar energy can be converted into store-able chemical energy, in the form of H2, through water splitting. During photo-catalyzed water splitting, photons, absorbed inside a semiconducting material, generate free charges that then facilitate the oxidation of H2O and the reduction of the resultant H+ into molecular hydrogen, which can be stored for use in hydrogen fuel cells.Since the oxidation and reduction reactions require free charges to come into contact with water, semi-conducting nanomaterials have been extensively studied as promising photocatalysts for improving the efficiency of water splitting devices.2 The large surface area to volume ratio of nanomaterials maximizes the amount of charge transported to the interface between the photo-catalyst and the water. Whilst there is an abundance of inorganic semiconductors that convert light into electron–hole pairs, inorganic nanoparticulates are typically wide band gap semiconductors that only absorb in the ultra-violet region,3 which only accounts for a few percent of the Sun's radiation reaching the Earth's surface.
In contrast, organic semiconductors often have smaller band gaps, making them active in a wider region of the visible spectrum. The challenge in developing efficient organic semiconductors is that an absorbed photon leads to the creation of an exciton, a bound state of an electron hole pair. Excitons have a high binding energy and short diffusion length before they decay. As a consequence only those excitons generated within ∼10 nm of the semiconductor surface are likely to disassociate into the unbound electrons/holes required for the reduction/oxidation reactions, significantly inhibiting the efficiency of devices based on such nanoparticles. One promising route to overcome this challenge is to make the nanoparticles from binary mixtures of organic materials that phase separate, creating internal interfaces.4,5 Solar cells based on such mixtures are often referred to as bulk heterojunction (BHJ) devices, with the best performing conventionally being mixtures of an organic electron donor and a fullerene based electron acceptor.6 Due to poor thermal and photo-chemical stability, more recent attention has turned to non-fullerene based electron acceptors.7
Kosco et al.4 and Yang et al.5 recently showed that careful engineering of the internal structure of a BHJ nanoparticle, comprised of a polymeric donor and an organic non-fullerene acceptor, can significantly enhance the hydrogen evolution rate. In a BHJ, disassociation of photo-generated excitons is enhanced at internal donor:acceptor interfaces due to the difference in electron affinity between the two phases. The electrons and holes are then free to diffuse through the acceptor/donor phases. If the internal structure is such that there is no chemical preference for one phase over the other to enrich the surface of the nanoparticle, then both electrons and holes are able to reach the surface with equal probability, maximizing the subsequent water splitting reaction, and hence hydrogen evolution rate. Other recent advances in methodologies for controlling the microstructure and dispersion of semi-conducting nanoparticles, including surfactant free techniques such as precipitation8 and electrostatic stabilisation through illumination,9,10 demonstrate that there remain opportunities for further improving the power conversion efficiency of nanoparticulate based devices.
Due to the complexity of the photo-chemical pathway from absorbed photons to free charges, it can be challenging to experimentally determine how the formulation and/or synthetic methodology impact upon charge generation and hence hydrogen evolution. Modeling is a valuable tool to complement experimental materials design, enabling the prediction of structure – property relations, and providing insights in the mechanisms that determine performance. Electronic properties of photo-active molecules can be effectively predicted using density functional theory,11 but elucidating the role of microstructure on the scale of tens of nanometres in BHJs requires a mesoscale approach, in which effects such as charge generation, exciton dissociation and recombination, and the hopping of charges are coarse-grained in a drift-diffusion model. We also use a coarse-grained phase-field approach to create the internal microstructure of the bulk heterojunction. The timescales associated with the microstructure formation are many orders of magnitude greater than those that are accessible to molecular dynamics simulations, even when atomistic details are coarse-grained into bead-spring polymer models.12
We have previously shown how mesoscale modeling, using both drift-diffusion and kinetic Monte Carlo methods, can be invaluable in predicting structure–property relations in organic solar cells. Such modeling has enabled us to highlight the potential of block co-polymer microstructures as efficient active layers;13 to quantify how surface wetting layers can reduce device efficiency;14 to demonstrate the importance of sharp, rather than diffuse, interfaces between phases within the BHJ15 for increasing device efficiency; and to clarify the impact of delocalized charge transfer states on the efficiency of fullerene based devices.
In this paper, we extend our drift-diffusion model16 to predict how the internal and surface microstructure of a BHJ nanoparticle affects the number of photo-generated electrons and holes that reach the surface of the nanoparticle. From this, we elucidate the role that morphology plays in the extraction of current from the polymer photovoltaic nanoparticles. We believe that our model will provide an invaluable tool for interrogating the complex physical and chemical processes at play in determining the efficiency of BHJ nanoparticles for photo-generated charge extraction, providing surfactant free methods have recently been developed.
2 Methodology
The modeling workflow is summarized in Fig. 1. The morphologies are obtained from the Flory–Huggins Cahn–Hilliard microstructure evolution model, a polymer specific phase field model. The photogeneration of excitons are obtained from a finite-difference time-domain solar absorption model. The output from both the microstructure and solar absorption modeling serve as inputs for the drift diffusion model. The drift diffusion model consists of iteratively solving Poisson's equation and the drift diffusion equations in turn using the conjugate gradient method. In other words, four systems of simultaneous equations have to be solved at each time step. The Scharfetter–Gummel method is used to discretize the drift diffusion equation and ensure numerical stability, with the linear equations detailed in Buxton and Clarke.16 The simulation progresses until sufficient convergence has occurred.2.1 Microstructure modeling
The Flory–Huggins Cahn–Hilliard model is used to capture polymer nanoparticle morphologies. The free energy is of the form: | (1) |
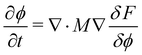 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 polymer mixture is shown in Fig. 2a. The system undergoes spinodal decomposition and different phases of incompatible polymer emerge quite early on. Over time these domains coarsen.
50 polymer mixture is shown in Fig. 2a. The system undergoes spinodal decomposition and different phases of incompatible polymer emerge quite early on. Over time these domains coarsen.
2.2 Solar absorption modeling
The absorbed power density of solar light by a nanoparticle is captured using the finite-difference time-domain. In particular, the software MEEP is used to calculate the local absorbed power density in a dispersive polymeric material.20 The deposition of small (on the order of 1 nm) metal co-catalysts was found to be negligible in terms of the absorption of solar light. A two-dimensional system containing the nanoparticle in the center (with a radius of 42 nm) is bounded with perfectly matched layers. The wavelengths of light that comprise sunlight are initiated from a line source of light in the model. This allows the absorbed power density, Si(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) to be calculated as a function of position within the nanoparticle. The photo-generation of excitons is given by
) to be calculated as a function of position within the nanoparticle. The photo-generation of excitons is given by  , where Φi is the incident photon flux (an experimentally obtained table of values can be obtained in ref. 21). The Drude–Lorentzian susceptibility that is assumed for the organic material is depicted in Fig. 2b, while the absorbed power density in the nanoparticle is shown in Fig. 2c.
, where Φi is the incident photon flux (an experimentally obtained table of values can be obtained in ref. 21). The Drude–Lorentzian susceptibility that is assumed for the organic material is depicted in Fig. 2b, while the absorbed power density in the nanoparticle is shown in Fig. 2c.
2.3 Drift diffusion model
The two-dimensional drift-diffusion model is comprised of Poisson's equation and three equations that evolve in time the concentrations of electrons (n), holes (p) and excitons (x),| ∇·(ε∇ψ) = −q(p − n) | (3) |
 | (4) |
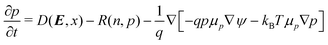 | (5) |
 | (6) |
The first equation is Poisson's equation, which is used to calculate the electrostatic potential, ψ, in terms of the concentration of charged particles. ε is the permittivity and q the elementary charge. The second and third equations are the continuity equations for the electron and hole concentrations, respectively. μn is the mobility of electrons, μp is the mobility of holes, μx is the mobility of excitons, kB is the Boltzmann constant and T is the temperature. Note that the flux of these charge carriers involves both drift (dictated by the gradient of the electrostatic potential) and diffusion (dictated by gradients in the charge carrier concentrations themselves). The last equation captures the evolution of the exciton concentrations, which contains a diffusion term.
The charge carriers can be created via the dissociation of excitons and this is described by Onsager's theory for electrolyte dissociation and given by22
 | (7) |
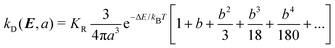 | (8) |
The charge carriers can recombine prior to dissociation, and this is captured with a recombination term, R(n,p); the rate of recombination is taken to be of the Langevin form, R(n,p) = q(μn + μp)pn/ε. A fraction (commonly taken as  ) recombine to form singlet excitons and, therefore, this term also appears in the continuity equation for excitons. The above dissociation term also appears in the continuity equation for excitons, as exciton dissociation reduces the concentration of excitons. However, if excitons do not dissociate they may recombine, or decay. The recombination rate of excitons is R(x) = x/τx, where τx is the average lifetime of an exciton.
) recombine to form singlet excitons and, therefore, this term also appears in the continuity equation for excitons. The above dissociation term also appears in the continuity equation for excitons, as exciton dissociation reduces the concentration of excitons. However, if excitons do not dissociate they may recombine, or decay. The recombination rate of excitons is R(x) = x/τx, where τx is the average lifetime of an exciton.
A field-dependent carrier mobility of the Poole–Frenkel form is used to capture the hopping process that occurs during the current transport in organic semiconductors,  .25 We adopt the strategy of Ruhstaller et al.26 for simulating the hopping process at internal interfaces, where it is assumed that the hopping rate between two sites differing in energy by ΔE is proportional to exp[−(ΔE + Ep)2/4kBTEp], where Ep is the polaron binding energy. The metal-semiconductor interface at the metal co-catalysts, and the water-semiconductor interfaces, are simulated using the boundary conditions of Scott and Malliaras.27 The precise form of the current in these Schottky barriers can be found in either Barker et al.28 or Lacic and Inganas.29 Metal co-catalysts (occupying a single site in the discrete lattice) are randomly dispersed on the surface of the polymer nanoparticle. All four equations (that update the concentrations, and Poisson's equation) are solved using the conjugate gradient method at each time step. This allows us to capture the current density into the metal cocatalysts as a consequence of the polymer nanoparticle morphology and the distribution of cocatalysts on the surface of the nanoparticle.
.25 We adopt the strategy of Ruhstaller et al.26 for simulating the hopping process at internal interfaces, where it is assumed that the hopping rate between two sites differing in energy by ΔE is proportional to exp[−(ΔE + Ep)2/4kBTEp], where Ep is the polaron binding energy. The metal-semiconductor interface at the metal co-catalysts, and the water-semiconductor interfaces, are simulated using the boundary conditions of Scott and Malliaras.27 The precise form of the current in these Schottky barriers can be found in either Barker et al.28 or Lacic and Inganas.29 Metal co-catalysts (occupying a single site in the discrete lattice) are randomly dispersed on the surface of the polymer nanoparticle. All four equations (that update the concentrations, and Poisson's equation) are solved using the conjugate gradient method at each time step. This allows us to capture the current density into the metal cocatalysts as a consequence of the polymer nanoparticle morphology and the distribution of cocatalysts on the surface of the nanoparticle.
2.4 Numerical parameters
Following our previous work, we illustrate the capabilities of the model using parameters that are typical of organic bulk heterojunction materials.13 We take the zero-field mobility of the electrons in the acceptor and donor to be 1 × 10−8 m2 V−1 s−1 and 1 × 10−9 m2 V−1 s−1, respectively. Holes generally have a higher mobility than electrons and, therefore, we take the zero-field hole mobility in the acceptor and donor to be 2 × 10−8 m2 V−1 s−1 and 2 × 10−9 m2 V−1 s−1, respectively. The exciton mobility, μx = 3.86 × 10−9 m2 V−1 s−1, takes into consideration a diffusion length of 10 nm and a lifetime, τx, of 1 μs. The field-dependent mobility parameter is taken to be γ = 5 × 10−4 m2 V−2. The polaron binding energy is 0.1 eV, the band offset between donor and acceptor is taken to be 0.7 eV, the exciton binding energy is 0.5 eV and the Schottky barrier height is 0.5 eV. The built-in voltage is assumed to be 0.5 V. The fundamental parameters that act as inputs for our models could, in principle, be determined using a multiscale modeling scheme incorporating, for example, density functional theory, molecular mechanics and non-adiabatic molecular dynamics. The development of such multiscale modeling is challenging with many issues regarding how to bridge between the different time and length scales unresolved. A detailed discussion of the state-of-the-art of multiscale modeling of photocatalytic materials and the challenges can be found in Samamta et al.113 Results and discussion
A typical example morphology generated from the microstructure modeling is shown in Fig. 2a.Assuming that electrons and holes extracted into the water or the co-catalysts will instantly recombine, in Fig. 3 we show the difference in currents extracted from the system, corresponding to the electron current minus the hole current into the co-catalysts and the hole current minus the electron current into the water. Fig. 3a shows these differences in current as a function of the concentration of donor and acceptor polymers. When the ratio of donor to acceptor concentration is 30% to 70% the donor material exists as islands in a matrix of acceptor material. Electrons, therefore, have a clear path from the donor–acceptor interfaces to the co-catalyst particles around the outside of the nanoparticle. The electron current extracted from the device via the co-catalysts is at its greatest. The difference in current, holes minus electrons, to the surrounding water is negative as more electrons exit into the water than holes. At the other extreme, where the donor–acceptor ratio is 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 and islands of acceptor are surrounded by donor material, electrons are not efficiently extracted from the device. Small regions of acceptor material are at the surface, and electrons may be able to travel through this acceptor material to the co-catalysts particles. However, a large amount of acceptor material exists as isolated islands. Electrons dissociated in these regions will find it more difficult to be extracted from the device as they will have to travel across donor material to reach the co-catalyst particles around the outside of the nanoparticle. The optimum morphology would be near the 50
30 and islands of acceptor are surrounded by donor material, electrons are not efficiently extracted from the device. Small regions of acceptor material are at the surface, and electrons may be able to travel through this acceptor material to the co-catalysts particles. However, a large amount of acceptor material exists as isolated islands. Electrons dissociated in these regions will find it more difficult to be extracted from the device as they will have to travel across donor material to reach the co-catalyst particles around the outside of the nanoparticle. The optimum morphology would be near the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 donor–acceptor ratio, where both electrons can reach the co-catalyst particles and holes can reach the surrounding water. During the phase separation process one phase of the polymer blend may preferentially wet to the surface, giving rise to a core–shell type morphology. Fig. 3b shows how such morphological changes affect the currents. In Fig. 4, we show that preferential attraction of the platinum co-catalysts to the acceptor material can increase the extracted current by approximately 36%.
50 donor–acceptor ratio, where both electrons can reach the co-catalyst particles and holes can reach the surrounding water. During the phase separation process one phase of the polymer blend may preferentially wet to the surface, giving rise to a core–shell type morphology. Fig. 3b shows how such morphological changes affect the currents. In Fig. 4, we show that preferential attraction of the platinum co-catalysts to the acceptor material can increase the extracted current by approximately 36%.
The difference in current is plotted as a function of the preferred phase (negative for acceptor and positive for donor) and the strength of the interaction. The surface interaction is represented in our model by the parameter Vϕs. A value of Vϕs = −0.1, correspond to a shell of donor material surrounding the core of the nanoparticle, a value of Vϕs = −0.01 is a core partially, but not completely, surrounded by a shell of donor material, a value of Vϕs = 0 is the usual 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 bulk heterojunction morphology, and a value of Vϕs = +0.1 results in a system with an acceptor shell. Note that even in a system with a shell of acceptor material around the outside of the nanoparticle, there exists many regions of acceptor material isolated from this shell in the center of the nanoparticle. This is why even for a system with a shell of acceptor material, the electrons are not as easily extracted as in a bulk heterojunction morphology.
50 bulk heterojunction morphology, and a value of Vϕs = +0.1 results in a system with an acceptor shell. Note that even in a system with a shell of acceptor material around the outside of the nanoparticle, there exists many regions of acceptor material isolated from this shell in the center of the nanoparticle. This is why even for a system with a shell of acceptor material, the electrons are not as easily extracted as in a bulk heterojunction morphology.
Fig. 5 depicts the concentrations of electrons, holes and excitons in a bulk-heterojunction morphology, a nanoparticle with a donor–acceptor ratio of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 and a nanoparticle with a shell of donor material around the outside. In this bulk-heterojunction morphology within the islands of donor or acceptor, surrounded by acceptor or donor, respectively, there are no low energy pathways to charge extraction, leading to the accumulation of charge, hence the concentrations of holes and electrons will be larger in these regions (Fig. 5a and b). Closer to the outside of the nanoparticle, holes and excitons are more easily extracted from the nanoparticle. The excitons are dissociated at the interface between donor and acceptor and, in all the systems considered here, the concentrations of excitons are smallest at the donor–acceptor interfaces (Fig. 5c, f and i). In the system with a donor–acceptor ratio of 30
70 and a nanoparticle with a shell of donor material around the outside. In this bulk-heterojunction morphology within the islands of donor or acceptor, surrounded by acceptor or donor, respectively, there are no low energy pathways to charge extraction, leading to the accumulation of charge, hence the concentrations of holes and electrons will be larger in these regions (Fig. 5a and b). Closer to the outside of the nanoparticle, holes and excitons are more easily extracted from the nanoparticle. The excitons are dissociated at the interface between donor and acceptor and, in all the systems considered here, the concentrations of excitons are smallest at the donor–acceptor interfaces (Fig. 5c, f and i). In the system with a donor–acceptor ratio of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 there are electrons flowing through the matrix acceptor material to the co-catalysts (Fig. 5d), but the islands of donor material trap holes in the system and result in large concentrations of holes (Fig. 5e). In a system with donor material around the outside the electrons accumulate at the donor–acceptor interface of the shell material, especially in regions near the co-catalyst particles (Fig. 5g). However, the electrons will have to flow through the donor material if they are reach the co-catalysts and this limits the current in these devices. Even the holes, which when dissociated in the shell region can be easily extracted, can be limited because there exists islands of donor material within the nanoparticle separate from the donor shell (Fig. 5h). Therefore, the optimum morphology which allows both electrons and holes to be extracted is the bulk heterojunction morphologies with continuous pathways of acceptor material to the co-catalysts and donor material to regions of water.
70 there are electrons flowing through the matrix acceptor material to the co-catalysts (Fig. 5d), but the islands of donor material trap holes in the system and result in large concentrations of holes (Fig. 5e). In a system with donor material around the outside the electrons accumulate at the donor–acceptor interface of the shell material, especially in regions near the co-catalyst particles (Fig. 5g). However, the electrons will have to flow through the donor material if they are reach the co-catalysts and this limits the current in these devices. Even the holes, which when dissociated in the shell region can be easily extracted, can be limited because there exists islands of donor material within the nanoparticle separate from the donor shell (Fig. 5h). Therefore, the optimum morphology which allows both electrons and holes to be extracted is the bulk heterojunction morphologies with continuous pathways of acceptor material to the co-catalysts and donor material to regions of water.
4 Conclusions
In summary, we have shown that drift-diffusion modeling is a powerful tool for probing structure-performance modeling of nanoparticle photocatalysts for water splitting. We find that the effect of the core–shell morphology is to only reduce the current generation by a factor of ∼2, whereas Kosco et al.4 find that the evolution of hydrogen improves by a factor of ∼10, when the morphology is changed from core–shell to a uniform bulk heterojunction throughout the nanoparticle. This suggests that lack of preferential wetting is insufficient on its own to account for the performance enhancement observed by Kosco et al.4 Based on our results, we suggest that the observed loss of performance is partly due to core–shell nanoparticles not possessing an optimum bulk heterojunction microstructure within the core. When a shell of one component forms then the material in the core is depleted of that component resulting in a droplet-like phase separated structure, rather than a BHJ microstructure. We find that the droplet microstructure has a more dramatic effect on the current, with, for example, the flow of hole current into the water becoming negative when the D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio is 40
A ratio is 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 or less. We note however, that with the parameterization used in our model, some electrons are able to flow through the donor material, and so the detrimental effects of the core–shell morphology with a bulk heterojunction core microstructure might be more pronounced in systems with larger ΔE (the binding energy, minus the difference in electron affinity between the phases).
60 or less. We note however, that with the parameterization used in our model, some electrons are able to flow through the donor material, and so the detrimental effects of the core–shell morphology with a bulk heterojunction core microstructure might be more pronounced in systems with larger ΔE (the binding energy, minus the difference in electron affinity between the phases).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
NC acknowledges valuable conversations with members of COST Action CA18234 (CompNanoEnergy), supported by COST (European Cooperation in Science and Technology) www.cost.eu. The authors are grateful to Alex Ramadan at The University of Sheffield for discussions that were invaluable in improving our understanding of the complex physico-chemical processes associated with photo-catalytic water splitting.Notes and references
- A. Fujishima and K. Honda, Nature, 1972, 238, 37 CrossRef PubMed.
- J. Joy, J. Mathew and S. C. George, Int. J. Hydrogen Energy, 2018, 43, 4804–4817 CrossRef.
- M. Ismael, Sol. Energy, 2020, 211, 522–546 CrossRef.
- J. Kosco, M. Bidwell, H. Cha, T. Martin, C. T. Howells, M. Sachs, D. H. Anjum, S. Gonzalez Lopez, L. Y. Zou, A. Wadsworth, W. M. Zhang, L. S. Zhang, J. Tellam, R. Sougrat, F. Laquai, D. M. DeLongchamp, J. R. Durrant and I. McCulloch, Nat. Mater., 2020, 19, 559 CrossRef PubMed.
- Y. J. Yang, D. H. Li, P. Wang, X. Zhang, H. J. Zhang, B. C. Du, C. H. Guo, T. Wang and D. Liu, Polymer, 2022, 244, 124667 CrossRef.
- G. Dennler, M. C. Scharber and C. J. Brabec, Adv. Mater., 2009, 21, 1323–1338 CrossRef.
- C. Q. Yan, S. Barlow, Z. H. Wang, H. Yan, A. K. Y. Jen, S. R. Marder and X. W. Zhan, Nat. Rev. Mater., 2018, 3, 18003 CrossRef.
- D. Darwis, N. Holmes, D. Elkington, A. L. D. Kilcoyne, G. Bryant, X. Zhou, P. Dastoor and W. Belcher, Sol. Energy Mater. Sol. Cells, 2014, 121, 99–107 CrossRef.
- P. Marlow, F. Manger, K. Fischer, C. Sprau and A. Colsmann, Nanoscale, 2022, 14, 5569–5578 RSC.
- F. Manger, P. Marlow, K. Fischer, M. Noeller, C. Sprau and A. Colsmann, Adv. Funct. Mater., 2022, 32, 2202566 CrossRef.
- B. Samanta, A. Morales-Garcia, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hutter, F. Libisch, A. B. Munoz-Garcia, M. Pavone and M. C. Toroker, Chem. Soc. Rev., 2022, 51, 3794–3818 RSC.
- A. Arbe, F. Alvarez and J. Colmenero, Polymers, 2020, 12, 8257–8270 CrossRef PubMed.
- G. A. Buxton and N. Clarke, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 085207 CrossRef.
- B. P. Lyons, C. Groves and N. Clarke, J. Phys. Chem. C, 2011, 115, 22572–22577 CrossRef.
- B. P. Lyons, N. Clarke and C. Groves, Energy Environ. Sci., 2012, 5, 7657 RSC.
- G. A. Buxton and N. Clarke, Modell. Simul. Mater. Sci. Eng., 2007, 15, 13–26 CrossRef.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- O. Kuksenok, D. Jasnow, J. Yeomans and A. C. Balazs, Phys. Rev. Lett., 2003, 91, 108303 CrossRef PubMed.
- S. C. Glotzer and W. Paul, Annu. Rev. Mater. Res., 2002, 32, 401–436 CrossRef.
- A. F. Oskooi, D. Roundy, M. Ibanescu, P. Bermel, J. D. Joannopoulos and S. G. Johnson, Comput. Phys. Commun., 2010, 181, 687–702 CrossRef.
- A. L. Fahrenbruch and R. H. Bube, Fundamentals of Solar Cells, Academic Press, New York, 1983 Search PubMed.
- T. Goliber and J. Perlstein, J. Chem. Phys., 1984, 80, 4162–4167 CrossRef.
- C. L. Braun, J. Chem. Phys., 1984, 80, 4157–4161 CrossRef.
- J. Nelson, Curr. Opin. Solid State Mater. Sci., 2002, 6, 87–95 CrossRef.
- J. Frenkel, Phys. Rev., 1938, 54, 647 CrossRef.
- B. Ruhstaller, S. Carter, S. Barth, H. Riel, W. Riess and J. Scott, J. Appl. Phys., 2001, 89, 4575–4586 CrossRef.
- J. C. Scott and G. G. Malliaras, Chem. Phys. Lett., 1999, 299, 115–119 CrossRef.
- J. A. Barker, C. M. Ramsdale and N. C. Greenham, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 075205 CrossRef.
- S. Lacic and O. Inganäs, J. Appl. Phys., 2005, 97, 075205 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |





