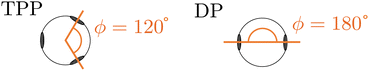Open Access Article
Open Access ArticleActivity affects the stability, deformation and breakage dynamics of colloidal architectures
H. J.
Jonas
 *a,
P.
Schall
b and
P. G.
Bolhuis
*a,
P.
Schall
b and
P. G.
Bolhuis
 a
a
avan 't Hoff Institute for Molecular Sciences, University of Amsterdam, PO Box 94157, 1090 GD Amsterdam, The Netherlands. E-mail: P.G.Bolhuis@uva.nl
bvan der Waals-Zeeman Institute, Institute of Physics, University of Amsterdam, PO Box 94485, 1090 GL Amsterdam, The Netherlands
First published on 26th January 2024
Abstract
Living network architectures, such as the cytoskeleton, are characterized by continuous energy injection, leading to rich but poorly understood non-equilibrium physics. There is a need for a well-controlled (experimental) model system that allows basic insight into such non-equilibrium processes. Activated self-assembled colloidal architectures can fulfill this role, as colloidal patchy particles can self-assemble into colloidal architectures such as chains, rings and networks, while self-propelled colloidal particles can simultaneously inject energy into the architecture, alter the dynamical behavior of the system, and cause the self-assembled structures to deform and break. To gain insight, we conduct a numerical investigation into the effect of introducing self-propelled colloids modeled as active Brownian particles, into self-assembling colloidal dispersions of dipatch and tripatch particles. For the interaction potential, we use a previously designed model that accurately can reproduce experimental colloidal self-assembly via the critical Casimir force [Jonas et al., J. Chem. Phys., 2021, 135, 034902]. Here, we focus primarily on the breakage dynamics of three archetypal substructures, namely, dimers, chains, and rings. We find a rich response behavior to the introduction of self-propelled particles, in which the activity can enhance as well as reduce the stability of the architecture, deform the intact structures and alter the mechanisms of fragmentation. We rationalize these findings in terms of the rate and mechanisms of breakage as a function of the direction and magnitude of the active force by separating the bond breakage process into two stages: escaping the potential well and separation of the particles. The results set the stage for investigating more complex architectures.
1 Introduction
Structural architectures in living cells, such as the cytoskeleton in muscle or plant tissue, are both viscoelastic and active, i.e. undergo continuous injection of energy, leading to remarkable collective, non-equilibrium properties. Networks made of these living polymer filaments can be viewed as active gels,1 a fascinating class of materials that show rich, responsive and functional mechanical properties, reminiscent of cell motility, replication and growth, and tissue repair.2,3 Therefore, such soft biological materials are of great fundamental and technological relevance. Indeed, one of the promising directions in material science is to mimic driven biological systems in the form of active (gel) architectures, where active particles provide continuous energy injection.4 While much research is being done in this area, both on biological materials3,5–9 as well as simplified physical systems,10–15 there is a need for well-controlled model systems that would allow us to investigate the fundamental physical properties of such driven materials in a systematic way. In this work we investigate activated breakage of self-assembled colloidal architectures relevant for networks and gels.Experimental breakthroughs in nanostructure assembly and active matter provide such prototypical systems. For instance, novel synthesis routes enable the design of colloidal particles surface-decorated with DNA16,17 or patches of a materials with different surface properties compared to bulk enabling formation of directed bonds.18–21 Suspending the latter type of patchy particles in a near-critical binary liquid mixture (e.g. water and lutidine), induces attractive directed bonds between the patches on the surface of neighboring particles via a solvent mediated critical Casimir force. These attractive bonds allow the controlled self-assembly into complex structures such as chains, rings, and networks.18,22–25 Experiencing thermal motion, such patchy particles obey the Boltzmann distribution, and thus can be seen as mesoscopic analogs of atoms. As they can be directly observed with e.g., confocal microscopy, patchy particles can act as an experimental model system to explore complex self-assembled colloidal architectures analogous to their molecular counterparts.24–27
At the same time, well-controlled self-propelling particle systems allow experimental control of microscopic energy injection.28,29 Examples of these particles are gold coated Janus particles that are self-propelled by catalysis of e.g. hydrogen peroxide, or colloids that are driven via external electric, magnetic or optical fields. These processes induce an active force aligned along the particle orientation. As the particle is still free to rotate in the suspension, such active particles' dynamics are often modeled as Active Brownian particles (ABPs). Previous studies have addressed the self-assembly and motility induced phase separation of ABPs with isotropic interactions.30–32
Here, we combine the above-mentioned two experimental breakthroughs in a simulation study to explore the collective non-equilibrium response of patchy colloidal architectures to the introduction of activity. We aim to obtain microscopic insight into the two main effects of introducing activity: (1) how does the active force lead to the breaking of colloidal chains? In particular, what effect does activity have on the bond configurations before escaping the potential well, and how does activity affect separating the particles into the bulk? Specifically, we look into the breakage mechanisms, – positions and – rates. (2) how is the dynamics of a colloidal architecture, such as a ring or a network, altered by such active forces? For that, we investigate global bending modes of ring structures.
To address these questions, we combine ABPs with patchy particles interacting via the critical Casimir force in Brownian dynamics simulations. To make a connection to the experimental realization of these systems, we would like to stay as close as possible to the experimental conditions. Therefore, we employ our accurate potential model for patchy particle systems that was benchmarked on experiments.33
We find that the response to activity yields a rich behavior, in which activity can both enhance and reduce the stability of architecture, as well as alter the mechanism of fragmentation. In addition, although activity distorts the ring configuration, it leaves the dominance of global bending modes unaffected.
The paper is organized as follows. In the next section we introduce the systems, the potential model, simulation and analysis methods. In Section 3, we present and discuss the simulation results for dimers, decamers and rings. We end with concluding remarks.
2 Methods
2.1 Patchy particle architectures
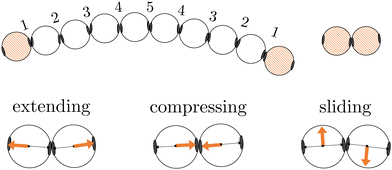
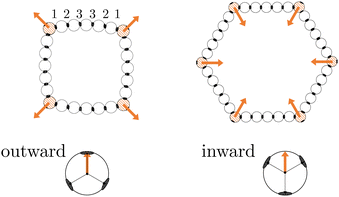
In this work, we investigate two types of self-assembled structures: chains, and rings. The chains are composed of colloidal divalent patchy, or dipatch (DP), particles that have two attractive patches at opposite sites of the particle (Fig. 1). We consider two chain lengths: dimers consisting of just two, and decamers consisting of ten self-assembled DP particles. The outer two particles in the chains are made active by considering self-propelled forces acting on the centers of the particles in three qualitatively different ways, by compressing, extending, and sliding along the patch–patch bond (see Fig. 2). In contrast to a dimer, for which the activity is directly mediated by a single bond, the decamer can and must propagate the active force along the passive particles in the chain. For analysis purposes, we give each bond in the decamer an index; due to symmetry, there are only five irreducible bond numbers (Fig. 2).The ring structures are symmetric and composed of four or six trigonal planar patchy (TPP) particles connected via 5 or 15 DP particles. Fig. 3 illustrates the structures T4D5 and T6D5 where the number after the T indicates the number of TPP particles, and after the D the number of DP particles connecting the TPP particles in the chain. Also the bonds in the rings are labeled; due to symmetry, there are only three or eight irreducible bond numbers for the 5 and 15 DP particle-based rings, respectively. The square structures with four TPP particles naturally contain an additional tension due to the mismatching bond angle of the TPP particle. Fig. 3 shows how, depending on the experimental realisation, the self-propulsion forces acting on the TPP particle either point toward the patch and creates outward-facing forces with respect to the ring, or between two patches resulting in inward-facing forces with respect to the ring. The ring simulations are performed in the presence of a gravitational potential that makes the particles sediment to a horizontal surface with a gravitational height of 0.13 times the diameter σ similar to the typical experimental setup employing critical Casimir forces.33
2.2 Interaction potential
The effective anisotropic pair interaction between two patchy particles i and j with orientation Ωi and Ωj, respectively, and interparticle distance rij is given by| Vpair(rij,Ωi,Ωj) = VYukawa(rij) + VC(rij)S(Ωi,Ωj), | (1) |
The anisotropy of the patch interactions is captured by two switching functions S′(θ) that are in principle a function of the orientations Ω of both particles, but are simplified to a dependency on the angles θ of each particle
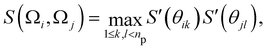 | (2) |
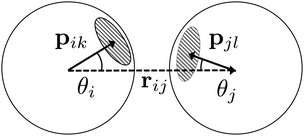 | ||
| Fig. 4 A schematic illustration of the inter-particle vector r (dotted arrow), patch vectors p on each particle (solid arrows), and the angles θ. | ||
The critical Casimir interaction is dependent on how close the system is to its critical point in terms of temperature Tc and composition cc. In an experimental setup, typically, the composition is kept constant and the temperature is used to control the attraction between patchy particles. The temperature difference from Tc is captured by the parameter dT = Tcx − T, where Tcx is the coexistence temperature of the binary liquid (Tcx = 0.08 + Tc) and T is the temperature (T < Tc). The strength of the attraction increases upon lowering dT.33
Fig. 5 shows the optimized patchy particle potential that is capable of reproducing the experimental system of DP particles. The exact functional forms of the Yukawa electrostatic repulsion, critical Casimir attraction, and the switching functions S′ can be found in the Appendix A and ref. 33 Appendix B.
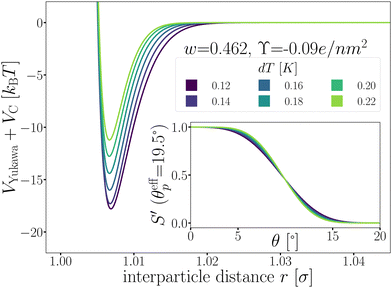 | ||
| Fig. 5 The patchy particle radial potential for dipatch particles composed of Yukawa repulsion VYukawa (eqn (18)) and critical Casimir attraction VC (eqn (20)) for several values of dT. The inset shows the switching functions S′ that are additionally a function of dT. | ||
The total potential energy of the system is the sum of all patchy particle pair interactions, and an external gravitational potential Vext(zi)
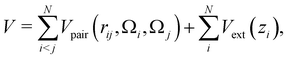 | (3) |
2.3 Equations of motion
The dynamical motion of colloidal particles is described by overdamped Langevin dynamics, i.e. brownian molecular dynamics (BMD), that includes the stochastic thermal motion of the particles.34 The translational equation of motion of a Brownian particle is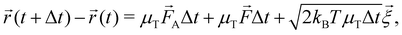 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) is the positional vector of the particle, and t the time. The timestep Δt = 5.0 μs was tested to be suitable for the strongest interaction strength at dT = 0.12 K, and used for all potentials. The conservative force
is the positional vector of the particle, and t the time. The timestep Δt = 5.0 μs was tested to be suitable for the strongest interaction strength at dT = 0.12 K, and used for all potentials. The conservative force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) follows from the (gradient of the) potential V (eqn (3)), and the active force
follows from the (gradient of the) potential V (eqn (3)), and the active force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A is only non-zero for the active particles. The translational mobility tensor
A is only non-zero for the active particles. The translational mobility tensor 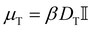 with DT = 0.0034σ2 s−1 as experimentally measured for dipatch particles with diameter σ = 3.2 μm,
with DT = 0.0034σ2 s−1 as experimentally measured for dipatch particles with diameter σ = 3.2 μm, 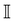 the identity matrix, β = 1/kBT = 1 the inverse temperature with the Boltzmann constant kB, and the temperature T.23 The stochastic noise
the identity matrix, β = 1/kBT = 1 the inverse temperature with the Boltzmann constant kB, and the temperature T.23 The stochastic noise ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) is a vector where each element is i.i.d., with a zero mean and unit variance over time.
is a vector where each element is i.i.d., with a zero mean and unit variance over time.
The rotational equation of motion is given by
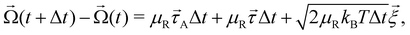 | (5) |
![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) is the torque acting on the particle coming from V (eqn (3)), and
is the torque acting on the particle coming from V (eqn (3)), and 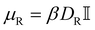 is the rotational mobility tensor with DR = 0.05 rad2 s−1.35 We integrate the equations of motion numerically.34
is the rotational mobility tensor with DR = 0.05 rad2 s−1.35 We integrate the equations of motion numerically.34
A widely used model to simulate self-propelling colloidal particles is the active Brownian particle (ABP). It consists of a self-propulsion force acting on the center of mass of the colloidal particle
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A = FAêA A = FAêA | (6) |
In an experimental setup, the Janus particle aligns its motion parallel to the wall, due to the applied AC field. Furthermore, the continuous presence of gravity prevents the active particles to self-propel against the gravitational field away from the wall.36 As the exact response of the Janus particles to the AC field is quite complex,37 we mimic this behavior by including an effective alignment torque with magnitude38–40
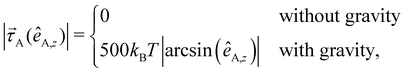 | (7) |
The self-propulsion force FA acting on the ABP is often expressed using the Péclet number:
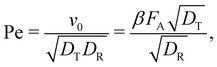 | (8) |
The active forces FA = 0, 10, 50, and 100kBT/σ would correspond to Pe = 0, 2.6, 13.1, and 26.1, respectively, and are achievable in a typical experimental system. The Pe number is also dependent on the effective particle radius when using a soft repulsion instead of a hard-sphere model.11
2.4 Monte Carlo
The BMD simulations are started from configurations that are equilibrated and decorrelated. Note that this passive initial distribution is often also taken as a starting point in experiments. Relaxation to a steady state is fast for low activity. Moreover, a non-equilibrium steady state approach prohibits the exploration of the high activity limit. To create this collection of starting configurations, we use Monte Carlo (MC).33 For a given colloidal architecture, only single particle MC moves are performed and those MC steps that lead to bond breakage, i.e. Epair ≥ 0, are rejected. In the single particle move, a randomly selected particle is randomly rotated (50% of the MC steps) around their center of mass with a randomly selected rotation magnitude dq ∈ [0,θmax] or randomly translated with a magnitude dr ∈ [0,rmax]. When the gravitational potential is applied, the z-direction of the random translation is divided by 10 to prevent placing the particle inside the wall or against the gravitational field which leads to unfavorable energies.2.5 Analysis of the bond breakage process
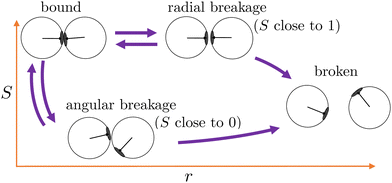
Starting from equilibrated structures, we conducted straightforward, “brute force” BMD simulations to analyze bond breakage. Due to the random fluctuations or with the aid of the active force, a bonded particle pair can escape its attractive well. The particle pair either rebinds going back into the attractive well, or increases their interparticle distance to r = 1.5σ at which we assume the probability of rebinding is sufficiently low.43 Only the latter criterion is considered a true bond breakage upon which the simulation is halted.To analyze the bond breakage mechanism and lifetime, we separate the bond phase space into four regions indicating a strongly bound (1), weakly bound (2), diffusive (3), and truly broken (4) state as illustrated in Fig. 6. We define these four regions using the reduced energy Eλ, which is a parameter between zero and one:
| Eλ = VC(rλ)·S/EC,min, | (9) |
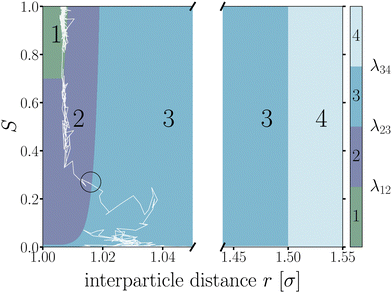 | ||
| Fig. 6 Contour map of the bond breakage order parameter λ(r,S). An example trajectory of a breaking bond is shown with the white solid line for which its bond breakage mechanism is measured when crossing λ23 as highlighted by the black circle. The four states strongly bound (1), weakly bound (2), free diffusion (3), and fully broken (4) as defined in Table 1. The breaking trajectory undergoes two stages: I. Escaping the potential well from state 1 → 3, and II. Separating the particles from state 2 → 4. | ||
| Region | Energy | Distance | |
|---|---|---|---|
| 1 | Strongly bound | E λ ≤ 0.70 | |
| 2 | Weakly bound | 0.70 < Eλ ≤ 0.01 | |
| 3 | Diffusive | E λ > 0.01 | |
| 4 | Truly broken | r λ > 1.50σ |
We used the label λ as a (fictitious) order parameter that determines whether a configuration is inside a certain region, and, more importantly, when crossing a boundary between these regions. We denote the boundary (a.k.a. an interface) between region i and j as λij. Initiated from the strongly bound region 1, trajectories can only escape via region 2 and 3 to finally reach region 4, crossing the interface λ34, after which the bond is considered truly broken and the simulation is halted. This strict condition is necessary, as even after escaping the attractive well and entering region 3, the particles diffuse around and actually have a significant chance of rebinding. Counting trajectories that enter region 3 as being broken thus would severely underestimate the lifetime. However, since the time to diffuse the particles from the λ23- to the λ34-interface is very dependent on the location of λ34, the instantaneous bond lifetime τ itself is measured as the last timestamp the trajectory crossed the λ23-interface. We stress that the exact location of the interfaces does itself not influence the lifetime estimate.
The lifetime of the bond is strongly related to the rate constant for the breaking process. Considering bond-breaking as a two state dissociation process, we can express the corresponding rate as the inverse of the bonds' average lifetime (a.k.a. residence time) kbreak = 1/〈τ〉. An alternative way to compute the rate constant for breakage is to compute the flux for trajectories starting in the strongly bound state to escape:44
| kbreak = Φλ12P(λ23|λ12)Psep, | (10) |
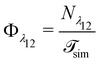 | (11) |
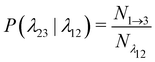 | (12) |
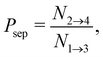 | (13) |
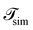 is the total duration of all the simulations used for the estimate, Nλ12 the number of positive crossings through the λ12 interface, i.e. from region 1 toward 2, and N1→3 (N2→4) is the number of times region 3(4) is reached given that one came from 1(2), or, in other words, the number of first crossings of λ23 (λ34) subsequent to λ12 (λ23). One can quickly verify that the breakage rate is then, as expected,
is the total duration of all the simulations used for the estimate, Nλ12 the number of positive crossings through the λ12 interface, i.e. from region 1 toward 2, and N1→3 (N2→4) is the number of times region 3(4) is reached given that one came from 1(2), or, in other words, the number of first crossings of λ23 (λ34) subsequent to λ12 (λ23). One can quickly verify that the breakage rate is then, as expected, 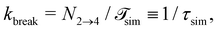 with τsim the average simulated bond lifetime.
with τsim the average simulated bond lifetime.
Measuring the quantities in eqn (10)–(13) per bond provides microscopic insight into the influence of activation on the breakage dynamics. The first stage of bond breakage, i.e. escaping the potential well, is defined by Φesc = Φλ12P(λ23|λ12) which expresses the rate at which the particles escape their potential well. The second stage of bond breakage, i.e. successfully separating the particles to r = 1.5σ, is expressed as the probability Psep. Separating the breakage process into two stages helps to identify the role of activity as stage I is mainly defined by the shape and depth of the pair potential and buckling of the bond, while stage II by, for example, the position of the bond in the structure, or crowding effects by other particles.
As patchy particles have rotational and translational degrees of freedom, one can characterize the mechanism of breaking a critical Casimir induced bond between two particles as a combination a two qualitatively different limiting cases. Fig. 7 schematically illustrates the two breakage mechanisms along the λ(r,S)-order parameter: (1) a pure radial mechanism, where particles move away from each other along the bond vector, keeps the particles' patches aligned and S = 1. And (2) a purely rotational, angular mechanism in which particles rotate along each other perpendicular to the bond vector, until the overlap area between the patches is vanishing, makes S = 0. In practice, both routes are available to the particles and the breakage mechanism is naturally a combination of these limiting routes. Accordingly, we can follow the breakage mechanism along the value of S as it can distinguish between radial (S = 1) or angular (S = 0) trajectories.
For analyzing the breakage mechanism, we again use the separation of the two stages of breakage. In the first stage, the system escapes the potential well and reaches the λ23-interface for the first time at a particular S-value, which we denote Smech. These Smech-values are counted as n1→3(Smech) which' probability distribution is given by eqn (14). Note that the counts Ni→j from eqn (12) and (13) equal the sum over all Smech-values as 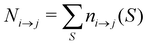 . Continuing the simulation, the trajectory either rebinds, adding a count to n3→1(Smech), or breaks, adding a count to n2→4(Smech). Then, noting that n1→3(S) = n2→4(S) + n3→1(S), the probability of breaking at given S is written in eqn (15). Only upon true breakage, the last n2→4(Smech) is counted and normalized as the breakage mechanism probability Pmech in eqn (16). One can see that the breakage mechanism probability also follows from Pmech(S) = P1→3(S)P2→4(S)Psep−1 where Psep−1 is the normalization.
. Continuing the simulation, the trajectory either rebinds, adding a count to n3→1(Smech), or breaks, adding a count to n2→4(Smech). Then, noting that n1→3(S) = n2→4(S) + n3→1(S), the probability of breaking at given S is written in eqn (15). Only upon true breakage, the last n2→4(Smech) is counted and normalized as the breakage mechanism probability Pmech in eqn (16). One can see that the breakage mechanism probability also follows from Pmech(S) = P1→3(S)P2→4(S)Psep−1 where Psep−1 is the normalization.
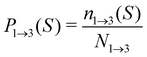 | (14) |
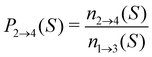 | (15) |
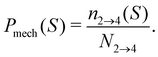 | (16) |
By only considering the values of S at λ23 under the condition the system came from region 1, λ23-recrossing events are filtered out of the breakage mechanism analysis. Recrossing events, as observed for the example trajectory in Fig. 6 where the trajectory recrosses λ23 at S ≈ 0.1 after escaping the well at S ≈ 0.3, are mainly determined by free diffusion and do not contain information on how the system escaped the potential well.
Many of the observables, e.g. the bond lifetime, show an exponential decay over time. Therefore, we report averages with a 95% confidence interval of the mean calculated using block averaging. As the start configurations are equilibrated before the measurements start, and the breakage itself is a rare event, all breakage events are uncorrelated and we take blocks of minimal 100 simulations.45,46
3 Results and discussion
In this section, we present and discuss the numerical simulations. We start with the simplest colloidal architectures in Sections 3.1 and 3.2: the dimers and decamers. We performed 1000 brute force BMD simulations at various attraction depths, tuned by the critical Casimir interaction via the temperature dT. The activity is tuned by the force magnitude FA and direction (see Methods and Fig. 2).In Section 3.3, we increase the complexity of the architectures toward rings, and evaluate the influence on strained and relaxed rings of different sizes. Here we include the gravitational field to mimic the experimental setup.
3.1 Dimer
Before the bond breaks, activity naturally affects the exploration of phase space and we show this effect with probability histograms in Fig. 8. Measurements are taken at each timestep during BMD simulations in a volume or isosurface of interest. For the effect on the bond orientation of the dimer, we measure S inside the bonding volume, i.e. region 1 and 2, at which the bond is intact (Fig. 8a) and we observe that activity does not significantly buckle the bond as the histogram of S of passive and active dimers overlap.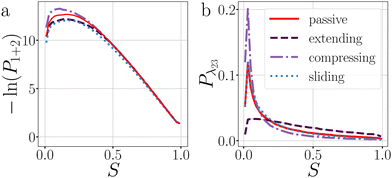 | ||
| Fig. 8 Exploring the potential well of passive and active dimers at dT = 0.12 K. The probability histogram of S (eqn (2)) of a passive dimer (red solid line) and active dimers with FA = 100kBT/σ and force directions: extending, compressing, and sliding. The measurements are taken in (a) the full bonding volume, i.e. region 1 + 2, and (b) when crossing (positively and negatively) the λ23-interface. There are 50 bins for S ∈ [0.0,1.0]. As the λ23-interface has a minimal value of S = 0.01 (at Eλ = 0.01), the first bin in (b) is approximately twice as low as the second bin. | ||
The histogram shown in Fig. 8b shows the distribution of the S-values at crossing the λ23-interface positively and negatively. In equilibrium, this histogram, if taken as − ln(P), represents the free energy in units of kBT and we observe that bonds mostly sample values with θ > 0°. Each particle in the bond can rotate around the interparticle vector to maintain S′(θ) and r at a constant value (Fig. 4), resulting in a bonding volume proportional to sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Such behavior leads to an entropic contribution to the free energy, and configurations with θ > 0° are found to be more prevalent.
θ. Such behavior leads to an entropic contribution to the free energy, and configurations with θ > 0° are found to be more prevalent.
Activity has a specifically large effect where the gradient of the potential is comparable or smaller than the active force, such as when crossing λ23 (Fig. 8b). Under extending forces, the probability density shift to higher S-values compared to the passive case. This has two reasons: first, the particles start out in the strongly bound region 1 where S is close to one and activity pulls the particles apart, keeping S high. Second, recrossing λ23 at low S-values will be suppressed for extending forces as they direct away from the λ23-interface. Both effects are indirectly measured using P1→3 and P2→4, see below. Conversely, under compressing forces, the active forces' direction is reversed and thus more density is observed at low S-values.
 | ||
| Fig. 9 Analysis of the breakage mechanism of the dimers by P1→3, P2→4, and Pmech from eqn (14)–(16), respectively. (a)–(c) Passive dimers at dT = 0.12–0.22 K. (d)–(i) Active dimers at dT = 0.12 (d)–(f) and 0.22 K (g)–(i) with extending, compressing, and sliding active forces at FA = 100kBT/σ. Each row shows its legend on the right. Colored bands indicate 95% confidence interval. | ||
Starting with the passive case, Fig. 9a shows that to reach λ23, the patches rotate significantly more in the strong attraction potential (dT = 0.12 K) compared to the weak attraction potential (dT = 0.22 K). At the same time, the conditional probability to break P2→4(S) peaks around S ≈ 0 (i.e. the patches are rotated away), decreases quickly, and plateaus at a low value for S > 0.5 (Fig. 9b). The peak at low S is reduced for stronger attraction. Since P1→3(S) and P2→4(S) show opposing trends, the effect of dT on the breaking mechanism is reduced (Fig. 9c). Nevertheless, the majority of bond breakage events clearly occur via the angular mechanism. The maximum of Pmech(S) shifts from Smax ≈ 0.2 to Smax ≈ 0.1 with increasing attraction strength.
Although the translational and rotational diffusion constants have no influence on equilibrium distributions, they do play a critical role in bond breakage dynamics as demonstrated in ref. 42 and 47. Hence, the introduction of active particles that experience directional enhanced translation is expected to significantly impact the breakage mechanism. As hypothesized above, when using extending forces, P1→3(S) shows a shift toward high S-values (Fig. 9d and g), indicating radial breakage, as the active force pulls the particles from high S in region 1 toward the λ23-interface. Subsequently, the probability of successfully separating the particles increases for all values of S (Fig. 9e and h), as extending forces are directed away from the bonding volume (see Fig. 10 for a schematic illustration). The breakage mechanism probability distribution in Fig. 9f and i shows that for extending forces both angular and radial routes are likely, with only a small bias toward smaller S, i.e. angular breakage. In contrast, for compressing forces, P1→3(S) shows a shift toward lower S-values, indicating angular breakage, with respect to the passive case. Moreover, the corresponding P2→4(S) indicates that configurations with S > 0.5 are completely blocked from particle separation as the compressing active force restores the particles back into the bound state (Fig. 10). The breakage mechanism probability distribution Pmech(S) shows now a significant shift toward lower S-values indicating that all bonds must break via the angular route. Finally, sliding forces results in a distribution P1→3 similar to that of compressing forces, while P2→4 shows a large increase at S < 0.5. Therefore, one would expect a shift of Pmech(S) toward angular breakage. However, as sliding forces also increase Psep = N2→4/N1→3 (see Fig. 11d). the breakage mechanism probability Pmech(S) is similar to the passive dimers, even if the two stages of breakage are very different from passive breakage.
 | ||
| Fig. 10 For a configuration at λ23, its probability to rebind depends on the overlap between the bonding volume (purple region between patches), and the positional density distribution (orange halo around the particles) which' probability is amplified in the direction of the active force(orange arrow). This is a schematic representation and not based on simulations.48 See Fig. 9 for measured P2→4(S) = 1 − Prebind(S) at the various force directions. | ||
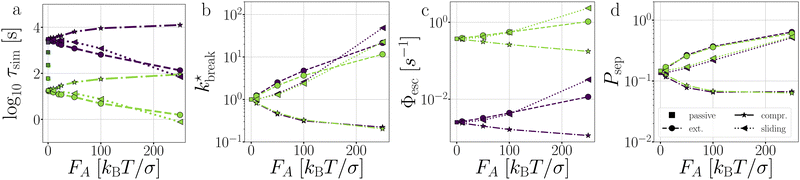 | ||
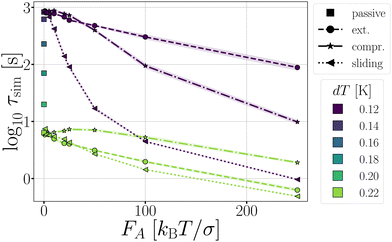
Fig. 11 Passive and active dimers. (a) The measured average bond lifetime τsim in the passive case at dT = 0.12–0.22 K and in the active cases at dT = 0.12 and 0.22. The scaled rate constant 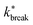 (b), stage I (Φesc) (c), and stage II (Psep) (d) at dT = 0.12 and 0.22 K and FA = 10, 50, 100, and 250kBT/σ. The color coding indicates the dT, similar to Fig. 5, and the line coding is shown in figure on the right. (b), stage I (Φesc) (c), and stage II (Psep) (d) at dT = 0.12 and 0.22 K and FA = 10, 50, 100, and 250kBT/σ. The color coding indicates the dT, similar to Fig. 5, and the line coding is shown in figure on the right. | ||
This analysis clearly indicates that the breakage mechanism of dimers is strongly affected by the separation probability P2→4, both in the passive or active case, and at strong or weak interaction strength.
 the flux out of the potential well (stage I) Φesc, and the separation probability Psep of stage II. Naturally, in the passive case, the bond lifetimes τsim depend strongly on dT, as a shallower potential leads to exponentially faster breakage (Fig. 11a).49,50 Under the influence of activity, τsim can either be enhanced or suppressed depending on the direction of the applied force.
the flux out of the potential well (stage I) Φesc, and the separation probability Psep of stage II. Naturally, in the passive case, the bond lifetimes τsim depend strongly on dT, as a shallower potential leads to exponentially faster breakage (Fig. 11a).49,50 Under the influence of activity, τsim can either be enhanced or suppressed depending on the direction of the applied force.
As expected, only stage I of breakage (Fig. 11c), i.e. the rate of escaping the potential well, depends on the potential depth as determined by dT. Compressing and extending forces, respectively, exponentially decrease and increase the rate constant of stage I proportional to the magnitude of FA. Because in the dimer the particles are bound with directed patches, forming a relatively stiff bond, and which maintain the active forces at a ±180 angle, the effect of activity inside the potential well of the dimer resembles an equilibrium problem in an effective tilted potential along the direction of r.51 This effect can be qualitatively captured with an Arrhenius type expression
| ktilt(FA) = νe−βV(r)+βαFAΔr | (17) |
The effect of activity on stage II of breakage, i.e. successful particle separation, was qualitatively explained using Fig. 10 and quantitatively measured in Fig. 9. Fig. 11d confirms that extending and sliding forces enhance the probability of separation Psep, while compression reduces it. Additionally, Psep does not show a potential depth dependency.
Considering that activity can be viewed as an effective tilt on the potential, and Psep is dT independent, the contribution of the potential depth can be separated from the activity by dividing the breakage rate constant kbreak by the rate constant at zero activity, as shown in Fig. 11b as  . Consequently, for the active dimer, activity with the same magnitude and direction have an equivalent effect on the breakage rate.
. Consequently, for the active dimer, activity with the same magnitude and direction have an equivalent effect on the breakage rate.
3.2 Decamer
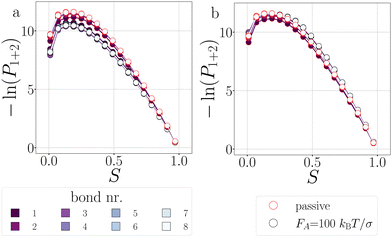
In contrast to a dimer, a longer chain can transmit stresses resulting from active forces exerted on its outer particles through the other bonds in the chain (Fig. 2). Although the breakage mechanism of the bonds in decamers remains qualitatively similar to that of dimers (see Fig. 18 in Appendix B), activity has a significant impact on the dynamics and conformational distributions of the chain, leading to opposing effects in bond lifetime compared to a dimer.10Before any bond has broken, activity already affects the bond distributions, causing the chain to buckle or straighten.52Fig. 12 shows the probability distribution of S for each bond in a passive chain and active chains with FA = 100kBT/σ at dT = 0.12 K. In the freely moving passive chain, all nine bonds are statistically identical, in line with Boltzmann's equipartition theorem, and appear as a single (red) curve.
 | ||
| Fig. 12 Deformations in decamers at dT = 0.12 K. The probability histogram of S (eqn (2)) of a passive chain (red solid line) and active chain with FA = 100kBT/σ (dots) and the force directions: extending (a), compressing (b), and sliding (c). The measurement is taken at regions 1 and 2. The colored dots indicate the reduced bond number as shown in the legend. | ||
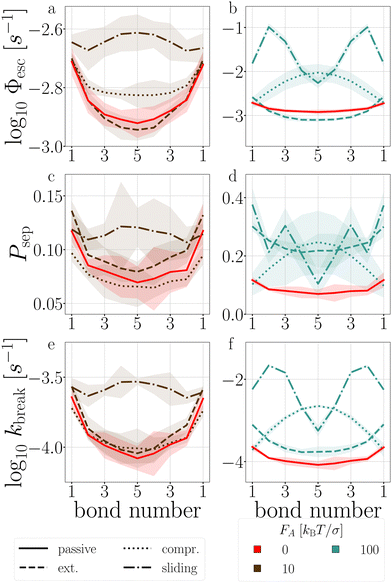 | ||
| Fig. 13 Passive and active decamer at dT = 0.12 K with FA = 10 (left) and 100 (right) kBT/σ. Plotted are the Stage I escape flux Φesc (see eqn (12)) (a) and (b), the Stage II separation probability Psep (c) and (d) (see eqn (13)), and the breakage rate kbreak (e) and (f) as a function of the bond index (see Fig. 2). Color and line coding in the legends at the bottom. Colored bands indicate the 95% confidence interval. The logarithmic plots handle the sometimes large scale differences between the curves. The passive decamer shows mostly breakage at the edges, while compressing and sliding active forces shift the breaking rate profile to bonds in the middle of the chain. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(Epair) (see Fig. 19 in Appendix B). This stabilization impacts stage I of breakage with FA = 100, and to a lesser extent with FA = 10: bond 2 to 5 diffuse slower out of the well compared to the passive chain as shown in Fig. 13a and b, respectively.
P(Epair) (see Fig. 19 in Appendix B). This stabilization impacts stage I of breakage with FA = 100, and to a lesser extent with FA = 10: bond 2 to 5 diffuse slower out of the well compared to the passive chain as shown in Fig. 13a and b, respectively.
The stabilization of the chain and lowering of the rate of stage I would predict an increased lifetime. However, Fig. 14 indicates τsim exponentially decreases with the extending force magnitude FA. It is the increase of stage II probability Psep, that is tripled when FA = 100, that is primarily responsible for the decrease in the decamer's lifetime (Fig. 13c and d).58 The increase of the stage II probability is bond number independent, leaving the breakage profile in Fig. 13e and f largely unaffected compared to the passive decamer.
3.3 Ring structures
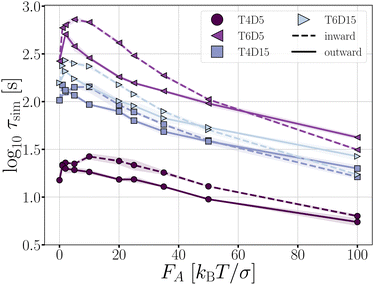
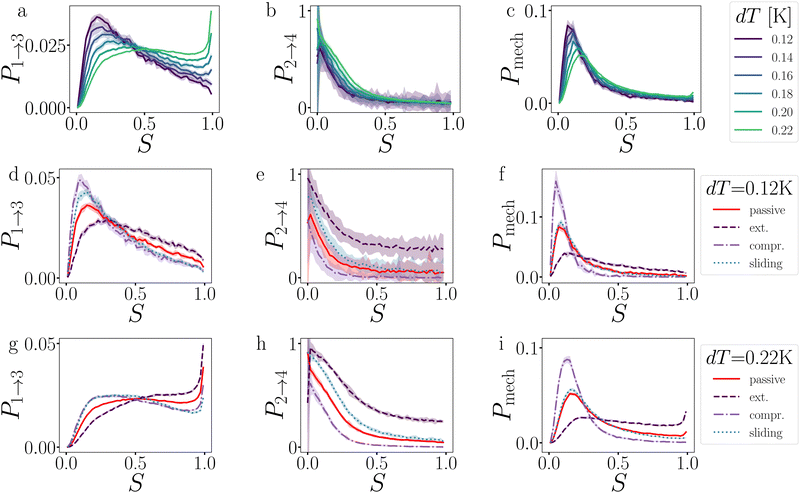
Complex networks or gels, in contrast to freely moving chains, can contain tension even when energy minimized at zero temperature. The simplest architecture for which such tension can occur, is a ring structure. In our assessment, we consider two types of rings: a four TPP particle ring, which is under tension, and a six TPP particle ring, which is tension free (see Fig. 3). Additionally, we vary the length of the DP-chain from 5 to 15 particles, which can mediate the tension within the rings. We set the critical Casimir temperature to dT = 0.16 K, striking a balance between ensuring a reasonable simulation length until breakage and allowing the structures to remain intact long enough to observe the effects of activity on the deformations in the architectures.The average bond lifetime of the rings is presented in Fig. 15. As anticipated, the presence of tension reduces the lifetime of the structures, and larger number of bonds leads breakage. The lifetimes τsim of the structures follow the order T4D5 ≪ T4D15 < T6D15 < T6D5. For all structures and both directions of active forces, the lifetime of the rings initially increases with increasing active force, but eventually decreases.
We use the T6D15 structure for an in-depth analysis of how the deformations (Fig. 16) and breakage rate are affected by the active forces (Fig. 17). This structure does not suffer from the misalignment of the TPP-DP bond nor from a limited number of bonds that can mediate the activity.
 | ||
| Fig. 16 Deformations in T6D15 at dT = 0.16 K. The probability histogram of S (eqn (2)) of a passive and active rings with FA = 100kBT/σ and the force directions: inward (a), and outward (b). The measurement is taken in region 1 + 2. The inner color of the dots indicate the position of the bond, and the edgecolor the passive (red) or active ring (black). | ||
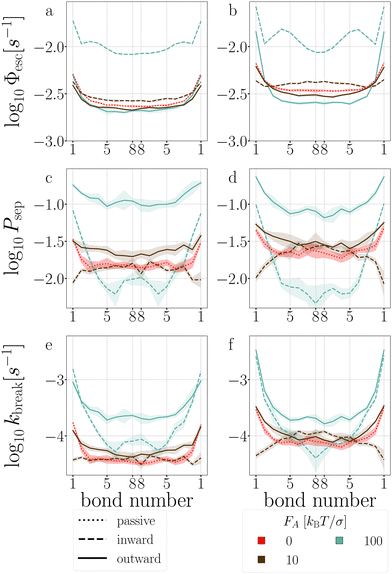 | ||
| Fig. 17 Stage I (a) and (b), stage II (c) and (d), and breakage rate (e) and (f) per bond of T6D15 (a), (c) and (e), and of T4D15 (b), (d) and (f). Colored bands indicate 95% confidence interval. | ||
In the passive case and at low activity, we observe that the tension is evenly distributed over all bonds as T6D15 and T4D15 show the same shape of stage I and stage II versus bond number. However, T4D15 is faster in both stages.
At high activity, in the first stage with outward-facing forces, all bonds in T6D15 straighten and strengthen, while for T4D15, the straightening of the chain between the active particles expose the misalignment of the TPP-DP bond, making it prone to break, as shown in Fig. 17b, where Φesc at bond 1–2 is higher and bond 3–8 lower than the passive case.60 Both structures shows similar increased stage II throughout all the bonds. Using inward-facing forces, bond 1, and 4 to 6 are faster in stage I in T4D15. However, in both structures, Psep (stage II) of bond 4–8 is below 1% and the differences of stage I cannot be observed in the breakage rate kbreak. Thus, for both force directions, the largest difference is observed at bond 1, which indeed is the misaligned TPP-DP bond.
4 Conclusions
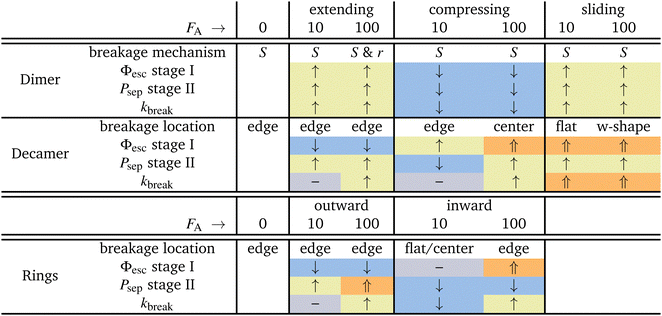
In this work, we have given microscopic insight into the effect of activity, modeled as active patchy Brownian particles connected to various patchy particle architectures: dimers, decamers, and rings. To do so, we separated the contribution on the two stages of breakage: the rate of escaping the pair potential well (stage I) and the probability of successful particle separation (stage II). We unraveled the observed behavior in the bond breakage rate, breakage mechanism, and breakage profile and identify at which stage the influence of activity dominates.Table 2 summarizes the effects of small and large active forces on dimers and decamers with FA directions: extending, compressing and sliding.
For the dimers, the effect of activity on the first stage of bond breakage resembles an equilibrium problem in an effective tilted potential along the radial direction, and the second stage of bond breakage was potential depth independent. Therefore, the effect of activity on the bonds' lifetime is roughly a function of the magnitude and direction of the active force only. When active forces point toward or away from the bonding volume, the bond life time τ increases or decreases, respectively.
The dimers and decamers showed qualitatively similar breakage mechanisms in both passive and active systems. Under extending (compressing) forces, the mechanism shifted to a radial (angular) route which is explained by the direction of the active force pointing away (toward) from the bonding volume. The sliding mechanism lies in between these two extremes.
The active decamers showed under all force directions and magnitudes reduced or comparable lifetimes compared to passive decamers. Extending forces straighten the chain, energetically stabilize the bonds, and suppress the rate constant of stage I. However, the chains still show an exponentially decaying lifetime proportional to the magnitude of the active force because simultaneously stage II is enhanced. For sliding and large compressing forces, the chains buckle and weaken their bonds leading to breakage peaked around the highest curvature in the chain. The weakened bond strength (stage I) dominates in explaining the effect of activity on the decreased lifetimes. However, at small compressing forces, stage II is suppressed at the ends of the chain and balances the effect of stage I. The active chain then shows an approximately equal breakage rate compared to passive chains.
All ring structures, with and without tension, show an initial stabilization of the structures upon small active forces (FA = 10). The initial stabilization of the structure is caused by a minor suppression of stage I. Subsequently, for inward-facing forces, we observe an significant suppression of stage II in bonds close to the active force leading to a strong enhancement of the lifetime τ. However, for the outward-facing forces, the opposite is observed. The minor stabilization of stage I is followed by a minor enhancement of stage II leading to lifetimes approximately equal to the passive case.
At larger activity (FA = 100), the bond lifetime τ has reduced significantly and converges for both directions of the forces to the same value. Additionally, this case shows most breakage near the active force at bond 1. However, the two directions of the force each target a different breakage stage. Inward facing forces induce buckling in the ring and weaken all bonds. Stage I shows an overall enhancement, but stage II is only enhanced at bonds close to the active force and suppressed at the bond in the center. Outward-facing forces show very little effect on the conformations of the ring as well as on stage I; it is stage II that has the largest effect on the breakage rate.
Lastly, we looked at the effect of the misaligned bond (bond 1) in the T4D15 structure compared to T6D15. At low activity and in the passive case, the tension caused by the misalignment can be distributed over all bonds. The lifetime of T4D15 is lower than T6D15, but there is no enhanced reactivity in bond 1; only at large forces, we observe differences. Outward- and inward-facing forces expose the weakness of bond 1 and enhance stage I of its breakage significantly. Simultaneously, as observed in T6D15, the second stage at bond 4 to 8 is very low as Psep is less than 1%. Effectively, both directions of the force leads to enhanced breakage at the misaligned bond via stage I.
We can draw some general conclusions from our findings, summarized in Table 2. First of all, the preferred breakage mechanism is in all cases via an angular mechanism. This might at first seem surprising, since it seems only natural that a bond breaks along the radial axis. However, the entropic contribution of larger angles is substantially enlarged to counteract this, and most bonds will break at low S value, i.e. via the angular mechanism.
Second, it is a well-known fact that breakage is a combination of an activated well escape stage, and a diffusive separation stage. When applying an active force most of the time both stages will respond qualitatively identically: for the dimer extending and sliding force will enhance breakage rate, while compression will suppress it. For the decamer and the rings things are different: the extending/outward forces surprisingly lower the escape probability due to stiffening of the chain. However, the final result is still that breakage is enhanced, as the separation stage compensates. In contrast, sliding is significantly enhancing chain breakage. Compressing forces are most complex, they enhance stage I but decrease stage II. The contrasting effect of forces occurring in ring structure: inward force first stabilize rings, before they enhance breakage at higher forces.
It is clear that activity can both enhance and suppress breakage rates and mechanisms, depending on the precise magnitude and direction. We expect therefore that activity also will have a large effect on the dynamical behavior of network formation in colloidal patchy particle systems.
Our findings will thus be important for designing adaptive and responsive active physical gels, and rationalizing their behavior. In addition, if one wants to control breakage – and formation – of bonds one might target the different stages of breakage using activity. In a future study, we will report on how colloidal gels self-assembled from patchy particle mixtures respond to activity. On the other hand, one might extend the current investigation to other architectures, such as stars, multiple rings, and 3D structures.
The predictions made in this work can be experimentally tested by using particle systems that behave according to the potential used here.33 Using microscopy the breaking behavior can be followed and tracked, see e.g. ref. 61 and 62.
While our predictions were made specifically for critical Casimir interactions, we believe that they can be generalized to a large class of patchy interaction potentials, that are qualitatively similar: strong short range attractions induced by a relatively small patch in combination with ABP dynamics. As long as the rotational and translational diffusion constants behave similarly to those of the colloids we consider here, and the ABP model applies to the self-propulsion mechanism, the resulting breakage dynamics should be qualitatively similar, irrespective of the origin of the attraction and the self-propulsion.
Appendices
A Potentials
A.1 The patchy particle pair potential
The pair potential that governs patchy particles is composed of an isotropic repulsive component and a directed attractive critical Casimir component mediated through the patches (eqn (1)). In a previous study, dipatch particles were immersed at a surface coverage of 30 area% in a 30–70 vol% lutidine–water mixture with 1 mM MgSO4 to form chains of specific lengths and stiffness depending on the strength of the interaction.25 To reproduce the observed chain length distributions and bending rigidities across a range of weak to strong interactions as a function of temperature, we optimized the patchy particle potential based on the physical dimensions of the dipatch particles and theoretical critical Casimir potentials in ref. 33.The repulsive potential is given by the electrostatic Yukawa potential:
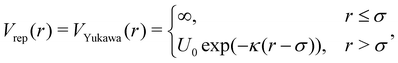 | (18) |
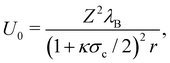 | (19) |
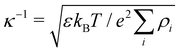 where ρi is the number density of monovalent ions in the solvent.63 The values of σc = 2.0 μm, λB = 2.14 nm, κ−1 = 2.78 nm, and the optimized γ = −0.09e nm−2 have been used in the model.33
where ρi is the number density of monovalent ions in the solvent.63 The values of σc = 2.0 μm, λB = 2.14 nm, κ−1 = 2.78 nm, and the optimized γ = −0.09e nm−2 have been used in the model.33
The attractive potential is based on the (isotropic) critical Casimir potential VC between two spherical particles:
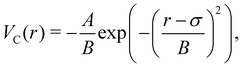 | (20) |
The switching function was obtained by explicit integration using VYukawa and VC at an effective patch width of θeffp = 19.5° and fitted to the functional form:
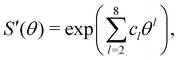 | (21) |
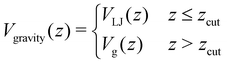 | (22) |
 | (23) |
B Decamers' breakage mechanism
Fig. 18 presents the P1→3, P2→4, and Pmech of passive and active dimers and decamers at dT = 0.12 K and FA = 100kBT/σ.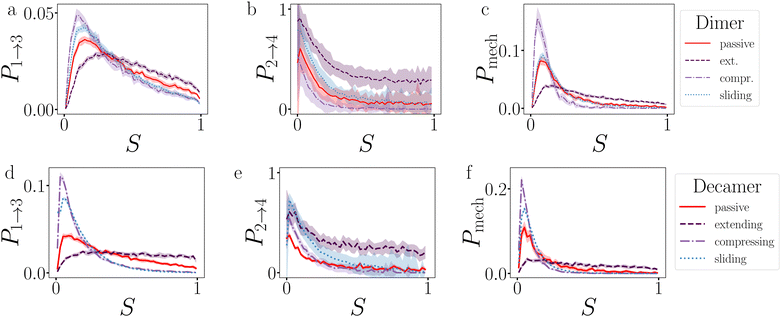 | ||
| Fig. 18 Analysis of the breakage mechanism by P1→3, P2→4, and Pmech from eqn (14)–(16), respectively. Dimers (a)–(c) and decamers (d)–(f) with dT = 0.12 K and active force directions with extending, compressing, and sliding active forces at FA = 100kBT/σ. Note that breakage mechanism and both stages are in principle bond number dependent, but here we take the average over the whole chain. | ||
Stage I of breakage in a decamer is affected by the shape of the chain. As shown in Fig. 12 by the distribution of S per bond, and in Fig. 19 the distribution of Epair, under activity the decamer changes its shape. This shape change: straightening under extending forces, and buckling under compressing and sliding forces, is reflected in the P1→3 of Fig. 18d as a shift toward high and low S meaning radial and angular breakage, respectively.
Fig. 18b and e show that the effect of activity on probability of successful particles separation in the decamer is lower than in the dimer, especially at S < 0.5. The particles in the chains are not freely diffusing in region 3, as they may be still bound to their neighbours. This effect is explicitly measured in Fig. 13c, which shows that the ends of the chain separate twice as successful compared to the center.
Comparing the breakage mechanism of the dimer and decamer (Fig. 18c and f), we observe qualitative similarities. The passive case it is practically similar, the active case shows an exaggeration of the shift in breakage mechanism. Extending forces: no preferred breakage route, and compressing and sliding forces: angular breakage.
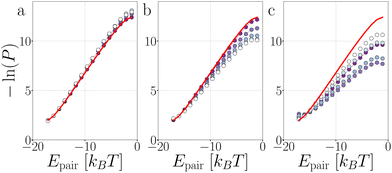 | ||
| Fig. 19 Passive and active decamers. The probability histogram of Epair (eqn (1)) of a passive chain (red solid line) and active chain with FA = 100kBT/σ (dots) and the force directions: extending (a), compressing (b), and sliding (c). Due to symmetry, only the first to fifth bond are shown with symbols as depicted with the colored dots in the legend of Fig. 12. The inset shows a zoom out of the distributions. The measurement is taken at Epair < 0 kBT. | ||
C Fluctuations
To be able to understand the response of the ring structures to the introduction of activity, we can analyze their dynamical fluctuations using principle component analysis (PCA).64 We perform PCA on long straightforward Brownian dynamics simulation trajectories of rings using the MDAnalysis software package.65,66 We focus on the ring system with 4 TPP and 15 DP particles (T4D15), as this system contains long chains that allow significant buckling, but is smaller than the 6 TPP structures and thus decorrelates significantly faster.We start with the analysis of the influence of active forces on the fluctuation dynamics and deformations of an elastic ring using principal component analysis (PCA), as depicted in Fig. 20 and reported Table 3. To enhance the likelihood of observing intact structures during the fluctuation and deformation simulations, we set the interaction strength to dT = 0.12 K.
We conducted Principal Component Analysis (PCA) on long trajectories, with all simulations lasting at least 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds. However, for an inward-directed active force FA = 15, the simulation duration was reduced to 5000 seconds due to observed buckling and a high probability of breaking.
000 seconds. However, for an inward-directed active force FA = 15, the simulation duration was reduced to 5000 seconds due to observed buckling and a high probability of breaking.
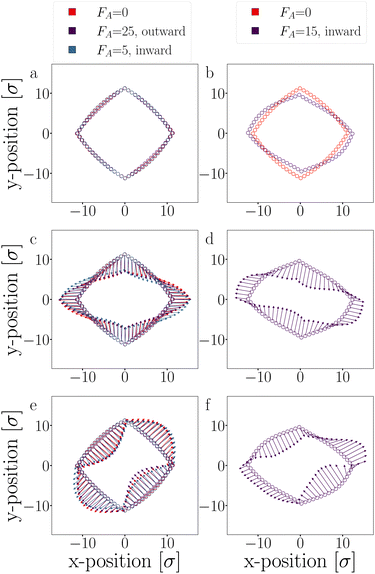
The eigenvectors corresponding to the two dominant modes, which account for approximately 80% of the variance, are depicted in Fig. 20, and their respective eigenvalues are listed in Table 3. These dominant modes are particularly prevalent since they correspond to the lowest curvature in the semi-flexible polymers, resulting in minimal energy cost.
For small outward-directed forces up to FA ≤ 25 and inward-directed forces up to FA ≤ 5, no significant deformations were observed, and the contribution to the variance was not notably different from the passive case (see Fig. 20a, c and e). Any observed differences between the systems can be attributed to limited sampling. Conversely, larger inward-facing active forces (FA ≥ 15) caused the DP-particle chains to buckle, as evidenced by the average positions of these trajectories (Fig. 20b). The buckling is caused by the movement of the first mode (Fig. 20d) which indeed shows a significantly higher contribution compared to the passive case (Table 3).62 In this deformed structure, the two dominant modes still exist, albeit with different amplitudes. Note that an even higher inward force inevitably led to buckling and breaking.
Since the active force, whether inward or outward, primarily affects the radial part of the potential through the translational displacement of particles, it is not expected to have a substantial impact on the fluctuation spectrum. The fluctuations primarily depend on the bending rigidity, as defined by the shape of the S′-function. Moreover, the active force is fixed to the particles and constrained by two bonds. Consequently, the active force cannot reorient along fluctuation modes to drive them, as observed in the actuated elastic solid in ref. 67.
Author contributions
HJJ – equal: conceptualization, formal analysis, investigation, methodology, writing – original draft, writing – review and editing. Lead: data curation, software, validation, visualization. PS – support: conceptualization, investigation, supervision, writing – review and editing. Equal: funding acquisition, project administration. PGB – equal: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, writing – original draft, writing – review and editing. Support: software. Lead: supervision.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
The authors acknowledge the funding (Grant No. 680.91.124) from the Foundation for Fundamental Research on Matter (FOM), which is part of The Netherlands Organization for Scientific Research (NWO).Notes and references
- J. Prost, F. Jülicher and J.-F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- E. H. Barriga, K. Franze, G. Charras and R. Mayor, Nature, 2018, 554, 523–527 CrossRef CAS PubMed.
- F. Burla, Y. Mulla, B. E. Vos, A. Aufderhorst-Roberts and G. H. Koenderink, Nat. Rev. Phys., 2019, 1, 249–263 CrossRef.
- G. L. Jackson, J. M. Dennis, N. D. Dolinski, M. van der Naald, H. Kim, C. Eom, S. J. Rowan and H. M. Jaeger, Macromolecules, 2022, 55, 6453–6461 CrossRef CAS.
- M. P. Murrell and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20820–20825 CrossRef CAS PubMed.
- J. Alvarado, M. Sheinman, A. Sharma, F. C. Mackintosh and G. H. Koenderink, Nat. Phys., 2013, 9, 591–597 Search PubMed.
- C. Alkemade, H. Wierenga, V. A. Volkov, M. Preciado López, A. Akhmanova, P. R. ten Wolde, M. Dogterom and G. H. Koenderink, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1–12 CrossRef.
- Y. Mulla, M. J. Avellaneda, A. Roland, L. Baldauf, W. Jung, T. Kim, S. J. Tans and G. H. Koenderink, Nat. Mater., 2022, 21, 1019–1023 CrossRef CAS PubMed.
- H. N. Verwei, G. Lee, G. Leech, I. I. Petitjean, G. H. Koenderink, R. M. Robertson-Anderson and R. J. McGorty, J. Vis. Exp., 2022, 1–27 Search PubMed.
- R. G. Winkler, J. Elgeti and G. Gompper, J. Phys. Soc. Jpn., 2017, 86, 101014 CrossRef.
- D. Rogel Rodriguez, F. Alarcon, R. Martinez, J. Ramírez and C. Valeriani, Soft Matter, 2020, 16, 1162–1169 RSC.
- S. Joo, X. Durang, O.-C. Lee and J.-H. Jeon, Soft Matter, 2020, 16, 9188–9201 RSC.
- A. Militaru, M. Innerbichler, M. Frimmer, F. Tebbenjohanns, L. Novotny and C. Dellago, Nat. Commun., 2021, 12, 2446 CrossRef CAS PubMed.
- J. Zhang, T. Huang, G. Xu and Y. Chen, Commun. Theor. Phys., 2022, 74, 075601 CrossRef.
- Y. Kim, S. Joo, W. K. Kim and J.-H. Jeon, Macromolecules, 2022, 55, 7136–7147 CrossRef CAS.
- X. Xia, H. Hu, M. P. Ciamarra and R. Ni, Sci. Adv., 2020, 6, 1–8 Search PubMed.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 CrossRef.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS.
- Z. Gong, T. Hueckel, G.-R. Yi and S. Sacanna, Nature, 2017, 550, 234–238 CrossRef PubMed.
- R. Khalaf, A. Viamonte, E. Ducrot, R. Mérindol and S. Ravaine, Nanoscale, 2023, 15, 573–577 RSC.
- Y. Shelke, S. Marín-Aguilar, F. Camerin, M. Dijkstra and D. J. Kraft, J. Colloid Interface Sci., 2023, 629, 322–333 CrossRef CAS PubMed.
- T. Nguyen, A. Newton, D. Kraft, P. G. Bolhuis and P. Schall, Materials, 2017, 10, 1265 CrossRef.
- S. G. Stuij, H. J. Jonas, Z. Gong, S. Sacanna, T. E. Kodger, P. G. Bolhuis and P. Schall, Soft Matter, 2021, 17, 8291–8299 RSC.
- P. J. M. Swinkels, S. G. Stuij, Z. Gong, H. Jonas, N. Ruffino, B. van der Linden, P. G. Bolhuis, S. Sacanna, S. Woutersen and P. Schall, Nat. Commun., 2021, 12, 2810 CrossRef CAS PubMed.
- S. Stuij, J. Rouwhorst, H. J. Jonas, N. Ruffino, Z. Gong, S. Sacanna, P. G. Bolhuis and P. Schall, Phys. Rev. Lett., 2021, 127, 108001 CrossRef CAS PubMed.
- I. Chakraborty, D. J. G. Pearce, R. W. Verweij, S. C. Matysik, L. Giomi and D. J. Kraft, ACS Nano, 2022, 16, 2471–2480 CrossRef CAS.
- P. J. M. Swinkels, Z. Gong, S. Sacanna, E. G. Noya and P. Schall, Nat. Commun., 2023, 14, 1524 CrossRef CAS.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
- H. Seyforth, M. Gomez, W. B. Rogers, J. L. Ross and W. W. Ahmed, Phys. Rev. Res., 2022, 4, 023043 CrossRef CAS.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E, 2013, 88, 012305 CrossRef PubMed.
- G. S. Redner, C. G. Wagner, A. Baskaran and M. F. Hagan, Phys. Rev. Lett., 2016, 117, 148002 CrossRef.
- C. F. Lee, Soft Matter, 2017, 13, 376–385 RSC.
- H. J. Jonas, S. G. Stuij, P. Schall and P. G. Bolhuis, J. Chem. Phys., 2021, 155, 034902 CrossRef CAS PubMed.
- I. M. Ilie, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2015, 142, 114103 CrossRef.
- S. G. Stuij, PhD thesis, University of Amsterdam, 2020.
- K. Dietrich, D. Renggli, M. Zanini, G. Volpe, I. Buttinoni and L. Isa, New J. Phys., 2017, 19, 065008 CrossRef.
- N. Oikonomeas-Koppasis, S. Ketzetzi, D. J. Kraft and P. Schall, Power-law intermittency in the gradient-induced self-propulsion of colloidal swimmers, 2023, https://arxiv.org/abs/2310.17384.
- B. Szabó, G. J. Szöllösi, B. Gönci, Z. Jurányi, D. Selmeczi and T. Vicsek, Phys. Rev. E, 2006, 74, 061908 CrossRef.
- S. van Teeffelen and H. Löwen, Phys. Rev. E, 2008, 78, 020101 CrossRef PubMed.
- S. Henkes, Y. Fily and M. C. Marchetti, Phys. Rev. E, 2011, 84, 040301 CrossRef PubMed.
- L. Fang, L. Li, J. Guo, Y. Liu and X. Huang, Phys. Lett. A, 2022, 427, 127934 CrossRef CAS.
- A. C. Newton, J. Groenewold, W. K. Kegel and P. G. Bolhuis, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15308–15313 CrossRef CAS.
- A. Vijaykumar, P. R. ten Wolde and P. G. Bolhuis, Mol. Phys., 2018, 116, 3042–3054 CrossRef CAS.
- T. S. van Erp, D. Moroni and P. G. Bolhuis, J. Chem. Phys., 2003, 118, 7762–7774 CrossRef CAS.
- G. Cowan, Statistical data analysis, Oxford University Press, USA, 1998 Search PubMed.
- H. Flyvbjerg and H. G. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- A. Vijaykumar, P. G. Bolhuis and P. R. ten Wolde, Faraday Discuss., 2016, 195, 421–441 RSC.
- J. K. G. Dhont, G. W. Park and W. J. Briels, Soft Matter, 2021, 17, 5613–5632 RSC.
- H. Kramers, Physica, 1940, 7, 284–304 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- A. Geiseler, P. Hänggi and G. Schmid, Eur. Phys. J. B, 2016, 89, 175 CrossRef.
- L. Natali, L. Caprini and F. Cecconi, Soft Matter, 2020, 16, 2594–2604 RSC.
- J. Paturej, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, J. Chem. Phys., 2011, 134, 224901 CrossRef CAS PubMed.
- A. Zaccone, I. Terentjev, L. Di Michele and E. M. Terentjev, J. Chem. Phys., 2015, 142, 114905 CrossRef CAS PubMed.
- C. F. Lee, J. Phys.: Condens. Matter, 2015, 27, 275101 CrossRef PubMed.
- C. F. Lee, J. Phys.: Condens. Matter, 2018, 30, 315102 CrossRef PubMed.
- M. Razbin, P. Benetatos and A. A. Moosavi-Movahedi, Soft Matter, 2019, 15, 2469–2478 RSC.
- A. Ghosh, D. I. Dimitrov, V. G. Rostiashvili, A. Milchev and T. A. Vilgis, J. Chem. Phys., 2010, 132, 204902 CrossRef CAS PubMed.
- A. Mondal and G. Morrison, J. Chem. Phys., 2022, 157, 104903 CrossRef CAS PubMed.
- A. M. Lorenzo, E. M. De La Cruz and E. F. Koslover, Soft Matter, 2020, 16, 2017–2024 RSC.
- S. Stuij, J. M. van Doorn, T. Kodger, J. Sprakel, C. Coulais and P. Schall, Phys. Rev. Res., 2019, 1, 023033 CrossRef CAS.
- S. G. Stuij, A. Biebricher, Z. Gong, S. Sacanna, E. Peterman, I. Heller and P. Schall, Phys. Rev. Mater., 2022, 6, 035603 CrossRef CAS.
- V. A. Parsegian, van der Waals Forces, Cambridge University Press, 2005, pp. 1–380 Search PubMed.
- S. Henkes, C. Brito and O. Dauchot, Soft Matter, 2012, 8, 6092 RSC.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105 Search PubMed.
- P. Baconnier, D. Shohat, C. H. López, C. Coulais, V. Démery, G. Düring and O. Dauchot, Nat. Phys., 2022, 18, 1234–1239 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |