Finite size effects during the penetration of objects in a granular medium
Valentin
Paume
,
Pascale
Aussillous
 and
Olivier
Pouliquen
and
Olivier
Pouliquen
 *
*
Aix-Marseille Université, CNRS, IUSTI, Marseille, France. E-mail: valentin.paume@univ-amu.fr
First published on 30th November 2023
Abstract
In many industrial or geotechnical applications, objects move through a granular medium and an important issue is the prediction of the force that develops during the motion of the intruder. In this paper, we experimentally study the vertical penetration of intruders into granular media and analyze both the average force and the fluctuations during motion. We investigate configurations where the size of the intruder becomes close to a few grain sizes, a regime that has not been studied before. Finite size effects are observed, showing that both the mean force and the fluctuations significantly increase when decreasing the ratio of the intruder size to the particle size, and scaling laws are identified to characterize this effect. The role of a conical tip in front of the cylinder to facilitate the penetration is also studied, showing that it is more efficient when the aspect ratio between the intruder size and the grain size is low.
1 Introduction
The study of the force experienced by an object moving in a fluid represents an entire branch of fluid mechanics. While most studies focus on Newtonian fluids, research on the motion of objects in soft materials such as polymers,1,2 foams,3,4 mud5,6 or sand7 is gaining more and more interest, showing that the rheological properties of the medium have a strong and non-trivial influence on the force experienced by the objects. This is particularly true in the case of granular media, which are the focus of the present study, devoted to the penetration of a cylinder in a packing of grains.The problem of the force generated by an object moving in a granular medium is a central issue in many industrial applications (mixing, mining applications, soil testing in geotechnics, locomotion of animals and robots on sand,8–10 anchoring strategies,11etc.). From a fundamental point of view, different configurations have been studied: objects pulled horizontally in a granular material,12,13 plates or cylinders rotating in the medium,14,15 intruders penetrating vertically in the grains,16–19 objects impacting the granular packing,20,21etc. In all these situations the forces are controlled to first order by the frictional nature of the rheology of granular materials,22 in which the shear stresses are proportional to the compressive stress.23 As in all the above configurations the packing lies under gravity, the compressive stress is controlled by the hydrostatic pressure, and one therefore expects that the depth at which the intruder moves in the material plays a fundamental role in the resistance force to movement.
This explains the first important result observed in previous studies, showing that the resistive force on an object moving slowly in a granular material is proportional to the depth at which it is moving multiplied by the cross section of the object. In the case of a fully immersed intruder moving horizontally at depth z, the force thus increases linearly with z. When the intruder is partially immersed (typically a vertical cylindrical plow pulled horizontally), the cross section being itself proportional to the depth, the force varies with the square of the depth z. As the velocity of the motion increases, inertial effects eventually becomes important and a velocity-dependence is observed,24 a situation typically encountered in impact problems.21 Other parameters like the preparation of the packing25 or the number of cycling of the motion also modify the penetration forces.26
A second non-trivial important result is the existence of a lift force on an object moving horizontally in grains, even if the object is symmetrical, an effect explained by the presence of the gravity-induced pressure gradient, which breaks the top/bottom symmetry.27,28 More generally, the shape of the object and the direction of its motion relative to gravity influence the total force experienced by the object. An attempt to predict the force for arbitrary shaped objects has been proposed in the framework of a resistance force theory (RFT).29–31 In this approach, the surface of the object is divided into elementary surfaces, and the total force is assumed to be the sum of the forces that the surfaces would experienced if there were alone in the same position with the same inclination. This approach provides good predictions when the object is moving near the free surface.
In this paper we focus on the configuration of a cylinder penetrating vertically a granular material, a system reminiscent of the penetration test in geotechnics and extensively studied in the literature.32,33 Cone penetration test (CPT) consists in pushing a cylinder with a conical tip in the soil, and in monitoring the forces experiences both by the cone and the cylinder during penetration. The evolution of the forces along the depth provides information about the structure of the soil and the composition of the different layers. Considering the model configuration of a cylinder penetrating a cohesionless granular material, the penetration force F is known to be proportional to cylinder cross-section S times the depth of penetration z: F = KnρpgzS, where ρp is the particle density and g the gravity intensity.17,34 The dimensionless coefficient Kn depends on the properties of the granular material. Assuming that the granular material behaves like a Mohr–Coulomb plastic material, Kn can be computed17,35 and is found to be a function of the friction coefficient μ of the material, increasing exponentially with μ. Experimental measurement of the penetration force in different materials with different friction coefficients are well predicted by this theory in the limit of large intruders compared to the grain size.17
Our goal in this study is to examine how the penetrating force deviates from this prediction as the intruder size approaches the grain size, a situation encountered in many applications. In this regime where granular flows occur on sizes less than 10 particle diameters, finite size effects are known to play a major role as observed in shear bands, in flows of thin layers,36 in flows around small objects,28etc. These finite size effects are a subject of an active research and have been attributed to the presence of non local effects, which are described by more elaborate constitutive laws than the simple Mohr Coulomb or μ(I) rheology.37–39 The existence of finite size effects during penetration of object has been observed in experimental studies18,40 and has been investigated by Miyai et al.19 using quasi-2D simulations. The authors reported that the penetration force increases with particle size and correlated this variation with the change in the width of the shear bands created during motion. In this paper, we experimentally investigate how finite size effects influence the average penetration force of an object penetrating a 3D granular material, but also how they strongly affect the force fluctuations. We also analyse the role of a conical tip at the head of the cylinder in facilitating the penetration.41
The setup and experimental procedure are presented in Section 2. In Section 3, we show that finite size effects play a major role in significantly increasing not only the average penetration force, but also the fluctuations that are enhanced as the size of the intruder approaches that of the particle. In Section 4, we investigate how sharpening the cylinder tip may facilitate penetration, especially in the regime of finite size effects. Section 5 presents conclusions and perspectives.
2 Experimental method
The experimental setup is shown in Fig. 1. A cylindrical container of diameter Dc = 200 mm is filled with particles to a height H = 130 mm. An intruder is moved vertically through the granular material by a vertical linear actuator (ZEMA, Zwick Roell). A force sensor placed between the actuator and the intruder provides an accurate measurement of the penetration force during the movement. We used two different sensors with a nominal force of 10 N and 100 N (accuracy of 0.5%) and we record the data at a frequency of 50 Hz. The intruders are 3D printed in PLA with a 0.4 mm nozzle and a layer thickness of 0.1 mm. We checked that the results are quantitatively identical using smooth metal intruder of the same shape, showing that the tiny roughness induced by the layering inherent to 3D printing does not play a role in the regime investigated in this study.The intruders used are mainly cylindrical with a length L = 110 mm and different diameters D = 3, 5, 10, 15, 20, 30, 40, 50 mm. Other shapes are also tested with different cross sections as shown in Fig. 1b (rectangular and triangular cross section). For these shapes, an equivalent diameter D is defined as  , where Sn is the intruder cross section area. The influence of the presence of a conical tip is also studied for D = 10 mm, by varying the tip angle θ in the range 20, 60, 80, 100 and 120 deg. All the experiments are performed in the limit of a large container, whose diameter Dc is large compared to the intruder size and to penetration depth, to ensure that the container walls do not influence the results and that there is no Janssen effect.
, where Sn is the intruder cross section area. The influence of the presence of a conical tip is also studied for D = 10 mm, by varying the tip angle θ in the range 20, 60, 80, 100 and 120 deg. All the experiments are performed in the limit of a large container, whose diameter Dc is large compared to the intruder size and to penetration depth, to ensure that the container walls do not influence the results and that there is no Janssen effect.
The granular media are made of monodisperse spherical glass beads of density ρp = 2500 kg m−3 with different mean diameters dp = 0.135, 0.52, 1.2, 3.0 and 4.5 mm, supplied by SiLiBeads (Deco Beads) and by Bellco (for dp = 3.0 mm).
Prior to the intruder penetration, the granular packing is prepared as follows. The grains are stirred with a spatula. Then the container is slightly shaken horizontally to obtain a flat surface. After this preparation, we expect the granular medium to be in a critical state, with the initial volume fraction estimated to be around 0.58. The intruder initially above the granular free surface is then moved vertically downward at a slow and constant speed v = 0.5 mm s−1 to ensure that the entire penetration process remains in a quasi-static regime.7 During penetration, the vertical displacement and the vertical drag force are recorded. Each experiment is repeated 4 to 10 times.
Fig. 2a shows the evolution of the raw force as a function of the penetration depth z, for a cylindrical intruder D = 30 mm in a granular medium dp = 3 mm. We define the position of the granular medium surface, z = 0, when the vertical force reaches the threshold value F = max(0.5ρpgSD, 10 mN). As expected, we observe that the force increases almost linearly with the penetration depth. The signal also shows that fluctuations are present around the average increase of the force. To analyse the signal, we decompose the raw force into an average and a fluctuating part F(z) = 〈F〉(z) + ΔF(z). The smoothed average force is computed using the LOcally WEighted Scatterplot Smoothing (LOWESS) algorithm,42 based on a weighted local averaging over a spatial window λav. In the following, the smoothing window is chosen equal to λav = 6dp, motivated by the observation discussed later in the paper that the typical period of the fluctuation is proportional to the particle diameter (≈3dp). The smoothed force 〈F〉(z) resulting from this average procedure is plotted as a solid line in Fig. 2a and the fluctuating part ΔF(z) is plotted in Fig. 2b as a function of displacement. In the next section, we analyse how the average force and the fluctuations vary with the experimental parameters for flat bottomed intruders, with a focus on the role of the aspect ratio between the intruder size and the grain size.
3 Penetration of flat-bottomed intruders
In this section we focus on the case of flat-bottomed intruders shown in Fig. 1(i)–(iv). To characterise the evolution of the force during penetration, we consider a classical description developed in previous approaches,18,19 based on the assumption that the material behaves as a frictional plastic material. The resistance force is written as a sum of two contributions related respectively to the tip and to the side walls. The first contribution Fn is due to the normal stress that applies to the front flat surface of the intruder as it pushes the granular material in front of it. It is proportional to the local pressure in the medium and can be written as Fn = KnρpgzSn, where Kn is a dimensionless constant, ρp the density of the grains, z the penetration depth and Sn = πD2/4 the cross-section of the intruder. In the framework of a Mohr–Coulomb material, Kn can be computed as a function of the friction coefficient μ of the granular material.17,35 The second contribution is due to tangential stress induced by the friction of the grains sliding on the side walls of the intruder and can be written as , where Kt is a dimensionless constant related to the wall/grains friction coefficient. Defining the dimensionless force
, where Kt is a dimensionless constant related to the wall/grains friction coefficient. Defining the dimensionless force ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = 4F/ρpgπD3 based on an Archimedes scaling and the dimensionless penetration depth
= 4F/ρpgπD3 based on an Archimedes scaling and the dimensionless penetration depth ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = z/D, the force can then be expressed as follows:
= z/D, the force can then be expressed as follows:〈![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 〉 = c0 + Kn 〉 = c0 + Kn![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) + 2Kt + 2Kt![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 2. 2. | (1) |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) fit = [0.3;1]. The lower limit takes into account the initial non-linear regime. The upper limit insures that the fitting region is large enough, while remaining in the linear regime. Once Kn is determined, we also measure the coefficient Kt of the nonlinear term by a quadratic fit on the whole curve.
fit = [0.3;1]. The lower limit takes into account the initial non-linear regime. The upper limit insures that the fitting region is large enough, while remaining in the linear regime. Once Kn is determined, we also measure the coefficient Kt of the nonlinear term by a quadratic fit on the whole curve.
Fig. 3 shows for two different granular media of increasing size dp, how the dimensionless force ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) varies as a function of the dimensionless penetration depth
varies as a function of the dimensionless penetration depth ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) for different cylindrical intruder diameters D. The first observation is that for the case of the finest grains Fig. 3a, all curves obtained for different intruder sizes collapse indicating that the scaling chosen for the non-dimensionalized force correctly captures the influence of the intruder size. However, the collapse becomes less accurate when increasing the grain size (Fig. 3b). In coarse grains, we observe that both the smoothed average force (solid lines) and the fluctuations seem to increase when decreasing the intruder diameter.
for different cylindrical intruder diameters D. The first observation is that for the case of the finest grains Fig. 3a, all curves obtained for different intruder sizes collapse indicating that the scaling chosen for the non-dimensionalized force correctly captures the influence of the intruder size. However, the collapse becomes less accurate when increasing the grain size (Fig. 3b). In coarse grains, we observe that both the smoothed average force (solid lines) and the fluctuations seem to increase when decreasing the intruder diameter.
 | ||
Fig. 3 Dimensionless force ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) as a function of the penetration depth as a function of the penetration depth ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) for cylindrical intruders of various diameters D in granular material of size (a) dp = 0.52 mm and (b) dp = 3 mm. for cylindrical intruders of various diameters D in granular material of size (a) dp = 0.52 mm and (b) dp = 3 mm. | ||
3.1 Size effect on the smoothed average force
From the evolution of the smoothed force, we compute for each particle size and intruder diameter the coefficient Kn. Fig. 4 shows how Kn varies with the intruder diameter for a fine and a coarse granular medium. We observe that for the fine particles (dp = 0.52 mm) the coefficient Kn is constant and does not depend on the intruder size D as found by Kang et al.17 However, for larger particles (dp = 4.5 mm), the coefficient Kn increases significantly when decreasing the intruder size.19 This suggests that in this regime, when the intruder size is close to the grain size, finite size effects are present, where the discrete nature of the granular medium is no longer negligible. | ||
| Fig. 4 Evolution of the coefficient Kn as a function of the cylinder diameter D for two different particle sizes dp. The dashed lines represent the coefficient Kn∞ in the limit of large aspect ratio D/dp. Inset: Evolution of the coefficient Kn∞ as a function of the friction angle δ for experimental data from this study and the work of Kang et al.,17 compared with the theoretical model of Kang et al.17 | ||
This behavior disappears when D ≫ dp, and the coefficient Kn tends towards a constant that we note Kn∞, which we measure for each granular medium. We also measure for each medium the friction angle δ using a rotating drum, which values are reported in Table 1. In the inset of Fig. 4 we compare our measurements of Kn∞ with those obtained by Kang et al.17 and with the theoretical model they developed in the continuum framework of the Mohr–Coulomb criterion, predicting the variation of Kn with the angle of friction δ. We observe a good agreement between the experimental values of Kn∞ and the model, showing that the Mohr Colomb description is relevant to predict Kn∞ when the aspect ratio between the intruder and the grains is large.
| d p (mm) | Friction angle δ (°) | Measured Kn∞ |
|---|---|---|
| 0.135 ± 0.03 | 25 ± 1 | 27 |
| 0.52 ± 0.10 | 23 ± 1 | 16.3 |
| 1.20 ± 0.07 | 24 ± 1 | 19.3 |
| 3.0 | 22 ± 1 | 11.4 |
| 4.5 | 26 ± 1 | 20.2 |
To characterise the finite-size effects observed when D/dp decreases, we plot in Fig. 5a the ratio Kn/Kn∞ as a function of the aspect ratio D/dp for all experiments performed. We observe that all data collapse in this representation, suggesting that the relative increase in the coefficient Kn is controlled by the size ratio between the diameter of the intruder and the particle diameter. The transition between the finite-size regime to the continuum regime occurs for D ≈ 4.5dp. We also reported in Fig. 5a data for other shapes (triangular and rectangular), showing that the shape of the intruder does not play a role. This was observed by Kang et al.17 in the high aspect ratio limit, and we show here that it is also true in the finite size regime.
 | ||
| Fig. 5 (a) Evolution of the normalised coefficient Kn/Kn∞versus the ratio D/dp. The dot-dashed line corresponds to eqn (2). (b) Ktversus the ratio D/dp. The dot-dashed line corresponds to the best fit by a constant Kt = 1.0. The symbols correspond to the different intruders cross section: circular (●), square (□), rectangles (◊), equilateral triangle (△), rectangular triangle (▽). | ||
To explain the role of the particle size, a simple model has been proposed14,19 assuming that the intruder has an effectif diameter equal to D + dp. The force should then be equal to Fn = Kn∞ρpgz(D + dp)2π/4, which according to our definition of Kn is also equal to Fn = KnρpgzD2π/4. This leads to the following prediction
| Kn/Kn∞ = (1 + dp/D)2 | (2) |
We also measure the coefficient Kt characterising the departure from linear Archimedes' law due to the frictional interaction on the sides of the intruder. The coefficient Kt is measured in all experiments, and Fig. 5b shows how it varies with the aspect ratio D/dp. Due to the fitting procedure, the data are more noisy for Kt than for Kn, but no systematic influence of the aspect ratio D/dp is observed, and the coefficient can be considered as constant with the best fit giving Kt ≈ 1.0. We can then conclude that no finite size effects is observed for the quadratic term of the force as notice in simulation.19 This observation is coherent with the fact that Kt is related to the wall/grains friction, which for smooth surfaces as used for our intruders is expected to be roughly independent of the grain size, although the value 1 is higher than expected for a wall friction coefficient. We now turn to the analyse of the fluctuating part of the force, which also appears to be sensitive to the finite size effect as observed in the raw data of Fig. 3.
3.2 Force fluctuations
During penetration, the intruder experiences significant force fluctuations, especially when moving in a coarse media. To characterize them, we systematically measure the fluctuations ΔF = F − 〈F〉, which like the mean force are expected to grow linearly with the depth. We then define the dimensionless fluctuations by dividing ΔF(z) by the mean force experienced by the intruder in the continuous limit of very fine grains equal to Kn∞ρpgzSn. The dimensionless fluctuations then writes: | (3) |
An example of  as a function of the dimensionless penetration depth
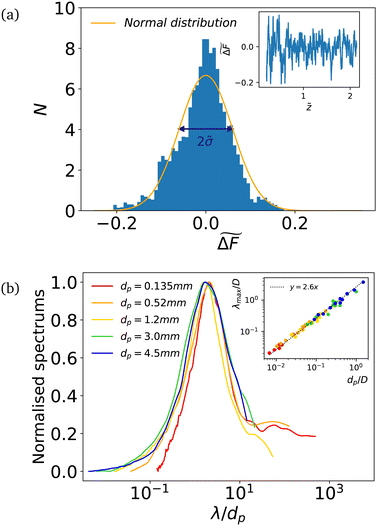
as a function of the dimensionless penetration depth ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) is plotted in the inset of Fig. 6a. The dimensionless signal fluctuates around zero with an amplitude that is constant during the penetration, meaning that ΔF grows linearly with the depth as anticipated by the nondimensionlization of eqn (3). The same feature is observed in all our experiments. We first analyze the spatial period of the fluctuations, by applying a FFT transform to the signal. The average spectrum obtained for D = 10 mm and different dp are plotted in Fig. 6b as a function of the wavelength divided by the particle diameter λ/dp. All the spectrum collapse, with a maximum obtained for λmax/dp ≈ 2.6. This shows that a well defined periodicity exists in the fluctuations, which is controlled by the grain size dp and is independent of the intruder size D, as shown inset of Fig. 6b showing that λmax/D varies linearly with dp/D. This suggest that the fluctuations take their origin in the particle rearrangements at the grains size. This observation justifies a posteriori the choice of an average window λav = 6dp ≈ 2λmax to smooth the force curve.
is plotted in the inset of Fig. 6a. The dimensionless signal fluctuates around zero with an amplitude that is constant during the penetration, meaning that ΔF grows linearly with the depth as anticipated by the nondimensionlization of eqn (3). The same feature is observed in all our experiments. We first analyze the spatial period of the fluctuations, by applying a FFT transform to the signal. The average spectrum obtained for D = 10 mm and different dp are plotted in Fig. 6b as a function of the wavelength divided by the particle diameter λ/dp. All the spectrum collapse, with a maximum obtained for λmax/dp ≈ 2.6. This shows that a well defined periodicity exists in the fluctuations, which is controlled by the grain size dp and is independent of the intruder size D, as shown inset of Fig. 6b showing that λmax/D varies linearly with dp/D. This suggest that the fluctuations take their origin in the particle rearrangements at the grains size. This observation justifies a posteriori the choice of an average window λav = 6dp ≈ 2λmax to smooth the force curve.
To further characterize the fluctuations, we plot in Fig. 6a a typical distribution of the normalised fluctuations amplitude, showing that they follow a centred normal distribution. From the distribution we extracted the standard deviation ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) for all our runs, for all grains and intruder sizes. Unlike the period of the fluctuations, the amplitude
for all our runs, for all grains and intruder sizes. Unlike the period of the fluctuations, the amplitude ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) varies with the size of the intruder D. The data are plotted in Fig. 7 showing how
varies with the size of the intruder D. The data are plotted in Fig. 7 showing how ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) varies as a function of the aspect ratio D/dp. All the data obtained in the different granular media, for different sizes and shapes of intruders collapse on a single curve well approximated by a power law. The best fit gives:
varies as a function of the aspect ratio D/dp. All the data obtained in the different granular media, for different sizes and shapes of intruders collapse on a single curve well approximated by a power law. The best fit gives:
 | (4) |
 | ||
Fig. 7 Amplitude of the force fluctuation ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) as a function of D/dp. The dashed line corresponds to eqn (4). The symbols correspond to different intruder cross sections: circular (•), square (□), rectangles (◊), equilateral triangle (△), rectangular triangle (▽). as a function of D/dp. The dashed line corresponds to eqn (4). The symbols correspond to different intruder cross sections: circular (•), square (□), rectangles (◊), equilateral triangle (△), rectangular triangle (▽). | ||
In conclusion of our measurements on the flat bottom intruders, we can infer that the ratio of the intruder size to the particle size influences both the average force and the fluctuations. Penetrating a coarse granular media is thus twice penalising if one consider the maximum force necessary to continuously move in the material. In the next section we investigate how a sharper shape may reduce this effect.
4 Influence of a conical tip
The intruder used in this section are cylindrical intruders of diameter D = 10 mm with a conical tip with zenith angles varying in the range θ = 20, 60, 80, 100, 120, 180°, the case θ = 180 deg corresponding to the flat case without conical tip. Fig. 8 shows the penetration force as a function of the depth for 3 different tip angles (θ = 20, 100 and 180 deg) and for two granular medium dp = 0.52 mm and dp = 3 mm. The position z = 0 is defined when the tip first touches the granular medium. The penetration of the tip initially gives rise to a non linear evolution of the force identified in the figure by the bold part of the curves. This non linearity is due to the increase of the section of the cone during penetration.34 In order to analyse to which extend the presence of the tip facilitates the subsequent penetration of the cylinder, we analyse the evolution of the force once the tip is fully immersed in the grains at the same penetration depth, i.e. in the yellow region in Fig. 8. Two observations can be made. First the force increment necessary to move the cylinder behind the tip seems smaller for sharp tips i.e. small θ compared to flat intruders. Secondly the fluctuations around the mean force seem to be attenuated by the presence of the tip. These two effects are even more pronounced in the case of the penetration in the coarse material (Fig. 8b).To quantitatively characterize the influence of the tip, we interpolate the smoothed force by a linear function in the yellow region and define the slope Kθn = d![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) /d
/d![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) , which characterises the difficulty of the cylinder to penetrate behind the tip. Fig. 9a shows the evolution of the ratio
, which characterises the difficulty of the cylinder to penetrate behind the tip. Fig. 9a shows the evolution of the ratio  as a function of the tip angle θ for different grain sizes (θ = 180° corresponding to the flat cylinder). The ratio decreases when decreasing θ below 120°, meaning that the sharpest the tip, the easiest the penetration of the cylinder behind the tip. The gain is about 40% for the tip with an angle 20% compare to the flat cylinder. This tendency is similar for all the grain size, although it is more pronounced in the coarse grains, meaning that the facilitation by the tip seems more efficient in presence of finite size effects. The observation that tips with an angle less than 120° do not influence Kn could be linked to the presence of a conical dead zone that exists even with a flat intruder. Adding a conical tip may not change the flow until it is sharper than the natural dead cone.
as a function of the tip angle θ for different grain sizes (θ = 180° corresponding to the flat cylinder). The ratio decreases when decreasing θ below 120°, meaning that the sharpest the tip, the easiest the penetration of the cylinder behind the tip. The gain is about 40% for the tip with an angle 20% compare to the flat cylinder. This tendency is similar for all the grain size, although it is more pronounced in the coarse grains, meaning that the facilitation by the tip seems more efficient in presence of finite size effects. The observation that tips with an angle less than 120° do not influence Kn could be linked to the presence of a conical dead zone that exists even with a flat intruder. Adding a conical tip may not change the flow until it is sharper than the natural dead cone.
 | ||
Fig. 9 (a) Coefficient  and (b) normalized force fluctuation amplitude and (b) normalized force fluctuation amplitude ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) θ/ θ/![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 180° as a function of the tip angle θ for different particle diameters. 180° as a function of the tip angle θ for different particle diameters. | ||
The presence of the tip also modifies the fluctuations, but only its amplitude and not the period. We have checked that the spectral analysis of the force signal obtained with conical tips reveals the same well defined period given by λmax ≈ 3d. However, the amplitude is significantly affected by the presence of the tip. Fig. 9b shows the standard deviation of the force on intruders with conical tips normalised by the standard deviation for a flat cylinder ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) θ/
θ/![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 180° as a function of the zenith angle θ for different grains sizes. Different behaviors are observed depending on the grains size. For the finer granular materials dp = 0.135 mm and dp = 0.52 mm, the standard deviation is more of less independent of the tip angle, with even a small increase observed for the finest grains. However, for coarser grains, a significant decrease of the fluctuation amplitude is observed when decreasing the zenith angle. Fluctuations for dp = 4.5 mm are 75% less for the sharp tip θ = 20° than for the flat cylinder. The interpretation of the fluctuation attenuation by the tip is not obvious, but might be understood by a geometrical effect: the conical tip pushes the grains on the side when penetrating into the interstices, when the flat cylinder pushes frontally on the grains. This might be less true for the smallest grains, as our 3D printed intruder are rounded at the tip over a typical size of 300 μm, which may explain why the attenuation in the force fluctuations in Fig. 9b is not observed for the two smallest grains.
180° as a function of the zenith angle θ for different grains sizes. Different behaviors are observed depending on the grains size. For the finer granular materials dp = 0.135 mm and dp = 0.52 mm, the standard deviation is more of less independent of the tip angle, with even a small increase observed for the finest grains. However, for coarser grains, a significant decrease of the fluctuation amplitude is observed when decreasing the zenith angle. Fluctuations for dp = 4.5 mm are 75% less for the sharp tip θ = 20° than for the flat cylinder. The interpretation of the fluctuation attenuation by the tip is not obvious, but might be understood by a geometrical effect: the conical tip pushes the grains on the side when penetrating into the interstices, when the flat cylinder pushes frontally on the grains. This might be less true for the smallest grains, as our 3D printed intruder are rounded at the tip over a typical size of 300 μm, which may explain why the attenuation in the force fluctuations in Fig. 9b is not observed for the two smallest grains.
Before concluding this section on the role of a conical tip, we address another question of interest for applications. Is it advantageous to have a conical tip in front of the cylinder if one want to introduce a certain length of the cylinder in the granular medium. In other words, we want to compare the work necessary to achieve the situations sketched in Fig. 10a, where the same amount of the cylindrical part of the intruder reaches a depth zmax. On one hand, adding a tip that has to penetrate first costs some additional work, but on the other hand we know from the above results that the presence of the tip also decreases the force necessary to further move the cylinder behind the tip, meaning that a trade-off might exist. In Fig. 10b and c we compute from the experimental measurements the work necessary to achieve different depths zmax, and plot it as a function of the tip angle for the finest (Fig. 10b) and the largest grains (Fig. 10c) used in our study. Whereas for the fine grains, the minimum work for all depth studied in the experiments is always achieved using a flat cylinder, when penetrating coarse grains an optimum exists: to introduce 6 cm of the cylinder in the medium, it is better to use a conical tip with an angle 50°. This result might explain the use of teeth in some mining applications when working in coarse grains.
5 Conclusion
In this paper, we studied the penetration of cylindrical intruders into a granular medium in a regime where the cylinder size approaches the grain size. We then depart from the continuous limit, and important finite size effects controlled by the aspect ratio between the cylinder size and grains size have been identified.First of all, the average penetration force increases significantly when the size of the object drops below ten grain sizes, to reach values almost three times greater when the size aspect ratio is one. To account for this increase, the explanation in terms of an increase of the effective cross-section by one grain diameter14,19 is not totally satisfactory because it predicts a too soft transition, and is based on an oversimplified description of the flow. Another interpretation may be that the observed finite size effects are the signature of a non local rheology. It would then be interesting to test whether recent continuous approaches accounting for finite size effects by non-local terms37,39 are able to capture the force amplification or not.
We also observed that the ratio of object size to grain size plays a crucial role in the fluctuations of the force. The force signal during penetration exhibits a well defined periodicity corresponding to a length scale equal to about 3 particle diameters and the amplitude of the force fluctuations follows a −3/2 power law with the aspect ratio. The theoretical approach considering that the fluctuations are simply controlled by an averaging process of the inter-particle forces on a volume which scales with the cylinder size provides a good prediction of the scaling law.
From an application perspective, the concomitant growth of the average force and fluctuation as the size of the object decreases (or the size of the grains increases) is crucial in predicting the maximum forces and thus the resistance that the objects will have to undergo during their use. In mining applications, teeth are also often used to dig into coarse granular material. We have analyzed the intuitive idea that a pointed object penetrates more easily a granular material. We have shown that the presence of a conical tip at the head of the cylinder has a quantitative effect on the penetration coefficient Kn, with a decrease varying of about 40% when decreasing the aspect ratio between the object and the grains. The point effect is even more noticeable on the force fluctuations, whose amplitude decreases by nearly 80% when the aspect ratio between the intruder and the grains approaches one. Understanding these intuitive effects is far from trivial. A first step could be the generalization of the plasticity calculation based on a Mohr–Coulomb model to a conical geometry.
Finally, we have restricted our analyse to the case of a single cylinder penetrating a granular medium. However, many applications use systems with several teeth to pick up or mix the grains. The interaction between the objects moving in a granular material is a problem that start to be studied43–46 and for which finite size effects certainly play an important role.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: theoretical estimate of the force fluctuations amplitude
The instantaneous force F experienced by the intruder is equal to F = PzzD2, where Pzz is the instantaneous normal stress averaged over the intruder section. Pzz can be estimated from the interparticle forces by , where fcz is the vertical component of the force at contact c, bcz the vertical component of the branch vector relating the center of the two particles in contact, and V the representative volume of averaging. The variance of the pressure is then related to the variance of the interparticle force:
, where fcz is the vertical component of the force at contact c, bcz the vertical component of the branch vector relating the center of the two particles in contact, and V the representative volume of averaging. The variance of the pressure is then related to the variance of the interparticle force: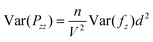 | (5) |
 | (6) |
This implies that the relative standard deviation of the force  follows a power law:
follows a power law:  . One should notice that the dimensionless standard deviation
. One should notice that the dimensionless standard deviation ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) defined in Section 3 is equal to
defined in Section 3 is equal to  , and then according to the above argument should not follows strictly the power law as Kn/Kn∞ is also a function of D/dp.
, and then according to the above argument should not follows strictly the power law as Kn/Kn∞ is also a function of D/dp.
Author contributions
VP did the experiments measurements. VP, PA and OP contributed to the conception and analysis of the experiments and to the writing of the paper.Acknowledgements
This work has been funded by Safe Metal. We thank J.-F. Carton, F. Marchand and O. Falcoz for fruitful discussion.Notes and references
- J. R. Gladden and A. Belmonte, Phys. Rev. Lett., 2007, 98, 224501 CrossRef.
- H. Tabuteau, P. Coussot and J. R. de Bruyn, J. Rheol., 2007, 51, 125–137 CrossRef CAS.
- B. Dollet, F. Elias, C. Quilliet, C. Raufaste, M. Aubouy and F. Graner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 031403 CrossRef PubMed.
- Z. Jing, S. Wang and Z. Wang, Langmuir, 2016, 32, 2419–2427 CrossRef CAS.
- N. P. Chafe and J. R. de Bruyn, J. Non-Newtonian Fluid Mech., 2005, 131, 44–52 CrossRef CAS.
- P. Coussot, J. Non-Newtonian Fluid Mech., 2014, 211, 31–49 CrossRef CAS.
- R. Albert, M. Pfeifer, A.-L. Barabási and P. Schiffer, Phys. Rev. Lett., 1999, 82, 205 CrossRef CAS.
- C. Li, T. Zhang and D. I. Goldman, Science, 2013, 339, 1408–1412 CrossRef CAS PubMed.
- R. D. Maladen, Y. Ding, C. Li and D. I. Goldman, Science, 2009, 325, 314–318 CrossRef CAS.
- N. D. Naclerio, A. Karsai, M. Murray-Cooper, Y. Ozkan-Aydin, E. Aydin, D. I. Goldman and E. W. Hawkes, Sci. Rob., 2021, 6, 2922 CrossRef PubMed.
- J. Featherstone, R. Bullard, T. Emm, A. Jackson, R. Reid, S. Shefferman, A. Dove, J. Colwell, J. E. Kollmer and K. E. Daniels, Planet. Sci. J., 2021, 2, 243 CrossRef.
- A. Seguin, Y. Bertho, P. Gondret and J. Crassous, Phys. Rev. Lett., 2011, 107, 048001 CrossRef CAS PubMed.
- M. Kobayakawa, S. Miyai, T. Tsuji and T. Tanaka, Phys. Rev. E, 2018, 98, 052907 CrossRef CAS.
- R. Soller and S. A. Koehler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021305 CrossRef PubMed.
- F. Guillard, Y. Forterre and O. Pouliquen, Phys. Rev. Lett., 2013, 110, 138303 CrossRef.
- T. G. Murthy, E. Gnanamanickam and S. Chandrasekar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061306 CrossRef.
- W. Kang, Y. Feng, C. Liu and R. Blumenfeld, Nat. Commun., 2018, 9, 1101 CrossRef.
- Y. Feng, R. Blumenfeld and C. Liu, Soft Matter, 2019, 15, 3008–3017 RSC.
- S. Miyai, M. Kobayakawa, T. Tsuji and T. Tanaka, Granular Matter, 2019, 21, 1–21 CrossRef.
- H. Katsuragi and D. J. Durian, Nat. Phys., 2007, 3, 420–423 Search PubMed.
- H. Katsuragi and D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052208 CrossRef PubMed.
- B. Andreotti, Y. Forterre and O. Pouliquen, Granular media: between fluid and solid, Cambridge University Press, 2013 Search PubMed.
- P. Jop, Y. Forterre and O. Pouliquen, Nature, 2006, 441, 727–730 CrossRef CAS PubMed.
- F. Q. Potiguar and Y. Ding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012204 CrossRef PubMed.
- F. Tapia, D. Espndola, E. Hamm and F. Melo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 014201 CrossRef PubMed.
- B. Darbois-Texier and A. Seguin, Phys. Rev. E, 2022, 106, 014906 CrossRef CAS PubMed.
- Y. Ding, N. Gravish and D. I. Goldman, Phys. Rev. Lett., 2011, 106, 028001 CrossRef.
- F. Guillard, Y. Forterre and O. Pouliquen, Phys. Fluids, 2014, 26, 043301 CrossRef.
- S. Agarwal, A. Karsai, D. I. Goldman and K. Kamrin, Sci. Adv., 2021, 7, eabe0631 CrossRef PubMed.
- S. Agarwal, A. Karsai, D. I. Goldman and K. Kamrin, Soft Matter, 2021, 17, 7196–7209 RSC.
- S. Agarwal, D. I. Goldman and K. Kamrin, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2214017120 CrossRef CAS.
- T. Lunne, J. J. Powell and P. K. Robertson, Cone penetration testing in geotechnical practice, CRC Press, 2002 Search PubMed.
- P. K. Robertson, Can. Geotech. J., 2009, 46, 1337–1355 CrossRef.
- T. A. Brzinski III, P. Mayor and D. J. Durian, Phys. Rev. Lett., 2013, 111, 168002 CrossRef.
- G. Meyerhof, Géotechnique, 1951, 2, 301–332 CrossRef.
- O. Pouliquen, Phys. Fluids, 1999, 11, 542–548 CrossRef CAS.
- K. Kamrin and G. Koval, Phys. Rev. Lett., 2012, 108, 178301 CrossRef.
- M. Bouzid, M. Trulsson, P. Claudin, E. Clément and B. Andreotti, Phys. Rev. Lett., 2013, 111, 238301 CrossRef PubMed.
- M. Bouzid, A. Izzet, M. Trulsson, E. Clément, P. Claudin and B. Andreotti, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 125 CrossRef.
- M. D. Bolton, M.-W. Gui, J. Garnier, J. F. Corte, G. Bagge, J. Laue and R. Renzi, Géotechnique, 1999, 49, 543–552 CrossRef.
- F. Patino-Ramirez and C. O'Sullivan, Acta Geotech., 2023, 18, 1–20 CrossRef.
- W. S. Cleveland, J. Am. Stat. Assoc., 1979, 74, 829–836 CrossRef.
- F. Pacheco-Vázquez and J. Ruiz-Suárez, Nat. Commun., 2010, 1, 123 CrossRef.
- R. L. De La Cruz and G. Caballero-Robledo, J. Fluid Mech., 2016, 800, 248–263 CrossRef.
- S. Pravin, B. Chang, E. Han, L. London, D. I. Goldman, H. M. Jaeger and S. T. Hsieh, Phys. Rev. E, 2021, 104, 024902 CrossRef CAS.
- B. Chang and A. Kudrolli, Phys. Rev. E, 2022, 105, 034901 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |