Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of shear-induced crystallization on the complex viscosity of lamellar-structured concentrated surfactant solutions†
Parth U.
Kelkar
 a,
Matthew
Kaboolian
a,
Matthew
Kaboolian
 a,
Ria D.
Corder
a,
Ria D.
Corder
 ab,
Marco
Caggioni
c,
Seth
Lindberg
c and
Kendra A.
Erk
ab,
Marco
Caggioni
c,
Seth
Lindberg
c and
Kendra A.
Erk
 *a
*a
aSchool of Materials Engineering, Purdue University, West Lafayette, IN 47907, USA. E-mail: erk@purdue.edu
bSchool of Mechanical Engineering, Purdue University, West Lafayette, IN 47907, USA
cCorporate Engineering, The Procter & Gamble Company, West Chester, OH 45069, USA
First published on 20th March 2024
Abstract
Material relationships at low temperatures were determined for concentrated surfactant solutions using a combination of rheological experiments, cross-polarized microscopy, calorimetry, and small angle X-ray scattering. A lamellar structured 70 wt% solution of sodium laureth sulfate in water was used as a model system. At cold temperatures (5 °C and 10 °C), the formation of surfactant crystals resulted in extremely high viscosity. The bulk flow behavior of multi-lamellar vesicles (20 °C) and focal conic defects (90 °C) in the lamellar phase was similar. Shear-induced crystallization at temperatures higher than the equilibrium crystallization temperature range resulted in an unusual complex viscosity peak. The effects of processing-relevant parameters including temperature, cooling time, and applied shear were investigated. Knowledge of key low-temperature structure–property-processing relationships for concentrated feedstocks is essential for the sustainable design and manufacturing of surfactant-based consumer products for applications such as cold-water laundry.
Introduction
Consumer cleaning products including shampoos and detergents often contain a large amount of water,1 a critical component during formulation and production that is typically required at all stages of the product's lifecycle.2 Concentrating products like detergents would lead to reduced water usage, waste generation, and transportation costs.3–5 The average 5 L concentrate bottle can be the equivalent of 500 separate ready-to-use spray bottles, potentially saving up to 29.3 kg of plastic trash over a product's lifetime.6–8 If industries only produced and sold concentrated products, it is projected that up to 20% of the world's disposable plastic packaging by weight could be replaced with reusable packaging.9Making concentrated formulations, however, is more complicated than simply removing as much water as desired. Surfactants are a key component in consumer cleaning products, and the microstructure and rheology of surfactant solutions radically changes with concentration and exposure to forces during processing.10–13 As the surfactant concentration rises, surfactant solutions typically transform from optically isotropic micellar solutions to optically birefringent infinitely ordered14 liquid crystalline assemblies like the hexagonal and lamellar phases. The lyothermotropic phase transitions of surfactant solutions have traditionally been modeled using the critical packing parameter (CPP)15 or spontaneous curvature considerations.14 Micellar solutions are most often Newtonian fluids while the liquid crystalline phases display non-Newtonian flow behavior.16–19 The influence of supramolecular aggregates on viscosity has been extensively studied in literature.20,21 Interestingly, the apparent viscosity of the more concentrated lamellar phase is often lower than that of the less concentrated hexagonal phase.22,23 Due to its microstructure of closely packed cylindrical micelles, the high-viscosity hexagonal phase can be very difficult to process and is generally avoided by industrial formulators.24 In contrast, the lamellar phase has a microstructure composed of stacked parallel surfactant bilayers which flows easily when exposed to shear forces and requires less energy inputs during processing.22,23
The flow behavior of the lamellar phase in surfactant systems has previously been investigated for a range of systems, as summarized in a review by Berni et al.12 However, the rheology of highly concentrated surfactant systems is rarely studied. Pasch et al. reported high yield stress values and shear-dependent orientation phenomenon at 20 °C in several non-ionic systems at high surfactant concentrations (50–75 wt% surfactant in water).25 Robles-Vasquez et al. analyzed room temperature dynamic and steady-state rheological responses of an aqueous ionic surfactant solution as a function of concentration to detect structural defects and shear thinning flow behavior.26 Mongondry et al. used small-angle X-ray scattering and rheology of a highly concentrated ternary mixed surfactant system (70–90 wt% surfactant in water) to study the flow behavior (at 25 °C and 45 °C) and temperature-dependent crystal to liquid crystal transition.27 Rheology and scattering (SAXS, SANS, SALS) were used to report the dynamic phase behavior and flow induced microstructural transitions for deuterated solutions of a homologous series of non-ionic polyoxyethylene alkyl ether surfactants (C12E3, C12E4, C12E5) at varying surfactant concentrations (40–60 wt%) and temperatures (20–72 °C).28–30 Veronico et al. recently reported a phase diagram for the nonionic surfactant Brij L4 (10–90 wt%)–water binary system at 25 °C.31
Caicedo-Casso et al. used steady-state rheometry and ultrasonic velocimetry at 22 °C to investigate the rheological behavior of aqueous sodium lauryl ether sulfate (SLES) solutions as a function of surfactant concentration (20–70 wt%).23 At the highest concentration, the presence of significant flow instabilities such as wall slip, shear banding, and plug flow was detected.23,32 An industrial workhorse used extensively in cleaning product formulations,33 aqueous solutions of anionic SLES were chosen because they can easily recreate the raw feedstocks and microstructures often observed in consumer products. Even though SLES is a common component of many commercial products, there has been limited published research on its flow behavior, temperature dependence, and phase evolution in pure systems. Hendrikse et al. used dissipative particle dynamics to simulate the first full-phase diagram of SLES in water at 25 °C33 and molecular dynamics to investigate conformation changes in SLES molecules at various surfactant concentrations.34 Recently, Ferraro et al. investigated the linear rheological behavior of aqueous SLE3S solutions (25–72 wt%) from 30–60 °C and used polarized optical microscopy to report the presence of four phases (micellar (L1), hexagonal (H), cubic (V1) and lamellar (Lα)) at room temperature.35
Due to a lack of knowledge of predictable structure–property-processing relationships, instability initiation and evolution are not well understood and it is currently unclear if flow instabilities can help or hinder the formulation and production of concentrated products.36 Additionally, the type of equipment used for processing and the selected operating conditions can change the structure of the product, which can subsequently affect its physical properties like viscosity and ultimately the product's performance, including shelf-life stability and end-use properties.
Consumer cleaning products begin as raw feedstock and progress through a series of temperature zones before being fully utilized by the end user. However, most prior work on the rheological behavior of highly concentrated surfactant systems, including the aforementioned studies, has primarily focused on room temperature behavior. Thus, there remains a need to study low-temperature flow behavior and characterize the rheological signature of specimens across multiple temperature zones.
The impacts of temperature variation on the material relationships of concentrated surfactant solutions are particularly important to investigate as industries are encouraging consumers to use products like detergents at lower temperatures,37,38 and studies have shown that simply lowering the wash temperature can have significant economic and environmental benefits.39,40 For instance, in a European study, heating water required for washing accounted for 60% of the carbon footprint associated with laundry.41 By reducing wash temperatures from 40 °C to 30 °C, annual CO2 emissions in Europe can be reduced by almost 4.9 million metric tons – comparable to taking over a million cars off the road.40,42 Naturally, decreasing the temperature to 20 °C would contribute to an even greater reduction in emissions.43,44 Hot water also hastens the breakdown of clothes and promotes microplastic shedding. It is estimated that the conventional laundering of synthetic clothes is responsible for 35% of primary microplastics in world oceans45 and that a single 6 kg domestic laundry cycle can generate up to 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 microplastic particles.46,47 High concentrations of these microplastics are regularly found downstream of water treatment facilities48,49 and they can eventually end up in our potable water sources.50–52 Research has shown that laundering at colder temperatures can have outsized positive impacts on microplastic generation and garment longevity. Lant et al. estimate a 30% reduction in microplastic generation for a washing cycle at 15 °C for 30 min, as opposed to 40 °C for 85 min.53 Cotton et al. concluded that in addition to energy savings, reducing laundry time and temperature results in significantly lesser color loss, dye transfer, and microfiber release.54
000 microplastic particles.46,47 High concentrations of these microplastics are regularly found downstream of water treatment facilities48,49 and they can eventually end up in our potable water sources.50–52 Research has shown that laundering at colder temperatures can have outsized positive impacts on microplastic generation and garment longevity. Lant et al. estimate a 30% reduction in microplastic generation for a washing cycle at 15 °C for 30 min, as opposed to 40 °C for 85 min.53 Cotton et al. concluded that in addition to energy savings, reducing laundry time and temperature results in significantly lesser color loss, dye transfer, and microfiber release.54
Temperature variation – and in particular, temperature reductions – are known to drastically change the material relationships of surfactant solutions. As surfactant solutions cool, crystallization can be a source of concern.55 It can be a desired result in some applications, and crystallization methods are frequently employed for separation, purification, and product definition.56 For instance, in the production of sunscreens or moisturizers, crystalline surfactant aggregations act as emulsifiers and improve product stability.57 It can however also have negative impacts such as pipe blockage or the formation of unwanted precipitates in other areas of the product development process. Considering differences in geography, climatic conditions, and water sources, the annual average tap water temperature in the United States of America varies from 7 °C to 22 °C.58,59 Laundering at these colder temperatures with concentrated products will have significant economic and environmental benefits. However, before that is feasible, it is critical to better understand the impacts of crystallization in concentrated surfactant solutions as well as the factors that can help control and tune crystallization.
The goal of the present experimental study was to develop low-temperature structure–property-processing-performance relationships for lamellar structured concentrated sodium lauryl ether sulfate (SLES) solutions. The impacts of three key processing variables – temperature, time, and applied shear forces – were investigated. For this study, three temperature zones were evaluated: (1) low temperature, <15 °C; (2) room temperature, 15 °C < 40 °C; and (3) high temperature, 40 °C to 90 °C. To characterize the flow behavior, shear, and oscillatory rheometry tests were carried out. The microstructure evolution was investigated by polarized optical microscopy and small angle X-ray scattering (SAXS) measurements in conjunction with temperature ramps. The structure–property-processing relationships identified by this work for anionic surfactants can better enable the sustainable design and manufacturing of low-water concentrated cleaning products with the desired performance.
Experimental section
Materials
A concentrated surfactant solution with anionic 70 wt% sodium lauryl ether sulfate (SLES) in water (STEOL® CS-170 UB, Stepan Company) was used as received. It has an average hydrophobic chain length of 12 carbon (C) atoms, a range of C10–C16, and a single ethoxy group.Rheometry
All rheometry experiments were performed on an Anton Paar Modular Compact Rheometer (MCR 702) configured with a CC10 concentric cylinder fixture (bob diameter = 10.0 mm, bob length = 14.9 mm, measurement gap = 0.422 mm) with Peltier temperature control. The concentric cylinder geometry was chosen to minimize water evaporation. The samples were examined using shear and small amplitude oscillatory shear (SAOS) protocols and new specimens from the same surfactant solution batch were used for all experiments. To ensure that all samples had as close to an identical shear history as possible, they were pre-sheared at 5 s−1 for 1 min and rested for 2 min. The magnitude of applied oscillations (strain amplitude, γ0 = 0.1% and angular frequency, ω = 10 rad s−1) was kept within the sample's linear viscoelastic range (LVER) at all studied temperatures (Fig. S1, ESI†). Unless specified otherwise, the temperature was changed at 1 °C min−1, with an uncertainty of ± 0.1 °C.A cycle of forward (0.001–100 s−1) and backward (100–0.001 s−1) rate-controlled flow sweep experiments were performed (7 s per point, 20 points per decade). Data from the second forward shear rate ramp is presented (Fig. S2, ESI†). To investigate thermal history effects, starting temperatures for oscillatory temperature ramps were varied from 5 °C to 25 °C. Following the heating ramp, samples were cooled from 35 °C back to the starting temperature. To investigate cooling rate effects, quiescent cooling rates varied from 5 °C min−1 to 0.5 °C min−1, and samples were cooled from 20 °C to 10 °C. In a separate thermal aging study, samples were held at constant temperatures for 20 min. The hold temperature varied from 20 °C to 5 °C and the effect of small oscillations was investigated. All experiments were carried out in triplicate.
Small angle X-ray scattering (SAXS)
Scattering experiments were performed using an Anton Paar SAXSPOINT 2.0 with a Cu-α source. Samples were placed in the PasteCell N sample holder inside of the thermally controlled TCStage 150. Samples were cooled from 20 °C to 5 °C at 0.5 °C min−1 with a thermal equilibration time of 3 minutes. At each temperature of interest, three, 1-minute, 2-dimensional frames were recorded using an Eiger X-ray detector at a sample-detector distance of 575 mm. The three scattering frames were averaged, the shadow of the beam stop was removed, and then integrated using a pie radial integration with a radius of 4 mm, an angle of 60°, and aligned with the positive y-axis.Dynamic scanning calorimetry (DSC)
All experiments were performed using a TA Instruments Q2000 DSC and hermetically sealed Tzero aluminum pans and lids. Temperature was changed at a rate of 1 °C min−1 and the temperature range compliments the corresponding rheometry experiments.Cross-polarized optical microscopy
Cross-polarized images were captured using a Keyence VHX-F series microscope equipped with a Dual-Objective VH-ZST Zoom Lens (magnification range 20× to 2000×) with polarizers. For in-situ temperature ramping, a digitally controlled Linkam Peltier stage was mounted on the microscope. The initial and end temperatures, as well as the ramp speeds, were pre-programmed. Small volumes (∼0.2 mL) of sample were carefully put on a glass slide, followed by a cover slip.Data analysis
Experimental data was fitted to theoretical models using Origin 2022 (OriginLab)Results and discussion
Fig. 1 shows the temperature-dependent microstructure evolution and Fig. 2 displays the shear-dependent flow behavior of the concentrated SLES solution maintained at various temperatures. At 5 °C (Fig. 1(a)), the lamellar Lα structure (the liquid crystalline bilayer phase with non-tilted sheets and disordered hydrocarbon chains60) was accompanied by opaque crystalline domains that interacted differently with light.61,62 At room temperature (20 °C) and 35 °C, oily streaks and multilamellar vesicles (MLVs) could be seen (Fig. 1(b) and (c)) which were indicative of the Lα structure.16 While it is beyond the practical scope of this study, at the highest investigated temperature (90 °C), focal conic defects (FCDs) were seen within the lamellar structure. Fig. 1(d) shows FCDs that formed between the oily streaks and Fig. 1(e) and (f) are zoomed-in micrographs. Color variation in the polarized optical microscopy images was orientation-dependent and could be analyzed using a Michel-Levy interference chart.63 However, the quantification of interference colors in these relatively thick (0.1 mm) samples was complex and beyond the scope of this study. | ||
| Fig. 2 Flow curves at different temperatures. Samples were loaded into the fixture at 20 °C, cycled to the predetermined temperature with applied oscillations, and rested for 2 min before shearing. Corresponding Herschel–Bulkley76,77 fits for shear stress vs. shear rate at low shear rates are shown in Fig. S3 (ESI†). | ||
As shown in Fig. 2, these solutions were shear thinning at all tested temperatures. The low temperature (5 °C and 10 °C) viscosities were significantly higher than the corresponding values at room temperature and high temperature. Interestingly, the flow behavior and viscosity at 20 °C, 35 °C, and 90 °C across the range of shear rates examined were very similar with slight deviations at the highest applied shear rates that were most likely due to shear-induced flow instabilities.23 The presence of significant flow instabilities in rotational experiments23 was a key driving factor for utilizing oscillatory tests in this study. The apparent viscosity of a polymer or surfactant solution typically will increase with decreasing temperature.64 Here, as temperature >0 °C, the aqueous component of the solutions was not expected to freeze. Thus, this high viscosity at low temperatures was attributed to a combination of normal viscosity-temperature behavior65,66 as well as a phase transformation (e.g., Fig. 1(a), the presence of opaque crystalline domains at 5 °C).
MLVs are a kind of surfactant aggregate that exhibit Maltese cross patterns (Fig. 1(b)) and are made up of many concentric layers of lamellar sheets rolled up like an “onion”.23,67,68 The effects of different flow conditions (Fig. 2) on the formation and rheological behavior of MLVs have been studied in the literature. Medronho et al. utilized deuterium rheo-NMR to study shear-induced lamellar bilayer to MLV transition in a non-ionic surfactant system.69,70 Sadtler et al.,71 Kosaka et al.,72 and Ito et al.73 investigated the temperature dependence of the same shear-induced transition. Kawabata et al. focused on deciphering the effects of interlamellar interactions on MLV formation.74 Diat et al.10,67,68 and Pommella et al.75 studied morphology and shear-thinning flow behavior of MLVs, consistent with results shown in Fig. 2.
FCDs are a common structural defect in lamellar phases (Fig. 1(d)–(f)) and the flow behavior of FCD rich lamellar phase is shown in Fig. 2. They were identified about a century ago by G. Friedel78 and have since been the topic of various studies. Apart from the fundamental papers by Friedel,78 Bragg,79 and Bouligand,80 studies by Honglawan et al.81 and Guo et al.82 developed methods to control the generation and morphology of FCDs. Currently, it is unclear whether FCDs in concentrated surfactant solutions are induced by temperature, shear, or a combination of the two, and additional investigations are necessary. Gharbi et al.83 and Ma et al.84 focused on leveraging the hierarchical architecture of FCDs for the development of advanced functional materials. Further, Fujii et al. explored relationships between defect structures in lamellar phases85 and observed similarities between the rheological behavior of FCDs and MLVs.86 This is consistent with the similar flow behaviors at 20 °C and 90 °C shown in Fig. 2.
To gain insight into the temperature range of crystallization and the resulting high viscosity at low temperatures, SAXS experiments were performed, and the results displayed in Fig. 3. At 20 °C, the Lα lamellar phase was evident following the characteristic 1, 2 … q* peak pattern.87 At 20 °C the primary q* peak occurred at 1.55 nm−1 and a secondary peak at 3.06 nm−1. The location of the primary peak corresponded to a lamellar periodicity spacing of 4.08 nm.23 Due to the similarities in scattering patterns, it was clear that the Lα phase's temperature region extended from greater than 20 °C down to 10 °C.87 Within this region there was an increase in the lamellar periodicity spacing from the 4.08 nm at 20 °C to 4.20 nm at 10 °C. At 7.5 °C and below the original second peak became unidentifiable from the background. Interestingly, the primary peak exhibited severe convolution at 7.5 °C with a large broadening of the scattering ring before complete separation of the ring at 5 °C indicative of a more complicated morphology.88 SAXS studies on comparable length cetostearyl alcohols have exhibited similar peak broadening at low temperature prior to complex crystallization.88 The possibility of the observed behavior having been ice crystallization can be disregarded due to the location of primary scattering intensity differing from that of both Cubic (Ic) and Hexagonal (Ih) ice crystals, both occurring at ∼1.07 nm−1.89 However, the lowest q, highest intensity peak varied from 1.547 nm−1 at 20 °C to 1.292 nm−1 at 5 °C, significantly different from the classic ice peak.89
 | ||
| Fig. 3 SAXS patterns as the solution was cooled from 20 °C to 5 °C at 0.5 °C min−1 with an equilibration time of 3 minutes. | ||
Complementary rheometry, calorimetry and polarized optical imaging experiments were performed (Fig. 4) to obtain further insight into the crystallization temperature range, microstructure evolution with cooling, and the rheological behavior. As the specimens were cooled, the growth of an opaque crystalline front was observed (Fig. 4(a)–(f)). In Fig. 4(h), cooling from 20 °C showed crystallization beginning at 7.8 °C and a slow corresponding complex viscosity increase below 15 °C (Fig. 4(g)) – the complex viscosity at 5 °C was 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 Pa s. The subsequent heating ramp from 5 °C displayed a melting between 5.7 °C and 11 °C (Fig. 4(h)) and a gradual decrease in complex viscosity (152 Pa s) up to 25 °C (Fig. 4(g)). The range of melting and crystallization temperatures (i.e., broad peaks) in the DSC data was most likely due to the different tail lengths (C10–C16) in the as-received SLES solution. Interestingly, the complex viscosity changes in Fig. 4(g) provided an earlier indication of crystallization and a lagging indicator of melting - at warmer temperatures before the actual crystallization/melting transitions were observed in the DSC data in Fig. 4(h).
610 Pa s. The subsequent heating ramp from 5 °C displayed a melting between 5.7 °C and 11 °C (Fig. 4(h)) and a gradual decrease in complex viscosity (152 Pa s) up to 25 °C (Fig. 4(g)). The range of melting and crystallization temperatures (i.e., broad peaks) in the DSC data was most likely due to the different tail lengths (C10–C16) in the as-received SLES solution. Interestingly, the complex viscosity changes in Fig. 4(g) provided an earlier indication of crystallization and a lagging indicator of melting - at warmer temperatures before the actual crystallization/melting transitions were observed in the DSC data in Fig. 4(h).
Significant hysteresis in complex viscosity between the cooling ramp from 20 °C to 5 °C and the subsequent heating ramp from 5 °C to 35 °C was also observed in Fig. 4(g). For example, the viscosity difference between the cooling and heating ramps at 10 °C was nearly 5 × 104 Pa s. This hysteresis indicated the influence of thermal history on complex viscosity. To investigate this further, the solution's complex viscosity response during temperature ramps was determined for different starting temperatures (Fig. 5).
 | ||
| Fig. 5 Effect of starting temperature. Samples at 20 °C were loaded into the fixture set to a pre-determined temperature, pre-sheared and rested before the temperature sweep. The samples were heated up to 35 °C and immediately cooled back to the temperature of interest. The G′ and G′′ profiles for ramp starting at 10 °C are shown in Fig. S4 (ESI†). | ||
The complex viscosity was indeed influenced by the sample's thermal history. For example, the complex viscosity at 25 °C for a ramp starting at 5 °C was 170 Pa s – significantly higher than the corresponding complex viscosity values for ramps starting at higher temperatures: 90 Pa s and 52 Pa s for 10 °C and 15 °C starting temperatures, respectively. Fig. 5 also displays an unusual complex viscosity peak observed for the ramp started at 10 °C. When the ramp was started at 15 °C, 20 °C, and 25 °C, the complex viscosity of these solutions was relatively low and nearly constant, consistent with flow curve behavior in Fig. 2.
To better understand how the surfactant solutions were impacted by thermal processing history, complementary DSC experiments were performed at starting temperatures of 5 °C and 10 °C (Fig. 6(a) and (b)). When the temperature ramp was started at 5 °C (Fig. 6(a)), crystallization and melting peaks were observed between 5 °C and 9 °C, similar to the range in Fig. 4(h). Heating the specimen from 5 °C resulted in a melting transition peak at 7.8 °C and caused a slow decrease in complex viscosity until to 20 °C. Cooling resulted in crystallization beginning at 6.7 °C and a sharp increase in complex viscosity which was only partially captured in the experiment due to temperature range limitations. In an interesting contrast, for a temperature ramp beginning at 10 °C (Fig. 6(b)), there were no significant endothermic or exothermic peaks visible in the DSC data that corresponded to the complex viscosity peak observed from 10 °C to 25 °C.
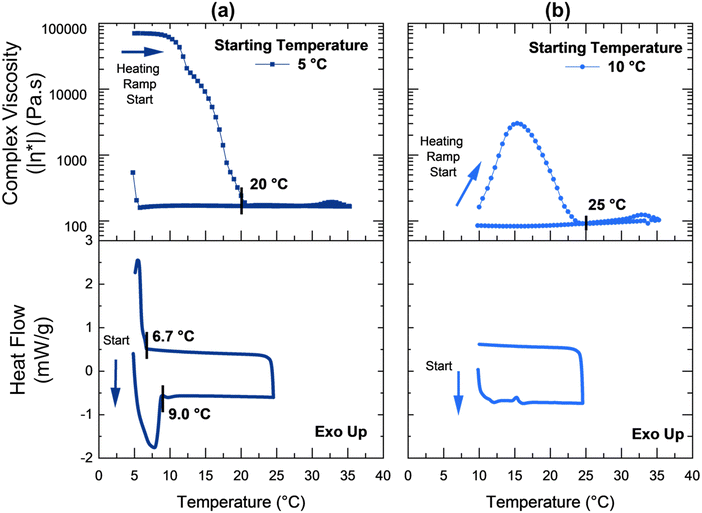 | ||
| Fig. 6 Oscillatory temperature ramps and complementary DSC data for ramps at different starting temperatures: (a) 5 °C, and (b) 10 °C. The temperature ramp rate was 1 °C min−1. | ||
The complex viscosity peak that results during heating from 10 °C (Fig. 5 and 6b) was hypothesized to be the result of applied oscillations promoting crystallization of the surfactant molecules at temperatures higher than the crystallization range determined by static DSC experiments (of 5 to 9 °C, Fig. 6(a)). During additional oscillation experiments, this peak was confirmed to exist in a narrow temperature range from 10 °C to 12.5 °C (Fig. S5, ESI†). This small temperature range was consistent with previous findings for some other dilute surfactant systems.90,91 There is a substantial body of research on the effect of applied shear forces on crystallization below the crystallization point in a wide range of complex fluids92,93 such as polymer melts,94,95 colloidal glasses,96,97 and multi-component surfactant systems.98,99 However, the literature on shear-driven crystallization in surfactant solutions above the crystallization temperature range is limited.100,101 Rathee et al. reported a reversible shear-induced crystallization in a cationic–anionic mixed ternary surfactant system. Rheo-optical tests were used to show that the pre-ordering of the isotropic bilayer mesophase102 in a shear-induced lamellar phase was a precursor to the nucleation of the crystalline phase.100
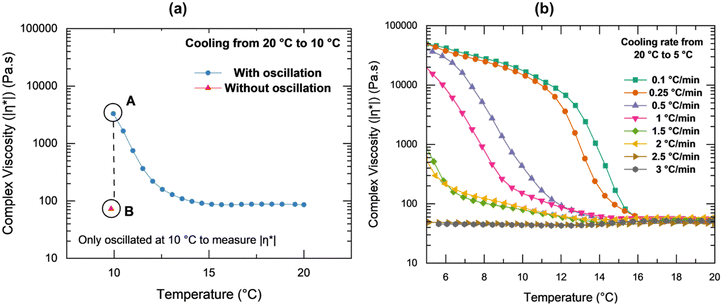
To further investigate the hypothesized occurrence of shear-induced crystallization, the data displayed in Fig. 7(a) depicts the specific influence of small applied oscillations on the solution's complex viscosity. Fig. 7(a) includes data from two different specimens: both cooled from 20 °C to 10 °C at 1 °C min−1, one with applied oscillations during cooling (blue circles) and the other was cooled without any applied oscillations (red triangle). At 10 °C, the complex viscosity for the sample oscillated during cooling was 3300 Pa s (point A) while the complex viscosity for the sample at rest during cooling was 73 Pa s (point B). Inspired by the theory of the metastable zone in the classical work of Nyvlt et al.,103 specimens were cooled at from 20 °C to 5 °C at cooling rates varying from 0.1 °C min−1 to 3 °C min−1 with small oscillations (Fig. 7(b)). Rates higher than 3 °C min−1, were too fast for the rheometer and it struggled to achieve a steady thermal state. At the slowest rates (0.1 °C min−1 and 0.25 °C min−1), the effects of shear on nucleation and growth were pronounced and visible significantly above the equilibrium crystallization temperature. The magnitude of complex viscosity at 10 °C for the higher cooling rates (2.5 °C min−1 and 3 °C min−1) was comparable to point B in Fig. 7(a) where no oscillations were applied while cooling. Thus, as the solution was cooled, while small oscillations within the linear viscoelastic regime affected the microstructure and acted to promote crystallization, this effect was dependent on the cooling rate.
Fig. 8 displays the effect of applied oscillations at a constant temperature. To decouple the effect of applied oscillations from temperature changes, specimens were loaded at 20 °C, cooled to a specified temperature and held there for 20 mins. At each corresponding temperature, Fig. 4 (a)–(f) are indicative of the microstructure before pre-shear, rest, and hold in Fig. 8. On an observable timescale, the complex viscosity plateaus reflect the maximum possible shear-induced crystallization, and the slopes of the curves before the plateau indicate the amount of time required to accomplish maximum crystallization. The time to reach the plateau is a function of temperature (samples at 12.5 °C and 15 °C have not reached a plateau after 1200 seconds).
 | ||
| Fig. 8 Thermal aging of specimens at pre-determined temperatures for 20 min. The specimens were cooled from 20 °C to a pre-determined temperature (e.g., 5 °C) at 0.5 °C min−1 without oscillation, pre-sheared, and rested before the aging experiment. G′ and G′′ profiles at selected temperatures are shown in Fig. S6 (ESI†). | ||
Applied oscillations enhanced crystallization at temperatures higher than the crystallization temperature range by primarily enhancing growth. The complex viscosity at t = 0 can be used as an indicator of the effect of the nucleation process. The small applied oscillations increase the rate of mass transfer of surfactant molecules to the crystal surface and promote growth. They can also cause collision breeding, further enhancing growth.103,104 This was seen clearly in the data sets at 7.5 °C, 10 °C, and 12.5 °C in Fig. 8. The increased complex viscosity was an indicator of increased shear-induced crystallization with time. At 5 °C, the temperature was at the lower end of the crystallization temperature range and the effect of oscillations was not as pronounced.
As shown in Fig. 9(a) and (c), strains within the LVER (0.01% and 0.1%) had the same influence on complex viscosity at temperatures where the solution was at equilibrium (20 °C – Lα lamellar phase and 5 °C – crystalline phase). The response is different at 10 °C because the surfactant solution is in a non-equilibrium transient state and small oscillations induce crystallization. The frequency dependence at all temperatures (Fig. 9(b), (d) and (f)) is rather more straightforward. The complex viscosity of the solution decreased as the frequency was increased, with a lower baseline complex viscosity at 20 °C. The shear-thinning nature of concentrated lamellar-structured SLES solution (Fig. 2) was posited to account for this behavior.
Having investigated the impacts of crystallization temperature range and applied oscillations, the effects of cooling time on rheological behavior were explored. The specimens were cooled from 20 °C to 10 °C at different rates without oscillations and the quiescent cooling time was found to impact the viscosity and microstructure. 10 °C was selected because a complex viscosity peak was previously observed when oscillations were initiated at this temperature (Fig. 5) and because it was higher than the crystallization range determined by static DSC experiments (Fig. 6). As shown in Fig. 10, the slowest cooling rate (0.5 °C min−1) resulted in a significant complex viscosity peak during the subsequent heating ramp with oscillations. The slower quiescent cooling rate essentially promoted the development of more crystal nucleation sites which subsequent oscillations then helped to grow. The faster cooling rates provided less time for ordered arrangements and nucleation sites to form at 10 °C and resulted in low complex viscosity peaks.103
 | ||
| Fig. 10 Effect of pre-ramp quiescent cooling rate on the viscosity during a temperature ramp. The specimens were cooled from 20 °C to 10 °C at different rates without oscillations and immediately heated up to 25 °C at 1 °C min−1 with oscillations. Effects of pre-ramp quiescent cooling rates on the microstructure are presented in Fig. S7 (ESI†). | ||
The observed complex viscosity peak can now be attributed to an interplay of three factors: shear-induced crystallization, cooling time, and temperature range. As seen in Fig. 5, if the solution was allowed to equilibrate to a low enough temperature that was close to the upper limit of the crystallization temperature range (e.g., 10 °C), the effect of applied oscillations dominated over the increasing temperature and promoted crystallization during a subsequent temperature ramp. This shear-induced crystallization manifested as an increase in complex viscosity. When the temperature was high enough, the temperature took precedence over oscillations, and the crystalline surfactant domains began to melt, resulting in a decrease in complex viscosity. Thus, the cold temperature rheological behavior of concentrated surfactant solutions was extremely sensitive to shear induced ordering of surfactant molecules.
Modelling and implications
The sigmoidal nature of isothermal shear-induced crystallization (Fig. 8) was analyzed using a modified five-parameter logistic (5PL) model (eqn (1)).105 Typically used to model immunoassays such as enzyme-linked immunosorbent assays (ELISA) and radioimmunoassay (RIA), the 5PL non-linear regression model builds on the four-parameter logistic model and incorporates an additional parameter (S) to characterize the curve asymmetry.106 | (1) |
 and
and  respectively are the complex viscosities at time (t) = 0 and infinity, tinflection is the time at which curvature changes direction (time at which
respectively are the complex viscosities at time (t) = 0 and infinity, tinflection is the time at which curvature changes direction (time at which  , h is the slope of the curves before the plateau and s is the asymmetry factor (when s = 1, the curve is symmetric). Corresponding 5PL fits are shown in Fig. S8 (ESI†). The inflection times increase with increasing temperature – ranging from 325 s at 5 °C to 8814 s at 15 °C. At 5 °C, the temperature is at the lower end of the equilibrium crystallization temperature and the inflection time represents the time required to complete the crystallization. The inflection time for the curve at 20 °C can be disregarded as there is no crystallization at 20 °C. The ratio,
, h is the slope of the curves before the plateau and s is the asymmetry factor (when s = 1, the curve is symmetric). Corresponding 5PL fits are shown in Fig. S8 (ESI†). The inflection times increase with increasing temperature – ranging from 325 s at 5 °C to 8814 s at 15 °C. At 5 °C, the temperature is at the lower end of the equilibrium crystallization temperature and the inflection time represents the time required to complete the crystallization. The inflection time for the curve at 20 °C can be disregarded as there is no crystallization at 20 °C. The ratio, 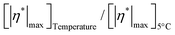 can be used to estimate the extent of crystallization.
can be used to estimate the extent of crystallization.
The temperature dependence of inflection times at 5 °C, 7.5 °C, 10 °C and 12.5 °C was described using an Arrhenius equation (eqn (2))107,108 and is shown in Fig. 11(a).
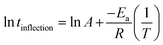 | (2) |
 | ||
| Fig. 11 (a) Arrhenius and (b) Avrami fit for isothermal crystallization with small oscillations. Fit parameters are tabulated in the Supplementary section (ESI†). | ||
Originally developed to model the extent of phase transitions, the Johnson–Mehl–Avrami–Kolmogorov (JMAK)110–112 formalization, commonly referred to as the Avrami equation (eqn (3)), was used to model the kinetics of isothermal crystallization (Fig. 11(b)).113
 | (3) |
Beyond laundry and personal care, controlled tailoring of microstructures in lamellar phases can have significant applications. For example, polymerizing lamellar phases, such as lyotropic liquid crystal (LLC) templating, has been shown to improve the mechanical and thermal properties of lamellar phases.114 Clapper et al. ordered macromolecules within a lamellar phase and developed nanostructured cross-linked biodegradable hydrogels with enhanced swelling and permeability.115 Bandegi et al. tuned the degree of LLC crystallinity to create ion gels with enhanced mechanical strength and ionic conductivity.116 Qavi et al. created antimicrobial membranes and ultrafiltration (UF) membranes with superior contamination resistance and water permeability compared to commercial UF membranes.117
Conclusions
In this experimental study, low-temperature structure–property relationships for concentrated SLES solutions were developed. At all temperatures and shear rates tested, these solutions were shear thinning (Fig. 2). The presence of crystals at low temperatures resulted in extremely high viscosity. Despite the presence of FCDs at high temperatures, the viscosity and rheological behavior at 20 °C and 90 °C were very similar. Room temperature viscosity was influenced by the thermal history (Fig. 5) and a crystallization temperature range was identified (Fig. 3 and 6). The peculiar viscosity peaks with increasing temperature were ascribed to a combination of cooling time, shear-induced crystallization, and temperature range. Temperature (Fig. 5), applied oscillations and cooling rates (Fig. 7–9), and quiescent cooling time (Fig. 10) are critical processing variables that directly impact the microstructure and rheological properties of concentrated surfactant solutions. Isothermal shear induced crystallization was modelled using a five-parameter logistic model and a relevant activation energy was estimated.The presence of crystals and the resulting high viscosity at low temperatures can make cold water laundry problematic. The concentrated product may take longer to dissolve in the washer, lengthening the load cycle and thereby increasing energy use. Oscillations during processing or transit can affect the appearance and performance of finished products. On one hand, oscillating pipelines can cause issues like uneven mixing, blockage, and drippage. On the other hand, if a precise amount of crystallization in a finished product is desired, it could be induced by vibrating the final package for a specific time.
The workflows developed herein for neat SLES solutions can be applied to study the phase evolution, microstructure, and flow behavior of systems with industrially relevant additives. Research into the impact of temperature, shear, and additives on the formation of MLVs and FCDs could provide valuable insights into defect mechanisms in lamellar bilayers. Techniques to control transitions of lamellar bilayers to specific proportions of sheets, MLVs, and FCDs, could be invaluable tools in the formulator's and process engineer's toolbox. Considering the recent sustainability efforts to develop concentrated products for low-temperature applications, knowledge of multiscale structure–property-processing relationships for industrially relevant systems is critical.
Author contributions
P. U. K.: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft; M. K.: formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing; R. D. C.: conceptualization, writing – review & editing; M. C.: conceptualization; S. L.: conceptualization, funding acquisition, resources, writing – review & editing; K. A. E.: conceptualization, data curation, funding acquisition, project administration, visualization, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
P. U. K. acknowledges support from the National Science Foundation (NSF) through GOALI Grant No. CBET-2112956. R. D. C. acknowledges support from the Lillian Gilbreth Postdoctoral Fellowship from Purdue University College of Engineering.References
- S. Liu, L. G. Papageorgiou and N. Shah, Comput. Ind. Eng., 2020, 139, 106189 CrossRef.
- J. B. Aguiar, A. M. Martins, C. Almeida, H. M. Ribeiro and J. Marto, Sustain. Prod. Consum., 2022, 32, 35–51 CrossRef.
- E. Saouter, G. van Hoof, C. A. Pittinger and T. C. J. Feijtel, Int. J. Life Cycle Assess., 2001, 6, 363–372 CrossRef CAS.
- A. Kapur, C. Baldwin, M. Swanson, N. Wilberforce, G. McClenachan and M. Rentschler, Int. J. Life Cycle Assess., 2012, 17, 377–387 CrossRef CAS.
- M. Giagnorio, A. Amelio, H. Grüttner and A. Tiraferri, J. Cleaner Prod., 2017, 154, 593–601 CrossRef.
- A. Koehler and C. Wildbolz, Environ. Sci. Technol., 2009, 43, 8643–8651 CrossRef CAS PubMed.
- The Cleaning Collective, The Benefits of Using Concentrated Cleaning Products, https://www.thecleaningcollective.co.uk/news/cleaning-tips/the-benefits-of-using-concentrated-cleaning-products, (accessed June 9, 2023).
- R. Rocca, F. Acerbi, L. Fumagalli and M. Taisch, Clean. Waste Syst., 2022, 3, 100057 CrossRef.
- A. Wicker, Could just-add-water products save us? https://www.vox.com/the-goods/2019/7/30/20727387/just-add-water-dehydrated-cleaning-beauty-environmental, (accessed June 9, 2023).
- D. Roux, F. Nallet and O. Diat, Europhys. Lett., 1993, 24, 53–58 CrossRef CAS.
- W. Richtering, Curr. Opin. Colloid Interface Sci., 2001, 6, 446–450 CrossRef CAS.
- M. G. Berni, C. J. Lawrence and D. Machin, Adv. Colloid Interface Sci., 2002, 98, 217–243 CrossRef CAS PubMed.
- L. Gentile, B. F. B. Silva, S. Lages, K. Mortensen, J. Kohlbrecher and U. Olsson, Soft Matter, 2013, 9, 1133–1140 RSC.
- E. F. Marques and B. F. B. Silva, in Encyclopedia of Colloid and Interface Science, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 1290–1333 Search PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525 RSC.
- F. B. Rosevear, J. Am. Oil Chem. Soc., 1954, 31, 628–639 CrossRef CAS.
- R. G. Laughlin, The Aqueous Phase Behavior of Surfactants, Academic Press, 1994 Search PubMed.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford Academic Press, 1998 Search PubMed.
- K. Holmberg, B. Jönsson, B. Kronberg and B. Lindman, Surfactants and Polymers in Aqueous Solution, John Wiley & Sons, Ltd., 2002 Search PubMed.
- A. Chattopadhyay and K. Mittal, Surfactants in Solution, CRC Press, 1996 Search PubMed.
- R. Zana, Dynamics of Surfactant Self-Assemblies, CRC Press, 1st edn, 2005 Search PubMed.
- P. A. Hassan, G. Verma and R. Ganguly, in Functional Materials, Elsevier, 2012, pp. 1–59 Search PubMed.
- E. A. Caicedo-Casso, J. E. Bice, L. R. Nielsen, J. L. Sargent, S. Lindberg and K. A. Erk, Rheol. Acta, 2019, 58, 467–482 CrossRef CAS.
- M. Wlodzimierz Sulek and A. Bak, Int. J. Mol. Sci., 2010, 11, 189–205 CrossRef PubMed.
- S. Paasch, F. Schambil and M. J. Schwuger, Langmuir, 1989, 5, 1344–1346 CrossRef CAS.
- O. Robles-Vásquez, S. Corona-Galván, J. F. A. Soltero, J. E. Puig, S. B. Tripodi, E. Vallés and O. Manero, J. Colloid Interface Sci., 1993, 160, 65–71 CrossRef.
- P. Mongondry, C. W. Macosko and T. Moaddel, Rheol. Acta, 2006, 45, 891–898 CrossRef CAS.
- L. Gentile, M. A. Behrens, S. Balog, K. Mortensen, G. A. Ranieri and U. Olsson, J. Phys. Chem. B, 2014, 118, 3622–3629 CrossRef CAS PubMed.
- Y. Suganuma, M. Imai, T. Kato, U. Olsson and T. Takahashi, Langmuir, 2010, 26, 7988–7995 CrossRef CAS PubMed.
- L. Gentile, M. A. Behrens, L. Porcar, P. Butler, N. J. Wagner and U. Olsson, Langmuir, 2014, 30, 8316–8325 CrossRef CAS PubMed.
- L. Veronico and L. Gentile, ACS Appl. Nano Mater., 2023, 6, 720–728 CrossRef CAS.
- R. G. Larson, Rheol Acta, 1992, 31, 213–263 CrossRef CAS.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed.
- R. L. Hendrikse, A. E. Bayly, P. K. Jimack and X. Lai, J. Phys. Chem. B, 2023, 127, 4676–4686 CrossRef CAS PubMed.
- R. Ferraro and S. Caserta, Rheol. Acta, 2023, 62, 365–375 CrossRef CAS.
- A. Talmon and E. Meshkati, Slurry Technology – New Advances, IntechOpen, 2022 Search PubMed.
- E. Thomasson and B. Lewis, A hard sell? Companies struggle to promote green consumption, https://www.reuters.com/article/us-climatechange-summit-consumers/a-hard-sell-companies-struggle-to-promote-green-consumption-idUKKBN0TQ23M20151207, (accessed June 4, 2023).
- Procter & Gamble, Leading detergent brands to European consumers: Wash cold, https://www.politico.eu/sponsored-content/leading-detergent-brands-to-european-consumers-wash-cold/, (accessed June 4, 2023).
- L. Golsteijn, R. Menkveld, H. King, C. Schneider, D. Schowanek and S. Nissen, Environ. Sci. Eur., 2015, 27, 23 CrossRef PubMed.
- Association of Issuing Bodies, European Residual Mixes – Results of the calculation of Residual Mixes for the calendar year 2020, 2021.
- E. Saouter and G. van Hoof, Int. J. Life Cycle Assess., 2002, 7, 103–114 CrossRef CAS.
- Electrolux, The Truth About Laundry, https://www.electroluxgroup.com/en/electrolux-study-reveals-current-laundry-practices-out-of-step-with-climate-concerns-32373/, (accessed June 9, 2023).
- S. J. Kenway, R. Scheidegger, T. A. Larsen, P. Lant and H.-P. Bader, Energy Build., 2013, 58, 378–389 CrossRef.
- S. J. Kenway, A. Binks, R. Scheidegger, H.-P. Bader, F. Pamminger, P. Lant and T. Taimre, Energy Build., 2016, 131, 21–34 CrossRef.
- J. Boucher and D. Friot, Primary microplastics in the oceans: A global evaluation of sources, IUCN International Union for Conservation of Nature, 2017.
- I. E. Napper and R. C. Thompson, Mar. Pollut. Bull., 2016, 112, 39–45 CrossRef CAS PubMed.
- L. Tiffin, A. Hazlehurst, M. Sumner and M. Taylor, J. Text. Inst., 2022, 113, 558–566 CrossRef CAS.
- T. Hoellein, M. Rojas, A. Pink, J. Gasior and J. Kelly, PLoS One, 2014, 9, e98485 CrossRef PubMed.
- M. Eriksen, S. Mason, S. Wilson, C. Box, A. Zellers, W. Edwards, H. Farley and S. Amato, Mar. Pollut. Bull., 2013, 77, 177–182 CrossRef CAS PubMed.
- R. C. Thompson, Y. Olsen, R. P. Mitchell, A. Davis, S. J. Rowland, A. W. G. John, D. McGonigle and A. E. Russell, Science, 1979, 2004(304), 838 CrossRef PubMed.
- G. L. Lattin, C. J. Moore, A. F. Zellers, S. L. Moore and S. B. Weisberg, Mar. Pollut. Bull., 2004, 49, 291–294 CrossRef CAS PubMed.
- R. Z. Miller, A. J. R. Watts, B. O. Winslow, T. S. Galloway and A. P. W. Barrows, Mar. Pollut. Bull., 2017, 124, 245–251 CrossRef CAS PubMed.
- N. J. Lant, A. S. Hayward, M. M. D. Peththawadu, K. J. Sheridan and J. R. Dean, PLoS One, 2020, 15, e0233332 CrossRef CAS PubMed.
- L. Cotton, A. S. Hayward, N. J. Lant and R. S. Blackburn, Dyes Pigm., 2020, 177, 108120 CrossRef CAS.
- L. A. Smith, A. Duncan, G. B. Thomson, K. J. Roberts, D. Machin and G. McLeod, J. Cryst. Growth, 2004, 263, 480–490 CrossRef CAS.
- L. A. Smith, K. J. Roberts, D. Machin and G. McLeod, J. Cryst. Growth, 2001, 226, 158–167 CrossRef CAS.
- S. M. Mawazi, J. Ann, N. Othman, J. Khan, S. O. Alolayan, S. S. Al Thagfan and M. Kaleemullah, Cosmetics, 2022, 9, 61 CrossRef CAS.
- L. A. C. Steele Alfred, Engineered Plumbing Design II, 2004 Search PubMed.
- K.-F. S. Rosen Marc, Cogeneration and District Energy Systems – Modeling, Analysis and Optimization, 2016 Search PubMed.
- M. Kranenburg and B. Smit, J. Phys. Chem. B, 2005, 109, 6553–6563 CrossRef CAS PubMed.
- P. T. Spicer and R. W. Hartel, Aust. J. Chem., 2005, 58, 655–659 CrossRef CAS.
- N. Zhang, A. Xu, B. Liu, N. Godbert and H. Li, ChemPhysMater, 2023, 2, 134–140 CrossRef.
- B. E. Sørensen, Eur. J. Mineral., 2013, 25, 5–10 CrossRef.
- H. H. Nouri and P. J. Root, in All Days, SPE, 1971.
- J. Wang and R. S. Porter, Rheol. Acta, 1995, 34, 496–503 CrossRef CAS.
- C. J. Seeton, Tribol. Lett., 2006, 22, 67–78 CrossRef CAS.
- O. Diat and D. Roux, J. Phys. II, 1993, 3, 9–14 CrossRef CAS.
- O. Diat, D. Roux and F. Nallet, J. Phys. II, 1993, 3, 1427–1452 CrossRef CAS.
- B. Medronho, S. Shafaei, R. Szopko, M. G. Miguel, U. Olsson and C. Schmidt, Langmuir, 2008, 24, 6480–6486 CrossRef CAS PubMed.
- B. Medronho, M. Rodrigues, M. G. Miguel, U. Olsson and C. Schmidt, Langmuir, 2010, 26, 11304–11313 CrossRef CAS PubMed.
- V. M. Sadtler, M. Guely, P. Marchal and L. Choplin, J. Colloid Interface Sci., 2004, 270, 270–275 CrossRef CAS PubMed.
- Y. Kosaka, M. Ito, Y. Kawabata and T. Kato, Langmuir, 2010, 26, 3835–3842 CrossRef CAS PubMed.
- M. Ito, Y. Kosaka, Y. Kawabata and T. Kato, Langmuir, 2011, 27, 7400–7409 CrossRef CAS PubMed.
- Y. Kawabata, R. Bradbury, S. Kugizaki, K. Weigandt, Y. B. Melnichenko, K. Sadakane, N. L. Yamada, H. Endo, M. Nagao and H. Seto, J. Chem. Phys., 2017, 147, 034905 CrossRef CAS PubMed.
- A. Pommella, S. Caserta, V. Guida and S. Guido, Phys. Rev. Lett., 2012, 108, 138301 CrossRef PubMed.
- W. H. Herschel and R. Bulkley, Kolloid-Z., 1926, 39, 291–300 CrossRef.
- T. Divoux, C. Barentin and S. Manneville, Soft Matter, 2011, 7, 8409 RSC.
- F. Grandjean and G. Friedel, Bull. Mineral., 1910, 409–465 Search PubMed.
- W. Bragg, Trans. Faraday Soc., 1933, 29, 1056–1060 RSC.
- Y. Bouligand, J. Phys. France, 1972, 33, 525–547 CrossRef.
- A. Honglawan, D. A. Beller, M. Cavallaro, R. D. Kamien, K. J. Stebe and S. Yang, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 34–39 CrossRef CAS PubMed.
- W. Guo, S. Herminghaus and C. Bahr, Langmuir, 2008, 24, 8174–8180 CrossRef CAS PubMed.
- M. A. Gharbi, I. B. Liu, Y. Luo, F. Serra, N. D. Bade, H.-N. Kim, Y. Xia, R. D. Kamien, S. Yang and K. J. Stebe, Langmuir, 2015, 31, 11135–11142 CrossRef CAS PubMed.
- L.-L. Ma, M.-J. Tang, W. Hu, Z.-Q. Cui, S.-J. Ge, P. Chen, L.-J. Chen, H. Qian, L.-F. Chi and Y.-Q. Lu, Adv. Mater., 2017, 29, 1606671 CrossRef PubMed.
- S. Fujii, Nano/Micro Science and Technology in Biorheology, Springer, Japan, Tokyo, 2015, pp. 77–97 Search PubMed.
- S. Fujii, S. Komura and C.-Y. Lu, Materials, 2014, 7, 5146–5168 CrossRef CAS PubMed.
- P. Alexandridis, U. Olsson and B. Lindman, Langmuir, 1998, 14, 2627–2638 CrossRef CAS.
- W. Karl, R. Perla, C. Gérard, C. Franck, N.-M. Luc, B. Hayat and F. Denis, J. Therm. Anal. Calorim., 2016, 123, 1411–1417 CrossRef CAS.
- J. C. F. Michielsen, J. Dings and J. van der Elsken, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 4068–4071 CrossRef CAS PubMed.
- D. Constantin, É. Freyssingeas, J.-F. Palierne and P. Ostwald, Langmuir, 2003, 19, 2554–2559 CrossRef CAS.
- G. C. Kalur, B. D. Frounfelker, B. H. Cipriano, A. I. Norman and S. R. Raghavan, Langmuir, 2005, 21, 10998–11004 CrossRef CAS PubMed.
- A. Ya Malkin and V. G. Kulichikhin, Appl. Rheol., 2015, 25, 40–53 Search PubMed.
- A. Ya Malkin, Adv. Colloid Interface Sci., 2021, 290, 102381 CrossRef PubMed.
- L. Li and W. H. de Jeu, Phys. Rev. Lett., 2004, 92, 075506 CrossRef PubMed.
- L. Li, D. Lambreva and W. H. de Jeu, J. Macromol. Sci., Part B: Phys., 2004, 43, 59–70 CrossRef.
- Y. L. Wu, D. Derks, A. van Blaaderen and A. Imhof, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10564–10569 CrossRef CAS PubMed.
- L. T. Shereda, R. G. Larson and M. J. Solomon, Phys. Rev. Lett., 2010, 105, 228302 CrossRef PubMed.
- G. Mazzanti, A. G. Marangoni and S. H. J. Idziak, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 041607 CrossRef PubMed.
- G. Mazzanti, S. E. Guthrie, A. G. Marangoni and S. H. J. Idziak, Cryst. Growth Des., 2007, 7, 1230–1241 CrossRef CAS.
- V. Rathee, R. Krishnaswamy, A. Pal, V. A. Raghunathan, M. Impéror-Clerc, B. Pansu and A. K. Sood, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 14849–14854 CrossRef CAS PubMed.
- P. K. Bera, V. Rathee, R. Krishnaswamy and A. K. Sood, Langmuir, 2021, 37, 6874–6886 CrossRef CAS PubMed.
- A. Pal, G. Pabst and V. A. Raghunathan, Soft Matter, 2012, 8, 9069 RSC.
- J. Nyvlt, O. Sohnel, M. Matuchova and M. Broul, The Kinetics of industrial crystallization, Elsevier, Amsterdam, 1985 Search PubMed.
- R. E. A. Mason and R. F. Strickland-Constable, Trans. Faraday Soc., 1966, 62, 455 RSC.
- P. G. Gottschalk and J. R. Dunn, Anal. Biochem., 2005, 343, 54–65 CrossRef CAS PubMed.
- J. J. Z. Liao and R. Liu, J. Chemom., 2009, 23, 248–253 CrossRef CAS.
- S. Arrhenius, Z. Phys. Chem., Stoechiom. Verwandtschaftsl., 1889, 4, 226–248 CrossRef.
- M. Peleg, Crit. Rev. Food Sci. Nutr., 2018, 58, 2663–2672 CrossRef PubMed.
- R. M. Miller, A. S. Poulos, E. S. J. Robles, N. J. Brooks, O. Ces and J. T. Cabral, Cryst. Growth Des., 2016, 16, 3379–3388 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- K. Shirzad and C. Viney, J. R. Soc., Interface, 2023, 20(203) DOI:10.1098/rsif.2023.0242.
- Y. Saadat, O. Q. Imran, C. O. Osuji and R. Foudazi, J. Mater. Chem. A, 2021, 9, 21607–21658 RSC.
- J. D. Clapper, S. L. Iverson and C. A. Guymon, Biomacromolecules, 2007, 8, 2104–2111 CrossRef CAS PubMed.
- A. Bandegi, J. L. Bañuelos and R. Foudazi, Soft Matter, 2020, 16, 6102–6114 RSC.
- S. Qavi, A. P. Lindsay, M. A. Firestone and R. Foudazi, J. Membr. Sci., 2019, 580, 125–133 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Amplitude sweeps at different temperatures, shear stress vs. shear rate data at low shear rates with Herschel–Bulkley fits, temperature range for complex viscosity peak, G′ and G′′ for selected temperature ramps, cross-polarized micrographs showing the effect of pre-oscillation quiescent cooling rate, 5 parameter logistic and avrami fits for isothermal shear-induced crystallization. See DOI: https://doi.org/10.1039/d3sm01198d |
| This journal is © The Royal Society of Chemistry 2024 |