Open Access Article
Open Access ArticleEffect of non-linear strain stiffening in eDAH and unjamming†
Xiaofan
Xie
 a,
Frank
Sauer
a,
Frank
Sauer
 a,
Steffen
Grosser
a,
Steffen
Grosser
 a,
Jürgen
Lippoldt
a,
Jürgen
Lippoldt
 a,
Enrico
Warmt
a,
Enrico
Warmt
 a,
Amit
Das
a,
Amit
Das
 b,
Dapeng
Bi
b,
Dapeng
Bi
 b,
Thomas
Fuhs
b,
Thomas
Fuhs
 a and
Josef A.
Käs
a and
Josef A.
Käs
 *a
*a
aSoft Matter Physics Division, Peter Debye Institute for Soft Matter Physics, University of Leipzig, Germany. E-mail: jkaes@uni-leipzig.de; Tel: +49 341 1248944
bDepartment of Physics, Northeastern University, Boston, MA 02115, USA
First published on 5th January 2024
Abstract
In cell clusters, the prominent factors at play encompass contractility-based enhanced tissue surface tension and cell unjamming transition. The former effect pertains to the boundary effect, while the latter constitutes a bulk effect. Both effects share outcomes of inducing significant elongation in cells. This elongation is so substantial that it surpasses the limits of linear elasticity, thereby giving rise to additional effects. To investigate these effects, we employ atomic force microscopy (AFM) to analyze how the mechanical properties of individual cells change under such considerable elongation. Our selection of cell lines includes MCF-10A, chosen for its pronounced demonstration of the extended differential adhesion hypothesis (eDAH), and MDA-MB-436, selected due to its manifestation of cell unjamming behavior. In the AFM analyses, we observe a common trend in both cases: as elongation increases, both cell lines exhibit strain stiffening. Notably, this effect is more prominent in MCF-10A compared to MDA-MB-436. Subsequently, we employ AFM on a dynamic range of 1–200 Hz to probe the mechanical characteristics of cell spheroids, focusing on both surface and bulk mechanics. Our findings align with the results from single cell investigations. Specifically, MCF-10A cells, characterized by strong contractile tissue tension, exhibit the greatest stiffness on their surface. Conversely, MDA-MB-436 cells, which experience significant elongation, showcase their highest stiffness within the bulk region. Consequently, the concept of single cell strain stiffening emerges as a crucial element in understanding the mechanics of multicellular spheroids (MCSs), even in the case of MDA-MB-436 cells, which are comparatively softer in nature.
1 Introduction
We have recently done extensive work on the contribution of cell contractility to tissue surface tension, as well as on shape-induced unjamming.1–4 Despite being two fundamentally distinct effects, our studies have demonstrated their significant mechanical impact on tissues. Both effects come with a common secondary effect: highly deformed elongated cells and nuclei. The deformation is so strong that we leave the linear regime, resulting in the strain stiffening of cells. This effect, previously overlooked in research, must be considered as we investigate the mechanical behavior of multicellular spheroids (MCSs). While it is not surprising that the contractility-based tissue surface tension leads to elongated cells on the outside and strain stiffening results in a stiffer shell, the surprising aspect is observed in unjamming. Here, strain stiffening leads to the highest mechanical resistance of an unjammed fluid phase. In our study, we used AFM measurements on cells adhering to glass, although not directly linked to the collective behavior of tissues, it is a clear demonstration of cell stiffening correlated with highly elongated nuclei. We use this foundation to illustrate the effect in spheroids, where we observe strongly deformed elongated cells on the surface of MCF-10A MCSs and in the bulk of MDA-MB 436 MCSs, indicating a higher mechanical resistance of tissues.Jamming describes a rigidity transition caused by mutual steric hindrance5 and it is crucial for the homeostasis of healthy epithelial tissues.2,6–11 It is also relevant for the pathologic mechanical changes in tumor tissue that are quintessential for cancer progression.12,13 From previous studies, we know that there are two collective cellular states of matter in solid tumors: an amorphous glass-like state with characteristics of 3D cell jamming, and a disordered fluid state.4 In primary solid tumors, cancer cells are mainly confined in cell clusters surrounded by stroma. In these clusters, solid regions of jammed round cancer cells are embedded in a fluid sea of elongated motile cancer cells. Cancer cell unjamming enables the cells to leave the clusters and thereby fosters distant metastasis.14,15 In 3D cell spheroids, cancerous mesenchymal cells tend to elongate, and the changes in cell and nuclear shape correlate with an increase of tissue fluidity, whereas round healthy epithelial cells show a solid-like collective behavior. From this, it has been inferred that cell unjamming regulates the fluid or solid bulk mechanics of tissues.16,17 Shifting from a larger fraction of unjammed, motile cells to more jammed, immobile cells, the system moves from more fluid-like to more solid-like behavior.4 However, the characteristic time of fluidization by shape-induced unjamming is on the order of several hours. Here, we probe the short-term mechanical behavior by atomic force microscopy (AFM), which has been previously ignored.
MCSs are held together by cell–cell adhesion. According to the differential adhesion hypothesis (DAH), this causes a TST (tissue surface tension) that stabilizes the MCS boundary.18 However, since the DAH does not consider cell jamming, it failed to correctly predict the behavior that we observed in MCSs.2 More recently, we have shown that collective cell contractility can significantly contribute to the TST described by the extended differential adhesion hypothesis (eDAH).19 Epithelial cells show a contractility based on the actin cortex1,20–28 and form a collective contractile cortex surrounding MCSs which leads to a strong TST. This is particularly noteworthy since the MCSs from epithelial cells are in a jammed state and classical mechanisms to generate a surface tension do not work in a solid. The collective cortex around the MCSs strongly contracts to generate the TST and strongly stretches the cells at the MCS surface.
We have chosen a MCS as our model system, which is reproducible and suited for quantitative measurements, to systematically investigate how strongly the deformation of cells on its own changes the mechanical properties in contractility-based TST and shape-induced cell unjamming, and how the two collective behaviors impact the mechanical behavior of cell clusters in biological tissue. The basic principle of producing MCSs is to lower the adhesion between the cells and the substrate of the cell culture dish, allowing cells to self-assemble into a spheroid to minimize surface tension. MCSs are the most common in vitro 3D analogs to examine cellular tissues.29 MCSs capture some of the essential features of cell clusters in physiological tissue (e.g., 3D structure and cell–cell interactions), while they do not typically capture more complex interactions of cells with the microenvironment such as interactions with fibrotic stroma or vascularization.30–37 Even as a rather simple model for tissues, the MCS already shows a complex, emergent rheological behavior.4 Here, we investigate the short-term mechanical behavior by AFM. We particularly focus on cell jamming (solid) versus unjamming (fluid) as well as on epithelial versus mesenchymal contractility. We have chosen spheroids made from healthy epithelial MCF-10A and cancerous mesenchymal MDA-MB-436 cells as representatives of solid, jammed and fluid, unjammed MCSs, respectively.4 Moreover, MCF-10A cells form a strong collective contractile cortex, which is not the case for MDA-MB-436 cells.1
To understand the mechanical response of the MCS to AFM indentation, we split our investigations into measurements with small indentations (i.e., small forces) targeting the surface-tension-like effects stemming from the outermost layer(s) of cells and those with large indentations (i.e., large forces) probing the core of the spheroid. At the corresponding loading forces of 5 nN for small indentations and 100 nN for large indentations, we used superimposed sinusoidal oscillations with an amplitude of 15 nm over a wide frequency range (1–200 Hz) to capture the viscoelastic behavior of the spheroids.38–40 A modified Hertz model provides the real and imaginary parts of the complex shear modulus, describing the elastic energy stored and the viscous energy dissipated within the cell at different oscillatory frequencies.41 Although by AFM we cannot directly access the ultra-low frequency range that is relevant to fluidization by cell unjamming, we have addressed long time responses previously.4 For unjamming, cells must maintain a fluid and elongated state throughout the fusion of spheroids,4 which means the stiffening effect is present all the time. Similarly, for the contractility-based tissue surface tension effect, the contractile ring persists as long as it is formed.1 In this case, although we focus on the short time scale stiffness behavior, the strain stiffening will always be there as long as the deformation does not relax and thus can be correlated with long-time scale effects such as unjamming and eDAH. Furthermore, we employed the fractional element (FE) model42 to reduce the frequency-resolved data to two fundamental parameters μ and α of power-law rheology. These parameters describe the elasticity and fluidity of the tissue, respectively.43–47
In agreement with previous results, we describe the mechanics of cells and cellular tissues by a power law behavior.48 The power-law scaling is rooted in the underlying cellular cytoskeleton of single cells that can be described by an extended soft glassy rheological behavior over a broad range of timescale.49 The cytoskeleton also significantly contributes to the stiffening at larger strains.50–52 Moreover, active actomyosin-based contractility significantly contributes to cell and tissue mechanics.20,21,53 Contractility can be generated by actin stress fibers21,54 and the acto-myosin based cell cortex.55–58 Actin stress fibers are contractile actin bundles, which form a highly regulated acto-myosin structure prevalent within mesenchymal cells,1,59,60 whereas the acto-myosin cell cortex directly underlying the plasma membrane dominates in epithelial cells.58,61
Here, we characterize in MCSs the mechanical role of strongly deformed cells required for shape-induced cell unjamming and TST generated by cell contractility. For both collective effects, strong cell deformation leads to measurable stiffening in the relevant regions of the MCSs. We used cytoskeletal drugs to investigate the role of the actin cytoskeleton in MCS mechanics. The jammed MCSs showed a significant reaction to the drugs, while in unjammed regions of the MCSs, the cells are so strongly deformed that the mechanical response of the cells is dominated by the rigid cell nuclei (which are not targeted by the drugs). We find that contractile TST and cell unjamming require such a high degree of cell and nucleus deformation that strain stiffening causes a more rigid behavior. This seems somewhat counterintuitive for unjamming since softer cells squeeze by each other more easily.
2 Methods and materials
2.1 Cell culture
MCF-10A (ATCC, Cat. No. CRL-10317) is a non-tumorigenic epithelial breast cell line.62 It was cultured in medium consisting of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Dulbecco's Modified Eagle's Medium (DMEM) and Ham's F12 medium (PAA, E15-813 with L-glutamine) supplemented with 5% Horse Serum (PAA, A15-151), 20 ng per ml epidermal growth factor (EGF), 10 μg per ml insulin (Sigma-Aldrich, I6634 or I9278), 100 ng per ml cholera toxin (Sigma-Aldrich, C8052), 500 ng per ml hydrocortisone (Sigma-Aldrich, H0888 or H0396), and 1% 10
1 mixture of Dulbecco's Modified Eagle's Medium (DMEM) and Ham's F12 medium (PAA, E15-813 with L-glutamine) supplemented with 5% Horse Serum (PAA, A15-151), 20 ng per ml epidermal growth factor (EGF), 10 μg per ml insulin (Sigma-Aldrich, I6634 or I9278), 100 ng per ml cholera toxin (Sigma-Aldrich, C8052), 500 ng per ml hydrocortisone (Sigma-Aldrich, H0888 or H0396), and 1% 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 U per ml penicillin/streptomycin (Sigma, P0781). MDA-MB-436 (ATCC, Cat. No. HTB130) is a cancerous mesenchymal cell line.63 It was cultured in medium consisting of 89% DMEM (PAA, E15-810), 10% fetal calf serum (FCS; Sigma-Aldrich, S0615) and 1% penicillin–streptomycin (Sigma-Aldrich, P0781). Both cell types were incubated at 37 °C and 5% CO2.
000 U per ml penicillin/streptomycin (Sigma, P0781). MDA-MB-436 (ATCC, Cat. No. HTB130) is a cancerous mesenchymal cell line.63 It was cultured in medium consisting of 89% DMEM (PAA, E15-810), 10% fetal calf serum (FCS; Sigma-Aldrich, S0615) and 1% penicillin–streptomycin (Sigma-Aldrich, P0781). Both cell types were incubated at 37 °C and 5% CO2.
2.2 MCS preparation and drug treatment
To generate MCSs, cells were trypsinized using 0.25 g per l trypsin (Sigma-Aldrich, T4049) and 2000 cells were transferred to a low adhesion U-bottom 96-well plate (BRAND, 781900) per well with 250 μl medium. They were incubated for about 24 hours during which the spheroids formed.4 To alter the cytoskeleton of cells in spheroids, 25 μM (−)-blebbistatin (Sigma-Aldrich, B0560) or 100 nM cytochalasin D (Sigma-Aldrich, C8273) was added to the respective culture medium for 24 hours during spheroid formation, avoiding the drug concentration that cells are exposed to varies from the spheroid surface to the core. As spheroid formation and drug treatment are time dependent (see Fig. S1, ESI†), the time period to start observation is set for 24 hours in this study to guarantee the comparability throughout the used model systems.2.3 AFM and sample preparation
Microrheology measurements were performed using an atomic force microscope (AFM) (NanoWizard® 4 XP NanoScience, JPK, Berlin, Germany) with a 300 μm hybrid stage combined with an Axio Zoom V16 microscope (Zeiss, Oberkochen, Germany). The device was controlled using JPK NanoWizard® software with the MicroRheology software module. A heating stage was used to maintain physiological temperature (37 °C) connected with a 5% CO2 supply hose during measurements. For MCS measurements, spheroids were transferred to a glass-bottom Petri dish (Cellvis, D60-30-1.5-N) coated with 0.01% poly-L-lysine (Sigma-Aldrich, P4832). Measurements were carried out in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 MCF-10A/MDA-MB-436 culture medium for both cell lines to guarantee comparable medium conditions. Before starting the AFM measurement, the MCSs were allowed to settle and slightly attach to the Petri dish for one hour. A flat, tipless cantilever (TL-FM, NANOSENSORS, 28 ± 7.5 μm cantilever width) was used for all MCS measurements to achieve a relatively broad indented area to deform the whole spheroid rather than individual cellular structures. The effective spring constant of the cantilever was calibrated using the thermal noise method.64 During the initial MCS attachment phase, the cantilever was immersed in the medium to reach thermal equilibrium before calibration. We used a custom force-ramp consisting of a force-indentation segment, followed by sinusoidal oscillations at 1, 3, 10, 30, 100, and 200 Hz with a 15 nm amplitude. Two different indentation forces were used in this study: a 5 nN force indented the MCSs by 2–3 μm (the average spheroid size was 150–200 μm in diameter) and 100 nN indented them by 8–10 μm, which still stay within the limits of the linear Hertz model with respect to the MCS diameter (see Fig. S2a, ESI†). The cantilever tip was positioned as close to the center of the spheroids as possible. For each experimental condition, 10–30 individual spheroids were measured, while each MCS was repeatedly measured 3–5 times.
50 MCF-10A/MDA-MB-436 culture medium for both cell lines to guarantee comparable medium conditions. Before starting the AFM measurement, the MCSs were allowed to settle and slightly attach to the Petri dish for one hour. A flat, tipless cantilever (TL-FM, NANOSENSORS, 28 ± 7.5 μm cantilever width) was used for all MCS measurements to achieve a relatively broad indented area to deform the whole spheroid rather than individual cellular structures. The effective spring constant of the cantilever was calibrated using the thermal noise method.64 During the initial MCS attachment phase, the cantilever was immersed in the medium to reach thermal equilibrium before calibration. We used a custom force-ramp consisting of a force-indentation segment, followed by sinusoidal oscillations at 1, 3, 10, 30, 100, and 200 Hz with a 15 nm amplitude. Two different indentation forces were used in this study: a 5 nN force indented the MCSs by 2–3 μm (the average spheroid size was 150–200 μm in diameter) and 100 nN indented them by 8–10 μm, which still stay within the limits of the linear Hertz model with respect to the MCS diameter (see Fig. S2a, ESI†). The cantilever tip was positioned as close to the center of the spheroids as possible. For each experimental condition, 10–30 individual spheroids were measured, while each MCS was repeatedly measured 3–5 times.
For single cell measurements, a soft pyramid-shaped cantilever (PPP-BSI, NANOSENSORS, 28 ± 7.5 μm cantilever width) with a 6 μm diameter bead glued to its tip was used. A smaller 0.5 nN indentation force was chosen to prevent going beyond the limits of the linear Hertz model (see Fig. S2d, ESI†), resulting in indentation depths between 0.5 and 1.0 μm, less than 10% of the average cell height (∼10 μm) with respect to the glass substrate. More details about this approach have been described elsewhere by Mahaffy et al.65 For fluorescence experiments with DNA-stained (0.1 μM SPY515-DNA, Spirochrome) single cells, a compact light source (HXP 200C, Mercury short arc reflector lamp) and a CCD camera sensitive to fluorescence (setting of exposure time: 1s) were added. Each cell was repeatedly measured at least 10 times, while 10–60 individual cells were measured per experiment.
2.4 Data processing and modeling
AFM data were first analyzed with JPK data processing software (version 7.1.18) to calculate Young's modulus using a Hertz fit to the smoothed and baseline corrected force indentation curves (Fig. S2b, ESI†). For a flat cantilever pressing on a spheroid, by assuming the cantilever as an infinitely large sphere, the relation between the force applied to the cantilever F and indentation depth δ can be expressed as follows:38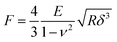 | (1) |
The data were then post-processed with a custom-written MATLAB program (MathWorks, Natick, MA, USA) to apply a modified extended Hertz model38 to calculate the complex shear modulus G* for different deformation frequencies. To determine the frequency dependent shear modulus G* for small amplitudes, eqn (1) can be approximated with the first term of the Taylor expansion for indentation depth δ and the extended Young's Modulus can be expressed as40
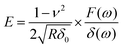 | (2) |
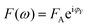 ,
, 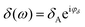 . The phase shift between force and indentation is Δφ = φF − φδ, and thus the Fourier transform of force and indentation can be expressed as follows: F(ω) = FA(cos
. The phase shift between force and indentation is Δφ = φF − φδ, and thus the Fourier transform of force and indentation can be expressed as follows: F(ω) = FA(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δφ + isin
Δφ + isin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δφ), δ(ω) = δA.39 By using the shear modulus expression G = E/2(1 + ν),66eqn (2) can be derived as
Δφ), δ(ω) = δA.39 By using the shear modulus expression G = E/2(1 + ν),66eqn (2) can be derived as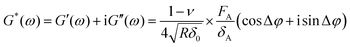 | (3) |
G*(ω) data were then fitted to the fractional element (FE) model based on a fractal ladder of Maxwell models and introduced by Helmut Schiessel and Alexander Blumen in 1995.42 This has shown its applicability to describe the frequency dependent rheological behavior of eukaryotic cells45 and human tissues.67 In this model, the complex shear modulus G*(ω) = G′(ω) + iG′′(ω) is described as68
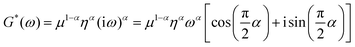 | (4) |
2.5 Spheroid staining and fluorescence microscopy
Spheroids were fixed with 10% formalin solution (Sigma, MKCK5986) for 20 min, then rinsed twice with PBS buffer. After the fixation, the spheroids were left overnight in a solution consisting of 1% Triton-X (Sigma, 91K0094). For fluorescence staining, spheroids were firstly washed with PBS, then stained with both 0.1 μM SiR-DNA (Spirochrome, SC007) and Alexa-Fluor 488 Phalloidin (Thermo-Fisher, Waltham) for about 24 hours. Spheroids were then transferred to a flat 18-well μ-slide (ibidi, 81816) and immersed in ibidi mounting medium (ibidi, 50001) for fluorescence imaging. The imaging was done on a confocal microscope (Leica TCS SP2) with a Leica HC PL APO 20X/0.7 CS Corr IMM objective. A few drops of immersion oil (ibidi, 50101) were used to avoid index mismatching.42.6 Segmentation and cell shape analysis
The segmentation process and image analysis are done using a self-written MATLAB algorithm. Standard detection models of StarDist and watershed are used to detect the nuclei in MATLAB. A detailed description of our image analysis process can be found in Grosser et al.4 and a benchmarking of the image analysis in Gottheil et al.3 We took the confocal image stacks to determine the cell and nuclei outlines. The distance of the detected foreground pixels to the background was calculated and smoothed, and its maxima were found as nucleus seeds. Utilizing the nucleus seeds as initialization points and the edges of the cancer clusters as constraints, we employed a watershed algorithm to approximate the cell outlines and applied the watershed function to the actin signal around wells (gaps between the nucleus and the actin cortex) obtained from the nuclear signal to determine the cell shape. We computed an ellipsoidal fit to the cell and nucleus shapes and determined the corresponding aspect ratios (AR) for a given cell or nucleus based on the second moment tensor of the cell or nucleus.4 During AFM measurements, only the 2D projected area and AR of nuclei can be measured simultaneously. The nuclear AR in 2D is generally smaller than that in 3D since cells have one more degree of freedom on the z-axis in monolayers.3 Results
3.1 Strongly deformed, elongated cell and nuclear shapes in MCSs
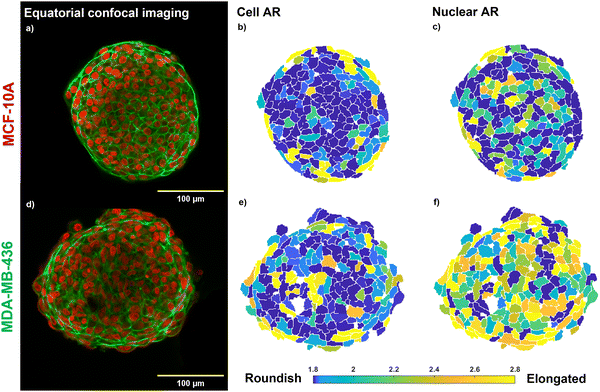
The confocal images of the equatorial plane of fixed and DNA/actin-stained MCF-10A and MDA-MB-436 spheroids (Fig. 1(a) and (d)) show that both cell lines form compact and stable MCSs. An elongated cell shape becomes visible for the direct surface of the MCF-10A MCS and elongated nuclei are seen for the entire bulk of the MDA-MB-436 MCS. In cell clusters, collective effects such as shape-induced cell unjamming or TST generated by cell contractility led to highly elongated cell and nuclear shapes.4 As shown in the heatmap of the ARs of cell and nuclear shapes in Fig. 1(b), (e), (c), (f), the jammed MCF-10A MCS shows pronounced elongated cell shapes at the outer boundary cell layer, while cells and nuclei display roundish shapes in the bulk. In MCF-10A spheroids, the cells form a cortical rim of actomyosin, spanning the spheroid surface. This cortical rim was formed by reorganization of the cells’ actin cortical networks to a collective structure on the surface of the spheroids.1,19 The contractility of the collective cortical rim strongly contributes to the TST as described in the eDAH.19 The generated TST of this collective cortical rim leads to a very smooth spheroid surface.4 The cells in the core are jammed in agreement with a rounder cell and nuclear shape. Since the core of the MCF-10A spheroid is a jammed solid the spheroid cannot generate a TST in a classical way, the cortical contractility is thus the sole mechanism that can cause a TST.In the MDA-MB-436 spheroids, cells are in a fluid unjammed state, where cells can move in the bulk.4 On the other hand, no collective cortical rim can be observed, and the spheroid surface remained rough (Fig. 1(d)). The TST can be only generated by cell–cell adhesion similar to a fluid droplet and is thus much weaker. Since the spheroids are close to volume fraction 1 (i.e., no noticeable gaps present in the spheroids),4 the fluid motile behavior in the bulk of the spheroid requires elongated cell and nuclear shapes for shape induced unjamming, as can be seen in a particularly pronounced fashion for the ARs of the nuclei in Fig. 1(f).
3.2 Cell mechanics and nuclear shape
As demonstrated in Fig. 1, contractility based TST and cell unjamming cause elongated cell and nuclear shapes. To determine the influence of cell and nucleus elongation on the mechanics, we performed AFM-based rheology on separate single cells of the investigated cell lines (MCF-10A and MDA-MB-436) on glass substrates. We live-stained the DNA in the nucleus for both cell types and simultaneously performed fluorescence microscopy in the AFM-setup. In this way, we are able to precisely target the nuclear region with the AFM and simultaneously extract the shape of the nucleus (see Fig. S3, ESI†). Next, we correlate the cell nuclear shape, more precisely their AR, and the stiffness of the nucleus. We use the nuclear AR as a measure of the deformation. The single cells on the substrate show the full spectrum from round to highly elongated shapes. We probe cell mechanics by AFM with a 6 μm bead attached to the tip of the cantilever, indenting the nucleus at the cell center. To avoid substrate effects when probing on rigid glass substrates, we have chosen 0.5 nN as our loading force, corresponding to an indentation depth of 0.5–1.0 μm, which is less than 10% of the average cell height of 10 μm with respect to the substrate. The low loading force allowed us to use the linear Hertz model (indentation depth δ < 0.3R, where R represents the radius of the attached bead) to probe thin cells (δ < 0.1h, where h represents the thickness of our cells) (see Fig. S1c and d, ESI†).65 We apply the identical FE model,42–44 to describe the frequency-dependent rheological behavior of the single cells (also see Section 2.4). For both cell lines, the magnitude of μ increases and α decreases with nucleus elongation (see Fig. 2). An increase in μ with elongation indicates that the change in shape is accompanied by mechanical changes. Nuclear elongation leads to stiffening and solidification. For the MCF-10A cells, their resistance against deformation shows a pronounced, roughly linear increase with nuclear elongation (see Fig. 2(a)). The observed increase for MDA-MB-436 cells is less pronounced but also roughly linear (see Fig. 2(b)). We choose the median nuclear AR of single MCF-10A cells (i.e., AR = 1.3) as the threshold to group our MCF-10A and MDA-MB-436 cells into two populations: more roundish cells below the threshold and more elongated cells above the threshold. For MCF-10A cells, we see a significant stiffening between round (AR < 1.3) cells and elongated (AR > 1.3) cells; we have μ = (0.78 ± 0.41) kPa for round cells and μ = (1.20 ± 0.65) kPa for elongated cells, which is also accompanied by a significant drop in fluidity from α = (0.28 ± 0.06) to α = (0.23 ± 0.05). For MDA-MB-436 cells, we see a trend with α = (0.26 ± 0.14) kPa and α = (0.33 ± 0.13) for round cells and μ = (0.36 ± 0.26) kPa and α = (0.27 ± 0.09) for elongated cells (see Table 1). While in MCF-10A more elongated cells are also less fluid (i.e., more solid-like or elastic), the MDA-MB-436 cells do not display this behavior – here also elongated cells can have a high fluidity. Overall, the healthy MCF-10A cells are more rigid and have a lower fluidity than the cancerous MDA-MB-436 cells.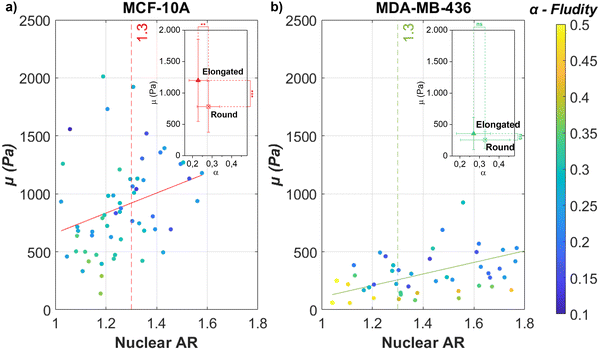 | ||
| Fig. 2 The individual epithelial MCF-10A and mesenchymal MDA-MB-436 cells show an increase in stiffness when elongated. Nuclear elongation (measured in AR) for (a) MCF-10A single cells and (b) MDA-MB-436 single cells in comparison with their respective FE model parameters μ (y-axis, stiffness parameter) and α (heatmap, fluidity parameter) [N = 60 cells (MCF-10A); N = 50 (MDA-MB-436)]. The continuous lines represent linear regression for all data that give (a) μ = 865.232AR − 204.676(R2 = 0.086) and (b) μ = 498.319AR − 389.001(R2 = 0.273). Both cell lines show a trend toward a stiffer cell behavior for more elongated nuclei. This tendency is more pronounced for MCF-10A cells, which also show a pronounced elongated cell shape on the surface of the MCS (see Fig. 1(b)), while for the fluid MDA-MB-436 MCS, the cell nuclei show a pronounced elongation (see Fig. 1(f)). In the subfigure, the median value (AR = 1.3) of scattered MCF-10A nuclear AR was chosen as the threshold for comparing round (AR < 1.3) and elongated (AR > 1.3) cells. For all conditions, without drug treatment, 24 hours culture time, ****p < 0.0001, ***p < 0.001, **p < 0.01, *p < 0.05, p > 0.05, non-significant by Welch's t-test. | ||
| MCF-10A | MDA-MB-436 | |||||
|---|---|---|---|---|---|---|
| Group | IF (nN) | μ (kPa) | α | μ (kPa) | α | |
| SC | Round | 0.5 | (0.78 ± 0.41) | (0.28 ± 0.06) | (0.26 ± 0.14) | (0.33 ± 0.13) |
| Elongated | 0.5 | (1.20 ± 0.65) | (0.23 ± 0.05) | (0.36 ± 0.26) | (0.27 ± 0.09) | |
| All | 0.5 | (0.96 ± 0.56) | (0.26 ± 0.06) | (0.32 ± 0.23) | (0.29 ± 0.10) | |
| MCS | WT | 5 | (1.07 ± 0.44) | (0.37 ± 0.05) | (0.36 ± 0.28) | (0.38 ± 0.12) |
| WT | 100 | (0.40 ± 0.18) | (0.32 ± 0.02) | (1.23 ± 0.60) | (0.23 ± 0.02) | |
| Cyto. D | 5 | (0.40 ± 0.24) | (0.40 ± 0.03) | — | — | |
| Cyto. D | 100 | — | — | (1.27 ± 0.83) | (0.28 ± 0.08) | |
| (−)-Bleb. | 100 | (1.63 ± 0.47) | (0.29 ± 0.02) | (0.97 ± 0.48) | (0.21 ± 0.03) | |
With this background information about the elongation-induced stiffening of single cells, we started probing the MCF-10A and MDA-MB-436 MCSs with AFM-based rheology. From our previous experiments,4 we know that especially MCF-10A spheroids have a distinctive different structure between the outer cell layers and the core of the spheroids. The core is jammed, while the outside surface is unjammed and surrounded by a collective contractile actin cortex.1 To probe the surface and the bulk of the MCS, we use varying loading forces to achieve different indentation depths. Loading forces of 5 nN resulted in an indentation depth of 2–3 μm, corresponding to 1–2% of the spheroid diameter, thus probing only the outer layers of the spheroids. While loading forces of 100 nN reached indentations of 8–10 μm (5–10% of the spheroid diameter). With both indentation forces, the deformations stay within the limits of the linear Hertz model (see Fig. S1, ESI†). Data were recorded frequency-resolved and then evaluated within the FE model to obtain the stiffness parameter μ and fluidity parameter α.42
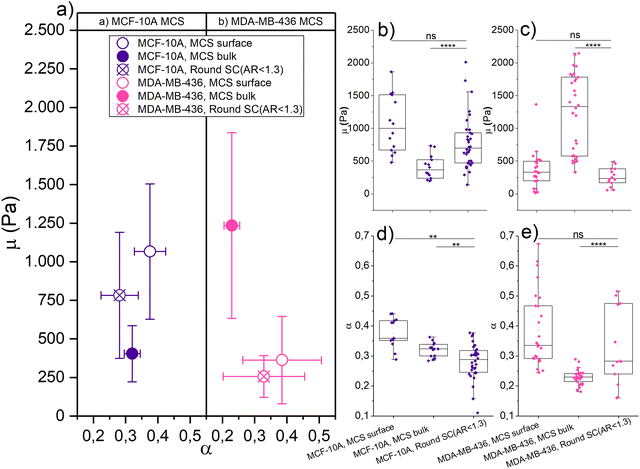
Fig. 3 shows the μ and α of jammed, epithelial MCF-10A spheroids and unjammed, mesenchymal MDA-MB-436 spheroids using different loading forces and measurements of single cells with roundish nuclei (i.e., AR < 1.3) as a reference. We choose round single cells as a reference for their non-distorted mechanical ground state in terms of mechanical resistance. For probing the MCS surface, we get μ = (1.07 ± 0.44) kPa and α = (0.37 ± 0.05) for MCF-10A spheroids, and μ = (0.36 ± 0.28) kPa and α = (0.38 ± 0.12) for MDA-MB-436 spheroids. For probing the bulk, we measure μ = (0.40 ± 0.18) kPa and α = (0.32 ± 0.02) for MCF-10A spheroids, and μ = (1.23 ± 0.60) kPa and α = (0.23 ± 0.02) for MDA-MB-436 spheroids. The round single cells adhered to the glass substrate were probed using 0.5 nN as the indentation force, and we get μ = (0.78 ± 0.41) kPa and α = (0.28 ± 0.06) for MCF-10A cells, and μ = (0.26 ± 0.14) kPa and α = (0.33 ± 0.13) for MDA-MB-436 cells (see Table 1).
We see a significant difference between the surface and bulk resistance for the MCF-10A spheroids. We have a stiffer outer shell with a softer core: μ is 63% lower in the bulk than at the surface, the round single cells fall in between core and surface stiffness. Despite the bulk forming a jammed heterogeneous solid,4 the cells at the MCS boundary are stiffer due to their elongated cell shape. While the jammed cells in the bulk are even rounder than the single cells and thus have an even lower mechanical resistance. The stiffening due to elongation observed in Fig. 2 has according to these observations a dominant role in the studied MCS. Moreover, the active contractility of the MCS surface also fosters higher fluidity, which is probably due to the increased activity in contractile cells.
The unjammed, fluid MDA-MB-436 spheroids are softer on the outside and stiffer in the core. While on the surface μ has not changed significantly between single cells and spheroids, μ increased nearly 2.5-fold from the outside to the core. The pronounced stiffening in the bulk agrees with the elongated cell and in particular nuclear shapes that cause cell stiffening. However, fluidity decreases in the bulk. This cannot be attributed to the single cell behavior under strong deformations and may be due to the increased nuclear friction in the bulk.3,4
The mechanics of our MCS significantly differs between epithelial and mesenchymal cell lines. At the surface, MDA-MB-436 spheroids are softer (μ is 66% lower) than MCF-10A, which is a larger difference than that between the single cells. The cortical contractility at the surface of the MCF-10A MCS, which causes a high TST, leads to highly elongated shapes and consequently stiff cells. For larger indentations, the behavior of the bulk becomes dominant. For the spheroid cores, the situation is inverted: the resistance of the cancerous mesenchymal cell line is now nearly three times the value of the healthy epithelial cell line. Despite the round single MDA-MB-436 cells being softer than MCF-10A, the bulk of the unjammed, more fluid-like MDA-MB-436 MCSs with highly elongated nucleus shapes reaches the highest mechanical resistance. The cancerous MDA-MB-436 MCSs are unjammed and thus require elongated cells and nuclear shapes in the bulk. Note that the fluidization caused by unjamming occurs on a much longer time scale than probed in our experiments. A lower α here means less dissipation on a short time scale. Furthermore, MDA-MB-436 cells have large nuclei, which are more compact in the center of the MCS (Fig. S4, ESI†), leading to an increased steric hindrance. Thus, the highly elongated shapes required for unjamming and consequential fluidization on long time scales lead to strong stiffening on the short time scales that we probe here.
3.3 Perturbation of the cytoskeleton
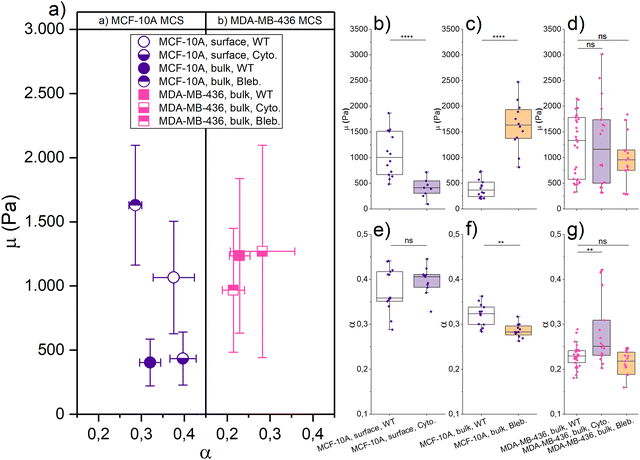
We have recently shown that cell unjamming depends on the mechanics of the cellular cytoskeleton and of the nucleus.3,4,12 This motivates us to investigate how the cytoskeleton and nucleus contribute to the observed cell deformation, induced stiffening in regions of high TST or unjammed fluid behavior. It is difficult to alter the mechanical properties of the nucleus. Thus, we use cytoskeletal drugs to determine the mechanical contribution of the cytoskeleton and its indirect role with respect to the nucleus. We perturbed the cells’ cytoskeleton, by depolymerizing actin filaments with cytochalasin D and blocking myosin motors with (−)-blebbistatin, to get a more detailed view on the contractility-based TST and shape-induced unjamming.As shown in Fig. 4, the mechanical resistance at the surface of healthy epithelial MCF-10A spheroids softens with cytochalasin D by 63% to μ = (0.40 ± 0.24) kPa, while the fluidity α = (0.40 ± 0.03) practically remained unchanged. The structural integrity of the MCF-10A spheroids was highly destabilized due to the loss of contractility-induced TST when the collective actin cortex is destroyed. Therefore, we can only apply a 5 nN indentation force to our cytochalasin D treated spheroids, as higher forces caused the disintegration of the spheroids. Thus, we cannot probe the bulk properties with cytochalasin D. With (−)-blebbistatin, a 100 nN indentation force is applied to probe the bulk of the MCS. The boundary could not be evaluated with a lower indentation force due to large background noise. The MCF-10A spheroids showed a significant stiffening, and the fitting results were μ = (1.63 ± 0.47) kPa and a decrease of fluidity with α = (0.29 ± 0.02). By adding (−)-blebbistatin, μ was increased nearly threefold in the core compared to the WT and α was slightly decreased. The drastic stiffening effect of (−)-blebbistatin on the bulk is somewhat surprising since the jammed round cells should not be heavily influenced by (−)-blebbistatin which impacts the collective cortical rim. On the other hand, the effect on the collective rim suggests that Blebbistatin weakens the mechanical strength of the actin cortex of all cells. We expect that the loss of cytoskeletal integrity is pronounced enough that the nuclei start to dominate the bulk behavior. Since the nuclei are much stiffer, this leads to the pronounced stiffening that we observe in the bulk. The strong effect of cytoskeletal drugs on contractility-controlled TST in MCSs clearly demonstrates that the stiffening we observe in elongated MCF-10A cells can be attributed to the cytoskeleton.
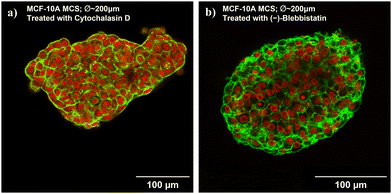
We took confocal images of fixed and DNA/actin-stained MCF-10A spheroids treated with the cytoskeletal drugs for a more detailed analysis of the loss of MCS stability (see Fig. 5). The images of the equatorial plane show a strongly reduced collective actin cortex at the MCS boundary for both drugs. Cytochalasin D, by directly capping the plus end of actin filaments and depolymerizing the filaments, made it harder for MCF-10A cells to aggregate and the cell cluster formed a less smooth and round cluster boundary (Fig. 5). The actin structure is less sharply localized at the spheroid boundary, and no pronounced collective actin cortex surrounding the MCS is formed. The actin distribution shifts more to the interior of the MCS, and visible actin cortex structures can be also found in the actin cortex. No more elongated, stretched out cells can be found at the surface of the MCS after drug treatments. All cells and nuclei in the MCS have a rounder shape. All together, these observations demonstrate that the TST is drastically lowered, which explains the mechanical instability of the spheroids. (−)-Blebbistatin, as an inhibitor of myosin II, keeps myosin in an actin-detached state,71 preventing the actomyosin cortex from active contractions. The MCSs no longer form a collective contractile cortex surrounding that would lead to a strong TST. The spheroids have a little bit less irregular and rough shapes, and still the images are characteristic of a lower TST (Fig. 5). This also agrees with the more ellipsoidal and less round spheroid shape. In particular, no elongated cell and nuclear shapes can be found on the spheroid surface. Despite MCSs being no longer compressed by a high TST, we can see that the cell nuclei are more densely packed in the core of the spheroids and the actin bundles are shorter and more disordered. The reduced cytoskeleton permits a smaller distance between the nuclei. The (−)-blebbistatin-treated MCS are more mechanically stable than the cytochalasin D-treated spheroids. With a significantly weakened yet a still existing actomyosin cortex and the resulting closer spacing of the nuclei, the integrity of the MCS remains stable enough for cantilever probing. The remaining cytoskeleton permits the cells to adhere to each other and the closer spacing of the nuclei generates a more rigid behavior. We are probing now rather the stiff nuclei instead of cytoskeletal structures, and this might explain why we got the highest resistance in the bulk of (−)-blebbistatin-treated MCS.
For the cancerous mesenchymal MDA-MB-436 spheroids, both cytochalasin D and (−)-blebbistatin have no significant effect on the bulk mechanics. With cytochalasin D, we got for the bulk μ = (1.27 ± 0.83) kPa and α = (0.28 ± 0.08), and μ = (0.97 ± 0.48) kPa and α = (0.21 ± 0.03) with (−)-blebbistatin, and all fitting results are listed in Table 1. Since the MDA-MB-436 spheroids do not react to cytoskeletal drugs, we conclude that the cytoskeleton is not the main determinant of the bulk mechanics of unjammed, fluid MDA-MB-436 spheroids and the strongly deformed nuclei that we found in this region. The fluid behavior occurs on much longer time scales than we can probe with the AFM. Recent research by Grosser et al.4 and Gottheil et al.3 has shown that the nuclei and their viscoelasticity have a major impact on the unjamming behavior. From Fig. S4 (ESI†) and Fig. 1, it becomes visible that the MDA-MB-436 cells have larger nuclei which are also more deformed in the bulk than the MCF-10A cells (Fig. 1(d)). As shown in Fig. 2, single MDA-MB-436 cells show a less pronounced stiffening with increasing nucleus elongation. Nevertheless, as cytoskeletal drugs have no effect, we attribute the stiffening of the elongated cells in the bulk to the mechanical behavior of the nuclei with their pronounced deformations (Fig. 1(f)). The observed stiffening effect in the MDA-MB-436 MCSs is however much stronger than our single cell data.
Based on our experiments, the stiffening of highly elongated cells in MCSs can be attributed either to the actin cytoskeleton in the case of the observed TST effects or to the cell nuclei for the unjamming events in the bulk. Our finding agrees with recent results from cell migration experiments through narrow constrictions, where actomyosin-based contractility is used by MCF-10A cells to squeeze through constrictions. Mesenchymal MDA-MB-436 cells did not pass through the narrow constrictions.53 The highly squeezed MDA-MB-436 cells are too rigid to pass through the constriction.
4 Discussion
We measured and compared the viscoelasticity of MCSs from healthy and cancerous cell lines. The observed power law behavior for the studied times, much shorter than unjamming, indicates a complex dynamic system with no dominant frequency or time scale with respect to the shear relaxation in the investigated frequency range of 1–200 Hz (see Fig. S5, ESI†), which agrees with the previously observed behavior in cells and tissues.2,4,12,38 Despite our measurements concerning more about TST effects and the mechanical resistance against fast indentations than fluidization through unjamming, which is a much slower process occurring over several hours to days,4 the strain stiffening due to cell and nucleus elongation will always be present as long as the deformation does not relax and thus can be correlated with the long-time scale effect such as unjamming and eDAH. We study relatively simple models of cellular tissues. Yet, they display already complex, emergent behaviors such as those described in the eDAH and in shape-induced cell unjamming. Both phenomena result in strongly deformed, elongated cells and nuclei.A central, previously unanswered question is to what extent the mechanical properties of MCS are modulated not solely by the collective mechanical effects of eDAH and unjamming, but also directly through changes in the mechanical behavior of individual cells under large deformations beyond the behavior described by linear elasticity. A complex interplay between collective and individual cell properties shapes the mechanical behavior of MCSs. As for collective effects, we have previously shown that unjamming controls cell motility and long-term fluidity2–4,12 and that cortical contractility stabilizes cell boundaries.1 On the individual cell level, a combination of in vivo magnetic resonance elastography and single cell elasticity measurements recently showed that the dissipative behavior of brain tumors is determined by the dissipation behavior of individual cancer cells.67 Single cell properties mostly determine the mechanics of cell aggregates indirectly, as softer cells favor shape-induced cell unjamming,12 higher cell–cell adhesion fosters cell streaming,28 and cortical cell contractility contributes to the TST.1
Here, we have found on the single cell level that strong deformations go beyond the linear elastic response, and the cells and nuclei stiffen with elongated shape. Both TST and unjamming effects required pronounced elongated cells and nuclear shapes, which leads to linear stiffening with increasing strain. The strain stiffening with elongation can be caused by the actin cytoskeleton in the case of the TST of MCF-10A MCSs as well as by the nucleus in the case of unjamming in MDA-MB-436 MCSs. This agrees with the finding that semiflexible polymers, such as F-actin or DNA, will undergo strain hardening under deformation.72–74 In this sense, the observed stiffening in MCSs either in regions of TST or in the unjammed area is a consequence of the elongated cell and nuclear shapes.
The epithelial MCF-10A cells display an actin-cortex-based contractility and a cooperative cage formed by the rigid outer cells that generates a sharp and stable boundary.4 We find for MCF-10A MCSs highly elongated cell shapes at the spheroid boundary which is also the stiffest region of these spheroids. The active cortical tension and the strain stiffening through elongated shape, both generated by the actin cytoskeleton, contribute to this high resistance of the outside surface. The epithelial cells are ideally suited for this purpose since they display an actin-cortex-based contractility that fosters the formation of a collective contractile spheroid shell. In the absence of the cortex cell layer, the spheroid loses its mechanical integrity. Concerning the generated TST, the collective cortical contractility is the primary cause, while the elongation serves as a secondary effect. Both factors lead to strain stiffening and cannot be completely separated from each other. Most remarkably, we observe this significant TST in an otherwise jammed spheroid in contrast to the convention that only fluid systems can generate a surface tension. Thus, a contractility based TST enhanced by strain stiffening is the optimal way to stabilize the MCS boundary in jammed spheroids. We expect that the stiffening of elongated cells at the boundary of epithelial tissues helps to mechanically stabilize these tissues.
The MDA-MB-436 MCSs do not show an outer boundary of cells that are more elongated and strongly deformed. Thus, we find no indications of a strong TST. Instead, we find elongated cell and nuclear shapes in the bulk, which permit shape induced unjamming, necessary for the motile behavior in the spheroids. Softer cells favor unjamming since cancer cells have to squeeze by each other.12 As a matter of fact, single MDA-MB-436 cells are softer than MCF-10A cells (see Fig. 2) and form unjammed MSCs. However, somewhat surprisingly the unjammed areas in the MDA-MB-436 MCSs show the highest stiffness that we have measured (see Fig. 3). While we are unable to directly measure the stiffness of the nuclei, observations with cytoskeletal drugs indicate that the mechanical properties of cancerous MCSs undergo minimal changes. Therefore, the primary factor contributing to increasing the resistance in the bulk of MCSs is likely the strain stiffening originating from the nuclei. The strong deformation of the nuclei of the unjammed cells leads to a considerable increase in the mechanical resistance in the bulk of these spheroids. We observe this effect despite individual MDA-MB-436 cells only showing a weak tendency to stiffen with deformation (see Fig. 2(b)).
Our results show that, even for such simple tissue models as spheroids made from a single cell line, Aristotle's saying applies: the whole is greater than the sum of its parts. The mechanical behavior of our cell spheroids is not simply determined by collective effects or single cell stiffness. We find a complex interplay between collective effects and the mechanical properties of individual cells. We have previously demonstrated that the unjamming state diagram strongly depends on the nucleus (see Fig. S6, ESI†).3 Consequently, we anticipate a pronounced mechanical impact resulting from nucleus elongation. In the paper, we observe the cancerous spheroids are stiffer in the bulk, and we know that is the area, which is, according to the state diagram, nuclei dominated. The stiffening is particularly strong in such areas where nuclei are “densely packed”. Thus, we could draw a conclusion that elongated cell and nuclear shapes are a good indicator for predicting the mechanical rigid regions in the MCS, caused by both contractility-based TST and shape-induced cell unjamming.
5 Summary
In this paper, we measured and compared the viscoelastic properties of MCSs derived from both healthy and cancerous cell lines. We focused on short-time-scale effects, such as mechanical resistance to immediate deformations, rather than the slower process of fluidization through unjamming. The mechanical properties of MCSs were found to result from a complex interplay between collective effects, such as cell unjamming and eDAH, and individual cell properties, including cell stiffness and adhesion. Strong deformations caused cells and nuclei to undergo strain stiffening, and naturally this stiffening was associated with elongated cell and nuclear shapes. This behavior was attributed to factors like the actin cytoskeleton and nucleus, both of which can undergo strain stiffening under deformation. Overall, we revealed that the mechanical behavior of MCSs is influenced by both collective effects, unjamming and eDAH, with elongated cell and nuclear shapes serving as indicators of mechanically stiff regions within the spheroids.Code and data availability
You could find the analysis code for single cell measurements on AFM and all data we used in the paper on the link: https://github.com/XiaofanXie/Effect-of-Non-linear-Strain-Stiffening-in-eDAH-and-Unjamming. Custom MATLAB scripts for cell-nuclei tracking and cell segmentation are available at https://github.com/steffengrosser/smart-3D-registration-2019 and https://github.com/JuergenLippoldt/On-Motility-and-Form.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was funded by the European Research Council (ERC-741350) and the Open Access Publishing fund of Leipzig University supported by the German Research Foundation within the program Open Access Publication Funding.References
- E. Warmt, S. Grosser, E. Blauth, X. Xie, R. Stange, J. Tomm, F. Sauer, J. Schnauß, M. von Bergen and J. A. Käs, New J. Phys., 2021, 23, 103020 CrossRef CAS.
- S. Pawlizak, A. W. Fritsch, S. Grosser, D. Ahrens, T. Thalheim, S. Riedel, T. R. Kießling, L. Oswald, M. Zink and M. L. Manning, New J. Phys., 2015, 17, 083049 CrossRef.
- P. Gottheil, J. Lippoldt, S. Grosser, F. Renner, M. Saibah, D. Tschodu, A.-K. Poßögel, A.-S. Wegscheider, B. Ulm and K. Friedrichs, Phys. Rev. X, 2023, 13, 031003 CAS.
- S. Grosser, J. Lippoldt, L. Oswald, M. Merkel, D. M. Sussman, F. Renner, P. Gottheil, E. W. Morawetz, T. Fuhs and X. Xie, Phys. Rev. X, 2021, 11, 011033 CAS.
- L. Oswald, S. Grosser, D. M. Smith and J. A. Käs, J. Phys. D: Appl. Phys., 2017, 50, 483001 CrossRef PubMed.
- J.-A. Park, J. H. Kim, D. Bi, J. A. Mitchel, N. T. Qazvini, K. Tantisira, C. Y. Park, M. McGill, S.-H. Kim and B. Gweon, Nat. Mater., 2015, 14, 1040–1048 CrossRef CAS PubMed.
- J. J. Fredberg and D. Stamenovic, J. Appl. Physiol., 1989, 67, 2408–2419 CrossRef CAS PubMed.
- J. Fredberg, J. Mitchel, J. H. Kim and J. A. Park, FASEB J., 2016, 30, 1296.1292 Search PubMed.
- M. G. Castro, S. E. Leggett and I. Y. Wong, Soft Matter, 2016, 12, 8327–8337 RSC.
- G. Biroli, Nat. Phys., 2007, 3, 222–223 Search PubMed.
- T. E. Angelini, E. Hannezo, X. Trepat, M. Marquez, J. J. Fredberg and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4714–4719 CrossRef CAS PubMed.
- T. Fuhs, F. Wetzel, A. W. Fritsch, X. Li, R. Stange, S. Pawlizak, T. R. Kießling, E. Morawetz, S. Grosser, F. Sauer, J. Lippoldt, F. Renner, S. Friebe, M. Zink, K. Bendrat, J. Braun, M. H. Oktay, J. Condeelis, S. Briest, B. Wolf, L.-C. Horn, M. Höckel, B. Aktas, M. C. Marchetti, M. L. Manning, A. Niendorf, D. Bi and J. A. Käs, Nat. Phys., 2022, 18, 1510–1519 Search PubMed.
- E. Frittoli, A. Palamidessi, F. Iannelli, F. Zanardi, S. Villa, L. Barzaghi, H. Abdo, V. Cancila, G. V. Beznoussenko and G. Della Chiara, Nat. Mater., 2022, 1–12 Search PubMed.
- K. Wolf, M. Te Lindert, M. Krause, S. Alexander, J. Te Riet, A. L. Willis, R. M. Hoffman, C. G. Figdor, S. J. Weiss and P. Friedl, J. Cell Biol., 2013, 201, 1069–1084 CrossRef CAS PubMed.
- M. Sadati, N. T. Qazvini, R. Krishnan, C. Y. Park and J. J. Fredberg, Differentiation, 2013, 86, 121–125 CrossRef CAS PubMed.
- W. Wang, S. Goswami, E. Sahai, J. B. Wyckoff, J. E. Segall and J. S. Condeelis, Trends Cell Biol., 2005, 15, 138–145 CrossRef CAS PubMed.
- M. F. Staddon, D. Bi, A. P. Tabatabai, V. Ajeti, M. P. Murrell and S. Banerjee, PLoS Comput. Biol., 2018, 14, e1006502 CrossRef PubMed.
- M. S. Steinberg, Science, 1963, 141, 401–408 CrossRef CAS PubMed.
- J. D. Amack and M. L. Manning, Science, 2012, 338, 212–215 CrossRef CAS PubMed.
- C. M. Kraning-Rush, J. P. Califano and C. A. Reinhart-King, PLoS One, 2012, 7, e32572 CrossRef CAS PubMed.
- C. T. Mierke, D. Rösel, B. Fabry and J. Brábek, Eur. J. Cell Biol., 2008, 87, 669–676 CrossRef CAS PubMed.
- J. Kim, J. Feng, C. A. Jones, X. Mao, L. M. Sander, H. Levine and B. Sun, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- T. Fischer, N. Wilharm, A. Hayn and C. T. Mierke, Convergent Sci. Phys. Oncol., 2017, 3, 044003 CrossRef.
- T. M. Koch, S. Münster, N. Bonakdar, J. P. Butler and B. Fabry, PLoS One, 2012, 7, e33476 CrossRef CAS PubMed.
- M. Yilmaz and G. Christofori, Cancer Metastasis Rev., 2009, 28, 15–33 CrossRef PubMed.
- S. Kumar and V. M. Weaver, Cancer Metastasis Rev., 2009, 28, 113–127 CrossRef PubMed.
- J. L. Ouderkirk and M. Krendel, Cytoskeleton, 2014, 71, 447–463 CrossRef CAS PubMed.
- O. Ilina, P. G. Gritsenko, S. Syga, J. Lippoldt, C. A. La Porta, O. Chepizhko, S. Grosser, M. Vullings, G.-J. Bakker and J. Starruß, Nat. Cell Biol., 2020, 22, 1103–1115 CrossRef CAS PubMed.
- S. A. Langhans, Front. Pharmacol., 2018, 9, 6 CrossRef PubMed.
- S. Kozubek and G. Erzgraber, Multicellular spheroids as an in vitro tumor model, J. Inst. Nucl. Res., 1982, No. JINR(E19-82), 589 Search PubMed.
- W. Mueller-Klieser, J. Cancer Res. Clin. Oncol., 1987, 113, 101–122 CrossRef CAS PubMed.
- G. Hamilton, Cancer Lett., 1998, 131, 29–34 CrossRef CAS PubMed.
- L. Kunz-Schughart, Cell Biol. Int., 1999, 23, 157–161 CrossRef CAS PubMed.
- T.-M. Achilli, J. Meyer and J. R. Morgan, Expert Opin. Biol. Ther., 2012, 12, 1347–1360 CrossRef CAS PubMed.
- G. Mehta, A. Y. Hsiao, M. Ingram, G. D. Luker and S. Takayama, J. Controlled Release, 2012, 164, 192–204 CrossRef CAS PubMed.
- S. Nath and G. R. Devi, Pharmacol. Ther., 2016, 163, 94–108 CrossRef CAS PubMed.
- X. Cui, Y. Hartanto and H. Zhang, J. R. Soc., Interface, 2017, 14, 20160877 CrossRef PubMed.
- R. E. Mahaffy, C. K. Shih, F. C. Mackintosh and J. Käs, Phys. Rev. Lett., 2000, 85, 880–883 CrossRef CAS PubMed.
- J. Alcaraz, L. Buscemi, M. Puig-De-Morales, J. Colchero, A. Baró and D. Navajas, Langmuir, 2002, 18, 716–721 CrossRef CAS.
- J. Alcaraz, L. Buscemi, M. Grabulosa, X. Trepat, B. Fabry, R. Farré and D. Navajas, Biophys. J., 2003, 84, 2071–2079 CrossRef CAS PubMed.
- J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980 Search PubMed.
- H. Schiessel and A. Blumen, Macromolecules, 1995, 28, 4013–4019 CrossRef CAS.
- F. Sauer, L. Oswald, A. A. de Schellenberger, H. Tzschätzsch, F. Schrank, T. Fischer, J. Braun, C. T. Mierke, R. Valiullin and I. Sack, Soft Matter, 2019, 15, 3055–3064 RSC.
- J. Braun, H. Tzschätzsch, C. Körting, A. Ariza de Schellenberger, M. Jenderka, T. Drießle, M. Ledwig and I. Sack, Magn. Reson. Med., 2018, 79, 470–478 CrossRef CAS PubMed.
- V. D. Djordjević, J. Jarić, B. Fabry, J. J. Fredberg and D. Stamenović, Ann. Biomed. Eng., 2003, 31, 692–699 CrossRef PubMed.
- A. Bonfanti, J. L. Kaplan, G. Charras and A. Kabla, Soft Matter, 2020, 16, 6002–6020 RSC.
- H. Tzschätzsch, J. Guo, F. Dittmann, S. Hirsch, E. Barnhill, K. Jöhrens, J. Braun and I. Sack, Med. Image Anal., 2016, 30, 1–10 CrossRef PubMed.
- E. Moeendarbary and A. R. Harris, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2014, 6, 371–388 Search PubMed.
- B. Fabry, G. N. Maksym, J. P. Butler, M. Glogauer, D. Navajas and J. J. Fredberg, Phys. Rev. Lett., 2001, 87, 148102 CrossRef CAS PubMed.
- P. Kollmannsberger and B. Fabry, Annu. Rev. Mater. Res., 2011, 41, 75–97 CrossRef CAS.
- I. Elbalasy, P. Mollenkopf, C. Tutmarc, H. Herrmann and J. Schnauß, Soft Matter, 2021, 17, 3954–3962 RSC.
- T. Golde, M. Glaser, C. Tutmarc, I. Elbalasy, C. Huster, G. Busteros, D. M. Smith, H. Herrmann, J. A. Käs and J. Schnauß, Soft Matter, 2019, 15, 4865–4872 RSC.
- C. Ficorella, H. M. Eichholz, F. Sala, R. M. Vázquez, R. Osellame and J. A. Käs, New J. Phys., 2021, 23, 083028 CrossRef CAS.
- M. L. Gardel, I. C. Schneider, Y. Aratyn-Schaus and C. M. Waterman, Annu. Rev. Cell Dev. Biol., 2010, 26, 315–333 CrossRef CAS PubMed.
- P. Chugh and E. K. Paluch, J. Cell Sci., 2018, 131, jcs186254 CrossRef PubMed.
- M. Gyger, R. Stange, T. R. Kießling, A. Fritsch, K. B. Kostelnik, A. G. Beck-Sickinger, M. Zink and J. A. Käs, Eur. Biophys. J., 2014, 43, 11–23 CrossRef CAS PubMed.
- M. Murrell, P. W. Oakes, M. Lenz and M. L. Gardel, Nat. Rev. Mol. Cell Biol., 2015, 16, 486–498 CrossRef CAS PubMed.
- G. Salbreux, G. Charras and E. Paluch, Trends Cell Biol., 2012, 22, 536–545 CrossRef CAS PubMed.
- T. E. Kreis and W. Birchmeier, Cell, 1980, 22, 555–561 CrossRef CAS PubMed.
- S. Tojkander, G. Gateva and P. Lappalainen, J. Cell Sci., 2012, 125, 1855–1864 CAS.
- D. Pesen and J. H. Hoh, Biophys. J., 2005, 88, 670–679 CrossRef CAS PubMed.
- H. D. Soule and C. M. McGrath, In Vitro Cell. Dev. Biol., 1986, 22, 6–12 CrossRef CAS PubMed.
- P. Y. Desprez, C. Q. Lin, N. Thomasset, C. J. Sympson, M. J. Bissell and J. Campisi, Mol. Cell. Biol., 1998, 18, 4577–4588 CrossRef CAS PubMed.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- R. E. Mahaffy, S. Park, E. Gerde, J. Käs and C. K. Shih, Biophys. J., 2004, 86, 1777–1793 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Quantum mechanics: non-relativistic theory, Elsevier, 2013 Search PubMed.
- F. Sauer, A. Fritsch, S. Grosser, S. Pawlizak, T. Kießling, M. Reiss-Zimmermann, M. Shahryari, W. C. Müller, K.-T. Hoffmann and J. A. Käs, Soft Matter, 2021, 17, 10744–10752 RSC.
- D. Klatt, C. Friedrich, Y. Korth, R. Vogt, J. Braun and I. Sack, Biorheology, 2010, 47, 133–141 Search PubMed.
- B. Derrick, D. Toher and P. White, The Quantitative Methods in Psychology, 2016, p. 12 Search PubMed.
- G. D. Ruxton, Behav. Ecol., 2006, 17, 688–690 CrossRef.
- M. Kovács, J. Tóth, C. Hetényi, A. Málnási-Csizmadia and J. R. Sellers, J. Biol. Chem., 2004, 279, 35557–35563 CrossRef PubMed.
- D. Humphrey, C. Duggan, D. Saha, D. Smith and J. Käs, Nature, 2002, 416, 413–416 CrossRef CAS PubMed.
- M. L. Gardel, F. Nakamura, J. H. Hartwig, J. C. Crocker, T. P. Stossel and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1762–1767 CrossRef CAS PubMed.
- N. Orakdogen, B. Erman and O. Okay, Macromolecules, 2010, 43, 1530–1538 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00630a |
| This journal is © The Royal Society of Chemistry 2024 |