Open Access Article
Open Access ArticleAbsolute control over the quantum yield of a photodissociation reaction mediated by nonadiabatic couplings
Ignacio R.
Sola
 *a and
Alberto
García-Vela
*a and
Alberto
García-Vela
 *b
*b
aDepartamento de Química Física, Universidad Complutense de Madrid (and Unidad Asociada I+D+I al CSIC), 28040 Madrid, Spain. E-mail: isolarei@ucm.es
bInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 123, 28006 Madrid, Spain. E-mail: garciavela@iff.csic.es
First published on 23rd August 2024
Abstract
Control of molecular reaction dynamics with laser pulses has been developed in the last decades. Among the different magnitudes whose control has been actively pursued, the branching ratio between different product channels constitutes the clearest signature of quantum control. In polyatomic molecules, the dynamics in the excited state is quagmired by non-adiabatic couplings, which are not directly affected by the laser, making control over the branching ratio a very demanding challenge. Here we present a control scheme for the CH3I photodissociation in the A band, that modifies the quantum yield of the two fragmentation channels of the process. The scheme relies on the optimized preparation of an initial superposition of vibrational states in the ground potential, which further interfere upon the excitation with a broad pump pulse. This interference can suppress any of the channels, regardless of its dominance, and can be achieved over the whole spectral range of the A band. Furthermore, it can be accomplished without strong fields or direct intervention during the dynamics in the excited states: the whole control is predetermined from the outset. The present work thus opens the possibility of extensive and universal control of the channel branching ratio in complex photodissociation processes.
Introduction
Quantum control of molecular reaction dynamics has been actively pursued over the last decades.1–11 Among these reactions, the near ultraviolet photolysis of CH3I in the first absorption band (the A band, ranging from 220 to 350 nm with a maximum at about 260 nm) has been considered as a prototypical photodissociation reaction. The relatively small size of this polyatomic molecule favors its study both experimentally and theoretically. In addition, the presence of a conical intersection between the two main excited valence states produces interesting nonadiabatic effects in the photodissociation dynamics. The A band absorption spectrum of CH3I was measured almost fifty years ago.12 After this pioneering work, a variety of experimental techniques were applied to investigate the CH3I photodissociation dynamics in the A band. This process was the first one investigated by ion imaging by Chandler and Houston13 at 266 nm, later followed by velocity map imaging (VMI) measurements by Eppink and Parker14,15 over nearly the whole band (240–334 nm). Time-resolved studies were pioneered by Zewail and coworkers,16 and then a series of time-resolved VMI experiments were reported for different regions of the A band.17–20 Photoelectron imaging experiments in the range 245.5–261.6 nm were also reported.21 The first theoretical study on the photolysis dynamics of CH3I in the A band consisted of a two-dimensional wave packet model by Shapiro and Bersohn.22 This model was later improved by Guo,23 by adding a third degree of freedom. Then, wave packet models including four,20 five,24 and the full nine25 dimensions of the system were reported. Those models used either the six-dimensional,26 or the full-dimensional,27ab initio potential-energy surfaces of CH3I calculated by Morokuma and coworkers, further refined by Xie et al.28Quantum control of molecular processes takes advantage of the coherent properties of light. Several control schemes applying both strong and weak laser fields have been proposed for different molecular reactions.29–46 Rather surprisingly, control of the prototypical photodissociation dynamics of CH3I has been the subject of very few works. In fact, to the best of our knowledge only two theoretical31,47 only one theoretical31 and two experimental43,45 quantum control works on the CH3I photolysis in the A band have been reported. The two excited states mainly involved in the photodissociation, namely 3Q0 and 1Q1, are connected by a conical intersection and give rise to two different product channels forming CH3 + I*(2P1/2) and CH3 + I(2P3/2), respectively. The branching ratio between these two channels should in principle be susceptible to be controlled. However, with the exception of ref. 31, 43 and 47, no attempts in this sense have been reported.
In this work we suggest a quantum control scheme that aims at modifying the branching ratio of the two product channels of the CH3I photodissociation, CH3 + I*(2P1/2) and CH3 + I(2P3/2), over the whole energy range of the A band. Recognizing the crucial role of the initial coherences in the control of ultrafast processes,48–51 our scheme reverses the order of the pulses in the “orthodox” two-step approach. Instead of first applying a strong ultrashort pump pulse, which ignites the dynamics creating a vibronic wave packet in the excited states, and then the control pulse, guiding the dynamics by adjusting or modifying the phases along the reaction coordinate, as necessary (where in many practical implementations both pulses can be integrated into a single pulse of complex structure), we first apply a control pulse that prepares the coherences in the ground electronic state, and then use the ultrafast pump pulse to pump the proper wave packet in the desired excited state. The method can be seen as a generalization of one of the Brumer–Shapiro coherent control scenarios,31 where we generate a superposition of vibrational states using the geometrical optimization (GO) procedure,52–56 optimizing variationally the superposition coefficients in order to maximize a given functional which in our case is the desired branching ratio, either [I*]/([I*] + [I]) or [I]/([I*] + [I]), over the different wavelengths of the A band. This implies a different and more complex derivation of the optimal equations, leading to non-linear eigenvalue equations, as shown in the Methodology. The optimization procedure is driven by the output of wave packet simulations on the CH3I photodissociation dynamics, and by the interference between the superposition coefficients. Since the control scheme applied relies on interference, only a weak laser field is required to pump CH3I to the excited states, thus avoiding potential problems associated with intense fields. In this way, the control scheme suggested allows to maximize the yield of any of the two product channels at different wavelengths in the A band, with respect to the natural yield obtained in the absence of control.
Methodology
The control scheme
Photodissociation of CH3I in the A band involves a dominant parallel 3Q0 ←![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1 transition and two perpendicular transitions, 1Q1 ←
1A1 transition and two perpendicular transitions, 1Q1 ← ![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1 and 3Q1 ←
1A1 and 3Q1 ← ![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1, of lower intensity. The photodissociation process is schematically depicted in Fig. 1. The 1Q1 and 3Q1 states correlate asymptotically to the same fragments, CH3 + I(2P3/2), while 3Q0 correlates to the CH3 + I*(2P1/2) products. For simplicity, hereafter these two product channels will be referred to as the I and I* channels, respectively. The asymptote of 3Q0 is separated from that of 1Q1 and 3Q1 by the iodine spin–orbit splitting, 0.943 eV.14 In addition, a conical intersection (CI) connects the 3Q0 and 1Q1 states, so a wave packet initially excited to any of these two states will bifurcate at the CI, producing both CH3 + I and CH3 + I* fragments.
1A1, of lower intensity. The photodissociation process is schematically depicted in Fig. 1. The 1Q1 and 3Q1 states correlate asymptotically to the same fragments, CH3 + I(2P3/2), while 3Q0 correlates to the CH3 + I*(2P1/2) products. For simplicity, hereafter these two product channels will be referred to as the I and I* channels, respectively. The asymptote of 3Q0 is separated from that of 1Q1 and 3Q1 by the iodine spin–orbit splitting, 0.943 eV.14 In addition, a conical intersection (CI) connects the 3Q0 and 1Q1 states, so a wave packet initially excited to any of these two states will bifurcate at the CI, producing both CH3 + I and CH3 + I* fragments.
In the following, we describe briefly the GO procedure on which the control scheme applied in this work is based. The cross section for the photodissociation of CH3I in the electronic channel e (I or I*) can be written, in its time-dependent formulation, as
 | (1) |
We can write the expression for the total cross section in channel e in a very succinct way, as
 | (2) |
 is the projection operator over the desired scattering state, and
is the projection operator over the desired scattering state, and | (3) |
 , eqn (2) becomes
, eqn (2) becomes  . Now, if instead of a single eigenstate, the initial state is a coherent superposition of N vibrational eigenstates of the ground state potential
. Now, if instead of a single eigenstate, the initial state is a coherent superposition of N vibrational eigenstates of the ground state potential  , the photodissociation cross section will be proportional to
, the photodissociation cross section will be proportional to | (4) |
 , and the coefficients of the superposition were arranged as a column vector c (or its conjugate transpose row vector cT). As long as Se has non-diagonal elements, σe will exhibit interference patterns, such that one can maximize the quantum yield over the desired channel by optimizing the initial superposition state.
, and the coefficients of the superposition were arranged as a column vector c (or its conjugate transpose row vector cT). As long as Se has non-diagonal elements, σe will exhibit interference patterns, such that one can maximize the quantum yield over the desired channel by optimizing the initial superposition state.
To do so, we define a functional of the quantum yield on channel I, χI = σI/σdis, where the total photodissociation cross section is σdis = σI + σI*, and we calculate its gradient with respect to cT (or c). Imposing constraints over the norm of the initial wave function, cTc = 1, we obtain the nonlinear eigenvalue equation
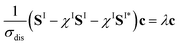 | (5) |
The maximum yield can be obtained from the eigenvector with largest eigenvalue cop, which provides the optimal initial superposition Ψ(0), as
 | (6) |
Notice that Ψ(0) is obtained in a completely different way from the optimal superpositions that maximize absolute yields, as found in previous derivations using the geometrical optimization.52,53,56 The same procedure can be followed to maximize the quantum yield in channel I*.
Wave packet calculations
In the present dynamical simulations, methyl iodide is represented as a CXI pseudotriatomic molecule,23 where the pseudoatom X = H3 is located at the center-of-mass of the three H atoms. In this model, three degrees of freedom represented by the (R, r, θ) Jacobi coordinates are included, where the dissociation coordinate R is the distance between I and the CH3 (or C–X) center-of-mass, r is the C–X distance and it represents the umbrella bend of the C–H3 group (ν2), and θ is the angle between the vectors associated with R and r and it represents the X–C–I bend (ν6). The assumption of modeling the umbrella mode of the C–H3 group in CH3I as a C–X stretching has been justified by a number of theoretical works,18–20,22,23,28 which were successful in reproducing most of the experimental data. In the simulations, zero total angular momentum (J = 0) is assumed for the system.The Hamiltonian and the potential-energy surfaces (PES) have been described in detail elsewhere.18,19 In summary, the ![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1 ground state PES is represented as a sum of three potential interactions in the RC–I (the C–I internuclear distance), r, and θ coordinates, respectively. The interaction potential in the RC–I coordinate is taken from the two-dimensional (2D) ground-state potential for CH3I, obtained by means of multireference spin–orbit configuration interaction ab initio calculations.57 The potential interactions in the r, and θ coordinates are modeled by harmonic oscillator functions. For the 3Q0 and 1Q1 excited electronic states and the nonadiabatic coupling between them, we have used the ab initio surfaces reported by Xie et al.,28 which are an improved version of the previous nine-dimensional surfaces of Amatatsu et al.,27 where the remaining six coordinates are fixed at their equilibrium values. The 2D ab initio PES of Alekseyev et al.,58 was used for the 3Q1 excited state, modelling the θ dependence of the potential surface.19 The electric-dipole moment functions coupling radiatively
1A1 ground state PES is represented as a sum of three potential interactions in the RC–I (the C–I internuclear distance), r, and θ coordinates, respectively. The interaction potential in the RC–I coordinate is taken from the two-dimensional (2D) ground-state potential for CH3I, obtained by means of multireference spin–orbit configuration interaction ab initio calculations.57 The potential interactions in the r, and θ coordinates are modeled by harmonic oscillator functions. For the 3Q0 and 1Q1 excited electronic states and the nonadiabatic coupling between them, we have used the ab initio surfaces reported by Xie et al.,28 which are an improved version of the previous nine-dimensional surfaces of Amatatsu et al.,27 where the remaining six coordinates are fixed at their equilibrium values. The 2D ab initio PES of Alekseyev et al.,58 was used for the 3Q1 excited state, modelling the θ dependence of the potential surface.19 The electric-dipole moment functions coupling radiatively ![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1 with the three excited electronic states were also taken from the work of Alekseyev et al.58
1A1 with the three excited electronic states were also taken from the work of Alekseyev et al.58
The dynamical simulations solve the time-dependent Schrödinger equation.18,19 Computational details on the basis set used to represent the wave packet, on the calculation of the initial state, and on the wave packet propagation have been given elsewhere.19 The initial states propagated consisted of the direct product φv(R)ρ(r, θ), where ρ(r, θ) is the ground vibrational state associated with the r and θ coordinates, and φv(R) is the vibrational state associated with the R mode. Six different initial vibrational states φv(R)ρ(r, θ) with v = 0–5 were propagated. The initial state amplitude is pumped from ![[X with combining macron]](https://www.rsc.org/images/entities/char_0058_0304.gif) 1A1 to the three excited states by means of a laser field of the form ε(t) = A(t)
1A1 to the three excited states by means of a laser field of the form ε(t) = A(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt + ϕ), where A(t) is a Gaussian function, ω is the photon frequency of the incident radiation, and ϕ = 0 for simplicity. Three different excitation wavelengths were used, namely 316 nm (3.92 eV), 266 nm (4.66 eV), and 216 nm (5.74 eV). Four different laser pulses were applied with pulse durations of 5, 15, 30, and 60 fs (full width at half maximum, FWHM). The intensity of the pulses ranges in the weak-field regime (of the order of 109 W cm−2). The intensity of the different pulses was scaled with appropriate factors to ensure a constant pulse area ∫dt|ε(t)|2 in all the simulations. The wave packet propagation was carried out for a total time tf = 300 fs, with a time step of 0.1 fs. This propagation time ensures that all the wave packet amplitude reaches the asymptotic region.
cos(ωt + ϕ), where A(t) is a Gaussian function, ω is the photon frequency of the incident radiation, and ϕ = 0 for simplicity. Three different excitation wavelengths were used, namely 316 nm (3.92 eV), 266 nm (4.66 eV), and 216 nm (5.74 eV). Four different laser pulses were applied with pulse durations of 5, 15, 30, and 60 fs (full width at half maximum, FWHM). The intensity of the pulses ranges in the weak-field regime (of the order of 109 W cm−2). The intensity of the different pulses was scaled with appropriate factors to ensure a constant pulse area ∫dt|ε(t)|2 in all the simulations. The wave packet propagation was carried out for a total time tf = 300 fs, with a time step of 0.1 fs. This propagation time ensures that all the wave packet amplitude reaches the asymptotic region.
Partial photodissociation cross sections are computed along time by projecting out the asymptotic wave packet onto the corresponding fragment states, by means of the method of Balint-Kurti et al.59,60
 | (7) |
| kvi,ν,j = [2m(E − VSOδi1 − Eν,j)]1/2, | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where χν(j)(r) are the rovibrational states of C–X in the umbrella mode (with associated rovibrational energies Eν,j) and Pj(cos
θ), where χν(j)(r) are the rovibrational states of C–X in the umbrella mode (with associated rovibrational energies Eν,j) and Pj(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) are Legendre polynomials. Ψi,v(Rc, r, θ, t′) is the wave packet in the excited electronic state i at time t′. Eqn (7) is the expanded form of the more compact eqn (1). In the same way, the expanded form of Ave,n(E) that appears in eqn (2) [or Aje,n(E) and Ake,n(E) that appear in eqn (4)] is
θ) are Legendre polynomials. Ψi,v(Rc, r, θ, t′) is the wave packet in the excited electronic state i at time t′. Eqn (7) is the expanded form of the more compact eqn (1). In the same way, the expanded form of Ave,n(E) that appears in eqn (2) [or Aje,n(E) and Ake,n(E) that appear in eqn (4)] is | (9) |
Results and discussion
Photodissociation of CH3I in the absence of control
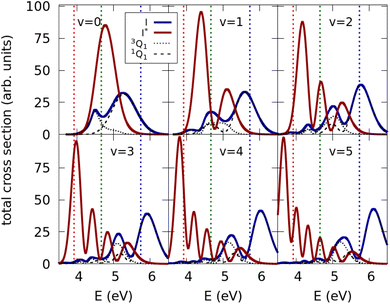
The photodissociation dynamics of CH3I in the A band has been computed for six different initial vibrational states of the ground electronic potential, corresponding to the v = 0–5 vibrations of the CH3–I stretching mode. From these simulations, the corresponding Ave,n(E) quantities are obtained (see the Methodology section), and with them, the optimized quantum yields of the I and I* channels are found by means of eqn (4)–(6). Before discussing the results of the optimization, it is interesting to analyze the absorption spectra calculated from a single vibrational state v, i.e., in the absence of control, when the photodissociation cross section is obtained with eqn (1) instead of (4). Such spectra are displayed in Fig. 2 for the initial states corresponding to v = 0–5. Each panel of Fig. 2 shows three spectra corresponding to the 3Q0, 1Q1, and 3Q1 electronic states. The spectra are calculated as the square of the Fourier transform of the autocorrelation function of the time-dependent wave packet evolving on each excited electronic state. We note that the 3Q0 state contributes to the I* fragmentation channel, while both the 1Q1 and 3Q1 states contribute to the I channel.The three spectra associated with each v state reflect the nodal pattern of the corresponding vibrational wave function, as expected from the reflection principle in repulsive electronic states.61 The absorption spectrum of CH3I was measured by Gedanken and Rowe,12 and they found that the ratio between the maximum of intensity of the sub-bands associated with the 3Q0, 1Q1, and 3Q1 states were 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, respectively. From the spectra of Fig. 2, it is seen that, when using the best currently available ab initio potential-energy surfaces, as done in the present work, the intensity of the 1Q1 and 3Q1 sub-bands is overestimated (and particularly that of 3Q1). The population of the different v states is determined by a Boltzmann distribution at the temperature at which CH3I is prepared in the photodissociation experiment. At typical experimental temperatures, most of the population of this distribution is at v = 0, and drops very fast for v > 0. Thus the CH3I absorption spectrum in the A band is essentially dominated by that corresponding to v = 0. Indeed, this is why the spectra of the v = 0 panel of Fig. 2 are quite similar to those measured by Gedanken and Rowe12 (leaving apart the differences in intensity of the 1Q1 and 3Q1 sub-bands; see Fig. 4 of ref. 12).
3, respectively. From the spectra of Fig. 2, it is seen that, when using the best currently available ab initio potential-energy surfaces, as done in the present work, the intensity of the 1Q1 and 3Q1 sub-bands is overestimated (and particularly that of 3Q1). The population of the different v states is determined by a Boltzmann distribution at the temperature at which CH3I is prepared in the photodissociation experiment. At typical experimental temperatures, most of the population of this distribution is at v = 0, and drops very fast for v > 0. Thus the CH3I absorption spectrum in the A band is essentially dominated by that corresponding to v = 0. Indeed, this is why the spectra of the v = 0 panel of Fig. 2 are quite similar to those measured by Gedanken and Rowe12 (leaving apart the differences in intensity of the 1Q1 and 3Q1 sub-bands; see Fig. 4 of ref. 12).
Focusing on the v = 0 spectra of Fig. 2, we have chosen three energy regions in order to illustrate the universality of our approach. These three regions are denoted by the three vertical lines displayed in the panels of Fig. 2. One energy region is centered at 266 nm (4.66 eV), where the 3Q0 sub-band is clearly the dominant one. A second region is around 216 nm (5.74 eV), where the 1Q1 sub-band dominates. Finally, we consider a third region around 316 nm (3.92 eV), at the tail of the spectra, where the yields of the I and I* channels are similar.
Optimization of the quantum yield of the I fragment channel at 266 nm
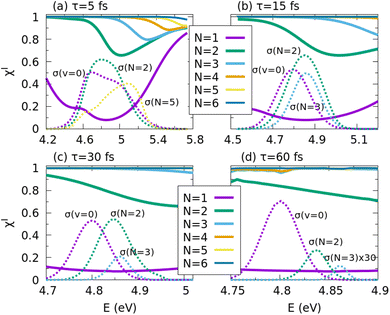
First, we maximize the yield of the I channel in the region around 266 nm, where the I* channel dominates. For this purpose, pulses of different duration, τ = 5, 15, 30, and 60 fs, are applied to induce the photodissociation from the optimized initial wave functions formed as superpositions of the N lowest vibrational excitations of the CH3–I stretching mode, where N varies from 2 to 6. The vibrational quantum of energy of this mode is E1 − E0 = 490.8 cm−1, where Ev is the energy of the v vibrational state. In the 266 nm energy region, CH3I is mainly excited to the 3Q0 state. After passing the conical intersection, the molecule dissociates producing mostly CH3 + I* fragments. A much smaller amount of CH3I + I products is formed (see the v = 0 panel of Fig. 2) as a result of the dissociation in 1Q1 after a 1Q1 ← 3Q0 transition at the conical intersection, added to the fragmentation of the population initially excited to 1Q1 and 3Q1.The results of maximizing the quantum yield of the I channel at 266 nm are shown in Fig. 3. The energy range of the four panels of Fig. 3 changes because it is related to the spectral bandwidth of the different pulses. For the 5 fs pulse, its spectral FWHM is 3536 cm−1, while for the 60 fs pulse, the bandwidth is 295 cm−1, twelve times smaller. The I channel cross sections  , displayed in the panels for three of the optimal initial superpositions, show the energy range covered by the superpositions. For the ground state v = 0, labelled as N = 1, the I channel quantum yield can be as small as 0.1. This result should be taken as the reference value in order to assess the degree of control achieved with the optimized initial superpositions. Interestingly, already with the N = 2 superposition (including v = 0 and 1), the I channel yield increases typically up to 0.7–0.9. And for N ≥ 3 the yield becomes 1 or nearly 1 in practically all the relevant excitation energy range, which implies maximizing the I yield by a factor as large as 9–10 with respect to the N = 1 initial state. Therefore, by optimizing the initial superposition state, one can fully revert the fraction of fragments in the ground state I, over that in the excited state I*. Remarkably, throughout the spectral region encompassing the pump pulse bandwidth, one can obtain quantum yields very close to unity, using only the three lowest vibrational states, regardless of the pump pulse duration. This degree of control is probably only possible when the superposition state involves excitations of the CH3–I stretching mode, which correlates with the reaction coordinate.
, displayed in the panels for three of the optimal initial superpositions, show the energy range covered by the superpositions. For the ground state v = 0, labelled as N = 1, the I channel quantum yield can be as small as 0.1. This result should be taken as the reference value in order to assess the degree of control achieved with the optimized initial superpositions. Interestingly, already with the N = 2 superposition (including v = 0 and 1), the I channel yield increases typically up to 0.7–0.9. And for N ≥ 3 the yield becomes 1 or nearly 1 in practically all the relevant excitation energy range, which implies maximizing the I yield by a factor as large as 9–10 with respect to the N = 1 initial state. Therefore, by optimizing the initial superposition state, one can fully revert the fraction of fragments in the ground state I, over that in the excited state I*. Remarkably, throughout the spectral region encompassing the pump pulse bandwidth, one can obtain quantum yields very close to unity, using only the three lowest vibrational states, regardless of the pump pulse duration. This degree of control is probably only possible when the superposition state involves excitations of the CH3–I stretching mode, which correlates with the reaction coordinate.
For the control to be possible, different pathways must connect the initial states with the same final scattering state at energy Efinal = Ev + ℏωblue = Ev+1 + ℏωred, where ωblue and ωred are blue-shifted or red-shifted components of the pump pulse. Broadband pulses allow this interference between vibrational states to happen naturally. Indeed, the energy difference between v = 0 and v = 5 for the CH3–I stretching mode is 2472 cm−1, which can be covered by the bandwidth of the 5 and 15 fs pulses. Thus, pathways emerging from all these states can interfere between themselves and contribute almost equally. This is not the case for pulses of 60 fs (or even for 30 fs). The bandwidth of a 60 fs pulse allows interference only between energetically adjacent vibrational states. Moreover, at an energy E = E0 + ℏω, the amplitude of the field that allows excitation from E1, ε(ω − ωCH3–I), is only ∼0.05% of the peak amplitude, ε(ω). Control over the quantum yield of a given channel is achieved by almost suppressing the photodissociation in the other channel from the different vibrational states. This is the reason why, in controlling the yield, the value of the cross section in the I channel is mostly conserved with respect to the cross section obtained from the single v = 0 initial state, while the cross section in the I* channel is almost suppressed when using the shorter pulses (τ = 5 and 15 fs). For these pulses, the interference terms between the different vibrational states [see eqn (4)] are strong, allowing to suppress the I* yield while still conserving the intensity of σIop as N increases. The I yield is maximized without reducing its cross section. For longer pulses, and particularly for τ = 60 fs, the smaller bandwidth leads to remarkably fewer and weaker interference terms in eqn (4), which are much smaller than the diagonal terms except at the edges of the spectra for the different vibrational states (shown in Fig. 2), where σv(E) is small. Hence, control over the yield can only be achieved at the expense of reducing the cross section of the I channel as N increases. That is, fewer molecules are excited, but those excited produce almost exclusively I fragments.
Optimization of the quantum yield of the I* and I fragment channels at 316 and 216 nm
In Fig. 4 the performance of the control scheme is illustrated at the two edges of the CH3I A band, in the regions around 316 and 216 nm, by applying a τ = 5 fs pulse. For excitations around 316 nm, the yields of the I and I* channels are very low (see the v = 0 panel of Fig. 2). The N = 1 (v = 0) yield of Fig. 4a and c show that up to 3.9 eV the I yield is completely dominant over the I* yield, but for larger excitation energies the situation is gradually inverted. Thus, this energy region reflects a similar situation for the two channels in the absence of control, namely the passage of small yield to nearly unity or vice versa. When the control is exerted by optimizing the initial state, it is found that a yield of unity is achieved in practically all of the energy range for both fragmentation channels. Interestingly, a yield of unity is already obtained for most of the energies with the simplest and smallest N = 2 (v = 0 and 1) superposition. Moreover, in the case of the I* channel, the cross section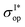 increases for N = 2 and 3 with respect to N = 1, as shown in Fig. 4a. Thus, the control scheme can maximize the yield of both channels in the same energy region, reverting situations of small (and nearly zero) yield to achieve yields of 1.
increases for N = 2 and 3 with respect to N = 1, as shown in Fig. 4a. Thus, the control scheme can maximize the yield of both channels in the same energy region, reverting situations of small (and nearly zero) yield to achieve yields of 1.
In the region around 216 nm, the I channel is dominant, as shown in the v = 0 panel of Fig. 2. This is reflected in the very high yield (typically >0.9) found for the single v = 0 initial state in the absence of control in Fig. 4d. The corresponding yield of the I* channel is typically <0.1, as shown in Fig. 4b. Clearly, no much more optimization of the I channel yield can be achieved by optimizing the initial superpositions, but still this yield is remarkably maximized at energies <5.7 eV when the size of the superposition is increased in Fig. 4d. The real maximization is achieved for the I* channel yield, which varies from typically less than 0.1 to nearly unity as N increases, as found in Fig. 4b. However, the maximization of the I* channel yield is obtained at the expense of reducing its absolute cross section, which decreases rapidly as N increases. The reason behind this result is similar to that governing the optimization with increasing N with a 60 fs pulse. The large difference between the cross sections of the I and I* channels at 216 nm (see the v = 0 panel of Fig. 2), with the I* cross section being very small, causes the terms of interference between the vibrational states to be small enough to prevent the suppression of the I yield, except at the edges of the spectra of the different v states, where the I* cross section also decreases remarkably. Using a pulse with a peak excitation energy around 5.3–5.4 eV (instead of the 5.74 eV associated with 216 nm), where the difference between the I and I* cross sections is not so large (as seen in the v = 0 spectra of Fig. 2), would lead to maximizing the I* yield up to unity without reducing significantly the I* cross section, resembling the situation found in Fig. 3a. We chose, however, the extreme situation for the I* channel at excitation energies around 216 nm in order to show that even in those unfavorable conditions our control scheme can maximize the yield of a channel with a very low intensity.
Experimental implementations
In the following, we discuss two possible experimental implementations. The scheme essentially consists of two steps: (a) preparation of the optimized initial superposition, and (b) excitation of the prepared superposition to the excited electronic states with a weak short visible-ultraviolet (VUV) laser pulse. Since the second step can be performed routinely nowadays,18,20 we will focus on the first step.The most direct method to prepare the superposition of vibrational states uses infrared (IR) lasers. In the case of the CH3–I stretching mode, the carrier frequency must be near 500 cm−1. Because the energy separation between the six lowest vibrational states is much larger than the pulse carrier frequency (∼2500 cm−1 between v = 0 and v = 5), single-photon excitation of all the states by a broadband IR pulse is not possible. In addition, a weak field would not provide enough amplitude in the excited vibrational states to allow for an effective interference between them. Thus, a strong IR pulse will be needed to reach the upper states by multiphoton absorption. The duration of the pulse should be chosen to overcome the anharmonicity of the vibrational spectrum, which is just ∼24 cm−1 in our case, for which a 19.6 μm picosecond pulse could be used. The optimization can be achieved by pulse shaping, applying an adaptive feedback genetic algorithm.5,8,11,32 Indeed, the strategy is to generate the optimal combination of (complex) amplitudes in the different vibrational states of the initial superposition, such that these amplitudes interfere in the proper way to produce the desired final quantum yield. Such amplitudes can be prepared by using an IR pulse able to excite all the vibrational states of the superposition, properly shaped by the iterative adaptive feedback genetic algorithm to generate the required optimal combination. Although most acousto-optic modulators operate in the near IR,62 some new techniques have been reported that can be used for pulses with wavelengths up to 20 μm as in our case.63 Alternatively, free-electron laser facilities could be used to generate the required fields.64,65
This scheme can be substantially simplified when the initial superposition involves only two vibrational states, which can already improve the initial yield by more than 500% for most energies, as shown in Fig. 3 and 4. Then the optimized superposition can be prepared by just controlling two parameters: the intensity of the IR pulse, that accounts for the relative populations in the superposition, and the time-delay between the IR pulse and the VUV pulse, which allows to fix the relative phase between the coefficients of the superposition at the time the wave packet is pumped to the excited state. No pulse shaper is then needed. The simplicity of this experimental scheme should endorse the possibility of its practical implementation.
Finally, a superposition of vibrational states can also be prepared by stimulated Raman using two ultrashort pulses.29,66,67 In this case, the dynamics follows through a pump–dump–pump process, where the second pump can be identical to the first one. The first excursion in the excited dissociative states is used to displace the wave packet from the Franck–Condon region, creating the initial superposition, which can be further optimized using pulse shapers and genetic algorithms in the usual manner. The second excursion leads to fragmentation.
Conclusions
In summary, a robust control scheme to modify extensively the quantum yields of the different channels of a molecular nonadiabatic photodissociation process is proposed. The scheme relies on preparing and optimizing an initial coherent superposition of vibrational states of the molecule in the ground electronic state, which is pumped to the excited states by a simple weak ultrashort (fs), Gaussian-type laser pulse. Interference between the amplitudes of the optimized superposition is what allows maximization of the yields of the different fragmentation channels. The control scheme is applied to the CH3I photodissociation in the A band, where it is shown that the scheme can maximize up to unity the yield of the two fragmentation channels of the process over the whole spectral range of the band. We show that the coherences encoded in the initial state are enough to guide the dynamics in this polyatomic molecule, under the presence of strong non-adiabatic (uncontrolled) couplings, such that absolute control over the quantum yield of any of the two fragmentation channels can be achieved. The control mechanism is based on destructive interference over the quantum pathways that lead to the undesired fragment. But using ultrashort pulses, we demonstrate that the high branching ratios are not achieved at the expense of small absolute photodissociation cross sections. Experimental implementations of the control scheme are suggested, some of them being simple enough as to guarantee its development in practice. The magnitude of the control effects found in this work is large enough as to be easily demonstrated experimentally. The proposed scheme is envisioned as general and universal in its application to molecular photodissociation processes.Data availability
All the data related to this work are available upon request to the authors.Author contributions
I. R. S. and A. G.-V. conceptualized and designed the project, performed the calculations, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Ministerio de Ciencia e Innovación of Spain (MICINN), Grant No. PID2021-122796NB-I00. This project has received funding from the COST Action CA21101 (COSY). The Centro de Supercomputación de Galicia (CESGA, Spain) is acknowledged for the use of its resources.Notes and references
- S. A. Rice and M. Zhao, Optical Control of Molecular Dynamics, Wiley, New York, 2000 Search PubMed.
- M. Shapiro and P. Brumer, Quantum control of molecular processes, John Wiley & Sons, Hoboken, 2012 Search PubMed.
- H. Rabitz, R. de Vivie-Riedle, M. Motzkus and K. Kompa, Science, 2000, 288, 824–828 CrossRef CAS PubMed.
- T. Brixner and G. Gerber, ChemPhysChem, 2003, 4, 418 CrossRef CAS PubMed.
- M. Wollenhaupt, V. Engel and T. Baumert, Annu. Rev. Phys. Chem., 2005, 56, 25–56 CrossRef CAS PubMed.
- G. G. Balint-Kurti, S. Zou and A. Brown, Adv. Chem. Phys., 2008, 138, 43–94 CrossRef CAS.
- V. Engel, C. Meier and D. J. Tannor, Adv. Chem. Phys., 2009, 29–101 CrossRef CAS.
- C. Brif, R. Chakrabarti and H. Rabitz, New J. Phys., 2010, 12, 075008 CrossRef.
- D. Townsend, B. J. Sussman and A. Stolow, J. Phys. Chem. A, 2011, 115, 357–373 CrossRef CAS PubMed.
- P. v. d. Hoff, S. Thallmair, M. Kowalewski, R. Siemering and R. d. Vivie-Riedle, Phys. Chem. Chem. Phys., 2012, 14, 14460–14485 RSC.
- I. R. Sola, B. Y. Chang, S. A. Malinovskaya and V. S. Malinovsky, Adv. At., Mol., Opt. Phys., 2018, 67, 151–256 Search PubMed.
- A. Gedanken and M. D. Rowe, Chem. Phys. Lett., 1975, 34, 39–43 CrossRef CAS.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1998, 109, 4758–4767 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1999, 110, 832–844 CrossRef CAS.
- M. H. M. Janssen, M. Dantus, H. Guo and A. H. Zewail, Chem. Phys. Lett., 1993, 214, 281–289 CrossRef CAS.
- P. C. Samartzis, B. L. G. Bakker, D. H. Parker and T. N. Kitsopoulos, J. Phys. Chem. A, 1999, 103, 6106–6113 CrossRef CAS.
- R. de Nalda, J. Durá, A. García-Vela, J. G. Izquierdo, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2008, 128, 244309 CrossRef PubMed.
- L. Rubio-Lago, A. García-Vela, A. Arregui, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 174309 CrossRef CAS PubMed.
- A. García-Vela, R. de Nalda, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2011, 135, 154306 CrossRef PubMed.
- C. Hu, S. Pei, Y.-L. Chen and K. Liu, J. Phys. Chem. A, 2007, 111, 6813–6821 CrossRef CAS PubMed.
- M. Shapiro and R. Bersohn, J. Chem. Phys., 1980, 73, 3810–3817 CrossRef CAS.
- H. Guo, J. Chem. Phys., 1992, 96, 6629–6642 CrossRef CAS.
- A. D. Hammerich, U. Manthe and R. Kosloff, J. Chem. Phys., 1994, 101, 5623–5646 CrossRef.
- C. R. Evenhuis and U. Manthe, J. Phys. Chem. A, 2011, 115, 5992–6001 CrossRef CAS PubMed.
- Y. Amatatsu, K. Morokuma and S. Yabushita, J. Chem. Phys., 1991, 94, 4858–4876 CrossRef CAS.
- Y. Amatatsu, S. Yabushita and K. Morokuma, J. Chem. Phys., 1996, 104, 9783–9794 CrossRef CAS.
- D. Xie, H. Guo, Y. Amatatsu and R. Kosloff, J. Phys. Chem. A, 2000, 104, 1009 CrossRef CAS.
- D. J. Tannor and S. A. Rice, J. Chem. Phys., 1985, 83, 5013–5018 CrossRef CAS.
- D. Tannor, R. Kosloff and S. A. Rice, J. Chem. Phys., 1986, 85, 5805 CrossRef CAS.
- P. Brumer and M. Shapiro, Chem. Phys. Lett., 1986, 126, 541–546 CrossRef CAS.
- R. S. Judson and H. Rabitz, Phys. Rev. Lett., 1992, 68, 1500 CrossRef CAS PubMed.
- A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber, Science, 1998, 282, 919 CrossRef CAS PubMed.
- P. Anfirud, R. de Vivie-Riedle and V. Engel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8328–8329 CrossRef PubMed.
- T. Brixner, N. H. Damrauer, P. Niklaus and G. Gerber, Nature, 2001, 414, 57 CrossRef CAS PubMed.
- R. J. Levis, G. M. Menkir and H. Rabitz, Science, 2001, 292, 709 CrossRef CAS PubMed.
- C. Daniel, J. Full, L. González, C. Lupulescu, J. Manz, A. Merli, S. Vajda and L. Wöste, Science, 2003, 299, 536–539 CrossRef CAS PubMed.
- M. Sukharev and T. Seideman, Phys. Rev. Lett., 2004, 93, 093004 CrossRef PubMed.
- B. J. Sussman, D. Townsend, M. Y. Ivanov and A. Stolow, Science, 2006, 314, 278–281 CrossRef CAS PubMed.
- H. Goto, H. Katsuki, H. Ibraim, H. Chiba and K. Ohmori, Nat. Phys., 2011, 7, 383–385 Search PubMed.
- L. S. Cederbaum, Y.-C. Chiang, P. V. Demekhin and N. Moiseyev, Phys. Rev. Lett., 2011, 106, 123001 CrossRef PubMed.
- A. García-Vela, J. Phys. Chem. Lett., 2012, 3, 1941–1945 CrossRef.
- M. E. Corrales, J. González-Vázquez, G. Balerdi, I. R. Sola, R. de Nalda and L. Bañares, Nat. Chem., 2014, 6, 785 CrossRef CAS PubMed.
- A. García-Vela and N. E. Henriksen, J. Phys. Chem. Lett., 2015, 6, 824–829 CrossRef PubMed.
- M. E. Corrales, R. de Nalda and L. Bañares, Nat. Commun., 2017, 8, 1345 CrossRef PubMed.
- A. García-Vela, Phys. Rev. Lett., 2018, 121, 153204 CrossRef PubMed.
- A. Serrano-Jiménez, L. Bañares and A. García-Vela, Phys. Chem. Chem. Phys., 2019, 21, 7885 RSC.
- K. B. Møller, N. E. Henriksen and A. H. Zewail, J. Chem. Phys., 2000, 113, 10477–10485 CrossRef.
- B. Amstrup and N. E. Henriksen, J. Chem. Phys., 1992, 97, 8285–8295 CrossRef CAS.
- S. Meyer and V. Engel, J. Phys. Chem. A, 1997, 101, 7749–7753 CrossRef CAS.
- N. Elghobashi and L. González, Phys. Chem. Chem. Phys., 2004, 6, 4071–4073 RSC.
- B. Y. Chang, S. Shin and I. R. Sola, J. Phys. Chem. Lett., 2015, 6, 1724–1728 CrossRef CAS PubMed.
- B. Y. Chang, S. Shin and I. R. Sola, J. Chem. Theory Comput., 2015, 11, 4005–4010 CrossRef CAS PubMed.
- B. Y. Chang, S. Shin and I. R. Sola, J. Phys. Chem. A, 2015, 119, 9091–9097 CrossRef CAS PubMed.
- B. Y. Chang, S. Shin, V. Engel and I. R. Sola, J. Phys. Chem. A, 2017, 121, 8280–8287 CrossRef CAS PubMed.
- C. G. Arcos, A. García-Vela and I. R. Sola, J. Phys. Chem. Lett., 2024, 15, 1442 CrossRef PubMed.
- A. B. Alekseyev, H.-P. Liebermann, R. J. Buenker and S. N. Yurchenko, J. Chem. Phys., 2007, 126, 234102 CrossRef PubMed.
- A. B. Alekseyev, H.-P. Liebermann and R. J. Buenker, J. Chem. Phys., 2007, 126, 234103 CrossRef PubMed.
- G. G. Balint-Kurti, R. N. Dixon and C. C. Marston, J. Chem. Soc., Faraday Trans., 1990, 86, 1741 RSC.
- G. G. Balint-Kurti, R. N. Dixon and C. C. Marston, Int. Rev. Phys. Chem., 1992, 11, 317 Search PubMed.
- R. Schinke, Photodissociation Dynamics: Spectroscopy and Fragmentation of Small Polyatomic Molecules, Cambridge University Press, Cambridge, 1993 Search PubMed.
- A. M. Weiner, Rev. Sci. Instrum., 2000, 71, 1929–1960 CrossRef CAS.
- A. Cartella, S. Bonora, M. Först, G. Cerullo, A. Cavalleri and C. Manzoni, Opt. Lett., 2014, 39, 1485–1488 CrossRef PubMed.
- P. O'Shea and H. Freund, Science, 2001, 292, 1853–1858 CrossRef PubMed.
- C. Feng and H.-X. Deng, Nucl. Sci. Tech., 2018, 29, 160 CrossRef.
- L. Dhar, J. A. Rogers and K. A. Nelson, Chem. Rev., 1994, 94, 157–193 CrossRef CAS.
- U. Banin, A. Bartana, S. Ruhman and R. Kosloff, J. Chem. Phys., 1994, 101, 8461–8481 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |