Origin of copper dissolution under electrocatalytic reduction conditions involving amines

Abstract

Cu dissolution has been identified as the dominant process that causes cathode degradation and losses even under cathodic conditions involving methylamine. Despite extensive experimental research, our fundamental and theoretical understanding of the atomic-scale mechanism for Cu dissolution under electrochemical conditions, eventually coupled with surface restructuring processes, is limited. Here, driven by the observation that the working Cu electrode is corroded using mixtures of acetone and methylamine even under reductive potential conditions (−0.75 V vs. RHE), we employed Grand Canonical density functional theory to understand this dynamic process under potential from a microscopic perspective. We show that amine ligands in solution directly chemisorb on the electrode, coordinate with the metal center, and drive the rearrangement of the copper surface by extracting Cu as adatoms in low coordination positions, where other amine ligands can coordinate and stabilize a surface copper–ligand complex, finally forming a detached Cu–amine cationic complex in solution, even under negative potential conditions. Calculations predict that dissolution would occur for a potential of −1.1 V vs. RHE or above. Our work provides a fundamental understanding of Cu dissolution facilitated by surface restructuring in amine solutions under electroreduction conditions, which is required for the rational design of durable Cu-based cathodes for electrochemical amination or other amine involving reduction processes.

---

1. Introduction

The electrochemical reductive amination is a green way for the conversion of biomass,^1–3e.g. levulinic acid,^4,5 which is a longer-chain ketone. Thus, it is of great importance to rationally design catalysts that are effective and stable under reaction conditions.

Cu demonstrates high efficiency in facilitating electrochemical amination^2,3,6–11 reactions, where Mürtz et al.³ named copper as a green cathode material for the reductive amination of acetone (the first representative of levulinic acid's homologous series) with methylamine (a simple primary amine) as nitrogen source and obtained N-methylpropan-2-amine in a yield of 65% (±2%). Copper is also used for a large ensemble of electroreduction reactions, such as CO and CO₂ electroreduction into C₁ and C₂₊ products,^12–14 where amines could be a co-reactant, for example in the case of the electroreduction of amine-captured CO₂.¹⁵ Numerous studies have shown that under electrochemical reduction conditions, Cu suffers from instability and the arrangement of Cu surface atoms has a profound effect on performance.^16–18 Even though several experimental instruments, such as liquid cell transmission electron microscopy (TEM)^19–21 and in situ electron microscopy,²² can monitor the morphological evolution of electrocatalysts under reaction conditions,^22–25 where the specific morphological features^26,27 are responsible for a given activity and selectivity, the transient Cu-cation species in solution are straggling to be fully grasped since experimental conclusions are largely drawn from samples that have been removed from the electrochemical environment and evaluated in the absence of an applied potential. However, these redox processes play a role in Cu-reconstruction, including dissolution and re-deposition.²⁸ During the cell startup, when the working electrode experiences cathodic potentials, a dissolution–redeposition of Cu species in solution occurs and induces changes in the catalyst morphology and total exposed surface.^22,29,30 This kind of changes are in need to be explored in order to design durable catalysts.

Here, after a 30 minute electrolysis of an acetone/methylamine mixture, the concentration of Cu in the solution was measured, showing that at −0.75 V vs. RHE, the concentration can still hold a value of around 13 ppm. To probe the underlying mechanism, grand canonical DFT was used to understand the reconstruction and dissolution of copper by complexation with soluble amine ligands. These ligands initially adsorb on the Cu surface in electroreduction conditions and then enable transient restructuring and dissolution of Cu by forming coordination complexes with Cu cations. NH₃ is considered as a model amine in our calculations but, in addition, ligand effects are explored by performing calculations for two other amines as ligands. Our study offers essential insights into the dynamic process of the Cu surface during electrochemical reduction, vital for designing durable Cu-based cathodes for a large array of processes.

2. Results and discussion

2.1 Experimental observations

Building upon the research conducted by Mürtz et al.,³ we utilized the reductive amination technique to synthesize N-methylpropan-2-amine from acetone and methylamine. The electrolysis setup involved Cu‖Pb electrodes with a N-324 membrane (Cu 99.98% from Manufacture Aldrich), using 0.5 M KH₂PO₄ (pH = 8.3) as the electrolyte (the following nomenclature will be used: cathode‖anode, with ‖ being the N-324 membrane). Additionally, a cooling phase lasting 18 minutes was implemented to achieve the desired temperature of 10 °C before starting the electrolysis process. This procedure is crucial for forming the intermediate N-methylpropan-2-imine, as its equilibrium with acetone and methylamine is temperature dependent (Scheme 1).

Scheme 1 The equilibrium reaction of acetone and methylamine is a condensation and yields N-methylpropan-2-imine. The imine can be reduced and results in N-methylpropan-2-amine.

Subsequently, a current density of −40 mA cm⁻² was applied for electrolysis, yielding an amine amount of 3.9% (±0.2%) as measured by quantitative ¹H-NMR spectroscopy (depicted as the first set of bars in Fig. 1), representing a 61% decrease compared to a prior study.³ Notably, corrosion was evident on the copper electrode surface (Fig. S1†), and that corrosion was initiated by methylamine in the reaction solution (Fig. S2†). Initially, after an 18 minute cooling period, copper concentration in solution reached approximately 84 ppm measured via ICP-OES. Employing a cathodic potential around −0.16 V vs. RHE stabilized the working electrode during cooling, where at this stabilizing potential no electrochemical hydrogenation occurred as indicated by the absence of faradaic currents in CV measurements (Fig. S3†). Consequently, the copper concentration decreased to 19 ppm in the acetone–methylamine mixture, leading to an amine yield of 30% (±2%) after subsequent electrolysis. This was still 35% lower than that in the prior work³ but 26% higher than that obtained from the initial test (illustrated in the second set of bars in Fig. 1). The reduced copper concentration and increased amine yield underscore the feasibility of stabilizing the cathode in the presence of methylamine. To assess performance without a cooling phase, a third electrolysis experiment was conducted, yielding an amine of 51% (±2%), albeit still lower than the reported value,³ yet exhibiting the highest yield.

Fig. 1 Examining the influence of the cooling interval and its modification on the electrochemical reductive amination of acetone with methylamine. The resulting yields of N-methylpropan-2-imine (Y_Imine), N-methylpropan-2-amine (Y_Amine) and isopropanol (Y_Alcohol) are depicted. Additionally, the conversion of acetone (X) is illustrated. Carbon balance (C.B.): 80–81%. Experimental conditions include Cu‖Pb electrode with N-324 membrane (was previously used at least 3 times with Pb as anode); current density (j) of −40 mA cm⁻²; Faraday equivalents (F_eq.) = 1; solvent: 0.5 M KH₂PO₄ (pH 8.3); substrates concentrations: acetone: 2.4 M, methylamine: 2.9 M; temperature (T) maintained at 10 °C; pH at 10 °C: 12.9; anolyte: 25% H₃PO₄.

These observations suggest that the cathode surface underwent dissolution during the cooling phase, inhibiting the electrochemical reduction of the imine while promoting water splitting.

As it was observed that a cathodic potential stabilized the copper electrode during the cooling period, the relationship between copper dissolution and applied potential will be investigated next. Four distinct potentials ranging from 0.25 V to −1.25 V vs. RHE were employed for a duration of 30 minutes, followed by measuring the concentration of dissolved copper (depicted in Fig. 2). Generally, enhanced stability of copper is observed at −1.25 V vs. RHE, evidenced by the lower concentration of Cu in the reaction solution post-electrolysis compared to potentials of −0.75 V, −0.25 V, and 0.25 V vs. RHE. This suggests that the stability of copper in the presence of methylamine is contingent upon the applied potential, indicating a critical minimum cathodic potential below which the copper electrode experiences stronger stabilization.

Fig. 2 The effect of the applied potential on copper dissolution from the cathode in the presence of an acetone/methylamine mixture after 30 minutes of electrolysis is examined. Experimental conditions include Cu‖Pb electrodes with a usage of a N-324 membrane (previously utilized at least 3 times with Pb as anode); solvent: 0.5 M KH₂PO₄ (pH 8.3); substrate concentrations: acetone: 2.4 M, methylamine: 2.9 M; temperature (T) maintained at 10 °C; pH at 10 °C: 12.9; anolyte: 25% H₃PO₄.

2.2 Theoretical investigations

The above experimental measurements trigger the question: why does dissolution happen in electroreduction potential (e.g. at −0.75 V vs. RHE)? Here, we computationally determined the mechanism of evolution of the Cu surface in the presence of amine ligands in water and formation of dissolved Cu complexes at different potential conditions using grand canonical density functional theory^31–34 (GC-DFT). Since we consider a negative potential vs. RHE, we modeled a reduced Cu surface, in the absence of O species, as previously experimentally shown in similar reducing conditions.^35,36 The study was performed using the PBE³⁷ exchange correlation functional with dDsC van der Waals correction³⁸ and including implicit solvation effects through the VASPsol³⁹ framework, as reported in the Methods section. A Cu(843) surface presenting step and kink sites and a flat Cu(111) surface were considered to assess the role of low coordination site atoms (kink sites) and close-packed high coordination domains, respectively. Methylamine, NH₂–CH₃, chemisorbs on Cu surfaces by forming strong Cu–N bonds. The –CH₃ group in methylamine introduces additional geometric degrees of freedom. For simplicity, our starting model amine is NH₃, replacing CH₃ with H. In Section 2.2.4, the ligand's effects by itself will be discussed again using other four different amines.

In the simulations, the mechanism of Cu dissolution was then determined from the energetics of formation and transformation of metal–amine complexes, on the Cu surface and their detachment in solution, with various amine counts, under different potential conditions. The formation Gibbs free energy of surface amine complexes is calculated with a reference to the Gibbs free energy of bare Cu slab G_slab and of amine ligands in solution G_ligand, (formula (1) where G_{slab–ligands} is the Gibbs free energy of the restructured Cu slab with chemisorbed amine ligands), while the formation of the dissolved complex is expressed with a reference to the chemical potential of Cu μ_Cu and to the Gibbs free energy of ligands G_ligand in solution (formula (2)). We give here the example of the formation of a dissolved Cu(NH₃)₄²⁺ complex, but other cases will be also described later. Detailed mathematical derivation including entropy terms in the Gibbs free energy are provided in ESI Note 2.1.†

G_formation = G_{slab–ligands} − G_slab − n × G_ligand (1)

G_formation = (G_{Cu(NH3)4²⁺} − 2eU) − μ_Cu − 4 × G_ligand (2)

Additional method information can be found in Section 4.

2.2.1 Restructuring and dissolution process on kink sites of Cu(843). We use the Cu(843) surface to model low coordination defects present on the Cu electrode, as steps or kinks (Fig. 3). The chemisorption of methylamine or NH₃ on the kink sites, which possesses metallic coordination of 6 instead of 9 for the dense Cu(111) terrace, is significantly stronger than that on the (111) terrace (by about 0.5 eV, although the difference is potential dependent) (Fig. 3), while the step site's adsorption is intermediate. Considering that methylamine is interacting with the surface through an occupied lone pair orbital on N, injecting electrons at the surface by going to a more negative potential destabilizes the adsorption, which becomes endergonic for a potential more negative than −2 V vs. RHE. Our starting model amine, NH₃, provides similar adsorption energy compared to methylamine.

Fig. 3 (A) Three different chemisorption sites on Cu(843), including kink site (blue), (100) step site (orange) and (111) terrace site (green). Cu atoms of the upper terrace are in brown for clarity. Free energy of adsorption of methylamine (B) or NH₃ (C) on the three different sites of Cu(843) as a function of potential. pH equals 12.9.

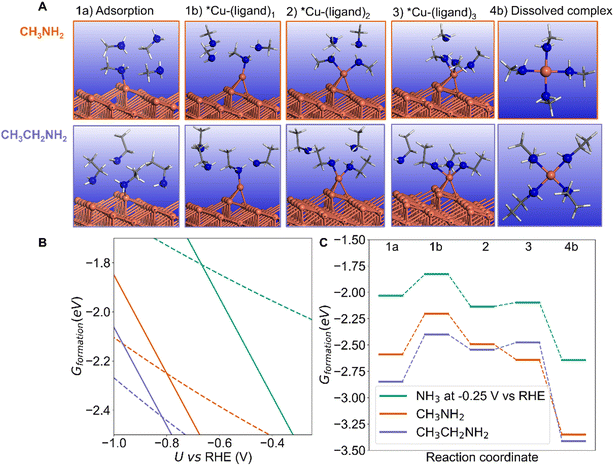
The stronger chemisorption of NH₃ makes the kink site a good candidate for the dissolution process and mechanism.^40,41 We start with one NH₃ molecule adsorbed on the kink site (Fig. 4A – structure 1a). We were not able to locate a stable configuration with two NH₃ molecules bound to the kink atom. However, upon one NH₃ adsorption, the kink Cu atom can be displaced on the terrace as an adatom with low metallic coordination of 3 (Fig. 4A – structure 1b). The energy required to form that NH₃ capped Cu adatom is low (+0.1 to +0.3 eV depending on the potential, Fig. 4C), and this process creates a new kink atom, previously a neighbor of the former kink site. In addition, the formed Cu adatom can accept a second NH₃, in a stabilizing process if the potential is less negative than −0.7 V vs. RHE (Fig. 4A – structure 2). A third NH₃ can bind forming a pseudo-threefold Cu(NH₃)₃ surface complex (Fig. 4A – structure 3). The binding of the fourth NH₃ is slightly more difficult and adopts a “butterfly” C_2v geometry (Fig. 4A – structure 4a).

Fig. 4 Dissolution of the Cu(843) surface in the presence of NH₃ in water as a function of the potential, initiated at the kink site. (A) mechanisms and intermediates during the dissolution; 1a: adsorption of one NH₃ on the Cu kink site, 1b: diffusion of the NH₃-capped kink site Cu atom forming a Cu adatom on the nearby terrace; adsorption of a second (2), third (3) and fourth (4a) NH₃ on the formed Cu adatom; (4b) Cu(NH₃)₄²⁺, Cu(NH₃)₃⁺, and Cu(NH₃)₂²⁺ complexes formation and detachment. (B) Free energy of the NH₃ induced surface or dissolved intermediates described in (A). The vertical blue dashed line describes the threshold potential above which the dissolved complex becomes most stable. (C) Potential dependent reaction pathway for NH₃ adsorption, surface complex formation and detachment, where labels refer to (A). pH equals 12.9.

The surface complex can finally be detached to form a Cu–amine complex in solution,^42–45 in a stabilizing process (Fig. 4A –structures 4b1, 4b2 and 4b3). Complexes with multiple number of ligands or Cu oxidation states can be formed.^43,45–47 It is known that Cu²⁺ with four NH₃ ligands adopts a (quasi)-planar structure.^43–45 Besides, Cu²⁺ can also be complexed by two NH₃ ligands in a linear structure. Cu⁺ should also be considered, where it is reported that this cation forms a tetrahedron configuration with four NH₃ or a planar structure with three NH₃.^42,48 Our detailed explorations of Cu⁺/Cu²⁺ with a maximal number of four NH₃ ligands is reported in ESI Note 2.4.† Our calculations show that for Cu²⁺, the square planar complex is more stable than the tetrahedron by 0.15 eV. Besides, the linear two-ligand complex Cu(NH₃)₂²⁺ is 0.37 eV more stable than the square planar structure. With regard to Cu⁺, if one NH₃ in the tetrahedron complex moves away, it forms a planar structure with three NH₃, which is 0.07 eV more stable. Therefore, a 4-NH₃ square planar Cu²⁺, a 3-NH₃ planar Cu⁺, and 2-NH₃ linear Cu²⁺ structures were chosen to represent the final dissolved complexes. From the calculations, Cu(NH₃)₂²⁺ appears as the most stable dissolution product in our conditions, and dissolution is thermodynamically favored vs. the NH₃ covered Cu surface until a potential of −1.1 V vs. RHE. However other complexes could also be formed, Cu(NH₃)₃⁺ and Cu(NH₃)₄²⁺ being more stable than NH₃ covered Cu surface until −0.9 V and −0.8 V vs. RHE respectively. These threshold stability potentials are dependent on the pH, where lower pH would shift the values to more negative potential, extending the potential range where dissolution occurs. For example, at pH = 10 (compared to 12.9 on Fig. 4), the threshold potentials would be more negative by about 0.1 V.

We will discuss here the formation of the Cu complex with the maximal number of NH₃ ligands (four) as illustrated in Fig. 4C (structure 4b). The overall free energy profile for complexation and dissolution depends on the applied potential. At positive (+0.5 V vs. RHE) or zero potential the process is very easy and thermodynamically limited by the formation of the NH₃ capped Cu adatom. At negative potential, the process becomes limited by the formation of the Cu(NH₃)₄ surface complex. At −0.7 V vs. RHE, the formation of that Cu(NH₃)₄ surface complex represents a reasonable thermodynamic barrier of 0.51 eV. It can be underlined that forming the four-ligand surface complex Cu(NH₃)₄ is not mandatory, since starting from the surface Cu(NH₃)₃ complex, the approach of the fourth NH₃ can be concerted with the detachment of the complex from the surface. In that case, the thermodynamic barrier is only 0.21 eV at −0.7 V vs. RHE. For a potential more negative than −0.8 V vs. RHE, the calculations show that the dissolution process forming Cu(NH₃)₄²⁺ is not thermodynamically favored, and NH₃ adsorption on the kink site becomes more favorable than the formation and detachment of the Cu(NH₃)₄²⁺ complex. This is clearly seen in Fig. 4B, which represents the free energy of the various intermediates as a function of the potential. For more positive potential the dissolved Cu(NH₃)₄²⁺ complex is more stable than chemisorbed NH₃ (structure 1a), while at more negative potential, the chemisorbed NH₃ is more stable. Note that other complexes (Cu(NH₃)₂²⁺, Cu(NH₃)₃⁺) can be stable on a slightly more negative potential zone. We assume here that the various processes have low activation energy, which is typically the case for adsorption and metal atom diffusion at metal surfaces. The dissolution of the kink Cu atom generates a new kink atom on the surface, and the process can continue. It should be underlined that in the absence of an NH₃ ligand, the displacement of the kink Cu atom on the terrace as an adatom is uphill by ∼1 eV so NH₃ is crucial for that restructuring (ESI Note 2.2 and Fig. S5†).

At pH 12, the Pourbaix diagram of Cu in water shows the formation of Cu(OH)₂ at a potential more positive than +0.4 vs. RHE, while the Cu surface is stable at more negative potentials.⁴⁹ Our simulations show the formation of OH adsorbates on the Cu(843) surface at a potential more positive than 0.25 V vs. RHE (ESI Fig. S7 and S8†). The presence of NH₃ therefore results in a considerable potential shift for the stability domain of the Cu electrode, favoring dissolution by formation of the Cu(NH₃)_n complex until a potential of −0.8 V to −1.1 V vs. RHE, depending on the Cu complex formed. The implication is that Cu electrocatalysts cannot be used in a stable manner for electroreduction in the presence of amines.

2.2.2 Restructuring and dissolution process on the Cu(111) surface. The dissolution process starting from a dense Cu(111) surface requires to extract a high coordination atom (coordination 9). We have explored two scenarios. These both start by the chemisorption of one NH₃ on the Cu(111) surface (Fig. 5A, 1a), which is slightly less stable than that on the Cu(843) kink. The second step extracts the surface atom to form an NH₃-capped adatom on the terrace (Fig. 5A, 1b). This forms a surface vacancy. In the first scenario (ESI Fig. S9†), the vacancy is kept as is and the process is highly endergonic (by around 1.50 eV) making it unfavorable. As a second scenario, we suppose that one atom diffuses from the bulk in a concerted way and refills the vacancy. In this condition, the formation of the NH₃-capped Cu adatom is only uphill by 0.24 eV at 0 V vs. RHE, compared to 0.20 eV for the Cu(843) kink site. The formation of the Cu adatom in the absence of the NH₃ ligand is very unfavorable even if the vacancy is refilled (ESI Fig. S5†). The formation of the surface Cu complex occurs in a similar way as that seen for Cu(843), with the coordination of a second, third, and fourth NH₃ molecule, accompanied with the detachment of the Cu complex. Planar Cu(NH₃)₄²⁺, planar Cu(NH₃)₃⁺ and linear Cu(NH₃)₂²⁺ have been again considered. The process is globally less favorable than on the kink atom of the Cu(843) surface. For example, at U = 0 V vs. RHE, the formation of the 4-coordinated surface complex (4a) on Cu(111) is less stable by 0.39 eV compared to the initial adsorbed structure for one NH₃ molecule (1a), while it was slightly more stable for the kink site. The limited stability of the 4-coordinated surface complex can be also illustrated by the unusually long distance for two C–N bonds, 2.6 Å compared to 2.1 Å in the other cases. This reduced stability is explained by lateral repulsion between NH₃ ligands and the flat Cu(111) surface, compared to the somewhat convex situation in the vicinity of the kink site, with more space to fit the ligands.

Fig. 5 Dissolution of the Cu(111) surface in the presence of NH₃ in water, featuring the case where the vacancy is compensated by the concomitant migration of a Cu atom from the bulk, as a function of the potential. (A) mechanisms and intermediates during the dissolution; 1a: adsorption of one NH₃ on the Cu surface, 1b: diffusion of the NH₃-capped Cu atom forming a Cu adatom on the surface, where the accompanying vacancy formation is compensated by the diffusion of a Cu atom from the bulk to the vacancy site; adsorption of a second (2), third (3) and fourth (4a) NH₃ on the formed Cu adatom; (4b) Cu(NH₃)₄²⁺, Cu(NH₃)₃⁺, and Cu(NH₃)₂²⁺ complexes formation and detachment. (B) Free energy of the NH₃ induced surface or dissolved intermediates described in (A). The vertical dashed line describes the threshold potential above which the dissolved complex becomes most stable. (C) Potential dependent reaction pathway for NH₃ adsorption, surface complex formation, and detachment, where labels refer to (A). pH equals 12.9.

The potential thresholds for the stability of the dissolved Cu(NH₃)₂²⁺ is −1.1 V, for that of Cu(NH₃)₃⁺ is −0.9 V and for that of Cu(NH₃)₄²⁺ is −0.8 V vs. RHE, which are the same values as that for Cu(843).This is due to the fact that the binding energy of the kink atom on Cu(843) is equal to the binding energy of Cu in the bulk. In the case of the Cu(111) surface, if the vacancy is filled by a bulk atom, then the dissolution process is equivalent to the detachment of a bulk atom.

Therefore, the dissolution of an atom from a (111) terrace of Cu is possible, if we assume that the formed vacancy can be refilled in a concomitant way by a Cu atom from the bulk. It is somewhat less favorable, however, than the dissolution of a kink atom. In contrast, if the vacancy at the (111) surface is maintained, then the formation of the surface complex and its dissolution become highly endergonic.

2.2.3 Analysis of the Cu dissolution from a chemical bonding perspective. The strength of the chemical bond between the formed Cu adatom and the surface along the surface complex formation can be estimated from the integrated Crystal Orbital Hamilton Population (–ICOHP) value, obtained from the one-electron band structure of the surface (Fig. 6 – A1 and B1). If we start from structure 1b, with one NH₃ ligand, we see that increasing the number of ligands leads to a weakening of the bond between the Cu atom of the surface complex and Cu atoms of the surface. The effect becomes especially strong if four NH₃ ligands are placed on the surface complex, with a reduction by about a factor of two for the case of the kink Cu(843) surface. The effect is similar to that on the (111) surface (in the hypothesis where one bulk atom diffuses and immediately fills the vacancy created by the extracted atom), even if the bond weakening is not as large. This decrease of the Cu–Cu bond strength by NH₃ adsorption is a key feature explaining the Cu atom extraction and dissolution. From there it follows that the detachment of the complex should be easier starting from the surface complex involving four NH₃ ligands, since the bond between the Cu adatom and the surface is markedly weakened. As a result, Cu(NH₃)₄²⁺ should form initially, but could transform in the other complexes upon reaction in the solution. The origin of the weakening of the bond between the Cu adatom and the surface resides in the formation of Cu–N bonds via ligand bonding. Per Cu–N -ICOHP is very comparable on (843) and (111) surfaces for 1, 2, or 3 ligands (1a, 1b, 2, and 3 structures), and the sum of –ICOHP follows a very similar trend. However, when it comes to the fourth ligand binding (4a), the kink surface shows a better capacity to hold it, which is consistent with the higher summed –ICOHP between adatom Cu and surface Cu on Cu(843) and the better stability of the four-NH₃ surface complex.

Fig. 6 Chemical bond strength as quantified by the –ICOHP between extracted Cu in the surface complex and the three bonded surface Cu sites, as a function of the number of NH₃ ligands, on Cu(843) (A1) or Cu(111) (B1). Chemical bond strength as quantified by the -ICOHP between extracted Cu in the surface complex and N atoms of the NH₃ ligands, as a function of the number of NH₃ ligands, on Cu(843) (A2) or Cu(111) (B2). Labels on the x-axis refer to structures in Fig. 4 for Cu(843) and Fig. 5 for Cu(111).

2.2.4 Influence of the nature of the amine ligand on the dissolution process. As discussed above, the NH₃ ligands enable the formation of a surface complex Cu(NH₃)_n (n = 1 to 4) that detaches as a dissolved Cu(NH₃)_n cation. The ligands move the threshold potential for this Cu dissolution to a more negative value (from −0.8 V to −1.1 V vs. RHE depending on the complex formed), compared to the case of water. Here we will discuss how this effect depends on the choice of the amine ligand. Two other ligands were checked, methylamine and ethylamine, on the Cu(843) surface (ESI Fig. S10†). We will consider the formation of the square planar Cu(NH₃)₄²⁺ complex, but a similar conclusion would arise for the formation of other complexes.

If we consider the kinked Cu(843) surface, the initial adsorption of one NH₃ molecule is stabilized if one H is replaced by a methyl or ethyl group (Fig. 7B) since these electron donor substituents increase the reactivity of the amine. If we now look at the energy of the final CuL₄ dication (where L is the amine ligand), we see on the right part of Fig. 7B that it is also markedly stabilized by electron donor substituents, as well known. The bonding stability between N and Cu²⁺ is following the sequence: ethylamine ≈ methylamine > NH₃. Ethylamine is very comparable with methylamine, which is because even though ethylamine has a slightly larger alkyl group, providing a greater electron-donating inductive effect compared to methylamine, its longer carbon chain has slightly higher steric hindrance compared to methylamine. On the thermodynamic aspect, dissolution is more favorable for substituted amines and the thermodynamic potential threshold (the crossing points in Fig. 7B) is even more negative than that of NH₃, in the order ethylamine ≈ methylamine < NH₃.

Fig. 7 Influence of the type of amines on the structure and energy of the intermediate surface complexes on Cu(843) and of the dissolved dication, using three amines as ligands, including NH₃, methylamine, and ethylamine. (A) structure of the adsorbed amine on the kink site (1a), of the displaced adatom with one ligand (1b), with two ligands (2), three ligands (3), and the corresponding detached complex (4b). (B) energy diagram comparing ligand adsorption on the kink atom (structure 1a, dashed lines) and dissolved complex (4b, solid lines) for the three considered ligands: NH₃ (green), methylamine (orange) and ethylamine (purple). (C) Free energy profile at 0 V vs. RHE for each ligand type for the adsorption of one ligand on the kink atom of Cu(843) (1a), the formation of the surface complex with one ligand (1b), two ligands (2), three ligands (3), and finally the dissolved dication CuL₄ complex (4b). pH equals 12.9.

However, the stability of the intermediate surface Cu complexes does not follow the same trend. The initial extraction of the Cu kink atom with one ligand to form an amine-capped Cu adatom (from structure 1a to 1b) is slightly uphill in energy at −0.25 V vs. RHE for NH₃ and methylamine (0.20 eV and 0.39 eV resp.) but more difficult for ethylamine: 0.45 eV (Fig. 7C). From there, the formation of the surface complex with 2 and 3 ligands from 1b is exothermic for NH₃, methylamine and ethylamine. Calculations therefore show that the formation of the surface complex is more difficult for the substituted ethylamine even at U = −0.25 V vs. RHE. Changing the potential provides a consistent trend: the dissolution is easier at a less negative potential, and always more difficult at a more negative potential (ESI Fig. S11–S13†). Calculations hence show that the dissolution process can be kinetically controlled by changing the substituent on the amine, with a slower dissolution for substituted amines. Experiments with NH₃, methylamine and ethylamine at a potential −0.25 V show that dissolution occurs in each case but that the amount of Cu in solution is lower for the substituted amines (Fig. S14†). Secondary or tertiary amines were not included in our study since they cannot be used for the synthesis of secondary amines from carbonylic compounds in the considered amination reaction under alkaline conditions in water.^2,3,10

3. Conclusions

In complement to observations of the dissolution of copper (Cu) and its negative impact on the performance for the reductive amination of acetone with methylamine as nitrogen sources, even under reductive potential conditions (−0.75 V vs. RHE), this study employs Grand Canonical density functional theory to delve into this dynamic phenomenon from a microscopic perspective. The findings illustrate that amine ligands in solution directly chemisorb onto the electrode, coordinating with the metal center and driving surface rearrangement by moving Cu atoms into low coordination adatom positions. Subsequently, other ligands stabilize the formed copper–ligands complex on the Cu surface, eventually leading to the dissolution of a Cu–amine cationic complex, even under negative potential conditions. Calculations indicate that dissolution is predicted to be thermodynamically favored in the case of ammonia ligands at a potential of −1.1 V vs. RHE or higher, with a small dependence of this threshold potential on the nature of the complex formed, Cu(NH₃)₄²⁺, Cu(NH₃)₂²⁺ or Cu(NH₃)⁺. Besides, the electron-donating group in the amine ligands will contribute to the thermal stability of the complex, but can also partially hinder the formation of the surface complex as shown for ethylamine. The dissolution of the Cu atom is facilitated by the weakening of the Cu–Cu bond, itself promoted by the multiple coordination of amine ligands on the Cu adatom. This work significantly advances our fundamental understanding of Cu dissolution facilitated by surface restructuring in amine solutions under electroreduction conditions. Such insights are crucial for the rational design of durable Cu-based cathodes for electrochemical amination and other amine-involving reduction processes.

4. Methods

4.1 Experimental measurements

The electrolysis experiments were performed in a divided cell, whereby the cathode and anode chamber were separated by a Nafion-324 membrane. The Nafion-324 membrane was used at least three times with lead as anode before these experiments were performed. The half-cells had a cylindrical geometry (r = 1 cm, h = 1 cm). The cathode compartment was cooled by cryostat (Julabo CORIO CD-200F) to 10 °C from the back of the working electrode. A three-electrode setup consisting of the working (cathode), counter (anode), and reference electrode was used. The cathode was copper, while lead was the anode. As reference electrode, a 1 M Hg/HgO electrode was applied. The galvanostatic or potentiostatic electrolysis experiments were performed by using a Metrohm Autolab PGSTAT 302N potentiostat/galvanostat. Before each electrolysis, copper and lead were freshly wet sanded using a 1000 and 2000 grid.

4.1.1 Galvanostatic experiments: stability of the copper electrode and its performance in the reductive amination reaction of acetone. A reaction volume of 2.8 mL was used that contained 2.4 M acetone (0.50 mL, 1 eq.) and 2.9 M methylamine (1.2 eq., 40% methylamine solution: 0.70 mL). Both substrates were added to an aqueous 0.5 M KH₂PO₄-solution (pH 8.3) (1.61 mL). For the anode compartment, 2.8 mL of an aqueous 25% H₃PO₄ solution was used. The solutions were transferred into the respective half-cell chamber. When a cooling phase was applied, the solution was stirred at 250 rpm for 18 min and, if necessary, −1 V vs. Hg/HgO (−0.16 V vs. RHE) was applied during this time. At 10 °C, the acetone/methylamine mixture had a pH of 12.9. The stirrer was turned off after the cooling period, and cyclic voltammetry measurements were carried out with a scan rate of 50 mV s⁻¹ between −1.12 V and 0.06 V vs. RHE. In galvanostatic experiments, a current density of −40 mA cm⁻² was used. The electrolysis was stopped after 1 F_eq. was passed.

4.1.2 Potentiostatic experiments: stability of the copper electrode at different potentials. A reaction volume of 2 mL was used that contained 2.4 M acetone (0.36 mL, 1 eq.) and 2.9 M methylamine (1.2 eq., 40% methylamine solution: 0.50 mL). Both substrates were added to an aqueous 0.5 M KH₂PO₄-solution (pH 8.3) (1.14 mL). For the anode compartment, 2 mL of an aqueous 25% H₃PO₄ solution were used. The solutions were transferred into the respective half-cell chamber. At 10 °C, the acetone/methylamine mixture had a pH of 12.9. After transferring the reaction solutions into the half cells, the respective potential (0.25 V, −0.25 V, −0.75 V, or −1.25 V vs. RHE) was applied for 30 min. Afterward, the product solution was immediately removed, and the copper concentration was measured by ICP-OES.

4.1.3 Potentiostatic experiments: stability of the copper electrode in the presence of different amines. A reaction volume of 2.8 mL was used that contained 2.4 M acetone (0.50 mL, 1 eq.) and 2.9 M of the respective amine. As amines, ammonia (1.2 eq., 29% ammonium hydroxide solution: 1.10 mL), methylamine (1.2 eq., 40% methylamine solution: 0.70 mL) and ethylamine (1.2 eq., 69% ethylamine solution: 0.65 mL) were tested. Acetone and amine were mixed to an aqueous 0.5 M KH₂PO₄-solution (pH 8.3), that was used as solvent. For the anode compartment, 2.8 mL of an aqueous 25% H₃PO₄ solution were used. The solutions were transferred into the respective half-cell chamber. At 25 °C, the acetone/amine mixtures had a pH of 12.3. The stability test of copper in the presence of various amines was performed at 25 °C, as a precipitate formed in a mixture of acetone/ammonia at 10 °C and could therefore not be handled. No precipitated was formed at 25 °C. After transferring the reaction solutions into the half cells, −0.25 V vs. RHE was applied for 30 min. Afterward, the product solution was immediately removed, and the copper concentration was measured by ICP-OES.

4.1.4 Nuclear magnetic resonance spectroscopy. Yields, conversions, and carbon balances (C.B.) were determined by quantitative ¹H-NMR spectroscopy. DMSO-d₆ (2.50 ppm) was utilized as the solvent and 1,3,5-trioxane (δ_H: 5.07 ppm) as well as 1,4-dioxane (δ_H: 3.52 ppm) were used as internal standards for the cathode and anode solutions, respectively. The internal standard (∼20–36 mg) was dissolved in DMSO-d₆ (0.8 mL) and frozen in the fridge in the meantime. After electrolysis, 0.2 mL of the product solution was added to the half-thawed DMSO-d₆/internal standard mixture. The quantitative ¹H-NMR measurements were done with a Bruker Avance spectrometer (400 MHz) at room temperature with 16 scans in each case and setting the d₁ time to 10 s. The NMR spectra were processed using apodization (0.3 Hz), zero filling (128 k), phase correction (manually), and baseline correction (Bernstein polynomial fit (manually)). The quantification was done based on the absolute areas of the signals and using eqn (3).n_{substance X}: amount of substance X after electrolysis [mol]. n_IS: amount of substance of the internal standard in the NMR sample solution [mol]. H_{theo IS}: number of protons the area of the used signal of the internal standard should theoretically represent [–]. H_{substance X}: number of protons the area of the used signal of substance X should theoretically represent [–]. A_{substance X}: Measured area of the used signal of substance X [–]. A_IS: measured area of the used signal of the internal standard [–]. m_product: mass of the product solution after electrolysis [g]. m_NMR: mass of the product solution used for the NMR analysis [g].

Methylamine: ¹H-NMR (400 MHz, DMSO-d₆) δ2.17 (s, 1H).

Acetone: ¹H-NMR (400 MHz, DMSO-d₆) δ2.06 (s, 6H).

N-Methylpropan-2-imine: ¹H-NMR (400 MHz, DMSO-d₆) δ2.87 (s, 3H), 1.81 (d, J = 49.1 Hz, 6H).

N-Methylpropan-2-amine: ¹H-NMR (400 MHz, DMSO-d₆) δ 2.58–2.45 (m, 1H), 2.16 (s, 3H), 0.92 (d, J = 6.3 Hz, 6H).

Isopropanol: ¹H-NMR (400 MHz, DMSO-d₆) δ 3.76 (hept, J = 6.1 Hz, 1H), 1.02 (d, J = 6.1 Hz, 6H).

Signals used for the calculation of yield, conversion and C.B. are printed in bold.

4.1.5 ICP-OES. The ICP-OES data were measured externally by the microanalytical laboratory Kolbe (Oberhausen, Germany). After the microwave digestion with a MARS 6 device from CEM, the metal content of the samples was measured with a Spectro acros ICP device from Spectro.

4.1.6 Material. Chemicals used in this work are listed in Table 1. They were used without purification.

Table 1 Manufacture and the substance or material that were used in this work

Substance/material	Manufacture	Purity
Acetone	Chemsolute	99.50%
Ammonium hydroxide	Honeywell Fluka	29%
Copper	Aldrich	99.98%
Dimethylsulfoxide-d6	Deutero	99.80%
1,4-Dioxane	Emsure	99.50%
Ethylamine	Aldrich Chemistry	69%
Methylamine	Merck	40%
Monopotassium phosphate	Fluka	99%
Nafion N-324 (0.15 mm, Teflon fabric reinforced)	Thermo scientific
Phosphoric acid	Merck	85%
Potassium hydroxide	Chemsolute	85%
1,3,5-Trioxane	Aldrich	99%

---

4.2 Theoretical calculations

Vienna ab initio simulation package (VASP) was used to carry out all the periodic DFT calculations.⁵⁰ The Perdew–Burke–Ernzerhof (PBE) parametrization of the generalized gradient approximation (GGA) of the exchange-correlation functional was employed, along with the dDsC dispersion correction to account for van der Waals interaction.^37,38 The cut off energy was 400 eV. The interactions between the atomic cores and electrons were described by the projector augmented wave (PAW) method.⁵¹ All structures were optimized under vacuum firstly until the force and energy on each atom was less than 0.01 eV Å⁻¹ and 10⁻⁶ eV. Then geometry optimization based on implicit solvation provided by VASPsol³⁹ was used to reach the force and energy on each atom less than 0.02 eV Å⁻¹ and 10⁻⁶ eV.

The Cu(843) was modeled by an around 3-layer (1 × 1) supercell with a cell dimension of 8.08 Å × 8.44 Å. The bottom layer (0–2 Å region) was fixed as the bulk region. Meanwhile, a 3-layer (3 × 3) supercell of Cu(111) termination was used, where the bottom one layer was fixed. A vacuum slab of 15 Å thickness was added in the Z direction. When it comes to solvation optimization and Surface Charging, all structures are symmetrized and the box thickness in the Z direction is 60 Å for the implicit solvation region. To be specific, five layers were used with adsorbates on both sides. The Brillouin zone was sampled using 5 × 5 × 1 Gamma-centered k-point grids for structure optimization. The COHP analysis was performed using the LOBSTER program with the pbeVaspFit2015 basis set,⁵² where self-consistent calculation used a denser k-point grid of 8 × 8 × 1. The Gibbs free energies for adsorbates on the surface are obtained from the DFT energies with ZPE and entropy corrections determined from frequency calculations performed for all the considered structures using the Harmonic Oscillator approximation.

4.2.1 Grand canonical density functional theory (GCDFT) calculations. The grand canonical free energy was evaluated by grand canonical density functional theory (GCDFT) calculations, which is a surface charging technique. Details can be found in our previous work, and here we summarize the key points.^31–34 The net charge of the surface n_surface is obtained as:

n_surface = N_surface − N_{surface, neutral}

where N_surface and N_{surface, neutral} is the number of electrons on the surface and the number of electrons in the neutral state. DFT energy for the charged surface is obtained as:

E_surface = E_surface,raw + ε_fermishiftn_surface

where E_surface,raw is the raw electronic energy of the surface and ε_fermishiftn_surface is the correction term accounting for the difference (ε_fermishift) in the reference energy of the electron between the “internal” reference level and vacuum. Then, the grand canonical electronic energy of a surface model, Ω(U) is obtained as:

Ω(U) = E_surface − n_surfaceμ_electron

where μ_electron is the chemical potential of an electron, which is defined as:

μ_electron = qU_vac = −eU_vac

where U_vac is the potential of the system with reference to the vacuum level and q is the charge of an electron. The potential of the system with reference to the vacuum can be determined by two components, the Fermi level (ε_F) with reference to the “internal” zero energy reference and the Fermi shift which is the difference between the “internal” energy reference and the vacuum level:

−eU_vac = ε_F + ε_fermishift

For the metallic systems, the potential-dependent grand canonical energy, Ω(U), exhibits a quadratic behaviour around the potential of zero charge (U₀) in the vacuum scale:

where C is the capacitance of the surface. The potential of the system with respect to the standard hydrogen electrode (SHE) can be converted from U_vac as:

U_SHE = U_vac − 4.44

The linearized Poisson Boltzmann implicit solvation model implemented in VASPsol⁵³ is used to represent the polarizable electrolyte region. The dielectric constant of water, 78.4, and the Debye screening length corresponding to 0.1 M concentration of electrolytes, 9.6 Å, were used. The surface slab is symmetrized along the z-axis to avoid asymmetric potential in the implicit solvation region. Here the implicit solvent thickness is set to 60 Å for the symmetrized slab.

Data availability

Data for this article, including experimental data (yield, conversion, carbon balance and copper concentration) and theoretical data (calculated structures) are available at Zenodo at https://doi.org/10.5281/zenodo.13241433.

Author contributions

Yani Guan performed calculations and drafted the manuscript. Justus Kümpe conducted the experimental work and drafted the experimental part of the manuscript. Sonja D. Mürtz and Simran Kumari assisted with data analysis and manuscript writing. Peter J. C. Hausoul aided in data analysis and manuscript revision. Regina Palkovits conceived the experiments, oversaw the work at RWTH Aachen and reviewed the manuscript. Philippe Sautet conceived the calculations, supervised the study, and edited and finalized the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

Y. G., S. K. and P. S. acknowledge support from the National Science Foundation award 2140374. Computational resources for this work were provided by the UCLA-shared cluster Hoffman2 and the Expanse cluster through the allocation CHE170060 at the San Diego Supercomputing Center through ACCESS. J. K., S. M., P. H. and R. P. gratefully acknowledge the German Research Foundation for funding this project within PA1689/17-1 as well as in the frame of NFDI4Cat (ID 441926934). Part of this work was supported by the Cluster of Excellence Fuel Science Center (EXC 2186, ID: 390919832) funded by the Excellence Initiative by the German federal and state governments to promote science and research at German universities. J. K., S. M., P. H. and R. P. also acknowledge funding by the Federal Ministry of Food and Agriculture granted by the Agency for Renewable Resources (FNR, 2220NR101X). S. M. thanks Cusanuswerk e.V. for funding.

References

1. C. Fernández-Dacosta, V. Stojcheva and A. Ramirez, J. CO₂ Util., 2018, 23, 128–142.
2. J. J. Roylance and K.-S. Choi, Green Chem., 2016, 18, 5412–5417.
3. S. D. Mürtz, N. Kurig, F. J. Holzhäuser and R. Palkovits, Green Chem., 2021, 23, 8428–8433.
4. S. V. Vassilev, D. Baxter, L. K. Andersen and C. G. Vassileva, Fuel, 2010, 89, 913–933.
5. Y. M. Bar-On, R. Phillips and R. Milo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6506–6511.
6. Q.-L. Yang, X.-Y. Wang, J.-Y. Lu, L.-P. Zhang, P. Fang and T.-S. Mei, J. Am. Chem. Soc., 2018, 140, 11487–11494.
7. X. Yang, Q.-L. Yang, X.-Y. Wang, H.-H. Xu, T.-S. Mei, Y. Huang and P. Fang, J. Org. Chem., 2020, 85, 3497–3507.
8. T. Ghosh, H. Kaizawa, S. Funato, M. A. Rahman, N. Sasaki, T. Nokami, M. Abe and T. Nishikata, ChemElectroChem, 2024, 11, e202300636.
9. P. J. L. Broersen, T. de Groot, D. F. Bruggeman, E. S. Caarls, J. A. Trindell, D. Anastasiadou, M. C. Figueiredo, G. Rothenberg and A. C. Garcia, ChemCatChem, 2024, 16, e202301370.
10. T. Pienemann and H.-J. Schäfer, Synthesis, 1987, 1987, 1005–1007.
11. T. Kim, D. I. Park, S. Kim, D. Yadav, S. Hong, S. H. Kim, H. J. Yoon and K. Jin, Chem. Commun., 2023, 59, 4818–4821.
12. R. Chen, X. Zu, J. Zhu, Y. Zhao, Y. Li, Z. Hu, S. Wang, M. Fan, S. Zhu, H. Zhang, B. Ye, Y. Sun and Y. Xie, Adv. Mater., 2024, 36, 2314209.
13. P. Trogadas, L. Xu and M.-O. Coppens, Angew. Chem., 2024, 136, e202314446.
14. X. Meng, H. Huang, X. Zhang, L. Hu, H. Tang, M. Han, F. Zheng and H. Wang, Adv. Funct. Mater., 2024, 34, 2312719.
15. K. Shen, D. Cheng, E. Reyes-Lopez, J. Jang, P. Sautet and C. G. Morales-Guio, Joule, 2023, 7, 1260–1276.
16. D. Cheng, A. N. Alexandrova and P. Sautet, J. Phys. Chem. Lett., 2024, 1056–1061.
17. D. Cheng, Z. Wei, Z. Zhang, P. Broekmann, A. N. Alexandrova and P. Sautet, Angew. Chem., 2023, 135, e202218575.
18. Z. Zhang, J. Li and Y.-G. Wang, Acc. Chem. Res., 2024, 57, 198–207.
19. N. De Jonge and F. M. Ross, Nat. Nanotechnol., 2011, 6, 695–704.
20. F. M. Ross, Science, 2015, 350, aaa9886.
21. M. L. Taheri, E. A. Stach, I. Arslan, P. A. Crozier, B. C. Kabius, T. LaGrange, A. M. Minor, S. Takeda, M. Tanase, J. B. Wagner and R. Sharma, Ultramicroscopy, 2016, 170, 86–95.
22. V. Beermann, M. E. Holtz, E. Padgett, J. F. De Araujo, D. A. Muller and P. Strasser, Energy Environ. Sci., 2019, 12, 2476–2485.
23. G.-Z. Zhu, S. Prabhudev, J. Yang, C. M. Gabardo, G. A. Botton and L. Soleymani, J. Phys. Chem. C, 2014, 118, 22111–22119.
24. S. F. Tan, S. W. Chee, Z. Baraissov, H. Jin, T. L. Tan and U. Mirsaidov, J. Phys. Chem. Lett., 2019, 10, 6090–6096.
25. A. Impagnatiello, C. F. Cerqueira, P.-E. Coulon, A. Morin, S. Escribano, L. Guetaz, M.-C. Clochard and G. Rizza, ACS Appl. Energy Mater., 2020, 3, 2360–2371.
26. Y. Li and W. Shen, Chem. Soc. Rev., 2014, 43, 1543–1574.
27. X. Wang, K. Klingan, M. Klingenhof, T. Möller, J. Ferreira de Araújo, I. Martens, A. Bagger, S. Jiang, J. Rossmeisl, H. Dau and P. Strasser, Nat. Commun., 2021, 12, 794.
28. J. Vavra, G. P. L. Ramona, F. Dattila, A. Kormányos, T. Priamushko, P. P. Albertini, A. Loiudice, S. Cherevko, N. Lopéz and R. Buonsanti, Nat. Catal., 2024, 1–9.
29. S. J. Raaijman, N. Arulmozhi and M. T. M. Koper, ACS Appl. Mater. Interfaces, 2021, 13, 48730–48744.
30. S. Popovic, M. Bele and N. Hodnik, ChemElectroChem, 2021, 8, 2634–2639.
31. X. Fu, D. Cheng, C. Wan, S. Kumari, H. Zhang, A. Zhang, H. Huyan, J. Zhou, H. Ren, S. Wang, Z. Zhao, X. Zhao, J. Chen, X. Pan, P. Sautet, Y. Huang and X. Duan, Adv. Mater., 2023, 35, 2301533.
32. S. Kumari, T. Masubuchi, H. S. White, A. Alexandrova, S. L. Anderson and P. Sautet, J. Am. Chem. Soc., 2023, 145, 5834–5845.
33. Elucidation of the Active Site for the Oxygen Evolution Reaction on a Single Pt Atom Supported on Indium Tin Oxide, https://pubs.acs.org/doi/epdf/10.1021/acs.jpclett.3c00160, accessed 2 October 2023.
34. D. Cheng, Z. Wei, Z. Zhang, P. Broekmann, A. N. Alexandrova and P. Sautet, Angew. Chem., 2023, 135, e202218575.
35. A. A. Permyakova, J. Herranz, M. El Kazzi, J. S. Diercks, M. Povia, L. R. Mangani, M. Horisberger, A. Pătru and T. J. Schmidt, ChemPhysChem, 2019, 20, 3120–3127.
36. S. B. Scott, T. V. Hogg, A. T. Landers, T. Maagaard, E. Bertheussen, J. C. Lin, R. C. Davis, J. W. Beeman, D. Higgins, W. S. Drisdell, C. Hahn, A. Mehta, B. Seger, T. F. Jaramillo and I. Chorkendorff, ACS Energy Lett., 2019, 4, 803–804.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930.
39. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
40. B. Eren, D. Zherebetskyy, L. L. Patera, C. H. Wu, H. Bluhm, C. Africh, L.-W. Wang, G. A. Somorjai and M. Salmeron, Science, 2016, 351, 475–478.
41. B. Eren, R. S. Weatherup, N. Liakakos, G. A. Somorjai and M. Salmeron, J. Am. Chem. Soc., 2016, 138, 8207–8211.
42. M. Pavelka and J. V. Burda, Chem. Phys., 2005, 312, 193–204.
43. T. E. Da-yang, J. J. Fifen, A. Malloum, S. Lahmar, M. Nsangou and J. Conradie, New J. Chem., 2020, 44, 3637–3653.
44. J. Hu, Q. Chen, H. Hu, Z. Jiang, D. Wang, S. Wang and Y. Li, J. Phys. Chem. A, 2013, 117, 12280–12287.
45. A. Bérces, T. Nukada, P. Margl and T. Ziegler, J. Phys. Chem. A, 1999, 103, 9693–9701.
46. R. J. Deeth and L. J. A. Hearnshaw, Dalton Trans., 2005, 3638.
47. N. R. Texler and B. M. Rode, J. Phys. Chem., 1995, 99, 15714–15717.
48. H. D. Pranowo, A. H. Bambang Setiaji and B. M. Rode, J. Phys. Chem. A, 1999, 103, 11115–11120.
49. J. Gambino, J. Robbins, T. Rutkowski, C. Johnson, K. DeVries, D. Rath, P. Vereecken, E. Walton, B. Porth, M. Wenner, T. McDevitt, J. Chapple-Sokol and S. Luce, in 2008 15th International Symposium on the Physical and Failure Analysis of Integrated Circuits, 2008, pp. 1–4.
50. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
51. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
52. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
53. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01944j

---