Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling the mechanisms of triplet state formation in a heavy-atom free photosensitizer†
Thomas P.
Fay
 *a and
David T.
Limmer
*abcd
*a and
David T.
Limmer
*abcd
aDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: tom.patrick.fay@gmail.com; dlimmer@berkeley.edu
bKavli Energy Nanoscience Institute, Berkeley, CA 94720, USA
cChemical Science Division Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
dMaterial Science Division Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 2nd April 2024
Abstract
Triplet excited state generation plays a pivotal role in photosensitizers, however the reliance on transition metals and heavy atoms can limit the utility of these systems. In this study, we demonstrate that an interplay of competing quantum effects controls the high triplet quantum yield in a prototypical boron dipyrromethene-anthracene (BD-An) donor–acceptor dyad photosensitizer, which is only captured by an accurate treatment of both inner and outer sphere reorganization energies. Our ab initio-derived model provides excellent agreement with experimentally measured spectra, triplet yields and excited state kinetic data, including the triplet lifetime. We find that rapid triplet state formation occurs primarily via high-energy triplet states through both spin–orbit coupled charge transfer and El-Sayed's rule breaking intersystem crossing, rather than direct spin–orbit coupled charge transfer to the lowest lying triplet state. Our calculations also reveal that competing effects of nuclear tunneling, electronic state recrossing, and electronic polarizability dictate the rate of non-productive ground state recombination. This study sheds light on the quantum effects driving efficient triplet formation in the BD-An system, and offers a promising simulation methodology for diverse photochemical systems.
I. Introduction
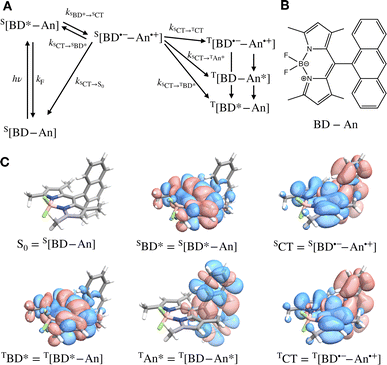
Photosensitizers harvest photons and transfer energy to other molecules, enabling new chemistry and photophysics, for applications ranging from photocatalysis,1–4 bioimaging,5–7 and photon upconversion.8–11 For photosensitizers to function efficiently, the electronic excitation needs to be generated in high yield and persist for a long time. One strategy to achieve this is to engineer the sensitizer to rapidly convert short-lived singlet excited states that are generated through photoexcitation into triplet excited states through intersystem crossing. Relaxation of triplet excited states to the singlet ground state is spin-forbidden, allowing the excitation to persist for orders of magnitude longer than in singlet excited states. In many photosensitizers, efficient intersystem crossing is facilitated by the presence of heavy atoms, such as transition metals, which enhance the spin–orbit coupling between singlet and triplet excited states. Recently, a large class of heavy-atom free triplet photosensitizers have been developed, capable of producing long-lived triplet excited states in high yields without the presence of heavy atoms.12–16 Understanding how triplet formation happens in these systems is essential for the design of other photocatalysts and photosensitizers. Using explicit molecular simulations of ab initio derived models, we reveal the mechanism by which triplet state formation occurs in a molecule made of only light elements.In this work we focus on a prototypical heavy-atom-free photocatalyst, the boron-dipyrromethene-anthracene (BD-An) dyad (chemical structure in Fig. 1B).5,17–19 BD-An has recently found applications in synthetic chemistry20–22 and its derivatives have been investigated for phototheraputic applications.23 The competing photophysical processes and the electronic excited states involved are summarized in Fig. 1. BD-anuses excited state charge transfer from an anthracenyl (An) group to the photoexcited SBD* forming an SCT state, to enable rapid triplet TBD* formation with a high experimental yield, ΦT = 0.93–0.96.18,24 Naively one might expect excited state charge transfer to reduce the triplet quantum yield, since the charge transfer state provides a charge recombination pathway for relaxation to the singlet ground state. However experiments indicate that charge recombination is suppressed by the large charge recombination free energy change, pushing this reverse electron transfer deep into the Marcus inverted regime, where increasing the free energy change increases the activation energy.18 This effect is captured qualitatively by Marcus' theory for the reaction rate constant25,26
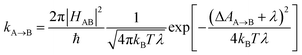 | (1) |
![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0041_20d1.gif) B is the free energy change of the reaction and λ is the reorganization energy, which encodes how solvent fluctuations and intramolecular vibrations control electronic state transitions, ℏ is Planck's constant and kBT is Boltzmann's constant times the temperature. Spin conserving charge recombination to the ground state is in the Marcus inverted regime, −ΔAA→B ≫ λ, which requires a significant activation energy to proceed, whilst for the spin–orbit coupled charge transfer to the triplet excited state −ΔAA→B ≈ λ, the reaction is approximately activation-less and thus this spin-forbidden process is competitive, despite HAB being much smaller for the spin-forbidden charge recombination. However, Marcus theory is not accurate in the inverted regime due to significant nuclear quantum effects, and alternate triplet formation pathways via high-energy triplet states could contribute, as has been observed in TREPR studies wherein TCT and TAn* intermediates were detected at low temperatures.24
B is the free energy change of the reaction and λ is the reorganization energy, which encodes how solvent fluctuations and intramolecular vibrations control electronic state transitions, ℏ is Planck's constant and kBT is Boltzmann's constant times the temperature. Spin conserving charge recombination to the ground state is in the Marcus inverted regime, −ΔAA→B ≫ λ, which requires a significant activation energy to proceed, whilst for the spin–orbit coupled charge transfer to the triplet excited state −ΔAA→B ≈ λ, the reaction is approximately activation-less and thus this spin-forbidden process is competitive, despite HAB being much smaller for the spin-forbidden charge recombination. However, Marcus theory is not accurate in the inverted regime due to significant nuclear quantum effects, and alternate triplet formation pathways via high-energy triplet states could contribute, as has been observed in TREPR studies wherein TCT and TAn* intermediates were detected at low temperatures.24
We aim to investigate the efficiency of BD-An triplet state generation in solution, going beyond the Marcus picture through first principles computational and theoretical methods, in order to explain how spin-crossover competes with charge recombination and fluorescence in solution. To this end, we interrogate each of the photophysical processes outlined in Fig. 1A by combining electronic structure calculations, molecular dynamics simulations and non-adiabatic rate theories.26,27 Our aim is to develop models that quantitatively predict experimental observables and give physical insight into mechanisms of triplet formation. We find that effects not captured by Marcus theory, including nuclear tunneling and zero-point energy, have a large effect on the non-adiabatic reaction rate constants, and must be accounted for in our description of these systems.27–30 Furthermore, Marcus theory relies on weak coupling between charge transfer states that does not hold for some of the important processes in BD-An, which we investigate with numerically exact open-system quantum dynamics calculations.31–34
The importance of solvent effects poses a particular challenge in developing a first principle understanding of triplet state formation, because this necessitates the use of explicit solvent models and molecular dynamics.27 However common general force fields for organic molecules are only applicable to describe the ground electronic state of these systems. Previous studies have primarily used gas phase electronic structure calculations to rationalize observed behavior,18,19 but these have not attempted to quantitatively predict rate constants from first principles. To address these challenges, we have developed a protocol for excited state force field parameterization, enabling us to accurately describe solvent fluctuations that control charge transfer processes in ground and excited states. With these tools, we show that the photophysics of BD-An can be quantitatively predicted and mechanisms of triplet formation can be understood in detail. We start by providing a brief description of the computational methods used in this study. We then show our results for predicted spectra, free energy changes and rate constants, followed by a discussion of how these can be used to understand efficient triplet formation in BD-An.
II. State energies and spectra
To validate our molecular model, we have computed the BD-An absorption and fluorescence spectra (shown in Fig. 2). We calculated gas phase energies of the excited states using high-level wave-function based the DLPNO-STEOM-CCSD/def2-TZVP(-f) method35,36 (or DLPNO-CCSD(T)/def2-TZVP(-f) for the TBD* and TAN* states37), with geometries for each of the excited states obtained from TDA-TDDFT38,39 with the ωB97X-D3/def2-SVP functional40 and basis set.41 All calculations were performed with Orca 5.0.3.42–44 We found that wave-function based methods, which account for orbital relaxation in the excited state are required in order to obtain an accurate S0–SCT gap.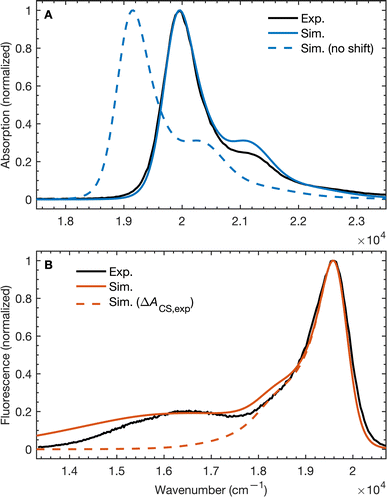 | ||
| Fig. 2 (A) Absorption and (B) emission spectra of BD-An comparing calculated and experimental spectra with and without shifts in the excited state energies. The simulated line-shapes are obtained from the spin-boson mapping described in the main-text with bespoke force-fields for the excited states. The energy differences between excited states were obtained from DLPNO-STEOM-CCSD/def2-TZVP(-f) calculations combined with solvation energies from molecular dynamics. Experimental spectra obtained from ref. 18. | ||
In the absence of solvation effects, the SBD* state is lower in energy than the SCT state by about 0.5 eV (see ESI† for list of energies), which is inconsistent with the fluorescence spectrum, which shows a clear peak from the CT state at lower energies than the SBD* peak. Thus in order to predict solvation effects and spectral line-shapes, we constructed bespoke force-fields for the ground and excited states of BD-An, which enabled us to perform molecular dynamics simulations to efficiently compute spectra with the spin-boson mapping.45 Geometries and Hessians from TDA-TDDFT to were used to parameterize intramolecular force-fields46,47 based on the OPLS-AA force-field.48,49 Electronic polarizability was accounted for using the Drude oscillator model.50 We used the same procedure to parameterize both polarizable50 and non-polarizable force-fields for the acetonitrile (ACN) solvent, with further non-bonded parameter refinement targeting the dielectric properties of the solvent. The BD-An molecule was solvated in a box of 512 ACN molecules, and energy gap correlation functions were calculated from NVE trajectories, initial after NPT and NVT equilibration (full details are given in the ESI†).
From the molecular dynamics (MD) trajectories, the spin-boson mapping was constructed, from which spectra were then calculated.45,51,52 In this approach the full anharmonic potential energy surfaces VJ are mapped onto effective harmonic potential energy surfaces. Observables of this harmonic model are fully determined by the spectral density 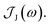 We fit the spectral distribution
We fit the spectral distribution 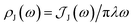 from the energy gap correlation function obtained from molecular dynamics,29
from the energy gap correlation function obtained from molecular dynamics,29
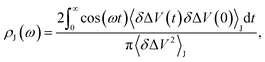 | (2) |
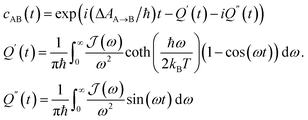 | (3) |
The absorption, AJ(ω), and fluorescence, FJ(ω), spectra (with unit area) are then given by
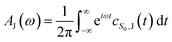 | (4) |
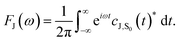 | (5) |
Further details of force-field development and the spin-boson mapping are provided in the ESI.†
The unshifted spectra calculated from the spin-boson mapping using DLPNO-STEOM-CCSD/def2-TZVP(-f) gas phase energy gaps are shown in Fig. 2 as dashed lines. Our calculated spectra show good overall agreement in the spectral line shapes, without any additional fitting, capturing the narrow SBD* peak in the absorption and fluorescence spectra, including a small vibronic side band at about 1500 cm−1 from the main peak, as well as the broad SCT fluorescence band. The agreement in the vibronic structure in the SBD* peaks suggests the fitted force fields capture the reorganization energies between excited states relatively well. However we see that the unshifted absorption spectrum calculations underestimates the SBD* energy, which we attribute to the fact that the triple zeta def2-TZVP(-f) basis set is likely still not sufficient for this system. As a result, we shifted all excited states by 805 cm−1 in order to fit the experimental absorption spectrum. This simple shift is justified by the fact that all excited states shift by ∼0.15 eV on increasing the basis set size from def2-SVP to def2-TZVP(-f), but differences between excited state energies change by much less (see ESI† for details). Furthermore it has been found the EOM-CCSD has typical errors of around 0.3 eV ≈ 2400 cm−1 for charge transfer states, so introducing a shift of 805 cm−1 seems justifiable. This shift is also used later in the free energy and rate calculations.
Using the shift from the absorption spectrum, the fluorescence spectrum (Fig. 2B) was calculated as a weighted sum of the SCT and SBD* emission spectra, with weights given by the transition dipole moments from DLPNO-STEOM-CCSD, μSBD*,S02 = 7.59 a.u. and μSCT,S02 = 0.54 a.u., and equilibrium populations of the two states given by the free energy change of charge separation ΔACS, i.e.
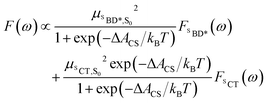 | (6) |
The assumption of equilibrium between the SBD* and SCT states is justified by the fact the time-scale of equilibration of these states is ∼103 times shorter than the lifetime of these states (as we will discuss shortly). We have also computed the fluorescence spectrum assuming the populations of the SBD* and SCT states are given by the experimental estimate, ΔACS,exp, based on the approximate Weller equation, which is about 0.2 eV larger than our estimate.18 Because ΔACS,exp > 0, the SCT state is significantly less populated relative to the SBD* state and the SCT fluorescence peak is almost completely suppressed, which does not agree with the experimental spectrum. This suggests that the Weller equation cannot be used reliably when free energy changes are close to zero. As an interesting aside, the strongest SCT–Sn coupling (see Table 1) is to the S0 state, by over a factor of 10, which indicates that the intensity borrowing effect responsible for the SCT emission arises primarily from mixing between SCT and S0 states, rather than SCT and SBD* states, as has previous been assumed.24
| A | B | Calc. ΔAA→B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (eV) (eV) |
Exp. ΔAA→Bb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (eV) (eV) |
λ (eV) | |HAB|d (cm−1) | k A→B (s−1) |
|---|---|---|---|---|---|---|
| a Free energy changes calculated with non-polarizable ACN, from thermodynamic integration/MBAR. b Estimated free energy changes from ref. 18 calculated with the Rehm–Weller equation ΔA ≈ ΔG = e(ED − EA) − ΔE* − e2/(4πε0εrrDA). c Reorganization energies from equating the pGaussianJ(ε = 0) with pJ(ε = 0) (see ESI for details). d Couplings averaged over gas-phase equilibrium geometries of A and B, |HAB|2 = (|HAB,A|2 + |HAB,B|2)/2. Details of calculations given in ESI. Ref. 18, estimated from spectroscopic measurements. e Rate constants from spin boson mapping. f Linear response value: λ = (〈ΔV〉B − 〈ΔV〉A)/2. g Radiative rate constant (eqn (9)). h With recrossing correction and. i Without recrossing correction. j Estimated from spectroscopic measurements.18 k Using reorganization energy from non-polarizable umbrella sampling calculations (see ESI). | ||||||
| SBD* | SCT | −0.057 ± 0.005 | +0.13 | 0.550 ± 0.002 | 99 | (1.46 ± 0.04) × 1011 |
| SBD* | S0 | −2.4542 ± 0.0004 | −2.460 | (8.77 ± 0.08) × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
— | (1.0747 ± 0.0006) × 108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
| SCT | S0 | −2.397 ± 0.003 | −2.59 | 0.483 ± 0.003 | 1904 | (3.4 ± 0.5) × 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h/(3.6 ± 0.6) × 107i h/(3.6 ± 0.6) × 107i |
| SCT | TBD* | −0.826 ± 0.005 | −0.97 | 0.584 ± 0.001 | 0.79 | (7.9 ± 0.2) × 107 |
| SCT | TAN* | −0.524 ± 0.004 | — | −0.477 ± 0.002 | 0.63 | (9.7 ± 0.1) × 107 |
| SCT | TCT | −0.112 ± 0.001 | — | −0.119 ± 0.002 | 0.21 | (2.86 ± 0.02) × 107 |
| TAN* | TBD* | −0.302 ± 0.003 | — | 0.565 ± 0.002 | 2.57 | (1.09 ± 0.01) × 109 |
| TBD* | S0 | −1.638 ± 0.001a | −1.62j | 0.512 ± 0.002k | 0.19 | (1.045 ± 0.006) × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
III. Charge separation and recombination
A. Thermodynamics
Charge separation, the SBD* → SCT process, and charge recombination, the SCT → S0 process, both play an important role in efficient triplet formation. Efficient charge separation is required to suppress fluorescence from the SBD* state, but slow charge recombination is needed to enable intersystem crossing to occur to generate triplet states. From our excited state force-fields, we have calculated free energy changes associated with these processes from molecular dynamics and the multi-state Bennett acceptance ratio (MBAR).53,54 As discussed above, the calculated free energy change for charge separation is −0.057 eV, thus population of the SBD* state is reduced and fluorescence is suppressed.We have also calculated the rates of these processes from the same MD simulations, by calculating the probability of two states being at resonance. This probability controls the classical Fermi's Golden rule (FGR) rate for the transition between A and B.55 The free energy along the energy gap coordinate, ΔV = VB − VA, is related to the energy gap distribution pJ(ε) = 〈δ(ΔV − ε)〉J by27
| AJ(ε) = −kBTln(pJ(ε)) + (AB − AJ) | (7) |
![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0041_20d1.gif) B = (2π/ℏ)|HAB|2e−AA(ε=0)/kBT.27 If the free energy curve is perfectly quadratic, then this reduces exactly to Marcus theory [eqn (1)].25,26,29 For the charge recombination the crossing point occurs outside of the sampled region, so we extrapolated to the crossing point using a quadratic polynomial ansatz for the free energy, fitted to the cumulative distribution function. This procedure was found to result in very little loss in accuracy when compared to umbrella sampling/weighted histogram analysis56 calculations performed using the non-polarizable ACN model (see ESI† for details).
B = (2π/ℏ)|HAB|2e−AA(ε=0)/kBT.27 If the free energy curve is perfectly quadratic, then this reduces exactly to Marcus theory [eqn (1)].25,26,29 For the charge recombination the crossing point occurs outside of the sampled region, so we extrapolated to the crossing point using a quadratic polynomial ansatz for the free energy, fitted to the cumulative distribution function. This procedure was found to result in very little loss in accuracy when compared to umbrella sampling/weighted histogram analysis56 calculations performed using the non-polarizable ACN model (see ESI† for details).
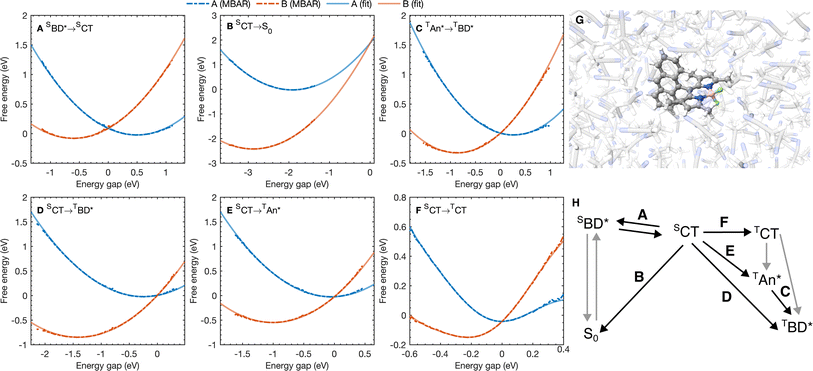 | ||
| Fig. 3 (A–F) Free energy curves for the six A → B processes considered with the reaction A → B labeled on each figure. Points correspond to free energy curves calculated with MBAR and lines correspond to polynomials fitted to the MBAR cumulative distribution functions (see ESI† for details). (G) A snapshot for molecular dynamics simulations on the S0 potential energy surface. (H) A scheme highlighting the processes in (A–F). | ||
The free energy curves for charge separation and charge recombination are shown in Fig. 3A and B, where we see charge separation lies in the Marcus normal regime, whereas charge recombination is deep in the Marcus inverted regime, with a much larger free energy barrier. Using diabatic state couplings calculated from the generalized Mulliken–Hush method57 with DLPNO-STEOM-CCSD calculations, we can directly calculate the classical FGR rates for these processes (couplings |HAB| are shown in Table 1). The classical FGR charge separation rate is 4.8 × 1010 s−1, about a factor of 10 smaller than the experimentally observed rate of 5.4 × 1011 s−1, however the charge recombination rate is predicted to be 1.1 × 10−17 s−1, which is more than 1024 times too small compared to the experimental estimate of 2.3 × 107 s−1.18 This enormous discrepancy can be attributed to nuclear quantum effects, in particular the important role of nuclear tunneling in the inverted regime.
B. Quantum effects on rates
In order to include nuclear quantum effects in the rate calculations, we employed the same spin-boson mapping approach as was used to compute the spectra. The full FGR rate constant is given by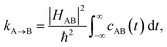 | (8) |
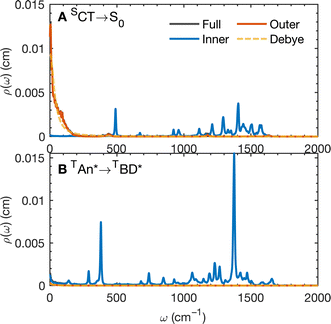
The calculated spectral distributions ρJ(ω) can be decomposed into inner sphere, outer sphere and cross-correlated contributions, by decomposing the energy gap into molecular and the remaining environment contributions ΔV = ΔVmol + ΔVenv. We find that the cross-correlated contribution is generally negligible for all processes in BD-An, so the reorganization energy is well-described by a simple sum of inner and outer sphere contributions. The inner and outer sphere spectral distributions are calculated with the non-polarizable ACN/solute model, with the outer sphere contribution scaled down to match the polarizable model outer sphere contributions. As can be seen in Fig. 4A, the low frequency proportion of the spectral distribution for the SCT → S0 transition is dominated by the outer sphere contribution arising from solvent molecule fluctuations, making up ∼50% of the reorganization energy, which is well approximated by the Debye model.32 In contrast, the high frequency region of the spectral density is dominated by the inner sphere contribution from changes in equilibrium bond lengths in the BD-An molecule on charge transfer. The inner sphere spectral distribution has contributions over a range of frequencies from around 500 to 1600 cm−1, all of which contribute to tunneling enhancement of the SCT → S0 rate, although the dominant mode at ∼1400 cm−1 likely corresponds to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching motion within the aromatic rings. Qualitatively similar spectral distributions were found for the other charge transfer processes. For processes which do not involve charge transfer the spectral distribution is dominated by the inner sphere contribution, as can be seen for the TAN* → TBD* process in Fig. 4B.
C stretching motion within the aromatic rings. Qualitatively similar spectral distributions were found for the other charge transfer processes. For processes which do not involve charge transfer the spectral distribution is dominated by the inner sphere contribution, as can be seen for the TAN* → TBD* process in Fig. 4B.
When accounting for nuclear quantum effects, the SBD* → SCT rate goes up by a factor of ∼3 to 1.46 × 1011 s−1, and the SCT → S0 rate goes up by over 1024 to 1.0 × 108 s−1, and both calculated rates are now much closer to the experimentally measured values, agreeing much better with the experimental value. Application of Marcus–Levich–Jortner theory with the same inner and outer sphere reorganization energies and a characteristic inner-sphere frequency of 1500 cm−1 also predicts about a 1024-fold increase in the rate constant, compared to Marcus theory. This suggests that the large increase is robust to the details of the spectral density. Electronic polarizability is essential to account for in calculating the charge recombination rate. When a non-polarizable model is used instead, the free energy change of the reaction is effectively unchanged but the reorganization energy goes up by nearly 0.1 eV. This lowers the activation energy and accelerates the rate by around a factor of three.
Care should however be taken when using FGR to calculated the charge recombination rate. This is because the diabatic coupling for charge recombination process, HAB = 1904 cm−1, is about 20 times larger than kBT, and thus higher-order diabatic coupling effects beyond FGR, may be important (although large nuclear quantum effects in the FGR rate have been observed to reduce the importance of higher order effects).34 The large difference in couplings arises from the BD π orbitals involved in the transitions. The SBD* → SCT coupling involves an interaction between πAn and πBD (Fig. 5A) orbitals, whereas SCT → S0 coupling involves the πAn and  (Fig. 5B) orbitals. As can be seen in Fig. 5 the πBD has minimal density on the carbon atom bonded to the An, group, whereas the
(Fig. 5B) orbitals. As can be seen in Fig. 5 the πBD has minimal density on the carbon atom bonded to the An, group, whereas the  orbital does. In order to investigate the potential role of higher-order diabatic coupling effects in the SCT → S0 transition, we have performed Hierarchical Equations of Motion (HEOM) calculations a simple model for this transition. The spectral density for the transition is coarse-grained down to a low-frequency outer-sphere portion described with a Debye spectral density and the inner sphere portion is described with a single under-damped Brownian oscillator spectral density, with a characteristic frequency of 1400 cm−1. The coarse-grained spectral density is shown in Fig. 6A. For this simplified model the exact open quantum system dynamics can be obtained using the HEOM method, and from this the rate constant as a function of HAB can be obtained. These rates are shown in Fig. 6B. We see that the rate constant is still fortuitously very well described by Fermi's Golden rule for this model, with only a factor of ∼0.9 reduction in the rate constant at the calculated value of HAB. We include this as a correction to the Fermi's Golden rule kSC
orbital does. In order to investigate the potential role of higher-order diabatic coupling effects in the SCT → S0 transition, we have performed Hierarchical Equations of Motion (HEOM) calculations a simple model for this transition. The spectral density for the transition is coarse-grained down to a low-frequency outer-sphere portion described with a Debye spectral density and the inner sphere portion is described with a single under-damped Brownian oscillator spectral density, with a characteristic frequency of 1400 cm−1. The coarse-grained spectral density is shown in Fig. 6A. For this simplified model the exact open quantum system dynamics can be obtained using the HEOM method, and from this the rate constant as a function of HAB can be obtained. These rates are shown in Fig. 6B. We see that the rate constant is still fortuitously very well described by Fermi's Golden rule for this model, with only a factor of ∼0.9 reduction in the rate constant at the calculated value of HAB. We include this as a correction to the Fermi's Golden rule kSC![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0054_20d1.gif) S0 that we calculated with the full spectral density.
S0 that we calculated with the full spectral density.
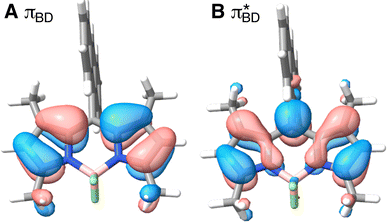 | ||
Fig. 5 BD orbitals involved in charge separation and recombination (A) πBD and (B) 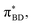 calculated with ωB97X-D3/def2-TZVPP/CPCM(ACN) at the S0 equilibrium geometry. calculated with ωB97X-D3/def2-TZVPP/CPCM(ACN) at the S0 equilibrium geometry. | ||
 | ||
| Fig. 6 (A) The coarse-grained model spectral distribution for the SCT → S0 transition, consisting of a low frequency Debye contribution ρD(ω) = (1/2π)/(1 + (ω/ωD)2), with βωD = 0.1831, and an under-damped Brownian oscillator contribution ρBO(ω) = (1/2π)γΩ2/((ω2 − Ω2)2 + γ2ω2) with βγ = 4 and βΩ = 6.76. The reorganization energy for the Brownian oscillator portion is βλ = 8.6780 and for the Debye portion is βλ = 10.1459. (B) The rate constant from HEOM calculations for the coarse-grained spectral density as a function of HAB together with the FGR predictions. The value of HAB for the SCT → S0 transition is also indicated. Calculations were performed using the heom-lab code58 using the HEOM truncation scheme from ref. 59. | ||
Radiative recombination from the SCT state can also occur in BD-An, either through thermally activated delayed fluorescence via the SBD* state, or directly. The radiative rates can be calculated from the fluorescence spectra obtained from the spin-boson mapping as26,60
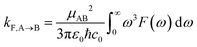 | (9) |
IV. Triplet state formation and lifetime
As with the charge separation and charge recombination processes, we have calculated the free energy changes and free energy profiles for the three triplet formation pathways: from the SCT state to the TCT, TAN* and TBD* states (Fig. 3D–F). Free energy calculations reveal that the three pathways are thermally accessible, with all three states lying lower in energy than the SCT state. Furthermore all three pathways are approximately activation-less, which is at first surprising given that each process has a very different free energy change. The TBD* pathways has a larger |ΔAA→B|, than the TAN* pathway, but the TAN* pathway has smaller inner and outer sphere reorganization energies, so this pathway is also approximately activation-less. The TCT pathway has a very small reorganization energy which is dominated (∼90%) by the inner sphere contribution, at only 0.11 eV. This is because the SCT and TCT states have the same orbitals occupied, so the reorganization energy is dictated only by differences in the exchange energy which alters bonds lengths. However the net exchange energy difference between these states is small because the unpaired electrons have low spatial overlap, so overall the reorganization energy is low and this transition is approximately activation-less. Much like the spin-conserving charge separation and charge recombination, about 50% of the reorganization energies for the charge transfer processes is outer sphere, with the remaining 50% arising from inner sphere reorganization, although there is a significant range of reorganization energies for the charge transfer processes, from 0.48 eV to 0.58 eV. In contrast, the reorganization energies of processes which do not involve charge transfer are dominated by the inner sphere contribution, 89% for the SCT → TCT spin-crossover and 99% for the TAN* → TBD* triplet–triplet energy transfer, as illustrated in Fig. 4B. The triplet–triplet energy transfer still has a reorganization energy comparable to the charge transfer processes, at 0.57 eV, due to a large change in bond order in both the BD and An units in this process. Further analysis of the inner/outer sphere reorganization energies are given in the ESI† together with all calculated spectral densities.We have also calculated the SOC couplings between the different SCT and triplet states using TDDFT (ωB97X-D3/def2-TZVPP/CPCM(ACN)) and the spin–orbit mean-field (SOMF) treatment of spin–orbit coupling.61,62 The two spin–orbit coupled charge transfer (SOCT) pathways have the largest SOC couplings, at 0.79 cm−1 and 0.63 cm−1 for the TBD* and TAN* whilst the formally El-Sayed's rule forbidden pathway has a smaller coupling at 0.21 cm−1. Using these couplings and the spin-boson mapping, we find that two El-Sayed's rule allowed transitions, viaTAN* and TBD*, occur at very similar rates, with SCT → TBD* occurring only about 20% faster than the SCT → TAN* formation. The triplet–triplet TAN* → TBD* energy transfer is also activation-less (Fig. 3C), and has a coupling from fragment energy/charge density (FED/FCD) calculations47,63,64 of 2.57 cm−1, and so occurs about 10 times faster than the triplet formation rate, accelerated by a factor of 1.6 by nuclear quantum effects, so the steady state population of TAN* would be difficult to observe spectroscopically at room temperature. The El-Sayed's rule forbidden transition to the TCT state also contributes to triplet formation, although it occurs about 4.5 times slower than TBD* formation. The TCT state very rapidly recombines to the TAN* or TBD* states, with these spin allowed transitions occurring at least ∼104 times faster than the corresponding spin-forbidden transitions, so the TCT state would be very difficult to observe directly at room temperature. Overall the TCT TAN*, and TBD* pathways contribute 14%, 47%, and 39% respectively to the overall triplet formation. Surprisingly the most significant pathway is the TAN* pathway and not the direct TBD* pathway, which can be rationalized by the lower activation barrier for the TAN* spin–orbit coupled charge recombination. The observation is consistent with TREPR experiments in which all three triplet states were observed, although at much lower temperatures (80 K) in a very different medium (a dichloromethane/isopropanol solid matrix). This work shows that multiple triplet formation pathways, including those forbidden by El-Sayed's rule, can contribute at room temperature in polar solvents. The presence of multiple triplet recombination pathways may also explain the large spread of effective spin–orbit coupled charge transfer rates observed in the family of BD-Aryl molecules studied in ref. 18.
Using all of the computed rates, we have estimated the observed charge separation and charge recombination rates, as well as the triplet yield. The effective charge separation rate corresponds to the observed equilibration rate between SBD* and SCT states i.e. kCS,eff = kSBD*→SCT + kSCT→SBD*. Likewise the effective charge recombination rate corresponds to the observed decay rate of the SCT state, which under a pre-equilirbium approximation for the SBD* ⇌ SCT interconversion is given by
| kCR,eff = pSCT(kCR + kF,SCT→S0) + pSBD*kF,SBD*→S0 | (10) |
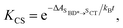 kF,SBD* is the calculated fluorescence rate from the SBD* state back to the S0 state and kCR is the total recombination rate from the SCT state, i.e.
kF,SBD* is the calculated fluorescence rate from the SBD* state back to the S0 state and kCR is the total recombination rate from the SCT state, i.e.kCR = kSCT→S0 + kSCT→TCT + kSC![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0054_20d1.gif) TAN* + kSCTT→BD*. TAN* + kSCTT→BD*. | (11) |
The triplet quantum yield ΦT is calculated as ΦT = pSCT(kSCT→TCT + kSCT→TAN* + kSCT→TBD*)τCR, with τCR = 1/kCR,eff, and the fluorescence yield ΦF is ΦF = pSBD*kF,SBD*τCR. We also computed the fraction of non-radiative transitions which produce a triplet state, ϕCRT = ΦT/(1 − ΦF), as measured in ref. 18.
The calculated and experimental values of the rates and yields are summarized in Table 2. Overall we see excellent agreement between the calculated rates/yields and the experimental measurements from ref. 18 and 24, with less than a factor of 4 error in the charge separation rate and only a factor of ∼1.6 error in the charge recombination rate. Similar we only slightly underestimate the triplet yield, with our calculations yielding 0.80, compared to the experimental measurements between 0.93 and 0.96. If we only included the dominant SCT → TBD* triplet formation pathway, the triplet quantum yield would only be ∼0.6, and the error in the rate would be over a factor of 3. We also find that suppression of the charge recombination also plays a large role in efficient triplet formation, which is facilitated by polarizability and recrossing effects. Without including electronic polarizability, the charge recombination rate would be enhanced to ∼1.0 × 108 s−1, which would reduce the triplet quantum yield to ∼0.63. This corroborates the conclusions drawn in ref. 18, although we find that multiple triplet pathways also enable the triplet formation to compete with charge recombination, which is suppressed by several effects. The net fluorescence quantum yield from SBD* that we calculate, 0.045, is also in good agreement with the experimental values, between 0.01 and 0.018. These results suggest that the intersystem crossing rates are being slightly underestimated by our models, possibly due to errors in the reorganization energies or the spin–orbit couplings obtained from TD-DFT, which are all less than 1 cm−1.
The triplet lifetime τT = 1/kTBD*→S0 plays an important role in determining the utility of a triplet sensitizer or photocatalyst, with longer-lived triplet states allowing more time for diffusive encounters with other molecules enabling more efficient energy transfer. We have also calculated the triplet lifetime for BD-Anusing the methods described above, and we also find good agreement between our calculated value for τT and experimental measurements (Table 2), with an error of only ∼20%. From a simulation perspective, this requires an accurate calculation of the free-energy barrier, which requires enhanced sampling since the transition is very deep in the Marcus inverted regime, since it displays a highly non-quadratic free energy curve. This was achieved using the non-polarizable model with umbrella sampling65 on the energy gap coordinate ΔV sampled with the Fast-Forward Langevin algorithm.66 Use of the non-polarizable model is justified because over 99% of the reorganization energy is inner sphere for both ACN models, and solvent polarizability has less than a 1 meV effect on the free energy of the TBD* state. As with the spin-conserving charge recombination, because the transition is deep in the inverted regime and the spectral distribution is dominated by high frequency inner sphere contributions, there is a very large nuclear quantum effect of over 107 in the rate constant. One significant source of uncertainty in this is the validity of the spin-boson mapping, where rates calculated from the spectral distribution obtained from TBD* and S0 dynamics vary by about 50%. This means that methods that more rigorously account for asymmetry and anharmonicity in the potential energy surfaces, while also accounting for nuclear quantum effects, may be needed to more accurately compute triplet lifetimes for this system and other related systems.55,67,68 However given the simplicity of the spin-boson mapping and its accuracy in this case, it is clearly still useful in prediction of non-adiabatic rates.
V. Concluding remarks
Through this study, we have found that triplet formation in the photosensitizer BD-An hinges on a subtle balance of effects. Firstly charge separation occurs efficiently, which suppresses radiative decay from the SBD* state. Secondly multiple triplet recombination pathways can operate, due to the range of reorganization energies and free energy changes associated with the rate-limiting intersystem crossing steps in each pathway, and in fact the high-lying triplet pathways make-up the major contribution to triplet formation, rather than direct SOCT to the ground triplet state. Thirdly, spin-conserving charge recombination to the S0 state is slowed down a high free energy barrier, with the transition being deep in the inverted regime, as well as diabatic recrossing effects, a significant portion of which arises due to electronic polarizability. The SCT state energy plays an important role in triplet formation, since an increase in energy would increase fluorescence from SBD*, but a decrease in its energy would reduce the barrier for spin-conserving charge recombination because this process is in the Marcus inverted regime. Capturing all of these effects depends on a complete description of the photophysics including accurate calculations of electronic state couplings, explicit solvent fluctuations, polarizability, to capture outer sphere reorganization energies, as well as an accurate description of molecular potential energy surfaces and inner sphere contributions to reorganization energies, as well as the nuclear quantum effects arising due to high frequency vibrations, which accelerate some processes by many orders of magnitude. Enhanced sampling techniques are also necessary to obtain accurate free energy barriers for important processes, namely the triplet decay.The simulation techniques and bespoke force-field parametrization approach developed here paves the way for a quantitative modeling of other triplet photosensitizers and related systems,69 possibly even enabling straightforward computational screening for properties such as the triplet lifetime. Comparison between simulated and experimental optical spectra indicates that a major source of error is in gas phase energies of excited states. Even the popular wave-function-based DLPNO-STEOM-CCSD method appears to significantly underestimate transition energies, although the ground-state DLPNO-CCSD(T) method which can be used to calculate the T1–S0 gap seems robust. We also note that whilst the approximate spin-boson mapping seems fairly reliable for these systems, its application to deep inverted regime processes requires scrutiny. Thus BD-Ancould provide an interesting test-bed for recently developed approaches to calculating non-adiabatic transition rates applicable to high-dimensional anharmonic systems.34,55,67,68,70–79 The SCT → S0 transition poses a particular challenge, since it is deep in the inverted regime, nuclear quantum effects are very large and strong diabatic coupling means there may be some effects missed by FGR, which we have estimated using open quantum dynamics simulations. Furthermore in this study we have neglected non-Condon effects80 and potential spin-vibronic effects,81 which could also play a role in determine the rates of conversion between excited states in this system. Future investigations into these potential effects could provide further insight into triplet formation in BD-An.
Overall, we believe the mechanistic insights gained from this study, which would be difficult to probe directly with experiment alone, could help light the path towards the development of novel and interesting photochemistry in related systems. The observation that high-energy triplet pathways dominate at room temperature opens the door to the intriguing possibility of engineering triplet anti-Kasha's rule systems,82 in which higher energy triplet states could be used to drive photochemistry. This could be particularly promising since triplet-triplet energy transfer is strongly distance dependent,83 so spatial separation of chromophore units could be used to extend the lifetime of high-lying triplet states. In summary, our comprehensive study highlights the intricate balance of factors influencing triplet formation, including the significance of charge separation efficiency, multiple recombination pathways, and nuclear quantum effects. Moving forward, this mechanistic understanding could steer the development of novel photochemical systems, with a wide range of potential applications.
Abbreviations
| ACN | Acetonitrile |
| An | Anthracene |
| BD | BODIPY, boron dipyrromethane |
| CPCM | Conductor-like polarizable continuum |
| CR | Charge recombination |
| CS | Charge separation |
| CT | Charge transfer |
| DLPNO-STEOM-CCSD | Domain local pair natural orbital similarity transformed equation of motion coupled cluster singles and doubles |
| DLPNO-CCSD(T) | Domain local pair natural orbital coupled cluster singles and doubles with perturbative triples |
| EOM-CCSD | Equation of motion coupled cluster singles and doubles |
| FGR | Fermi's golden rule |
| HEOM | Hierarchical equations of motion |
| MBAR | Multi-state Bennett acceptance ratio |
| MD | Molecular dynamics |
| NPT | Constant particle number/pressure/temperature molecular dynamics |
| NVE | Constant particle number/volume/energy molecular dynamics |
| NVT | Constant particle number/volume/temperature molecular dynamics |
| WHAM | Weighted histogram analysis |
| SOCT | Spin–orbit coupled charge transfer |
| TDA | Tamm-Dancoff approximation |
| TDDFT | Time dependent density functional theory |
| TREPR | Time resolved electron paramagnetic resonance |
Data availability
OpenMM force field files and example scripts to run energy gap calculations, together with initial geometries, can be found at https://doi.org/10.5281/zenodo.10719345. Other data that is not available in the manuscript or ESI† is available from the corresponding authors upon a reasonable request.Author contributions
T. P. F.: conceptualization, data curation, formal analysis, investigation, software, writing – original draft, writing – review & editing (equal). D. T. L.: funding acquisition, supervision, writing – review & editing (equal).Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We would like to thank Tomoyasu Mani for providing data for the experimental absorption and emission spectra for BD-An and for his comments on the manuscript. We would also like to thank Zachariah Page for a useful discussion, and his suggestion of triplet anti-Kasha's rule photochemistry. T. P. F. and D. T. L. were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, CPIMS Program Early Career Research Program under Award DE-FOA0002019.References
- N. A. Romero and D. A. Nicewicz, Organic Photoredox Catalysis, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed.
- S. Fukuzumi and K. Ohkubo, Selective photocatalytic reactions with organic photocatalysts, Chem. Sci., 2013, 4, 561–574 RSC.
- D. P. Hari and B. König, The Photocatalyzed Meerwein Arylation: Classic Reaction of Aryl Diazonium Salts in a New Light, Angew. Chem., Int. Ed., 2013, 52, 4734–4743 CrossRef CAS PubMed.
- J. Zhao, W. Wu, J. Sun and S. Guo, Triplet photosensitizers: from molecular design to applications, Chem. Soc. Rev., 2013, 42, 5323 RSC.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, H. Savoie, K. J. Flanagan, C. Sy, E. Sitte, M. Telitchko, F. Laquai, R. W. Boyle and M. O. Senge, Generation of Triplet Excited States via Photoinduced Electron Transfer in meso -anthra-BODIPY: Fluorogenic Response toward Singlet Oxygen in Solution and in Vitro, J. Am. Chem. Soc., 2017, 139, 6282–6285 CrossRef CAS PubMed.
- J. P. Celli, B. Q. Spring, I. Rizvi, C. L. Evans, K. S. Samkoe, S. Verma, B. W. Pogue and T. Hasan, Imaging and Photodynamic Therapy: Mechanisms, Monitoring, and Optimization, Chem. Rev., 2010, 110, 2795–2838 CrossRef CAS PubMed.
- P. Kaur and K. Singh, Recent advances in the application of BODIPY in bioimaging and chemosensing, J. Mater. Chem. C, 2019, 7, 11361–11405 RSC.
- J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Upconversion Luminescent Materials: Advances and Applications, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed.
- J. Zhao, S. Ji and H. Guo, Triplet–triplet annihilation based upconversion: from triplet sensitizers and triplet acceptors to upconversion quantum yields, RSC Adv., 2011, 1, 937 RSC.
- T. N. Singh-Rachford and F. N. Castellano, Photon upconversion based on sensitized triplet–triplet annihilation, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- R. S. Khnayzer, J. Blumhoff, J. A. Harrington, A. Haefele, F. Deng and F. N. Castellano, Upconversion-powered photoelectrochemistry, Chem. Commun., 2012, 48, 209–211 RSC.
- J. Peng, X. Guo, X. Jiang, D. Zhao and Y. Ma, Developing efficient heavy-atom-free photosensitizers applicable to TTA upconversion in polymer films, Chem. Sci., 2016, 7, 1233–1237 RSC.
- V.-N. Nguyen, Y. Yan, J. Zhao and J. Yoon, Heavy-Atom-Free Photosensitizers: From Molecular Design to Applications in the Photodynamic Therapy of Cancer, Acc. Chem. Res., 2021, 54, 207–220 CrossRef CAS PubMed.
- X. Zhang, Z. Wang, Y. Hou, Y. Yan, J. Zhao and B. Dick, Recent development of heavy-atom-free triplet photosensitizers: molecular structure design, photophysics and application, J. Mater. Chem. C, 2021, 9, 11944–11973 RSC.
- J. Zhao, K. Chen, Y. Hou, Y. Che, L. Liu and D. Jia, Recent progress in heavy atom-free organic compounds showing unexpected intersystem crossing (ISC) ability, Org. Biomol. Chem., 2018, 16, 3692–3701 RSC.
- M. A. Filatov, Heavy-atom-free BODIPY photosensitizers with intersystem crossing mediated by intramolecular photoinduced electron transfer, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- Z. Wang and J. Zhao, Bodipy–Anthracene Dyads as Triplet Photosensitizers: Effect of Chromophore Orientation on Triplet-State Formation Efficiency and Application in Triplet–Triplet Annihilation Upconversion, Org. Lett., 2017, 19, 4492–4495 CrossRef CAS PubMed.
- J. T. Buck, A. M. Boudreau, A. DeCarmine, R. W. Wilson, J. Hampsey and T. Mani, Spin-Allowed Transitions Control the Formation of Triplet Excited States in Orthogonal Donor-Acceptor Dyads, Chem, 2019, 5, 138–155 CAS.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. J. Flanagan, M. Telitchko, T. Wiesner, F. Laquai and M. O. Senge, Control of triplet state generation in heavy atom-free BODIPY–anthracene dyads by media polarity and structural factors, Phys. Chem. Chem. Phys., 2018, 20, 8016–8031 RSC.
- S. Abuhadba, M. Tsuji, T. Mani and T. V. Esipova, meso -Antracenyl-BODIPY Dyad as a New Photocatalyst in Atom-Transfer Radical Addition Reactions, ACS Omega, 2021, 6, 32809–32817 CrossRef CAS PubMed.
- K.-K. Chen, S. Guo, M.-J. Ding, T.-B. Lu and Z.-M. Zhang, Heavy-Atom-Free Photosensitizers for High-Yield CO 2 -to-CO Conversion, CCS Chem., 2023, 5, 2650–2662 CrossRef CAS.
- A. Uddin, S. R. Allen, A. K. Rylski, C. J. O'Dea, J. T. Ly, T. A. Grusenmeyer, S. T. Roberts and Z. A. Page, Do The Twist: Efficient Heavy-Atom-Free Visible Light Polymerization Facilitated by Spin-Orbit Charge Transfer Inter-system Crossing, Angew. Chem., Int. Ed., 2023, 62, e202219140 CrossRef CAS PubMed.
- S. Callaghan, B. E. Vindstad, K. J. Flanagan, T. B. Melø, M. Lindgren, K. Grenstad, O. A. Gederaas and M. O. Senge, Structural, Photophysical, and Photobiological Studies on BODIPY-Anthracene Dyads, ChemPhotoChem, 2021, 5, 131–141 CrossRef CAS.
- Z. Wang, A. A. Sukhanov, A. Toffoletti, F. Sadiq, J. Zhao, A. Barbon, V. K. Voronkova and B. Dick, Insights into the Efficient Intersystem Crossing of Bodipy-Anthracene Compact Dyads with Steady-State and Time-Resolved Optical/Magnetic Spectroscopies and Observation of the Delayed Fluorescence, J. Phys. Chem. C, 2019, 123, 265–274 CrossRef CAS.
- R. A. Marcus, On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley, 1st edn, 2011 Search PubMed.
- J. Blumberger, Recent Advances in the Theory and Molecular Simulation of Biological Electron Transfer Reactions, Chem. Rev., 2015, 115, 11191–11238 CrossRef CAS PubMed.
- J. S. Bader, R. A. Kuharski and D. Chandler, Role of nuclear tunneling in aqueous ferrous–ferric electron transfer, J. Chem. Phys., 1990, 93, 230–236 CrossRef CAS.
- J. E. Lawrence and D. E. Manolopoulos, Confirming the role of nuclear tunneling in aqueous ferrous–ferric electron transfer, J. Chem. Phys., 2020, 153, 154114 CrossRef CAS PubMed.
- J. Blumberger and G. Lamoureux, Reorganization free energies and quantum corrections for a model electron self-exchange reaction: comparison of polarizable and non-polarizable solvent models, Mol. Phys., 2008, 106, 1597–1611 CrossRef CAS.
- L. Zusman, The theory of electron transfer reactions in solvents with two characteristic relaxation times, Chem. Phys., 1988, 119, 51–61 CrossRef CAS.
- M. Sparpaglione and S. Mukamel, Dielectric friction and the transition from adiabatic to nonadiabatic electron transfer in condensed phases. II. Application to non-Debye solvents, J. Chem. Phys., 1988, 88, 4300–4311 CrossRef CAS.
- M. Sparpaglione and S. Mukamel, Dielectric friction and the transition from adiabatic to nonadiabatic electron transfer. I. Solvation dynamics in Liouville space, J. Chem. Phys., 1988, 88, 3263–3280 CrossRef CAS.
- J. E. Lawrence, T. Fletcher, L. P. Lindoy and D. E. Manolopoulos, On the calculation of quantum mechanical electron transfer rates, J. Chem. Phys., 2019, 151, 114119 CrossRef PubMed.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, Exploring the Accuracy of a Low Scaling Similarity Transformed Equation of Motion Method for Vertical Excitation Energies, J. Chem. Theory Comput., 2018, 14, 72–91 CrossRef CAS PubMed.
- A. K. Dutta, F. Neese and R. Izsák, Towards a pair natural orbital coupled cluster method for excited states, J. Chem. Phys., 2016, 145, 034102 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- Z. R. Wiethorn, K. E. Hunter, T. J. Zuehlsdorff and A. Montoya-Castillo, Beyond the Condon limit: Condensed phase optical spectra from atomistic simulations, J. Chem. Phys., 2023, 159, 244114 CrossRef CAS PubMed.
- R. Wang, M. Ozhgibesov and H. Hirao, Analytical hessian fitting schemes for efficient determination of force-constant parameters in molecular mechanics, J. Comput. Chem., 2018, 39, 307–318 CrossRef CAS PubMed.
- C.-H. Yang and C.-P. Hsu, A multi-state fragment charge difference approach for diabatic states in electron transfer: Extension and automation, J. Chem. Phys., 2013, 139, 154104 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- T. A. Halgren and W. Damm, Polarizable force fields, Curr. Opin. Struct. Biol., 2001, 11, 236–242 CrossRef CAS PubMed.
- D. Loco, S. Jurinovich, L. Cupellini, M. F. S. J. Menger and B. Mennucci, The modeling of the absorption lineshape for embedded molecules through a polarizable QM/MM approach, Photochem. Photobiol. Sci., 2018, 17, 552–560 CrossRef CAS PubMed.
- T. J. Zuehlsdorff, A. Montoya-Castillo, J. A. Napoli, T. E. Markland and C. M. Isborn, Optical spectra in the condensed phase: Capturing anharmonic and vibronic features using dynamic and static approaches, J. Chem. Phys., 2019, 151, 074111 CrossRef PubMed.
- M. R. Shirts and J. D. Chodera, Statistically optimal analysis of samples from multiple equilibrium states, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- X. S. Li, B. Van Koten, A. R. Dinner and E. H. Thiede, Understanding the sources of error in MBAR through asymptotic analysis, J. Chem. Phys., 2023, 158, 214107 CrossRef CAS PubMed.
- J. E. Lawrence and D. E. Manolopoulos, An improved path-integral method for golden-rule rates, J. Chem. Phys., 2020, 153, 154113 CrossRef PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- R. J. Cave and M. D. Newton, Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- T. P. Fay, A simple improved low temperature correction for the hierarchical equations of motion, J. Chem. Phys., 2022, 157, 054108 CrossRef CAS PubMed.
- L. P. Lindoy, A. Mandal and D. R. Reichman, Quantum dynamical effects of vibrational strong coupling in chemical reactivity, Nat. Commun., 2023, 14, 2733 CrossRef CAS PubMed.
- T. P. Fay and D. T. Limmer, Coupled charge and energy transfer dynamics in light harvesting complexes from a hybrid hierarchical equations of motion approach, J. Chem. Phys., 2022, 157, 174104 CrossRef CAS PubMed.
- F. Neese, Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- B. De Souza, G. Farias, F. Neese and R. Izsák, Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics, J. Chem. Theory Comput., 2019, 15, 1896–1904 CrossRef CAS PubMed.
- J. Tölle, L. Cupellini, B. Mennucci and J. Neugebauer, Electronic couplings for photo-induced processes from subsystem time-dependent density-functional theory: The role of the diabatization, J. Chem. Phys., 2020, 153, 184113 CrossRef PubMed.
- Y.-C. Wang, S. Feng, W. Liang and Y. Zhao, Electronic Couplings for Photoinduced Charge Transfer and Excitation Energy Transfer Based on Fragment Particle–Hole Densities, J. Phys. Chem. Lett., 2021, 12, 1032–1039 CrossRef CAS PubMed.
- G. Torrie and J. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- M. Hijazi, D. M. Wilkins and M. Ceriotti, Fast-forward Langevin dynamics with momentum flips, J. Chem. Phys., 2018, 148, 184109 CrossRef PubMed.
- G. Trenins and J. O. Richardson, Nonadiabatic instanton rate theory beyond the golden-rule limit, J. Chem. Phys., 2022, 156, 174115 CrossRef CAS PubMed.
- E. R. Heller and J. O. Richardson, Instanton formulation of Fermi's golden rule in the Marcus inverted regime, J. Chem. Phys., 2020, 152, 034106 CrossRef CAS PubMed.
- Z. Tong, X. Gao, M. S. Cheung, B. D. Dunietz, E. Geva and X. Sun, Charge transfer rate constants for the carotenoid-porphyrin-C60 molecular triad dissolved in tetrahydrofuran: The spin-boson model vs the linearized semiclassical approximation, J. Chem. Phys., 2020, 153, 044105 CrossRef CAS PubMed.
- J. E. Lawrence and D. E. Manolopoulos, Analytic continuation of Wolynes theory into the Marcus inverted regime, J. Chem. Phys., 2018, 148, 102313 CrossRef PubMed.
- E. R. Heller and J. O. Richardson, Semiclassical instanton formulation of Marcus–Levich–Jortner theory, J. Chem. Phys., 2020, 152, 244117 CrossRef CAS PubMed.
- I. M. Ansari, E. R. Heller, G. Trenins and J. O. Richardson, Instanton theory for Fermi's golden rule and beyond, Philos. Trans. R. Soc., A, 2022, 380, 20200378 CrossRef CAS PubMed.
- E. Mulvihill and E. Geva, A Road Map to Various Pathways for Calculating the Memory Kernel of the Generalized Quantum Master Equation, J. Phys. Chem. B, 2021, 125, 9834–9852 CrossRef CAS PubMed.
- J. R. Mannouch and J. O. Richardson, A mapping approach to surface hopping, J. Chem. Phys., 2023, 158, 104111 CrossRef CAS PubMed.
- J. E. Runeson and D. E. Manolopoulos, A multi-state mapping approach to surface hopping, J. Chem. Phys., 2023, 159, 094115 CrossRef CAS PubMed.
- J. E. Lawrence, J. R. Mannouch and J. O. Richardson, Recovering Marcus Theory Rates and Beyond without the Need for Decoherence Corrections: The Mapping Approach to Surface Hopping, J. Phys. Chem. Lett., 2024, 15(3), 707–716 CrossRef CAS PubMed.
- G. Amati, M. A. C. Saller, A. Kelly and J. O. Richardson, Quasiclassical approaches to the generalized quantum master equation, J. Chem. Phys., 2022, 157, 234103 CrossRef CAS PubMed.
- A. Kelly, N. Brackbill and T. E. Markland, Accurate nonadiabatic quantum dynamics on the cheap: Making the most of mean field theory with master equations, J. Chem. Phys., 2015, 142, 094110 CrossRef PubMed.
- J. E. Runeson, T. P. Fay and D. E. Manolopoulos, Exciton dynamics from the mapping approach to surface hopping: comparison with Förster and Redfield theories, Phys. Chem. Chem. Phys., 2024, 26, 4929–4938 RSC.
- S. S. Skourtis, I. A. Balabin, T. Kawatsu and D. N. Beratan, Protein dynamics and electron transfer: Electronic decoherence and non-Condon effects, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3552–3557 CrossRef CAS PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin-Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- A. P. Demchenko, V. I. Tomin and P.-T. Chou, Breaking the Kasha Rule for More Efficient Photochemistry, Chem. Rev., 2017, 117, 13353–13381 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, M. J. James, M. Teders, L. Pitzer and F. Glorius, Energy transfer catalysis mediated by visible light: principles, applications, directions, Chem. Soc. Rev., 2018, 47, 7190–7202 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details on electronic structure calculations and bespoke force-field parameterization. Details of rate constant calculations. MD simulation details. Supplemental tables of solvent model properties, gas phase state energies, and reorganization energies. See DOI: https://doi.org/10.1039/d4sc01369g |
| This journal is © The Royal Society of Chemistry 2024 |