Transient-absorption spectroscopy of dendrimers via nonadiabatic excited-state dynamics simulations

Abstract

The efficiency of light-harvesting and energy transfer in multi-chromophore ensembles underpins natural photosynthesis. Dendrimers are highly branched synthetic multi-chromophoric conjugated supra-molecules that mimic these natural processes. After photoexcitation, their repeated units participate in a number of intramolecular electronic energy relaxation and redistribution pathways that ultimately funnel to a sink. Here, a model four-branched dendrimer with a pyrene core is theoretically studied using nonadiabatic molecular dynamics simulations. We evaluate excited-state photoinduced dynamics of the dendrimer, and demonstrate on-the-fly simulations of its transient absorption pump–probe (TA-PP) spectra. We show how the evolutions of the simulated TA-PP spectra monitor in real time photoinduced energy relaxation and redistribution, and provide a detailed microscopic picture of the relevant energy-transfer pathways. To the best of our knowledge, this is the first of this kind of on-the-fly atomistic simulation of TA-PP signals reported for a large molecular system.

---

I. Introduction

An efficient light harvesting and subsequent lossless electronic energy funnel are among the most important requirements in natural photosynthesis and in the development of organic electronic devices like solar cells, light-emitting diodes, electronic sensors, and so on.^1,2 Here, conjugated dendrimers emerged as artificially designed multi-chromophoric molecular systems that are able to closely mimic the natural photosynthetic systems due to their well-defined three-dimensional structural arrangements. Their treelike structure consists of several equivalent light absorber branches connected to a specific central core, yielding an efficient branches-to-core energy funnel.^3–10 The molecular design of dendrimers via varying the number and chemical properties of the branches and/or the characteristics of the core, targets optimization of their optical properties, intra- and inter-branch energy transfer efficiency and unidirectional funnelling.^11–13

The photoinduced dynamics of dendrimers and their building blocks have been analysed using a variety of theoretical^14–27 and experimental approaches.^28–36 These studies reveal their rich excited-state dynamics involving processes such as intramolecular electronic and vibrational energy relaxation and redistribution, radiative and nonradiative decay, effects of static and dynamic disorder, coherences, transient exciton self-trapping, molecular scrambling, structural rearrangements, and planarization. These complex and simultaneous processes can be explored in detail using on-the-fly atomistic non-adiabatic excited state molecular dynamics simulations. This task can be afforded by using mixed quantum/classical approaches to describe non-adiabatic dynamics.^37,38 Different computational codes enable these simulations in realistic molecular or materials systems, such as NEWTON-X,^39–41 SHARC,^42–44 PYXAID,^45,46 NWChem,^47,48 and NEXMD,^49–51 to name a few. Particularly, the NEXMD software package^49,50 can deal with large conjugated molecules featuring multiple coupled electronic excited states. This code has been previously used for the simulations of different types of dendrimers^{11,22,24,31,52,53} showing its suitability for the analysis of their photoexcited energy relaxation, redistribution and transfer.

Experimental monitoring of ultrafast photoinduced non-adiabatic dynamics in such molecular systems can be accomplished by transient-absorption (TA) spectroscopy with laser pulses which have specific temporal envelopes and polarizations.^54–59 Simulations of these signals have been performed by using several theoretical methods.^60–68 For example, on-the-fly simulations of TA pump probe (TA-PP) signals of different polyatomic chromophores have been performed using the cumulant/harmonic approximation for the evaluation of vibrational contributions^61–63 and real-time time-dependent density-functional theory (RT-TDDFT).^64–66,69 However, virtually all ab initio simulations of spectroscopic signals are performed in the impulsive limit (Dirac delta-function pulse envelopes) and without proper orientational averaging (aligned samples). More recently, a practical approach for the ab initio simulations of femtosecond TA-PP signals of nonadiabatic dynamics in molecular systems has been proposed.^70,71 This approach combines the classical approximation to the doorway-window (DW) representation introduced by Mukamel and coworkers^72–74 with the on-the-fly trajectory simulations. This methodology, which showed its efficiency in the simulations of TA signals of pyrazine,⁷⁰ phenylene ethynylene dendrimers building blocks²⁷ and azomethane,⁷⁵ was further extended to the simulation of photoelectron,⁷⁶ electronic two dimensional⁷⁷ and femtosecond pump – X-ray probe signals.⁷⁸ The TA-PP signal is calculated as the product of the doorway operator (at the initial time, t = 0) and the window operator (at the time delay t between the pump and probe pulses), averaged over all quantum-classical nonadiabatic excited-state trajectories. Trajectory surface hopping algorithms^{37,38,79–82} were commonly used in these simulations.

Herein, we demonstrate how TA signals can be simulated – without extra computational cost – with proper (e.g. experimental) pulse envelopes and polarizations as well as orientational averaging. Specifically, we employ the DW formalism to model an efficient energy funnel that takes place during nonadiabatic excited state molecular dynamics of large multi-chromophoric conjugated realistic systems like the tetra-branched dendrimer T1 (see Fig. 1(a)) with a pyrene as a core and fluorene/carbazole as dendrons. The calculated TA spectra agree well with experiments.³² We show that the simulated signals monitor in real time photoinduced energy relaxation and redistribution in the T1 dendrimers and provide a detailed microscopic picture of the relevant energy-transfer pathways. To the best of our knowledge, this is the first of this kind of on-the-fly atomistic simulation of TA-PP signals reported for large molecular systems.

Fig. 1 (a) Chemical structure of the dendrimer T1; (b) superposition of snapshots obtained from the ground state molecular dynamics simulations at room temperature indicating conformational flexibility of the molecule; (c) calculated linear absorption spectra (black dashed) from these snapshots with separate contributions (colors) from the different excited states. Vertical lines mark oscillator strength values obtained at the optimized ground state geometry, and the corresponding spatial distribution of electronic transition densities of S₁ and S₂ states calculated at the optimized ground state geometry, are shown in the insets. The black solid line shows the experimental linear absorption spectra.³²

II. Results and discussion

We start with the energy-level structure of the tetra-branched dendrimer T1 depicted in Fig. 1(a). A superposition of conformational structures of T1 during ground state molecular dynamics simulations at ambient conditions (see Methods) is shown in Fig. 1(b). We find that the T1 branches experience free rotations at room temperature around the dihedral angles that connect the different intramolecular chromophores. This conformational flexibility is expected to affect the exciton localization/delocalization patterns in the excited state dynamics. Fig. 1(c) displays the simulated absorption spectra calculated from the structures in Fig. 1(b) with separate contributions from different excited states and the corresponding experimental spectra. The spatial distributions of electronic transition densities of the states S₂, and S₁, calculated in the ground state geometry, are shown as insets. The first 5 excited-states feature Frenkel-exciton character. The calculation the corresponding natural orbitals for the different excited state, shown in ESI Fig. S8,† indicates the absence of charge transfer character in these states. Despite the degree of delocalization, the transition densities of S₁ and S₂ are mainly localized on dendrons and pyrene, respectively. The validity of the semiempirical electronic structure method used (see Methods) is justified by a good agreement with the experimental absorption spectra,³² showing a low energy band at ∼2.5 eV (∼500 nm) corresponding to the S₁ state and a larger peak centered at ∼3.15 eV (∼393 nm).

The electronic states of the tetra-branched dendrimer T1 can be grouped into three energetically separated regions; {0} is the ground state; {I} involves a manifold of states that can be initially excited by the pump pulse from the ground state; and {II} comprises a manifold of the states that can be excited by the probe pulse from states {I}.^70,71 The energies of the states from the groups {I} and {II} match ≈E_pu and ≈2E_pu, respectively. For the pump pulse centered at E_pu = 426 nm, the lowest five excited states are included in the manifold {I} (see also Fig. 1(c)), and the next 295 states are included in the manifold {II}. Table 1 summarizes the vertical excitation energies (VEEs) of the first five excited electronic states from {I}, as well as the transition dipole moments μ_x,y,z,tot with respect to a body-fixed reference frame with the x, and y axes defined in the plane of pyrene according to ESI Fig. S1.† Although the molecule formally belongs to the C_2h symmetry group, the high flexibility of the branches under thermal fluctuation leads to significant deviations from the symmetric configurations. Nevertheless, the molecular excited state structure can be analyzed as a set of coupled chromophore units; i.e., a central core pyrene moiety and four equivalent branches. In this sense, the Frenkel exciton model becomes an ideal reduced framework allowing to rationalize properties of the first five low-lying electronic excitations (see ESI† for details on the corresponding Frenkel Hamiltonian model). According to this model, the first excitation is mainly located in the pyrene moiety, while the subsequent excited states S_2–4 have contributions coming from the branches. Although thermal fluctuations drive the system away from this idealization, some general trends can be seen in the absorption spectra (Fig. 1(c)). S₁ state is well separated from the other low-lying excited states because it corresponds mostly to the contribution coming from the central core. The S₂ oscillator strength is the smallest among the first five low-lying excited states because a symmetric superposition of the branches cancels the net transition dipole moment. S_3,4 are quasi-degenerate states having similar oscillator strengths coming from the alternating branch contributions, leading to distinct transition dipole orientations. The spatial distributions of the respective electronic transition densities indicating the orientation of their corresponding transition dipole moments (μ) for the five lowest energy electronic states are shown in ESI Fig. S9.†

Table 1 Vertical excitation energies (VEEs) and transition dipole moments (μ) of the five lowest energy electronic states obtained at the ground state geometry

	VEE (eV)	μ (a.u.)
		x	y	z	Tot.
S1	2.40	−0.45	5.13	−0.14	5.15
S2	2.88	−0.03	0.01	0.01	0.03
S3	2.90	5.67	1.42	0.17	5.85
S4	2.90	−5.88	−1.29	0.00	6.02
S5	3.01	−0.28	0.36	−0.55	0.71

---

The photoexcited state population dynamics in T1 is succinctly presented in Fig. 2. Panel (a) illustrates the evolution of populations of electronic states within manifold {I}. The pump pulse centered at E_pu = 426 nm (2.91 eV) (see Section IV.A) populates states S₃ and S₄ that experience ultrafast relaxation to the S₂ state on the timescale of ∼100 and ∼20 femtoseconds, respectively (see ESI Fig. S2† for a more detailed description of the short-time dynamics). After the S₂ state is populated, it experiences a slower relaxation to the S₁ state approaching a picosecond timescale. Throughout the internal conversion process, the dendrimer undergoes ultrafast branches-to-pyrene energy transfer, manifested through discernible changes in the spatial localization of its transition density (see Methods) as visualized in Fig. 2(b). During the first ∼30 fs after photoexcitation, the S₂ population reaches its maximum value. Then approximately half of the transition density, which is initially localized in the branches, is transferred to the pyrene, suggesting delocalization of the S₂ state between the branches and the pyrene units. The subsequent S₂ → S₁ transfer further increases the exciton localization in the pyrene trap. The overall internal conversion process, calculated by fitting the raise of the S₁ population using a mono-exponential function, yields the lifetime of ∼437 fs. This signifies the effective channeling of the initially harvested light energy towards the core.

Fig. 2 (a) Evolution of average populations of electronic states calculated from the fraction of trajectories in a particular state at a given time after the initial laser excitation; (b) evolution of the average fraction of the transition density δ^α_X(t) on the branches and the pyrene core.

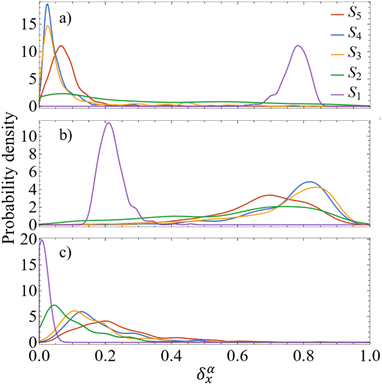
As detailed in the Methods section, a more intricate picture of intramolecular energy redistribution can be obtained using the diagonal elements (ρ^0α)_ii of transition density matrices between excited states, defined in terms of the atomic orbital (AO) basis. These quantities (ρ^0α)_ii reflect changes of the electronic density on AO i during a transition from the ground state to the excited state α. After applying the normalization condition , the fraction of the transition density (ρ^0α(t))²_X localized on each specific X chromophore can be obtained (see the Methods section), being X = pyrene, fluorenes, and carbazoles. Fig. 3 illustrates the fraction of transition density on pyrene (a), fluorene (b), and carbazole (c) in the electronic states S_α of manifold {I} throughout the internal conversion process. The exciton localization on carbazoles, δ^α_carbazole(t), decreases with the decreasing order in energy of states (Fig. 3(c)). The opposite trend is observed for δ^α_pyrene(t), whose values are larger for the S₁ state with respect to other states (Fig. 3(a)). Very low values of δ^α_pyrene(t) are observed for the other states, except S₂ that exhibits a broad distribution of this value. This indicates that S₂ is the most responsive among the states to conformational distortions introduced at room temperature. Most of states experience their main exciton localization on fluorene units δ^α_fluorene(t), except S₁ (Fig. 3(b)). Since the initial pump pulse populates mainly states S₃ and S₄, the fluorene → pyrene path represents the main exciton redistribution during the internal conversion. A detailed picture of this process is shown in ESI Fig. S3,† where the evolution of the average fraction of the transition densities δ^α_carbazole(t), δ^α_fluorene(t), and δ^α_pyrene(t) are tracked. The initial excitation is mainly localized in the fluorenes and a minor portion in the carbazole. The fraction in the carbazole is then quickly redistributed yielding a slower fluorene → pyrene transfer to dominate the process.

Fig. 3 Distribution of the average fraction of the transition density matrix (δ^α_X(t)) localized on the (a) pyrene, (b) fluorenes, and (c) carbazoles as the system evolves in the different S_α states during the internal conversion process.

In order to analyze the inter-branch exciton exchange, we have followed the time-evolution of the spatial localization of the transition density on the different branches (dendrons), δ^α_X(0) (X = A, B, C, D). Once we define the branch A as the branch with the highest initial value of δ^α_X(0), branches B, C, and D can be uniquely labeled as shown in Fig. 4(a). Fig. 4(b) and (c) illustrates that the exciton is initially mainly localized in the branch A (as per definition) with some minor delocalization in the branch B. Following photoexcitation, there is no substantial inter-branch exciton exchange. The initially excited branch A appears to undergo direct relaxation to the pyrene with minor participation of the other branches.

Fig. 4 (a) Chemical structure of the dendrimer T1 showing the labeling of its branches. The branch A has the highest initial value of δ^α_X(0); (b) and (c) evolution of the average fraction of the transition density δ^α_X(t) on the branches and the pyrene core, with branch notation as adopted above.

The integral TA-PP signals of the T1 dendrimer simulated with the on-the-fly DW approach (see Methods) are shown in Fig. 5 and 6 for s_pu = s_pr and s_pu⊥s_pr, respectively. The figures depict the GSB, SE, ESA contributions and the total signal. In the frequency domain, the signals cover a broad energy range, indicating the presence of multiple transitions between manifolds {0} and {I} as well as between {I} and {II}. In the time domain, the signals display underdamped (GSB) and slightly damped (SE, ESA) oscillations, mirroring the wavepacket motion in manifolds {0} and {I}. Qualitatively, similar signals are frequently detected in various polyatomic molecular complexes probed by a broad-band high-resolution TA-PP spectroscopy (see ref. 83 and 84 and references therein).

Fig. 5 The GSB, SE, and ESA contributions and the total TA-PP signal for pump and probe pulses with parallel polarizations, s_pu = s_pr. The calculated signals are plotted as a function of delay time between pump and probe and probe pulse frequency.

Fig. 6 Same as Fig. 5 but for the TA-PP signal for pump and probe pulses with orthogonal polarizations, s_pu⊥s_pr.

The GSB signal probes transitions from the ground state S₀ to manifold {I} states. In the case of (Fig. 5), the primary contribution corresponds to E_pr ≈ 2.9 eV, representing electronic transitions between the states S₀ and S₃, S₄. In contrast, for the case , the main contribution corresponds to E_pr ≈ 2.5 eV (Fig. 6), which reveals transitions between the S₀ and S₁ states. This difference can be explained by analyzing Table 1. While μ₀₃ and μ₀₄ are essentially oriented in the direction of the x-axis, μ₀₁ is oriented in the y-axis, i.e., orthogonal to them. In the time domain, the underdamped oscillations unveil the wavepacket motion in the electronic ground state. These oscillations, similarly obtained in the DW simulation of short model dendrimers,²⁷ are indicative of pronounced non-Condon effects. These effects arise from a significant dependence of the transition dipole moments between manifolds {0} and {I} on nuclear configurations.

The SE signal depicts the projection of the nuclear motion in the current excited state onto the ground state. It provides detailed information on the nonadiabatic transitions, offering insights beyond the population dynamics presented in Fig. 2(a). The ultrafast S_n → S₂ internal conversion is manifested as a redshift of the SE signal in the frequency domain. Hence the SE spectrum, which is initially localized at E_pr ≈ 2.9 eV, shifts to the red in less than 50 fs after the photoexcitation. Further on, the S₂ → S₁ transition causes depopulation of these contributions from the S₂ state, which is located at E_pr ≈ 2.8 eV. As such, the signal shifts to E_pr ≈ 2.3 eV, revealing the S₁ state. After ∼500 fs, the S₁ state receives half of the population, and the maximum of the SE intensity corresponds to this state. As previously noted, the intramolecular fluorene → pyrene transfer takes place during the photoinduced dynamics in manifold {I} (see Fig. 3). This process is similarly reflected in the GSB and SE signals. Namely, the initial SE intensity at E_pr ≈ 2.8 eV is higher for the 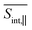signal than that for the signal. However, the situation becomes opposite for E_pr ≈ 2.3 eV at longer times. Nevertheless, the SE contribution at E_pr ≈ 2.8 eV persists for longer times in the signal compared to the signal. This arises due to the orthogonal orientations of μ₀₃ and μ₀₄ with respect to μ₀₁.

As evident in Fig. 6, the final signal is centered at ∼2.3 eV, whereas the GSB signal is centered at ∼2.5 eV. This difference is attributed to the influence of nuclear wavepacket evolution on S₁, resulting in a redshift that is also manifested in the steady-state fluorescence spectra.³² This redshift is frequently observed as a result of the excited state dynamics in multichromophoric conjugated molecular systems. It is associated to a specific planarization that enhances the extent of π-conjugation across the chromophore units.⁸⁵ No oscillations are detected during the S₂ → S₁ transition, owing to the time-delocalized character of this transfer.

A detailed short-time dynamics of the TA-PP signals are displayed in ESI Fig. S4 and S5† for 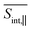and , respectively. During the first ∼50 fs, the SE signal exhibits oscillations around E_pr ≈ 2.8 eV due to the evolution of the molecular system on S₂. These oscillations are less pronounced in the GSB signal since the latter depends on the nuclear propagation in the electronic ground state. Hence, these findings emphasize the distinction in nuclear dynamics between the excited and ground states even at short times. This difference is primarily induced by the reorganization energy, representing the displacement of the equilibrium position of the nuclear modes in the excited electronic states relative to the ground state. Owing to the substantial number of (generally anharmonic) nuclear degrees of freedom involved, the oscillations do not exhibit a well-defined period. However, the distance between the first two SE maxima is approximately 15–20 fs, supporting the observation in ref. 27 regarding short dendrimers. ESI Fig. S10† shows the dominant contributions of the non-adiabatic coupling singular value decomposition for transitions from S_3/4 to S₂. Although the dendrimer high level of flexibility misaligns the non-adiabatic couplings vectors in real space, we can single out some features. The characteristic directions include CC double bonds in the pyrene unit, CC double bonds in the fluorene units, and the CC triple bonds connecting the carbazole and fluorene units, in agreement with the delocalized nature of S₂. These vibrational motions are activated when the electronic wavefunction reaches the excited state S₂. The corresponding nuclear oscillations are responsible for the pronounced oscillatory behavior of the SE and ESA contributions of the TA-PP during the first 15–20 fs, as shown in Fig. 5 and 6. It is essential to clarify that both the ESA and SE signals reveal the same photoinduced nuclear wavepacket motion in manifold {I}. However, these signals employ different “spectacle states” for delivering this information. While the SE signal monitors the nuclear wavepacket propagating in a current state of manifold {I} projected on the electronic ground state, the ESA signal reflects the projection of the nuclear motion in the current state of manifold {I} to higher-energy excited states of manifold {II}.

The total pump–probe signals and 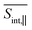are obtained as a sum of the GSB, SE, and ESA contributions. In the frequency domain, the net signals are dominated by ESA at lower E_pr and by the GSB+SE at higher E_pr. At short times (<100 fs), the high-energy state contributions are more intense in (Fig. 5 and ESI Fig. S4†) compared to (Fig. 6 and ESI Fig. S5†). At longer times, the S₁ state signatures become more pronounced in . As explained above, this effect is attributed to the transition dipole moment orientations in the S₁ state. Importantly, the S_n → S₂ and S₂ → S₁ transitions clearly visible in the SE signal, are obscured in the total TA-PP signal, because the GSB signal dominates over the SE contribution. However, these transitions can be monitored through the raise and decay of the ESA contributions, which do not interfere with their GSB and SE counterparts in the total signal.

To compare our simulations with the experimental TA-PP measurements reported in ref. 32, Fig. 7 shows (a) the total TA-PP spectrum 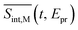; two cuts of this spectrum at t = 0.3 and 1.2 ps evaluated at magic angle between pump- and probe-pulse polarizations, and (c) the corresponding experimental signal at t = 0.3 and 1 ps. The total TA-PP spectrum is qualitatively similar to its and counterparts. We will further concentrate on the cuts of the spectrum shown in panel (b) and their experimental counterparts in panel (c). The experimental TA-PP spectra reveal three negative bands in the region of approximately 420–640 nm (∼1.9–2.9 eV), resulting from the superposition of GSB and SE signals. Additionally, two spectral features around 470 and 580 nm arise from the partial cancellation of the positive ESA and negative GSB+SE contributions. Wavelengths higher than 640 nm are attributed to the ESA signals. The overall shape of the experimental spectra Fig. 7(c) is well reproduced by our simulations Fig. 7(b). Furthermore, our simulations not only recover the major features, such as a pronounced GSB+SE band in the blue part of the spectrum. The calculated TA-PP spectra detail a number of finer features of the experimental signals and faithfully describe their temporal evolution. This includes an increase in the intensity of the hump around 470 nm and a decrease around 580 nm, as well as a notable reduction of the GSB+SE shoulder within the 520–580 nm range over time. However, some discrepancies exist, the most prominent being a slight redshift of the simulated GSB+SE band compared to the experimental results. This can be caused by a number of factors, for example, by immobilization of T1 in the polymer matrix, by non-Gaussian shape of the experimental pump pulses, and by the difference between the experimental and simulated excitation frequencies of the pump pulses. In addition, our simulations slightly overestimate “positiveness” of the peak around 580. However, this is not surprising since this feature is a result of a delicate balance and significant mutual cancellation of the GSB+SE and ESA contributions. In summary, this brief analysis demonstrates the reliability of our theoretical predictions and provides further validation for our methodology in simulating the nonlinear spectroscopic responses of large molecular systems.

Fig. 7 The total TA-PP signal (a) and two cuts of the signal at t = 0.3 and 1.2 ps, (b) evaluated at the magic angle (54.7°) between polarizations of the pump and probe pulses , and (c) measured experimentally.³²

III. Conclusions

In this contribution we report calculations of transient absorption pump–probe spectra delivering detailed information on photoexcited dynamics of a large four branched dendrimer with a pyrene core. This modelling of transient absorption spectra directly relies on the atomistic on-the-fly nonadiabatic excited state molecular dynamics simulations. We further employ the doorway-window methodology and simulation protocol.^72–74 Our analysis reveals an ultrafast intra-branch energy relaxation that takes place before the final exciton capture by the pyrene trap. Following an initial ultrafast carbazole → fluorene energy transfer, there is a subsequent, slower fluorene → pyrene funnelling. We demonstrate that the simulated pump–probe spectra permit a direct visualization of the photoinduced energy-transfer dynamics and pathways through the real-time monitoring of cascades of the S₄ → S₂, S₃ → S₂, and S₂ → S₁ interconversion processes accompanied by coherent wavepacket oscillations. Importantly, this information cannot be conveniently extracted from the GSB+SE contribution to the total transient signals coming from the low-lying excited electronic states, because it is “contaminated” by the GSB. However, the same information can be directly obtained from the spectrally separated ESA contribution to the total TA-PP signal. Hence, the ESA signal can be used as a messenger signifying the photoinduced dynamics in large chromophores.

The conformational flexibility and size of the dendrimer has required substantial modifications and improvements of the previously developed DW methodology.^70,71 Namely, we employed sampling of the initial trajectories from the doorway function, and incorporated orientational averaging of the signals into the simulation protocol. These techniques allowed us to simulate and analyze polarization-sensitive TA-PP signals. As the input, our DW protocol requires only electronic energies and transition dipole moments evaluated along (quasi)classical trajectories in the electronic ground state and lower-lying excited states. This renders the present methodology particularly attractive for the on-the-fly simulations of femtosecond responses of large molecular systems. Specifically, the present simulation protocol permits to (i) realistically simulate transient-absorption signals obtained with arbitrary pulse envelops and polarizations; (ii) evaluate anisotropy and any other polarization-sensitive transient absorption signals; (iii) straightforwardly generalize ab initio simulation protocols of all existing nonlinear spectroscopic signals towards the inclusion of realistic pulse envelops and arbitrary pulse polarization vectors; (iv) perform ab initio studies of various schemes of controlling and engineering photophysical processes via optimally tuned laser pulses; (v) dissect simulated spectroscopic signals into specific spectroscopic pathways by adopting the proper polarization schemes. A good agreement with reported experimental pump–probe spectra³² further substantiates the efficacy of the current methodology in simulating the nonlinear spectroscopic responses of large molecular systems. As such, work is in progress on the extension of the TA-PP protocol to electronic two-dimensional (2D) spectra and general four-wave-mixing signals.

IV. Methods

A. Non-adiabatic excited-state molecular dynamics

The photoinduced excited state dynamics in the tetra-branched dendrimer T1, shown in Fig. 1(a), has been simulated with Non-adiabatic EXcited state Molecular Dynamics (NEXMD) software.^49,50 This code was specifically designed to simulate on-the-fly non-adiabatic photoexcited dynamics in large conjugated molecules and able to treat multiple coupled electronic states with different hybrid quantum-classical methods. In the present work, the Tully's Fewest Switches Surface Hopping (FSSH) algorithm⁷⁹ is used. As implemented in NEXMD, excited state energies, gradients and non-adiabatic coupling terms are obtained at the configuration interaction singles (CIS) level and the semiempirical AM1 Hamiltonian model.⁸⁶

Particularly, the NEXMD software package^49,50 uses semiempirical Hamiltonian models and minimalistic configurational interactions singles description for electronically excited states. This reduced quantum mechanical description and on-the-fly propagation algorithms allow to model photoexcited dynamics in large conjugated molecules featuring multiple coupled electronic excited states. This code has been previously used for the simulations of different types of dendrimers^{11,22,24,31,52,53} showing its suitability for the analysis of their photoexcited energy relaxation, redistribution and energy transfer. Benchmarks against more accurate Time-Dependent Density Functional Theory (TD-DFT) calculations and comparisons with experimental spectra in terms of electronic transition energies and oscillator strengths have shown semiquantitative accuracy of the NEXMD package for simulating electronic excitations, excited state dynamics and spectroscopy.⁴⁹

Within the framework of NEXMD, transition density matrices between excited states are defined in atomic orbital (AO) basis⁸⁷ as (ρ^0α)_ij = ϕ_α|c^†_ic_j|ϕ₀, with ϕ₀ and ϕ_α being the wavefunctions corresponding to the adiabatic ground and excited states, respectively. c^†_i and c_j are the respective creation and annihilation operators acting over AO labeled with i and j indices. The diagonal elements (ρ^0α)_ii are relevant to the changes of the electronic density on AO i during a transition from the ground state to the excited state α. Therefore, it is possible to analyze the localization of the excited state wavefunction via the fraction of the transition density on each specific fragment of the dendrimer, obtained as:

where the index n_A runs over all the AO of atoms localized in the fragment X. Transition dipole moment vectors between the ground state and excited states (μ_0α(R₀)) and between excited-states (μ_αβ(R_α)) are calculated according to ref. 88, where R₀ and R_α are the corresponding molecular ground and excited state geometries, respectively.

The initial conditions for excited state simulations are obtained from 1 ns-long equilibrated ground state molecular dynamics simulation of the dendrimer at room temperature (T = 300 K) using the Langevin thermostat with a friction coefficient γ = 20.0 ps⁻¹. The following nonadiabatic excited state simulations are performed at a constant energy with five hundred (500) individual excited state trajectories propagated. As it has been pointed out in our previous work,⁸⁹ is a sufficient number of trajectories to achieve a reasonable statistical convergence of the results for similar systems. For each trajectory, the initial (subscript “in”) excited states α are sampled from the positively-defined doorway function,⁷¹

D_in(R₀, P₀, E_pu) = ε²_pr(E_pu − E_0α(R₀))|μ_0α(R₀)|² (2)

which is proportional to the probability of excitation of the molecular system with the pump pulse. Here

ε_pu(E_pu − E_0α(R₀)) = exp[−2π²σ²(E_pu − E_0α(R₀))²] (3)

where ε_pu(ω) and E_pu are the spectrum and the carrier frequency of the pump pulse, and E_0α is the energy of the αth state with respect to the ground state. Here we include up to 300 excited states to simulate TA-PP signals. We assume that the pump pulse is tuned into the maximum of the absorption spectrum, E_pu = 426 nm (see Fig. 1(c)), and has a Gaussian envelope ε_pu(t) = exp(−t²/2σ²) in the time domain with σ = 42.5 fs which corresponds to the FWHM (Full Width at Half Maximum) of 100 fs. Classical time steps of 0.5 and 0.1 fs are used for nuclei propagation in the ground state and excited state trajectories, respectively. A quantum time step of 0.025 fs is selected to propagate the electronic coefficients. Specific treatments of decoherence⁹⁰ and trivial unavoided crossings⁹¹ are used in these simulations along with other default options.⁵⁰ More details about the NEXMD theory, implementation, advantages and testing parameters can be found in our previous works.^49–51

B. TA-PP signal

Following Gelin et al.^70,71 the integral TA-PP can be evaluated through (semi)classical trajectories following the DW simulation protocol, which is based on the sampling of initial nuclear coordinates and momenta from the Wigner distribution. In this work, we modify and extend the protocol of ref. 70 in two directions. First, due to the high flexibility of the dendrimer, we do not use Wigner sampling. Instead, the initial conditions are obtained from snapshots collected during a long-equilibrated ground state molecular dynamics simulation (see Section IV.A). Second, we take into account orientational averaging and consider polarization-sensitive detection of TA-PP signals (cf. ref. 27). Hence we need to evaluate partial TA-PP signals S^(abcd)_int(t, E_pr), where the indexes a, b, c, d = x, y, z correspond to orientation of the transition dipole moments responsible for the interaction with the pump (a, b) and probe (c, d) pulses along the axes x, y, z along a certain (arbitrary) reference frame, and E_pr is the carrier frequency of the probe pulse. Subsequently, the DW simulation protocol of the present work looks as follows. The partial TA PP signals are evaluated according to the formula

S^(abcd)_int(t, E_pr) ∼ 〈D^(ab)(R₀)(W^int(cd)₀(R₀(t), P₀(t), E_pr) + W^int(cd)_I(R_α(t), P_α(t), E_pr) − W^int(cd)_II(R_α(t), P_α(t), E_pr))〉, (4)

where the three terms in eqn (4) represent the ground state bleach (GSB), stimulated emission (SE), and excited-state absorption (ESA). While the angular brackets represent averaging over quasi-classical trajectories sampled from the doorway function of eqn (2). The tensor DW functions are defined as

W^int(cd)₀(R₀(t), P₀(t), E_pr) = ε²_pr(E_pr − E_0α(R₀(t)))μ^(c)_0α(R₀(t))μ^(d)_0α(R₀(t)) (6)

W^int(cd)_I(R_α(t), P_α(t), E_pr) = ε²_pr(E_pr − E_0α(R_α(t)))μ^(c)_0α(R_α(t))μ^(d)_0α(R_α(t)) (7)

W^int(cd)_II(R_α(t), P_α(t), E_pr) = ε²_pr(E_pr − E_αβ(R_α(t)))μ^(c)_αβ(R_α(t))μ^(d)_αβ(R_α(t)) (8)

Here the subscripts 0 and α, β denote, respectively, the ground and excited electronic states, R₀, P_0, and R_α(t), P_α(t) are the nuclear positions and momenta in these states, E_0α(R₀(t)) and E_αβ(R_α(t)) are the energy differences between the electronic energies along trajectories. The superscripts (a, b, c, d = x, y, z) denote projections of the transition dipole moments μ_0β(R_α(t)) and μ_αβ(R_α(t)) on the axes of the reference frame, and ε_pr(ω) = ε_pu(ω) is the spectrum of the probe pulse. Finally, to be consistent with the selection of initial 0 → α excitations (eqn (2)), α → β excitations required for the ESA contribution follow an equivalent procedure. That is, a β state is selected at each time according to weight proportional to ε_pr²(E_pr − E_αβ(R_α))|μ_0α(R₀)|².

After the partial S^(abcd)_int(t, E_pr) have been obtained, the orientationally-averaged TA PP signal can be evaluated as

where s_pu and s_pr are the unit vectors along linear polarizations of the pump and probe pulses, respectively (the explicit dependence of S^(abcd)_int on t and E_pr is dropped for brevity). The derivation of eqn (9) can be found at ESI Section S1.† In this work, we analyze the situations with s_pu∥s_pr (s_pus_pr = 1), s_pu⊥s_pr, (s_pus_pr = 0) and (so-called magic angle). The corresponding signals are denoted as , , and , respectively (the subscript M stands for magic). Note that . The dispersed TA-PP spectra can be simulated in a similar manner, by replacing the “integral” window functions W^int(cd)_k (k = 0, I, II) by their “dispersed” counterparts defined in ref. 70 and 71.

Data availability

All study data are included in the article and/or ESI.† The Non-adiabatic EXcited state Molecular Dynamics (NEXMD) Program code, license, and documentation may be accessed at http://github.com/lanl/NEXMD.

Author contributions

R. P.-C. performed the non-adiabatic simulations and calculated and analyzed the TA-PP signals. V. M. F. helped in deriving, computing and analyzing the TA-PP signals and supervised the project. S. M., A. M.-M., and L. U.-P. contributed to write the manuscript. S. T. contributed to write the manuscript and supervised the project. M. F. G. derived, supervised the calculation and analysis of the TA-PP signals and contributed to write the manuscript. S. F-A. designed and supervised the project and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by CONICET, UNQ, ANPCyT (PICT-2018-2360). S. T. gratefully acknowledge support from the Chemical Sciences, Geosciences, and Bio-Sciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy (DOE), through award DE-SC0019484 and under Triad National Security, LLC (“Triad”) contract grant # 89233218CNA000001 (FWP: LANLE3T1). The work at Los Alamos National Laboratory (LANL) was performed in part at the Center for Integrated Nanotechnologies (CINT), a U.S. Department of Energy, Office of Science User Facility. This research used resources provided by the LANL Institutional Computing Program. We would like to thank professors Zujin Zhao and Yan Wan who kindly shared the experimental data presented in Fig. 1 and 7(c).

References

1. H. Hoppe and N. S. Sariciftci, Organic Solar Cells: An Overview, J. Mater. Res., 2004, 19, 1924–1945.
2. G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Light Harvesting for Organic Photovoltaics, Chem. Rev., 2017, 117(2), 796–837.
3. A. Nantalaksakul, D. Reddy, C. Bardeen and S. Thayumanavan, Light Harvesting Dendrimers, Photosynth. Res., 2006, 87(1), 133–150.
4. V. Balzani, P. Ceroni, M. Maestri and V. Vicinelli, Light-Harvesting Dendrimers, Curr. Opin. Chem. Biol., 2003, 7(6), 657–665.
5. T. Aida, D.-L. Jiang, E. Yashima and Y. Okamoto, A New Approach to Light-Harvesting with Dendritic Antenna, Thin Solid Films, 1998, 331(1–2), 254–258.
6. X. Xu, P. Zhang, B. Wu, Y. Xing, K. Shi, W. Fang, H. Yu and G. Wang, Photochromic Dendrimers for Photoswitched Solid-to-Liquid Transitions and Solar Thermal Fuels, ACS Appl. Mater. Interfaces, 2020, 12, 50135–50142.
7. A. Bar-Haim, J. Klafter and R. Kopelman, Dendrimers as Controlled Artificial Energy Antennae, J. Am. Chem. Soc., 1997, 119(26), 6197–6198,  DOI:10.1021/ja970972f.
8. A. BarHaim, J. Klafter and R. Kopelman, The Development of Light-Emitting Dendrimers for Displays, J. Am. Chem. Soc., 1997, 119, 6197–6198.
9. N. Kubota, Y. Segawa and K. Itami, N6-Cycloparaphenylene Transition Metal Complexes: Synthesis, Structure, Photophysical Properties, and Application to the Selective Monofunctionalization of Cycloparaphenylenes, J. Am. Chem. Soc., 2015, 137(3), 1356–1361,  DOI:10.1021/ja512271p.
10. S.-C. Lo and P. L. Burn, Development of Dendrimers: Macromolecules for Use in Organic Light-Emitting Diodes and Solar Cells, Chem. Rev., 2007, 107(4), 1097–1116.
11. V. Bonilla, V. M. Freixas, S. Fernandez-Alberti and J. F. Galindo, Impact of the Core on the Inter-Branch Exciton Exchange in Dendrimers, Phys. Chem. Chem. Phys., 2023, 25(17), 12097–12106,  10.1039/d2cp06009d.
12. O. P. Varnavski, J. C. Ostrowski, L. Sukhomlinova, R. J. Twieg, G. C. Bazan and T. Goodson, Coherent Effects in Energy Transport in Model Dendritic Structures Investigated by Ultrafast Fluorescence Anisotropy Spectroscopy, J. Am. Chem. Soc., 2002, 124(8), 1736–1743,  DOI:10.1021/ja011038u.
13. R. Kishi, T. Minami, H. Fukui, H. Hideaki Takahashi and M. Nakano, Core Molecule Dependence of Energy Migration in Phenylacetylene Nanostar Dendrimers: Ab Initio Molecular Orbital-Configuration Interaction Based Quantum Master Equation Study, J. Chem. Phys., 2008, 128, 244306.
14. S. Mukamel, Trees to Trap Photons, Nature, 1997, 388, 425–427.
15. S. Tretiak and S. Mukamel, Density Matrix Analysis and Simulation of Electronic Excitations in Conjugated and Aggregated Molecules, Chem. Rev., 2002, 102(9), 3171–3212,  DOI:10.1021/cr0101252.
16. J. Huang, L. Du, J. Wang and Z. Lan, Photoinduced Excited-State Energy-Transfer Dynamics of a Nitrogen-Cored Symmetric Dendrimer: From the Perspective of the Jahn-Teller Effect, J. Phys. Chem. C, 2015, 119(14), 7578–7589,  DOI:10.1021/jp512496z.
17. R. Dani and N. Makri, Excitation Energy Transfer in Bias-Free Dendrimers: Eigenstate Structure, Thermodynamics, and Quantum Evolution, J. Phys. Chem. C, 2022, 126(25), 10309–10319.
18. J. Liu and W. Thiel, An Efficient Implementation of Semiempirical Quantum-Chemical Orthogonalization-Corrected Methods for Excited-State Dynamics, J. Chem. Phys., 2018, 154103, 154103–154114.
19. O. P. Dimitriev, Dynamics of Excitons in Conjugated Molecules and Organic Semiconductor Systems, Chem. Rev., 2022, 122(9), 8487–8593.
20. J. C. Kirkwood, C. Scheurer, V. Chernyak and S. Mukamel, Simulations of Energy Funneling and Time- and Frequency-Gated Fluorescence in Dendrimers, J. Chem. Phys., 2001, 114(5), 2419–2429.
21. S. Tretiak, V. Chernyak and S. Mukamel, Localized Electronic Excitations in Phenylacetylene Dendrimers, J. Phys. Chem. B, 1998, 102, 3310–33155.
22. V. M. Freixas, D. Keefer, S. Tretiak, S. Fernandez-Alberti and S. Mukamel, Ultrafast Coherent Photoexcited Dynamics in a Trimeric Dendrimer Probed by X-Ray Stimulated-Raman Signals, Chem. Sci., 2022, 13(21), 6373–6384,  10.1039/d2sc00601d.
23. V. M. Freixas, A. J. White, T. Nelson, H. Song, D. V. Makhov, D. Shalashilin, S. Fernandez-Alberti and S. Tretiak, Nonadiabatic Excited-State Molecular Dynamics Methodologies: Comparison and Convergence, J. Phys. Chem. Lett., 2021, 12(11), 2970–2982,  DOI:10.1021/acs.jpclett.1c00266.
24. M. C. Aguilera, A. E. Roitberg, V. D. Kleiman, S. Fernandez-Alberti and J. F. Galindo, Unraveling Direct and Indirect Energy Transfer Pathways in a Light-Harvesting Dendrimer, J. Phys. Chem. C, 2020, 124(41), 22383–22391,  DOI:10.1021/acs.jpcc.0c06539.
25. C. Robertson and G. A. Worth, Modelling the Non-Radiative Singlet Excited State Isomerization of Diphenyl-Acetylene: A Vibronic Coupling Model, Chem. Phys., 2018, 510, 17–29.
26. E. K.-L. Ho and B. Lasorne, Diabatic Pseudofragmentation and Nonadiabatic Excitation-Energy Transfer in Meta-Substituted Dendrimer Building Blocks, Comput. Theor. Chem., 2019, 1156, 25–36.
27. D. Hu, J. Peng, L. Chen, M. F. Gelin and Z. Lan, Spectral Fingerprint of Excited-State Energy Transfer in Dendrimers through Polarization-Sensitive Transient-Absorption Pump-Probe Signals: On-the-Fly Nonadiabatic Dynamics Simulations, J. Phys. Chem. Lett., 2021, 12(39), 9710–9719,  DOI:10.1021/acs.jpclett.1c02640.
28. V. D. Kleiman, J. S. Melinger and D. Mc Morrow, Ultrafast Dynamics of Electronic Excitations in a Light-Harvesting Phenylacetylene Dendrimer, J. Phys. Chem. B, 2001, 105, 5595–5598.
29. T. Nomoto, H. Hosoi, T. Fujino, T. Tahara and H. Hamaguchi, Excited-State Structure and Dynamics of 1,3,5-Tris(phenylethynyl)benzene as Studied by Raman and Time-Resolved Fluorescence Spectroscopy, J. Phys. Chem. A, 2007, 111(15), 2907–2912.
30. E. Atas, Z. H. Peng and V. D. Kleiman, Energy Transfer in Unsymmetrical Phenylene Ethynylene Dendrimers, J. Phys. Chem. B, 2005, 109(28), 13553–13560.
31. J. Galindo, E. Atas, A. Altan, D. Kuroda, S. Fernandez-Alberti, S. Tretiak, A. Roitberg and V. Kleiman, Dynamics of Energy Transfer in a Conjugated Dendrimer Driven by Ultrafast Localization of Excitations, J. Am. Chem. Soc., 2015, 137(36), 11637–11644.
32. D. Huo, M. Li, Z. Zhao, X. Wang, A. Xia, P. Lu and Y. Wan, Delocalized Excitation or Intramolecular Energy Transfer in Pyrene Core Dendrimers, J. Phys. Chem. Lett., 2021, 12, 7717–7725,  DOI:10.1021/acs.jpclett.1c02182.
33. S. Peng, G. Shao, K. Wang, X. Chen, J. Xu, H. Wang, D. Wu and J. Xia, Efficient Energy Transfer in a Rylene Imide-Based Heterodimer: The Role of Intramolecular Electronic Coupling, J. Phys. Chem. Lett., 2023, 14(13), 3249–3257,  DOI:10.1021/acs.jpclett.3c00477.
34. L. J. Patalag, J. Hoche, M. Holzapfel, A. Schmiedel, R. Mitric, C. Lambert and D. B. Werz, Ultrafast Resonance Energy Transfer in Ethylene-Bridged BODIPY Heterooligomers: From Frenkel to Förster Coupling Limit, J. Am. Chem. Soc., 2021, 143(19), 7414–7425,  DOI:10.1021/jacs.1c01279.
35. M. Ranasinghe, M. Hager, C. Gorman and T. Goodson, Time-Resolved Fluorescence Investigation of Energy Transfer in Compact Phenylacetylene Dendrimers, J. Phys. Chem. B, 2004, 108(25), 8543–8549.
36. J. S. Melinger, Y. C. Pan, V. D. Kleiman, Z. H. Peng, B. L. Davis, D. McMorrow and M. Lu, Optical and Photophysical Properties of Light-Harvesting Phenylacetylene Monodendrons Based on Unsymmetrical Branching, J. Am. Chem. Soc., 2002, 124(40), 12002–12012.
37. R. Crespo-Otero and M. Barbatti, Recent Advances and Perspectives on Nonadiabatic Mixed Quantum-Classical Dynamics, Chem. Rev., 2018, 118(15), 7026–7068,  DOI:10.1021/acs.chemrev.7b00577.
38. B. F. E. Curchod and T. J. Martínez, Ab Initio Nonadiabatic Quantum Molecular Dynamics, Chem. Rev., 2018, 118(7), 3305–3336,  DOI:10.1021/acs.chemrev.7b00423.
39. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Newton-X: A Surface-Hopping Program for Nonadiabatic Molecular Dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(1), 26–33,  DOI:10.1002/wcms.1158.
40. S. Mai, P. Marquetand and L. González, NEWTON-X, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
41. M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, The On-the-Fly Surface-Hopping Program System Newton-X: Application to Ab Initio Simulation of the Nonadiabatic Photodynamics of Benchmark Systems, J. Photochem. Photobiol., A, 2007, 190(2–3), 228–240,  DOI:10.1016/j.jphotochem.2006.12.008.
42. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, SHARC: Ab Initio Molecular Dynamics with Surface Hopping in the Adiabatic Representation Including Arbitrary Couplings, J. Chem. Theory Comput., 2011, 7(5), 1253–1258,  DOI:10.1021/ct1007394.
43. S. Mai, P. Marquetand and L. González, Nonadiabatic Dynamics: The SHARC Approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
44. F. Plasser, S. Gómez, M. Menger, S. Mai and L. González, Highly Efficient Surface Hopping Dynamics Using a Linear Vibronic Coupling Model, Phys. Chem. Chem. Phys., 2019, 21, 57–69.
45. A. V. Akimov and O. V. Prezhdo, The PYXAID Program for Non-Adiabatic Molecular Dynamics in Condensed Matter Systems, J. Chem. Theory Comput., 2013, 9(11), 4959–4972,  DOI:10.1021/ct400641n.
46. A. V. Akimov and O. V. Prezhdo, Advanced Capabilities of the PYXAID Program: Integration Schemes, Decoherence Effects, Multiexcitonic States, and Field-Matter Interaction, J. Chem. Theory Comput., 2014, 10(2), 789–804,  DOI:10.1021/ct400934c.
47. H. Song, S. A. Fischer, Y. Zhang, C. J. Cramer, S. Mukamel, N. Govind and S. Tretiak, First Principles Nonadiabatic Excited-State Molecular Dynamics in NWChem, J. Chem. Theory Comput., 2020, 16(10), 6418–6427,  DOI:10.1021/acs.jctc.0c00295.
48. H. Song, V. M. Freixas, S. Fernandez-Alberti, A. J. White, Y. Zhang, S. Mukamel, N. Govind and S. Tretiak, An Ab Initio Multiple Cloning Method for Non-Adiabatic Excited-State Molecular Dynamics in NWChem, J. Chem. Theory Comput., 2021, 17(6), 3629–3643,  DOI:10.1021/acs.jctc.1c00131.
49. T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Non-Adiabatic Excited-State Molecular Dynamics: Theory and Applications for Modeling Photophysics in Extended Molecular Materials, Chem. Rev., 2020, 120(4), 2215–2287,  DOI:10.1021/acs.chemrev.9b00447.
50. W. Malone, B. Nebgen, A. White, Y. Zhang, H. Song, J. A. Bjorgaard, A. E. Sifain, B. Rodriguez-Hernandez, V. M. Freixas, S. Fernandez-Alberti, A. E. Roitberg, T. R. Nelson and S. Tretiak, NEXMD Software Package for Nonadiabatic Excited State Molecular Dynamics Simulations, J. Chem. Theory Comput., 2020, 16(9), 5771–5783,  DOI:10.1021/acs.jctc.0c00248.
51. T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nonadiabatic Excited State Molecular Dynamics: Modeling Photophysics in Organic Conjugated Materials, Acc. Chem. Res., 2014, 47, 1155–1164.
52. D. Ondarse-Alvarez, N. Oldani, A. E. Roitberg, V. Kleiman, S. Tretiak and S. Fernandez-Alberti, Energy Transfer and Spatial Scrambling of an Exciton in a Conjugated Dendrimer, Phys. Chem. Chem. Phys., 2018, 20, 29648–29660,  10.1039/C8CP05852K.
53. D. Ondarse-Alvarez, S. Kömürlü, A. Roitberg, G. Pierdominici-Sottile, S. Tretiak, S. Fernandez-Alberti and V. Kleiman, Ultrafast Electronic Energy Relaxation in a Conjugated Dendrimer Leading to Inter-Branch Energy Redistribution, Phys. Chem. Chem. Phys., 2016, 18(36), 25080–25089.
54. L. R. Khundkar and A. H. Zewail, Ultrafast Molecular Reaction Dynamics in Real-Time: Progress over a Decade, Annu. Rev. Phys. Chem., 1990, 41, 15–60.
55. J. L. Martin and M. H. Vos, Femtosecond Biology, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 199–222.
56. G. Beddard, Molecular Photophysics, Rep. Prog. Phys., 1993, 56, 63–171.
57. M. Fushitani, Applications of Pump-Probe Spectroscopy, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2008, 104, 272–297.
58. T. Elsaesser, Introduction: Ultrafast Processes in Chemistry, Chem. Rev., 2017, 117(16), 10621–10622,  DOI:10.1021/acs.chemrev.7b00226.
59. M. Maiuri, M. Garavelli and G. Cerullo, Ultrafast Spectroscopy: State of the Art and Open Challenges, J. Am. Chem. Soc., 2020, 142(1), 3–15,  DOI:10.1021/jacs.9b10533.
60. I. Conti, G. Cerullo, A. Nenov and M. Garavelli, Ultrafast Spectroscopy of Photoactive Molecular Systems from First Principles: Where We Stand Today and Where We Are Going, J. Am. Chem. Soc., 2020, 142, 16117–16139.
61. D. Polli, P. Altoe, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies and E. Al, Conical Intersection Dynamics of the Primary Photoisomerization Event in Vision, Nature, 2010, 467, 440–443.
62. A. Nenov, R. Borrego-Varillas, A. Oriana, L. Ganzer, F. Segatta, I. Conti, J. Segarra-Marti, J. Omachi, M. Dapor and S. Taioli, et al., UV-Light-Induced Vibrational Coherences: The Key to Understand Kasha Rule Violation in Trans-Azobenzene, J. Phys. Chem. Lett., 2018, 9, 1534–1541.
63. R. Borrego-Varillas, D. C. Teles-Ferreira, A. Nenov, I. Conti, L. Ganzer, C. Manzoni, M. Garavelli, A. Maria de Paula and G. Cerullo, Observation of the Sub-100 Fs Population of a Dark State in a Thiobase Mediating Intersystem Crossing, J. Am. Chem. Soc., 2018, 140, 16087–16093.
64. T. S. Nguyen, J. H. Koh, S. Lefelhocz and J. Parkhill, Black-Box, Real-Time Simulations of Transient Absorption Spectroscopy, J. Phys. Chem. Lett., 2016, 7, 1590–1595.
65. F. P. Bonafé, F. J. Hernández, B. Aradi, T. Frauenheim and C. G. Sánchez, Fully Atomistic Real-Time Simulations of Transient Absorption Spectroscopy, J. Phys. Chem. Lett., 2018, 9, 4355–4359.
66. J. Krumland, A. M. Valencia, S. Pittalis and C. A. Rozzi, Understanding Real-Time Time-Dependent Density-Functional Theory Simulations of Ultrafast Laser-Induced Dynamics in Organic Molecules, J. Chem. Phys., 2020, 153, 054106.
67. T. Zimmermann and J. Vaníček, Efficient On-the-Fly Ab Initio Semiclassical Method for Computing Time-Resolved Nonadiabatic Electronic Spectra with Surface Hopping or Ehrenfest Dynamics, J. Chem. Phys., 2014, 141, 134102.
68. T. Begušić, J. Roulet and J. Vaníček, On-the-Fly Ab Initio Semiclassical Evaluation of Time-Resolved Electronic Spectra, J. Chem. Phys., 2018, 149, 244115.
69. N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni and A. A. Correa, et al., Octopus, a Computational Framework for Exploring Light-Driven Phenomena and Quantum Dynamics in Extended and Finite Systems, J. Chem. Phys., 2020, 152, 124119.
70. M. F. Gelin, X. Huang, W. Xie, L. Chen, N. Došlić and W. Domcke, Ab Initio Surface-Hopping Simulation of Femtosecond Transient-Absorption Pump-Probe Signals of Nonadiabatic Excited-State Dynamics Using the Doorway-Window Representation, J. Chem. Theory Comput., 2021, 17(4), 2394–2408.
71. M. F. Gelin, L. Chen and W. Domcke, Equation-of-Motion Methods for the Calculation of Femtosecond Time-Resolved 4-Wave-Mixing and n-Wave-Mixing Signals, Chem. Rev., 2022, 122, 17339–17396.
72. Y. J. Yan, L. E. Fried and S. Mukamel, Ultrafast Pump-Probe Spectroscopy: Femtosecond Dynamics in Liouville Space, J. Phys. Chem., 1989, 93, 8149–8162.
73. Y. J. Yan and S. Mukamel, Femtosecond Pump-Probe Spectroscopy of Polyatomic Molecules in Condensed Phases, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6485–6504.
74. L. E. Fried and S. Mukamel, A Classical Theory of Pump–Probe Photodissociation for Arbitrary Pulse Durations, J. Chem. Phys., 1990, 93, 3063–3071.
75. C. Xu, K. Lin, D. Hu, F. L. Gu, M. F. Gelin and Z. Lan, Ultrafast Internal Conversion Dynamics through the On-the-Fly Simulation of Transient Absorption Pump–Probe Spectra with Different Electronic Structure Methods, J. Phys. Chem. Lett., 2022, 13, 661–668.
76. T. Pitesa, M. Sapunar, A. Ponzi, M. F. Gelin, N. Doslic, W. Domcke and P. Decleva, Combined Surface-Hopping, Dyson Orbital, and B-Spline Approach for the Computation of Time-Resolved Photoelectron Spectroscopy Signals: The Internal Conversion in Pyrazine, J. Chem. Theory Comput., 2021, 17, 5098–5109.
77. X. Huang, W. Xie, N. Došlić, M. F. Gelin and W. Domcke, Ab Initio Quasiclassical Simulation of Femtosecond Time-Resolved Two-Dimensional Electronic Spectra of Pyrazine, J. Phys. Chem. Lett., 2021, 12, 11736–11744.
78. T. Kaczun, A. L. Dempwolff, X. Huang, M. F. Gelin, W. Domcke and A. Dreuw, Tuning UV Pump X-Ray Probe Spectroscopy on the Nitrogen K Edge Reveals the Radiationless Relaxation of Pyrazine: Ab Initio Simulations Using the Quasiclassical Doorway–Window Approximation, J. Phys. Chem. Lett., 2023, 14, 5648–5656.
79. J. C. Tully, Molecular Dynamics with Electronic Transitions, J. Chem. Phys., 1990, 93, 1061–1071.
80. L. J. Wang, A. Akimov and O. V. Prezhdo, Recent Progress in Surface Hopping: 2011–2015, J. Phys. Chem. Lett., 2016, 7, 2100–2112.
81. S. Mai, P. Marquetand and L. González, Nonadiabatic Dynamics: The SHARC Approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(6), 1–23,  DOI:10.1002/wcms.1370.
82. M. Persico and G. Granucci, An Overview of Nonadiabatic Dynamics Simulations Methods, with Focus on the Direct Approach versus the Fitting of Potential Energy Surfaces, Theor. Chem. Acc., 2014, 133, 1526.
83. S. Rafiq and G. D. Scholes, From Fundamental Theories to Quantum Coherences in Electron Transfer, J. Am. Chem. Soc., 2019, 141, 708–722.
84. S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Interplay of Vibrational Wavepackets during an Ultrafast Electron Transfer Reaction, Nat. Chem., 2021, 13, 70–76.
85. I. Franco and S. Tretiak, Electron-Vibrational Dynamics of Photoexcited Polyfluorenes, J. Am. Chem. Soc., 2004, 126(38), 12130–12140.
86. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, The Development and Use of Quantum-Mechanical Molecular-Models.76.AM1 - A New General Purpose Quantum-Mechanical Molecular-Model, J. Am. Chem. Soc., 1985, 107, 3902–3909.
87. S. Tretiak, C. M. Isborn, A. M. N. Niklasson and M. Challacombe, Representation Independent Algorithms for Molecular Response Calculations in Time-Dependent Self-Consistent Field Theories, J. Chem. Phys., 2009, 130(5), 054111,  DOI:10.1063/1.3068658.
88. S. Tretiak and V. Chernyak, Resonant Nonlinear Polarizabilities in the Time-Dependent Density Functional Theory, J. Chem. Phys., 2003, 119, 8809–8823.
89. T. Nelson, S. Fernandez-Alberti, V. Chernyak, A. E. Roitberg and S. Tretiak, Nonadiabatic Excited-State Molecular Dynamics (NA-ESMD). Numerical Tests of Convergence and Parameters, J. Chem. Phys., 2012, 136, 54108.
90. T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nonadiabatic Excited-State Molecular Dynamics: Treatment of Electronic Decoherence, J. Chem. Phys., 2013, 138(22), 224111.
91. S. Fernandez-Alberti, A. E. Roitberg, T. Nelson and S. Tretiak, Identification of Unavoided Crossings in Nonadiabatic Photoexcited Dynamics Involving Multiple Electronic States in Polyatomic Conjugated Molecules, J. Chem. Phys., 2012, 137(1), 014512,  DOI:10.1063/1.4732536.

---

Footnote

† Electronic supplementary information (ESI) available: Section S1 presents computational protocol to deduct the orientational averaging pump–probe signal; Section S2 presents the Frenkel Exciton Hamiltonian model; Fig. S1 shows the axis of the body-fixed reference frame used; Fig. S2 presents populations of electronic states at short times; Fig. S3 displays the evolution in time of the average fraction of the transition densities in different chromophores; and Fig. S4 and S5 shows the TA-PP signals at short time using s_pu = s_pr and s_pu⊥s_pr orientations, respectively; Fig. S6 and S7 displays GSB, SE, ESA at two different delay times for and 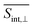, respectively; Fig. S8 displays hole–electron pairs calculated for the first 5 excited states; Fig. S9 shows the spatial distributions of electronic transition densities indicating the orientation of their corresponding transition dipole moments (μ) for the five lowest energy electronic states; Fig. S10 presents the bigger contributions of the singular value decomposition for the non-adiabatic couplings corresponding to the transitions from excited states S_3/4 to S₂. See DOI: https://doi.org/10.1039/d4sc01019a

---