Open Access Article
Open Access ArticleTracing mechanistic pathways and reaction kinetics toward equilibrium in reactive molten salts†
Luke D.
Gibson
 a,
Santanu
Roy
a,
Santanu
Roy
 *b,
Rabi
Khanal
a,
Rajni
Chahal
b,
Ada
Sedova
c and
Vyacheslav S.
Bryantsev
*b,
Rabi
Khanal
a,
Rajni
Chahal
b,
Ada
Sedova
c and
Vyacheslav S.
Bryantsev
 *b
*b
aComputational Sciences and Engineering Division, Oak Ridge National Laboratory, P.O. Box 2008, Oak Ridge, TN 37831, USA
bChemical Science Division, Oak Ridge National Laboratory, P.O. Box 2008, Oak Ridge, TN 37831, USA. E-mail: roys@ornl.gov; bryantsevv@ornl.gov
cBioscience Division, Oak Ridge National Laboratory, P.O. Box 2008, Oak Ridge, TN 37831, USA
First published on 22nd January 2024
Abstract
In the dynamic environment of multi-component reactive molten salts, speciation unfolds as a complex process, involving multiple competing reaction pathways that are likely to face free energy barriers before reaching the reaction equilibria. Herein, we unravel intricate speciation in the AlCl3–KCl melt compositions with rate theory and ab initio molecular dynamics simulations. We find that the compositions with 100 and 50 mol% AlCl3 exclusively comprise neutral Al2Cl6 dimers and charged AlCl4− monomers, respectively. In intermediate AlCl3–KCl compositions, the chemical speciation proves to be a very complex process, requiring over 0.5 nanosecond to reach an equilibrium distribution of multiple species. It is a consequence of the competitive formation and dissociation of additional species, including charged Al dimers, trimers, and tetramers. Here, the species formation occurs through ion exchange events, which we explain by computing free energy landscapes and employing a Marcus-like rate theory. We show that both interspecies and intraspecies ion exchanges are probable and are dictated by the local structural reorganization reflected in the change of local coulombic fields. The species distributions are validated by comparing computed Raman spectra and neutron structure factors with the available experimental data. We find an excellent simulation-experiment agreement in both cases. Nevertheless, Raman spectroscopy turns out to be particularly advantageous for distinguishing between unique species distributions because of the distinct vibrational signatures of different species. The mechanistic insight into reaction dynamics gained in this study will be essential for the advancement of molten salts as reactive media in high-temperature energy applications.
Introduction
Understanding speciation in molten salts (MS) is fundamentally critical to advancing next-generation high-temperature batteries, concentrated solar power plants, and nuclear reactors.1–5 Due to the dependency on temperature and chemical environment, speciation can span across various length scales. It ranges from the formation of monomeric and small oligomeric species caused by corrosion of materials or fission reactions to the formation of larger nanoscale ion chains in MS media.6–18 These microscopic speciation events can directly impact macroscale MS properties such as ion solubility, viscosity, diffusivity, and conductivity.19–23 Despite such importance and implications of speciation, the mechanistic understanding of how chemical species form and interconvert in reactive MS remains ambiguous and requires comprehensive investigation. A few recent kinetic studies15,17,18 indicate that processes occurring at short length and time scales, such as ion exchange, can influence species formation or dissociation, consequently influencing the properties of MS. However, the direct relationship between them remains unclear and continues to be a subject of ongoing research.Herein, we intend to achieve a mechanistic understanding of speciation reactions in the AlCl3-based MS. These systems exhibit a wide spectrum of speciation-related chemical reactions of fundamental importance24–28 and also show promise for use as electrolytes in high-temperature battery applications.29 For example, although the Al–Cl interactions are mostly ionic, molecular species are still prevalent in the AlCl3-based MS despite the extreme environments (namely, high temperature and purely ionic medium).28,30 Furthermore, they are often used as reference solvent media with known chloride activity24–26 determined by the following acid–base reaction equilibrium:
| 2AlCl4− ⇌ Al2Cl7− + Cl− | (1) |
Several potentiometric and spectroscopic studies31–34 found that when additional metal ions are added as solutes, the chloride activity changes, providing insight into the stability and chemical equilibria of the chloro-coordination species formed in MS. Nevertheless, speciation in the AlCl3-based MS mixtures can be remarkably complex, resulting in profound controversies. For instance, the neutron scattering measurements combined with the reverse Monte Carlo method reported the existence of polymeric corner-linked tetrahedral units in liquid AlCl3.27 This contradicts many studies including Raman spectroscopic measurements,28,35–40 suggesting that liquid AlCl3 consists exclusively of discrete edge-shared Al2Cl6 dimers. The oligomeric species other than dimers can only appear in appreciable concentrations if AlCl3 is mixed with alkali halides at a concentration greater than 50 mol% AlCl3. From these studies, it is clear that a variety of Al species likely co-exist in the AlCl3-based systems, with their distribution intricately dependent on the AlCl3 concentration in the melt. Consequently, the questions that require answers to achieve a unified understanding of speciation are: What are the precise structures and relative populations of different species at different AlCl3 concentrations? What is the origin of the discrepancy between the findings of neutron scattering and Raman spectroscopy? How does the variation in the AlCl3 concentration impact the mechanism and kinetics governing the speciation reactions? A rigorous multimodal theoretical investigation is necessary to address these questions, which we conduct here by combining molecular dynamics (MD) simulations, modeling of neutron scattering and Raman spectra, and rate theory for treating the reaction kinetics.
We recognize that simulating the AlCl3-based MS with force field-based MD, even with a polarizable21,41–43 ion model (PIM), has notable limitations. While there exists a PIM model for the pure AlCl3 melt,35,44 parameterized to reproduce structures in both solid and liquid phases, a different PIM model45 had to be developed for an equimolar mixture of AlCl3 and alkaline chlorides. This observation underscores the inherent difficulty in creating a single PIM model that can reliably treat a range of melt compositions, necessitating the utilization of the more-accurate ab initio molecular dynamics (AIMD) simulation. Nevertheless, the AIMD simulations of these systems conducted thus far have been limited to short times (∼10 picoseconds (ps)),46,47 yielding conclusions based on insufficient sampling, which further exacerbates the existing controversies. One AIMD study46 showed that liquid AlCl3 predominantly consists of oligomeric species larger than the edge-shared dimer, in direct contrast to another AIMD study,47 which indicated that dominant contributions come from dimers, accompanied by ring-like trimers. None of these short AIMD simulations are expected to provide statistically converged species distributions. The bond-forming/breaking phenomena that cause shifts in the distribution of species in molten AlCl3 are likely rare events. Therefore, at least several hundreds of picoseconds to nanoseconds (ns) of simulation time are required to accurately determine the reaction kinetics and the distributions of species at equilibrium.
In this work, by carrying out a series of nanoseconds of AIMD simulations, we unravel the complexities of Al speciation across various AlCl3–KCl compositions. Our extensive sampling efforts have allowed us to observe the gradual convergence of species distributions toward equilibrium. It is evident from our results that the equilibrium liquid structure of pure AlCl3 is composed exclusively of edge-shared dimers, with larger oligomeric species only emerging when AlCl3 is mixed with KCl at concentrations exceeding 50 mol% AlCl3. We have systematically investigated a wide range of interconversion pathways between various Al species and have demonstrated that, in certain instances, achieving a speciation equilibrium can require a minimum of 0.5 ns. Surprisingly, the computed neutron structure factors (S(q)) obtained from two differing species distributions (i.e., actively evolving vs. equilibrated) of the same composition were nearly indistinguishable, underscoring the insensitivity of S(q) to the unique distribution of species in the melt. This finding raises concerns, as it suggests that one can accidentally attain a good modeling-experiment agreement despite poor configurational sampling and draw inaccurate, controversial conclusions on speciation, as exemplified previously.27,46,47 In contrast, the computed Raman spectra exhibit a strong sensitivity to the variation of the species distribution and match well with the measured spectra,39,40 but only when computed for the equilibrium species distribution. Thus, Raman spectroscopy offers a significant advantage in effectively solving speciation-related problems, allowing cross-examination of neutron scattering data.
What stands out most prominently is the connection between the distribution of various species across the AlCl3–KCl compositions and the trend in the local ion exchange mechanism and kinetics. A Marcus-like theory17,48 and free-energy landscape analyses have been employed to provide insight into both intraspecies and interspecies ion exchanges. An interesting observation is that the reorganization of solvent ions around species induces changes in the local electrostatic environment, which in turn facilitates interspecies ion exchange and the formation of new species. Furthermore, the oligomeric species themselves undergo transitions between corner- and edge-shared configurations to allow the intraspecies Cl− exchange and migration. This detailed fundamental study of ion exchange substantially contributes to our insight into speciation in reactive MS, a necessary step toward understanding MS properties and reactivity.
Results and discussion
Simulation strategy to attain chemical equilibrium in MS
While extensive AIMD is the main simulation drive in this study, PIM simulations can be useful for the initial system preparation before AIMD simulations (see ESI† for details). We performed 2 ns PIM simulations of AlCl3 + KCl systems with 100 mol%, 66.7 mol%, 58 mol%, and 50 mol% of AlCl3 using the most-recent parameters35,44,45 and used the PIM-equilibrated structures for the AIMD simulations. However, visual inspection and preliminary –Al–Cl–Al– type aggregate analysis of the PIM trajectories showed that the systems form mostly large polymeric structures such as tetramers and pentamers that are unrealistic for 100 mol% and 58 mol% of AlCl3. Further, when starting with the PIM-equilibrated configuration, the initial AIMD run for the pure AlCl3 melt contained a pentameric structure that remained intact even after 100 ps, indicating that the lifetime of this metastable species likely exceeds the feasible timescale of AIMD simulations. This serves as a cautionary tale for how not to take the results of relatively short AIMD simulations for granted without considering the existence of kinetically trapped states.47,50 Therefore, further editing of the structures was necessary to obtain meaningful results before running additional computationally expensive AIMD simulations.Based on the data from the Raman spectroscopy,38–40 we built the pure AlCl3 system from neutral dimers (Al2Cl6) in which 4 Cl− coordinate to each Al3+ and two of these 4 Cl− are shared between the two Al3+. For 66.67 mol% of AlCl3, we intended to generate two independent initial ensembles, 16 Al2Cl7− and (16 AlCl4− + 8 Al2Cl6), denoted as Bias 1 and Bias 2, respectively. Likewise, for 58 mol% of AlCl3, we aimed for two independent initial ensembles as well, (20 AlCl4− + 4 Al2Cl6) and (12 AlCl4− + 8 Al2Cl7−), respectively as Bias 1 and Bias 2. We performed tens of picosecond restrained/biased AIMD for each of these cases, wherein we biased each Al3+ to have the desired number of Cl− and Al3+ neighbors required to generate these ensembles. 200 kcal mol−1 harmonic force constant was used for these biased AIMDs. While these biased simulations removed many structural artifacts of the PIM model, the systems of the 66.7 mol% and 58 mol% of AlCl3 still remained far from what is expected in the equilibrium. Then, we lifted the bias and followed with unbiased AIMD in each case for about a nanosecond. These extensive simulations starting from two very different configurations allowed us to observe how equilibrium speciation is reached over time for the systems that exhibit slow reaction kinetics toward equilibrium. An alternative strategy for building the initial configurations for 58 and 66.7 mol% AlCl3 mixtures could have been a random placement of the preoptimized monomeric and dimeric Al species together with the K+ cations in the periodic box. For the specific case of 16 Al2Cl7− and 16 K+, test calculations over 100 ps revealed that this strategy did not provide an obvious advantage for reaching equilibrium faster. For pure AlCl3 initially made of dimeric configurations, AIMD was performed for at least 360 ps, wherein the dimeric configurations remained intact. For 50 mol% of AlCl3, the PIM simulations generated good initial structures for AIMD, comprising mostly monomeric configurations, which persisted throughout the entire AIMD simulation, which was conducted for ∼130 ps.
In the following subsections, we will provide a full structural, dynamical, and spectroscopic characterization of different species resolved in the AIMD simulations. First, we will discuss how equilibrium distributions of species are attained in terms of the time evolution of their populations obtained from –Al–Cl–Al– type aggregate analysis. Then, we will compare the computed neutron structure factors and Raman spectra with available experimental data for validation of our theoretical findings and conclude on the viability of these techniques. Finally, we will show how different species are formed through ion exchange kinetics using rate theory in conjunction with free energy surface analysis.
Time-evolution of the population of metastable species
The equilibrium distribution of species is well understood experimentally for the compositions with 100 mol% and 50 mol% of AlCl3. While the former is composed of only dimeric configurations, the latter consists exclusively of monomers. As mentioned above, the AIMD simulations do agree with these findings if started with such initial configurations and continued for several hundreds of picoseconds. Speciation is more complex and obscure for the intermediate compositions, namely for 58 mol% and 66.7 mol% of AlCl3. Nevertheless, two independent AIMD simulations starting from two different distributions (Bias 1 and Bias 2) for each of these compositions have helped us examine and ensure that the converged equilibrium distributions of species have been attained. Although the exact speciation is unknown for these compositions, the presence of K+ ions suggests that charged species would be favored over neutral species and oligomers would likely become more unstable as their size increases. In conjunction with these considerations, the converged distributions were expected to exhibit a stable set of species over an extended period of time (≥150 ps) with relatively constant concentrations. The resulting distributions of species based on these criteria are shown in a later section to produce an excellent agreement between the computed and experimental Raman spectra, validating our choice of criteria. Fig. 1 illustrates the time-evolution of these converged distributions expressed in terms of the relative population of each species. For element-specific speciation, one must factor in the number of Al3+ atoms in each cluster. For 66.7 mol% of AlCl3, Bias 2 never reached a converged distribution and is shown in Fig. S1 in ESI.† The most notable features of Fig. 1 are the timescales (>500 ps) required to converge to equilibrium for each composition. This further emphasizes the importance of sufficient sampling in these molten salt mixtures where metastable complex ions can form and persist for hundreds of ps.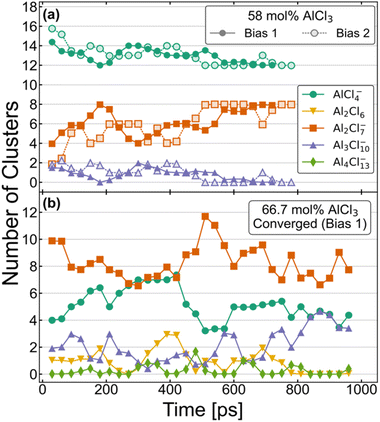 | ||
| Fig. 1 Aggregate analysis showing how equilibrium distribution of different species in AIMD simulations for (a) 58 mol% and (b) 66.7 mol% of AlCl3 are reached at long simulation times. | ||
The distributions for the 58 mol% AlCl3 composition in Fig. 1a show a gradual convergence toward the equilibrium distribution of species, which consists of a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of charged monomers (AlCl4−) to charged dimers (Al2Cl7−). This ratio means that if AlCl3 is added, it will predominantly react with AlCl4− to form Al2Cl7−. The only other species that is found in a very small quantity is a charged Al3Cl10− trimer; these consistently appear, disappear, and reappear throughout the simulation for both Bias 1 and Bias 2. We find that the formation and dissociation of Al3Cl10− follows the SN2 reaction mechanism, which involves nucleophilic attacks by Cl atoms on the electrophilic Al centers:
2 ratio of charged monomers (AlCl4−) to charged dimers (Al2Cl7−). This ratio means that if AlCl3 is added, it will predominantly react with AlCl4− to form Al2Cl7−. The only other species that is found in a very small quantity is a charged Al3Cl10− trimer; these consistently appear, disappear, and reappear throughout the simulation for both Bias 1 and Bias 2. We find that the formation and dissociation of Al3Cl10− follows the SN2 reaction mechanism, which involves nucleophilic attacks by Cl atoms on the electrophilic Al centers:
| Al2Cl7− + Al2Cl7− ⇌ Al3Cl10− + AlCl4−, | (2) |
Due to the relatively low overall population of Al3Cl10− during the simulation time >500 ps, the reaction equilibrium in eqn (2) is strongly shifted to the left. We note that SN2 reactive events are much more prevalent than what is suggested by Fig. 1a—a large majority of reactions are symmetrical and do not affect the distribution of species (e.g., AlCl4− + Al2Cl7− ↔ Al2Cl7− + AlCl4−). Consistent with Raman spectroscopic observations (discussed below), neutral dimers and larger complex ions with >3 Al3+ appear to be unstable at 58 mol% AlCl3.
The speciation for the 66.7 mol% AlCl3 composition during equilibration is more complex as it includes additional species and takes more time to reach the dynamic equilibrium (Fig. 1b). Considering only a strongly downhill reaction between the excess AlCl3 and AlCl4−,49 the 66.7 mol% AlCl3 composition would be nominally comprised of Al2Cl7− dimers and K+ counterions. However, according to eqn (2), Al2Cl7− is in equilibrium with AlCl4− and Al3Cl10−, resulting in a much larger increase in Al3Cl10− concentration at this composition. In fact, there is an extended period of time toward the end of the simulation (Bias 1), where only these three species are present. The estimated equilibrium constant in eqn (2) based on this part of the trajectory is K2 = 0.33. This suggests that as the concentration of the monomer decreases, the likelihood of trimer formation increases. The computed value is remarkably close to the value of K2 = 0.53 at T = 498.15 K obtained using the potentiometric and vapor pressure measurements29 from the model with the most realistic description of the reactions in the AlCl3–NaCl melt.
One important difference compared to 58 mol% AlCl3 is the appearance of neutral Al2Cl6 dimers, mostly as the result of breaking up larger aggregates, such as trimers and tetramers
| Al3Cl10− ⇌ AlCl4− + Al2Cl6 | (3) |
| Al4Cl13− ⇌ Al2Cl7− + Al2Cl6 | (4) |
Al2Cl6 exhibits high reactivity in these systems and, although from one to three Al2Cl6 dimers are present over hundreds of ps, their lifetimes are relatively short as they rapidly react and reform through Reactions 3 and 4. As equilibration progressed, their formation along with the appearance of tetramers was largely suppressed. Nevertheless, Al2Cl6 and Al4Cl13− can occasionally form in the mixture containing only AlCl4−, Al2Cl7−, and Al3Cl10−. This means they need to be considered as a part of the 66.7 mol% AlCl3 composition. The precise determination of Al2Cl6 and Al4Cl13− concentrations at equilibrium is limited by the relatively small size of the simulation cell used in our AIMD simulations. We also find that larger complex ions are involved in ion exchange through an SN2 mechanism analogous to eqn (2), but at a slower rate, because the nucleophilic ability of negatively charged AlnCl3n+1− ions decreases with their size (n). A very small concentration of dianionic species such as AlnCl3n+22− (<0.35%) indicates that these are truly transient species appearing only for a short time (<100 fs) during the reactive events.
We have used the converged parts of the trajectories for analysis, which are the last 290 ps for 58% Bias 2 and 150 ps for 66.7% Bias 1. We have also chosen unconverged parts of the trajectories, namely the 200–300 ps window for 58% Bias 2 and the last 150 ps for 66.7% Bias 2 to check the degree to which the computed structure functions are sensitive to speciation. The Raman spectra for the last 60 ps of the unconverged windows were also computed and compared with the converged simulations wherein only charged monomers and dimers are present in 58 mol% AlCl3 and additionally a trimer is present in 66.7 mol% AlCl3.
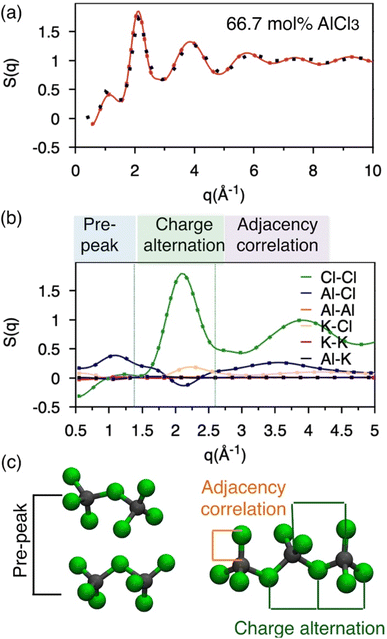
Neutron S(q): calculation and existing measurement
Molten salts are made of ions that exhibit correlation across length scales. For example, there can be adjacency (nearest-neighbor) correlation accompanied by charge alternation in a network of ions, which are reflected in the distances (d) between the ions with opposite and like charges. Further, one can find parallel networks of ions spaced by a specific distance indicating the existence of an intermediate-range ordering. The structure factor, S(q), can provide a measure of these structural correlations, where q, the scattering vector (aka momentum transfer) is equivalent to the distance metric through Braggs' diffraction condition, d: q ≈ 2π/d. Therefore, to discern between these correlations for the AlCl3 + KCl systems, we have computed the neutron S(q) from two independent AIMD trajectories of 66.7 mol% AlCl3, by Fourier-transforming the radial distribution functions (RDFs) using the I.S.A.A.C.S. program,50 and have compared with existing51 experimental S(q) in Fig. 2a. The calculated and the measured S(q)s are in excellent agreement despite the fact that one of the AIMD trajectories (Bias 2) did not converge to an equilibrium population of species (as discussed earlier). This is both encouraging and concerning: it means that AIMD is accurate enough to describe the pair-wise interactions encoded in S(q), but also that the relative populations of different species have a negligible impact on S(q). The RDFs presented in Fig. S1† also agree with this observation. Nevertheless, all of the aforementioned different structural correlations appear to be contributing to S(q) when it is decomposed into the pairwise contributions in Fig. 2b. In the lower q region (q ∼ 1 Å−1), which is commonly known as the pre-peak region, the Al–Cl and Cl–Cl interactions contribute predominantly. When two Al dimers are in close contact as shown in Fig. 2c, the distances (d) between Al or Cl in one dimer and Cl in another dimer correspond to the lower range of q through the relation, q ≈ 2π/d (see d = r > 6 Å region in the Al–Cl and Cl–Cl RDFs in Fig. S1† to link S(q) to d). While the close contacts of the dominating dimeric species should contribute the most to the pre-peak, the close contacts of any of the four species (i.e., monomers, dimers, trimers, and tetramers) satisfying the said Al–Cl and Cl–Cl distance correlations should contribute to the pre-peak as well. It is noticeable that while the Al–Al interactions also have a similar distance correlation, they do not significantly contribute to S(q) due to the relatively small scattering length, explaining the insensitivity of the total S(q) to structural variations caused by Al clustering. Next, q ∼2.0 Å−1 represents charge alternation in –Al–Cl–Al–Cl– networks in dimers and larger oligomers, characterized jointly by the positive-trending Cl–Cl peak and the negative-trending Al–Cl peak (aka anti-peak) and confirmed by the corresponding distance correlations in the RDFs shown in Fig. S1.† However, the nearest neighbor K–Cl interactions positively contribute to this region and cancel the negative Al–Cl contribution, suggesting that the Cl–Cl correlation dominates the charge alternation feature. Finally, consistent with the Al–Cl RDF, the shortest realistic structural correlation is represented by the Al–Cl nearest–neighbor interactions at around q ∼3.5 Å−1. All these structural correlations are also present in the 58 mol% of AlCl3 and illustrated in Fig. S2.† It should be noted that both RDFs and S(q) for 58 mol% AlCl3 analyzed for the nonequilibrium and equilibrium parts of the AIMD trajectory are almost identical, reconfirming the insensitivity of the total pair correlation function to the species distribution.Free energy surfaces revealing coordination environments
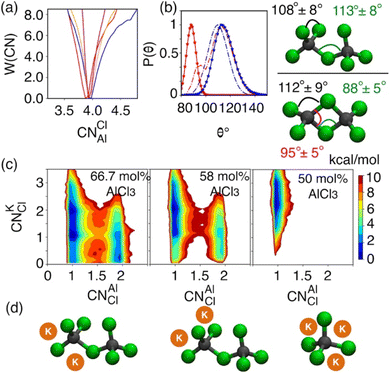
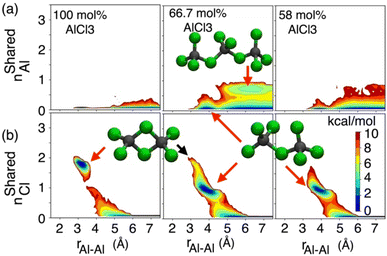
While the S(q)s or RDFs provide a detailed understanding of pair correlation and structural ordering, analyses of free energy surfaces are needed to gain insight into metastable coordination environment of different species. The coordination environment in molten salts continuously fluctuates in the high-temperature thermal equilibrium and rearranges to overcome free energy barrier to interconvert between different metastable states, which can be straightforwardly gleaned from free energy surfaces. We determined free energy surfaces for the AlCl3 + KCl systems by computing the joint probability distributions involving the Cl− coordination around Al3+ (CNClAl), along with the Al3+ and K+ coordination around Cl− (CNAlCl and CNKCl) in Fig. 3. The number of shared Cl− or Al3+ between two different Al3+ ions (nSharedCl and nSharedAl) is shown in Fig. 4. As defined in the ESI,† these collective variables vary smoothly with time, capturing the continuous fluctuation and rearrangement of the coordination environment in the AlCl3 + KCl systems.The free energy, W(CNAlCl), shown in Fig. 3a, suggests that the Cl− coordination number of the Al3+ ions is four and is preserved for all AlCl3 concentrations. The reader is reminded that the pure AlCl3 melt is composed entirely of neutral Al–Al dimers that persist throughout the simulations. In these dimers, there are six Cl− ions—therefore, given that CNAlCl = 4, two of these Cl− ions are shared between those two Al3+ ions. In Fig. 4, where we show the free energy surfaces, W(rAl–Al, nSharedAl) and W(rAl–Al, nSharedCl), confirm these findings by illustrating that for any close Al–Al contact (rAl–Al < 3.8 Å) there is no 3rd Al3+ that coordinates jointly with those two Al3+, while there are always two Cl− ions found between them. The Cl–Al–Cl and Al–Cl–Al angle distributions (see Fig. 3b) calculated for these dimers suggest that the dimers persist in the form of two slightly distorted tetrahedrons connected through edge-sharing. At the region where they share their edges through 2 Cl− ions, the Cl–Al–Cl and Al–Cl–Al angles are almost equal and restricted to ∼90°, while the other Cl–Al–Cl angles are around 112°. For 66.7 mol% and 58 mol% of AlCl3, Fig. 4 suggests that two adjacent Al3+ ions predominantly share one Cl− between them, while the 2 Cl−-shared state rarely appears. Therefore, the dimers (or low-populated larger oligomers) are made of tetrahedrons mostly connected through corner-sharing. These tetrahedrons satisfy ideal tetrahedrality as indicated by the Cl–Al–Cl angle distribution in the CNAlCl = 4 state (see Fig. 3b) that centers around 108°. It is also noticeable from W(rAl–Al, nSharedAl) in Fig. 4 for 66.7 mol% of AlCl3 that two Al3+ separated by a distance of ∼6.5 Å share coordination with a different Al3+ between them, confirming the existence of trimers as thermodynamically stable species at this composition. While these trimers occasionally appear in the 58 mol% of AlCl3, they are energetically disfavored at this composition, as discussed earlier.
The 2D free energy surfaces in Fig. 3c and the snapshots in Fig. 3d illustrate how the cationic environment changes around a Cl− ion as the AlCl3 concentration decreases. For both 66.7 mol% and 58 mol% of AlCl3, a Cl− ion can have either one (in monomeric, dimeric, or larger oligomeric complexes) or two Al3+ (in dimeric or larger oligomeric complexes) neighbors. Obviously, the reduced number of Al3+ allows more K+ neighbors to interact a Cl− ion. For example, a Cl− ion with one Al3+ interacts with 1, 2, and even 3 K+. These K+-bound states frequently interconvert due to small free energy barriers. It is noticeable that the likelihood of finding a Cl− ion with two Al3+ neighbors is more probable in the mixture with 66.7 mol% of AlCl3 than in the mixture with 58 mol% of AlCl3, which is consistent with the respective populations of larger oligomeric complexes (≥2Al3+) in Fig. 1. For 50 mol% of AlCl3, there is only one Al3+ neighbor around a Cl− ion as there are only monomers present at this concentration of AlCl3, allowing 2–3 K+ ions to coordinate with this chloride.
Raman spectra: sensitivity towards the distribution of Al3+ species
Raman spectra generally are very sensitive to the local coordination environment. For example, in our previous study13 on the molten MgCl2 and its mixture with KCl, a large blue-shift in the Raman spectrum was observed for the composition with 50 mol% of MgCl2 (dominated by CNClMg = 4) when compared with the pure MgCl2 case (dominated by CNClMg = 5). Herein, for the AlCl3 + KCl systems, the tetrahedral coordination geometry (CNClAl = 4) is preserved across all concentrations of AlCl3. However, since the cationic coordination around a chloride (represented by CNAlCl and CNKCl in Fig. 3) and the distribution of coordination species vary drastically across the AlCl3 compositions, changes in the spectral lineshape, frequency shift, and appearance of new peaks or disappearance of existing peaks are expected. To examine the spectral changes and their causes with varying the MS composition, we have compared the computed and experimental39,40 Raman spectra in Fig. 5 for 50 mol%, 58 mol%, 66.7 mol%, and 100 mol% AlCl3.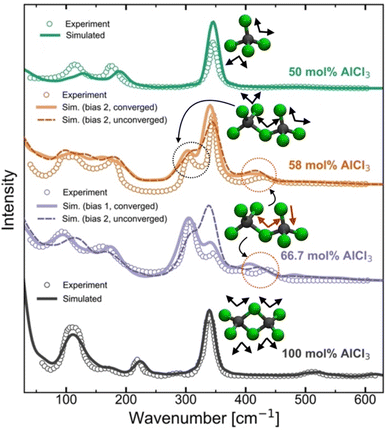 | ||
| Fig. 5 Computed and experimental40 Raman spectra for pure AlCl3 and the mixtures with KCl, revealing through the change in the vibrational bands how the ensemble of neutral dimers in pure AlCl3 convert to a mixture of monomers and anionic dimers due to the presence of KCl at 66.7 mol% AlCl3 and 58 AlCl3 mol%, and finally to an ensemble of monomers at 50 mol% of AlCl3. | ||
For pure AlCl3, all measured Raman bands perfectly align with the computed peaks from a trajectory that contains exclusively edge-shared neutral Al2Cl6 dimers. From a density functional theory-based gas-phase Raman spectrum calculation on the optimized Al2Cl6 dimer (Fig. S4†), it is clear that the peak around 340 cm−1 represents the symmetric stretching (breathing) mode of the Al–Cl bonds. A comparison with the significantly red-shifted gas-phase spectrum for the neutral trimer (Al3Cl9) confirms that trimers or larger oligomers do not exist in the pure AlCl3 melt. For the 50 mol% of AlCl3, the agreement between the computed and experimental spectra is also very good, confirming the experimental39,40 assignment of the Raman bands to the AlCl4− species. The symmetric mode is noticeably blue-shifted to ∼350 cm−1 due to shorter Al–Cl bonds in the AlCl4− species relative to those in neutral Al2Cl6. Our AIMD results do not indicate any association reactions between AlCl4− species at 50 mol% of AlCl3, which is fully consistent with the unfavorable reaction free energy for eqn (1) (pK = 7.05 at 448 K) established via potentiometric measurements.24,25 However, it disagrees with a recent PIM study45 that predicted the existence of 1.6% of Al3+ ions in the form of Al2Cl7− dimers.
Increasing the AlCl3 concentration from 50 to 58 mol%, two new peaks (at ∼310 cm−1 and ∼430 cm−1) appear in the experimental Raman spectrum, which were both attributed38–40 to the Al2Cl7− dimer. This assignment is supported by our simulations, albeit for a different structure with the bent (along the Al–Cl–Al angle) molecular geometry as shown in Fig. 3, rather than the linear one as assumed previously.39,40 Further, based on the gas-phase Raman spectrum of the charged dimer (Fig. S4†), we find that the mode at ∼310 cm−1 is the symmetric stretching mode wherein all Al–Cl bonds exhibit in-phase vibrations, while the high-frequency mode at ∼430 cm−1 arises due to the vibrations of the terminal Al–Cl bonds that are out-of-phase with the vibrations of the Al–Cl bonds bridging the Al ions. The spectrum of the charged trimer in the gas phase (Fig. S4†) suggests that these species can also contribute to the symmetric mode, but the contribution is likely insignificant due to their low population. It is noticeable from Fig. 5 that the Raman spectra for converged and unconverged parts of the AIMD trajectory are very similar. This is because the converged part has no charged trimers and only one or two charged trimers are present in the unconverged part. The speciation is not drastically different in these two parts of the trajectory. Nevertheless, the Raman spectrum computed from the converged part reproduces the experimental spectrum more faithfully, showing a more developed peak at ∼310 cm−1 and a closer match in the 100–200 cm−1 region. This suggests that even if the trimers are present in the 58 mol% of AlCl3, they are only at a very small concentration below the detection limit of Raman spectroscopy.
The Raman spectra for the 66.7 mol% AlCl3 computed from two different initial biases are very dissimilar. While the 66.7 mol% AlCl3 composition ideally corresponds to a population of purely Al2Cl7− dimers, the observed presence of AlCl4− indicated by the Raman band at 350 cm−1, necessitates the existence of species larger than Al2Cl7−.38–40 If only charged monomers (13.9%), dimers (44.1%), and trimers (41.7%) are present (the proportion of each species is given in parentheses as a percentage of aluminum ions) in the converged simulation, the agreement between the simulated and the experimental Raman spectra is excellent. The relative positions and amplitudes of the main peaks are reproduced to a high degree of detail, such as the relative magnitudes of the breathing modes of Al2Cl7− and AlCl4− respectively at ∼310 cm−1 and ∼350 cm−1. Therefore, the relative populations of these species should be regarded as our best estimates. Interestingly, despite the same mole-to-mole ratio for AlCl4− and Al3Cl10−, only a single small peak at 395 cm−1 was directly attributed to the charged trimer in the experimental spectrum,38–40 which can be matched with a peak at 410 cm−1 in the simulated spectrum. Another small peak at ∼480 cm−1 in the simulated spectrum arises from the symmetric Al–Cl stretching of the central Al atom in the trimer, which is also observed experimentally41 but at the higher 75 mol% AlCl3 concentration. It should be noted that the Bias 2 simulation did not reach the thermodynamic equilibrium even after 0.8 ns of simulation time. Compared to the converged species distribution above, this simulation shows a diminished population of charged trimers, a larger presence of tetramers, and also the appearance of a significant portion of neutral dimers. The resulting simulated Raman spectrum is inconsistent with the experimental one, showing enhanced features at ∼120 cm−1 and 340 cm−1 due to the presence of the neutral dimer that are not observed experimentally at this composition. This suggests that AIMD simulations do not completely exclude the possibility of neutral dimers at this composition, but if they are present, they are likely to be at a low concentration, since they are not detectable by the experimental Raman spectra.
The reader is reminded that, in stark contrast to the above Raman spectroscopic findings, the neutron scattering spectra (Fig. 2) computed from two different initial biases for the 66.7 mol% of AlCl3 show essentially no difference. Very little sensitivity of the total S(q) to changes in speciation is observed because the total neutron scattering signal is dominated by the Cl–Cl and Al–Cl correlations (Fig. 2b) that are largely insensitive to a specific cluster formed. As gleaned from the RDFs in Fig. S2,† the only distinction found between the two simulations is a very small difference in the Al–Al interaction strength, which again has a negligible contribution to the total neutral S(q) due to the small neutron scattering length of 27Al. This explains the difficulty of using the reverse Monte Carlo in determining the correct structure of these melts in the absence of the isotopic data, even for the simplest case of pure AlCl3,27,47 where such models incorrectly suggested the possibility of the formation of corner-shared neutral Al2Cl6 dimers and larger aggregates.
Ion exchange dynamics underpinning speciation
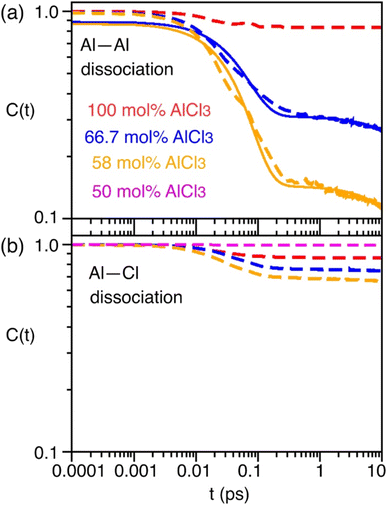
As indicated earlier through population analysis of different species, reaching speciation equilibrium takes a very long time (sub-nanosecond) for compositions that exhibit high reactivity, namely the compositions with 66.7 mol% and 58 mol% of AlCl3. It is expected that the dissociation of existing species or formation of new species would depend on the rates at which Al–Cl and Al–Al (through chloride sharing) contacts dissociate or form. To investigate this, we have computed the time-correlation function of the survival probability of the Al–Cl and Al–Al pairs for pure AlCl3 and different mixture melts of AlCl3 and KCl and have depicted them in Fig. 6. The survival probability for the Al–Al dimers remains close to 1 for pure AlCl3 as the system persists in the neutral dimeric states throughout the simulation. The correlation decay rate gets faster with decreasing AlCl3 concentration until 58 mol%. The faster Al–Al dissociation for the 58 mol% of AlCl3 can be attributed to the change in underlying physical and chemical conditions, namely the relatively higher (by 75 K) temperature and the increased concentration of KCl, which is known to break ion networks of companion salts with multivalent cations.16,52 The survival probability correlation exhibits extremely slow dynamics for Al–Cl dissociation for all cases. From 100 mol% to 58 mol% of AlCl3, the decay rate increases but becomes the slowest for 50 mol%. For 66.7 mol% and 58 mol%, the dissociation of Al–Cl is correlated with the Al–Al dissociation. This is because as the larger species break into smaller ones, the chloride shared between the two Al3+ ions must dissociate as well from one of these Al3+ ions. Since for 58 mol% of AlCl3 Al–Al contacts dissociate faster, Al–Cl bonds must also break faster. However, since the terminal Al–Cl bonds that do not participate in the Al–Al bridging are extremely stable, they effectively slow down the overall Al–Cl breaking events to much slower timescales. For 50 mol% of AlCl3, there exist only monomers with terminal Al–Cl bonds that are extremely stable showing no indication of breaking. We note that while it is common practice to employ exponential fitting to the correlation curves to determine the underlying timescales, herein the fitting timescales would not be quantitatively accurate because the correlation curves are far from zero at the maximum correlation time (10 ps) considered. A more appropriate rate-theory-based analysis is discussed below for a quantitative characterization of the timescales.To gain thermodynamic and kinetic insight into how Al–Al chloride-shared close contacts dissociate, converting larger species into smaller (and vice versa), we have explored the utility of electric field as a reaction coordinate along with the conventional Al–Al distance. MS are coulombic fluids—local electrostatic interactions are expected to change as any local structural reorganization occurs during the process of bond forming and breaking. In Fig. 7, we show the free energy changes as a function of the Al–Al distance (r) and the electric field (E) exerted by all ions on one of them along the Al–Al distance unit vector (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ). The 1D profile, W(r), indicates that the dissociation of an Al–Al contact is exergonic (Fig. 7a) for the 58 mol% of AlCl3, while it is endergonic (Fig. 7d) for the 66.7 mol% of AlCl3, meaning that the dissociation events are favored more for the former. For both AlCl3 concentrations, the 2D surface depicts that when two Al3+ ions are in close contact (rAl–Al ∼ 4.0 Å), predominantly through one shared Cl−, one of the Al3+ ions experience a net positive field along
). The 1D profile, W(r), indicates that the dissociation of an Al–Al contact is exergonic (Fig. 7a) for the 58 mol% of AlCl3, while it is endergonic (Fig. 7d) for the 66.7 mol% of AlCl3, meaning that the dissociation events are favored more for the former. For both AlCl3 concentrations, the 2D surface depicts that when two Al3+ ions are in close contact (rAl–Al ∼ 4.0 Å), predominantly through one shared Cl−, one of the Al3+ ions experience a net positive field along ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) . The field is weak due to screening by this Cl− ion. When a negatively charged species (namely, AlCl4−) initiates a nucleophilic attack (SN2 reaction) on one of the two terminal Al3+ in a larger species (e.g., a charged trimer shown in Fig. 7g), the field gets further weakened along with the slight increase in the Al–Al separation leading to a transition state. Then as the SN2 reaction proceeds, the larger species subsequently transforms into a smaller one (e.g., the charged trimer converts into the charged dimers, as shown in Fig. 7g). In this product state represented by a large Al–Al separation distance (rAl–Al ∼ 6.5 Å), the net field on the Al3+ ion along
. The field is weak due to screening by this Cl− ion. When a negatively charged species (namely, AlCl4−) initiates a nucleophilic attack (SN2 reaction) on one of the two terminal Al3+ in a larger species (e.g., a charged trimer shown in Fig. 7g), the field gets further weakened along with the slight increase in the Al–Al separation leading to a transition state. Then as the SN2 reaction proceeds, the larger species subsequently transforms into a smaller one (e.g., the charged trimer converts into the charged dimers, as shown in Fig. 7g). In this product state represented by a large Al–Al separation distance (rAl–Al ∼ 6.5 Å), the net field on the Al3+ ion along ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) centers around zero due to the cancelation of fields exerted from different ions in the isotropic environment. The minimum free energy path (MFEP) on the 2D surface computed using the string method55 illustrates this most-likely (r, E)-dependent pathway of oligomer dissociation.
centers around zero due to the cancelation of fields exerted from different ions in the isotropic environment. The minimum free energy path (MFEP) on the 2D surface computed using the string method55 illustrates this most-likely (r, E)-dependent pathway of oligomer dissociation.
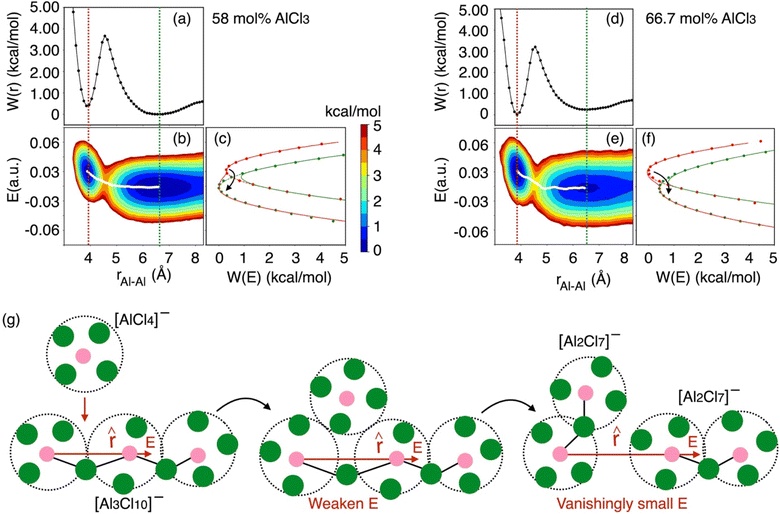 | ||
Fig. 7 Free energy surfaces describing dissociation of Al–Al contacts for (a–c) 58 mol% and (d–f) 66.7 mol% of AlCl3: W(r) represents 1D free energy profile as a function of Al–Al distance, rAl–Al, while the 2D free energy surface, W(rAl–Al, E), relates between rAl–Al and the electric field experienced by one of the Al3+ ions along their distance unit vector (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ). The diabats, W(E), are extracted from the 2D surfaces for the equilibrium close-contact (red slice) and solvent-separated (green slice) distances. The transition path through the crossing point of these diabats is consistent with the MFEP (white line) on the 2D surface, suggesting that reorganization of the coordination environment via SN2 reaction reflected in the change in the local electrostatic environment (weaken electric field) leads to an unstable transition state. Then the (g) Al–Al dissociation of a larger species (e.g., a charged trimer) is triggered, resulting in smaller species (e.g., two charged dimers). The colorbar indicates the free energy levels for both concentrations. While the reaction in eqn (2) is provided as an example, the description is equally applicable to reactions in eqn (3) and (4) as well. ). The diabats, W(E), are extracted from the 2D surfaces for the equilibrium close-contact (red slice) and solvent-separated (green slice) distances. The transition path through the crossing point of these diabats is consistent with the MFEP (white line) on the 2D surface, suggesting that reorganization of the coordination environment via SN2 reaction reflected in the change in the local electrostatic environment (weaken electric field) leads to an unstable transition state. Then the (g) Al–Al dissociation of a larger species (e.g., a charged trimer) is triggered, resulting in smaller species (e.g., two charged dimers). The colorbar indicates the free energy levels for both concentrations. While the reaction in eqn (2) is provided as an example, the description is equally applicable to reactions in eqn (3) and (4) as well. | ||
It is obvious that reorganization of the solvent ions is necessary for a charge species to initiate the nucleophile attack on a larger species, which is again reflected in the change in the local electrostatic environment. Therefore, a Marcus theory53,54 based rate theory formalism that we recently extended for electric fields17,48 can be employed to determine the effective Al–Al dissociation rates (see ESI† for details). For this purpose, we have extracted slices through the 2D surface for the Al–Al distances that represent the Al–Al close-contacts (red slice; the reactant state) and the Al–Al solvent-separated contacts (blue slice; the product state) as shown in Fig. 7c and f. These slices represent the reactant and product diabats, which are ideal parabolas (established through fitting) that cross at a point treated as the transition state for the dissociation reaction. Considering a harmonic coupling between these diabats, the higher and lower adiabatic surfaces are generated. Then, as discussed in the ESI,† the reactant-to-product transition rate takes the form of:
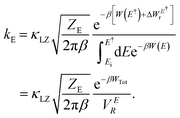 | (5) |
Here, W(E) = W−(E) is the lower adiabatic free energy surface and W(E†) is the barrier height on this surface. 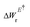 is the additional barrier along the Al–Al distance, providing a total barrier of WTot. β = 1/kBT represents inverse thermal energy and kB is the Boltzmann constant. The integral from Ei to E† provides the “reactant volume” in the electric field space (VER). 1/ZE is the mass associated with the motion of the electric field. κLZ is the transmission coefficient obtained by employing the semiclassical approach of Landau and Zener. κLZ is introduced to account for any barrier-recrossing events that slow down the rates—it depends on the probability (P) of reactive transitions, κLZ = 2P/(P + 1), as the diabats cross at the “normal region”. P again depends on several factors such as the coupling strength between the diabats at the crossing point and the mean traversal velocity of the electric field trajectories at the crossing point. All parameters of this rate theory formalism are reported in Table S1.†
is the additional barrier along the Al–Al distance, providing a total barrier of WTot. β = 1/kBT represents inverse thermal energy and kB is the Boltzmann constant. The integral from Ei to E† provides the “reactant volume” in the electric field space (VER). 1/ZE is the mass associated with the motion of the electric field. κLZ is the transmission coefficient obtained by employing the semiclassical approach of Landau and Zener. κLZ is introduced to account for any barrier-recrossing events that slow down the rates—it depends on the probability (P) of reactive transitions, κLZ = 2P/(P + 1), as the diabats cross at the “normal region”. P again depends on several factors such as the coupling strength between the diabats at the crossing point and the mean traversal velocity of the electric field trajectories at the crossing point. All parameters of this rate theory formalism are reported in Table S1.†
Utilizing eqn (5), we find that the timescale for dissociating any Al–Al contact is 2.8 ps and 5.3 ps, respectively, for the 58 mol% and the 66.7 mol% of AlCl3. From Table S1,† we find that the barrier effects for both cases are very similar. The slower Al–Al dissociation timescale for the 66.7 mol% of AlCl3 is mainly caused by relatively small κLZ (κLZ = 0.63), which again is a result of the reduction in the reactive transition probability due to a weaker reactant-product coupling strength (C in Table S1†). Interestingly, utilizing the detailed balance condition of reaction equilibrium, kdissociationLZVER = kassociationLZVEP, where VEP is the “product volume” defined in the same way as the “reactant volume” in eqn (5), the timescales for the product-to-reactant transition are slower (4.5 ps) and faster (3.1 ps), respectively for the 58 mol% and 66.7 mol% of AlCl3. The equilibrium constants are therefore, respectively, >1 (1.61) and <1 (0.59), suggesting that the concentration of 58 mol% of AlCl3 drives a dissociative reaction, while 66.7 mol% of AlCl3 is prone to an associative reaction. This explains why at 66.7 mol% of AlCl3, dimers are predominant, coexisting with larger oligomers, while at 58 mol% of AlCl3 the monomers dominate, accompanied by dimers, with only a minimal presence of trimers. In accordance with our earlier research,16,55 when introducing KCl into the mixture with multivalent cation salts, specifically MgCl2 or LaCl3, the ion network and chains formed by the multivalent cations undergo a reduction in size. A similar effect is observed in the case of AlCl3, where an increase in KCl concentration leads to a greater prevalence of smaller species, such as monomers. With the highest electron density, these monomers readily initiate nucleophilic attacks on larger species, dissociating them into smaller ones. We recognize that the effective multivalent Al–Al dissociation/association timescales are two orders of magnitude faster than the timescale of reaching an overall speciation equilibrium. This can be attributed to the multitude and multidimensionality of speciation reactions (eqn (1)–(4)) that collectively slow down the equilibration process. Another contributing factor could be the small simulation box, which is known to slow down kinetic events such as solvent exchange.56 If a larger simulation box is considered (currently out of the scope of AIMD), the overall speciation kinetics might be faster, but would still be much slower than the effective Al–Al dissociation timescale due to the said multitude/multidimensionality of reactions.
It is critical to realize that whenever there is an association or dissociation event of the Al species there is a possibility of Cl− exchange between them at the reactive region. For example, at 58 mol% of AlCl3 most of the speciation reactions are symmetrical, AlCl4− + Al2Cl7− ↔ Al2Cl7− + AlCl4−, where interspecies Cl− exchange can take place. In Fig. 8, we show the 2D free energy surface, W(r, E), describing dissociation of a Cl− ion from an Al3+ ion during Cl− exchange events at 58 mol% of AlCl3. When a Cl− is bound to an Al3+, it experiences high electric fields along the unit Al–Cl distance vector (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ). By following the MFEP that drops almost vertically to a near zero field in the bound state, it is obvious that two species (e.g., a monomer and a dimer as shown in Fig. 8b) have associated by sharing their Cl− ions. These shared Cl− ions experience effectively near zero field due to the two nearest Al3+ ions that are exerting fields in the opposite directions from the same distance. The two-Cl−-shared state (or the five-coordination state of the Al3+ ions) is unstable, triggering immediate dissociation and allowing a Cl− exchange event to take place. After dissociation at a large Al–Cl distance, the field on the exchanged Cl− becomes negative as indicated by the MFEP. This is because the field from the Al3+ to which the Cl− ion was originally bound is now weak, while the field from the nearest Al3+ ion is strong—the projection of which along
). By following the MFEP that drops almost vertically to a near zero field in the bound state, it is obvious that two species (e.g., a monomer and a dimer as shown in Fig. 8b) have associated by sharing their Cl− ions. These shared Cl− ions experience effectively near zero field due to the two nearest Al3+ ions that are exerting fields in the opposite directions from the same distance. The two-Cl−-shared state (or the five-coordination state of the Al3+ ions) is unstable, triggering immediate dissociation and allowing a Cl− exchange event to take place. After dissociation at a large Al–Cl distance, the field on the exchanged Cl− becomes negative as indicated by the MFEP. This is because the field from the Al3+ to which the Cl− ion was originally bound is now weak, while the field from the nearest Al3+ ion is strong—the projection of which along ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) is negative. It should be noted that even if the association between two species takes place as shown in Fig. 8, Cl− exchange may not occur, as Al species may simply associate and dissociate with their own Cl−. This suggests that the actual breaking of the Al–Cl bond is comparatively less frequent than the dissociation of Al–Al contacts following the formation of a transient complex. This is also reflected in the ∼3 times higher free energy barrier for the former.
is negative. It should be noted that even if the association between two species takes place as shown in Fig. 8, Cl− exchange may not occur, as Al species may simply associate and dissociate with their own Cl−. This suggests that the actual breaking of the Al–Cl bond is comparatively less frequent than the dissociation of Al–Al contacts following the formation of a transient complex. This is also reflected in the ∼3 times higher free energy barrier for the former.
While the interspecies Cl− exchange demonstrated by Fig. 8 for 58 mol% of AlCl3 is also feasible for 66.7 mol% AlCl3, the free energy surface analysis interestingly points to a more-favorable intraspecies (intramolecular) Cl− exchange for the latter. In Fig. 9, the MFEP on the 2D surface suggests that the electric field on an Al3+-bound Cl− ion drops to a near zero field, but instead of going negative, it remains positive as the Cl− ion leaves the Al3+ ion. This is possible only when the Cl− migration takes place between two connected monomer units in a larger oligomer such as dimer, trimer, or tetramer. For example, in a charged dimer (Fig. 9b) a Cl− ion bound to the first Al3+ ion gets shared with the second Al3+ ion as the two monomer units rotate. This sharing weakens the field experienced by the Cl− ion to nearly zero, which again increases as it moves away from the first Al3+ ion and becomes bound only to the second Al3+ ion. This positive gain in the field value after the Cl− transfer is due to the reduced cancelation effects between the fields due to the two Al3+ ions.
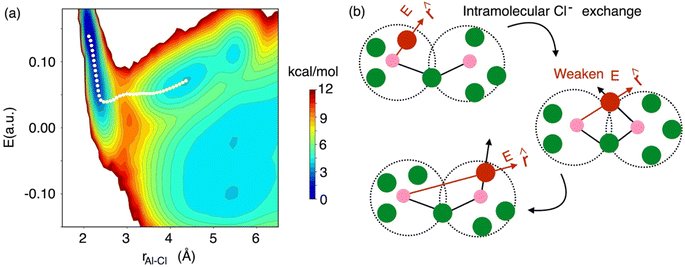 | ||
| Fig. 9 The 2D free energy surface (a, same as Fig. 8), highlighting (b) intraspecies chloride exchange at the concentration of 66.7 mol% of AlCl3. | ||
Conclusion
In summary, we have employed a multimodal approach based on a series of nanosecond AIMD simulations, modeling of neutron scattering and Raman spectra, free energy surface analysis, and rate theory, to elucidate underlying reactions that establish chemical equilibrium in molten AlCl3 + KCl mixtures. Such long ab initio simulations, despite their huge computational costs, are necessary to treat reactive systems that inherently exhibit a variety of solvent-composition-dependent reactions that govern speciation. Indeed, the AIMD simulations conducted here reveal that—depending on the AlCl3 concentration in the AlCl3 + KCl systems (namely, in going from the 66.7 mol% to 58 mol% of AlCl3)—a range of species such as monomers, dimers, trimers, and tetramers can be present. Reaching their equilibrium populations through interconversion reactions (eqn (1)–(4)) requires at least 500 ps. For the pure and 50 mol% of AlCl3, the systems preserve their species throughout the simulations in the form of neutral dimers and charged monomers, respectively. It is worth noting that the monomers have a tetrahedral geometry, while in the oligomeric species these monomer tetrahedrons connect to each other either through sharing their corners (e.g., charged dimers/trimers) or edges (e.g., neutral dimers).By taking advantage of available experimental data on these systems, we have validated our theoretical findings. For instance, excellent agreement between the computed and measured neutron structure factors is found. This agreement confirms the existence of the short-range nearest neighbor and charge-alternation correlations in different species along with the intermediate-range structural ordering that involves association (cross-correlation) of these species. However, the structure factor computed from the part of the AIMD trajectory that is not fully equilibrated is almost identical to the one computed from the equilibrated portion, raising concerns about the applicability of the simulation and modeling approaches that typically utilize short trajectories to model and interpret scattering observables. Such an approach may provide a completely wrong picture of speciation. For cases where force fields are not applicable and AIMD is necessary, the latter must be performed for long simulation times to examine the convergence of the species distribution. Relying solely on the comparison of computed and experimental structure factors may not suffice in such cases. While modeling the scattering observables faces such challenges, the Raman spectra show ultra-sensitivity to species distribution and clearly distinguish the nonequilibrium segment of the AIMD trajectories from the equilibrium portion. Considering all AlCl3 concentrations, the computed spectra from the equilibrium portions and measured Raman spectra are in excellent agreement in terms of the relative peak heights, spectral lineshapes, and frequency shifts caused by the changes in the species distribution. For example, when transitioning from 58 mol% to 66.7 mol% of AlCl3, the peak height for the Al–Cl symmetric stretching mode assigned to monomers drops, while those assigned to dimers/trimers increase. The notable sensitivity of Raman spectroscopy to speciation makes it a crucial technique for determining species distribution, particularly when combined with species populations derived from AIMD and their associated simulated Raman spectra.
Finally, a Marcus-like theory using electric field as a reaction coordinate shows that the effective Al–Al dissociation timescales are faster at 58 mol% than at 66.7 mol% of AlCl3. By obtaining the backward (association) reaction rates, and thereby the effective equilibrium constants, we find that Al3+ ions are prone to dissociation at 58 mol% of AlCl3, while they prefer to associate at 66.7 mol% of AlCl3. This explains why the higher populations of dimers and larger oligomers are observed at 66.7 mol% of AlCl3, while monomers dominate at 58 mol% of AlCl3. From a macroscopic perspective, we realize that the increased concentration of the structure-breaking KCl plays a role here—they tend to break networks of companion salts of multivalent ions. Higher concentrations of KCl favor smaller Al species such as negatively charged monomers, which in turn are more likely to engage in nucleophilic attacks on larger species leading to frequent Al–Al dissociation events and the formation of smaller species. One of the interesting findings is that both the interspecies and intraspecies Cl− migration and exchange appear to be plausible from the free energy surface analysis. When two Al species associate, a two-Cl−-shared (i.e., edge-shared) state between the interacting Al3+ ions is created. Due to thermodynamic instability, this state dissociates allowing the two Al3+ ions to exchange their shared Cl− ions. The intraspecies Cl− exchange events are probable through the transition from the one-Cl−-shared (i.e., corner-shared) state to the two-Cl−-shared (i.e., edge-shared) state in oligomeric species. The intraspecies Cl− exchange is likely to occur more at the 66.7 mol% of AlCl3 due to the existence of more oligomeric species, while interspecies Cl− exchanges are more frequent at the 58 mol% AlCl3 through many nucleophile reactions.
Overall, this study provides critical insight into the connection between chemical speciation and ion exchange processes, while examining the applicability of different methods for assessing species distribution. This knowledge is essential for advancing our understanding of molten salt properties. Investigating properties such as solubility, viscosity, diffusivity, and conductivity, and connecting them directly to ion exchange and speciation, is out of the scope of this AIMD study. However, in the future, through the development of accurate machine learning30,57,58 interatomic interaction potentials trained on ab initio forces and energies, accessing both large length scales and long simulation times will be possible. This will help establish the property-speciation-ion exchange relations, providing a means to enhance the performance of the high-temperature energy storage and production technologies.
Author contributions
SR and VSB designed the project and performed simulations. All authors performed partial data analysis. The original manuscript draft was prepared by LDG, SR, and VSB. All authors proofread and approved the manuscript.Data availability
Computational data are available from the corresponding authors upon reasonable request.Notes
This manuscript has been authored in part by UT Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doepublic-access-plan).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Office of Materials and Chemical Technologies within the Office of Nuclear Energy, U.S. Department of Energy. This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. Additionally, this research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.References
- S. Guo, J. Zhang, W. Wu and W. Zhou, Prog. Mater. Sci., 2018, 97, 448–487 CrossRef CAS.
- R. Roper, M. Harkema, P. Sabharwall, C. Riddle, B. Chisholm, B. Day and P. Marotta, Ann. Nucl. Energy, 2022, 169, 108924 CrossRef CAS.
- R. Jiang, M. Gao, X. Mao and D. Wang, Curr. Opin. Electrochem., 2019, 17, 38–46 CrossRef CAS.
- S. V. Volkov, Chem. Soc. Rev., 1990, 19, 21–28 RSC.
- E. González-Roubaud, D. Pérez-Osorio and C. Prieto, Renewable Sustainable Energy Rev., 2017, 80, 133–148 CrossRef.
- A. I. Bhatt, H. Kinoshita, A. L. Koster, I. May, C. Sharrad, H. M. Steele, V. A. Volkovich, O. D. Fox, C. J. Jones, B. G. Lewin, J. M. Charnock and C. Hennig, in Separations for the Nuclear Fuel Cycle in the 21st Century, ed. G. J. Lumetta, K. L. Nash, S. B. Clark and J. I. Friese, American Chemical Society, Washington, DC, 2006, vol. 933, pp. 219–231 Search PubMed.
- A. T. Motta, A. Couet and R. J. Comstock, Annu. Rev. Mater. Res., 2015, 45, 311–343 CrossRef CAS.
- H. O. Nam, A. Bengtson, K. Vörtler, S. Saha, R. Sakidja and D. Morgan, J. Nucl. Mater., 2014, 449, 148–157 CrossRef CAS.
- H. O. Nam and D. Morgan, J. Nucl. Mater., 2015, 465, 224–235 CrossRef CAS.
- N. Winner, H. Williams, R. O. Scarlat and M. Asta, J. Mol. Liq., 2021, 335, 116351 CrossRef CAS.
- S. T. Lam, Q.-J. Li, J. Mailoa, C. Forsberg, R. Ballinger and J. Li, J. Mater. Chem. A, 2021, 9, 1784–1794 RSC.
- M. S. Emerson, S. Sharma, S. Roy, V. S. Bryantsev, A. S. Ivanov, R. Gakhar, M. E. Woods, L. C. Gallington, S. Dai, D. S. Maltsev and C. J. Margulis, J. Am. Chem. Soc., 2022, 144, 21751–21762 CrossRef CAS PubMed.
- S. Roy, M. Brehm, S. Sharma, F. Wu, D. S. Maltsev, P. Halstenberg, L. C. Gallington, S. M. Mahurin, S. Dai, A. S. Ivanov, C. J. Margulis and V. S. Bryantsev, J. Phys. Chem. B, 2021, 125, 5971–5982 CrossRef CAS PubMed.
- H. Wang, R. S. DeFever, Y. Zhang, F. Wu, S. Roy, V. S. Bryantsev, C. J. Margulis and E. J. Maginn, J. Chem. Phys., 2020, 153, 214502 CrossRef CAS PubMed.
- S. Roy, F. Wu, H. Wang, A. S. Ivanov, S. Sharma, P. Halstenberg, S. K. Gill, A. M. Milinda Abeykoon, G. Kwon, M. Topsakal, B. Layne, K. Sasaki, Y. Zhang, S. M. Mahurin, S. Dai, C. J. Margulis, E. J. Maginn and V. S. Bryantsev, Phys. Chem. Chem. Phys., 2020, 22, 22900–22917 RSC.
- F. Wu, S. Sharma, S. Roy, P. Halstenberg, L. C. Gallington, S. M. Mahurin, S. Dai, V. S. Bryantsev, A. S. Ivanov and C. J. Margulis, J. Phys. Chem. B, 2020, 124, 2892–2899 CrossRef CAS PubMed.
- S. Roy, S. Sharma, W. V. Karunaratne, F. Wu, R. Gakhar, D. S. Maltsev, P. Halstenberg, M. Abeykoon, S. K. Gill, Y. Zhang, S. M. Mahurin, S. Dai, V. S. Bryantsev, C. J. Margulis and A. S. Ivanov, Chem. Sci., 2021, 12, 8026–8035 RSC.
- S. Roy, Y. Liu, M. Topsakal, E. Dias, R. Gakhar, W. C. Phillips, J. F. Wishart, D. Leshchev, P. Halstenberg, S. Dai, S. K. Gill, A. I. Frenkel and V. S. Bryantsev, J. Am. Chem. Soc., 2021, 143, 15298–15308 CrossRef CAS PubMed.
- A. Zhadan, A. Carof, V. Sarou-Kanian, L. Del Campo, L. Cosson, R. Vuilleumier, M. Malki and C. Bessada, J. Phys. Chem. C, 2023, 127, 11186–11194 CrossRef CAS.
- A. Zhadan, V. Sarou-kanian, L. Del Campo, L. Cosson, M. Malki and C. Bessada, J. Phys. Chem. C, 2022, 126, 17234–17242 CrossRef CAS.
- M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Phys. Chem. B, 2007, 111, 4678–4684 CrossRef CAS PubMed.
- B. Koo, H. Lee, S. Hwang and H. Lee, J. Phys. Chem. C, 2023, 127, 5676–5682 CrossRef CAS.
- A. D. Wilson and C. J. Orme, RSC Adv., 2015, 5, 7740–7751 RSC.
- G. Mamantov and G. Torsi, Inorg. Chem., 1971, 10, 1900–1902 CrossRef CAS.
- H. A. Hjuler, A. Mahan, J. H. Von Barner and N. J. Bjerrum, Inorg. Chem., 1982, 21, 402–406 CrossRef CAS.
- B. Trémillon and G. Letisse, J. Electroanal. Chem. Interfacial Electrochem., 1968, 17, 371–386 CrossRef.
- Y. S. Badyal, D. A. Allen and R. A. Howe, J. Phys.: Condens.Matter, 1994, 6, 10193–10220 CrossRef CAS.
- R. L. Harris, R. E. Wood and H. L. Ritter, J. Am. Chem. Soc., 1951, 73, 3151–3155 CrossRef CAS.
- S. J. Percival, L. J. Small and E. D. Spoerke, J. Electrochem. Soc., 2018, 165, A3531–A3536 CrossRef CAS.
- M. Bu, T. Feng and G. Lu, J. Mol. Liq., 2023, 375, 120689 CrossRef CAS.
- W. Gau and I. Sun, J. Electrochem. Soc., 1996, 143, 914–919 CrossRef CAS.
- J. H. Von Barner and N. J. Bjerrum, Inorg. Chem., 1973, 12, 1891–1896 CrossRef CAS.
- J. H. Von Barner, N. J. Bjerrum and K. Kiens, Inorg. Chem., 1974, 13, 1708–1712 CrossRef CAS.
- J. H. V. Barner, L. E. McCurry, C. A. Joergensen, N. J. Bjerrum and G. Mamantov, Inorg. Chem., 1992, 31, 1034–1039 CrossRef.
- L. Bernasconi, P. A. Madden and M. Wilson, PhysChemComm, 2002, 5, 1 RSC.
- Z. Varga, M. Kolonits and M. Hargittai, Struct. Chem., 2012, 23, 879–893 CrossRef CAS.
- R. Ruberto, G. Pastore, Z. Akdeniz and M. P. Tosi, Mol. Phys., 2007, 105, 2383–2392 CrossRef CAS.
- G. Torsi and G. Mamantov, Inorg. Nucl. Chem. Lett., 6, 553–560 Search PubMed.
- H. A. Øye, E. Rytter, P. Klæboe, S. J. Cyvin, I. Lagerlund and L. Ehrenberg, Acta Chem. Scand., 1971, 25, 559–576 CrossRef.
- E. Rytter, S. J. Cyvin and B. N. Cyvin, J. Inorg. Nucl. Chem., 2003, 35, 1185–1198 CrossRef.
- M. Wilson and P. A. Madden, J. Phys.: Condens.Matter, 1994, 6, 159–170 CrossRef CAS.
- M. Wilson and P. A. Madden, J. Phys.: Condens.Matter, 1993, 5, 6833–6844 CrossRef CAS.
- M. Salanne and P. A. Madden, Mol. Phys., 2011, 109, 2299–2315 CrossRef CAS.
- F. Hutchinson, M. K. Walters, A. J. Rowley and P. A. Madden, J. Chem. Phys., 1999, 110, 5821–5830 CrossRef CAS.
- M. Salanne, L. J. A. Siqueira, A. P. Seitsonen, P. A. Madden and B. Kirchner, Faraday Discuss., 2012, 154, 171–188 RSC.
- B. Kirchner, A. P. Seitsonen and J. Hutter, J. Phys. Chem. B, 2006, 110, 11475–11480 CrossRef CAS PubMed.
- A. L. L. East and J. Hafner, J. Phys. Chem. B, 2007, 111, 5316–5321 CrossRef CAS PubMed.
- S. Roy, G. K. Schenter, J. A. Napoli, M. D. Baer, T. E. Markland and C. J. Mundy, J. Phys. Chem. B, 2020, 124, 5665–5675 CrossRef CAS PubMed.
- A. A. Fannin, L. King and D. Seegmiller, J. Electrochem. Soc., 1972, 119, 801 CrossRef CAS.
- S. Le Roux and V. Petkov, J. Appl. Crystallogr., 2010, 43, 181–185 CrossRef CAS.
- M. Blander, E. Bierwagen, K. G. Calkins, L. A. Curtiss, D. L. Price and M.-L. Saboungi, J. Chem. Phys., 1992, 97, 2733–2741 CrossRef CAS.
- W. E., W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103 CrossRef PubMed.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- F. Wu, S. Roy, A. S. Ivanov, S. K. Gill, M. Topsakal, E. Dooryhee, M. Abeykoon, G. Kwon, L. C. Gallington, P. Halstenberg, B. Layne, Y. Ishii, S. M. Mahurin, S. Dai, V. S. Bryantsev and C. J. Margulis, J. Phys. Chem. Lett., 2019, 10, 7603–7610 CrossRef CAS PubMed.
- S. Roy and V. S. Bryantsev, J. Phys. Chem. B, 2018, 122, 12067–12076 CrossRef CAS PubMed.
- R. Chahal, S. Roy, M. Brehm, S. Banerjee, V. Bryantsev and S. T. Lam, JACS Au, 2022, 2, 2693–2702 CrossRef CAS PubMed.
- W. Liang, G. Lu and J. Yu, ACS Appl. Mater. Interfaces, 2021, 13, 4034–4042 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical definition of CNClAl, CNAlCl, nSharedCl, and nSharedAl; expression for survival probability correlation function; formalism of extended Marcus theory and corresponding parameters; details of PIM and AIMD simulations; details of Raman spectra calculations and alignment with experimental spectra; speciation and reaction analysis; species distribution at 66 mol% AlCl3 for Bias 1 and Bias 2; all RDFs; S(q) for the 58 mol% of AlCl3. See DOI: https://doi.org/10.1039/d3sc06587a |
| This journal is © The Royal Society of Chemistry 2024 |