Chemometric sensing of stereoisomeric compound mixtures with a redox-responsive optical probe

Abstract

The analysis of mixtures of chiral compounds is a common task in academic and industrial laboratories typically achieved by laborious and time-consuming physical separation of the individual stereoisomers to allow interference-free quantification, for example using chiral chromatography coupled with UV detection. Current practice thus impedes high-throughput and slows down progress in countless chiral compound development projects. Here we describe a chemometric solution to this problem using a redox-responsive naphthoquinone that enables chromatography-free click chemistry sensing of challenging mixtures. The achiral probe covalently binds amino alcohols within a few minutes at room temperature and generates characteristic UV_A and CD_A spectra that are intentionally altered via sodium borohydride reduction to provide a second, strikingly different chiroptical data set (UV_B and CD_B). Chemometric partial least squares processing of the chiroptical outputs then enables spectral deconvolution and accurate determination of individual analyte concentrations. The success of this approach is demonstrated with 35 samples covering considerably varied total analyte amounts and stereoisomeric ratios. All chemicals and machine learning algorithms are readily available and can be immediately adapted by any laboratory.

---

Introduction

The ubiquity and general importance of chirality in the chemical, materials and health sciences together with the widespread use of automated equipment demand practical analytical assays that can handle increasingly complicated stereoisomeric compound mixtures and at the same time satisfy today's high-throughput sample processing expectations. Most promising for such task are methods that do not require sample purification and are compatible with multi-well plate technology and parallel data acquisition. The quantification of enantiomers and diastereomers has often been a major bottleneck or even a roadblock in chiral compound development projects and generally relies on cumbersome separation steps prior to the analysis. Despite remarkable progress with high-speed separations,¹ chiral GC, SFC and HPLC are typically time-consuming and liquid chromatography can generate large amounts of solvent waste. To address these shortcomings, alternative strategies based on mass spectrometry,² UV³ and fluorescence spectroscopy,⁴ gas-phase rotational resonance spectroscopy,⁵ IR thermography,⁶ circular dichroism,⁷ NMR spectroscopy,⁸ and biochemical methods⁹ have been introduced.

Optical chirality sensing with circular dichroism (CD) probes is generally fast, robust, operationally simple, compatible with high-throughput screening platforms and amenable to parallel analysis of hundreds of samples which is an inherent advantage over serial chromatography.¹⁰ In recent years, remarkable progress in this field has been made with several demonstrations of crude asymmetric reaction analysis¹¹ and through the introduction of powerful probe designs that conquer challenging chirality space and overcome limitations of traditional NMR and HPLC methods.¹² Additional noteworthy advances are the report of a unified CD sensing protocol that gives ee and concentration results without the common need for concomitant UV measurements,¹³ the use of computer generated calibration curves to eliminate trial-and-error method development,¹⁴ and the combination with machine learning tools that address the problem of CD spectral overlap in multicompound analysis.¹⁵ Methods that allow optical chromatography-free chiral compound mixture analysis are anxiously awaited by both academic and industrial laboratories that need to streamline their development processes to increase throughput at reduced cost, waste and workload. Despite recent advances this field is still in its early stages.¹⁶ Remaining shortcomings of chemometric chiral compound mixture sensing include elaborate sample treatments that require filtration or isolation steps, insufficient accuracy and robustness, and limited tolerance of sample composition variations. We now wish to introduce a commercially available, inexpensive naphthoquinone probe and demonstrate its use in chemometric chirality analysis of challenging binary to quaternary compound mixtures that vary substantially in the overall amount and stereoisomeric composition. This is achieved through a combination of click chemistry, fast generation of two UV/CD data sets and partial least squares data processing, which altogether eliminate typically required laborious and time-consuming physical separation steps, a long-standing goal and improvement highly sought-after by many chemists (Fig. 1).

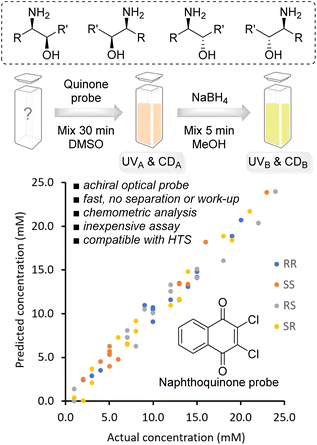Fig. 1 Chemometric sensing of complicated stereoisomeric mixtures with a redox-responsive chirality probe.

Results and discussion

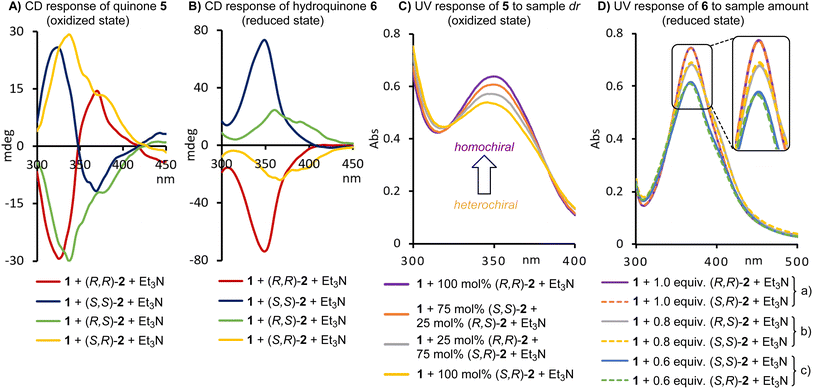
For this study we selected the dichlorobenzoquinone 1 which we expected to undergo smooth carbon–nitrogen bond formation with amino alcohols like 2–4. Indeed, NMR, UV and CD spectroscopic analysis showed that the replacement of one chloride occurs within 30 minutes at room temperature (Scheme 1 and ESI†). The substitution coincides with a characteristic color change to orange and we were able to grow a single crystal of (R,S)-5 obtained with a heterochiral 1,2-diphenylaminoethanol substrate to confirm the reaction outcome. The solution of 5 can then be used directly in the reduction step with sodium borohydride to generate the naphthohydroquinone 6. This transformation is complete within a few minutes which was evident from the colorimetric change from orange to pale yellow and by NMR analysis. Both reactions are quantitative and we did not observe formation of by-products. This well-defined reaction sequence set the stage for the evaluation of the chirotical properties of the stereoisomeric quinone and hydroquinone products 5 and 6.

Scheme 1 Reaction of naphthoquinone 1 with amino alcohols 2–4 to 5 and reduction to the hydroquinone derivative 6. The crystal structure shown is derived from the reaction between 1 and (R,S)-2.

The amino alcohols 2–4 were chosen as test compounds because they display two chirality centers and are commercially available in all four stereoisomeric forms. This allowed us to examine if 1 is capable of producing distinct UV and CD signals in three separate cases and to prepare a diverse sample set of quaternary mixtures for chemometric analysis, see below. In addition, they represent cyclic and acyclic compounds with or without aromatic moieties.

To this end, it is noteworthy that chiral compounds with an aromatic group in close proximity to the chiral center are conducive to exciton-coupled CD inductions and are therefore often privileged sensing targets while purely aliphatic ones are much more difficult to work with. In some chiroptical assays, the presence of aryl groups in the substrate proved to be highly advantageous or even necessary for the generation of sufficiently strong chiroptical signals that can be quantified without interference from chiral impurities with inherent CD activity, a complication that is most likely in the spectral region below 300 nm.⁷ Accordingly, a chiroptical assay that does not rely on chromophoric contributions from the analyte and generally produces red-shifted CD effects that avoid these obstacles is regarded much more useful.

With these considerations in mind, we applied 1 in the reaction with each stereoisomer of amino alcohol 2. We were pleased to find that each of the corresponding naphthoquinones 5 displays strong CD signals above 300 nm at low concentrations (Fig. 2A). The enantiomers of the heterochiral amino alcohol products have a strong CD maximum around 340 nm at 0.33 mM while the homochiral naphthoquinones give quite different CD couplets centered at approximately 350 nm. The in situ reduction toward the naphthohydroquinones resulted in remarkable chiroptical changes (Fig. 2B). The signs of the Cotton effects of the heterochiral products were reversed. For example, the positive CD signal obtained by sensing of (R,S)-2 in the oxidized state 5 was transformed into a negative CD response and the maximum was slightly red-shifted in the (R,S)-hydronaphthoquinone 6 (yellow lines in Fig. 2A and B). The opposite was observed with the (S,R)-enantiomer of 2 (green lines in Fig. 2A and B). The shape of the couplets of the homochiral enantiomers also changed substantially upon reduction and we obtained very strong maxima around 350 nm at 0.26 mM (blue and red lines in Fig. 2A and B). Altogether, the oxidized and reduced states 5 and 6, respectively, have significantly different CD signatures which we envisioned to be crucial for the chemometric analysis of quaternary amino alcohol mixtures.

Fig. 2 CD and UV responses of the quinone/hydroquinone redox couple derived from amino alcohol 2. Conditions: (A) CD measurements were conducted at 0.33 mM in DMSO. (B) CD spectra were obtained at 0.26 mM in DMSO : MeOH (3 : 1). (C) UV measurements at 0.225 mM in DMSO. (D) The UV concentrations in DMSO : MeOH (3 : 1) in order of decreasing signal intensities: (a) purple and dashed red lines, 0.23 mM (1, Et₃N and 2); (b) grey and dashed orange lines, as under (a) but [2] was 0.18 mM; (c) blue and dashed green lines, as under (A) but [2] was 0.14 mM.

We then studied the UV characteristics of 5 and 6. Since our probe is achiral, we do not introduce additional chiral information and the naphthoquinones produced from enantiomeric substrates give identical UV signals at 350 nm. Further analysis with 5 revealed that the UV absorption steadily increases when the heterochiral enantiomers of 2 are replaced with the homochiral isomers. As a result, the UV analysis of 5 is sensitive to the diastereomeric composition of 2 (Fig. 2C). In the reduced state 6 the UV maximum is shifted to 370 nm and independent of the stereoisomeric composition (Fig. 2D). A titration experiment confirmed that this UV absorption is only responding to the total amount of initially present 2. The same redox sensing analysis with the amino alcohols 3 and 4 revealed that the resultant enantiomeric and diastereomeric naphthoquinones and naphthohydroquinones also exhibit remarkably distinct CD profiles (see ESI†). This suggests that a rigid substrate structure and the presence of aryl groups in the analyte are not strict requirements for sensing with 1. It is important to point out that the quinone probe is used in slight excess to ensure quantitative conversion toward 5 and to rule out the possibility of a second substitution reaction which was not observed. The mild assay conditions are noteworthy as well and 5 does not undergo ring closure via attack of the alcohol moiety at the adjacent electrophilic carbon carrying the remaining chloride. We also conducted time studies of both the oxidized and the reduced states to show that the products 5 and 6 do not undergo noticeable epimerization even after several hours (see ESI†). This provides a very comfortable time frame during which the assay can be conducted.

As mentioned above, the quantification of mixtures containing up to four stereoisomers is a very challenging task and typically requires time-consuming separation of the individual compounds with chromatographic methods prior to the analysis. To replace undesirable chromatography by direct mixture chemosensing one needs to be able to deconvolute a large amount of spectral information hidden under widely overlapping CD and UV absorption bands. We expected that this would be possible by combining the multi-modal spectral output generated by our redox-responsive chiroptical assay with chemometric data processing.

Fifteen samples containing the stereoisomers of 2-amino-1,2-diphenylethanol at varying concentrations in DMSO were prepared and subjected to analysis with probe 1. For each sample, 5 single point UV measurements in DMSO were taken at 351 nm and averaged. The diastereomeric ratio was calculated using UV measurements of the oxidized state (see ESI† for details). Upon addition of NaBH₄ another 5 single point UV measurements were taken in 3 : 1 DMSO : MeOH at 370 nm and averaged to determine the overall sample concentration.¹⁷ The results from the linear regressions of the UV absorptions of the naphthoquinone and hydronaphthoquinone products, and the CD spectra of the oxidized and the reduced states were used to quantify individual stereoisomer concentrations using partial least squares (PLS) regression.

PLS is commonly utilized in chemometrics to construct predictive models and extract valuable insights from convoluted chemical datasets, especially in spectroscopic analyses. It proves particularly beneficial for the treatment of highly correlated variables, noisy data, and scenarios involving a limited number of samples relative to variables. The main objective of PLS is to establish relationships between input variables, such as spectral data and total sample concentrations, and output variables, for example individual concentrations of each stereoisomer. This is achieved by creating a small set of uncorrelated latent variables called components, which capture the maximum covariance between the input and output variables. PLS offers several advantages. It effectively handles highly correlated variables by capturing and extracting the shared variance among them, leading to improved predictions and enhanced interpretability. PLS is well-suited for situations with a small sample size compared to the number of variables, as it reduces dimensionality and extracts relevant information from a smaller set of components. It robustly handles noisy data by focusing on the covariance between input and output variables, resulting in more reliable predictions and improved data analysis. Additionally, PLS allows for simultaneous analysis of multiple variables, enabling the modeling of complex relationships and the capture of interactions among various variables. However, PLS also has limitations. The interpretation of PLS models and connection of dimensionally reduced variables to the original data can be challenging. PLS can be sensitive to outliers, and extreme values that deviate significantly from the overall data pattern can disproportionately influence the model's outcomes. Furthermore, as the number of variables increases, PLS models may become complex, hindering interpretation and making it difficult to determine the true importance of independent variables. Lastly, PLS assumes a linear relationship between input and output variables, limiting its ability to adequately capture nonlinear relationships. The viability of this approach was verified by CD reconstitution and leave-one-out cross-validation (see ESI†). During spectra reconstitution the data that have been reduced in dimensionality through PLS regression are reversed to the original dimension. This can illustrate whether there is data loss during processing. The spectra reconstitutions of selected samples showing minimal data loss are shown in Fig. 3.

Fig. 3 Reconstitution of CD spectral information obtained by sensing stereoisomeric mixtures of 2 with naphthoquinone 1 (oxidized state). See ESI† for details.

The results of the chemometric analysis of samples 1–15 are shown in Table 1. Despite the complexity of the mixtures we were able to determine individual stereoisomer concentrations with good accuracy and with an averaged absolute error of only 0.8 mM. For example, the sensing of sample 4 containing 13.0 mM of (R,R)-2, 2.0 mM of (S,S)-2, 7.0 mM of (R,S)-2, and 8.0 mM of (S,R)-2 gave 13.5 mM, 2.5 mM, 7.3 mM, and 8.0 mM, respectively. Larger deviations were observed with sample 2 showing the maximum absolute error across all analyses. In this case, our assay predicted 3.5 mM of the (R,R), 18.2 mM of the (S,S), 16.1 mM of the (R,S) and 0.1 mM of the (S,R) isomer deviating between 0.5 to 2.2 mM form the actual concentrations.

Table 1 Chemometric chiroptical sensing results of 15 samples containing the four stereoisomers of 2 in varying amounts^a

Sample	RR actual (mM)	RR predicted (mM)	Absolute error	SS actual (mM)	SS predicted (mM)	Absolute error	RS actual (mM)	RS predicted (mM)	Absolute error	SR actual (mM)	SR predicted (mM)	Absolute error
a See ESI for details.
1	20.0	20.7	0.7	5.0	5.7	0.7	22.0	20.4	1.6	3.0	2.1	0.9
2	4.0	3.5	0.5	16.0	18.2	2.2	18.0	16.1	1.9	2.0	0.1	1.9
3	19.0	18.9	0.1	4.0	4.5	0.5	10.0	10.1	0.1	12.0	11.0	1.0
4	13.0	13.5	0.5	2.0	2.5	0.5	7.0	7.3	0.3	8.0	8.0	0.0
5	10.0	10.7	0.7	7.0	6.6	0.4	15.0	15.1	0.1	3.0	3.7	0.7
6	15.0	14.2	0.8	5.0	5.3	0.3	1.0	1.4	0.4	19.0	18.4	0.6
7	3.0	2.9	0.1	22.0	20.4	1.6	7.0	7.3	0.3	18.0	18.9	0.9
8	2.0	2.4	0.4	23.0	23.9	0.9	24.0	24	0.0	1.0	0.4	0.6
9	10.0	10.5	0.5	13.0	13.4	0.4	1.0	0.0	1.0	21.0	21.7	0.7
10	15.0	14.1	0.9	5.0	4.0	1.0	12.0	12.5	0.5	8.0	9.2	1.2
11	14.0	13.1	0.9	6.0	4.8	1.2	9.0	10.5	1.5	6.0	7.3	1.3
12	15.0	14.8	0.2	5.0	5.4	0.4	15.0	14.1	0.9	7.0	6.5	0.5
13	10.0	9.1	0.9	14.0	13.4	0.6	12.0	13.3	1.3	7.0	6.6	0.4
14	12.0	11.6	0.4	13.0	11.6	1.4	7.0	8.1	1.1	14.0	14.8	0.8
15	9.0	11.0	2.0	5.0	6.3	1.3	8.0	6.3	1.7	13.0	11.7	1.3

---

The reliability and robustness of our chemometric sensing method are illustrated in Fig. 4. The heatmap in Fig. 4A provides a visual representation of the algorithm's sensing accuracy, with each box indicating the actual concentration of the individual stereoisomer present in the samples. The color gradient, ranging from green to yellow, corresponds to an absolute error between 0.0 and 2.2 mM. Fig. 4B displays a scatterplot that showcases the outstanding correlation between the predicted and actual concentrations without substantial outliers.

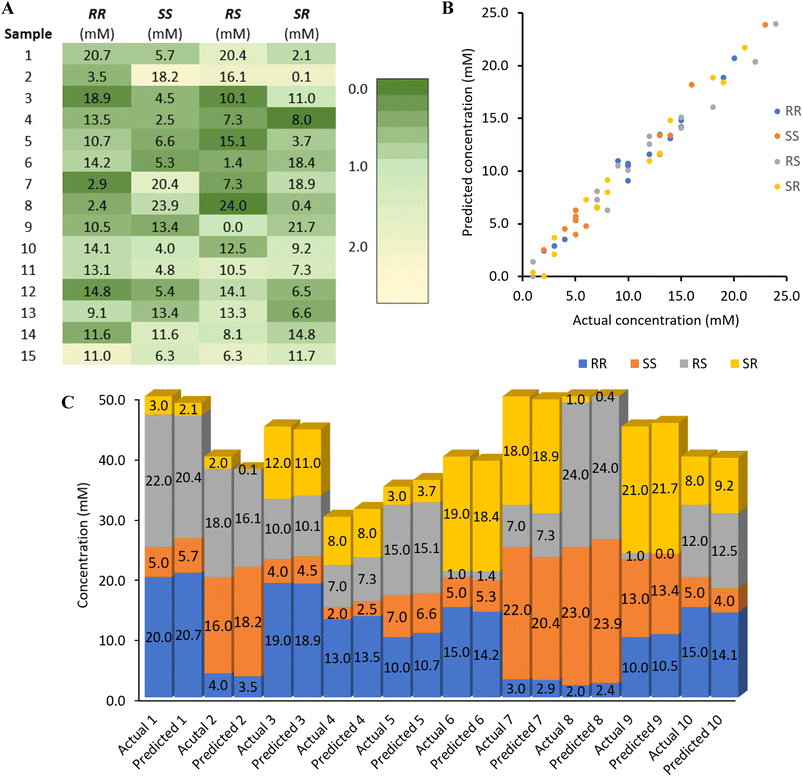Fig. 4 Heat map, plot of actual versus predicted stereoisomer concentrations, and bar chart of the first ten samples. (A) The heatmap represents the absolute %error ranging from 0.0 (dark green) to the maximum of 2.2% (light yellow). (B) Plot showing the consistently small assay inaccuracy and robustness over a 25 mM range for each stereoisomer. (C) The bar chart compares the assay results together with the overall sample concentrations which was varied from 30.0 mM to 50.0 mM. The complete bar chart with all 15 samples can be found in the ESI.†

Finally, Fig. 4C is a comprehensive comparison of actual and predicted values in a stacked column chart, which reveals that chemometric sensing with 1 does allow accurate quantification of each amino alcohol stereoisomer even when the total analyte concentrations vary from 30.0 to 50.0 mM. This highlights an important advance over the scope of previously reported multinary chiral compound sensing work that was limited to samples with constant total analyte quantities.^15d

To further validate the chiroptical assay, we applied it to samples that intentionally do not contain all four stereoisomers, an inherently more challenging chemometric task. In the case of binary samples, both enantiomeric as well as diastereomeric mixtures were prepared. Twenty samples containing either two or three stereoisomers of 2 at varying concentrations were subjected to the chemometric process described above (Table 2 and ESI†). We were pleased to find that the results obtained by PLS were in close agreement with the actual sample compositions. For the binary samples, the highest absolute error increased only slightly to 3.2 mM (see entries 6 and 7 in Table 2). Meanwhile, we found that the absolute error range for ternary mixtures is comparable to that of quaternary mixtures. For example, the analysis of a sample composed of 20.1 mM of (S,S)-2, 9.0 mM of (R,S)-2 and 11.1 mM of (S,R)-2 gave 20.3 mM, 9.2 mM and 10.8 mM, respectively (entry 16). It is noteworthy that our assay predicted 8.8 mM of (R,R)-2, 5.0 mM of (S,S)-2, and 16.9 mM of (S,R)-2 for a sample consisting of these isomers in 8.3 mM, 6.8 mM, and 15.1 mM, respectively, representing the largest deviation of 1.8 mM from the actual sample composition across all measurements (entry 20).

Table 2 Chiroptical analysis of mixtures with two or three stereoisomers^a

Sample		(R,R)-2 (mM)	(S,S)-2 (mM)	(R,S)-2 (mM)	(S,R)-2 (mM)
a See ESI for details and results obtained with all 20 samples.
1	Actual	9.9	20.1	0.0	0.0
	Predicted	9.2	23.1	0.4	0.0
2	Actual	33.5	0.0	16.5	0.0
	Predicted	32.1	0.0	16.1	2.5
3	Actual	9.9	0.0	20.1	0.0
	Predicted	10.2	0.0	22.8	0.5
4	Actual	26.8	0.0	0.0	13.2
	Predicted	28.2	0.0	0.4	13.8
5	Actual	13.2	0.0	0.0	26.8
	Predicted	15.7	0.0	0.0	27.1
6	Actual	0.0	20.1	9.9	0.0
	Predicted	0.0	23.3	11.3	0.0
7	Actual	0.0	13.2	26.8	0.0
	Predicted	1.1	16.4	25.1	0.0
8	Actual	0.0	20.1	0.0	9.9
	Predicted	0.0	19.7	0.2	11.5
9	Actual	0.0	13.2	0.0	26.8
	Predicted	0.0	14.4	0.1	26.5
10	Actual	0.0	0.0	9.9	20.1
	Predicted	0.0	1.0	9.1	21.4
11	Actual	13.2	13.2	13.2	0.0
	Predicted	13.6	12.4	13.7	0.0
12	Actual	11.0	9.0	0.0	20.0
	Predicted	10.4	9.3	0.1	20.0
13	Actual	21.4	0.0	9.2	0.0
	Predicted	24.0	0.0	8.3	0.0
14	Actual	0.0	22.1	0.0	7.4
	Predicted	0.0	23.2	0.0	7.6
15	Actual	26.0	0.0	0.0	14.0
	Predicted	25.5	0.7	0.4	13.5
16	Actual	0.0	20.1	9.0	11.1
	Predicted	0.0	20.3	9.2	10.8
17	Actual	19.9	0.0	0.0	29.8
	Predicted	20.3	2.3	0.0	28.2
18	Actual	15.2	0.0	6.8	8.4
	Predicted	15.7	0.0	7.0	8.6
19	Actual	6.7	8.2	0.0	14.9
	Predicted	7.7	7.8	0.0	16.1
20	Actual	8.3	6.8	0.0	15.1
	Predicted	8.8	5.0	0.0	16.9

---

Summary

In conclusion, we have demonstrated practical chromatography-free analysis of stereoisomeric mixtures of chiral compounds using organic reaction based dual-mode optical sensing combined with chemometric processing of UV and CD spectra that are produced with a readily available dichloronaphthoquinone. This achiral probe covalently binds the target molecules in a few minutes at room temperature and generates characteristic UV and CD spectra that are intentionally altered by reduction of the quinone motif to provide a second chiroptical data set. Chemometric PLS processing of the optical measurements enables spectral deconvolution of inherently broad and largely overlapping absorption bands generated during simultaneous recognition of up to four amino alcohol stereoisomers. The realization of quantitative in situ chirality sensing was verified by accurate determination of individual analyte concentrations using 35 samples with largely varying amounts and stereoisomeric ratios, thus advancing the scope of previously reported multinary chiral compound sensing methods. It is noteworthy that this method is adaptable to automation and high-throughput screening of hundreds of samples with commercially available microplate readers is possible. Of course, any methodological advance has some remaining drawbacks. We found that the chemosemesing assay is limited to a total analyte concentration range from 30 to 50 mM. The strong absorbance and fluorescence of the quinone adducts and of the corresponding hydroquinone compounds start interfering with the CD measurements above 50 mM and we noticed a deviation from the linear relationship between the CD amplitudes and the enantiomeric excess of the analytes. Below 30 mM, the CD and UV intensities of some species are too weak for accurate differentiation between them. In addition, PLS regression analysis of samples with only two or three analytes is still challenging. While the averaged error increases only slightly compared to samples that contain all four stereoisomers, the absence of one or two was not consistently detected. Although this was not a problem with 90% of the samples, in two out of twenty cases our chemometric processing incorrectly predicted the concentration of an absent stereoisomer as 2.0 and 2.5 mM, respectively. Nevertheless, we believe that chemometric sensing with redox-responsive optical probes like 1 bears considerable potential to accelerate chiral compound development projects in numerous academic and industrial laboratories.

Data availability

General procedures, probe development studies, UV and CD spectra, and chemometric details are available in the ESI.†

Author contributions

J. S. S. K. F. performed all UV and CD experiments and mechanistic studies. D. S. H. conducted the chemometric analysis. C. W. supervised the project. All authors interpreted the results, contributed to writing the manuscript and approved the final version.

Conflicts of interest

The authors declare no competing conflicts.

Acknowledgements

We gratefully acknowledge financial support from the U.S. National Science Foundation (CHE-1764135 and CHE-2246747).

References

1. (a) C. J. Welch, Chirality, 2009, 21, 114–118; (b) D. C. Patel, M. F. Wahab, D. W. Armstrong and Z. S. Breitbach, J. Chromatogr. A, 2016, 1467, 2–18; (c) C. L. Barhate, L. A. Joyce, A. A. Makarov, K. Zawatzky, F. Bernardoni, W. A. Schafer, D. W. Armstrong, C. J. Welch and E. L. Regalado, Chem. Commun., 2017, 53, 509–512.
2. (a) J. Guo, J. Wu, G. Siuzdak and M. G. Finn, Angew. Chem., Int. Ed., 1999, 38, 1755–1758; (b) M. T. Reetz, M. H. Becker, H.-W. Klein and D. Stöckigt, Angew. Chem., Int. Ed., 1999, 38, 1758–1761; (c) C. Markert and A. Pfaltz, Angew. Chem., Int. Ed., 2004, 43, 2498–2500; (d) C. A. Müller, C. Markert, A. M. Teichert and A. Pfaltz, Chem. Commun., 2009, 1607–1618; (e) C. Ebner, C. A. Müller, C. Markert and A. Pfaltz, J. Am. Chem. Soc., 2011, 133, 4710–4713; (f) S. Piovesana, R. Samperi, A. Laganà and M. Bella, Chem.–Eur. J., 2013, 19, 11478–11494.
3. (a) R. Eelkema, R. A. van Delden and B. L. Feringa, Angew. Chem., Int. Ed., 2004, 116, 5123–5126; (b) D. Leung, S. O. Kang and E. V. Anslyn, Chem. Soc. Rev., 2012, 41, 448–479.
4. L. Pu, Chem. Rev., 2004, 104, 1687–1716.
5. R. E. Sonstrom, J. L. Neill, A. V. Mikhonin, R. Doetzer and B. H. Pate, Chirality, 2021, 34, 114–125.
6. (a) M. T. Reetz, M. H. Becker, K. M. Kühling and A. Holzwarth, Angew. Chem., Int. Ed., 1998, 37, 2647–2650; (b) P. Tielmann, M. Boese, M. Luft and M. T. Reetz, Chem.–Eur. J., 2003, 9, 3882–3887.
7. (a) C. Wolf and K. W. Bentley, Chem. Soc. Rev., 2013, 42, 5408–5424; (b) P. Metola, S. M. Nichols, B. Kahr and E. V. Anslyn, Chem. Sci., 2014, 5, 4278–4282; (c) B. T. Herrera, S. L. Pilicer, E. V. Anslyn, L. A. Joyce and C. Wolf, J. Am. Chem. Soc., 2018, 140, 10385–10401.
8. (a) M. T. Reetz, A. Eipper, P. Tielmann and R. Mynott, Adv. Synth. Catal., 2002, 344, 1008–1016; (b) M. A. Evans and J. P. Morken, J. Am. Chem. Soc., 2002, 124, 9020–9021; (c) M.-S. Seo and H. Kim, J. Am. Chem. Soc., 2015, 137, 14190–14195; (d) Y. Zhao and T. M. Swager, J. Am. Chem. Soc., 2015, 137, 3221–3224; (e) H. Huang, G. Bian, H. Zong, Y. Wang, S. Yang, H. Yue, L. Song and H. Fan, Org. Lett., 2016, 18, 2524–2527; (f) L. Yang, T. Wenzel, R. T. Williamson, M. Christensen, W. Schafer and C. J. Welch, ACS Cent. Sci., 2016, 2, 332–340; (g) G. Bian, S. Yang, H. Huang, H. Zong, L. Song, H. Fan and X. Sun, Chem. Sci., 2016, 7, 932–938; (h) Q. H. Luu, K. G. Lewis, A. Banerjee, N. Bhuvanesh and J. A. Gladysz, Chem. Sci., 2018, 9, 5087–5099.
9. (a) G. A. Korbel, G. Lalic and M. D. Shair, J. Am. Chem. Soc., 2000, 123, 361–362; (b) P. Abato and C. T. Seto, J. Am. Chem. Soc., 2001, 123, 9206–9207; (c) F. Taran, C. Gauchet, B. Mohar, S. Meunier, A. Valleix, P. Y. Renard, C. Créminon, J. Grassi, A. Wagner and C. Mioskowski, Angew. Chem., Int. Ed., 2002, 114, 132–135; (d) M. Matsushita, K. Yoshida, N. Yamamoto, P. Wirsching, R. A. Lerner and K. D. Janda, Angew. Chem., Int. Ed., 2003, 42, 5984–5987; (e) T. A. Feagin, D. P. Olsen, Z. C. Headman and J. M. Heemstra, J. Am. Chem. Soc., 2015, 137, 4198–4206; (f) S. M. Ramos De Dios, V. K. Tiwari, C. D. McCune, R. A. Dhokale and D. B. Berkowitz, Chem. Rev., 2022, 122, 13800–13880.
10. S. L. Pilicer, J. M. Dragna, A. Garland, C. J. Welch, E. V. Anslyn and C. Wolf, J. Org. Chem., 2020, 85, 10858–10864.
11. D. S. Hassan, F. S. Kariapper, C. C. Lynch and C. Wolf, Synthesis, 2022, 54, 2527–2538.
12. (a) M. B. Minus, A. L. Featherston, S. Choi, S. C. King, S. J. Miller and E. V. Anslyn, Chem, 2019, 5, 3196–3206; (b) Z. A. De los Santos and C. Wolf, J. Am. Chem. Soc., 2020, 142, 4121–4125; (c) F. Y. Thanzeel, K. Balaraman and C. Wolf, Angew. Chem., Int. Ed., 2020, 59, 21382–21386; (d) E. Nelson, J. S. S. K. Formen and C. Wolf, Chem. Sci., 2021, 12, 8784–8790; (e) J. J. Dotson, E. V. Anslyn and M. S. Sigman, J. Am. Chem. Soc., 2021, 143, 19187–19198; (f) J. S. S. K. Formen and C. Wolf, Angew. Chem., Int. Ed., 2021, 133, 27031–27038.
13. A. Sripada, F. Y. Thanzeel and C. Wolf, Chem, 2022, 8, 1734–1749.
14. J. R. Howard, A. Bhakare, Z. Akhtar, C. Wolf and E. V. Anslyn, J. Am. Chem. Soc., 2022, 144, 17269–17276.
15. (a) B. T. Herrera, S. R. Moor, M. McVeigh, E. K. Roesner, F. Marini and E. V. Anslyn, J. Am. Chem. Soc., 2019, 141, 11151–11160; (b) Z. A. De los Santos, S. MacAvaney, K. Russell and C. Wolf, Angew. Chem., Int. Ed., 2019, 132, 2461–2469; (c) Y. Sasaki, S. Kojima, V. Hamedpour, R. Kubota, S. Takizawa, I. Yoshikawa, H. Houjou, Y. Kubo and T. Minami, Chem. Sci., 2020, 11, 3790–3796; (d) D. S. Hassan and C. Wolf, Nat. Commun., 2021, 12, 6451.
16. (a) K. W. Busch, I. M. Swamidoss, S. O. Fakayode and M. A. Busch, J. Am. Chem. Soc., 2003, 125, 1690–1691; (b) Y. Wanga, F. Zhang, J. Liang, H. Lib and J. Kong, Spectrochim. Acta, Part A, 2007, 68, 279–283; (c) S. O. Fakayode, P. N. Brady, D. A. Pollard, A. K. Mohammed and I. M. Warner, Anal. Bioanal. Chem., 2009, 394, 1645–1653; (d) Q. Li, Y. Huang, J. Duan, L. Wu, G. Tang, Y. Zhu and S. Min, Spectrochim. Acta, Part A, 2013, 101, 349–355.
17. It is important that excess of NaBH₄ is used to protect the reduced state from partial re-oxidation by air during the UV and CD measurements.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experimental conditions and sensing conditions, chemometric analysis, and crystallographic data. CCDC 2155745. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc05706b

---