Open Access Article
Open Access ArticleThermodynamic characterization of amyloid polymorphism by microfluidic transient incomplete separation†
Azad
Farzadfard‡
 ab,
Antonin
Kunka‡
ab,
Antonin
Kunka‡
 a,
Thomas Oliver
Mason
a,
Jacob Aunstrup
Larsen
a,
Thomas Oliver
Mason
a,
Jacob Aunstrup
Larsen
 a,
Rasmus Krogh
Norrild
a,
Rasmus Krogh
Norrild
 a,
Elisa Torrescasana
Dominguez
a,
Soumik
Ray
a,
Elisa Torrescasana
Dominguez
a,
Soumik
Ray
 a and
Alexander K.
Buell
a and
Alexander K.
Buell
 *a
*a
aProtein Biophysics Group, Department of Biotechnology and Biomedicine, Technical University of Denmark, Søltofts Plads, Building 227, Kgs. Lyngby, 2800, Denmark. E-mail: alebu@dtu.dk
bInterdisciplinary Nanoscience Center (iNANO), Aarhus University, Gustav Wieds Vej 14, 8000, Aarhus C, Denmark
First published on 8th January 2024
Abstract
Amyloid fibrils of proteins such as α-synuclein are a hallmark of neurodegenerative diseases and much research has focused on their kinetics and mechanisms of formation. The question as to the thermodynamic stability of such structures has received much less attention. Here, we newly utilize the principle of transient incomplete separation of species in laminar flow in combination with chemical depolymerization for the quantification of amyloid fibril stability. The relative concentrations of fibrils and monomer at equilibrium are determined through an in situ separation of these species based on their different diffusivity inside a microfluidic capillary. The method is highly sample economical, using much less than a microliter of sample per data point and its only requirement is the presence of aromatic residues (W, Y) because of its label-free nature, which makes it widely applicable. Using this method, we investigate the differences in thermodynamic stability between different fibril polymorphs of α-synuclein and quantify these differences for the first time. Importantly, we show that fibril formation can be under kinetic or thermodynamic control and that a change in solution conditions can both stabilise and destabilise amyloid fibrils. Taken together, our results establish the thermodynamic stability as a well-defined and key parameter that can contribute towards a better understanding of the physiological roles of amyloid fibril polymorphism.
Introduction
Amyloid fibrils are a specific class of protein aggregates characterized by a highly ordered, elongated molecular architecture formed by repeating intermolecular β-sheet motifs. Their accumulation in intra- or extracellular deposits is a common denominator of numerous severe pathologies including Alzheimer's disease (AD), Parkinson's disease (PD), or Amyotrophic lateral sclerosis (ALS).1 The individual building blocks of amyloid fibrils are structurally distinct from their soluble precursors which range from short peptides,2 intrinsically disordered proteins (IDPs3), to natively folded proteins,4–7 indicating a certain universality of the “amyloid fold”.8 Conversely, cryo-electron microscopy of several amyloid-forming proteins revealed a high degree of structural polymorphism, i.e., a single polypeptide chain adopting several distinct conformations within the amyloid core.9–11 Fibril polymorphism is strongly modulated by extrinsic factors and consequently, structures of fibrils formed in vitro often do not correspond to those isolated ex vivo from patients' tissues.11 Moreover, several polymorphs have been identified in a single test tube in which initially highly pure soluble protein (α-synuclein) aggregated under well-defined solution conditions.12 Altogether, it is becoming increasingly apparent that the free-energy landscape of amyloids is much more degenerate than perhaps originally thought, and that fibril polymorphism is a consequence of the interplay between kinetic factors and stability of individual conformations.The thermodynamic stability of amyloids fibrils can provide the missing link for understanding the mechanisms driving fibril polymorphism. In contrast to the kinetics of amyloid formation which has been extensively studied13–15 and characterized in detail for many pathologically relevant proteins such as amyloid-β,16 Tau,17 or α-Synuclein (αSyn),18,19 systematic analysis of amyloid stability has only recently started to gain more attention.20 The thermodynamic stability of amyloid fibrils may contribute to defining their persistence in vivo, which is influenced by many factors including posttranslational modifications,21,22 proteasomal degradation,23 or clearance by chaperones.24–26 The dysregulation and insufficient efficiency of these clearance mechanisms leads to pathological states.
In general, thermodynamic stability is defined by the concentration of different species in equilibrium, e.g., folded (N), and unfolded (U) states for protein conformational stability (eqn (1)). Similarly, the thermodynamic stability of amyloid fibrils can be defined by the concentration of soluble precursors (herein termed monomers) in equilibrium with the insoluble fibrils. At sufficiently high total concentration, the equilibrium concentration of monomer is independent of the molar concentration of fibrils and relates to fibril stability according to eqn (2).
U ⇌ N; then ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln([N]eq/[U]eq) ln([N]eq/[U]eq) | (1) |
[F]n + [M] ⇌ [F]n+1; then ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/[M]eq); ln(1/[M]eq); | (2) |
Chemical depolymerization offers several advantages including simplicity and scalability. Experimental techniques used in chemical depolymerization experiments can be categorized into two groups: (i) separation-based, and (ii) bulk methods. The first group relies on physical separation of the soluble protein from the fibrils, and their subsequent quantification. Methods including (ultra) centrifugation41 or chromatography (HPLC) are often used, although they are time and sample consuming. Techniques from the second group rely on monitoring changes in specific features of fibrils or monomers as a function of increasing denaturant concentration, and include, for example, circular dichroism, light scattering, intrinsic fluorescence, or thioflavin-T fluorescence.35 Spectroscopic techniques have the advantage of analyzing mixtures without the need for separation, which enables fast and high-throughput analysis. However, these methods provide relative measurements rather than absolute concentrations of the species involved which introduces some degree of uncertainty during analysis. Furthermore, they might require the presence of specific environmentally sensitive fluorophores (tryptophan residues) and can be limited by strong scattering (circular dichroism).
Here, we describe a new method for measuring fibril stability using a combination of chemical depolymerization and transient incomplete separation (TIS) of fibrils and monomers based on their different diffusivity in a laminar flow. TIS occurs under experimental conditions (mobilization pressure, capillary dimensions) where monomers and fibrils experience different hydrodynamic regimes. Specifically, monomers fulfil the two conditions of Taylor dispersion (i.e., negligible axial diffusion, characteristic diffusion time much shorter than the average elution time),48,49 whereas the mass transfer of the fibrils is dominated by convection50 which allows their incomplete separation and quantification of the soluble species. The theoretical and experimental basis of TIS have been derived and demonstrated using SDS micelles and polystyrene particles.51–54 The principle was recently utilized for accurate determination of protein complex affinities by incomplete separation and quantification of the free and bound protein (ACTIS – accurate constant via transient incomplete separation).55–57 The same group demonstrated that the change in the hydrodynamic regime is not a prerequisite, and even mixtures of solutes with similar diffusivities in the Taylor regime can be resolved.57 This was recently utilized for studying aggregation of amyloid-beta 1–40 and 1–42 peptides and their mixtures.42–44 The deconvolution of Taylorgrams of complex mixtures at different reaction times enabled to quantitatively describe the differences between aggregation mechanisms of the two peptides in terms of temporal evolution of size and populations of different species.43
To the best of our knowledge, the present study is the first to use Taylor dispersion-based analysis in conjunction with chemical depolymerization to study amyloid fibril stability. Our approach is rapid, fully automated, amenable to high throughput, label-free, utilizes a commercially available instrument, and uses minute amounts of sample. We demonstrate its advantages by benchmarking it against four commonly used techniques using αSyn and PI3K-SH3 fibrils as the test cases. Using our newly developed approach we compare stability of fibrils at different experimental conditions and quantify thermodynamic stability differences between distinct fibril polymorphs. We believe that our method is a versatile and useful tool for probing rugged amyloid energy landscapes in a quantitative, and efficient manner.
Results
Analysis of particles in laminar flow beyond the Taylor regime
The method described utilizes differences between diffusivity of large particles (i.e. fibrils) and soluble species (i.e., monomers) to measure the thermodynamic stability of αSyn and PI3K-SH3 fibrils. The classical Taylor dispersion analysis48 is used to measure the size of the particles based on their diffusivity in a laminar flow defined by low values of the Reynolds number (Re < 2000; typical scenarios in FIDA experiments feature 0.1 < Re < 10 in water and 25 °C). In the laminar flow regime, the fluid travels in parallel layers that move smoothly next to each other without turbulent mixing. The central layers are the fastest while the outermost layers in contact with the capillary wall are immobile, giving rise to the characteristic parabolic flow velocity profile. It has been demonstrated both theoretically and experimentally, that for a given carrier solvent at fixed temperature, the mass transfer of solutes depends on (i) their diffusivity, (ii) capillary dimensions (internal diameter, length, and effective length, i.e., distance between point of injection and detection window), and (iii) flow velocity (i.e., mobilization pressure).48,49,58 The relationship between these parameters and the hydrodynamic regime of solute mass transfer in the laminar flow is defined by the characteristic diffusion time (τ) and Péclet number (Pe) according to eqn (3) and (4):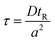 | (3) |
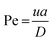 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59) the dispersion in the axial direction of the capillary can be neglected and the mass transfer between the individual fluid layers in the directions perpendicular to the flow is achieved by radial diffusion (see ESI movie 1†). Small particles (e.g., small molecules, protein monomers) diffuse between the layers and travel with the average flow velocity (Fig. 1a, and ESI movie 1,† blue species) resulting in a Gaussian distribution of their concentration at the point of the detection. Their diffusion coefficients (Dapp) can be obtained by fitting the resulting Taylorgrams by equations (eqn (5) and (6)) and used to determine their hydrodynamic radii (Rh) according to the Stokes–Einstein equation (eqn (7)).60,61
59) the dispersion in the axial direction of the capillary can be neglected and the mass transfer between the individual fluid layers in the directions perpendicular to the flow is achieved by radial diffusion (see ESI movie 1†). Small particles (e.g., small molecules, protein monomers) diffuse between the layers and travel with the average flow velocity (Fig. 1a, and ESI movie 1,† blue species) resulting in a Gaussian distribution of their concentration at the point of the detection. Their diffusion coefficients (Dapp) can be obtained by fitting the resulting Taylorgrams by equations (eqn (5) and (6)) and used to determine their hydrodynamic radii (Rh) according to the Stokes–Einstein equation (eqn (7)).60,61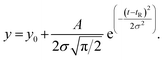 | (5) |
| Dapp = tRa2/24σ2 | (6) |
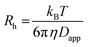 | (7) |
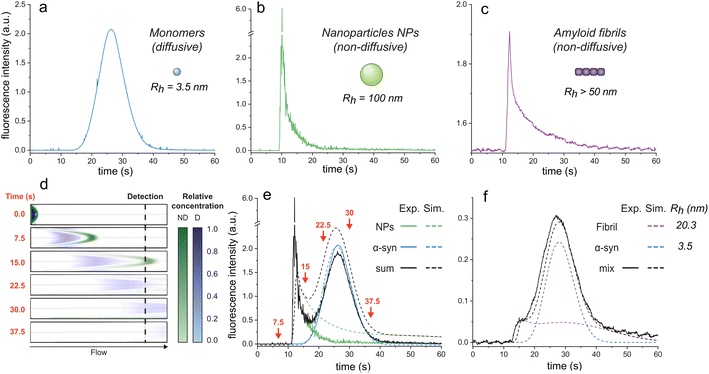 | ||
| Fig. 1 Elution profiles of diffusive and non-diffusive particles. Elution profiles of (a) monomeric αSyn (Rh = 3.5 nm), (b) fluorescent nanoparticles (Rh = 100 nm), and (c) F94W αSyn amyloid fibrils (non-sonicated large fibrils, Rh > 50 nm). Experiments were recorded under the experimental conditions (i.e., 1500 mbar mobilization pressure) described in the materials and methods. (d)–(f) COMSOL simulations of elution profiles using a mixture of monomeric αSyn and nanoparticles. (d) Snapshots of the mixture separating in the capillary (i.d. = 75 μm, l = 1 m) at different time-points (see ESI movie 1† for the whole simulation). Concentrations of the non-diffusive (ND) and diffusive (D) particles in the flow are indicated by the colour-gradients shown on the right. (e) Overlay of the simulated elution profiles shown on the left with the sum of the experimentally measured profiles of D and ND species, corresponding to curves in (a) and (b). The arrows correspond to the time points shown as snapshots in (d). (f) Comparison of experimental (black line) and simulated (dashed lines) data for a mixture of F94W αSyn monomers (blue) and sonicated fibrils (purple; Rh = 20.3 nm) in 1 M urea. | ||
Conversely, larger particles (e.g., liposomes, large nanoparticles, protein aggregates) cannot radially diffuse under the same experimental conditions (or diffuse marginally within the experimental time scale) and remain in the same flow layer during the experiments. Their mass transfer is dominated by convection, resulting in the deformed, asymmetrical distribution of their signal at the detector (Fig. 1b and c; ESI movie 1,† green species).
Here, we exploit this phenomenon to separate non-diffusive aggregates from the diffusive monomers to determine the stability of amyloid fibrils. To better understand the regime of the diffusive and non-diffusive particles in the laminar flow under the given experimental conditions, we first numerically simulated the experiment using the COMSOL software (COMSOL Multiphysics® v. 6.1. COMSOL AB, Stockholm, Sweden). In the simulations, a small plug (20 s, 75 mbar) containing nanoparticles (NPs, D = 2.5 × 10−12 m2 s−1, corresponding to Rh = 100 nm) or protein monomers (D = 7.0 × 10−11 m2 s−1, corresponding to Rh = 3.5 nm derived from Taylor dispersion analysis (TDA) measurements of αSyn monomer) was injected into the one meter-long capillary with internal diameter of 75 μm, and their time-dependent distribution in the flow mobilized by 1500 mbar was analyzed (Fig. 1d and e; ESI movie 1†). Expectedly, the radially diffusing monomers formed a wide uniform zone which travels with the average flow speed (Fig. 1d and e; ESI movie 1†). In contrast, the non-diffusive NPs follow the parabolic shape of the flow speed with their major fraction being pushed ahead of the plug, followed by the gradually decreasing fraction moving in the slower layers. This translates to a highly skewed distribution (i.e., transient) at the point-of-detection (84 cm from the injection) with sharp increase in signal followed by its slow gradual decrease over time (Fig. 1d and e; ESI movie 1†). A COMSOL simulation of different particle sizes is shown in ESI Fig. S1.†
To validate our simulations, we carried out the experiment with the FIDA1 instrument using αSyn monomers (WT or F94W mutant) and fluorescent carboxylate-modified polystyrene NPs (d = 200 nm; FluoSpheres™, Thermo Fisher) as the models of diffusive and non-diffusive particles, respectively (Fig. 1a–c). The experimental flow profiles of the two types of species match almost perfectly those obtained by the COMSOL simulations (Fig. 1e). Moreover, the behaviour of the non-diffusive particles can be well approximated by an analytical solution derived in our parallel study of Taylor dispersion-induced phase separation (TDIPS62). As predicted by both the simulations and the analytical equations, the arrival time of the fastest non-diffusive particles is almost exactly half of the average monomer residence time. Similar observations have been made by others in systems where mass transfer is dominated by convection.51–54,63,64
Transient incomplete separation of amyloid fibrils and soluble monomers
Following the successful modelling and experimental validation of the NPs behaviour beyond the Taylor dispersion regime, we extended the methodology to the analysis of amyloid fibrils (Fig. 1f). We used αSyn fibrils equilibrated in 1 M urea to allow their partial dissociation to monomers and analyzed the resulting mixture using the FIDA1 instrument (Fig. 1f). The profile resembled the one obtained as the sum of NPs and monomeric αSyn (Fig. 1e), suggesting similar, non-diffusive behaviour of the fibrils. Such transient incomplete separation (TIS) of diffusive and non-diffusive species and different approaches for the data analysis have been previously described.51–57 Here, we analyzed the curve using numerical COMSOL simulations assuming two species and obtained diffusion coefficients of 7.0 × 10−11 and 1.2 × 10−11 m2 s−1 for αSyn monomer and fibril, respectively. Both values are in excellent agreement with those measured by TDA of αSyn monomers (Rh = 3.5 nm), and DLS analysis of fibrils (Rh = 20.3 ± 0.5 nm). The latter corresponds to a fibrillar species of around 100 nm length with 10 nm width based on the models of rod-like particles derived elsewhere.65 The shape of the curve for sonicated fibrils (Fig. 1f) is shallower than the non-sonicated fibril curve (Fig. 1c) due to their different size distributions which, however, both fall outside the regime for Taylor dispersion and form transient curves under our experimental conditions (ESI Fig. S1†). Together, our results clearly demonstrate that the FIDA1 instrument is a suitable experimental platform for separation and individual quantification of diffusive soluble proteins from their mixtures with non-diffusive particles.Chemical depolymerization of αSyn fibrils studied by transient incomplete separation
Next, we repeated the experiment in a range of urea concentrations to derive the full depolymerization curve of the αSyn fibrils. First, we tested fibrils of the αSyn tryptophan-containing mutant (F94W) to obtain a higher signal-to-noise ratio compared to the wild type in the intrinsic fluorescence-based detection system. We analyzed F94W αSyn fibrils equilibrated in a range of urea concentrations from 0 to 5.4 M using the same experimental conditions as described above (Fig. 2). For each sample, a buffer with the matching concentration of urea was used to mobilize the sample plug to avoid artefacts from dilution or viscosity gradients. In low concentrations of urea, the resulting elution profiles were characteristic of the two-component TIS regime described above, i.e., a sum of asymmetrical and Gaussian peaks (Fig. 2). The amplitude of the former gradually decreased and completely disappeared at high urea concentrations (>2.3 M), indicating complete fibril dissociation to monomers which are in the TDA regime. Similar to the experiments described above, the monomer diffusion in the complex mixture was mostly unaffected by the larger species and behaved in a predictable manner which could be accurately modelled and analyzed (Fig. 2, middle panel). Conversely, the signal from protein aggregates was less reproducible due to the unspecific self-interaction or interaction with the capillary surface resulting in signal spikes or delayed elution (sometimes appearing in the washing step). Therefore, we concluded that absolute quantification of monomers, rather than relative quantification of fibrils and monomer is a more robust and reproducible approach and used it for further analysis. We also verified that fluorescence and hydrodynamic radius of the monomer are not affected by the denaturant by performing control experiments with monomeric αSyn in increasing concentrations of urea (ESI Fig. S2†).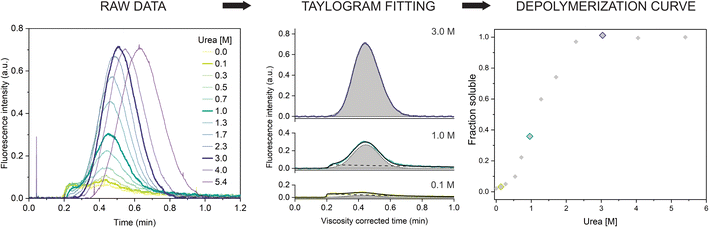 | ||
| Fig. 2 Chemical depolymerization of amyloid fibrils using TIS. (left) Raw Taylorgrams of F94W fibrils (c = 20 μM) equilibrated in increasing concentrations of urea. (middle) Quantification of monomer concentration from the elution profiles (after correction for the urea viscosity, see materials and methods). Fitting of three representative curves (highlighted in the panel (a)) by the sum of the equations describing asymmetrical (dotted line) and Gaussian (dashed lines) distributions (eqn (9) and (10)). The area of the Gaussian peak (gray) is proportional to the monomer concentration. (right) Depolymerization curve of F94W αSyn fibrils. The points correspond to the ratio of monomer concentrations derived from the deconvolution of the elution profiles in the total protein concentration as a function of urea. | ||
The quantification of monomer was carried out in several different ways. First, we removed the signal contribution from the fibrils by subtracting a manually generated linear baseline connecting the hypothetical intersections of the two distinct peaks and integrated the remaining monomer peak to obtain the corresponding area (ESI Fig. S3, ESI Table S1†). Although simple, the procedure is lengthy and subjective regarding the selection of the intersects. To overcome these limitations, we fitted the viscosity-corrected data to the sum of the two distributions described by eqn (9) and (10) (see Materials and methods for details) to obtain the deconvoluted areas under the Gaussian peaks. The procedure worked well for curves where the two distributions could be clearly distinguished. In cases where the contribution from one of the peaks to the overall signal was minimal (0 to 10%), analysis was more challenging and often resulted in overfitting due to the high number of parameters. We solved this by writing a custom python script (provided in the associated content with a link at the end of the manuscript) that globally fits the Taylorgrams across the whole urea concentration range by parametrizing the monomer peak area using ΔG and m-value from the isodesmic model and sharing the rest of the parameters from eqn (9) and (10) (except the area of the asymmetric fibril peak). The global analysis gives well defined confidence intervals of the fitted parameters, albeit sometimes at the expense of quality of the individual fits. In such cases, individual fits with higher quality can be obtained with the same script. Finally, we verified the results using deconvolution of the curves by numerical analysis in COMSOL. The depolymerization curves obtained by the four methods are almost identical and yield similar energy parameters (within error) when analyzed within the isodesmic depolymerization model framework (ESI Fig. S3, ESI Table S1†). We primarily chose the global fitting approach for analysis of further experiments owing to its reliability, speed, and automation.
TIS is a robust method for the analysis of amyloid fibril thermodynamic stability
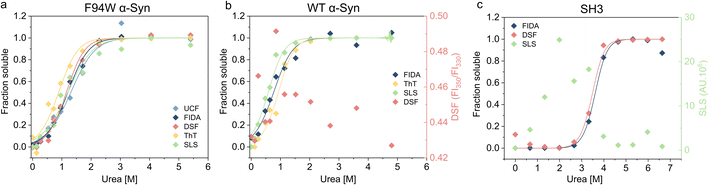
To validate our newly developed FIDA analysis, we measured the thermodynamic stability of the WT and F94W mutant of αSyn, and PI3-SH3 fibrils using other available techniques including DSF (differential scanning fluorimetry), static light scattering (SLS) intensity, thioflavin T fluorescence, and ultracentrifugation (UCF) followed by quantification of the monomer in the supernatant using UV-absorbance (Fig. 3, Table 1). Depolymerization curves obtained by each method were fitted to the isodesmic model and compared based on the resulting ΔG values (Table 3). The isodesmic model is conceptually simpler than the cooperative model which limits overfitting by reducing the number of free parameters, particularly in cases where only a single protein concentration is measured.38 We obtained excellent agreement between experiments for the F94W αSyn with nearly overlapping depolymerization curves (apart from that obtained by ThT fluorescence) and differences between ΔG values within the range of fitting errors (Fig. 3a, Table 1). Since both FIDA and DSF are based on the detection of intrinsic fluorescence, we decided to test their limits by repeating the experiment using fibrils of wild type αSyn which does not contain tryptophan, but only 4 tyrosine residues as fluorophores (Fig. 3b, Table 1). The fibrils were prepared according to the same protocol used for the F94W mutant and depolymerized at two-times higher final concentration (40 μM) to compensate for the lower signal. The sensitivity of the FIDA proved to be sufficient and we were able to obtain a well-defined depolymerization curve (Fig. 3b). Based on our results, we conclude that the limits of detection for wild type and F94W αSyn monomers are ca. 5 and 1 μM, respectively. In contrast, DSF which utilizes the shift of the tryptophan fluorescence emission spectrum induced by changes in its local environment (e.g., monomeric vs. fibrillar state66,67) did not yield any meaningful results for WT αSyn fibrils (Fig. 3b), confirming that the tyrosine residues lack the environmental sensitivity necessary to distinguish aggregated from soluble states. Interestingly, the stability of WT fibrils was ca. 4 kJ mol−1 lower compared to the F94W mutant (Table 1). Arguably, the mutation alters the energy landscape of αSyn and is therefore not a non-invasive probe for analysis of αSyn fibril stability. This is an important finding since similar effects might be, in principle, observed in studies of amyloid forming proteins lacking tryptophan and that use engineered Trp variants instead.| Analytical technique | F94W αSyn | WT αSyn | SH3 | |||
|---|---|---|---|---|---|---|
| ΔG (kJ mol−1) | m (kJ M−1 mol−1) | ΔG (kJ mol−1) | m (kJ M−1 mol−1) | ΔG (kJ mol−1) | m (kJ M−1 mol−1) | |
| a UCF – ultracentrifugation, FIDA – flow-induced dispersion analysis, ThT – thioflavin T assay, SLS – static light scattering, DSF – differential scanning fluorimetry, n.m. – not measured, n.d. – ΔG could not be determined. | ||||||
| UCF | −34.0 ± 0.9 | 6.5 ± 0.8 | n.m. | n.m. | ||
| FIDA | −34.6 ± 1.0 | 7.6 ± 0.9 | −30.1 ± 0.7 | 8.3 ± 0.97 | −59.8 ± 4.7 | 10.0 ± 1.3 |
| DSF | −35.4 ± 1.2 | 8.6 ± 1.1 | n.d. | −58.6 ± 5.1 | 10.0 ± 1.5 | |
| ThT | −32.8 ± 0.8 | 8.2 ± 0.9 | −33.0 ± 0.4 | 10 ± 0.3 | n.m. | |
| SLS | −33.1 ± 0.8 | 6.3 ± 0.7 | −29.5 ± 0.3 | 9.8 ± 0.1 | n.d. | |
In contrast to αSyn, PI3K-SH3 naturally contains a single tryptophan which gives the protein two distinct fluorescence emission spectra in the monomeric and fibrillar states (fluorescence is fully quenched in the fibrillar state), making it an ideal probe for studying fibril stability by DSF.38 Our analysis of PI3K-SH3 fibril stability by FIDA agreed well with DSF measured here (Fig. 3c, Table 1) and published previously.38 In contrast, the SLS signal was noisy at low denaturant concentrations, presumably due to higher order assembly of fibrils and sedimentation, and could not be used for the fitting.
Using three model cases we successfully verified the general applicability of our novel approach for analyzing fibril stability. The only other method which could be successfully applied to all three cases was ThT fluorescence which is also simple, fast, and scalable. However, different fibrils have distinct sensitivity to ThT, and some fibril polymorphs are even “ThT-invisible” and cannot be monitored by this fluorescent dye.68–71 Although applicable in some cases, scattering techniques (SLS and DLS) suffer from large dependency of scattered light intensity on aggregate size, hindering reliable normalization of the depolymerization curves when small amounts of residual aggregates are present in the depolymerized samples at high urea concentrations. Similar issues apply to ultracentrifugation, which additionally requires higher volumes of sample (>30 μL), specialized equipment, and long centrifugation times (>1.5 h) at high-speed (>150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g) to ensure complete removal of the aggregates.
000×g) to ensure complete removal of the aggregates.
Thermodynamic stability as potential indicator of aSyn fibril polymorphism
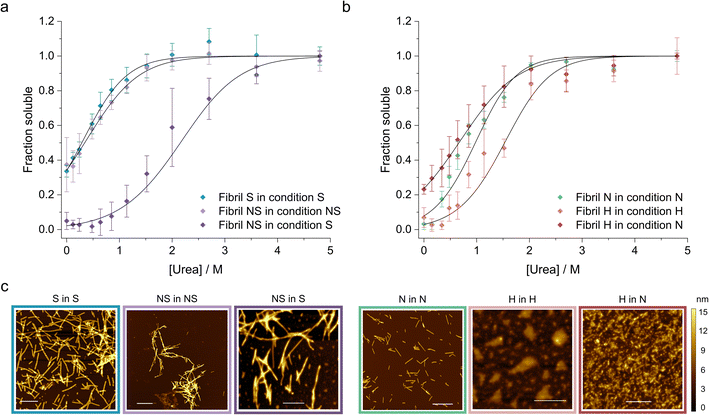
Finally, we applied our newly developed methodology to study how the solution conditions dictate the stability of WT αSyn fibrils (Table 2). First, we selected two well characterized αSyn fibril polymorphs – fibrils (polymorph S) assembled under physiological conditions (50 mM Tris–HCl, pH 7.4, 150 mM KCl; i.e., salt condition), and ribbons (polymorph NS) assembled in the absence of salt (5 mM Tris–HCl pH 7.4, i.e., no salt condition).72 We prepared the two fibril polymorphs using established protocols72 and confirmed their morphology using AFM (Fig. 4c). Fibrils of polymorph S are composed of two protofilaments (8.23 ± 1.17 nm height) that twist with an average pitch length of 204 ± 63 nm. In contrast, the ribbons were thinner (6.59 ± 0.87 nm height), had no detectable twist, and were often found in bundles (Fig. 4c). Both polymorphs were sonicated and depolymerized using increasing concentrations of urea in (i) their original buffer (native conditions) and in (ii) buffer with salt to allow direct comparison of their stability. The change of conditions was achieved by diluting the fibrils (200 μM) 5 times using a modified salt and pH solution, resulting in the final desired condition. We also verified that 3 days of incubation time was long-enough to ensure that equilibrium was reached in all urea concentrations (ESI Fig. S4 and SI Table S2†). Interestingly, although the two polymorphs showed similar stability in their native buffers, polymorph NS was 8.5 kJ mol−1 more stable than polymorph S when measured in the presence of salt (Fig. 4a). Notably, the propensity of fibrils NS to form bundles and clumps did not change significantly in the new condition based on our AFM analysis (Fig. 4c), indicative that the stabilizing effect does not stem from their increased lateral association. It has been shown by ssNMR that polymorph NS is formed by regular long β-strands whereas polymorph S has an irregular pattern of shorter β-strands.73 The higher stability of polymorph NS observed here can thus arguably reflect the stronger network of hydrogen bonds within its cross-β-sheet architecture and/or higher number of residues forming the amyloid core.| Fibril polymorph | Condition | ΔG (kJ mol−1) | m-Value (kJ M−1 mol−1) | Buffer |
|---|---|---|---|---|
| S | S | −25.6 ± 0.1 | 6.4 ± 0.4 | 50 mM Tris, 150 mM KCl pH 7.5 |
| NS | −34.2 ± 0.5 | 4.8 ± 0.3 | ||
| NS | NS | −25.6 ± 0.3 | 5.3 ± 0.4 | 5 mM Tris pH 7.5 |
| N | N | −30.6 ± 0.8 | 7.0 ± 0.7 | 20 mM NaP, 150 mM NaCl pH 7.4 |
| H | −27.0 ± 0.6 | 4.9 ± 1.2 | ||
| H | H | −33.3 ± 1.6 | 6.3 ± 1.2 | 20 mM NaAc, 150 mM NaCl pH 5 |
Next, we studied the effect of pH on fibril stability. We prepared αSyn fibrils at pH 7.4 (neutral (N) polymorph) and pH 5 (acidic (H) polymorph) in the presence of 150 mM NaCl to mimic cytosolic and lysosomal pH, respectively.74 We characterized their morphology using AFM and found that the neutral polymorph has an average pitch length of 162 ± 47 nm and height of 5.2 ± 0.7 (Fig. 4c). The morphology of acidic polymorph was difficult to assess due to the higher order assembly of individual fibrils into large particles observed by AFM (Fig. 4c). When depolymerized in their native conditions, the acidic polymorph was more stable compared to the neutral polymorph (Fig. 4b). However, its stability decreased significantly when transferred to the neutral condition, to below the stability of the neutral polymorph (Fig. 4b, Table 2). Arguably, this shift of fibril stability is caused by the higher solubility of αSyn in the neutral pH compared to the acidic one leading to (partial) fibril dissociation upon the pH jump. Similar destabilization of αSyn fibrils upon change in pH was observed by others and could be an important phenomenon occurring in vivo.74
Moreover, an exploration was conducted to identify aggregation intermediate species in the soluble fraction of the samples. This involved reanalyzing the FIDA curves by introducing additional species to the fitting process or varying the size of soluble species. These analyses, however, could not distinguish monomers from dimers to decamers (ESI Section 1, ESI Fig. S5†). Consequently, DLS and FIDA were applied to the soluble fraction of the samples after centrifugation, revealing an absence of significant fractions of intermediate species (ESI Section 1, ESI Fig. S6†).
In general, the stability of αSyn fibrils measured here is low (ΔG ∼ −35 to −25 kJ mol−1) which translates to relatively high solubility (low μM range) compared to other amyloids whose solubility is often in the low nM range.41 We therefore calculated the values of ΔG in the absence of urea based on the eqn (2) and compared it to the ones obtained from the isodesmic model (Table 2). We observed that although there is a correlation between the two values, they are not equal. (ESI Fig. S7†). We speculate that this is primarily due to the uncertainty in the estimation of the concentrations in the absence of urea based on the FIDA analysis, since they fall below the 5 μM threshold in most cases. This highlights the value of the chemical depolymerisation method to determine fibril stability, even for fibrils with relatively low stability, such as those of αSyn.
Discussion
TIS is a robust, sensitive, and sample-economical method for analysis of fibril stability
Several different experimental methods are used to probe thermodynamic stability of amyloid fibrils (Table 3).35,38,41 These include methods based on separation of aggregates and soluble monomers from each other (e.g., ultracentrifugation), or those detecting the spectroscopic or scattering signatures from mixtures of fibrils and soluble protein (e.g., ThT, DSF, SLS). Ultracentrifugation, followed by quantification of soluble protein in the supernatant, is considered a standard method for the quantification of the solubility at any given set of conditions. Despite being conceptually simple and straightforward, it is time-consuming and has relatively low throughput. Furthermore, in our study, we failed to separate extensively sonicated fibrils from monomer even by centrifugation at 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g for 1 hour. The resulting supernatant was ThT positive, indicating the presence of residual fibrils or oligomers (ESI Fig. S8†).
000×g for 1 hour. The resulting supernatant was ThT positive, indicating the presence of residual fibrils or oligomers (ESI Fig. S8†).
| Technique | Detection/species | Advantages | Disadvantages |
|---|---|---|---|
| a 5 μL is the minimal working volume for sample injection, <250 nL of sample is used for the analysis. b Based on the method used here which includes washing steps. c Asymmetric peak = not diffusive or slowly diffusive aggregates; spikes = large, non-diffusive aggregates; absence of spikes and asymmetric peak = large and macroscopic aggregates that do not enter the capillary. d Removal of most aggregates by centrifugation followed by FIDA allows more reliable sizing of the residual soluble species. e Using Type 42.2 Ti Fixed-Angle Titanium Rotor (Beckman). f e.g. pipetting in and out of the centrifugation tubes and absorbance measurement off-line. g Using 384-well plates and 30 min read time/plate. h ThT signal is not always linearly dependent on fibril concentration. i Using DSF capillary-based platforms such as Prometheus Panta (NanoTemper). FIDA – flow-induced dispersion analysis, UCF – ultracentrifugation, ThT – thioflavin T assay, SLS – static light scattering, DLS – dynamic light scattering, DSF – differential scanning fluorimetry. HTP – high-throughput, LOD – limit of detection. | |||
| FIDA | Intrinsic fluorescence/monomer | Quantification of monomer, sizing of the soluble species, 5 μL per sample (>95% recoverablea), 15 samples per hourb in autonomous manner from 96 well-plate, qualitative information about fibril sizec, can be used in tandem with centrifugationd, label-free | Requires presence of at least one Y/W in the sequence (LOD of αSyn WT (4 × Y) and F94W (4 × Y, 1 × W) ca. 5 and 1 μM, respectively), parallel measurements not possible |
| UCF | Absorbance/monomer | Quantification of monomer, medium throughput (72 samples per rune), sensitivity dependent on the protein quantification assay and can be optimized | Labor-intensivef, large sample volume (∼30 μL), no sizing of soluble species available, presence of soluble aggregates in the supernatant |
| ThT | Extrinsic fluorescence/fibril | High throughput (768 samples per hourg), low sample consumption (15 μL), autonomous, continuous monitoring of multiple samples during equilibration possible (depolymerization kinetics) | Low or no sensitivity to certain fibrils (i.e., ThT invisible polymorphs), indirect measurementh, interference with other molecules (e.g., DNA), no information about the soluble species which can render normalization difficult |
| SLS, DLS | Light scattering/fibrils | Simple and fast, high throughput (48 samples per runi), low sample consumption (10 μLi). Label-free, no specific protein amino acid requirements, continuous monitoring of multiple samples during equilibration possible (depolymerization kinetics) | Large dependence of scattering intensity on aggregate size, no information about the concentration of the soluble species leading to errors in data normalization, low signal/noise ratio |
| DSF | Intrinsic fluorescence/both | Simple and fast, high throughput (48 samples per runi), low sample consumption (10 μLi), continuous monitoring of multiple samples during equilibration possible (depolymerization kinetics) | Requires presence of tryptophan residues and measurable difference of their fluorescence spectra in the monomeric versus fibrillar state |
Higher-order assemblies and aggregates of proteins strongly scatter light which can be used for determination of fibril stability.75,76 The analysis of stability curves determined by DLS or SLS can be cumbersome due to the large uncertainty in quantification of soluble monomers in samples with small amounts of large aggregates that dominate the scattering signal which consequently hinders correct normalization of the depolymerization curves. Moreover, aggregates that precipitate out of solution do not show any scattering signal (e.g. SH3 fibrils, Fig. 3c). The Thioflavin-T (ThT) assay is an extensively used and popular method for quantification of fibrils, mostly in kinetic analysis of fibril formation, owing to its simplicity, throughput, and use of commonly available fluorescence plate readers. One of the main disadvantages of ThT-based (or other fluorescent probes such as ANS) detection is the great sensitivity of the fluorescence intensity of the dye towards solution conditions or structural features of the fibrils.68–71,77 DSF is an attractive method due to its high throughput and low sample consumption. However, it requires the presence of tryptophan residues localized such that their structural context within the protein changes between monomeric and fibrillar states and is accompanied by sufficiently large shift of its fluorescence spectrum.38 Unfortunately, tryptophan is a relatively rare amino acid78,79 and its introduction into the wild type by mutagenesis can affect the protein's free energy landscape, as demonstrated here in a case of αSyn (Fig. 3a and b). The output of spectroscopic and scattering techniques reports only on relative concentrations of the species and the resulting data analysis requires making assumptions which might be incorrect. Specifically, the normalization of data may suffer from errors if the fibrils are partially dissociated in the absence of urea or not completely depolymerized in the highest urea concentration, where the relative monomer concentration is normalized to zero and one.
In contrast, the methodology described here combines fast, in situ separation of the two species using ultra-low sample volume (5 μL minimal sample volume with only a few hundred nL sample consumption per data point) on relatively short time scales (minutes) in an automated, high throughput-amenable manner. The intrinsic fluorescence detector is sensitive enough to detect species of protein that do not contain tryptophan. Here, down to 5 μM of monomeric unlabelled WT αSyn (ε280 = 5960 M−1 cm−1; four tyrosine residues) could be quantified. The quantification of monomer concentration enables straightforward and reliable data normalization. Moreover, absolute concentration of monomer can be obtained if it can be independently demonstrated that the samples are fully monomeric at the highest denaturant concentrations. Otherwise, a calibration curve with known monomer concentrations can be used.
Although not considered in detail in our present analysis, the fluorescence signal of the fibrils during FIDA provides valuable qualitative information about their properties. Fibrils that are prone to self-association form larger aggregates that are detected as signal spikes whose intensity is related to their size. Conversely, isolated, and homogenized (sonicated) fibrils are often small enough to appear as continuous signal of non-diffusive particles (Fig. 1c). Such information can be useful in attempts to optimize solution conditions towards favouring well-defined individual fibrils, something that is a requirement for structural analyses of amyloid fibrils, e.g. by AFM or cryoEM.
Thermodynamic stability of aSyn fibrils is a valuable probe of fibril polymorphism
Multiple polymorphs of αSyn fibrils have been observed in both patient samples80,81 and in vitro studies using recombinant monomer.82,83 The structural variation of fibrils assembled in vitro is dictated by the solution conditions of the aggregation assay, including pH, salt concentration, incubation temperature, or shaking.82,83 Conversely, the diversity of fibril polymorphs isolated ex vivo may be attributed to the unique cellular environments84 characteristic for each disease (similarly to what has been observed for the tau protein9). These include dopaminergic neurons in PD and oligodendrocytic glial cells in different brain regions in MSA.80,85 This is supported by the finding of unknown electron densities in the structures of both disease-related αSyn polymorphs, indicating a cell specific “aggregation co-factor” whose absence explains the inability to replicate these structures in vitro using seeded experiments.11 While it is plausible for different fibril polymorphs to nucleate in a cellular environment, disease-specific polymorph evidence suggests that only one polymorph emerges as the dominant competitor, propagating itself due to higher stability, faster kinetics, or better compatibility with the cellular environment, including ligands or post-translational modifications (PTMs).We studied the effect of salt and pH separately on the thermodynamic stability of the fibrils. We first prepared the fibrils in the absence or presence of salt (150 mM KCl) as well as neutral (pH 7.4) and acidic (pH 5) conditions. It has been reported that a distinct dominant polymorph is formed in each condition72,86 which is supported by the morphological differences observed in our AFM analysis of the fibrils (Fig. 4c).
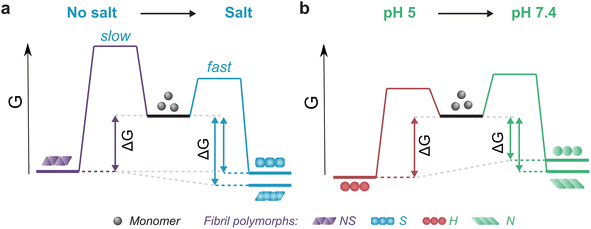
The thermodynamic stability of the polymorph S (salt condition) and NS (non-salt) was similar when assayed under the conditions in which they were formed (Fig. 5a). However, the polymorph NS was more stable than polymorph S when measured in the buffer conditions in which the latter was formed (Fig. 5a). The result was unexpected since the kinetics of fibril formation was faster at high salt, both in terms of nucleation and elongation (ESI Fig. S9†). In contrast, the aggregation of αSyn in the absence of salt was slow and the reaction had to be promoted by sonication during the time course of reaction to achieve complete conversion of monomers to fibrils. Analysis of the aggregation kinetics in the presence of preformed seeds revealed that elongation saturates already at low μM concentrations of monomer, which might explain the need for sonication which promotes formation of new elongation-competent fibril ends and greatly accelerates the overall conversion of monomer to fibrils (ESI Fig. S5b,† right panel). To rationalize all our observations, we consider that αSyn can adopt different conformations during fibril formation.82,83 At high ionic strength the electrostatic repulsion between monomers and fibrils is largely screened.87 Consequently, the fibril conformations with lowest energy barrier of nucleation/elongation are formed first, i.e., the structural polymorphism is dominated by kinetic factors (Fig. 5a, polymorph S in S, light blue). This might lead to structures that are not minimising electrostatic repulsion inside the fibril, because such minimisation is not necessary under highly screened conditions. In contrast, the high electrostatic repulsion in the absence of salt creates an energy barrier leading to slower aggregation (Fig. 5a, polymorph NS in NS, violet). In this scenario, the formation of amyloid fibrils is driven by αSyn conformations with an optimally minimized set of unfavourable electrostatic interactions and maximization of favourable interactions to ensure fibril stability under such unfavourable conditions. In other words, fibril structure is primarily governed by thermodynamic stability of the resulting fibrils under such unfavourable conditions. These polymorphs exhibit enhanced stability compared to the kinetically controlled ones when transferred to the conditions where electrostatic forces are attenuated (high salt, right side of energy landscape diagram in Fig. 5a). The NS polymorph represents a low and possibly the global energy minimum on the rugged conformational landscape for neutral pH conditions which is unlikely to be sampled in the physiologically relevant context due to the easier accessibility of other fibril morphologies at physiological ionic strength. However, it provides important insights into the delicate interplay between kinetic and thermodynamic factors and their influence on fibril stability and polymorphism.
Changes in fibril stability in response to pH variation are likely to have more physiological relevance. It has been reported that fibrils formed under conditions that simulate the acidic cellular compartments (lysosomes, endosomes) are destabilized when transferred to the neutral pH of the cytosolic environment.74 Our results agree with such observations and provide a quantitative view of this phenomenon. Aggregation of αSyn under acidic pH conditions is faster and the resulting fibrils (H) are slightly more stable compared to neutral pH (Fig. 4b, 5b; ESI S5c and d†). In contrast to the case above, the solubility differs between the fibril-forming conditions which explains the higher stability of fibrils at pH 5. However, the stability of H fibrils decreases upon transfer to physiological pH even below the stability of fibrils formed under such conditions (right side of Fig. 5b). This indicates that a given fibril structure can be well-adapted to a given set of solution conditions, while a change in solution conditions can severely destabilize the structure. A change in pH can lead to a significant change in charge state of a protein and hence can lead to the emergence of additional unfavourable electrostatic interactions that render the given structure ill-adapted to the new solution environment.
To conclude, we demonstrate the importance of thermodynamic stability measurements in probing the rugged amyloid landscape and provide a useful novel methodology for its analysis. We believe that future studies, which link thermodynamic stability of fibril polymorphs with high resolution structural information can provide a missing link between the observed structural polymorphism of amyloid fibrils and some of the properties relevant for disease.
Materials and methods
Protein purification and sample preparation
Human wild type or F94W mutant αSyn were expressed in E. coli BL21 (DE3) cells transformed by the pT7-7 plasmid carrying the respective gene (Addgene plasmid # 36046; http://n2t.net/addgene:36046; RRID: Addgene_36046 (ref. 88)). Transformed cells were used to inoculate 1 L LB medium containing ampicillin (50 μg ml−1 final concentration) as a selection marker. The cell suspension was incubated at 37 °C and αSyn expression induced by IPTG (1 mM final concentration) at OD600 ∼ 0.6–0.8. The cells were harvested by centrifugation (5000×g, 20 minutes) following the 4 hour expression at 37 °C. Cell pellet corresponding to 1 L culture was resuspended in 20 mL of Tris buffer (10 mM Tris–HCl, 1 mM EDTA, pH 8.0) with 1 mM PMSF (phenylmethylsulfonyl fluoride). The suspension was sonicated with a probe ultrasonicator for 8 min (10 s on time, 30 s off time, 12 rounds with 40% amplitude). 1 μL benzonase (DNAse) was added to the cell lysate and the insoluble fraction was removed by centrifugation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g, 30 min at 4 °C). The resulting cell-free extract was boiled for 20 min and the heat-precipitated proteins removed by centrifugation (20
000×g, 30 min at 4 °C). The resulting cell-free extract was boiled for 20 min and the heat-precipitated proteins removed by centrifugation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g for 20 min at 4 °C). αSyn was precipitated by addition of saturated (NH4)2SO4 (4 mL per 1 mL of supernatant). The solution was incubated on a rocking platform at 4 °C for 15 min and then centrifuged (20
000×g for 20 min at 4 °C). αSyn was precipitated by addition of saturated (NH4)2SO4 (4 mL per 1 mL of supernatant). The solution was incubated on a rocking platform at 4 °C for 15 min and then centrifuged (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g, 20 min, 4 °C) to obtain a protein pellet. The pellet was dissolved in 7 mL of 25 mM Tris–HCl pH 7.7 with 1 mM DTT. Protein was dialyzed against the same buffer for 16–18 h with a buffer exchange after 12 h of dialysis at 4 °C. The dialyzed protein was then subjected to anion exchange chromatography (AEC) (HiTrap Q Hp 5 ml, GE healthcare) followed by size exclusion chromatography (SEC) (HiLoad 16/600 Superdex 200 pg. column). The monomeric fraction of αSyn eluted in 10 mM of sodium phosphate buffer (pH 7.4) was collected, and the protein concentration determined by UV-absorption at 280 nm with theoretical molar extinction coefficients calculated from the protein sequence using ProtParam80 (Expasy, Switzerland).
000×g, 20 min, 4 °C) to obtain a protein pellet. The pellet was dissolved in 7 mL of 25 mM Tris–HCl pH 7.7 with 1 mM DTT. Protein was dialyzed against the same buffer for 16–18 h with a buffer exchange after 12 h of dialysis at 4 °C. The dialyzed protein was then subjected to anion exchange chromatography (AEC) (HiTrap Q Hp 5 ml, GE healthcare) followed by size exclusion chromatography (SEC) (HiLoad 16/600 Superdex 200 pg. column). The monomeric fraction of αSyn eluted in 10 mM of sodium phosphate buffer (pH 7.4) was collected, and the protein concentration determined by UV-absorption at 280 nm with theoretical molar extinction coefficients calculated from the protein sequence using ProtParam80 (Expasy, Switzerland).
Fibril preparation
The αSyn fibrils were prepared using a single monomer batch which was transferred to different buffer conditions (200 μM final monomer concentration) followed by incubation in the benchtop thermo-shaker with constant agitation (1200 rpm) at 37 °C for 7 days. Fibril samples were frozen and stored at −20 °C. Prior to the experiment, fibrils were thawed and sonicated using an ultrasonic probe (Hielscher UP200St). Sonication was carried out in repeating pulses of 3 second duration with 20% amplitude separated by 12 second pauses for 5 minutes (one minute total sonication time) to prevent sample overheating.Flow analysis of non-diffusive particles
The flow-induced dispersion experiments were carried out using FIDA1 instrument (FidaBio, Denmark). For each measurement, the following method was used unless stated otherwise:1 – Wash 1 (1 M NaOH): 45 s, 3500 mbar.
2 – Wash 2 (MQ water): 45 s, 3500 mbar.
3 – Equilibration (buffer): 30 s, 3500 mbar.
4 – Sample application (protein/NP stock): 20 s, 75 mbar.
5 – Measurement and detection (buffer): 75 s, 1500 mbar.
All experiments were performed at 25 °C. The resulting elution profiles were corrected for the viscosity of urea according to the following empirical formula derived in ref. 89:
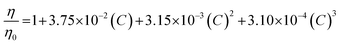 | (8) |
The monomer quantification was carried out using four different methods of Taylorgram deconvolution following the reasoning that (i) the observed signal is a sum of contributions from diffusive particles (i.e., monomers) with a Gaussian distribution, and non-diffusive particles (i.e., fibrils/nanoparticles) exhibiting an asymmetrical distribution, and (ii) that the monomer concentration is proportional to the signal amplitude of the former.
Method 1: baseline subtraction
The contribution from the non-diffusive particles was subtracted from the monomer signal using a linear baseline connecting manually selected points at the intersects of the two distributions using OriginPro (OriginLab, USA). The monomer concentration was determined from the integral of the resulting peak.Method 2: independent fitting
Each elution profile was fitted to the sum of the Gaussian and asymmetrical distributions (Asym2Sig; OriginPro 2021) described by the eqn (9) and (10), respectively.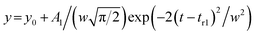 | (9) |
| y = [A2/(1 + exp(−(t − tr2 + w1/2)/w2))][1 − 1/(1 + exp(−(t − tr2 − w1/2)/w3))] | (10) |
Method 3: global fitting
Fits of individual elution profiles often suffered from overparameterization and did not converge, most notably in cases where the contribution from the non-diffusive particles to the overall signal was low (0–10%). To overcome this, elution profiles across the whole urea depolymerization series were analyzed globally.A global fit allows shared parameters across all data to be obtained for one series of measurements at different denaturant concentrations, which restricts the model and makes fitting more robust. The residency time (retention time) of the samples should be independent of urea concentration after normalizing the data based on the viscosity increase and was therefore shared between all samples. The hydrodynamic radius of the monomer was shown to be independent of denaturant and could thus be represented with Gaussian curves with shared widths (eqn (9)) but different total areas which were defined by the isodesmic polymerization model (eqn (11),38) multiplied with a constant to relate fluorescence to concentration.
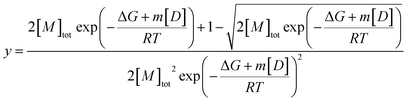 | (11) |
We found that the signal for the fibrils changed slightly with urea concentration, however this change could not be directly modelled by the empirical fit using the asymmetric distribution (eqn (10)). Also, the amount of fibrils present in the signal was stochastically changing in each sample due to sticking, sampling-issues due to heterogeneous samples and sedimentation, etc. To limit the over-parameterization and correlation between parameters in the fit, which made the estimation of monomer unreliable, the global analysis therefore used a shared asymmetric distribution curve to account for the fibril signal in all samples, and only the total area of the fibril signal was an independent fit parameter for each individual measurement. Because clumping fibrils caused spikes in the signal, all samples were smoothed using a median filter with a window size of 31 data points. Least squares fits were performed with lmfit in Python using the Levenberg–Marquardt algorithm.
Method 4: COMSOL simulation
Monomer and fibril transport were simulated using COMSOL Multiphysics 5.6 (COMSOL AB, Sweden) finite element analysis software. The simulated geometry was a straight capillary 1 m in length aligned along the z-axis with a cylindrical 500 μm detector region at z = 840 mm.Using the “Transport of Diluted Species” interface, a Poiseuille velocity field was imposed in the channel, with the magnitude determined by a parameterized pressure/viscosity term that was variable in time. In the first 20 seconds of the simulation, the velocity corresponded to an inlet pressure of 75 mbar, and two solute species were introduced by concentration constraint at the inlet, resulting in the introduction of a sample “plug”. After 20 seconds, the concentration constraint at the inlet was set to zero and the pressure parameter increased to a value corresponding to the desired experimental velocity. The concentration of each species at the detector was recorded as a function of simulation time.
The simulation output was calibrated against experimental data from monomer-only runs. As the total protein concentration was constant (20 μM), and only the leading edge of the peak was used as reference data (avoiding confounding effects from adsorption of fibrils to the capillary walls), a separate calibration factor for fibrils was computed. The hydrodynamic radius of the monomer was experimentally determined using the FIDA 1 instrument, and its diffusion coefficient used as determined (7.0 × 10−11 m2 s−1). An approximate fibril diffusion coefficient (Df) was derived from a COMSOL fit to an experimental FIDA run for fibrils and confirmed by calculation of approximate expected values for fibrils of the experimentally determined average length (1.2 × 10−11 m2 s−1).
Using the “Parameter Estimation interface”, the free monomer concentration, fibril diffusion coefficient and fibril concentration/signal calibration multiplier were used as fitting parameters with the first 30 seconds of each experimental run as reference data. The fibril signal calibration value was entered as a fitting parameter to verify consistency of results.
DSF and static light scattering (SLS)
Intrinsic fluorescence and light scattering of the fibrils equilibrated at different concentrations of urea were measured using the Prometheus Panta instrument (NanoTemper, Germany). Samples were loaded into the standard grade capillaries and their fluorescence and light scattering recorded for 30 min at 25 °C. Scattering intensity was averaged over the measured timespan and normalized based on the assumption that fibrils at the lowest (0) and the highest concentration of urea (5.4 M) contain negligible amounts of free monomer or are completely dissociated, respectively.Thioflavin T (ThT) fluorescence
In the ThT experiments, 10 μM ThT was added to the equilibrated samples (3 days, 25 °C), and their fluorescence (ex./em. = 440/480 nm) was recorded in a 384-well plate (Corning® 384-well Black and Clear Bottom; Corning 3544) using a FLUOstar Omega fluorescence plate reader (BMG Labtech, Germany).Aggregation kinetics
Aggregation kinetics of wt αSyn were monitored under seeded and non-seeded conditions by ThT assay (ex./em. = 440/480 nm, 50 μM ThT). In the seeded experiments, 2.5 μM of sonicated seeds pre-formed under the same conditions as the respective experiment were added to varying concentrations of fresh monomeric αSyn. The elongation kinetics were measured in the 384-well low volume non-binding black plates with clear bottom (Corning 3544) under quiescent conditions at 37 °C. Quantification of the residual monomer at the end of the aggregation reaction was carried out for samples with the highest initial monomer concentration by FIDA and used to convert the ThT signal into concentration of the fibrils (in monomer equivalents). The apparent elongation rates were obtained from slopes of the linear curves fitted into the initial timepoints (5 hours).In the non-seeded experiments, varying concentrations of monomeric WT αSyn in different buffer conditions were incubated with a single glass bead (d = 1 mm) in the 384-well low volume non-treated polystyrene plates (Corning 3540) at 37 °C and the ThT fluorescence was monitored during continuous shaking (300 rpm, double orbital). Resulting datasets were fitted individually to a purely empirical logistic function described by the eqn (12).
| y = y0 + A/(1 + exp(−k(t − t0.5))) | (12) |
The y0 is the pre-transition baseline, A is the signal amplitude, k is the apparent growth rate, and t0.5 is the midpoint of the transition, i.e., half-time.90
Ultracentrifugation
Fibril samples equilibrated for 72 hours at different concentrations of urea were ultracentrifuged (180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g, 1 h, 25 °C) to pellet the aggregated fraction. The supernatant was carefully collected in an Eppendorf tube and the concentration of the residual monomer determined by UV absorption using a NanoDrop instrument (ThermoFisher, USA) and the extinction coefficients of the respective variants (WT or F94W).
000×g, 1 h, 25 °C) to pellet the aggregated fraction. The supernatant was carefully collected in an Eppendorf tube and the concentration of the residual monomer determined by UV absorption using a NanoDrop instrument (ThermoFisher, USA) and the extinction coefficients of the respective variants (WT or F94W).
AFM imaging and analysis of the fibrils
Fibrils were diluted to 5 μM monomer equivalent concentration and 10 μL of the solution was pipetted onto freshly cleaved mica substrates. Following 10 min of incubation, the substrates were cleaned extensively with milli-Q water and dried under air flow. All fibrils were imaged in tapping mode in air using a DriveAFM (Nanosurf, Liestal, Switzerland) using PPP-NCLAuD cantilevers (Nanosensors, Neuchatel, Switzerland).Amyloid fibrils are characterized by pitch length and height. Fibril pitch is analyzed from fibril height profiles along the fibril length extracted using Gwyddion. Multiple pixel averages have been used to measure slightly curved fibrils. This is acceptable for analysis since the absolute height of the fibrils does not influence pitch analysis. Additionally, length profiles shorter than 300 nm are excluded from the analysis. The Fourier transforms of the fibril height profiles were computed, using the fft and fftfreq modules of the scipy.fft python library. To avoid the frequency domain being dominated by measurement noise and the mean fibril profile, frequencies translating to length scales below 5 pixel-lengths and above 1/3 of the full fibril or profile length are excluded. From the remaining frequency domain, the primary frequency peak is identified as the frequency of fibril rotation and converted to length to obtain the periodicity. The pitch length (full 360° rotation) is calculated as twice the length of a single fibril rotation. Fibril height is analyzed from fibril cross-section profiles extracted using Gwyddion. The surface baseline is calculated as the median height of the cross-section and fibril height is calculated from the peak of the cross-section.
DLS analysis of the soluble species in the fibril supernatants
Fibrils S, NS, N, and H, equilibrated in their respective native buffers in the presence of 0, 1, and 2 M urea for three days were centrifuged (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g, 1 h, 25 °C) and the supernatant carefully removed. The supernatant was loaded into the standard grade capillaries (NanoTemper, Germany) and the DLS measurements of the samples were carried out using the Prometheus Panta instrument (NanoTemper, Germany). In total, ten 5 second acquisitions were carried out for each sample and the resulting correlation curves automatically analysed by the software using the size distribution fit.
000×g, 1 h, 25 °C) and the supernatant carefully removed. The supernatant was loaded into the standard grade capillaries (NanoTemper, Germany) and the DLS measurements of the samples were carried out using the Prometheus Panta instrument (NanoTemper, Germany). In total, ten 5 second acquisitions were carried out for each sample and the resulting correlation curves automatically analysed by the software using the size distribution fit.
Data availability
The data of this study can be found on the Zenodo repository, at DOI: 10.5281/zenodo.10479393.Author contributions
AF, AK, SR, and AKB conceptualized the study. AF and AK carried out the investigation. AF, AK and AKB analysed the data and wrote the manuscript. TOM performed the COMSOL simulations. RKN wrote the code for automated data analysis. JAL prepared script for analysis of AFM data. ETD performed the AFM experiments. AKB supervised and was the main coordinator of the project. All authors contributed to the manuscript preparation and review.Conflicts of interest
Authors declare no conflict of interest.Acknowledgements
A. F., R. K. No., T. O. M., J. A. L. and A. K. B. thank the Novo Nordisk Foundation (grant number: NNF17SA0028392) for funding. T. O. M. and A. K. B. acknowledge funding from the Lundbeck Foundation (grant no: R400-2022-911) for funding. S. R. (grant no: 101062241) and A. K. (grant number 101106115) would like to acknowledge a Horizon MSCA individual postdoctoral fellowship for funding. A. F. and A. K. B. thank the Michael J. Fox Foundation for funding (grant no: MJFF-021293). This research was also co-funded by the European Union (ERC CoG 101088163 EMMA). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.References
- F. Chiti and C. M. Dobson, Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress Over the Last Decade, Annu. Rev. Biochem., 2017, 86, 27–68 CrossRef CAS PubMed.
- N. Louros, K. Konstantoulea, M. De Vleeschouwer, M. Ramakers, J. Schymkowitz and F. Rousseau, WALTZ-DB 2.0: an updated database containing structural information of experimentally determined amyloid-forming peptides, Nucleic Acids Res., 2020, 48(D1), D389–D393 CrossRef CAS PubMed.
- S. Mehra, L. Gadhe, R. Bera, A. S. Sawner and S. K. Maji, Structural and Functional Insights into alpha-Synuclein Fibril Polymorphism, Biomolecules, 2021, 11(10), 1419 CrossRef CAS PubMed.
- M. Sunde, L. C. Serpell, M. Bartlam, P. E. Fraser, M. B. Pepys and C. C. Blake, Common core structure of amyloid fibrils by synchrotron X-ray diffraction, J. Mol. Biol., 1997, 273(3), 729–739 CrossRef CAS PubMed.
- M. G. Iadanza, R. Silvers, J. Boardman, H. I. Smith, T. K. Karamanos, G. T. Debelouchina, Y. Su, R. G. Griffin, N. A. Ranson and S. E. Radford, The structure of a beta(2)-microglobulin fibril suggests a molecular basis for its amyloid polymorphism, Nat. Commun., 2018, 9(1), 4517 CrossRef PubMed.
- C. Roder, N. Vettore, L. N. Mangels, L. Gremer, R. B. G. Ravelli, D. Willbold, W. Hoyer, A. K. Buell and G. F. Schroder, Atomic structure of PI3-kinase SH3 amyloid fibrils by cryo-electron microscopy, Nat. Commun., 2019, 10(1), 3754 CrossRef PubMed.
- L. J. G. Hoppenreijs, L. Fitzner, T. Ruhmlieb, T. R. Heyn, K. Schild, A. J. van der Goot, R. M. Boom, A. Steffen-Heins, K. Schwarz and J. K. Keppler, Engineering amyloid and amyloid-like morphologies of β-lactoglobulin, Food Hydrocolloids, 2022, 124 Search PubMed.
- E. Gazit, The “Correctly Folded” state of proteins: is it a metastable state?, Angew. Chem., Int. Ed., 2002, 41(2), 257–259 CrossRef CAS PubMed.
- Y. Shi, W. Zhang, Y. Yang, A. G. Murzin, B. Falcon, A. Kotecha, M. van Beers, A. Tarutani, F. Kametani, H. J. Garringer, R. Vidal, G. I. Hallinan, T. Lashley, Y. Saito, S. Murayama, M. Yoshida, H. Tanaka, A. Kakita, T. Ikeuchi, A. C. Robinson, D. M. A. Mann, G. G. Kovacs, T. Revesz, B. Ghetti, M. Hasegawa, M. Goedert and S. H. W. Scheres, Structure-based classification of tauopathies, Nature, 2021, 598(7880), 359–363 CrossRef CAS PubMed.
- U. Ghosh, K. R. Thurber, W. M. Yau and R. Tycko, Molecular structure of a prevalent amyloid-beta fibril polymorph from Alzheimer’s disease brain tissue, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(4), e2023089118 CrossRef CAS PubMed.
- S. Lovestam, M. Schweighauser, T. Matsubara, S. Murayama, T. Tomita, T. Ando, K. Hasegawa, M. Yoshida, A. Tarutani, M. Hasegawa, M. Goedert and S. H. W. Scheres, Seeded assembly in vitro does not replicate the structures of alpha-synuclein filaments from multiple system atrophy, FEBS Open Bio., 2021, 11(4), 999–1013 CrossRef PubMed.
- M. Ziaunys, A. Sakalauskas, K. Mikalauskaite and V. Smirnovas, Polymorphism of Alpha-Synuclein Amyloid Fibrils Depends on Ionic Strength and Protein Concentration, Int. J. Mol. Sci., 2021, 22(22), 12382 CrossRef CAS PubMed.
- T. P. Knowles, C. A. Waudby, G. L. Devlin, S. I. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, An analytical solution to the kinetics of breakable filament assembly, Science, 2009, 326(5959), 1533–1537 CrossRef CAS PubMed.
- G. Meisl, J. B. Kirkegaard, P. Arosio, T. C. Michaels, M. Vendruscolo, C. M. Dobson, S. Linse and T. P. Knowles, Molecular mechanisms of protein aggregation from global fitting of kinetic models, Nat. Protoc., 2016, 11(2), 252–272 CrossRef CAS PubMed.
- T. C. T. Michaels, A. Saric, J. Habchi, S. Chia, G. Meisl, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Chemical Kinetics for Bridging Molecular Mechanisms and Macroscopic Measurements of Amyloid Fibril Formation, Annu. Rev. Phys. Chem., 2018, 69, 273–298 CrossRef CAS PubMed.
- S. I. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. Knowles, Proliferation of amyloid-beta42 aggregates occurs through a secondary nucleation mechanism, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(24), 9758–9763 CrossRef CAS PubMed.
- F. Kundel, L. Hong, B. Falcon, W. A. McEwan, T. C. T. Michaels, G. Meisl, N. Esteras, A. Y. Abramov, T. J. P. Knowles, M. Goedert and D. Klenerman, Measurement of Tau Filament Fragmentation Provides Insights into Prion-like Spreading, ACS Chem. Neurosci., 2018, 9(6), 1276–1282 CrossRef CAS PubMed.
- C. Galvagnion, A. K. Buell, G. Meisl, T. C. Michaels, M. Vendruscolo, T. P. Knowles and C. M. Dobson, Lipid vesicles trigger alpha-synuclein aggregation by stimulating primary nucleation, Nat. Chem. Biol., 2015, 11(3), 229–234 CrossRef CAS PubMed.
- A. K. Buell, C. Galvagnion, R. Gaspar, E. Sparr, M. Vendruscolo, T. P. Knowles, S. Linse and C. M. Dobson, Solution conditions determine the relative importance of nucleation and growth processes in alpha-synuclein aggregation, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(21), 7671–7676 CrossRef CAS PubMed.
- A. K. Buell, Stability matters, too - the thermodynamics of amyloid fibril formation, Chem. Sci., 2022, 13(35), 10177–10192 RSC.
- S. Donzelli, S. A. Osullivan, A.-L. Mahul-Mellier, A. Ulusoy, G. Fusco, S. T. Kumar, A. Chiki, J. Burtscher, M. L. D. Boussouf, I. Rostami, A. D. Simone, D. A. Di Monte and H. A. Lashuel, Post-fibrillization nitration of alpha-synuclein abolishes its seeding activity and pathology formation in primary neurons and in vivo, bioRxiv, 2023 DOI:10.1101/2023.03.24.534149.
- M. F. Altay, A. K. L. Liu, J. L. Holton, L. Parkkinen and H. A. Lashuel, Prominent astrocytic alpha-synuclein pathology with unique post-translational modification signatures unveiled across Lewy body disorders, Acta Neuropathol. Commun., 2022, 10(1), 163 CrossRef CAS PubMed.
- R. Cliffe, J. C. Sang, F. Kundel, D. Finley, D. Klenerman and Y. Ye, Filamentous Aggregates Are Fragmented by the Proteasome Holoenzyme, Cell. Rep., 2019, 26(8), 2140–2149 CrossRef CAS PubMed.
- A. Wentink, C. Nussbaum-Krammer and B. Bukau, Modulation of Amyloid States by Molecular Chaperones, Cold Spring Harbor Perspect. Biol., 2019, 11(7), a033969 CrossRef CAS PubMed.
- A. Franco, P. Gracia, A. Colom, J. D. Camino, J. A. Fernandez-Higuero, N. Orozco, A. Dulebo, L. Saiz, N. Cremades, J. M. G. Vilar, A. Prado and A. Muga, All-or-none amyloid disassembly via chaperone-triggered fibril unzipping favors clearance of alpha-synuclein toxic species, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(36), e2105548118 CrossRef CAS PubMed.
- Z. L. Almeida and R. M. M. Brito, Amyloid Disassembly: What Can We Learn from Chaperones?, Biomedicines, 2022, 10(12), 3276 CrossRef CAS PubMed.
- E. Hellstrand, B. Boland, D. M. Walsh and S. Linse, Amyloid beta-protein aggregation produces highly reproducible kinetic data and occurs by a two-phase process, ACS Chem. Neurosci., 2010, 1(1), 13–18 CrossRef CAS PubMed.
- M. R. Sawaya, M. P. Hughes, J. A. Rodriguez, R. Riek and D. S. Eisenberg, The expanding amyloid family: Structure, stability, function, and pathogenesis, Cell, 2021, 184(19), 4857–4873 CrossRef CAS PubMed.
- J. Kardos, K. Yamamoto, K. Hasegawa, H. Naiki and Y. Goto, Direct measurement of the thermodynamic parameters of amyloid formation by isothermal titration calorimetry, J. Biol. Chem., 2004, 279(53), 55308–55314 CrossRef CAS PubMed.
- B. Morel, L. Varela and F. Conejero-Lara, The thermodynamic stability of amyloid fibrils studied by differential scanning calorimetry, J. Phys. Chem. B, 2010, 114(11), 4010–4019 CrossRef CAS PubMed.
- T. Ikenoue, Y. H. Lee, J. Kardos, M. Saiki, H. Yagi, Y. Kawata and Y. Goto, Cold denaturation of alpha-synuclein amyloid fibrils, Angew. Chem., Int. Ed., 2014, 53(30), 7799–7804 CrossRef CAS PubMed.
- R. K. Norrild, N. Vettore, A. Coden, W. F. Xue and A. K. Buell, Thermodynamics of amyloid fibril formation from non-equilibrium experiments of growth and dissociation, Biophys. Chem., 2021, 271, 106549 CrossRef CAS PubMed.
- J. H. M. van Gils, E. van Dijk, A. Peduzzo, A. Hofmann, N. Vettore, M. P. Schutzmann, G. Groth, H. Mouhib, D. E. Otzen, A. K. Buell and S. Abeln, The hydrophobic effect characterises the thermodynamic signature of amyloid fibril growth, PLoS Comput. Biol., 2020, 16(5), e1007767 CrossRef CAS PubMed.
- F. Meersman and C. M. Dobson, Probing the pressure-temperature stability of amyloid fibrils provides new insights into their molecular properties, Biochim. Biophys. Acta, 2006, 1764(3), 452–460 CrossRef CAS PubMed.
- T. Narimoto, K. Sakurai, A. Okamoto, E. Chatani, M. Hoshino, K. Hasegawa, H. Naiki and Y. Goto, Conformational stability of amyloid fibrils of beta2-microglobulin probed by guanidine-hydrochloride-induced unfolding, FEBS Lett., 2004, 576(3), 313–319 CrossRef CAS PubMed.
- S. Raimondi, P. P. Mangione, G. Verona, D. Canetti, P. Nocerino, L. Marchese, R. Piccarducci, V. Mondani, G. Faravelli, G. W. Taylor, J. D. Gillmore, A. Corazza, M. B. Pepys, S. Giorgetti and V. Bellotti, Comparative study of the stabilities of synthetic in vitro and natural ex vivo transthyretin amyloid fibrils, J. Biol. Chem., 2020, 295(33), 11379–11387 CrossRef CAS PubMed.
- M. I. Sulatsky, A. I. Sulatskaya, O. V. Stepanenko, O. I. Povarova, I. M. Kuznetsova and K. K. Turoverov, Denaturant effect on amyloid fibrils: Declasterization, depolymerization, denaturation and reassembly, Int. J. Biol. Macromol., 2020, 150, 681–694 CrossRef CAS PubMed.
- N. Vettore and A. K. Buell, Thermodynamics of amyloid fibril formation from chemical depolymerization, Phys. Chem. Chem. Phys., 2019, 21(47), 26184–26194 RSC.
- M. M. Santoro and D. W. Bolen, Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants, Biochemistry, 1988, 27(21), 8063–8068 CrossRef CAS PubMed.
- M. M. Smulders, M. M. Nieuwenhuizen, T. F. de Greef, P. van der Schoot, A. P. Schenning and E. W. Meijer, How to distinguish isodesmic from cooperative supramolecular polymerisation, Chemistry, 2010, 16(1), 362–367 CrossRef CAS PubMed.
- A. J. Baldwin, T. P. Knowles, G. G. Tartaglia, A. W. Fitzpatrick, G. L. Devlin, S. L. Shammas, C. A. Waudby, M. F. Mossuto, S. Meehan, S. L. Gras, J. Christodoulou, S. J. Anthony-Cahill, P. D. Barker, M. Vendruscolo and C. M. Dobson, Metastability of native proteins and the phenomenon of amyloid formation, J. Am. Chem. Soc., 2011, 133(36), 14160–14163 CrossRef CAS PubMed.
- M. Deleanu, O. Deschaume, L. Cipelletti, J. F. Hernandez, C. Bartic, H. Cottet and J. Chamieh, Taylor Dispersion Analysis and Atomic Force Microscopy Provide a Quantitative Insight into the Aggregation Kinetics of Abeta (1-40)/Abeta (1-42) Amyloid Peptide Mixtures, ACS Chem. Neurosci., 2022, 13(6), 786–795 CrossRef CAS PubMed.
- M. Deleanu, J. F. Hernandez, L. Cipelletti, J. P. Biron, E. Rossi, M. Taverna, H. Cottet and J. Chamieh, Unraveling the Speciation of beta-Amyloid Peptides during the Aggregation Process by Taylor Dispersion Analysis, Anal. Chem., 2021, 93(16), 6523–6533 CrossRef CAS PubMed.
- M. Deleanu, J. F. Hernandez, H. Cottet and J. Chamieh, Taylor dispersion analysis discloses the impairment of Abeta peptide aggregation by the presence of a fluorescent tag, Electrophoresis, 2023, 44(7–8), 701–710 CrossRef CAS PubMed.
- S. Lovestam, D. Li, J. L. Wagstaff, A. Kotecha, D. Kimanius, S. H. McLaughlin, A. G. Murzin, S. M. V. Freund, M. Goedert and S. H. W. Scheres, Disease-specific tau filaments assemble via polymorphic intermediates, Nature, 2024, 625(7993), 119–125 CrossRef CAS PubMed.
- E. Prada Brichtova, M. Krupova, P. Bour, V. Lindo, A. Gomes Dos Santos and S. E. Jackson, Glucagon-like peptide 1 aggregates into low-molecular-weight oligomers off-pathway to fibrillation, Biophys. J., 2023, 122(12), 2475–2488 CrossRef CAS PubMed.
- A. D. Williams, S. Shivaprasad and R. Wetzel, Alanine scanning mutagenesis of Abeta(1-40) amyloid fibril stability, J. Mol. Biol., 2006, 357(4), 1283–1294 CrossRef CAS PubMed.
- G. I. Taylor, Dispersion of soluble matter in solvent flowing slowly through a tube, Proc. R. Soc. London, Ser. A, 1953, 219(1137), 186–203 CAS.
- R. Aris, On the dispersion of a solute in a fluid flowing through a tube, Proc. R. Soc. London, Ser. A, 1956, 235(1200), 67–77 Search PubMed.
- J. Chamieh, L. Leclercq, M. Martin, S. Slaoui, H. Jensen, J. Ostergaard and H. Cottet, Limits in Size of Taylor Dispersion Analysis: Representation of the Different Hydrodynamic Regimes and Application to the Size-Characterization of Cubosomes, Anal. Chem., 2017, 89(24), 13487–13493 CrossRef CAS PubMed.
- M. Harada, T. Kido, T. Masudo and T. Okada, Solute distribution coupled with laminar flow in wide-bore capillaries: what can be separated without chemical or physical fields?, Anal. Sci., 2005, 21(5), 491–496 CrossRef CAS PubMed.
- T. Okada, Hydrodynamic Chromatography in Narrow and Wide-Bores; Whether Radial Diffusion Is Essential or Not, J. Liq. Chromatogr. Relat. Technol., 2010, 33(9–12), 1116–1129 CrossRef CAS.
- T. Okada, M. Harada and T. Kido, Resolution of small molecules by passage through an open capillary, Anal. Chem., 2005, 77(18), 6041–6046 CrossRef CAS PubMed.
- C. N. Trumbore, M. Grehlinger, M. Stowe and F. M. Keleher, Further experiments on a new, fast method for determining molecular weights of diffusing species in a liquid phase, J. Chromatogr. A, 1985, 322, 443–454 CrossRef CAS.
- N. Sisavath, J. L. Rukundo, J. C. Y. Le Blanc, V. A. Galievsky, J. Bao, S. Kochmann, A. S. Stasheuski and S. N. Krylov, Transient Incomplete Separation Facilitates Finding Accurate Equilibrium Dissociation Constant of Protein-Small Molecule Complex, Angew. Chem., Int. Ed., 2019, 58(20), 6635–6639 CrossRef CAS PubMed.
- J. L. Rukundo, S. Kochmann, T. Y. Wang, N. A. Ivanov, J. C. Y. Le Blanc, B. I. Gorin and S. N. Krylov, Template Instrumentation for “Accurate Constant via Transient Incomplete Separation”, Anal. Chem., 2021, 93(34), 11654–11659 CrossRef CAS PubMed.
- T. Y. Wang, J. L. Rukundo, A. T. H. Le, N. A. Ivanov, J. C. Y. Le Blanc, B. I. Gorin and S. N. Krylov, Transient Incomplete Separation of Species with Close Diffusivity to Study the Stability of Affinity Complexes, Anal. Chem., 2022, 94(44), 15415–15422 CrossRef CAS PubMed.
- H. Cottet, J. P. Biron and M. Martin, On the optimization of operating conditions for Taylor dispersion analysis of mixtures, Analyst, 2014, 139(14), 3552–3562 RSC.
- N. N. Poulsen, N. Z. Andersen, J. Ostergaard, G. Zhuang, N. J. Petersen and H. Jensen, Flow induced dispersion analysis rapidly quantifies proteins in human plasma samples, Analyst, 2015, 140(13), 4365–4369 RSC.
- M. E. Pedersen, J. Ostergaard and H. Jensen, Flow-Induced Dispersion Analysis (FIDA) for Protein Quantification and Characterization, Methods Mol. Biol., 2019, 1972, 109–123 CrossRef CAS PubMed.
- H. Jensen and J. Ostergaard, Flow induced dispersion analysis quantifies noncovalent interactions in nanoliter samples, J. Am. Chem. Soc., 2010, 132(12), 4070–4071 CrossRef CAS PubMed.
- T. M. Rasmus Norrild, Lars Boyens-Thiele ,Soumik Ray ,Joachim Mortensen ,Anatol Fritsch ,Juan Iglesias-Artola ,Louise Klausen ,Emil Stender ,Henrik Jensen ,Alexander Buell Taylor-dispersion induced phase separation for the efficient characterisation of protein condensate formation, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-1ztrt.
- S. Latunde-Dada, R. Bott, J. Crozier, M. Trikeriotis, O. I. Leszczyszyn and D. Goodall, Rapid determination of hydrodynamic radii beyond the limits of Taylor dispersion, J. Chromatogr. A, 2016, 1472, 66–73 CrossRef CAS PubMed.
- S. Latunde-Dada, R. Bott, K. Hampton and O. I. Leszczyszyn, Application of the Exact Dispersion Solution to the Analysis of Solutes beyond the Limits of Taylor Dispersion, Anal. Chem., 2015, 87(15), 8021–8025 CrossRef CAS PubMed.
- J. G. Garcia de la Torre and V. A. Bloomfield, Hydrodynamic properties of complex, rigid, biological macromolecules: theory and applications, Q. Rev. Biophys., 1981, 14(1), 81–139 CrossRef CAS PubMed.
- C. A. Royer, Probing protein folding and conformational transitions with fluorescence, Chem. Rev., 2006, 106(5), 1769–1784 CrossRef CAS PubMed.
- Protein Fluorescence, in Principles of Fluorescence Spectroscopy, ed. Lakowicz, J. R., Springer US, Boston, MA, 2006, pp. 529–575 Search PubMed.
- A. Sidhu, J. Vaneyck, C. Blum, I. Segers-Nolten and V. Subramaniam, Polymorph-specific distribution of binding sites determines thioflavin-T fluorescence intensity in alpha-synuclein fibrils, Amyloid, 2018, 25(3), 189–196 CrossRef CAS PubMed.
- S. A. Hudson, H. Ecroyd, T. W. Kee and J. A. Carver, The thioflavin T fluorescence assay for amyloid fibril detection can be biased by the presence of exogenous compounds, FEBS J., 2009, 276(20), 5960–5972 CrossRef CAS PubMed.
- M. Ziaunys, A. Sakalauskas and V. Smirnovas, Identifying Insulin Fibril Conformational Differences by Thioflavin-T Binding Characteristics, Biomacromolecules, 2020, 21(12), 4989–4997 CrossRef CAS PubMed.
- M. Biancalana and S. Koide, Molecular mechanism of Thioflavin-T binding to amyloid fibrils, Biochim. Biophys. Acta, 2010, 1804(7), 1405–1412 CrossRef CAS PubMed.
- L. Bousset, L. Pieri, G. Ruiz-Arlandis, J. Gath, P. H. Jensen, B. Habenstein, K. Madiona, V. Olieric, A. Bockmann, B. H. Meier and R. Melki, Structural and functional characterization of two alpha-synuclein strains, Nat. Commun., 2013, 4, 2575 CrossRef PubMed.
- J. Gath, L. Bousset, B. Habenstein, R. Melki, A. Bockmann and B. H. Meier, Unlike twins: an NMR comparison of two alpha-synuclein polymorphs featuring different toxicity, PLoS One, 2014, 9(3), e90659 CrossRef PubMed.
- B. Eymsh, A. Drobny, T. R. Heyn, W. Xiang, R. Lucius, K. Schwarz, J. K. Keppler, F. Zunke and P. Arnold, Toxic Metamorphosis-How Changes from Lysosomal to Cytosolic pH Modify the Alpha-Synuclein Aggregation Pattern, Biomacromolecules, 2020, 21(12), 4673–4684 CrossRef CAS PubMed.
- A. M. Streets, Y. Sourigues, R. R. Kopito, R. Melki and S. R. Quake, Simultaneous measurement of amyloid fibril formation by dynamic light scattering and fluorescence reveals complex aggregation kinetics, PLoS One, 2013, 8(1), e54541 CrossRef CAS PubMed.
- C. L. Shen, G. L. Scott, F. Merchant and R. M. Murphy, Light scattering analysis of fibril growth from the amino-terminal fragment beta(1-28) of beta-amyloid peptide, Biophys. J., 1993, 65(6), 2383–2395 CrossRef CAS PubMed.
- F. De Giorgi, F. Laferriere, F. Zinghirino, E. Faggiani, A. Lends, M. Bertoni, X. Yu, A. Grelard, E. Morvan, B. Habenstein, N. Dutheil, E. Doudnikoff, J. Daniel, S. Claverol, C. Qin, A. Loquet, E. Bezard and F. Ichas, Novel self-replicating alpha-synuclein polymorphs that escape ThT monitoring can spontaneously emerge and acutely spread in neurons, Sci. Adv., 2020, 6(40), eabc4364 CrossRef CAS PubMed.
- V. N. Uversky, The alphabet of intrinsic disorder: II. Various roles of glutamic acid in ordered and intrinsically disordered proteins, Intrinsically Disord. Proteins, 2013, 1(1), e24684 CrossRef PubMed.
- V. Vacic, V. N. Uversky, A. K. Dunker and S. Lonardi, Composition Profiler: a tool for discovery and visualization of amino acid composition differences, BMC Bioinf., 2007, 8, 211 CrossRef PubMed.
- M. Shahnawaz, A. Mukherjee, S. Pritzkow, N. Mendez, P. Rabadia, X. Liu, B. Hu, A. Schmeichel, W. Singer, G. Wu, A. L. Tsai, H. Shirani, K. P. R. Nilsson, P. A. Low and C. Soto, Discriminating alpha-synuclein strains in Parkinson's disease and multiple system atrophy, Nature, 2020, 578(7794), 273–277 CrossRef CAS PubMed.
- T. Strohaker, B. C. Jung, S. H. Liou, C. O. Fernandez, D. Riedel, S. Becker, G. M. Halliday, M. Bennati, W. S. Kim, S. J. Lee and M. Zweckstetter, Structural heterogeneity of alpha-synuclein fibrils amplified from patient brain extracts, Nat. Commun., 2019, 10(1), 5535 CrossRef PubMed.
- W. Hoyer, T. Antony, D. Cherny, G. Heim, T. M. Jovin and V. Subramaniam, Dependence of alpha-synuclein aggregate morphology on solution conditions, J. Mol. Biol., 2002, 322(2), 383–393 CrossRef CAS PubMed.
- S. A. M. Holec, S. L. Liu and A. L. Woerman, Consequences of variability in alpha-synuclein fibril structure on strain biology, Acta Neuropathol., 2022, 143(3), 311–330 CrossRef CAS PubMed.
- C. Peng, R. J. Gathagan, D. J. Covell, C. Medellin, A. Stieber, J. L. Robinson, B. Zhang, R. M. Pitkin, M. F. Olufemi, K. C. Luk, J. Q. Trojanowski and V. M. Lee, Cellular milieu imparts distinct pathological alpha-synuclein strains in alpha-synucleinopathies, Nature, 2018, 557(7706), 558–563 CrossRef CAS PubMed.
- M. Schweighauser, Y. Shi, A. Tarutani, F. Kametani, A. G. Murzin, B. Ghetti, T. Matsubara, T. Tomita, T. Ando, K. Hasegawa, S. Murayama, M. Yoshida, M. Hasegawa, S. H. W. Scheres and M. Goedert, Structures of alpha-synuclein filaments from multiple system atrophy, Nature, 2020, 585(7825), 464–469 CrossRef CAS PubMed.
- A. Peduzzo, S. Linse and A. K. Buell, The Properties of alpha-Synuclein Secondary Nuclei Are Dominated by the Solution Conditions Rather than the Seed Fibril Strain, ACS Chem. Neurosci., 2020, 11(6), 909–918 CrossRef CAS PubMed.
- A. K. Buell, P. Hung, X. Salvatella, M. E. Welland, C. M. Dobson and T. P. Knowles, Electrostatic effects in filamentous protein aggregation, Biophys. J., 2013, 104(5), 1116–1126 CrossRef CAS PubMed.
- K. E. Paleologou, A. W. Schmid, C. C. Rospigliosi, H. Y. Kim, G. R. Lamberto, R. A. Fredenburg, P. T. Jr Lansbury, C. O. Fernandez, D. Eliezer, M. Zweckstetter and H. A. Lashuel, Phosphorylation at Ser-129 but not the phosphomimics S129E/D inhibits the fibrillation of alpha-synuclein, J. Biol. Chem., 2008, 283(24), 16895–16905 CrossRef CAS PubMed.
- K. Kawahara and C. Tanford, Viscosity and density of aqueous solutions of urea and guanidine hydrochloride, J. Biol. Chem., 1966, 241(13), 3228–3232 CrossRef CAS PubMed.
- P. Arosio, T. P. Knowles and S. Linse, On the lag phase in amyloid fibril formation, Phys. Chem. Chem. Phys., 2015, 17(12), 7606–7618 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Figures and tables demonstrating additional experimental details and simulations (DOC). Supplementary video: COMSOL simulation of diffusive (D) and non-diffusive (ND) particles in FIDA (AVI). Supplementary python code: the script for the curve deconvolution using the global fitting (IPYNB). See DOI: https://doi.org/10.1039/d3sc05371g |
| ‡ Authors with equal contribution to the work. |
| This journal is © The Royal Society of Chemistry 2024 |