Open Access Article
Open Access ArticleLnDOTA puppeteering: removing the water molecule and imposing tetragonal symmetry†
Anna Schannong
Manvell‡
 a,
Rouven
Pfleger‡§
a,
Rouven
Pfleger‡§
 ab,
Niels Andreas
Bonde
ab,
Niels Andreas
Bonde
 ac,
Matteo
Briganti
ac,
Matteo
Briganti
 *d,
Carlo Andrea
Mattei
*d,
Carlo Andrea
Mattei
 d,
Theis Brock
Nannestad
d,
Theis Brock
Nannestad
 a,
Høgni
Weihe
a,
Høgni
Weihe
 a,
Annie K.
Powell
a,
Annie K.
Powell
 b,
Jacques
Ollivier
b,
Jacques
Ollivier
 c,
Jesper
Bendix
c,
Jesper
Bendix
 *a and
Mauro
Perfetti
*a and
Mauro
Perfetti
 *d
*d
aDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark. E-mail: jesper.bendix.chem@gmail.com
bInstitute of Inorganic Chemistry, Karlsruhe Institute of Technology, Engesserstrasse 15, 76131 Karlsruhe, Germany
cInstitut Laue-Langevin, 71 avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
dDepartment of Chemistry U. Schiff, Via della Lastruccia 3, 50019, Sesto Fiorentino, Italy. E-mail: matteo.briganti@unifi.it; mauro.perfetti@unifi.it
First published on 12th December 2023
Abstract
Complexes of lanthanide(III) ions (Ln) with tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetate (DOTA) are a benchmark in the field of magnetism due to their well-investigated and sometimes surprising features. Ab initio calculations suggest that the ninth ligand, an axial water molecule, is key in defining the magnetic properties because it breaks the potential C4 symmetry of the resulting complexes. In this paper, we experimentally isolate the role of the water molecule by excluding it from the metal coordination sphere without altering the chemical structure of the ligand. Our complexes are therefore designed to be geometrically tetragonal and strict crystallographic symmetry is achieved by exploiting a combination of solution ionic strength and solid state packing effects. A thorough multitechnique approach has been used to unravel the electronic structure and magnetic anisotropy of the complexes. Moreover, the geometry enhancement allows us to predict, using only one angle obtained from the crystal structure, the ground state composition of all the studied derivatives (Ln = Tb to Yb). Therefore, these systems also provide an excellent platform to test the validity and limitations of the ab initio methods. Our combined experimental and theoretical investigation proves that the water molecule is indeed key in defining the magnetic anisotropy and the slow relaxation of these complexes.
Introduction
The tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetic acid (H4DOTA) forms stable coordination compounds with almost all metal ions in the periodic table,1 and its complexes with lanthanide ions (Ln) are particularly studied due to their magnetic properties. Magnetic resonance imaging contrast agents based on LnDOTA·H2O are commercial and very efficient under both low2 and high3–5 magnetic fields. Moreover, the LnDOTA·H2O complexes are nowadays a benchmark in the field of molecular magnetism due to their well-investigated magnetic anisotropy6 and Single Molecule Magnet (SMM) properties.7–9 The two factors that rule the magnetic and the relaxometric responses are the magnetic anisotropy of the lanthanide ion and its coordination environment.5,10 In the case of LnDOTA·H2O (structure reported in Fig. 1a), the apically coordinated water molecule is the key ligand in determining the magnetic anisotropy. The hydrogen atoms of the water molecule make it a non-linear ligator in the angular overlap model formalism, disrupting the potential C4 symmetry of the DOTA ligand sphere. It was theoretically predicted11 that the water ligation is sufficient to remove the degeneracy in the carboxylic oxygen plane, and its orientation can magnetically favour only one direction (easy axis).6,8,12 Symmetry breakings are also important for SMM properties and can be detrimental for the slow relaxation, especially at low temperatures, where the quantum tunnelling (QT) process dominates.13 Moreover, the axial position of the oxygen atom of the water molecule reduces the equatorial character of the Crystal Field (CF) in the 9-coordinate complexes.14,15The rationalization of the magnetic anisotropy of these complexes was not easy to rationalize. The coordinated carboxylic oxygens are the main source of electrostatic field around the 4f orbitals, stabilizing |mJ〉 states with a “prolate” distribution of the electron density. Therefore, the states with the largest |mJ〉 projection are the most stabilised for the ions Er3+, Tm3+ and Yb3+, and an easy axis along the Ln–OH2 bond is observed. On the other side, for the ions with the largest |mJ〉 states displaying an “oblate” shape of the electron density, such as Tb3+ and Dy3+, an easy plane of magnetisation should have been observed. However, the asymmetry induced by the apical water molecule and the distortions of the DOTA ligand due to the bond network promoted by the counterions prevented the observation of this easy plane/easy axis trend along the whole series.6 In particular, for complexes with ions such as Dy3+, the ground state anisotropy is easy axis in the carboxylic plane but an easy plane-like magnetic anisotropy is recovered at higher temperatures, when excited states with nearly perpendicular easy magnetisation axes become populated.6 Also, the relative effects on the anisotropy of the asymmetries induced by the DOTA distortion (packing effects) and the water orientation were unclear, i.e., which were necessary and/or sufficient conditions to observe an easy plane behaviour in ions where the largest mJ values are associated with an oblate distribution of the electron density.
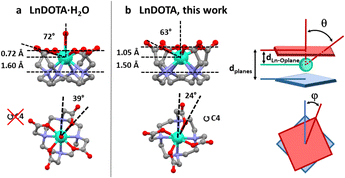 | ||
| Fig. 1 Structural comparison between (a) LnDOTA·H2O and (b) LnDOTA (this work). Angles and distances in the figure are averaged along the entire series. See Table S2† for individual values. dLn–Oplane: distance between the Ln ion and the plane formed by the coordinating oxygen atoms; θ: angle between the (pseudo)-C4 axis and the Ln–O(carboxylic) bonds; dplanes: distance between the planes formed by the oxygen and nitrogen atoms; φ: dihedral O–Ln–N angle. Colour code: Ln: aquamarine, O: red, N: blue, C: grey. H atoms, counterions and co-crystallised molecules were omitted for clarity. | ||
In this work we have successfully removed the water molecule from the metal coordination sphere and, at the same time, imposed rigorous tetragonal symmetry on seven LnDOTA complexes (Ln = Y and Tb to Yb) in the solid state. In order to isolate the influence of the symmetry on the magnetic anisotropy, we have performed an extensive magnetometric and spectroscopic characterization as well as ab initio calculations. We present here the experimental answers to two much debated questions: (I) Does removing the water molecule cause a change in anisotropy (easy axis to easy plane) in complexes with a lanthanide ion characterised by an “oblate” electronic shape for the largest mJ values (e.g. Tb3+ and Dy3+)? (II) Does the removal of the water molecule enhance the equatorial CF around the metal centre therefore boosting the slow relaxation for lanthanide complexes where the largest |mJ〉 states display a “prolate” distribution of the electron density (e.g. Er3+ and Yb3+)? Answering to these questions allows to investigate the magneto-structural correlations and the real nature of the lanthanide coordination bond by employing an observable that is purely originating from electrons in the 4f orbitals: the magnetic anisotropy.
Results and discussion
Synthesis and crystal structure
In literature, two routes towards exclusion of the apical water ligand in the solid state have been pursued. One approach has been the modification of the carboxylic arms of the DOTA ligand leading to tetragonal symmetry, at the cost of altering the CF.16–18 In other cases the DOTA ligand was kept unchanged, but in poorly symmetric environments generated by the dense network of intermolecular interactions.19–21Excluding the apical ligand from coordination in a complex where the DOTA ligand is unaltered and concurrently imposing tetragonal symmetry is a challenging task. The use of non-coordinating solvents under inert gas could appear a tempting strategy, however the solubility of the DOTA ligand and most lanthanide precursors can limit this synthetic route. As an alternative path, we have considered to act on the solution ionic strength. Indeed, studies on Ln3+ complexes with DOTA-like ligands in solution revealed that structure and metal coordination sphere are sensitive to variations of the ionic strength.22,23
Along the past years, the need of more effective contrast agents directed many efforts towards a better comprehension of the factors governing the water exchange rate (i.e. the equilibrium between the LnDOTA and the LnDOTA·H2O species).24 These complexes undergo an equilibrium in solution between Twisted Square Antiprismatic (TSA, N–Ln–O torsion angle < 30°) and Square Antiprismatic (SA, N–Ln–O torsion angle ca. 40°) diastereoisomers.23–26 Both forms were recently isolated also in the solid state.27 The water exchange rate is faster in the TSA isomers.24 Indeed, it seems to be facilitated by its interaction with the bulk water (outer sphere) which is stronger in the TSA form because the Ln3+ ion sinks into the DOTA pocket,19,27–29 making the Ln–OH2 bond longer (i.e. the interaction weaker). In fact, it has been suggested that the water exchange proceeds via a dissociative mechanism with an early transition state.19,30 Such a structural change can also be detected by looking at the isotropic shift values for complexes with paramagnetic ions.31 Subtle variations of enthalpy and entropy terms can govern the described isomeric and coordinative equilibrium28,32 that, for the purpose of this paper (i.e. removing the water molecule), must be shifted towards the TSA isomers. The high stability constants of lanthanide complexes with DOTA ligands allow for a reasonable comparison between solution and solid state situations.33 It was shown that higher ionic strength favours the TSA isomer over the SA isomer, but notably it was concluded that “This shift in equilibrium, which is entropy driven, does not result from the effect of low water activity on stabilizing species without inner sphere water […]”.23 This conclusion is of direct relevance to our goal. Indeed, it underlines the necessity for working at high ionic strength and combining lattice effects for stabilizing the desired 8-coordinate complexes.
Accordingly, the choice of counter ion(s) is central and only ions compatible with tetragonal packing are reasonable candidates. The solution behaviour of Ln(DOTA-like) complexes is dependent on the nature of the dissolved ions.23,34,35 For instance, strong Lewis acids such as fluoride anions can significantly alter the outer coordination sphere but are likely to bind the metal centre substituting to the water coordinated molecule.36–38 A good compromise seems to be offered by the use of the chloride anion which should prevent the coordination of any apical ligand.23
The combination of all the mentioned information has led us to the choice of Me4NOH as deprotonating agent and of Me4NCl as ionic strength enhancer. The Me4N+ cation is compatible with tetragonal symmetry and prevents the network of bonds that leads to symmetry breakings in, e.g., Na[LnDOTA·H2O] complexes.8,9 At the same time, the Cl− counterion does not coordinate to the metal ion.23 By using ionic strength and packing effects as “threads of a puppeteer”, we have developed a synthetic protocol able to remove a player from the scene and produce crystalline 8-coordinated [Ln(DOTA)]− complexes in decent yield (30–40%).
In a typical synthesis, 4 equivalents of Me4NOH were added to a water solution of H4DOTA and the lanthanide chloride salt. After filtration, 10.5 equivalents of Me4NCl were added and the resultant solution was allowed to slowly concentrate at ca. 50 °C. After few hours to few days needle shaped crystals suitable for single crystal X-ray diffraction studies were obtained. More details about the synthesis are reported in ESI.†
All derivatives crystallise in the P4bm space group with the general formula [Me4N][LnDOTA]·2Me4NCl·5H2O (Ln = Y, Tb, Dy, Ho, Er, Tm, Yb). In Fig. S1† we reported the powder X-ray diffractograms for the whole series. From now on we will refer to the complexes with the symbol of the lanthanide ion in bold. The principal symmetry axis of the structure (C4) passes through the lanthanide, making the complexes rigorously tetragonal. Details about the metrics of the complexes are reported in Table S1.† Here, we examine some relevant structural parameters to assess how the absence of the apical water molecule from the metal coordination sphere changes the CF around the Ln3+ ion. The formal removal of the water molecule impacts three main geometrical parameters showed in Fig. 1. We will discuss all of them using angles and distances averaged along the entire series, while exact values for each structure are reported in Table S2.† (I) The Ln3+ ion sinks inside the macrocyclic cavity: this can be seen by the increase in the distance (dLn–Oplane in Fig. 1) between the Ln ion and the plane formed by the coordinating oxygen atoms (ca. 1.05 Å vs. 0.72 Å) as well as by the smaller angle (θ in Fig. 1) between the (pseudo)-C4 axis and the Ln–O(carboxylic) bonds (ca. 63° vs. 72°). (II) The molecular packing increases the distance (dplanes in Fig. 1) between the planes formed by the oxygen and nitrogen atoms, respectively, by approximately 10% and (III) the dihedral O–Ln–N angle (φ in Fig. 1) gets reduced to 24° (39° in LnDOTA·H2O). All structural information indicate that the compounds are isolated as TSA diastereoisomers. In the following paragraphs we will show the impact that these modifications have on the electronic structure and magnetic properties of the complexes.
Electronic structure and magnetic properties
The electronic structure and magnetic properties have been unravelled using a combined spectroscopic and magnetometric study. The energy level structure has been experimentally investigated by combining Inelastic Neutron Scattering (INS), Luminescence, and Electron Paramagnetic Resonance (EPR). The magnetometric characterization has been performed using dc and ac measurements.All spectroscopic and magnetometric data for each anisotropic complex have been merged using a single home-written MATLAB programme based on EASYSPIN39 and the MINUIT minimization subroutine.40 to conduct a global fit using a Hamiltonian containing a Crystal Field and a Zeeman term:
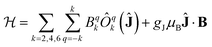 | (1) |
The C4 molecular symmetry allows to restrict the number of CF parameters from 27 to 7: three diagonal parameters (B02, B04 and B06), and four off-diagonal parameters (B44, B−44, B46 and B−46). A rotation of the reference frame can be used to set one of the out of diagonal parameters to zero, therefore we decided to set B−44 = 0 reducing the number of fitted parameters to 6.
As initial guess we have used the CF parameters calculated ab initio and reported in Table S3.† Computational details about the ab initio calculations are reported in ESI.† The values of the CF parameters extracted from the fit are given in Table S4.† Noticeably, the parameters have the same sign (in Wybourne notation) for all the studied derivatives, as expected for an isostructural series. The fitted parameters and the simulated electronic structure allowed us to extract a coherent picture of all the data from the different experimental techniques, as discussed below.
INS has been used several times to study the energy level structure of lanthanide complexes of relevance in molecular magnetism.41 In order to have a broad view of the electronic structure along the series we have studied Tb, Dy, Ho and Er. In Fig. 2 we reported the scattering function S(Q,ω) recorded at T = 1.6 K and with an incident neutron wavelength λ = 4.8 Å. The scattering function is the Fourier transform in space and time of the time-dependent pair correlation function. This function contains all the necessary information from an INS experiment. The Q-dependence of S(Q,ω) is related to the structure, i.e. where atoms or electron density is; the ω-dependence gives information about dynamics. Yellow spots correspond to signals (see Table 1). The energy resolution broadening of the neuron spectra does not allow a direct discrimination of the components. This has been made through an appropriate fit. Q-Cuts evidencing the magnetic peaks are reported in Fig. S2–S5.† We have identified 2 peaks for Tb, one for Dy and three for Ho, while Er was silent. Both the ab initio calculations and experimental fit reproduce these observations very well, as reported in Table 1.
 | ||
| Fig. 2 Scattering function S (Q,ω) plots recorded at T = 1.6 K and λ = 4.8 Å for Tb, Dy, Ho and Er. The black arrows indicate the magnetic transitions. | ||
| E/cm−1 | Exp | Fit | Ab initio |
|---|---|---|---|
| Tb | 2.5–9.5 | 7.45 | 6.9 |
| 10–14 | 11.5* | 8* | |
| Dy | 10–11.6 | 10.0 | 13.6 |
| Ho | 0–4 | 3.05* & 3.7 | 0.3 |
| 5–8 | 9.30* | 1.3 | |
| 12–14 | 13 | 21 | |
| Er | — | — | — |
All derivatives have been investigated using luminescence spectroscopy at 77 K to reveal the CF splitting of the ground multiplet. Only Tb and Dy exhibited resolved luminescence spectra. For both derivatives well-resolved transitions to the ground state could be observed (Fig. S6–S9†). The barycentre of the visible excited states is reported in Tables S5 and S6.† The energy levels extracted from ab initio and experimental fit are reported on top of the experiments in Fig. S6 and S9† and are in agreement with the experimental results. It is interesting to notice that both compounds show low lying excited states, as expected from the equatorial nature of DOTA ligand.
The magnetically diluted versions of all the Kramers derivatives (molar ratio ca. Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln = 98
Ln = 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) were also investigated using low temperature EPR spectroscopy to gain information about the ground state composition. The results are reported in Table 2 and Fig. S10–S12.† The anisotropy of the ground doublet is easy plane for YDy and easy axis for YEr and YYb. Both for Er and Yb, however, large transversal g-factors are observed. Both the ab initio calculations and the experimental fit are in excellent agreement with the experiments. Table S7† contains other parameters extracted from the fitting, such as the hyperfine couplings.
2) were also investigated using low temperature EPR spectroscopy to gain information about the ground state composition. The results are reported in Table 2 and Fig. S10–S12.† The anisotropy of the ground doublet is easy plane for YDy and easy axis for YEr and YYb. Both for Er and Yb, however, large transversal g-factors are observed. Both the ab initio calculations and the experimental fit are in excellent agreement with the experiments. Table S7† contains other parameters extracted from the fitting, such as the hyperfine couplings.
| Ground g components (g⊥, g∥) | |||
|---|---|---|---|
| Exp | Fit | Ab initio | |
| YDy | 9.46, — | 9.97, 1.03 | 10.1, 0.573 |
| YEr | 3.52, 11.58 | 3.51, 12.3 | 3.37, 11.938 |
| YYb | 2.89, 4.22 | 2.90, 4.26 | 2.82, 4.34 |
Dc magnetometric measurements have been performed on all derivatives. The shape of the χT vs. T plots is characteristic of Ln complexes. In all samples, the decrease observed in all samples at low temperature can be attributed to the depopulation of the CF levels. The room temperature χT values are close to the Curie constant for all derivatives except Tm and Yb (5.5 vs. 7.15 and 1.88 vs. 2.57 emu K mol−1 for Tm and Yb, respectively), suggesting a significantly larger CF splitting of these two derivatives compared to the others (see Table S8†). Interestingly, none of the LnDOTA·H2O complexes showed such a low value of the χT at room temperature.6 While the experiments and fitting result are in excellent agreement (Fig. 3a, see also Fig. S13† for separate plots) the ab initio calculations fail in reproducing the relatively low room temperature χT value of Tm and Yb (see Fig. S14†). The reason for this discrepancy must be attributed to an underestimation of the total CF splitting. This is immediately evident by comparing the energy level splitting of all the studied derivatives (Fig. S15†). Tables S9–S14 and S15–S21† report the energy levels and their composition for fit and ab initio, respectively. In order to quantify the discrepancy between ab initio and fitting, we have calculated the CF strength:42,43
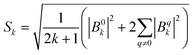 | (2) |
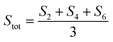 | (3) |
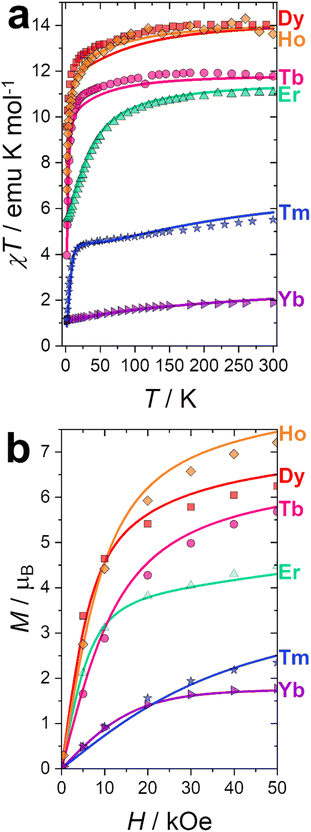 | ||
| Fig. 3 (a) χT vs. T experimental curves (symbols) and best fits (solid lines) obtained at H = 1000 Oe. (b) Magnetisation curves (symbols) and best fit (solid lines) obtained at T = 2 K. | ||
The CF strengths are reported in Fig. S16 (fit) and S17 (ab initio).† As expected, the value of the Tm total CF strength (Stot, reported in Fig. S16†) obtained from the experimental fit is the highest along the series, while the one extracted ab initio is comparable with the others (Fig. S17†).
Our CF analysis suggests that Tm should retain a significant fraction of its low temperature anisotropy even at room temperature. We have calculated the room temperature anisotropy of the magnetic susceptibility (Δχ = χpar − χperp) at H = 0.1 T and normalized it for the T = 2 K value. Tm retains 2% of its low temperature susceptibility anisotropy, more than 3.5 times the average normalized Δχ for the other derivatives (0.55%).
Magnetisation curves at T = 2 K were recorded for all derivatives and reported in Fig. 3b. Curves at other temperatures are reported in Fig. S18 (fit) and S19 (ab initio).† Also in this case, the experiments and fitting result are in excellent agreement. The ab initio computed magnetization curves are in fair agreement with the experimental data for Kramers ions while we see a larger deviations for non-Kramers ions (Fig. S19†). This is not surprising: non-Kramers ions possess, for this series, singlet ground states, therefore small differences in the eigenvalue of the first excited state could cause dramatic changes in the shape and magnitude of the magnetization curves. Interestingly, adding the 8th order CF parameters, usually neglected, improves the agreement between experiments and theory. This is especially significant for Tb (see Fig. S20†). The necessity to employ operators with order higher than 6 is an indication that the CF approximation is not entirely valid for Tb, and some degree of covalency should be considered, i.e., the 4f-ligand coordination bond is not a purely electrostatic interaction.44,45 This finding is also in agreement with the observed reduction of the covalency in the 4f coordination bond along the series, as computed through the electronic and relativistic nephelauxetic effects (see next section).
Anisotropy of the complexes
The results of the experimental fit and the ab initio calculations allow us to describe in detail the anisotropy of these complexes. Fig. 4 represents the low temperature low field magnetic susceptibility calculated for Dy and Er (as representatives of complexes with ions where the electron density of the states with the largest |mJ〉 projections displays an oblate or prolate distribution, respectively). The DOTA ligand alone acts as a textbook equatorial ligand: ions such as Tb3+, Dy3+ and Ho3+ show easy plane anisotropy, while the ions Er3+, Tm3+ and Yb3+ display easy axis anisotropy. This is evident from the g values obtained from EPR (see Table 2). Moreover, the low temperature magnetic anisotropy type is maintained, for these derivatives, up to room temperature at all fields. The situation was different in the LnDOTA·H2O derivatives, where the low temperature and high temperature magnetic anisotropy did not coincide for some derivatives.6 We can conclude that the tetragonal geometry stabilizes a well-defined type of anisotropy for all derivatives at all experimental conditions.The mJ compositions of the states reported in Tables S9–S14† (fitted) and Tables S15–S21† (ab initio) corroborates the overall equatorial nature of the DOTA ligand: the states with the largest mJ components are the highest in energy for Tb, Dy and Ho, while they are the ground or first excited ones for Er, Tm and Yb.
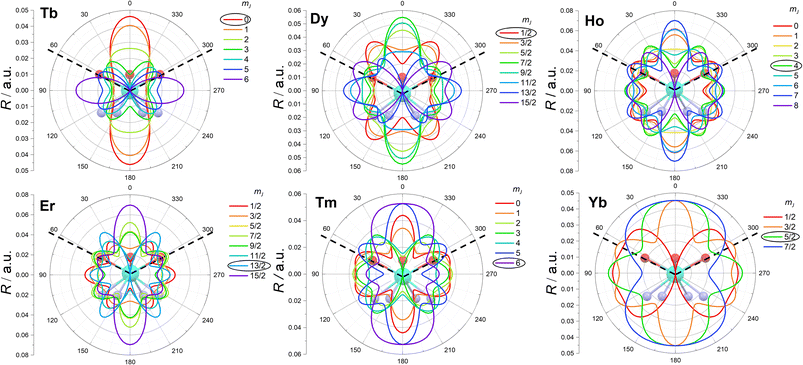
The enhanced symmetry achieved thanks to the absence of the water molecule renders the studied compounds sufficiently simple for a meaningful analysis of the electron density of each mJ state.15Ab initio calculations on the LnDOTA·H2O systems have revealed that the nitrogen ligators of the macrocyclic ligand do not contribute significantly to the ligand field, compared to the highly charged carboxylic oxygen atoms.11 In the hypothesis of low tetragonal mixing, we argue that the mJ state with less electron density at ca. 63° (the θ angle in Fig. 1, see also Table S2†) should be the most stabilized. This analysis can be seen as a simpler version of the electrostatic models proposed by Baldovì,46 Chilton12 and Jiang,47 and a more refined approach compared to the one proposed by Rinehart and Long.14
In Fig. 5 we report a polar plot of the mJ states superimposed to the chemical structure of the complexes. The dotted lines represent the position of the carboxylic ligators. In the second column of Table 3 we report the result obtained from this model. Considering the gross assumption of negligible wave functions mixing, and negligible contribution of the N atoms, the model provides excellent agreement with both experiments and theory. The model correctly predicts the main contribution to the ground state obtained from the fit for all derivatives. However, the results of our analysis disagree with the ground state composition predicted by ab initio calculations for Dy and Ho. In both cases, the disagreement can be explained considering that in these ions several mJ states provide very similar charge density at the selected angle (see Fig. S21†). For example, the states with mJ = 3/2 and 1/2 of Dy provide almost equal contributions.
| Charge density | Fit | Ab initio | |
|---|---|---|---|
| Tb | 0 | 0 | 0 |
| Dy | 1/2 | 1/2 | 3/2 |
| Ho | 4 | 4 | 2 |
| Er | 13/2 | 13/2 | 13/2 |
| Tm | 6 | 6 | 6 |
| Yb | 5/2 | 5/2 | 5/2 |
Since our electrostatic model and the results of the global fit of the experiments were completely compatible, we also analysed the composition of the other states. Notably, our simple model also correctly identifies the composition of the first excited state of all derivatives. Even more impressively, the entire mJ ladder can be correctly predicted for Tm and Yb.
An insight on this scenario comes from the analysis of the electronic structure within the framework of the ab initio ligand field theory (AILFT).48 Using this approach, we evaluated the covalent contribution to the 4f coordination bonding. Since the CASSCF methodology is known to underestimate ligand field parameters, the outcomes of the AILFT calculations cannot be interpreted as a quantitative result but, despite its limitations, they provide qualitative trends of covalency along the lanthanide series.49 The contribution of the 4f orbitals to the coordination bond can be assessed through the electronic and relativistic nephelauxetic effects.50 The first one is the reduction of the 4f interelectronic repulsion (Racah E3 parameter) with respect to the free ion, that arises from the expansion of the 4f electronic cloud due to the orbital hybridization with the ligands. Analogously, the relativistic nephelauxetic effect is the reduction of the spin–orbit coupling ζ, which is also a radial expansion effect akin to the 4f orbital hybridization with the ligands upon complex formation.51 The analysis of both quantities shows the same trend (see Table S22†): the computed nephelauxetic ratios with respect to the free ion for both E3 and ζ parameters increase for the late lanthanides, and this reduction in covalency is practically linear as a function of the Z atomic number. This means that the nephelauxetic effect is more pronounced for early lanthanide ions, suggesting a higher degree of covalency in the bonds. This trend is in agreement with previous studies where the same trend has been observed,52 and is also coherent with the previous study by some of us on [Dy(DOTA)H2O]−, where a covalent contribution has been computed for the Dy–H2O bond, i.e. around 25%.11 However, it is worth stressing that this analysis is purely based on the magnetic/spectroscopic properties arising from the electrons in the 4f orbitals. Summarizing, since only the 4f electrons are included in the active space in the multiconfigurational calculation, this shows how the 4f shell alone contributes to the lanthanide coordination bonds. A complete view of the covalency trends along the group could be computed only when including inside the active space the 5d and 6s shells, whose contribution to the metal–ligand bonding is not negligible. Since the model that we have developed in this paper is based on electrostatic considerations, we expect high accuracy for late lanthanides and some discrepancies for ions where the shape of the states with the largest |mJ〉 projections is oblate, as observed.
These considerations suggest that a refinement of the simple electrostatic model presented in this paper (Fig. 5) by including a correction with some degree of covalency could be a simple yet powerful tool for the prediction of eigenvectors in lanthanide complexes, with the additional advantage of being computationally inexpensive.
It appears now interesting to discuss if the anisotropy change compared to the LnDOTA·H2O species is here caused by the water removal, by the symmetry enhancement or by both effects combined. Sample ab initio calculations on DyDOTA·H2O have shown that an hypothetical removal of the water molecule without any geometric alteration would still produce a markedly easy axis anisotropy.11 Moreover, we have also performed ab initio calculations keeping unaltered the structure of the symmetric DyDOTA and adding a water molecule in apical position (Dy+H2O model). The Dy–O bond length and Dy-O-H angles were set to the values found for the optimized structure of the asymmetric DyDOTA·H2O. The computational results (Table S23†) show that even the small perturbation induced by the water's H atoms produce a marked easy axis anisotropy (gzca. 17) of the ground and first excited doublet. Both the easy axis of the ground and of the first excited state now lie in the carboxylic plane and they are almost perpendicular to each other (87.5°). We can conclude that both the removal of the water molecule and the symmetry enhancement are necessary conditions to observe the ideal behaviour expected in an equatorial CF for an ion where the largest |mJ〉 state projection is depicted by an oblate distribution of the electron density.
Single molecule magnet behaviour
The LnDOTA·H2O derivatives show a systematic magnetic behaviour along the series: only Kramers ions exhibit in-field SMM behaviour.6,9 DyDOTA·H2O shows also a fast QT-driven relaxation (τ ≈ 5 10−6 s) in zero applied field.7 In principle, a simple removal of the apical water molecule (without any structural change) should increase the relaxation times of thermally activated processes in ions where the states with the larger and smaller |mJ〉 projections show a prolate and oblate electron distribution, respectively. In contrast, ions characterised by an oblate shape for those states with the larger |mJ〉 projections and a prolate electron distribution for the states with smaller |mJ〉 projections should ideally not display any slow relaxation. However, our structural analysis has evidenced that the position of the lanthanide ion inside the macrocyclic cavity is perturbed by the absence of coordinating water (i.e. the metal ion sinks inside the cavity). The innermost location of the Ln3+ ion in the DOTA ligand cavity gives rise to a less equatorial charge disposition of the oxygen atoms around the metal ion. Such structural modification of the Ln3+ ion coordination environment results in an electron density arrangement that overall affects the slow magnetisation dynamic of ions such as Er3+ and Yb3+ (i.e. prolate electron distribution for the states with the larger |mJ〉 projections) in a more subtle way compared to the naive hypothesis of perfect equatorial character of the ligand. At the same time, the symmetrisation of the structure should slow down QT for all derivatives.13 The slow relaxation must be therefore interpreted as the result of the subtle balance between these effects.The ions of the series where the states with an oblate electron distribution is associated to the larger |mJ〉 projections did not show any significant fraction of slowly relaxing molecules, as expected. The main relaxation process for all these derivatives was QT. Ac measurements on these systems are reported in the ESI (Fig. S22–S29†).
No zero-field signal could be detected in the investigated frequency window for complexes containing lanthanide ions displaying a prolate shape of the states with the larger |mJ〉 projections. This result is expected for Tm since the symmetry causes mixing of the mJ = +6 and −6 states in third order, effectively removing the degeneracy and stabilizing a singlet ground state. Conversely, the absence of zero field relaxation might seem counterintuitive for Er and Yb. However, due to the metal ion sinking, the oxygen atoms of the carboxylic groups are less equatorial in our system compared to the hydrated complex. As reported in Table 3, the ground states of neither Er nor Yb are dominated by the highest mJ projection.
The application of a magnetic field slows down the relaxation in both Er and Yb. The relaxation times were extracted from the concomitant fit of the in-phase and out-of-phase magnetic susceptibility components using an extended Debye model. The field and temperature dependence of the relaxation times were fitted using the following equation.53,54
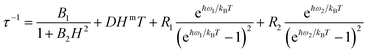 | (4) |
The four terms in eqn (4) refer to QT, direct process, and two Raman processes, respectively.54 For each derivative we have minimized the number of fitting parameters by setting to zero the less relevant ones in the equation (vide infra).
A field scan at T = 2 K reveals that Er has a complex relaxation pathway, with multiple allowed relaxation processes (Fig. S30†). Attempts in fitting the experimental data did not provide any reasonable estimation of the relaxation time because the maxima are outside the experimental frequency window. At H = 1000 Oe one dominant relaxation process is present. This external applied field was chosen to study the dynamic magnetic behaviour of Er at different temperatures (Fig. S31†). The shift of the peak towards high frequencies with increasing the temperature is indicative of the thermally activated nature of the process. Also the values of the relaxation time distribution (α, Fig. S32†) are moderate and decrease with increasing temperature, as observed for thermally activated processes. Indeed, the application of a fit procedure combining a direct mechanism and one Raman process (i.e. the second and third terms in eqn (4)) produces values in good agreement with the experiments (see Fig. S33†). The best fit values are: D = 1.35(1) s−1 K−1 Oe−m, m = 1.0(1), R1 = 1.57(4) × 105 s−1, ω1 = 13(1) cm−1. The value of the frequency is in agreement with previously reported values for lanthanide Single Ion Magnets (SIMs), where the lowest in energy vibrations at Γ are the main driver of the Raman relaxation.53,55 The quality of the fit was not significantly improved by inclusion of QT and/or an Orbach process (with an effective barrier fixed to the energy value of the first excited state). It should be noted that the field dependence of the direct process is here linear, while usually a higher exponent is observed.56
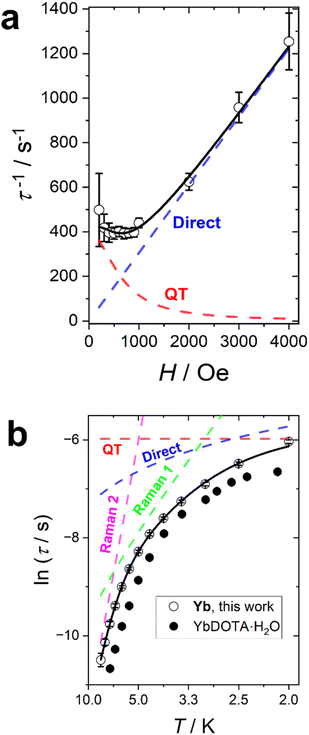
The Yb complex also shows an in-field SMM behaviour. A field scan at T = 2 K reveals a single identifiable relaxation process for applied fields below 4000 Oe (Fig. S34†). The application of higher fields produces a dramatic increase of the distribution of the relaxation times suggesting the presence of multiple relaxation processes. Since the measurements were taken at T = 2 K, the field dependence of the relaxation rate was fitted with a combination of QT and direct processes (the only ones significant at such low temperature) as reported in Fig. 6a. The best fit yields: B1 = 394(31) s−1, B2 = 2.4(5) × 10−6 Oe−2, D = 0.153(3) s−1 K−1 Oe−m and m = 1.0(1). As for Er, the field dependence of the direct process is linear.
We have performed a temperature scan at the optimum field of H = 1000 Oe (Fig. S35†). As for Er, the α values, reported in Fig. S36,† are rather small in the entire temperature range, suggesting a thermally activated process. The temperature dependence of the slow relaxation (Fig. 6b) has been fitted by fixing all the terms obtained in the field scan and adding two Raman terms. Therefore, our fit included four free parameters: the weights (R1 and R2) and the energies of the phonons (ω1 and ω2) of the Raman processes. The best fit was obtained with R1 = 3.57(0.73) × 105 s−1, R2 = 2.37(1.37) × 107 s−1, ω1 = 9.5(5) cm−1, ω2 = 38(3) cm−1. The lowest frequency is very close to the one found for Er, as expected from the isostructural nature of the whole series. In this case, however, it is important to note that a single Raman process was not sufficient to reasonably reproduce the experimental data. Moreover, the inclusion of an Orbach term (with the effective barrier fixed to the gap between the ground and the first excited state obtained either from fit or ab initio) did not produce reasonable results.
It is interesting to notice that the relaxation time recorded for Yb is consistently longer than the one of its hydrated congener (Fig. 6b), while the opposite is true for Er (see Fig. S33†). We note that the optimization of relaxation times in lanthanide SMMs often is challenged by concurrent variations in electron density shape and ion size. With dominating Raman relaxation mechanisms the stiffening of the complexes with the smaller central ions provide reason for the observed variation, although the subtle balance between the removal of the water molecule (axiality increasing) and the sinking of the ion inside the cavity (axiality decreasing) need to be considered in the temperature and field regimes influenced by thermally activated relaxation. Table 4 summarizes the main relaxation mechanisms and optimal fields for all the studied derivatives.
| H/Oe | Slow relaxation process | Fast relaxation process | |
|---|---|---|---|
| Dy | 5000 | QT | QT |
| Ho | 4000 | QT | QT |
| Er | 1000 | Direct + Raman | |
| Yb | 1000 | QT + direct + Raman | |
Conclusions
In this paper we reported the synthesis, experimental characterization and modelling of seven strictly tetragonal new complexes in which the DOTA ligand coordinates a single lanthanoid ion without the presence of the usual apical water molecule. The preparation of the samples does not require dry conditions, but instead was conducted using water as a solvent: the modulation of the solution ionic strength was the key for isolating the complexes without any water molecule in the metal coordination sphere.Such a formal removal of the coordinated water, compared to the previous LnDOTA·H2O examples, causes a sinking of the Ln3+ ion inside the DOTA cavity that has a strong impact on the magnetic properties. The room temperature values of the χT product significantly deviate from the Curie constants for Tm and Yb, suggesting surprisingly large CF splittings for these ions. Our combined spectroscopic, computational, and magnetometric study shows that removing the apical water molecule and enhancing the symmetry changes from easy axis to easy plane the magnetic anisotropy of complexes where the lanthanide ion displays an oblate electronic shape of the states with the larger |mJ〉 projections (Tb, Dy and Ho). The high symmetry of our systems was also used to correctly predict the ground state composition of all anisotropic derivatives by using a simple electrostatic model based on the electron densities of the mJ states. However, this study shed further light on the subtle coexistence of covalent and electrostatic contributions in the lanthanide coordination bond. The covalent contribution cannot be completely neglected, although it becomes progressively less relevant along the series.
As a consequence of the Ln3+ ion innermost location in the DOTA ligand cavity, the oxygen atoms generate a less equatorial field around the metal ion. Therefore, the new Ln3+ ion coordination environment provides an electron density arrangement that modulates the slow magnetisation dynamic of ions such as Er3+ and Yb3+ (i.e. prolate and oblate electron distribution for the states with the larger and smaller |mJ〉 projections, respectively) in a more complex way compared to the assumption of an ideal equatorial character of the ligand. In particular, the slow relaxation is faster in Er and slower in Yb compared to their LnDOTA·H2O congeners. In the context of the use of these systems in relaxometry studies, the moderate and opposed effects on the magnetic relaxation of removing the axial water for Yb and Er could be interesting and potentially exploitable.
Author contributions
MP and JB designed the project. AM, RP, CAM, AKP and JB performed the synthetic procedures. AM, MP and HW performed the EPR characterization and modelling. NB, MP, JB and JO performed the INS measurements and modelling. MB performed the ab initio calculations. TBN and AM performed the luminescence measurements. AM, JB and MP performed the magnetic characterization and modelling. The manuscript was written by MP and CAM with inputs from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funded by the European Union (ERC, ELECTRA, 101039890). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The financial support provided by the MUR – Dipartimenti di Eccellenza 2023-2027 (DICUS 2.0) to the Department of Chemistry “Ugo Schiff” of the University of Florence is acknowledged. RP and AKP acknowledge the Karlsruhe House of Young Scientists (KHYS) for the Research Travel Grant and the Networking Grant and the German Research Foundation (DFG) Collaborative Research Centre (CRC) 1573 "4f for Future".References
- N. Viola-Villegas and R. P. Doyle, Coord. Chem. Rev., 2009, 253, 1906–1925 CrossRef CAS.
- D. G. Mitchell, J. Magn. Reson. Imaging, 1997, 7, 1–4 CrossRef CAS PubMed.
- T. C. Soesbe, J. Ratnakar, Z. Kovacs and A. D. Sherry, J. Am. Chem. Soc., 2013, 135(40), 14904–14907 CrossRef PubMed.
- T. C. Soesbe, S. J. Ratnakar, M. Milne, S. Zhang, Q. N. Do, Z. Kovacs and A. D. Sherry, Magn. Reson. Med., 2014, 71, 1179–1185 CrossRef CAS PubMed.
- D. Cicolari, F. Santanni, L. Grassi, F. Brero, M. Filibian, T. Recca, P. Arosio, M. Perfetti, M. Mariani, R. Sessoli and A. Lascialfari, J. Chem. Phys., 2021, 155, 214201 CrossRef CAS PubMed.
- M. Briganti, E. Lucaccini, L. Chelazzi, S. Ciattini, L. Sorace, R. Sessoli, F. Totti and M. Perfetti, J. Am. Chem. Soc., 2021, 143, 8108–8115 CrossRef CAS PubMed.
- P. E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751–3753 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- M. E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 125, 368–372 CrossRef.
- D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, Acc. Chem. Res., 2020, 53, 1520–1534 CrossRef CAS PubMed.
- M. Briganti, G. F. Garcia, J. Jung, R. Sessoli, B. Le Guennic and F. Totti, Chem. Sci., 2019, 10, 7233–7245 RSC.
- N. F. Chilton, D. Collison, E. J. McInnes, R. E. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 CrossRef PubMed.
- M. A. Sørensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolomé, G. G. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolomé, S. Piligkos, H. Weihe, L. H. Doerrer, J. van Slageren, H. M. Rønnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1292 CrossRef PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J. Sievers, Z. Phys. B: Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- H. Nakai, J. Seo, K. Kitagawa, T. Goto, K. Nonaka, T. Matsumoto and S. Ogo, Inorg. Chem., 2016, 55, 6609–6615 CrossRef CAS PubMed.
- R. Janicki, A. Kędziorski and A. Mondry, Phys. Chem. Chem. Phys., 2016, 18, 27808–27817 RSC.
- F. Avecilla, J. A. Peters and C. F. Geraldes, Eur. J. Inorg. Chem., 2003, 2003, 4179–4186 CrossRef.
- F. Benetollo, G. Bombieri, L. Calabi, S. Aime and M. Botta, Inorg. Chem., 2003, 42, 148–157 CrossRef CAS PubMed.
- P. Thuéry, CrystEngComm, 2009, 11, 2319–2325 RSC.
- R. Janicki and A. Mondry, Dalton Trans., 2019, 48, 3380–3391 RSC.
- M. Marques, C. Geraldes, A. Sherry, A. E. Merbach, H. Powell, D. Pubanz, S. Aime and M. Botta, J. Alloys Compd., 1995, 225, 303–307 CrossRef CAS.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. Geraldes, D. Pubanz and A. E. Merbach, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- P. Caravan, D. Esteban-Gómez, A. Rodríguez-Rodríguez and C. Platas-Iglesias, Dalton Trans., 2019, 48, 11161–11180 RSC.
- S. Aime, A. Barge, M. Botta, A. S. De Sousa and D. Parker, Angew. Chem., Int. Ed., 1998, 37, 2673–2675 CrossRef CAS PubMed.
- D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. Howard, Chem. Rev., 2002, 102, 1977–2010 CrossRef CAS PubMed.
- M. S. Thomsen, S. Parsons and T. J. Sørensen, Dalton Trans., 2022, 51, 15725–15733 RSC.
- L. Di Bari and P. Salvadori, ChemPhysChem, 2011, 12, 1490–1497 CrossRef CAS PubMed.
- M. S. Thomsen, H. O. B. Andersen and T. J. Sørensen, Dalton Trans., 2022, 51, 14118–14124 RSC.
- D. Parker, H. Puschmann, A. S. Batsanov and K. Senanayake, Inorg. Chem., 2003, 42, 8646–8651 CrossRef CAS PubMed.
- R. S. Dickins, D. Parker, J. I. Bruce and D. J. Tozer, Dalton Trans., 2003, 1264–1271 RSC.
- M. Botta, Eur. J. Inorg. Chem., 2000, 39, 399–407 CrossRef.
- J. F. Desreux, Inorg. Chem., 1980, 19, 1319–1324 CrossRef CAS.
- A. L. Thompson, D. Parker, D. A. Fulton, J. A. Howard, S. U. Pandya, H. Puschmann, K. Senanayake, P. A. Stenson, A. Badari and M. Botta, Dalton Trans., 2006, 5605–5616 RSC.
- A. Barge, M. Botta, D. Parker and H. Puschmann, Chem. Commun., 2003, 1386–1387 RSC.
- O. A. Blackburn, N. F. Chilton, K. Keller, C. E. Tait, W. K. Myers, E. J. McInnes, A. M. Kenwright, P. D. Beer, C. R. Timmel and S. Faulkner, Angew. Chem., 2015, 127, 10933–10936 CrossRef PubMed.
- O. A. Blackburn, J. D. Routledge, L. B. Jennings, N. H. Rees, A. M. Kenwright, P. D. Beer and S. Faulkner, Dalton Trans., 2016, 45, 3070–3077 RSC.
- O. A. Blackburn, A. M. Kenwright, P. D. Beer and S. Faulkner, Dalton Trans., 2015, 44, 19509–19517 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- F. James, MINUIT Function Minimization and Error Analysis (version 94.1), Geneva, Switzerland, pp. 1994–1998 Search PubMed.
- M. Dunstan, R. Mole and C. Boskovic, Eur. J. Inorg. Chem., 2019, 8, 1090–1105 CrossRef.
- B. M. Flanagan, P. V. Bernhardt, E. R. Krausz, S. R. Lüthi and M. J. Riley, Inorg. Chem., 2002, 41, 5024–5033 CrossRef CAS PubMed.
- N. A. Bonde, J. B. Petersen, M. A. Sørensen, U. G. Nielsen, B. r. Fåk, S. Rols, J. Ollivier, H. Weihe, J. Bendix and M. Perfetti, Inorg. Chem., 2019, 59, 235–243 CrossRef PubMed.
- L. Ungur and L. F. Chibotaru, Chem.–Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem.–Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967 CrossRef PubMed.
- S.-D. Jiang and S.-X. Qin, Inorg. Chem. Front., 2015, 2, 613–619 RSC.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- J. Jung, M. Atanasov and F. Neese, Inorg. Chem., 2017, 56, 8802–8816 CrossRef CAS PubMed.
- D. Aravena, M. Atanasov and F. Neese, Inorg. Chem., 2016, 55, 4457–4469 CrossRef CAS PubMed.
- F. Neese and E. I. Solomon, Inorg. Chem., 1998, 37, 6568–6582 CrossRef CAS PubMed.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco and S. A. Kozimor, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef PubMed.
- S. Mondal and A. Lunghi, J. Am. Chem. Soc., 2022, 144, 22965–22975 CrossRef CAS PubMed.
- F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860–5871 RSC.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
- E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2281615–2281620 and 2281329. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03928e |
| ‡ These authors have equally contributed to this work. |
| § Current address: Department of Biological and Chemical Engineering, Åbogade 40, 8200 Aarhus N, Denmark. |
| This journal is © The Royal Society of Chemistry 2024 |