Critiquing lab technique videos prior to class: can it improve demonstrated technique?
Stephanie M.
Tenney
 ,
Arlene A.
Russell
,
Arlene A.
Russell
 and
Jennifer R.
Casey
and
Jennifer R.
Casey
 *
*
Department of Chemistry and Biochemistry, University of California, Los Angeles, 607 Charles E. Young Drive, Los Angeles, California 90095-1569, USA. E-mail: jrcasey@chem.ucla.edu
First published on 22nd April 2024
Abstract
During COVID-19 remote instruction, instructors were tasked with providing students with authentic laboratory experiences in an out-of-classroom environment. One solution developed for our introductory general chemistry laboratory involved students critiquing readily available technique videos to distinguish between correct and incorrect laboratory technique. After returning to in-person labs in Fall 2021, we incorporated this assessment into the pre-lab assignments in an effort to reduce the cognitive load of learning a new technique. Here we explore whether this critical-review exercise translates into improved technique as measured by precision and accuracy when using a 10 mL volumetric pipet. Additionally, we consider the impact of the pre-lab assignment given the involvement level of the TA, as some TAs are more willing to provide feedback on student technique during the lab period. We found that while students self-report the exercise as useful towards their learning, there are no significant changes in performance for most students. We did, however, find a reduction in the overall outliers and saw improvements when additional feedback (through a TA) was provided as well. These findings indicate that the exercise may be most useful for students who make large errors and who receive little individualized feedback.
Introduction
The development of laboratory skills is a critical aspect of STEM undergraduate education. For instance, in order for a chemistry department to grant an ACS-certified bachelor's degree, students must complete 400 hours of laboratory work (Undergraduate professional education in chemistry: ACS guidelines and evaluation procedures for bachelor's degree programs, 2015). The chemistry lab is viewed as a place where important skills can be developed, such as problem solving, safety awareness, communication, and teamwork. While there may not be complete consensus on the purpose of laboratory practice (Reid and Shah, 2007; Seery, 2020), many agree that lab is a place where students can learn technical skills (Bruck and Towns, 2013; Connor et al., 2023). The focus on the development of technical skills is to ensure that graduates can safely and accurately work in a laboratory environment, as dictated by the Quality Assurance Agency (The Quality Assurance Agency for Higher Education, 2022). Unfortunately, employers often feel that graduates do not possess these required skills (From analysis to action: Undergraduate education in science, mathematics, engineering, and technology, 1996; Hanson and Overton, 2010; Sarkar et al., 2019).Much effort has been directed at improving the technical skills of students. According to a comprehensive review conducted by DeMeo, this includes performing live demonstrations, providing opportunities for practice, assigning pre-lab activities, and engaging in “elbow instruction,” where an instructor observes students as they work and corrects errors accordingly (DeMeo, 2001). The use of pre-lab activities has been particularly popular, given that the preparation availed by the pre-lab may allow for more meaningful learning to occur during the lab itself (Johnstone, 1997). While pre-laboratory assignments vary in terms of focus, those designed to introduce lab techniques frequently utilize video demonstrations of equipment usage. Many studies indicate that assigning pre-lab activities can be beneficial; students who complete pre-lab assignments tend to be more efficient in the lab, receive higher assessment scores, and feel an increase in self-confidence (Nadelson et al., 2015; Canal et al., 2016b; Jolley et al., 2016; Stieff et al., 2018). These benefits of prelab activities have been attributed to a reduction in the cognitive load for students when they enter the lab itself (Agustian and Seery, 2017). With that said, it is unclear if these efforts are resulting in better lab technique. A recent study done by Sanchez applied quality control methods to assess student laboratory results (Sanchez, 2022). The labs under investigation required the use of basic laboratory skills (e.g., weighing, solution preparation, use of volumetric equipment), yet a surprisingly large number of results were considered incorrect or questionable—despite the fact that students were enrolled in upper-division lab courses and had received 240 to 330 hours of lab training. The primary source of error came from poor lab skills, either from improper weighing procedures or the incorrect use of volumetric glassware.
Part of the difficulty stems from misalignment between instructor goals and assessments. Lab technique is often not evaluated nor graded, making it difficult for students to recognize the importance of mastering these skills (Seery, 2020). While instructors see the lab as a place to improve technical proficiency, students tend to be more concerned about finishing the lab quickly, thereby forgoing opportunities to improve their technique (DeKorver and Towns, 2015). In an attempt to address this issue, some instructors have begun to explicitly incorporate skills assessment into the laboratory. This includes the lab practical (Hancock and Hollamby, 2020), digital badging (Towns et al., 2015; Hensiek et al., 2016; Seery et al., 2017), and structured chemistry examinations (SChemES) (Kirton et al., 2014). While the implementation varies for each of these methods, they all require students to demonstrate specific lab skills, either in person or through videos.
Motivation
With the start of the COVID-19 pandemic and the abrupt transition to remote learning, chemistry students around the world were denied the key essence of lab: “the lab must allow students to make [their own] observations and measurements and then seek to interpret them” (Reid, 2021). Despite our best efforts, our students were unable to practice important manipulative skills such as quantitatively transferring materials or making solutions of precise concentrations. In the absence of in-person labs, lab faculty at our university fell back on the 40 year-old practice of showing students how to do the lab via videos – an instructional practice pioneered by one of the authors (Russell and Mitchell, 1979). We embedded videos into our learning management system (LMS) and had students view them prior to analyzing instructor-provided data; however, students were unable to assess the mastery of their technique through the accuracy and precision of their own data.In an effort to better align our teaching beliefs with our practices, we changed the modality of the video instruction so that students could evaluate multiple videos using a detailed task inventory that identified the many nuanced and subtle steps involved in mastering a specific technique. Students were shown two to three videos of people demonstrating the use of a particular piece of equipment (e.g., volumetric pipet, volumetric flask); one of these videos was an exemplar, while the others contained a few small mistakes. Students then used a task inventory to evaluate the accuracy of the technique demonstrated in the video (see Appendix 1 for an example task inventory).
When in-person classes resumed, we were interested in continuing the critiquing of lab technique, but now as part of a pre-lab report. Prior student data showed wide deviations in both accuracy and precision–results that far exceeded the manufacturer's tolerance for the equipment and gave rise to results that were difficult to interpret. Our hypothesis was that by breaking the skill down into manageable steps and providing an opportunity to work with this information prior to entering the lab, students could then focus during the lab on putting all the steps together in order to achieve high accuracy and precision. While digital badging has been used in large laboratory courses to encourage better technique (Towns et al., 2015; Hensiek et al., 2016), we were interested in determining if a more manageable intervention could achieve positive results as well. A similar experiment was performed by Accettone et al., where students were given two technique videos, one of which showed the technique performed properly while the other video contained mistakes (Accettone et al., 2023). Students were asked to distinguish between the two videos, as well as identify the errors and the potential consequences of these errors. Students viewed the activity positively and generally reported feeling more confident in performing the technique in lab, but the study did not determine whether specific techniques improved as a result of the intervention.
The majority of studies interested in improving student technique focus on student experience (Towns et al., 2015; Canal et al., 2016b; Hensiek et al., 2016; Jolley et al., 2016; Seery et al., 2017), and for those studies that do consider technique as an outcome, the emphasis tends to be on general observations and analysis of a final result that relies on a combination of techniques (Kempa and Palmer, 1974; Canal et al., 2016a; Stieff et al., 2018). For this reason, we wanted to investigate the impact our intervention had specifically on student mastery of a particular technique. We chose the use of a 10 mL volumetric pipet since this is a critical skill that students are known to struggle with (Prichard, 1999; Sanchez, 2022), and the accuracy and precision can easily be determined and is directly connected to correct usage of the equipment.
Theoretical framework
The design of the intervention was based upon the principles of cognitive load theory (CLT). It is understood that the cognitive load of a task is related to both the interactivity of its elements as well as the manner in which it is taught. Intrinsic cognitive load is related to the complexity of the material itself, while extraneous and germane cognitive load are related to how the material is presented. While extraneous cognitive load is caused by distractions to learning, germane cognitive load focuses on enhancing processes which benefit learning.The laboratory is well known for being an environment that can induce cognitive overload, and this is in fact one of the reasons why pre-laboratory activities are commonly implemented (Johnstone and Wham, 1982; Johnstone, 1984). But in watching a technique video, a student must assimilate multiple individual manipulative steps each with its own set of sub-technique procedures. Even more challenging, students must distinguish these specific steps themselves. The hope is that students can separate the ‘noise’ from the ‘message’, but that can be quite challenging for a novice.
The use of a task inventory for critiquing pipetting technique was done in an effort to direct students’ attention to the important procedural steps, thereby reducing extraneous cognitive load and increasing germane cognitive load. The idea of using an organizer, such as the inventory used here (see Appendix 1), is a well-known technique in CLT (Ausubel, 1963; Robinson et al., 1998). It has also been shown that sequencing tasks into isolated elements can improve learning, especially for novices (Pollock et al., 2002). While pipetting may not seem to be a particularly advanced technique, it does require high element interactivity – the ten steps can be written out as separate items, but all ten steps must be perfectly executed together in order to achieve high accuracy and precision. By using an “isolated elements” procedure, we provide students with an initial opportunity to familiarize themselves with the technique, so that they can then focus on the process of interacting elements once in the lab.
The use of an exemplary video followed by a video containing minor errors was based in part on work by Hendry, which highlights exemplars as a means for students to better understand expectations before performing a task (Hendry, 2013; Hendry and Anderson, 2013). Additionally, including a video that contained errors simulates the process of peer review, which can engage students in reflection on their own work (Nicol et al., 2014).
Research question
Does prior critiquing of a technique using a task inventory translate into improved technique (as measured by precision and accuracy when using a 10 mL volumetric pipet) compared to passively watching an exemplary video?Methods
Study setting
The study occurred at a large public research university in the southwest United States during the Winter 2019 and Fall 2021 quarters. The study focused on the first chemistry laboratory class taken in the chemistry series designed for Life Science majors. The breakdown of students was: 11.3% first year, 68.0% second year, 18.4% third year, and 2.3% fourth year for Winter 2019, and 3.5% first year, 75.4% second year, 17.2% third year, and 3.9% fourth year for Fall 2021. This course is not necessarily taken concurrently with general chemistry lecture; the second quarter of general chemistry lecture is a co- or pre-requisite. The course consists of a 50 minute lecture and a 170 minute lab each week during a ten-week quarter. The lecture is focused on exploring the chemistry concepts behind the experiments, while the lab section is focused on performance of the experiments and data collection. The lab sections are run by graduate teaching assistants (TAs), who usually give a short (∼10 min) presentation on the experiment before students begin. Data analysis is done outside of the lab, and lab reports are submitted weekly. The course consists of a midterm and final exam but does not involve any lab practical. IRB (#21-001672) classified the collection of student data and TA observations in this study as exempt.Pipetting experiment
The pipetting assignment (Fig. 1) begins by first practicing the transfer of water using a 10 mL volumetric pipet. Once students feel they have had sufficient practice, students (1) weigh three empty vials on an analytical balance, (2) transfer a 10 mL aliquot of water to each vial using the 10 mL volumetric pipet, and (3) re-weigh the vials that now contain the 10 mL aliquots of water. During the lab section, students record the mass of the empty vials, the mass of the vials with the 10 mL aliquot of water, and the temperature of the water. In the post-lab report, students are asked to convert the mass of water transferred to volume using the appropriate density given the water temperature, and then to calculate the average volume transferred as well as the percent relative average deviation (%RAD). Regardless of the values they obtained, students could receive full points simply by correctly interpreting the accuracy and precision of their data. They were made aware of this policy prior to turning in the post-lab to discourage them from recording false measurements.Implementation of video critique pre-lab assignment
In Winter 2019, the lecture and lab sections were taught in-person. The pre-lab assignment for the pipetting assignment consisted of filling in a partially completed flowchart and noting what values would be recorded during the lab period as well as what calculations would be required after completing the lab work. During the lab period, the TAs were instructed to show an exemplary technique video on pipetting before students attempted to use the equipment themselves (Use of A Pipette Pump, n.d.). This cohort contained 434 students and will be known as the “control group.”In Fall 2021, the lecture and lab sections were also taught in-person. The pre-lab assignment for the pipetting assignment consisted of a drag-and-drop flowchart, followed by two technique videos (both were implemented through our university LMS). Students were asked to watch the technique videos and then analyze them using a provided task inventory (summary in Table 1, full inventory in Appendix 1). Every student was assigned the same exemplary video used in Winter 2019 (Use of A Pipette Pump, n.d.). The second video was randomly assigned from a series of online published videos (Lab Technique Video, 2014; The Volumetric Pipet and Pipetting Technique, 2014; Calibration and Use of a Volumetric Pipet, 2017; General and Organic Chemistry – Use of a Pipet, 2017). Links to these videos are provided in their references. Students had a week before their lab section met to complete the pre-lab assignment, and three attempts to show mastery of the assignment without penalty. The TAs were not asked to show the students any technique videos during the lab section. This cohort contained 451 students and will be known as the “treatment group.”
| Step number | Task |
|---|---|
| 1 | Check to see if the pipet is clean |
| 2 | Rinse the pipet with solution to be transferred |
| 3 | Place the pipet pump onto the pipet |
| 4 | Draw the liquid above the calibration mark |
| 5 | Wipe off the outside of the pipet tip |
| 6 | Lower the liquid level to the calibration mark |
| 7 | Touch the pipet tip to a dry wall of the container holding solution |
| 8 | Transfer the pipet to the receiving vessel and release pressure |
| 9 | Allow the pipet to drain freely while touching the wall of the receiving vessel |
| 10 | Leave the residual fluid in the tip after draining pipet |
Collection of student data
Although students calculated the average mass and %RAD within their post-lab report, the raw values recorded for weight of water were tabulated for each student, and the %RAD and average mass were recalculated for this study to avoid potential student calculation errors. A temperature of 20 °C was assumed. Student feedback about the usefulness of the pre-lab assignment was collected through an instructor-designed anonymous mid-course survey with a 70% response rate.Data analysis
Statistical analyses were performed using R version 4.1.1. A two-tailed independent t-test was conducted to compare both the accuracy and precision of student data from Winter 2019 and Fall 2021 and a p value of <0.05 was considered statistically significant. Extreme values were defined as greater than 3× the manufacturer's tolerance of the pipet, to provide a standardized range for comparison across distributions. Outliers were also identified by finding values both above and below 1.5× the interquartile range but were not removed from the data reported in the main text figures since they are informative about whether the pipet was used properly or not (see the Appendix for the analysis excluding outliers, although general conclusions remain the same). Chi-square analysis was done on the breakdown of student results into categories based on the number of goals they met, and a p < 0.05 was considered significant. Cramer's V was used to measure the effect size. Logistic regression was conducted to test the association between TA involvement and student performance for the treatment group only. The odds ratio represents the odds of a successful outcome in one group compared to another, in this case reaching their expected accuracy or precision target as determined by the tolerance rating of the volumetric pipet. A p < 0.05 was also considered statistically significant for these odds ratios.Positionality statement
We acknowledge that the identities and experiences of researchers influence their work, both implicitly and explicitly. We come into this work in various ways. All three authors hold PhDs in the field of Chemistry, although SMT was a graduate student during the time of the project. JRC and AAR are instructional faculty and have prior experience with discipline-based education research. Our social identities include women (AAR, JRC, SMT) and White (AAR, JRC, SMT).Results and discussion
Impact of video critique on student pipetting technique
In order to determine whether actively critiquing technique videos is a more effective primer for learning lab skills than passively watching an exemplary video, we compared student results after implementation of the critique to a control group of students who completed the traditional pre-lab assignment (Fig. 1). We chose to conduct this study for the first laboratory experiment in the course because the quantitative results obtained by the students can be directly correlated to the quality of their pipetting technique. The average mass of water (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) delivered provides us with a measure of how accurately a student used the 10 mL volumetric pipet. Although the temperature, which affects the water density, was not rigorously held constant across each laboratory room, we discount the negligible contribution of temperature fluctuations to error (details in Appendix 2) and generally expect the 10 mL volumetric pipet to deliver 10.00 ± 0.02 mL (or 9.98 ± 0.02 g). Similarly, the percent relative average deviation (%RAD), eqn (1) is a measure of the spread in a data set, and as such it provides us with information on the precision of the collected data.
) delivered provides us with a measure of how accurately a student used the 10 mL volumetric pipet. Although the temperature, which affects the water density, was not rigorously held constant across each laboratory room, we discount the negligible contribution of temperature fluctuations to error (details in Appendix 2) and generally expect the 10 mL volumetric pipet to deliver 10.00 ± 0.02 mL (or 9.98 ± 0.02 g). Similarly, the percent relative average deviation (%RAD), eqn (1) is a measure of the spread in a data set, and as such it provides us with information on the precision of the collected data.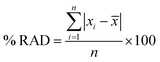 | (1) |
Examining the interquartile range of the student data for both the control and treatment groups reveal that the majority of students are near the expected values, but outside of the desired range (Fig. 2a and b, full distributions with outliers shown in Appendix 3, Fig. 5). There was not a significant difference in the average mass between the control and treatment groups (p = 0.50), but the mean was closer to the target (9.98 g) in the treatment group at 9.95 g compared to 9.92 g in the control. The statistics are summarized in Tables 2 and 3. Similarly, there was not a significant difference in %RAD for treatment and control groups (p = 0.17) but the same trend of an improvement in the mean is observed. In the treatment group, the mean %RAD was 0.627% compared to 0.967% in the control group. Overall, a greater portion of students are within the acceptable range for precision than accuracy, which may indicate that students are prone to making an error but doing so consistently for each trial. For both average mass and %RAD, the median is nearly unchanged by the implementation of the video critique exercise, indicating that the exercise does not seem to have a strong impact for the class as a whole.
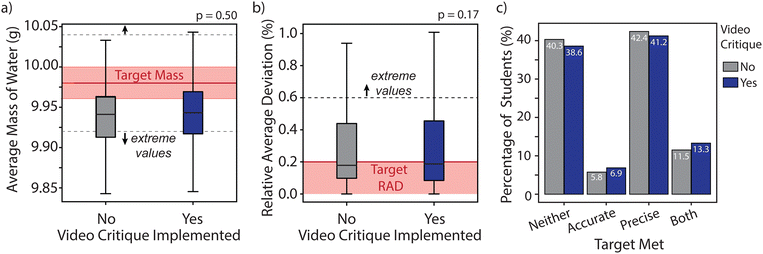 | ||
| Fig. 2 The overall distributions of student data for the control group (no video critique, grey) compared to the treatment group (video critique, blue). (a) The average mass informs about the accuracy while (b) the %RAD informs about the precision of pipet measurements. Only the interquartile ranges are shown to highlight the acceptable range of values if the pipet was used properly (red shaded region), with the red line indicating the expected value (full distributions are shown in Fig. 5). The target mass was calculated assuming a room temperature of 20 °C. The dashed lines and arrows indicate the regions where data were assigned as “extreme values,” quantified as 3× the manufacturer's tolerance of the pipet. (c) The categorical breakdown of student outcomes. Each student's data was evaluated as whether it fell within the acceptable range or not and then subsequently categorized by how many targets were met. The percentage of students within each category is given within the bars. | ||
| Measurement | Accuracy | Accuracy | Precision | Precision |
|---|---|---|---|---|
| Video implementation | No (control) | Yes (treatment) | No (control) | Yes (treatment) |
| Sample size | 434 | 451 | 434 | 451 |
| Mean | 9.92 g | 9.95 g | 0.976% | 0.623% |
| Median | 9.94 g | 9.94 g | 0.179% | 0.187% |
| Standard deviation | 0.38 g | 0.59 g | 4.16% | 3.14% |
| Extreme values (%) | 37 | 33 | 21 | 17 |
| Outliers (%) | 16 | 14 | 13 | 10 |
| Outlier treatment | Measurement | Accuracy | Precision |
|---|---|---|---|
| Included (reported in main text) | t statistic | −0.681 | 1.383 |
| p value | 0.50 | 0.17 | |
| 95% confidence interval | (−0.091, 0.044) | (−0.146, 0.842) | |
| Effect size (Cohen's d) | 0.060 | 0.096 | |
| t statistic | −2.116 | −1.107 | |
| Excluded | p value | 0.035 | 0.269 |
| 95% confidence interval | (−0.011, 0) | (−0.048, 0.013) | |
| Effect size (Cohen's d) | 0.153 | 0.079 | |
Since our goal of this study is to help students pipet both accurately and precisely, it is also important to evaluate if students are improving on only one or both metrics. If we classify each student's data as either agreeing with the expected value or not, we can categorically group students by whether they met one or both of their targets (Fig. 2c). Overall, ∼40% of students met neither target, while less than 15% met both targets. The remaining students only met a single target, the majority of which was precision (∼40%) as opposed to accuracy (∼6–7%). We did find about a 1.7% reduction in students who met neither of their targets with implementation of the intervention, a 1.1% increase in accuracy only, a 1.2% reduction in precision only, and a 1.8% increase in both. We tested the association between video critique treatment and categorical performance breakdown with a Chi-square test for independence and found no statistically significant effect (χ2 = 1.24, p = 0.7, V = 0.02, details found in Table 4 and Appendix 4).
| Group | Neither | Accurate | Precise | Both | Sum |
|---|---|---|---|---|---|
| Control | 175 | 25 | 184 | 50 | 434 |
| Treatment | 174 | 31 | 186 | 60 | 451 |
| Sum | 349 | 56 | 370 | 110 | 885 |
Because we found no significant improvement, the video critique exercise does not seem to address the errors that most students seem to be making. Given that the median for accuracy was very close but just under the target, it is possible that the consistent inaccuracy comes from incorrect lowering of the meniscus or from droplets being left behind on the walls of the pipet. We observed some students during the experiment and noted that the most commonly skipped steps were the rinsing of the pipette and drawing the meniscus above the line before carefully lowering it to the correct volume. In post-lab feedback, many students noted that they would set the meniscus level while the pipet tip was submerged, but it would lower when they lifted the tip out of the water for transfer (leading them to deliver slightly less). This was not discussed in the videos and can explain why ∼75% of students deliver under the expected value.
While most students are already near their targets and see little to no impact from the video critique implementation, this exercise may be effective for students who would otherwise make large procedural errors and collect outlying values as data. We first classified a set range for “extreme values” (Fig. 2a and b, dashed lines and arrows) as 3× the accepted manufacturer's tolerance of the pipet (more details in Table 2). This removes the dependence of outlying values on the IQR as the distributions may encompass a different spread in values. We found that the percentage of students with extreme values reduces with implementation of the video critique exercise from 37% to 33% for average mass and 21% to 17% for %RAD, although these differences are not significant (Table 2). We also evaluated outliers, classified as greater than 1.5× the IQR. Similarly, the percentage of students with outlying data reduces with implementation of the video critique exercise from 16% to 14% for average mass and 13% to 10% for %RAD (Table 2). The reduction of outliers has been seen in other pre-lab interventions and may by itself be an important finding (Canal et al., 2016b). A study investigating common sources of struggle in the laboratory found that one major concern is when tools did not perform as expected (Keen and Sevian, 2022). The authors found that students’ common response was to assume the tool was broken or guess about the expected result rather than addressing the origin of the discrepancy. It can be difficult for a student to draw meaning from an anomalous result, so reducing these types of outliers is certainly a desired outcome.
Overall, we did not find any significant evidence of improvement in student performance with implementation of the video-critique exercise. Our results show that there may be some effect if considering the percent of “extreme values” reported, but in general the median student performance remains similar. Given that students are still performing outside of the expected tolerance of the pipet, it seems our efforts to reduce the cognitive load required during the experiment were insufficient and students still struggled to master the overall skill.
The association between teaching assistant involvement and technique performance
According to Johnstone's ten commandments, meaningful learning requires feedback and assurance in addition to limiting the amount of information to be processed (Johnstone, 1997). Another intent of the intervention was to mimic the process of engaging in feedback, yet this approach may have been insufficient. Rather than try to incorporate a more time-intensive intervention such as digital badging, our hope was that implementing the critical evaluation of technique videos would provide some form of evaluation that could potentially offset the lack of structured feedback.Despite our best efforts to standardize all lab sections, we recognize that variability in the level of TA-student interaction remains. While our hope is that the TAs, who undergo a ten-week training process and work with no more than 20 students in a lab section, would provide some elbow instruction to students, we recognize that may not be the case. Yet given that studies suggest online pre-lab activities help standardize the laboratory experience across TAs (Nadelson et al., 2015; Stieff et al., 2018), we had hoped that the intervention may compensate for those TAs who are less involved.
To investigate whether the intervention could potentially alleviate differences in the level of individual feedback provided by TAs, we first ranked each TA's level of involvement during lab within the treatment group (more information in Appendix 5). This was done by conducting observations of TAs during the lab periods where students were completing the pipet assignment. In Fig. 3, we compare student data within the low and high TA involvement sections for the treatment group. The ranges are set to highlight the IQR, and the full range with all outlying values is shown in Appendix 6, Fig. 6.
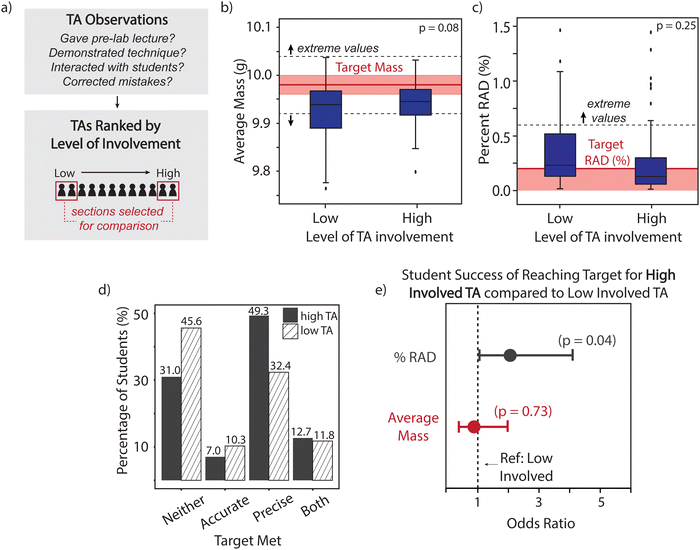 | ||
| Fig. 3 Student results when stratified by the level of TA involvement in their section. (a) Observations were used to rank each TA's level of involvement, and student data from the two lowest (n = 68) and two highest (n = 71) were used for further analysis. The comparison of high and low TA involvement for (b) average mass (accuracy) and (c) percent relative average deviation (precision). Note that only the IQR region is shown although outlying values were not excluded from the data set, and these outliers affect the reported p-values (see Fig. 6 for full range). The dashed lines and arrows indicate the regions where data was assigned as “extreme values,” quantified as 3× the manufacturer's tolerance of the pipet. (d) The categorical breakdown of performance for high TA sections (solid) compared to low TA sections (dashed). (e) The odds ratio of student success in precision (grey) and accuracy (red) for students in a high TA section compared to a low TA section. Error bars indicate the 97.5% confidence intervals. | ||
While we found no significant differences between the means of the distribution when comparing high to low TA involvement (Fig. 3b and c), we did find improvement in the mean, median, and standard deviation in high TA involvement sections (statistics summarized in Appendix 7, Tables 5 and 6). For average mass, when comparing high to low TA involvement we observe a mean of 9.960 g compared to 9.879 g (target = 9.98 g), a median of 9.945 g compared to 9.939 g, and a standard deviation of 0.172 compared to 0.336. For %RAD we observe similar results when comparing high to low TA involvement sections—a mean of 0.319% compared to 1.460% (target ≤0.2%), median of 0.129% compared to 0.232%, and a standard deviation of 0.611 compared to 8.035. The percentages of extreme and outlying values were also lower for high TA involvement sections. These results demonstrate that although the mean performance is largely skewed by outliers (leading to non-significance in p values), the middle 50% of the students demonstrate better technique in high TA involvement sections compared to low TA involvement sections. Categorical breakdown of targets met (Fig. 3d) also showed that although the percentage of students meeting both targets are similar for high and low TA, there are large differences when only one or none of the targets are met. Highly involved TAs resulted in a lower frequency of students meeting no targets, and a higher frequency of students meeting precision. A Chi-square analysis shows that the effect of TA on performance is not statistically significant (χ2 = 4.32, p = 0.2) but does show a small effect size (V = 0.1). These results may be an outcome of having a small number of students in some categories when stratified by TA and number of goals met (Appendix 8, Table 7), so we further analyzed performance by determining if students were likely to meet their targets or not in Fig. 3e.
We use logistic regression to determine the odds ratio of student success if they are in a section with a high involvement TA compared to a low involvement TA (Fig. 3e). The odds ratio (OR) is a measure of association between an outcome (in this case, proper technique) and an exposure (the student's TA). An OR = 1 means the two groups can expect the same outcome; an OR > 1 means the group in question has higher odds of a successful outcome than the reference; an OR < 1 means the reference group has higher odds of a successful outcome. We plot the ORs and their 97.5% confidence intervals, to highlight the increased or decreased odds of the group (indicated in the x-axis) having a successful outcome compared to the reference group (dashed line). The odds of high TA involvement sections meeting their accuracy target are equal (no significant difference, OR = 0.87, p = 0.73) to the low TA involvement students, while the odds of reaching the precision target are significantly higher (twice as high) for students with a highly-involved TA than for students with low TA involvement (OR = 2.06, p = 0.04). A full description of results is provided in Appendix 9, Table 8. These results imply that the level of TA involvement may be a predictor of student success, in this case demonstrating proper technique, and suggests the importance of instructor feedback during the experiment. Also noteworthy is that TA involvement seems to affect precision more strongly than accuracy. One plausible explanation of this could be that the students are following a standard procedure but a highly-involved TA may be more likely to encourage students with a wide spread in their measurements to redo a trial.
While it is promising to see that the odds of achieving accurate results were the same for all students, we do not know if this is a result of the intervention itself. Unfortunately, we did not collect data on TA involvement in Winter 2019, and therefore cannot speak to whether the intervention alleviated disparities in TA involvement when it came to using the pipet accurately. The precision results point to the importance of having more direct forms of feedback during the experiment—those TAs designated as high involvement were all reported to frequently check on the students during the lab and help correct student technique in the moment. This type of constructive input appears to have an impact on student's ability to use the pipet consistently.
Student perceptions of video critique usefulness
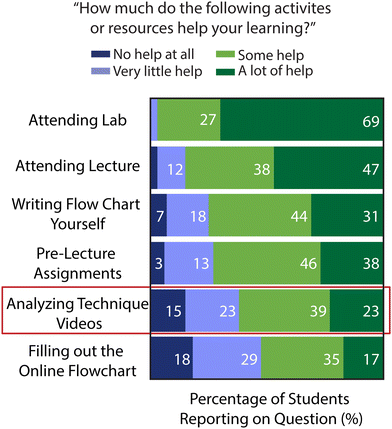
Another important consideration with any intervention is student perception; therefore, we asked students for feedback on how helpful the technique video critique exercise was in their learning process through a mid-quarter survey (see Fig. 4). The survey contained questions with numerical rankings as well as free-response entries. When the treatment group was asked about analyzing the technique videos in the pre-lab assignment, only 23% stated it was a “a lot of help” (other responses from the treatment group included: “some help” (39%), “very little help” (23%), and “no help at all” (15%)). Although the majority of our students self-reported this resource as useful, most of the class still saw no significant improvement compared to the control cohort. This is line with literature where students’ confidence in their skills was shown to improve with online preparation videos, but their cognitive performance was not necessarily correlated (Altowaiji et al., 2021). While it has been demonstrated that students generally perceive skills-based assignments as having a positive impact on their learning, it may not be enough to look at student perceptions of what is helpful (Accettone et al., 2023).The main complaint students in the treatment group expressed in regards to the intervention was having to carefully watch the videos for the pre-lab as they were graded on their responses. Even with three attempts, some felt like it was “nit-picky” and therefore seemed to focus more on getting the right answer than critically evaluating the technique. Selected quotes expressing frustration from students within the treatment group on the mid-quarter survey:
“The most difficult part of the pre-lab is analyzing the videos because when completing these questions, students are more concerned about getting the answer right than actually learning the lab procedure.”
“[The biggest challenge of this course is] a sense of frustration when completing flowcharts and technique analysis videos during prelab.”
“The flowcharts and analyzing the technique videos are very frustrating. […] When analyzing the videos, sometimes the person in the video did part of a step, so I don’t really know to answer yes or no if they completed it correctly.”
Accettone et al. reported similar findings, in that students expressed difficulty with determining how many errors were present in a video (Accettone et al., 2023). Following their recommendations, students may feel less frustrated if they are allowed to miss one error without being penalized. It is also recommended to select technique videos that contain more obvious mistakes, thereby avoiding ambiguities that may lead to unnecessary frustration. This too may help with reducing extraneous cognitive load, as it seems we may have inadvertently introduced new distractions via the types of videos selected.
Limitations
One major limitation of this study is that the control group completed their chemistry laboratory coursework before the COVID-19 pandemic and were not disrupted by virtual learning. The treatment group completed this course just after the return to in-person instruction, meaning their preparation from any previous laboratory courses was most likely impacted by the pandemic and they may have had less exposure to technical skills that require hands-on manipulation. This must be considered in the context of our results as an additional confounding factor—the treatment group may very well have had a lower baseline of technical skills even before introducing the pre-lab exercise.Another potential limitation is the fact that there was up to a week-long delay between the completion of the video critique and the actual implementation of the skill. There is evidence that in order to minimize extraneous cognitive load, the time between the presentation of the supporting information and the integration of the information should be minimized (Kester et al., 2001). Furthermore, the integration of procedural information during the task is advisable, yet we did not directly provide students with the task inventory while they were in lab (Van Merriënboer et al., 2003). While students could have accessed that resource themselves, they were not encouraged to do so.
Because we recognized TA involvement as a potential confounding variable only after data were collected, the section “The Association Between Teaching Assistant Involvement and Technique Performance” has several limitations. The criteria used to determine which TAs were high and low involvement were not rigorously defined and as such, we felt compelled to use the extreme cases for comparison; this in turn limited our sample size. Finally, we were unable to compare the control and treatment group, thus preventing us from investigating whether the intervention can help to alleviate differences in TA involvement. Given the data analysis we have performed here, this is now an avenue we plan to more rigorously investigate in future studies.
Implications
Overall, our work demonstrates that mastering a lab technique may require more intervention than the pre-lab critique exercise presented here. In addition to this pre-lab exercise, it may be more effective to incorporate active feedback such as in the form of working in pairs to critique each other's technique, self-assessments by recording and then comparing a student's own technique to the exemplary video, or structured feedback from the TA or undergraduate learning assistants through means such as digital badging.Along with providing personal feedback, we believe that it may also be necessary for students to receive sufficient interleaved practice to master a lab skill—one lab period dedicated to pipetting technique may not have provided sufficient practice. Interleaved practice gives students periods of rest between sessions when they are actively learning or practicing and has been shown to be effective for higher cognitive learning in math, science, and physics as well as in the development of motor skills (Brown et al., 2014; Eglington and Kang, 2017; Foster et al., 2019; Samani and Pan, 2021). As pipetting is a technical skill that is used repeatedly in subsequent experiments, a future study looking at how the students improve over the duration of the course may give insight on when students master the skill and whether there is a latent effect of a higher cognitive preparation.
Conclusions
To better prepare students for learning a new lab skill, we implemented a pre-lab exercise which involved students watching a technique video (volumetric pipetting) and completing a critique of the demonstration through a task inventory. After the pre-lab exercise, students then completed a volumetric pipet lab, and we compared their data to a cohort who did not complete the same video critique pre-lab assignment. We found that using this pre-lab exercise alone was not enough to significantly improve the students’ performance, despite their perception of the assignment as being useful towards their learning. Consistent with others reports (Seery et al., 2024) we found that a potential predictor of student success is access to an instructor who directly assists them with learning proper technique.While we did not find significant improvement in accuracy and precision after implementing the video critique exercise, we did discover that this intervention gives similar results as showing technique videos during class. This means that instructors could have flexibility to move this activity to outside-of-class time and maximize the valuable in-class time for interaction with instructors and peers. This may be especially useful if lab periods are short and/or if a particular lab takes up the entire period.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix 1. Video critique exercise task inventory form
| Identification | |||
| Title: use of a pipet | URL: https://www.youtube.com/watch?v=YMjy2sK_kBo | ||
| Video clip (if applicable) | 5:04–12:06 minutes | ||
| Procedure performance | |||
| Correct | Incorrect or omitted | ||
| 1 | Checking to see if the pipet is clean by observing whether droplets cling to the inside of the pipet | _______ | _______ |
| 2 | Rinsing the pipet including a portion of the stem above the calibration mark with small amounts of the solution to be transferred | _______ | _______ |
| 3 | Carefully placing the pipet pump or bulb on the top of the pipet | _______ | _______ |
| 4 | (a) Bulb suction: holding the pipet with one hand and moving the INDEX finger (not thumb) to the top of the pipet when the liquid has been drawn above the calibration mark with the bulb in the other hand | _______ | _______ |
| (b) Pipet pump: holding the pipet with one hand and manipulating the pipet wheel with the thumb of the other hand to draw the liquid up the pipet above the calibration mark | |||
| 5 | Wiping off the outside of the tip of the pipet while the liquid is above the calibration mark | _______ | _______ |
| 6 | Slowly lowering the liquid level just to the calibration mark by (a) lessening the pressure of the index finger on the pipet top by turning the pipet (not lifting the finger off the pipet) if you are using a bulb or (b) turning the wheel slowly to lower the plunger if using a pipet pump | _______ | _______ |
| 7 | Touching the tip of the pipet to a dry edge of the container holding the solution before moving the pipet to the receiving container | _______ | _______ |
| 8 | Transferring the pipet to the receiving vessel and releasing the pressure by lifting the finger completely or pressing the release valve on the pump | _______ | _______ |
| 9 | Allowing the pipet to drain freely while touching the inside wall of the receiving vessel above the level of the liquid | _______ | _______ |
| 10 | Leaving residual liquid in the tip after draining appears complete | _______ | _______ |
| Safety | |||||||
| Proper PPE | Eye protection | Yes | _______ | No | ________ | Not visible | _______ |
| Lab coat | Yes | _______ | No | ________ | Not visible | _______ | |
| Badge certification recommendation (select one) | ||
| Recommended | Provisional | Not recommended |
| All procedure steps correctly performed, PPE used if visible | One or two steps omitted or incorrect; proper PPE used if visible | Improper PPE if visible and/or more than two steps omitted or incorrectly performed |
| Feedback: (no more than three sentences) based on recommendation | ||
| Positive: (what was done correctly) | ||
| Constructive: (what was omitted and/or what experimenter should do to improve incorrectly performed steps) | ||
Appendix 2. Error analysis of water density fluctuations
The volumetric pipet is rated to deliver 10.00 ± 0.02 mL at 20 °C which, in mass, is equivalent to 9.98 ± 0.02 g. Because this study was conducted over 24 different laboratory sections it was not possible to ensure that the temperature of the room was always held constant. As such, we evaluated how the temperature fluctuations would contribute to the error of the expected volume.We first assume that the room temperature was held within a range of 15–25 °C. The density is expressed by:
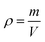 | (2) |
| ρ at 15 °C = 0.9991 g mL−1 | (3) |
| ρ at 20 °C = 0.9982 g mL−1 | (4) |
| ρ at 25 °C = 0.9970 g mL−1 | (5) |
 | (6) |
| ΔmassH2O = 0.0233 | (7) |
Appendix 3. Average mass and percent RAD distributions for the entire class
We assigned student results to being “extreme values” if they fell outside of 3× the acceptable manufacturer error. For accuracy, this included values outside of 9.92–10.04 g (accepted range 9.98 ± 0.02 g). For precision, this included values greater than 0.6% RAD (accepted range <0.2% RAD). We chose to use this metric in addition to the number of outliers, because the outliers are calculated by 1.5× the IQR, which changes in spread from one distribution to another. To test for significance in the frequency of extreme values we ran a Chi-square test of independence. For average mass we obtained χ2 = 1.6 (df = 1, p = 0.2, V = 0.04). For % RAD we obtained χ2 = 1.3 (df = 1, p = 0.3, V = 0.04). Neither result showed statistical significance. See Fig. 5.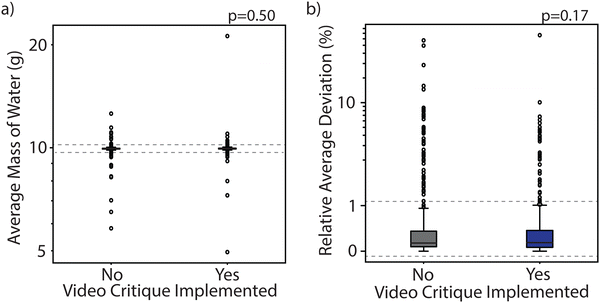 | ||
| Fig. 5 The full distributions of all student data for (a) accuracy and (b) precision. The grey dashed lines indicate the data show in Fig. 2 (the IQR ranges), and the outliers are represented by the circles. | ||
Appendix 4. Frequency table and Chi-squared test for categorical breakdown of performance
We ran a Chi-Squared test of independence to test whether the breakdown of performance is associated with pre-lab style. We obtained a χ2 = 1.2 (df = 3, p = 0.7). The Cramer's V effect size is V = 0.02. These results indicate that there is no statistically significant effect between the treatment and performance.Appendix 5. TA evaluation of involvement
All TAs included in this study participated in a required general training program through the chemistry department (30 hour total), in addition to one-hour weekly TA meetings for the specific course to discuss the experiments and logistics. We chose to evaluate the TAs on their involvement with student learning by conducting observations in the treatment group during the pipet experiment. The control group could not be evaluated because the study was designed after the control data was collected. The observations were done by a non-instructor (graduate student investigator) who was neither recognizable to the students nor had any influence on grades for either the students or the TAs. The TAs were informed that observations of students were being collected for a study but were not informed that their involvement was also being recorded so as to capture their most typical behavior. Students were not informed about the observations. The investigator did not communicate with the students about their skills in any way and any questions from students were directed to the TA to answer.Criteria for TA involvement was determined prior to entering the classroom and the observer was assessing:
(1) Did the TA give a pre-lab lecture?
(2) Did the TA give a demonstration of proper technique to the entire class?
(3) Did the TA walk around as the students were practicing with the pipet?
(4) Did the TA demonstrate any attempts to correct mistakes they saw?
When determining whether a TA met certain criteria, a binary response was given – either yes or no. The frequency and quality of the interaction were not rated, and as such, no rubric was devised. TAs who demonstrated all 4 criteria were identified as “high involvement”, TAs who demonstrated 2–3 criteria were identified as “intermediate involvement”, and any TA who only demonstrated 1 criterion was identified as “low involvement”. From the four criteria listed, the low involvement TAs only gave a pre-lab lecture, and therefore did not provide students with any feedback about pipet usage. Two TAs with high involvement and two TAs with low involvement were selected for further analysis. These groups contained 68 students with a low involvement TA and 71 students with a high involvement TA.
Appendix 6. Full distributions for average mass and precision by TA invovlement
See Fig. 6. | ||
| Fig. 6 The full distributions of student data for (a) average mass and (b) percent RAD comparing the students in sections where a TA demonstrated low involvement compared to high involvement. The outliers are shown in these plots, while they are not in Fig. 4 for clarity of visualizing the IQR. | ||
Appendix 7. Average mass and percent RAD distribution statistics for the high and low TA groups
See Tables 5 and 6.| Measurement | Accuracy | Accuracy | Precision | Precision | |
|---|---|---|---|---|---|
| Outlier treatment | Video implementation | Yes (treatment) | Yes (treatment) | Yes (treatment) | Yes (treatment) |
| TA involvement | High | Low | High | Low | |
| Included (shown in main text) | Sample size | 71 | 68 | 71 | 68 |
| Mean | 9.9600 g | 9.8785 g | 0.3188 | 1.4600 | |
| Median | 9.9454 g | 9.9390 g | 0.1294 | 0.2316 | |
| Standard deviation | 0.1721 g | 0.3363 g | 0.6110 | 8.0346 | |
| Extreme values (%) | 30 | 38 | 13 | 16 | |
| Outliers (%) | 7 | 10 | 11 | 12 | |
| Excluded | Sample size | 64 | 52 | 64 | 52 |
| Mean | 9.945 g | 9.948 g | 0.1974 | 0.2250 | |
| Median | 9.946 g | 9.952 g | 0.1026 | 0.1669 | |
| Standard deviation | 0.0390 g | 0.0418 g | 0.2226 | 0.1715 | |
| Outlier treatment | Measurement | Accuracy (treatment) | Precision (treatment) |
|---|---|---|---|
| Included | t statistic | −1.788 | 1.168 |
| p value | 0.08 | 0.25 | |
| Confidence interval | (−0.172, 0.009) | (−0.808, 3.091) | |
| Effect size (Cohen's d) | 0.305 | 0.200 | |
| Excluded | t statistic | 0.7083 | 0.7523 |
| p value | 0.48 | 0.45 | |
| Confidence interval | (−0.046, 0.097) | (−0.045, 0.100) | |
| Effect size (Cohen's d) | 0.091 | 0.137 | |
Appendix 8. Frequency table and Chi-squared test for categorical breakdown of performance stratified by TA involvement
We ran a Chi-Squared test of independence to test whether the breakdown of performance is associated with TA involvement. We obtained a χ2 = 4.32 (df = 3, p = 0.2). The Cramer's V effect size is V = 0.1. These results indicate that there is a small but statistically insignificant effect, which may be a result of having a small sample size. See Table 7.| Group | Neither | Accurate | Precise | Both | Sum |
|---|---|---|---|---|---|
| Low TA | 31 | 7 | 22 | 8 | 68 |
| High TA | 22 | 5 | 35 | 9 | 71 |
| Sum | 53 | 12 | 57 | 17 | 139 |
Appendix 9. Summary of logistic regression results
See Table 8.| Outlier treatment | Measurement | Accuracy | Precision |
|---|---|---|---|
| Group | Treatment | Treatment | |
| Included | Odds ratio of high TA | 0.87 | 2.06 |
| p value | 0.73 | 0.04 | |
| 97.5% CI upper | 0.38 | 1.05 | |
| 2.5% CI lower | 1.97 | 4.10 | |
| Excluded | Odds ratio of high TA | 0.69 | 1.62 |
| p value | 0.39 | 0.21 | |
| 97.5% CI upper | 3.39 | 1.31 | |
| 2.5% CI lower | 0.62 | 0.28 | |
Acknowledgements
This work was funded by UCLA Instructional Improvement Grant #21-10. The authors would like to thank Dr K. Supriya and the Center for Education Innovation and Learning in the Sciences (CEILS) at UCLA for helpful guidance and discussion on data analysis. We also thank the reviewers for helpful comments.References
- Accettone S. L. W., DeFrancesco C., King C. A. and Lariviere, M. K., (2023), Laboratory Skills Assignments as a Teaching Tool to Develop Undergraduate Chemistry Students’ Conceptual Understanding of Practical Laboratory Skills, J. Chem. Educ., 100, 1138–1148 DOI:10.1021/acs.jchemed.2c00710.
- Agustian H. Y. and Seery M. K., (2017), Reasserting the role of prelaboratory activities in chemistry education: a proposed framework for their design, Chem. Educ. Res. Pract., 18, 518–532 10.1039/C7RP00140A.
- Altowaiji S., Haddadin R., Campos P., Sorn S., Gonzalez L., Villafañe S. M. and Groves M. N., (2021), Measuring the effectiveness of online preparation videos and questions in the second semester general chemistry laboratory, Chem. Educ. Res. Pract., 22, 616–625 10.1039/D0RP00240B.
- Ausubel D. P., (1963), The Psychology of Meaningful Verbal Learning, Grune & Stratton.
- Brown P. C., III H. L. R. and McDaniel M. A., (2014), Make It Stick: The Science of Successful Learning, Cambridge, MA: Belknap Press.
- Bruck A. D. and Towns M., (2013), Development, Implementation, and Analysis of a National Survey of Faculty Goals for Undergraduate Chemistry Laboratory, J. Chem. Educ., 90, 685–693 DOI:10.1021/ed300371n.
- Calibration and Use of a Volumetric Pipet, (2017), https://www.youtube.com/watch?v=0NmbYqERfoo.
- Canal J. P., Hanlan L., Key J., Lavieri S., Paskevicius M., Sharma D., (2016a), Chemistry Laboratory Videos: Perspectives on Design, Production, and Student Usage, Technology and Assessment Strategies for Improving Student Learning in Chemistry, ACS Symposium Series, American Chemical Society, pp. 159–177 DOI:10.1021/bk-2016-1235.ch009.
- Canal J. P., Lowe J. and Fong R., (2016b), Improving Students’ Practical Laboratory Techniques through Focused Instruction and Assessment, Technology and Assessment Strategies for Improving Student Learning in Chemistry, ACS Symposium Series, American Chemical Society, pp. 137–157 DOI:10.1021/bk-2016-1235.ch008.
- Connor M. C., Rocabado G. A. and Raker J. R., (2023), Revisiting faculty members’ goals for the undergraduate chemistry laboratory, Chem. Educ. Res. Pract., 24, 217–233 10.1039/D2RP00215A.
- DeKorver B. K. and Towns M. H., (2015), General Chemistry Students’ Goals for Chemistry Laboratory Coursework, J. Chem. Educ., 92, 2031–2037 DOI:10.1021/acs.jchemed.5b00463.
- DeMeo S., (2001), Teaching Chemical Technique. A Review of the Literature, J. Chem. Educ., 78, 373 DOI:10.1021/ed078p373.
- Eglington L. G. and Kang S. H. K., (2017), Interleaved Presentation Benefits Science Category Learning, J. Appl. Res. Memory Cognition, 6, 475–485 DOI:10.1016/j.jarmac.2017.07.005.
- Foster N. L., Mueller M. L., Was C., Rawson K. A. and Dunlosky J., (2019), Why does interleaving improve math learning? The contributions of discriminative contrast and distributed practice, Mem. Cogn., 47, 1088–1101 DOI:10.3758/s13421-019-00918-4.
- From analysis to action: Undergraduate education in science, mathematics, engineering, and technology, (1996), National Academy of Science, Washington, DC: The National Academy Press.
- General and Organic Chemistry – Use of a Pipet, (2017), https://www.youtube.com/watch?v=YMjy2sK_kBo.
- Hancock L. M. and Hollamby M. J., (2020), Assessing the Practical Skills of Undergraduates: The Evolution of a Station-Based Practical Exam, J. Chem. Educ., 97, 972–979 DOI:10.1021/acs.jchemed.9b00733.
- Hanson S. and Overton T., (2010), Skills required by new chemistry graduates and their development in degree programmes, Higher Education Acadamy UK Physical Sciences Centre, University of Hull.
- Haynes W. M., (2016), CRC Handbook of Chemistry and Physics, 97th edn, Boca Raton: CRC Press DOI:10.1201/9781315380476.
- Hendry G. D., (2013), Using exemplars to scaffold learning, in: Merry M., Carless D. P. and Taras M. (ed.), Reconceptualising Feedback in Higher Education, Abingdon: Routledge, pp. 133–141.
- Hendry G. D. and Anderson J., (2013), Helping students understand the standards of work expected in an essay: using exemplars in mathematics pre-service education classes, Assess. Eval. Higher Educ., 38, 754–768 DOI:10.1080/02602938.2012.703998.
- Hensiek S., DeKorver B. K., Harwood C. J., Fish J., O’Shea K. and Towns M., (2016), Improving and Assessing Student Hands-On Laboratory Skills through Digital Badging, J. Chem. Educ., 93, 1847–1854 DOI:10.1021/acs.jchemed.6b00234.
- Johnstone A. H., (1984), New Stars for the Teacher to Steer by?, 61, 847–849.
- Johnstone A. H., (1997), Chemistry Teaching – Science or Alchemy? 1996 Brasted Lecture, J. Chem. Educ., 74, 262 DOI:10.1021/ed074p262.
- Johnstone A. H. and Wham A. J. B., (1982), The demands of practical work, Educ. Chem., 19, 71–73.
- Jolley D. F., Wilson S. R., Kelso C., O’Brien G. and Mason C. E., (2016), Analytical Thinking, Analytical Action: Using Prelab Video Demonstrations and e-Quizzes To Improve Undergraduate Preparedness for Analytical Chemistry Practical Classes, J. Chem. Educ., 93, 1855–1862 DOI:10.1021/acs.jchemed.6b00266.
- Keen C. and Sevian H., (2022), Qualifying domains of student struggle in undergraduate general chemistry laboratory, Chem. Educ. Res. Pract., 23, 12–37 10.1039/D1RP00051A.
- Kempa R. F. and Palmer C. R., (1974), The Effectiveness of Video-tape Recorded Demonstrations in the Learning of Manipulative Skills in Practical Chemistry, Br. J. Educ. Technol., 5, 62–71 DOI:10.1111/j.1467-8535.1974.tb00623.x.
- Kester L., Kirschner P. A., van Merrienboer J. J. G. and Baumer A., (2001), Just-in-time information presentation and the acquisition of complex cognitive skills, Comput. Hum. Behav., 17, 373–391 DOI:10.1016/S0747-5632(01)00011-5.
- Kirton S. B., Al-Ahmad A. and Fergus S., (2014), Using Structured Chemistry Examinations (SChemEs) As an Assessment Method To Improve Undergraduate Students’ Generic, Practical, and Laboratory-Based Skills, J. Chem. Educ., 91, 648–654 DOI:10.1021/ed300491c.
- Lab Technique Video: Pipetting, (2014), https://www.youtube.com/watch?v=IXLgDnUVc3I.
- Nadelson L. S., Scaggs J., Sheffield C. and McDougal O. M., (2015), Integration of Video-Based Demonstrations to Prepare Students for the Organic Chemistry Laboratory, J. Sci. Educ. Technol., 24, 476–483 DOI:10.1007/s10956-014-9535-3.
- Nicol D., Thomson A. and Breslin C., (2014), Rethinking feedback practices in higher education: a peer review perspective. Assess. Eval. Higher Educ., 39, 102–122 DOI:10.1080/02602938.2013.795518.
- Pollock E., Chandler P. and Sweller J., (2002), Assimilating complex information, Learn. Instruction, 12, 61–86 DOI:10.1016/S0959-4752(01)00016-0.
- Prichard E., (1999), Basic skills of analytical chemistry: do we take too much for granted?, Accred Qual. Assur., 4, 37–39 DOI:10.1007/s007690050308.
- Reid N., (2021), The Johnstone Triangle: The Key to Understanding Chemistry, Royal Society of Chemistry.
- Reid N. and Shah I., (2007), The role of laboratory work in university chemistry, Chem. Educ. Res. Pract., 8, 172–185 10.1039/B5RP90026C.
- Robinson D. H., Katayama A. D., Dubois N. F. and Devaney T., (1998), Interactive Effects of Graphic Organizers and Delayed Review on Concept Application, J. Exp. Educ., 67, 17–31 DOI:10.1080/00220979809598342.
- Russell A. A. and Mitchell B. L., (1979), The use of videotapes in large lab courses, J. Chem. Educ., 56, 753 DOI:10.1021/ed056p753.
- Samani J. and Pan S. C., (2021), Interleaved practice enhances memory and problem-solving ability in undergraduate physics. npj Sci. Learn., 6, 1–11 DOI:10.1038/s41539-021-00110-x.
- Sanchez J. M., (2022), Are basic laboratory skills adequately acquired by undergraduate science students? How control quality methodologies applied to laboratory lessons may help us to find the answer, Anal. Bioanal. Chem., 414, 3551–3559 DOI:10.1007/s00216-022-03992-x.
- Sarkar M., Overton T., Thompson C. D., Rayner G., 2019. Academics’ perspectives of the teaching and development of generic employability skills in science curricula, High. Educ. Res. Dev., 39, 346–361 DOI:10.1080/07294360.2019.1664998.
- Seery M. K., (2020), Establishing the Laboratory as the Place to Learn How to Do Chemistry, J. Chem. Educ., 97, 1511–1514 DOI:10.1021/acs.jchemed.9b00764.
- Seery M. K., Agustian H. Y., Doidge E. D., Kucharski M. M., O’Connor H. M. and Price A., (2017), Developing laboratory skills by incorporating peer-review and digital badges, Chem. Educ. Res. Pract., 18, 403–419 10.1039/C7RP00003K.
- Seery M. K., Agustian H. Y., Christiansen F. V., Gammelgaard B. and Malm R. H., (2024), 10 Guiding principles for learning in the laboratory, Chem. Educ. Res. Pract., 25, 383–402 10.1039/D3RP00245D.
- Stieff M., Werner S. M., Fink B. and Meador D., (2018), Online Prelaboratory Videos Improve Student Performance in the General Chemistry Laboratory, J. Chem. Educ., 95, 1260–1266 DOI:10.1021/acs.jchemed.8b00109.
- The Quality Assurance Agency for Higher Education, (2022), Subject Benchmark Statement: Chemistry, The Quality Assurance Agency for Higher Education.
- The Volumetric Pipet and Pipetting Technique, (2014), https://www.youtube.com/watch?v=HC44xjs7dho.
- Towns M., Harwood C. J., Robertshaw M. B., Fish J. and O’Shea K., (2015), The Digital Pipetting Badge: A Method To Improve Student Hands-On Laboratory Skills, J. Chem. Educ., 92, 2038–2044 DOI:10.1021/acs.jchemed.5b00464.
- Undergraduate professional education in chemistry: ACS Guidelines and evaluation procedures for bachelor's degree programs, (2015), Washington, DC: American Chemical Society.
- Use of A Pipette Pump, n.d. https://www.molsci.ucla.edu/downloads/Use_of_a_pipette_pump.mp4.
- Van Merriënboer J. J. G., Kirschner P. and Kester P., (2003), Taking the Load Off a Learner's Mind: Instructional Design for Complex Learning, Educ. Psychol., 38, 5–13 DOI:10.1207/S15326985EP3801_2.
| This journal is © The Royal Society of Chemistry 2024 |