Use of machine learning to analyze chemistry card sort tasks
Logan
Sizemore
 *a,
Brian
Hutchinson
*a,
Brian
Hutchinson
 ac and
Emily
Borda
b
ac and
Emily
Borda
b
aDepartment of Computer Science, Western Washington University, Bellingham, WA, USA. E-mail: sizemol@wwu.edu; Brian.Hutchinson@wwu.edu
bDepartments of Chemistry and Science, Math, and Technology Education (SMATE), Western Washington University, Bellingham, WA, USA. E-mail: bordae@wwu.edu
cComputing and Analytics Division, Pacific Northwest National Laboratory, 902 Battelle Blvd., Richland, WA 99354-1793, USA
First published on 7th November 2023
Abstract
Education researchers are deeply interested in understanding the way students organize their knowledge. Card sort tasks, which require students to group concepts, are one mechanism to infer a student's organizational strategy. However, the limited resolution of card sort tasks means they necessarily miss some of the nuance in a student's strategy. In this work, we propose new machine learning strategies that leverage a potentially richer source of student thinking: free-form written language justifications associated with student sorts. Using data from a university chemistry card sort task, we use vectorized representations of language and unsupervised learning techniques to generate qualitatively interpretable clusters, which can provide unique insight in how students organize their knowledge. We compared these to machine learning analysis of the students’ sorts themselves. Machine learning-generated clusters revealed different organizational strategies than those built into the task; for example, sorts by difficulty or even discipline. There were also many more categories generated by machine learning for what we would identify as more novice-like sorts and justifications than originally built into the task, suggesting students’ organizational strategies converge when they become more expert-like. Finally, we learned that categories generated by machine learning for students’ justifications did not always match the categories for their sorts, and these cases highlight the need for future research on students’ organizational strategies, both manually and aided by machine learning. In sum, the use of machine learning to analyze results from a card sort task has helped us gain a more nuanced understanding of students’ expertise, and demonstrates a promising tool to add to existing analytic methods for card sorts.
Introduction
Making sense of new information is dependent on one's ability to organize knowledge into a framework that facilitates its retrieval and use (Gentner and Medina, 1998; Bransford et al., 2000). Card sort tasks, in which individuals are asked to group cards representing problems by similarity, have been used as a means to understand how students organize their knowledge and investigate the development of expertise, e.g., (Chi et al., 1981).In chemistry, a specific dimension of one's knowledge organization is their ability to connect three levels of understanding or representation described in Johnstone's (1982) chemistry triplet: submicroscopic, macroscopic, and symbolic. This triplet was originally proposed to expose the difficulty that linking such levels of representation and understanding poses to a novice, and establish that connections between these levels requires instructional support. In an earlier study, we developed a card sort task to investigate students’ ability to connect these three triplet levels by recognizing common principles among problems represented on different levels (Irby et al., 2016). Although on average, the sorting data showed a positive correlation between the amount of one's formal chemistry instruction and their ability to sort by underlying principles, there were several sorts and verbal justifications for sorts that were difficult to make sense of. We wondered if there were patterns in students’ thinking that were not easily captured by this card sort and associated analytic techniques.
Here we report the use of machine learning techniques to analyze a larger dataset captured with the same card sort task. The results from the use of machine learning to analyze both the sorts and the sorting justifications suggest novel ways of approaching the card sort task, with associated implications for students’ knowledge structures when learning chemistry. Our method also adds tools and analytic approaches to support future studies using card sorts.
Theoretical framework
In this work we investigate the use of a card sort task to investigate students’ expertise in chemistry. A dimension of expertise we drew upon to design and interpret results from this task is the idea of schemas. Schemas are described as mental representations of a problems created by individuals engaged in problem-solving tasks (Eysenck and Keane, 2005; Galotti, 2014). Research suggests schemas change with learning (Revlin, 2012), and that the more abstract and principle-based, vs. context-bound, the schema, the more readily an individual can apply it across problems with similar underlying principles, even if those problems might look distinct on the surface (Chen, 1999). Thus, the development of expertise involves, at least in part, the modification of schemas to become more abstract and generalizable, a process called re-representation (Gentner, 2005).A separate but related lens through which to view expertise is that of knowledge organization. The cognitive science literature tells us expertise requires not only a breadth of factual knowledge, but also a conceptual framework that organizes the knowledge in a way that facilitates retrieval (Bransford et al., 2000). A well-defined knowledge structure facilitates long term storage and easy retrieval of factual information (Mayer, 2012). Studies show knowledge structures become more interconnected through the acquisition of expertise (Acton et al., 1994). This finding may also relate to schemas becoming more abstract as an individual gains expertise, as discussed above, where a more interconnected knowledge structure is more abstract and generalizable. Studies performed using an organic chemistry reactions card sort task show consolidation of knowledge structures with more expertise (Galloway et al., 2018). Card sorts are also a way of investigating categories that guide one's knowledge structure. Open-ended card sort tasks have been used to surface different categories or “bins” individuals use to express similarities between problems or information represented on the cards (Yamauchi, 2005). These categories can reflect the quality of a learner's knowledge structure, in terms of how well information linked together in a category facilitates the application of that information to a range of different types of problems and tasks. For this reason, card sort studies often ask individuals to name the groups they create, and almost always have a qualitative component asking the individual to justify their groupings.
The chemistry triplet, originally proposed by Johnstone in 1982 (Johnstone, 1982), combines ideas about knowledge organization and representation in describing expertise in chemistry. As expertise grows, individuals are able to better connect the three levels of understanding and representation in the triplet: macroscopic, submicroscopic, and symbolic (Irby et al., 2016). The macroscopic level represents human-scale observations, which can be aided by instrumentation. An example of a macroscopic scale set of observations is that when table salt is added to water, it yields a clear, colorless liquid that nevertheless tastes different from pure water. In addition, this mixture conducts electricity, whereas pure water does not. The submicroscopic scale usually represents a small particle model or explanation for what is happening with molecules, atoms, and/or ions, to produce the results observed on the macroscopic scale. A submicroscopic-scale explanation would be that sodium chloride splits up into positively- and negatively-charged ions that are surrounded by water molecules which are attracted through their partial charges to the ions. These ions can move in response to external charges, to which they are attracted or repelled. The symbolic scale expresses observations or small particle models with symbols, such as mathematical or chemical equations, or graphs. A symbolic-scale description of the dissolution of salt in water might be expressed through this chemical equation: NaCl(s) → Na+(aq) + Cl−(aq). While a novice might think about the chemical equation and whatever problem solving tasks they might encounter involving it as separate from a drawing, simulation, or even mental representation of small particles of sodium chloride breaking up into charged ions and being surrounded by water, and might further separate the observations of salt water forming from the dissolution of salt in water and conducting electricity from the equation and/or small particle model, an expert tacitly links the three domains of knowledge to form a knowledge structure that is explanatory, predictive, and generalizable. Studies have shown, for example, that novices can successfully work problems oriented at the symbolic level while failing to successfully work problems that integrate representations of more than one level of the chemistry triplet (Jaber and BouJaoude, 2012).
The problem of connecting components of the chemistry triplet is in part related to an individual's ability to decode representations, an activity that is not necessarily straightforward to novices (Kern et al., 2010). In addition, the process of making such connections is thought to be more than a question of representational competence, and in fact, is part of what it means to understand concepts and principles in chemistry (Johnstone, 1982; Taber, 2013). For example, one's ability to visualize sodium and chloride ions being solubilized in water while observing salt being added to water is evidence of their ability to create a model or explanation for what is going on that can be used to make predictions. Indeed, creating and using models, explanations, and arguments is central to any scientific endeavor (National Research Council, 2012) and in chemistry, necessarily involves linking these three levels of understanding/representation. In this sense, connecting the components of the chemistry triplet in the service of solving a problem, making a prediction, or constructing an explanation can be thought of as developing an abstract schema that connects two or more parts of the chemistry triplet.
Card sorts as methods for investigating expertise
Individuals’ schemas, knowledge organization, and specifically in chemistry, their ability to integrate components of the chemistry triplet, are all dimensions of expertise that are difficult to investigate through traditional knowledge inventories or surveys. This is because these dimensions focus on how students connect and use different components of their knowledge; e.g., what they do with that knowledge, not necessarily to what extent they have acquired that knowledge. We relied on a card sort task because when students sort cards, they are demonstrating their thinking about how concepts are related, or unrelated, to each other.Classification and card sort tasks have been widely used to investigate expertise in various domains (Chi et al., 1981; Smith, 1992; Kozma and Russell, 1997; Lajoie, 2003; McCauley et al., 2005; Domin et al., 2008; Stains and Talanquer, 2008; Lin and Singh, 2010; Mason and Singh, 2011; Smith et al., 2013; Irby et al., 2016; Krieter et al., 2016; Graulich and Bhattacharyya, 2017; Davidson et al., 2022; Lapierre et al., 2022). A finding on which much of this literature has converged is that novices tend to focus on surface features and experts focus on underlying principles and concepts when sorting cards displaying problems (Singer et al., 2012). This finding, developed in physics (Chi et al., 1981) and reproduced in biology (Nehm and Ridgway, 2011; Smith et al., 2013), chemistry (Irby et al., 2016; Krieter et al., 2016; Graulich and Bhattacharyya, 2017; Galloway et al., 2018), and geology (Davidson et al., 2022), is undergirded by research on schemas from the problem solving literature.
Card sort data are often quantitatively analyzed by how close they are to the canonical sorts upon which their design is based; for example, edit distances (Deibel et al., 2005; Smith et al., 2013) describe the smallest number of rearrangements necessary to change the sort into one or the other canonical sorts, while sorting coordinates (Irby et al., 2016) describe the sort's “distance” from the canonical sorts. Subsequent researchers have used edit distance in conjunction with normalized minimum spanning-trees to measure the orthogonality of sorts given by participants of an administered single-criterion card sort task (Fossum and Haller, 2005; McCauley et al., 2005). Gelphi maps have also been used to graphically depict common groupings (Galloway et al., 2018; Lapierre et al., 2022). In order to find clusters of common sorts produced by participants in a card sort study, cluster techniques, including k-means clustering, have been effectively employed (Ewing et al., 2002; Bussolon, 2009; Paul, 2014; Shinde et al., 2017; Stiles-Shields et al., 2017; Macías, 2021; Paea et al. 2021; Carruthers et al., 2019; Gläscher et al., 2019). Our work describes the use of clustering on the free-form responses students gave for their card sort, which to our knowledge, has not been done before in the context of card sort tasks. Card sort tasks are often accompanied by interviews asking students to name and/or justify their sorts. These qualitative data are also most often analyzed by what type(s) of canonical sorts are represented. While these can be effective ways of determining whether a student organizes their knowledge around underlying principles or surface-level representations, often in practice neither a student's knowledge nor their sort are purely principle- or representation-based. Any method of analysis relying solely on how close a given student's sort is to a canonical sort will lose the potentially nuanced justification for that student's sort. These types of analyses also assume students who sort alike think alike, and that there is some unique relationship between the way a student sorts and their schemas. Instead, it would be beneficial for a researcher to be able to utilize a student's language justification of their sort, a potentially richer signal of their thought processes. Leveraging the language used to justify a student's sort may provide insight into ways of organizing knowledge that combine, or fall outside of, the canonical principle or representation categories upon which the cards are based.
Although qualitative data analysis is crucial to adding the nuances described above to card sort studies, it is labor intensive. In most of the card sort studies cited here, manual coding was used to analyze qualitative data coming from participants’ verbalization or written justifications for their groupings. In some cases, codes were used to develop emergent themes for students’ sorting patterns (e.g., Stains and Talanquer, 2008; Galloway et al., 2018), while in other studies codes reflect hypothesized novice and expert sorts upon which tasks were originally created (e.g., Smith et al., 2013; Irby et al., 2016). These methods can be highly labor intensive and difficult to apply consistently, especially with large datasets, and may cause researchers to miss ways of grouping that were not initially hypothesized when the card sorts were created. As Fincher and Tenenberg (2005) highlight, there are computational techniques that can help in overcoming the challenges associated with analyzing card sort data, especially for large datasets. In this paper, we further extend this line of work by describing the use of machine learning methods to analyze card sort data. We applied these methods to a card sort task we designed to investigate students’ abilities to connect the three levels of understanding and representation in the chemistry triplet (Irby et al., 2016). In this task, general chemistry problems on three different topics are represented primarily on one of the three levels of the chemistry triplet, so that level of representation competes with the underlying principle needed to solve the problems. We hypothesized that as individuals gain expertise, they would more readily cross between levels of representation to group cards by the underlying principles needed to solve the problem. Although the quantitative evidence from the students’ sorts largely supported this hypothesis, much of the qualitative data from interviews in which participants justified their sorts were impossible to categorize into novice and expert anchor points. Thus, we used machine learning methods to uncover alternate sorting frameworks students used in order to help us investigate students’ schemas and knowledge structures in a more nuanced way, potentially aiding in the exploration of the development of expertise, which is arguably less well understood than the differences between novices and experts (Stains and Talanquer, 2008).
Research questions
The research questions guiding our study are: (1) How can machine learning be applied to help us better understand card sort data – both the sorts themselves and the justifications for the sorts, and (2) What new understandings of students’ schemas can be uncovered through the use of machine learning to analyze a chemistry card sort task crossing levels of the chemistry triplet with general chemistry principles?Methods
In this paper, we describe a variety of unsupervised machine learning approaches to analyze students’ card sorts and their free-form written justifications using the chemistry card sort task (Irby et al., 2016). Unsupervised machine learning (Hastie et al., 2009) is a term that encompasses a collection of techniques aimed at learning from data or discovering patterns therein without explicit annotations, labels, or other guidance from a researcher. Our primary goal for analysis is to place each student in our dataset within a space such that students who sort or justify their sorts similarly are positioned closer to one another, and students who sort or justify their sorts dissimilarly are positioned far from each other. We use machine learning techniques to assign each student a sequence of coordinates defining their position in a high dimensional space. This sequence is called a vector. From these vectors we can identify and characterize potential themes. In this work we create two spaces: a “sort space” based on students’ sorts and a “language space” based on students’ justifications for their sorts. These two spaces enable us to identify separate themes related to sorts and justifications, potentially uncovering more nuanced ways students organize their knowledge around the chemistry problems. We can also begin to address whether students who sort alike also justify their sort in a similar way, and vice versa.Data collection methods
Our data were collected from students in general and organic chemistry courses at a medium sized, master's-granting regional university. All students were given course credit for completing the task, and only data from those who consented to participate in the study in our IRB-approved informed consent process were included in the data set for analysis. Participants completed an online version of the chemistry card sort task, in which they were told to sort chemistry problems (cards) into different groups representing related concepts needed to solve the problems. The same general procedure and prompts described in Irby, et al. (2016) were used, including the requirement that students had to create between two and eight groups (i.e., they could not put all of the nine cards into one group, nor could they put each card in its own individual group). Initial data from a pilot of the online task showed similar sorting patterns as in the original study done via face to face interviews, reinforcing the finding that students with more chemistry preparation sorted, on average, increasingly by underlying principle. The online sort task included fields for students to write a title and justification for each group a student created. Responses were discarded if the student did not consent to participate in the study; gave duplicate responses; responded in fewer than five minutes; gave an incomplete response; gave inaccurate information about themself, their instructor, or their class; or if they responded in such a way that showed that they failed to read the card sort task instructions. In total, 1722 responses were deemed acceptable for analysis. These came from students enrolled in general or organic chemistry, as described in Table 1. Data from these students were aggregated to give a wide breadth of responses in order to allow us to develop machine learning methods of analysis.| Chemistry course | Classes | Unique instructors | Students |
|---|---|---|---|
| General chemistry 1 | 16 | 11 | 611 |
| General chemistry 2 | 10 | 8 | 513 |
| General chemistry 3 | 6 | 6 | 402 |
| Organic chemistry 1 | 4 | 3 | 146 |
Card sort task
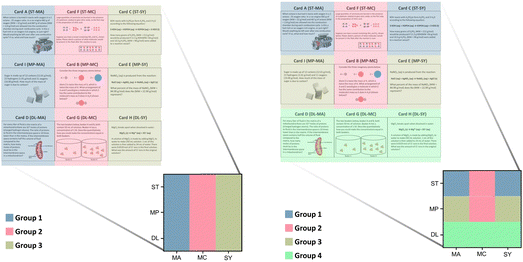
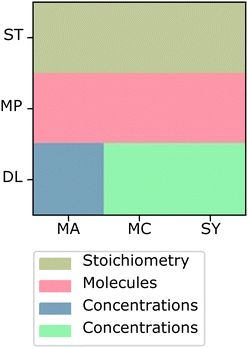
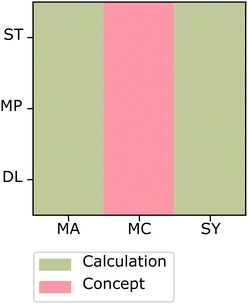
The card sort task used in this study (Irby et al., 2016) consists of 9 cards, each representing a typical problem from a general chemistry course. The card set crosses three underlying principles stoichiometry (ST), mass percent (MP), and dilution (DL) with the three levels of representation in the chemistry triplet, macroscopic (MA), submicroscopic (SA), and symbolic (SY), such that each card presents a unique combination of underlying principle and level of representation (Fig. 1). Participants are given these nine problems in random order and asked to sort the cards based on similar concepts one would need to solve each problem. This task was designed to have two canonical sortings, both of which consist of three groups of three cards each: a principle sort and a representation sort (the rows and columns, respectively, of Fig. 1). While participants may sort the cards any way they feel is appropriate, our previous study with this sorting task has shown that those with more chemistry preparation tend to sort the cards based on underlying principles, while those with less chemistry preparation sort their cards based on the representation of the cards or surface-level features (Irby et al., 2016).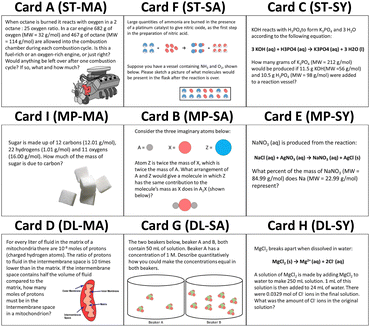 | ||
| Fig. 1 Card sort task (Irby et al., 2016). Each row corresponds to an underlying principle and each column corresponds to a representation. Underlying principles and representations are shortened to two letter identifiers. Stoichiometry (ST), mass percent (MP), dilution (DL), submicroscopic (SA), macroscopic (MC), and symbolic (SY). | ||
Methods for clustering students’ responses
Card sort tasks can be useful assessments of students’ knowledge organization, and clustering can reveal patterns in students’ knowledge structures, potentially providing insight into their schemas. Below we describe how we generated vectorized representations of both the language students used to justify their sorts, and the sorts themselves. Unsupervised machine learning techniques then used these representations to generate interpretable clusters, or groups, of similar data.Using sorting coordinates, we calculated the distance from each student sort to each other student sort, resulting in vectors containing 1722 integers for each of the 1722 student responses. These distances define an implicit sort space, where similar sorts occupy a similar location within that space. We can use this sort space to identify groups (clusters) with similarities we may not have uncovered through a manual sorting study.
Clustering students’ responses
Once we have defined a space for both the language and the sorts students produce, we can divide up this space into clusters of student responses, where the responses in each cluster are more similar to each other than the those outside their assigned cluster.We used the k-means algorithm to identify clusters of data within the language and sort spaces. The expectation is that students who used similar language to justify their sort will be assigned to the same language space cluster. Likewise, students who sorted in a similar way will belong to the same sort space cluster, allowing us to identify potential new common sorting patterns.
| Wr = (Wc/Tc)/(Wo/To) |
Results
We used the k-means clustering algorithm to address our first research question regarding how we can use machine learning to understand card sort data. Each cluster generated from this procedure potentially represents a theme within the dataset, helping us to identify emergent themes that would be difficult to detect through manual coding. By uncovering emergent themes, we can begin to address our second research question regarding how we can use machine learning gather new understandings of students’ knowledge structures, which, as discussed above, may be related to their schemas. Because the acquisition of expertise involves the organization of factual information into categories for easy retrieval and application, an alternative perspective on the way that students categorize information could also shed light on how students acquire expertise. In this section we describe the clusters generated first in the language space then in the sort space. Finally, we characterize intersections between the two.Language clustering
The justifications were processed into numerical vectors, or embeddings. As described in Methods, this was done by passing each student justification through a pre-trained BERT language model and taking the mean of the word embeddings to produce a single sentence embedding. Using these BERT sentence embeddings, we were able to generate clusters of similar responses. Metrics like the silhouette score did not indicate how many clusters ought to be made for the language clusters, primarily because there was no clear trend as a function of the number of clusters. Instead, we analyzed the dataset a number of times with different numbers of clusters and chose the number we thought generated the most informative themes.The Sankey diagram in Fig. 3 summarizes the different clusters that were uncovered as a greater number of clusters were chosen for the k-means clustering algorithm, with lines representing clusters and ribbons representing changes in group membership as different numbers of clusters were chosen. The width of each ribbon scales with the number of justifications it represents. We gave each cluster a label based on manual examination of the justifications, as quantitative metrics were insufficient to uncover the themes.
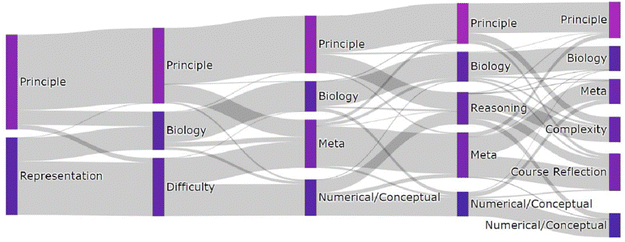 | ||
| Fig. 3 Sankey diagram representing the distribution of justifications from two to six clusters in the language space. | ||
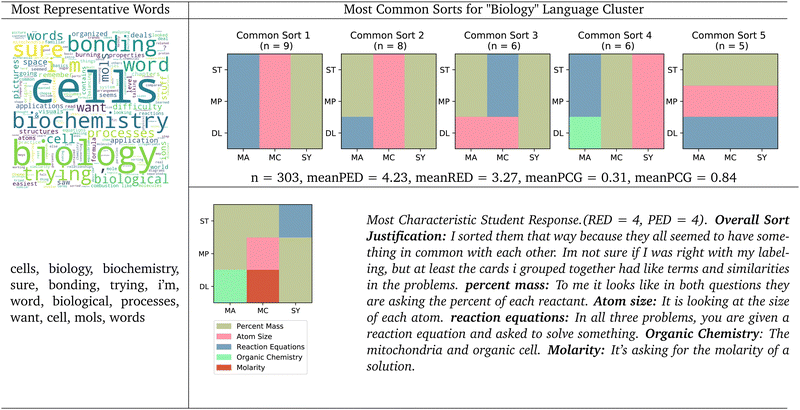
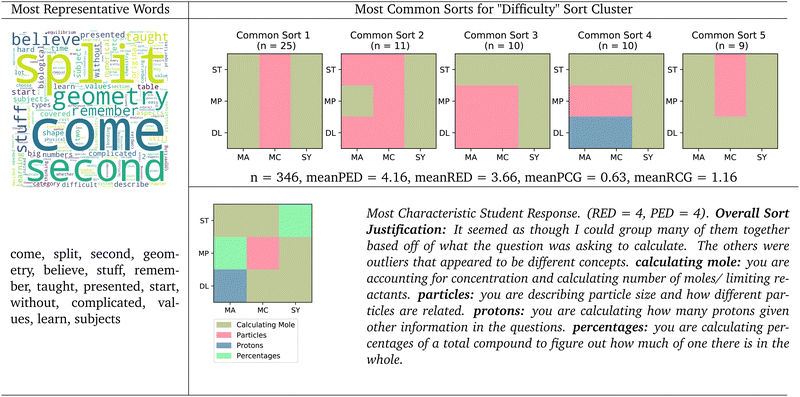
Regardless of how many clusters were specified, there seemed to be clusters that we could qualitatively characterize as a principle-based. As more language clusters were specified, the justified “principle” cluster's average PED approaches zero, indicating that underlying principle language is closely tied to the underlying principle sort. In contrast, representation as a theme in the language data was no longer evident when three or more clusters were specified. Instead, various distinct themes perhaps tied to representation-based justifications became evident. For example, the “Representation” cluster is split into two from step two to three in the Sankey diagram. The first of these two new clusters was characterized as “Biology”, where students used unique language related to biological concepts. This theme remains from three clusters onward. The other new cluster in the transition from two clusters to three is characterized by us as “Difficulty”, which consists of justifications expressing some level of difficulty in addressing the card sort task, including words like “difficult”, “harder”, “hard”, and “help”.
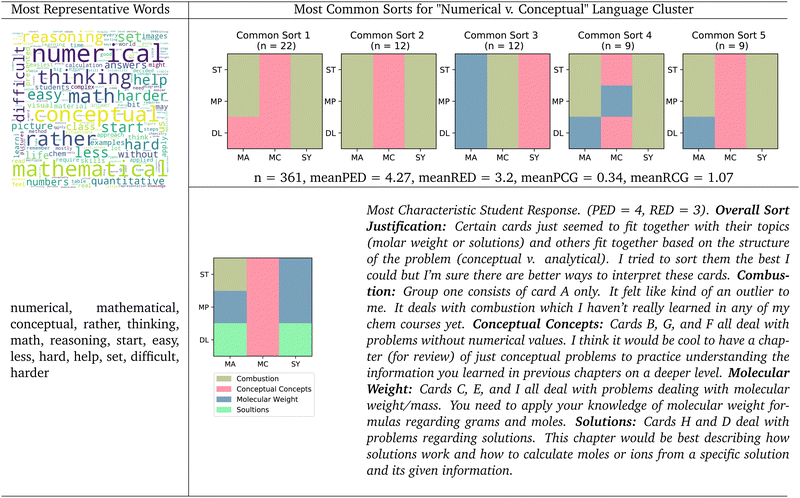
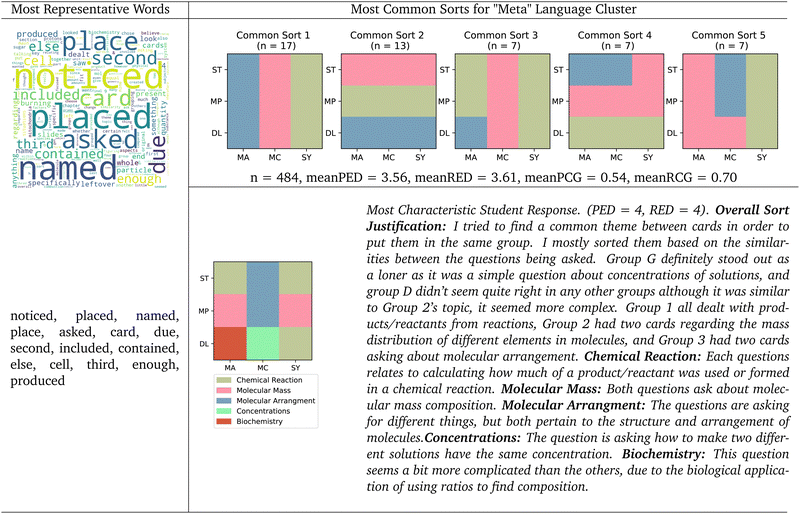
When four clusters were specified, subsets of the “Difficulty” and “Principle” clusters combined to form a “Meta” cluster, where students justified their sorts by focusing on the mechanics of the task itself, instead of the underlying concepts. Students in the “Meta” cluster often described the constraints of the task or the act of placing the cards. There continued to be a justifiable “Meta” theme with up to six clusters. The remaining subset of the difficulty cluster is best characterized as a “Numerical vs. Conceptual” cluster, containing responses expressing a perceived dichotomy between problems requiring math and problems requiring understanding of one or more concepts.
As five clusters were specified, there remained qualitatively justifiable “Principle”, “Biology”, “Meta”, and “Numerical vs. Conceptual” clusters. In addition to these four clusters, we characterized the new cluster as a “Reasoning” cluster, which was created from a subset of the “Numerical vs. Conceptual” and “Principle” clusters. The “Reasoning” cluster is composed of responses revealing the methods of solving a problem that include words like “applied”, “solved”, and “reasoning.” These justifications suggest process-oriented thinking in approaching the task.
When six clusters were specified, four clusters shared a characterization from the five clusters specification: “Principle”, “Biology”, “Meta”, and “Numerical vs. Conceptual.” In addition, we characterized two new clusters: “Complexity” and “Course Reflection.” The “Complexity” cluster is primarily a subset of the reasoning cluster that contains words like “complex”, “basics”, and “intro”, suggesting expressions of how complex or basic students perceive a chemistry problem to be. The “Course Reflection” cluster is primarily composed of a subset of the “Meta” cluster and a subset of the “Reasoning” cluster and contains words like “time”, “learning”, and “taught”, which partially suggest recollection of learned knowledge. The most representative student response in this cluster: “I chose the particular groups based on my previous knowledge of chemistry and how it has been taught to me in the past” further supports this characterization.
Finally, we found that a cluster that could be justifiably characterized as “Underlying Principle” could be found regardless of the number of language clusters specified. The students whose responses were categorized in this cluster also tended to sort according to the underlying principle canonical group. However, there was not a single cluster that could be justifiably characterized as belonging to our representation-based canonical grouping beyond when two clusters were specified. Instead, the representation cluster seemed to split into many different themes, perhaps suggesting the external representations of the cards were less meaningful to students than the other themes. Although there is no clear method for choosing a number of clusters, one could argue that all of the themes uncovered in the analysis of the different sets of clusters are potentially elements of students’ schemas when presented with chemistry problems represented in different ways. Further, the observation that the principle-based themes seemed more stable than representation-based themes in the clustering analysis may lead to insights about the relative stability of these ways of organizing knowledge, and support claims that principle-based sorting is associated with more expertise. insights relate to our first research question regarding how machine learning can be applied to help us better understand card sort data.
The most characteristic student response seems to support our earlier analysis. This student also seemed to identify some underlying principles, as one group was titled “Percent Mass”, which appears to relate to the “Mass Percent” canonical grouping, and another group was titled “Molarity”, seemingly relating to the “Dilutions” canonical grouping. However, these student groups only represent the underlying principle canonical groups in name only, as the cards within these student groups do not resemble what we would expect from a student who organizes their knowledge around underlying principles. Still, this student's use of language seems to show that they were able to identify these underlying principles as meaningful group categories. In a similar way, this student created a group titled “reaction equations”, which relates to the “symbolic” surface-level representation canonical sort, but only contains the symbolic-stoichiometry card.
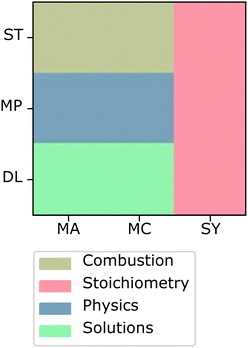
The most characteristic student response illustrates this dichotomy. This student justified their sort by suggesting that some of the cards “fit together based on the structure of the problem (conceptual vs. analytical).” This student's second group was named “conceptual concepts”, and they sorted the cards within that group because the student thought that they did not require calculations. The third and fourth group justifications make reference to “formulas” and making calculations, as opposed to a “concept.” This student also showed some lack of certainty in the way they sorted their cards, as they indicate in their overall sort justification by suggesting that there may be some better way that these cards could be sorted. Additionally, this student indicates that they were unsure about how to sort the cards in their first group titled “Combustion”. The language this student uses, along with their uncertain justifications, support the idea that this is a cluster of students who see a “conceptual vs. mathmatical” divide among these problems, but there is also some expression of the difficulty of the task.
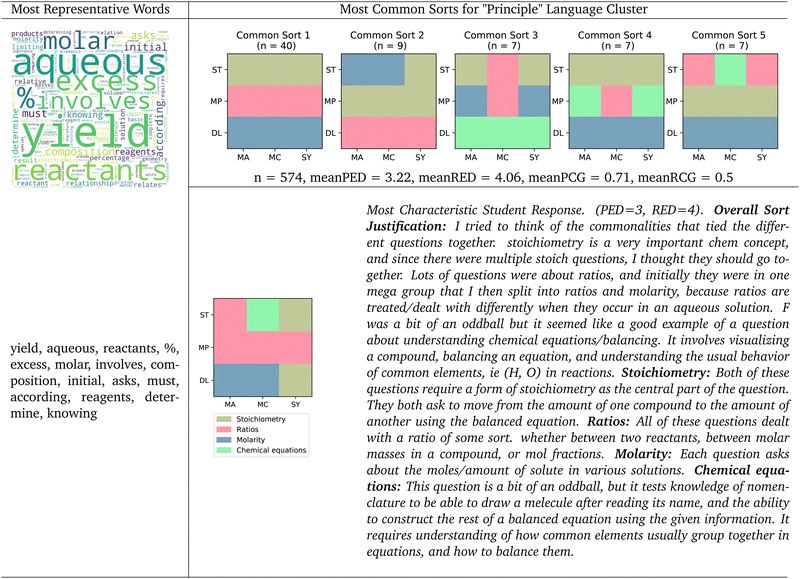
The most characteristic justification for this cluster suggested the student was able to identify the underlying principles of the problems printed on the cards among the various surface-level representations. Of these students’ four groups, three seem to map onto the three underlying principles built into the task. This student called their first group “stoichiometry”, and proceeded to describe the principle. The student continued to describe their second group as “ratios”, describing how this group included cards that have to do with molar masses and mole fractions, indicating a conceptual understanding of the “mass percent” chemistry underlying principle. This student's third group is called “molarity” and they describe how all the questions in that group had to do with “moles of solute in various solutions,” which maps to a dilutions canonical underlying principle group. While this student seemed to do well in identifying the underlying principles present in the task, they struggled to place the cards into canonical principle groups. Despite this student's justification being the most representative response of the principle language cluster, this student achieved a PED of 3 and a RED of 4, which is neither close to the underlying principle canonical sort nor the surface-level representation canonical sort. In this case, looking at the sort scoring metrics alone would not have captured this student's sort as based in underlying principles.
While the most common sort within a cluster may provide valuable information to a researcher, its primary function is to quantify the dominant pattern in a data set. However, it does not necessarily reflect the unique characteristics and nuanced features of a specific cluster. The primary goal of our analysis seeks to capture more than frequency. For instance, in the principle language cluster, while a large plurality of students provided a canonical principle-based sort, this uniformity can only offer insights into what is prevalent but not necessarily what is distinctive.
The ‘most characteristic student response’ better captures the essence of a cluster by identifying a response that is the most representative of the characteristics defined by the cluster's centroid, which might show subtleties and specificities that are potentially lost by analyzing the ‘most common sort.’ Researchers in Irby et al. found that students who sorted based on principles exhibited principle-based reasoning in their sort justification (Irby et al., 2016), and that is consistent with what we find in this paper. However, we are interested in the characteristic response that embodies the distinct features of the principle language cluster, which may or may not align with the most common sort.
The analytical techniques described in this paper aligns with the affordances offered by machine learning, allowing researchers to analyze a large amount of data, identify underlying patterns, and glean insights that would be infeasible to uncover using traditional qualitative methods.
Clustering in the sort space
We can compare to what extent students’ justifications match their actual sorts by defining, and creating clusters within, a “Sort Space”. The sort space was created by assigning each student a vector containing a series of distances between that student's sort and the sort of every other student. Students who made similar sorts were positioned near one another in this sort space, while students who made dissimilar sorts were positioned far from one another. We created these clusters using the k-means clustering algorithm. Each cluster can be interpreted a theme found in the student card sort responses. A student's sort is indicative of the way they organize their knowledge. This helps us understand how the student approaches the material, what sort of knowledge they prioritize, and can potentially provide a window into their schemas. As in the previous section, the names chosen for these clusters were qualitatively determined by considering the most common sorts, the most representative words, and the various quantitative methods used to characterize groups of student responses, including edit distance and triplet occurrence (Fig. 7 and 8).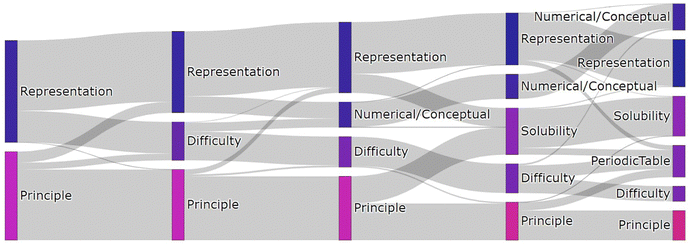 | ||
| Fig. 8 Sankey diagram representing the distribution of justifications from two to six clusters in the sort space. | ||
When five clusters were specified, the previous four groups carried forward with the addition of a new cluster, which we characterized as a “Solubility” cluster. This cluster is composed primarily of two subsets of sorts belonging to the “Underlying Principle” and “Surface-Level Representation” clusters when four clusters were specified. These sorts tended to be closer to the underlying principle canonical sorting, but they emphasized the microscopic surface-level representation. As six clusters were specified, five of the clusters could be justifiably characterized with the same titles as the previous clusters, with the sixth characterized as a “Periodic Table” cluster. Responses in this cluster included language suggesting students based their sorts on information and trends found in the periodic table.
In this case we were able to use a silhouette score to determine the ideal number of clusters, as the silhouette score peaked when three clusters were specified. This is especially interesting considering the card sort task was originally designed with two methods of sorting in mind. Because our primary goal was to investigate the utility of machine learning to analyze the language data, we do not describe the sort clusters in detail here. This information can be found in the appendix. The most notable findings from this exercise for the purposes of our study are that students’ language did not always match their sorts, and that different types of groups outside of the principle and representation canonical sorts were defined in the two spaces. These findings are further explored below, where the language and sort spaces are compared.
Language and sort cluster intersections
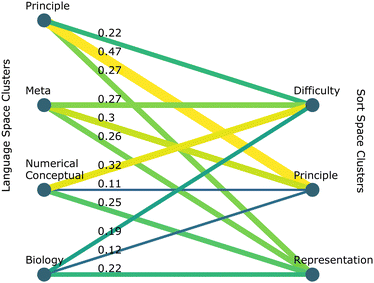
It is conceivable that students who sort alike do not think alike, and vice versa. Examining the intersection between the clusters of students who sort alike and the clusters of students who use similar language can shed light on students’ knowledge structures and potentially the schemas they use to approach problems.About a third of students within the difficulty sort cluster produced language that put them into the numerical vs. conceptual language cluster. A key feature of this cluster was the prevalence of language expressing difficulty in completing the card sort task. There is relatively equal representation of the other three language clusters within the difficulty sort cluster, with the biology language cluster least represented. A more detailed analysis of a subset of these sort intersections can be found in the appendix.
By clustering in both the sort space and the language space, we find that there is no clear one-to-one relationship between the language that students use and the sort that they make, especially as it relates to a non-expert level ways of organizing knowledge. However, we find that expert ways of sorting cards tend to use similar kinds of language because there is greater crossover between the principle language cluster and principle sort cluster than the other clusters. This suggests novice students who sort similarly may not organize their knowledge similarly. Similarly, novice students with similar knowledge structures may sort in diverging ways.
Conclusion
Discussion
In this paper we describe methods involving machine learning to analyze results from a card sort task and its associated language data. These methods helped to uncover nuances in student thinking that are potentially associated with their representational schemas related to the chemistry triplet. One important finding is that students had many different ways of expressing their ideas about how the problems were related to each other, especially when their sorts took on more characteristics of surface-level sorts. They characterized problems by difficulty, by discipline, or by the process needed to solve the problem.Notably, several students shared a particular sort but justified their sorts in different ways. For example, the canonical surface-level representation group was a member of the top five most common sorts of the biology language cluster, the numerical vs. conceptual language cluster, and the meta language cluster. This shows the sorts themselves don’t tell the whole story about students’ reasoning, and that analysis of students’ language is necessary to gain a fuller picture of how they organize knowledge. This is an illustration of the potential richness that machine learning can add to a card sort analysis, as the identification of more than one reasoning type for a single sort would have been very difficult through manual analysis. Machine learning is one way to supplement existing methods to further unpack justifications in cases like these.
Further, unpacking these results potentially adds finer detail to the conceptual framework on which it is based. The card sort task was developed with two canonical sorts related to principle- to representation-level thinking, based upon the concept of the chemistry triplet (Johnstone, 1982). When clustering the language into four clusters, we found there was a distinct underlying principle cluster, but that there was not an explicit, unique surface-level representation language cluster. Instead, the three remaining clusters (meta, numerical vs. conceptual, and biology) seemed to act as different kinds of surface-level feature clusters. The fact that more surface-level feature clusters were created, compared to principle-based clusters, suggests that students used a greater diversity of distinct language when justifying surface-level features sorts that grouped each triplet level together, while students used more homogenous language when justifying underlying principle sorts, where the three levels of the chemistry triplet were combined. One potential implication of this finding is that there are several ways to organize knowledge within each of the three levels of the triplet, but fewer ways to connect them. In order for a chemistry novice to make a sort based on the chemistry triplet, the novice must have enough chemistry expertise to identify the chemistry triplet among the cards. Some students struggled to make any connections between the cards, and they ended up creating few groups with many cards or many groups with few cards. This seems to suggest that there is a lower “level” sort below what we defined as the novice sort. Additionally, making connections between the levels of the triplet may show expertise, but it also may show random pairings due to a complete lack of expertise.
Our work demonstrates the potential usefulness of machine learning methods to analysis of results from card sort data. When paired with human expertise, judgment, and interpretation, machine learning can provide ways of gaining insights that may not be easily uncovered through other methods for analyzing card sort tasks. Traditional qualitative analysis alone often requires a high investment of resources, and still may not capture certain nuances in student thinking, especially regarding categories or organizational schemes that the card sort task was not originally designed to elicit. Here we demonstrate that machine learning techniques in association with a card sort task can enhance the analysis of language data and potentially uncover novel ways of organizing and reasoning with the cards. Further, machine learning techniques may be used to develop and validate new card sort tasks, allowing researchers to create a task where the language used by students and the sort they give closely align. Such alignment may provide evidence that a student's sort closely approximates their knowledge structure and may give valid insight into their schema.
Limitations
A primary limitation in our method comes from our choice to use the k-means clustering algorithm. Recall that the k-means clustering algorithm places centroids, or the average vector of the points belonging to a cluster, within the clustering space and then adds data points to each of the clusters based on their proximity to the cluster centroids. The placement of these centroids is somewhat random. This does not mean that the clusters themselves are random, and the clusters in this analysis tend to closely align between random states, but the random variation makes it difficult to make claims about cross-sectional or longitudinal changes between student groups. Future work may include new strategies that can allow a researcher to make claims about how students transition between these clusters with more domain-specific knowledge preparation. As of this time, these methods may be best used as a means of characterizing a dataset as a whole. Future work may involve the use of different methods of clustering data.Within the sort space, we were able to determine an optimal number of clusters. An optimal cluster is one that minimizes the variance within a cluster while maximizing the distinctness between clusters. However, there was no clear optimal number of clusters for the language space. Though the clusters within the language space are still qualitatively interpretable (i.e., there is a justifiable qualitative explanation for why those students ought to be placed in the same cluster), a quantitative metric to justify an optimal clustering does not exist. Future studies could explore the use of various algorithms to find optimal numbers of clusters.
For many of the clusters created using the k-means algorithm, a commonality could be found between the cards in that cluster. However, sometimes a cluster seemed to be characterized primarily by what was most unique about a sort or a written justification. For example, many students in the “Biology” language cluster tended to provide language relating to biology, but the remainder of their sort often reflected a diversity of different ways of thinking when qualitatively analyzed. This suggests machine learning techniques may provide insight into general themes that can summarize the collected data, but do not always uncover themes related to knowledge structures or schemas. This issue points to the necessity of human qualitative analysis to make judgments about the meaningfulness of data and suggests machine learning may represent a starting point or supplement to qualitative data analysis.
Another potential limitation is that we based our study on the assumption that a student's written justification for their sort provides another valid window into their knowledge structure that can complement the information from their sort. However, in some cases, students' sorts appeared not to align with their justifications. This calls into question the extent to which either the sorts themselves or the justifying language can be validly linked through machine learning techniques to students’ knowledge structures. There are limitations in both the card sort, which was designed with particular anchors in mind and chose three among many potential general chemistry topics for underlying principles, and students’ written justifications, as students are not always facile with expressing their ideas in writing. Although we did conduct think-aloud interviews during pilot stages of this study, our dataset was not large enough to capture differences between verbal and written expression. The techniques outlined in this paper could potentially be adapted to an interview-based data collection strategy, which could add to the research by comparing clusters arrived at through analysis of verbal versus written justifications. In such a study, it may be possible with the ability to probe students’ thinking through follow-up prompts, to establish links between students’ sorts, language, and knowledge structures. This limitation further illustrates that machine learning should only be used as a supplement to, not a substitute for, human intervention and analysis.
Finally, the structure of the card sort task itself limited what we were able to learn from a machine learning analysis of the sorts and justifications. This particular task was designed with clear novice and expert anchors in mind, which limited the number of interesting and meaningful sorts and justifications outside of those two anchors. An open-ended card sort task, such as that in Yamauchi (2005) coupled with machine learning might generate a more authentic window into students’ knowledge structures, and potentially also their schemas.
Implications for instruction
Ultimately, machine learning methods for analyzing the results from card sort tasks are only useful if they add knowledge that can guide instructional practice. We learned several things from our machine learning analysis of the triplet-oriented card sort tasks that have implications for instruction. One such implication is that students first need to recognize the ideas presented in a problem in order to be able to create useful schema for solving them, and it seems that for many students, the representations depicted on the cards neither helped nor hindered their ability to do this. The implication is that strategies for concept recognition should be explicitly taught and practiced, and this necessitates the interleaving of problems from a range of different topics, something that is not always done in a general chemistry classroom. Once students are able to recognize some of the underlying principles of the problems, it appears they are better able to organize their knowledge and justify it consistent with these principles.Our finding that students’ justifications and sorts do not always overlap suggests that when formatively assessing students’ expertise, especially when it comes to connecting or categorizing multiple ideas, more than one data point is necessary. Sources of evidence should include opportunities for students to express their thinking in an open-ended manner. When students’ explanations do not seem consistent with their performance on other tasks, it is an opportunity to inquire further into their thinking (as well as the assessment methods), rather than assuming a position along the continuum from novice to expert. It may be that students have a truly novice level of expertise and require further instruction, but it may also be that they have difficulty expressing their ideas or knowledge structures, or even that they have a different way of thinking about or organizing concepts that could be fruitful to build upon.
Finally, our finding that many students were unable to recognize the underlying principles and sorted based on type of representation, perceived difficulty, or even discipline, reinforces a need to explicitly teach students about the different levels of the chemistry triplet. This should go beyond including multiple representations in problems, but should explicitly connect those representations in ways that show their roles in scientific modeling. In this way, helping students develop their ability to make connections between these levels engages them in using important scientific practices.
Conflicts of interest
No conflicts of interest to report.Appendices
Appendix
Analysis of three sort clusters
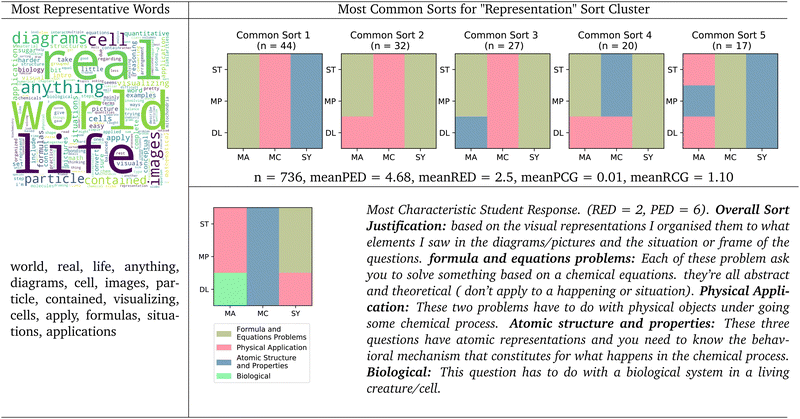
As before with the language clusters, we can characterize the sort clusters using the various techniques we outlined in the methods section. These include the most representative words, the most characteristic student response, the most common sorts, and various quantitative metrics.The representative language of this “Representation” cluster also supports this characterization. Students used words like “diagrams”, “images”, and “visualizing”, potentially referring to the actual representations on the card and how they are visualizations of chemistry principles. Students also used words and phrases like “real life” and “real world”, potentially referring to how many cards within the representation sorting seem to have some relation to an observable phenomena on the macroscopic scale. Relatedly, students used words like “applications”, “situations”, and “apply”, potentially referring to how the representations on the cards apply to underlying principles of chemistry.
The most characteristic student response for this cluster also supports this cluster's characterization as a “surface-level representation” cluster. This student had a RED score of 2 and a PED score of 6, showing that they sorted closer to the surface level representation canonical sort than to the underlying principle canonical sort. This student justified their sort by stating that it was “based on the visual representations” and that they “organised [their cards] to what elements [they] saw in the diagrams/pictures and the situation or frame of the questions.” This student made 4 groups, three of which map neatly onto the three canonical surface-level representation groupings based on the language justifications. This student's first group was selftitled as “formula and equations problems” and corresponds to the “Symbolic” canonical grouping; the student's second group was self-titled as “Physical application”, which seems to align with the “Macroscopic” canonical grouping; and the student's third group was self-titled as ”Atomic structure and properties”, which matches the “submicroscopic” canonical group. The student's final group was titled “biological” and contained one card involving mitochondria in the cell. Considering that the most representative student of this cluster created groups that mapped closely to canonical surface-level representation groups suggests that the characterization of this cluster as a “surface-level representation” cluster is reasonable.
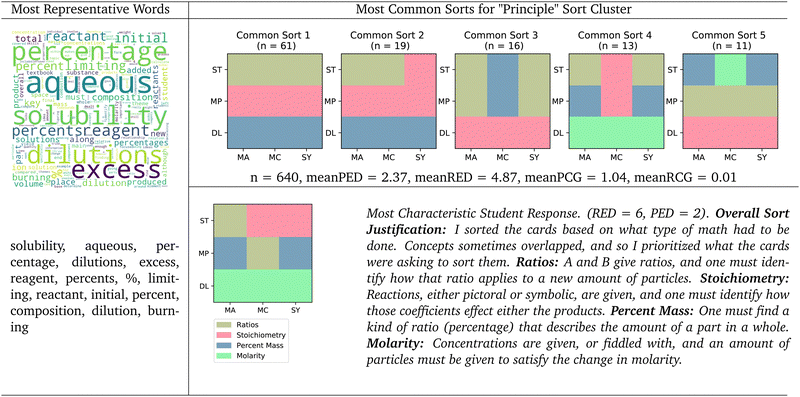
The language that students used within this cluster supports our categorization of this cluster as an “Underlying Principle” cluster. Students in this cluster used words like “solubility”, “aqueous”, “dilutions”, “dilution”, and “reagent”, which all seem to refer to the “Dilution” canonical grouping (DL). Students also used words like “percentage”, “percent”, and “composition”, words that indicate that students are describing the mass percent (MP) canonical grouping. Lastly, students used words like “excess”, “limiting”, “reactant”, and “initial”, which seems to suggest that students are describing the stoichiometry canonical grouping (ST). All the most representative words of this cluster can be qualitatively used to infer a categorization of that cluster.
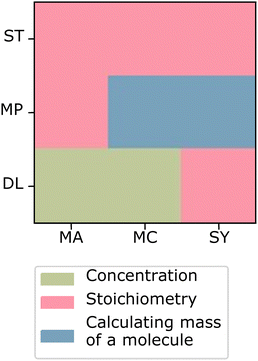
The most characteristic student response for this cluster also supports this cluster's characterization as an “underlying principle” cluster. This student had a RED score of 6 and a PED score of 2, showing that they sorted closer to the underlying principle canonical sort than to the surface-level representation canonical sort. This student based their sort on “the math that had to be done” to solve the problems. Four groups were created by this student, three of which correspond closely to how we would expect a student to justify the three canonical underlying principle groups. The first group this student generated was titled “Ratios”, containing two cards that supposedly required the ratio of particles, which does not correspond to a canonical group. The second group was titled “Stoichiometry Reactions”, which relates directly to the “Stoichiometry” underlying principle canonical group; the third student group was titled “Percent Mass”, which again relates directly to the “Mass Percent” underlying principle canonical group; and the fourth group was titled “Molarity Concentrations”, which seems to map to the “Dilution” underlying principle canonical group. Because the most characteristic student response within this cluster created groups that seem to correspond to what we would expect in an “Underlying Principle” canonical sort, it suggests that this cluster can be characterized as an “Underlying Principle” cluster.
It is difficult to characterize this cluster with the principle and representation binary as the average sort within this cluster is far from both the canonical underlying principle sort and the canonical underlying principle sort. From the language, we can see that some of the most representative words for this cluster were “believe,” “remember,” “taught,” “complicated,” “presented,” “learn” and “subjects”, possibly indicating that these students are struggling to recall information that they learned from class to identify specific underlying principles or concepts relevant to make an informed sort. Based on these representative words, we categorized this cluster as a “Difficulty” cluster, as students were finding it difficult to recall information and identify relevant information that would help them perform this task.
The justification for the most characteristic sort for this cluster suggested the student was able to identify some underlying principles, but perceived the rest of the cards as both unique and unrelated. This student reported that they made one group that was based on the kind of calculation each question was asking, and the rest were deemed to be “outliers that appeared to be different concepts.” This student made four groups, one with five of the nine cards, and three more groups containing the remaining four cards. The first group was titled “calculating moles” because, according to this student, “you are accounting for concentration and calculating number of moles/limiting reactants.” This justification seems to suggest that the student identified two underlying principles, dilutions and stoichiometry, but they didn’t see those concepts as distinct enough to separate them out into their own groups. Instead, this student elected to make one large group containing a majority of the cards. The remaining cards were separated out into their own small groups, two of which only had one card each, suggesting that this student struggled to identify information that united those cards together. This student sort captures the difficulty that a student may have in identifying relevant information necessary to find the similarities and differences among chemistry problems.
Intersection characteristic sort
Much like how we found representative student responses for each individual cluster, we can find the most representative responses in the same way for each intersection between clusters. Looking at the most characteristic student sorts for some of the intersections between the sort clusters and the language clusters can provide valuable insight into the relationship between student sorts and their language.Acknowledgements
We would like to thank students and instructors, who were gracious enough to assist with data collection. We would also like to thank Spenser Stumpf and Matt Smiley for their contributions to this work. And, we offer our thanks to the Washington NASA Space Grant Consortium for contributing to the funding this project.References
- Acton W. H., Johnson P. J. and Goldsmith T. E., (1994), Structural Knowledge Assessment: Comparison of Referent Structures, J. Educ. Psychol., 86(2), 303–311.
- Bransford J. D., Brown A. L. and Cocking R. R., (2000), How People Learn: Brain, Mind, Experience, and School, Washington, DC: National Academy Press.
- Bussolon S., (2009), Card sorting, category validity, and contextual navigation, J. Inf. Archit., 5–29.
- Carruthers S. P., Gurvich C. T., Meyer D., Bousman C., Everall I. P., Neill E., Pantelis C., Sumner P. J., Tan E. J. and Thomas E. H., (2019), Exploring heterogeneity on the Wisconsin card sorting test in schizophrenia spectrum disorders: a cluster analytical investigation, J. Int. Neuropsychol. Soc., 25(7), 750–760.
- Chen Z., (1999), Schema induction in children's analogical problem solving, J. Educ. Psychol., 91(4), 703–715.
- Chi M. T. H., Feltovich P. J. and Glaser R., (1981), Categorization and representation of physics problems by experts and novices, Cognitive Sci., 5(2), 121–152.
- Davidson A., Addison C. and Charbonneau J., (2022), Examining Course-Level Conceptual Connections Using a Card Sort Task: A Case Study in a First-Year, Interdisciplinary, Earth Science Laboratory Course, Teach. Learn. Inquiry, 10, 1–20.
- Deibel K., Anderson R. and Anderson R., (2005), Using edit distance to analyze card sorts, Expert Systems, 22(3), 129–138.
- Devlin J., Chang M.-W., Lee K. and Toutanova K., (2018), Bert: pre-training of deep bidirectional transformers for language understanding, arXiv, preprint, arXiv:1810.04805.
- Domin D. S., Al-Masum M. and Mensah J., (2008), Students’ categorizations of organic compounds, Chem. Educ. Res. Pract., 9(2), 114–121.
- Ewing G., Logie R., Hunter J., McIntosh N., Rudkin S. and Freer Y., (2002), A new measure summarising ‘Information’ conveyed in cluster analysis of card-sort data, IDAMAP 2002, 4, 25.
- Eysenck M. W. and Keane M. T., (2005), Cognitive Psychology: A Student's Handbook, 5th edn, New York: Psychology Press.
- Fincher S. and Tenenberg J., (2005), Making sense of card sorting data, Expert Systems, 22(3), 89–93.
- Fossum T. and Haller S., (2005), Measuring card sort orthogonality, Expert Systems, 22(3), 139–146.
- Galloway K. R., Leung M. W. and Flynn A. B., (2018), A Comparison of How Undergraduates, Graduate Students, and Professors Organize Organic Chemistry Reactions, J. Chem. Educ., 95(3), 355–365.
- Galotti K. M., (2014), Cognitive Psychology In and Out of the Laboratory, 5th edn, Los Angeles: SAGE Publications.
- Gentner D., (2005), The development of relational category knowledge, in Gershkoff-Stowe L. and Rakison D. H. (ed.) Building object categories in developmental time, Hillsdale, NJ: Erlbaum.
- Gentner D. and Medina J., (1998), Similarity and the development of rules, Cognition., 65(2–3), 263–297.
- Gläscher J., Adolphs R. and Tranel D., (2019), Model-based lesion mapping of cognitive control using the Wisconsin Card Sorting Test, Nat. Commun., 10(1), 20.
- Graulich N. and Bhattacharyya G., (2017), Investigating students’ similarity judgments in organic chemistry, Chem. Educ. Res. Pract., 18(4), 774–784.
- Hastie T., Tibshirani R. and Jerome F., (2009), The Elements of Statistical Learning Data Mining, Inference, and Prediction, Second edn, Springer.
- Irby S., Phu A., Borda E. J., Haskell T., Steed N. and Meyer Z., (2016), Use of a card sort task to assess students’ ability to coordinate three levels of representation in chemistry, Chem. Educ. Res. Pract., 17(2), 337–352.
- Jaber L. Z. and BouJaoude S., (2012), A Macro-Micro-Symbolic Teaching to Promote Relational Understanding of Chemical Reactions, Int. J. Sci. Educ., 34(7), 973–998.
- Johnstone A. H., (1982), Macro- and micro-chemistry, School Sci. Rev., 64, 377–379.
- Kern A. L., Wood N. B., Roehrig G. H. and Nyachwaya J., (2010), A qualitative report of the ways high school chemistry students attempt to represent a chemical reaction at the atomic/molecular level, Chem. Educ. Res. Pract., 11(3), 165–172.
- Kozma R. B. and Russell J., (1997), Multimedia and understanding: expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 34(9), 949–968.
- Krieter F. E., Julius R. W., Tanner K. D., Bush S. D. and Scott G. E., (2016), Thinking Like a Chemist: Development of a Chemistry Card-Sorting Task To Probe Conceptual Expertise, J. Chem. Educ., 93(5), 811–820.
- Lajoie S. P., (2003), Transitions and Trajectories for Studies of Expertise, Educ. Res., 32(8), 21–25.
- Lapierre K. R., Streja N. and Flynn A. B., (2022), Investigating the role of multiple categorization tasks in a curriculum designed around mechanistic patterns and principles, Chem. Educ. Res. Pract., 23(3), 545–559.
- Lin S.-Y. and Singh C., (2010), Categorization of Quantum Mechanics Problems by Professors and Students.
- Macías J. A., (2021), Enhancing Card Sorting Dendrograms through the Holistic Analysis of Distance Methods and Linkage Criteria, J. Usability Stud., 16(2), 73–90.
- MacQueen J., (1967), Some methods for classification and analysis of multivariate observations, in the proceedings of the Berkeley symposium on mathematical statistics and probability, in Fifth Berkeley Symposium on Mathematical Statistics and Probability, Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, Berkeley, USA: University of California Press, pp. 281–297.
- Martine G. and Rugg G., (2005), That site looks 88.46% familiar: quantifying similarity of Web page design, Expert Systems, 22(3), 115–120.
- Mason A. and Singh C., (2011), Assessing expertise in introductory physics using categorization task, Phys. Rev. ST Phys. Educ. Res., 7(2), 020110.
- Mayer R. E., (2012), Information Processing, in APA Educational Psychology Handbook, WA: American Psychological Association, pp. 85–99.
- McCauley R., Murphy L., Westbrook S., Haller S., Zander C., Fossum T., Sanders K., Morrison B., Richards B. and Anderson R., (2005), What do successful computer science students know? An integrative analysis using card sort measures and content analysis to evaluate graduating students’ knowledge of programming concepts, Expert Systems, 22(3), 147–159.
- Mikolov T., Chen K., Corrado G. and Dean J., (2013), Efficient estimation of word representations in vector space, arXiv, preprint, arXiv:1301.3781.
- National Research Council, (2012), A framework for K-12 science education: Practices, crosscutting concepts, and core ideas, Washington, DC: The National Academies Press.
- Nehm R. H. and Ridgway J., (2011), What do experts and novices “see” in evolutionary problems? Evolution: Educ. Outreach. 4(4), 666–679.
- Paea S., Katsanos C. and Bulivou G., (2021), Information architecture: Using K-Means clustering and the Best Merge Method for open card sorting data analysis, Interact. Comput., 33(6), 670–689.
- Paul C. L., (2014), Analyzing Card-Sorting Data Using Graph Visualization, J. Usability Stud., 9(3), 87–104.
- Revlin R., (2012), Cognition: Theory and Practice, 1st edn, New York: Worth Publishers.
- Rousseeuw P. J., (1987), Silhouettes: a graphical aid to the interpretation and validation of cluster analysis, J. Comput. Appl. Math., 20, 53–65.
- Sanders K., Fincher S., Bouvier D., Lewandowski G., Morrison B., Murphy L., Petre M., Richards B., Tenenberg J., Thomas L., Anderson R., Anderson R., Fitzgerald S., Gutschow A., Haller S., Lister R., McCauley R., McTaggart J., Prasad C., Scott T., Shinners-Kennedy D., Westbrook S. and Zander C., (2005), A multi-institutional, multinational study of programming concepts using card sort data, Expert Systems, 22(3), 121–128.
- Shinde P., Szwillus G. and Keil I. R., (2017), Application of Existing k-means Algorithms for the Evaluation of Card Sorting Experiments, PhD thesis, Paderborn University Paderborn, Germany.
- Singer S. R., Nielsen N. R. and Schweingruber H. A., (2012), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, Washington, DC: National Academies Press.
- Smith M. U., (1992), Expertise and the organization of knowledge: unexpected differences among genetic counselors, faculty, and students on problem categorization tasks, J. Res. Sci. Teach., 29(2), 179–205.
- Smith J. I., Combs E. D., Nagami P. H., Alto V. M., Goh H. G., Gourdet M. A. A., Hough C. M., Nickell A. E., Peer A. G., Coley J. D. and Tanner K. D., (2013), Development of the Biology Card Sorting Task to Measure Conceptual Expertise in Biology, Cbe-Life Sci. Educ., 12(4), 628–644.
- Stains M. and Talanquer V., (2008), Classification of chemical reactions: stages of expertise, J. Res. Sci. Teach., 45(7), 771–793.
- Stiles-Shields C., Montague E., Lattie E. G., Kwasny M. J. and Mohr D. C., (2017), What might get in the way: Barriers to the use of apps for depression, DIGITAL HEALTH. 3, 2055207617713827.
- Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14(2), 156–168.
- Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A. N., Kaiser L. and Polosukhin I., (2017), Attention is all you need, arXiv, preprint, arXiv:1706.03762.
- Yamauchi T., (2005), Labeling Bias and Categorical Induction: Generative Aspects of Category Information, J. Exp. Psychol. Learn., Memory, Cognition, 31(3), 538–553.
| This journal is © The Royal Society of Chemistry 2024 |