Effect of defects and framework Sn on the stability and activity of Pt clusters for ethane dehydrogenation in chabazite zeolite

Abstract

With increasing interest in new catalytic materials based on atomically dispersed transition metals on various supports (e.g., zeolites or oxides), it is necessary to have an atomic level understanding of the factors that determine their structural and electronic properties as well as catalytic activity. Encapsulated Pt atoms and sub-nanometer Pt clusters in Sn-substituted zeolitic frameworks have demonstrated extended catalytic stability and remarkable selectivity for alkane dehydrogenation to alkenes. Despite efforts to characterize these materials, the bonding environment of the dispersed atoms in the presence of framework Sn or of defect silanols is uncertain. We have employed ab initio molecular dynamics simulations and electronic structure calculations to identify and characterize electronically stable Pt active site motifs in chabazite (CHA) and Sn-CHA at low Pt loadings. The activity of several active site motifs was assessed by microkinetic simulations. We demonstrate that framework Sn and silanol defects can promote the dispersion of Pt species. Unexpectedly, we find that in the presence of silanol nests, the dispersed Pt species statistically prefer to coordinate with the silanols and not with the framework Sn. We show that Pt and Sn are bonded via a 3-center-4-electron bond (O:–Sn–:Pt), affirm the absence of Pt–O–Sn bonding, and thus resolve the ambiguity related to the coordination of Pt to framework Sn. We predict that the O:–Sn–:Pt and Sn–O–Pt–Pt–Si bonding motifs in Sn-CHA are stable and active for ethane dehydrogenation. We relate our findings and conclusions to recent experimental characterization of Pt in Sn-BEA zeolite, point out the close alignment in several aspects and suggest that the effect of framework Sn on the dispersion of low nuclearity Pt species and on the formation of stable and efficient active sites should be largely independent of the framework itself.

---

Introduction

Supported single platinum atoms (SAs) and sub-nanometer clusters have been garnering attention for the selective, high-temperature alkane dehydrogenation to alkenes.¹ These catalysts show high atom efficiency, i.e., high activity per atom,² making them a cost-effective alternative to the conventional PtSn/Al₂O₃ catalyst. Such low-nuclearity Pt-based catalysts present fewer Pt–Pt bonds, which reduces the propensity for C–C cracking and coking, and thereby are more selective for alkenes.³ What hinders the industrial deployment of these catalysts is their stability. The large cohesive energy of bulk platinum provides a strong thermodynamic driving force for sintering. Indeed, this has been reported in several experimental reports of Pt clusters on alumina support.^4,5

Encapsulating small Pt clusters in microporous zeolite frameworks has shown great promise for preventing sintering. It has been hypothesized that the zeolite can trap the small Pt clusters within its micropores, creating a physical barrier to sintering. Liu et al.⁶ and Kistler et al.⁷ have reported the synthesis of trapped single Pt atoms in the 6-membered cages of the zeolites Y and KLTL, confirmed by aberration-corrected STEM studies. In this configuration, zeolite Y showed a five-fold increase in turnover frequency for n-hexane isomerization relative to nanoparticles and selectivity of around 98%. In KLTL, the single Pt atoms remained isolated even after the CO oxidation reaction. Therefore, the encapsulated Pt sub-nanometer clusters satisfy the four tenets of a promising catalyst: high activity, high selectivity, extended stability, and improved sustainability due to high noble-atom efficiency.

Incorporating heteroatoms and engineering silanol defects in the zeolite framework has been shown to enhance the stability of single metal atoms and sub-nanometer metal clusters under reaction conditions. Lezcano-González et al.⁸ reported extended catalytic stability and reduced sintering of small Pt clusters in a highly defective, isomorphously substituted Sn-MFI framework. Extensive characterization suggested that the silanol defects and the framework Sn provided anchoring sites to the small clusters. Xu et al.⁹ reported extended stability of small Pt clusters in Sn-BEA under dehydrogenation conditions. They, too, reasoned that the framework Sn and geometric constraints can stabilize small Pt clusters. Recently, Lefton et al.¹⁰ extensively characterized low-nuclearity Pt clusters synthesized by wetness impregnation of dealuminated BEA and of Sn-BEA, at 0.03 wt% Pt loading. They concluded that framework Sn or silanol nests could promote the thermodynamic dispersion of the embedded Pt atoms. There is less certainty regarding the bonding environment of the dispersed Pt species. Lefton et al.¹⁰ concluded that only Pt–Sn bonding was likely because attempts to fit Pt–O–Sn paths to their XAS spectra had resulted in nonsensical coordination numbers, whereas Ma et al.¹¹ had previously reported only Pt–O–Sn bonding. Both moieties are plausible active site motifs and lack of consensus may be due to differences in the synthesis method or sample pre-treatment,^10,11 but they have distinctly different electronic structures and, likely, activity. The reported coordination of Pt by –SiOH groups¹⁰ is related to the dispersive effect of silanol nests but this bonding structure, too, is ambiguous. Microscopy-based methods like HAADF-STEM often cannot detect ultrasmall Pt clusters or single atoms, and adsorption or scattering spectra (e.g., EXAFS) are ensemble averages. This makes it difficult to unequivocally determine the coordination environment of low-nuclearity Pt clusters using only experimental characterization methods.

In this contribution, we wish to address and resolve these uncertainties and add electronic level clarity to the bonding structures of the active site motifs that result from the dispersion of the Pt atoms. We restricted ourselves to low Pt loadings as only low-nuclearity Pt clusters seem to have been active when catalyst samples were tested for propane dehydrogenation.¹⁰ Taking advantage of the low-nuclearity of the active Pt species, and for computational efficiency, we chose to work with the CHA framework, with only 36 base atoms in its primitive unit cell. CHA is sufficiently flexible to accommodate a Sn atom in its lattice and there is only one distinct crystallographic position where the substitution can take place. Using the Pt–Pt and Pt–Sn atomic separations as order parameters, to distinguish between associated and dissociated states, we performed ab initio molecular dynamics (AIMD) free energy simulations to compute the corresponding free energy profiles and sample configurations that belong to the attractive basins of the reduced free energy landscape. Structures from these ensembles were subsequently quenched to identify attractors of the potential energy surface. The optimized structures were used for analysis of their electronic configurations and of their catalytic activity for ethane dehydrogenation. Microkinetic simulations were performed to obtain kinetic parameters. Last, we discuss insights into activity trends across the different local environments and strategies for achieving Pt dispersion.

Methods

Periodic electronic structure calculations

The CHA unit cell, consisting of 36T-sites, was taken from the International Zeolite Association (IZA) website. The framework contains three types of rings, 4-, 6- and 8-membered. There is only one crystallographic site that substitutional atoms can occupy. To build the Sn-substituted model, a Si atom in the unit was replaced by Sn and the model was reoptimized. Periodic density-functional theory (DFT) calculations^12,13 were performed at the Perdew–Burke–Ernzerhof (PBE)¹⁴ theory level with D3 dispersion¹⁵ in CP2K.¹⁶ The DZVP-MOLOPT-GTH basis set was used with a plane-wave cutoff of 400 Ry. The core electrons were treated with the Goedecker–Teter–Hutter (GTH) pseudopotentials, and the valence electrons were treated with the Gaussian and plane waves (GPW) approach implemented in CP2K. The self-consistent field (SCF) calculations were converged to 1 × 10⁻⁶ Ha, and the geometric optimizations were performed using the conjugate gradients (CG) optimizer. The forces were converged to 4.5 × 10⁻⁴ Ha per Bohr. Silanol defects were created by removing an –Si–O–Si– moiety and adding hydrogens to the unsaturated –Si–O– bonds. This created a 6-membered defect ring which is typically more stable than the 4-membered one (created by removing a single Si atom) in which the 4 closely packed –Si–OH groups experience repulsive forces. There are three ways to remove an Si–O–Si moiety from the CHA framework: across the 4- and 6- membered rings; across the 6- and 8-membered rings; and across the 4- and 8-membered rings. The lowest energy structure results from Si–O–Si deletion from the 6- and 8-membered ring. This is the structure used in this study.

Finite cluster electronic structure calculations

Cluster models were carved out of the optimized Pt_n/support periodic structures as spheres of radius 6.5 Å centred on the Pt atoms. The Si dangling bonds were saturated with H atoms in the direction of the Si–O– bonds present in the periodic Ptn/support structure. All electronic structure calculations with the cluster models were performed using Gaussian 09, version d01.¹⁷ The C, Si, O, H atoms were modelled at the B3LYP^18,19/TZVP theory level and the Pt, Sn atoms were modelled at the B3LYP/LANL2DZ theory level.²⁰ An empirical dispersion correction by Grimme²¹ was added to the DFT energies. Transition states were confirmed by vibrational frequency analysis (single imaginary frequency) and by intrinsic reaction coordinate (IRC) calculations. Thermal corrections to the electronic energies were obtained within the harmonic oscillator approximation at 900 K using the pMuTT²² utility (version 1.2.12); frequencies below 100 cm⁻¹ were set to 100 cm⁻¹ for all intermediates.²³ To mimic the rigidity of the zeolitic framework, the peripheral hydrogens were kept frozen during optimization and frequency calculations. Natural bond orbital analysis was performed in the NBO6 program.²⁴

Microkinetic simulations

Microkinetic analysis for a fixed bed reactor (FBR) was performed in CHEMKIN.²⁵ Kinetic analysis across the active site models was performed at a conversion of 3% at reaction temperature (898.15 K). Reaction conditions chosen for the models are summarized in section S3, Table S3.1;† they were chosen to ensure that the kinetic analyses are performed at differential conditions. The feed flow rate was adjusted across the models to fix conversion at 3% at the reaction temperature. CHEMKIN uses the DASPK solver; the absolute and relative tolerances of the differential equations were set to 10⁻¹⁰ and 10⁻⁸, respectively. Specifically, the tolerance values correspond to the gas mole fractions and intermediate coverages (quantities bounded between 0 and 1).

Ab initio molecular dynamics simulations

The AIMD simulations were carried out in the canonical ensemble (NVT) at 900 K, using a chain of three Nosé–Hoover thermostats²⁶ with a relaxation time of 500 fs. For systems containing hydrogen, we observed oscillations in the temperature associated with the Toda demon²⁷ and in order to eliminate them the thermostat mass was set to 10⁻² times the default value for each system. All calculations were performed at the Perdew–Burke–Ernzerhof (PBE)¹⁴ theory level with a D3 dispersion correction of Grimme et al.¹⁵ in CP2K. The equations of motion were integrated using the velocity Verlet algorithm²⁸ with the time step of 2.5 fs for the frameworks without hydrogen atoms and 1 fs for the hydrated frameworks. The SCF cycles were converged to 1 × 10⁻⁶ eV and the energy cutoff was set to 400 Ry.

Thermodynamic integration (TI) free energy calculations²⁹ were performed using either the Pt–Pt or the Pt–Sn interatomic distance (d_Pt–Pt, d_Pt–Sn) as the collective variable. The free energy difference between the two configurations corresponding to the reaction coordinate values of l₀ and l₁ was calculated using eqn (1)

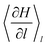where is the generalized force associated with the constraint on the reaction coordinate in the MD simulations. A δl of 2.5 nm was used to define each window and the constraint on either the Pt–Pt bond or the Pt–Sn bond was enforced using the RATTLE algorithm.³⁰ Each window consisted of trajectories of 9 ps long (3 ps equilibration and 6 ps production).

Results and discussion

Stable active site motifs

Using the Pt–Pt and Pt–Sn atomic separations as order parameters to distinguish between associated and dissociated states, we performed TI free energy simulations to compute the corresponding free energy profiles and sample configurations of active site motifs for one or two Pt atoms per unit cell. The simulations were performed at 900 K (representative of dehydrogenation conditions) in pristine CHA (Fig. S1a†); in CHA with silanol defects created as described in Methods (def-CHA; Fig. S1b†); in Sn-CHA (Fig. S1c†); and in Sn-CHA with silanol defects (def-Sn-CHA; Fig. S1d†).

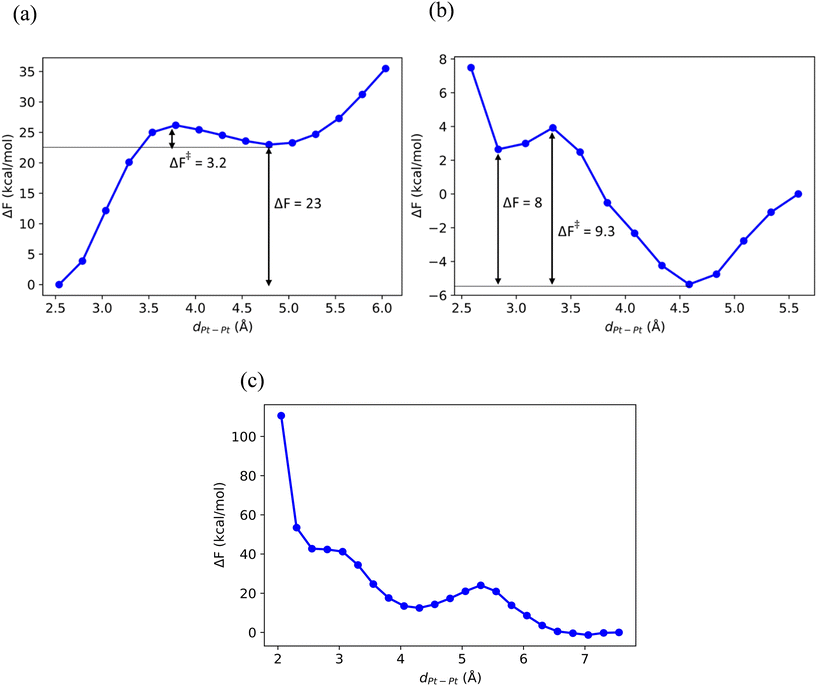
Fig. 1 shows the Pt–Pt potential of mean force (pmf) as a function of their separation d_Pt–Pt in CHA, def-CHA and Sn-CHA. In pristine, stoichiometric CHA (Fig. 1a), association of the two Pt atoms is thermodynamically favored over the dissociated state by 23 kcal mol⁻¹, and it is reasonable to deduce that Pt growth in the pristine material will only be limited by the pore size. In def-CHA (Fig. 1b), the Pt–Pt pmf is essentially repulsive at short d_Pt–Pt, with only a very shallow local minimum at 2.8 Å, and the Pt atoms seem to be dispersed by the defect silanols. This behavior is reminiscent of the dispersion of Pt atoms by surface hydroxyls on hydrated Al₂O₃ (110).³¹ In pristine Sn-CHA with Sn : Pt ratio of 1 : 1, the Pt–Pt pmf is similarly repulsive at short d_Pt–Pt (Fig. 1c). Visual inspection of the MD trajectories in the free energy well at d_Pt–Pt ≈ 7 Å revealed that each of the two Pt atoms prefers to coordinate with a framework Sn. We confirmed the facile Pt–Sn association in Sn-CHA by computing the Pt–Sn potential of mean force, which is shown in Fig. 2a. Evidently, Pt–Sn binding is thermodynamically favorable by ΔF = −11 kcal mol⁻¹ relative to the local free energy minimum at which the Pt and Sn atoms are 4.8 Å apart. These results are quite pleasing because not only do they agree with experimental reports about the stability of dispersed Pt in Sn-BEA and Sn-MFI under dehydrogenation conditions conditions,^9,10,32 but they strongly suggest that the thermodynamics of the dispersion of Pt particles in the presence of Sn is rather agnostic to the framework. We also investigated the thermodynamics of Pt–Sn binding in def-Sn-CHA and the results were quite surprising. The Pt–Sn pmf in def-Sn-CHA, shown in Fig. 2b, is clearly repulsive. At the minimum at d_Sn–Pt ≈ 5 Å, inspection of the MD trajectories revealed that Pt prefers coordination to the silanol defects to binding to the framework Sn (Table 1).

Fig. 1 Potential of mean force between two Pt atoms in (a) CHA, (b) def-CHA, and (c) Sn-CHA.

Fig. 2 Potential of mean force between Pt and Sn atoms on (a) Sn-CHA, and (b) def-Sn-CHA.

Table 1 Average O–Pt–Si and O–Pt–H bond angles along the Pt–Pt nucleation trajectory in CHA and defected-CHA, respectively

Pristine CHA		Defect CHA
d Pt–Pt (Å)	∠OPtSi	d Pt–Pt (Å)	∠OPtH
2.5 Å	97°	2.8 Å	89°
3.8 Å	97°	3.3 Å	88°
4.8 Å	88°	4.6 Å	96°

---

Next, we analyzed the bonding structures of representative configurations belonging to the free energy minima identified above. To that end, these structures were quenched by DFT optimization.

We began by analyzing quenched structures corresponding to the two minima in the Pt–Pt potential of mean force in pristine CHA. As we saw earlier, dispersion of the Pt atoms is thermodynamically less favorable than Pt–Pt bonding. The two Pt atoms prefer to be bonded. The quenched structure corresponds to the dispersed state in which each of the separated Pt atoms is wedged in an Si–Pt–O bonding structure between a 6- and 4-membered ring, elongating the framework Si–O bond from 1.63 to 2.84 Å (Fig. S1a†); such a stable geometry in siliceous zeolites has been reported before.³³ According to natural bond orbital (NBO) analysis of a representative cluster model (Fig. 3a), the Pt atom in Si–Pt–O is sd-hybridized and its two bonds are at 87°, consistent with the spatially orthogonal topology of the sd-hybrids (Fig. S3a†). In this Si–Pt–O bonding structure, Pt acquires some positive charge (q_Pt = 0.27 e). Although this positive charge is not sufficient to ascertain oxidation of the Pt atom, it should nevertheless manifest itself in a blue shift in the IR spectrum of a probe CO molecule. Trapped Pt atoms in the frameworks of the Y⁶) and KLTL⁷ zeolites have been confirmed by aberration-corrected STEM. In the quenched configuration (Fig. S2a†) associated with the thermodynamically more stable Pt₂ state in pristine CHA, the two Pt atoms are in a Pt–Pt(Si)(O) bonding structure. In this, the two Pt atoms acquire distinctly different electronic characteristics. The “central” Pt, which is bonded to Pt, Si and O (bond angles 85–95°), is wedged between the 4- and 6-membered rings, interrupting their Si–O bond and, based on NBO analysis (model in Fig. 4a), it is sd²-hybridized, which explains the mutually orthogonal bonds (Fig. S6a†). It is also positively charged with q_Pt = 0.4 e, namely, it is more charge depleted than isolated Pt atoms in the O–Pt–Si moieties described earlier (cf., q_Pt = 0.27 e) and one should expect stronger blue shift in the CO IR spectrum. The second Pt atom in Pt–Pt(Si)(O) is inside the cage formed by the 4- and 6-membered rings and negatively charged (q_Pt = −0.3 e). This Pt atoms is not hybridized and is bonded to the “central” Pt with its 6 s-orbital. We will see later that the mononuclear Si–Pt–O active site is a lot less active than the dinuclear Pt–Pt(Si)(O) for C–H activation.

Fig. 3 DFT optimized cluster models of the Pt₁ species in different local environments (a) CHA, (b) def-CHA, (c) Sn-CHA, and (d) def-Sn-CHA (H, white; O, red; Si, green; Pt, blue; Sn, dark green).

Fig. 4 DFT optimized cluster models of the Pt₂ species in different local environments (a) CHA (b) def-CHA, and (c) Sn-CHA (H, white; O, red; Si, green; Pt, blue; Sn, dark green).

We described earlier that silanol defects in unsubstituted CHA (def-CHA) dispersed the Pt atoms (Fig. 1b) and that visual inspection of the trajectories showed coordination of the Pt atoms to –SiOH nests. Quenching of configurations associated with the free energy well centered at d_Pt–Pt ≈ 4.5 Å yielded the Si–O–Pt–H bonding structures, namely, the dispersed Pt atoms inserted themselves in O–H bonds using their sd-hybrid orbitals (Fig. S1b†). NBO analysis (model in Fig. 3b) showed that in this configuration Pt acquires again positive partial charge q_Pt = 0.39 e. We also quenched sampled configurations corresponding to the thermodynamically less stable (by only ca. 8 kcal mol⁻¹) dinuclear state Pt₂. We found the bonding structure Si–O–Pt–Pt–H after 1,2-insertion of Pt₂ in the O–H bond of a defect silanol (Fig. 4b). Here, again, the Pt atoms are sd-hybridized but, interestingly, the Pt bonded to the O atom is electronically depleted, with q_Pt = 0.4 e, whereas the Pt bonded to the H atom is nearly neutral, with q_Pt = −0.02 (Fig. S6c†). Furthermore, the NBO analysis indicated the presence of a 3-center-4-electron bond (3c-4e), O:–Pt–:O(H), between the Pt and O atoms in boldface type in –Si–O–Pt–Pt–H and a proximal –SiOH oxygen atom. In this 3c–4e resonance state, the participating O atoms take turns—not necessarily with equal probabilities—in bonding with the Pt atom, and when one of them is σ-bonded to Pt, the other donates an electron pair to the corresponding antibonding orbital.

As we noted earlier, the MD simulations showed that, in def-Sn-CHA, Pt–Sn is not thermodynamically stable (Fig. 2b) and that visual inspection of the trajectories indicated, quite unexpectedly, that the dispersed Pt atoms associated with the silanol nests and not with the framework Sn. Quenching of sampled configurations in the free energy attractor of the Pt–Sn potential of mean force shown in Fig. 2b, yielded the Si–O–Pt–H (Fig. S1d†) bonding structure, similar to that in def-CHA. Unsurprisingly, the sd-hybrized Pt atom is positively charged, with q_Pt = 0.39 e (Orbitals shown in Fig. S5c†).

Only in the absence of silanol defects did we see dispersion of Pt by framework Sn in Sn-CHA. The quenched structure (Fig. S1c†) corresponding to the free energy well at d_Pt–Pt ≈ 7 Å shows the Pt atom being coordinated to a framework Sn–O bond. NBO analysis (model shown in Fig. 3c) showed that the Pt atom actually participates in a 3c–4e bond, O:–Sn–:Pt. In this hybrid state, the Pt atom is 60% in a state in which the Pt donates a d-lone pair to the orbital, and 40% in a state in which the O donates a 2p-lone pair to the orbital (Fig. S5b†). The Pt in this bonding structure is not as electronically depleted (q_Pt = 0.17 e) as in the bonding structures we have described so far and in which the Pt atom was stabilized by inserting itself in the O–H bond of defect silanols.

As we mentioned in the Introduction, Lefton et al.¹⁰ recently concluded by EXAFS analysis that only Pt–Sn bonding was present in Pt–Sn-deAlBEA samples at low Pt loading (0.03 wt%) because attempts to fit Pt–O–Sn paths to their XAS spectra had resulted in nonsensical coordination numbers. Direct Pt–Sn bonding has also been recently reported by Dou et al.³² in the Sn-MFI framework, although the authors in that work claimed that Sn was in the 2+ rather than 4+ oxidation state. Our simulations and analysis indicate direct Pt–Sn bonding and the absence of Pt–O–Sn bonding, more in agreement with the findings of Lefton et al.¹⁰ In contrast, Ma et al.¹¹ have reported only Pt–O–Sn bonding in the XAS spectra of Pt–Sn-deAlBEA samples. Although further characterization studies might be needed to resolve this disagreement, it is conceivable that it is due to differences in the synthesis of Sn-BEA and the bonding structure of the Sn atom in the framework, namely, “closed” Sn(SiO)₄versus “open” (SiO)₃SnOH. Whereas Lefton et al.¹⁰ used the sequential dealumination and impregnation approach, Ma et al.¹¹ used the hydrothermal structural reconstruction method. In the latter work, ¹¹⁹Sn NMR analysis indicated the formation of the octahedral “open” structures (Si–O)₃(H₂O)₂Sn^(IV)–OH. Ma et al.¹¹ further asserted that ¹¹⁹Sn MAS NMR, UV-vis and in situ XPS suggested that the Pt atom anchors itself to the hydroxyl group on the “open” Sn site, which upon H₂ reduction results in the (Si–O)₂Sn^(II)–O–Pt_{n (n=1–15)} bonding structure.

For completeness, in the activity studies presented below, we also considered for Sn-CHA the Sn–O–Pt–Pt–Si bonding motif, formed by 1,2-insertion of Pt₂ in one of the four Si–O bonds next to Sn (Fig. S2c†). For this bonding structure, the NBO analysis (Fig. 4c) showed that the two Pt atoms acquired different electronic characteristics, much like the Pt–Pt(Si)(O) structure in pristine CHA. The “central” Pt (bonded to O) in Sn–O–Pt–Pt–Si is sd hybridized and positively charged with q_Pt = 0.6 e, namely it is more depleted than the “central” Pt in the Pt–Pt(Si)(O) structure in CHA. The second Pt atom (bonded to Si) is sd² hybridized and nearly neutral (q_Pt = −0.06 e) (orbitals shown in Fig. S6b†).

Before we turn our attention to the activity of the active site motifs described above, we should make an additional note related to the characterization of Pt–Sn-deAl-BEA.¹⁰ In that work, pyridine-IR studies for moderate−high Pt loading showed a significant reduction in the peak intensity corresponding to pyridine interaction with Sn, suggesting that at the higher Pt loadings some Pt clusters were anchored near Sn. In the same work, EXAFS analysis of Pt–Sn-deAlBEA samples at low Pt-loading (0.03 wt%) showed minimal Pt–Sn interactions and more Pt–O than Pt–Pt interactions. This suggests that at low Pt loadings, a greater fraction of isolated Pt atoms was coordinated with the silanol nests, forming Pt–O–H bonds, which agrees with our free energy calculations for Pt in def-Sn-CHA (Fig. 2b). The authors also reported two CO stretch frequencies in the IR spectra of Pt–Sn-deAlBEA samples at low Pt loading.¹⁰ The lower of the two frequencies was ascribed to Pt interacting with Sn and the higher was ascribed to a positively charged Pt species since a blue shift is related to diminished π back-donation to CO. From our simulations and analysis of Pt in def-Sn-CHA, Pt atoms participating in Si–O–Pt–H bonding with silanol nests are more depleted electronically than those coordinating to framework Sn via 3c-4e O:–Sn–:–Pt bonding. Therefore, the positively charged Pt atoms associated with the high CO stretch frequency reported by Lefton et al.¹⁰ must be those coordinating to the silanol nests, while the Pt atoms assigned to the low CO frequency should be those in the O:–Sn–:–Pt motif.

Overall, the presence of silanol defects and framework Sn provides coordination environments that stabilize single Pt atoms, which afford excellent selectivity towards ethylene formation in non-oxidative dehydrogenation.³

Activity

So far, we have identified the most likely Pt sites in various local environments. Summarizing, they are: Si–Pt–O in pristine CHA (Fig. 3a), Si–O–Pt–H in def-CHA (Fig. 3b), O:–Sn–:Pt in Sn-CHA (Fig. 3c), Si–O–Pt–H in def-Sn-CHA (Fig. 3d); and the dinuclear Pt sites: Pt–Pt(Si)(O) in pristine CHA (Fig. 4a), Si–O–Pt–Pt–H in def-CHA (Fig. 4b) and Sn–O–Pt–Pt–Si in Sn-CHA (Fig. 4c). In the following we present ethane dehydrogenation activity results from DFT calculations for all seven sites listed above. On all the sites, the reaction takes place on the singlet spin state.

Formally, ethane dehydrogenation entails two consecutive H deletions and H₂ recombination (Fig. S7 and S8† as well as Table S5† show the Gibbs free energy and electronic energy diagrams respectively).

The C–H bond is activated homolytically on a Pt atom across all the active site motifs listed above. In the case of sites with two Pt atoms, the catalytically active Pt is the one directly bonded to an O atom. The homolytic mechanism was inferred by NBO analysis of the respective transition states, which showed singly occupied lone orbitals on the α-C and the abstracted H. With the exception of the O:–Sn–:Pt site in Sn-CHA, the partial charge of the catalytically active Pt on the rest of the sites increased (Table 2), but not in any significant way to infer a change in the oxidation state of Pt. This is reminiscent of oxidative addition to Pt complexes which, according to Low et al.,³⁴ can proceed without a change in the formal oxidation state of Pt, but rather with an increase in its maximum covalency. Here, upon C–H scission, the Pt atom loses a bond to one of the atoms in its coordination sphere (O or Pt) but forms two new bonds, with the ethyl radical and the H atom.

Table 2 Partial charge on the central Pt atom across the active sites

Active site	q Pt in	q Pt in TS^C–H
O:–Sn–:Pt/Sn–CHA	0.02 e	0.02 e
Si–O–Pt–H/def-CHA	0.4 e	0.55 e
Si–O–Pt–H/def-Sn-CHA	0.4 e	0.55 e
Pt–Pt(Si)(O)/CHA	0.4 e	0.7 e
Sn–O–Pt–Pt–Si/Sn-CHA	0.6 e	0.75 e
Si–O–Pt–Pt–H/def-CHA	0.4 e	0.8 e

---

In Fig. 5a, we plot the C–H activation barriers on the different sites. The site O:–Sn–:Pt in Sn-CHA, and the site –Si–O–Pt–H, found in both def-CHA and def-Sn-CHA, are the most active for C–H activation, with potential energy barriers in the range of 5–10 kcal mol⁻¹. The rest display moderate activity, except for –Si–Pt–O– in pristine CHA which is totally inactive. Thus, a rather general trend that emerges is that the dimeric Pt species are less active than the monomeric for C–H activation. The reason for this seems to be the degree of polarization of the –Pt–O– and –Pt–Pt– bonds. NBO analysis of the C–H scission transition states and of the intermediate preceding it showed substantial second-order mixing (see Table S1†) between the singly occupied 2p orbital of the α-C with the in the –Si–O–Pt–H structure or the in the dimeric active site motifs, weakening the respective bonds. Therefore, the C–H activation barriers should correlate with the strength of the –Pt–O– and –Pt–Pt– bonds. The NBO analysis indicated that the former should be generally weaker because it is more polarized, which makes intuitive sense since the O atom is more electronegative (for more details see Table S2 in the ESI†).

Fig. 5 (a) Electronic energy barrier (intrinsic) for the C–H activation. (b) Electronic energy barrier (intrinsic) for the β-H elimination.

Fig. 5b shows the intrinsic activation barriers for the β-H elimination. The first, salient observation is a change in the activity trend described above. The dimeric species, Pt⋯Pt(Si)(O) in pristine CHA, Si–O–Pt⋯Pt–H in def-CHA, and Sn–O–Pt⋯Pt–Si in Sn-CHA, seem to be more effective than the isolated Pt sites for β-H elimination. Here, we use the notation –Pt⋯Pt– to signify that after the C–H activation the dimeric sites are nominally so because the Pt–Pt bond is broken, as we noted above. Looking for possible explanations for the change in the activity trend, we first note that, from a mechanistic point of view, the β-H elimination is not as straightforward because it does not proceed through the same mechanism across all the active site motifs. On the mononuclear sites (Si–O⋯Pt–H in def-CHA, O:–Sn–:Pt in Sn-CHA, and Si–O⋯Pt–H in def-CHA and def-Sn-CHA), the β-H of the Pt–ethyl complex is abstracted by the Pt center itself (the notation “⋯” is again to remind that the Pt–O bond is broken after C–H activation). On the dimeric sites, Si–O–Pt⋯Pt–H and Sn–O–Pt⋯Pt–Si, on the other hand, the β-H of the Pt–ethyl complex is abstracted by the neighboring Pt atom. The Pt⋯Pt(O)(Si) site in CHA is yet another exception as the β-H is abstracted by the Pt of the Pt–ethyl complex because, as noted earlier, the neighboring Pt atom is trapped in a cage and inaccessible. So what is the explanation for the change in trend? On the Si–O–Pt⋯Pt–H and Sn–O–Pt⋯Pt–Si sites, the Pt atom that used to be bonded to the Pt of the metal-ethyl complex is undercoordinated, as it is only bonded either to an H or to a Si atom and can readily abstract the β-H of the metal–ethyl complex. On the mononuclear sites (Si–O⋯Pt–H, O:–Sn–:Pt, and Si–O⋯Pt–H), however, we were not able to locate transition states in which the β-H transferred to the O atom of the dissociated siloxide ligand. This is not surprising in light of the fact that the C–H activation takes place homolytically and that the Pt atom retains the s¹d⁹ configuration. Therefore, subsequent transfer of the β-H atom to a neighboring O atom would entail a proton-coupled-electron-transfer mechanism and reduction of the Pt atom.

It is therefore difficult to deduce the most active motifs by simply inspecting or analyzing the free energy profiles along the reaction pathway. To that end, we performed microkinetic simulations (conditions in Table S3†) and the ethane dehydrogenation turnover frequencies (TOF) on the different sites are plotted in Fig. 6a; the corresponding apparent activation energies are plotted in Fig. 6b. Table 3 lists the reaction orders and most abundant intermediate across the sites. Four active site motifs, three of which involving dimeric Pt₂ species, showed similar high activity, although the first in the list below was more active than the rest by about an order of magnitude: Pt–Pt(O)(Si) in CHA; Sn–O–Pt–Pt–Si in Sn-CHA; Si–O–Pt–Pt–H in def-CHA and def-Sn-CHA; and O:–Sn–:Pt in Sn-CHA.

Fig. 6 (a) TOF at 3% ethane conversion (plotted on logscale) and (b) apparent activation energy across the different Pt active site motifs.

Table 3 Reaction orders and most abundant reaction intermediate (MARI) across the active sites

Active site	Rxn order in ethane	MARI
O:–Sn–:Pt/Sn-CHA	0.5
Si–O–Pt–H/def-CHA	1	Active site
Si–O–Pt–H/def-Sn-CHA	1	Active site
Pt–Pt(Si)(O)/CHA	1	Active site
Sn–O–Pt–Pt–Si /Sn-CHA	1	Active site
Si–O–Pt–Pt–H /def-CHA	1	Active site

---

In Table S4,† we show results from sensitivity analysis to identify the rate-limiting elementary steps on the various active sites. On Pt–Pt(O)(Si) in CHA, the rate is controlled by both the C–H activation and the β-H elimination. On Sn–O–Pt–Pt–Si and O:–Sn–:Pt in Sn-CHA, the rate is only sensitive to the β-H elimination, whereas on Si–O–Pt–Pt–H in def-CHA the rate is determined by the C–H activation alone.

Even though the isolated Pt atoms activate the C–H bond rather readily, they do not always show the expected high activity. The reason is that the isolated Pt sites over-stabilize the Pt–alkyl intermediate and that makes the β-H very slow. It is also worth noting that while the geometrically constrained Pt–Pt(O)(Si) motif in CHA shows the highest activity, its propensity for sintering could shorten its catalytic lifetime. Thus, the O:–Sn–:Pt and Sn–O–Pt–Pt–Si motifs in Sn-CHA, and the Si–O–Pt–Pt–H bonding structure in def-CHA should be the most active and stable catalysts among the sites investigated.

Interestingly, the Pt–Pt(O)(Si) motif in CHA as well as the O:-Sn-:Pt and Sn-O-Pt–Pt-Si motifs in Sn-CHA show lower apparent activation energies (by less than 10 kcal mol⁻¹) than the sites with corresponding nuclearities (Pt₂, Pt₂Sn, PtSn) on the conventional alumina support³⁵ highlighting the crucial role of the support and of the oxidation state of the Sn atom (Sn(IV) in CHA, Sn(0) on alumina) on activity. The sites on alumina show facile activation of the C–H bond on account of being undercoordinated. However, their overall activity is reduced by intermediate coverages and the high barrier of the β-H elimination.

Conclusions

We have performed ab initio molecular dynamics simulations and electronic structure calculations to identify and characterize stable Pt active site motifs in CHA and Sn-CHA, with and without silanol defects, at low Pt loadings. The activity of several active site motifs was evaluated by microkinetic modeling.

In contrast to pristine CHA, which promotes Pt–Pt association, silanol defects and framework Sn promote Pt dispersion. In the presence of silanol defects in Sn-CHA, the dispersed Pt species statistically prefer to coordinate with the silanols and not with the framework Sn, which agrees with a recent characterization of Pt species in Sn-BEA by Lefton et al.¹⁰ We further resolved the ambiguity related to the coordination of Pt in the presence of framework Sn by showing that the Pt atom is directly bonded to the Sn atom via a 3-center-4-electron O:–Sn–:Pt bond and by affirming the absence of Pt–O–Sn bonding, in agreement with the recent suggestion by Lefton et al.¹⁰

We identified four active site motifs, three of which involving dimeric Pt₂ species, that exhibited high activity for ethane dehydrogenation: the Pt–Pt(O)(Si) site motif in CHA; the Sn–O–Pt–Pt–Si in Sn-CHA; the Si–O–Pt–Pt–H in def-CHA and def-Sn-CHA; and the O:–Sn–:Pt in Sn-CHA. The first on the list, Pt–Pt(O)(Si), is more active than the rest by about an order of magnitude. However, we argue that it should likely have high propensity for sintering, which could shorten its catalytic lifetime. Therefore, the O:–Sn–:Pt and Sn–O–Pt–Pt–Si motifs in Sn-CHA, are predicted to be catalytically active and stable.

Our results and conclusions are related to the CHA framework. However, they are closely aligned with those made by Lefton et al. and by Dou et al. regarding Pt species at low loadings in Sn-BEA and Sn-MFI, respectively. We believe that this agreement strongly suggests that the effect of framework Sn on the dispersion of Pt species and on the formation of stable and efficient active sites, with bonding structures similar to those presented above, is largely independent of the framework itself.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the US Department of Energy (DOE), award number DE-SC0024085. The computations were partially supported by Information Technologies (IT) resources at the University of Delaware, specifically the high-performance computing resources. The research was supported in part by the University of Delaware's high-performance computing resources and Information Technologies (IT) resources. The authors thank Dr. Jeff Frey and Alfred Worrad for helping with software installation on the high-performance computing cluster. The authors also thank Prof. Raul Lobo, Roshaan Surendhran, Dr. Tso-Hsuan Chen and Dr. Pavel Kots for several helpful discussions.

References

1. W. Zhang, H. Wang, J. Jiang, Z. Sui, Y. Zhu, D. Chen and X. Zhou, Size Dependence of Pt Catalysts for Propane Dehydrogenation: from Atomically Dispersed to Nanoparticles, ACS Catal., 2020, 10(21), 12932–12942.
2. A. Bruix, Y. Lykhach, I. Matolínová, A. Neitzel, T. Skála, N. Tsud, M. Vorokhta, V. Stetsovych, K. Ševčíková, J. Mysliveček, R. Fiala, M. Václavů, K. C. Prince, S. Bruyère, V. Potin, F. Illas, V. Matolín, J. Libuda and K. M. Neyman, Maximum Noble-Metal Efficiency in Catalytic Materials: Atomically Dispersed Surface Platinum, Angew. Chem., Int. Ed., 2014, 53(39), 10525–10530.
3. Y. Nakaya and S. Furukawa, Tailoring Single-Atom Platinum for Selective and Stable Catalysts in Propane Dehydrogenation, ChemPlusChem, 2022, 87(4), e202100560.
4. Y. F. Chu and E. Ruckenstein, On the sintering of platinum on alumina model catalyst, J. Catal., 1978, 55(3), 281–298.
5. P. Tabib Zadeh Adibi, V. P. Zhdanov, C. Langhammer and H. Grönbeck, Transient Bimodal Particle Size Distributions during Pt Sintering on Alumina and Silica, J. Phys. Chem. C, 2015, 119(2), 989–996.
6. Y. Liu, Z. Li, Q. Yu, Y. Chen, Z. Chai, G. Zhao, S. Liu, W.-C. Cheong, Y. Pan, Q. Zhang, L. Gu, L. Zheng, Y. Wang, Y. Lu, D. Wang, C. Chen, Q. Peng, Y. Liu, L. Liu, J. Chen and Y. Li, A General Strategy for Fabricating Isolated Single Metal Atomic Site Catalysts in Y Zeolite, J. Am. Chem. Soc., 2019, 141(23), 9305–9311.
7. J. D. Kistler, N. Chotigkrai, P. Xu, B. Enderle, P. Praserthdam, C.-Y. Chen, N. D. Browning and B. C. Gates, A Single-Site Platinum CO Oxidation Catalyst in Zeolite KLTL: Microscopic and Spectroscopic Determination of the Locations of the Platinum Atoms, Angew. Chem., Int. Ed., 2014, 53(34), 8904–8907.
8. I. Lezcano-González, P. Cong, E. Campbell, M. Panchal, M. Agote-Arán, V. Celorrio, Q. He, R. Oord, B. M. Weckhuysen and A. M. Beale, Structure-Activity Relationships in Highly Active Platinum-Tin MFI-type Zeolite Catalysts for Propane Dehydrogenation, ChemCatChem, 2022, 14(7), e202101828.
9. Z. Xu, Y. Yue, X. Bao, Z. Xie and H. Zhu, Propane Dehydrogenation over Pt Clusters Localized at the Sn Single-Site in Zeolite Framework, ACS Catal., 2020, 10(1), 818–828.
10. N. G. Lefton and A. T. Bell, Effects of Structure on the Activity, Selectivity, and Stability of Pt–Sn-DeAlBEA for Propane Dehydrogenation, ACS Catal., 2024, 3986–4000.
11. Y. Ma, X. Chen, Y. Guan, H. Xu, J. Zhang, J. Jiang, L. Chen, T. Xue, Q. Xue, F. Wei and P. Wu, Skeleton-Sn anchoring isolated Pt site to confine subnanometric clusters within *BEA topology, J. Catal., 2021, 397, 44–57.
12. H. Wang, J.-X. Liu, L. F. Allard, S. Lee, J. Liu, H. Li, J. Wang, J. Wang, S. H. Oh, W. Li, M. Flytzani-Stephanopoulos, M. Shen, B. R. Goldsmith and M. Yang, Surpassing the single-atom catalytic activity limit through paired Pt-O-Pt ensemble built from isolated Pt1 atoms, Nat. Commun., 2019, 10(1), 3808.
13. H. V. Thang, G. Pacchioni, L. DeRita and P. Christopher, Nature of stable single atom Pt catalysts dispersed on anatase TiO2, J. Catal., 2018, 367, 104–114.
14. J. P. Perdew, K. Burke and M. Ernzerhof, Perdew, Burke, and Ernzerhof Reply, Phys. Rev. Lett., 1998, 80(4), 891.
15. J. Antony, R. Sure and S. Grimme, Using dispersion-corrected density functional theory to understand supramolecular binding thermodynamics, Chem. Commun., 2015, 51(10), 1764–1774.
16. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103.
17. M. J. Frisch, Gaussian 03 Rev. E.01, 2004, http://www.gaussian.com/.
18. A. D. Becke, Density-functional thermochemistry, III, The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652.
19. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789.
20. J. Kua, X. Xu, R. A. Periana and W. A. Goddard, Stability and Thermodynamics of the PtCl2 Type Catalyst for Activating Methane to Methanol: A Computational Study, Organometallics, 2002, 21(3), 511–525.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
22. J. Lym, G. R. Wittreich and D. G. Vlachos, A Python Multiscale Thermochemistry Toolbox (pMuTT) for thermochemical and kinetic parameter estimation, Comput. Phys. Commun., 2020, 247, 106864.
23. M. John, K. Alexopoulos, M.-F. Reyniers and G. B. Marin, Effect of zeolite confinement on the conversion of 1-butanol to butene isomers: mechanistic insights from DFT based microkinetic modelling, Catal. Sci. Technol., 2017, 7(14), 2978–2997.
24. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural bond orbital analysis program, J. Comput. Chem., 2013, 34(16), 1429–1437.
25. M. E. Coltrin, R. J. Kee, F. M. Rupley and E. Meeks, Surface chemkin-iii: A fortran package for analyzing heterogeneous chemical kinetics at a solid-surface-gas-phase interface; Sandia National Lab.(SNL-NM), Albuquerque, NM, United States, 1996.
26. D. J. Evans and B. L. Holian, The Nose–Hoover thermostat, J. Chem. Phys., 1985, 83(8), 4069–4074.
27. B. L. Holian, A. F. Voter and R. Ravelo, Thermostatted molecular dynamics: How to avoid the Toda demon hidden in Nos\'e-Hoover dynamics, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52(3), 2338–2347.
28. N. S. Martys and R. D. Mountain, Velocity Verlet algorithm for dissipative-particle-dynamics-based models of suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59(3), 3733–3736.
29. G. Ciccotti, R. Kapral and E. Vanden-Eijnden, Blue Moon Sampling, Vectorial Reaction Coordinates, and Unbiased Constrained Dynamics, ChemPhysChem, 2005, 6(9), 1809–1814.
30. V. Kräutler, W. F. van Gunsteren and P. H. Hünenberger, A fast SHAKE algorithm to solve distance constraint equations for small molecules in molecular dynamics simulations, J. Comput. Chem., 2001, 22(5), 501–508.
31. T.-H. Chen, D. G. Vlachos and S. Caratzoulas, Ab Initio Molecular Dynamics Study of Pt Clustering on γ-Al2O3 and Sn-Modified γ-Al2O3, J. Phys. Chem. C, 2023, 127(39), 19778–19787.
32. X. Dou, W. Li, K. Zhang, H. Hou, Z. He, C. Zhu, D. M. Meira, M. Lopez-Haro, Z. Xia, P. He, H. Xiao and L. Liu, Size-Dependent Structural Features of Subnanometer PtSn Catalysts Encapsulated in Zeolite for Alkane Dehydrogenation, ACS Catal., 2024, 14(5), 2859–2871.
33. D. Hou, L. Grajciar, P. Nachtigall and C. J. Heard, Origin of the Unusual Stability of Zeolite-Encapsulated Sub-Nanometer Platinum, ACS Catal., 2020, 10(19), 11057–11068.
34. J. J. Low and W. A. Goddard, III, Theoretical studies of oxidative addition and reductive elimination: hydrogen + diphosphineplatinum.fwdarw. dihydridodiphosphineplatinum, J. Am. Chem. Soc., 1984, 106(23), 6928–6937.
35. Y. Liu, X. Zong, A. Patra, S. Caratzoulas and D. G. Vlachos, Propane Dehydrogenation on PtxSny (x, y ≤ 4) Clusters on Al2O3(110), ACS Catal., 2023, 13(5), 2802–2812.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00187g

---