Pyrolysis and gasification of 5–20 mm tyre rubber cubes under carbon dioxide flow

Abstract

The thermal behaviour of waste tractor tyre tread was investigated using 5-, 10-, 15- and 20 mm cubes and video recording of the process – an experimental approach for which no precedent could be found in the literature. Pyrolysis and gasification under CO₂ flow in the range of 400 °C to 1000 °C were studied using a pre-heated tube furnace under near-isothermal reaction conditions. The video-graphic timeline and thermal history observations were used to correlate the results with first-order heat-transfer calculations and TGA-derived kinetics published previously. For pyrolysis, heat-transfer becomes the rate limiting step in the region 800–900 °C and above. Experimental evidence shows that the full pyrolysis time may be estimated from the algebraic sum of the local kinetic component and a heat-transfer component. The pressure build-up due to the release of gaseous products results in shattering of the solid into sub-millimetre char fragments. The kinetics of the reverse-Boudouard reaction can be described by a standard gas–solid shrinking particle model; however the character of the charred remains complicates this. Mass transfer limits are predicted only to become significant above 1200 °C, for a well-characterised char surface.

---

1 Introduction

The research reported here forms part of a development program at the South African Nuclear Energy Corporation SOC Ltd. (Necsa) for the plasma-assisted treatment of various wastes, including end-of-life tyres, as feed material to produce CO-rich synthesis gas suitable for use in, e.g., electricity-generation equipment. This paper builds on the existing body of work to arrive at a semi-quantitative description of the rubber pyrolysis–gasification process with the overall aim of providing heuristics for estimating pyrolysis and gasification times for rubber samples in the 5–20 mm range, for the design of a mobile plasma-based waste-to-energy system.

The peer-reviewed literature with respect to the thermal treatment of waste tyre rubber has demonstrated increasing activity over the past few years, undoubtedly due to mounting environmental and energy concerns. A Scopus search¹ using the key words ‘waste AND tyre AND rubber AND pyrolysis’ reveals an exponential rise in the number of papers being published since 2000, with the current rate at >60 per annum.

Of direct relevance to the work presented here, are: research reports containing TGA derived kinetics from mg sample sizes; results with respect to the thermal behaviour of macroscopic rubber samples; and heat-and mass transfer models for the pyrolysis and gasification of macroscopic rubber crumbs; and articles on reactor development at TRL 4 and higher.

Papers on pyrolysis and gasification go back many years as evidenced, for example, by a series of review articles between 1963 and 2020.^2–11 Reaction kinetics are mainly studied by TGA^2,12 and according to ICTAC guidelines^13–15 and done at different heating rates under either isothermal or, mostly, dynamic conditions. In order to eliminate bulk diffusion and heat transfer effects, particles of ∼100 μm size and mg sample mass range, are used so that chemical kinetics are rate-determining. In industrial scale processes, however, the cost of feedstock size reduction can quickly become prohibitive.¹⁶ Several authors have suggested that, above about 2 mm particle size, heat- and mass transfer effects must be taken into account in modelling studies.

The distinction between primary and secondary pyrolysis stages of 13 mm particles progressively disappears as the heating rate is increased, for which Senneca et al.¹⁷ propose a mechanistic model.

Gao et al.¹⁸ found that for identical heating rates the mass loss curve for 1 cm cubes shifts to higher temperature w.r.t. 0.07 to 0.8 mm powder samples due to heat transfer effects.

In a recent paper Ramírez Arias et al.¹⁹ analyzed the pyrolysis of 0.3 mm and 5 mm rubber particles at several heating rates. The results for the kinetic triplet depended on the model used and the values found increased with particle size due to heat transfer effects.

In their study of the influence of particle size on the pyrolysis process, Haydary et al.²⁰ used rubber particles from 48 mm in size and include some images of the product obtained at different residence times. They correlated data obtained from an isothermal auger reactor with those obtained by TGA, much as was done in this study but using a different experimental approach. Their model couples the chemical kinetics as energy sink to Fourier II, in spherical co-ordinates, with appropriate boundary and initial conditions. The sample surface temperature is assumed to be the furnace temperature. They report reaction times of 50–130 s for particles of sizes 4–8 mm, measured by iso-thermal TGA at 550 °C. Correspondence between model and data is good. They concluded that using average heat transfer values does not lead to significant errors in the modelling. We used their experimental rather than their modelled times.

The model developed by Larsen et al.²¹ is even more comprehensive. It includes both convective and radiative heat transfer, along with phase change.

Bouvier et al.²² studied the relationship between pyrolysis time, sample dimensions (520 mm cubes) and temperature. Above 460 °C the pyrolysis time increased linearly with the square of the side length and the rate is under heat transfer control. Below 460 °C this relationship no longer holds, indicating chemical and physical kinetics control. They include a rough thermal model assuming uniform temperature distribution for their relatively large samples, along with simple kinetic modelling. They fitted their dynamic mass-loss data to simple sigmoidal curves, and demonstrated good correspondence between model and experiment.

Yang and co-workers²³ investigated the isothermal vacuum pyrolysis of 40 mm dia. × 60 mm cylindrical tyre samples up to 480 °C, following the thermal history by an embedded thermocouple. They proposed a mechanism whereby the reaction front involves solid–plastic–solid phase changes with devolatilization via bubbling of the plastic phase. Our imaging results have shown this to be so. They calibrated their model against measurements taken on a rubber sample, substantially larger than the one in this study – a 40 mm OD × 60 mm height cylinder – and for temperatures up to 480 °C.

Kim et al.²⁴ studied the influence of isothermal pyrolysis time on small (≤1.2 mm) rubber particles in a thermobalance up to 500 °C at different heating rates. The isothermal pyrolysis time was directly proportional to the frequency factor, inversely proportional to the activation energy and heating rate and increase linearly with particle size.

Aylon et al.²⁵ pyrolyzed ≤2 mm particles at different heating rates, and temperatures up to 600 °C in a fixed-bed (platinum basket) TGA set-up. They noted that the heating rate does have an influence at low temperatures where low heating rates led to higher conversion, due to the sample residence time being longer. Up to 500 °C, at a constant heating rate, only a higher final temperature improved the conversion. Their kinetic model predictions showed good agreement with experimental results obtained in a fixed bed reactor. They concluded that for their size range, the influence of the heat transfer rate was negligible, and used the sub-1 mm material for the rest of their investigation, the samples being more representative and homogeneous in composition. This agrees with our findings. Their work was done using a constant heating rate, however, and therefore their reaction times could not be directly correlated with the data in this study.

In their work Larsen et al.²¹ pyrolyzed 7.5–22 mm dia. × 32 mm rubber cylinders, using two samples atop one another and enclosed in a steel mesh basket to contain swelling. They introduced a local devolatilization conversion in their modeling to compensate for the physical changes in the sample and the changing heat capacity and thermal conductivity. Validation of their model against experimental observations led them to conclude that the devolatilization of large rubber particles is controlled by heat transfer and chemical kinetics.

Ahmed and Gupta²⁶ numerically simulated the effects of particle size, porosity and temperature on char conversion at different Damkohler numbers. At large numbers the reaction rate is much faster than the rate of diffusion and the process is diffusion rate controlled with reaction is mainly on the surface of the particle. As the reaction proceeds, the Damkohler number decreases as the particle shrinks, becomes more porous, the diffusion rate increases, and the process becomes chemical reaction rate controlled.

Oyedun et al.¹⁶ have developed a model for energy optimization for tyre pyrolysis by considering the effect of shredding, particle size, and heating rate on the overall energy balance. As can be expected, pyrolysis completion time reduces as particles become smaller. However, the overall process energy requirement reduces with increasing particle size, having spent less energy on shredding and grinding.

During the gasification of rubber waste the material passes through an initial pyrolysis phase at 300 °C to 600 °C producing CO, H₂ and light hydrocarbon gases, volatile (condensable) hydrocarbon compounds and char. Gasification of the char then proceeds at a rate relevant to the gasification agent, be it O₂, air, steam or CO₂, or gas mixtures. Investigations by standard TGA are limited to the mg sample range and the requirement of using a representative sample which is as homogeneous as possible. This implies taking an aliquot from a large sample which has been ground down to typically 10–100 micron particles. As mentioned, that for particles up to about 2 mm, heat transfer phenomena do not affect the kinetics materially.²⁵ However, for industrial applications, the appreciable cost of grinding waste rubber down to these sizes militates against this size range. Modelling of heat transfer together with chemical kinetics thus becomes desirable for understanding the pyrolysis–gasification process.^16,18,27

The modelling referred to in the paragraphs above, invariably use finite-difference discretization of the governing equations, and purpose-written code. One publication has appeared recently reporting a more computationally-intensive model of rubber pyrolysis, viz., by Khiari et al.²⁸ They report a finite-difference model, using commercial software. The model was developed for cubic samples, using; five simultaneous chemical reactions with kinetic parameters taken from Cheung et al.;²⁷ convective heat transfer to the sample surface; volatile flows from inside the sample; and physical property values varying with degree of conversion. They explored temperatures below our range of interest. For a 20 mm at 550 °C, they predict a period of 3300 s to arrive at a 0.6–0.65 degree of conversion – about an order of magnitude longer than the experimental results reported here, testifying to the complexity of the problem.

In a recent paper²⁹ we reported the derivation of engineering kinetic parameters from isothermal and dynamic TGA data, from room temperature to 1100 °C, for the pyrolysis and the reaction of <100 μm tyre rubber crumbs with CO₂. Workable, rather than definitive, models could be derived: Jander 3-D diffusion for the first pyrolysis event up to 550 °C; the Mampel mechanism for high-temperature pyrolysis in the absence of CO₂ above 550 °C; and shrinking-particle chemical-reaction control as the rate limiting step for the reverse-Boudouard reaction. These model equations performed better than the empirical Sestak–Berggren equation.

The objective of the present exploratory study was to extend and test the applicability of the microscale work done previously by TGA²⁹ to large particles in the form of 5–20 mm cubes cut from tractor-tyre rubber. No study could be found showing images of samples at different pyrolysis stages, nor of short method for estimating reaction times, and no data with respect to the reaction with CO₂ is available.

Here we present novel real-time imaging of such behaviour. A heuristic pyrolysis model is derived from the videographic data and our previous TGA-derived kinetics; it is an engineering rule-of-thumb method for estimating pyrolysis time as function of temperature and rubber-sample size. Conversion of the char residue to CO by reaction with CO₂ is a slower process and is shown to fit reasonably to gas–solid shrinking-particle model, provided the size of the char granules, not the initial rubber sample size, is taken into account.

We observed and recorded the pyrolysis and gasification behaviour of different-sized particles in a tube furnace under N₂ and CO₂ flow using in situ videography a novel approach for which no precedent could be found in the literature and correlated with first order heat-transfer and kinetic predictions. Char yields obtained under various conditions of temperature and residence time were determined. The morphology of the chars were examined by scanning-electron microscopy/energy-dispersive X-ray spectroscopy (SEM/EDX) and microphotography.

2 Experimental

2.1 Experimental planning

The experimental work investigated the effects of particle size, temperature and residence time on pyrolysis and gasification of different-sized rubber cubes under CO₂ atmosphere. Some runs were done under N₂ for comparative purposes. The schedule was developed before data analysis was performed. The experimental conditions, sorted by cube dimensions for the results reported here, are summarized in Table 1. The variation in the masses of similar-sized cubes attests to the difficulty of accurately cutting the samples by hand.

Table 1 Summary of experimental conditions

Exp. no	Process gas	Cube nom. side length (mm)	Cube nom. volume (cm^3)	Initial mass (g)	Cube true volume (calc.) (cm^3)	Temperature (°C)	Time (min)
220329_2	CO2	5	0.13	0.1676	0.147	863	23
220224_1	N2	10	1.00	1.0989	0.965	635	22
220324_3	CO2	10	1.00	1.3710	1.204	863	20
220329_1	CO2	15	3.38	3.6440	3.199	456	21
220302_1	N2	15	3.38	3.2836	2.843	640	22
220302_2	CO2	15	3.38	3.9789	3.493	635	20
220310_1	CO2	15	3.38	2.8566	2.508	873	10
220322_1	CO2	15	3.38	3.7040	3.252	864	14
220310_2	CO2	15	3.38	3.5488	3.116	882	20
220318_1	CO2	15	3.38	3.6196	3.178	860	20
220316_1	CO2	15	3.38	2.8935	2.540	861	45
220324_1	CO2	15	3.38	3.8303	3.363	862	20
220505_1	CO2	15	3.38	4.2275	3.712	990	20
220328_1	CO2	20	8.00	9.2394	8.112	864	23

---

2.2 Materials

The samples used in this study were cut from a section of delaminated tractor tyre tread, obtained from the scrap stockpile of a local dealership in South Africa. The rubber contained no textile or steel. The density of this material, 1140 kg m⁻³, determined by the Archimedes method, corresponds to that of other rubber reported in the literature.³⁰ Cubes of 5-, 10-, 15- and 20 mm side length were manually cut from the source material using glycerine as lubricant (Fig. 1).

Fig. 1 Typical examples of rubber cubes cut from tractor tyre tread.

The proximate and ultimate analyses of the rubber used in this study are summarized in Table 2. Gases used in the experiments were obtained from Afrox (Pty) Ltd.

Table 2 Rubber properties

Property	Mass %
Fixed carbon	19.0
Volatiles	70.8
Ash	10.2
C	82.9
H	7.3
N	0.3
S	2.4
O (by difference)	7.3

---

2.3 Analytical instruments

SEM was done on the rubber and char samples using a Quanta FEI 200 D instrument with an acceleration voltage of 15 kV and samples were pre-coated with carbon. During capturing of the micrographs, EDX analyses were done using an EDAX Octane detector and a spot size parameter of 6.5 mm. TEAM Elemental qualification software was used for visualisation and data processing, A Zeiss Discovery V20 Stereo Microscope equipped with a 5 MP digital camera and imaging software was used to obtain images of rubber and char surface morphology.

The proximate analysis was performed on single-particle samples cut from the parent rubber, using an SDT Q600 V20.9 Build 20 TGA instrument. Ultimate analyses of the rubber and char was done in a Thermo Scientific Flash 2000 organic element analyzer. C, H, N and S could be quantified and the oxygen concentration was determined by difference.

2.4 Equipment

The experimental set-up is illustrated by the schematic in Fig. 2. Samples were heated in a 2340 W Carbotherm Model GHA 12/300 programmable horizontal tube furnace (1). The furnace has a heated length of 300 mm and is capable of sustained operation at 1100 °C. The alumina furnace tube (84 mm OD, 74 mm ID and ∼700 mm long) (14) was plugged at both ends with insulating brick (12) through which were passed thermocouples (3, 4) and thin (1.2 mm) braided stainless-steel wire (10) for drawing a sample pan (18) into and out of the heated zone (positions 17 and 18, respectively). The working gas (Ar, N₂, CO₂), feed to the furnace was regulated by rotameter (11) and pre-heated in a 4.6 m long, 6.4 mm (1/4 inch) OD stainless-steel tube (15), coiled to fit inside the furnace tube. The gas exited the heating coil at the end of the tube next to the observation port (8). A stainless-steel mesh support platform (16) was fitted inside the gas heating coil to allow the sample to be drawn into and out of the furnace. Mechanical stops at each end of the mesh ensured repeatable positioning of the sample pan. The stop at the hot end was positioned so that the sample pan would rest in the centre of the furnace heating zone during processing. A stainless-steel gauze (0.2 mm wire, 16 mesh) sample support basket was placed in a rectangular stainless-steel pan (64 × 40 × 14 mm) with an empty weight of 42.2088 g. The pan was intended to collect any spills from the sample basket and allowed the processing residue to be weighed without having to transfer the sample to a weighing pan. Temperatures at the waste gas outlet (1), initial sample position (2), and the working position at the centre of the furnace (3) were recorded by K-type thermocouples and a Yokogawa Model DX 2030-3-4-2 digital multichannel recorder.

Fig. 2 Schematic of tube furnace set-up. Not to scale, data logger not shown. (1) Tube furnace; (2)–(4) thermocouples connected to a multichannel datalogger; (5) ventilation shroud; (6) borosilicate glass rod; (7) 12 V LED lamp; (8) quartz observation port; (9) camera; (10) braided drawing cable; (11) rotameter; (12) insulating brick end plugs; (13) flexible ventilation duct; (14) furnace tube; (15) gas heating coil; (16) support grid, (17); sample pan (initial position); (18) sample pan (working position).

The interior of the furnace tube was illuminated by a commercially available 12 V LED lamp (7) mounted at one end of a 12 mm borosilicate rod (6) passed through the furnace end plug. The ends of the glass rod were sanded to an opaque finish, to provide uniform illumination.

Video footage of the sample behaviour in the furnace was recorded by a tripod-mounted Canon DSLR camera (9) via a 40 mm dia. quartz observation port (8) set up at the hot end of the furnace.

A ventilation shroud (5), placed around the cold outlet of the furnace tube was connected directly to the laboratory fume extraction system by flexible aluminium air conditioning ducting (13). The hot off gas exiting the furnace (12) was cooled and diluted by room air drawn through the annulus between the shroud (5) and furnace tube (14).

General views of the furnace equipment and camera set-up are shown in Fig. 3 and 4 respectively. Fig. 4 shows the imaging equipment set up on-axis outside the viewing port at the hot end of the furnace, including thermocouples TC3 and TC4 and the cable for drawing the sample boat into the furnace hot zone. The LED is shown mounted on a borosilicate glass rod for illuminating the inside of the furnace, especially at temperatures below 800 °C.

Fig. 3 General view of the experimental apparatus.

Fig. 4 Views of the imaging set up.

2.5 Experimental method

Experiments were routinely carried out by pre-programming the furnace heating cycle for a particular series of runs. For all working temperatures up to 860 °C, the ramp up heating rate was set to 15 °C min⁻¹. The control thermocouple of the furnace was situated near the heating elements. Experience showed that for the furnace tube size used here, the furnace set point had to be some 50 °C above the desired operating temperature due to the temperature gradient between the elements and the interior of the furnace tube. For temperatures above 860 °C the heating was ramped up at 50 °C min⁻¹ to 100 °C below the set point and then at 15 °C min⁻¹ up to the final temperature to minimize overshoot.

Examples of the rubber cubes are shown in Fig. 1. The stainless-steel sample pan, together with the gauze basket and the sample, was weighed before each experiment. The sample pan containing the residual material was weighed after each experiment. The mass loss of the sample was obtained by difference.

The sample pan containing the sample was placed on the stainless-steel mesh support platform at the cold end of the furnace (position 17, Fig. 2). Braided 1.2 mm stainless-steel cables, passing through the plugs at either end of the furnace tube, were then attached to the sample pan to so that it could be moved between the cold and the heated zones of the furnace. The camera was pre-focussed on the sample at rest in the hot zone (position 18 of Fig. 2). After replacing the plug at the cold end, the ventilation shroud was moved into position. Free movement of the sample assembly was checked before starting the inert purge gas flow (N₂ or Ar) at 7.7 NL min⁻¹ during temperature ramp-up.

At this point in time, the furnace and data recorder were switched on with the sample positioned at the cold end. The quoted operating temperatures were as measured in the centre of the furnace by thermocouple TC4 and at the cold end by thermocouple TC3. The thermocouples were situated at roughly 10 mm below the respective sample positions and the resulting temperature gradients were considered insignificant in the context of this investigation.

Once the temperature at the centre of the furnace (TC4) was within 5 °C of the intended working temperature, the purge gas was changed to CO₂. The video recording was started and after a stabilisation time of typically 2 minutes the sample was drawn into the hot zone and the reaction recorded. Once the pre-determined reaction time had lapsed, the sample was withdrawn to the cold end of the furnace (position 17, Fig. 2), the furnace switched off and purged with Ar while the sample pan cooled sufficiently for removal and weighing.

We estimate the accuracy of the measurements to be of the order of 5%.

2.6 Data acquisition

Temperature data were captured every 2 s throughout each run, downloaded and converted to Microsoft Excel format for analysis. Reaction times could be determined with good accuracy by examining the temperature record of thermocouples TC3 and TC4 positioned respectively in the cold and hot zones of the furnace tube. Inserting the sample into the hot zone caused a dip in temperature TC4 and, upon withdrawing it, a spike in temperature TC3. The difference between these two times was taken as the residence time, t_r, of which a typical example is illustrated in Fig. 5.

Fig. 5 Effect of sample insertion and extraction on temperature. t_r refers to the residence time in the hot zone.

Video- and photographic data were routinely captured by a digital DSLR camera. Videos were recorded for up to 30 min for observation of the physical changes of the samples during pyrolysis and devolatilization. Still photographs were taken every 5 min thereafter, if necessary, until completion of the run to record the much slower gasification process.

During play-back of the videos using VLC Media Player® (version 3.0.18.0) software, ‘snapshots’ were taken and run times noted by stopping the recordings at the moment of insertion in the hot zone, the initiation of pyrolysis and devolatilisation, and at selected times thereafter. The moment of sample insertion (typically 2 min into the video) was taken as t₀ and this value was subsequently subtracted from the video run time to obtain the reaction time at any given point. In this way the video content could be correlated with the temperature history from the process data recorder. The heating/devolatilisation process was judged to be complete when fumes were no longer visible, the sample no longer changed form and the image had a uniform colour. These times were then used for further data analysis.

Still photographs and video snapshots were edited in XnView® (version 1.98.5) by cropping and normalizing the colour images using the program's default settings. Colour images could also be transformed to 64 bit greyscale as required. The sample pan containing the residue was weighed after completion of the experiment and the weight-loss recorded.

3 Results and discussion

3.1 General observations

Video data clearly showed the physical changes taking place in samples during heating. The general observation was a distinct heat front moving into the bulk of the sample at low temperatures, with concomitant blistering or bubbling of the heated rubber and evolution of smoky vapour. At higher temperatures the sample disintegrated vigorously, literally popping apart due to rapid devolatilisation, forming a friable char.

From previous TGA results,²⁹ it is known that only pyrolysis takes place below 500 °C irrespective of whether nitrogen or carbon dioxide is used as carrier gas. The residue after pyrolysis was 33–38% of the starting material. Above 500 °C under nitrogen, only a slight further mass loss was observed. Under carbon dioxide, however, the reverse-Boudouard reaction starts at just above 800 °C, the char gasifying with one mole of CO₂ yielding 2 moles of CO. At the typical TGA heating rates, the process is complete between 1000 °C and 1200 °C, leaving only the inorganic ash. Thus, the process takes place in two steps, viz., pyrolysis followed by gasification, as also reported by many previous researchers, e.g., by Cetin et al.³¹

The process is illustrated by time-lapse images for 10 mm and 15 mm cube undergoing pyrolysis at a furnace temperature of 635 °C under a N₂ and CO₂ flow in Fig. 6 and 7 respectively, and the pyrolysis–gasification behavior of a 15 mm cube under a CO₂ flow at 990 °C in Fig. 8. The images were close-cropped to show the effects of the processing more clearly. Due to the geometry of the equipment the sample could not be positioned on the centre-line of the furnace, which, in addition to initial the shielding effect of the cold sample pan, led to the clearly asymmetrical heating of the sample visible in Fig. 6. Gas flow to the furnace was regulated at 7.7 NL min⁻¹ in all experiments reported here, except for 220302_2, (8.5 NL min⁻¹).

Fig. 6 Time lapse images, (a)–(f), of pyrolysis. 10 mm rubber cube at 635 °C under N₂ flow (Exp. 220224_1).

Fig. 7 Time-lapse images, (a)–(h), of pyrolysis. 15 mm rubber cube at 635 °C under CO₂ flow (Exp. 220302_2).

Fig. 8 Time lapse images, (a)–(l), of pyrolysis and gasification. 15 mm rubber cube under CO₂ flow at 990 °C (Exp. 220505_1).

3.2 Pyrolysis under N₂ and CO₂ atmosphere

The images in Fig. 6(a)–(f) illustrate the progression of the heat and reaction zone during pyrolysis and devolatilisation. The stainless steel gauze sample support was complimented by a gauze restraint over the top of the sample to keep it in position during the transfer in and out of the furnace and to mitigate mass loss during crumbling while the sample was being heated.

Fig. 6(a) shows the sample at the moment it was drawn up against the stop in the centre of the furnace hot zone, i.e., t = 0. After 10 s (Fig. 6(b)) blistering of the material has become clearly visible. Fig. 6(c) and (d) show the progression of the reaction front after 15 and 18 s reaction time, respectively. After 21 s, (Fig. 6(e)), the visible blistering is complete and the sample has started crumbling. Fig. 7(a)–(h) presents time lapse images of the thermal behaviour of a 15 mm rubber sample at 635 °C under a CO₂ atmosphere when allowed to expand freely.

The time-lapse images in Fig. 7(a)–(h) show the volume change of a 15 mm cube as pyrolysis under CO₂ at 635 °C proceeds. In this case the sample was contained in a gauze basket without a restraining cover, unlike the set-up shown in Fig. 6. Larsen et al.²¹ specifically constrained their pyrolysis samples in a gauze basket to combat the effects of swelling. In an industrial process, however, the swelling and granulation is inherently part of the process, and should be taken into account when sizing the reactor. In this case, by measuring the relative height of the material directly from the video footage at t = 0 (40 mm) and t = 3 min (68 mm), when it reaches a maximum, the estimated volume increase is roughly 70%.

3.3 Pyrolysis and gasification under CO₂ atmosphere

The time lapse images of the pyrolysis and gasification of a 15 mm cube at 990 °C under CO₂ flow presented in Fig. 8 show the initial vigorous decomposition of the sample at this temperature.

Fig. 8(a) shows the sample at rest at the moment of introduction into the furnace at time t = 0 s and sample temperature of 22 °C before introduction. The first smoky-vapour evolution is already visible (top right hand quadrant) and reaches more or less steady state after 9 s (Fig. 8(b)). The blistering observed during the initial phase of pyrolysis, at 635 °C (Fig. 6) was, however, not evident here, which leads to the conclusion that the heat transfer at high temperature is so fast that blistering was no longer observable, even when recording at 30 frames per second. Particles were almost immediately ejected from the surface as shown by the light-shaded tracks visible in the upper left-hand quadrant of Fig. 8(b), and the sample is starting to crumble.

Sudden bursts of smoke and faint particle tracks are visible in the upper left quadrant, in Fig. 8(c). Fig. 8(d) and (e) show whole portions of the charring mass being ejected, visible as blurred areas in the lower right-hand quadrant. The smoky cloud begins to subside after about 150 s, but the tracks of hot ejected particles are still visible (Fig. 8(e)). The mass eventually reaches temperature equilibrium with its surroundings after 182 s (Fig. 8(f)) as evidenced by the uniform colour of the image in the foreground and the disappearance of the smoky vapour cloud, suggestive of complete devolatilisation.

The crumbling of the char shows that, once the pyrolysis is complete, the gasification rate should be controlled by the gasification kinetics as determined by TGA (chemical reaction control, shrinking particle), transport of reagent gas and products through, and inter-particle heat transfer in, the resultant particle bed. In the reverse-Boudouard gasification, the chemical reaction will be the rate determining step. The receding surface of the char visible in the upper left quadrants of Fig. 8(g) and (l) give a qualitative indication of the gasification rate. The average heating rate of the sample between introduction (22 °C) and the temperature equilibrium point at 990 °C was 5.3 °C s⁻¹, in comparison to the 50 °C min⁻¹ (∼0.8 °C s⁻¹) during the “isothermal” TGA experiments.

3.4 Sample morphology

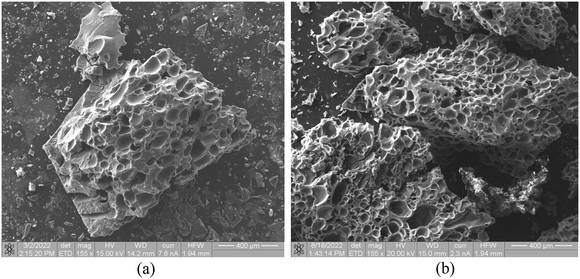
Images of the surface morphology of an original rubber sample and the char residues obtained at 650 °C under N₂ flow and 1000 °C under CO₂ flow, are presented in Fig. 9 and 10 respectively. The images of an untreated rubber sample, Fig. 9(a) and (b) show granular material spread out on the cut surface. The X-ray-excitation K lines obtained from the light-coloured granular material in Fig. 9(b) showed a strong presence of Ti, Si, O, and some Fe, suggestive of inorganic filler material.

Fig. 9 Surface morphology of the untreated rubber sample. Optical microscope image (×10 magnification) (a) and combined secondary electron/backscatter electron SEM image (×1000 magnification) (b).

Fig. 10 SEM images of the surface morphology of the residue (a) after 20 min at 650 °C under N₂ flow (Exp. 220302_1), and (b) after 20 min at 990 °C under CO₂ (Exp. 220505_1). Both are at a ×155 magnification.

The images in Fig. 10(a) and (b), show the morphology of the residue after 20 min at 650 °C under N₂ and after 20 min at 990 °C under CO₂ flow respectively, obtained by combined SEM-BSE (back-scattered electron mode) and SEM-SE (secondary-electron mode) images at ×155 magnification. Although not immediately evident from the video-graphic data, the pore morphology clearly suggests that the rubber melts with the evolving gases collecting in bubbles in the molten phase.²³ The increasing degree of pyrolysis results in loss of elasticity by the molten phase and increased charring. At some point the charred material is unable to yield to the gas build up, and the material crumbles. At low temperatures the process proceeds slowly (Fig. 6), suggesting the growth of larger gas pockets (typically 100 μm) as evidenced in Fig. 10(a) before charring and mechanical breakage. At high temperatures (Fig. 8) the heating rate is fast and the typical pore size is about 50 μm (Fig. 10(b)). It should be noted that in many cases the particles and dust scattered by the explosive gas release could not be collected in full, causing substantial errors in our experimental residue-mass data.

3.5 Data analysis

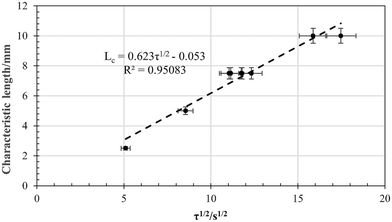
In Fig. 11 below, the time taken for pyrolysis at 860 °C is plotted as function of the size of the rubber cubes. The reaction times were extracted from the video material and taken to be the point at which no further gas evolution could be discerned and temperature equilibrium uniform colour with the surroundings was achieved. The reaction times range from less than 1 minute for a 5 mm cube, to between 4 and 5 minutes for a 20 mm cube. The trend is clearly parabolic, suggesting that the process is heat-transfer driven.

Fig. 11 Dependence of devolatilisation time on nominal cube dimensions at 860 °C.

A plot of characteristic length, taken to be half the cube side length, as function of the square root of the reaction time, is presented in Fig. 12. The trend is linear within 5% error.

Fig. 12 Evaluation of thermal diffusivity at 860 °C.

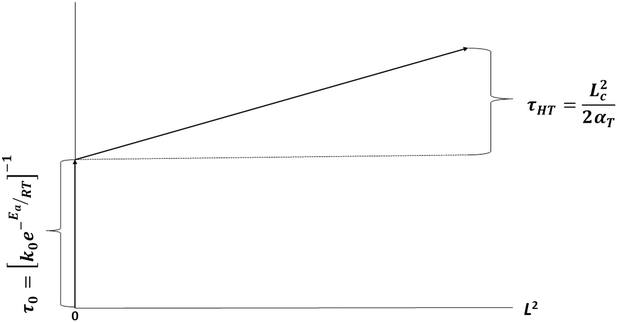
The conductive heat transfer in a body is roughly described in terms of the characteristic length L_c, the thermal diffusivity α_T, and the characteristic time τ_c by

L_c = (2α_Tτ_c)^1/2 (1)

where the thermal diffusivity is, per definition, the ratio of the thermal conductivity κ, to the product of the specific heat capacity C_p and the density of the material ρ (e.g. ref. 32), i.e.Note that the intercept has a finite negative value, not having been forced through zero. The rubber thermal diffusivity may be estimated from the gradient. The value of 0.194 mm² s⁻¹ arrived at for the thermal diffusivity compares well with values calculated from physical properties taken from the literature as presented in Table 3.

Table 3 Comparative physical properties

Material	α T (mm^2 s^−1)	κ (W m^−1 K^−1)	C p (J kg^−1 K^−1)	ρ (kg m^−3)
a Thermtest database.^33 b Yang et al.^23
This study	0.194	—	—	—
Butadiene–acrylonitrile rubber + carbon^a	0.22	0.418	1443	1340
Styrene–butadiene rubber + carbon black^a	0.14	0.243	1757	1000
Tyre rubber^b	0.281	0.38	1230	1100

---

The kinetic triplet previously derived for the pyrolysis process²⁹ is described as adaptable to estimate the effect of particle size. The Jander 3D diffusion equation is given by eqn (3) (see, e.g., ref. 34):

The variable and parameters have their usual meaning and are listed in the nomenclature table: α is the extent of reaction defined in terms of mass m as [(m₀ − m_t)]/[m₀ − m_fin] with the subscripts 0, t, and fin indicating initial, at time t, and final respectively; k(T) and k′(T) are Arrhenius-type rate constants, units of inverse time and extension per unit time; D is the diffusion constant of the migrating species through the solid product layer, the gaseous products released during pyrolysis; and R₀ is the initial sample radius.

We previously extracted the coefficient of t on the right-hand side of eqn (3) as a single temperature-dependent Arrhenius rate constant (the inverse of τ) from TGA data. The sample comprised <100 μm rubber crumbs. As a first approximation for using the expression to estimate pyrolysis times for larger particles, it was adapted by multiplying by the square of average experimental particle radius, then dividing by the square of the starting radius of the crumb. This proved less than satisfactory, however, and unnecessary, as will be shown below. The parameters used for this paper, taken from our previous work,²⁹ are listed in Table 5.

Eqn (3) is derived for spherical particles. In deriving the kinetic triplet from TGA data, fourteen solid state models were compared. The Jander 3D model came out marginally better only.²⁹ No complementary investigations were performed. In light of well-documented misgivings about the derivation of solid-state kinetics from TGA data,^35,36eqn (3) should thus be taken to have suggestive physical meaning only; rather it is an algebraic expression for evaluating the extent of reaction as function of time and temperature, smoothing through the chemical complexity of the pyrolysis process. In the spirit of the engineering approach taken in this paper, we have also not distinguished between spherical and rectangular co-ordinates, and have taken L_c ∼ R₀, and the cubic dimension L = 2L_c ∼ 2R₀.

3.6 Comparison with the literature

Systematic studies of the pyrolysis of rubber samples in the 10 mm range have been published. In general the data generated were used to calibrate numerical solutions of Fourier II for the pyrolysis process. Here we use the data of Bouvier et al.,²² Larsen et al.,²¹ and Haydary et al.,²⁰ as summarized in Table 4: summary of thermal diffusivities and L = 0 pyrolysis-time intercepts along with our own data.

Table 4 Summary of thermal diffusivities and L = 0 pyrolysis-time intercepts

T/°C	τ 0,model/s	τ 0,experimental/s	α T/(mm^2 s^−1)	Ref.
490	312.9	256.8	0.126	Haydary et al.^20
501	228.7	93.8	0.161	Bouvier et al.^22
544	72.8	25.1	0.147	Bouvier et al.^22
550	62.7	70.1	0.149	Larsen et al.^21
590	24.3	9.5	0.173	Bouvier et al.^22
620	12.6	110.5	0.178	Haydary et al.^20
840	0.3	17.8	0.209	Haydary et al.^20
860	0.2	0	0.194	This work
Average:			0.166 ± 0.026

---

Full pyrolysis times as function of particle size and temperature, extracted from these papers, are plotted along with our data in Fig. 13. These τ_pyrolysisvs. L² plots, i.e., plots of full pyrolysis time vs. the square of the sample dimension, are linear, with very little variation in slope values, and with τ_pyrolysis intercepts that increase with lowering temperature, and approaching zero at around the 900 °C mark.

Fig. 13 Raw pyrolysis data taken from the literature.^21,22,37

The intercept values correspond very satisfactorily with full pyrolysis times calculated from the Jander 3D-diffusion expression we have derived for pyrolysis of <100 μm particles,²⁹i.e., eqn (5) in Table 5, taking full pyrolysis times as the inverse of the rate constant for any given temperature. Experimental and model data are plotted in Fig. 14. Since the y-intercepts in Fig. 13 are extrapolated values for zero-diameter particles, this makes perfect sense.

Table 5 Summary kinetic data²⁹ for pyrolysis and reverse Boudouard reaction, in integral form

g(α)	τ (min)		Equation #
Pyrolysis
Here: CCO2 is the partial pressure of the CO2, expressed in mass per unit volume; ρ is the density with the subscript indicating either carbon or carbon dioxide; DCO2 is the self-diffusion constant of CO2; Sh is the Sherwood number, Re the Reynolds number, Sc the Schmidt number; and μCO2 is the CO2 viscosity.
[1 − (1 − α)^1/3]^2		k 0 = 7.337 × 10^8 min^−1	(5)
		E a = 1.40 × 10^5 J mol^−1 K^−1

---

Reverse Boudouard – chemical reaction control
1 − (1 − α)^1/3		k 0 = 2.580 × 10^6 min^−1	(6)
		E a = 1.689 × 10^5 J mol^−1 K^−1

---

Reverse Boudouard – mass-transfer control
1 − (1 − α)^2/3		Sh = 2 + 0.522Re^1/2Sc^1/3	(7)

---

Fig. 14 Model and experimental pyrolysis times for L ∼ 0 mm.

The conclusion can thus be drawn that full-pyrolysis times of cm-sized rubber samples may be estimated from the algebraic sum of the pyrolysis time for sub-mm pyrolysis rubber crumbs, τ₀, and the thermal diffusion time τ_HT for the larger sample, i.e.:

The process heuristics are illustrated graphically in Fig. 15. Since we were not able to trace a derivation of expression (4) in the literature, it is given in ESI† Appendix A.

Fig. 15 Heuristics for estimating rubber pyrolysis time.

Experimental values from the literature,^20–22 and values estimated from eqn (4), the dotted line, using the parameters given in Tables 4 and 5, are compared in Fig. 16: the absolute percentage difference is ∼20%.

Fig. 16 Pyrolysis time estimates for experimental values taken from the literature, for T ≥ 490 °C.

3.7 Estimation of reaction times

Rubber pyrolysis times as function of temperature and dimension are presented in Fig. 17, using eqn (4). Between 800 °C and 900 °C the chemical pyrolysis time becomes less than 1 s, and for all practical purposes, negligible, and the rate of the process is controlled by heat transfer only. Note that eqn (4) is temperature-independent, and is a rule-of-thumb rather than an accurate expression. One fact that it doesn't address is the reaction and charring becoming so fast at higher temperatures that the pressure build-up due the gaseous products becomes high enough for the material to explode, ripping apart the geometry and invalidating the use of the expression. In the temperature range for the work reported here, the line yields a workable limit for the expected pyrolysis rates, and is a useful engineering estimation tool.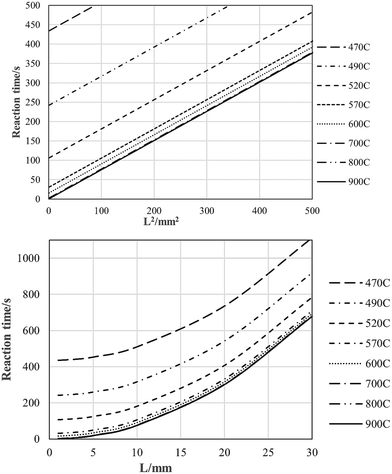

Fig. 17 Pyrolysis reaction regimes for rubber: mixed chemical-reaction and heat-transfer rate control above solid line; effective heat-transfer control only below solid line.

For the reverse Boudouard reaction one would anticipate that at some stage the supply of CO₂ might become the rate limiting factor. To assess at what temperature and sample size this might occur, and whether this might become problematic, one may estimate the mass transfer rate and compare it to the chemical reaction rate for the shrinking-particle case. The set of equations used to evaluate the mass-transfer limited shrinking-particle case is listed in Table 5. The derivation of eqn (6) may be found in Levenspiel,³⁸ and that of eqn (7) in ESI† as Appendix B.

Fig. 18 shows the predicted reaction times for the reverse-Boudouard gasification only – i.e. pyrolysis not included – for various temperatures and sample sizes. Mass-transfer controlled reaction times were calculated for a typical range on Re values (8–250), in the temperature range 200–1200 °C. The CO₂ gas-phase properties were generated using the thermodynamic software package Terra (version 4.5e).^39,40 For lower temperatures the mass-transfer rates are substantially higher than chemical reaction rates. For the larger sample dimensions the predicted mass-transfer rates converge with the chemical-reaction controlled rates only at 1200 °C. For temperatures higher than this, the chemical reaction rates are more rapid than the mass-transfer rates and mass transfer is expected to become rate determining. The target plasma-gasification temperature range is 900–1100 °C, and, for pure CO₂, mass transfer control can reasonably be excluded for well mixed conditions without bulking of the charred rubber feedstock.

Fig. 18 Reaction times predicted for various rubber samples sizes for chemical reaction and mass-transfer (MT) shrinking particles.

3.8 Modelling

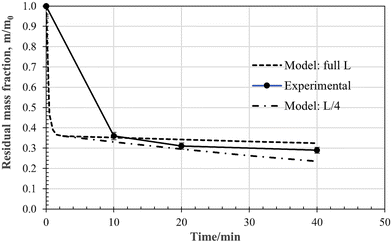
The time-dependent values of the fractional residue for a 15 mm cube at a furnace temperature of 860 °C, under a pure CO₂ atmosphere, are plotted in Fig. 19. The initial mass loss due to devolatilisation is rapid, and is followed by a much slower rate due to gasification by the reverse-Boudouard reaction. The major issue with using the shrinking-particle chemical-control model, i.e., eqn (5), is the size of the sample. During pyrolysis, as discussed above, the sample pops apart, retaining some of its general shape, but fragmenting into a heap of sub-mm agglomerated fragments. For accurate modelling, characterization of particle-size size distribution, particle morphology, and porosity would be necessary. This is beyond the scope of the current more exploratory research presented here, where the search is for broad, semi-quantitative guidelines only. Model predictions for the full and a quarter of initial cubic dimension are superimposed on the experimental data points. The experimental data fall reasonably inside this band.

Fig. 19 Time dependent fractional residue for 15 mm rubber cubes at 860 °C under CO₂ flow.

The residual char and ash mass fractions obtained after 20 min reaction time at 860 °C under CO₂ flow, are plotted in Fig. 20 as function of cube size. For the 20 mm cubes the reverse Boudouard gasification process has hardly started at the 20 min mark. For the 5 mm case, it is well on its way. Again, model predictions are superimposed on the experimental data points, generated for sample dimension L and L/4, and fall reasonably inside the band.

Fig. 20 Size dependent fractional residue after 20 min at 860 °C under CO₂ flow.

As mentioned in the introduction, many modelling and experimental studies on rubber pyrolysis are available in the open literature. The reported results are by and large in agreement with the experimental findings in this study. Some results are not useable, however, because they were gathered in different regimes of interest. No results could be traced in the open literature with respect to large-sample work using CO₂ gasification.

4 Conclusions

For the purposes of designing a reactor for the pyrolysis and reverse-Boudouard gasification of scrap-tyre granules operating in the target temperature range of 900 °C to 1100 °C, the relevant results may be summarised as follows:

1) The rate of first pyrolysis step is controlled by heat-transfer only, and the chemical kinetics may be ignored. For accurate energy requirements, both the enthalpy for heating and bond breaking/formation, i.e., pyrolysis, will obviously have to be taken into account.

2) Upon pyrolysis the rubber chunks char and split into sub-millimetre fragments.

3) For accurate modelling, the geometry, morphology, surface area, porosity, etc., of the char would have to be characterised.

4) The char fragments readily undergo the reverse-Boudouard reaction, with the rate impacted by the ambient CO₂ partial pressure.

5) Only above 1200 °C is the rate of the reverse-Boudouard expected to be limited by CO₂ diffusion to the reacting char solid surface, for char with accessible reaction surfaces.

6) If a plasma torch running on gases other than CO₂ is used, the dilution has to be accounted for.

Nomenclature

α	Extent of reaction (—)
α T	Thermal diffusivity (mm^2 s^−1 or m^2 s^−1)
A	Area (mm^2 or m^2)
C	Concentration (kg m^−3)
C P	Specific heat at constant pressure (J kg^−1 K^−1)
D	Diffusion constant or diameter (mm^2 s^−1 or m^2 s^−1)
E a	Activation energy (J kg^−1)
h	Mass transfer coefficient (kg m^−2 s^−1)
κ	Thermal conductivity (W m^−1 K^−1)
k	Reaction constant (generally s^−1 or min^−1)
k 0	Pre-exponential factor (s^−1 or min^−1)
L	Cubic dimension and/or diameter
L c	Characteristic length (mm or m), L/2
m	Mass (kg)
ρ	Density (g cm^−3 or kg m^−3)
r	Radius (mm or m)
R	Ideal gas constant (8.314 J mol^−1 K^−1)
R 0	Initial radius (mm or m)
Re	Reynolds number (—)
S	Volumetric enthalpy source or sink (W m^−3)
Sc	Schmidt number (—)
Sh	Sherwood number (—)
τ	Full time for any process (s or min)
t	Time (s or min)
t r	Residence or holding time (min)
T	Absolute temperature (K)
u	Linear velocity (m s^−1)
μ	Viscosity (P s)

Author contributions

AAJ: conceptualization, equipment, methodology, investigation, data curation, writing – original draft; JSG: experimental, equipment, data collection; IJvdW: equipment, methodology, supervision, project administration, funding acquisition, writing – review and editing; PLC: conceptualization, data curation, formal analysis, model development, investigation, methodology, software, visualization, writing – original draft.

Conflicts of interest

We have no conflicts of interest to report.

Acknowledgements

AAJ thanks the University of Pretoria and Suid-Afrikaanse Akademie vir Wetenskap en Kuns for financial support. The staff, equipment and analytical facilities made available by Necsa are gratefully acknowledged. PLC thanks Dr Gawie Nothnagel for demonstrating innovative ways of interpreting PDFs, once upon a time.

References

1. Scopus, waste AND tyre AND rubber AND pyrolysis, https://www.scopus.com, 2023.
2. A. W. Coats and J. P. Redfern, Analyst, 1963, 88, 906–924.
3. J. D. Martınez, N. Puy, R. Murillo, T. García, M. V. Navarro and A. M. Mastral, Renewable Sustainable Energy Rev., 2013, 23, 179–213.
4. A. Quek and R. Balasubramanian, J. Anal. Appl. Pyrolysis, 2013, 101, 1–16.
5. P. T. Williams, Waste Manage., 2013, 33, 1714–1728.
6. I. Janajreh and I. Adeyemi, Effect of Process Parameters on Gasification: Review, Proceedings of The 2014 IAJC-ISAM International Conference, 2014, ISBN 978-1-60643-379-9.
7. E. Muzenda, presented in part at the Int'l Conf. on Chemical Engineering & Advanced Computational Technologies (ICCEACT' 2014) Pretoria (South Africa), Nov. 24–25, 2014, 2014.
8. M. Labaki and M. Jeguirim, Environ. Sci. Pollut. Res., 2017, 24, 9962–9992.
9. B. O. Oboirien and B. C. North, J. Environ. Chem. Eng., 2017, 5, 5169–5178.
10. L. Waldheim, Gasification of waste for energy carriers A review, IEA Bioenergy, 2018.
11. M. Arabiourrutia, G. Lopez, M. Artetxe, J. Alvarez, J. Bilbao and M. Olazar, Renewable Sustainable Energy Rev., 2020, 129, 109932.
12. S. Vyazovkin and C. A. Wight, Int. Rev. Phys. Chem., 1998, 17, 407–433.
13. S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19.
14. S. Vyazovkin, K. Chrissafis, M. L. Di Lorenzo, N. Koga, M. Pijolat, B. Roduit, N. Sbirrazzuoli and J. J. Suñol, Thermochim. Acta, 2014, 590, 1–23.
15. S. Vyazovkin, A. K. Burnham, L. Favergeon, N. Koga, E. Moukhina, I. A. S. Pérez-Maqueda and N. Sbirrazzuoli, Thermochim. Acta, 2020, 689, 178597.
16. A. Oyedun, K.-L. Lam, M. Fittkau and C.-W. Hui, Fuel, 2012, 95, 417–424.
17. O. Senneca, P. Salatino and R. Chirone, Fuel, 1999, 78, 1575–1581.
18. N. Gao, A. Li and W. Li, Waste Manage. Res., 2009, 27, 242–250.
19. A. M. Ramírez Arias, J. C. Moreno-Piraján and L. Giraldo, ACS Omega, 2022, 7, 16298–16305.
20. J. Haydary, L. Jelemenský, L. Gasparovic and J. Markoš, J. Anal. Appl. Pyrolysis, 2012, 97, 73–79.
21. M. B. Larsen, L. Schultz, P. Glarborg, L. Skaarup-Jensen, K. Dam-Johansen, F. Frandsen and U. Henriksen, Fuel, 2006, 85, 1335–1345.
22. J. M. Bouvier, F. Charbel and M. Gelus, Resour. Conserv., 1987, 15, 205–214.
23. J. Yang, P. A. Tanguy and C. Roy, Chem. Eng. Sci., 1995, 50, 1909–1922.
24. S. Kim, Korean J. Chem. Eng., 1996, 13, 559–564.
25. E. Aylon, M. S. Callen, J. M. Lopez, A. M. Mastral, R. Murillo, M. V. Navarro and S. Stelmach, J. Anal. Appl. Pyrolysis, 2005, 74, 259–264.
26. I. I. Ahmed and A. K. Gupta, Appl. Energy, 2011, 88, 4667–4677.
27. K.-Y. Cheung, K.-L. Lee, K.-L. Lam, C.-W. Lee and C. W. Hui, Fuel Process. Technol., 2011, 92, 856–863.
28. B. Khiari, S. Kordoghli, D. Mihoubi, F. Zagrouba and M. Tazerout, Waste Manage., 2018, 78, 337–345.
29. A. A. Jansen, I. J. van der Walt and P. L. Crouse, Thermochim. Acta, 2022, 708, 179104.
30. S. M. Al-Salem, P. Lettieri and J. Baeyens, J. Hazard. Mater., 2009, 172, 1690–1694.
31. E. Cetin, R. Gupta and B. Moghtaderi, Fuel, 2005, 84, 328–1334.
32. J. R. Welty, G. L. Rorrer and D. G. Foster, Fundamentals of Momentum, Heat and Mass Transfer, John Wiley & Sons, Singapore, 6th edn, 2014.
33. Thermtest, Materials Thermal Properties Database, https://thermtest.com/thermal-resources/materials-database, (accessed 220606, 2022).
34. E. Segal, Rev. Roum. Chim., 2012, 57, 491–493.
35. A. K. Galwey, Thermochim. Acta, 2004, 413, 139–183.
36. A. K. Galwey, React. Kinet., Mech. Catal., 2015, 114, 1–29.
37. J. Haydary, L. Jelemenský, J. Markoš and J. Annus, Kautsch. Gummi Kunstst., 2009, 62, 661–665.
38. O. Levenspiel, Chemical Reaction Engineering, John Wiley and Sons, USA, 3rd edn, 1999.
39. G. B. Sinyarev, N. A. Vatolin, B. G. Trusov and G. K. Moiseev, Application of computers for thermodynamic calculations of metallurgical processes, Nauka Publishing House, Moscow, 1982, p. 263.
40. B. G. Trusov, TERRA software system for modeling phase and chemical equilibria in plasma-chemical systems, in Proceedings 3rd International Symposium on Theoretical and Applied Plasma Chemistry, Ivanovo, Sat materials, 2002.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00577a

---