Advancing 2D material predictions: superior work function estimation with atomistic line graph neural networks

Abstract

Despite the increased research and scholarly attention on two-dimensional (2D) materials, there is still a limited range of practical applications for these materials. This is because it is challenging to acquire properties that are usually obtained by experiments or first-principles predictions, which require substantial time and resources. Descriptor-based machine learning models frequently require further density functional theory (DFT) calculations to enhance prediction accuracy due to the intricate nature of the systems and the constraints of the descriptors employed. Unlike these models, research has demonstrated that graph neural networks (GNNs), which solely rely on the systems' coordinates for model description, greatly improve the ability to represent and simulate atomistic materials. Within this framework, we employed the Atomistic Line Graph Neural Network (ALIGNN) to predict the work function, a crucial material characteristic, for a diverse array of 2D materials sourced from the Computational 2D Materials Database (C2DB). We found that the ALIGNN algorithm shows superior performance compared to standard feature-based approaches. It attained a mean absolute error of 0.20 eV, whereas random forest models achieved 0.27 eV.

---

1 Introduction

The exploration of innovative two-dimensional (2D) materials for diverse applications has witnessed a surge in research efforts subsequent to the groundbreaking discovery of graphene, which led to the prestigious Nobel Prize in Physics in 2010.¹ Due to their distinctive amalgamation of physical, chemical, and optical characteristics, coupled with their elevated surface-to-volume ratio, 2D materials have garnered considerable interest as prospective contenders for various applications within the realm of materials science investigation. These applications encompass but are not limited to energy storage and/or conversion technologies.^2–6 This progress has been fueled by the ongoing discovery of novel 2D materials and the emerging concept of lateral and vertical 2D heterostructures, which opens up whole new avenues for designing materials with specialised and superior properties.^7–10

The work function is a fundamental characteristic of a material that quantifies the minimal energy necessary to extract an electron from the Fermi level and transfer it to a vacuum state. In addition to its significance in surface science, the work function of a 2D-material holds relevance in several fields such as catalysis, energy storage/conversion, and electronics.^11–14 It has been shown that fluorinating graphene at varying concentrations has been used as work function grading to enhance electron extraction in inverted structures.¹⁵ Deng and co-workers¹⁶ revealed that graphene cover enclosing Fe nanoparticles displayed both high activity and great stability which is due to the work function difference between outer cover and the inner nanometal. He et al. showed that due to the very high work function value, CuBiP₂Se₆ acts as the most stable intrinsic p-type 2D material.¹⁷

Researchers frequently employ sophisticated first principles approaches such as density functional theory (DFT)¹⁸ in their pursuit to unravel electronic characteristics, encompassing crucial attribute like work function. Although these techniques provide valuable insights, their computing requirements can be challenging, particularly when dealing with a wide range of materials. Significantly, a comprehensive collection of materials, carefully developed via extensive and meticulous research, reveals promising opportunities for the application of machine learning (ML) in the investigation of new 2D materials.^19–23 Predictive machine learning models offer practical alternatives to computationally demanding DFT calculations by providing statistical predictions for these important characteristics. These models are trained using either existing or newly curated data. Databases such as the computational 2D materials database (C2DB)²⁴ and 2DMatPedia,²⁵ for example, systematically document the thermodynamic, and electronic characteristics of 2D materials, providing essential assets for expediting the process of material exploration and design. Recently Roy et al. performed ML for the prediction of the work function of 2D-materials²⁶ where they used the descriptor based analysis. Descriptor-based models may encounter difficulties in accurately reflecting intricate linkages and non-linear interactions within materials data. These limitations are particularly evident when working with high-dimensional or unstructured data.^27,28

Graph neural networks (GNNs)²⁹ are a revolutionary method for representing and modelling atomistic materials. They go beyond traditional machine learning models that rely on predefined descriptors like bond distances, angles, or local atomic environments. In contrast to descriptor-based models, GNNs naturally capture the complex and frequently non-linear connections between atoms by explicitly representing the graph-like arrangement of materials. In this representation, atoms are considered as nodes and interatomic bonds as edges. GNNs utilize a graph-based representation to effectively learn the fundamental physical and chemical interactions. This enables a more precise and reliable modelling of intricate material behaviours, which is essential for accurately predicting properties in new materials and comprehending phenomena at the quantum level. The ALIGNN (atomistic line graph neural network), proposed by Choudhary et al.,³⁰ represents the latest achievements in this field. What sets ALIGNN apart from other GNN models is the inclusion of not only the atomic positions but also the related bond lengths and bond angles as explicit input characteristics. By incorporating an extra level of data, ALIGNN is able to accurately capture the intricate geometric and topological aspects of atomic structures, resulting in very accurate forecasts of material characteristics.

This manuscript examines the predicted accuracy of the ALIGNN approach, emphasizing its potential to greatly improve the overall comprehension of work functions. The validity of our research is strengthened by thorough validation, performed on both artificial and real-world datasets, which clearly shows the model's excellent predicting ability. The findings highlight the model's capacity as a fundamental tool for future study and practical applications, expanding beyond work functions to include a broad spectrum of materials' properties.

2 Atomistic line graph neural network (ALIGNN)

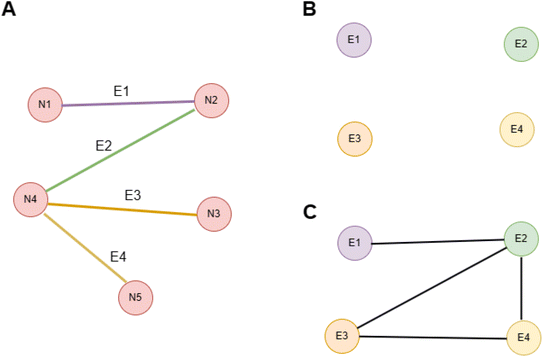
ALIGNN, as proposed by Choudhary and co-workers,³⁰ introduced a novel neural network architecture aimed to enhance materials property predictions. The model architecture of ALIGNN is composed of several key components. First the atomic structure inputs are transformed into graphs, a potent tool for encapsulating the local atomic environment of a material. The construction process involves replacing each atom in the structure with a node and each atomic bond with an edge. Then the construction of line graph takes place. In a line graph, nodes represent the bonds connecting two atoms of the atomistic graph. An edge is drawn between two nodes (bonds) in the line graph if they are linked to the same atom in the atomistic graph. The line graph helps to incorporate the bond angle information as an edge feature. Fig. 1 shows the construction of line graphs for basic understanding. The illustration depicts the process of constructing a line graph from an initial graph, beginning with the original graph (Panel A), where five nodes {N₁, N₂, N₃, N₄, N₅} are interconnected by four edges {E₁, E₂, E₃, E₄}. In the first step (Panel B), these edges of the original graph are transformed into nodes in the line graph, resulting in the new nodes {E₁, E₂, E₃, E₄}, which are initially unconnected. The second step (Panel C) involves drawing edges between these new nodes in the line graph, based on whether the corresponding edges in the original graph share a common node. Specifically, edges are drawn between E₁ and E₂ (sharing node N₂), E₂ and E₃ (sharing node N₄), E₂ and E₄ (sharing node N₄), and E₃ and E₄ (sharing node N₄), thereby completing the line graph. This process effectively translates the relationships between edges in the original graph into the connections between nodes in the line graph, providing a new perspective on the structure of the original graph. Then an edge-gated graph convolution (EGCN) was applied on the line graph to refresh pair and triplet features. These updated pair features are then propagated to the edges of the atomistic graph and further refreshed through a second edge-gated graph convolution applied to the atomistic graph. The hidden representations of nodes undergo an update using the refreshed pair and triplet features. This update process employs a neural network that intakes the current hidden representation of a node along with the updated pair and triplet features. The ALIGNN layer can collaborate with other layers within the neural network architecture, such as fully connected layers, to enhance overall model performance.

Fig. 1 Line graph construction: this illustration shows different steps involved in constructing a line graph. (A) shows the graph for which we intend to make a line graph. Its nodes are labelled by {N₁, N₂, N₃, N₄, N₅} and edges are labelled by {E₁, E₂, E₃, E₄}. Step 1 (B and C) is to draw nodes in line graph corresponding to the edges in atomistic graph. Here the nodes of line graph will be {E₁, E₂, E₃, E₄}. Step 2 is to draw edges in line graph. We will draw an edge between two nodes in line graph if there is a common node for them in the original graph. So we are drawing edges between nodes {E₁, E₂}, {E₂, E₄}, {E₂, E₃} and {E₃, E₄}.

In Fig. 2, we present the schematic representation of the ALIGNN model for predicting the work function. The initial step is the conversion of the chemical structure into two separate graph representations. The initial representation is a conventional molecular graph, wherein atoms are depicted as nodes and bonds as edges. The second type of graph is a line graph, which provides a more conceptual depiction in which the bonds are plotted as nodes, and the edges reflect the shared atoms between the bonds. The aforementioned graph representations are subsequently inputted into the ALIGNN model, which has been specifically engineered to concurrently process both the graph and line graph. The inputs utilized by the model facilitate the acquisition of intricate linkages within the molecular structure, thereby providing a comprehensive representation of both atomic interactions and bond connectivity. In the subsequent step, the processed data is employed to make predictions regarding the work function of the molecule.

Fig. 2 Schematic representation of the ALIGNN model for predicting the work function.

The Fig. 3 illustrates a comprehensive flowchart outlining the methods utilized in the construction of a predictive model employing the ALIGNN framework. The proposed model is specifically designed for the purpose of predicting the work function of materials. The initial stage involves the acquisition of molecular data, which functions as the fundamental dataset. The molecular data is subsequently subjected to two separate channels of processing: one that represents the data in the form of a conventional graph, wherein atoms are represented as nodes and bonds are represented as edges, and another that generates a line graph, capturing more complex relationships by considering the bonds of the original graph as nodes. Following the representation of molecular data in these two formats, an embedding procedure is employed to transform both the graph and line graph representations into a space of higher dimensions. The aforementioned step holds significant importance in capturing the intricate and non-linear interactions that are present in the molecular structure. The higher-dimensional embeddings maintain the inherent duality of the data, hence preserving both the graph and line graph representations. Once the embedding phase is completed, the data undergoes additional processing using the ALIGNN layer. This particular neural network layer has been specifically built to efficiently acquire knowledge from atomistic line graphs, hence facilitating the model's comprehension of complex interactions among atoms and their bonds. These interactions play a crucial role in defining the properties of materials. Following the completion of data processing by the ALIGNN layer, the process of average pooling is implemented. The aforementioned procedure consolidates the data from several dimensions, resulting in a concise statistical measure that encompasses the fundamental characteristics of the molecular design. Ultimately, the aggregated data is processed by means of a basic linear layer, which functions to convert the consolidated characteristics into a precise forecast—in this instance, the material's work function.

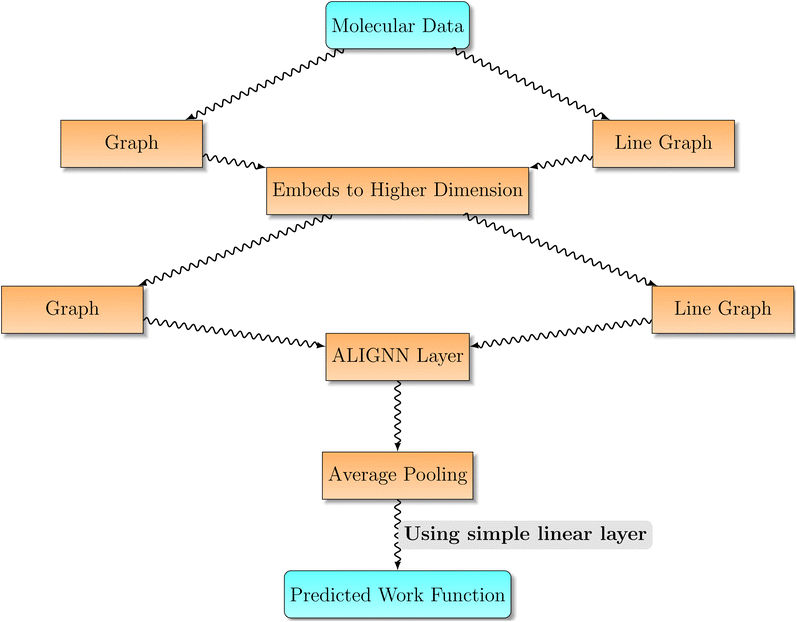Fig. 3 Overall methodology utilized for developing our model, describing the architecture of ALIGNN framework.

3 Results & discussion

3.1 Implementation of the model

The implementation of the model utilizes PyTorch, the Deep Graph Library (DGL), and PyTorch Geometric to effectively handle graph-based data by using their own capabilities. The foundation of our approach is based on the initial construction of the ALIGNN, which serves as the fundamental structure of our model. During the training process, we aim to reduce the Mean Square Error (MSE) loss function. This involves optimising the model parameters over 700 epochs using the AdamW optimiser. The weight decay is set to 10⁻⁵ to mitigate overfitting, and we use a batch size of 64 to optimise training efficiency. The learning rate is adaptively modified using a One-Cycle learning rate scheduler, with the upper limit of the learning rate set at 0.001, guaranteeing a seamless convergence. The training process is enhanced by implementing the OneCycleLR approach, which effectively controls the learning rate during the full 700 epochs. In addition, our model architecture incorporates 2 ALIGNN layers and 2 EGCN layers to accurately capture the complex interactions within the graph data. Importantly, the method does not set a fixed random state, which introduces some level of randomness in the process of training the model.

Table 1 provides a concise overview of the essential technical aspects of the ALIGNN model, emphasising its structure and settings. The model is composed of 2 ALIGNN layers and 2 EGCN layers. These layers are essential for capturing intricate interactions within the graph representations of molecules or materials. The concealed feature space is determined by a vector of 256 dimensions, enabling the model to efficiently acquire knowledge and analyse data. In addition, the bond length and bond angle undergo transformation through the use of Radial Basis Function (RBF) expansion. The output sizes for the bond length and bond angle transformations are 80 and 40, respectively. This technique allows for the capture of more complex patterns in the data. The RBF expansion embedding size is set to 128 to encode the enlarged features into a fixed-size vector that is acceptable for the model's processing. Understanding these specifications is crucial for assessing the model's ability to accurately predict material properties.

Table 1 ALIGNN only technical details

ALIGNN model's technical details
ALIGNN layers	2
EGCN layers	2
Hidden features	256
Bond length RBF expansion output size	80
Bond angle RBF expansion output size	40
RBF expansion embedding size	128

---

3.2 Application of our model on dataset

3.2.1 Description of dataset. The first step in creating a strong ML model is to choose a large and diverse dataset that includes enough variation. In order to accomplish this, we make use of the Computational 2D Materials Database (C2DB), which is a publicly accessible repository specifically created for the computation of 2D materials. This database contains an extensive collection of pertinent characteristics for a diverse selection of 2D materials. The original paper by Haastrup et al.²⁴ utilized state-of-the-art density functional theory (DFT) within the many-body perturbation theory framework to compute various properties. The attributes encompass structural, thermodynamic, elastic, electrical, magnetic, and optical properties for a wide range of 2D materials. Furthermore, all unit cells in the database have undergone relaxation using spin-polarization computations to guarantee precise depiction of their fundamental states. This methodical methodology yields a comprehensive and dependable dataset that is crucial for training and evaluating our machine learning models.

The provided Fig. 4 illustrates a violin plot, graphically portraying our dataset's distribution. The plot illustrates a symmetrical distribution centered around a work function of zero. Fig. 4 shows that the work function dataset has a broad distribution that closely follows the law of normal distribution. Table 2 illustrates the detailed configuration for our model. The dataset has 7208 data points. It contains 4977 data points after null values are removed. These are broken down into 3982 (80% of total data) training, 497 testing, and 498 validation instances. For model implementation, we used a k-nearest neighbours (k = 12) approach with a mini-batch size of 64. To train the neural network, we employ a five-fold cross validation strategy.

Fig. 4 Violin plot demonstrating the distribution of values of work function.

Table 2 Details of the dataset

Parameter	Value
Total data points	4977
Training set	3982
Testing set	497
Validation set	498
Neighbours	12
Mini batch size	64

---

3.2.2 Prediction of work function. The following part explores the outcomes derived from implementing the ALIGNN model to predict the work function, a crucial characteristic in the field of material science that impacts the effectiveness of electronic devices. This investigation emphasises the model's ability to effectively predict the work function in different material systems, demonstrating its capacity to represent the intricate interactions and dependencies present in atomic structures. The model exhibits substantial predictive capability by utilizing the ALIGNN design, which incorporates geometric and topological information via its distinctive atomistic line graph neural network structure.

Fig. 5 presents a detailed representation of the performance of the ALIGNN model. It includes a parity plot in the left panel and training-validation loss curves in the right panel. The parity plot in the left panel illustrates the comparison between the predicted values and the actual values for both the training and test datasets. The bulk of data points strongly overlap with the diagonal reference line, which is shown by an orange dashed line. This indicates that the model's predictions nearly match the true values throughout the dataset. This alignment indicates that the model exhibits strong generalization abilities and has successfully captured the fundamental patterns in the data, resulting in minimum discrepancy between the anticipated and actual values.

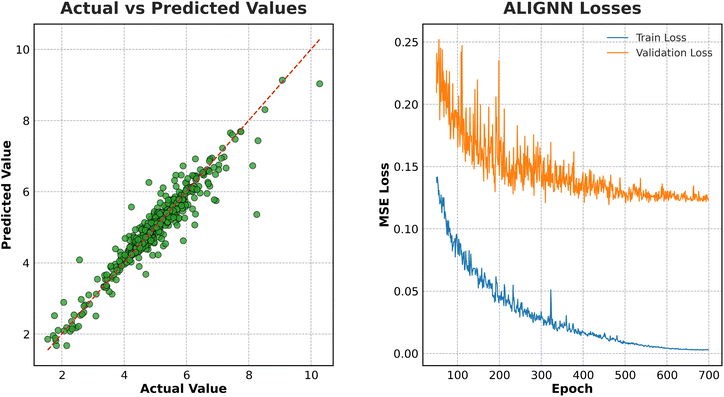Fig. 5 (left) Actual vs. predicted values showing their correlation. (right) Training and validation loss for ALIGNN.

The right panel of Fig. 5 displays the evolution of the training and validation losses during 700 epochs. At the beginning of training, the validation loss shows noticeable variations, indicating that the model's capacity to generalise is unstable. As the training advances, both the training and validation losses increasingly diminish, eventually reaching a stable area. By around 700 epochs, the disparity between the training and validation losses diminishes, suggesting that the model has successfully mitigated overfitting. Currently, the validation loss reaches a stable point, indicating that additional training would not result in substantial enhancements, but would instead raise the risk of overfitting.

The ALIGNN model ultimately attains a mean absolute error (MAE) of 0.20 eV on the test set, surpassing alternative models. Comparatively, a random forest model produces a mean absolute error (MAE) of 0.27 eV, whilst a conventional artificial neural network (ANN) model generates an MAE of 0.25 eV. The ALIGNN model's lower MAE indicates its improved predictive accuracy for this assignment, showcasing its capacity to more efficiently capture intricate material features. The results indicate that ALIGNN is a reliable model option for predicting work functions, as it demonstrates superior accuracy and generalization capabilities compared to traditional machine learning models.

During the ALIGNN model setup, we detected a validation loss of 0.0960 eV, which serves as a crucial measure of the model's capacity to effectively adapt to new data. The validation loss is comparatively minimal, indicating that the model successfully caught the fundamental patterns in the training data without overfitting. In addition, the model obtained a training loss of 0.0045 eV, indicating its high level of competency in learning from the training data. The significant disparity between the training and validation losses suggests that the model possesses a robust ability to learn, while also maintaining a high level of generalisation, which is essential for the effectiveness of machine learning models.

In addition, the Mean Absolute Error (MAE) was measured at 0.2033 eV. The MAE quantifies the average size of errors between the expected and actual values, regardless of their direction. The MAE value offers a straightforward measure of the model's prediction accuracy, indicating that, on average, the forecasts differ by around 0.2033 eV from the actual work functions. The precision achieved in this study is comparable to the current norms in the area, especially for models that predict energy attributes based on first-principles calculations.

The residual plot depicted in Fig. 6 provides additional confirmation of these findings. Residuals, which are the discrepancies between the observed and model-predicted work functions, serve as a crucial diagnostic tool for assessing model performance. Our research revealed that around 60% of the data points in the test set exhibited residuals falling within a range of 0.20 eV. This discovery is important since it indicates that most of the model's forecasts are closely matched with the actual values, coming within a small margin of error. The selection of the 0.20 eV threshold is intentional as it corresponds to the level of accuracy commonly attained by machine learning models that forecast properties such as adsorption energies, nanostructure stabilities, and electronic band gaps. These properties are frequently derived from density functional theory (DFT) or comparable first-principles techniques.^31,32

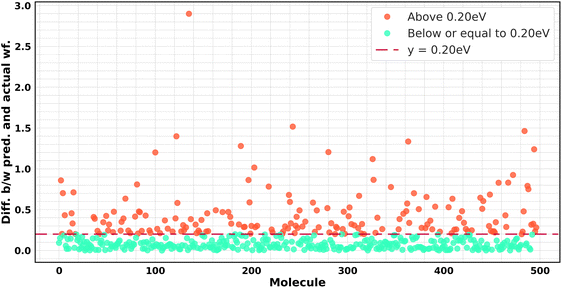Fig. 6 Visualization of absolute differences between the actual and predicted values on the validation dataset using both models.

One important component of our study is the novel use of graph properties in the ALIGNN framework, which sets our work apart from earlier studies. Previous models did not include graph-based features. We believe that including this technique will improve the model's performance, especially when dealing with intricate porous materials. This innovative technique has the capacity to surpass conventional models in forecasting the characteristics of such materials, indicating that additional investigation in this direction could produce even more precise and dependable predictive models. This development has the potential to have a substantial impact on the sector by offering a fresh approach to constructing machine learning models that can accurately forecast the characteristics of advanced materials.

3.2.3 Comparison with previous research. ML models have progressively been utilized to predict the work function of two-dimensional materials, resulting in substantial improvements in accuracy compared to conventional first-principles methods. As for example, Roy et al.²⁶ designed a feature-based model to predict the work function of MXenes, a category of two-dimensional materials with adjustable surface chemistries. This model attained a mean absolute error (MAE) of 0.25 eV on the testing dataset, illustrating the viability of machine learning-based work function predictions within particular material categories. The reliance on manual properties constrains generalizability, particularly among various 2D materials with varying bonding conditions. Zhang et al.³³ presented GT-Net, a hybrid model that integrates GNNs with transformers to predict the work function of boron-doped graphene. GT-Net attained a high accuracy (R² = 0.975) by modeling local and global interactions across more than 30 000 combinations of doped graphene. The integration of GNNs and transformers facilitated an intricate depiction of the atomic structure without predetermined descriptors; nonetheless, the model's sensitivity to boron-doped graphene indicates that retraining may be necessary for generalization to other materials. Our research enhances existing developments by employing the ALIGNN, which supplements conventional GNNs by integrating a secondary line graph to explicitly represent bond angles and connectivity in conjunction with atomic–level interactions. ALIGNN's dual representation facilitates the modeling of atomic and bond-level interactions, resulting in a MAE of 0.20 eV across a diverse array of 2D materials in the C2DB database. The ALIGNN architecture's capacity to incorporate geometric and topological characteristics of atomic structures allows it to surpass descriptor-based models and traditional GNNs, providing a more resilient and adaptable approach for predicting work functions in various 2D materials.

4 Discussion

GNNs are especially beneficial for estimating the work function of 2D materials due to their intrinsic ability to represent the non-Euclidean structure of atomic configurations, a constraint in conventional feature-based machine learning and standard neural networks. In a GNN, atoms are depicted as nodes, while bonds or interatomic interactions are represented as edges, enabling the model to learn directly from a material's atomic graph without the necessity for manually produced features. This framework allows GNNs to discern intricate, localized interactions within the material, encompassing coordination environments and atomic neighborhoods, which are essential for features such as work function that rely on both electronic structure and spatial atomic arrangement. The work function is affected by both individual atomic contributions and extensive electronic interactions inside the material, a complexity that GNNs can effectively describe using iterative message-passing processes. This enables the encoding of both local and global information, which is crucial in 2D materials where surface effects and interlayer interactions are significant.

ALIGNN enhances this capability by integrating bond-level specifics via a dual representation that has a secondary“line graph” wherein each bond in the primary atomic graph is seen as a node. This secondary network represents bond angles as links between bond-nodes, enabling ALIGNN to capture more complex geometric and topological features such as bond lengths and angles. This additional precision is essential for precisely predicting properties like the work function, which is significantly dependent on the material's electronic and atomic structure. The sensitivity of the work function to bonding conditions and bond angles is crucial, as these elements directly affect electron distribution and Fermi levels. By acquiring both atomic and bond-level data, ALIGNN improves prediction accuracy, surpassing traditional feature-based machine learning models and typical graph neural networks.

Feature-based machine learning models often necessitate comprehensive, domain-specific feature engineering to achieve generalization across materials, but ALIGNN's graph-based architecture directly learns these dependencies from the data. Conventional GNNs capture atomic configurations but do not incorporate bond-angle information, which ALIGNN integrates, rendering ALIGNN particularly effective for intricate materials such as 2D structures. The dual graph methodology renders ALIGNN exceptionally applicable in material science, where minor structural variations significantly influence surface properties, providing an advanced model architecture that is both versatile and highly precise across various configurations and compositions. This architecture enhances ALIGNN as a powerful tool for the discovery and prediction of electronic properties, including the work function, across a diverse range of 2D materials.

4.1 Future scope of work

Despite the progress made with ALIGNN in predicting the work function of 2D materials, additional investigation in this domain could augment both the model's predictive accuracy and its applicability. Future research may concentrate on creating models that incorporate supplementary structural properties, like defects, grain boundaries, and strain effects, which frequently occur in practical applications and can profoundly influence electronic properties. Incorporating these properties would enable ALIGNN and analogous models to yield more precise predictions for real-world materials. Furthermore, expanding ALIGNN to predict additional electronic properties, including bandgap, conductivity could enhance its utility in materials design, particularly for multifunctional materials employed in optoelectronics, energy storage, and catalysis.

A further potential enhancement entails integrating ALIGNN with reinforcement learning or optimization algorithms to proactively direct material design. By establishing target work function ranges, such hybrid models could facilitate the discovery or engineering of materials with specified electronic properties tailored for certain applications. Furthermore, augmenting the training dataset with a broader array of 2D material systems may enhance the generalizability of ALIGNN across various chemical compositions, hence increasing its effectiveness in high-throughput materials screening initiatives.

5 Conclusion

The work function of materials is an essential inherent characteristic that greatly impacts their performance in various applications, such as catalysis, energy storage and conversion, and electronic devices. Hence, it is crucial to comprehend and precisely forecast the work function for the purpose of designing and optimising materials in these domains. Recent progress in computational techniques, specifically GNNs, has shown more effectiveness in modelling and describing atomistic materials compared to conventional descriptor-based machine learning models. For this study, we utilized the ALIGNN model, an advanced GNN framework, to predict the work function of materials. ALIGNN successfully updates the atomic features encoded inside the nodes of the graph via its layers, resulting in accurate predictions of the task function. The results of our study emphasize the capability of ALIGNN and GNN methods to transform the field of material science. These approaches offer accurate and dependable predictions of material properties, which can lead to advancements in a wide range of technological applications.

Data availability

Data and code developed in this study are available in this link: https://drive.proton.me/urls/X1TV3NRHJ8#DzOjNMigjVe8.

Author contribution

C. C. conceptualized the project. C. C., H. S. and J. B. performed the calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. C. acknowledges SERB, India for the funding (PDF/2021/003445). CSIR-CLRI Communication No. 2046.

References

1. A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191.
2. J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, D. Akinwande and C. J. Brennan, et al., A review on mechanics and mechanical properties of 2d materials—graphene and beyond, Extreme Mech. Lett., 2017, 13, 42–77.
3. V. Varshney, E. Bianco, A. Apte, A. Roy, E. Ringe, N. R. Glavin, R. Rao and P. M. Ajayan, Emerging applications of elemental 2d materials, Adv. Mater., 2020, 32, 1904302.
4. D. Pakulski, A. Aliprandi, A. Ciesielski, C. Anichini, W. Czepa and P. Samorì, Chemical sensing with 2d materials, Chem. Soc. Rev., 2018, 47, 4860–4908.
5. G. Liu, B. Luo and L. Wang, Recent advances in 2d materials for photocatalysis, Nanoscale, 2016, 8, 6904–6920.
6. M. Audiffred, P. Miró and T. Heine, An atlas of two-dimensional materials, Chem. Soc. Rev., 2014, 43, 6537–6554.
7. H. Chen, G. Deng, J. Wang, Z. Li and X. Niu, Recent advances in 2d lateral heterostructures, Nano-Micro Lett., 2019, 11, 1–31.
8. L. Colombo, G. Iannaccone, F. Bonaccorso and G. Fiori, Quantum engineering of transistors based on 2d materials heterostructures, Nat. Nanotechnol., 2018, 13, 183–191.
9. M. Perucchini, G. Fiori, E. G. Marin, D. Marian and G. Iannaccone, Lateral heterostructure field-effect transistors based on two-dimensional material stacks with varying thickness and energy filtering source, ACS Nano, 2020, 14, 1982–1989.
10. Y. Shi, M.-Y. Li, C.-H. Chen and L.-J. Li, Heterostructures based on two-dimensional layered materials and their potential applications, Mater. Today, 2016, 19, 322–335.
11. N. K. Dutta, R. Garg and N. R. Choudhury, Work function engineering of graphene, Nanomaterials, 2014, 4, 267–300.
12. G. Zhang, Y. Cai and Y.-W. Zhang, Layer-dependent band alignment and work function of few-layer phosphorene, Sci. Rep., 2014, 4, 6677.
13. S. Pescetelli, A. Di Vito, D. Rossi, A. Pecchia, M. Auf der Maur, A. Liedl, R. Larciprete, D. V. Kuznetsov, A. Agresti and A. Pazniak, et al., Titanium-carbide mxenes for work function and interface engineering in perovskite solar cells, Nat. Mater., 2019, 18, 1228–1234.
14. C. Huang, Z. Bian, M. Tian, H. Chen, R. Duan, L. Wang, Z. Liu, T. Zhang, J. Miao and J. Qiao, 2d semimetal with ultrahigh work function for sub-0.1 v threshold voltage operation of metal-semiconductor field-effect transistors, Mater. Des., 2023, 112035.
15. H.-I. Joh, J.-S. Yeo, J.-H. Yu, C.-H. Lee and S.-I. Na, Synergetic effects of solution-processable fluorinated graphene and pedot as a hole-transporting layer for highly efficient and stable normal-structure perovskite solar cells, Nanoscale, 2017, 9, 17167–17173.
16. X. Chen, G. Wang, L. Jin, X. Pan, J. Deng, G. Sun, D. Deng, L. Yu and X. Bao, Iron encapsulated within pod-like carbon nanotubes for oxygen reduction reaction, Angew. Chem., Int. Ed., 2013, 52, 371–375.
17. P. Yu, W. He, L. Kong and G. Yang, Record-high work-function p-type cubip2se6 atomic layers for high-photoresponse van der waals vertical heterostructure phototransistor, Adv. Mater., 2023, 35, 2209995.
18. N. Argaman and G. Makov, Density functional theory: An introduction, Am. J. Phys., 2000, 68, 69–79.
19. H. Pu, M. K. Y. Chan, B. Ryu, L. Wang and J. Chen, Understanding, discovery, and synthesis of 2d materials enabled by machine learning, Chem. Soc. Rev., 2022, 51, 1899–1925.
20. D. Jariwala, N. C. Frey, D. Akinwande and V. B. Shenoy, Machine learning-enabled design of point defects in 2d materials for quantum and neuromorphic information processing, ACS Nano, 2020, 14, 13406–13417.
21. N. R. Knøsgaard, P. M. Lyngby, S. Manti, M. K. Svendsen and K. S. Thygesen, Exploring and machine learning structural instabilities in 2d materials, npj Comput. Mater., 2023, 9, 33.
22. G. I. Vega Bellido, B. Anasori, Y. Gogotsi, N. C. Frey, J. Wang and V. B. Shenoy, Prediction of synthesis of 2d metal carbides and nitrides (mxenes) and their precursors with positive and unlabeled machine learning, ACS Nano, 2019, 13, 3031–3041.
23. B. Focassio, G. R. Schleder and A. Fazzio, Machine learning for materials discovery: Two-dimensional topological insulators, Appl. Phys. Rev., 2021, 8, 031409.
24. M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen, A. C. Riis-Jensen, S. Haastrup and M. Strange, et al., The computational 2d materials database: High-throughput modeling and discovery of atomically thin crystals, 2D Mater., 2018, 5, 042002.
25. M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang, J. Zhou and L. Shen, et al., 2dmatpedia, an open computational database of two-dimensional materials from top-down and bottom-up approaches, Sci. Data, 2019, 6, 86.
26. S. W. Koh, H. Li, P. Roy, L. Rekhi and T. S. Choksi, Predicting the work function of 2d mxenes using machine-learning methods, J. Phys.: Energy, 2023, 5, 034005.
27. B. Miasojedow, S. Szymkuć, E. P. Gajewska, B. A. Grzybowski, G. Skoraczyński, P. Dittwald and A. Gambin, Predicting the outcomes of organic reactions via machine learning: Are current descriptors sufficient?, Sci. Rep., 2017, 7, 3582.
28. A. Habrard, A. Bellet and M. Sebban, A survey on metric learning for feature vectors and structured data, arXiv, 2013, preprint, arXiv:1306.6709,  DOI:10.48550/arXiv.1306.6709.
29. A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. Van Hoesel, H. Schopmans, T. Sommer, P. Reiser and M. Neubert, et al., Graph neural networks for materials science and chemistry, Commun. Mater., 2022, 3, 93.
30. K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7, 1–11.
31. J. R. Boes, O. Mamun, K. T. Winther and T. Bligaard, A bayesian framework for adsorption energy prediction on bimetallic alloy catalysts, npj Comput. Mater., 2020, 6, 177.
32. M. G. Taylor, J. Dean and G. Mpourmpakis, Unfolding adsorption on metal nanoparticles: Connecting stability with catalysis, Sci. Adv., 2019, 5, eaax5101.
33. N. Liao, Y. Lu, J. Zhang, C. Zhang, Q. Zhang, L. Cai and K. Zeng, Work function prediction by graph neural networks for configurationally hybridized boron-doped graphene, Langmuir, 2024, 40, 7087–7094.

---