Computational evaluation of the oxidation of superoxide to molecular dioxygen mediated by NNNN-tetradentate copper complexes

Abstract

Free radicals such as superoxide are reactive species that, upon accumulation, lead to oxidative stress. The superoxide dismutase (SOD) enzyme mitigates this stress by converting superoxide into hydrogen peroxide and oxygen. However, the probable lack of SOD supplementation has driven the search for alternatives, with copper complexes emerging as promising candidates. This study employs density functional theory (DFT) to evaluate the Gibbs reaction energies of nine copper complexes, suggesting their potential to catalyze the conversion of superoxide into molecular oxygen as all complexes exhibit thermodynamically favorable mechanisms for mimicking SOD. Furthermore, a topological analysis using Bader's quantum theory of atoms in molecules (QTAIM) was conducted to investigate the present interactions between copper, superoxide, and molecular oxygen species. The latter reveals that the interaction between copper and superoxide is partially covalent and attractive, transitioning to a closed-shell interaction upon charge redistribution to form the product. These findings suggest that copper complexes could effectively mimic SOD, offering a promising approach to reducing oxidative stress, a key factor in neurodegenerative diseases like Alzheimer's Disease (AD). This work provides a robust framework for assessing copper complexes as potential therapeutic agents in combating oxidative stress-related conditions.

---

Introduction

Free radicals are highly reactive species continuously produced during regular biological processes in human cells, such as cellular respiration, mitochondrial ATP production, fatty acid breakdown, and cellular detoxification.¹ While they possess crucial functions, including the regulation of gene expression, cellular growth regulation, and defense against pathogens, the accumulation of free radicals represents a potential health risk.² Under oxidative stress conditions, the production of these species can exceed the organism's control capacity, leading to an imbalance known as oxidative stress.³ The latter has been implicated in a diverse range of diseases, for instance: Alzheimer's and cancer.¹ As a defensive strategy, living organisms produce a variety of species known as antioxidants, whose main role is to mitigate the damage caused by oxidative stress. Among the known antioxidants, the main group consists of three enzymes: superoxide dismutase, catalase, and glutathione peroxidase.⁴ As mentioned above, these play an important role in neutralizing the excess of free radicals, with superoxide dismutase (SOD) being the most efficient agent against oxidative stress.⁵ SOD is ubiquitously present in all living organisms and serves as a key enzyme for cellular survival. In these regards, it catalyzes the conversion of the superoxide radical into hydrogen peroxide and oxygen, as shown in eqn (1).

SOD supplements have been employed as a component of treatments for oxidative stress-associated diseases. However, these supplements often entail significant costs and face several biological limitations.⁶ In this context, intensive research has been conducted to identify and propose alternative approaches, being the most promising one the use of coordination complexes based on manganese, nickel, zinc, and copper as SOD mimics.^7–11 Among these metals, manganese complexes have garnered the most extensive investigation,¹² whereas fewer studies have explored copper^13,14 and zinc systems.^15,16

Copper is present in metalloenzymes like superoxide dismutase (SOD), cytochrome C oxidase, ascorbate oxidase, and ceruloplasmin.¹⁷ Its regulated release from synaptic vesicles plays a crucial role in neurotransmission and is essential for neuropeptide synthesis and the proper functioning of the immune system.¹⁸ Nevertheless, copper also can participate in redox reactions, catalyzing the production of reactive oxygen species, including superoxide and hydrogen peroxide, which exacerbate neuronal damage.¹⁹

In this chain of reactions shown in Fig. 1, superoxide has been reported as a key intermediate.^21–23 In this sense, a therapeutic approach relies on the prevention of superoxide formation by using chelating ligands for metal cations.¹⁹ However, an alternative is the design of molecules capable of reverting the reaction using the superoxide transformation into molecular dioxygen (reversed step 1 in Fig. 1):

Cu²⁺L + O₂˙⁻ → Cu⁺L + O₂ (2)

Fig. 1 Mechanism proposed for the generation of hydrogen peroxide mediated by Cu–Aβ complexes. Aβ stands for the amyloid-beta peptide. Adapted from Alí-Torres, et al.²⁰

On the other hand, Salen-type ligands are employed in coordination with copper, serving as versatile chelating agents in coordination chemistry. The synthesis of these ligands is straightforward and typically achieved through a condensation reaction between salicylaldehyde and an ethylenediamine derivative.²⁴ Upon coordination with metal ions, Salen ligands form metal complexes that exhibit a wide range of catalytic properties and chemical reactivity, rendering them valuable in various applications. Metal–Salen complexes have attracted attention for their role in promoting a variety of catalytic reactions, including cycloaddition, A³-coupling reactions,²⁵ and asymmetric synthesis.²⁶ Furthermore, recent in vitro studies have demonstrated their potential as therapeutic agents, particularly exhibiting anticancer properties.²⁷ Moreover, metal Salen complexes are employed as enzyme mimics, in biosensing and bioimaging applications, for their antimicrobial activity and applications in nanotechnology.²⁸

In this work, we performed computational calculations based on density functional theory (DFT) to determine the Gibbs reaction energies of nine copper complexes with salen-type ligands, and through this, their potential to promote the oxidation of superoxide to molecular dioxygen (eqn (2)). These nine complexes were selected because, in a previous study, they demonstrated suitable standard reduction potentials to function as SOD mimics. Furthermore, we selected the most stable conformation of these complexes studied by Puentes-Díaz et al.²⁹

We have also performed a topological analysis using Bader's quantum theory of atoms in molecules (QTAIM) to gain deeper insights into the underlying interactions. This approach allowed us to explore the detailed nature of the interactions between copper, the superoxide radical, and molecular dioxygen. The DFT + QTAIM description provides a comprehensive framework for assessing the potential of copper complexes in modulating oxidative processes, which are closely linked to oxidative stress and their implications in neurodegenerative diseases such as Alzheimer's disease (AD).

Computational details

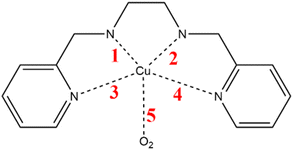
As mentioned above, we selected a set of copper complexes with potential application in neurodegenerative diseases as proposed by Puentes-Diaz et al.^29,30 This set of complexes was chosen because their calculated standard reduction potentials lie in the range of the oxidation and reduction potentials of the superoxide radical (−0.16 and 0.89 V vs. standard hydrogen electrode).³¹ The structures and abbreviations of the copper complexes are presented in Fig. 2, the IUPAC nomenclature of each complex is listed in Table S1.†

Fig. 2 Structures and abbreviations of the copper complexes evaluated in this study.

Possible reaction intermediaries were evaluated for the dismutation reaction of the superoxide radical mediated by copper complexes. These intermediates were proposed based on mechanisms reported in the literature for the SOD enzyme (eqn (3) to (8)), where M(ox) and M(red) stand for the oxidized and reduced states of the metals, respectively. We will refer to the mechanism described by Valko et al. as Mechanism 1 (eqn (3) and (4)),² Mechanism 2 will denote the one reported by Miller et al. (eqn (5) and (6)),³² and Mechanism 3 will represent the mechanism proposed by Bull and Fee (eqn (7) and (8)).³³

SOD − M(ox)(OH⁻) + O₂˙⁻ + H⁺ → SOD − M(red)(OH₂) + O₂ (3)

SOD − M(red)(OH₂) + O₂˙⁻ + H⁺ → SOD − M(ox)(OH⁻) + H₂O₂ (4)

SOD − M(ox) + O₂˙⁻ + H⁺ → SOD − M(red)(H⁺) + O₂ (5)

SOD − M(red)(H⁺) + O₂˙⁻ + H⁺ → SOD − M(ox) + H₂O₂ (6)

SOD − M(ox) + O₂˙⁻ → SOD − M(red) + O₂ (7)

SOD − M(red) + O₂˙⁻ + 2H⁺ → SOD − M(ox) + H₂O₂ (8)

Following the latter, the mechanisms considered for the nine complexes are:

Ligand_x − Cu(II)(OH⁻) + O₂˙⁻ + H⁺ → Ligand_x − Cu(I)(OH₂) + O₂ (9)

Ligand_x − Cu(I)(OH₂) + O₂˙⁻ + H+ → Ligand_x − Cu(II)(OH⁻) + H₂O₂ (10)

Ligand_x − Cu(II) + O₂˙⁻ + H⁺ → Ligand_x − Cu(I)(H⁺) + O₂ (11)

Ligand_x − Cu(I)(H⁺) + O₂˙⁻ + H⁺ → Ligand_x − Cu(II) + H₂O₂ (12)

Ligand_x − Cu(II) + O₂˙⁻ → Ligand_x − Cu(I) + O₂ (13)

Ligand_x − Cu(I) + O₂˙⁻ + 2H⁺ → Ligand_x − Cu(II) + H₂O₂ (14)

Note that the subscript of the ligand corresponds to the complex abbreviation (from systems 1 to 9):

The free reaction energy changes were calculated by fully optimizing the structures of the reactants, products, and intermediates. All the calculations were performed with the M06-2X density functional and the all-electron basis set 6-311++G(d,p) for all atoms. It is important to point out that this combination of functional and basis sets was previously calibrated by our group, and it provides accurate results for the molecular properties of copper complexes, particularly the standard reduction potential.^29–31,34 The optimizations were conducted including the solvent effects (water) with the SMD continuous model.³⁵ All calculations were carried out with the Gaussian16 suite of programs.³⁶

It is important to comment that the quantum-mechanical description of both the reactant and product complexes associated to eqn (2) represents a challenge due to the nature of the electronic and spin states of the involved species. In these regards, it must be considered that the complexes containing Cu²⁺ and the superoxide O₂˙⁻ are open-shell systems presenting a doublet state, while the complexes bearing Cu⁺ are singlet close-shell cases. On the other hand, it is well-known that the electronic state of the O₂ molecule with the lowest energy corresponds to the triplet. Despite this diversity of spin states, it must be noted that both, the Cu²⁺L/O₂˙⁻ and Cu⁺L/O₂ systems, present total charge and multiplicity of 1+ and 3, respectively. To ensure the adequate spin state in the different species of the reactant and product complexes, the following protocol was employed: (i) The isolated CuL system with either 1+ or 2+ oxidation state was optimized considering the correct charge and multiplicity. (ii) Upon obtaining the equilibrium geometry, an O₂˙⁻ or O₂ molecule was added close to the metallic center of the Cu²⁺L or Cu⁺L system, respectively. (iii) A subsequent optimization process was performed, leaving only the oxygen atoms of O₂˙⁻ or O₂ free while keeping the atoms of the CuL complex frozen. (iv) Finally, a spin density analysis was performed to evaluate the spin distribution across the complex, ensuring that the correct spin state was accurately represented in the computational model.

Quantum Theory of Atoms in Molecules (QTAIM) provides a framework that links chemical concepts such as structure, bonding, and reactivity to the topology of the electron density (ρ(r)) within a chemical species ρ(r) is characterized by critical points, which are locations where the electron density possesses maxima, minima, or saddle points.^37,38 These critical points are classified into four types: nuclear-critical points (NCP, maxima), bond-critical points (BCP, saddle), ring-critical points (RCP, saddle), and cage-critical points (CCP, minima). The classification of these points is based on the Laplacian of the electron density (∇²ρ(r)), and the number of each type of critical points within a molecule follows a topological rule known as the Poincaré–Hopf, which states that the difference between the number of NCPs and the sum of BCPs, RCPs, and CCPs equals one.^39,40

To investigate the interaction between copper complexes and the superoxide radical, we analyzed the reactants and intermediates described in Mechanism 3 using various QTAIM descriptors to characterize the interactions at selected bond-critical points (BCPs, Fig. 3). We focused on the electron density (ρ(r_BCP)), the Laplacian of the electron density (∇²ρ(r_BCP)), the absolute value of the ratio between potential energy density and gradient kinetic energy density (|V(r_BCP)|/G(r_BCP)), and the total electronic energy density (H(r_BCP)). The ρ(r_BCP) correlates with bond orders and binding energies, providing insight into bond strength. The sign of ∇²ρ(r_BCP) indicates whether electron density is concentrated (negative) or depleted (positive) at that point. The ratio |V(r_BCP)|/G(r_BCP) is an indicator for identifying atomic interactions, while the H(r_BCP), helps assess the degree of covalence in the interaction. A negative H(r_BCP) value that implies electron sharing, a characteristic of covalent bonds. These descriptors enable the classification of interactions into two main categories: shared shell interactions, which are associated with covalent bonds, and closed-shell interactions, which are related to ionic bonds. Beyond these parameters, another important characteristic for describing bond properties is ellipticity (ε = (λ₁/λ₂) − 1). This measure indicates the cylindrical symmetry of a bond; for instance, bonds like single C–C, have an ellipticity of zero. In contrast, aromatic bonds, such as those found in benzene, display an ellipticity of about 0.23, while the double bond in ethylene exhibits an ellipticity of 0.45. It is important to remind that, in QTAIM analysis, the electron density is partitioned into regions or basins around each atom, charges are assigned based on the density within each basin and the spin density is computed by separating the total electron density into components based on spin.^41–45 The topology analysis calculations were performed using the MULTIWFN software,⁴⁶ utilizing the optimized wavefunction extracted from the Gaussian output files.

Fig. 3 Bond critical points (BCP) considered for the evaluated complexes.

Results and discussion

In this section, we first report on the reaction-free energy changes for the three mechanisms considered in eqn (9) to (14) mediated by each of the nine copper complexes. In the second part, we detail the topological analysis of the interaction between the copper complexes and oxygen species. Lastly, we compare the interaction energies of the copper complexes with the oxygen species. The equation used to calculate the reaction free energies and the primary Gibbs energy values is given in Table S2 of the ESI.†

Reaction free energies

Since we were focused on the role of the copper complexes interacting with the oxygen species, we evaluated the Gibbs reaction energies for the intermediate formation in each mechanism. These energies are shown in Table 1, where it is observed that all the reaction free energies are negative, indicating that the processes are thermodynamically favorable. As a general trend, the larger changes in the Gibbs reaction energy occur in Mechanism 2, followed by Mechanism 1, and the smaller changes in Mechanism 3 (the free energy for the full reactions is presented in Table S3 of the ESI†). Considering that all the ΔG values are negative, it is possible to suggest that the complexes can initiate the mimicking process of the SOD enzyme in all three considered mechanisms. From this table, it also can be seen that the exergonicity of the reaction is more dependent on the mechanism of the nature of the copper complex.

Table 1 Changes in the Gibbs energy of reaction (kcal mol⁻¹) for obtaining the intermediates in the three considered mechanisms

Complexes	ΔG (kcal mol^−1)
	Mechanism 1	Mechanism 2	Mechanism 3
1	−2.0	−80.8	−79.4
2	−6.1	−84.3	−77.5
3	−6.9	−75.5	−81.0
4	−7.1	−75.6	−80.4
5	−7.3	−76.3	−82.1
6	−9.3	−75.2	−83.0
7	−7.2	−73.4	−81.5
8	−7.2	−75.4	−81.2
9	−9.6	−76.0	−80.8

---

Regarding the geometries, the reaction intermediates for the first mechanism present some geometrical changes compared to the isolated Cu²⁺ complex 4 depicted in Fig. 4A (the geometrical features of the remaining 8 complexes are reported in the ESI†). The geometry of this first intermediate (Fig. 4B), reveals the coordination of the water molecule to the copper center. Notably, this coordination results in an elongation of the Cu–N distances. In contrast, the intermediate of the second mechanism (Fig. 4C) involves binding a hydrogen atom to the nitrogen 1. This binding significantly alters the coordination sphere of the copper, which is solely coordinated by nitrogen atoms 3 and 4, leading the complex toward a more linear geometry upon reduction.

Fig. 4 Optimized structures and distances between copper and nitrogen for (A) complex 4-Cu²⁺; (B) reaction intermediate Cu⁺–H₂O; (C) reaction intermediate Cu(I)–H⁺; (D) reaction intermediate Cu⁺–O₂. Distances are given in angstroms.

Consequently, the distances between nitrogen 1 and 2 and the copper cation are greater than those between nitrogen 3 and 4, and the metal center. Finally, in the intermediates of the third mechanism, illustrated in Fig. 4D, an oxygen molecule coordinates to the copper through one of its oxygen atoms. This interaction induces an elongation of all the Cu–N distances and causes a more pronounced distortion of the initial square-planar configuration of the Cu²⁺ coordination sphere. However, due to the constraints imposed by the ligand, the coordination center does not fully transition to the pyramidal shape typically associated with Cu⁺ complexes.

Topological analysis

The topological analysis focused on the interaction between oxidized and reduced complexes and the oxygen species, considering the interaction of Cu²⁺ with the superoxide as the reactants and Cu⁺ with oxygen as products. Therefore, the systems considered for the reactants are a biradical, where one unpaired electron lies on the copper and the other on the superoxide. In contrast, the oxygen in the products is a diradical with two unpaired electrons, as confirmed by the analysis of the electron spin density. These changes can be observed in Fig. 5, where the electron spin density of the two moieties in the reactants is centered on Cu²⁺ and O₂˙⁻, whereas in the products, the spin density is centered on O₂. Table 2 summarizes the charges and spin densities for complexes 1 and 4, where the systems were accurately described (charges and spin densities for all the complexes considered are detailed in SI).

Fig. 5 Electron spin density isosurfaces for (A) complex 1 and (B) complex 4 in reactant and product states. The isosurface was set to 0.003 a.u.

Table 2 Atomic charges and spin densities for the copper cation and oxygens involved in the dismutation reaction for complexes 1 and 4

Complex 1 – superoxide			Complex 4 – superoxide
Atom	Atomic charge	Spin density	Atomic charge	Spin density
Cu^2+	1.3993	0.8257	1.5226	0.8271
O	−0.4720	0.5178	−0.4708	0.5243
O	−0.4887	0.4685	−0.4586	0.4763

---

Complex 1 – dioxygen			Complex 4 – dioxygen
Atom	Atomic charge	Spin density	Atomic charge	Spin density
Cu^+	0.6128	0.0051	1.1267	0.0106
O	−0.0072	0.9950	−0.0061	0.9931
O	−0.0118	0.9953	−0.0094	0.9896

---

For the oxidized forms of complexes 1, 2, 4, 5, 7, 8, and 9, the interactions between the copper and nitrogen atoms exhibit similar values for both ρ(r_BCP) and ∇²ρ(r_BCP), with both being positive (see Tables S13 to S21 in the ESI†). These results suggest that the aliphatic and aromatic nitrogen atoms bond to the copper atom with comparable strength. Additionally, the ratio |V(r_BCP)|/G(r_BCP) is consistently around 1.11 across all the oxidized forms of the complexes. The total electronic energy density, H(r_BCP), also shows similar negative values, approximately −0.010 a.u., indicating comparable covalent characteristics. Furthermore, the ellipticity analysis reveals that the N–Cu interactions in the oxidized forms possess strong cylindrical symmetry, corresponding to a sigma-type interaction between the atoms. In the case of Cu–O interactions, the values for ρ(r_BCP) and ∇²ρ(r_BCP) are also positive but approximately half and one-third, respectively, of those observed in the N–Cu interactions. The ratio |V(r_BCP)|/G(r_BCP) and H(r_BCP) to Cu–O interactions are like those found in the N–Cu interactions. However, the ellipticity for Cu–O is consistently higher, compared to the N–Cu interactions. This indicates that the Cu–O interaction is less symmetric, with the curvature of the electron density being more pronounced in one direction within the plane perpendicular to the bond path for these interactions, this can be observed in Fig. 6. Similar observations can be made in the oxidized forms of complexes 3 and 6; however, in these cases, the ellipticity is similar between N–Cu and Cu–O interactions. For the reduced forms of complexes 1–9, a decrease in electron density at the BCPs corresponding to the Cu–N and Cu–O interactions is observed. However, the decrease is more pronounced in the latter case. Additionally, for the Cu–O interaction, there is a decrease in the |V|/G ratio, an increase in H(r) reaching a positive value, and a rise in ellipticity. These factors, together with the elongation of the Cu–O distance, suggest that the reduced form involves the decoordination of the O₂ molecule (see eqn (7) and (8)).

Fig. 6 3D NCI plots for (A) complex 1 and (B) complex 4, the reduced gradient isosurface was set to 0.5 a.u. and colored with the sign(λ₂)ρ(r). Each complex is accompanied by the corresponding 2D NCI plot. For both, 3D and 2D plots the color scale sign(λ₂)ρ(r) in a.u. is the same. On the left are the structures of the Cu(II) complexes with superoxide, while on the right are the structures of the Cu(I) complexes with dioxygen.

The plot of the reduced gradient differs from QTAIM by revealing both covalent and non-covalent interactions.⁴⁷ The analysis of the plots of the reduced gradient extends beyond QTAIM by identifying regions in space where electron density accumulates, thereby identifying areas where non-covalent interactions occur.^48,49 Additionally, it offers the advantage of mapping reduced gradient isosurfaces with a color scale that reflects the electron density multiplied by the sign of the second eigenvalue of the Hessian matrix. This feature allows for the differentiation of interaction types, such as steric/repulsive (λ₂ > 0), van der Waals-like (λ₂ ≈ 0), and attractive (λ₂ < 0) interactions. Fig. 6 shows the isosurfaces of the reduced gradient. On the left, the structures of the Cu²⁺ complexes with O₂˙⁻ (reactants) are displayed, while on the right, the structures of the Cu⁺ complexes with O₂ (products) are presented. The corresponding reduced gradient vs. sign(λ₂)ρ(r) (NCI plot 2D) plots are also included. For the reactants, a relatively strong interaction between the superoxide and Cu can be observed, with a density at the BCP of approximately 0.04 a.u. in both cases A and B. This interaction corresponds to the third peak from left to right in the nciplot 2D graph. In both cases, the first two peaks, one at ∼ −0.08 and the other at ∼−0.07 (sign(λ₂)ρ(r)), correspond to the N(1,2)–Cu and N(3,4)–Cu interactions, respectively. The first noticeable feature in the products is the decrease in interaction strength, expressed as a reduction in the isocontour volume and its associated density. This interaction appears as a peak at approximately −0.012 in sign(λ₂)ρ(r), which falls within the range of what could be considered as a van der Waals interaction. Additionally, there is a decrease in the strength of the interactions between the nitrogen atoms and the Cu⁺ atom, with a shift in the peak corresponding to the N(1,2)–Cu interactions from approximately −0.08 to −0.04. This decrease is less pronounced in the N(3,4)–Cu interactions, which shift from −0.07 to −0.06. These observations suggest a modification in the Cu complexes and a decrease in the Cu–O interaction strength, consistent with our previous findings.

Finally, the interaction energies (ΔE) between the copper complexes and oxygen species for the reactants and products were calculated. To minimize the basis set superposition error (BSSE), we applied the counterpoise method, treating the system as two fragments: the copper complex and the oxygen.⁵⁰ The BSSE-corrected results are shown in Table 3, where it is observed that the Cu²⁺ interaction with the superoxide is much stronger than the interaction between Cu⁺ and oxygen in agreement with the results derived from the topological analysis. This lower interaction energy in the reduced complex is an indication of the plausible decoordination of the oxygen, in this way neutralizing the superoxide.

Table 3 Interaction energies (ΔE) of the Cu(II) complexes with superoxide and Cu(I) with oxygen. The interaction energy is calculated as the difference between the free energy of the copper-oxygen adduct and the sum of the free energies of the separated copper and oxygen species

Complex	ΔE (kcal mol^−1)
	Cu(II) complexes – superoxide	Cu(I) complexes – dioxygen
1	−91.4	−4.9
2	−91.6	−4.3
3	−77.1	−5.0
4	−92.0	−4.9
5	−92.0	−4.9
6	−92.1	−4.9
7	−91.1	−5.1
8	−91.8	−5.1
9	−92.2	−5.2

---

The combined analysis of the reaction free energies for the intermediate formation together with the topological analysis as well as the evaluation of the interaction of the oxygen species before and after copper reduction confirm that the participation of these complexes in facilitating the conversion of superoxide into molecular dioxygen is feasible. This behavior is similar in the 9 evaluated complexes.

Conclusions

We presented the free energy changes in water for the formation of reaction intermediates in nine copper complexes across three different mechanisms in the conversion of superoxide to molecular oxygen at the M06-2X level of theory. The results indicate that all the complexes can mimic the SOD enzyme through any of the mechanisms considered in this study, suggesting their potential effectiveness in facilitating the desired biochemical reactions. Additionally, we performed a topological analysis of the electron density distribution for the nine complexes interacting with the superoxide radical. The analysis revealed that the interaction between copper(II) and the superoxide radical is partially covalent and attractive. In the products, the copper(I) complexes and dioxygen the interaction shifts to a closed-shell (CS) type, which is indicative of a significant change in the nature of the interaction. This change, combined with the observed variations in interaction energy between the copper complexes and oxygen species, supports the idea that these complexes could effectively facilitate the conversion of superoxide into molecular dioxygen. The combined analysis of the reaction free energies for intermediate formation, topological features of the electron density, and interaction energies before and after copper reduction confirms that the participation of these complexes in the conversion of superoxide to molecular dioxygen is feasible. This behavior is consistently observed across all 9 evaluated complexes, reinforcing their potential as effective mimics of the SOD enzyme.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. M. M. and J. A. T. thank the Universidad Nacional de Colombia for the financial support (Research Project No. 57575). J. A.-T. would like to dedicate this article to Eduardo Ruiz-Durantez (RIP). A. F.-G. thanks, Universidad Militar Nueva Granada for the financial support. This is a product derived from the project INV-CIAS-3408 funded by Vicerrectoría de Investigaciones Universidad Militar Nueva Granada – Validity 2021. FJT thanks the financial support of this project through the USFQ's POLIGRANTS program. The calculations in the present work were carried out using the USFQ's High Performance Computing System (HPC-USFQ) and the Advanced Computing Laboratory of Universidad del Rosario computational resources.

References

1. Y. Gilgun-Sherki, E. Melamed and D. Offen, Neuropharmacology, 2001, 40, 959–975.
2. M. Lawson, K. Jomova, P. Poprac, K. Kuča, K. Musílek and M. Valko, Free Radicals and Antioxidants in Human Disease, in Nutritional Antioxidant Therapies: Treatments and Perspectives, ed. A. K. Hussain and I. Laher, Springer, Cham, 2017, pp. 283–305.
3. M. Martínez-Cayuela, Biochimie, 1995, 77, 147–161.
4. O. M. Ighodaro and A. Akinloye, Alexandria J. Med., 2018, 54, 287–293.
5. S. B. Chidambaram, A. Ben Khedher, M. S. Vaithilingam, G. Shanmugavelu and S. Perumalsamy, IBRO Neurosci. Rep., 2024, 16, 373–394.
6. O. Iranzo, Bioorg. Chem., 2011, 39, 73–87.
7. M. Baudry, L. R. Etienne, A. Ruizan, J. M. Gilders and L. S. Marino, Biochem. Biophys. Res. Commun., 1993, 192, 964–968.
8. X. Hou, X. Liang, Y. Wang, D. Cai, Y. Kang and W. Huang, Polyhedron, 2024, 260, 117097.
9. S. Signorella, C. Palopoli and G. Ledesma, Coord. Chem. Rev., 2018, 365, 75–102.
10. C. Policar, J. Bouvet, H. C. Bertrand and N. Delsuc, Curr. Opin. Chem. Biol., 2022, 67, 102109.
11. G. Schanne, S. Demignot, C. Policar and N. Delsuc, Coord. Chem. Rev., 2024, 514, 215906.
12. C. Policar, J. Bouvet, H. C. Bertrand and N. Delsuc, Curr. Opin. Chem. Biol., 2022, 67, 102109.
13. T. P. Ribeiro, L. M. Freitas, G. Lima, J. S. Oliveira and S. S. Moura, Free Radical Biol. Med., 2015, 80, 67–76.
14. E. Mathieu, A. E. Tolbert, K. J. Koebke, C. Tard, O. Iranzo, J. E. Penner-Hahn, C. Policar and V. Pecoraro, Chem. - Eur. J., 2020, 26, 249–258.
15. M. Bashir, A. A. Dar and I. Yousuf, ACS Omega, 2023, 8, 3026–3042.
16. J. L. Moore, B. K. Ellis, E. S. Jones and P. G. Thompson, Inorg. Chem., 2022, 61, 19983–19997.
17. Y. H. Hung, A. I. Bush and R. A. Cherny, J. Biol. Inorg. Chem., 2010, 15, 61–76.
18. M. Bost, J. A. Aschiero, E. McQueen, R. Pujol and B. Yates, J. Trace Elem. Med. Biol., 2016, 35, 107–115.
19. N. Puentes-Díaz, D. Chaparro, D. Morales-Morales, A. Flores-Gaspar and J. Alí-Torres, ACS Omega, 2023, 8, 4508–4526.
20. J. Alí-Torres, A. Mirats, J.-D. Maréchal, L. Rodríguez-Santiago and M. Sodupe, J. Phys. Chem. B, 2014, 118, 4840–4850.
21. A. Mirats, J. Alí-Torres, L. Rodríguez-Santiago and M. Sodupe, Theor. Chem. Acc., 2016, 135, 1–9.
22. A. Mirats, J. Alí-Torres, L. Rodríguez-Santiago, M. Sodupe and G. La Penna, Phys. Chem. Chem. Phys., 2015, 17, 27270–27274.
23. K. Reybier, J. P. Henry, F. Carrière, A. Guilloteau and P. Marchand, Angew. Chem., Int. Ed., 2016, 55, 1085–1089.
24. M. A. Todarwal, S. K. Tadavi, R. S. Sancheti and R. S. Bendre, Eurasian J. Chem., 2024, 15, 128–142.
25. A. Singh, A. Maji, A. Mohanty and K. Ghosh, New J. Chem., 2020, 44, 18399–18418.
26. J. C. Pessoa and I. Correia, Coord. Chem. Rev., 2019, 388, 227–247.
27. N. Mohan, K. Subramanian, V. Srinivasan and A. Rajesh, New J. Chem., 2022, 46, 12540–12550.
28. A. Erxleben, Inorg. Chim. Acta, 2018, 472, 40–57.
29. N. Puentes-Díaz, D. Chaparro, V. Reyes-Marquez, D. Morales-Morales, A. Flores-Gaspar and J. Alí-Torres, J. Alzheimer's Dis., 2024, 99, S383–S396.
30. N. Puentes-Díaz, D. Chaparro, D. Morales-Morales, J. Alí-Torres and A. Flores-Gaspar, Chempluschem, 2023, 88, e202300405.
31. D. Chaparro and J. Alí-Torres, J. Mol. Model., 2017, 23, 1–8.
32. A. F. Miller, K. Padmakumar, D. L. Sorkin, A. Karapetian and C. K. Vance, J. Inorg. Biochem., 2003, 93, 71–83.
33. C. Bull and J. A. Fee, J. Am. Chem. Soc., 1985, 107, 3295–3304.
34. D. Chaparro, A. Flores-Gaspar and J. Alí-Torres, J. Alzheimer's Dis., 2021, 82, S179–S193.
35. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robb, et al. Gaussian16 Rev. C.01, Gaussian, Inc., Wallingford, CT, 2016.
37. C. Lepetit and M. L. Kahn, Res. Chem. Intermed., 2021, 47, 377–395.
38. L. E. Seijas, A. Lunar, L. Rincón and R. Almeida, J. Mol. Struct., 2022, 1261, 132898.
39. P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536.
40. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
41. P. Macchi, Coord. Chem. Rev., 2003, 238–239, 383–412.
42. F. Cortes-Guzmán and R. Bader, Coord. Chem. Rev., 2005, 249, 633–662.
43. W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057.
44. L. E. Seijas, C. H. Zambrano, R. Almeida, J. Alí-Torres, L. Rincón and F. J. Torres, Int. J. Mol. Sci., 2023, 24, 5271.
45. L. E. Seijas, L. M. Belandria, P. J. Vivas, M. Guillén, J. L. Burgos, A. N. Fitch, J. Wright, L. Rincón, G. E. Delgado and A. J. Mora, J. Mol. Struct., 2022, 1261, 132898.
46. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
47. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
48. L. E. Seijas, A. Lunar, L. Rincón, R. Almeida and J. Comput, Methods Sci. Eng., 2017, 17, 1–9.
49. R. A. Boto, J. Contreras-García, J. Tierny and J.-P. Piquemal, Mol. Phys., 2016, 114, 1406–1414.
50. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07126c

---