Synthesis, structural characterization, and theoretical analysis of novel zinc(II) schiff base complexes with halogen and hydrogen bonding interactions

Abstract

In this article, we present the synthesis and characterization of three zinc(II) complexes, [Zn^II(HL¹)₂] (1), [Zn^II(HL²)₂]·2H₂O (2) and [Zn^II(HL³)₂] (3), with three tridentate Schiff base ligands, H₂L¹, H₂L², and H₂L³. The structures of the complexes were confirmed by single-crystal X-ray diffraction analysis. DFT calculations were performed to gain insights into the self-assembly of the complexes in their solid-state structures. Complex 1 exhibits dual halogen-bonding interactions (Br⋯Br and Br⋯O) in its solid-state structure, which have been thoroughly investigated through molecular electrostatic potential (MEP) surface calculations, alongside QTAIM and NCIPlot analyses. Furthermore, complex 2 features a fascinating hydrogen-bonding network involving lattice water molecules, which serves to link the [Zn^II(HL²)₂] units into a one-dimensional supramolecular polymer. This network has been meticulously examined using QTAIM and NCIplot analyses, allowing for an estimation of the hydrogen bond strengths. The significance of H-bonds and CH⋯π interactions in complex 3 was investigated, as these interactions are crucial for the formation of infinite 1D chains in the solid state.

---

Introduction

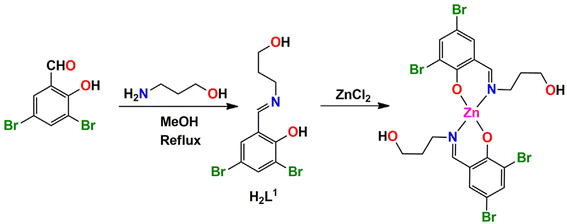
Zinc is an eco-friendly and inexpensive metal. Zinc complexes have attracted intense research interest among synthetic inorganic chemists, supramolecular chemists and biochemists for their wide-ranging application in material science, crystal engineering and inorganic biochemistry.^1–19 It shows a stable oxidation state (+2) and a variety of coordination geometries, e.g., tetrahedral, trigonal bipyramidal, square pyramidal, octahedral etc., depending mainly on the steric demand of the ligand.^20–26 Many hydrolytic enzymes with vital biochemical functions of the living body contain zinc in their active site structure, and many model complexes of these enzymes have been synthesised and characterized by several research groups.^27–34 Zinc complexes have also been used to synthesize many optoelectronic materials.^35–37

Moreover, the exploration of supramolecular interactions, e.g., hydrogen bonding, π⋯π stacking, cation⋯π, C–H⋯π, lone pair⋯π and anion⋯π interactions, in the solid-state structure of many complexes is an interesting research area in structural biology and crystal engineering.^38–47 Supramolecular chemists and theoretical chemists are also interested in the solid-state structure of transition and non-transition metal complexes to explore σ-hole interactions.^48–50 Usually, the σ-hole indicates a region of lower electron density compared to its neighbouring regions. It is produced by the anisotropic distribution of the electron density along the σ-skeleton.⁵¹ In this article, we shall concentrate on the halogen-bonding interaction, which is an example of σ-hole interaction between the σ-hole created on a halogen atom in a molecular entity and an electron-rich region in another, or the same, molecular entity.^52,53 Other types of σ-hole interactions are also known to crystal engineers, such as spodium bonding (for group 12), tetrel bonding (for group 14), chalcogen bonding (for group 16) etc.^54–57

In the present work, three tridentate N,N,O-donor Schiff bases (H₂L¹, H₂L² and H₂L³) were used to form three zinc complexes, [Zn^II(HL¹)₂] (1), [Zn^II(HL²)₂]·2H₂O (2) and [Zn^II(HL³)₂] (3) H₂L¹ = 2-(3-hydroxypropylimino)methyl-4,6-dibromo phenol; H₂L² = 2-(1-hydroxybutan-2-ylimino)methyl-6-ethoxyphenol; H₂L³ = 2-(1-hydroxy-2-methylpropan-2-ylimino)methyl-4-bromophenol). Two types of halogen-bonding interactions (characterized by Br⋯Br and Br⋯O contacts) were observed in the solid-state structures of complex 1, as confirmed by DFT calculations. Furthermore, an interesting R₄⁴(8) supramolecular ring was observed in the solid-state structure of complex 2. This provides a high degree of stabilization and explains the basis of co-crystallization of complex 2 with two water molecules. The optimization and QTAIM analysis elucidated the strength and orientation of these H-bonds. For complex 3, the relative importance of H-bonds and CH⋯π interactions was investigated, as they determine the formation of infinite 1D chains in the solid state.

Experimental

All starting materials and solvents were commercially available, reagent grade, and used as purchased from Sigma-Aldrich without further purification.

Synthesis of the ligands

2-(3-Hydroxypropylimino)methyl-4,6-dibromo phenol (H₂L¹). A methanol (15 mL) solution of 3,5-dibromo-2-hydroxybenzaldehyde (280 mg, ∼1 mmol) was refluxed with 3-aminopropan-1-ol (0.1 mL, ∼1 mmol) for 2 hours, leading to the formation of a yellow Schiff base ligand, H₂L¹. The ligand was not isolated, and the methanol solution was used directly for the preparation of complex 1.

2-(1-Hydroxybutan-2-ylimino)methyl-6-ethoxyphenol (H₂L²). H₂L² was prepared by refluxing a methanol solution (15 mL) of 2-aminobutan-1-ol (∼1 mmol, 0.1 mL) and 3-ethoxy-2-hydroxybenzaldehyde (∼1 mmol, 170 mg) for ca. 2 h. The ligand was not isolated, and the methanol solution was used directly for the preparation of complex 2.

2-(1-Hydroxy-2-methylpropan-2-ylimino)methyl-4-bromophenol (H₂L³). The Schiff base ligand HL³ was prepared by refluxing an acetonitrile solution (15 mL) of 2-amino-2-methylpropan-1-ol (∼1 mmol, 0.1 mL) and 5-bromo-2-hydroxybenzaldehyde (∼1 mmol, 205 mg) for ca. 2 h. The ligand was not isolated, and the methanol solution was used directly for the preparation of complex 3.

Synthesis of the complexes

[Zn^II(HL¹)₂] (1). A methanol solution of the Schiff base ligand, H₂L¹, was added to the acetonitrile solution of zinc(II) chloride (140 mg, ∼1 mmol) with constant stirring, and the stirring was continued for an additional 1 h. X-ray quality yellow block single crystals were collected after two weeks.

Yield: 472 mg (∼64%) based on zinc(II). Anal. calc. for C₂₀H₂₀Br₄N₂O₄Zn (FW: 737.37): C, 32.58; H, 2.73; N, 3.80. Found: C, 32.60; H, 2.71; N, 3.81%. FT-IR (KBr, cm⁻¹): 3576–3177 (ν_O–H), 3058–2841 (ν_C–H), 1620 (ν_CN). UV-vis, λ_max (nm), [ε_max (L mol⁻¹ cm⁻¹)] (MeOH): 376 (1.132 × 10⁴).

[Zn^II(HL²)₂]·2H₂O (2). To a 15 mL methanol solution of the ligand, H₂L², was added a methanol solution of zinc(II) acetate dihydrate (220 mg, ∼1 mmol) with constant stirring at room temperature. After six days, yellow needle-shaped crystals with X-ray quality clarity emerged at the beaker's bottom. These were gathered and allowed to dry naturally.

Yield: 369.16 mg (∼65%) based on zinc(II). Anal. calc. for C₂₆H₃₄N₂O₈Zn (FW: 567.94): C, 54.98; H, 6.03; N, 4.93. Found: C, 55.01; H, 6.15; N, 4.92%. FT-IR (KBr, cm⁻¹): 3477–3215 (ν_OH2, ν_OH), 2974–2854 (ν_C–H), 1610 (ν_CN). UV-vis, λ_max (nm), [ε_max (L mol⁻¹ cm⁻¹)] (MeOH): 375 (1.124 × 10⁴).

[Zn^II(HL³)₂] (3). An acetonitrile solution (10 mL) of zinc(II) chloride (140 mg, ∼1 mmol) was added to a methanol solution (15 mL) of the Schiff base ligand, H₂L³, with constant stirring until a light-yellow solution was observed. To avoid precipitation, a few drops of DMSO were added in the reaction mixture, then it was kept in an open atmosphere to grow single crystals. After four weeks, single yellow crystals of X-ray quality were gathered.

Yield: 431 mg (∼71%) based on zinc(II). Anal. calc. for C₂₂H₂₆Br₂N₂O₄Zn (FW: 607.64): C, 43.49; H, 4.31; N, 4.61. Found: C, 43.50; H, 4.32; N, 4.62%. FT-IR (KBr, cm⁻¹): 3549–3107 (ν_OH), 2958–2926 (ν_C–H), 1622 (ν_C=N). UV-vis, λ_max (nm), [ε_max (L mol⁻¹ cm⁻¹)] (MeOH): 371 (1.048 × 10⁴).

Physical measurement. Elemental analysis (carbon, hydrogen and nitrogen) of the complexes was performed on a PerkinElmer 240C elemental analyzer. Infrared spectra in KBr (4500–500 cm⁻¹) were recorded using a PerkinElmer RXI FT-IR spectrophotometer. Absorption and emission spectra in methanol solvent were recorded on a Duetta-1621 fluorescence and absorbance spectrophotometer. The detailed information on the Hirshfeld surface analysis is presented in the ESI.†
X-ray crystallography. Suitable single crystals of all the complexes were used for data collection using a Bruker D8 QUEST area detector diffractometer equipped with graphite-monochromated Mo K_α radiation (λ = 0.71073 Å). Molecular structures were solved by direct methods and refined by full-matrix least squares on F² using the SHELXL-18/6 package.⁵⁸ Non-hydrogen atoms were refined with anisotropic thermal parameters. All other hydrogen atoms were placed in their geometrically idealized positions and constrained to ride on their parent atoms. Multi-scan empirical absorption corrections were applied to the data using the program SADABS.⁵⁹ One pendant –CH₂OH group in complex 1 and one OEt group in complex 2 are disordered over two sites. In 2, the hydrogen atoms bonded to the oxygen atom of the lattice water molecule could not be located. The crystallographic data and refinement details are presented in Table 1. Selected bond lengths and angles are listed in Tables 2 and 3, respectively.

Table 1 Crystal data and refinement details of complexes 1–3^a

Complex	1	2	3
a (^ξ)R1 = Σ||Fo| − |Fe||/Σ|Fo|; (^ψ) wR2 = Σw(|Fo|^2 − |Fe|^2)^2/Σw|Fo|^2)^1/2.
Formula	C20H20Br4N2O4Zn	C26H34N2O8Zn	C22H26Br2N2O4Zn
Formula weight	737.37	567.94	607.64
Temperature (K)	273	273	273
Crystal system	Monoclinic	Orthorhombic	Monoclinic
Space group	C2/c	A b a 2	P21/n
a (Å)	21.561(1)	21.494(2)	12.5138(5)
b (Å)	4.595(2)	13.8469(13)	11.9667(4)
c (Å)	25.047(1)	9.6418(1)	16.7858(7)
β	110.368(1)	(90)	108.173(1)
Z	4	4	4
V (Å^3)	2326.44(17)	2869.6(5)	2388.27(16)
dcalc (g cm^−3)	2.105	1.315	1.690
μ (mm^−1)	7.956	0.903	4.405
F(000)	1424.0	1192.0	1216.0
Total reflections	48 902	24 328	33 325
Unique reflections	3637	2572	5297
Observed data [I > 2σ(I)]	4428	2091	3785
No. of parameters	147	188	281
R(int)	0.0396	0.0494	0.0681
^ξR1, ^ψwR2 (all data)	0.0541, 0.1008	0.0641, 0.1437	0.0923, 0.2249
^ξR1, ^ψwR2 [I > 2σ(I)]	0.0396, 0.0915	0.0494, 0.1314	0.0681, 0.2004
CCDC no.	2346042	2346043	2346044

---

Table 2 Selected bond lengths (Å) of complexes 1–3

Bonds	Complex 1	Complex 2	Complex 3
Zn(1)–O(1)	1.933(2)	1.912(6)	2.054(4)
Zn(1)–N(1)	2.009(2)	2.020(7)	2.073(5)
Zn(1)–O(2)	—	—	2.288(4)
Zn(1)–O(3)	—	—	1.955(5)
Zn(1)–O(4)	—	—	2.355(6)
Zn(1)–N(2)	—	—	2.093(5)

---

Table 3 Selected bond angles (°) of complexes 1–3^a

Angles	Complex 1	Complex 2	Complex 3
a Symmetry transformation = ^i = 1 − x, y, 1.5 − z, ^ii = 1 − x, 1 − y, z.
O(1)–Zn(1)–N(1)	94.95(8)	95.10(2)	89.80(15)
O(1)–Zn(1)–O(1)^i	123.27(8)	—	—
O(1)–Zn(1)–O(1)^ii	—	117.60(2)	—
O(1)–Zn(1)–N(1)^i	111.87(8)	—	—
O(1)–Zn(1)–N(1)^ii	—	112.80(2)	—
N(1)–Zn(1)–N(1)^i	122.27(9)	—	—
N(1)–Zn(1)–N(1)^ii	—	125.30(3)	—
O(1)–Zn(1)–O(2)	—	—	158.81(16)
O(1)–Zn(1)–O(3)	—	—	100.46(17)
O(1)–Zn(1)–O(4)	—	—	87.35(18)
O(1)–Zn(1)–N(2)	—	—	99.10(17)
O(1)–Zn(1)–N(1)	—	—	89.80(15)
O(2)–Zn(1)–O(3)	—	—	96.87(18)
O(2)–Zn(1)–O(4)	—	—	78.35(19)
O(2)–Zn(1)–N(1)	—	—	74.31(16)
O(2)–Zn(1)–N(2)	—	—	92.34(19)
O(3)–Zn(1)–O(4)	—	—	166.10(2)
O(3)–Zn(1)–N(1)	—	—	103.38(18)
O(3)–Zn(1)–N(2)	—	—	92.02(18)
O(4)–Zn(1)–N(1)	—	—	88.00(2)
O(3)–Zn(1)–N(2)	—	—	92.02(18)
O(4)–Zn(1)–N(2)	—	—	75.30(2)
N(1)–Zn(1)–N(2)	—	—	160.56(17)

---

Theoretical methods. For the calculations, the X-ray coordinates were used, and only the H-atoms were optimized. These geometries were used to analyze the energetic features at the PBE0 (ref. 60)-D3 (ref. 61)/def2-TZVP⁶² level of theory. The Gaussian-16 program⁶³ was used for the optimizations and energetic calculations. Molecular electrostatic potential (MEP) surfaces were computed at the same level of theory and represented using 0.001 a.u. isovalue of electron density to map the electrostatic potential. The QTAIM⁶⁴ and NCIplot analyses⁶⁵ were performed using the AIMAll program at the same level of theory.⁶⁶ For the NCIplot analysis, the following setting were used: S = 0.5, ρ cut-off = 0.04 a.u., color scale −0.035 ≤ sign(λ₂)ρ ≤ −0.035 a.u. For the evaluation of HB energies using QTAIM analysis, the equations proposed in the literature were used.⁶⁷

Results and discussion

Synthesis

The N, O donor Schiff bases (H₂L¹–H₂L³) were prepared by refluxing the appropriate propanol amines and salicylaldehyde derivatives in 1 : 1 molar ratio in methanol/acetonitrile according to literature methods.^68–77 These Schiff bases were not isolated and purified; the methanol/acetonitrile solution of the Schiff bases were used in situ for the synthesis of Zn(II) complexes, [Zn(HL¹)₂] (1), [Zn(HL²)₂]·2H₂O (2) and [Zn(HL³)₂] (3), by adding zinc(II) chloride and zinc(II) acetate dehydrate with constant stirring for the formation of the complexes 1, 2 and 3 respectively (in a 1 : 1 molar ratio), as shown in Scheme 1. Additionally, in complex 2, the cocrystallized water molecules are assumed to come from the precursor zinc(II) acetate dihydrate salt used during the course of the reaction. The synthetic routes to complexes 1, 2 and 3 are shown in Schemes 1–3, respectively.

Scheme 1 Synthetic route to complex 1.

Scheme 2 Synthetic route to complex 2. Lattice water molecules are omitted for clarity.

Scheme 3 Synthetic route to complex 3.

IR, electronic and fluorescence spectra

In the IR spectra for all the complexes, a distinct band due to azomethine (C=N) stretching vibration appears at 1610–1622 cm⁻¹.^78,79 Bands in the region of 3058–2841 cm⁻¹ may be assigned as C–H stretching vibrations.^80,81 The appearance of a broad band around 3576–3107 cm⁻¹ indicates the presence of O–H stretching vibrations⁸² of the hydroxyl groups of the complexes and the coordinated water molecule in the case of complex 2. The IR spectra of the complexes are shown in Fig. S1–S3 (ESI).†

The electronic spectra of complexes 1–3 were recorded in methanol. There is only one band in the UV-vis spectra of all the complexes. The band at 376 nm (in 1), 375 (in 2) and 371 (in 3) may be attributed as π → π* or n → π* transition.^83–85 There is no band corresponding to d–d electronic transitions, as expected for zinc(II) complexes with d¹⁰ electronic configuration.⁸⁶ The UV spectra of complexes 1, 2 and 3 are shown in Fig. S4–S6 (ESI),† respectively.

Upon excitation at 380 nm in methanol solution, complex 3 shows strong emission of around 461 nm.⁸⁷ This emission may be tentatively attributed to the intra-ligand transitions modified by metal coordination. The fluorescence spectrum of the complex is shown in Fig. S7 (ESI).†

Description of structures

[Zn^II(HL¹)₂] (1). Single-crystal X-ray diffraction analysis reveals that complex 1 consists of a discrete mononuclear unit [Zn(HL¹)₂] in which the zinc atom occupies a two-fold axis. The complex crystallizes in monoclinic space group, C2/c. The perspective view of complex 1 is shown in Fig. 1.

Fig. 1 The perspective view of complex 1. ⁱ = Symmetry transformation = 1 − x, y, 1.5 − z. Only the major component of the pendant disordered –CH₂OH group is shown.

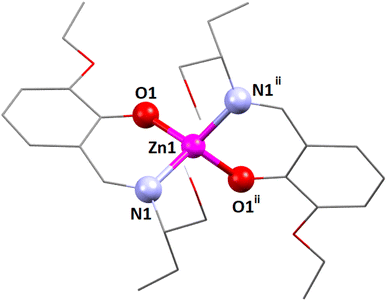
The coordination polyhedron around the zinc(II) centre is best described as a distorted tetrahedral with a ZnN₂O₂ chromophore, furnished by two imine nitrogen atoms [N(1) and its symmetry-related counterpart, N(1)ⁱ] and two phenolate oxygen atoms [O(1) and its symmetry-related counterpart, O(1)ⁱ] of the tridentate Schiff base ligand (ⁱ = symmetry transformation = 1 − x, y, 1.5 − z). Two well-known geometries for a tetra-coordinated metal ion are square planar and tetrahedral. The geometry of the tetra-coordinated zinc(II) centre is distorted tetrahedral, as confirmed by calculating the τ₄ index, which is defined as τ₄ = {360 − (α + β)}/141, where α and β are the two largest ligand–metal–ligand angles in the coordination sphere.⁸⁸ The τ₄ index is equal to 0 for a perfectly square planar geometry. Similarly, the τ₄ index is equal to 1 for a regular tetrahedral geometry. In the present case, the τ₄ index is 0.81, which confirms that the geometry of the zinc(II) centre is distorted tetrahedral. The unsaturated six-membered chelate ring [Zn(1)–N(1)–C(7)–C(6)–C(1)–O(1)] presents an envelope conformation (Fig. S8, ESI†) with puckering parameters q = 0.1575(16) Å; θ = 55.6(7)°; ϕ = 5.3(10)°.^89,90

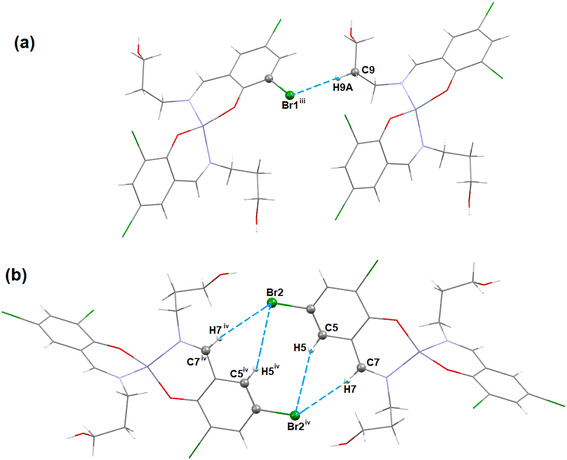
In complex 1, there are Br⋯Br and Br⋯O halogen-bonding interactions involving neighboring molecules. The bromine atom Br(1) of the Schiff base unit forms halogen bonds (HaB) (Fig. 2) with the bromine atom Br(1)ⁱⁱⁱ of the neighboring molecule (symmetry transformation = ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z) to form a supramolecular dimer. On the other hand, the oxygen atom, O(2A), forms a HaB with the bromine atom, Br(2)^iv, of the neighbouring molecule (symmetry transformation = ^iv = 1 − x, −y, 1 − z) to form a supramolecular dimer. The details of HaB interactions are presented in Table 4.

Fig. 2 The perspective views of the HaB interactions of complex 1. Hydrogen atoms are omitted for clarity. Symmetry transformation = ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z, ^iv = 1 − x, −y, 1 − z.

Table 4 Halogen interactions in complex 1

Complex	Br⋯Br/O	Br⋯Br/O (Å)	Symmetry transformation
1	Br(1)⋯Br(1)^iii	3.7487(5)	^iii = 1.5 − x, −1/2 + y, 1.5 − z
	Br(2)^iv⋯O(2A)	3.768(6)	^iv = 1 − x, −y, 1 − z

---

In complex 1, three C–H⋯Br hydrogen-bonding interactions with the neighbouring molecules are present. The hydrogen atom H(9A) attached to the carbon atom C(9) of the Schiff base unit forms a hydrogen bond with the bromine atom Br(1)ⁱⁱⁱ of the neighbouring molecule to form a supramolecular dimer (Fig. 3a) (symmetry transformation = ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z). Another two hydrogen atoms H(5) and H(7), which are attached to the carbon atoms C(5) and C(7), respectively, of the Schiff base, form hydrogen bonds with the bromine atom Br(2)^iv of the neighbouring molecule (symmetry transformation = ^iv = 1 − x, −y, 1 − z) to form a supramolecular dimer (Fig. 3b). The geometrical parameters are presented in Table 5.

Fig. 3 The perspective views of the hydrogen-bonding interactions of complex 1, involving Br(1) (a) and Br(2) (b) atoms. Symmetry transformation = ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z, ^iv = 1 − x, −y, 1 − z.

Table 5 Hydrogen bond distances and angles in complexes 1 and 3

Complex	C–H⋯X	C–H (Å)	H⋯X (Å)	C–H⋯X (Å)	∠C–H⋯X (°)	Symmetry transformation
1 (X= Br)	C(7)–H(7)⋯Br(2)^iv	0.930	3.10	4.026(2)	171.5	^iv = 1 − x, −y, 1 − z
	C(5)–H(5)⋯Br(2)^iv	0.930	3.34	4.215(3)	156.8
	C(9)–H(9A)⋯Br(1)^iii	0.970	3.53	4.135(3)	122.3	^iii = 1.5 − x, −1/2 + y, 1.5 − z
3 (X = O)	O(2)–H(2O)⋯O(1)^iii	0.929	1.81	2.668(6)	151.5

---

[Zn(HL²)₂]·2H₂O (2). The structure of complex 2 is quite similar to that of complex 1, with the metal atom situated on a two-fold axis. Single-crystal X-ray diffraction analysis reveals that complex 2 consists of a discrete, centrosymmetric, mononuclear unit [Zn(HL¹)₂] and two non-coordinated water molecules. The complex crystallizes in orthorhombic space group Aba2. The perspective view of complex 2 is shown in Fig. 4.

Fig. 4 The perspective view of complex 2. Only the relevant hydrogen atoms are shown, for clarity. Lattice solvent molecules are omitted for clarity. Symmetry transformation ⁱⁱ = 1 − x, 1 − y, z. Only the major component of the pendant disordered –OEt group is shown.

The zinc(II) center's coordination polyhedron can be best understood as a deformed tetrahedral with a ZnN₂O₂ chromophore, comprised by two imine nitrogen atoms [N(1) and its symmetry-related counterpart, N(1)ⁱⁱ] and two phenolate oxygen atoms [O(1) and its symmetry-related counterpart, O(1)ⁱⁱ] of the tridentate Schiff base ligand (ⁱⁱ = symmetry transformation = 1 − x, 1 − y, z). The zinc(II) center's deformed tetrahedral geometry is confirmed by the τ₄ index of 0.83. The unsaturated six-membered chelate ring [Zn(1)–N(1)–C(9)–C(7)–C(8)–O(1)] presents an envelope conformation (Fig. S9, ESI†) with puckering parameters q = 0.182(5) Å; θ = 111(2)°; ϕ = 179(2)°.^89,90

[Zn(HL³)₂] (3). Based on the determination of the X-ray crystal structure, this complex crystallizes in the monoclinic space group P21/n. The perspective view of complex 3, along with the selective atom-numbering scheme, is shown in Fig. 5. The zinc(II) centre is hexa-coordinated, being bonded with two imine nitrogen atoms, [N(1) and N(2)], one phenoxo oxygen atom, O(3), and one hydroxyl oxygen atom, O(4), of the Schiff base ligand (HL³)⁻ to form an equatorial plane, and the axial position is occupied by one phenoxo along with one hydroxyl oxygen atom [O(1) and O(2)] from the Schiff base unit (HL³)⁻. The distance between the phenoxo oxygen atom and the zinc(II) center varies from 1.955(5) to 2.054(4) Å, and the distance between the hydroxyl oxygen atom and zinc(II) center varies from 2.288(4) to 2.355(6) Å. The saturated five-membered chelate ring [Zn(1)–N(1)–C(8)–C(11)–O(2)] presents an envelope conformation (Fig. S10, ESI†) with puckering parameters q = 0.407(7) Å; ϕ = 110.2(7)°.^89,90 The saturated six-membered chelate ring [Zn(1)–N(1)–C(19)–C(22)–O(4)] presents an envelope conformation with puckering parameters q = 0.418(7) Å; ϕ = 243.7(8)°.^89,90 The unsaturated six-membered chelate ring [Zn(1)–N(1)–C(7)–C(6)–C(1)–O(1)] presents a screw-boat conformation (Fig. S11, ESI†) with puckering parameters q = 0.186(4) Å; θ = 115.4(15)°; ϕ = 194.8(18)°.^89,90 The unsaturated six-membered chelate ring [Zn(1)–N(2)–C(18)–C(17)–C(12)–O(3)] presents a screw-boat conformation with puckering parameters q = 0.126(5) Å; θ = 70(2)°; ϕ = 40(2)°.^89,90

Fig. 5 The perspective view of complex 3. Only the relevant hydrogen atoms are shown, for clarity.

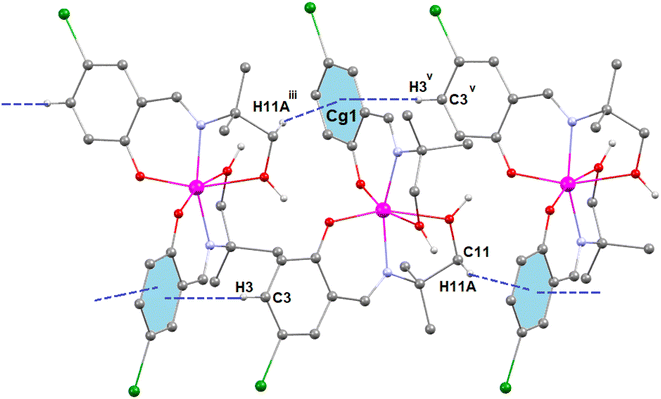
In complex 3, there is one O–H⋯O hydrogen-bonding interaction present with the symmetry-related neighbouring molecule. The hydrogen atom H(2O) attached to the oxygen atom O(2) of the Schiff base ligand (HL³)⁻ forms a hydrogen bond with the oxygen atom O(1)ⁱⁱⁱ of the symmetry-related neighbouring molecule, thus forming a one-dimensional supramolecular chain (Fig. 6) of complex 1 (symmetry transformation ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z). The hydrogen bond distance and angle are presented in Table 5.

Fig. 6 Perspective view of the hydrogen-bonding interactions of complex 3. Only the relevant hydrogen atoms are shown, for clarity. Symmetry transformation ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z.

In complex 3, two C–H⋯π interactions are present with the symmetry-related neighbouring molecules. The aromatic ring R(1), containing carbon atoms C(12)–C(13)–C(14)–C(15)–C(16)–C(17), is involved in two C–H⋯π interactions with two hydrogen atoms, H(11A)ⁱⁱⁱ and H(3)^v, which are attached to carbon atoms C(11)ⁱⁱⁱ and C(3)^v, respectively, of the Schiff base ligand (HL³)⁻ of the symmetry-related neighbouring molecules to form a supramolecular chain (Fig. 7). Symmetry transformation ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z and ^v = 1.5 − x, −1/2 + y, 1.5 − z. The geometric parameters of C–H⋯π interactions are presented in Table 6.

Fig. 7 Perspective view of the C–H⋯π interactions of complex 3. Only the relevant hydrogen atoms are shown, for clarity. Symmetry transformation = ⁱⁱⁱ = 1.5 − x, −1/2 + y, 1.5 − z; v = 1.5 − x, 1/2 + y, 1.5 − z.

Table 6 Geometric parameters of the C–H⋯π interactions in complex 3

Complex	C–H⋯π	H⋯π (Å)	C–H⋯π (Å)	∠C–H⋯Cg (°)	Symmetry transformation
3	C(11)^iii–H(11A)^iii⋯Cg(1)	2.66	3.56	153.6	^iii = 1.5 − x, −1/2 + y, 1.5 − z
	C(3)^v–H(3)^v⋯Cg(1)	3.07	3.49	109.8	^v = 1.5 − x, −1/2 + y, 1.5 − z

---

Hirshfeld surface analysis

The Hirshfeld surfaces of the complexes were mapped over d_norm, and the curvedness and shape index (range −0.1 Å to 1.5 Å) are shown in Fig. S12–S14 (ESI).† The surface is shown as transparent to allow visualization of the molecular moiety around which they are calculated. The dominant interactions of the complexes are Br⋯H/H⋯Br, O⋯H/H⋯O and C⋯H/H⋯C, which can be seen in the Hirshfeld surfaces as red spots on the d_norm surface in Fig. S12–S14 (ESI).† Other visible spots in the Hirshfeld surfaces correspond to H⋯H contacts. The small extent of area and light colour on the surface indicate weaker and longer contacts other than hydrogen bonds. Br⋯H/H⋯Br, O⋯H/H⋯O and C⋯H/H⋯C interactions appear as distinct spikes in the 2D fingerprint plots (Fig. 8–10). Complementary regions are visible in the fingerprint plots where one molecule acts as a donor (d_e > d_i) and the other as an acceptor (d_e < d_i). The fingerprint plots can be decomposed to highlight contributions from different interaction types, which overlap in the full fingerprint.⁹¹

Fig. 8 Fingerprint plot: different contacts contributed to the total Hirshfeld surface area of complex 1.

Fig. 9 Fingerprint plot: different contacts contributed to the total Hirshfeld surface area of complex 2.

Fig. 10 Fingerprint plot: different contacts contributed to the total Hirshfeld surface area of complex 3.

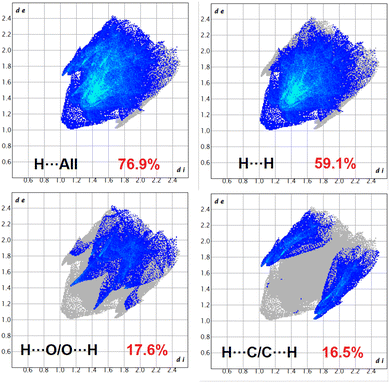
In complex 1, the O⋯H/H⋯O interactions comprise 16.7% of the Hirshfeld surfaces of the complex. This O⋯H/H⋯O interaction appears as two distinct spikes in the 2D fingerprint plot. The O⋯H interaction is represented by the lower spike (d_i = 1.1 and d_e = 0.75 Å), and the H⋯O interaction is represented by the upper spike (d_i = 0.75 and d_e = 1.1 Å), which can be viewed as bright-red spots on the d_norm surface. Similarly, the Br⋯H/H⋯Br and C⋯H/H⋯C interactions comprise 30.1% and 9.7% of the Hirshfeld surfaces of the complex. The Br⋯H interaction is represented by the lower spike (d_i = 1.8 and d_e = 1.1 Å), and the H⋯Br interaction is represented by the upper spike (d_i = 1.1 and d_e = 1.8 Å), which can be viewed as bright-red spots on the d_norm surface. The C⋯H interaction is represented by the lower spike (d_i = 2.2 and d_e = 1.5 Å), and the H⋯C interaction is represented by the upper spike (d_i = 1.5 and d_e = 2.2 Å), which can be viewed as bright-red spots on the d_norm surface. The Br⋯Br interactions comprise 3.6% and Br⋯O/O⋯Br interactions comprise 1.3% of the Hirshfeld surfaces of complex 1.

In complex 2, the O⋯H/H⋯O interaction comprises 17.6% of the Hirshfeld surfaces of the complex. This O⋯H/H⋯O interaction appears as two distinct spikes in the 2D fingerprint plot. The O⋯H interaction is represented by the lower spike (d_i = 1.45 and d_e = 1.15 Å), and the H⋯O interaction is represented by the upper spike (d_i = 1.15 and d_e = 1.45 Å), which can be viewed as bright-red spots on the d_norm surface. Similarly, the C⋯H/H⋯C interactions comprise 16.5% of the Hirshfeld surfaces of the complex. The C⋯H interaction is represented by the lower spike (d_i = 1.7 and d_e = 1.0 Å), and the H⋯C interaction is represented by the upper spike (d_i = 1.0 and d_e = 1.7 Å), which can be viewed as bright-red spots on the d_norm surface.

In complex 3, the O⋯H/H⋯O interactions comprise 6.2% of the Hirshfeld surfaces of the complex. This O⋯H/H⋯O interaction appears as two distinct spikes in the 2D fingerprint plots. The O⋯H interaction is represented by lower spike (d_i = 1.15 and d_e = 0.7 Å), and the H⋯O interaction is represented by upper spike (d_i = 0.7 and d_e = 1.15 Å), which can be viewed as bright-red spots on the d_norm surface. Similarly, the Br⋯H/H⋯Br and C⋯H/H⋯C interactions comprise 24.4% and 20.8% of the Hirshfeld surfaces of the complex. The Br⋯H interaction is represented by the lower spike (d_i = 1.85 and d_e = 1.1 Å), and the H⋯Br interaction is represented by the upper spike (d_i = 1.1 and d_e = 1.85 Å), which can be viewed as bright-red spots on the d_norm surface. The C⋯H interaction is represented by the lower spike (d_i = 1.6 and d_e = 1.1 Å), and the H⋯C interaction is represented by the upper spike (d_i = 1.1 and d_e = 1.6 Å), which can be viewed as bright-red spots on the d_norm surface.

Theoretical study

In the solid-state structure of complex 1, two distinct types of halogen-bonding interactions are observed, as depicted in Fig. 11. The first interaction involves C–Br⋯Br–C contacts, where the distances at 3.748(1) Å fall slightly longer than Bondi's van der Waals radii sum (3.66 Å) yet remain shorter than Batsanov's van der Waals radii sum (3.80 Å). The C–Br⋯Br angle, measured at 162.3(3)°, aligns with the σ-hole interaction's expected characteristics. These contacts connect the 1D columns that further organize into 2D supramolecular assemblies by means of Br⋯Br interactions, as illustrated in Fig. 11a. Concurrently, the other Br atom engages in C–Br⋯O contacts (3.321(2) Å), driving the extension of the monomer into a 1D supramolecular polymer, as shown in Fig. 11b. Here, the C–Br⋯O angle is 151.0(3)°, smaller than that of C–Br⋯Br, raising questions about whether it is indeed the positive part of the Br atom interacting with the electron-rich O atom. Both types of interactions are thoroughly examined in this section.

Fig. 11 Partial views of the X-ray structures of complex 1 (a and b), 2 (c) and 3 (d). Distances in Å. H-atoms omitted for clarity (in complex 2, the water H atoms could not be located).

Complex 2, lacking halogen atoms, demonstrates the significant impact of co-crystallization with two water molecules on the packing. Specifically, these water molecules, in synergy with the alcohol groups and the ethoxy–phenoxy O atoms of the Schiff-base complex, form a complex H-bonding network, although the hydrogen atoms could not be located because of disorder. However, it is clear from Fig. 11 that the hydrogen atoms form a central ring of hydrogen bonds that could run either clockwise or anticlockwise. This network is pivotal in the propagation of complex 2 into a 1D supramolecular polymer. The characteristics and significance of the H-bonding network are detailed through QTAIM and NCIplot analyses.

Complex 3, despite having a Br atom, does not engage in halogen bonding. Instead, it forms infinite 1D chains propagated by H-bonding interactions involving the phenoxido atoms as acceptor and the hydroxyl groups as donor (see Fig. 11d). The characteristics and energetic significance of such 1D chain have also been analyzed through QTAIM and NCIPlot analyses.

First, we calculated the molecular electrostatic potential (MEP) surfaces for complexes 1–3, presented in Fig. 12. For complex 1, the MEP's maximum value is found at the hydrogen atom of the hydroxyl groups (+50 kcal mol⁻¹), while its minimum is at the phenoxy oxygen atoms (−33 kcal mol⁻¹). In Fig. 12a, the MEP surface surrounding the bromine atoms, depicted using a reduced scale (±10 kcal mol⁻¹), reveals the anisotropy around the bromine atom. This illustrates a σ-hole along the extension of the C–Br bond (+9.4 kcal mol⁻¹) and a surrounding area of negative potential (−10.0 kcal mol⁻¹). Notably, the σ-hole cone angle measures 35°, indicating that the C–Br⋯O interaction observed in complex 1 (Fig. 11b) can be classified as a σ-hole interaction. However, this interaction is anticipated to be relatively weak because it occurs in a region near the bromine atom where the MEP is approximately zero (electroneutral). In complex 2, the MEP's highest value is at the hydroxyl group (+55 kcal mol⁻¹), with the lowest in the area influenced by both ethoxy and phenoxy oxygen atoms. Additionally, the oxygen atom of the hydroxyl group, serving as an intramolecular hydrogen bond donor, also displays a significantly negative MEP value (−39 kcal mol⁻¹), highlighting its potential role as H-bond acceptor. Two different views of the MEP surface of complex 3 are presented in Fig. 12c. The MEP maximum is located at the hydroxyl group (+59 kcal mol⁻¹), highlighting its potential role as an H-bond donor. This value is significantly more positive than that of complex 2, due to the coordination of the hydroxyl's oxygen atom to the Zn metal center, which increases the acidity of the hydroxyl proton. The minimum is located at the coordinated phenoxide oxygen atoms (−47 kcal mol⁻¹), indicating their potential role as H-bond acceptors. The MEP is also negative at the belt of the bromine atom (−20 kcal mol⁻¹) and over the aromatic ring (−17 kcal mol⁻¹). Additionally, the MEP is positive at the hydrogen atoms of the alkyl chain connecting the imino nitrogen atoms of the Schiff-base ligand.

Fig. 12 MEP surfaces of complexes 1 (a), 2 (b) and 3 (c) using the 0.001 a.u. isovalue. The energies at selected points are given in kcal mol⁻¹.

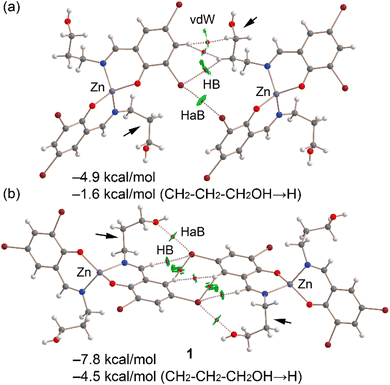
Fig. 13a displays the QTAIM/NCIplot analysis for the Br⋯Br dimer of complex 1, extracted from the assembly depicted in Fig. 11a. The halogen-bonding interaction is confirmed by QTAIM analysis through a bond critical point (displayed as a fuchsia sphere) and a dashed bond path connecting the two Br atoms. The QTAIM analysis also uncovered a CH⋯Br interaction involving an aliphatic CH bond and several hydrophobic C_sp²–H⋯H–C_sp³ interactions. Small, green reduced density gradient (RDG) isosurfaces, aligned with the bond critical points, further elucidate the halogen-bonding (HaB), hydrogen-bonding (HB), and hydrophobic interactions, demonstrating their attractive nature (λ₂ < 0). The interaction energy for this dimer is modest, at −4.9 kcal mol⁻¹. To discern the contribution of halogen bonding, we calculated a mutated dimer where the propanol arm is substituted with a hydrogen atom, isolating the HaB interaction. This modification reduces the interaction energy to −1.6 kcal mol⁻¹, indicating the HaB's contribution. This small interaction is consistent with the long Br⋯Br experimental distance and the small MEP value at the σ-hole.

Fig. 13 Combined QTAIM and NCIplot analyses (see Theoretical methods for settings) of the Br⋯Br (a) and Br⋯O (b) dimers of complex 1. The dimerization energies of the dimers and the mutated dimers are also indicated. Only intermolecular interactions are indicated. The propanol arms replaced by H-atoms in the mutated dimers are marked with small arrows.

Fig. 13b presents the combined QTAIM/NCIplot analysis of the self-assembled Br⋯O dimer. Here, bond critical points (BCPs) and bond paths link the Br and O atoms, highlighting the Br⋯O interaction. Additional CH⋯Br and C_sp²H⋯HC_sp² interactions are identified, characterized by their respective BCPs, bond paths, and green RDG isosurfaces. The dimerization energy is −7.8 kcal mol⁻¹, attributed to all identified interactions. To assess the HaBs' contribution specifically, a mutated dimer was analyzed, in which the propanol arms (indicated by small arrows) were replaced by hydrogen atoms, thus eliminating the HaBs. This alteration leads to an interaction energy of −4.5 kcal mol⁻¹. The difference in dimerization energies (−3.3 kcal mol⁻¹) is ascribed to the energy of the HaBs, with each Br⋯O contact contributing −1.65 kcal mol⁻¹.

The hydrogen-bonding network of complex 2 was meticulously examined. The positions of the hydrogen atoms were determined through optimizations using the PBE0-D3/def2-SVP level of theory, while the coordinates of the heavier atoms were kept fixed. These positions of necessity break the two-fold symmetry of the crystal structure and indicate that the crystal structure must be disordered to accommodate two possible hydrogen bond patterns, clockwise as shown in Fig. 14, or anticlockwise. This disorder may well account for the hydrogen atoms not being located in the crystal structure. Subsequent single-point calculations were carried out at the PBE0-D3/def2-TZVP level. The energy associated with each hydrogen bond was approximated by the potential energy density (V_g) at the BCP identifying each H-bond. These findings, illustrated in Fig. 14, reveal an intermolecular OH⋯O hydrogen bond between the central water molecules and a sequential orientation of H-bonds, forming a R₄⁴(8) supramolecular ring. This includes the intramolecular OH⋯O hydrogen bond between the hydroxyl groups on the pendant arms. This configuration does not align with the Aba2 point group observed for this complex, suggesting a potential disorder in the hydrogen atoms' positioning, allowing for both clockwise and anticlockwise orientations of the R₄⁴(8) supramolecular ring. Furthermore, the water molecules form two bifurcated hydrogen bonds with the oxygen atoms of the ethoxy and phenoxy groups. Consequently, a total of eight strong hydrogen bonds are established, contributing to a significant stabilization energy of −44.2 kcal mol⁻¹, which accounts solely for the intermolecular hydrogen bonds. This substantial interaction energy correlates with the dark-blue RDG isosurfaces characterizing the R₄⁴(8) supramolecular ring, with HB energies ranging from −8.3 to −8.9 kcal mol⁻¹. The bifurcated hydrogen bonds, though weaker, exhibit energies between −3.5 and −6.3 kcal mol⁻¹. This analysis confirms the importance of the H-bonding network dictating the solid-state architecture of complex 2.

Fig. 14 Combined QTAIM and NCIplot analyses (see Theoretical methods for settings) of the H-bonding network in complex 2. The energies of the HBs are indicated.

Finally, a dimer extracted from the infinite 1D chain presented in Fig. 11c was analyzed. The QTAIM and NCIplot analyses support the strong nature of the OH⋯O bond (see Fig. 15), as also anticipated by the MEP surface analysis. The RDG isosurface characterizing the H-bond is strongly blue, and the calculated energy using the V_g predictor is −10.4 kcal mol⁻¹, stronger than that determined for the H-bonding network of complex 3. The total dimerization energy is −15.4 kcal mol⁻¹, primarily due to the OH⋯O H-bond. The QTAIM analysis also reveals the existence of an ancillary CH⋯O H-bond that accounts for −0.9 kcal mol⁻¹. Interestingly, the QTAIM/NCIplot analysis also reveals the presence of a CH⋯π interaction characterized by a bond critical point (BCP) and bond path linking the aliphatic hydrogen atom to one carbon atom of the ring. The formation of this contact is consistent with the MEP surface analysis (Fig. 12c), which showed negative MEP over the π-system and positive MEP at the aliphatic hydrogen atoms. The π-nature of the interaction is clearly revealed by the NCIplot analysis, which shows a green RDG isosurface embracing most of the aromatic ring. The contribution of the CH⋯π interactions can be roughly estimated by the difference between the total contribution of the H-bonds (−11.3 kcal mol⁻¹) and the dimerization energy (−15.4 kcal mol⁻¹), resulting in −4.1 kcal mol⁻¹.

Fig. 15 Combined QTAIM and NCIplot analyses (see Theoretical methods for settings) of a selected dimer of complex 3. The energies of the HBs are indicated in red.

Conclusions

Three new Zn(II) complexes were synthesized and X-ray characterized. DFT calculations evidence that complex 1 exhibits two types of halogen-bonding interactions, characterized by C–Br⋯Br–C and C–Br⋯O contacts. The first interaction involves C–Br⋯Br–C contacts, where the distances fall slightly longer than the sum of Bondi's van der Waals radii, yet remain shorter than those using Batsanov's values. The C–Br⋯Br angle aligns with the σ-hole interaction's expected characteristics. These contacts connect the 1D columns that further organize into 2D supramolecular assemblies by means of Br⋯Br interactions. Concurrently, the other Br atom engages in C–Br⋯O contacts, driving the extension of the monomer into a 1D supramolecular polymer. Here, the C–Br⋯O angle is smaller than that of C–Br⋯Br, raising questions about whether it is indeed the positive part of the Br-atom interacting with the electron-rich O-atom. These interactions interconnect the 1D columns, forming 2D supramolecular assemblies. Despite the relatively weak nature of these interactions, as indicated by modest interaction energies, they are significant in guiding the directional assembly of the molecules into organized structures. Complex 2, lacking halogen atoms, demonstrates the significant impact of co-crystallization with two water molecules involved in the packing. Specifically, these water molecules, in synergy with the alcohol groups and the ethoxy–phenoxy O-atoms of the Schiff-base complex, form a complex H-bonding network. This network is pivotal in the propagation of complex 2 into a 1D supramolecular polymer. The complex hydrogen-bonding network is crucial for its structural integrity. The optimization and QTAIM analysis elucidate the strength and orientation of these H-bonds, forming an interesting R₄⁴(8) supramolecular ring with a high degree of stabilization and explaining the co-crystallization of 2 with two water molecules. It is proposed that complex 2 presents flexibility in the hydrogen-bonding network, allowing for different orientations (clockwise and anticlockwise) of the R₄⁴(8) to align with its point group symmetry. Complex 3, despite having a Br atom, does not engage in halogen bonding. Instead, it forms infinite 1D chains propagated by H-bonding interactions involving the phenoxido atoms as acceptor and hydroxyl groups as donor. The characteristics and energetic significance of such 1D chain were also analyzed through QTAIM and NCIPlot analyses. The analyses reveal the strong nature of the OH⋯O bond, with an energy of −10.4 kcal mol⁻¹, and the presence of ancillary CH⋯O and CH⋯π interactions, contributing to the overall stability of the dimer and playing a crucial role in its propagation into an infinite 1D chain.

The implications of the results are not restricted to the development of the single crystals of different zinc complexes only. The results may point to the wider importance of understanding halogen and hydrogen bonding in the context of numerous physical and chemical phenomena in catalysis, materials science, ion transport and recognition etc. We trust that these findings will captivate not only the crystal engineering community but also researchers in supramolecular chemistry and theoreticians.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for compounds 1–3 have been deposited at the CCDC with CCDC numbers 2346042, 2346043 and 2346044.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. Gishan thanks UGC, India, for awarding a Junior Research Fellowship (JRF). P. Middya thanks UGC, India, for awarding a Senior Research Fellowship (NFSC-SRF). AF thanks MICIU/AEI of Spain (project PID2020-115637GB-I00 FEDER funds) for financial support.

References

1. L. Ni, J. Wang, C. Liu, J. Fan, Y. Sun, Z. Zhou and G. Diao, Inorg. Chem. Front., 2016, 3, 959–968.
2. Z.-F. Wang, Q.-X. Nong, H.-L. Yu, Q.-P. Qin, F.-H. Pan, M.-X. Tan, H. Liangd and S.-H. Zhang, Dalton Trans., 2022, 51, 5024–5033.
3. M. Porchia, M. Pellei, F. D. Bello and C. Santini, Molecules, 2020, 25, 5814.
4. E. A. Ermakova, J. A. Golubeva, K. S. Smirnova, L. S. Klyushova, I. V. Eltsov, A. A. Zubenko, L. N. Fetisov, A. E. Svyatogorova and E. V. Lider, Polyhedron, 2023, 230, 116213.
5. H. R. Zhang, Y. C. Liu, Z. F. Chen, J. Guo, Y. X. Peng and H. Liang, Russ. J. Coord. Chem., 2018, 44, 322.
6. R. Brahma and J. B. Baruah, ACS Omega, 2020, 5, 3774–3785.
7. P. Middya, M. Karmakar, R. M. Gomila, M. G. B. Drew, A. Frontera and S. Chattopadhyay, New J. Chem., 2023, 47, 9346–9363.
8. B. Liu, L.-Y. Pang, L. Hou, Y.-Y. Wang, Y. Zhang and Q.-Z. Shi, CrystEngComm, 2012, 14, 6246–6251.
9. A. Terenzi, A. Lauria, A. M. Almerico and G. Barone, Dalton Trans., 2015, 44, 3527–3535.
10. C. A. Barboza, J. C. Germino, A. M. Santana, F. J. Quites, P. A. M. Vazquez and T. D. Z. Atvars, J. Phys. Chem. C, 2015, 119, 6152–6163.
11. J. A. Kübler, B. Pfund and O. S. Wenger, JACS Au, 2022, 2, 2367–2380.
12. M. A. Fuchs, C. Altesleben, S. C. Staudt, O. Walter, T. A. Zevaco and E. Dinjus, Catal. Sci. Technol., 2014, 4, 1658–1673.
13. S. Bhunia, R. A. Molla, V. Kumari, S. M. Islam and A. Bhaumik, Chem. Commun., 2015, 51, 15732–15735.
14. J.-J. Chen, Y.-C. Xu, Z.-L. Gan, X. Peng and X.-Y. Yi, Eur. J. Inorg. Chem., 2019, 1733–1739.
15. Z. Mahmood, N. Rehmat, S. Ji, J. Zhao, S. Sun, M. D. Donato, M. Li, M. Teddei and Y. Huo, Chem.–Eur. J., 2020, 26, 14912–14918.
16. T. Basak, A. Bhattacharyya, K. Harms and S. Chattopadhyay, Polyhedron, 2019, 157, 449–457.
17. L. M. Berreau, A. Saha and A. M. Arif, Dalton Trans., 2006, 183–192.
18. M. Shyamal, A. Panja and A. Saha, Polyhedron, 2014, 69, 141–148.
19. U. C. Saha, B. Chattopadhyay, K. Dhara, S. K. Mandal, S. Sarkar, A. R. Khuda-Bukhsh, M. Mukherjee, M. Helliwell and P. Chattopadhyay, Inorg. Chem., 2011, 50, 1213–1219.
20. B. Mondal, B. Sen, E. Zangrando and P. Chattopadhyay, J. Chem. Sci., 2015, 127, 1747–1755.
21. T. Basak, M. G. B. Drew and S. Chattopadhyay, Inorg. Chem. Commun., 2018, 98, 92–98.
22. M. Karmakar and S. Chattopadhyay, Polyhedron, 2020, 184, 114527.
23. P. Middya, D. Medda and S. Chattopadhyay, Inorg. Chim. Acta, 2023, 554, 121540.
24. M. Karmakar, R. M. Gomila, A. Frontera and S. Chattopadhyay, New J. Chem., 2022, 46, 1845–1856.
25. S. Banerjee and A. Saha, J. Coord. Chem., 2016, 69, 3092–3106.
26. S. Hazra, L. K. Das, S. Giri, M. G. B. Drew and A. Ghosh, Inorg. Chim. Acta, 2018, 471, 691–697.
27. C. Pathak, S. K. Gupta, M. K. Gangwar, A. P. Prakasham and P. Ghosh, ACS Omega, 2017, 8, 4737–4750.
28. G. Parkin, Chem. Rev., 2004, 104, 699–768.
29. S. Albedyhl, M. T. Averbuch-Pouchot, C. Belle, B. Krebs, J. L. Pierre, E. Saint-Aman and S. Torelli, Eur. J. Inorg. Chem., 2001, 1457–1464.
30. N. Dutta, S. Haldar, G. Vijaykumar, S. Paul, A. P. Chattopadhyay, L. Carrella and M. Bera, Inorg. Chem., 2018, 57, 10802–10820.
31. C. Pathak, M. K. Gangwar and P. Ghosh, Polyhedron, 2018, 145, 88–100.
32. R. Sanyal, X. Zhang, P. Kundu, T. Chattopadhyay, C. Zhao, F. A. Mautner and D. Das, Inorg. Chem., 2015, 54, 2315–2324.
33. R. Sanyal, A. Guha, T. Ghosh, T. K. Mondal, E. Zangrando and D. Das, Inorg. Chem., 2014, 53, 85–96.
34. A. Zianna, E. Vradi, A. G. Hatzidimitriou, S. Kalogiannisb and G. Psomas, Dalton Trans., 2022, 51, 17629–17641.
35. S. Konar, A. Dey, S. R. Choudhury, K. Das, S. Chatterjee, P. P. Ray, J. Ortega-Castro, A. Frontera and S. Mukhopadhyay, J. Phys. Chem. C, 2018, 122, 8724–8734.
36. P. K. Mudi, L. Singla, A. Chamuah, S. Bhattacharya, A. R. Choudhury and B. Biswas, CrystEngComm, 2022, 24, 2418–2428.
37. P. D. Akhtaruzzaman, S. Khan, S. Maity, S. Naaz, S. Islam, P. Ghosh, P. P. Ray and M. H. Mir, New J. Chem., 2019, 43, 16071–16077.
38. M. Karmakar, A. Frontera and S. Chattopadhyay, CrystEngComm, 2020, 22, 6876–6885.
39. P. Middya, M. Karmakar, A. Frontera and S. Chattopadhyay, Inorg. Chim. Acta, 2023, 553, 121516.
40. M. Bazargan, M. Mirzaei, A. S. Hamid, Z. H. Kafshdar, H. Ziaekhodadadian, E. Momenzadeh, J. T. Mague, D. M. Gil, R. M. Gomila and A. Frontera, CrystEngComm, 2022, 24, 6677–6687.
41. I. Mondal, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 3391–3397.
42. T. Basak, A. Frontera and S. Chattopadhyay, RSC Adv., 2021, 11, 30148–30155.
43. A. G. Tskhovrebov, A. S. Novikov, O. V. Odintsova, V. N. Mikhaylov, V. N. Sorokoumov, T. V. Serebryanskaya and G. L. Starova, J. Organomet. Chem., 2019, 886, 71–75.
44. D. S. Bolotin, M. V. Il’in, A. S. Novikov, N. A. Bokach, V. V. Suslonov and V. Y. Kukushkin, New J. Chem., 2017, 41, 1940–1952.
45. M. Bulatova, A. A. Melekhova, A. S. Novikov, D. M. Ivanov and N. A. Bokach, Z. Kristallogr.–Cryst. Mater., 2018, 233(6), 371–377.
46. S. V. Baykov, S. I. Filimonov, A. V. Rozhkov, A. S. Novikov, I. V. Ananyev, D. M. Ivanov and V. Y. Kukushkin, Cryst. Growth Des., 2020, 20, 995–1008.
47. A. V. Rozhkov, I. V. Ananyev, D. M. Ivanov, A. S. Novikov, N. A. Bokach and V. Y. Kukushkin, CrystEngComm, 2020, 22, 554–563.
48. S. Thakur, R. M. Gomila, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 5087–5096.
49. L. E. Zelenkov, A. A. Eliseeva, S. V. Baykov, V. V. Suslonov, B. Galmés, A. Frontera, V. Y. Kukushkin, D. M. Ivanov and N. A. Bokach, Inorg. Chem. Front., 2021, 8, 2505–2517.
50. M. N. Ahmed, M. Madni, S. Anjum, S. Andleeb, S. Hameed, A. M. Khan, M. Ashfaq, M. Nawaz Tahir, D. M. Gil and A. Frontera, CrystEngComm, 2021, 23, 3276–3287.
51. A. Frontera, Crystals, 2020, 10, 721.
52. M. Karmakar, W. Sk, R. M. Gomila, M. G. B. Drew, A. Frontera and S. Chattopadhyay, RSC Adv., 2021, 13, 21211–21224.
53. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Primagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
54. S. Burguera, A. K. Sahu, A. Frontera, H. S. Biswal and A. Bauzá, Inorg. Chem., 2023, 62, 18524–18532.
55. A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321.
56. Q. Zhang, K. Luo, W. Zhou, A. Li and Q. Hi, J. Am. Chem. Soc., 2024, 146, 3635–3639.
57. D. Manna and G. Mugesh, J. Am. Chem. Soc., 2012, 134, 4269–4279.
58. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
59. G. M. Sheldrick, SADABS, V2014/5, Software for Empirical Absorption Correction, University of Göttingen, Institute fur Anorganische Chemieder Universitat, Gottingen, Germany.
60. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
61. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
62. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
64. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
65. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
66. T. A. Keith, TK Gristmill Software, AIMAll (Version 19.10.12), Overland Park KS, USA, 2019, https://aim.tkgristmill.com/.
67. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
68. Z.-L. You, H.-L. Zhu and W.-S. Liu, Z. Anorg. Allg. Chem., 2004, 630, 1617.
69. S. Ponsico, H. Gulyas, M. Martnez-Belmonte, E. C. Escudero-Adan, Z. Freixa and P. W. N. M. van Leeuwen, Dalton Trans., 2011, 40, 10686.
70. S. Majumder, L. Mandal and S. Mohanta, Inorg. Chem., 2012, 51, 8739.
71. B. Miroslaw, B. Cristovao and Z. Hnatejko, Molecules, 2018, 23, 1761.
72. K. Zhang, H. Qian, L. Zhang and W. Huang, Inorg. Chem., 2015, 54, 675.
73. M. Azam and S. I. Al-Resayes, J. Mol. Struct., 2016, 1107, 77.
74. D. Majumdar, M. S. S. Babu, S. Das, J. K. Biswas, M. Mondal and S. Hazra, J. Mol. Struct., 2017, 1138, 161.
75. G. Consiglio, S. Failla, P. Finocchiaro, I. P. Oliveri, R. Purrello and S. D. Bella, Inorg. Chem., 2010, 49, 5134–5142.
76. T. Basak, A. Bhattacharyya, M. Das, K. Harms, A. Bauza, A. Frontera and S. Chattopadhyay, ChemistrySelect, 2017, 2, 6286–6295.
77. G. Consiglio, I. P. Oliveri, S. Failla and S. D. Bella, Inorg. Chem., 2016, 55, 10320–10328.
78. T. Basak, D. Das, P. P. Ray, S. Banerjee and S. Chattopadhyay, CrystEngComm, 2020, 22, 5170–5181.
79. T. Basak, R. M. Gomila, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 2703–2710.
80. M. Karmakar, T. Basak and S. Chattopadhyay, New J. Chem., 2019, 43, 4432–4443.
81. I. Mondal, T. Basak, S. Banerjee and S. Chattopadhyay, CrystEngComm, 2020, 22, 3005–3019.
82. A. Banerjee, A. Frontera and S. Chattopadhyay, Dalton Trans., 2019, 48, 11433–11447.
83. T. Basak, A. Bhattacharyya, M. Das, K. Harms, A. Bauza, A. Frontera and S. Chattopadhyay, ChemistrySelect, 2017, 2, 6286–6295.
84. A. Hazari, L. K. Das, R. M. Kadam, A. Bauzá, A. Frontera and A. Ghosh, Dalton Trans., 2015, 44, 3862–3876.
85. K. Visvaganesan, R. Mayilmurugan, E. Suresh and M. Palaniandavar, Inorg. Chem., 2007, 46, 10294–10306.
86. C. W. Lange, B. J. Conklin and C. G. Plerpont, Inorg. Chem., 1994, 33, 1276–1283.
87. P. Middya, R. M. Gomila, A. Frontera and S. Chattopadhyay, Inorg. Chem. Commun., 2023, 157, 111436.
88. L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964.
89. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358.
90. D. Cremer, Acta Crystallogr., 1984, 40, 498–500.
91. M. A. Spackman and P. G. Byrom, Chem. Phys. Lett., 1997, 267, 215.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2346042–2346044. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ra06217e

---