Open Access Article
Open Access ArticleEffect of rare-earth ytterbium doping on the microwave absorption performance of nickel–cobalt ferrite
Guangming Wanga,
Zhijun Ma *ab,
Yunsheng Zhenga,
Liang Chenga,
Huiling Xinga and
Zhuomin Lia
*ab,
Yunsheng Zhenga,
Liang Chenga,
Huiling Xinga and
Zhuomin Lia
aCollege of Mining, Liaoning Technical University, Fuxin 123000, China. E-mail: zhijunma0930@126.com
bCollege of Materials Science & Engineering, Liaoning Technical University, Fuxin 12300, China
First published on 3rd December 2024
Abstract
In order to investigate the effect of different doping proportions of Yb3+ on the structure and microwave absorption properties of ferrite, a sol–gel method was proposed to prepare spinel Ni0.5Co0.5YbxFe2−xO4. The crystal shape, particle size, elements, microstructure, electromagnetic loss and microwave absorption properties of Ni0.5Co0.5YbxFe2−xO4 were characterized by X-ray diffraction, inductively coupled plasma emission spectrometry, transmission electron microscopy, scanning electron microscopy and vector network analysis. Results show that nickel–cobalt–ytterbium ferrite microwave absorbing materials can be prepared under optimal conditions, with an average particle size of 38.00–45.00 nm. With the increase in the doping amount, the microwave absorption performance first increases and then decreases. When Yb3+ = 0.02, Ni0.5Co0.5Yb0.02Fe1.98O4 has the best microwave absorption performance, the best reflection loss is −21.04 dB, and the effective microwave absorption bandwidth in the Ku band is 2.55 GHz (15.45–18.00 GHz). The prepared nickel–cobalt–ytterbium ferrite microwave absorbing material has the advantages of less thickness, light weight, strong reflection loss and simple synthesis method. The excellent absorbing properties of Ni0.5Co0.5Yb0.02Fe1.98O4 are attributed to the interaction between natural resonance and exchange resonance.
Introduction
With the development and progress of the information age, the problems of human health and ecological environment caused by electromagnetic pollution have attracted much attention.1,2 Therefore, it is of great significance to research, design and develop microwave absorbing materials for preventing and treating electromagnetic pollution.3–5 For national defense science and technology, the study of microwave absorbing materials is conducive to the development of China's cutting-edge stealth technology and can identify the “soft rib” of stealth technology to strengthen the national defense force.6–8 After years of development, many excellent microwave absorbing materials have been discovered, such as ferrite,9 barium titanate,10 polycrystalline iron fibers,11 and graphite materials.12 Among them, ferrite can absorb electromagnetic waves in high frequency, ultra-high frequency and microwave frequency bands.13 It can also be reused without affecting its microwave absorption performance, good corrosion resistance14 and high temperature resistance.15 Ferrite is suitable for use in various environments and has several other advantages. Therefore, it has very high research value for civil and military purposes.At present, ferrite preparation methods include liquid phase method, gas phase method and solid phase method. The liquid phase method has the advantages of high purity, good uniformity and accurate chemical composition control. The liquid phase method includes sol–gel method, hydrothermal method and chemical coprecipitation method.16,17 Ferrite materials prepared by hydrothermal method and chemical coprecipitation methods have the disadvantages of serious grain agglomeration and high density, and it is difficult to meet the requirements of “light, thin, wide and strong” microwave absorbing materials.18 The sol–gel method has the characteristics of easy control of material composition, good rheological properties, molecular level uniformity in a short time, and light product. Xiaogang Su et al.19 prepared rare earth Gd3+-doped ferrite (GdxFe3−xO4) microwave absorbing material by a solvothermal method. When the doping amount was x = 0.02, thickness = 5.1 mm, and frequency = 6.1 GHz, the minimum reflection loss was −48.90 dB. The effective absorption bandwidth was 5.53 GHz (2.79–6.77 GHz, 15.52–17.07 GHz). Hongwei Chen et al.20 prepared nano-M0.4Zn0.6PrxFe2−xO4 microwave absorbing materials doped with rare earth Pr3+ by hydrothermal synthesis method. For a doping amount of x = 0.03 and frequency = 16–18 GHz, the minimum reflection loss was −19.216 dB. Lei Guo et al.21 prepared Nd3+-doped spinel type NiNdxFe2−xO4 microwave absorbing material by the sol–gel method. When the doping amount was x = 0.02, thickness = 6.02 mm, and frequency = 7.92 GHz, the minimum reflection loss was −47 dB and the effective absorption bandwidth was 4.5 GHz.
In summary, spinel ferrites doped with rare earths have good wave-absorbing properties, and there are few research articles on rare earth ytterbium. Hence this study chooses rare earth ytterbium doped nickel–cobalt ferrite to study its wave absorbing properties.
Experimental
Materials
(1) Reagents: C6H8O7·H2O, Ni(NO3)2·6H2O, Co(NO3)2·6H2O, Fe(NO3)3·9H2O, Yb(NO3)3·5H2O, NH3·H2O, all analytical grade (AR), distilled water.(2) Instrument: X-ray diffractometer (XRD), a D8 ADVANCE model. Inductively coupled plasma emission spectrometer (ICP-OES), Agilent 5110 model. Transmission electron microscope (TEM), JEM-2010 model. Scanning electron microscope (SEM), GeminiSEM 300 model. Vector Network Analysis (VNA), HP8722ES type.
Experimental: synthesis steps
(1) The metal ions of nitrate and citric acid were weighed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (the doping ratio of Yb3+ in ferrite is Ni0.5Co0.5YbxFe2−xO4 (x = 0.00, 0.02, 0.04, 0.06, 0.08)) and mixed in 50 mL distilled water.
1 ratio (the doping ratio of Yb3+ in ferrite is Ni0.5Co0.5YbxFe2−xO4 (x = 0.00, 0.02, 0.04, 0.06, 0.08)) and mixed in 50 mL distilled water.
(2) Ultrasonic dispersion was carried out with an ultrasonic cleaner, ultrasonic treatment was performed for 10 min, stirring by glass rod was done, and then ultrasonic treatment was continued for 10 min.
(3) The obtained mixed solution was poured into a four-mouth flask and stirred in a constant temperature water bath at 80 °C for 10 min. Ammonia water was added at the rate of 3 s per drop, the pH was adjusted to 7 and then stirred in a constant temperature water bath for 4 h; the speed was 120 rpm.
(4) The sol was put into a vacuum drying oven and dried at 120 °C for 4 h to obtain the gel, then cooled at room temperature for 15 min.
(5) The gel was placed in a muffle oven, heated to 200 °C at 15 °C min−1 and kept warm for 5 min.
(6) The obtained product was ground and placed in a muffle furnace. It was heated to 950 °C at a rate of 5 °C min−1 and kept at that temperature for 180 minutes to obtain nano nickel–cobalt–ytterbium ferrite.
Characterization
(1) The phase composition of the sample was tested using a D8 ADVANCE X-ray diffractometer (XRD). The conditions were: Cu target Kα radiation, wavelength 0.15406 nm, working voltage 40 kV, tube current 30 mA, scanning speed 10° min−1, scanning range 5–80°.(2) An Agilent 5110 inductively coupled plasma emission spectrometer (ICP-OES) was used to analyze the elemental content of the samples. The power was 1250 W, the plasma gas flow was 12.0 L min−1, the auxiliary gas flow was 1.0 L min−1, the atomizer gas flow was 0.70 L min−1, and three replicates were recorded.
(3) The morphology and particle size of the crystals were analyzed by a JEM-2010 transmission electron microscope (TEM). The resolution was 0.1–0.2 nm, the acceleration voltage was 200 kV, and the magnification was 20×–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×.
000×.
(4) The morphology of the samples was analyzed by a GeminiSEM 300 scanning electron microscope (SEM). The resolution was 0.8–1.4 nm and the magnification was 12–2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×.
000×.
(5) The complex permittivity and complex permeability of the samples in the frequency range of 0–18 GHz were measured by the coaxial line method using an HP8722ES vector network analyzer (VNA). The sample powder was mixed with paraffin wax in a ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. After mixing evenly, it was pressed into a ring with a mold to make a circular composite material with a thickness of 2 mm. The electromagnetic parameters of the samples were determined by a vector network analyzer.
3. After mixing evenly, it was pressed into a ring with a mold to make a circular composite material with a thickness of 2 mm. The electromagnetic parameters of the samples were determined by a vector network analyzer.
Results and discussion
Crystal structure analysis
Fig. 1 shows the XRD characterization results of Yb3+ with different doping ratios. The diffraction peak intensity of each doping ratio is roughly the same, indicating that the crystallization effect of ferrite prepared by the sol–gel method is better. The 2θ diffraction angles are 18.4°, 30.3°, 35.7°, 37.3°, 43.4°, 53.8°, 57.4°, 63.0°, 71.5°, 74.6°, and 75.6° corresponding to the (111), (220), (311), (222), (400), (422), (511), (440), (620), (533), and (622) crystal planes. The diffraction peak of the sample was compared with PDF#86-2267 standard card, and no miscellaneous peak appeared.22 The results show that pure spinel-type nickel–cobalt–ytterbium ferrite has been prepared. From the XRD patterns in Fig. 1, it can be seen that the strongest diffraction peak intensity is the (311) crystal plane, indicating that the preferred crystallization orientation of the crystal is (311). The distance between the crystal faces of the sample (d) was calculated according to Bragg's formula. The mean particle size (D) and lattice constant (α) of the sample were calculated according to Scherrer's formula.
nλ = 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (1) |
D = k1λ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (2) |
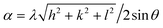 | (3) |
| Structural formula | 2θ/(°) | d/nm | α/nm | (311) priority crystallization diffraction peak | |
|---|---|---|---|---|---|
| FWHM/(°) | D/nm | ||||
| Ni0.5Co0.5Fe2O4 | 35.67 | 0.2515 | 0.8341 | 0.00213 | 67.6 |
| Ni0.5Co0.5Yb0.02Fe1.98O4 | 35.52 | 0.2525 | 0.8374 | 0.00375 | 38.4 |
| Ni0.5Co0.5Yb0.04Fe1.96O4 | 35.53 | 0.2524 | 0.8371 | 0.00363 | 39.7 |
| Ni0.5Co0.5Yb0.06Fe1.94O4 | 35.54 | 0.2523 | 0.8367 | 0.00346 | 41.6 |
| Ni0.5Co0.5Yb0.08Fe1.92O4 | 35.57 | 0.2521 | 0.8361 | 0.00325 | 44.3 |
According to the comprehensive analysis in Fig. 1 and Table 1, sample Ni0.5Co0.5Yb0.02Fe1.98O4 has the best crystallinity, the strongest diffraction peak and the smallest grain size. Therefore, the content of the main elements in Ni0.5Co0.5Yb0.02Fe1.98O4 was detected, as shown in Fig. 2.
According to the analysis in Fig. 2, the contents of Fe, Ni, Co and Yb are 46.32%, 12.45%, 12.61% and 0.48%, respectively. The ratio between the elements is approximately 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which meets the stoichiometric ratio of Ni0.5Co0.5Yb0.02Fe1.98O4, thus proving that the types and contents of elements in the sample conform to the characteristics of Ni0.5Co0.5Yb0.02Fe1.98O4.
1, which meets the stoichiometric ratio of Ni0.5Co0.5Yb0.02Fe1.98O4, thus proving that the types and contents of elements in the sample conform to the characteristics of Ni0.5Co0.5Yb0.02Fe1.98O4.
Morphological analysis
Fig. 3 shows the TEM characterization results of Ni0.5Co0.5YbxFe2−xO4 sample. As can be seen from the figure, the ferrite doped with Yb3+ has an irregular structure, and the average grain size can reach 38–45 nm, which is basically consistent with the results calculated by Scherrer's formula in XRD. However, the crystal surface could not be observed from the TEM results; thus, the sample of Ni0.5Co0.5YbxFe2−xO4 was tested by SEM, and the results are shown in Fig. 4. It can be clearly seen from Fig. 4 that the grain size of the ferrite doped with Yb3+ is significantly smaller than that without doping, which corresponds to the results in Table 1. The overall appearance of an irregular shape and flat surface is consistent with the TEM results. However, its dispersion is poor and its distribution is uneven. The reason is that the nickel–cobalt–ytterbium ferrite particles have magnetic attraction and intermolecular force, and the particles attract each other and connect into larger aggregates. At the same time, the magnetostatic energy is reduced, and the growth rate is difficult to control, resulting in uneven distribution. | ||
| Fig. 3 TEM images of doping with different Yb3+ ratios ((A) Ni0.5Co0.5Fe2O4, (B) Ni0.5Co0.5Yb0.02Fe1.98O4, (C) Ni0.5Co0.5Yb0.04Fe1.96O4, (D) Ni0.5Co0.5Yb0.06Fe1.94O4, (E) Ni0.5Co0.5Yb0.08Fe1.92O4). | ||
Microwave-absorbing performance analysis
Fig. 5 shows the relationship between reflection loss, frequency and thickness of the Ni0.5Co0.5YbxFe2−xO4 sample. According to formula (4), (5), (6), (7),23,24 the relation curve between microwave absorption reflectivity and frequency is calculated as follows.
RL(dB) = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg|Zin − Z0)/(Zin + Z0)| lg|Zin − Z0)/(Zin + Z0)|
| (4) |
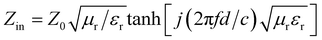 | (5) |
| εr = ε′ − jε′′ | (6) |
| μr = μ′ − jμ′′ | (7) |
As can be seen from Fig. 5, with the increase in the Yb3+ doping ratio, the microwave absorption performance presents a trend of first increase and then decrease. When Yb3+ = 0.00, the minimum reflection loss is −16.15 dB at the absorption layer thickness of 3.0 mm and frequency of 17.32 GHz. When Yb3+ = 0.02, the minimum reflection loss is −21.04 dB at the absorption layer thickness of 2.5 mm and frequency of 17.15 GHz. When Yb3+ = 0.04, the minimum reflection loss is −7.17 dB at an absorption layer thickness of 3.5 mm and frequency of 13.75 GHz. When Yb3+ = 0.06, the minimum reflection loss is −2.87 dB at an absorption layer thickness of 3.0 mm and frequency of 16.47 GHz. When Yb3+ = 0.08, the minimum reflection loss is −1.72 dB at the absorption layer thickness of 3.0 mm and frequency of 17.41 GHz. When doped with Yb3+ = 0.02, the microwave absorption effect is the best, and the effective band width of <−10.00 dB is 2.55 GHz (15.45–18.00 GHz). The reason why Ni0.5Co0.5Yb0.02Fe1.98O4 has better microwave absorption performance is that in nano Ni0.5Co0.5YbxFe2−xO4, Yb3+ preferentially occupies the octahedral position (i.e., B site) in each unit cell. As the proportion of Yb3+ doping increases, the lattice constant gradually decreases and the crystal orientation boundary decreases, resulting in a decrease in the demagnetization energy, an increase in magnetic moment, and an increase in hysteresis loss. When the doping ratio is too high, Yb2+ appears in the octahedron (B-site), and Yb3+ and Yb2+ electron exchange exists, while electron exchange between Fe3+ and Fe2+ disappears, resulting in the reduction of exchanged electrons, the weakening of electrical conductivity and the reduction of dielectric loss.25 Therefore, the microwave absorption performance of Ni0.5Co0.5YbxFe2−xO4 can be effectively enhanced by doping the appropriate proportion.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) can be used to represent the value of electromagnetic wave loss. It contains the tangent value of the electrical loss angle (tan
δ) can be used to represent the value of electromagnetic wave loss. It contains the tangent value of the electrical loss angle (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δe) and the tangent value of the magnetic loss angle (tan
δe) and the tangent value of the magnetic loss angle (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δm). Formula (8) (ref. 26) is as follows:
δm). Formula (8) (ref. 26) is as follows:
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = tan δ = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δe + tan δe + tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δm = (ε′′/ε′) + (μ′′/μ′) δm = (ε′′/ε′) + (μ′′/μ′)
| (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δe, and the ratio of the imaginary part μ′′ to the real part μ′ of the complex magnetic permeability is tan
δe, and the ratio of the imaginary part μ′′ to the real part μ′ of the complex magnetic permeability is tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δm. Also, the larger the tan
δm. Also, the larger the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value, the better the microwave absorbing performance of the material.
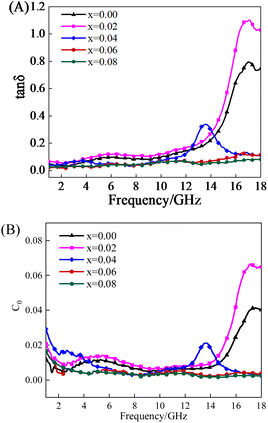
δ value, the better the microwave absorbing performance of the material.Fig. 6(A) and (B) respectively show the relationship curves of dielectric loss tangent value and magnetic loss tangent value of Ni0.5Co0.5YbxFe2−xO4 with frequency changes, both of which show nonlinear changes. It can be seen from Fig. 6(A) that when doped Yb3+ = 0, 0.02, 0.04, 0.06, ferrite has an obvious formant. In the frequency range of 1.00–17.00 GHz, the dielectric loss value of Yb3+ = 0.02 ferrite is higher than that of other doping ratios. The maximum dielectric loss tangent value is 0.18 at a frequency of 16.73 GHz. It can be seen from Fig. 6(B) that when doped Yb3+ = 0 and 0.02, ferrite has an obvious formant. In the frequency range of 14.50–18.00 GHz, the magnetic loss value of Yb3+ = 0.02 ferrite is higher than that at other doping ratios. The maximum magnetic loss tangent value is 0.94 at a frequency of 17.15 GHz. In the whole frequency band, the tangent value curve of dielectric loss first increases and then decreases, but the overall trend is increasing, while the tangent value curve of magnetic loss shows a gradual increasing trend.
Fig. 7(A) shows the relationship between the loss angle tangent value and the frequency change of Ni0.5Co0.5YbxFe2−xO4, which presents a nonlinear change. Ni0.5Co0.5Yb0.02Fe1.98O4 has the largest loss angle tangent value, which is tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1.10. It also verified that Ni0.5Co0.5Yb0.02Fe1.98O4 has a higher loss factor, which is one of the reasons for its better microwave absorption performance compared with other doping ratios. The tangent value of the magnetic loss of Ni0.5Co0.5Yb0.02Fe1.98O4 is greater than the tangent value of the electrical loss in the whole absorbing frequency band, which indicates that the dielectric loss is very small and the absorption of microwave mainly comes from the magnetic loss. Therefore, Fig. 7(B) analyzes the forms of magnetic loss at different frequency bands. Fig. 7(B) shows the relationship between magnetic loss C0 and frequency variation of Ni0.5Co0.5Yb0.02Fe1.98O4. According to formula (9),27
δ = 1.10. It also verified that Ni0.5Co0.5Yb0.02Fe1.98O4 has a higher loss factor, which is one of the reasons for its better microwave absorption performance compared with other doping ratios. The tangent value of the magnetic loss of Ni0.5Co0.5Yb0.02Fe1.98O4 is greater than the tangent value of the electrical loss in the whole absorbing frequency band, which indicates that the dielectric loss is very small and the absorption of microwave mainly comes from the magnetic loss. Therefore, Fig. 7(B) analyzes the forms of magnetic loss at different frequency bands. Fig. 7(B) shows the relationship between magnetic loss C0 and frequency variation of Ni0.5Co0.5Yb0.02Fe1.98O4. According to formula (9),27
| C0 = μ′′/((μ′)2f) | (9) |
It can be seen from the figure that the curve of the Ni0.5Co0.5YbxFe2−xO4 sample (x = 0, 0.02, 0.04, 0.06, 0.08) fluctuates in a wide range at low frequency in the range of 1.00–10.00 GHz, indicating the magnetic loss caused by natural resonance at this frequency. Natural resonance generally occurs at low frequency bands and is usually caused by shape anisotropy and magnetocrystalline anisotropy.28,29 At frequencies ranging from 6.00 GHz to 18.00 GHz, the curves of samples Ni0.5Co0.5Yb0.06Fe1.94O4 and Ni0.5Co0.5Yb0.08Fe1.92O4 show a small fluctuation range, indicating the magnetic loss caused by eddy current loss at this frequency.30 The samples Ni0.5Co0.5Fe2O4, Ni0.5Co0.5Yb0.02Fe1.98O4 and Ni0.5Co0.5Yb0.04Fe1.96O4 have obvious resonance peaks in the frequency range of 10.00–18.00 GHz, indicating the magnetic loss caused by exchange resonance. Exchange resonances generally occur at high frequency bands and are usually caused by surface anisotropy and energy exchange between grains.31 Therefore, the magnetic loss form of Ni0.5Co0.5Yb0.02Fe1.98O4 in this frequency band is the joint action of natural resonance and exchange resonance. The results show that different doping ratios can affect the magnetic loss form of nickel–cobalt–ytterbium ferrite.
High-quality microwave absorbing materials have two characteristics: attenuation properties and impedance matching. Attenuation characteristics mean that electromagnetic waves will be converted into other forms of energy after entering the material, and the higher the attenuation constant, the better the microwave absorption effect.32 Impedance matching means that before electromagnetic waves enter the interior of the material, some electromagnetic waves will be reflected because the impedance matching between the air and the surface of the material is inconsistent. At the frequency with the best microwave absorption effect, the closer the impedance matching is to 1, the stronger the performance.33
Fig. 8 shows the relationship between the attenuation constant and frequency of the Ni0.5Co0.5YbxFe2−xO4 sample. Here, the attenuation constant is α, which is plotted according to formula (10).34
 | (10) |
It can be seen from the figure that the peaks of Ni0.5Co0.5Yb0.06Fe1.94O4 and Ni0.5Co0.5Yb0.08Fe1.92O4 samples fluctuate between 1.00 GHz and 18.00 GHz, but the fluctuations are not obvious. The attenuation constant of sample Ni0.5Co0.5Yb0.02Fe1.98O4 is the highest, reaching 242.89 at a frequency of 17.15 GHz. This also confirms that the good absorption effect of sample Ni0.5Co0.5Yb0.02Fe1.98O4 is due to its high attenuation constant.
Fig. 9 is the impedance matching diagram of the Ni0.5Co0.5Yb0.02Fe1.98O4 sample. According to formula (11),35
 | (11) |
 | ||
| Fig. 9 Impedance matching, reflection loss and frequency relationship curve of the Ni0.5Co0.5YbxFe2−xO4 sample. | ||
According to the above results, the Ni0.5Co0.5Yb0.02Fe1.98O4 sample has the best microwave absorption effect and the largest attenuation constant. Therefore, only the impedance matching diagram of the Ni0.5Co0.5Yb0.02Fe1.98O4 sample with different thicknesses is discussed here. It can be seen from the figure that when the absorption layer thickness of Ni0.5Co0.5Yb0.02Fe1.98O4 is 2.5 mm and the frequency is 17.15 GHz, the minimum reflection loss value is −21.03 dB, and the impedance matching value Z is 1.16. Compared with the minimum reflection loss of other thicknesses, the impedance matching value at the corresponding frequency is closer to 1. It is also verified that Ni0.5Co0.5Yb0.02Fe1.98O4 not only has a larger attenuation constant at the frequency with the best microwave absorption effect but the impedance matching is also closer to 1.
Conclusions
In summary, in this paper, the sol–gel method has been used to prepare pure spinel-type nickel–cobalt–ytterbium ferrite without impurity peaks under the conditions of solution pH 7, molar ratio of citric acid to metal ion = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, crystallization temperature 950 °C and crystallization time 3 h. With the increase in the doping amount, the microwave absorption performance first increases and then decreases. Through the correlation calculation after XRD and the observation by transmission electron microscopy, it is mutually confirmed that the grain size is in the range of 38–45 nm. The microwave absorption performance is the best when doped with Yb3+ = 0.02. At an absorption layer thickness of 2.5 mm and frequency of 17.15 GHz, the reflection loss is the smallest, which is −21.03 dB. The effective microwave absorption frequency band is 2.55 GHz (15.45–18.00 GHz). Compared with undoped nickel–cobalt ferrite, the reflection loss is increased by 30.28%, and the microwave absorption performance is significantly improved. Ni0.5Co0.5Yb0.02Fe1.98O4 is dominated by magnetic loss in the whole frequency band, and its magnetic loss mechanism is mainly the interaction of natural resonance and exchange resonance. At a frequency of 17.15 GHz, the attenuation constant α = 242.89 and the impedance matching Z = 1.16. These results show that Ni–Co ferrite doped with rare earth ytterbium has the advantages of thin thickness, low cost, strong reflection loss and simple synthesis method. It is a kind of microwave absorbing material with high application prospect.
1, crystallization temperature 950 °C and crystallization time 3 h. With the increase in the doping amount, the microwave absorption performance first increases and then decreases. Through the correlation calculation after XRD and the observation by transmission electron microscopy, it is mutually confirmed that the grain size is in the range of 38–45 nm. The microwave absorption performance is the best when doped with Yb3+ = 0.02. At an absorption layer thickness of 2.5 mm and frequency of 17.15 GHz, the reflection loss is the smallest, which is −21.03 dB. The effective microwave absorption frequency band is 2.55 GHz (15.45–18.00 GHz). Compared with undoped nickel–cobalt ferrite, the reflection loss is increased by 30.28%, and the microwave absorption performance is significantly improved. Ni0.5Co0.5Yb0.02Fe1.98O4 is dominated by magnetic loss in the whole frequency band, and its magnetic loss mechanism is mainly the interaction of natural resonance and exchange resonance. At a frequency of 17.15 GHz, the attenuation constant α = 242.89 and the impedance matching Z = 1.16. These results show that Ni–Co ferrite doped with rare earth ytterbium has the advantages of thin thickness, low cost, strong reflection loss and simple synthesis method. It is a kind of microwave absorbing material with high application prospect.
Data availability
All the data from this study are available, and raw data can be provided for editors and reviewers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the financial support received through the National Natural Science Foundation (52274265).Notes and references
- J. W. Zhang, X. Meng, X. F. Wei, G. Fu, C. Putson, B. Rabah, H. Abdelowahed and F. Belhora, Sens. Actuators, A, 2023, 363, 114757 CrossRef CAS.
- B. S. Zhu, W. P. Mu, Y. F. Gao, G. M. Li and Y. M. Tian, Surf. Interfaces, 2023, 42, 103354 CrossRef CAS.
- K. Mandeep, K. G. Sachin and B. Shalini, J. Magn. Magn. Mater., 2024, 600, 172158 CrossRef.
- K. Parveen, N. Praveen, K. D. Alok, B. B. Himangshu, K. Sumit, K. M. Ashish and K. Ashavani, Mater. Chem. Phys., 2024, 319, 129360 CrossRef.
- G. V. Kostishin, M. I. Isaev and V. D. Salogub, Polym., 2024, 16, 1003 Search PubMed.
- H. Ahmad, A. Tariq, A. Shehzad, M. S. Faheem, M. Shafiq, I. A. Rashid, A. Afzal, A. Munir, M. T. Riaz, H. T. Haider, A. Afzal, M. B. Qadir and Z. Khaliq, Polym. Compos., 2019, 40, 4457–4472 CrossRef CAS.
- V. G. Kostishyn, I. M. Isaev, R. I. Shakirzyanov, D. V. Salogub, A. R. Kayumova and V. K. Olitsky, Tech. Phys., 2024, 68, S178–S184 CrossRef.
- I. M. Isaev, V. G. Kostishin, R. I. Shakirzyanov, A. R. Kayumova, V. K. Olitsky and D. V. Salogub, Tech. Phys., 2024, 68, S552–S561 CrossRef.
- J. L. Song, Y. Gao, G. G. Tan, Q. k. Man and Z. Wang, Ceram. Int., 2022, 48, 22896–22905 CrossRef CAS.
- J. H. Ha, S. Lee, B. Park, J. Lee and I. H. Song, J. Aust. Ceram. Soc., 2020, 56, 1–11 CrossRef.
- D. D. Min, J. L. Jiang, Y. C. Qing, X. Y. Gao, G. Hu and M. Zhou, J. Alloys Compd., 2023, 948, 169817 CrossRef CAS.
- E. Y. He, T. M. Yan, X. C. Ye, Q. Gao, C. Yang, P. Yang, Y. S. Ye and H. H. Wu, J. Mater. Sci., 2023, 58, 11647–11665 CrossRef CAS.
- S. V. R. Rama, J. Mater. Sci., 2022, 33, 13198–13206 Search PubMed.
- R. A. Sadrolhosseini and M. Naseri, Prot. Met. Phys. Chem. Surf., 2019, 55, 72–79 CrossRef.
- A. D. Bamburov, A. A. Markov, I. A. Leonidov and M. V. Patrakeev, J. Solid State Electrochem., 2018, 22, 899–907 CrossRef CAS.
- L. J. Xu, Z. Li, F. N. Xiao, Y. C. Zhao, Y. C. Zhou and S. Z. Wei, Tungsten, 2022, 5, 481–502 CrossRef.
- Y. A. Khalafallah, A. M. Siddig, A. O. Algethami, A. A. Elbadawi and S. A. Mohammed, Mater. Res. Express, 2024, 11, 055003 CrossRef.
- W. Li, Z. L. Zhang, Y. Y. Lv, Z. Wu, L. Yang, W. X. Zou and Y. H. Zou, Appl. Surf. Sci., 2022, 571, 151349 CrossRef CAS.
- X. G. Su, J. Wang, M. J. Han and Y. Q. Liu, New Chem. Mater., 2023, 51, 157–161, DOI:10.19817/j.cnki.issn1006-3536.2023.11.051.
- H. W. Chen, X. Y. Weng, Z. J. Ma and Z. H. Guan, Chin. J. Rare Met., 2020, 44, 1339–1344 Search PubMed.
- L. Guo, J. H. Yu, Z. J. Li, P. Wang, Z. J. Ding and B. Du, J. Magn. Magn. Mater., 2013, 44, 19–22+27 CAS.
- B. Laxmikant and A. Sadhana, Curr. Appl. Phys., 2023, 56, 47–65 CrossRef.
- J. Gao, Z. J. Ma, F. L. Liu and X. Y. Weng, Rare Met., 2023, 1, 254–262 CrossRef.
- C. Tang, J. Y. Yang, W. B. Deng, Y. H. Bai, B. W. Han, Z. L. Xu, Z. W. Liu, K. Zhao and Y. F. Tang, Carbon, 2024, 218118697 Search PubMed.
- Z. J. Ma, C. Y. Mang, J. C. Wang, X. Y. Weng, L. W. Si and Z. H. Guan, Chin. J. Mater. Res., 2017, 12, 909–917 Search PubMed.
- B. Trinadh, J. Suresh, G. R. Patta, B. K. Vijaya, C. Komali, B. B. Vikram, D. K. Anjani, M. B. Sathish and K. Samatha, Solid State Commun., 2023, 376, 115360 CrossRef CAS.
- W. Q. Guo, B. Hong, J. C. Xu, Y. B. Han, X. L. Peng, H. L. Ge, J. Li, H. W. Chen and X. Q. Wang, Diamond Relat. Mater., 2024, 141110699 Search PubMed.
- F. Tian, Y. Gao, A. P. Wang, L. Xiang, Q. K. Man, H. Xu and B. G. Shen, J. Magn. Magn. Mater., 2023, 587, 171229 CrossRef CAS.
- C. Wang, N. K. Chen, Y. Y. Xiao, J. H. He, R. Han and N. N. Song, Ceram. Int., 2023, 49, 36233–36243 CrossRef CAS.
- S. P. Chi, S. J. Zhu, Y. Zhu, S. J. Feng, X. S. Liu, Q. R. Lv, X. C. Kan and W. Sun, J. Supercond. Novel Magn., 2023, 36, 1703–1708 CrossRef CAS.
- Y. X. Xie, Y. Y. Guo, T. T. Cheng, L. B. Zhao, T. Wang, A. Meng, M. Zhang and Z. J. Li, Chem. Eng. J., 2023, 457, 141205 CrossRef CAS.
- D. R. Li, X. H. Liang, B. Quan, Y. Cheng, G. B. Ji and Y. W. Du, Mater. Res. Express, 2017, 4, 035604 CrossRef.
- H. Z. Du, W. M. Zhang, L. Wang, S. Q. Shen, W. W. Dong, Y. F. Hu, S. U. Rehman, H. P. Zou and T. X. Liang, J. Alloys Compd., 2023, 968, 172129 CrossRef CAS.
- Y. H. Zhou, G. X. Zhu, P. An and S. Y. Du, Nanotechnology, 2020, 31, 395203 CrossRef CAS PubMed.
- Y. Q. Ge, C. P. Li, G. I. N. Waterhouse, Z. M. Zhang and L. M. Yu, Ceram. Int., 2021, 47, 1728–1739 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |