Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultra-high Q-factor and amplitude-tunable Fano resonance in vanadium dioxide–silicon hybrid metamaterials
Kun Dengab,
Yachen Gao c,
Yang Gaoc and
Tong Wu
c,
Yang Gaoc and
Tong Wu *ab
*ab
aKey Laboratory of Medical Electronics and Digital Health of Zhejiang Province, Jiaxing University, Jiaxing, 314001, China. E-mail: wutongjx@zjxu.edu.cn
bEngineering Research Centre of Intelligent Human Health Situation Awareness of Zhejiang Province, Jiaxing University, Jiaxing, 314001, China
cElectronic Engineering College, Heilongjiang University, Harbin, 150080, China
First published on 25th April 2024
Abstract
As the resonance response in magnetic systems usually occurs at low frequencies, previously known as terahertz high Q-factor resonances, are mainly excited by electrical resonances. In this paper, we present a metamaterial based on vanadium dioxide–silicon arrays capable of achieving a Q-factor of up to 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198; the ultra-high Q-factor Fano resonance excited by the proposed metamaterial is mainly affected by strong magnetic resonance. The analysis of diffractive coupling theory, electric field, magnetic field and current distribution shows that strong magnetic resonance is mainly realized by coupling localized plasmon resonance with the lattice resonance. Due to the conductivity-tunable nature of vanadium dioxide, the proposed metamaterial features an amplitude tunable function with a modulation depth of 98.8%. The spectral response of the analyte demonstrates the capability of the proposed metamaterial for application as a sensor with a maximum sensitivity of 69.52 GHz per RIU and a figure of merit of 15
198; the ultra-high Q-factor Fano resonance excited by the proposed metamaterial is mainly affected by strong magnetic resonance. The analysis of diffractive coupling theory, electric field, magnetic field and current distribution shows that strong magnetic resonance is mainly realized by coupling localized plasmon resonance with the lattice resonance. Due to the conductivity-tunable nature of vanadium dioxide, the proposed metamaterial features an amplitude tunable function with a modulation depth of 98.8%. The spectral response of the analyte demonstrates the capability of the proposed metamaterial for application as a sensor with a maximum sensitivity of 69.52 GHz per RIU and a figure of merit of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456. The ultra-high Q-factor performance and amplitude tunability of the proposed structure can be applied to terahertz devices, such as ultrasensitive sensors, filters and optical switches.
456. The ultra-high Q-factor performance and amplitude tunability of the proposed structure can be applied to terahertz devices, such as ultrasensitive sensors, filters and optical switches.
1. Introduction
Terahertz wave is a sub-millimeter wave in the frequency range of 0.1–10 THz. It has the characteristics of microwaves and far-infrared waves because it is in the range where both wave types overlap.1,2 In recent years, the development of terahertz technology has provided new means for the development of many disciplines, such as biology, chemistry, and physics.3–5 Terahertz sensing is an important research direction for the evaluation of terahertz sensing performance as well, where the quality factor (Q-factor) is an important parameter. The key to realizing a high Q-factor resonance is to reduce the dipole radiation loss.6,7 In plasmon structures, Fano resonance can reduce or even completely suppress radiation loss.8 It can produce an anomalous asymmetric and narrow bandwidth line shape through the interference of narrowband dark and broadband bright modes.9The emergence of metamaterials provides an effective solution for the excitation of Fano resonance, which is characterized by the ability to artificially design the geometry of structural units.10–12 Enhanced manipulation of terahertz waves and the response of their fields to matter is possible by combining multiple materials and designing different cell structures.13 Metamaterial-excited Fano resonance has become an important research direction.14–17 With the development of tunable materials, such as graphene and VO2, multifunctional sensors based on metamaterials have progressed significantly.18 For example, in 2023, Xin et al. used a metal structure and GaAs to prepare a Fano-resonant metamaterial that could achieve a sensitivity of 513 GHz per RIU and a maximum modulation depth of 96.5% by an adjustment of the conductivity of GaAs.19 In 2023, Ma et al. designed an all-media metamaterial based on silicon and reported strong intrinsic chirality of the planar cross resonance and a high Q-factor for it.20 In the same year, Feng et al. proposed a metamaterial, whose unit structure consisted of asymmetric triple-parallel silicon rectangles and recorded a high Q-factor and high robustness for it.21 In 2023, Wang et al. proposed a two-band metamaterial absorber at terahertz frequency with a periodically patterned metallic structure on the top of the wafer, which exhibited perfect absorption properties and a high Q-factor in two bands, 0.89 THz and 1.36 THz.22 In 2023, He et al. proposed a four-band tunable narrow-band terahertz absorber that had a perfect multimodal absorption in the 1–9 THz range and could sense with high sensitivity.23 However, it is worth noting that as the resonant response in magnetic systems usually occurs at low frequencies, previously reported terahertz high Q-factor resonance was mainly excited by electrical resonances.24 There are still only a few metamaterials with tunable Fano resonances to achieve the ultra-high Q-factor, and most such metamaterials are sensitive to the polarization of the incident wave, limiting their application scenarios.
In this paper, we design an ultra-high Q-factor metamaterial that can be used for sensing and optical switching. The unit structure of this metamaterial consists of vanadium dioxide (VO2) and silicon rings that are periodically arranged and can be insensitive to incident polarization. In addition, the field distributions and currents of the proposed metamaterial at the resonance frequency indicate that the ring resonator is capable of exciting significant electric quadrupole resonance and magnetic dipole resonance. The diffraction coupling theory analysis concludes that significant second-order (1,1) surface lattice resonance (SLR) occurs at the Fano resonance frequency. The proposed metamaterial achieves extremely narrow Fano resonance peaks via coherent Fano interactions between the localized plasmon resonance (LPR) of individual ring resonators and SLR of the array. The far-field radiation losses are also suppressed due to the destructive interference of the metamaterial resonator with the scattered field of the substrate, resulting in ultra-high Q-factor Fano resonance. In terms of sensing performance, proposed metamaterials can achieve a sensitivity of 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 and a figure of merit (FoM) of 15
198 and a figure of merit (FoM) of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456. The Fano resonance peak amplitude is also modulated by changing the conductivity of VO2.
456. The Fano resonance peak amplitude is also modulated by changing the conductivity of VO2.
2. Structural design and methods
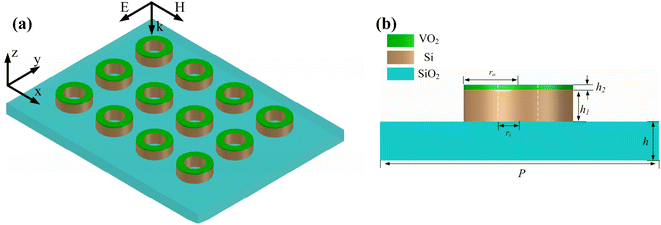
Fig. 1 illustrates an overall schematic and the front view of the proposed metamaterial. The substrate consists of a 20 μm-thick silicon dioxide (SiO2) layer with a dielectric constant of 1.49.25 As a phase-change material, VO2 has a low carrier concentration, and it is an insulating material at a temperature of 28 °C. When the temperature is increased to 68 °C, VO2 reaches a conductivity of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 S m−1 and achieves an insulating-to-metallic transition, which can occur at sub-picosecond rates.26 Compared to metal-based metasurfaces, dielectric-based metasurfaces have lower losses to the incident wave. Thus, the proposed resonator unit of the metasurface is realized by a combination of silicon and vanadium dioxide.27 The resonator unit on the substrate consists of silicon and VO2 rings, which are stacked and distributed in an array with a period of 400 μm. The inner and outer ring radius of the silicon and VO2 ring embraces are 50 μm and 75 μm and thicknesses are 35 μm and 0.2 μm, respectively. The permittivity of silicon is 3.45.28 The centrosymmetric feature of the proposed metamaterial unit enables it to possess the advantage of being insensitive to the electromagnetic field polarization of the incident wave.
000 S m−1 and achieves an insulating-to-metallic transition, which can occur at sub-picosecond rates.26 Compared to metal-based metasurfaces, dielectric-based metasurfaces have lower losses to the incident wave. Thus, the proposed resonator unit of the metasurface is realized by a combination of silicon and vanadium dioxide.27 The resonator unit on the substrate consists of silicon and VO2 rings, which are stacked and distributed in an array with a period of 400 μm. The inner and outer ring radius of the silicon and VO2 ring embraces are 50 μm and 75 μm and thicknesses are 35 μm and 0.2 μm, respectively. The permittivity of silicon is 3.45.28 The centrosymmetric feature of the proposed metamaterial unit enables it to possess the advantage of being insensitive to the electromagnetic field polarization of the incident wave.
The permittivity of VO2 can be obtained by ε(ω) = ε∞ − [ωp2(σ)/ω(ω + iγ)], where ε∞ = 12 is the high-frequency permittivity; ωp(σ) is the conductivity-dependent plasma frequency, and γis the collision frequency. In addition, ωp(σ)and σ are proportional to the free carrier density. Therefore, the plasma frequency at σ frequency can be roughly expressed as ωp2(σ) = σωp2(σ0)/σ0, where σ0 = 3 × 103 Ω−1 S−1, ωp(σ0) = 1.4 × 1015 rad s−1, and γ = 5.75 × 1013 rad s−1.29,30 Terahertz plane wave was positively incident along the z-axis to the proposed metamaterial. The S parameter can be calculated by the FDTD theory, and the transmission T can be obtained by T = |S21|2.31
3. Results and discussion
The initial incident wave polarization was set to be in the x direction, and the initial conductivity of VO2 was 0. The transmission properties of the proposed metamaterial in the terahertz band were numerically calculated using the FDTD algorithm, and the results are shown in Fig. 2(a) as red circles. It can be observed that an asymmetric Fano curve with a narrow line width exists at 0.743063 THz. Furthermore, we analyzed Fano characteristics using eqn (1), where a1 + ia2 denotes the background transmission without the resonator and comprises real numbers; γ is the damping loss, and ω0 is the resonant frequency.
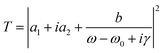 | (1) |
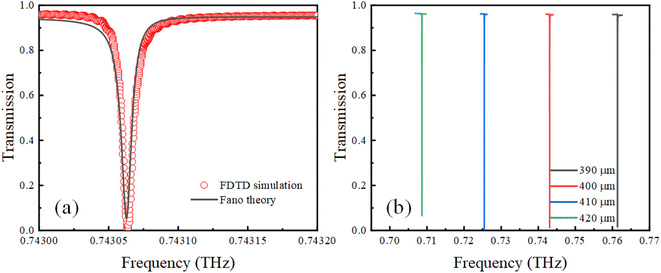 | ||
| Fig. 2 (a) Transmission spectra calculated by FDTD simulation and Fano theory, (b) transmission spectra with different metasurface periods. | ||
The fitting results are shown as the black line in Fig. 2. It can be seen that theoretical fitting results are in good agreement with numerical simulation results. Correspondingly, the Q-factor is approximately 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 from the formula, Q = Re(ω)/2Im(ω) = ω0/2γ.32
198 from the formula, Q = Re(ω)/2Im(ω) = ω0/2γ.32
In this work, in-plane SLR could be generated in the metamaterial due to the periodic arrangement of the resonator units in the design. When the resonance frequency of a single resonator is close to the SLR frequency, a strong energy transfer can be achieved from the incident terahertz wave to the local plasma, resulting in a sharp plasma resonance.33,34
Based on the diffractive coupling theory,35 the resonant frequency of the SLR can be expressed as eqn (2).
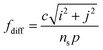 | (2) |
To gain a deeper understanding of the physical mechanisms of Fano resonance, we simulate and analyze the distribution of electric field, magnetic field, current and charge at Fano resonance frequency. In Fig. 3(a), we see that there is an obvious enhancement of the electric field on both sides of the ring resonator. In addition, we can see that along with the excitation of the second-order (1,1) lattice resonance in the absence of a resonator unit, the two sides of the substrate still produce an obvious electric field resonance, indicating that the electric quadrupole is excited along with the second-order (1,1) SLR. In Fig. 3(b), we can see that the charge distribution on the ring is “+ − + −” along four clockwise parts, which can be recognized as an electric quadrupole resonance mode. In Fig. 3(c), we can see that a significant magnetic field enhancement occurs in each of the resonator units, exciting a magnetic resonance that was constrained by a strong field on the surface of the substrate. Furthermore, according to the propagation direction of the magnetic field at the Fano resonance frequency, the magnetic field of a single resonator propagates in the opposite direction to that in the substrate, which in turn generates interfering couplings at the second-order SLR. Therefore, the electromagnetic wave energy can be efficiently confined to the metamaterial without combining with the free space. Fig. 3(d) illustrates the current distribution in the x–z cross-section of the metamaterial; it can be seen that currents with opposite vector directions are formed on both sides of the resonator and circulate inside the resonator. The presence of such circulating currents causes the resonator to produce a magnetic dipole moment m on the y-axis, as shown in Fig. 3(c).37,38 The multipole expansion method shows that for magnetic dipole resonances, the radiation losses are influenced by the magnetic moment m or equivalent current element J. Since currents on both sides of the ring resonator are in opposite directions, forming a cancellation, the equivalent current is almost zero. Thus, almost no radiation is lost, which in turn contributes to the formation of the ultra-high Q-factor Fano resonance.6
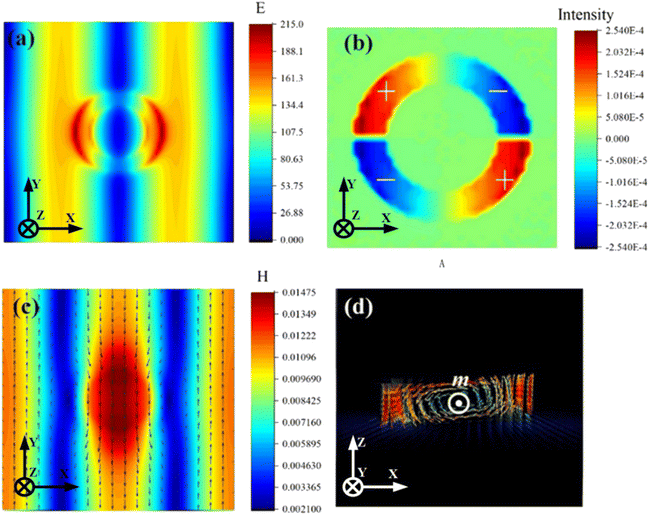 | ||
| Fig. 3 (a) Electric field distribution, (b) charge distribution, (c) magnetic field distribution and (d) x–z cross-sectional current in the proposed design. | ||
From the above analysis, it is concluded that the scattered field excited at each metamaterial unit resonates at the substrate surface and produces interference phenomena, leading to in-plane confinement of the scattered field and reduction of radiation losses. The coupling of the magnetic dipole and electric quadrupole to the SLR confines the electromagnetic energy in the lattice, which greatly suppresses radiative damping and ultimately leads to a high Q-factor of more than 106 in the terahertz band.
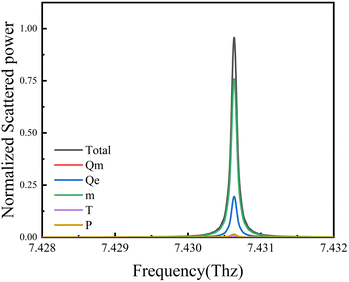
To quantitatively analyze the ultra-high Q-factor Fano resonance mechanism, we calculated the radiative components of the magnetic dipole (m), magnetic quadrupole (Qm), electric quadrupole (Qe), electric dipole (P) and toroidal dipole (T) using eqn (3) (ref. 39 and 40)
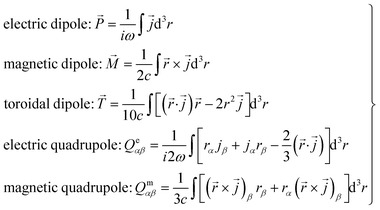 | (3) |
Fig. 4 shows the results of the multipole analysis, where modes excited at the Fano resonance frequency are mainly magnetic dipole resonance and electric quadrupole resonance; these observations are consistent with those shown in Fig. 3(c) and (d), and thus, magnetic resonance is dominant at the Fano resonance frequency.
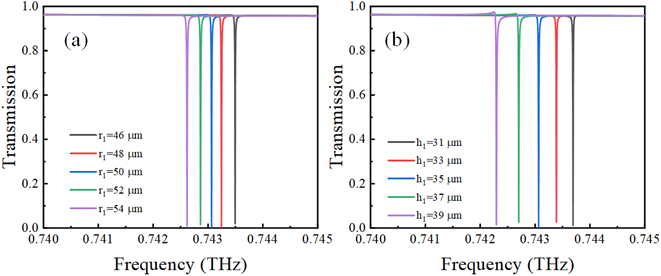
The parameters of the structure have an important influence on the performance of magnetic resonance. The effect of fabrication defects on the magnetic resonance must be considered in the actual preparation process. Fig. 5(a) demonstrates the effect of transmission spectra for different inner ring radii (r1) while keeping a constant ring width. It was found that the Fano resonance frequency gradually moves to lower frequencies with the increase in the inner ring radius. In Fig. 5(b), it is shown that as the silicon ring height increases, the Fano resonance frequency also exhibits a shift toward lower frequencies. This is because in the plasma resonance mode, the resonance frequency can be effectively controlled by the properties and structural parameters of the material.41
As a phase change material, vanadium dioxide can undergo phase change from an insulator state to a metallic state by various methods, such as temperature, light, and electric field, thereby producing an adjustable conductivity of VO2.42,43 As shown in Fig. 6(a), the amplitude of the Fano resonance decreases as the VO2 conductivity (σ) decreases, and the Fano resonance almost disappears, when the conductivity is set at 150 s m−1. To demonstrate the impact of VO2 conductivity on Fano resonance more clearly, Fig. 6(b) shows the relationship between conductivity and transmittance at the lowest point of Fano resonance. Therefore, this design achieves an optical switching function, where the modulation depth can be up to 98.9% using MD = [(Tmax − Tmin)/(Tmax + Tmin)] × 100%.
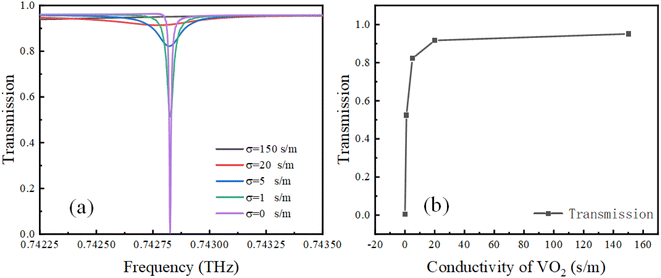 | ||
| Fig. 6 (a) Fano resonance transmission with different conductivities of VO2, (b) relationship between conductivity and transmittance at the lowest point of Fano resonance. | ||
To clarify the physical mechanism of this amplitude tunability, in Fig. 7, we show electric and magnetic fields calculated for the x–z cross-section of the metamaterial cell. From electric field distributions in Fig. 7(a–c), it can be observed that the electric field enhancement at the ring resonator gradually diminishes as the conductivity increases, and it disappears almost completely when the conductivity is 150 S m−1. According to magnetic field distributions in Fig. 7(d and e), when the VO2 conductivity is 0 S m−1, magnetic resonance is excited at the center of the ring resonator. As the conductivity increases, the magnetic resonance at the center of the ring weakens significantly. When the conductivity is 150 S m−1, the magnetic resonance almost disappears. This phenomenon illustrates that as the conductivity of VO2 increases, the excitation of the electrical and magnetic resonance sat the ring resonator ring are affected and weaken the coupling between the LPR and SLR, which ultimately leads to the disappearance of the ultra-high Q-factor Fano resonance. Here, it can be concluded that the increase in VO2 conductivity of the proposed metamaterial weakens the intensity of Fano resonance, resulting in the gradual disappearance of the Fano line in Fig. 6(a).
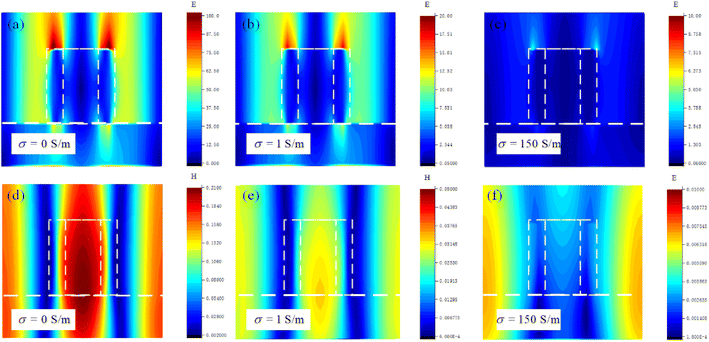 | ||
| Fig. 7 Distribution of (a)–(c) electric and (d)–(f) magnetic fields in the x–z cross-section of metamaterial with different conductivities of VO2. | ||
Enhancement of the electrical and magnetic fields on the surface of a metamaterial sensor can increase the interaction of incident electromagnetic waves with the analyte, which in turn improves the sensitivity of the sensor to the medium refractive index (RI). The ring-shaped resonator array proposed in our design can be considered a frequency-selective metasurface. Therefore, the LPR resonance frequency is estimated using eqn (4).44
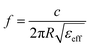 | (4) |
Due to the extremely narrow Fano resonance peak that can be achieved by our design, the resonance peak frequency will significantly change when the analyte RI changes. As shown in Fig. 8(a), as the analyte RI increases, the Fano resonance gradually moves to lower frequencies.
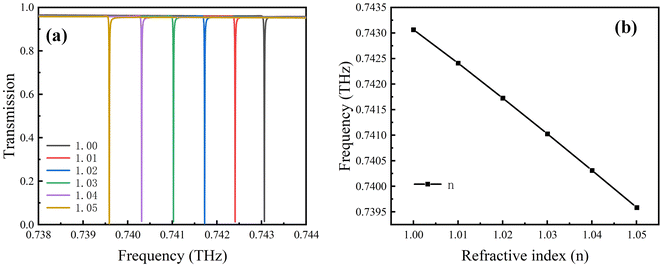 | ||
| Fig. 8 (a) Transmission and (b) Fano resonance frequency at different refractive indices of the analyte. | ||
The influence of the analyte RI on the Fano resonance frequency is shown in Fig. 8(b); it can be seen that there is a good linear relationship between frequency change and RI, which is favorable for the application of this metamaterial as a sensor. The sensitivity is calculated to be 0.06952 Thz per RIU using the relation, S = Δf/Δn. The FoM can be calculated using the equation, FOM = S/FWHM = S × Q/f, where FWHM is the full width at half maximum, and f refers to the resonance frequency. The present design can achieve a FoM value of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456.45
456.45
In Table 1, we summarize relevant sensors using metamaterials.41,46–48 It can be concluded that our proposed design has excellent performance (ultra-high Q-factor and FOM). In addition, our design can realize the optical switching function with modulation depths up to 98.8% by tuning the VO2 conductivity. The designed structure is also relatively simple and easy to prepare for future experiments.
4. Conclusions
In summary, we theoretically designed a metamaterial consisting of a periodic arrangement of VO2–silicon ring resonators, which is capable of achieving sensing functionality with an ultra-high Q-factor, along with optical switching functions with high modulation depth. It is demonstrated by electric field, magnetic field, current analysis and multipole analysis that the proposed metamaterial can excite obvious magnetic dipole resonance and electric quadrupole resonance. Coupling of the above two resonant modes to the SLR suppresses radiation loss and achieves a Q-factor as high as 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198. The Fano resonance frequency can be adjusted by changing the parameters of the resonance units of the proposed metamaterial. Due to the tunable conductivity of VO2, the metamaterial is also capable of optical switching with a modulation depth of 98.8%. In addition, we calculated the theoretical sensitivity to show that our design can realize a sensitivity of 69.52 Ghz per RIU and a high FoM of 15
198. The Fano resonance frequency can be adjusted by changing the parameters of the resonance units of the proposed metamaterial. Due to the tunable conductivity of VO2, the metamaterial is also capable of optical switching with a modulation depth of 98.8%. In addition, we calculated the theoretical sensitivity to show that our design can realize a sensitivity of 69.52 Ghz per RIU and a high FoM of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456. The proposed scheme provides a path to achieve tunable terahertz functional devices with an ultra-high Q-factor. The findings of this investigation are of great significance for the study of the suppression of radiation loss and enhancement of terahertz field interactions with matter.
456. The proposed scheme provides a path to achieve tunable terahertz functional devices with an ultra-high Q-factor. The findings of this investigation are of great significance for the study of the suppression of radiation loss and enhancement of terahertz field interactions with matter.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Humanity and Social Science Research Project of the Ministry of Education of China (College Counselors), grant number 22JDSZ3023 and the University-Industry Collaborative Education Program, grant number 220603372015422 and 220604029012441.References
- S. Han, L. Q. Cong, Y. K. Srivastava, B. Qiang, M. V. Rybin, A. Kumar, R. Jain, W. X. Lim, V. C. Achanta, S. S. Prabhu, Q. J. Wang, Y. S. Kivshar and R. Singh, All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum, Adv. Mater., 2019, 31(37), 1901921 CrossRef PubMed.
- T. L. Dong, Y. Zhang, Y. Li, Y. P. Tang and X. J. He, Dual-function switchable terahertz metamaterial device with dynamic tuning characteristics, Results Phys., 2023, 45, 106246 CrossRef.
- S. Zhang, J. F. Zhou, Y. S. Park, J. Rho, R. Singh, S. Nam, A. K. Azad, H. T. Chen, X. B. Yin, A. J. Taylor and X. Zhang, Photoinduced handedness switching in terahertz chiral metamolecules, Nat. Commun., 2012, 3, 942 CrossRef PubMed.
- J. Zhou, X. Zhao, G. R. Huang, X. Yang, Y. Zhang, X. Y. Zhan, H. Y. Tian, Y. Xiong, Y. X. Wang and W. L. Fu, Molecule-Specific Terahertz Biosensors Based on an Aptamer Hydrogel-Functionalized Metamaterial for Sensitive Assays in Aqueous Environments, ACS Sens., 2021, 6(5), 1884–1890 CrossRef CAS PubMed.
- K. L. Shih, P. Pitchappa, L. Jin, C. H. Chen, R. Singh and C. Lee, Nanofluidic terahertz metasensor for sensing in aqueous environment, Appl. Phys. Lett., 2018, 113(7), 071105 CrossRef.
- F. Yan, Q. Li, Z. W. Wang, H. Tian and L. Li, Extremely high Q-factor terahertz metasurface using reconstructive coherent mode resonance, Opt. Express, 2021, 29(5), 7015–7023 CrossRef PubMed.
- S. Y. Yang, C. C. Tang, Z. Liu, B. Wang, C. Wang, J. J. Li, L. Wang and C. Z. Gu, Simultaneous excitation of extremely high-Q-factor trapped and octupolar modes in terahertz metamaterials, Opt. Express, 2017, 25(14), 15938–15946 CrossRef CAS PubMed.
- G. Dayal, A. Solanki, X. Y. Chin, T. C. Sum, C. Soci and R. Singh, High-Q plasmonic infrared absorber for sensing of molecular resonances in hybrid lead halide perovskites, J. Appl. Phys., 2017, 122(7), 073101 CrossRef.
- D. G. Kotsifaki, V. G. Truong and S. N. Chormaic, Fano-Resonant, Asymmetric, Metamaterial-Assisted Tweezers for Single Nanoparticle Trapping, Nano Lett., 2020, 20(5), 3388–3395 CrossRef CAS PubMed.
- S. Zhang, D. A. Genov, Y. Wang, M. Liu and X. Zhang, Plasmon-induced transparency in metamaterials, Phys. Rev. Lett., 2008, 101(4), 047401 CrossRef PubMed.
- Y. D. Gong, Z. Zhang, J. X. Tang, L. Ma and K. Pang, Research progress on terahertz achromatic broadband polarization wave plates, Opt. Laser Technol., 2023, 166, 109633 CrossRef.
- Y. Zhu, J. Cheng, Z. Yi, B. Tang, J. Chen, J. Zhang, X. Xu, C. Tang and T. Sun, Spectrally selective solar absorber and thermal infrared suppression based on hollow cylindrical microstructures, Opt. Commun., 2023, 549, 129910 CrossRef CAS.
- F. Yan, Q. Li, H. Hu, Z. W. Wang, H. Tian, L. Li, Y. Luo and Q. J. Wang, Terahertz high-Q magnetic dipole resonance induced by coherent Fano interactions, Appl. Phys. Lett., 2022, 121(20), 201704 CrossRef CAS.
- X. Y. He and W. H. Cao, Tunable terahertz hybrid metamaterials supported by 3D Dirac semimetals, Opt. Mater. Express, 2023, 13(2), 413–422 CrossRef CAS.
- B. X. Ruan, E. D. Gao, M. Li, X. Chang, Z. B. Zhang and H. J. Li, Tunable Fano resonance and optical switching in the one-dimensional topological photonic crystal with graphene, J. Appl. Phys., 2023, 133(21), 213101 CrossRef CAS.
- Y. Z. Hu, M. Y. Tong, S. Y. Hu, W. B. He, X. A. Cheng and T. Jiang, Reassessing Fano Resonance for Broadband, High-Efficiency, and Ultrafast Terahertz Wave Switching, Adv. Sci., 2023, 10(2), 2204494 CrossRef CAS PubMed.
- Y. Y. Lu, T. T. Li, M. S. Yang, H. Y. Yao, L. J. Liang, X. Yan, K. K. Lv, M. Wang, Q. L. Yang, C. Y. Wei, J. D. Shao and J. Q. Yao, Dual control of multi-band resonances with a metal-halide perovskite-integrated terahertz metasurface, Nanoscale, 2022, 14(35), 12703–12712 RSC.
- W. Lu, Z. Yi, J. Zhang, X. Xu, B. Tang, G. Li, L. Zeng, J. Chen and T. Sun, A tunable broadband absorber in the terahertz band based on the proportional structure of a single layer of graphene, Diamond Relat. Mater., 2023, 140, 110481 CrossRef CAS.
- X. Yan, C. C. Huang, Z. J. Zhang, F. Qiu, W. J. Liu, R. C. Xu, Z. Q. Wang, Z. H. Li, X. F. Hu, C. Wang, Y. G. Zhang, H. Y. Yao, L. J. Liang and J. Q. Yao, GaAs-enabled tunable multifunctional devices based on three coupling mechanisms for terahertz metamaterials, Opt. Mater. Express, 2023, 13(2), 423–433 CrossRef CAS.
- T. Ma, J. K. Tian, W. Sang, D. D. Wang and J. Li, High Q Chiroptical Responses Driven by Toroidal Dipole Resonance in All-Dielectric Metasurfaces, IEEE Photonics Technol. Lett., 2023, 35(17), 963–966 Search PubMed.
- G. Feng, Z. H. Chen, X. Y. Mi, F. Sun, Y. B. Yang, Y. Wang and S. Q. Chen, All-dielectric terahertz metasurfaces with high Q Fano resonance based on indirect perturbation and bound states in the continuum, Opt. Laser Technol., 2023, 164, 109578 CrossRef CAS.
- D. X. Wang, K. D. Xu, S. Y. Luo, Y. Q. Cui, L. Y. Zhang and J. L. Cui, A high Q-factor dual-band terahertz metamaterial absorber and its sensing characteristics, Nanoscale, 2023, 15(7), 3398–3407 RSC.
- L. He, Y. Yi, J. Zhang, X. Xu, B. Tang, G. Li, L. Zeng, J. Chen, T. Sun and Z. Yi, A four-narrowband terahertz tunable absorber with perfect absorption and high sensitivity, Mater. Res. Bull., 2024, 170, 112572 CrossRef CAS.
- T. J. Yen, W. J. Padilla, N. Fang, D. C. Vier, D. R. Smith, J. B. Pendry, D. N. Basov and X. Zhang, Terahertz Magnetic Response from Artificial Materials, Science, 2004, 15, 1494–1496 CrossRef PubMed.
- S. Jain, A. Paliwal, V. Gupta and M. Tomar, SPR based refractive index modulation of nanostructured SiO2 films grown using GLAD assisted RF sputtering technique, Surf. Interfaces, 2022, 34, 102355 CrossRef CAS.
- T. Driscoll, H.-T. Kim and B.-G. Chae, et al., Memory metamaterials, J. Sci., 2009, 325(5947), 1518–1521 CrossRef CAS PubMed.
- M. Yang, X. Yan and Z. Zhang, et al., Ultra-wideband low-loss control of terahertz scatterings via an all-dielectric coding metasurface, J. ACS Appl. Electron. Mater., 2020, 2(4), 1122–1129 CrossRef CAS.
- D. X. Yan, X. J. Li, C. Ma, G. H. Qiu, M. X. Cao, J. N. Li and S. H. Guo, Terahertz Refractive Index Sensing Based on Gradient Metasurface Coupled Confined Spoof Surface Plasmon Polaritons Mode, IEEE Sens. J., 2022, 22(1), 324–329 CAS.
- S. X. Wang, C. F. Cai, M. H. You, F. Y. Liu, M. H. Wu, S. Z. Li, H. G. Bao, L. Kang and D. H. Werner, Vanadium dioxide based broadband THz metamaterial absorbers with high tunability: simulation study, Opt. Express, 2019, 27(14), 19436–19447 CrossRef CAS PubMed.
- L. Gevorgyan, H. Haroyan, H. Parsamyan and K. Nerkararyan, Tunable ultra-broadband terahertz metamaterial absorber based on vanadium dioxide strips, RSC Adv., 2023, 13(18), 11948–11958 RSC.
- R. Zheng, Y. Liu, L. Ling, Z. Sheng, Z. Yi, Q. Song, B. Tang, Q. Zeng, J. Chen and T. Sun, Ultra wideband tunable terahertz metamaterial absorber based on single-layer graphene strip, Diamond Relat. Mater., 2024, 141, 110713 CrossRef CAS.
- Y. S. Wang, S. L. Yu, Z. A. Gao, S. Z. Song, H. Y. Li, T. G. Zhao and Z. H. Hu, Excitations of Multiple Fano Resonances Based on Permittivity-Asymmetric Dielectric Meta-Surfaces for Nano-Sensors, IEEE Photonics J., 2022, 14(1), 4613107 CAS.
- T. C. W. Tan, E. Plum and R. Singh, Lattice-Enhanced Fano Resonances from Bound States in the Continuum Metasurfaces, Adv. Opt. Mater., 2020, 8(6), 1901572 CrossRef CAS.
- T. C. Tan, Y. K. Srivastava, M. Manjappa, E. Plum and R. Singh, Lattice induced strong coupling and line narrowing of split resonances in metamaterials, Appl. Phys. Lett., 2018, 112(20), 201111 CrossRef.
- S. Y. Yang, Z. Liu, X. X. Xia, Y. W. E, C. C. Tang, Y. J. Wang, J. J. Li, L. Wang and C. Z. Gu, Excitation of ultrasharp trapped-mode resonances in mirror-symmetric metamaterials, Phys. Rev. B, 2016, 93(23), 235407 CrossRef.
- Y. K. Srivastava, R. T. Ako, M. Gupta, M. Bhaskaran, S. Sriram and R. Singh, Terahertz sensing of 7 nm dielectric film with bound states in the continuum metasurfaces, Appl. Phys. Lett., 2019, 115(15), 151105 CrossRef.
- V. Savinov, V. A. Fedotov and N. I. Zheludev, Toroidal dipolar excitation and macroscopic electromagnetic properties of metamaterials, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(20), 205112 CrossRef.
- P. De Vries, D. V. Van Coevorden and A. Lagendijk, Point scatterers for classical waves, Rev. Mod. Phys., 1998, 70(2), 447–466 CrossRef.
- T. Kaelberer, V. A. Fedotov, N. Papasimakis, D. P. Tsai and N. I. Zheludev, Toroidal Dipolar Response in a Metamaterial, Science, 2010, 330(6010), 1510–1512 CrossRef CAS PubMed.
- Z. Song, Q. Chu, C. Zhu, Q. Chen and W. Wang, Polarization-independent terahertz tunable analog of electromagnetically induced transparency, IEEE Photonics Technol. Lett., 2019, 31(15), 1297–1299 CAS.
- Z. Z. Li, S. M. Wang, Y. Y. Zhu, J. W. Fan, D. Guo and Y. E. Chen, E-shaped split ring resonator used for metasurface-based structure with an ultra-high Q-factor for terahertz application, Opt. Commun., 2023, 529, 129041 CrossRef CAS.
- Z. Zheng, Y. Luo, H. Yang, Z. Yi, J. Zhang, Q. Song, W. Yang, C. Liu, X. Wu and P. Wu, Thermal tuning of terahertz metamaterial absorber properties based on VO2, Phys. Chem. Chem. Phys., 2022, 24(15), 8846–8853 RSC.
- S. Lysenko, A. Rua, V. Vikhnin, J. Jimenez, F. Fernandez and H. Liu, Light-induced ultrafast phase transitions in VO2 thin film, Appl. Surf. Sci., 2006, 252(15), 5512–5515 CrossRef CAS.
- B. A. Munk, Frequency selective surfaces: theory and design [Book Review], IEEE Signal Processing Magazine, 2001, vol. 18, p. 94 Search PubMed.
- B. W. Liu, S. Chen, J. C. Zhang, X. Yao, J. H. Zhong, H. X. Lin, T. X. Huang, Z. L. Yang, J. F. Zhu, S. Liu, C. Lienau, L. Wang and B. Ren, A Plasmonic Sensor Array with Ultrahigh Figures of Merit and Resonance Linewidths down to 3 nm, Adv. Mater., 2018, 30(12), 1706031 CrossRef PubMed.
- J. W. Wu, T. T. Yuan, J. J. Liu, J. Y. Qin, Z. Hong, J. S. Li and Y. Du, Terahertz Metamaterial Sensor With Ultra-High Sensitivity and Tunability Based on Photosensitive Semiconductor GaAs, IEEE Sens. J., 2022, 22(16), 15961–15966 CAS.
- J. T. Zhong, X. C. Xu and Y. S. Lin, Tunable Terahertz Metamaterial with Electromagnetically Induced Transparency Characteristic for Sensing Application, Nanomaterials, 2021, 11(9), 2175 CrossRef CAS PubMed.
- S. L. Ma, S. S. Wen, X. W. Mi and H. P. Zhao, Terahertz optical modulator and highly sensitive terahertz sensor governed by bound states in the continuum in graphene-dielectric hybrid metamaterial, Opt. Commun., 2023, 536, 129398 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |