Open Access Article
Open Access ArticleAssessing the efficacy of aluminum metal clusters Al13 and Al15 in mitigating NO2 and SO2 pollutants: a DFT investigation†
Sajida Riffat Laraib a,
Ji Liu
a,
Ji Liu *a,
Yuan-gu Xiaa,
Yang-wen Wu
*a,
Yuan-gu Xiaa,
Yang-wen Wu a,
Mohsen Doust Mohammadib,
Nayab Fatima Noorc and
Qiang Lu
a,
Mohsen Doust Mohammadib,
Nayab Fatima Noorc and
Qiang Lu a
a
aNational Engineering Research Center of New Energy Power Generation, North China Electric Power University, Beijing 102206, China. E-mail: liujipower@ncepu.edu.cn
bSchool of Chemistry, College of Science, University of Tehran, Tehran 14176, Iran
cMilitary College of Signals, National University of Science and Technology, Rawalpindi, Pakistan
First published on 8th April 2024
Abstract
The present investigation delves into the adverse environmental impact of atmospheric pollutant gases, specifically nitrogen dioxide (NO2) and sulfur dioxide (SO2), which necessitates the identification and implementation of effective control measures. The central objective of this study is to explore the eradication of these pollutants through the utilization of aluminum Al13 and Al15 metal clusters, distinguished by their unique properties. The comprehensive evaluation of gas/cluster interactions is undertaken employing density functional theory (DFT). Geometric optimization calculations for all structures are executed using the ωB97XD functional and the Def2-svp basis set. To probe various interaction modalities, gas molecule distribution around the metal clusters is sampled using the bee colony algorithm. Frequency calculations employing identical model chemistry validate the precision of the optimization calculations. The quantum theory of atoms in molecules (QTAIM) and natural bond orbital (NBO) methodologies are applied for the analysis of intermolecular interactions. This research establishes the robust formation of van der Waals attractions between the investigated gas molecules, affirming aluminum metal clusters as viable candidates for the removal and control of these gases.
1. Introduction
Sulfur dioxide (SO2) and nitrogen dioxide (NO2) are deleterious gases with pronounced implications for both human health and environmental integrity.1–3 SO2 emanates predominantly from the combustion of sulfur-laden fossil fuels, such as coal and oil.4,5 Consequently, power plants and industrial facilities that utilize these fuels contribute significantly to atmospheric SO2 concentrations. This emission not only raises concerns for air quality and human health but also underscores the environmental impact of energy production.6,7 Upon release into the atmosphere, SO2 undergoes reactions with other compounds, precipitating the formation of fine particulate matter and thereby contributing to atmospheric pollution.2,8 Prolonged exposure to heightened concentrations of SO2 poses a significant threat to respiratory health,9 manifesting in conditions such as asthma10 and bronchitis.11 Conversely, NO2, another byproduct of combustion processes, also engenders the formation of fine particulate matter and ground-level ozone, exacerbating broader air quality concerns.12,13 Persistent exposure to elevated NO2 levels is associated with respiratory ailments and the exacerbation of pre-existing conditions. Moreover, both SO2 and NO2 are implicated in the acidification of soil and water bodies,14 thereby instigating ecological imbalances and adversely affecting aquatic ecosystems.15 Mitigating emissions of these pollutants is imperative to uphold human health standards and preserve environmental equilibrium.Diverse materials have been applicated in the mitigation of gases within various environmental contexts, notably in the realms of air purification and industrial procedures. For instance, activated carbon,16 distinguished by its expansive surface area and porous structure, is extensively utilized for gas adsorption owing to its capacity to entrap and retain a spectrum of pollutants, including volatile organic compounds and malodorous gases.17,18 Zeolites, crystalline aluminosilicate minerals, manifest selective adsorption properties, rendering them efficacious in the removal of specific gases and contaminants.19,20 Besides, metal–organic frameworks represent a contemporary material class characterized by tunable structures, proffering elevated surface areas and customized functionalities conducive to gas adsorption and separation.21,22 Furthermore, scrubbers employing liquid agents like sodium hydroxide or calcium oxide demonstrate proficiency in adsorbing and neutralizing acidic gases such as sulfur dioxide.23 Molecular sieves,24 silica gels,25 and activated alumina26 are other important materials used as gas removal compounds. The selection of gas removal materials is contingent upon factors such as the targeted gas pollutants, operational conditions, and the desired efficacy of the removal process. Ongoing research and advancements in material science persist in broadening the spectrum of options for efficacious gas removal across diverse applications.
Within the scope of adsorbing materials, aluminum metallic clusters have emerged as a compelling frontier, garnering significant attention from researchers globally.27 The distinctive properties and behaviors of these clusters have rendered them particularly intriguing. Notably, possessing an expansive surface-to-volume ratio, these nanoclusters exhibit a plethora of remarkable attributes that set them apart from their bulk aluminum counterparts.28,29 Their diminutive size and augmented surface area result in a profusion of active sites conducive to catalyzing chemical reactions, thereby establishing them as highly efficient catalysts for a diverse array of chemical transformations.30 Moreover, the utilization of synthesis techniques such as physical vapor deposition, chemical vapor deposition, and cluster beam methods facilitates the precise tailoring of aluminum nanocluster structures, encompassing control over their size, shape, and composition. This exceptional tunability empowers researchers to delve into the intricate interplay between structure and properties.31–33 Aluminum nanoclusters exhibit versatile applications across various disciplines. As a catalyst, their noteworthy catalytic activities prove advantageous for the creation of innovative and efficient catalysts, thereby impacting diverse industrial processes.34 Additionally, the incorporation of these nanoclusters into electronic systems presents a potential avenue for the advancement of electronic components characterized by enhanced performance and miniaturization.27,35,36
Broadly speaking, the employment of atomic metal clusters of transition metals, coupled with diverse nanocages, represents a prevalent approach in the utilization of material for the adsorption and regulation of polluting gases, the purification of liquids, and the remediation of environmental contaminants. Mohammadi et al.37 have demonstrated the potential of atomic clusters of gold and silver to adsorb the atmospheric polluting gases, specifically highlighting their impact on SO2 and NO2. Furthermore, a research conducted by the same group has unveiled the efficacy of zinc and zinc oxide clusters in the adsorption and containment of gases, including carbon dioxide, etc.38 In a distinct investigation, Hussain et al.39 have undertaken fundamental research to elucidate the interaction dynamics between B12N12 nanocage and Phosgene gas. In a research by Guardado et al.40 the prominent role of lithium atomic clusters in hydrogen gas storage has been highlighted. Numerous instances exemplify the pivotal role played by metal clusters, oxides,41 hydrides,42 and hydroxides,43 serving as highly pragmatic advanced materials primarily deployed in the fabrication of electronic devices,44 drug delivery systems,45,46 water purification technologies,47 and respiratory air purification methodologies,48,49 among other applications.
Aluminum metal clusters are poised as versatile assets with considerable utility across a spectrum of applications, particularly in the area of sensor innovation and gas purification technologies.50 Their unique electronic and chemical properties endow them with a diverse array of functionalities. In the domain of gas sensing, aluminum clusters serve as pivotal sensing elements, interacting with gas molecules to effect changes in electrical conductivity, optical characteristics, or surface reactivity.51 This inherent adaptability facilitates the discernment of a wide gamut of gases, including those of a hazardous nature, within industrial, environmental, and medical contexts. Furthermore, aluminum clusters assume a catalytic role, expediting chemical reactions essential to the mitigation of pollutants, thereby bolstering the efficacy of gas abatement methodologies for air decontamination and environmental remediation efforts.52 Moreover, the integration of aluminum clusters into porous substrates or nanocomposite matrices augments their capacity for gas adsorption, particularly towards species such as carbon dioxide, sulfur dioxide, and volatile organic compounds. This enhancement is of paramount significance in curtailing the emission of pollutants from industrial sources, vehicular exhausts, and indoor environments. Additionally, aluminum-based materials, inclusive of metal clusters, are under scrutiny for their potential in hydrogen storage applications. In this capacity, these clusters function as adept hydrogen adsorbents, enabling the reversible storage and release of hydrogen gas for utilization in fuel cell technologies and other energy-centric endeavors.53–55
The objective of the upcoming research is to use quantum mechanical calculations to study intermolecular interactions of SO2 and NO2 gases onto the exterior surface of aluminum atomic clusters of Al13 and Al15. In addition, the methodology employed for computing adsorption energy is explicated, accompanied by a brief theoretical discourse on various facets of the calculations. For the computational scrutiny of the specified systems, the initial imperative lies in determining the stable ground state of aluminum clusters. A comprehensive elucidation of the procedures for generating and identifying the most stable ground state, predicated upon the energy content of atomic clusters, is provided in Section 3.1. Section 3.2 delves into the electronic structure of the aforementioned clusters. Sections 3.3 and 3.4 of this study encompass an analysis of the interactions between the gas and the cluster, employing various methodologies such as natural bond orbital (NBO) and quantum theory of atoms in molecules (QTAIM). The examination involves a comprehensive investigation into the nature of these interactions. Subsequently, in Section 4, a succinct summary of the research findings will be presented. This final section encapsulates the overarching conclusions derived from the analytical processes conducted in the preceding sections.
2. Computational details
The ωB97XD functional, with a dispersion correction term, effectively predicts electronic structure and energetics, considering repulsive and interactive electron influences, notably addressing long-range van der Waals interactions. Hence, employing the ωB97XD functional.56 This approach extends the functionality of the prevalent ωB97 functional by amalgamating the empirical long-range correction (LC) articulated by Handy and Cohen with the PBE functional pioneered by Perdew, Burke, and Ernzerhof. The incorporation of dispersion corrections within the ωB97XD framework serves to accommodate van der Waals interactions, pivotal for an accurate depiction of non-covalent interplays among molecules, encompassing dispersion forces, π–π stacking, and hydrogen bonding. These enhancements in dispersion corrections substantially augment the fidelity of the method, especially in scenarios where non-covalent interactions wield pronounced influence, as observed in molecular aggregates, supramolecular complexes, and biomolecular systems. By integrating dispersion corrections, ωB97XD furnishes a more equitable portrayal of both short-range exchange–correlation interactions and long-range dispersion interactions, thereby engendering enhanced precision in the prognosis of diverse molecular attributes, spanning molecular geometries, energies, reaction barriers, and intermolecular interactions. This method excels in noncovalent interaction studies, reaction energies, pathways, and spectroscopic characteristics.57–59The Def2-svp basis set is recognized for accuracy in diverse chemical configurations, combines functions for valence electrons with polarization functions to address electron correlation effects and is chosen for its comprehensive coverage, elucidating complex interplays among molecular components, which is suitable for intermediate-sized molecules and moderately correlated systems.60,61 The research focuses on optimizing the geometries of Al13 and Al15 clusters, along with gaseous NO2 and SO2 species, and conducting frequency analysis to ensure the stability of complexes/monomers. The Def2-SVP (SVP stands for single valence with polarization) and Def2-TZVPP (TZVPP stands for triple zeta valence with polarization and diffuse functions) basis sets are both widely used in computational chemistry for quantum mechanical calculations. These basis sets are designed to provide increasingly accurate descriptions of molecular electronic structure by systematically including more basis functions. The Def2-SVP basis set includes a moderate number of basis functions, usually sufficient for calculations on small to medium-sized molecules. It comprises a single valence set with additional polarization functions to account for electron correlation effects and diffuse functions to capture the electronic behavior in regions of low electron density. On the other hand, the Def2-TZVPP basis set is more extensive, incorporating triple zeta valence quality functions with additional polarization and diffuse functions. This allows for a more accurate representation of the electronic wavefunction and can yield more precise results, especially for larger and more complex molecular systems. The advantage of using the Def2-SVP basis set lies primarily in its computational efficiency without compromising significantly on accuracy. Since it contains fewer basis functions compared to Def2-TZVPP, calculations using Def2-SVP typically require less computational resources in terms of memory and CPU time. This makes Def2-SVP particularly advantageous for preliminary studies, high-throughput screenings, or when computational resources are limited. Additionally, the moderate size of the Def2-SVP basis set can sometimes lead to more stable and reliable convergence behavior in electronic structure calculations compared to larger basis sets, especially for systems where electronic correlation effects are not dominant.
The investigation and analysis of the electronic characteristics of the structures mentioned above have been a subject of scholarly discourse. The focus of this examination primarily centers on the evaluation of the frontier molecular orbitals (FMOs). To achieve a comprehensive understanding of the nature of intermolecular interactions, analyses based on the quantum theory of atoms in molecules (QTAIM) and natural bond orbital (NBO) methodologies have been implemented. The geometry structures of the gaseous species NO2 and SO2 were constructed using Gauss View software,62 with optimization and stability evaluations conducted through the Gaussian 09 package.63 The extraction of precise geometric arrangements for the aluminum clusters Al13 and Al15 was accomplished using the ABCluster 3.1.64 This software incorporates a sophisticated module for the automated allocation of two gas molecules and clusters to disparate spatial coordinates. These spatial arrangements, hereinafter referred to as “configurations,” undergo geometric optimization to identify those demonstrating utmost stability in relation to their ground state energy content. Selected configurations are then subjected to further analysis. The NBO 3.1 software,65 integrated into the Gaussian 09 package, was employed for executing NBO and QTAIM calculations. Additionally, the Multiwfn66 package was utilized to elucidate and visualize the resultant findings based on electronic structure analyses.
The quantification of adsorption energy (Eads) is contingent upon the intricate framework of supramolecular theory referred to eqn (1).67,68 This methodology involves the energy contributions originating from both the self-contained cluster and the targeted gaseous entity. The amalgamation of these two distinct magnitudes results in the subsequent deduction of the aggregated energy value characterizing the gas@cluster configurations. Additionally, it is demonstrated that the correction pertaining to zero-point energy (ZPEC) is concurrently administered, and this correction is derived through frequency calculations.
| Eads = Ecomplex − (Egas + Ecluster) + ΔEZPEC | (1) |
The method employed for ascertaining the optimal structure of Al13 and Al15 clusters involved the initial generation of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries for each structural isomers of a cluster utilizing specialized ABCluster software, with subsequent determination of their total energy employing the CHARMM force field.69 Subsequently, isoenergies were subjected to a screening process, and a representative sample was chosen for each energy level. In the subsequent stage, 1000 structures were subjected to semi-empirical calculations using the xtb software,70 and the total energy of these systems was computed utilizing the PM7 method. Ultimately, 100 structures characterized by the most stable energy levels were identified and submitted to the Gaussian software for DFT calculations. This sequential approach facilitated a comprehensive exploration of the energy landscapes of the respective clusters, contributing to the identification of structurally the most stable configurations. Ultimately, the selection process led to the identification of the most stable cluster, and its corresponding XYZ structure is presented in Table S1 within the (ESI†) section. It is to note that all clusters have been thoroughly already examined at 273 K and 1 atmospheric pressure using Gaussian Package.
000 geometries for each structural isomers of a cluster utilizing specialized ABCluster software, with subsequent determination of their total energy employing the CHARMM force field.69 Subsequently, isoenergies were subjected to a screening process, and a representative sample was chosen for each energy level. In the subsequent stage, 1000 structures were subjected to semi-empirical calculations using the xtb software,70 and the total energy of these systems was computed utilizing the PM7 method. Ultimately, 100 structures characterized by the most stable energy levels were identified and submitted to the Gaussian software for DFT calculations. This sequential approach facilitated a comprehensive exploration of the energy landscapes of the respective clusters, contributing to the identification of structurally the most stable configurations. Ultimately, the selection process led to the identification of the most stable cluster, and its corresponding XYZ structure is presented in Table S1 within the (ESI†) section. It is to note that all clusters have been thoroughly already examined at 273 K and 1 atmospheric pressure using Gaussian Package.
3. Results and discussion
3.1 Geometry optimization
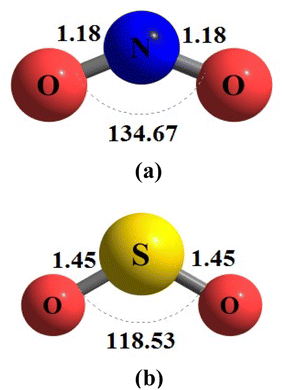
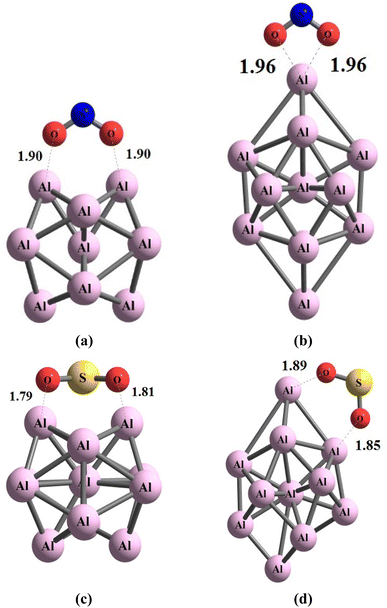
During the initial computational stage, it is imperative to verify the spatial morphology of aluminum clusters to identify their most stable configuration. The inherent lack of symmetry in these clusters complicates the determination of their optimal structure. Consequently, a specialized software ABCluster64 has been designed to address this challenge. This software facilitates the generation of diverse spatial shapes, which can then be transmitted as input files to the Gaussian 09 (ref. 63) software for subsequent DFT calculations. This research does not delve into the intricacies of the artificial bee colony algorithm, which is employed in the software; however, the comprehensive descriptions of the bee colony algorithm can be found in relevant ref. 64, 71 and 72.In Fig. 1, section (a), presents data on the bond length and interatomic angle of the NO2 molecule, wherein the interatomic angle measures 134.67 Radians (rad), and the oxygen–nitrogen bond length is quantified at 1.18 Angstroms (Å). Subsequently, Fig. 1b depicts corresponding metrics for the SO2 molecule, revealing an interatomic angle of 118.53 rad and a sulfur–oxygen bond length of 1.45 Å. The observed reduction in the interatomic angle in the SO2 molecule can be attributed to an increasement of lone pair electrons within the valence layer of the sulfur atom. Subsequent computations demonstrate alterations in these bond lengths and angles as a consequence of interactions with aluminum clusters. Fig. 2 depicts the structural representations of aluminum clusters comprising 13 and 15 atoms in part (a) and (b), respectively. Given the intricate nature of these structures, involving numerous angles and varied bond lengths, the XYZ coordinates corresponding to these clusters have been systematically tabulated in Table S1.† Subsequently, utilizing a graphic tool, a comprehensive visualization of these structures has been generated, allowing for a detailed examination of pertinent structural information. Symmetry plays a pivotal role in dictating the stability of molecular configurations, exemplified by aluminum clusters such as Al13 and Al15. Al13, characterized by its pronounced symmetry, assumes an icosahedral geometry, thereby facilitating optimal aluminum atom packing, thereby mitigating repulsive forces and augmenting stability. Conversely, Al15, owing to its larger size, tends to manifest a more intricate and asymmetrical configuration, leading to less efficient atom packing and potentially heightened internal strain. Consequently, the stability of Al15 typically pales in comparison to that of Al13. In essence, the heightened symmetry inherent in Al13 significantly bolsters its stability relative to the less symmetrical Al15 cluster, as symmetry profoundly influences atom arrangements within the cluster, thereby modulating their interactions and overall stability characteristics.
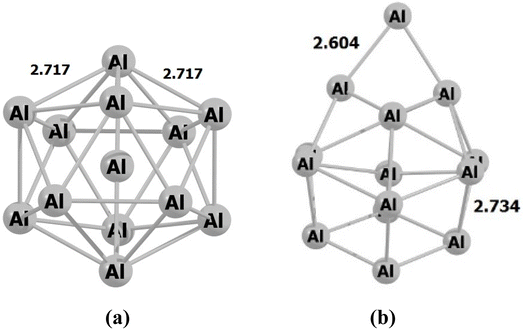 | ||
| Fig. 2 The figure illustrates an scheme of the geometry of the structures associated with (a) Al13 and (b) Al15 through optimization utilizing the ωB97XD/Def2-svp method. The values are in Å. | ||
The disparate interaction characteristics of SO2 gas with aluminum clusters, contingent upon whether the interaction occurs from the side of the sulfur atom or the oxygen atoms, result in distinct adsorption energies (Eads). Furthermore, the outer surface of aluminum clusters exhibits diverse adsorption sites, necessitating a comprehensive examination of the entire cluster environment. Consequently, it becomes imperative to systematically investigate the adsorption energies of SO2 or NO2 gas molecules around the cluster molecule from various orientations. This investigative process, conventionally labor-intensive, has prompted the development of a specialized module within the ABCluster software. This module facilitated the automated generation of diverse gas@cluster configurations, streamlining the exhaustive exploration of adsorption energies under varying spatial arrangements. The investigation entails the consideration of a myriad of gas@cluster configurations, necessitating the determination of their respective adsorption energies to identify the most stable configuration. The methodology employed for discerning the most stable gas@cluster configuration mirrors the approach delineated earlier for determining aluminum cluster isomers. This consistent methodological framework has been systematically applied, resulting in the identification and documentation of 10 stable configurations, which are detailed in the ESI† section, specifically outlined in Table S1.† It is pertinent to elucidate that the nomenclature “gas@cluster_n” signifies the desired configuration indexed by n.
The examination of adsorption behaviors of NO2 and SO2 onto aluminum clusters, specifically Al13 and Al15, reveals intriguing insights into the stability of the resulting structures and their respective adsorption energies. The adsorption energies of NO2 and SO2 gases on clusters Al13 and Al15 exhibit variability contingent upon the spatial orientation of the respective molecules. The tabulated values in Table 1 elucidate this discrepancy, revealing a range of adsorption energies between −2.61 and −3.1 eV for NO2 gas adsorption on the aluminum cluster with 13 atoms. Notably, the configuration NO2@Al13_4 (i.e. −3.1 eV) emerges as the most stable configuration within this context. Fig. 3, part (a), provides a visual representation of this system, although it is advisable to reference Table S1† for a more comprehensive understanding and a superior spatial visualization in graphical interfaces such as Gauss View. This approach allows for the observation and tracking of atomic angles, interatomic distances, and dihedral angles. The comprehensive presentation of such information within the textual narrative is deemed impractical and would not match the efficacy of a graphical interface. The variance in adsorption energy values observed between Al15 clusters and NO2 gas molecules spans from −2.49 to −3.97 eV, with these respective values corresponding to configurations NO2@Al15_6 and NO2@Al15_1. In Fig. 3, part (b), a schematic representation is presented illustrating the orientation of the NO2 gas molecule on the outer surface of the Al15 cluster, wherein the maximum adsorption energy is attained, signifying its optimal stability. Upon comparing the optimal configurations of Al13 and Al15 clusters in their interactions with NO2 gas, it is deduced that the aluminum cluster composed of 15 atoms exhibits a superior adsorption capacity in comparison to its 13-atom counterpart which enables Al15 to effectively hold NO2 on it surface. The aluminum cluster composed of 15 atoms exhibited a better ability to accept electrons with a higher electrophilicity value η (eV) of 2.61 eV.
| Systems | εHOMO (eV) | εLUMO (eV) | HLG (eV) | μ (eV) | η (eV) | ω | EE (HF) | Eads (eV) |
|---|---|---|---|---|---|---|---|---|
| Al13 | −7.1261 | −2.0126 | 5.1136 | 4.5693 | 2.5568 | 4.0830 | −3150.595438 | — |
| Al15 | −5.6140 | −1.9794 | 3.6346 | 3.7967 | 1.8173 | 3.9659 | −3635.319898 | — |
| NO2 | −10.0282 | −0.2057 | 9.8225 | 5.1170 | 4.9112 | 2.6657 | −204.848691 | — |
| SO2 | −11.2848 | −1.5842 | 9.7006 | 6.4345 | 4.8503 | 4.2681 | −548.2876908 | — |
| NO2@Al13_1 | −7.0597 | −2.0526 | 5.0072 | 4.5561 | 2.5036 | 4.1457 | −3355.554484 | −3.0029 |
| NO2@Al13_2 | −7.1223 | −2.2256 | 4.8967 | 4.6740 | 2.4483 | 4.4614 | −3355.539934 | −2.6070 |
| NO2@Al13_3 | −7.0611 | −2.0536 | 5.0074 | 4.5574 | 2.5037 | 4.1477 | −3355.554484 | −3.0029 |
| NO2@Al13_4 | −6.8690 | −2.1813 | 4.6877 | 4.5251 | 2.3439 | 4.3682 | −3355.558329 | −3.1075 |
| NO2@Al13_5 | −7.1231 | −2.2248 | 4.8983 | 4.6740 | 2.4492 | 4.4599 | −3355.539942 | −2.6072 |
| NO2@Al13_6 | −7.0603 | −2.0531 | 5.0072 | 4.5567 | 2.5036 | 4.1467 | −3355.554484 | −3.0029 |
| NO2@Al13_7 | −7.0595 | −2.0523 | 5.0072 | 4.5559 | 2.5036 | 4.1452 | −3355.554484 | −3.0029 |
| NO2@Al13_8 | −7.0608 | −2.0528 | 5.0080 | 4.5568 | 2.5040 | 4.1463 | −3355.554484 | −3.0029 |
| NO2@Al13_9 | −7.1229 | −2.2256 | 4.8972 | 4.6742 | 2.4486 | 4.4614 | −3355.539931 | −2.6069 |
| NO2@Al13_10 | −7.1337 | −1.7111 | 5.4227 | 4.4224 | 2.7113 | 3.6066 | −3355.551638 | −2.9255 |
| NO2@Al15_1 | −7.1672 | −1.9394 | 5.2279 | 4.5533 | 2.6139 | 3.9658 | −3840.314374 | −3.9670 |
| NO2@Al15_2 | −6.6331 | −1.8838 | 4.7492 | 4.2584 | 2.3746 | 3.8184 | −3840.294603 | −3.4290 |
| NO2@Al15_3 | −7.0437 | −2.2245 | 4.8191 | 4.6341 | 2.4096 | 4.4562 | −3840.296942 | −3.4927 |
| NO2@Al15_4 | −6.5343 | −2.1606 | 4.3737 | 4.3474 | 2.1868 | 4.3213 | −3840.277461 | −2.9626 |
| NO2@Al15_5 | −6.6649 | −1.8975 | 4.7674 | 4.2812 | 2.3837 | 3.8445 | −3840.309092 | −3.8233 |
| NO2@Al15_6 | −6.7898 | −2.1347 | 4.6551 | 4.4623 | 2.3275 | 4.2775 | −3840.260096 | −2.4900 |
| NO2@Al15_7 | −7.0328 | −2.2346 | 4.7982 | 4.6337 | 2.3991 | 4.4748 | −3840.296952 | −3.4929 |
| NO2@Al15_8 | −6.5917 | −2.0332 | 4.5585 | 4.3125 | 2.2792 | 4.0797 | −3840.283349 | −3.1228 |
| NO2@Al15_9 | −6.4388 | −1.8814 | 4.5574 | 4.1601 | 2.2787 | 3.7974 | −3840.287373 | −3.2323 |
| NO2@Al15_10 | −6.9520 | −2.3130 | 4.6390 | 4.6325 | 2.3195 | 4.6259 | −3840.295392 | −3.4505 |
| SO2@Al13_1 | −6.5525 | −2.6360 | 3.9165 | 4.5942 | 1.9583 | 5.3892 | −3698.983339 | −2.7269 |
| SO2@Al13_2 | −6.6366 | −1.9775 | 4.6591 | 4.3070 | 2.3296 | 3.9815 | −3698.991228 | −2.9415 |
| SO2@Al13_3 | −6.8907 | −3.6240 | 3.2667 | 5.2574 | 1.6334 | 8.4611 | −3698.918967 | −0.9752 |
| SO2@Al13_4 | −7.2034 | −2.1119 | 5.0915 | 4.6576 | 2.5458 | 4.2607 | −3698.889817 | −0.1820 |
| SO2@Al13_5 | −6.6096 | −1.8297 | 4.7800 | 4.2197 | 2.3900 | 3.7251 | −3699.014201 | −3.5666 |
| SO2@Al13_6 | −6.6369 | −1.9783 | 4.6586 | 4.3076 | 2.3293 | 3.9830 | −3698.991235 | −2.9417 |
| SO2@Al13_7 | −6.6175 | −1.8305 | 4.7870 | 4.2240 | 2.3935 | 3.7272 | −3699.014199 | −3.5666 |
| SO2@Al13_8 | −6.6113 | −1.8281 | 4.7832 | 4.2197 | 2.3916 | 3.7225 | −3699.014199 | −3.5666 |
| SO2@Al13_9 | −6.6344 | −1.9764 | 4.6580 | 4.3054 | 2.3290 | 3.9794 | −3698.991233 | −2.9417 |
| SO2@Al13_10 | −6.8875 | −3.6599 | 3.2275 | 5.2737 | 1.6138 | 8.6171 | −3698.918964 | −0.9751 |
| SO2@Al15_1 | −6.5033 | −1.8354 | 4.6678 | 4.1693 | 2.3339 | 3.7241 | −4183.741918 | −3.6553 |
| SO2@Al15_2 | −6.4382 | −1.7121 | 4.7261 | 4.0752 | 2.3630 | 3.5139 | −4183.729714 | −3.3232 |
| SO2@Al15_3 | −6.4352 | −1.7108 | 4.7244 | 4.0730 | 2.3622 | 3.5114 | −4183.729714 | −3.3232 |
| SO2@Al15_4 | −6.0015 | −1.7290 | 4.2725 | 3.8652 | 2.1362 | 3.4968 | −4183.719169 | −3.0362 |
| SO2@Al15_5 | −6.4379 | −1.7119 | 4.7261 | 4.0749 | 2.3630 | 3.5135 | −4183.729715 | −3.3232 |
| SO2@Al15_6 | −6.2739 | −1.9094 | 4.3644 | 4.0916 | 2.1822 | 3.8359 | −4183.767472 | −4.3506 |
| SO2@Al15_7 | −6.4276 | −1.6460 | 4.7816 | 4.0368 | 2.3908 | 3.4080 | −4183.732452 | −3.3977 |
| SO2@Al15_8 | −6.9063 | −2.1647 | 4.7416 | 4.5355 | 2.3708 | 4.3383 | −4183.717038 | −2.9783 |
| SO2@Al15_9 | −6.4369 | −1.7121 | 4.7247 | 4.0745 | 2.3624 | 3.5138 | −4183.729715 | −3.3232 |
| SO2@Al15_10 | −6.4184 | −1.6414 | 4.7770 | 4.0299 | 2.3885 | 3.3996 | −4183.732399 | −3.3963 |
Concerning the adsorption of SO2 gas on the Al13 cluster, it is observed that the lowest adsorption energy corresponds to configuration SO2@Al13_4, with a value of −0.18 eV, while the highest energy is associated with configuration SO2@Al13_8, yielding a value of −3.57 eV. Notably, the range of adsorption energy variations for SO2 is found to be more extensive than that for NO2 on the external surface of the Al13 cluster. The underlying rationale for this discrepancy lies in the spatial orientation and the nature of interaction between the two molecular species. This underscores the significance of the orientation of valence layer orbitals of the interacting species, as the ease with which electrons can be accommodated in bonded electrons profoundly influences the intensity of the interaction. Consequently, the juxtaposition of the valence layer orbitals assumes a pivotal role in modulating the strength of interaction between SO2 and the Al13 cluster. The final system under investigation pertains to the interaction between SO2 gas and an aluminum cluster comprising 15 atoms. Within the scope of the 10 scrutinized configurations, the configuration denoted as SO2@Al15_8 exhibits the lowest adsorption energy, quantified at −2.98 eV, while configuration SO2@Al15_6 attains the highest value at −4.35 eV. The spatial arrangement of the SO2 gas molecule in conjunction with the Al13 cluster is illustrated in Fig. 3, part (c), and similarly, in part (d), the depiction extends to the same gas juxtaposed onto the aluminum cluster comprising 15 atoms. Upon scrutinizing the adsorption energies derived from these configurations, it becomes evident that the most robust interaction is manifested in the case of the SO2 species and the Al15 cluster.
It is imperative to acknowledge that the validity of each optimized molecular configuration has been substantiated through frequency calculations, wherein the absence of negative or imaginary frequencies signifies that the optimized structures at the extremum point pertain to the respective local minima. Table 2 provides a comprehensive compilation of all pertinent details derived from thermochemical computations. Additionally, a spectrum of thermochemical parameters, including thermal energy (TE), heat capacity (CV), and total entropy (S), is systematically presented, furnishing an extensive dataset for the scrutiny and reflection of researchers.
| Systems | ZPEC (HF) | TE (kcal mol−1) | CV (cal mol−1 k−1) | S (cal mol−1 k−1) |
|---|---|---|---|---|
| Al13 | 0.0218 | 24.782 | 61.097 | 132.777 |
| Al15 | 0.0242 | 28.625 | 72.091 | 151.074 |
| NO2 | 0.0095 | 7.767 | 6.728 | 57.224 |
| SO2 | 0.0072 | 6.458 | 7.433 | 59.329 |
| NO2@Al13_1 | 0.0329 | 34.183 | 72.376 | 152.296 |
| NO2@Al13_2 | 0.0318 | 33.885 | 73.305 | 158.562 |
| NO2@Al13_3 | 0.0329 | 34.183 | 72.378 | 152.293 |
| NO2@Al13_4 | 0.0331 | 34.069 | 72.330 | 147.962 |
| NO2@Al13_5 | 0.0318 | 33.893 | 73.280 | 157.861 |
| NO2@Al13_6 | 0.0329 | 34.183 | 72.374 | 152.267 |
| NO2@Al13_7 | 0.0329 | 34.183 | 72.375 | 152.285 |
| NO2@Al13_8 | 0.0329 | 34.183 | 72.379 | 152.292 |
| NO2@Al13_9 | 0.0318 | 33.882 | 73.312 | 158.743 |
| NO2@Al13_10 | 0.0320 | 33.962 | 73.174 | 156.721 |
| NO2@Al15_1 | 0.0360 | 38.245 | 82.822 | 170.247 |
| NO2@Al15_2 | 0.0363 | 38.085 | 82.837 | 163.019 |
| NO2@Al15_3 | 0.0351 | 37.979 | 83.666 | 172.509 |
| NO2@Al15_4 | 0.0346 | 37.805 | 83.936 | 174.061 |
| NO2@Al15_5 | 0.0369 | 38.282 | 82.400 | 161.244 |
| NO2@Al15_6 | 0.0362 | 38.531 | 83.072 | 172.842 |
| NO2@Al15_7 | 0.0352 | 37.984 | 83.654 | 172.259 |
| NO2@Al15_8 | 0.0357 | 38.142 | 83.140 | 171.082 |
| NO2@Al15_9 | 0.0360 | 38.236 | 82.854 | 169.617 |
| NO2@Al15_10 | 0.0352 | 37.398 | 81.641 | 165.674 |
| SO2@Al13_1 | 0.0315 | 32.8020 | 72.883 | 146.172 |
| SO2@Al13_2 | 0.0289 | 32.0450 | 74.617 | 154.653 |
| SO2@Al13_3 | 0.0301 | 32.7400 | 73.933 | 158.716 |
| SO2@Al13_4 | 0.0296 | 33.0170 | 74.400 | 170.079 |
| SO2@Al13_5 | 0.0301 | 32.3530 | 73.750 | 149.842 |
| SO2@Al13_6 | 0.0289 | 32.0430 | 74.618 | 154.608 |
| SO2@Al13_7 | 0.0301 | 32.3480 | 73.763 | 149.872 |
| SO2@Al13_8 | 0.0301 | 32.3530 | 73.753 | 149.880 |
| SO2@Al13_9 | 0.0290 | 32.0490 | 74.607 | 154.592 |
| SO2@Al13_10 | 0.0300 | 32.1540 | 71.961 | 152.376 |
| SO2@Al15_1 | 0.0335 | 36.541 | 84.118 | 167.290 |
| SO2@Al15_2 | 0.0333 | 36.549 | 84.262 | 167.679 |
| SO2@Al15_3 | 0.0333 | 36.551 | 84.257 | 167.653 |
| SO2@Al15_4 | 0.0332 | 36.496 | 84.344 | 168.639 |
| SO2@Al15_5 | 0.0333 | 36.549 | 84.261 | 167.701 |
| SO2@Al15_6 | 0.0330 | 36.203 | 84.427 | 165.639 |
| SO2@Al15_7 | 0.0331 | 36.473 | 84.399 | 169.217 |
| SO2@Al15_8 | 0.0326 | 36.624 | 84.616 | 177.921 |
| SO2@Al15_9 | 0.0333 | 36.548 | 84.261 | 167.667 |
| SO2@Al15_10 | 0.0331 | 36.476 | 84.383 | 168.920 |
3.2 Electronic structure
In the preceding section, we addressed the influence of different orientations of gas molecules around an aluminum cluster on adsorption energies. The electron redistribution within molecules results in an uneven electron distribution, with one part exhibiting greater electron density and another part demonstrating lower density. This phenomenon prompts an exploration of molecular reactivity. Logically, when a highly reactive portion of a gas molecule interfaces with a larger segment of a reactive cluster, a more robust interaction ensues between the participating species, leading to heightened adsorption energy. Additionally, the alignment of gas and cluster orbitals in the correct spatial orientation is a critical consideration, necessitating an examination of the electronic structure of the involved species. Theoretical explanations pertaining to conceptual density functional theory (CDFT) are provided in the ESI† section. In brief, it is observed that in the analysis of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), a smaller energy gap corresponds to increased reactivity of the species. Additionally, a higher electrophilic index (ω) value indicates greater reactivity for a given species. These indices afford a global assessment of the reactivity of two molecules in relation to each other. However, this analysis does not concern itself with determining the specific region of a molecule exhibiting greater reactivity.Upon closer examination of the data presented in Table 1, it becomes evident that the ω values for aluminum clusters consisting of 13 and 15 atoms are distinctive, yet equally noteworthy, with respective magnitudes of 4.0830 and 3.9659. The presented data unequivocally indicates nearly identical reactivity between the two clusters under consideration, with Al13 exhibiting a slightly elevated level. Nevertheless, it is reasonable to assert, with a high degree of approximation, that the global reactivity of the two clusters is essentially equivalent. Based on the electrophilicity index values obtained for NO2 gas (2.7) and SO2 gas (4.3), it is observed that the latter exhibits higher reactivity. It is crucial to underscore that the proper spatial alignment, orbital interaction, and promotion of charge transfer processes collectively contribute to the enhancement of adsorption energy. The findings derived from the adsorption energies, as presented in the preceding section, indicate that the maximum adsorption energy is achieved by SO2 gas in conjunction with the aluminum cluster Al15. Furthermore, the outcomes from the reactivity analysis align consistently with this observation, affirming the accurate prediction of the aforementioned conclusion.
Electrostatic potential (ESP) map serves as valuable tools for elucidating the distribution of electric charge within a molecule or molecular system. In Fig. 4 and 5 the positive and negative regions are depicted by solid and dashed lines respectively. These maps, which visualize the electrostatic potential on a molecular surface, offer crucial insights into diverse facets of a molecule's chemical and physical attributes. The key information derived from ESP maps are details concerning charge distribution, aiding in the identification of regions with positive and negative charges that are pivotal for comprehending chemical reactivity and interactions. Additionally, these maps provide indications of molecular dipole moments, enabling an understanding of molecular polarity and its impacts on various properties. The identification of functional groups is facilitated by specific patterns in electrostatic potential maps, contributing to the interpretation of a molecule's chemical nature. Furthermore, ESP maps assist in predicting sites conducive to nucleophilic and electrophilic attacks in chemical reactions by highlighting regions with high and low electron density, respectively. Hydrogen bonding patterns, essential for predicting and explaining molecular interactions, are discernible through these maps. The inclusion of solvent molecules in electrostatic potential calculations allows for an understanding of a molecule's interaction with its environment and provides insights into solvation effects.
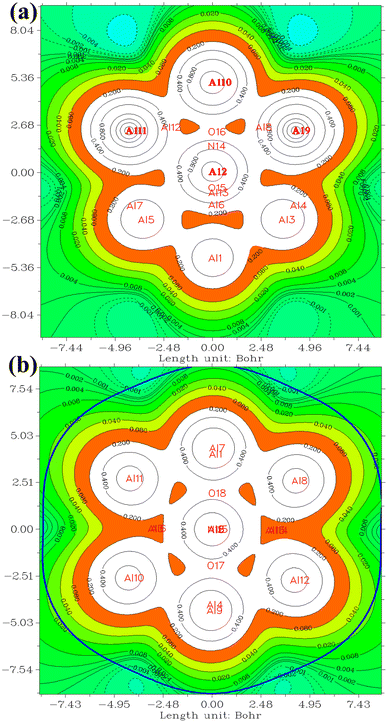
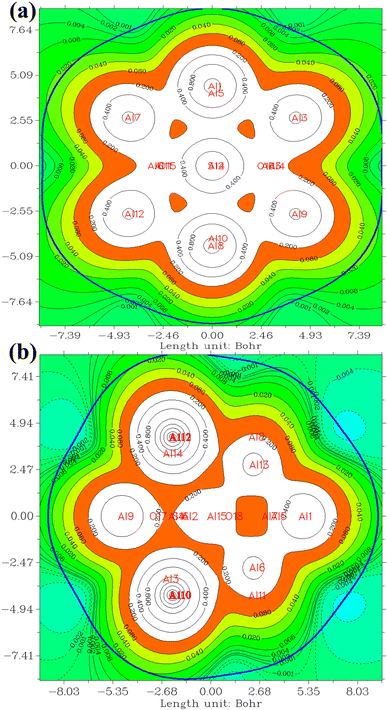
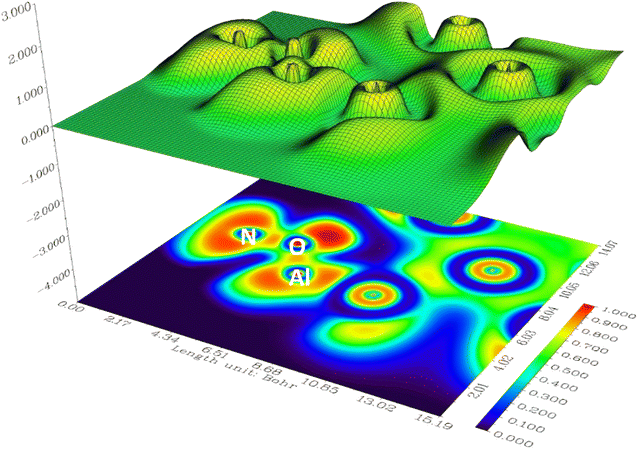
In the investigation of gas/cluster systems, the determination of electrophilic and nucleophilic sites within the adsorptive molecule often involves the utilization of ESP maps. The preceding section elucidated the process of sampling adsorption sites within the cluster molecule, wherein a comprehensive examination and sampling of the entire cluster were conducted. Subsequently, adsorption energy was calculated throughout the entirety of the cluster, resulting in a more extensive database than that derived solely from reactivity analysis. Reactivity analysis, conducted to identify electron-filled sites within the absorber molecule, entails placing the gas molecule in these identified areas and subsequently calculating the adsorption energy. Fig. 4 illustrates the interaction of NO2 gas with the cluster from the oxygen atom side, demonstrating a peak in the ESP map data. A similar observation is discernible in Fig. 5 concerning the interaction with SO2 gas.
3.3 NBO analysis
In computational chemistry, both natural bond orbital (NBO) analysis and Hartree–Fock (HF) theory constitute indispensable tools, each serving distinct purposes with inherent advantages. Unlike the delocalized depiction offered by HF theory, which encompasses the entire molecule, NBOs present a localized and chemically intuitive representation of electron density, focusing on specific atoms or bonds for enhanced clarity in understanding chemical bonding. Furthermore, NBO analysis facilitates a more straightforward interpretation of chemical bonds compared to the often-challenging interpretation of HF orbitals, particularly for complex molecules. Notably, NBO analysis excels in identifying and quantifying charge transfer, aiding in the comprehension of electron flow during chemical reactions, a feature less explicit in HF calculations. Additionally, while HF theory provides information about molecular orbitals, it may fall short in quantifying the strength of individual bonds, a limitation addressed by NBO analysis, which includes data on stabilization energies, thereby offering a quantitative measure of bond strength. Moreover, NBO results prove instrumental in predicting reactive sites within a molecule, contributing valuable insights into reaction mechanisms. Lastly, NBOs uniquely permit the quantification of electron delocalization, providing valuable information on the spread of electrons across multiple atoms or regions in a given molecular system.73–75Derived from electronic structure calculations, NBOs offer insights into the natural electron configurations associated with specific atoms or bonds within a molecule. By emphasizing localized orbitals, NBOs provide an intuitive and clear representation of electron distribution, enabling a comprehensive understanding of chemical bonding. The concept of “natural electron configuration” within NBO analysis pertains to the electron distribution in these localized NBOs, each with a defined electron occupancy. This analysis facilitates the identification of charge transfer, elucidates bonding characteristics, and quantifies the energetic stability of each orbital through occupancy and stabilization energy assessments. Additionally, NBO analysis enables the quantification of delocalization, shedding light on electron spread across different molecular regions.
Both NO2 and SO2 gases exhibit neutrality when considered in isolation, with distributed partial charges resulting in an overall charge of zero. The sulfur atom within the SO2 molecule carries a partial charge of 1.56, whereas each oxygen atom in this compound bears a charge of −0.78, as outlined in Table 3. Similarly, the partial charges for the nitrogen atom within the NO2 molecule are 0.54, and for each oxygen atom in the same molecule, the charge is −0.27. The distribution of electrons within the valence layer orbitals of each atom is presented in the natural electron configuration section of Table 3. Both analyses presented in this table furnish valuable data for comparing the isolated state of the specified gases with those engaged in interactions with aluminum clusters.
| System | Atom | Natural electron configuration | Natural charge |
|---|---|---|---|
| NO2 | N | [Core] 2S (1.17) 2p (3.21) 3S (0.03) 3p (0.03) 3d (0.02) | 0.5402 |
| O | [Core] 2S (1.74) 2p (4.52) 3p (0.01) 3d (0.01) | −0.2701 | |
| O | [Core] 2S (1.74) 2p (4.52) 3p (0.01) 3d (0.01) | −0.2701 | |
| SO2 | S | [Core] 3S (1.62) 3p (2.62) 4S (0.05) 3d (0.12) 4p (0.02) | 1.5600 |
| O | [Core] 2S (1.83) 2p (4.94) 3d (0.01) | −0.7800 | |
| O | [Core] 2S (1.83) 2p (4.94) 3d (0.01) | −0.7800 | |
| NO2@Al13_2 | N | [Core] 2S (1.46) 2p (3.09) 3S (0.03) 3p (0.02) 3d (0.02) | 0.3762 |
| O | [Core] 2S (1.72) 2p (5.04) 3p (0.01) | −0.7759 | |
| O | [Core] 2S (1.71) 2p (4.52) 3S (0.01) 3p (0.01) 3d (0.01) | −0.2543 | |
| NO2@Al15_1 | N | [Core] 2S (1.43) 2p (3.06) 3S (0.01) 3p (0.02) 3d (0.02) | 0.4515 |
| O | [Core] 2S (1.71) 2p (4.80) 3p (0.01) 3d (0.01) | −0.5200 | |
| O | [Core] 2S (1.71) 2p (4.80) 3p (0.01) 3d (0.01) | −0.5197 | |
| SO2@Al13_8 | S | [Core] 3S (1.60) 3p (3.29) 4S (0.01) 3d (0.06) 4p (0.02) | 1.0116 |
| O | [Core] 2S (1.76) 2p (5.29) | −1.0571 | |
| O | [Core] 2S (1.76) 2p (5.28) | −1.0479 | |
| NO2@Al15_6 | S | [Core] 3S (1.72) 3p (3.40) 4S (0.01) 3d (0.04) 4p (0.02) | 0.8184 |
| O | [Core] 2S (1.76) 2p (5.27) | −1.0425 | |
| O | [Core] 2S (1.79) 2p (5.37) | −1.1773 |
To ascertain the direction of charge transfer during the adsorption process—whether it occurs from the gas to the cluster or vice versa—a scrutiny of the algebraic sum of partial charges in the gas molecules suffices. As evident from the presented table, isolated gas molecules exhibit neutrality, with the algebraic sum of their partial charges equating to zero, as previously noted. Following the adsorption process, examination of NO2@Al13_2 configuration reveals that the sum of partial charges for gas atoms assume a value of −0.65. This observation indicates that a charge transfer has transpired from the Al13 cluster to the NO2 gas. One of the oxygen atoms within the gas molecule has exhibited a heightened significance in the charge transfer mechanism. Evidently, its partial charge has escalated from −0.27 to −0.78, concomitant with a modification in its associated orbital from 2p (4.52) to 2p (5.04). Furthermore, the 3d (0.01) subshell of this oxygen atom is found to be entirely unoccupied, with its electron density redistributed across alternative orbitals. The adsorption of NO2 on an Al15 cluster exhibits a similar behavior, albeit with a marginal reduction in the intensity of charge transfer. The algebraic summation of partial charges on NO2 gas atoms in the NO2@Al15_1 configuration yields a value of −0.59, indicating a slight attenuation compared to the preceding system's value of −0.65. Furthermore, alterations in the distribution of electron density within orbitals are discernible in this system. Specifically, the 2p orbital population for oxygen atoms has undergone an elevation from 4.52 to 4.80, while a noteworthy modification involves the upgrade of the nitrogen atom's 2S orbital from 1.17 to 1.43, as evident in the table.
The magnitude of charge transfer from aluminum clusters to SO2 gas surpasses that observed with NO2 gas, as evident in configuration SO2@Al13_8. The cumulative sum of partial gas charges equates to −1.09, indicating a notably substantial charge transfer. There are pronounced alterations in electron distribution within the orbitals, resulting in the complete vacuity of the 3d (0.01) orbital. Conversely, in oxygen atoms, the 2p orbitals have experienced an elevation from 4.94 to 5.29. Moreover, significant alteration have occurred in the valence layer of the sulfur atom, transitioning from [3S (1.62), 3p (2.62), 4S (0.05), 3d (0.12), 4p (0.02)] to [3S (1.60), 3p (3.29), 4S (0.01), 3d (0.06), 4p (0.02)]. In the NO2@Al15_6 system, pronounced charge transfer has been observed, reaching a maximum of −1.4. Notably, the 2p orbital of the oxygen atoms has undergone enhancement (i.e. 4.94 to 5.37), while the valence electron distribution of the sulfur atom has undergone a substantial transformation, resulting in the configuration of 3S (1.72), 3p (3.40), 4S (0.01), 3d (0.04), and 4p (0.02).
3.4 QTAIM analysis
The QTAIM methodology meticulously examines the characteristics and features of chemical bonds within molecular entities, providing an understanding of the spatial distribution of electron density and its topological aspects. The determination of electron density originates from quantum mechanical computations and encompasses the probability of locating an electron at a specific spatial coordinate. The QTAIM methodology is intricately complex and posits an alternative conceptualization of atomic interactions surpassing conventional chemical bonding. Detailed exposition is eschewed in this context, as numerous sources are available for the thorough examination of the theory.76,77 The ensuing discussion will focus exclusively on the interpretation of the results acquired. A concise introduction to this theory is attempted in the ESI† section for reference.Table 4 presents data concerning bond critical points (3, −1). A detailed analysis reveals electron density values within the narrow range of 0.03 to 0.045. This range serves as a crucial indicator of the strength and resilience of the intermolecular bonds dictating the behavior of the examined system. Notably, the electron density of bond critical points between NO2 and Al clusters is consistently lower than that of points between SO2, implying a more robust interaction between SO2 and Al clusters. This observation aligns with the higher adsorption energies of SO2. Of particular interest is the pervasive negative sign characterizing electron density Laplacian throughout the system. This distinctive attribute enhances the favorable nature of the system's electronic structure. Negative Laplacian indicate regions of maximum electron accumulation, reinforcing the significance of intermolecular forces governing interactions within the system. Fig. 6 provides a visual representation of bond critical points in the NO2@Al13 system. The minutely varied electron density values, coupled with the consistently negative Laplacian, underscore the intricate dynamics of intermolecular interactions within the system.
| Systems | Bond | ρ(r) | ∇2 ρ(r) | G(r) | V(r) | G(r)/|V(r)| | ELF | LOL |
|---|---|---|---|---|---|---|---|---|
| NO2@Al13_2 | O⋯Al | 0.0374 | −0.0122 | 0.0101 | −0.0233 | 0.4343 | 0.7422 | 0.2206 |
| O⋯Al | 0.0368 | −0.011 | 0.0092 | −0.0212 | 0.4348 | 0.4135 | 0.1725 | |
| NO2@Al15_1 | O⋯Al | 0.0367 | −0.0085 | 0.0093 | −0.0206 | 0.4484 | 0.7699 | 0.2243 |
| O⋯Al | 0.0366 | −0.0023 | 0.0092 | −0.019 | 0.4849 | 0.7604 | 0.2230 | |
| SO2@Al13_8 | O⋯Al | 0.036 | −0.0066 | 0.009 | −0.0197 | 0.4584 | 0.7301 | 0.2191 |
| O⋯Al | 0.0392 | −0.0055 | 0.0136 | −0.0286 | 0.4761 | 0.7262 | 0.2187 | |
| SO2@Al15_6 | O⋯Al | 0.0395 | 0.0133 | 0.0169 | −0.0304 | 0.5549 | 0.6736 | 0.2117 |
| O⋯Al | 0.0439 | −0.0094 | 0.0156 | −0.0336 | 0.4650 | 0.6951 | 0.2147 |
The index G(r)/|V(r)|, serves as an essential metric for revealing insights into the robustness of the bond formed between gas and aluminum clusters. Consider the case of the Al13 cluster and its interaction with NO2 gas, where a value of 0.43 is observed, slightly below the critical threshold of 0.5. As explained in ESI,† these numerical outcomes indicate the covalent nature of the interactions. For the Al15 cluster interacting with NO2 gas, the index exhibits values of 0.44 and 0.48, resembling a strong affinity between the aluminum cluster and NO2 gas molecules. Notably, this finding reinforces the established trend, corroborating previous meticulous analyses. It is noteworthy that the subtle disparity in favor of the Al13 cluster, as observed in these investigations, aligns with knowledge from prior inquiries.
The investigation of the interaction between SO2 gas and aluminum atomic clusters is examined through a comprehensive QTAIM analysis, aimed at elucidating the intricacies of this phenomenon. The results derived from this analysis reveal significant insights, particularly demonstrating that the intermolecular interactions between the gas and clusters exhibit characteristics akin to covalent bonds. By meticulous examination of the interaction between SO2 and the Al13 atomic cluster, the G(r)/|V(r)| index attains a noteworthy value of 0.37 at its maximum potency. The exploration of the adsorption process of this gas on the Al13 cluster reveals additional data points, with values of 0.45 and 0.47, underscoring the profound nature of the gas/cluster interaction. Similarly, the investigation into the interaction of SO2 gas with the Al15 cluster yields compelling observations. In this context, the G(r)/|V(r)| index manifests values of 0.46 and 0.55, further substantiating the robust nature of the bond formed during this process. Additionally, the G(r)/|V(r)| of SO2@Al13/15 exceeds that of NO2@Al13/15, aligning with the adsorption energies and indicating the increased stability of SO2 adsorption on the Al cluster. Notably, the G(r)/|V(r)| of SO2@Al15 surpasses others, corresponding to its highest adsorption energy.
In the context of these findings, it becomes evident that both SO2 gases are intricately entangled within the potential field of these aluminum clusters. The established bond exhibits remarkable strength, resisting facile attempts to disassociate it. The robustness of the gas-cluster bond holds paramount significance and presents substantial potential in addressing the deleterious environmental effects associated with these gases. Given the profound implications of this research, its applications are diverse. The newfound understanding of the formidable strength and stability of these gas-cluster interactions opens promising avenues for utilizing Al clusters as potent absorbents, offering a means to alleviate the environmental impact of SO2 gases. Innovative approaches leveraging these clusters hold great promise in fostering a cleaner and more sustainable future.
The electron localization function (ELF) serves as a valuable tool for scrutinizing the electron density distribution within a given molecular entity. Its utility extends to the provision of insights into the extent of electron localization or delocalization, thereby facilitating the identification of regions characterized by varying degrees of electron pairing strength. The interpretation of ELF results hinges upon the consideration of specific parameters, including low ELF values, which approximate zero and denote regions of electron delocalization, such as those found in aromatic systems or conjugated π systems. Conversely, high ELF values, approximating one, indicate localized regions where electrons are tightly bound or strongly paired, as observed around atoms participating in covalent bonds or lone pairs. Furthermore, ELF proves instrumental in the analysis of weak interactions, such as van der Waals forces or hydrogen bonding, with high ELF values in hydrogen bonding regions signifying pronounced electron localization.78,79 The LOL exhibits comparable expressions to the ELF. Specifically, the chemically significant regions highlighted by both LOL and ELF demonstrate qualitative similarities. However, Jacobsen80 has pointed out that LOL imparts a more decisive and clearer depiction than ELF. While LOL can be interpreted kinetically, similar to ELF, it also lends itself to an interpretation based on localized orbitals which leads to the clusters suitable for the eradication of pollutants.
Table 4 displays ELF values for the investigated systems, consistently indicating elevated and nearly unitary values. This observation suggests that the interatomic interactions within these systems are predominantly of a covalent nature. For instance, in NO2@Al13_2 system, the ELF attains a value of 0.7422, underscoring the robust and covalent nature of the bond between oxygen and aluminum atoms. Fig. 7 has been included to enhance comprehension, where regions corresponding to O–Al and N–O bonds are highlighted in red, denoting the presence of covalent interatomic interactions. Furthermore, the red coloring surrounding nitrogen (N) and oxygen (O) atoms signifies the existence of lone pairs of electrons. The tabular data reveals that interactions involving gas atoms and aluminum clusters exhibit a pronounced strength, indicating a proximity to covalency. This deduction aligns with the findings of the preceding section's topological analysis, wherein similarly robust interactions were anticipated.
4. Conclusions
This study investigates the intricate molecular interactions between NO2 and SO2 gases with Al13 and Al15 clusters. The clusters, characterized by adsorption energies surpassing the 2.0 eV threshold, display significant potential for efficiently eliminating noxious gases, making them viable candidates for further examination. Through systematic optimization of geometric configurations and rigorous analyses, valuable insights emerge. The electrophilicity index proves crucial in assessing cluster reactivity, with the SO2 gas demonstrating superior reactivity due to its compact arrangement. Natural electron configuration and natural charge analyses reveal the nature of charge transfer through gas/cluster interactions, with the SO2/Al15 system exhibiting intensive charge transfer properties. QTAIM analysis provides detailed insights into the robust covalent bonding between both gases and aluminum clusters, indicating exceptional bond strength. G(r)/|V(r)| index values further underscore the substantial bonding affinity of SO2 gas with both Al13 and Al15 clusters. These findings show promise in mitigating environmental pollution from SO2 gases, suggesting the potential application of clusters as adsorbents. Employing a comprehensive array of analytical tools, this study enhances our understanding of gas-cluster interactions, presenting new possibilities for environmental and industrial contexts. Further exploration using advanced computational methods holds the potential to unveil deeper insights, contributing to a cleaner and more sustainable future.Author contributions
Sajida Riffat Laraib: investigation, methodology, validation, writing – original draft, review & editing. Ji Liu: conceptualization, funding acquisition, supervision, writing – original draft, review & editing. Yuan-gu Xia: validation, writing – review & editing. Yang-wen Wu: validation, funding acquisition, writing – review & editing. Mohsen Doust Mohammadi: methodology, formal analysis. Nayab Fatima Noor: methodology, formal analysis. Qiang Lu: conceptualization, funding acquisition, writing – review & editing.Conflicts of interest
There is no conflict of interest for this manuscript.Acknowledgements
This work was supported by the National Natural Science Foundation of China (52376182, 52276189); Natural Science Foundation of Jiangsu Province (BK20221248); China Postdoctoral Science Foundation (2022M721131); and Fundamental Research Funds for the Central Universities (2023JC009).References
- D. Burtraw and E. Mansur, Environ. Sci. Techonl., 1999, 33, 3489–3494 CrossRef CAS.
- S. Oesch and M. Faller, Corros. Sci., 1997, 39, 1505–1530 CrossRef CAS.
- D. O. Johns and W. S. Linn, Inhalation Toxicol., 2011, 23, 33–43 CrossRef CAS PubMed.
- V. Perraud, J. R. Horne, A. S. Martinez, J. Kalinowski, S. Meinardi, M. L. Dawson, L. M. Wingen, D. Dabdub, D. R. Blake and R. B. Gerber, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13514–13519 CrossRef CAS PubMed.
- J. A. De Gouw, D. D. Parrish, G. J. Frost and M. Trainer, Earth's Future, 2014, 2, 75–82 CrossRef CAS.
- S. M. Serbula, J. S. Milosavljevic, J. V. Kalinovic, T. S. Kalinovic, A. A. Radojevic, T. L. A. Trujic and V. M. Tasic, Sci. Total Environ., 2021, 777, 145981 CrossRef CAS PubMed.
- B. Kamarehie, M. Ghaderpoori, A. Jafari, M. Karami, A. Mohammadi, K. Azarshab, A. Ghaderpoury, A. Alinejad and N. Noorizadeh, J. Adv. Environ. Health Res., 2017, 5, 44–50 CAS.
- B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100 RSC.
- P. Orellano, J. Reynoso and N. Quaranta, Environ. Int., 2021, 150, 106434 CrossRef CAS PubMed.
- A. L. Reno, E. G. Brooks and B. T. Ameredes, Environ. Health Insights, 2015, 9, 13–25 Search PubMed.
- Y. Khajeamiri, S. Sharifi, N. Moradpour and A. Khajeamiri, J. Air Pollut. Health, 2021, 5(4), 243–258 Search PubMed.
- Y.-K. Park and B.-S. Kim, Chem. Eng. J., 2023, 461, 141958 CrossRef CAS.
- B. Yang, K. M. Zhang, W. D. Xu, S. Zhang, S. Batterman, R. W. Baldauf, P. Deshmukh, R. Snow, Y. Wu and Q. Zhang, Environ. Sci. Technol., 2018, 52, 4574–4582 CrossRef CAS PubMed.
- Q. Yu, T. Zhang, X. Ma, R. Kang, J. Mulder, T. Larssen and L. Duan, Environ. Sci. Technol., 2017, 51, 9498–9506 CrossRef CAS PubMed.
- A. Bouwman, D. Van Vuuren, R. Derwent and M. Posch, Water, Air, Soil Pollut., 2002, 141, 349–382 CrossRef CAS.
- H.-C. Shin, J.-W. Park, K. Park and H.-C. Song, Environ. Pollut., 2002, 119, 227–236 CrossRef CAS PubMed.
- D. Das, V. Gaur and N. Verma, Carbon, 2004, 42, 2949–2962 CrossRef CAS.
- M. P. Cal, M. J. Rood and S. M. Larson, Sep. Purif. Technol., 1996, 10, 117–121 CrossRef CAS.
- M. W. Ackley, S. U. Rege and H. Saxena, Microporous Mesoporous Mater., 2003, 61, 25–42 CrossRef CAS.
- M. Ozekmekci, G. Salkic and M. F. Fellah, Fuel Process. Technol., 2015, 139, 49–60 CrossRef CAS.
- N. A. Khan, Z. Hasan and S. H. Jhung, J. Hazard. Mater., 2013, 244, 444–456 CrossRef PubMed.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- Y. Sun, E. Zwolińska and A. G. Chmielewski, Crit. Rev. Environ. Sci. Technol., 2016, 46, 119–142 CrossRef CAS.
- C. C. Lin, K. A. Dambrowitz and S. M. Kuznicki, Can. J. Chem. Eng., 2012, 90, 207–216 CrossRef CAS.
- J. Lee, S. Han and T. Hyeon, J. Mater. Chem., 2004, 14, 478–486 RSC.
- S. I. Alhassan, L. Huang, Y. He, L. Yan, B. Wu and H. Wang, Crit. Rev. Environ. Sci. Techonl., 2021, 51, 2051–2085 CrossRef CAS.
- A. Schnepf and H. Schnöckel, Angew. Chem., Int. Ed., 2002, 41, 3532–3554 CrossRef CAS.
- J. Demuynck, M. M. Rohmer, A. Strich and A. Veillard, J. Chem. Phys., 1981, 75, 3443–3453 CrossRef CAS.
- J. Koutecky and P. Fantucci, Chem. Rev., 1986, 86, 539–587 CrossRef CAS.
- S. Nigam and C. Majumder, Appl. Surf. Sci., 2021, 547, 149160 CrossRef CAS.
- G. Linti and H. Schnöckel, Coord. Chem. Rev., 2000, 206, 285–319 CrossRef.
- Z. Luo, A. Castleman Jr and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492 CrossRef CAS PubMed.
- P. Dumitraschkewitz, S. S. Gerstl, L. T. Stephenson, P. J. Uggowitzer and S. Pogatscher, Adv. Eng. Mater., 2018, 20, 1800255 CrossRef.
- S. Das, S. Pal and S. Krishnamurty, J. Phys. Chem. C, 2014, 118, 19869–19878 CrossRef CAS.
- V. S. Zharinov, T. Picot, J. E. Scheerder, E. Janssens and J. Van de Vondel, Nanoscale, 2020, 12, 1164–1170 RSC.
- A. Datta, S. S. Mallajosyula and S. K. Pati, Acc. Chem. Res., 2007, 40, 213–221 CrossRef CAS PubMed.
- M. D. Mohammadi, N. Patsalidis, S. Bhowmick, V. A. Harmandaris and G. Biskos, RSC Adv., 2023, 13, 18014–18024 RSC.
- M. D. Mohammadi, H. Louis, U. G. Chukwu, S. Bhowmick, M. E. Rasaki and G. Biskos, ACS Omega, 2023, 8, 20621 CrossRef PubMed.
- S. Hussain, R. Hussain, M. Y. Mehboob, S. A. S. Chatha, A. I. Hussain, A. Umar, M. U. Khan, M. Ahmed, M. Adnan and K. Ayub, ACS Omega, 2020, 5, 7641–7650 CrossRef CAS PubMed.
- A. Guardado, I.-R. Marisol, R. Mayén-Mondragón and M. Sánchez, J. Mol. Graph. Model., 2023, 122, 108491 CrossRef CAS PubMed.
- A. Azari, R. R. Kalantary, G. Ghanizadeh, B. Kakavandi, M. Farzadkia and E. Ahmadi, RSC Adv., 2015, 5, 87377–87391 RSC.
- M. Krstić, A. Zavras, G. N. Khairallah, P. Dugourd, V. Bonačić-Koutecký and A. Richard, Int. J. Mass Spectrom., 2017, 413, 97–105 CrossRef.
- F. Zare, M. Ghaedi, A. Daneshfar, S. Agarwal, I. Tyagi, T. A. Saleh and V. K. Gupta, Chem. Eng. J., 2015, 273, 296–306 CrossRef CAS.
- M. Mil’vidskii and V. Chaldyshev, Semiconductors, 1998, 32, 457–465 CrossRef.
- K. Bhattacharyya and S. Mukherjee, Bull. Chem. Soc. Jpn., 2018, 91, 447–454 CrossRef CAS.
- R. Sinha, G. J. Kim, S. Nie and D. M. Shin, Mol. Cancer Ther., 2006, 5, 1909–1917 CrossRef CAS PubMed.
- B. Huang, Z. Wu, H. Zhou, J. Li, C. Zhou, Z. Xiong, Z. Pan, G. Yao and B. Lai, J. Hazard. Mater., 2021, 412, 125253 CrossRef CAS PubMed.
- J. B. DeCoste and G. W. Peterson, Chem. Rev., 2014, 114, 5695–5727 CrossRef CAS PubMed.
- N. Vershinin, I. Balikhin, O. Efimov, E. Kabachkov and E. Kurkin, J. Phys. Conf., 2018, 1134, 012067 CrossRef.
- N. S. King, L. Liu, X. Yang, B. Cerjan, H. O. Everitt, P. Nordlander and N. J. Halas, ACS Nano, 2015, 9(11), 10628–10636 CrossRef CAS PubMed.
- R. Leuchtner, A. Harms and A. Castleman Jr, J. Chem. Phys., 1991, 94(2), 1093–1101 CrossRef CAS.
- R. Jones, Phys. Rev. Lett., 1991, 67(2), 224 CrossRef CAS PubMed.
- J. Akola, M. Manninen, H. Häkkinen, U. Landman, X. Li and L. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(19), 13216 CrossRef CAS.
- J. Akola, H. Häkkinen and M. Manninen, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(7), 3601 CrossRef CAS.
- D. Cox, D. Trevor, R. Whetten, E. Rohlfing and A. Kaldor, J. Chem. Phys., 1986, 84(8), 4651–4656 CrossRef CAS.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- D. Jacquemin, E. A. Perpete, I. Ciofini and C. Adamo, Theor. Chem. Acc., 2011, 128, 127–136 Search PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017 RSC.
- J. Witte, J. B. Neaton and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234105 CrossRef PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758 RSC.
- D. Phlip, Adv. Mater., 1996, 8(10), 866–868 CrossRef.
- B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels and S. Boresch, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wires. Comput. Mol. Sci., 2021, 11, e1493 CrossRef CAS.
- D. Karaboga and B. Akay, Appl. Math. Comput., 2009, 214, 108–132 CrossRef.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- F. Weinhold and C. R. Landis, Chem. Educ. Res Pract., 2001, 2, 91–104 RSC.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. Bader, Monatsh. Chem., 2005, 136, 819–854 CrossRef CAS.
- E. Matito, B. Silvi, M. Duran and M. Sola, J. Chem. Phys., 2006, 125, 024301 CrossRef PubMed.
- F. Hao, R. Armiento and A. E. Mattsson, J. Chem. Phys., 2014, 140, 18A536 CrossRef PubMed.
- H. Jacobsen, Can. J. Chem., 2008, 86, 695–702 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra00708e |
| This journal is © The Royal Society of Chemistry 2024 |