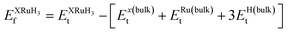DOI:
10.1039/D4RA00204K
(Paper)
RSC Adv., 2024,
14, 8385-8396
A DFT investigation on structural, electronic, magnetic, optical, elastic and hydrogen storage properties of Ru-based hydride-perovskites XRuH3 (X = Cr, V, Ni)
Received
8th January 2024
, Accepted 20th February 2024
First published on 11th March 2024
Abstract
The present investigation delves into various physical properties exhibited by CrRuH3, VRuH3 and NiRuH3. Notably adopting a stable cubic configuration, both compounds manifest a distinct metallic demeanor characterized by an absolute absence of band gap. In-depth analysis through Total Density of States (TDOS) and Partial Density of States (PDOS) justify this metallic conduct by distinctly showcasing peak conductivity at the Fermi level. The materials' magnetic behavior reveals an antiferromagnetic disposition for CrRuH3 and NiRuH3, while their intrinsic attributes emerge as anisotropic and rigid. Applying Poisson's ratio (ν) and the B/G ratio, all investigated compounds show ductility, but the CrRuH3 is superior among them. The heightened values of Young's modulus, Bulk modulus, and mean shear modulus observed in CrRuH3 underscore its enhanced rigidity as compared to VRuH3 and NiRuH3. Within the optical realm, CrRuH3 displays notable optical conductivity and absorption, particularly within the lower energy spectrum. Remarkably, at 0 eV, CrRuH3 showcases elevated reflectivity and refractive index as compared to the other investigated materials. On the hydrogen storage front, XRuH3 (X = Cr, V, Ni) exhibit promising potential, yet CrRuH3 emerges as the more favorable candidate for hydrogen storage applications.
1. Introduction
Technological advancements in modern societies have generated an escalating demand for energy. This surge in energy requirements can be attributed to improved living standards and population growth. The global energy agency confirms that fossil fuels continue to serve as the primary source fulfilling these mounting energy demands.1,2 It is imperative to acknowledge that while fossil fuels fulfill our energy needs, they concurrently release a significant volume of CO2, posing a grave environmental threat. Environmental pollution stems from the release of CO2 through the combustion of various fossil fuels. This emission plays a pivotal role in global warming and exerts detrimental effects on the natural environment.3,4 Astonishingly, CO2 emissions, which were approximately 20.7 billion tons in 1990, surged dramatically to an astounding 32.5 billion tons in 2006.5,6 Furthermore, a study examining hydrogen storage revealed a substantial CO2 emission rate of 35%.7 While a minor concentration of CO2 in the air poses no harm to humans, heightened emissions could potentially lead to health issues such as headaches, dizziness, and confusion. This concern extends to animals and aquatic life as well. Escalating CO2 emissions also exacerbate global warming, resulting in severe weather phenomena like floods, deforestation, and droughts. The continuous reliance on fossil fuels not only inflicts adverse impacts on the environment but also depletes finite natural resources, underscoring the critical need to explore renewable energy sources capable of meeting societal needs without inflicting environmental harm. Emerging as an auspicious alternative to fossil fuels due to its abundance and environmental compatibility, hydrogen deserves attention. Its combustion exclusively produces water, rendering it a clean choice.3 Crucially, hydrogen combustion avoids the release of carbon dioxide, positioning it as a genuinely green energy source. Despite hydrogen's threefold higher energy content by weight compared to gasoline, its volume energy content lags, a fact countered by the superior efficiency of hydrogen fuel cells when compared to gasoline engines.4,8 The applicability of hydrogen extends beyond vehicles to industries, promoting ecological sustainability. Recently, perovskite hydrides have garnered attention for hydrogen storage applications.9,10 Adhering to the ABX3 formula,10,11 with A and B representing cations and X denoting an anion, these materials prove adaptable. The anion X can be interchanged with oxygen as well as nitrogen and we can also change it with halogens and fluorine,12,13 rendering perovskite hydrides a versatile solution for hydrogen storage.7,14,15 A perovskite material assumes the designation “halide perovskite” upon the substitution of X with an element from the halide group. Correspondingly, it is commonly referred to as “nitride-perovskite”, “oxide-perovskite”, or “fluoro-perovskite” at the point when nitrogen, oxygen, or fluorine replaces X, respectively. These variants adhere to the general formulae16–19 ABO3, ABN3, and ABF3, with each fulfilling distinct roles: nitride-perovskites in electronic components, oxide-perovskites in photocatalytic applications, and fluoro perovskites in lens materials. Intriguingly, halide-perovskites have proven highly effective for modern solar cells.20–25 The introduction of hydrogen into ABX3 yields a hydride perovskite,26,27 denoted as ABH3. However, the challenge of employing hydrogen as a fuel lies in its intricate storage requirements.28–30 Significantly, the prospects for employing perovskite hydrides, denoted by the chemical configuration ABH3, as a resolution for hydrogen storage are quite promising.31–39 These compounds display fundamental attributes, such as strong hydrogen bonding, spacious gaps facilitating considerable hydrogen storage, catalytic properties that augment hydrogen uptake, and suitable gravimetric hydrogen storage capabilities. Generally, hydride perovskites demonstrate gravimetric densities spanning from 1.2 to 6.0 weight percent.33 The transition metal based hybrid perovskites XCuH3 (X = Co, Ni, Zn) possess a high gravimetric hydrogen storage capacity and are considered as a promising choice for hydrogen storage application.40 Compared to alternative methods, metal hydride perovskites offer a safer and more efficient option for hydrogen storage41–43 This comprehensive study investigates the structural, optical, electronic, mechanical, magnetic, and hydrogen storage properties of novel ternary perovskite hydrides incorporating XRuH3 (X = Cr, V, Ni). Through Density Functional Theory (DFT), we will analyze the properties of investigated compounds for hydrogen storage applications. The scrutiny spans an in-depth assessment of the structural, optical, electronic, mechanical, and magnetic attributes of XRuH3 (X = Cr, V, Ni). This leads us to an in-depth assessment of the structural, optical, electronic, mechanical, and magnetic properties of XRuH3 (X = Cr, V, Ni). We hope this research article significantly play a role as a bridge between theoretical and experimental literature and offers contribution to the scholarly corpus. We divide our research into different sections to make it reader friendly and more understandable: our first section which is actually an Introduction part where we discuss the scope, utility, hurdles and their solutions as well as the applications of perovskite hydride. Section 2 elaborates the computational work which we employed. In Section 3, we delve into outcomes and discussions concerning perovskite hydrides XRuH3 (X = Cr, V, Ni). Ultimately, Section 4 discuss the conclusion and findings of our research.
2. Computational methodology
The CASTEP package44 was utilized to finely tune the arrangement of the XRuH3 (X = Cr, V, Ni) hydride perovskites. This code, CASTEP, was also put to use to thoroughly examine various aspects of these materials. We adopted a method called the GGA exchange–correlation functional from ultra-soft USP plane wave PBE to delve into the characteristics of XRuH3 (X = Cr, V, Ni), including their shape, electrical properties, magnetic behavior, optical response, and mechanical strength. We employed the plane wave pseudopotential technique rooted in density functional theory (DFT) to address the Kohn–Sham equations. This technique creates a set of plane waves as a foundation, extending the concept through periodic boundary conditions.45,46 Then we employed first principles pseudopotentials to effectively manage interactions between electrons and ions within the Vanderbilt-type ultrasoft formulations, mimicking how they interact in reality.47 Prior research highlighted the superiority of the BFGS energy minimization approach in evaluating electron wave functions and charge distributions in crystalline materials. To facilitate this study, the Pulay density mixing approach was also applied.48,49 The Monkhorst–Pack technique was harnessed to meticulously sample unique points within the first Brillouin zone. An energy cutoff value of 600 eV was selected, complemented by k-points mesh featuring 6 × 6 × 6 points, chosen for greater precision. The discrepancy in energy per atom was confined to 2 × 10−5 eV. Notably, the ionic Hellmann–Feynman force was restricted to a maximum of 0.05 eV Å−1. Throughout the calculations, the stress was managed to stay within the confines of 0.1 GPa, while the most considerable atomic displacement was limited to 2 × 10−3 Å. For all calculations, a highly refined self-consistent field (SCF) convergence threshold and energy tolerance per atom were upheld. The PBE-GGA approach was additionally employed for the purpose of assessing elastic constants, a crucial aspect in the evaluation of structural integrity and correlated mechanical characteristics. In each instance of elongation or compression, a structured four-step methodology was implemented, employing a peak strain amplitude of 0.003 as the upper limit. The variance in energy per atom was maintained at a level of 4 × 10−6 eV, while the upper threshold for ionic Hellmann–Feynman force was confined to 0.01 eV Å−1. When examining the effects of compression, a maximum atomic displacement of 4 × 10−4 Å was selected. The application of an ultra-fine convergence threshold ensured accuracy both in optimizing geometry and evaluating measures of elasticity. The inquiry into these characteristics was undertaken only after confirming the optimal configuration of the fundamental building block.
3. Results and discussions
3.1. Structural properties
In this section, we present an examination of the structural attributes exhibited by hydrides following the perovskite-type arrangement, denoted as XRuH3 (X = Cr, V, Ni). These specific perovskite hydrides showcase a cubic crystal configuration, categorized within the pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with international number of 221. The depiction of the cubic crystal structure of XRuH3 (X = Cr, V, Ni) can be observed in Fig. 1. During the process of optimizing the unit cell, a systematic approach was adopted, involving the strategic positioning of X cations at the corners, with the central point occupied by the less abundant metal, Ru, and the face-centered sites adorned by hydrogen atoms. Detailed information regarding the lattice constants, volume, and band gap energy specific to the XRuH3 (X = Cr, V, Ni) perovskite hydrides is presented in Table 1. It's noteworthy that the lattice constant of VRuH3 surpasses that of CrRuH3 and NiRuH3, similarly reflecting a greater volume for VRuH3 in contrast to CrRuH3 and NiRuH3 perovskite hydrides. The formation enthalpy of all the compounds was calculated with the help of the following equation50
m space group with international number of 221. The depiction of the cubic crystal structure of XRuH3 (X = Cr, V, Ni) can be observed in Fig. 1. During the process of optimizing the unit cell, a systematic approach was adopted, involving the strategic positioning of X cations at the corners, with the central point occupied by the less abundant metal, Ru, and the face-centered sites adorned by hydrogen atoms. Detailed information regarding the lattice constants, volume, and band gap energy specific to the XRuH3 (X = Cr, V, Ni) perovskite hydrides is presented in Table 1. It's noteworthy that the lattice constant of VRuH3 surpasses that of CrRuH3 and NiRuH3, similarly reflecting a greater volume for VRuH3 in contrast to CrRuH3 and NiRuH3 perovskite hydrides. The formation enthalpy of all the compounds was calculated with the help of the following equation50
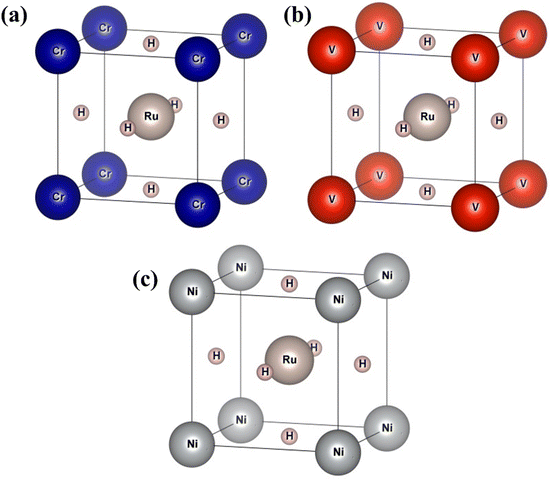 |
| | Fig. 1 Unit cell of (a) CrRuH3, (b) VRuH3 and (c) NiRuH3. | |
Table 1 The values of band gap energy, volume and lattice parameters
| Compound |
Lattice constant (Å) (a = b = c) |
Volume (Å)3 |
Band gap (eV) |
Reference |
| CrRuH3 |
3.350 |
37.597 |
0 |
Present study |
| VRuH3 |
3.385 |
38.004 |
0 |
Present study |
| NiRuH3 |
3.348 |
37.516 |
0 |
Present study |
| CoCuH3 |
3.328 |
36.882 |
0 |
40 |
| NiCuH3 |
3.324 |
36.742 |
0 |
40 |
| ZnCuH3 |
3.612 |
47.160 |
0 |
40 |
The formation energy is found −1.72, −1.09 and −1.30 eV per atom for CrRuH3, NiRuH3, and VRuH3 respectively. Further the stability of investigated compounds is also analyzed using the phonon spectra in Fig. 4 where the graph clearly depicts that the NiRuH3.has no negative frequencies as compared to the other two compounds. The resulting cohesive energy values of −5.11, −4.63 and −4.00 eV per atom affirm the robustness of the crystal structures of CrRuH3, VRuH3 and NiRuH3. However, in light of the more negative cohesive energy, the crystal structure of CrRuH3 holds a stronger recommendation for stability compared to the other investigated compounds. Moving beyond, we delve into the mechanical aspect of stability, gauged through an assessment of elastic constants. The outcome of this evaluation, as expounded in Section 3.4, reveals the mechanical stability of compounds under investigation.
3.2. Electronic band structure and density of states
When analyzing the electronic attributes of a substance, careful consideration of the examination of its electronic band structure and DOS becomes of utmost significance. The compound's electronic band arrangement can be comprehended through the application of TDOS and PDOS, elucidating the atomic interactions and the relaxation of these atoms contribute to the electronic band configuration.
Fig. 2 shows how atoms in XRuH3 (X = Cr, V, Ni) are arranged to create electronic bands. The point of zero energy, known as the Fermi level, is marked by a dashed black line at 0 eV in these bands. Think of the bands as different energy levels within the material. The upper part is like a busy highway for electrons, called the conduction band, while the lower part is like a resting area, called the valence band. The gap between them is called the band gap. But interestingly, for XRuH3 (X = Cr, V, Ni), these bands overlap, which means there's no clear band gap. This suggests that the material behaves more like a metal in this case. In Fig. 3, we have graphs that show the overall amount of energy states (TDOS) and partial density of states (PDOS) in XRuH3 (X = Cr, V, Ni). Think of these energy states as distinct positions within a framework. Some positions are more populated than others, indicating where energy levels gather. Specifically, in the valence region (analogous to the lower segment of this framework), energy levels reach their highest values at 0.60 eV, 0.99 eV, and 2.62 eV for CrRuH3, VRuH3, and NiRuH3 respectively, precisely aligned with the Fermi level. We also see more peaks at 17.45 eV, 17.10 eV, and 8.35 eV for CrRuH3, VRuH3, and NiRuH3 respectively. Looking deeper into how the electrons are arranged, the TDOS helps. In the valence area, the d-states contributes to energy levels from −10 to 0 eV, while the p-states affect energy levels from 10 to 20 eV in the upper region. Interestingly, the s-states do not play a big role in the lower part for any compound, but it's more active in the upper parts of all the materials we're studying. The coexistence of s-states and p-states at the Fermi level solidifies the metallic nature of these compounds, signifying their potential as novel materials for harnessing low-energy incident radiations. This unique property positions these compounds as capable hydrogen storage vessels owing to their intermetallic phase.51 Moving onward, CrRuH3 exhibits bond lengths of 1.68 Å (H–Ru) and 2.37 Å (H–Cr), VRuH3 exhibits bond lengths of 1.69 Å (H–Ru) and 2.39 Å (H–V), whereas NiRuH3 displays bond lengths of 1.67 Å (H–Ru) and 2.37 Å (H–Ni). Notably, the bond lengths within VRuH3 exceed those in CrRuH3 and NiRuH3 attributed to differences in ionic radii. This difference highlights the substantial bond strength present in these compounds, thereby enhancing their potential for hydrogen storage. The ionic radii of Cr, V, Ni, and Ru, measuring at 200, 179, 163, and 205 picometers respectively, could induce matrix distortion upon doping or substitution, resulting in matrix expansion. This expansion effectively increases interstitial sites, thus bolstering the capacity for hydrogen storage or absorption. Furthermore, these compounds are capable of experiencing the creation of intermetallic compounds through chemical reactions with hydrogen, contributing to the further enhancement of the storage process.
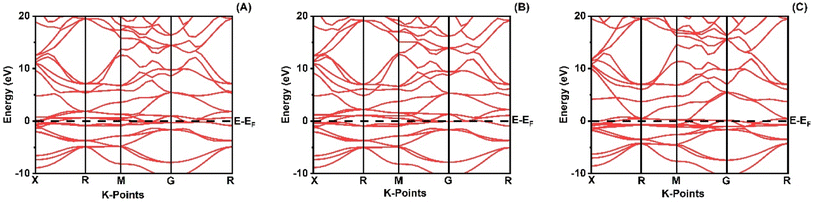 |
| | Fig. 2 Band structure of (A) CrRuH3, (B) VRuH3 and (C) NiRuH3. | |
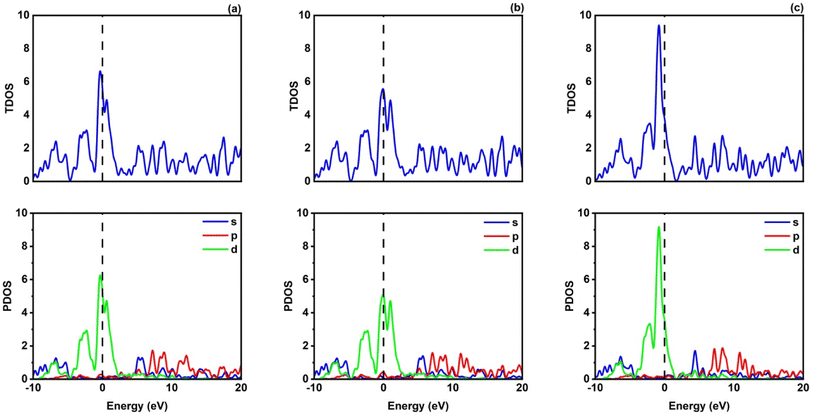 |
| | Fig. 3 TDOS and PDOS of (a) CrRuH3, (b) VRuH3 and (c) NiRuH3. | |
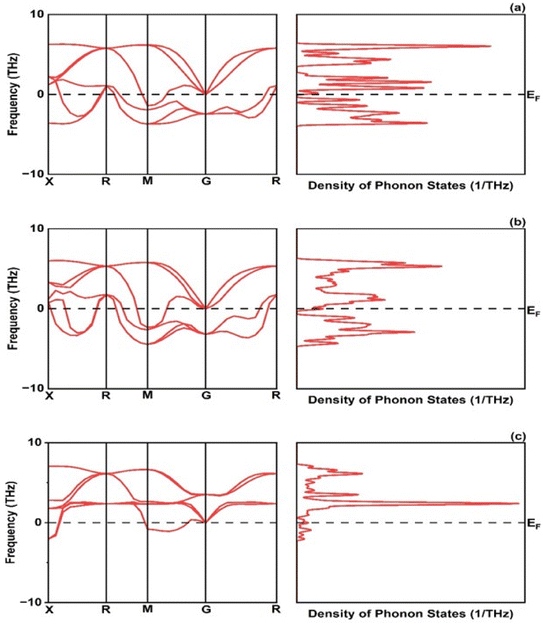 |
| | Fig. 4 Phonon dispersion and density of phonon states: (a) CrRuH3, (b) VRuH3 and (c) NiRuH3. | |
3.3. Magnetic properties
The magnetic properties of XRuH3 (X = Cr, V, Ni) arise due to a combination of inherent material traits and the specific arrangement of atoms. To understand these magnetic behaviors better, we conducted a detailed examination of the spin-polarized band structures of XRuH3 (X = Cr, V, Ni) using the PBE + GGA functional approach, which is a specific method for studying these materials. These band structures are like visual maps that show how electrons in the material's atoms behave. In these maps, the red lines represent electrons with one kind of spin (a property related to their movement), and blue lines represent electrons with a different spin. Similarly, when we looked at the density of different energy states, we used black lines for one type of spin and red lines for the other. The Fermi level is a special energy point in the material, and we indicated it with a red line on these maps, right at 0 eV. We looked at how different materials (XRuH3 where X is Cr, V, or Ni) behave when it comes to magnets. To do this, we checked the way the spins of the particles are arranged and how they affect the energy levels of the materials. In the pictures labeled Fig. 5 and 6, we showed how these spins affect the energy levels. Among the materials we studied, CrRuH3 and NiRuH3 don't act like magnets because their spins are like mirror images of each other, both in the parts with more energy and in the parts with less energy. This means they don't create any overall magnetic force. Our findings about how the spins are arranged in CrRuH3 and NiRuH3 support the idea that these materials don't act like regular magnets. This is because their spins cancel each other out; making them what we call “antiferromagnetic compounds”. In simple terms, the way their tiny magnetic forces add up is zero.52 Nevertheless, the VRuH3 demonstrates magnetic nature due to the imbalance noted in the spin up↑ and down↓ conditions. The magnetism attribute of VRuH3, being of a metallic disposition, renders it a distinctive substance for the storing of hydrogen. There were some variations in the spin behavior in VRuH3 compared to the others. This is linked to our earlier observation that there is no clear gap in energy levels (band gap) in both CrRuH3 and NiRuH3 compounds. Additionally, we noticed that the energy levels where electrons can be found were getting really close to each other, suggesting that these materials can easily conduct electricity. For a deeper understanding of how electrons are behaving and why the materials show magnetic properties, we also looked at the density of states with different spins. This gives us information about how many energy states are available for different types of electron spins. Fig. 6 illustrates these densities for the materials we studied. We marked the Fermi level with precision, and it's still at 0 eV. What's interesting is that the graphs representing densities for different spins look very similar to each other, except for VRuH3, where they seem to be like mirror images, just opposite to each other. This suggests that the overall magnetic behavior in these materials is neutral; they don't have a dominant magnetic direction. As a result, both CrRuH3 and NiRuH3 show an antiferromagnetic behavior, meaning their magnetic behavior opposes the usual magnetic patterns. This antiferromagnetic property is also noticeable when looking at certain energy states within the spin-polarized density of states. The spin-separated partial density of states for the s- and p-electrons also shows mirrored patterns in CrRuH3 and NiRuH3. This confirms that these materials behave in an antiferromagnetic way. It exerts a notable influence on both the electronic and magnetic characteristics of our compounds. These materials lack conventional macroscopic magnetization, the presence of antiferromagnetic order is important for understanding their unique magnetic behavior, which has implications for their suitability in hydrogen storage and other potential applications.
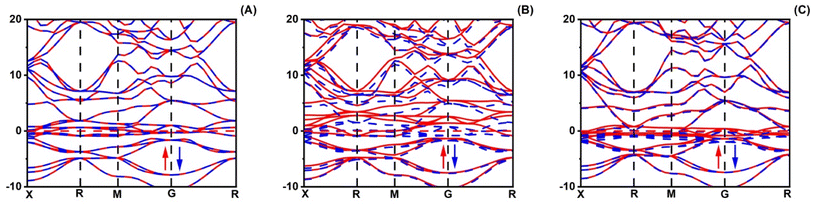 |
| | Fig. 5 Spin polarized band structure of (A) CrRuH3, (B) VRuH3 and (C) NiRuH3. | |
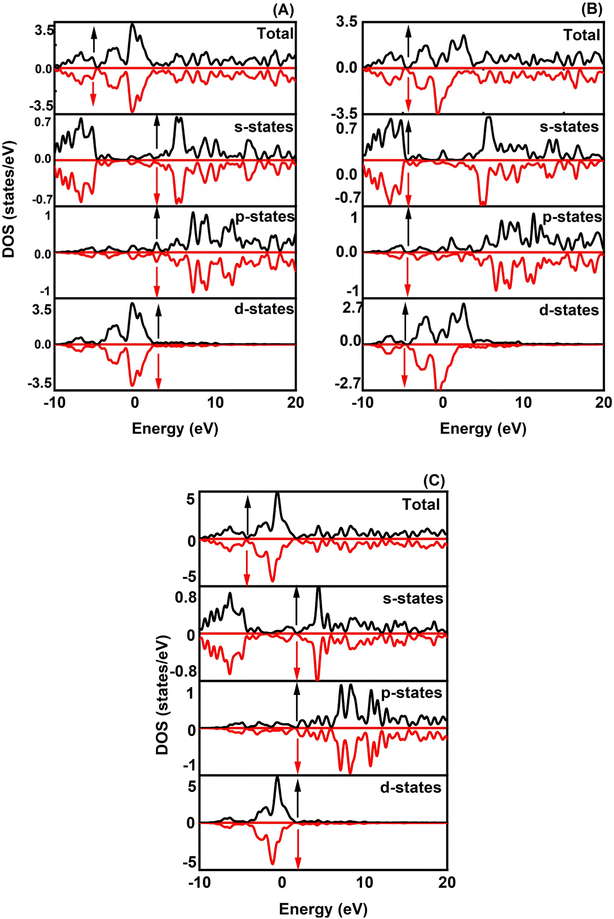 |
| | Fig. 6 Spin polarized TDOS and PDOS of (A) CrRuH3, (B) VRuH3 and (C) NiRuH3. | |
3.4. Optical properties
Optical parameters offer valuable insights into how materials interact with incident electromagnetic radiation. The intricate dielectric functions and other optical parameters that vary with frequency offer a holistic understanding of the optical characteristics of the materials under investigation. By analyzing reflectivity, we can effectively measure a material's ability to reflect incoming light. Fig. 7 illustrates the reflectivity graph for CrRuH3, VRuH3 and NiRuH3. Notably, the static values for CrRuH3, VRuH3 and NiRuH3 are 0.73, 0.8 and 0.61, respectively. The peak values stand at 0.53 (at 24.53 eV) for CrRuH3 and 0.50 (at 24.04 eV) for VRuH3 and 0.44 (at 24.14 eV) for NiRuH3. Beyond energies of 50 eV, 54 eV and 49 eV, respectively for CrRuH3, VRuH3 and NiRuH3, the reflectivity diminishes, ultimately reaching zero. The results clearly shows that reflectivity of CrRuH3 > VRuH3 > NiRuH3. The absorption coefficient, presented in Fig. 7, offers insights into how materials absorb photons. A high absorption coefficient signifies efficient photon absorption. CrRuH3, VRuH3 and NiRuH3 show no absorption when not exposed to incident radiations. For all compounds, absorption rises between 0 and 23 eV and decreases between 23 and 34 eV and then again increasing trend seen in all compounds from 38 to 50 eV. In contrast, CrRuH3 displays increasing absorption from 0.94 to 22.67 eV, followed by a continuous decrease beyond 22.67 eV. CrRuH3's maximum absorption occurs at 44.01 eV, VRuH3 shows maximum peak at 39 eV and NiRuH3's maximum peak of absorption is at 43.12 eV. At higher energies, all compounds show reduced absorption, reaching zero beyond 55.79 eV. Absorption graph clearly depicts that the absorption of CrRuH3, > VRuH3 > NiRuH3. The refractive index n(ω), depicted in Fig. 7, aids in predicting material transparency. The refractive index can be calculated using the equation53where R is the Fresnel's reflectance. Other optical properties such as reflectivity (R), energy loss (L), refractive index (n), and absorption coefficient (I) are computed using specific equations.| | |
ε(ω) = ε1(ω) + iε2(ω)
| (2) |
| | |
n(ω) = [ε1(ω)/2 + {ε12(ω) + ε12(ω)}1/2/2]1/2
| (3) |
| | |
L(ω) = −I′m(ε(ω)−1) = ε2(ω)/ε1(ω)2 + ε2(ω)2
| (4) |
| | |
I(ω) = 21/2ω[{ε12(ω) + ε12(ω)}1/2 − ε1(ω)]1/2
| (5) |
| | |
R(ω) = (n + k −1)/(n + k + 1)
| (6) |
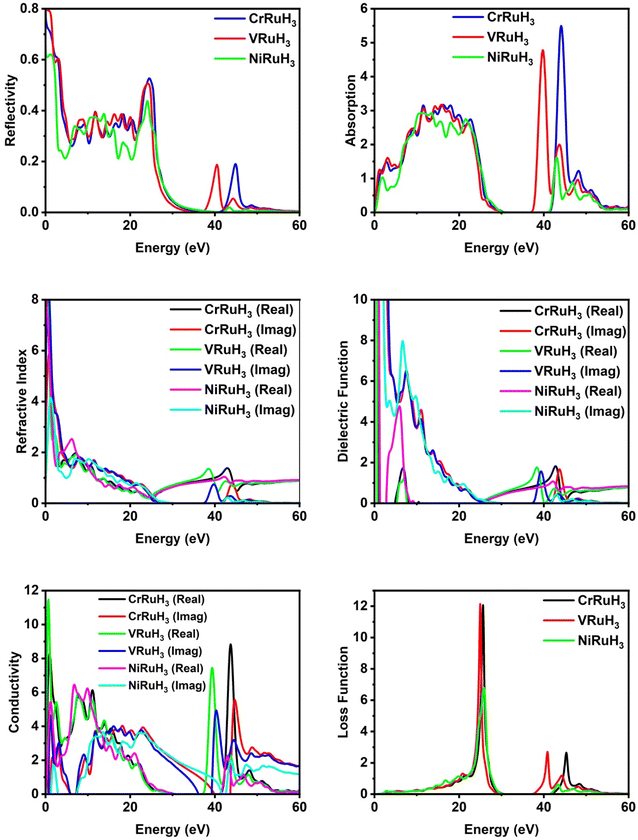 |
| | Fig. 7 Comparative analysis of optical properties of CrRuH3, VRuH3 and NiRuH3. | |
The static refractive index values for CrRuH3, VRuH3 and NiRuH3 are 3.68, 2.82 and 4.79, respectively. Furthermore, their peak refractive indices are 1.37 (at 42.89 eV) for CrRuH3, 1.35 (at 38.35 eV) for VRuH3 and 1.74 (at 6.77 eV) for NiRuH3. These values decrease as incident photon energy increases. The graph clearly depict that the refractive index of NiRuH3 > CrRuH3 > VRuH3. The dielectric function ε(ω) plays a pivotal role in assessing optical properties. Comprising real ε1(ω) and imaginary ε2(ω) parts, ε(ω) predicts polarization and photon dispersion. The real part reveals polarization, while the imaginary part indicates absorptive nature. The real and imaginary parts are combined through Kramers–Kronig's relation.54 The actual component of the dielectric function, ε1(ω), across all the compounds examined, displayed in Fig. 7, demonstrates stationary values of 1.05 eV for CrRuH3, 0.65 for VRuH3 and 1.33 for NiRuH3. Real peak values of ε1(ω) for CrRuH3, VRuH3 and NiRuH3 are 1.83 (at 42.72 eV), 1.76 (at 38.19 eV) and 4.73 (at 5.80 eV), respectively. Imaginary peak values occur at 7.27, 7.46 and 6.58 eV for CrRuH3, VRuH3 and NiRuH3, resulting in optical losses and poor transmission. Optical conductivity informs about conduction mechanisms due to photoelectrons. Real and imaginary parts of conductivity, as seen in Fig. 7, indicate the breaking of bonds. NiRuH3 exhibit zero conductivity in the absence of incident photons at 0 eV but CrRuH3, VRuH3 shows conductivity at 0 eV. CrRuH3 has higher conductivity, with a peak real conductivity value of 8.79 (at 43.68 eV) and imaginary conductivity of 5.51 (at 44.67 eV). The graph clearly shows that the conductivity of CrRuH3 > VRuH3 > NiRuH3. The energy loss function, shown in Fig. 7, indicates scattering probability of photoelectrons. The highest energy loss values are 12.12 (VRuH3) at 24.95 eV, 12.10 (CrRuH3) at 25.55 eV and 6.80 (NiRuH3) at 25.83 eV. Energy loss drops to zero beyond 50.83 eV. The results clearly shows that the loss function is VRuH3 > CrRuH3 > NiRuH3.
3.5. Mechanical properties
The evaluation of a material's response to applied forces necessitates the utilization of mechanical properties, particularly elastic constants. These elastic constants play a crucial role in exploring the mechanical behavior of the materials under investigation. In cubic crystals, such as the ones examined in this study, there are typically three elastic constants: C11, C12, and C44. The calculated elastic constants for CrRuH3, VRuH3 and NiRuH3 can be found in assessing the mechanical stability of crystal structures is of significant importance when investigating their mechanical properties. This stability in cubic crystals can be ascertained through the following criteria:55| | |
C11 + 2C12 > 0; C11 − C12 > 0; C44 > 0
| (7) |
Here, C11, C12, and C44 represent the elastic constants for cubic crystals. Both compounds fulfill these criteria, indicating their mechanical stability as given in the above equation. In Table 2, we showcase the anisotropic factor, Young's modulus, Poisson's ratio which are represented as A, E, ν respectively, and Pugh's index ratio for XRuH3 (X = Cr, V, Ni). These values were determined using the equations detailed below, shedding light on the material's mechanical properties and how it responds to external forces:56| | |
A = (2C44)/(C11 − C12)
| (8) |
| | |
Gv = (C11 − C12 + 3C44)/5
| (10) |
| | |
GR = 5C44(C11 − C12)/4C44 + 3(C11 − C12)
| (11) |
Table 2 The computed values for elastic constants and other parameters
| Parameters |
CrRuH3 |
VRuH3 |
NiRuH3 |
| C11 |
255.97 |
237.32 |
295.79 |
| C12 |
141.22 |
140.60 |
89.67 |
| C44 |
35.55 |
23.61 |
6.89 |
| A |
0.62 |
0.49 |
0.07 |
| B |
179.47 |
172.84 |
158.38 |
| Gv |
44.28 |
33.51 |
45.36 |
| GR |
41.93 |
29.69 |
10.99 |
| G |
43.11 |
31.60 |
28.18 |
| E |
119.73 |
89.35 |
79.80 |
| ν |
0.56 |
0.60 |
0.61 |
| B/G |
4.16 |
5.47 |
5.62 |
The equation stated above encompasses three distinct moduli: Gv, referred to as the Voigt modulus, which characterizes the upper bound; GR, which stands for the Reuss modulus, indicating the lower bound; and G, representing the mean shear modulus, capturing the average mechanical response of the material.
In the above equation, encompasses three pivotal moduli: the Bulk modulus (B), the mean shear modulus (G), and the Young's modulus (E), the latter symbolized as (E). These moduli collectively contribute to our understanding of the material's mechanical behavior.
| | |
ν = (3B − 2G)/2(2B + G)
| (14) |
In this context, B signifies the Bulk modulus, G represents the shear modulus, and ν provides insight into the Poisson's ratio. When considering cubic crystals, the elastic constants denoted as C11, C12, and C44 are expressed through eqn (4)–(7). These constants pave the way for assessing diverse mechanical properties once they are integrated. The anisotropy factor A serves as a tool for distinguishing whether the materials exhibit an isotropic or anisotropic nature. A numeric value of 1 indicates isotropy, while deviation from 1 signifies anisotropy. In this case, both materials exhibit an anisotropic nature due to the departure of A from 1. Bulk modulus (B) relates to material hardness. Both compounds exhibit positive bulk modulus values, indicating inherent hardness. CrRuH3, with a higher bulk modulus of 179.47, is comparatively harder than VRuH3 which has 172.84 and NiRuH3 which contains bulk modulus of 158.38. Mean shear modulus (G) and Young's modulus (E) corroborate the materials' inherent hardness, with CrRuH3 displaying greater hardness due to higher values of G and E. Poisson's ratio ν signifies material ductility or brittleness. All compounds under investigation exhibits ductile nature as results clearly shows that their ν > 0.26. The B/G ratio aids in characterizing ductile or brittle materials. Ductile materials have B/G > 1.75, reinforcing ductility of all investigated materials. Analyzing these mechanical properties indicates that CrRuH3 is a more favorable candidate for hydrogen storage devices as compared to other investigated compounds due to its desirable properties.
3.6. Hydrogen storage properties
Several challenges hinder the widespread adoption of hydrogen, as a potential fuel source, stands as one of the noteworthy contenders, which involves the lack of viable methods to efficiently contain hydrogen using sufficient gravimetric storage capacity. A key solution to this issue lies in the development of compounds capable of effectively reversing the accumulated hydrogen at higher densities. Diverse approaches to hydrogen storage exist, including solid-state, liquid, and gaseous methods. To address this goal, an extensive array of compounds has been explored, encompassing metal hydride perovskites. Assessing gravimetric hydrogen storage capacities proves instrumental in gauging a material's maximum ability to store hydrogen. For CrRuH3, VRuH3 and NiRuH3, these capacities are calculated using the formula:40| | |
Cwt% = [pMH/(Mcom + pMH)] × 100%
| (15) |
In this equation, p denotes the ratio of hydrogen atoms to material atoms, Mcom stands for the molar mass of the compound, and MH represents the molar mass of hydrogen. The gravimetric hydrogen storage capacity is quantified at 3.66%, 3.68% and 3.52% for CrRuH3, VRuH3 and NiRuH3, respectively. This establishes XRuH3 (X = Cr, V, Ni) as viable candidates for hydrogen storage applications. Notably, the gravimetric hydrogen storage capacity of XRuH3 lies within the range of 3.52 to 3.68% which makes a potential for hydrogen storage application.
4. Conclusion
The structural, electronic, optical, magnetic, hydrogen storage and mechanical characteristics of perovskites based on ruthenium hydrides XRuH3 (where X = Cr, V, Ni) have been systematically investigated utilizing the CASTEP computational tool. The calculations are performed employing the PBE exchange–correlation functional within the framework of generalized gradient approximation (GGA). Both compounds exhibit a stable crystal lattice arrangement and demonstrate metallic behavior, characterized by a complete absence of a band gap. The obtained lattice parameters match well with a previous study of transition metal based hydride perovskites. Notably, the Fermi level analysis through Total Density of States (TDOS) and Partial Density of States (PDOS) confirms the presence of maximum conductivity. An examination of the anisotropy factor ‘A’ reveals the inherent anisotropic nature of both materials. Further insight into mechanical properties discloses that CrRuH3 exhibits greater hardness than VRuH3 and NiRuH3, as evidenced by higher values of Young's modulus, bulk modulus and mean shear modulus. Additionally, the mechanical behavior is assessed through Poisson's ratio and B/G ratio, revealing that all compounds show ductile nature and results shows that CrRuH3 is the superior among them. The optical conductivity and absorption behaviors of these materials display pronounced characteristics in the lower energy spectrum. In terms of reflectivity CrRuH3 shows maximum peak and in terms of refractive index, NiRuH3 shows maximum value. The ability of the materials we studied to store hydrogen has been figured out. We found that VRuH3 can hold the most hydrogen by weight (about 3.68%), while NiRuH3 can hold the least (about 3.52%). When it comes to magnets, NiCuH3 and ZnCuH3 behave in an antiferromagnetic way, whereas VRuH3 is a strong magnetic material. All compounds under investigation demonstrate potential for hydrogen storage; however, CrRuH3 emerges as the superior choice, offering enhanced hydrogen storage capabilities. These theoretical calculations are expected to inspire researchers to create real CrRuH3, VRuH3, and NiRuH3 hydride perovskites in experiments. These materials are anticipated to have significant potential for use in hydrogen storage applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through research group program under grant number R.G.P. 2/570/44.
References
- A. Gencer, G. Surucu and S. Al, MgTiO3Hx and CaTiO3Hx perovskite compounds for hydrogen storage applications, Int. J. Hydrogen Energy, 2019, 44(23), 11930–11938 CrossRef CAS.
- I. Sreedhar, et al., A bird's eye view on process and engineering aspects of hydrogen storage, Renewable Sustainable Energy Rev., 2018, 91, 838–860 CrossRef CAS.
- L. Zhou, Progress and problems in hydrogen storage methods, Renewable Sustainable Energy Rev., 2005, 9(4), 395–408 CrossRef CAS.
- M. Granovskii, I. Dincer and M. A. Rosen, Environmental and economic aspects of hydrogen production and utilization in fuel cell vehicles, J. Power Sources, 2006, 157(1), 411–421 CrossRef CAS.
- M. R. Raupach, et al., Global and regional drivers of accelerating CO2 emissions, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(24), 10288–10293 CrossRef CAS PubMed.
- P. J. Pearson and T. J. Foxon, A low carbon industrial revolution? Insights and challenges from past technological and economic transformations, Energy Policy, 2012, 50, 117–127 CrossRef.
- Z. Guo, C. Shang and K. Aguey-Zinsou, Materials challenges for hydrogen storage, J. Eur. Ceram. Soc., 2008, 28(7), 1467–1473 CrossRef CAS.
- R. K. Ahluwalia, et al., Fuel economy of hydrogen fuel cell vehicles, J. Power Sources, 2004, 130(1–2), 192–201 CrossRef CAS.
- H. H. Raza, et al., First-principle investigation of XSrH3 (X= K and Rb) perovskite-type hydrides for hydrogen storage, Int. J. Quantum Chem., 2020, 120(24), e26419 CrossRef CAS.
- G. Surucu, et al., CaXH3 (X= Mn, Fe, Co) perovskite-type hydrides for hydrogen storage applications, Int. J. Energy Res., 2020, 44(3), 2345–2354 CrossRef CAS.
- M. A. H. Shah, et al., Exploring pressure induced thermoelectric properties of LiAeH3 (Ae= Ca, Sr, Ba) perovskite hydrides along with optoelectronic features, Mater. Sci. Semicond. Process., 2022, 137, 106238 CrossRef CAS.
- M. R. Kabli, et al., Structural, electronics and optical properties of sodium based fluoroperovskites NaXF3 (X= Ca, Mg, Sr and Zn): first principles calculations, Phys. Lett. A, 2021, 412, 127574 CrossRef CAS.
- J. ur Rehman, et al., First-principles calculations to investigate structural, electronic and optical properties of Na based fluoroperovskites NaXF3 (X= Sr, Zn), Solid State Commun., 2021, 334, 114396 CrossRef.
- M. Hirscher, et al., Materials for hydrogen-based energy storage–past, recent progress and future outlook, J. Alloys Compd., 2020, 827, 153548 CrossRef CAS.
- M. B. Ley, et al., Complex hydrides for hydrogen storage–new perspectives, Mater. Today, 2014, 17(3), 122–128 CrossRef CAS.
- A. Laref, et al., Impact of fluorine on organic cation for determining the electronic and optical properties of CH3− xFxNH3PbI3 (x= 0, 1, 2, 3) hybrid perovskites-based photovoltaic devices, Sol. Energy, 2019, 177, 517–530 CrossRef CAS.
- A. Abate, et al., Supramolecular halogen bond passivation of organic–inorganic halide perovskite solar cells, Nano Lett., 2014, 14(6), 3247–3254 CrossRef CAS PubMed.
- H.-S. Kim, S. H. Im and N.-G. Park, Organolead halide perovskite: new horizons in solar cell research, J. Phys. Chem. C, 2014, 118(11), 5615–5625 CrossRef CAS.
- B. M. Lefler, S. J. May and A. T. Fafarman, Role of fluoride and fluorocarbons in enhanced stability and performance of halide perovskites for photovoltaics, Phys. Rev. Mater., 2020, 4(12), 120301 CrossRef CAS.
- C. Ortiz-Cervantes, P. Carmona-Monroy and D. Solis-Ibarra, Two-dimensional halide perovskites in solar cells: 2D or not 2D?, ChemSusChem, 2019, 12(8), 1560–1575 CrossRef CAS PubMed.
- T. K. Ng, et al., Group-III-nitride and halide-perovskite semiconductor gain media for amplified spontaneous emission and lasing applications, J. Phys. D: Appl. Phys., 2021, 54(14), 143001 CrossRef CAS.
- X. Jiang and W.-J. Yin, High-throughput computational screening of oxide double perovskites for optoelectronic and photocatalysis applications, J. Energy Chem., 2021, 57, 351–358 CrossRef CAS.
- M. Sohail, et al., First-principal investigations of electronic, structural, elastic and optical properties of the fluoroperovskite TlLF 3 (L= Ca, Cd) compounds for optoelectronic applications, RSC Adv., 2022, 12(12), 7002–7008 RSC.
- W.-J. Yin, et al., Oxide perovskites, double perovskites and derivatives for electrocatalysis, photocatalysis, and photovoltaics, Energy Environ. Sci., 2019, 12(2), 442–462 RSC.
- Y.-W. Fang, et al., Lattice dynamics and ferroelectric properties of the nitride perovskite LaWN 3, Phys. Rev. B, 2017, 95(1), 014111 CrossRef.
- Y. Li, J. S. Chung and S. G. Kang, First-principles computational screening of perovskite hydrides for hydrogen release, ACS Comb. Sci., 2019, 21(11), 736–742 CrossRef CAS PubMed.
- M. A. H. Shah, et al., Hydrostatic pressure on XLiH3 (X= Ba, Sr, Ca) perovskite hydrides: an insight into structural, thermo-elastic and ultrasonic properties through first-principles investigation, Solid State Commun., 2021, 328, 114222 CrossRef CAS.
- S. Sharma and S. K. Ghoshal, Hydrogen the future transportation fuel: from production to applications, Renewable Sustainable Energy Rev., 2015, 43, 1151–1158 CrossRef CAS.
- S. Dutta, A review on production, storage of hydrogen and its utilization as an energy resource, J. Ind. Eng. Chem., 2014, 20(4), 1148–1156 CrossRef CAS.
- B. L. Salvi and K. Subramanian, Sustainable development of road transportation sector using hydrogen energy system, Renewable Sustainable Energy Rev., 2015, 51, 1132–1155 CrossRef CAS.
- Z.-M. Wang, et al., The improvement of dehydriding the kinetics of NaMgH3 hydride via doping with carbon nanomaterials, Metals, 2016, 7(1), 9 CrossRef.
- S. Benlamari, et al., Structural, electronic, elastic, and thermal properties of CaNiH3 perovskite obtained from first-principles calculations, Chin. Phys. B, 2018, 27(3), 037104 CrossRef.
- K. Ikeda, T. Sato and S.-i. Orimo, Perovskite-type hydrides–synthesis, structures and properties, Int. J. Mater. Res., 2008, 99(5), 471–479 CrossRef CAS.
- R. Sato, et al., Formation process of perovskite-type hydride LiNiH3: in situ synchrotron radiation X-ray diffraction study, Appl. Phys. Lett., 2013, 102(9), 091901 CrossRef.
- K. Ikeda, et al., Formation of perovskite-type hydrides and thermal desorption processes in Ca–T–H (T= 3d transition metals), Scr. Mater., 2006, 55(9), 827–830 CrossRef CAS.
- T. Sato, et al., Hydrides with the perovskite structure: general bonding and stability considerations and the new representative CaNiH3, J. Solid State Chem., 2005, 178(11), 3381–3388 CrossRef CAS.
- B. G. Yalcin, B. Salmankurt and S. Duman, Investigation of structural, mechanical, electronic, optical, and dynamical properties of cubic BaLiF3, BaLiH3, and SrLiH3, Mater. Res. Express, 2016, 3(3), 036301 CrossRef.
- K. Komiya, et al., Synthesis and decomposition of perovskite-type hydrides, MMgH3 (M= Na, K, Rb), J. Alloys Compd., 2008, 453(1–2), 157–160 CrossRef CAS.
- H. H. Raza, G. Murtaza and R. M. A. Khalil, Optoelectronic and thermal properties of LiXH3 (X= Ba, Sr and Cs) for hydrogen storage materials: a first principle study, Solid State Commun., 2019, 299, 113659 CrossRef CAS.
- S. Hayat, et al., First-principles investigations of the structural, optoelectronic, magnetic and thermodynamic properties of hydride perovskites XCuH3 (X= Co, Ni, Zn) for hydrogen storage applications, Optik, 2021, 228, 166187 CrossRef CAS.
- R. Khalil, et al., DFT based first principles study of novel combinations of perovskite-type hydrides XGaH3 (X= Rb, Cs, Fr) for hydrogen storage applications, AIP Adv., 2021, 11(2), 025032 CrossRef CAS.
- F. Schüth, B. Bogdanović and M. Felderhoff, Light metal hydrides and complex hydrides for hydrogen storage, Chem. Commun., 2004,(20), 2249–2258 RSC.
- S.-i. Orimo, et al., Complex hydrides for hydrogen storage, Chem. Rev., 2007, 107(10), 4111–4132 CrossRef CAS PubMed.
- S. J. Clark, et al., First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS.
- F. Bloch, Quantum mechanics of electrons in crystal lattices, Z. Phys., 1928, 52, 555–600 CrossRef CAS.
- N. Marzari, D. Vanderbilt and M. C. Payne, Ensemble density-functional theory for ab initio molecular dynamics of metals and finite-temperature insulators, Phys. Rev. Lett., 1997, 79(7), 1337 CrossRef CAS.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892 CrossRef PubMed.
- D. Alfe, Ab initio molecular dynamics, a simple algorithm for charge extrapolation, Comput. Phys. Commun., 1999, 118(1), 31–33 CrossRef CAS.
- G. Pilania, et al., Accelerating materials property predictions using machine learning, Sci. Rep., 2013, 3(1), 2810 CrossRef PubMed.
- M. Usman, et al., First-principles calculations to investigate structural, electronics, optical, and mechanical properties of Bi-based novel fluoroperovskites TBiF3 (T= Hg, Xe) for optoelectronic applications, Mater. Sci. Semicond. Process., 2023, 160, 107399 CrossRef CAS.
- P. Dantzer, Properties of intermetallic compounds suitable for hydrogen storage applications, Mater. Sci. Eng. A, 2002, 329, 313–320 CrossRef.
- S. Haid, et al., Thermoelectric, structural, optoelectronic and magnetic properties of double perovskite Sr2CrTaO6: first principle study, Mater. Sci. Eng. B, 2019, 245, 68–74 CrossRef CAS.
- J. U. Rehman, et al., First-principles calculations to investigate structural, electronics, optical and elastic properties of Sn-based inorganic halide-perovskites CsSnX3 (X= I, Br, Cl) for solar cell applications, Comput. Theor. Chem., 2022, 1209, 113624 CrossRef.
- K. Xiong, J. Robertson and S. Clark, Defect states in the high-dielectric-constant gate oxide LaAlO3, Appl. Phys. Lett., 2006, 89(2), 022907 CrossRef.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349 CrossRef.
- S. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Muhammad Bilal Tahirab,
Sania Ayuba,
Tarik E. Alic and
Hafiz Tariq Masoodd
*a,
Muhammad Bilal Tahirab,
Sania Ayuba,
Tarik E. Alic and
Hafiz Tariq Masoodd
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with international number of 221. The depiction of the cubic crystal structure of XRuH3 (X = Cr, V, Ni) can be observed in Fig. 1. During the process of optimizing the unit cell, a systematic approach was adopted, involving the strategic positioning of X cations at the corners, with the central point occupied by the less abundant metal, Ru, and the face-centered sites adorned by hydrogen atoms. Detailed information regarding the lattice constants, volume, and band gap energy specific to the XRuH3 (X = Cr, V, Ni) perovskite hydrides is presented in Table 1. It's noteworthy that the lattice constant of VRuH3 surpasses that of CrRuH3 and NiRuH3, similarly reflecting a greater volume for VRuH3 in contrast to CrRuH3 and NiRuH3 perovskite hydrides. The formation enthalpy of all the compounds was calculated with the help of the following equation50
m space group with international number of 221. The depiction of the cubic crystal structure of XRuH3 (X = Cr, V, Ni) can be observed in Fig. 1. During the process of optimizing the unit cell, a systematic approach was adopted, involving the strategic positioning of X cations at the corners, with the central point occupied by the less abundant metal, Ru, and the face-centered sites adorned by hydrogen atoms. Detailed information regarding the lattice constants, volume, and band gap energy specific to the XRuH3 (X = Cr, V, Ni) perovskite hydrides is presented in Table 1. It's noteworthy that the lattice constant of VRuH3 surpasses that of CrRuH3 and NiRuH3, similarly reflecting a greater volume for VRuH3 in contrast to CrRuH3 and NiRuH3 perovskite hydrides. The formation enthalpy of all the compounds was calculated with the help of the following equation50