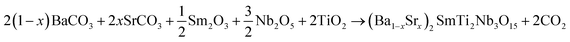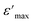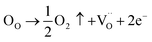Open Access Article
Open Access ArticleThe effects of Sr-substitution in Ba2SmTi2Nb3O15 ceramics: structural study, optical properties, and complex impedance spectroscopy†
Karim. Chourti *,
Ilyas. Jalafi,
Amine. Bendahhou
*,
Ilyas. Jalafi,
Amine. Bendahhou ,
Soufian El Barkany and
Mohamed. Abou-Salama
,
Soufian El Barkany and
Mohamed. Abou-Salama
Department of Chemistry, Laboratory of Molecular Chemistry, Materials and Environment, Faculty Multidisciplinary Nador, University Mohammed Premier, B.P. 300, Selouane, Nador 62700, Morocco. E-mail: chokarim@gmail.com; k.chourti@ump.ac.ma
First published on 14th March 2024
Abstract
Ceramics of (Ba1−xSrx)2SmTi2Nb3O15, denoted as BSxSTN (x = 0, 0.25 and 0.5), were synthesized by the conventional solid-state reactions route. The impact of Sr-substitution in Ba2SmTi2Nb3O15 ceramics on their structural, optical, and dielectric properties are investigated. The Rietveld method was employed to confirm the formation of tetragonal tungsten bronze with the P4bm space group, using X-ray diffraction data. The substitution of Ba by Sr resulted in a decrease in cell parameters, density, and the average crystallite size as determined by Scherrer's formula ranged from 29.4 to 32 nm. The compounds frequency-dependent dielectric properties were studied using complex impedance spectroscopy over a temperature range of 50 to 420 °C at different frequencies. Dielectric measurements revealed a high dielectric constant, and the compounds exhibited characteristics of diffuse ferroelectric behavior. As the Sr content increased, optical gap energy increases from 3.29 to 3.59 eV, diffusivity increased from 1.19 to 1.52, Curie temperature (Tc) decreased from 269 to 213 °C, and the dielectric loss at room temperature and 1 kHz significantly decreased from 3 × 10−3 to 7 × 10−4. The correlation between (Tc) and the off-center cationic displacement of Ti/Nb in the octahedral Ti/NbO6 was analyzed. Cole–Cole plots for each sample displayed a single semicircular arc, indicating the presence of a single relaxation process.
1. Introduction
The physical characteristics, including electrical, magnetic, optical, and dielectric properties, of materials featuring a tetragonal tungsten bronze (TTBs) structure have been thoroughly investigated. The standard formula for a TTB is (A1)2(A2)4(C)4(B1)2(B2)8O30.1–6 The pentagonal sites (A2) with a coordination number of 15 are capable of accepting sizable cations, including alkaline earth elements. On the other hand, the square sites (A1) with a coordination number of 12 are designed to accommodate moderately sized cations, such as rare earth elements. The triangular sites (C), with a coordination number of 9, are well-suited for hosting smaller cations like Li+.7,8 The octahedral sites (B1) and (B2) are typically occupied by highly charged cations like Ti4+, Ta5+, and Nb5+.9–11 The ferroelectric ordering in these materials is influenced by two primary factors: (i) the tilting of BO6 octahedra and (ii) the change in ionic radii of the (A) or (B) site ions.12,13 As a result, numerous studies have been carried to modify the properties of materials with a TTB structure, based on these two factors.Compounds with the formula Ba4−xSrxSmFe0.5Nb9.5O30 (x = 0, 1, 2, 3 and 4) have been identified as relaxor materials. The pronounced dielectric relaxation in these materials is attributed to the disorder of Ba/Sr cations in the (A) sites.14 In our investigation of the Sr2Sm1−xNdxTi2Nb3O15 solid solution, which exhibits a TTB structure with the space group P4bm. In this structure, large ions like Sr2+ occupy the pentagonal cavities (A2), medium-sized ions such as Sm3+ are located in the square sites (A1),14,15 and Ti4+/Nb5+ ions occupy the octahedral sites (B1 and B2), while the sites (C) with a coordinate number of 9 remain unoccupied. These compounds exhibit ferroelectric behavior, and the Curie temperature (TC) gradually decreases from 332 °C for Sr2SmTi2Nb3O15 to 246 °C for Sr2NdTi2Nb3O15. This trend correlates with the center displacement of the cation Ti/Nb(1) in the (B1) site.16 In another study, ceramics with the composition (SrxBa1−x)4Sm2Fe2Nb8O30 (x = 0, 0.1, 0.2, 0.3, 0.4) were investigated. These ceramics undergo a transition from a paraelectric to a ferroelectric phase, and this transition is influenced by the difference in radius (Δr) between the A1 and A2-site cations.17 Within the TTB structure, the substitution of specific cations with ions of different sizes and/or valences at the (A1), (A2) and/or (B) sites leads to the formation of either ferroelectric or relaxor-type materials.
The size of cations and their substitution ratio at different sites within the TTB structure significantly impact the dielectric properties and overall structure of these materials.18–21 Solid solutions, derived from a ferroelectric compound, involve cation substitutions either on the site (A1), as demonstrated in Ba2NdTi2Nb3O15,22,23 Ba2SmTi2Nb3O15,24 and Sr4R2Ti4Nb6O30 (R = Sm and Eu),25 or on the (A2) site, as observed in Sr2NdTi2Nb3O15,16 which shows ferroelectric behavior, and Ba2NdTi2Nb3O30 which exhibits relaxor behaviors.26
In their study, M. C. Stennett et al.27 investigated TTB-type ferroelectrics with the formula Ba2MTi2Nb3O15, were M = La, Nd, Sm, Gd, Bi. The researchers explored different composition, including Ba2LaTi2Nb3O15 (with a transition temperature, Tm∼−80 °C), Ba2BiTi2Nb3O15 (Tm∼−100 °C), Ba2NdTi2Nb3O15 (Tm∼165 °C), Ba2SmTi2Nb3O15 (Tm∼250 °C), and Ba2GdTi2Nb3O15 (Tm∼320 °C). In this family of Ba2MTi2Nb3O15 phases, the Curie temperature increases as the size of the M cation decreases. This observation suggests that the transition temperature is influenced by the dimensions of the cations M in TTB structure. The existence of ferroelectricity in these niobates is attributed to the occurrence of spontaneous polarization This phenomenon is usually a result of niobium displacements from the barycenter of the Ti/NbO6 octahedron formed by oxygen atoms.28,29
The objective of this study is to investigate the solid solution (Ba1−xSrx)2SmTi2Nb3O15 (x = 0, 0.25, 0.5). The specific aims of the research are as follows: (i) to examine the structural evolution within the solid solution, observing any changes or variations in the crystal structure as the substitution ratio of Ba and Sr cations is modified in the pentagonal site (A2); (ii) to investigate the dielectric properties of these phases with a specific focus on enhancing the dielectric constant while simultaneously minimizing dielectric losses. These properties provide insights into the material's response to an electric field and its energy dissipation behavior. Moreover (iii) to establish relationships between the crystalline structure and the dielectric and optical properties.
2. Materials and methods
BS0STN, BS0.25STN and BS0.5STN samples were prepared using the conventional solid-state reaction method. Reagent grade BaCO3, SrCO3, Sm2O3, TiO2 and Nb2O5, all supplied by Aldrich chemical, and high purity ≥99.9%, were employed. The starting powders were ground in an agate mortar to ensure homogeneity and reduce grain size. Sm2O3 powder was pre-dried at 750 °C for half an hour to remove traces of water and carbon dioxide. The mixtures were calcined in alumina crucibles at 1350 °C for 12 hours in air. The heating and cooling rates during the calcination process were maintained at 5 °C min−1. The fundamental chemical reaction for pure phase synthesis can be represented by:After calcination, the obtained powders were mixed with organic binders, specifically polyvinyl alcohol (PVA). The resulting mixture was then pressed into pellets with a diameter of 12 mm and 2 mm in thickness, applying a pressure of approximately 98 MPa. Subsequently, the disks were sintered at a temperature of 1400 °C in air for a duration of 2 h. This sintering step was conducted to facilitate the densification and consolidation of the pellets.
The X-ray diffraction (XRD) analysis was conducted at room temperature using CuKα radiation (λ = 1.5406 Å) to determine the crystal structure of the synthesized phases. XRD data were collected in the 2θ range of 5° to 120°, with a step size of 0.02° and a scanning speed of 1° min−1. This XRD analysis aimed to provide detailed information about the crystallographic characteristics of the synthesized materials.
The refinement of various parameters, including cell parameters, reduced coordinates, and thermal agitation coefficient, was conducted using the Jana 2006 software.30 The calculations were carried out in the same way for all compositions investigated. The visualization of the crystal structure of ceramics was taken by VESTA software.31 The average crystallite size was estimated for the strongest diffraction peak using the Scherrer equation.32
The UV-Shimadzu (1800) type of UV/visible spectrometer was utilized to examine the optical properties. For dielectric measurements, both surfaces of the pellets were coated with silver paste and annealed for 30 minutes at 300 °C to obtain good electrical contacts. The relative permittivity and dielectric losses were determined using a BioLogic impedance analyzer model MTZ-35. The measurements were conducted over a frequency range of 100 Hz to 1 MHz, and the furnace and sample temperatures were controlled using MT-lab software with a heating rate of 5 °C min−1.
The compositions studied are presented in the Table 1.
| x | Compositions | Formula |
|---|---|---|
| 0 | Ba2SmTi2Nb3O15 | BS0STN |
| 0.25 | (Ba0.75Sr0.25)2SmTi2Nb3O15 | BS0.25STN |
| 0.5 | (Ba0.5Sr0.5)2SmTi2Nb3O15 | BS0.5STN |
3. Results and discussion
3.1. Structural study
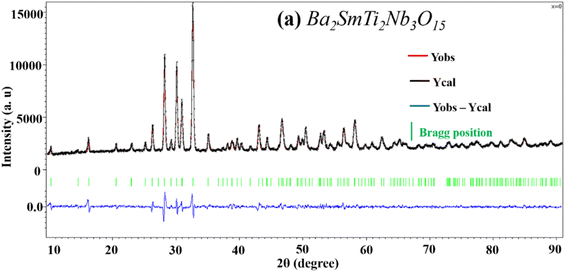
The diffractograms obtained for the compositions (Fig. 1) were successfully indexed in the tetragonal crystal system with the space group P4bm. The diffraction peaks were matched with structural model ICDD_PDF#38-1329, representing the TTB compound of the Ba6Ti2Nb8O30 formulation, as the initial patterns. The refinement of the different variables such as reduced coordinates and thermal agitation coefficient Uiso, was conducted using the Rietveld method.33 The calculations were consistently performed across all compositions. The shape of the X-ray diffraction peaks was approximated using the Pseudo Voigt function, expressed as PV = ηL + (1 − η)G, where η is the mixing factor, G corresponds to the Gaussian function, and L represents the Lorentzian function.34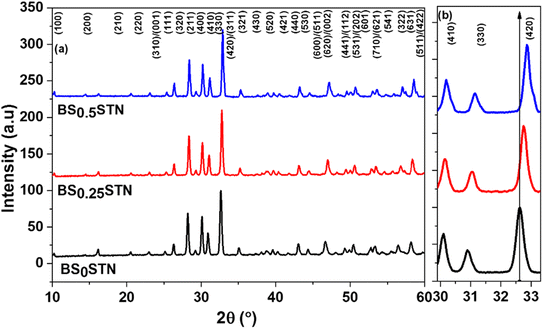 | ||
| Fig. 1 (a) X-ray diffraction patterns of BSxSTN powders, and (b) a shift of the diffraction peaks (410), (330) and (420). | ||
The peak shift in the XRD is based on the dopant size. If the dopant size is smaller Sr than the base metal Ba it occupies the interstitial position leading to change in the lattice structure and the d-spacing between the atoms become less and there is an increase in the X-ray diffraction resulting in higher angles. A decrease in peak intensity was observed as the Sr content increased (Fig. 1b). For certain reflection pairs, such as between (410) and (330), the difference in 2θ angles becomes more pronounced when compositions are rich in Ba. The shift of diffraction peaks towards higher angles corresponds to a reduction in the crystal lattice volume.
The replacement of Ba with Sr at the A2-site induces a shift of the diffraction peaks towards higher angles, indicating a decrease in the unit cell parameters. The obtained phases are pure, suggesting that the Sr element has diffused into the BSxSTN lattice. The refined unit cell parameters and crystallite size for the BSxSTN ceramics are provided in Table 2.
| Compounds | BS0STN | BS0.25STN | BS0.5STN |
|---|---|---|---|
| a = b (Å) | 12.2778(8) | 12.2598(7) | 12.2242(8) |
| c (Å) | 3.8980(3) | 3.8711(3) | 3.8540(3) |
| c/a | 0.317 | 0.316 | 0.315 |
| V (Å3) | 587.60(7) | 581.83(6) | 575.92(7) |
| Z | 2 | 2 | 2 |
| Crystallite size D (nm) | 29.4 | 31.9 | 32.0 |
| Profile function | Pseudo Voigt | Pseudo Voigt | Pseudo Voigt |
| u | 1.4265 | 1.1666 | 1.2547 |
| v | −0.7335 | −0.5705 | −0.7239 |
| w | 0.2061 | 0.1574 | 0.2058 |
| CuKα radiation (Å) | 1.5406 | 1.5406 | 1.5406 |
| Measuring range 2θ (°) | 5–120 | 5–120 | 5–120 |
| Step 2θ (°) | 0.02 | 0.02 | 0.02 |
| Number of refined parameters | 38 | 38 | 38 |
| Goodness-of-fit (Gof) | 2.84 | 2.71 | 2.26 |
| R-profile (Rp) (%) | 4.32 | 4.23 | 5.39 |
| R-weighted profile (Rwp) (%) | 5.85 | 5.85 | 7.40 |
| Expected residual factor (Rexp) (%) | 2.06 | 2.15 | 3.27 |
The refinement process was conducted within the P4bm space group. After several refinement cycles, the confidence factors, indicative of the refinement quality, stabilized within the following ranges: 4.3 ≤ Rp ≤ 5.4, 5.9 ≤ Rwp ≤ 7.4, and 2 ≤ Gof ≤ 3.3. These values suggest a satisfactory agreement between the observed and calculated XRD patterns (Fig. 2a, and S1 in ESI†).
Table 2 shows that the lattice parameters a, c, and cell volume V decreased with the substitution rate the compounds. This trend can be attributed to the small difference between the ionic radii of barium (rBa2+ with coordination number 15) = 1.65 Å, which is larger than strontium (rSr2+ with coordination number 15) = 1.50 Å.35 Additionally, the tetragonality c/a decreased from 0.317 in undoped BS0STN to 0.315 in BS0.5STN, indicating a decrease in distortions with increasing substitution. The Table 3 shows the refinement of structural parameters for BSxSTN.
| Atom | Site | x | y | z | Occupancy | Uiso |
|---|---|---|---|---|---|---|
| BS0STN | ||||||
| Ba | 4c | 0.1708(2) | 0.6708(2) | 0.067(6) | 1 | 0.025(16) |
| Sm | 2a | 0 | 0 | 0.020(6) | 1 | 0.033(2) |
| Ti1/Nb1 | 2b | 0 | 0.5 | 0.497(7) | 0.4/0.6 | 0.004(4) |
| Ti2/Nb2 | 8d | 0.0732(4) | 0.2143(4) | 0.538(6) | 0.4/0.6 | 0.006(16) |
| O1 | 2b | 0 | 0.5 | 0.134(19) | 1 | 0.008(6) |
| O2 | 4c | 0.2807(16) | 0.7807(16) | 0.484(17) | 1 | 0.008(6) |
| O3 | 8d | 0.063(2) | 0.1935(18) | 0.125(11) | 1 | 0.008(6) |
| O4 | 8d | 0.3493(17) | 0.0044(13) | 0.615(11) | 1 | 0.008(6) |
| O5 | 8d | 0.1308(17) | 0.078(2) | 0.615(10) | 1 | 0.008(6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| BS0.25STN | ||||||
| Sr/Ba | 4c | 0.1706(3) | 0.6706(3) | 0.084(7) | 0.25/0.75 | 0.024(19) |
| Sm | 2a | 0 | 0 | 0.021(7) | 1 | 0.031(2) |
| Ti1/Nb1 | 2b | 0 | 0.5 | 0.486(8) | 0.4/0.6 | 0.001(4) |
| Ti2/Nb2 | 8d | 0.0756(4) | 0.2175(4) | 0.544(7) | 0.4/0.6 | 0.002(15) |
| O1 | 2b | 0 | 0.5 | −0.830(3) | 1 | 0.013(7) |
| O2 | 4c | 0.2826(16) | 0.7826(16) | 0.600(2) | 1 | 0.013(7) |
| O3 | 8d | 0.062(2) | 0.1921(17) | 0.088(15) | 1 | 0.013(7) |
| O4 | 8d | 0.3492(18) | 0.0014(13) | 0.642(13) | 1 | 0.013(7) |
| O5 | 8d | 0.1382(17) | 0.076(2) | 0.480(14) | 1 | 0.013(7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| BS0.5STN | ||||||
| Sr/Ba | 4c | 0.1698(3) | 0.6698(3) | 0.036(6) | 0.50/0.50 | 0.029(2) |
| Sm | 2a | 0 | 0 | 0.052(6) | 1 | 0.027(2) |
| Ti1/Nb1 | 2b | 0 | 0.5 | 0.587(8) | 0.4/0.6 | 0.012(4) |
| Ti2/Nb2 | 8d | 0.0764(4) | 0.2159(4) | 0.562(6) | 0.4/0.6 | 0.003(16) |
| O1 | 2b | 0 | 0.5 | −0.025(17) | 1 | 0.025(6) |
| O2 | 4c | 0.289(2) | 0.789(2) | 0.475(15) | 1 | 0.025(6) |
| O3 | 8d | 0.068(3) | 0.199(2) | −0.015(11) | 1 | 0.025(6) |
| O4 | 8d | 0.3453(18) | 0.0001(16) | 0.474(12) | 1 | 0.025(6) |
| O5 | 8d | 0.129(2) | 0.082(2) | 0.461(10) | 1 | 0.025(6) |
In the BSxSTN crystal structure, specific ions occupy different sites. Ba2+ and Sr2+ occupy the pentagonal sites (A2), Sm3+ occupy the square sites (A1), and Ti4+ and Nb4+ occupy the octahedral sites. The sites (C) in the structure remain unoccupied. Examining the Ti/Nb(1)O6 octahedra reveals that the Ti/Nb(1)–O(1)′ bond length is consistently smaller than Ti/Nb(1)–O(1) across all compositions. In the Ti/Nb(2)O6 octahedra, there are variations in the Ti/Nb(2)–O distances for all compositions, suggesting that the Ti/Nb(2)O6 octahedra are more distorted or deformed compared to the Ti/Nb(1)O6 octahedra, a common observation in TTB structures. In the square sites (A1), it has been noted that the Sm-O(3) distance increases as the value of x increases. Conversely, for the pentagonal sites (A2), the Sr-O(5) distance rises with an increase in Ba content. As indicated in Table 4, all compositions exhibit centric displacements along the c-axis for both Ti and Nb cations within the Ti/Nb(1)O6 and Ti/Nb(2)O6 octahedra, as illustrated in Fig. 3b. Notably, the Ti/Nb(1)O6 octahedra in all compositions display an O(1)–Nb/Ti(1)–O(1) bond angle of 180°, indicating a linear arrangement. Moreover, these octahedra manifest four equal Ti/Nb(1)–O(4) bond lengths, as detailed in Table 4.
| Cation-O | Mul | BS0STN | BS0.25STN | BS0.5STN |
|---|---|---|---|---|
| Environment of Sr/Ba | ||||
| Sr/Ba-O(3) | ×2 | 3.2622(3) | 2.8803(10) | 3.2701(3) |
| ×2 | 3.4527(3) | 3.7383(13) | 3.2696(3) | |
| Sr/Ba-O(4) | ×2 | 3.0254(16) | 2.6917(8) | 2.8880(16) |
| ×2 | 2.7575(14) | 3.1682(10) | 2.7539(15) | |
| Sr/Ba-O(5) | ×2 | 3.4154(18) | 2.7907(8) | 3.3775(19) |
| ×2 | 2.9065(16) | 3.5572(11) | 3.0857(18) | |
| Sr/Ba-O(2) | ×1 | 2.9018(15) | 2.8260(8) | 2.8170(16) |
| ×1 | 2.7539(14) | 2.9954(9) | 2.6515(15) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Environment of Sm | ||||
| Sm-O(3) | ×4 | 2.3315(15) | 2.5588(9) | 2.6316(2) |
| Sm-O(5) | ×4 | 3.2470(18) | 3.3025(7) | 2.9357(16) |
| ×4 | 2.5317(13) | 2.5520(11) | 2.5704(14) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Environment of the octahedron Ti/Nb(1)O6 | ||||
| Ti/Nb(1)–O(1) | ×1 | 2.2647(19) | 2.1421(11) | 2.1112(17) |
| Ti/Nb(1)–O(1)′ | ×1 | 1.7330(12) | 1.7433(8) | 1.7434(14) |
| Ti/Nb(1)–O(4) | ×4 | 1.9109(12) | 2.0433(7) | 1.8539(14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Environment of the octahedron Ti/Nb(2)O6 | ||||
| Ti/Nb(2)–O(2) | ×1 | 1.9229(13) | 1.8880(7) | 1.9071(14) |
| Ti/Nb(2)–O(3) | ×1 | 2.2628(17) | 1.9370(9) | 2.1148(17) |
| ×1 | 1.7679(13) | 2.0611(9) | 1.7614(14) | |
| Ti/Nb(2)–O(4) | ×1 | 1.8691(12) | 1.7993(6) | 1.8836(14) |
| Ti/Nb(2)–O(5) | ×1 | 2.1773(14) | 1.9900(6) | 2.1608(16) |
| ×1 | 1.8926(12) | 2.2305(7) | 1.8308(14) | |
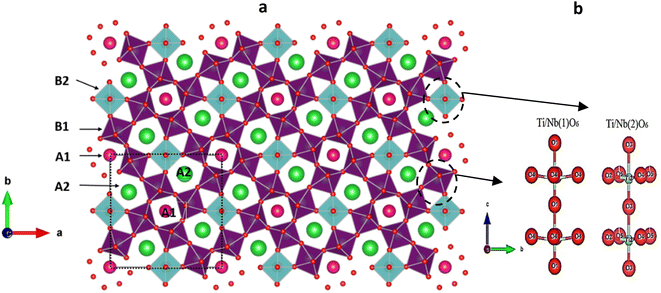 | ||
| Fig. 3 (a) Representation of the TTB structure of BSxSTN along the “c” axis. (b) Displacements of the Ti/Nb(1) and Ti/Nb(2) cations. | ||
Within the equatorial plane of the Ti(1)O6 octahedron, the O–Ti(1)–O angles, spanning from approximately 74° to 105°, suggest a relatively lower degree of distortion for this type of octahedron. Furthermore, the O(1)–Ti/Nb(1)–O(1) angle of 180° suggests a rotation of the octahedra around the b-axis.
The angles formed by O(3)–Ti(2)–O(3)′ surpass 150° and demonstrate an upward trend with increasing values of x, suggesting an expansion of these angles with the substitution from Ba to Sr increases. This observation implies an increasing distortion in the Ti(2)O6 octahedra as the composition undergoes changes. The diverse angles within the equatorial plane of the Ti(2)O6 octahedron, detailed in Table 5, additionally affirm that this octahedron is more distorted compared to the Ti(1)O6 octahedron.
| Angles (°) | BS0STN | BS0.25STN | BS0.5STN |
|---|---|---|---|
| O(1)–Ti(1)–O(1) | 180(0) | 180(0) | 180(0) |
| O(1)–Ti(1)–O(4) | 102.191(12) | 105.954(9) | 92.372(3) |
| 77.808(12) | 74.045(9) | 87.627(3) | |
| O(4)–Ti(1)–O(4) | 155.617(3) | 148.091(18) | 175.254(6) |
| O(2)–Ti(2)–O(3) | 96.599(17) | 95.143(5) | 92.757(8) |
| 110.002(10) | 82.785(4) | 98.432(4) | |
| O(2)–Ti(2)–O(4) | 89.789(0) | 86.076(0) | 95.970(0) |
| O(2)–Ti(2)–O(5) | 161.655(17) | 151.271(14) | 172.084(9) |
| 86.889(3) | 89.230(3) | 90.211(0) | |
| O(3)–Ti(2)–O(3) | 150.249(3) | 152.712(15) | 167.864(13) |
| O(3)–Ti(2)–O(4) | 87.735(14) | 88.882(15) | 89.817(4) |
| 104.941(0) | 118.209(0) | 93.655(0) | |
| O(3)–Ti(2)–O(5) | 66.377(0) | 113.512(10) | 81.438(5) |
| 70.456(10) | 94.534(18) | 93.777(10) | |
| O(4)–Ti(2)–O(5) | 157.368(3) | 147.195(18) | 169.537(7) |
Fig. 3a presents the crystallographic structure along the c-axis, depicting different sites such as pentagonal (A2), square (A1), triangular (C), and octahedral sites (B1, B2). The displacements of Ti/Nb(1) and Ti/Nb(2) cations within the Ti/NbO6 octahedra are shown in Fig. 3b.
3.2. Density of ceramic samples
The ceramic samples' experimental density (ρex) was measured using a KERN analytical balance based on Archimedes' method. The theoretical density (ρth) was calculated using lattice parameter values obtained from crystallographic data. And relative density (ρr) is the quotient obtained by diving the experimental density by theoretical density.14,36 The obtained results are summarized in Table 6. This calculation enabled the assessment of compactness and the inference of material in porosity. The results indicate that with an increase in x, the density decreases, accompanied by an increase in porosity.| Compounds | ρth (g cm−3) | ρex (g cm−3) | ρr (%) |
|---|---|---|---|
| BS0STN | 5.84 | 5.43 | 92.9 |
| BS0.25STN | 5.74 | 5.33 | 92.8 |
| BS0.5STN | 5.70 | 5.31 | 93.1 |
3.3. Optical properties
The optical transmittance spectrum for BS0STN, BS0.25STN, and BS0.5STN materials is presented in Fig. 4. Analysis of the spectra indicates that pure BS0STN exhibits higher optical transmittance than both BS0.25STN and BS0.5STN. The elevated optical transmittance might be a result of a reduced crystallite size in BS0STN. The optical gap energy (Eg) of the compounds were calculated by applying the Tauc law, as expressed in eqn (1).37
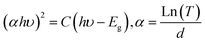 | (1) |
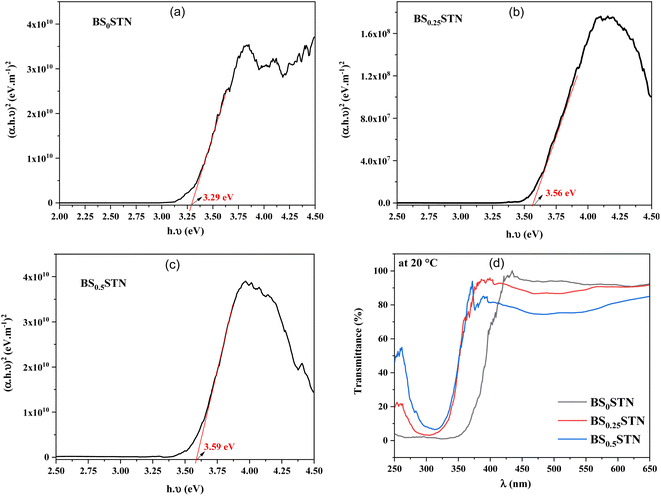 | ||
| Fig. 4 The (αhν)2 vs. (hν) of BSxSTN, where: (a) x = 0, (b) x = 0.25, (c) x = 0.5, and (d) optical transmittance spectrum. | ||
Firstly, a higher bandgap (Eg) means that electrons require greater energy or an elevated electric field to transition from the valence band to the conduction band. The increase in (Eg) from 3.25 to 3.59 eV with the rise in x suggests that the introduction of Sr into BSTN reduces the electron jump between these bands, potentially enhancing resistance to a higher applied electric field.41 Secondly, consequently, an increase in the band gap was observed with the Sr doping rate, appears to be associated with the enlargement of crystallite size, as indicated in the studies.42–45 Furthermore, the band gap46,47 is enhanced in the presence of strontium.
3.4. Study of dielectric properties
Indeed, the investigation of the dielectric properties of BSxSTN ceramics is crucial for gaining insights into their electrical behavior. It allows for establishing a correlation between the dielectric properties and the material's structure, providing valuable information about the material's electrical characteristics.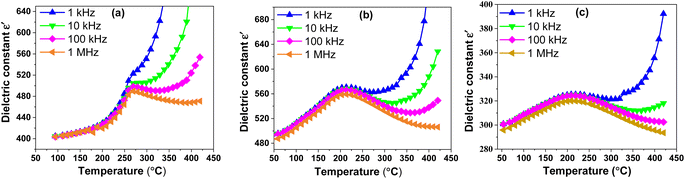 | ||
| Fig. 5 Thermal evolution of the dielectric constant ε′ of BSxSTN as a function of temperatures at different frequencies: (a) x = 0, (b) x = 0.25, and (c) x = 0.50. | ||
The variation in the maximum values of the dielectric constant (ε′max) with Sr content in the BSxSTN ceramics suggests that the substitution of Ba by Sr in the pentagonal site (A2) influences the dielectric behavior of the materials. The dielectric constant maximum values for BSxSTN ceramics at the Curie temperature and 1 MHz are as follows: 489.65 (BS0STN), 559.23 (BS0.25STN), and 319.96 (BS0.5STN). The minimum value of ε′max is observed for BS0.5STN, indicating that the substitution of Ba with Sr in the (A2) site leads to a decrease in the dielectric constant. This trend can be attributed to the influence of ionic radius. The larger ionic radius of Sr compared to Ba could lead to increased distortions or changes in the local coordination environments around the (A2) sites. This observation suggests that the dielectric properties of the BSxSTN ceramics are relatively sensitive to the Sr content. The higher ε′ value at low frequencies confirms the presence of various types of polarization, whereas at high frequencies, it is primarily attributed to electronic polarization. With increasing frequency, the dielectric permittivity may start to decrease, and the constant at 1 kHz is higher than that at 1 MHz. This could be attributed to phenomena such as partial reorientation of dipoles that cannot rapidly follow the electric field due to the higher frequency.48
The Curie temperature TC decreases with the increase of x, reaching a minimum value of 213 °C for the BS0.5STN composition. This change in Tc may be attributed to the influence of a slight displacement of Ti/Nb(1) cations along the c-axis, specifically indicated by the (O(1)–Ti/Nb(1)–O(1)′) in the Ti/NbO6 octahedra. This displacement is associated with alterations in the Ti/Nb(1)–O(1)′ bond distance, which inversely varies with the Ti/Nb(1)–O(1) distance (as shown in Table 4).
In ferroelectric materials, the ferroelectric ⇔ paraelectric transition is accompanied by a structural change. Below the transition temperature TC, the corresponding space group is P4bm (non-centrosymmetric and polar). Conversely, above TC, the structure often corresponds to P4/mbm (centrosymmetric and non-polar). It can be seen that the dielectric properties were closely related to the structure.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) δ). In Fig. 6, the temperature-dependent evolution of dielectric loss for BSxSTN is presented, measured at different frequencies (1 kHz–1 MHz) as a function of temperature (50 °C–420 °C). It is obviously observed that the BSxSTN ceramics exhibit low dielectric loss, which decreases with the increasing Sr content. The tangent losses appear to remain constant and start increasing after 300 °C. At room temperature and 1 kHz, the dielectric loss values are observed to be 3 × 10−3, 1 × 10−3, and 0.7 × 10−3 for different compositions, respectively. Remarkably, the dielectric loss values vary with the Sr content x, reaching a minimum of 0.7 × 10−3 for BS0.5STN. This behavior is attributed to the substitution of Ba by Sr in the pentagonal (A2) site. The dielectric loss tan
δ). In Fig. 6, the temperature-dependent evolution of dielectric loss for BSxSTN is presented, measured at different frequencies (1 kHz–1 MHz) as a function of temperature (50 °C–420 °C). It is obviously observed that the BSxSTN ceramics exhibit low dielectric loss, which decreases with the increasing Sr content. The tangent losses appear to remain constant and start increasing after 300 °C. At room temperature and 1 kHz, the dielectric loss values are observed to be 3 × 10−3, 1 × 10−3, and 0.7 × 10−3 for different compositions, respectively. Remarkably, the dielectric loss values vary with the Sr content x, reaching a minimum of 0.7 × 10−3 for BS0.5STN. This behavior is attributed to the substitution of Ba by Sr in the pentagonal (A2) site. The dielectric loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, increases with the rise in temperature, leading to a subsequent significant loss, possibly due to the increase in electrical conductivity.
δ, increases with the rise in temperature, leading to a subsequent significant loss, possibly due to the increase in electrical conductivity.
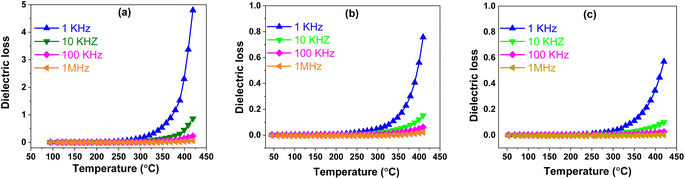 | ||
| Fig. 6 The thermal evolution of the dielectric loss for BSxSTN as a function of temperature at different frequencies: (a) x = 0, (b) x = 0.25, and (c) x = 0.5. | ||
Table 7 provides an overview of the dielectric characteristics of some TTBs. After comparing different types of TTB ceramics, it is observed that Ba2SmTi2Nb3O15 displays a higher dielectric constant ε′ and lower dielectric loss, indicating favorable results in comparison to Ba-based TTBs such as Ba4Sm2Ti4Ta6O30 and Ba3Nd3Ti5Ta5O30.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), maximum values of permittivity
δ), maximum values of permittivity  , and Curie temperature (TC) at a frequency of 1 MHz and room temperature (RT) of some type TTBs in previous literature
, and Curie temperature (TC) at a frequency of 1 MHz and room temperature (RT) of some type TTBs in previous literature
| Composition | ε′ (at RT) | Tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (at RT) δ (at RT) |
(at TC) | TC (°C) | Ref. |
|---|---|---|---|---|---|
| Ba4Sm2Ti4Ta6O30 | 159.6 | 3.5 × 10−3 | — | — | 49 |
| Ba3Sm3Ti5Ta5O30 | 134.4 | 4.6 × 10−3 | — | — | 49 |
| Sr4Eu2Ti4Nb6O30 | 125 | 50 × 10−3 | 210 | 402 | 50 |
| Sr5EuTi3Nb7O30 | 230 | 25 × 10−3 | 360 | 245 | 50 |
| Ba2NdTi2Ta3O15 | 136.9 | 0.7 × 10−3 | — | — | 51 |
| Ba3Nd3Ti5Ta5O30 | 103.1 | 8.8 × 10−3 | — | — | 51 |
| Ba5NdTi3Ta7O15 | 162.4 | 1.3 × 10−3 | — | — | 51 |
| Sr2NdTi2Nb3O15 | 106.4 | 2.7 × 10−3 | 127 | 246 | 16 |
| Sr2SmTi2Nb3O15 | 142.3 | 1.3 × 10−3 | 194 | 332 | 16 |
| (Ba0.5Sr0.5)2SmTi2Nb3O15 | 295.8 | 0.7 × 10−3 | 319.9 | 213 | This work |
| (Ba0.75Sr0.25)2SmTi2Nb3O15 | 570.6 | 1 × 10−3 | 559.2 | 218 | This work |
| Ba2SmTi2Nb3O15 | 403.8 | 3 × 10−3 | 489.6 | 269 | This work |
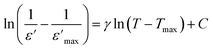 | (2) |
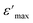 is the peak value of ε′ at Tmax, C is the modified Curie–Weiss constant, and γ is the diffusivity exponent. Fig. 7 shows the variation of
is the peak value of ε′ at Tmax, C is the modified Curie–Weiss constant, and γ is the diffusivity exponent. Fig. 7 shows the variation of 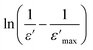 with ln(T − Tmax) at 1 MHz for BSxSTN. The diffusivity exponent values are determined by analyzing the slopes of individual curves, and these calculated values are then displayed in Table 8. The γ values range from 1 to 2, signifying a spectrum of ferroelectric behaviors. A γ value of 1 corresponds to a typical ferroelectric behavior in accordance with the Curie–Weiss law, while a γ value of 2 indicates a shift towards relaxation and a fully disordered ferroelectric system.54 This suggests a diffuse ferroelectric nature of the BSxSTN ceramics. The γ values indicate that the materials possess disorder. Furthermore, the increasing values of γ with Sr content suggest an increase in diffusivity.
with ln(T − Tmax) at 1 MHz for BSxSTN. The diffusivity exponent values are determined by analyzing the slopes of individual curves, and these calculated values are then displayed in Table 8. The γ values range from 1 to 2, signifying a spectrum of ferroelectric behaviors. A γ value of 1 corresponds to a typical ferroelectric behavior in accordance with the Curie–Weiss law, while a γ value of 2 indicates a shift towards relaxation and a fully disordered ferroelectric system.54 This suggests a diffuse ferroelectric nature of the BSxSTN ceramics. The γ values indicate that the materials possess disorder. Furthermore, the increasing values of γ with Sr content suggest an increase in diffusivity.
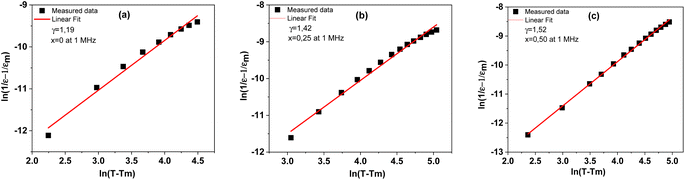 | ||
Fig. 7 Plots of 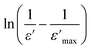 as a function of ln(T − Tmax) at 1 MHz for the BSxSTN ceramics: (a) x = 0, (b) x = 0.25, and (c) x = 0.5. The solid lines represent the linear fitted results. as a function of ln(T − Tmax) at 1 MHz for the BSxSTN ceramics: (a) x = 0, (b) x = 0.25, and (c) x = 0.5. The solid lines represent the linear fitted results. | ||
| Compounds | BS0STN | BS0.25STN | BS0.5STN |
|---|---|---|---|
| γ | 1.19 | 1.45 | 1.52 |
The diffuse nature of the phase transition in BSxSTN ceramics is suggested to be attributed to the presence of oxygen vacancies.55 In oxide materials, oxygen vacancies can easily be formed in oxide materials by the loss of oxygen from the crystal lattice, especially during heating at elevated temperatures (typically above 1300 °C).56 The Kröger–Vink notation provides a useful tool for understanding the occurrence of oxygen vacancies:
Indeed, the presence of oxygen vacancies  within the system can induce disorder and contribute to a diffuse-type ferroelectric-paraelectric phase transition.57
within the system can induce disorder and contribute to a diffuse-type ferroelectric-paraelectric phase transition.57
3.5. Complex impedance analysis (CIA)
Fig. 8 represents the variation of the imaginary part (Z′′) of impedance as a function of the real part (Z′) at different temperature. As depicted in the figure, an increase in temperature leads to a reduction in the size of the semicircle in the Cole–Cole plot for each sample, indicating a gradual decrease in compound resistance. The resistance values exhibit an increase ranging from 0.24 × 106 Ω for BS0STN to 2.747 × 106 Ω for BS0.5STN with the substitution rate. The observed arc corresponds to the grain response in the high-frequency range. In according with the brick model,58 the electrical properties of BSxSTN ceramics are well correlated with the internal microstructure.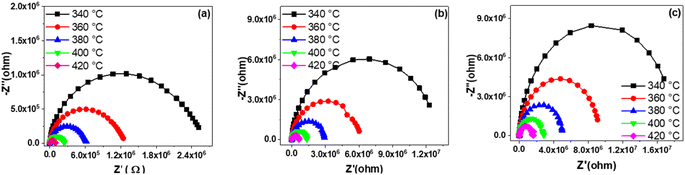 | ||
| Fig. 8 The variation of the imaginary part-Z′′ of impedance as a function of the real part Z′ at different temperatures for BSxSTN: (a) x = 0, (b) x = 0.25, and (c) x = 0.5. | ||
In order to extract the electrical properties of the materials, we employed an equivalent electrical circuit using the Zview 2.8d program, as shown in Fig. 9. The electrical model comprises the RQC circuit, associated to the grain contribution, grain resistance (Rg), grain capacitance (Cg), and the constant phase element (CPE). The introduction of the constant phase element is necessary to account for the non-ideal capacitive behavior observed in the circuit. This non-ideal grain behaviour may be due to the presence of more than one relaxation process.59
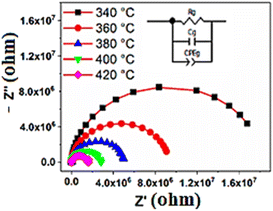 | ||
| Fig. 9 Adjusted Nyquist diagram for the BS0.5STN composition at different temperatures. The solid red lines show the adjusted data with the ZView software. | ||
The constant phase element “Q” is calculated using the following expression in eqn (3):60,61
| C = (R1−αQ)1/α | (3) |
For an ideal resistor and capacitor, the values of “α” are respectively zero and one.62 The good of agreement between the experimental data represented in points, and the theoretical values represented by the red line enables the validation of the proposed equivalent circuit (see Fig. 9). The different parameters employed for adjustments are displayed in Table 9.
| Compounds | T (°C) | Rg (MΩ) | Cg (nF) | Qg (nF sα−1) | α |
|---|---|---|---|---|---|
| BS0STN | 340 | 2.629 | 0.177 | 2.138 | 0.606 |
| 360 | 1.264 | 0.173 | 2.196 | 0.637 | |
| 380 | 0.620 | 0.168 | 2.396 | 0.660 | |
| 400 | 0.243 | 0.152 | 3.152 | 0.679 | |
| BS0.25STN | 340 | 13.21 | 0.186 | 0.255 | 0.759 |
| 360 | 6.274 | 0.175 | 0.195 | 0.833 | |
| 380 | 2.959 | 0.170 | 0.251 | 0.832 | |
| 400 | 1.349 | 0.157 | 0.290 | 0.857 | |
| BS0.5STN | 340 | 19.20 | 0.175 | 0.134 | 0.776 |
| 360 | 9.486 | 0.175 | 0.254 | 0.713 | |
| 380 | 5.093 | 0.172 | 0.261 | 0.733 | |
| 400 | 2.765 | 0.168 | 0.218 | 0.778 |
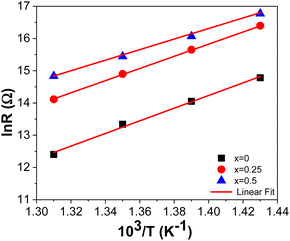
Table 9 shows that the grain resistance (Rg) decreases with increasing temperature, and (Rg) increases with the amount of Sr into the tungsten bronze structure, indicating effective conduction within the material. This suggests the presence of thermally activated conduction mechanisms in the grains. Fig. 10 shows the strength variation as a function of 103/T.
Table 10 presents the activation energy values determined for the BSxSTN ceramics. The grain activation energies decrease with the rate of substitution from 1.39 eV for BS0STN to 1.15 eV for BS0.5STN, within the temperatures range of 340 °C to 400 °C.
| Compounds | BS0STN | BS0.25STN | BS0.5STN |
|---|---|---|---|
| Ea (eV) | 1.39 | 1.34 | 1.15 |
The obtained Ea values suggest that oxygen vacancies are involved in the conduction mechanism of BSxSTN ceramics. Specifically, the activation energy of singly ionized vacancies typically falls within the range of 0.3 to 0.5 eV, while for doubly ionized oxygen vacancies, ranges from 0.6 to 1.2 eV.14,63,64 Consequently, it can be concluded that the Ea values for all samples are associated with the presence of doubly ionized oxygen vacancies.
4. Conclusion
In this study, oxides with the general formula (Ba1−xSrx)2SmTi2Nb3O15 (x = 0, 0.25, 0.5) were synthesized by solid-state method, which belong to the tetragonal tungsten bronze (TTB) family. Through a structural analysis using room temperature powder X-ray diffraction confirmed a pure TTB structure with the P4bm space group. Dielectric measurements conducted at room temperature and 1 kHz indicate that the synthesized compounds exhibit high dielectric constants (ε′) ranging from 325 to 570, with low dielectric losses (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) within the range of 10−4 to 10−3. The observed phase transition in these compounds is composition-dependent, with the dielectric constant of Ba2SmTi2Nb3O15 significantly higher than that of the Sr-doped compounds. All compounds demonstrated a diffuse-type ferroelectric-to-paraelectric phase transition. The results suggested that the phase transition temperature (TC) varied in correlation with the atomic displacement of Ti/Nb(1) within the octahedral Ti/NbO6. The optical transmittance spectra indicate that BS0STN exhibits higher transparency compared to BS0.25STN and BS0.5STN. The optical band gap energies (Eg) for BS0STN, BS0.25STN, and BS0.5STN were determined to be 3.25 eV, 3.56 eV, and 3.59 eV, respectively. Furthermore, as the rate of substitution of Ba by Sr increased, resistance values exhibited an increase, while activation energies of the grains decreased within the temperature range of 340 °C to 400 °C. Nyquists plots indicated an increase in resistance values with the rate of substitution, decreased with increasing temperature. The activation energy, obtained by fitting the Arrhenius formula at high temperatures, decreased within the substitution x from 1.39 to 1.15 eV. This suggests that doubly ionized oxygen vacancies are responsible for electrical conduction in (Ba1−xSrx)2SmTi2Nb3O15 ceramics.
δ) within the range of 10−4 to 10−3. The observed phase transition in these compounds is composition-dependent, with the dielectric constant of Ba2SmTi2Nb3O15 significantly higher than that of the Sr-doped compounds. All compounds demonstrated a diffuse-type ferroelectric-to-paraelectric phase transition. The results suggested that the phase transition temperature (TC) varied in correlation with the atomic displacement of Ti/Nb(1) within the octahedral Ti/NbO6. The optical transmittance spectra indicate that BS0STN exhibits higher transparency compared to BS0.25STN and BS0.5STN. The optical band gap energies (Eg) for BS0STN, BS0.25STN, and BS0.5STN were determined to be 3.25 eV, 3.56 eV, and 3.59 eV, respectively. Furthermore, as the rate of substitution of Ba by Sr increased, resistance values exhibited an increase, while activation energies of the grains decreased within the temperature range of 340 °C to 400 °C. Nyquists plots indicated an increase in resistance values with the rate of substitution, decreased with increasing temperature. The activation energy, obtained by fitting the Arrhenius formula at high temperatures, decreased within the substitution x from 1.39 to 1.15 eV. This suggests that doubly ionized oxygen vacancies are responsible for electrical conduction in (Ba1−xSrx)2SmTi2Nb3O15 ceramics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
It is to be acknowledged that the Department of Chemistry, Laboratory of Molecular Chemistry, Materials and Environment, at the Faculty Multidisciplinary in Nador (FPN), University Mohammed Premier, helped with the analysis this study needed.References
- I.-E. Nylund, C. R. Zeiger, D. Peng, P. E. Vullum, J. Walker, M.-A. Einarsrud and T. Grande, Chem. Mater., 2022, 35, 17–26 CrossRef.
- S. Dubey, K. Dubey, V. Sahu, A. Modi, G. Pagare, F. Z. Haque and N. K. Gaur, J. Mater. Sci.: Mater. Electron., 2023, 34, 2312 CrossRef CAS.
- E. Cavalli, G. Calestani, E. Bovero, A. Belletti and A. Migliori, J. Phys.: Condens.Matter, 2004, 16, 729 CrossRef CAS.
- J. Xing, F. Luo, Y. Qin, Y. Luo, Z. Gao, F. Shang and G. Chen, J. Am. Ceram. Soc., 2023, 106, 1074–1088 CrossRef CAS.
- X. Zuo, D. Song, Y. Zheng, Z. Hui, T. Guo, W. Dong, E. He, Y. Qin, B. Guan and J. Yang, Results Phys., 2023, 107230 Search PubMed.
- S. Chaudhary, S. Devi and S. Jindal, Mater. Chem. Phys., 2024, 312, 128580 CrossRef CAS.
- C. J. Huang, K. Li, X. Q. Liu, X. L. Zhu and X. M. Chen, J. Am. Ceram. Soc., 2014, 97, 507–512 CrossRef CAS.
- Y. B. Yao and C. L. Mak, J. Alloys Compd., 2012, 544, 87–93 CrossRef CAS.
- S. B. Rao, P. Viswarupachary and D. M. Potukuchi, Mater. Res. Express, 2019, 6, 66562 CrossRef CAS.
- E. H. Yahakoub, A. Bendahhou, K. Chourti, F. Chaou, I. Jalafi, S. El Barkany, Z. Bahari and M. Abou-salama, RSC Adv., 2022, 12, 33124–33141 RSC.
- I. Jalafi, A. Bendahhou, K. Chourti, F. Chaou, S. E. L. Barkany and M. Abou-Salama, Ceram. Int., 2023, 49, 10213–10223 CrossRef CAS.
- L. Wei, Z. Yang, R. Gu and H. Ren, J. Am. Ceram. Soc., 2010, 93, 1978–1983 CrossRef CAS.
- J. Fan, B. Yang, L. Wei and Z. Wang, Ceram. Int., 2016, 42, 4054–4062 CrossRef CAS.
- S. Wu, C. Sun, X. Yang, C. Hu, L. Liu and L. Fang, Ceram. Int., 2020, 46, 9240–9248 CrossRef CAS.
- Z. Guo, S. Wu, C. Hu, L. Liu and L. Fang, J. Alloys Compd., 2019, 773, 470–481 CrossRef CAS.
- K. Chourti, P. Marchet, Y. Elhafiane, A. Bendahhou, S. El barkany, M. Karroua and M. Abou-salama, Moroccan J. Chem., 2020, 8, 304–317 CAS.
- J. S. Hong, Y. H. Huang, X. Q. Liu, J. Li and Y. J. Wu, J. Alloys Compd., 2019, 770, 143–148 CrossRef CAS.
- F. Chaou, I. Jalafi, A. Bendahhou, S. El Barkany and M. Abou-Salama, Mater. Chem. Phys., 2023, 310, 128426 CrossRef CAS.
- A. Bendahhou, K. Chourti, F. Chaou, I. Jalafi, S. El Barkany and M. Abou-Salama, Mater. Res. Bull., 2023, 165, 112319 CrossRef CAS.
- I. Jalafi, F. Chaou, W. Bouazzati, A. Bendahhou, S. E. L. Barkany and M. Abou-Salama, J. Solid State Chem., 2023, 124506 Search PubMed.
- E. H. Yahakoub, A. Bendahhou, I. Jalafi, F. Chaou, S. EL Barkany, Z. Bahari and M. Abou-Salama, Heliyon, 2023, 9(11), 21037 CrossRef PubMed.
- S. Kamba, S. Veljko, M. Kempa, M. Savinov, V. Bovtun, P. Vaněk, J. Petzelt, M. C. Stennett, I. M. Reaney and A. R. West, J. Eur. Ceram. Soc., 2005, 25, 3069–3073 CrossRef CAS.
- X. L. Zhu, X. M. Chen, X. Q. Liu and X. G. Li, J. Appl. Phys., 2009, 105(12), 124110 CrossRef.
- M. Prades, H. Beltrán, N. Masó, E. Cordoncillo and A. R. West, J. Appl. Phys., 2008, 104(10), 104118 CrossRef.
- X. Zhu and X. Chen, Appl. Phys. Lett., 2010, 96, 32901 CrossRef.
- X. H. Zheng and X. M. Chen, J. Mater. Res., 2002, 17(7), 1664–1670 CrossRef CAS.
- M. C. Stennett, I. M. Reaney, G. C. Miles, D. I. Woodward, A. R. West, C. A. Kirk and I. Levin, J. Appl. Phys., 2007, 101, 104114 CrossRef.
- S. C. Abrahams, S. K. Kurtz and P. B. Jamieson, Phys. Rev., 1968, 172, 551 CrossRef CAS.
- M. Paściak, P. Ondrejkovic, J. Kulda, P. Vaněk, J. Drahokoupil, G. Steciuk, L. Palatinus, T. R. Welberry, H. E. Fischer and J. Hlinka, Phys. Rev. B, 2019, 99, 104102 CrossRef.
- V. Petrícek, M. Dusek and L. Palatinus, Z. fur Krist.–Cryst. Mater., 2014, 229(5), 345–352 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- P. Scherrer, in Kolloidchemie Ein Lehrbuch, Springer, 1912, pp. 387–409 Search PubMed.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- Z. Chchiyai, F. El Bachraoui, Y. Tamraoui, L. Bih, A. Lahmar, M. El Marssi, J. Alami and B. Manoun, J. Alloys Compd., 2022, 927, 166979 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- M. Arshad, H. Du, M. S. Javed, A. Maqsood, I. Ashraf, S. Hussain, W. Ma and H. Ran, Ceram. Int., 2020, 46, 2238–2246 CrossRef CAS.
- W. Huang, X. Du, S. K. Thatikonda, N. Qin, C. Yao, A. Hao and D. Bao, Ceram. Int., 2019, 45, 10475–10480 CrossRef CAS.
- J. Ruiz-Fuertes, O. Gomis, A. Segura, M. Bettinelli, M. Burianek and M. Mühlberg, Appl. Phys. Lett., 2018, 114(4) DOI:10.1063/1.5012111.
- A. R. F. Lima, J. C. Sczancoski, M. S. Li, E. Longo and E. R. Camargo, Ceram. Int., 2016, 42, 4709–4714 CrossRef CAS.
- D. Fan, R. Chong, F. Fan, X. Wang, C. Li and Z. Feng, Chin. J. Catal., 2016, 37, 1257–1262 CrossRef CAS.
- L. L. G. Al-mahamad, Heliyon, 2022, 8, e09966 CrossRef CAS PubMed.
- T. Badapanda, S. Sarangi, B. Behera, S. Parida, S. Saha, T. P. Sinha, R. Ranjan and P. K. Sahoo, J. Alloys Compd., 2015, 645, 586–596 CrossRef CAS.
- A. O. Turky, M. M. Rashad, A. M. Hassan, E. M. Elnaggar and M. Bechelany, Phys. Chem. Chem. Phys., 2017, 19, 6878–6886 RSC.
- A. Kumawat, S. Chattopadhyay, K. P. Misra, N. Halder, S. K. Jain and B. L. Choudhary, Solid State Sci., 2020, 108, 106379 CrossRef CAS.
- M. Rouchdi, E. Salmani, B. Fares, N. Hassanain and A. Mzerd, Results Phys., 2017, 7, 620–627 CrossRef.
- B. G. Hunashimarad, J. S. Bhat, P. V Raghavendra and R. F. Bhajantri, Opt. Mater., 2021, 114, 110962 CrossRef CAS.
- R. GopalaraoTanguturi, T. Bora, S. Ravi and D. Pamu, Phys. Procedia, 2014, 54, 70–74 CrossRef CAS.
- I. Jalafi, A. Bendahhou, K. Chourti, F. Chaou, S. El Barkany and M. Abou-Salama, Ceram. Int., 2023, 49(7), 10213–10223 CrossRef CAS.
- X. M. Chen, Y. H. Sun and X. H. Zheng, J. Eur. Ceram. Soc., 2003, 23, 1571–1575 CrossRef CAS.
- C. Hu, X. Peng, L. Fang, C. Li and B. Wu, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2011, 26, 311 CrossRef CAS.
- X. M. Chen and J. S. Yang, J. Eur. Ceram. Soc., 1999, 19, 139–142 CrossRef CAS.
- S. M. Pilgrim, A. E. Sutherland and S. R. Winzer, J. Am. Ceram. Soc., 1990, 73, 3122–3125 CrossRef CAS.
- I. W. Kim, C. W. Ahn, J. S. Kim, T. K. Song, J.-S. Bae, B. C. Choi, J.-H. Jeong and J. S. Lee, Appl. Phys. Lett., 2002, 80, 4006–4008 CrossRef CAS.
- G. A. Smolenskii, J. Phys. Soc. Jpn., 1970, 28, 26–37 Search PubMed.
- P. Ganguly and A. K. Jha, Phys. B, 2010, 405, 3154–3158 CrossRef CAS.
- C. K. Suman, K. Prasad and R. N. P. Choudhary, J. Mater. Sci., 2006, 41, 369–375 CrossRef CAS.
- F. A. Kröger and H. J. Vink, in Solid State Physics, Elsevier, 1956, Vol. 3, pp. 307–435 Search PubMed.
- J. R. Macdonald, Impedance spectroscopy, Ann. Biomed. Eng., 1992, 20, 289–305 CrossRef CAS PubMed.
- H. Ali, S. Karim, M. A. Rafiq, K. Maaz, A. U. Rahman, A. Nisar and M. Ahmad, J. Alloys Compd., 2014, 612, 64–68 CrossRef CAS.
- S. Rani, N. Ahlawat, R. Punia, K. M. Sangwan and P. Khandelwal, Ceram. Int., 2018, 44, 23125–23136 CrossRef CAS.
- H. Ma, K. Lin, L. Fan, Y. Rong, J. Chen, J. Deng, L. Liu, S. Kawaguchi, K. Kato and X. Xing, RSC Adv., 2015, 5, 71890–71895 RSC.
- J. R. Macdonald, J. Appl. Phys., 1985, 58, 1955–1970 CrossRef.
- X. Sun, J. Deng, L. Liu, S. Liu, D. Shi, L. Fang and B. Elouadi, Mater. Res. Bull., 2016, 73, 437–445 CrossRef CAS.
- K. Kumari, A. Prasad and K. Prasad, Am. J. Mater. Sci., 2016, 6, 1–18 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra00068d |
| This journal is © The Royal Society of Chemistry 2024 |